Analysis on errors due to photon noise and quantization process with multiple images

Analysis on errors due to photon noise and

quantization process with multiple images

The MIT Faculty has made this article openly available.

Please share

how this access benefits you. Your story matters.

Citation

Li, Fulu et al. “Analysis on Errors Due to Photon Noise and

Quantization Process with Multiple Images.” 2010 44th Annual

Conference on Information Sciences and Systems (CISS). Princeton,

NJ, USA, 2010. 1-6. Copyright © 2010, IEEE

As Published

http://dx.doi.org/10.1109/CISS.2010.5464908

Publisher

Institute of Electrical and Electronics Engineers

Version

Final published version

Citable link

http://hdl.handle.net/1721.1/65842

Terms of Use

Article is made available in accordance with the publisher's

policy and may be subject to US copyright law. Please refer to the

publisher's site for terms of use.

Analysis on Errors due to Photon Noise and Quantization Process

with Multiple Images

Fulu Li, James Barabas, Ankit Mohan, Ramesh Raskar

The Media Laboratory, MIT, Cambridge, MA USA 02139

Email: fulu@media.mit.edu

Abstract.

In the scenes with deflective and/or reflective medium such as fogs or mirrors, where the contrast levels among the intensity values of the pixels in the image are very small, even a small estimation improvement on the intensity value of each pixel could make a big difference for the perceptual quality of the final image if we want to subtract the interference components from the original image. In this paper we analyze the average quantization error, total error and photon noise from multiple images with fixed and varied exposure time. We observe that by properly controlling and varying exposure time with multiple images, one can obtain an image with better performance than that of the conventional wisdom, where multiple images are taken repeatedly with the same exposure time.

Keywords:

Photon Noise, Quantization Error, Images;

1.

Introduction

Image noise is an inherent and integral part of the digital imaging. In order to achieve the best performance from digital imaging, it is essential to understand the impact of noise, in particular the signal-dependent photon noise [18], on the estimation of the intensity values of each pixel in the image.

The motivation of this work is two-folds. First, for the scenarios in which the contrast levels among the intensity values of each pixel in the image are very small, even a small improvement for the estimation of the intensity values of the pixels in the image could significantly improve the perceptual quality of the final image. In other scenarios with reflective scenes by a mirror or with the masking process in computational photography , the contrast levels among the intensity values of each pixel in the resulted image are also very small. In this paper, we examine the tradeoffs to change or not to change exposure time in order to achieve the best performance from multiple images by collectively reducing the errors due to photon noise and quantization process, which will lead to a better resulted image. Second, the availability of the "burst" mode for commodity cameras provides new opportunities to get a better image from multiple images by taking many

978-1-4244-7417-2/10/$26.00 ©201 0 IEEE

images quickly. A conventional wisdom to reduce random noise is to take the average of multiple images [I2] by taking many images of the same scene repeatedly with the same exposure time. A natural question is that is this conventional wisdom the best way to go in order to get a better image from multiple images. In this paper, we tend to answer the above question by analyzing the trends of average quantization error, total error and photon noise with fixed and varied exposure time to take multiple images of the same scene.

The main results of this paper are as follows:

(a) Quantization error can not be overcome when the noise is zero with fixed exposure time.

(b) Quantization error can be reduced when the noise is zero and the exposure time is varied among different images.

(c) Quantization error can be reduced when the noise isfinite and the exposure time is fixed among different images.

(d) Quantization error can be further reduced with

high probability when the noise is finite and the

exposure time is varied among different images compared with that of the fixed exposure time for multiple images.

The rest of the paper is organized as follows: we discuss the related work in Section 2; we present preliminaries regarding the models in Section 3; we analyze average quantization errors, total errors and photon noise with multiple images in Section 4; the conclusions are presented in Section 5.

2. Related Work

Many researches have explored various ways to deal with image noise and the lack of quantization resolution in the face of small contrast levels in the image caused by interference components such as fogs. One natural way is to increase the number of quantization levels, which could lead to higher cost to produce the camera itself and it is also not trivial to do.

In [I2], Martinec conducted a systematic study on the sources of noise in digital imaging and presented some measurement results on image noise. The author also discussed some aspects of noise reduction on raw data.

In [12], Martinec also mentioned the conventional wisdom of repeatedly taking multiple images with the same exposure time to reduce random noise.

In [4], Grossberg and Nayar presented an algorithm to combine a few exposures to achieve high dynamic range. The authors proved that simple summation combines all the information in the individual exposures without loss. The approach in [4] to find the optimal exposures for a desired camera response function and a desired dynamic range is to minimize a function of the difference between the derivative of the camera response function and the derivative of the desired camera response function plus a term, which penalizes exposures that increase the noise variance. As will be seen in our analysis that a larger noise variance may not mean a larger quantization error when combining multiple images.

Schechner et al in [20] proposed techniques for instant dehazing using polarization to remove the effects of haze from images. The method presented in [20] uses multiple images taken through a polarizer at different orientations. Recent work by Fattal in [3] presented a new method of dehazing from single image by estimating the optical transmission in hazy scenes given a single input image. In [18], Ratner and Schechner presented a thorough and insightful treatment of noise mechanisms in digital imaging. The authors in [5,6,10,13] explored different ways for noise estimation based on noise distributions and camera response functions.

3. Preliminaries

In this section, we give a brief overview on the noise model, quantization error model, and the related theorems governing the corresponding statistical/random processes.

3.1 Camera Response Curve

The camera response curve is a curve showing the relationship between the amount of incoming light, which is often dictated by the length of exposure time, and the image pixel intensity values of a digital camera. In the following discussions, we assume linear camera response in terms of the length of exposure time and we have

veE)

=

a*

E+

P

(1)

where

E

indicates the duration of the exposure time,

a

and

fJ

are constant values. However, the principles discussed here are equally applicable to other camera response functions such as the logarithmic ones.

3.2 The Noise Model

As described in [12,13,18], image noise can be divided into two categories: dependent noise and

signal-independent noise. As the name suggests, signal-independent noise, signal-independent of the photon flux, is due to dark current, amplifier noise and the quantizer in the camera circuitry [18]. On the other hand, signal-dependent noise is determined by the photon flux and the uncertainty of the electron-photon conversion process that occurs in the camera detector [18].

In this study, we are mostly interested in examining the impact of photon shot noise, which is signal-dependent. It is well known in this literature that the stream of photons follow a Poisson distribution [6,12,13,18]. An important characteristic of the Poisson distribution is that the standard deviation of the fluctuations is equal to the square root of the average count itself The fluctuations in photon counts are perceived in images as noise, also known as Poisson noise or photon shot noise [12]. As discussed in [6] that if the mean of a Poisson distribution is relatively large, we can approximate a

Poisson distribution as a Gaussian distribution for photon noise. However, for very dark pixels, the

Gaussian approximation of image noise may not be that accurate.

3.3 The Quantization Error Model

Quantization error is due to digitization in the imaging process. There are two kinds of quantization errors: the

approximation error and the clipping error. The approximation error is caused by the "round -off' effect of the analog signal due to the lack of quantization resolution. The clipping error is due to inadequate quantizer range limit. In our discussion, we mainly consider the approximation error as the quantization error. For a uniform quantizer, the quantization error is bounded by the stepsize of the quantizer and we have

-~/2~qe ~~/2 (2)

where qedenotes the quantization error and ~is the stepsize of the quantizer.

4. Quantization Error and Total Error with

Multiple Images

Assume that a random variableX, representing the photon- flux signal, follows a probability distribution with a mean of J1 and a variance of a2, i.e.,

X ""'(J1, ( 2) . We have Nmeasurements of this random process in the form of Nimages of the same scene with the same exposure time, which are_{xl' X2 ,..., X}N . Notably, Xl' X2 ,... , XN are independent and identically

(6) (7) (8) (11) N

LI

Yi -

v.:

I

- ' i=l Xaqe=

-Likewise, let Xte represent the total error for

YI' Y2 ,..., Y N' meaning the difference between the

normalized average of the quantized values of Yi sand

the real signal value ofx , i.e., E{x} , and we have

N

LYi,q

- i=l ai x.«

=1

-

E{x}

I

N

-quantization error at each measurement and x»is the difference between the average of the quantized value at

each measurement and the real signal value of x, i.e., E{x}. Similarly, the same relationship applies to Xaqe

-

-Notably, the difference between Xaqe in Eq. (6) and Xte

in Eq. (10) is that xaqe is simply the average of the

Note that the measurement value of Yi is the real signal

value of aix, say aiE{x} , plus the signal-dependent

photon shot noise, say s; , which is the fluctuation of the photon counts. So, we have

Yi =aiE{x}+s; (9)

We need to emphasize that the term of s; in Eq. (9) is different from the term of Si in Eq. (7) in that the shapes

of the Poisson/Gaussian noise distribution are quite different in these two cases due to the fact that width of the "bell-shape" noise distribution curve is proportional to the square root of the real signal value.

Let Xte stand for the total error for Xl' X2 ,..., XN ,

meaning the difference between the average of the

quantized values of each individual measurement and the

real value ofx ,and we have N LXi,q ~te =1~-E{x}1 (10) N

-and Xte.

Regarding the quantization error with multiple measurements (multiple images in our case), we have the following observations:

N

LXi

where ~

=..i..=!- .

N

By changing the exposure time, we have the measurements ofYI' Y2 ,...y N. Assuminglinear camera

response function, we have

Yi=aix,l~i~N (4)

where ai is a positive scalar to indicate the signal

changes caused by varied exposure time. In this new setting, thenormalized average x is defined as follows:

N

L~

i=l ai

x = - - (5)

N

Let us further define XI,q' X2,q ,..., XN,q as the quantized

values forXl , X2 ,..., XN , respectively. Likewise, let

YI,q' Y2,q'· ..

,y

N,q denote the quantized values for

YI'Y2'···' YN, respectively.

N

In this paper, we only consider signal-dependent photon shot noise as most of the related work in this literature does [6]. The signal-independent noise can not be exploited for the reduction of quantization error and it can be dealt separately. Notably, the measurement value of Xi is the real signal value of x ,sayE{x} , plus the

signal-dependent photon shot noise, say si , which is the

fluctuation of photon counts. So, we have

Xi =E{X}+Si

-Let xaqedenote the average quantization error (AQE) for Xl' X2 ,..., XN ,meaning the average of the quantization

error at each measurement, and we have N

Llxi -Xi,q

I

i=l Xaqe =

photons, i.e., X, is Poisson distributed [6,12,18] and the

fluctuations in photon counts are considered as photon shot noise [12]. As an important property of a Poisson

distribution, we haveE{X}

=

Var(X) , i.e., f.1

=

(j2 in this case.

According to the Central Limit Theorem (CLT), we have

_ _ (j2

E{x}

=

f.1and Var(x)

=-

,

(3) N

-Likewise, let Xaqe indicate the average quantization error

for YI, Y2 ,..., Y N' meaning the normalized average of

the quantization error at each measurement, and we have

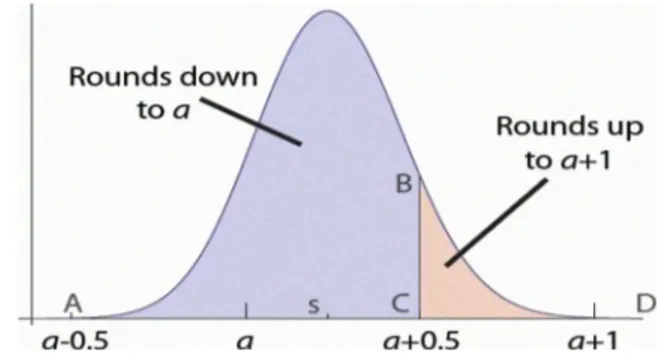
Lemma 1: Quantization error can not be overcome when the noise is zero with fixed exposure time.

To see this, let us have a look at the following quantization example in Fig. 1. Without loss of generality, let us assume that the signal value of xlands

(a) signal Yiis obtained with the exposure time of

e

_i seconds.

-error X teas defined in Eq. (11) can be reduced by the "cancelling-out" effect of " overest imates" (see Fig. 2.(b) )and " underest imates" (see Fig. 2.(a» if we take multiple images with controlled and varied exposure time.

between aand (a

+

0.5),

where ais an integer. The quantization error in this example is a - xin thi s example. If the noise is zero, the total error X te as defined in Eq. (10) will remain the same as Ia - xIno matter how many times we try the measurements.

a+ l C a+ O.5 s a A a- O.s

Lemma 3: Quantization error can be reduced when the

noise is finite and the exposure time is fixed among different image s.

Without loss of generality, let us look at the following example depicted in Fig. 3, where we have a real signal value of sand the photon shot noise, which oscillates around the signal value of swith a "bell-shape" distribution in terms of its density. The horizontal axis indicates possible measurement values and the vertical axis denotes the probability density function of the corresponding photon shot noise distribution. Let ndenote the random variable of photon noise

( nE[A - s,D - s] in this example). As we can see that

without noise, the quantization error will be (a - s) ,

where ais s's closest integer and (a - s)is a negative value in this case. With noise, if the value of the signal plus noise ( s+n_{i )} lands within the range of[A , C], where C is equal to a

+

0.5, the quantized value of

s

+

niis still the value of a, which leads to an underestimate of the real value of s. However, if the value of signal plus noise of (s+nj ) (the noise term of

nj varies among different images for the same pixel) lands within the range of [C, D], then the quantized value of (s

+

nj ) becomes a

+

1, which leads to an overestimate of the real value of s. If we repeat the

measurements for multiple times from multiple images with the fixed exposure time, the total error as defined in Eq. (10) from multiple measurements can be reduced due to the "cancelling-out" effect of "overestimates" and "underestimates". a +l a+l a+O.5 a+O.5 a x

Figure 1: An illustration of quantization error without noise.

Lemma 2: Quantization error can be reduced when the

noise is zero and the exposure time is varied among different images.

Assume that we have a linear response camera and the intensity value of a pixel is determined linearly by the duration of the exposure time when the image is taken. Without loss of generality, let us have a look at the examples illustrated in Fig. 2. In Fig. 2.(a), the signal value Yi will be truncated as a (Yi ' s closest integer

point), which leads to the quantization error of(a -Y i)' a

negative value. On the other hand, if we change the exposure time and the corresponding signal value of Yj could land in a different region from that of Y i 'S. By properlycontrolling the exposure time, it is possible that Yj lands in a region between (b +0.5)and (b +l), where b is an integer. As a result, the quantized value of

Yj would be(b+1) , which leads to the quantization error of (b+1-Yj ), a positive value. Therefore, the total

Figure 2:Anillustration of quantization error with varied exposure time.

(b) signal

Y

j is obtained with the exposure time of

e

j seconds.

b b+O.5

v,

b+l

Figure 3: An illustration of quantization error with photon shot noise.

Lemma 4: For the same limited number of images(N) , the total error can be further reduced with high probabilitywhen the noise is finite and the exposure time is varied properly among different image s even though the photon noise may not be further reduced compared

with multiple images with the same exposure time. More formally, by properly choosing varied exposure time,

-'

-with high probability we can have Xte ~ Xte for the same limited number of images (N) even tough the photon noise may not be further reduced compared with the case with fixed exposure time, i.e., we have

E{y;}= E{a;x}==a;xE{x}==_aif.1 , (12) where a; is a positive constant and 1~i~N .

Var(y;)=Var(a;x) ==a;xVar(x)==a;a- 2 , (13) where 1~i~N .

-

-Var(x )~Var(x). We further have

(16) (18) (14) N LaixE{x} i=l N La; xVar(x) i=l N N Var(LYi) (15)

(La_i)2 i~1 ;=1 N a-2xLa; i=l -

-Var(x )>Var(x) N LE{Yi} E{~}==_i=_l_ _ N Lai i=l ;=1 ;=1 i=l N LVar(Yi) Var(~)==_i=_l_

N-_-(L

a_i)2 i=l We further have N , LYi

Var(~ )==Var(i~l )= Lai

From (15), we have

Note that Y1' Y2 ,...,YN are independent measurements.

Note that _{aI' a2,..., aN are positive numbers. If and only} ifa1 ==a2== ...==aN, then we have

-' - a-2

Var(x )==Var(x)== - (17) N

Otherwise, we have First, let us look at the first part of the lemma stating that

byproperly choosing varied exposure time, we can have

-that the photon noise of Var(x) may not be further

reduced compared with Var(x) , which makes the results

of this lemma even more interesting and counter-intuitive.

Now let us prove the second part of the lemma stating

-

-

-Xte ~x«. Recall the definition ofXtein Eq. (10) that the total error for the case with fixed exposure time is simply the absolute value of the difference between the average of the quantized values (xi,qs) at each measurement and

the real value of the signal x. Likewise, the definition of

Xtein Eq. (11) states that the total error for the case with varied exposure time is the absolute value of the difference between the average of the normalized quantized values (Y;,q s) at each measurement and the

a;

real value of the signal x. Clearly, by properly choosing

a sequence of varied exposure time, with high probability thenormalized quantized values of Y;,q s could provide

a;

richer granularities for the "cancelling-out" effects of

"overestimates" and "underestimates" of the real value of the signalx, compared with the granularity of Xi,q s,

which is the quantization unit. Further, as we vary the exposure time, the signal-dependent photon noise also varies accordingly in the sense that the "bell shape" (see

illustrations in Fig. 3) of the photon noise

By properly choosing varied exposure time, the chances of the "cancelling-out" effect of "overestimates" and "underestimates" could be improved due to more diverse distributions of signal values of Y; s and the corresponding signal-dependent noises. Notably, x;s are independent and identically distributed , while Y; s are

independent but no longer identically distributed. Therefore, byproperly choosing varied exposure time,

-'

-withhigh probability we can have Xte ~ Xte .

As we can see that the expectation of

~'remains

the same as that of ~ but the variance (the photon noise)

-

-grows, i.e., Var(x )~Var(x).

What this lemma tells us is that photon noise is not necessarily correlated with the trend of the total error as defined in Eq. (10) or Eq. (11).

5. Conclusion

In this paper we present an indepth analysis on average quantization error, total error and photon noise from multiple images of the same scene with fixed or varied exposure time. In the scenarios with heavy fogs or reflective scenes where the contrast levels among the intensity values of the pixels in an image is very small, a small improvement on the accuracy of the estimated pixel value could make a big difference for the final perceptual quality of the image if we want to subtract the interference component from the original image. We examine the reduction of total error with multiple images of the same scene with fixed or varied exposure time.

Reference

[1] CHAVEZ, P. S., "An improved dark-object subtraction technique for atmonspheric scattering correction of multispectral data", Remote Sensing of Environment 24, 450--479, 1988.

[2] DEBEVEC, P. E., AND MALIK, 1., "Recovering high dynamic range radiance maps from photographs", in ACM SIGGRAPH 1997,369-378.

[3] FATTAL , R., "Single Image Dehazing", in Proc. of

ACM Siggraph '2008.

[4] GROSSBERG, M., S. K. NAYAR, "High Dynamic Range from Multiple Images: Which Exposures to Combine?", in IEEE Workshop CPMCV, 2003.

[5] HEALEY G. E., R. KONDEPUDY, "Radiometric ccd camera calibration and noise estimation", in IEEE

Trans. on PAMI, 1994.

[6] HUANG Y., 1. KIM, I. KWEON, "Sensor noise modeling using the Skellam distribution: Application to the color edge detection", in Proc. of IEEE CVPR '2007. [7] HYVRINEN , A., AND OJA, E., "Independent component analysis: algorithms and applications", Neural Networks 13, 411- 430, 2000.

[8] KAMGAR-PARSI 8. , 8. KAMGAR-PARSI , "Evaluation of Quantization Error in Computer Vision", in IEEE Trans. on PAM/, 1989.

[9] LARSON, G. W., RUSHMEIER, H., AND PIATKO,

c.,

"A visibility matching tone reproduction operator for high dynamic range scenes", IEEE Trans on Visualization and Computer Graphics 3, 4, 291-306, 1997.

[10] LIU,

c.,

W. T. FREEMAN, R. SZELISKI and S.8. KANG, "Noise estimation from a single image", in Proc.

of IEEE CVPR '2006.

[I I] LU, 1., AND D. M. Healy "Contrast enhancement via multi scale gradient transformation", in IEEE International Conference on Image Processing, 482--486, 1994.

[12] MARTINEC, E., "Noise, Dynamic Range and Bit Depth in Digital SLRs" , http ://theory.uchicago.edu/

ejm/pi x/20d/tests/noise/index .html.

[13] MATSUSHITA, Y., S. LIN, "A Probabilistic Intensity Similarity Measure based on Noise Distribution", in Proc. ofIEEE CVPR '2007.

[14] NARASIMHAN, S. G., AND NAY AR, S. K., "Chromatic framework for vision in bad weather", in Proceedings of IEEE CVPR, 598-605, 2000 .

[15] NAYAR, S. K., AND NARASIMHAN, S.G., "Vision in bad weather", in Proceedings of IEEE CVPR, 820, 1999.

[16] OAKLEY, 1. P., AND BU, H., "Correctio~ of simple contrast loss in color images", IEEE Transactions on Image Processing 16,2,511-522,2007.

[17] RAHMAN, Z., JOBSON, D., AND WOODELL, G.,"Multiscale retinex for color image enhancement", in Proc. of IEEE ICIP, 1996.

[18] RATNER, N., Y. SCHECHNER, "Illumination Multiplexing within Fundamental Limits", in Proc. of

IEEE CVPR '2007.

[19] ROSSUM, M. V., AND NIEUWENHUIZEN, T.,

"Multiple scattering of classical waves: microscopy, mesoscopy and diffusion", Reviews of Modern Physics, vol. 71,313-371,1999.

[20] SCHECHNER, Y., S. NARASIMHAN, S. K. NA YAR, "Instant Dehazing of Images Using Polarization", in Proc. oflEECVPR '200I.

[21] SHWARTZ, S., NAMER, E., Y , AND SCHECHNER, Y., "Blind haze separation", in Proceedings ofIEEE CVPR, 1984-1991 , 2006.

[22] SINGH, M., AND ANDERSON, 8. , "Toward a perceptual theory of transparency", Psychological Review, No. 109,492-519,2002.

[23] TAN , K., AND OAKLEY , 1. P.,"Enhancement of color images in poor visibility conditions", in ICIP 2000. [24] TAN, R.T.,"Visibility in bad weather from a single image", Proceedings ofIEEE CVPR, 2008.

[25] YUAN, L., SUN, 1., QUAN , L., AND SHUM, H.-Y., "Image deblurring with blurred/noisy image pairs", ACM Transactions on Graphics 26, 3, 1,2007.

[26] ZHANG, Y., GUINDON, 8., AND CIHLAR, 1., "An image transform to characterize and compensate for spatial variations in thin cloud contamination of landsat images", Remote Sensing of Environment 82 (October), 173-187, 2002.