Mme LE DUFF 1ère pro
1
Fiche méthode 3 : première. Etude du sens de variations d’une fonction. Méthode :
Déterminer la dérivée f’ (voir tableau des dérivées).
Etudier le signe de f’ (bien respecter l’intervalle donné dans l’énoncé pour les valeurs de x dans le tableau).
Si f’ est une constante alors son signe est évident (soit elle est positive, soit négative). Si f’ est une fonction affine (ax+b) :
Deux méthodes possibles :
o Résoudre ax+b=0. Placer cette valeur dans le tableau. f’ est du signe de a après cette valeur (si vous ne vous souvenez pas de cette règle, calculer avec des valeurs simples et regardez le signe du résultat, le signe restant constant dans chaque case, un calcul par intervalle suffit).
o Ou Résoudre ax+b≥0. Placer cette valeur dans le tableau. f’ est positive quand x répond au critère.
Si f’ est du second degré : voir méthode d’étude du signe d’un trinôme.
Si f’ est un quotient (en bac pro les intervalles sont donnés pour que le quotient ne pose pas de problème de définition) :
o Le dénominateur est un carré donc il sera toujours positif.
o Il faut étudier le signe du numérateur, c’est lui qui donnera le signe au quotient. Se ramener aux études de signes vues au-dessus en fonction du type de numérateur.
En déduire les variations de f : quand f’ est positive f est croissante, quand f’ est négative f est décroissante. Ne pas oublier de remplir les valeurs (toute sauf celles en ±∞) à l’aide du mode table de la calculatrice graphique.
Exemple (dérivée de type affine) :
Soit f la fonction définie sur
[ ]
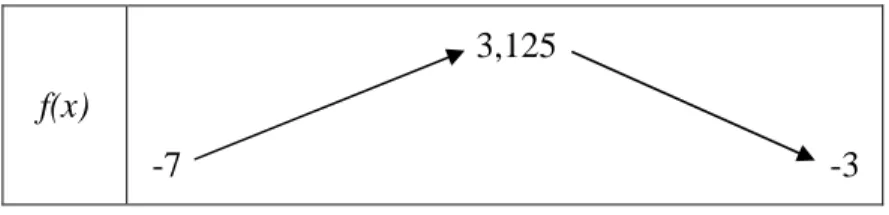
−1;3 par f(x)=−2x²+5x. Donner le tableau de variations de f. => f'(x)=−4x+5 −4x+5≥0(de signe +) −4x≥−5 4 5 4 5 = − − ≤x (x plus petit que 4 5 ) La fonction f' s'annule en 4 5
. Elle est positive « avant » 4 5 . x -1 4 5 3 f'(x) + 0 -
Mme LE DUFF 1ère pro
2
f(x)
3,125
-7 -3
Exemple (dérivée de type quotient avec numérateur de type constante) : Soit f la fonction étudiée sur
[ ]
2;9 par1 2 ) ( − = x x
f . Donner le tableau de variations de f.
1 2 − = = x v u 1 ' 0 ' = = v u
(
)
)² 1 ( 2 )² 1 ( 1 2 1 0 ) ( ' − − = − × − − × = x x x x f en utilisant la règle : ² ' ' 2 v uv v u v u = − (
)
2 1 −x est positif car c’est un carré, donc le quotient est du signe du numérateur : -2, qui est négatif. Donc on obtient le tableau suivant :
x 2 9 f '(x) - d f(x) 2 0,25 Car 2 1 2 1 2 2 ) 2 ( = = − = f et 0.25 4 1 8 2 1 9 2 ) 9 ( = = = − =
f (peuvent aussi être obtenues à l’aide du mode table de la calculatrice graphique).
Mme LE DUFF 1ère pro
3
Fiche méthode 4 : première. Déterminer l’équation d’une tangente.
GRAPHIQUEMENT :
La tangente à C au point d’abscissex a une équation de la forme 0 y =ax+b.
a est le coefficient directeur (c’est le nombre dérivé de f enx : 0 f'(x0)) ou pente de la droite. b est l’ordonnée à l’origine.
Exemple :
La droite D représentée ci-dessous est la tangente à Cf au point d’abscisse 0.
On obtient l’équation de la tangente D au point d’abscisse 0 : y =6x+2
PAR LE CALCUL :
La tangente à C au point d’abscissex a pour équation réduite :0 y= f'(x0)×
(
x−x0)
+ f(x0) On remplace x par la valeur donnée dans l’exercice. 0Mme LE DUFF 1ère pro
4
Calculer l’image de x par f’. 0 Calculer l’image de x par f. 0
Remplacer f'(x0) et f(x0)par les valeurs trouvées.
Exemple :
Soit f(x)=4x²−5x+1définie sur IR et C sa courbe représentative. Déterminer l’équation réduite de la tangente à C, au point de la courbe d’abscisse x =-1.
• Cette tangente a pour équationy = f'(−1)×
(
x−(−1))
+ f(−1) y= f'(−1)×(
x+1)
+ f(−1)• On calcule f'(x)=4×2x−5×1+0=8x−5
On en déduit f'(−1)=8×
( )
−1 +5=−8−5=−13• On calcule f(−1)=4×
( )
−12 −5×( )
−1 +1=4×1+5+1=4+6=10• Donc la tangente a pour équation : 10 ) 1 ( 13× + + − = x y y=−13x−13+10 y=−13x−3