Pour l’obtention du grade de
Docteur de l’Université de Poitiers
Faculté des Sciences Fondamentales et Appliquées
(Diplôme national – Arrêté du 7 août 2006)
Ecole Doctorale : Sciences Pour l’Ingénieur & Aéronautique
Secteur de recherche : Mécanique des solides, des matériaux, des structures et des surfaces
Présentée par :
Stéphen HEDAN
___________________________Mesures par voie optique de champs cinématiques pour l'étude du
comportement de plaques élastiques fissurées et chargées en mode I :
Formulation des déplacements 2D par confrontation
numérique/expérience en statique.
Analyse des effets 3D en dynamique.
___________________________Directeurs de thèse : Mario COTTRON
Valéry VALLE
Date de soutenance : 02 Décembre 2008 Devant la commission d’examen
JURY
M. A. VAUTRIN, Professeur, Ecole des Mines, Saint-Etienne Président Mme. S. POMMIER, Professeure, LMT, ENS de Cachan Rapporteur M. J.L. LATAILLADE, Professeur, LAMEFIP, ENSAM de Talence Rapporteur M. M. COTTRON, Professeur, LMS, Université de Poitiers Examinateur M. F. DUBOIS, Professeur, 3MSGC, Université de Limoges Examinateur M. L. HUMBERT, Chef de Travaux, LMSSMat, Ecole Centrale de Paris Examinateur M. N. MOËS, Professeur, GeM, Ecole Centrale de Nantes Examinateur M. V. VALLE, Professeur, LMS, Université de Poitiers Examinateur
Choisissez un travail que vous aimez et vous n'aurez pas à travailler
un seul jour de votre vie
.
Remerciements.
L'étude présentée dans ce mémoire a été réalisée au Laboratoire de Mécanique des Solides de l’Université de Poitiers (U.M.R. 6610) dirigé par Monsieur le Professeur O. Bonneau.
Je tiens à remercier Monsieur le Professeur Fabrice Brémand pour m'avoir permis d'entreprendre et de mener à bien cette recherche au sein de l'équipe Photomécanique et Rhéologie ainsi que pour son aide sur les simulations numériques par éléments finis.
Je suis particulièrement sensible à l'attention que m'ont portée Madame la Professeure Sylvie Pommier et Monsieur le Professeur Jean-Luc Lataillade en acceptant de juger ce mémoire.
Je remercie vivement Messieurs les Professeurs Frédéric Dubois, Nicolas Moës, Alain Vautrin et Monsieur Laurent Humbert pour l'intérêt qu'ils ont porté à mon travail en acceptant de participer au jury.
Je remercie également Monsieur le Professeur Mario Cottron pour avoir codirigé cette thèse, pour sa grande disponibilité, pour sa bonne humeur et par la rapidité de ces réponses aux nombreuses sollicitations que j'ai pu faire au cours de ces trois années.
Je voudrais exprimer toute ma reconnaissance et toute ma sympathie à Monsieur le Professeur Valéry Valle. Ses connaissances, explications et analyses ont très largement contribué à l'orientation et l'évolution permanente de cette étude. Son recul dans les domaines aussi variés que la mécanique, l'électronique, l'expérimental, la programmation, … et les nombreuses discussions que nous avons eues, m'ont permis de mener à bien ces travaux. Je t'adresse un grand merci pour ta confiance et l'aide que tu m'as apportée pour la recherche et pour les enseignements.
Je tiens à remercier les autres membres de l'équipe et plus particulièrement P. Doumalin pour les réalisations rapides de mes éprouvettes ainsi que pour son aide à
concilier enseignement et recherche et J.C. Dupré pour nos conversations scientifiques et "rugbalistiques".
Je souhaite également saluer les anciens doctorants de l'équipe Octavian, Eric et plus particulièrement Kossi pour nos nombreuses discussions "mathématiques" qui m'ont permis de faire avancer mes travaux, ainsi que les informaticiens Franck et Mathieu, l'électronicien Sébastien, les amis Arnaud, Ghina ..., les "sportifs" Tony, Eric D., pour leur disponibilité.
Je remercie très chaleureusement Arnaud qui, depuis 7 ans déjà, me supporte, m'aide dans les moments délicats et aussi pour nos nombreuses discussions parfois même tard le soir, que nous avons pu avoir et qui m'ont permis d'avancer au fil des années.
Je ne saurais terminer ces remerciements sans saluer ma famille : ma belle-sœur Sylvie, mes "beaux-parents" Marie-France et Jacques, mes frères Ludovic et Erwan et surtout mes parents Michelle et Yves qui ont toujours cru en moi, qui ont accepté et soutenu mes choix professionnels. La dernière personne que je tiens à remercier et qui tient une place essentielle tant personnellement que dans l'aboutissement de cette thèse, est Elodie, MERCI à toi…
Table des matières.
TABLE DES MATIERES. ...7
INTRODUCTION. ...13
1
MECANIQUE DE LA RUPTURE 2D ET METHODES OPTIQUES MISE EN
ŒUVRE EN FISSURATION. ...21
1.1 Introduction... 21
1.2 Théorie de la rupture et mode de fissuration. ... 23
1.3 Les solutions analytiques des contraintes et des déplacements... 24
1.4 Facteur d'Intensité des Contraintes (KI)... 30
1.4.1 Approche statique... 31
1.4.2 Approche dynamique. ... 32
1.4.3 Discussion... 35
1.5 Approche énergétique. ... 35
1.5.1 Théorie de Griffith et taux de restitution d'énergie (G). ... 35
1.5.2 Intégrale J de Rice... 37
1.6 Discussion. ... 40
1.7 Les méthodes optiques utilisées en mécanique de la rupture. ... 41
1.7.1 Méthodes optiques basées sur les interférences. ... 41
1.7.2 Méthodes optiques basées sur la variation du relief en pointe de fissure... 47
1.7.3 Méthodes optiques par suivi de motifs. ... 50
1.7.4 Méthodes optiques basées sur la variation d'indice optique... 54
1.8 Synthèse des méthodes optiques en mécanique de la rupture... 55
2.1 Introduction... 61
2.2 Etat de l'art en mécanique de la rupture statique. ... 62
2.2.1 Approches numériques et couplage numérique/expérimental... 62
2.2.2 Approches expérimentales... 64
2.3 Méthode optique choisie pour l'étude de fissures stationnaires. ... 67
2.4 Etude expérimentale des champs de déplacements dans le plan. ... 68
2.4.1 Détermination des caractéristiques mécaniques des matériaux. ... 70
2.4.2 Montage expérimental... 73
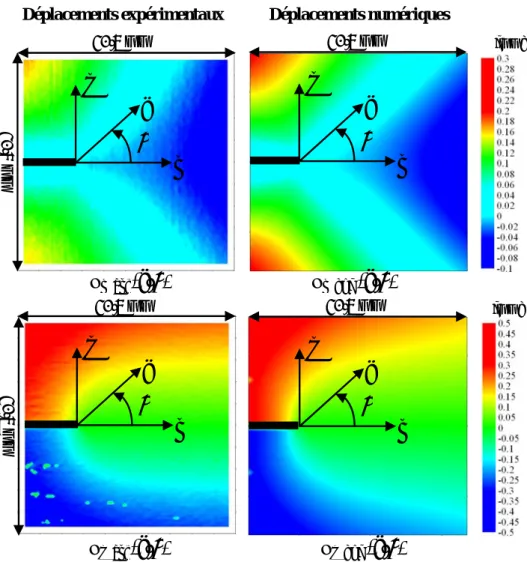
2.4.3 Présence de nodules sur les cartographies de phase. ... 74
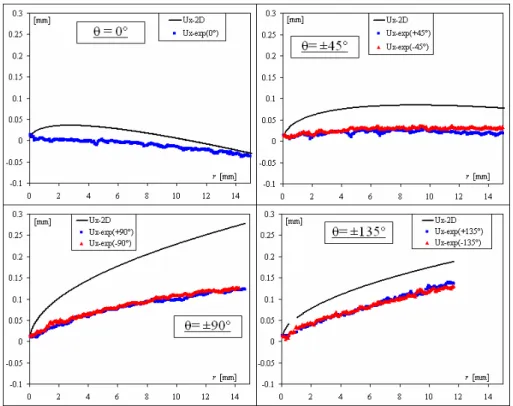
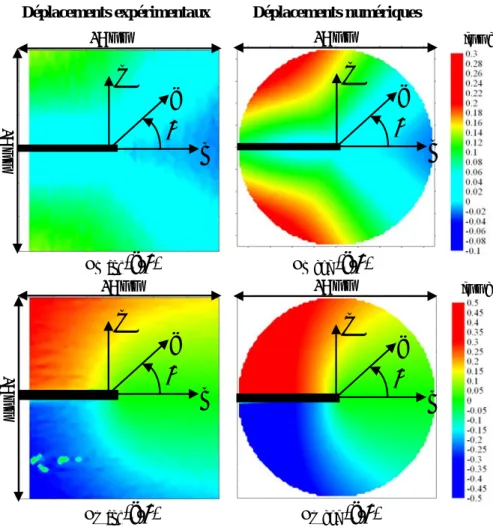
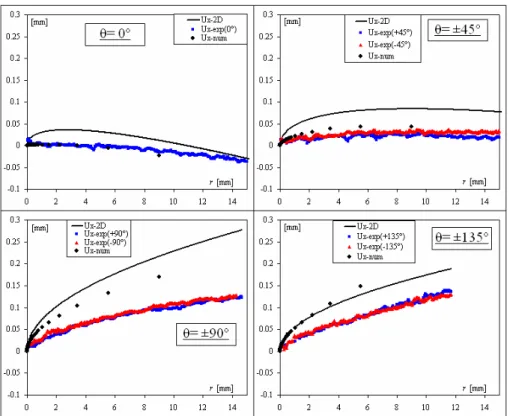
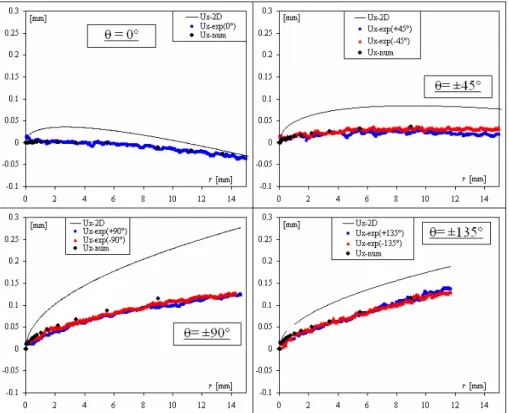
2.4.4 Etude des champs de déplacements expérimentaux et théoriques ux et uy. ... 77
2.4.5 Discussion et conclusions. ... 80
2.5 Etude numérique des champs de déplacements dans le plan. ... 80
2.5.1 Etude numérique pour une modélisation 3D de plaque infinie. ... 80
2.5.2 Etude numérique pour une modélisation 3D de plaque finie... 85
2.6 Calcul de l'intégrale J... 88
2.6.1 Gradients de déplacements de la formulation d'Arakawa. ... 88
2.6.2 Nouvelles formulations de ux et uy... 89
2.6.3 Calcul de l'intégrale J pour le PSM4. ... 94
2.7 Influence des effets de bords dans la modélisation numérique. ... 104
2.7.1 Calcul du facteur d'intensité des contraintes numériques KI_num... 105
2.7.2 Calcul des deux critères norm_x et norm_y. ... 106
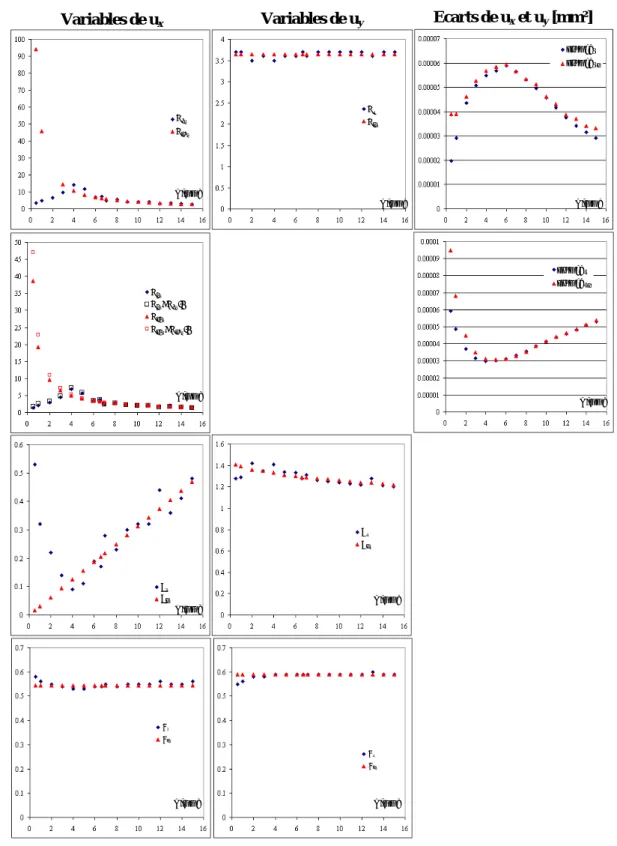
2.8 Etude des sept variables des formulations proposées ux et uy... 108
2.8.1 Influence de l'épaisseur (h) sur les sept variables. ... 108
2.8.2 Influence de la longueur de fissure (a) sur les sept variables. ... 112
2.8.3 Conclusions... 115
2.9 Conclusion générale. ... 115
3
PROPAGATION DE FISSURES : ETUDE DES DEPLACEMENTS
HORS-PLAN. ... 119
3.2 Etude de l'art en mécanique de la rupture dynamique. ... 120
3.2.1 Approches numériques... 120
3.2.2 Approches expérimentales... 122
3.2.3 Conclusion. ... 125
3.3 Méthode optique choisie pour l'étude lors de propagation de fissure... 125
3.3.1 La méthode MPC ("Modulated Phase Correlation"). ... 126
3.3.2 Caméra ultra-rapide... 128
3.4 Obtention des déplacements hors-plan en dynamique. ... 129
3.4.1 Approche théorique. ... 130
3.4.2 Moyens expérimentaux. ... 132
3.5 Etude expérimentale des champs de déplacement hors-plan lors de propagation de fissure... 134
3.5.1 Montage expérimental... 134
3.5.2 Les différents problèmes rencontrés. ... 135
3.5.3 Résultats expérimentaux. ... 140
3.5.4 Formulation tridimensionnelle du déplacement hors-plan... 147
3.6 Etendue de la zone tridimensionnelle. ... 159
3.6.1 Etendue de la zone 3D pour les cas expérimentaux. ... 160
3.6.2 Etude de la zone 3D en fonction du chargement () et de la vitesse (V)... 161
3.6.3 Normalisation des déplacements hors-plan théorique et expérimentaux... 163
3.6.4 Conclusion. ... 164
3.7 Etude post-mortem du faciès de rupture. ... 164
3.7.1 Principe. ... 166 3.7.2 Avantages et inconvénients. ... 167 3.7.3 Résultats... 168 3.7.4 Analyse... 170 3.7.5 Conclusion. ... 171 3.8 Conclusion générale. ... 171
CONCLUSIONS ET PERSPECTIVES. ... 173
REFERENCES BIBLIOGRAPHIQUES... 181
LISTE DES ILLUSTRATIONS... 189
PUBLICATIONS... 195
Introduction.
Aujourd'hui la réalité des marchés impose aux industriels de concevoir des ouvrages, des structures, des machines de plus en plus grandes, de plus en plus hautes, de plus en plus légères, de plus en plus performantes et ces conceptions doivent être réalisées le plus rapidement possible. Pour répondre à ces exigences, les entrepreneurs de ces ouvrages ou machines demandent aux fabricants de matériaux de satisfaire leurs besoins. C'est pour cela qu'une multitude de nouveaux matériaux sont créés (ex : composites, matériaux bio, alliages…). Toutefois, ces matériaux comme tous les autres, sont fabriqués avec des micro-défauts (cavités) à l'échelle microscopique, qui une fois sollicités provoquent des concentrations de contraintes préjudiciables sur la stabilité de la structure et peuvent faire apparaître des défauts macroscopiques non pris en compte par la mécanique des milieux continus. Pour appréhender ces problèmes, les mécaniciens ont entrepris l'étude de ces défauts au travers d'une discipline, en développant la mécanique de la rupture. D'autres défauts (ex : soudure), pouvant apparaître lors de la réalisation d'ouvrages, ainsi que le milieu ambiant peuvent entraîner la ruine d'une structure. Les récents accidents survenus à une fête foraine, où le bras d'une machine à sensation constitué d'un seul élément et supportant une nacelle à son extrémité, s'est littéralement fissuré en deux, montrent la nécessité de prendre en compte tous ces phénomènes dans la conception et dans la réalisation de tels ouvrages.
Les sollicitations extérieures (mécaniques, climatiques), les vibrations (séismes), les produits chimiques, les UV, etc. sont autant d'éléments pouvant réduire la durée de vie d'un ouvrage. La température aussi joue un rôle non négligeable lors des processus de fissuration. Par exemple, on constate régulièrement des ruptures brutales à basses températures. Si la rupture est brutale (fragile), la théorie de l'élasticité peut être appliquée, et une petite zone de plasticité apparaît restant confinée en pointe de fissure. A l'opposée, pour de fortes températures, la rupture entraîne des déformations plastiques non négligeables, dans une zone autour de la pointe de fissure, on parle alors de rupture ductile. La mécanique de la rupture linéaire est l'étude de structures élastiques à comportement fragile (sans plasticité), ayant des fissures macroscopiques et soumises à un chargement donné, afin de prédire les risques de rupture et de mieux comprendre les phénomènes de fissuration. Nous aborderons deux problèmes différents, l'un se rapportant à des conditions statiques dans le cas d'une plaque mince présentant une fissure stationnaire et l'autre traitant de la dynamique lorsqu'il y aura
Les développements en mécanique de la rupture bidimensionnelle fournissent des solutions asymptotiques des contraintes (xx, yy, xy) et du déplacement hors-plan (uz) et des
paramètres. Le facteur d'intensité des contraintes (K) et l'intégrale J de Rice sont deux paramètres largement utilisés pour prédire le risque de rupture d'une structure. Ces deux quantités s'obtiennent à partir de donnés numériques (ex : Eléments finis) ou expérimentales issues, de la photoélasticimétrie ou de la méthode des caustiques et plus récemment à partir de champs cinématiques, essentiellement par des mesures de champs de déplacements. Pour les déplacements dans le plan (ux, uy), les solutions théoriques sont connues et ne sont pas
asymptotiques. Dans l'approche bidimensionnelle du problème de la mécanique de la rupture, l'épaisseur (h) de la structure est négligée ainsi que toutes les grandeurs mécaniques suivant cette dimension. Cette hypothèse a permis d'exprimer analytiquement le problème d'une structure fissurée. Toutefois, la non-présence d'effets tridimensionnels au cœur d'une structure, induite par cette condition, a largement été contredite par de nombreux essais expérimentaux proche de la singularité géométrique.
L'étude des problèmes tridimensionnels de fissuration peut être mise en œuvre expérimentalement en utilisant les méthodes optiques, car elles sont sans contact, non destructives... Des expérimentations sur des fissures stationnaires et utilisant l'interférométrie ou la méthode des caustiques ont montré le caractère tridimensionnel proche de la singularité par comparaison des résultats expérimentaux et des formulations 2D. Parallèlement, des études numériques et volumiques ont aussi souligné le caractère 3D. Sur la surface libre de la structure, une zone dite "3D" égale à la demi-épaisseur de la plaque, a été observée. Proche de la pointe de fissure, l'évolution des reliefs est considérablement modifiée entre la théorie bidimensionnelle et les essais. Ainsi, l'expression du déplacement hors-plan 2D ne peut être appliquée pour des fissures stationnaires et donc une approche bidimensionnelle du problème de fissuration ne suffit pas pour visualiser le comportement mécanique dans une zone confinée en pointe de fissure.
Naturellement, un certain nombre de questions se pose. Si les déplacements hors-plan sont modifiés, qu'en est-il des champs de déplacements dans le plan ? Peut-on dimensionner la zone 3D à partir de champs cinématiques dans le plan ? Pouvons-nous étendre l'étude expérimentale du déplacement hors-plan proche de la fissure, lors de propagation de fissure ? Les formulations 2D du déplacement hors-plan sont-elles valides en dynamique ? Des effets autres, que les effets présents en statique, modifient-ils les champs cinématiques lors de
propagation de fissures ? La zone 3D évolue-t-elle en fonction de la vitesse de propagation de la fissure (V) ?
Actuellement, il devient nécessaire de répondre à ces questions pour permettre de valider les conditions aux limites des modèles numériques 3D pour des fissures stationnaires, et pour voir si une approche bidimensionnelle des modélisations numériques, très largement utilisée actuellement pour simuler des propagations de fissures, est suffisante pour étudier le comportement mécanique en pointe de fissure.
Ce mémoire présente deux approches expérimentales différentes pour l'étude des problèmes de fissurations en statique et en dynamique pour des plaques fissurées ayant un comportement élastique (nous négligeons la zone plastique confinée en pointe de fissure), sollicitées en mode I de chargement (écartement des lèvres de la fissure dans le plan de la plaque).
Concernant la partie statique et s'appuyant sur les précédents travaux qui ont permis de dimensionner une zone 3D à partir de méthodes optiques (interférométrie) [1], nous étudierons les champs de déplacements dans le plan d'une plaque fissurée. Parallèlement à ces travaux expérimentaux, la validité d'un modèle numérique tridimensionnel par éléments finis est étendue. Ces études expérimentales et numériques permettent, de développer deux formulations empiriques pour chacun des déplacements dans le plan, de mettre en évidence l'apparition d'effets de bord non négligeables lorsque la fissure n'est pas assez avancée dans la plaque, et de montrer la triaxialité du problème de rupture à partir de l'intégrale J. Ce travail expérimental a été mené sur deux polymères fragiles différents.
Pour la partie se rapportant à la dynamique, nous voulons étendre, à partir des données expérimentales de déplacements hors-plan, l'étude du comportement mécanique réalisée sur des fissures stationnaires. Pour cela, nous propageons une fissure dans une plaque sollicitée en mode I par l'impact d'une lame. Les écarts constatés entre la solution 2D et les résultats expérimentaux définissent une zone, appelée "zone 3D" rendant compte des effets 3D et des effets transitoires. La modification du chargement extérieur fait varier la vitesse de propagation (V), ainsi une étude de cette zone 3D est réalisée pour différentes valeurs de V. La principale difficulté réside dans l'obtention de données expérimentales des déplacements hors-plan proche de la pointe de fissure lors de sa propagation.
présenterons les différents modes de chargement, les différentes formes d'éprouvettes normalisées, les formulations théoriques des champs de contraintes et de déplacements. Ensuite, nous définirons les deux paramètres cités précédemment que sont le facteur d'intensité des contraintes en mode I noté KI et l'intégrale J de Rice. La septième partie du
chapitre 1 porte sur les méthodes optiques utilisées pour extraire des grandeurs mécaniques proches de la pointe de fissure. Nous présentons les méthodes optiques mettant à profit le phénomène d'interférence, basées sur la variation de relief en pointe de fissure, s'appuyant sur le suivi de motifs et celles basées sur la variation d'indice optique du matériau analysé. Dans la dernière partie, une conclusion sera faite sur les avantages et les inconvénients, sans toutefois choisir les méthodes optiques utilisées dans la suite des études expérimentales.
Il est à noter que seul le principe de chacune des méthodes est abordé, aucuns résultats de travaux numériques et expérimentaux en fissuration statique et dynamique ne seront présentés car une étude de l'art sera entreprise au début des chapitres (chapitre 2 et 3). Cette démarche permettra d'extraire les résultats importants des travaux antérieurs servant de référence pour les études menées dans ce mémoire.
Dans le deuxième chapitre, l'étude du comportement de plaques présentant une fissure stationnaire sera analysée. Dans les huit parties, nous commencerons d'abord par une étude de l'art des différents résultats expérimentaux et numériques. Le choix de la méthode des grilles pour obtenir les champs déplacements dans le plan est présenté. Puis suivra une étude expérimentale des champs de déplacements dans le plan, dans laquelle nous présenterons des essais sur des plaques en polyuréthane et polyméthacrylate de méthyle. Comme dans la littérature, des écarts entre les solutions théoriques 2D et les résultats expérimentaux apparaissent et deux formulations empiriques des déplacements basées sur le principe de superposition sont alors proposées. Ces expressions, dont les écarts sont minimisés entre les données expérimentales et ces nouvelles expressions permettent de décrire les champs de déplacements dans le plan. Le domaine de validité de ces expressions va être entendu au calcul des gradients. Ces derniers sont comparés aux gradients de déplacements numériques,. Cette démarche permettra de calculer l'intégrale J de Rice à partir de données expérimentales. Les champs numériques sont obtenus en réalisant une modification géométrique du modèle numérique 3D, actuellement utilisé au Laboratoire de Mécanique des Solides de Poitiers, pour tenir compte des conditions aux limites expérimentales, non prise en compte dans les précédentes simulations. A partir de ces différents essais expérimentaux et numériques, la triaxialité du problème de fissuration sera présentée en comparant les valeurs des différentes
intégrales J. Les formulations proposées comportent sept variables à identifier et nous choisissons d'étudier, à partir de champs numériques, l'évolution des sept variables en modifiant deux variables géométriques du modèle numérique (l'épaisseur et la longueur de fissure).
Pour l'étude du comportement mécanique lors de propagation de fissure, sept parties composent le chapitre 3, dans lesquelles différents aspects seront abordés. Nous relatons les travaux antérieurs liés aux problèmes de fissuration en dynamique. Pour cela, nous rappelons les différents résultats présentés dans le domaine expérimental à partir de méthodes optiques et dans le domaine numérique. Ainsi, nous constatons que la réalisation d'essais expérimentaux, permettant d'extraire des champs cinématiques lors d'événements dynamiques à haute vitesse de propagation, peut s'avérer extrêmement compliquée. Puis, nous présentons le montage expérimental retenu, les différents résultats de champs de déplacements hors-plan obtenus pour différentes vitesses de propagation de fissure (V). Comme en statique, nous proposons une expression dont les écarts sont minimisés par rapport aux déplacements hors-plan expérimentaux. Une étude de sensibilité de la formulation 3D du déplacement hors-plan est entreprise car lors de l'extraction des champs de déplacements, différentes hypothèses expérimentales sont imposées et nous en dénombrons quatre. Pour réaliser cette étude de sensibilité, nous rajoutons au relief imposé un bruit permettant la modélisation de ces différentes hypothèses. Cela nous permet de définir les limites maximales de chacune des hypothèses dans le but d'identifier physiquement et précisément les trois constantes (c1, c2 et
c3) de la formulation 3D en fonction de (V), la contrainte appliquée () et des caractéristiques
géométriques et mécaniques. La zone des effets 3D sera dimensionnée en fonction de la vitesse (V) et du chargement extérieur (), et la forme du relief en pointe de fissure sera étudiée. Après rupture des plaques, deux nouvelles surfaces sont créées, et une étude post-mortem des faciès de rupture sera effectuée. Pour cela, nous disposons au sein du laboratoire d'un interféromètre confocal en lumière blanche permettant de réaliser une topographie du relief sur de petits échantillons. Une comparaison est alors faite entre la rugosité calculée, l'aire développée générée par la création de la nouvelle surface et le chargement extérieur appliqué ().
CHAPITRE 1 :
Mécanique de la rupture 2D et méthodes
optiques mise en œuvre en fissuration.
1 Mécanique de la rupture 2D et méthodes
optiques mise en œuvre en fissuration.
1.1 Introduction.
La présence d'une fissure dans un milieu est caractérisée par une discontinuité géométrique de ce dernier. La mécanique des milieux continus pour un solide soumis à des sollicitations extérieures, prenant en compte des conditions aux limites spécifiques dues à la fissure, constitue la mécanique de la rupture. Les relations de la mécanique d'une part (équations d'équilibre, de compatibilité, loi de comportement, caractéristiques géométriques et mécaniques du milieu étudié), et les conditions aux limites relatives à la fissure d'autre part suffisent théoriquement à déterminer les champs cinématiques entourant la fissure. Pourtant, même dans le meilleur des cas (comportement élastique + géométrie simple), il s'avère difficile d'obtenir des expressions mathématiques concordant avec les conditions mécaniques et géométriques exprimées précédemment.
Pour étudier le comportement mécanique d'une plaque fissurée dans une zone entourant la pointe de fissure, différentes approches existent : soit à partir de relations théoriques, d'études expérimentales ou encore d'études numériques. Nous savons que l'approche théorique des grandeurs cinématiques en pointe de fissure n'est pas valide, dans une zone confinée en pointe de fissure, car elle considère qu'une plaque fissurée soumise à un chargement extérieur conduit à une contrainte infinie en pointe de fissure. Autrement dit, la plaque fissurée n'admet aucun chargement extérieur sinon il y a propagation de la fissure. C'est pour cela que des études tridimensionnelles numériques et expérimentales ont été entreprises, pour valider les hypothèses établies pour obtenir ces relations theéoriques 2D. L'approche expérimentale en mécanique de la rupture se réduit à l'utilisation presque systématiquement des méthodes optiques. Toutefois, les réseaux de Bragg [2] et les barres d'Hopkinson sont aussi largement utilisés pour étudier le comportement mécanique proche de la pointe de fissure. Lors d'un essai mécanique de fissuration, la mesure de la longueur d'onde au sein de la fibre de Bragg permet de déterminer l'écart de déformation en comparaison avec un état de référence. Le grand intérêt de cette méthode est son caractère tridimensionnel de la réponse optique enregistrée (indice de réfraction). Néanmoins, les propriétés mécaniques (élasticité, limite à la rupture) de la fibre de Bragg doivent être relativement proches de celles du matériau étudié,
d'éprouvettes incluant des réseaux de Bragg au sein de la structure à analyser, est une technique difficile et non maîtrisée dans notre laboratoire. De plus, les déformations non homogènes entourant la fibre sont difficilement appréhendables, c'est pourquoi nous choisissons de ne pas présenter les travaux en mécanique de la rupture avec inclusion de réseaux de Bragg dans le milieu étudié. Pour ce qui est de la mise en œuvre des barres d'Hopkinson [3] [4], cette méthode permet de calculer la déformation moyenne εx
t , lavitesse de déformation moyenne x
t et la contrainte moyenne x
t d'un échantillon au cours d'une sollicitation, à partir de deux jauges de déformation placées en amont et en aval de l'échantillon, ce qui en fait une technique parfaitement bien adaptée au mesure en dynamique rapide à haute vitesse de déformation. Lors d'un essai de compression en dynamique, un projectile impact une première barre dite "barre incidente", ce qui produit deux ondes. La première se propage dans le projectile et l'autre dans la barre incidente permettant de déterminer la déformation (i(t)) au niveau de la jauge 1 placée sur cette même barre. Laseconde onde ayant atteint l'échantillon se divise en deux nouvelles ondes appelées "onde de transmission" et "onde de réflexion" L'onde de transmission atteint la barre de transmission et passe sur la jauge 2 en donnant la déformation (t(t)). L'onde de réflexion passe par la jauge 1
et donne la déformation (r(t)).
Barre incidente Barre transmission
Projectile V
Echantillon
Jauge 1 Jauge 2
x
figure 1.1 : Schéma d'une barre d'Hopkinson en compression.
Avec la détermination de ces grandeurs, le calcul du (KI) et de la ténacité du matériau (KIc)
sont possibles [5]. Mais cette méthode donne une mesure ponctuelle et non une mesure de champs de ces grandeurs mécaniques, c'est pour cela que dans la suite de ce chapitre, nous ne présenterons pas cette méthode expérimentale pourtant largement utilisée en mécanique de la rupture [6].
Dans les paragraphes de ce chapitre, nous présentons d'abord les développements de la mécanique de la rupture 2D, puis le principe des différentes méthodes optiques et les grandeurs cinématiques déduites.
1.2 Théorie de la rupture et mode de fissuration.
Dans le but de clarifier et d'exprimer les formulations théoriques bidimensionnelles incluant chaque mode de chargement, nous allons d'abord présenter les différentes sollicitations d'une plaque fissurée. Une fissure sera schématisée par deux surfaces planes appelées lèvres supérieure et inférieure. Elles se coupent en une courbe appelée front de fissure. Nous limiterons l'étude aux plaques élastiques dont l'un des côtés est fissuré (SEN pour Single Edge Notch en anglais). Dans notre cas, les lèvres de la fissure sont toujours considérées comme perpendiculaires à la surface libre de la plaque.
Un système de coordonnées orthonormées direct (O, x ,y,z) est centré en pointe de fissure, d'axe z tangent au front de fissure, l'axe x se situe dans le prolongement de la fissure. Le plan passant par les axes x et z sera appelé ligament. Pour plus de simplicité dans la mise en équation, un système de coordonnées cylindriques (r,,z) est considéré où r est la distance au front de fissure et la coordonnée angulaire prise à partir de l'axe x (figure 1.2).
h
W
L
x
z
y
r
figure 1.2 : Représentation d'une éprouvette fissurée d'épaisseur (h) et sollicitée en mode I.
En fonction du chargement extérieur, tout problème de fissuration peut être ramené à trois mouvements élémentaires définissant trois modes de fissuration.
0 u ) , ( u u ) , ( u u z y y x x y x y x
MODE I MODE II MODE III
figure 1.3 : Différents modes de chargement d'une éprouvette fissurée.
Le mode I (mode d'ouverture) caractérise un déplacement des surfaces perpendiculaires au plan de la fissure, le mode II (mode de glissement dans le plan) une direction des déplacements normale au front de fissure et le mode III (mode de glissement anti-plan) un chargement tangent au front de fissure. Toutefois des combinaisons de ces modes sont possibles, on parlera alors de mode mixte. Pour chacun de ces trois modes, dans le cadre de la mécanique de la rupture bidimensionnelle, des expressions analytiques asymptotiques des contraintes et des déplacements valables près de la pointe de fissure existent.
1.3 Les solutions analytiques des contraintes et des déplacements.
Considérons une plaque fissurée de dimensions infinies, la détermination du vecteur déplacement u et du tenseur des contraintes σ se simplifie en un problème plan si le chargement est indépendant de z. Le déplacement u et le tenseur σ peuvent s'exprimer en se plaçant dans le cas de l'élasticité plane, par les deux approches connues sous le nom de déformations planes (DP) et de contraintes planes (CP). Les conditions supplémentaires ajoutées dans le cas de (DP) sont :
0 zz yz xz 0 xy y
(CP) 0 (DP) 0 zz xx yy yz xz
Rot tRotDans le cas des (CP), l'approche suppose que le tenseur ( σ ) ne dépend que de x et y et se simplifie par :
(1.2)
En négligeant les forces volumiques, en tenant compte de la loi de Hooke (=E) et en faisant l'hypothèse des petites perturbations (HPP), les équations d'équilibre se simplifient et conduisent aux expressions suivantes :
(1.3)
(1.4)
où est le coefficient de Poisson
En mécanique de la rupture, l'hypothèse des contraintes planes est très largement utilisée pour caractériser les grandeurs cinématiques pour des plaques fissurées de faible épaisseur (h). Les équations d'équilibre sont vérifiées par l'intermédiaire d'un tenseur de fonction de contraintes ( ) : (1.5) Avec : ) , ( A 0 0 0 0 0 0 0 0 y x
La fonction (A) est appelée fonction d'Airy et permet d'exprimer les contraintes sous la forme suivante : 2 2 xx A σ y ; 2 2 yy A σ x , y x A σ 2 xy
Westergaard [7] a résolu le problème symétrique d'une plaque infinie fissurée, chargée hydrostatiquement en développant la fonction d'Airy (A) l'aide d'une fonction complexe (Z).
Z Z yIm Re A ' Im y Re σyy Z Z (1.6) où Z z Z d d ; Z z Z d d ; ' d d Z z Z
Comme la fonction est analytique sur le domaine considéré, les dérivées peuvent être déterminées et les expressions des contraintes sont de la forme suivante :
σxx ReZyImZ'
(1.7) σxy yReZ'
Westergaard a proposé la fonction suivante dans le cas d'un chargement bi-axial constant (k=1, voir figure 1.4) d'une fissure de longueur (2a) contenue dans une plaque infinie sous chargement.
(1.8)
Les coordonnées (x) (y) sont liées au repère d'étude de la plaque suivante :
2a kσ σxx x σ σ y yy x y u w M r O
figure 1.4 : Plaque fissurée, milieu bidimensionnel infini en mode mixte.
iy x w a w σw Z 2 2
u 2 K u 2 aπ σ 2au σa a 2au u a u) σ(a Z I 2 2 2 0 u 2 3 cos 2 cos 2 sin 2 K ) , ( σ 2 3 sin 2 sin 1 2 cos 2 K ) , ( σ 2 3 sin 2 sin 1 2 cos 2 K ) , ( σ I xy I yy I xx θ θ θ πr θ r θ θ θ πr θ r θ θ θ πr θ r
2 cos 1 2 2 sin 2 K , u I 2 y θ θ r θ r d Westergaar
2 sin 1 1 2 cos 2 K , u I 2 x θ θ r θ r d WestergaarLa fonction ainsi proposée est une solution du problème. Afin de simplifier le champ de contraintes proche de la pointe de fissure, le terme (w) de l'équation (1.8) est remplacé par (a+u) avec u=rei, où (r,) sont les coordonnées cylindriques centrées en pointe de fissure (point O). En substituant la variable (u) dans l'équation (1.8), la fonction (Z) s'écrit au voisinage de la pointe de fissure lorsque |u|0 :
(1.9)
Le terme (KI), appelée Facteur d'Intensité des contraintes (FIC), est fonction uniquement du
chargement extérieur () et de la demie longueur de la fissure (a) et sera présenté ultérieurement. En tenant compte de la forme de (u) en coordonnées polaires et du comportement élastique, les contraintes et les déplacements en pointe de fissure peuvent être exprimés :
(1.10)
(1.11)
(1.12)
où =E/(2(1+)) représente le module de cisaillement, (E) le module d'Young et le coefficient de Poisson.
Il est à noter la présence de la singularité en r-1/2 pour les champs de contraintes et en r1/2 pour les champs de déplacements. D'autres approches comme celle Eftis et al [8] ont été
2 3 cos 2 cos 2 sin 2 K ) , ( σ 2 3 sin 2 sin 1 2 cos 2 K ) , ( σ σ k 1 2 3 sin 2 sin 1 2 cos 2 K ) , ( σ I xy I yy I xx θ θ θ πr θ r θ θ θ πr θ r θ θ θ πr θ r(figure 1.4). Cela conduit à une autre fonction complexe Z, que celle proposé par Westergaard. Les champs de contraintes se trouvent ainsi modifiés :
(1.13)
En considérant une loi de comportement élastique, les expressions de champs de déplacement dans le plan peuvent être obtenues :
(1.14)
(1.15)
On peut noter que l'on retrouve les solutions de Westergaard lorsque k=1. Si k=0 les conditions de sollicitations en mode I peuvent être appliquées pour un milieu infini. En 1977, Eftis et al [9] ont démontré que les conditions aux limites imposées pour obtenir les expressions des déplacements (1.14) (1.15) étaient seulement valables pour k=1. Ils ont alors développé une autre formulation complexe Z et ont obtenu les relations de déplacements suivantes : (1.16) (1.17) avec (CP) ν 1 ν 3 (DP) 4ν 3 κ
cos a
8 σ 1 κ k 1 2 sin 1 -κ 2 1 2 cos 2 K , u I 2 x r θ θ r θ θ r
r θ r θ
θ
rsinθ 8 σ κ -3 k 1 2 cos 1 κ 2 1 2 sin 2 K , u I 2 y
1 k cos E 2 sin 1 1 2 cos 2 K u I 2 2D -x r r
1 k sin E 2 cos 1 2 2 sin 2 K u I 2 2D -y r r (CP) E σa (DP) E ) ν σa(1 2 1)a (κ 2E ν) σ(1 ) u ( 2 0 x r
Avec cette solution (1.16), cela revient à un déplacement ux non nul en pointe de fissure. Pour
exemple, lorsqu'une plaque de dimensions infinies est soumise à un chargement uniaxial (k=0), le déplacement proche de la pointe de fissure s'écrit :
(1.18)
Nous traçons sur la figure suivante l'évolution des déplacements ux selon les formulations
(1.11) (1.14) et (1.16) pour (r,=0°) : r [mm] déplacement [m m] équation (1.16) équation (1.11) équation (1.14)
figure 1.5 : Déplacement ux selon les formulations (1.11), (1.14) et (1.16).
avec KI = 17,9631 MPamm, E = 2825 MPa et = 0,4
Sur la figure 1.5, l'équation (1.11) représente les déplacements pour un chargement bi-axial. Entre les équations (1.14) (1.16), seule la fonction Z change. Toutefois l'écart constaté entre ces deux équations s'apparente à un déplacement de solide rigide.
Pour la suite de notre travail, nous considérerons toujours les équations théoriques d'Eftis (1.14) (1.15) pour représenter les champs de déplacements (ux et uy) d'une éprouvette fissurée
et sollicitée en mode I de rupture (k=0). Concernant le déplacement hors-plan uz-2D de la
cte 2π 1 2 cos E h νK dz E ) σ ν(σ dz ) , , ( ε ) 2 / h , ( u I h/2 0 yy xx 2 / h 0 zz 2 -z
r θ z θ r z r,θ Dchargement uniaxial (k=0), nous obtenons la relation suivante en considérant un comportement élastique et un état de contraintes planes (CP) :
(1.19) avec 2 h σ E ν cte
où la coordonnée (z) est définie à partir du repère d'étude centré en fond de fissure.
En raison de la symétrie du problème, nous obtenons une expression de uz-2D identique au
signe près sur l'autre surface libre et dans la suite des travaux nous choisissons toujours un déplacement positif.
1.4 Facteur d'Intensité des Contraintes (K
I).
Dans le paragraphe précédent, l'étude de la fissuration est établie pour des éprouvettes de dimensions infinies ou semi-infinies. Mais lors de comparaison entre les solutions théoriques et des résultats expérimentaux, des écarts importants ont été constatés car expérimentalement l'hypothèse de plaques infinies est difficilement réalisable. Dans le but de normaliser les études en mécanique de la rupture, des éprouvettes standards ont été développées pour des dimensions finies, contenant des fissures "traversantes" dans l'épaisseur et ayant des géométries simples. Ci-dessous, nous présentons trois géométries d'éprouvettes normalisées les plus utilisées en fissuration pour une mode I de chargement.
Compact Tensile (CT)
Double Edge Notch (DEN)
Single Edge Notch (SEN)
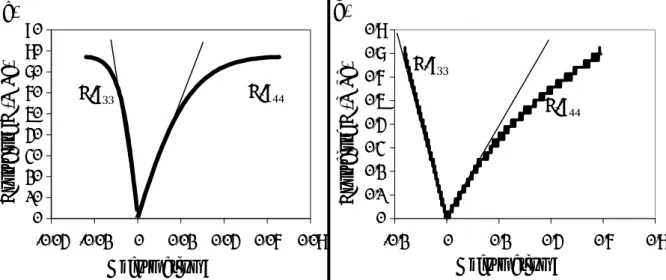
W a .Y πa σ KI 3 tada I 2W πa sin 1 0,37 W a 2,02 0,752 2W πa cos 2W πa 2tan . W h F K 1.4.1 Approche statique.
Le facteur d'intensité des contraintes donne physiquement une mesure de l'intensité de la singularité. Ce facteur caractérise à lui seul l'état mécanique à l'extrémité du front de fissure. Sa connaissance est donc suffisante pour décrire entièrement l'état de contraintes et le champ de déplacements au fond de fissure. C'est pourquoi l'un des axes importants de la mécanique de la rupture est la détermination des facteurs d'intensité des contraintes. Pour des éprouvettes à géométries simples, de dimensions finies et sollicités en mode I, on a l'habitude d'utiliser la formulation suivante:
(1.20)
Cela revient à reprendre la formulation de Westergaard (1.9) pondérée par un facteur multiplicatif (Y) qui est une fonction de forme dépendant de la géométrie de l'éprouvette et de la longueur de la fissure. Dans la littérature pour une éprouvette SEN sollicitée en mode I, une autre solution de (Y) [10] existe, mais en plus d'être fonction des paramètres précédents, elle est aussi fonction de la limite d'élasticité (e) du matériau étudié. Les expressions de Y les
plus souvent utilisées sont celles de Labbens [11] et celle de Tada et al [12] :
(1.21)
(1.22)
Ces deux formulations (1.21) (1.22) étant différentes, il est intéressant de les comparer et de définir une géométrie (longueur de fissure) où le choix de l'une des deux formulations n'influence pas ou peu la valeur des déplacements. Pour cela, nous définissons un critère empirique (Ratio) (1.23) à partir des deux expressions de KI précédentes. Ce critère est basé
sur la valeur moyenne (K ) des deux expressions (1.21) (1.22), ce qui permet de calculer I 4 3 2 labbens I W a 53,85 W a 38,48 W a 18,40 W a 0,41 1,99 a Wh F K
(1.23) avec : 2 K K KI Ilabbens Itada
Nous pouvons alors tracer en fonction de (a), l'évolution de l'équation (1.23) pour une des géométries des éprouvettes testées dans la suite de notre étude.
a[mm] R at io [% ]
figure 1.7 : Rapport entre l'expression de Labbens et l'expression de Tada.
D'après la figure précédente, quand la fissure est proche de a40 mm, le choix entre les deux expressions de KI n'a pas d'influence sur les valeurs des déplacements. L'évolution du critère
(Ratio) en fonction de (a) permet de définir la valeur maximale du critère qui peut être évaluée à 1,5%. Ainsi le choix de l'une des deux expressions affecte peu les champs théoriques lorsque a < 110 mm.
La détermination théorique du facteur d'intensité des contraintes est essentielle car c'est un paramètre faisant partie intégrante du processus de rupture fragile, qui intervient dans un critère d'initiation et de propagation de fissure.
1.4.2 Approche dynamique.
Aucun des termes présents dans les équations (1.21) (1.22) ne tient compte des aspects dynamiques liés à la propagation de fissure. Cela revient à dire que les champs de contraintes et de déplacements sont les mêmes que ce soit pour une longueur de fissure (a) stationnaire égale à une longueur de fissure a(t) (t = variable de temps) lors d'une propagation de fissure.
100 . K K -K Ratio I labbens I tada I
V f. K KId I
2
2 2 2 2 1 2 2 2 2 1 1 1 4 V f
2 1 1 1 E C2 L
1 2 E C2 TToutefois, des études [13] ont mis en évidence la présence d'effets transitoires directement liés à la vitesse de propagation (V). Différents travaux ont alors permis de prendre en compte les effets dynamiques dans le calcul empirique du facteur d'intensité des contraintes.
1.4.2.1 Terme correctif de Beinert et al [14].
Cette approche consiste à multiplier le facteur d'intensité des contraintes par un terme correctif f(V) tenant compte du caractère dynamique de l'expérience. Le facteur d'intensité des contraintes dynamiques (d-FIC) peut être déterminé analytiquement :
(1.24)
Pour obtenir la forme de f(V), les auteurs [14] ont fait une série d'essais pour différents matériaux et différentes vitesses de propagation de la fissure. En utilisant la méthode des caustiques (§ 1.7.2.2), les diamètres de celle-ci ont pu être analysés conduisant à une comparaison, entre le FIC statique et dynamique. Des divergences apparaissent, le KId
dynamique est toujours inférieur à KI statique et peut s'écrire sous la forme :
(1.25) avec 2 / 1 2 L 2 1 C V 1 et 2 / 1 2 T 2 2 C V 1
où CL et CT sont respectivement les célérités des ondes longitudinales et transversales.
A partir des équations de Navier, les expressions pour obtenir CL et CT sont les suivantes :
(1.26)
1.4.2.2 Terme correctif de Nilsson [15].
Dans son étude, Nilsson définit le FIC à partir du champ de contraintes tridimensionnel en fond de fissure.
2 2 2 2 1 1 I dyn ox 2 2 / 1 2 2 2 2 1 1 2 / 1 1 I Id x cos 2 1 cos B . 2 1 2 cos 1 2 2 cos 2 V B K , u θ r θ r c θ r θ r θ r
2 2 dyn 2 2 / 1 2 2 2 1 1 2 / 1 1 1 I Id y sin 1 sin B . 1 2 sin 1 2 2 sin 2 V B K , u θ r θ r c θ r θ r θ rSuivant le problème plan choisi et selon les conditions aux limites imposées, différentes expressions de KId peuvent être formulées. Tout d'abord, nous présentons les conditions aux
limites imposées dans les travaux de Nilsson :
(1) Pour y = L/2 : uy = uyo et xy=0
(2) Pour y = L/2 : uy = uyo et ux=0
avec xy la contrainte de cisaillement et uyo le déplacement constant induit par le chargement
extérieur suivant l'axe de chargement.
Nous limitons les expressions du d-FIC au cas d'un état de contraintes planes (CP).
(1.28)
(1.29)
1.4.2.3 Terme correctif d'Arakawa et al [16].
Dans le but d'étudier les d-FIC, à partir des mesures expérimentales dans le plan (moiré interférométrique § 1.7.1.3), les auteurs [16] ont réalisé deux essais pour obtenir les deux champs de déplacements plan (suivant l'axe x (ligament) et suivant l'axe y de chargement). Pour tenir compte de la propagation de fissure, les relations théoriques bidimensionnelles ont été modifiées : (1.30) (1.31)
2 / 1 2 1 2 2 2 1 2 2 1 y Id 4 1 4 1 L 4 .E. u K ) 1 (
2 / 1 2 2 1 2 2 2 2 1 2 2 / 1 y Id 1 1 4 L 2 . -1 -1 .E. u K ) 2 (
2 / 1 nom max yy R a 2 1 où
2
2 2 2 1 2 2 I 1 4 1 V B , yei j x j j r et dyn ox représente la contrainte éloignée
Pour obtenir les champs de déplacements dans le plan lors de propagation de fissure, cette approche permet de tenir compte de la vitesse (V) et ne se limite pas à une simple proportionnalité entre le FIC statique et le FIC dynamique.
1.4.3 Discussion.
Dans la suite de nos travaux, nous choisissons d'utiliser l'expression de Labbens KIlabbens pour
calculer les FIC empiriques en statique. En dynamique, nous multiplierons ce terme par la correction (F(V)) de Beinert et al [14] car ce terme permet d'exprimer directement la valeur du d-FIC au contraire des travaux de Nilsson et Arakawa où la détermination d'un champ cinématique est nécessaire.
1.5 Approche énergétique.
Parallèlement à ces travaux analytiques en mécanique en rupture, des développements visant à modifier l'approche du problème de fissuration ont été réalisés. C'est dans cette optique que des approches énergétiques ont été élaborées. Ainsi des paramètres nouveaux, caractérisant un milieu fissuré, ont été mis en évidence.
1.5.1 Théorie de Griffith et taux de restitution d'énergie (G).
Les premiers travaux sont l'œuvre d'Inglis [17] qui en supposant un milieu bidimensionnel et en utilisant la théorie de l'élasticité exprima analytiquement la contrainte maximale (yy)max
(équation (1.32)) suivant la direction de chargement (nom). Pour cela, il a considéré une
plaque incluant un trou elliptique, soumise à un chargement uniformément réparti à l'infini et perpendiculaire au grand axe.
(1.32)
avec (a) : la longueur du demi grand axe de l'ellipse, R : le rayon de courbure au point considéré.
Si (b) est la longueur du demi petit axe, R prend une valeur minimale à cet endroit et vaut b²/a. Dans un trou circulaire (R=a),
yy max est égale à 3nom. Il est à noter que dans le casd'une fissure, si l'on se place en pointe de fissure R0, la contrainte devient infinie, autrement dit la plaque fissurée ne supporte aucun chargement extérieur.
En se basant sur les travaux d'Inglis, Griffith [18] a été le premier à étudier la rupture d'un point de vue énergétique, et ces travaux ont permis d'éliminer la notion de contrainte infinie en pointe de fissure. Lorsqu'une plaque est chargée, les faces de la fissure le sont aussi. Le chargement tend à ouvrir et à croître la fissure, mais le matériau oppose une résistance et la fissure reste en équilibre. Si la pression croît, l'équilibre peut être rompu, et la fissure peut avancer de façon instable. Pour un milieu fragile idéal, l'énergie totale (E) du milieu s'écrit sous la forme suivante :
(1.33)
avec : (W) l'énergie de déformation du milieu et (Wext) le travail des forces appliquées, (dWS)
énergie dissipée dans la séparation et (Wcin) l'énergie cinétique.
Pour un processus adiabatique (pas d'échange de chaleur), (W) correspond également à l'énergie interne et dépend uniquement du tenseur des déformations ( ). Pour un milieu bidimensionnel, les quantités précédentes sont normalisées par rapport à l'unité d'épaisseur, l'énergie (dWS) s'écrit :
(1.34)
avec () l'énergie de création d'une surface libre. Le chiffre deux provient du nombre de surfaces créées.
Avant la propagation d'une fissure, il y a équilibre pour un système soumis à des sollicitations extérieures et présentant une fissure de surface (S). D'après (1.33), la fissure se propagera de façon instable si l'énergie cinématique dWcin > 0, ainsi nous obtenons l'expression suivante :
(1.35) 0 dW dW dW dW dE ext S cin da γ 2 dWS
W W
2 0 da d ext 2 / 1 * r a E
Ainsi, nous pouvons introduire le paramètre (G) appelé taux de restitution d'énergie
(1.36)
Dans las cas où (G=2), il n'y a pas augmentation de l'énergie cinétique (Wcin), on parle de
rupture contrôlée et de croissance stable de la fissure [19]. Lorsque le taux de restitution d'énergie (G) est supérieur à (2), une partie de l'énergie sert à créer de nouvelles surfaces (i.e. propagation d'une fissure). La propagation instable peut intervenir lorsque l'excès d'énergie ((G-2)da) est transformée en entièrement énergie cinétique. Toutefois, une partie de cette énergie est consommée par l'augmentation de l'énergie extérieure (Wext).
Suivant les travaux d'Inglis, Griffith a calculé l'énergie de déformation (W) dans le cas de la plaque élastique infinie (épaisseur unitaire) comportant un défaut elliptique de longueur (2a) :
(1.37)
avec E*=E/(1-²) pour un état de déformations planes (DP) et E*=E en contraintes planes
(CP).
En utilisant les expressions mathématiques (1.34), (1.35) et (1.36), un critère de rupture (r) a
pu être formulé, valide pour une plaque présentant un faible rayon de courbure, autrement dit une fissure :
(1.38)
Ce critère a été vérifié expérimentalement sur des matériaux purement élastiques tels que le verre. Un terme correctif a été apporté pour des matériaux ductiles présentant une zone ductile en pointe de fissure (énergie de déformation plastique) [20].
1.5.2 Intégrale J de Rice.
Dans le cas de la rupture ductile, le travail fourni par le chargement extérieur n'est pas seulement utiliser pour propager la fissure, mais une partie de cette énergie est stockée ou
W W 2 da d G ext * 2 nom 2 E a -W * 2 I E K G J ij ij W
Dans une première approche, la plaque est considérée comme homogène, de dimension deux avec un comportement purement élastique. En supposant que les forces massiques soient négligeables, le chargement extérieur (P) induit seul sur l'énergie stockée ou dissipée. De ce fait, l'intégrale de contour J s'écrit de la façon suivante :
(1.39)
avec (W()) : la densité d'énergie de déformation, (T(n)) : le vecteur contrainte, (ui) : le
vecteur déplacement et (ds) : l'élément de contour.
Dans l'expression (1.39), on peut observer que les deux termes (1.40) (1.41) sont égaux et de signe opposés, ce qui met en évidence l'indépendance de l'intégrale J vis-à-vis du contour d'intégration. On peut donc écrire l'intégrale J sous la forme suivante :
(1.40)
(1.41)
A partir des champs asymptotiques de contraintes ou de déplacements, nous obtenons pour un état de contraintes planes ou de déformations planes, la relation suivante qui n'est autre que le taux de restitution d'énergie (G).
(1.42)
D'autres formes de contours, ont été utilisées pour déterminer le paramètre (J) pour des matériaux fragiles [10] ou ductiles [22] [23] [24] comme le contour rectangulaire (figure 1.8b). Pour les matériaux élasto-plastique écrouissable, Hutchinson, Rice et Rosengreen (HRR) ont montré que l'intégrale J permet de caractériser les champs de contraintes et de déformations dans une enclave plastique.
ds x u n T dy W J i
x u x ds x u . n T i ij j iH1 V2 H2 V1 J -J -J J J
yy xx
2 yy yy xx 2 xx -1 E -1 E n y b) H2 V1 V2 H1 n y a)x
figure 1.8 : a) Contour d'intégration circulaire. b) Contour d'intégration rectangulaire. Le contour rectangulaire est divisé en lignes verticales (V1, V2) et en lignes horizontales (H1 et H2), cela permet de décomposer l'intégrale J et ainsi d'obtenir la relation suivante :
(1.43)
avec :
La détermination de l'intégrale J requiert les composantes des gradients (xx et uy/x), les
composantes des contraintes (xx, yy et xy) et l'énergie de déformation (W). Pour un
matériau à déformation élastique linéaire et pour un état de contraintes planes (CP), les composantes des contraintes s'écrivent de la forme suivante :
(1.44)
H2 xx xy y yy H2 H1 xx xy y yy H1 V2 y xy xx xx V2 V1 y xy xx xx V1 dx ε σ x u σ J dx ε σ x u σ J dy x u σ ε σ Wdy J dy x u σ ε σ Wdy J
2 xy yy xx 2 yy 2 xx 2 1 2 E 2 1 W 1 1 , 1 2 2 1 k k r θ θ θ r y r θ θ θ r x r θ θ θ r y r θ θ θ r x y y y yy y y y yx x x x xy x x x xx cos u sin u u F sin u cos u u F cos u sin u u F sin u cos u u F L'énergie de déformation (W) peut être calculée à partir de la relation suivante :
(1.45)
En substituant les équations (1.43), (1.44), (1.45) dans (1.39), nous pouvons exprimer l'intégrale, en fonction des gradients de déplacements (ux/x, uy/x, ux/y et uy/y)
(1.46)
avec:
Le calcul des gradients de déplacements est réalisé au moyen des équations suivantes [9] :
(1.47)
Pour calculer l'intégrale J pour différents contours (), des mesures de gradients de déplacements sont nécessaires en dérivant les champs de déplacements suivant les deux directions (x et y).
1.6 Discussion.
Il est difficile de fournir une expression analytique pour les champs asymptotiques dans un milieu fini tridimensionnel à l'échelle macroscopique. Pour cela, des développements théoriques et énergétiques ont permis de définir des critères et d'obtenir des formulations mathématiques bidimensionnelles des champs de contraintes et de déplacements. Cela implique la formulation d'hypothèses non représentatives des conditions expérimentales
x k k y k d y x u u x x u u y x u u 2 d x u y u x u y u y u x u x u y u ν 1 4 E J y y 1 y x 2 x x y x y x y x x y 1imposées. Les premiers développements réalisés par Westergaard [7] permettent d'obtenir des équations empiriques des champs cinématiques pour un état plan et pour un milieu infini soumis à un chargement bi-axial. D'autres expressions pour des sollicitations uni-axiales ont été proposées, notamment par Eftis [9]. L'approche énergétique relie des paramètres intrinsèques de la mécanique de la rupture (KI et J) pouvant être déterminés à partir de
grandeurs cinématiques, et notamment en utilisant les champs de déplacements. Le facteur d'intensité des contraintes (KI) permet de définir l'état de contraintes en pointe de fissure et
peut être déterminé empiriquement pour des géométries d'éprouvettes et des sollicitations mécaniques simples. L'intégrale J de Rice est obtenue à partir des approches énergétiques et permet de dimensionner l'énergie dissipée dans le milieu adjacent. Son grand avantage est qu'elle est indépendante du contour d'intégration ().
Dans ce chapitre, la présence de plasticité même confinée en pointe de fissure n'a pas été abordée, où l'existence de cette zone conduit à des contraintes bornées en pointe de fissure. Cette zone étant très faible, elle sera négligée pour le reste de notre étude. Dans l'étude de la mécanique de la rupture 2D, l'épaisseur du milieu étudié est systématiquement négligée. Cette hypothèse peut être étudiée en réalisant des essais expérimentaux à partir de méthodes optiques. Ces méthodes permettent d'extraire pour la plus part des champs cinématiques qui seront confrontés aux résultats théoriques bidimensionnels.
Dans les paragraphes suivants, l'étude expérimentale tridimensionnelle par voie optique de plaques minces fissurées en statique et en dynamique permet d'étudier l'influence de l'épaisseur sur les champs cinématiques. Ainsi, l'importance de ce paramètre sera évaluée. Pour cela, nous présentons le principe des différentes méthodes optiques pouvant être utilisées en mécanique de la rupture.
1.7 Les méthodes optiques utilisées en mécanique de la rupture.
Nous avons séparé les différentes méthodes en quatre groupes : les méthodes basées sur les interférences, celles s'appuyant sur le suivi de motifs, celles nécessitant une variation de relief de la surface et les méthodes mettant à profit la variation de l'indice optique du matériau.
1.7.1 Méthodes optiques basées sur les interférences.
1.7.1.1 Le phénomène d'interférences.
l'obscurité, d'où le nom de "paradoxe de l'interférence". Expérimentalement depuis le 19ième siècle, différents travaux sur les interférences lumineuses ont permis de réaliser des mesures précises grâce à une multitude d'interféromètres (Fizeau (1853), Michelson (1881), Rayleigh (1881), Mach-Zenden (1882), Fabry et Pérot (1899)). L'interférométrie est basée sur le phénomène provoqué par la superposition de deux ondes lumineuses et cohérentes dont nous allons présenter un exemple : l'interféromètre de Michelson.
1.7.1.2 L'interférométrie de Michelson.
Cet interféromètre permet de mesurer la variation de relief avec une amplitude de l'ordre de quelques micromètres. Pour cela (voir figure 1.9a), une source primaire (monochromatique) (S) est divisée à l'entrée en deux ondes (de même pulsation) par une lame semi réfléchissante inclinée à 45 degrés. L'une des ondes, appelée faisceau objet, se réfléchit sur la surface de l'objet et la seconde, appelée faisceau de référence, est réfléchie par un miroir (M). Puis les deux faisceaux retraversent la lame. Des interférences apparaissent, du fait du chemin optique différent entre la lame/objet et la lame/miroir, puis elles sont enregistrées par la caméra (C).
Miroir (M) LASER (S) = 514.5 nm Caméra (C) r x y Lame semi-réfléchissante Eprouvette SEN Fissure a) b) Interférogramme Fissure Pointe de fissure 3,8 mm Faisceau objet Faisceau de référence y x
figure 1.9 : a) Principe de l'interféromètre de Michelson. b) Interférogramme obtenu en pointe de fissure [1].
Cela permet d'étudier les variations d'épaisseur de la plaque analysée car les interférences ou franges visualisées sont directement liées au relief par l'équation suivante :
2 nλ
Δuz (1.48)
avec n : l'ordre de franges, : la longueur d'onde.
Pour une source lumineuse émettant dans le vert ( = 514,5 nm), on obtient à chaque interfrange un déplacement hors-plan uz de 0,257 m. Expérimentalement, l'état de la surface
et la réflexion influent fortement sur le contraste entre les franges sombres et claires. C'est pour cela, qu'un dépôt d'aluminium par vaporisation sous vide est réalisé à la surface des éprouvettes, l'épaisseur de ce dépôt n'excédant pas 50 nm.
Dans la nécessité d'entreprendre des mesures de champs en statique, l'interférométrie de Michelson permet d'obtenir automatiquement le déplacement hors-plan à une constante près. L'information mécanique contenue dans la phase (x,y) qui peut être extraite automatiquement en utilisant des techniques quasi-hétérodynes (i.e. décalage de phase). Ces techniques consistent, à l'aide d'au minimum trois images d'un même réseau de franges mais déphasées les unes par rapport au autres, à déterminer la phase de ce réseau. La nécessité d'acquérir plusieurs images réside dans le fait quand chaque pixel de l'interférogramme enregistré, l'expression mathématique de l'intensité lumineuse I(x,y) est généralement écrite sous la forme mathématique suivante :
(1.49)
où I(x,y), A(x,y), B(x,y) et (x,y) désignent respectivement au point de coordonnée (x,y) (figure 1.9), la valeur de l'intensité lumineuse du pixel en niveau de gris, l'amplitude de modulation, le fond continu et la fonction de phase.
Ainsi en enregistrant plusieurs images du même état mécanique, toutes les inconnues de l'équation (1.49) peuvent être obtenues. La résolution a été évaluée au 45ème d'interfranges (i.e. 6 nm) [25]. L'information de déplacement est alors contenue dans la phase (x,y) et par une relation optico-géométrique, nous pouvons avoir accès au relief uz(x,y) en tout point (x,y)
de l'image.
x,y A
x,y.cos
x,y Bx,yavec = angle d'incidence du faisceau objet sur la surface de l'éprouvette ( =/2).
En dynamique, cette méthode n'est pas plus difficile, à mettre en œuvre au premier abord. Toutefois, l'extraction de la phase (x,y) à partir des méthodes quasi-hétérodyne ne peut être utilisée car elle nécessite la prise de trois images, au minimum du même instant mécanique. Ceci s'avère impossible en mécanique de la rupture dynamique car la fissure progresse. Aujourd'hui, des techniques moins précises que les techniques quasi-hétérodyne sont développées permettant de déterminer la phase (x,y) à partir d'une seule image, ce qui permet de s'affranchir du caractère dynamique des essais, nous pouvons citer Robin et al [26] [30], Takeda et al [27], Gseisat et al [28], Servin et al [29], Surrel [31]. Ces différents algorithmes peuvent influencer la précision de mesure. Cette méthode optique convient parfaitement à la détermination du relief proche de la pointe de fissure en mécanique de la rupture dont l'amplitude est de l'ordre de quelques micromètres [32] [33].
1.7.1.3 Le moiré interférométrique.
1.7.1.3.1 Le principe de moiré.
Le principe de moiré consiste à superposer deux réseaux de traits dont les pas (p1 et p2) sont
voisins. Lorsque l'on superpose ces deux réseaux, on voit apparaître en général un troisième réseau dont le pas est plus important, on parle de moiré ou de moiré visible [34].
Np u 2 1 2 1 p p p . p i
En considérant le phénomène de moiré comme étant dû à un décalage du second réseau par rapport au premier, nous pouvons calculer l'interfrange (i) de moiré visible à partir des pas p1
et p2 des deux réseaux :
(1.51)
L'application de la méthode de moiré consiste à coller, sur l'objet à étudier et sur la surface de référence, un réseau de pas p. Au repos, nous observons une teinte plate, c'est-à-dire uniforme. Lorsque l'éprouvette est chargée, nous voyons apparaître le phénomène de moiré. Le déplacement (u) d'un point résultant du chargement est donc obtenu en fonction de l'ordre de frange N par la relation suivante :
(1.52)
1.7.1.3.2 Application à la mécanique de la rupture.
Basée sur le principe de moiré, le moiré interférométrique est une technique permettant d'extraire le déplacement autour de la pointe de fissure dans une direction à partir d'un réseau. Pour cela, un réseau de franges, de fréquence f=1/p (avec p = pas du réseau), est déposé par réplication ou par métallisation du réseau sur la surface libre de l'éprouvette. A l'état initial, compte tenu de la symétrie, les deux faisceaux incidents (faisceau 1 et 2) correspondants se superposent parfaitement, ne laissant voir qu'une teinte uniforme.
Ordre de franges N Lentille Faisceau incident 1 Réseau Faisceau incident 2 P P Franges d'interférences
![figure 1.9 : a) Principe de l'interféromètre de Michelson. b) Interférogramme obtenu en pointe de fissure [1]](https://thumb-eu.123doks.com/thumbv2/123doknet/7980935.267427/42.892.109.777.597.911/figure-principe-interféromètre-michelson-interférogramme-obtenu-pointe-fissure.webp)