Performance scolaire dans les écoles en présence d'asymétrie dans les effets de pairs

(1)

Performance scolaire dans les écoles en présence

d’asymétrie dans les effets de pairs

Mémoire présenté

à la Faculté des études supérieures et postdoctorales de l’Université Laval dans le cadre du programme de maîtrise en économique

pour l’obtention du grade de Maître ès sciences (M.Sc.)

DÉPARTEMENT D’ÉCONOMIQUE FACULTÉ DES SCIENCES SOCIALES

UNIVERSITÉ LAVAL QUÉBEC

2013

c

(2)

Dans ce mémoire, nous utilisons un modèle linéaire en moyenne pour évaluer l’impact des pairs sur les performances scolaires. Notre modèle, exploite la va-riation dans la taille des groupes comme source d’identification. Des effets fixes sont introduits pour tenir compte de l’effet des caractéristiques inobservées. Le modèle est estimé par la méthode du maximum de vraisemblance. Pour réali-ser les estimations, nous avons utilisé des données qui proviennent d’une base données du Ministère de l’Éducation du Loisir et du Sport de Québec. Cette base contenait des informations sur les notes, le niveau d’étude, l’âge, la langue parlée à la maison et le statut socio-économique des élèves ayant passé en Juin 2005, l’examen de fin de cycle du secondaire. Dans le cadre de cette étude, l’exa-men de l’impact des garçons sur les résultats des garçons, a mis en évidence des effets endogènes significatifs et positifs en mathématiques et en histoire. Cependant, l’impact des filles sur les performances des filles a quant à lui mis en évidence des effets endogènes significatifs et positifs en français, mathéma-tiques et histoire. L’effet endogène intra-genre, obtenu dans le sous groupe des garçons est de l’ordre 0,833 en mathématiques. Dans le sous groupe des filles, nous avons trouvé un estimé de l’ordre de 0,57 dans la même matière.

(3)

(4)

J’adresse mes remerciements au professeur Bernard Fortin. Je le remercie pour le choix du sujet, sa confiance en acceptant de m’encadrer comme directeur dans la réalisation de ce travail. J’exprime ma gratitude envers lui pour ses précieux conseils, sa patience et sa grande disponibilité.

Mes remerciements vont également à mon co-directeur le professeur Guy Lacroix pour ses remarques, commentaires et suggestions. Ce mémoire a été appuyé avec l’aide du centre de recherche CIRPÉE que je remercie pour le sou-tien financier.

Toute ma reconnaissance va à l’ensemble des chercheurs du départements d’Économique de l’Université Laval qui m’ont aidé dans l’élaboration de ce mémoire. Je remercie particulièrement Steeve Marchand pour toutes les heures qu’il a consacré à résoudre mes problèmes. Je remercie Habib Somé et Rokhaya Dieye ainsi que tous mes amis pour les services rendus.

La réalisation de ce travail ne serait possible sans le soutien de ma famille. Je souhaite exprimer toute ma gratitude envers mes parents et oncle Sidi Laouan. Vos encouragements m’ont énormément servi à aller de l’avant.

Enfin je remercie toutes les personnes qui ont contribué de près ou de loin à la réalisation de ce mémoire et que j’aurais oublié de mentionner.

(5)

Table des matières iv

Liste des tableaux v

Table des figures v

1 Introduction 1

2 Revue de littérature 4

2.1 Modélisation et critique de Manski . . . 5

2.2 Méthodes empiriques d’identification . . . 8

3 Méthode économétrique 13 3.1 Présentation du modèle . . . 13

3.1.1 Forme structurelle des garçons . . . 14

3.1.2 Forme structurelle des filles . . . 15

3.2 Stratégie d’identification et estimation . . . 16

4 Description des données de l’échantillon 21 5 Résultats d’estimation et interprétations 27 5.1 Effets endogènes . . . 28

5.2 Effets individuels et contextuels . . . 29

6 Conclusion 32

Bibliographie 35

(6)

(7)

A.1 Répartition des élèves en fonction des différentes caractéristiques dans les matières Français et Mathématiques . . . 39 A.2 Répartition des élèves en fonction des différentes caractéristiques

dans les matières Science et Histoire . . . 40 A.3 Statistiques descriptives sur les notes de Français et

Mathéma-tiques des élèves ayant passé l’examen de Juin 2005 . . . 41 A.4 Statistiques descriptives sur les notes de Science et Histoire des

élèves ayant passé l’examen de Juin 2005 . . . 42 A.5 Analyse des proportions d’élèves ayant des notes en dessous des

notes moyennes . . . 43 B.1 Résultat de l’impact des garçons et filles sur les performances

scolaires . . . 45 B.2 Résultat de l’impact des garçons sur la performance scolaires des

garçons . . . 46 B.3 Résultat de l’impact des filles sur les performances scolaires des

(8)

Introduction

L’analyse des interactions sociales dans les modèles économiques est un phénomène récent. Les effets d’interactions sociales, notamment les effets de pairs, correspondent aux effets résultant des relations interpersonnelles ayant une influence sur les comportements individuels.

La prise en compte de ces effets dans le cadre de l’analyse des comporte-ments économiques est au coeur des débats actuels. Leur internalisation dans cette sphère restreinte apparaît comme un moyen pour combler les insuffi-sances générées par les configurations partielles des modèles standards. Nom-breux sont les économistes qui ont souligné le rôle important joué par les pré-férences dans la détermination des comportements des agents économiques.

Avec l’avènement de nouvelles méthodes statistiques et la disponibilité des données devenue de plus en plus croissante, ce champ d’étude est devenu un sujet de premier choix auprès des économistes. Les travaux ont porté sur plusieurs domaines dont notamment l’éducation, la criminalité, l’obésité, la consommation de cigarettes, l’économie du travail, etc.

Ce mémoire met en évidence l’existence des effets de pairs en milieu sco-laire. De tels effets présentent un intérêt considérable pour les pouvoirs pu-bliques lorsqu’ils sont effectifs. Ils peuvent orienter de façon plus efficace les

(9)

politiques d’un système éducatif. Des politiques de mixité des élèves dans les classes ont été menées afin de favoriser une dynamique dans le processus d’ap-prentissage. Les effets de pairs peuvent aussi intensifier l’impact d’un pro-gramme à travers des effets multiplicateurs sociaux qu’ils génèrent. En effet, un programme de renforcement des capacités pourrait être bénéfique à des élèves ne faisant pas partie du programme à travers les effets du multiplicateur.

Nous allons, à l’aide d’un modèle linéaire en moyenne, montrer que des effets de pairs peuvent exister lorsque les élèves interagissent avec leurs cama-rades. Bien qu’il y ait plusieurs études sur le sujet, il existerait très peu d’ex-pansions sur les effets asymétriques.

En présence d’asymétrie dans les effets, l’impact sur les pairs est hétérogène. Ainsi, l’impact des résultats des bons élèves sur leurs pairs diffère de celui des moins bons élèves sur le reste de la classe. De même, il y a une asymétrie en ce qui concerne l’influence des résultats scolaires des garçons et des filles sur leurs pairs. En d’autres termes, les résultats scolaires des garçons et ceux des filles n’ont pas le même impact sur leurs pairs. Avec notre modèle économé-trique, nous envisagerons des configurations qui feront ressortir des aspects asymétriques selon le genre.

Cette recherche s’organise de la façon suivante. Dans le premier chapitre, nous présenterons une revue de littérature économique sur les effets de pairs. Nous évoquerons dans une première section les problèmes qui rendent diffi-cile l’identification des effets. Dans une seconde section, nous aborderons les différentes stratégies d’identification que recense la littérature.

Dans le second chapitre, nous présenterons notre démarche économétrique. Nous nous sommes inspirés des travaux deBramoullé et al.(2007) pour construire le modèle. Il s’agit d’un modèle linéaire en moyenne dans lequel nous distin-guons de façon séparée les effets de pairs filles et les effets de pairs garçons.

Nous présenterons dans le troisième chapitre les données utilisées pour quantifier ces influences. La base de données provient du Ministère de

(10)

l’Éduca-tion, du Loisir et du Sport de Québec. Nous avons utilisé le même échantillon que les travaux deBoucher et al.(2010) pour identifier nos effets. Nous discute-rons des résultats de la recherche dans le quatrième chapitre.

(11)

Revue de littérature

Au moment de la publication du rapport “Equity of Educational Opportu-nity”en 1966, personne ne se doutait que cela prendrait une proportion au-delà de toute espérance.

James Coleman et ses collaborateurs établirent les prémisses de l’influence par les pairs lorsqu’ils identifièrent les caractéristiques socioéconomiques et fa-miliales comme véritables déterminants des inégalités de chance de réussite aux États-Unis. On pouvait relever ainsi que la probabilité de réussite d’un élève quelle que soit sa race était conditionnée par la proportion des élèves de race blanche dans l’établissement (Moffitt 2001).

Plusieurs critiques furent adressées sur certains points du rapport. Si beau-coup restent sceptiques sur les vrais déterminants des réussites et échecs sco-laires, certains désapprouvent les procédures utilisées en raison des biais sta-tistiques occasionnés par la méthodologie employée. Des difficultés liées à la modélisation des effets de pairs vont contraindre beaucoup d’économistes à se désintéresser de ce champ d’études. Les travaux de Manski ainsi que d’autres économistes dans les années 90 vont contribuer à la recrudescence des efforts de vulgarisation.

(12)

2.1 Modélisation et critique de Manski

C’est à l’issue des travaux deManski(1993), que de véritables efforts seront consentis dans la modélisation des effets de pairs. Dans son article, il propose un modèle statique dans lequel il modélise le choix individuel en fonction du comportement du groupe de référence. Il ressort de cette interaction trois types d’effets que Manski met de l’avant dans son article. Il distingue l’effet endogène qui correspond à l’influence du comportement du groupe de référence sur le choix d’un individu. Un effet endogène positif signifie ceteris paribus que la per-formance d’un élève tend à influencer positivement la perper-formance des autres élèves du groupe (école, classe, quartier...etc). L’effet contextuel survient lorsque les caractéristiques exogènes des pairs ont un impact sur le comportement d’un individu. Un effet contextuel positif signifie que la réussite d’un élève varie dans le même sens que l’indice socio-économique du groupe auquel il appar-tient. Les effets corrélés sont difficilement mesurables et ils apparaissent en pré-sence de caractéristiques similaires inobservés que les individus d’un même groupe partagent. Les effets corrélés peuvent émerger même sans lien causal. Les effets endogènes et contextuels sont considérés comme phénomènes so-ciaux et présentent un intérêt en termes de politique publiques. Cependant la distinction de ces effets pose un véritable défi qui a été pendant de nombreuses années au coeur des débats sur les politiques éducatives.

LE PROBLÈME D’IDENTIFICATION

Le problème d’identification provient de la difficulté de pouvoir séparer, d’une part, les effets d’interactions sociales des effets corrélés, et d’autre part, les effets endogènes des effets contextuels. Les difficultés liées à l’identification de ces effets apparaissent en présence de simultanéité entre les comportements des individus et ceux de leurs groupes de références. Afin d’illustrer ce phé-nomène nous allons reprendre le modèle de Manski(1993). Ce dernier a servi de cadre d’analyse au développement de modèles statiques et dynamiques. Dans ce modèle, on évalue l’impact des pairs sur la performance des élèves en

(13)

estimant une fonction Y linéairement dépendante des caractéristiques indivi-duelles X, des caractéristiques E(X|g)du groupe et du résultat moyen E(Y|g)

comme suit :

Y =βE(Y|g) +α1X+α2E(X|g) +u (2.1)

Les paramètres α1, α2, et β sont respectivement l’effet individuel, contextuel et

endogène. Un terme d’erreur u est inclut pour compléter le modèle. En pré-sence d’interaction endogène positive (β 6= 0), le résultat moyen du groupe se retrouve parmi les variables explicatives dans la détermination des perfor-mances individuelles yi. Le problème de miroir (reflection problem) comme le

note Manski (1993) apparaît parce que le résultat moyen est lui-même déter-miné par les performances de chaque individu i si bien qu’il est difficile de sa-voir si c’est l’action individuelle qui exerce un impact sur le résultat de groupe, ou si c’est le groupe qui détermine le résultat de l’individu. Afin d’illustrer le problème, considérons le modèle suivant :

   yi =βyj+α1xi+α2xj+ui yj = βyi+α1xj+α2xi+uj (2.2)

où yi et yj représentent les résultats de i et j et xi et xj leurs caractéristiques

respectives. Le paramètre β capte l’effet endogène alors que α1 et α2 captent

respectivement les effets individuel et contextuel du modèle. Nous supposons également que le terme d’erreurs u n’est pas corrélé avec les variables xi et xj.

En effet :

E(u|xi, xj) =0

En présence de simultanéité, l’estimation par MCO des paramètres endogène et exogène du modèle (1.2) est biaisée puisque :

(14)

Ce résultat peut être facilement démontrer en utilisant les résidus de la forme réduite1Celle-ci est donnée pour i et j par la relation suivante :

           yi = α1 +βα₂ 1−β2 xi+α2 +βα₁ 1−β2 xj+vi vi = βuj+ui 1−β2 yj = α2 +βα1 1−β2 xi+ α1+βα2 1−β2 xj+vj vj = βui+uj 1−β2 (2.3)

Les paramètres identifiés à l’issue de l’estimation de l’équation (2.3) sont des paramètres composites qui englobent les effets endogènes et contextuels. Pour identifier les paramètres de la forme structurelle, il nécessaire d’utiliser les re-lations qui lient les paramètres du modèle (2.2) au modèle (2.3).Moffitt (2001) ainsi que d’autres chercheurs ont montré que les paramètres endogène et exo-gène ne peuvent être identifiés à partir de la forme réduite par MCO lorsque cov(yj, ui) 6=0, c’est à dire lorsque yjest endogène.

En effet4ui → 4vj qui à son tour se répercutera sur yjde la forme réduite. Il

apparait ainsi un biais d’endogénéité parce que le terme uiest corrélé avec yj.

L’environnement que partagent les individus peut présenter des facteurs qui affectent simultanément leurs comportements, leurs décisions ou même leurs résultats. Lorsque ces facteurs sont inobservés, et corrélés avec les carac-téristiques des individus, il apparait un second problème d’identification des effets de pairs : les paramètres composites (obtenus à l’issue de la régression par MCO de la forme réduite) ne pourront être utilisés pour retrouver les para-mètres de la forme structurelle. L’effet des caractéristiques inobservées (qualité de l’enseignement, ressources scolaires, ... etc.) peut être à l’origine de la ten-dance observée chez les élèves d’une classe ou d’une école en ce qui concerne leur réussite.

Un troisième problème d’identification apparaît lorsque les individus choi-sissent leurs groupes. C’est le cas lorsque les parents choichoi-sissent les écoles de leurs enfants, lorsque le personnel administratif assigne les élèves ayant des caractéristiques homogènes dans les mêmes classes : les bons élèves parmi les bons et les moins brillants ensembles. Ce critère d’assignation engendre un 1. La forme réduite exprime les variables dépendantes en fonction des variables explica-tives.

(15)

biais de sélection qui surestime les effets de pairs. Comme la sélection est en fait un problème d’effets corrélés, on parle également de sélection endogène des groupes.

2.2 Méthodes empiriques d’identification

Démêler les effets de pairs des autres influences est le défi que bon nombre d’économistes tentent jusqu’à présent de relever. Une première stratégie consiste à utiliser des données expérimentales afin d’éliminer les biais potentiels. Il s’agit d’expériences menées dans certaines grandes villes américaines où l’ef-fet d’une politique est analysée.Boozer et Cacciola(2001) etWhitmore(2005) ont utilisé les données du programme STAR2. Le projet avait pour but d’évaluer l’impact de la taille des classes sur la réussite académique. De telles expériences ont pour objet d’éliminer les biais dus aux facteurs inobservés en affectant aléa-toirement les élèves dans des classes ou dans les écoles.

Sacerdote(2001) etWinston et Zimmerman(2003) ont utilisé des données ran-domisées pour évaluer l’impact des caractéristiques des camarades de chambre sur la performance des nouveaux étudiants. Les auteurs ont estimé des effets significatifs et positifs de l’influence des caractéristiques des colocataires. Afin d’éliminer l’effet des facteurs inobservés responsable de la formation endogène des groupes, leurs stratégies reposaient sur l’assignation aléatoire des étudiants dans des dortoirs au Dartmouth College et au Williams College. En modélisant la note obtenue des nouveaux étudiants en fonction de la note des colocataires, Winston et Zimmerman (2003) trouve que les étudiants fraichement arrivés au Williams College ont une forte propension à intégrer une fraternité si leurs ca-marades de chambre en sont déjà membres. Sacerdote (2001) trouve pour sa part que la colocation améliore davantage les résultats des nouveaux étudiants lorsque ces derniers sont avec des étudiants assidus à leurs études. Les dortoirs et les chambres ne constituent pas les meilleurs environnements pour évaluer l’impact des pairs.Soetevent et Kooreman(2004) estiment que le comportement

(16)

et les préférences des élèves sont davantage modelés par des camarades de classes.Duflo et al.(2008) ont exploité les données d’une expérience réalisée en classe au Kenya pour identifier les effets de pairs.

En l’absence de données expérimentales, certains études ont eu recours à des méthodes d’appariement pour résoudre les problèmes d’identification. Ces techniques, consistent à intégrer dans le modèle, un ensemble de facteurs com-muns qui déterminent les performances des élèves. L’introduction des me-sures de ces variables, permet de capter les effets liées aux différences dans ces caractéristiques observables. Cependant, l’efficacité de cette méthode est remise en cause lorsque des caractéristiques difficilement mesurables (origines sociales, ensemble de valeurs transmises par les parents, ...etc), ne sont pas pris en compte et qui sont susceptibles d’affecter les performances des élèves. Aussi, cette stratégie ne traite pas le problème de simultanéité.Brock et Durlauf(2001) ont proposé des spécifications non linéaires pour solutionner le problème de simultanéité.

La technique des variables instrumentales reste la plus répandue dans les analyses lorsque les données ne permettent pas d’effectuer une randomisation. Cette stratégie s’appuie sur une source de variation exogène pour éliminer le biais d’endogénéité. Hoxby (2000) estime qu’une variation dans la composi-tion du genre est une source exogène crédible : elle ne dépend d’aucune dé-cision parentale. Elle trouve en effet qu’une augmentation de la proportion des filles d’une cohorte fait varier positivement la moyenne des élèves. En utili-sant les données provenant de plusieurs écoles primaires dans l’État du Texas, Hoxby (2000) démontre que le niveau moyen des élèves influence leurs résul-tats. D’autres études commeHanushek(2003) et al ont utilisé des valeurs retar-dées des caractéristiques des pairs comme source de variation exogène pour évaluer l’impact des pairs sur la réussite académique. Les auteurs ont validé le modèle en utilisant des données de panel. Ils ont aussi introduit des effets fixes à plusieurs niveaux (écoles, classes et individus) pour purger l’effet des carac-téristiques inobservées au cours de la période d’observation. Les résultats de leur étude ont montré qu’une augmentation d’un point dans la note moyenne en mathématiques des pairs améliore la note des élèves de 0,17.

(17)

L’approche par effets fixes a été utilisée aussi par Burke et Sass (2006) avec des données sur les écoles publiques de la Floride. Les auteurs ont trouvé dans leurs estimations que les effets sont moins importants lorsque l’effet fixe ensei-gnant est contrôlé. En effet une augmentation d’un point dans la note moyenne en mathématiques des pairs, améliore la note en mathématiques des élèves de 0,228 lorsque l’effet fixe enseignant n’est pas contrôlé et de 0,043 lorsque celui-ci est pris en compte.

Bien qu’il y ait divers travaux ayant discuté de l’existence des effets de pairs et de leurs conditions d’identification, très peu sont parvenus à séparer les ef-fets endogènes et exogènes. L’étude conduite parLee(2007) montre à l’aide d’un modèle linéaire en moyenne qu’on peut différencier les effets s’il y a suffisam-ment de variations dans la taille des groupes.

EFFETS ASYMÉTRIQUES

L’impact des pairs peut avoir des effets différents sur les bons et moins bons élèves. Schindler-Rangvid (2003) teste la présence d’une hétérogénéité dans la composition des groupes avec les données de l’enquête du PISA32000 au Da-nemark. Elle modélise plusieurs quantiles de la distribution des notes en litté-ratie et teste l’égalité des paramètres à différents points de la distribution. Les résultats mettent en évidence des différences significatives entre les quantiles extrêmes de la distribution. Schindler-Rangvid (2003) constate des effets substan-tiels de l’impact des pairs sur les moins bons élèves.4 Son modèle inclut dans les variables de contrôle des caractéristiques familiales responsables en grande partie de l’effet de sélection.

Schneeweis et Winter-Ebmer(2005) reprennent l’étude en introduisant des ef-fets fixes au niveau des écoles pour purger l’effet des caractéristiques inobser-vées. Avec des données autrichiennes, ils modélisent une fonction de produc-3. Program for International Student Assessment ou programme international pour le suivi des acquis des élèves

(18)

tion qui met en relation la note obtenue à l’examen du PISA et les variables suivantes : les caractéristiques individuelles, familiales et celles du groupe des pairs.5 Les résultats de leurs travaux montrent des effets de pairs significatifs et asymétriques à différents points de la distribution : les élèves en difficulté sont plus influençables par leurs pairs que les bons élèves.

La note obtenue est certainement l’élément qui distingue le bon du mau-vais élève dans cette étude.Lavy et al.(2008) s’appuient sur un critère autre que la note pour hiérarchiser les aptitudes des élèves. Ils trouvent que les résultats des élèves inscrits un an avant l’âge d’admissibilité sont meilleurs que ceux des élèves inscrits à l’âge normal. Ils assimilent les mauvais élèves à l’ensemble des élèves inscrits un an après leur âge d’admissibilité car leurs scores sont moins bons que ceux des élèves inscrits à l’âge normal. Lorsqu’ils évaluent l’impact de la qualité du groupe des pairs dans la détermination des performances indivi-duelles, ils constatent que les bons élèves n’ont aucun effet sur les performances des élèves réguliers mais que les mauvais élèves les affectent négativement.

Les effets de pairs masquent une hétérogénéité dans la composition du genre.Soetevent et Kooreman (2004), montrent dans une étude portant sur l’al-coolisme et le tabagisme, que les garçons et les filles n’ont pas les mêmes préfé-rences. Ils partitionnent les élèves en sous-groupes dans un modèle à choix dis-cret. Leurs estimations font apparaître des effets de pairs intra et inter-genre. Ils trouvent que les effets de pairs intra-genres sont plus larges que les effets inter-genre et que les garçons sont plus influençables que les filles.Lavy et al.(2009) utilisent les résultats des examens de fin de cycle dans les écoles anglaises pour partitionner les élèves en trois niveaux d’aptitudes. Ils construisent leurs indi-cateurs de mesure des effets de pairs sur la base de l’information collectée et comparent l’influence exercée par les plus brillants, les moyens et les moins ta-lentueux. Ils proposent des estimations non biaisées de l’impact des pairs avec des estimateurs à effets fixes. Les résultats indiquent que les élèves les plus talentueux affectent positivement la performance des filles (0,066) et négative-ment la performance des garçons (-0,052).6Les moins brillants affectent

néga-5. L’ensemble des élèves fréquentant la même école et ayant le même niveau scolaire 6. Une augmentation de 1% de la proportion des filles brillantes améliore le résultat des

(19)

tivement les résultats académiques des filles (-0,098) et des garçons (-0,076).7

filles de 0,077 point et réduit celui des garçons de 0,034. Une augmentation de 1% de la pro-portion des garçons talentueux améliore le résultat des filles de 0,037 point et réduit celui des garçons de 0,073.

7. Une augmentation de 1% de la proportion des filles moins brillantes réduit le résultat des filles et des garçons respectivement de 0,124 et 0,09 point. Une augmentation de 1% de la pro-portion des garçons moins talentueux réduit le résultat des filles et des garçons respectivement de 0,068 et 0,065 point.

(20)

Méthode économétrique

3.1 Présentation du modèle

Nous proposons une extension du modèle linéaire pour évaluer l’impact des pairs. Une analyse en terme de genre se proposera d’identifier les mesures dans lesquelles les effets peuvent être asymétriques. Nous nous inspirons des travaux deBramoullé et al.(2007) dont la forme structurelle du modèle est don-née par l’équation suivante :

yri =αr+β ¯yr−i+γxri+δ ¯xr−i+eri eri ∼ ℵ(0, σ2) (3.1)

Notre échantillon {i = 1, . . . M} est l’ensemble des élèves dont la performance est mesurée par la variable yri. La classe dont l’ensemble est {r = 1, . . . R} est

l’environnement dans lequel nous souhaitons étudier les effets de pairs. Nous supposons comme dans les travaux de Boucher et al. (2010) que les pairs de i sont les élèves dont le résultat académique et leurs caractéristiques indivi-duelles ont un impact sur son résultat académique. La performance moyenne du groupe r est donnée par la variable ¯yr−i1.

xri est un vecteur formé à partir des caractéristiques individuelles de i et

¯xr−i le vecteur formé à partir des caractéristiques moyennes de ses pairs.

(21)

αrest le paramètre qui capte l’effet des caractéristiques communes à tous les

élèves d’un même groupe.

E(eri|xr, αr) =0

Les effets d’interactions sociales (endogènes et contextuels) sont représentés respectivement par β et δ. L’effet des caractéristiques individuelles est capté par γ. Dans notre démarche nous allons élargir le modèle afin que les effets de pairs des filles puisses se différencier de ceux des garçons. L’effectif total des élèves observé dans un groupe mr peut être décomposé en ng garçons et nf

filles. Une décomposition des quantités ¯yr−i et ¯xr−i en fonction de ng, nf et mr

nous permettra d’observer deux formes structurelles : celle des garçons puis celle des filles.

¯yr−i = ∑i∈mr yri−yi

mr−1

Or ∑i∈mryri =∑i∈ngyig+∑i∈nf yi f =ng¯yg+nf¯yf

Ce qui implique ¯yr−i =

ng¯yg+nf¯yf

mr−1 ¯xr−i =

ng¯xg+nf¯xf

mr−1

3.1.1 Forme structurelle des garçons

En remplaçant ¯yr−i et ¯xr−i par leurs quantités respectives dans l’équation

(3.1), l’impact des pairs sur la performance des garçons est modélisé par :∀i ∈

ng,

yi=αr+βg f_mr−1n f ¯yf+βgg_mr−1ng−1¯y−i+γgxi+δg f_mr−1n f ¯xf+δgg_mr−1ng−1¯x−i+ei (3.2)

βg f et βgg apparaissent dans le modèle pour représenter les influences

endo-gènes respectivement des filles et garçons. βg f est l’effet du résultat moyen des

filles sur la réussite des garçons alors que βgg est l’effet qu’a le résultat moyen des garçons sur la réussite des élèves garçons. δg f est l’effet contextuel relatif

à l’influence des caractéristiques moyennes des filles. δgg est l’effet contextuel

(22)

des facteurs inobservables qui peuvent avoir un effet sur yidans le groupe r et

eri ∼ ℵ(0, σ2). La forme matricielle de l’équation (3.2) est donnée par :

yrg =1αr+βg fDryrf +βggGryrg+γgXgr +DrXrfδg f +δggGrXgr +erg (3.3)

où yrgde dimensions ng×1 comprend les performances des garçons dans chaque

groupe ; Xrde dimensions ng×k est la matrice formée par les k variables

expli-catives. E(e|x =0), E(ee0|x) = Σg 1=        1 1 .. . 1        ng×1 Dr = 1 mr−1     1 · · · 1 .. . . .. ... 1 · · · 1     ng×n f Gr = 1 mr−1        0 1 · · · 1 1 0 . .. ... .. . . .. 0 1 1 · · · 1 0        ng×ng

Suivant la formulation deBramoullé et al.(2007), Grest la matrice d’interaction

dont les éléments sont Gij = _m_r1−1 pour i 6= j et Gii = 0. La matrice d’écart

à la moyenne est donnée par la formule Jr = Ir − _n1_g101 avec Ir une matrice

identité de dimensions ng×ng. Pour (Ir−βggGr)inversible, la forme réduite

de l’équation est donnée par la relation qui suit :

Jrygr =JrXgr(Irγg+δggGr)(Ir−βggGr)−1+Jregr(Ir−βggGr)−1 (3.4)

3.1.2 Forme structurelle des filles

En remplaçant ¯yr−i et ¯xr−i par leurs quantités respectives dans l’équation

(3.1), l’impact des pairs sur la performance des filles est modélisé par :

∀i∈ nf,

yrf =1αr+βf gDrygr +βf fGryrf +γfXrf +DrXrgδf g+δf fGrXrf +erf (3.5) yrf de dimension nf ×1 est le vecteur qui indique les performances des filles

dans chaque groupe ; Xr de dimensions nf ×k est la matrice formée par les

k variables explicatives. Gr est une nouvelle matrice d’interaction de

dimen-sion nf ×nf. La matrice d’écart à la moyenne est donnée par la formule Jr = Ir −_n1_f101 avec Ir une matrice identité de dimensions nf ×nf. βf g et βf f

(23)

l’effet du résultat moyen des garçons sur la réussite des filles et βf f l’effet du

résultat moyen des filles sur la réussite des filles. δf g est l’effet contextuel qui

capte l’influence des caractéristiques moyennes des garçons sur la performance des filles. δf f capte l’influence des caractéristiques moyennes des filles sur la

performance scolaire des filles. Nous supposons que E(e|x=0), E(ee0|x) = Σf

1=        1 1 .. . 1        n f×1 Dr = 1 mr−1     1 · · · 1 .. . . .. ... 1 · · · 1     n f×ng Gr = 1 mr−1        0 1 · · · 1 1 0 . .. ... .. . . .. 0 1 1 · · · 1 0        n f×n f

L’inversibilité de (Ir−βf fGr) est nécessaire pour l’obtention de la forme

ré-duite qui est donnée par :

Jryrf =JrXrf(Irγf +δf fGr)(Ir−βf fGr)−1+Jrerf(Ir−βf fGr)−1 (3.6)

Dans notre modèle, les matrices Ir, Gret G2r pour les garçons et les filles sont

li-néairement indépendantes.Bramoullé et al.(2007) ont démontré l’identification des paramètres (αr, β, γ, δ) lorsque ces conditions sont satisfaites.

L’hypothèse d’une asymétrie dans les effets sera rejetée dans le cadre de notre étude si à l’issue des résultats d’estimation des modèles (3.2) et (3.3) nous obtenons d’une part que βgg = βg f = βf g = βf f = β et de l’autre que δgg =

δg f =δf g =δf f =δ.

3.2 Stratégie d’identification et estimation

Pour des raisons de commodité, nous allons présenter les étapes et condi-tions d’identification en considérant uniquement l’équation du modèle (3.2) car le processus est le même pour l’équation (3.3). Nous rappelons que l’équation (3.2) modélise l’impact des pairs garçons et filles sur la performance des gar-çons à travers la relation suivante :

(24)

La forme structurelle du modèle ne nous permet pas d’identifier les différents paramètres. Nous allons appliquer la transformation « within » afin d’obtenir la forme réduite du modèle. Soit ¯ygla moyenne de groupe pour les garçons. En

effet∀i∈ ng ¯yg =αr+βg f nf mr−1 ¯yf +βgg ng−1 mr−1 ∑−i∈ng ¯y−i ng +γg¯xg +δg f nf mr−1¯xf +δgg ng−1 mr−1 ∑−i∈ng ¯x−i ng +¯ei On sait que ∑−i∈ng ¯y−i ng = ¯yg ∑−i∈ng ¯x−i ng = ¯xg Ainsi : ¯yg =αr+βg f nf mr−1 ¯yf +βgg ng−1 mr−1 ¯yg+γg¯xg +δg f nf mr−1¯xf +δgg ng−1 mr−1¯xg +¯eg

Le modèle admet deux types d’effets fixes : il y’a αr qui est commun à tous

les individus du même groupe, ensuite les quantités βg f nf

mr−1¯yf et δg f

nf

mr−1 qui

sont communes à tous les garçons. En appliquant la transformation within, on élimine tous les facteurs susceptibles d’avoir un impact sur la variable d’intérêt yi. L’équation within du modèle(yi−¯yg)est donnée par la relation ci-dessous :

(1+ 1 mr−1βgg )(yi− ¯yg) = (γg− 1 mr−1δgg )(xi− ¯xg) + (ei−¯eg) (3.7) Posons y∗_i = (yi− ¯yg) x_i∗ = (xi− ¯xg) y∗_i = (γg(mr−1) −δgg mr−1+βgg )x_i∗+ mr−1 mr−1+βgge ∗ i (3.8)

Avec une équation puis trois inconnues, on ne peut pas récupérer les pa-ramètres du modèle. Pour que l’identification soit possible, il nous faudrait au

(25)

moins trois équations avec des tailles mr différentes.Bramoullé et al.(2007)

dé-montrent qu’en créant des variations dans la taille de groupe mr, on pourra

identifier les paramètres(βgg, δgg, γg).

La forme réduite de l’équation qui modélise l’impact des pairs garçons et filles sur la performance des filles est :∀i ∈nf

(yi− ¯yf) = ( γf(mr−1) −δf f mr−1+βf f )(xi− ¯xf) + mr−1 mr−1+βf f (ei−¯ef) (3.9)

L’estimation des paramètres du modèle sera conduite avec la méthode du maximum de vraisemblance.

Sous l’hypothèse de normalité des erreurs,

eri ∼ ℵ(0, σ2) Jre_ri ∼ ℵ(0, σ2(Ir− 1 ng1 0 1)) Ainsi Jryrg∼ ℵ(JrXgr (mr−1)γg−δgg mr−1+βgg , σ 2 g mr−1 mr−1+βgg [Ir− 1 ng1 0 1]) Soit : θ1 = (βggγg, δgg, σg); θ2= (βf f, γf, δf f, σf); Posons : ygr =Jry g r ; Xgr =JrX g r ; yfr =Jry f r ; Xfr =JrX f r

Suivant les notations deBramoullé et al.(2007) et deLee(2007), la vraisem-blance des garçons pour l’ensemble des groupes est donnée par :

L(yg1, yg2, ...ygR|m1, m2, ...mR, Xg1, Xg2, ...XgR, θ1) =

R

∏

r=0

(26)

La log vraisemblance est alors `₁ =c+_∑R_r₌₁(ng−1)log(mr−1+βgg) − (Ng −R 2 )log(σg2) − 1 2σ2 g ∑ R r=1( mr−1+βgg mr−1 ygr−Xgr (mr−1)γg−δgg mr−1 ) 0₍mr−1+βgg mr−1 ygr−Xgr (mr−1)γg−δgg mr−1 )

Sous l’hypothèse de normalité du terme d’erreur,

Jryrf ∼ ℵ(JrXrf (mr−1)γf −δf f mr−1+βf f , σ2_f mr−1 mr−1+βf f [Ir− 1 nf1 0 1])

La vraisemblance des filles pour l’ensemble des groupes est donnée par :

L(yf1, yf2, ...yfR|m1, m2, ...mR, Xf1, Xf2, ...XfR, θ1) =

R

∏

r=0

L(yfr|mr, Xfr, θ2)

La log vraisemblance est alors :

`₂ =c+_∑R_r₌₁(nf −1)log(mr−1+βf f) − ( Nf−R 2 )log(σ2f) − 1 2σ2_f ∑ R r=1( mr−1+βf f mr−1 yfr−Xfr (mr−1)γf−δf f mr−1 ) 0₍mr−1+βf f mr−1 yfr−Xfr (mr−1)γf−δf f mr−1 )

En maximisant les fonctions`₁et`₂séparément, on suppose que les groupes des garçons et des filles sont distincts. Or nous savons que dans notre modèle, nous pouvons avoir des garçons et des filles. La fonction de vraisemblance que nous maximisons est` = `1+ `2.

` =c+_∑R_r₌₁(ng−1)log(mr−1+βgg) − (Ng −R 2 )log(σg2) −_2σ12 g ∑ R r=1( mr−1+βgg mr−1 Jry g r −JrXgr (mr−1)γg−δgg mr−1 ) 0₍mr−1+βgg mr−1 Jry g r −JrXrg (mr−1)γg−δgg mr−1 )

(27)

+∑_rR₌₁(nf −1)log(mr−1+βf f) − ( Nf−R 2 )log(σ2f) − 1 2σ2_f ∑ R r=1( mr−1+βf f mr−1 Jry f r −JrXrf (mr−1)γf−δf f mr−1 ) 0₍mr−1+βf f mr−1 Jry f r −JrXrf (mr−1)γf−δf f mr−1 )

(28)

Description des données de

l’échantillon

L’échantillon que nous avons utilisé dans le cadre de cette recherche fut construit à l’issue de l’étude “Do peers affect student achievement ? Evidence from Canada using size variation”réalisée par Boucher et al.(2010). Il provient d’une base de données du Ministère de l’Éducation du Loisir et du Sport de Québec.

Pour construire l’échantillon, les auteurs ont tiré un échantillon aléatoire de 116 534 élèves parmi les 152 580 élèves inscrits aux examens de fin de pro-gramme du secondaire. Ces épreuves ministérielles ont lieu en Juin et Août mais la majorité des élèves passent ces épreuves durant la session de Juin. Ne disposant pas d’informations sur les candidats ayant passé les examens en Août de l’année 2005, les auteurs ont considéré uniquement les notes et ca-ractéristiques des élèves ayant passé les examens en Juin de l’année 2005. En examinant les tableauxA.1etA.2qui donnent les statistiques sur la répartition des élèves ayant passé l’examen dans les quatre disciplines à savoir Français, Science, Mathématiques et Histoire, nous pouvons faire le constat suivant :

L’échantillon renferme au total 167 587 observations. D’après le tableauA.1, il y a 41 778 notes en français dont 18 844 observations pour les filles et 22 934 pour les garçons. Les élèves ayant composé dans cette matière proviennent

(29)

essentiellement du secondaire 5 avec des taux de représentations de 98,24% chez les filles et 98,74% au niveau des garçons.

En Mathématiques nous avons enregistré 15 771 observations dont 7 260 au niveau des filles et 8 511 chez les garçons. Comme en Français, la plupart des élèves ayant composé dans cette discipline en Juin 2005 proviennent essen-tiellement du secondaire 5. Les taux de représentations sont respectivement de 93,72% et 97,44% en secondaire 5 pour les filles et les garçons. Les données du tableauA.1nous indiquent également qu’il y a moins de 12% d’élèves parlant une langue autre que le Français.

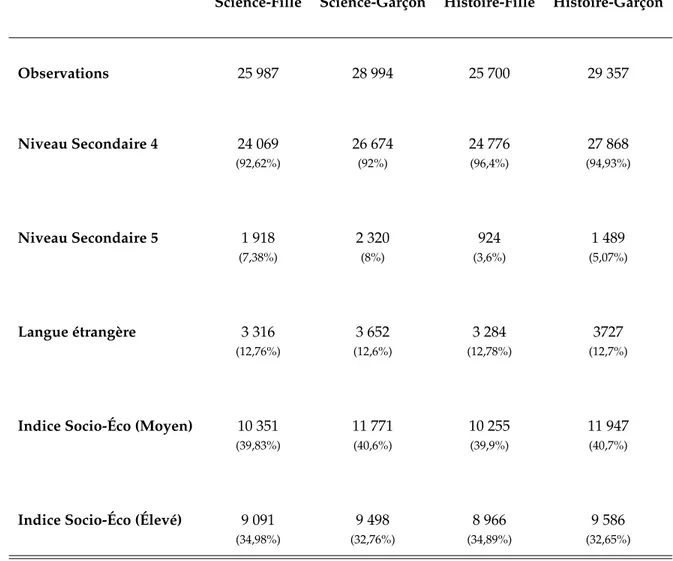
En Science 54 981 scores sont observés dont 25 987 chez les filles et 28 994 chez les garçons d’après le tableauA.2. Les filles et les garçons ayant composé dans cette discipline proviennent du secondaire 4. Les taux de représentations que nous avons enregistré à ce niveau d’étude sont respectivement de l’ordre de 92% et 92,62% chez les garçons et les filles. Toujours dans le même tableau, nous avons 55 057 observations en Histoire dont 25 700 pour les filles et 29 357 pour les garçons qui proviennent essentiellement du secondaire 4.

Les tableauxA.1et A.2, donnent également un aperçu de la répartition des notes en fonction de l’indice de milieu socio-économique. L’indice fut déve-loppé par le Ministère de l’Éducation du Loisir et du Sport de Québec à partir de deux variables : la proportion des familles dont les mères sont sous scola-risées dans une pondération de 2/3 et le taux d’inactivité parentale dans une pondération de 1/3. Le taux d’inactivité parentale correspond à la proportion de parents dont aucun ne travaille à temps plein. Les indices sont ensuite re-groupés puis classés suivant un rang décile. Plus ce rang est élevé (proche de 10), plus le milieu socio-économique est défavorable. Le ministère de l’Éduca-tion du Loisir et du Sport de Québec considère les trois premiers déciles comme étant les milieux les plus favorisés et les trois derniers déciles comme étant les milieux les plus défavorisés.

(30)

D’après les données du tableauA.1, 33,8% des filles et 31,86% des garçons qui avaient passé l’examen de français en Juin 2005 proviennent de milieux défavorisés, 40% des filles et 41% des garçons proviennent de milieux moyens. Parmi les filles issues des milieux défavorisés, 39,16% d’entre elles avaient des notes inférieures à la note moyenne des filles. Parmi l’effectif des garçons issus des milieux défavorisés, 33,38% d’entre eux avaient des notes inférieures à la note moyenne des garçons.

On note qu’environ 31% des filles ayant passé l’examen de Mathématiques de Juin 2005, proviennent des milieux défavorisés et 39% de milieux moyens. Dans le groupe des garçons, il y’a 29,39% qui proviennent de milieux défa-vorisés et 40,65% qui proviennent de milieux moyens. Nous avons remarqué que 44,34% des filles issues de milieux défavorisés et 48,9% des filles issues de milieux moyens avaient des notes de mathématiques en dessous de la note moyenne des filles. 44,94% des garçons issus des milieux défavorisés et 51,7% des garçons issus des milieux moyens avaient des notes de Mathématiques en dessous de la note moyenne des garçons.

D’après le tableau A.2, 34,98% des filles et 32,76% des garçons qui avaient passé l’examen de Sciences en Juin 2005 proviennent de milieux défavorisés. 40% des filles et environ 40,5% des garçons proviennent quant à eux de milieux moyens c’est à dire moins défavorisés. Parmi les filles issues des milieux défa-vorisés, 40,36% d’entre elles avaient des notes inférieures à la note moyenne des filles tandis que chez les filles issues des milieux moins défavorisés cette pro-portion était de l’ordre de 46,17%. Chez les garçons, il ressort dans le même ta-bleau que la proportion d’élèves ayant des notes supérieures à la note moyenne des garçons en sciences était plus élevée dans les milieux défavorisés que dans les milieux moyens.

On note également que 34,89% des filles et 32,65% des garçons qui avaient passé l’examen d’Histoire de Juin 2005 étaient issus de milieux défavorisés. Parmi les élèves issus de ces milieux, 41,41% de ces filles avaient aussi des notes (en Histoire) inférieures à la note moyenne des filles tandis que 41,19% des gar-çons avaient des notes inférieures à la note moyenne des gargar-çons. Le même

(31)

ta-bleau nous montre que 40% des filles et 41% des garçons ayant passé l’examen de Juin 2005 étaient issus de milieux moyens c’est à dire moins défavorisés. En comparaison par rapport aux milieux défavorisés, on retrouve une plus grande proportion d’élèves ayant des notes inférieures aux notes moyennes dans les milieux moins défavorisés : 48,46% des filles et 48,67% des garçons. La propor-tion des filles ayant des notes supérieures à la note moyenne des filles et qui proviennent des milieux moins défavorisés est de 51,54%. Dans le même temps, celle des garçons issus des mêmes milieux et ayant des notes supérieures à la note moyenne des garçons était de 51,33%.

Les données du tableauA.3enregistrent des notes moyennes en Français et en Mathématiques comprises entre 61,16 et 74,60 sur une échelle allant jusqu’à 100. La note moyenne en Français dans le groupe des filles s’élève à 70,25. Nous avons constaté que parmi les 18 844 observations enregistrées au niveau des filles, 44,04% étaient en dessous de 70,25 tandis que 55,96% étaient au dessus de cette note moyenne. Les filles ayant passé l’examen de Français enregistrent un écart type de 14,45 et des notes comprises entre 0 et 97. Légèrement supérieure à la note moyenne dans le groupe des filles, la note moyenne des garçons ayant composé l’examen de Français s’élève à 74,60. Parmi les 22 934 observations que nous avons enregistrées dans ce groupe, 38,88% étaient en dessous de cette note moyenne. Les notes sont en général comprises entre 0 et 97 avec un écart type d 13,46.

Toujours dans le même tableau, nous avons des notes en Mathématiques comprises entre 4 et 100 avec une note moyenne de 61,16 et un écart type de 15,72 dans le groupe des filles. Parmi les 7 260 scores observés chez les filles, 48,5% étaient en dessous de la note moyenne du sous groupe. Dans la même matière, chez les garçons les notes étaient comprises entre 0 et 100 avec un écart type 15,87 et une note moyenne de 62,87. Parmi les 8 511 scores observés chez les garçons, 47,98% d’entre eux étaient en dessous de cette note moyenne.

Les données du tableau A.4 enregistrent des notes moyennes en Science et en Histoire comprises entre 69,85 et 75,20 sur une échelle allant jusqu’à 100. Dans le groupe des filles, les notes en Science sont comprises entre 5 et 100 avec

(32)

une note moyenne de 74,11 et un écart type de 17,82. Parmi les 25 987 scores observés dans ce groupe, 45,58% étaient en dessous de la note moyenne. Dans cette même discipline, dans le groupe des garçons, les notes sont comprises entre 4 et 100. Parmi les 28 994 scores observés, 38,88% étaient en dessous de la note moyenne qui était établie à 75,20.

En Histoire, dans le groupe des filles, les notes sont comprises entre 4 et 100 avec un écart type de 16,86. Sur les 25 700 observations que nous avons enregistrées, 47,5% étaient inférieures à 75,20 qui est la note moyenne dans ce groupe. Par ailleurs, dans le groupe des garçons, et toujours en Histoire, les notes sont comprises entre 0 et 100 avec un écart type de 17,62. On note que sur les 29 357 scores que nous observons, 47,29% étaient en dessous de 69,85 qui est la note moyenne dans ce groupe.

L’examen des statistiques précédentes fait ressortir une forte proportion d’élèves en dessous des notes moyennes. Un aperçu des résultats du tableauA.5 nous montre que les proportions d’élèves ayant des notes en dessous des notes moyennes sont plus élevées parmi les élèves du secondaire 4 qui ont composé l’examen de Français et de Mathématiques. En effet on trouve en Mathéma-tiques que 61,18% des filles du secondaire 4 avaient des notes inférieures à 61,16, et 63,30% des garçons avaient des notes inférieures à 62,87. En Français c’est 76,81% des filles et 79,58% des garçons qui avaient des notes inférieures aux notes moyennes. Au secondaire 5, ces proportions sont revues à la baisse avec seulement 47,65% des filles et 47,58% des garçons en Mathématiques. La plupart des élèves ayant passé l’examen de Science et d’Histoire, l’ont fait lors-qu’ils étaient au secondaire 4. Ceux qui ont passé les examens au secondaire 5 ont eu de moins bonnes notes. C’est là bas aussi que nous avons relevé les proportions les plus élevées d’élèves en dessous des notes moyennes.

Les élèves parlant une langue étrangère (c’est à dire une langue autre que le français) représentent moins de 13% dans notre échantillon. Les statistiques révèlent qu’entre 46% à 53% de leurs effectifs avaient des notes inférieures aux notes moyennes dans les quatre disciplines.

(33)

Dans le groupe des filles, celles ayant un indice socio-économique moyen avaient moins de bonnes notes que celles qui avaient un indice socio-économique élevé. En Français, c’est 44,02% des filles ayant un indice socio-économique moyen qui avaient des notes en dessous de la note moyenne. En Mathéma-tiques c’est 48,91% et en Histoire c’est 48,46%. En comparaison avec celles ayant un indice socio-économique élevé, nous remarquons que seulement 39,16% d’entre elles avaient des notes inférieures à la note moyenne en Français ; 44,34% d’entre elles avaient des notes inférieures à la moyenne en Mathématiques. Le même constat est observé dans le groupe des garçons.

(34)

Résultats d’estimation et

interprétations

Nous avons utilisé les résultats dans cinq disciplines pour tester la significa-tivité des différents coefficients d’interaction. Les résultats sont consignés dans les tableauxB.1,B.2etB.3. Les paramètres estimés dans le premier tableau (B.1) sont issus du modèle qui estime conjointement les effets d’interaction des filles et des garçons. Nous avons reproduit dans les tableauxB.2 etB.3, les résultats de l’impact des garçons sur les performances des garçons et ceux l’impact des filles sur les performances des filles. Les coefficients qui sont significativement différents de zéro sont identifiés par un astérisque.

Dans les prochaines sections, nous allons procéder à l’interprétation de ces effets d’interactions. Nous nous intéresserons d’abord aux influences des effets endogènes, avant de passer aux interprétations des effets individuels et contex-tuels.

(35)

5.1 Effets endogènes

Nous avons mentionné auparavant que l’effet endogène est défini comme l’effet du résultat moyen du groupe sur la performance de chaque élève. Cet effet apparait dans chaque colonne du tableau à la première ligne.

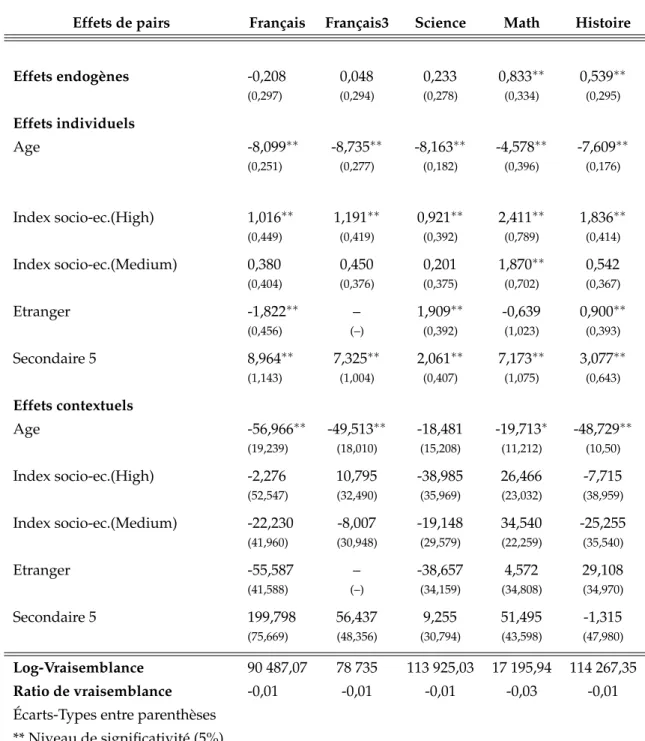
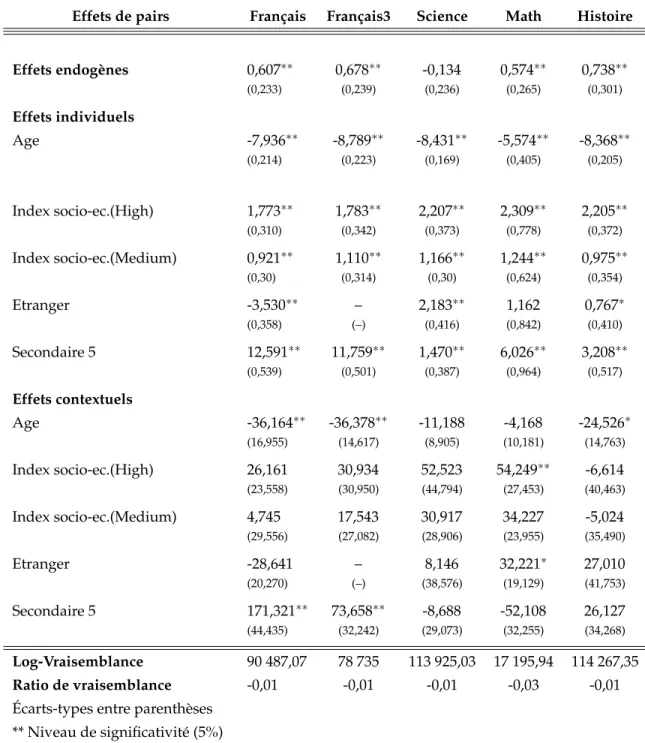
L’analyse des résultats du tableau B.1 montre que les notes moyennes en Mathématiques et en Histoire influencent de façon significative les performances des élèves. En Histoire par exemple, nous avons estimé un effet endogène po-sitif de 0,65. En effet une variation positive dans la note moyenne des autres élèves, toutes choses égales par ailleurs a un effet bénéfique sur la note de l’élève. Une analyse plus fine montre que dans les différentes matières, la si-gnificativité de l’effet endogène varie d’un sous échantillon à l’autre. L’effet en-dogène intra-genre dans le sous-groupe des garçons est seulement significatif en mathématiques. En effet d’après le tableau B.2, nous avons estimé en ma-thématiques chez les garçons un effet endogène et significatif de 0,833. L’effet endogène intra-genre dans l’échantillon des filles est significativement différent de zéro en Maths, Français et Histoire d’après le tableauB.3. Les paramètres es-timés dans ces matières sont tous positifs et sont respectivement de l’ordre de 0,574 ; 0,607 et 0,738 en Mathématiques, Français et Histoire. D’après les notes des élèves ayant passé l’examen de Juin 2005, c’est en Mathématiques que l’ef-fet endogène est significatif, non seulement dans l’échantillon, mais aussi dans les sous-groupes (garçons et filles) que nous avons défini. En examinant le de-gré de sensibilité de ces jeunes suites aux variations dans les notes moyennes de mathématiques, nous avons constaté que les garçons réagissent plus que les filles.

(36)

5.2 Effets individuels et contextuels

Les résultats présentés dans les tableaux B.2 et B.3 suscitent des commen-taires intéressants. Tout d’abord nous avons remarqué que la plupart des coef-ficients associés aux variables liées aux effets individuels sont significatifs et de signes positifs. Le signe négatif devant le coefficient de la variable âge indique plus l’âge des élèves augmente, moins ils ont de bonnes notes à l’école.

Concernant le statut socio-économique, on constate que les élèves ayant un indice élevé sont plus sensibles aux variations que ceux ayant un indice moyen. En effet comme le montrent les résultats du tableauB.1, le fait d’avoir un indice socio-économique élevé améliore de 2,01 les notes des élèves en His-toire. Alors que le fait d’avoir un indice socio-économique moyen améliore les notes des élèves en Histoires de seulement 0,795. Une comparaison intra-genre d’après les tableaux B.2 et B.3 nous montre que le fait d’avoir un in-dice socio-économique élevé a plus d’impact sur les notes des filles que sur les notes des garçons en Histoire. Nous avons estimé un effet de 2,205 dans le groupe des filles et 1,836 dans le groupe des garçons. En Mathématiques, l’impact de l’indice socio-économique élevé a plus d’effets sur les notes des garçons que sur les notes des filles. Nous avons estimé à ce niveau des coeffi-cients significatifs et positifs de l’ordre de 2,411 dans le sous-groupe des gar-çons et 2,309 dans le sous-groupe des filles. L’indice socio-économique moyen a aussi un impact significatif sur les performances des élèves d’après les ré-sultats du tableauB.1. Par ailleurs lorsque nous avons estimé les effets intra-genre, on a constaté que dans le sous-groupe des garçons, il n’est significatif qu’en Mathématiques. Dans le sous-groupe des filles, l’influence de l’indice socio-économique moyen est significatif dans les quatre matières.

Le niveau d’étude de l’élève est aussi un facteur déterminant les perfor-mances scolaires. Ainsi, le fait d’être en secondaire 5 améliore les notes dans toutes les matières dans le sous groupe des garçons comme dans celui des filles. Cependant, le fait d’être une fille en secondaire 5 a plus d’impacts sur les notes des filles en Français et Histoire. D’après le tableauB.3, les coefficients estimés

(37)

dans ce sous-groupe sont de l’ordre de 12,591 en Français et 3,208 en Histoire. Les mêmes estimations dans le sous-groupe des garçons ont donné des coef-ficients de l’ordre de 8,964 en Français et 3,077 en Histoire. Le fait d’être un garçon au secondaire 5 a plus d’impacts sur les notes des garçons en Science et en Mathématiques. D’après le tableauB.2, nous avons estimé un coefficient de 2,061 en Science, et un coefficient de 7,173 en Mathématiques. Les mêmes estimations dans le sous-groupe des filles a donné les résultats suivants : 1,470 en Science et 6,026 en Mathématiques.

L’estimation des effets contextuels a conduit à très peu de variables signi-ficatives. La variable âge figure parmi ces dernières. De signe négatif, le coef-ficient lié à cette variable indique que plus l’âge moyen des élèves de la classe augmente, moins les élèves auront de bonnes notes. En d’autres termes, plus les élèves sont âgés dans la classe, moins il y aura de bonnes notes. Dans le sous-groupe des garçons, une augmentation d’un an dans l’âge moyen rédui-rait toutes choses égales par ailleurs la note en français de 56,96. L’augmen-tation d’une année supplémentaire dans l’âge moyen des filles réduirait leurs notes de 36,164 dans la même matière.

Les coefficients liés aux statuts socioéconomiques, ceux liés au fait de ne pas parler le Français à la maison ainsi que le fait d’être en secondaire 5 ne sont pas significatifs chez les garçons. Chez les filles, l’indice socio-économique élevé est significatif et positif en Mathématiques. Nous avons trouvé aussi que le fait d’être en interaction avec les filles du secondaire 5 est significatif et positif en Français. D’après le tableauB.3, les coefficients significatifs estimés sont de l’ordre 54,249 en Mathématiques et 171,321 en Français.

TESTS D’HYPOTHÈSES

Nous souhaitons tester H0 :

βgg =βf f

γgg =γf f

(38)

Contre l’hypothèse alternative H1 : les coefficients sont tous différents. Sous H0, le Ratio de vraisemblance LR suit un Chi Carré χ(J)

LR= −2(log(L(θ∗) −log(L(θ))

Le modèle contraint comporte 14 variables alors que dans le modèle non contraint on en compte 28 variables. Les valeurs des fonctions de vraisemblances ainsi que les ratios de vraisemblances sont illustrées dans les tableauxB.2 etB.3. La valeur du ratio de vraisemblance étant inférieure à la valeur du Chi Carré lu sur la table, on ne peut pas rejeter l’hypothèse H0. En effet, on ne peut pas affirmer que le modèle non contrait est meilleur que le modèle contraint.

(39)

Conclusion

Nous avons présenté dans ce mémoire un schéma d’analyse s’inspirant des travaux récents pour identifier les effets de pairs en milieu scolaire. Le pro-cessus d’identification de ces effets est confronté aux problèmes de miroir (re-flection problem) et d’auto-sélection qui occasionnent des biais statistiques lors de l’estimation. Notre démarche empirique exploite la variation dans la taille des groupes comme source d’identification des effets endogènes et contextuels. Nous avons introduit des effets fixes pour purger l’effet des caractéristiques in-observées et avons estimé le modèle par la méthode du maximum de vraisem-blance.

Les résultats de cette recherche ont mis en évidence des effets significatifs de l’impact des pairs sur les performances des élèves de même genre. Nous avons trouvé chez les garçons des effets endogènes significatifs et positifs uniquement en mathématiques et en histoire. Par contre chez les filles, nous avons trouvé des effets endogènes significatifs et positifs en français, en mathématiques et en histoire. Toutefois, à l’exception de la variable Age, la plupart des coefficients relatifs aux effets contextuels ne sont pas significatifs.

L’analyse des effets de pairs soulève une question fondamentale en matière de reformes éducatives. Dans le but d’améliorer l’efficacité des méthodes d’ap-prentissage, quelle type de configuration serait convenable aux besoins des

(40)

élèves. En effet devrait-on opter pour un regroupement où les élèves sont assi-gnés dans les classes en fonction de leurs habiletés, résultats scolaires ou leurs sexes ? Epple et al. (2002) ont montré que le regroupement par habileté a un impact significatif sur les rendements des élèves. Selon les tenants de ce type de configuration, les élèves réussissent mieux lorsqu’ils sont assignés avec des camarades présentant les mêmes caractéristiques qu’eux. Le résultat est valide lorsque les élèves se trouvent dans des groupes présentant de fortes capacités intellectuelles. Dans les groupes à faible niveau intellectuel, les élèves subissent des effets négatifs qui font naître des inégalités et qui remettent en cause l’ef-ficacité de cette méthode. Les opportunités de recevoir un enseignement de bonne qualité peuvent différer à travers les groupes (Betts et Shkolnik(1999)). Le contenu des matières enseignées dans ces groupes, est généralement pré-senté de façon plus simpliste que dans les groupes où le niveau intellectuel est élevé. La diversité et l’hétérogénéité des élèves dans la classe s’avéreraient une pratique plus efficace pour corriger ces inégalités.Kang (2007) a montré dans une étude comparative que ce type d’organisation est plus efficient que le re-groupement homogène.

Selon Schneeweis et Winter-Ebmer (2005), le rôle des effets de pairs est de pouvoir relocaliser les élèves dans un environnement scolaire plus stimulant. En présence d’hétérogénéité dans les effets de pairs, on peut identifier les be-soins des différents groupes, réaffecter les ressources sans exiger de supplé-ments afin d’accroitre les performances des élèves. Il serait temps d’envisager des interventions ciblant les élèves issus des milieux défavorisés afin de ré-duire les inégalités des chances de réussites. Pour cela, il faut que les différents acteurs dans les milieux scolaires s’informent davantage sur les répercussions de ces effets sur le développement de l’élève. Il semble impératif de montrer que des gains d’efficacité peuvent être générés, puis bonifiés à travers les effets du multiplicateur en présence d’effets endogènes significatifs.

Nous avons estimé nos effets de pairs en intégrant les variables dans un modèle linéaire en moyenne. Ce type de spécification comporte des limites car il pourrait sous-estimer ou sur-estimer les effets lorsque l’effet moyen influence la variable d’intérêt de façon non linéaire. Nous avons certes estimé dans cette

(41)

recherche l’impact des filles sur les performances des filles et l’impact des gar-çons sur les performances des gargar-çons. Une autre limite que nous pouvons re-lever serait l’incapacité de notre modèle à estimer les effets croisés. En d’autres termes, notre modèle n’a pas estimé l’influence des filles sur les résultats des garçons et l’influence des garçons sur les résultats des filles. Dans les recherches à venir, il serait intéressant d’intégrer toutes ces limites dans des modèles plus avancés.

(42)

BETTS, J. R. et SHKOLNIK, J. L. (1999). The effects of ability grouping on student achievement and resource allocation in secondary schools. Economics of Edu-cation Review, 19(1):1–15.

BLUME, L. E., BROCK, W. A., DURLAUF, S. N. et IOANNIDES, Y. M. (2010). Iden-tification of social interactions. Economics Series 260, Institute for Advanced Studies.

BOOZER, M. A. et CACCIOLA, S. E. (2001). Inside the ’Black Box’ of Project STAR : Estimation of Peer Effects Using Experimental Data. Working Papers 832, Economic Growth Center, Yale University.

BOUCHER, V., BRAMOULLE, Y., DJEBBARI, H. et FORTIN, B. (2010). Do peers af-fect student achievement ? evidence from canada using group size variation. Cahiers de recherche, CIRPEE.

BRAMOULLÉ, Y., DJEBBARI, H. et FORTIN, B. (2007). Identification of peer effects through social networks. Cahiers de recherche 0705, CIRPEE.

BROCK, W. et DURLAUF, S. (2004). Identification of binary choice models with social interactions. Working papers 2, Wisconsin Madison Social Systems. BROCK, W. A. et DURLAUF, S. N. (2001). Discrete choice with social interactions.

Review of Economic Studies, 68(2):235–60.

BROCK, W. A. et DURLAUF, S. N. (2007). Identification of binary choice models with social interactions. Journal of Econometrics, 140(1):52–75.

BRODATY, T. (2010). Les effets de pairs dans l’éducation : une revue de littéra-ture. Revue d’économie politique, 120(5):739–757.

(43)

BURKE, M. A. et SASS, T. R. (2006). Classroom peer effects and student achie-vement. Working Papers wp2006, Department of Economics, Florida State University.

D’HAULTFOEUILLE, X., DAVEZIES, L. et FOUGÈRE, D. (2006). Identification of peer effects using group size variation. CEPR Discussion Papers 5865, C.E.P.R. Discussion Papers.

DUFLO, E., DUPAS, P. et KREMER, M. (2008). Peer effects, teacher incentives, and the impact of tracking : Evidence from a randomized evaluation in Kenya. NBER Working Papers 14475, National Bureau of Economic Research, Inc. EPPLE, D., NEWLON, E. et ROMANO, R. (2002). Ability tracking, school

compe-tition, and the distribution of educational benefits. Journal of Public Economics, 83(1):1–48.

GRAHAM, B. S. (2008). Identifying social interactions through conditional va-riance restrictions. Econometrica, 76(3):643–660.

HANUSHEK, E. A. (2003). Does peer ability affect student achievement ? Journal of Applied Econometrics, 18(5):527–544.

HOXBY, C. (2000). Peer effects in the classroom : Learning from gender and race variation. NBER Working Papers 7867, National Bureau of Economic Research, Inc.

KANG, C. (2007). Classroom peer effects and academic achievement : Quasi-randomization evidence from south korea. Journal of Urban Economics, 61(3): 458–495.

KOOREMAN, P. (2003). Time, money, peers, and parents : Some data and theo-ries on teenage behavior. IZA Discussion Papers 931, Institute for the Study of Labor (IZA).

LAVY, V., PASERMAN, M. D. et SCHLOSSER, A. (2008). Inside the black of box of ability peer effects : Evidence from variation in the proportion of low achie-vers in the classroom. NBER Working Papers 14415, National Bureau of Eco-nomic Research, Inc.

(44)

LAVY, V., SILVA, O. et WEINHARDT, F. (2009). The good, the bad and the ave-rage : Evidence on the scale and nature of ability peer effects in schools. NBER Working Papers 15600, National Bureau of Economic Research, Inc. LEE, L.-f. (2007). Identification and estimation of econometric models with

group interactions, contextual factors and fixed effects. Journal of Econome-trics, 140(2):333–374.

LEVIN, J. (2001). For whom the reductions count : A quantile regression analysis of class size and peer effects on scholastic achievement. Empirical Economics, 26(1):221–246.

MANSKI, C. F. (1993). Identification of endogenous social effects : The reflection problem. Review of Economic Studies, 60(3):531–42.

MOFFITT, R. (2001). Policy interventions, low-level equilibria, and social inter-actions. Edited by steven durlauf and peyton young, in Social Dynamics. SACERDOTE, B. (2001). Peer effects with random assignment : Results for

Dart-mouth roommates. The Quarterly Journal of Economics, 116(2):681–704.

SCHNEEWEIS, N. et WINTER-EBMER, R. (2005). Peer effects in Austrian schools. Economics Series 170, Institute for Advanced Studies.

SOETEVENT, A. R. et KOOREMAN, P. (2004). A discrete choice model with social interactions ; with an application to high school teen behavior. CCSO Wor-king Papers 200401, University of Groningen, CCSO Centre for Economic Research.

WHITMORE, D. (2005). Resource and peer impacts on girls’ academic achieve-ment : Evidence from a randomized experiachieve-ment. American Economic Review, 95(2):199–203.

WINSTON, G. et ZIMMERMAN, D. J. (2003). Peer effects in higher education. Williams Project on the Economics of Higher Education DP-64, Department of Economics, Williams College.

ZIMMERMAN, D. J. (2003). Peer effects in academic outcomes : Evidence from a natural experiment. The Review of Economics and Statistics, 85(1):9–23.

(45)

(46)

Tableau A.1 – Répartition des élèves en fonction des différentes caractéristiques dans les matières Français et Mathématiques

Français-Fille Français-Garçon Maths-Fille Maths-Garçon

Observations 18 844 22 934 7 260 8 511 Niveau Secondaire 4 332 289 456 218 (1,76%) (1,26%) (6,28%) (2,56%) Niveau Secondaire 5 18 512 22 645 6 804 8293 (98,24%) (98,74%) (93,72%) (97,44%) Langue étrangère 2 162 2 469 870 885 (11,47%) (10,77%) (11,98%) (10,40%)

Indice Socio-Éco (Moyen) 7 635 9 436 2 848 3 460

(40,52%) (41,14%) (39,23%) (40,65%)

Indice Socio-Éco (Élevé) 6 382 7 306 2 278 2 501

(33,87%) (31,86%) (31,38%) (29,39%)

(47)

Tableau A.2 – Répartition des élèves en fonction des différentes caractéristiques dans les matières Science et Histoire

Science-Fille Science-Garçon Histoire-Fille Histoire-Garçon

Observations 25 987 28 994 25 700 29 357 Niveau Secondaire 4 24 069 26 674 24 776 27 868 (92,62%) (92%) (96,4%) (94,93%) Niveau Secondaire 5 1 918 2 320 924 1 489 (7,38%) (8%) (3,6%) (5,07%) Langue étrangère 3 316 3 652 3 284 3727 (12,76%) (12,6%) (12,78%) (12,7%)

Indice Socio-Éco (Moyen) 10 351 11 771 10 255 11 947

(39,83%) (40,6%) (39,9%) (40,7%)

Indice Socio-Éco (Élevé) 9 091 9 498 8 966 9 586

(34,98%) (32,76%) (34,89%) (32,65%)

(48)

Tableau A.3 – Statistiques descriptives sur les notes de Français et Mathéma-tiques des élèves ayant passé l’examen de Juin 2005

Français-Fille Français-Garçon Maths-Fille Maths-Garçon

Note moyenne 70,25 74,60 61,16 62,87

% inf. à la note moyenne 44,04 38,88 48,50 47,98

% sup. à la note moyenne 55,96 61,12 51,50 52,02

Écart-type 14,45 13,46 15,72 15,87

Note minimale 0 0 4 0