HAL Id: hal-01527251
https://hal.archives-ouvertes.fr/hal-01527251
Submitted on 24 May 2017
HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
Une introduction à la théorie de la demande floue
Bernard Fustier
To cite this version:
Bernard Fustier. Une introduction à la théorie de la demande floue. [Rapport de recherche] Institut de mathématiques économiques (IME). 1982, 14 p., figures, bibliographie. �hal-01527251�
N°55
UNE INTRODUCTION A LA THEORIE DE LA DEMANDE FLOUE
Bernard FUSTIER Janvier 1982
Le but de cette collection est de diffuser rapidement une première version de travaux poursuivis dans le cadre de l'I.M.E. afin de provoquer des discussions scientifiques. Les lecteurs désirait entrer en rapport avec un auteur sont priés d'écrire à l'adresse
suivante: INSTITUT DE MATHEMATIQUES ECONOMIQUES
%VAUX DEJA PUBLIES
1 Michel PREYOT : Théorème du point fixe. Une étude topologique générale (juin 1974)
2 Daniel LEBLANC : L'introduction des consommations Intermédiaires dans le modèle de LEFEBER (juin 1974)
3 Colette BOUBON : Spatial Equilibrium of the Sector in Quasi-Perfect Competition (september 1974)
4 Claude PONSARD : L'imprécision et son traitement en analyse économique (septembre 1974)
5 Claude PONSARD : Economie urbaine et espaces métriques (septembre 1974) 6 Michel PREVOT : Convexité (mars 1975)
7 Claude PONSARD : Contribution à une théorie des espaces économiques imprécis (avril 1975)
8 Aimé VOGT : Analyse factorielle en composantes principales d'un caractère de dimension-n (juin 1975)
9 Jacques THISSE et Jacky PERREUR : Relation between the Point of Maximum Profit and the Point of Minimum Total Transportation Cost : A Restatement (juillet 1975)
10 Bernard FUSTIER : L'attraction des points de vente dans des espaces précis et imprécis (juillet 1975)
11 Régis DELOCHE : Théorie des sous-ensembles flous et classification en analyse économique spatiale (juillet 1975)
12 Gérard LASSIBILLE et Catherine PARRON : Analyse multicritère dans un con- texte imprécis (juillet 1975)
13 Claude PONSARD : On the Axiomatization of Fuzzy Subsets Theory (july 1975) 14 Michel PREVOT : Probability Calculation and Fuzzy Subsets Theory (august 1975) 15 Claude PONSARO : Hiérarchie des places centrales et graphes - flous
(avril 1 1976)
16 Jean-Pierre AURAY et Gérard DURU : Introduction à la théorie des espaces multiflous (avril 1976)
17 Roland LANTNER, Bernard PETITJEAN et Marie-Claude PICHERY : Jeu de simulation du circuit économique (août 1976)
18 Claude PONSARD : Esquisse de simulation d'une économie régionale : l'apport de la théorie des systèmes flous (septembre 1976)
19 Marie-Claude PICHERY : Les systèmes complets de fonctions de demande (avril l 1977)
20 Gérard LASSIBILLE et Alain MINGAT : L'estimation de modèles à variation dépendante dichotomique - La sélection universitaire et la réussite en première année d'économie (avril 1977)
1. 21 Claude PONSARD :
La région en analyse spatiale
(mai 1977)
�
0
22 Dan RALESCU :
Abstract
Models for Systems Identification
(juin 1977)
90 23 J. MARCHAL
et F. POULOT :
Multiplicateur,
graphes
et chaînes
de Markov
(décembre
1977)
40 24 Pietro BALESTRA :
Oeterminant
and Inverse
of a Sum of Matrices
with
Applications
in Economics
and Statistics
(avril
1978)
40 25 Bernard
FUSTIER :
Etude empirique
sur la notion
de région homogène
(avril 1978)
H9 26 Claude PONSARD :
On the Imprécision
of Consumer's
Spatial
Preferences
(avril 1978)
V 27 Roland LANTNER :
L'apport
de la théorie
des graphes
aux représentations
de l'espace
économique
(avril
1978)
N* 28 Emmanuel
JOLLES :
La théorie
des sous-ensembles
flous
au service
de la
décision :
deux exemples
d'application
(mai 1978)
IV°
29 Michel PREVOT :
Algorithme
pour la résolution
des systèmes
flous (mai 1978)
N° 30 Bernard
FUSTIER :
Contribution a
l'analyse
spatiale
de l'attraction
impré-
cise (juin 1978)
N° 31 TRAN QUI Phuoc : Régionalisation
de l'économie
française
par une méthode
de taxinomie
numérique
floue (juin 1978)
N° 32 Louis De MESNARD :
La dominance
régionale
et son imprécision,
traitement
dans le type général de structure
(juin 1978)
N° 33 Max PINHAS : Investissement
et taux
d'intérêt.
Un modèle stochastique
d'analyse
conjoncturelle
octobre 1978)
N° 34 Bernard
FUSTIER ,
Bernard
ROUGET :
La nouvelle
théorie
du consommateur
est-
elle testable ?
(janvier
1979)
.
N° 35 Didier DUBOIS :
Notes sur l'intérit
des sous-ensembles
flous
en analyse de
l'attraction
de points de vente (février
1979)
N° 36 Heinz SCHLEICHER :
Equity
Analysis
of Public Investments :
Pure and Mixed
Game-Theoretic
Solutions
(april
1979)
N° 37 Jean JASKOLD GABSZHWICZ :
Théories
de la concurrence
imparfaite :
illustra-
tions récentes
de thèmes
anciens
(juin 1979)
N° 38 Bernard
FUSTIER :
Contribution
à l'étude
d'un caractère
statistique
flou
(janvier
1980)
N° 39 Pietro BALESTRA :
Modèles de régression
avec variables
muettes
explicatives
(janvier
1980)
N° 40 Jean-Jacques
LAFFONT :
Théorie
des incitations
un exemple introductif
(février
1980)
N° 41 Claude PONSARD :
L'équilibre
spatial
du consommateur
dans un contexte
im-
précis (février
1980)
N° 42 Jean-Marie HURIOT : Rente foncière et modèles de production (avril 1980) N° 43 Claude PONSARD : Fuzzy Economic Spaces (april 1980)
N° 44 Alan KIRMAN : Imperfect Communication in Markets - A big world problem (april 1980)
N° 45 Michel PREVOT : Variétés différentielles (mai 1980)
N° 46 Claude PONSARD : Producer's spatial equilibrium with a fuzzy constraint (may 1930)
N° 47 Michel PREVOT : Théorie des catastrophes (mai 1980)
N° 48 Bernadette MARECHAL : Recherche de la forme d'un modèle à retards échelonnés application à la fonction d'investissement (novembre 1980)
N° 49 Bernard FUSTIER : Une méthode d'analyse multicritère, SPARTE, (mars 1981) N° 50 Jan SERCK-HANSSEN : On the Optimal Capital/Labour Ratios in Towns when
Demands for Outputs are Stochastic (may 1981)
N° 51 Claude PONSARD : Partial. Spatial Equilibria with Fuzzy Constraints (may 1981) N° 52 Xavier FREIXAS : Révélation des préférences dans l'allocation de biens
publics (juillet 1981)
N° 53 Bernard ROUGET : Equilibre spatial de consommation : quelques résultats (novembre 1981)
N° 54 Louis PHLIPS : Welfare and Price Discrimination : Optimal Departures from Uniform Pricing (november 1981)
N° 55 Bernard FUSTIER : Une introduction à la théorie de la demande floue (janvier 1982)
INTRODUCTION
Le graphique, dont nous reproduisons la photocopie ci-contre, ne provient pas d'un traité d'analyse économique moderne; il est extrait du "Cours d'Economie Politique" de Jean
MARCHAL (1). L'auteur considère que la demande prend la forme d'une "courbe-fuseau" lorsque la rationa- lité du consommateur s'affaiblit.
A l'heure où la théorie des sous-ensembles flous a donné ses premières applications en science économique, ce résultat est assez intuitif. Cependant, dans les lignes suivantes, nous pro- posons d'en rechercher la cause au niveau de l'imprécision qui caractérise les préférences du consommateur dont la rationalité devient, par ce fait, moins inhumaine que celle de l'homo-econo- micus.
En effet, nous savons que l'axiome d'existence d'un ordre pré- férentiel suppose un consommateur doté d'une supra-rationalité. Par exemple, une courbe d'indifférence étant l'expression d'une
infinité d'assortiments jugés équivalents, l'homo-economicus est censé pouvoir comparer un millième d'unité d'un bien X et dix unités d'un bien Y avec une infinité d'autres assortiments
de ces deux biens. Cet être de raison n'existe que pour la théorie économique, En réalité, les comparaisons et les choix s'effectuent sur des quantités qui n'ont pas la précision des nombres qu'elles représentent.
(1) J.MARCliAJ, "Cours d'Economie Politique" Tome 1 Librairie de Médicis. Paris. 11�52, 2d édition, p.559.
2
Après avoir rappelé le cadre traditionnel de la théorie de la demande (0), nous supposerons un consommateur capable d'effec- tuer des comparaisons entre des assortiments flous (I) c'est-à- dire de tenir pour équivalents "environ x unités du bien X avec un peu moins de y unités du bien Y" et "approximativement x' unités de X avec un peu plus de y' unités de Y". Une demande floue (II) dont la représentation graphique rappelle la "courbe- fuseau" de Jean MARCHAL, sera finalement dérivée en introduisant la contrainte budgétaire (au sens de la théorie traditionnelle des choix de consommation).
Cette rationalité "affaiblie" ne conduit pas à un appauvrisse- ment de la théorie de la demande. Au contraire elle débouche
sur un cas plus général où la courbe de la demande classique apparaît comme un cas particulier de l'expression graphique de la demande floue.
L'analyse des choix de consommation présentée dans cette intro- duction repose sur un exemple très simple qui ne fait pas appa- raître tous les concepts forgés par la théorie économique. Cette simplification s'imposait dans la mesure où il s'agit de dresser
présentement le cadre général de la théorie de la demande floue (1).
0 - ANALYSE TRADITIONNELLE DE LA DEMANDE - RAPPEL
Soit X et Y deux biens substituables dont les quantités consommées sont notées x et y respectivement. Les différentes valeurs de x et y sont combinées pour donner lieu à des assortiments jugés équivalents par un consommateur à un niveau donné d'utilité. Dans le plan xoy, un point A de coordonnées x et y définit un assortiment. Le ième assortiment, noté
Ai. est représenté par le couple (xi,yi). �
(1) ultérieurement nous nous proposons d'affiner les mécanismes du choix dans un environnement flou et de présenter certaines définitions élargies par la théorie des nombres flous (taux de substitution, élasticité, etc...)
3
D'après ce clui. précède, les variables x et y peuvent être assimi- liées 1 des caractères statistiques discrets dont les valeurs xi l et y. définissent des assortiments procurant le même niveau de satisfaction (ou d'utilité).
exemple 1.1. Le tableau suivant présente quelques assortiments jugés équivalents au niveau d'utilité U. puis U7
Pour une utilité d'ordre U les assortiments sont reliés par des segments de droite. Le résultat obtenu donne une approximation d'une courbe d'indifférence (cas continu) qui représente le lieu de toute les combinaisons des deux biens associés au même niveau de satisfaction (figure 1). La carte d'indifférence du consomma- teur est décrite par une série de courbes d'indifférence corres- pondant chacune à des utilités d'ordre d'autant plus élevé que la courbe d'indifférence se situe davantage vers le haut de la carte. On notera, enfin, que les courbes déduites du tableau précédent satisfont aux propriétés habituelles (convexité, deux courbes d'indifférence ne se coupent pas).
Toutefois, le champ de préférence du consommateur se trouve limité par ses disponibilités monétaires. La zone des assorti- ments accessibles est délimitée par la ligne de budget exprimée par l'équation R = x Py + y py
(R représente le revenu du consommateur, py et pY les prix uni- taires respectifs des biens X et Y). Lorsque le consommateur dépense l'intégralité de son revenu à l'achat des deux biens,
5
1'optimum est obtenu au point de tangence de 1a ligne de budget avec la courbe d'indifférence la plus élevée. (:'cst en ce point qu'il maximise son utilité.
Exempte 1.2. (cf . f igure 1). Soit pX = 4, py = 1 et R = 9. La ligne de budget représentée par la droite BC a pour équation y = - 4x + 9. L'équilibre est atteint au point A2 x = 1
1 Y = 5 Exemple 1.3. (cf.figure 1). On pose Px = 0,75 toutes choses égales par ailleurs. La nouvelle équation de la ligne de budget représentée par BC' est donnée par y = - 0,75 x + 9. Dans ces conditions, le consommateur maximise son utilité en choisissant l'assortiment
A3 Sx = 4
3 y = 6 ,
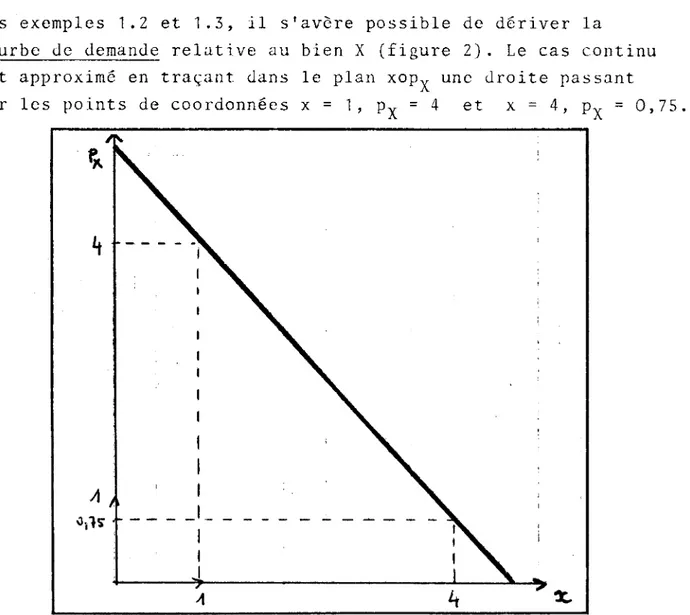
Des exemples 1.2 et 1.3, il s'avère possible de dériver la courbe de demande relative au bien X (figure 2). Le cas continu est approximé en traçant dans le plan xopx une droite passant
par les points de coordonnées x = 1, pX = 4 et x = 4, pX = 0,75.
6
I - ASSORTtMHNT tn,ou
La définition d'un assortiment flou repose sur la notion de nombre flou qu'il convient de rappeler et d'appliquer à l'ana- lyse des choix de consommation.
1.1 - Nombre flou
On considère maintenant que x etc sont des caractères statis- tiques flous (1) dont les valeurs, notées x_ et v, sont des nombres flous et représentent les quantités consommées de biens X et Y. Dans l'analyse des choix de consommation, les nombres flous prennent leurs valeurs dans l'ensemble des entiers posi- tifs N'.
I)ans ces conditions le nombre flou x. est défini par le sous- ensemble flou de N+ tc 1 que:
~1
où f et g désignent les fonctions d'appartenance des valeurs x et y aux nombres flous x. et y. respectivement. f(n) (respecti- vement g(n)) s'interprète comme le degré de plausibilité de la proposition "�i vaut x" (resp. "y. vaut y"). On impose qu'une valeur de N au moins soit telle que f(x) = 1 (resp. g(x) = 1); cette valeur est appelée valeur la plus plausible du nombre
flou cons.i.déré (2).
On conviendra d'appeler diagramme caractéristique d'un nombre flou x-, la représentation graphique des valeurs de la fonction
d'appartenance. Dans le cas le plus général on a:
(1) Pour un approfondissement de la notion de caractère statistique flou, cf. B.FUSTIER "Contribution à l'étude d'un caractère statistique flou". Document de Travail de l'I.M.E.,n°38, janvier 1980.
7
Figure 3. Diagramme caractéristique d'un nombre flou
c � x � a : f croissante au sens large
a � x � b : f(x) = 1 (la valeur la plus plausible est comprise entre a et b)
b � x � d : f décroissante au sens large.
Notons que si a = b = c = d = x* , , alors x. est un nombre entier ordinaire valant exactement x , car f(x) - 1 pour x = x et
f(x) = 0 �ix � x*; le nombre flou généralise le nombre classique (à condition toutefois que la fonction d'appartenance prenne la valeur 1 pour la valeur la plus plausible).
Exemple 2.1. Le tableau ci-dessous généralise l'exemple 1.1 en ce sens que, pour chaque nombre flou, les valeurs les plus plau- sibles coïncident avec les valeurs xi et y. du tableau précédent. Pour éviter une surcharge inutile, les valeurs associées à un degré de plausibilité nul ne sont pas prises en compte dans les nombres flous considérés (les applications ultérieures ne seront pas altérées par cette simplification).
8
1.2 - Couple flou. Assortiment flou
Par extension, un assortiment flou, noté Ai , est représenté par le couple de nombres flous (x.,y.). Il s'ensuit que A. est un sous-ensemble flou de N x N tel que:
Ai - ((x,y), h(x,y)) V (x, y) E N+ x N+
avec h(x,y) = f(x) A g(y) = degré de plausibilité du couple (x,y) au sous-ensemble flou Ai (resp. au couple flou (Ni'Yi)).
L'emploi de l'opérateur A se justifie dans la mesure où la défi- nition proposée ci-dessus généralise la notion de couple au sens traditionnel du terme.
9
Figure 4a - Diagramme caractéristique d'un couple (assortiment) flou (le couple (x ,y ) est l'él6ment le plus plausible: li(x O)YO) = 1)
Mais par la suite, nous adopterons la représentation simplifiée
ci-dessous:
Figure 4b - Représentation simplifiée d'un couple flou
Exemple 2.2. Les degrés de plausibilité des éléments de 1 sont donnés dans le tableau suivant:
10
L'ensemble des assortiments flous de l'exemple 2.1 1 est repré- senté sur la figure 5.
En reliant les points extrêmes de chaque assortiment flou pour un même niveau d'utilité, on obtient une approximation d'une
courbe d'indifférence floue. On vérifie que l'ensemble des valeurs les plus plausibles d'une telle courbe correspond à la courbe
classique traçée à partir de l'exemple 1.1 (ces courbes apparais- sent en trait plein sur la figure 5); la courbe floue généralise la courbe d'indifférence de la théorie traditionnelle.
II - DEMANDE FLOUE
II.1. Analyse des choix de consommation dans un environnement flou
En introduisant dans le schéma précédent la contrainte budgétaire (au sens traditionnel de la théorie des choix de consommation), l'équilibre du consommateur ne comporte généralement pas une solution unique.
11
Figure 5 - Analyse des choix de consommation dans un environnement flou
12 2
Exemple 2.3. Considérons la quantité demandée du bien X pour les données suivantes:
pX =
2, py = 1, R = 9. La ligne de budget a pour équation y = - 2x + 9 (cf.droite (2) sur la figure 5). Deux solutions apparaissent x = 2 au degré 0,5 et x = 3 au degré 0,6. Nous conviendrons de présenter les résultats sous la forme suivante
�2/0,5)(3/0,6)j .
D'après ce qui précède la quantité demandée du bien X, notée x(PX)' pour un prix donné de celui-ci est un sous-ensemble flou
de N : 1 1
Remarque : même si la valeur de �(x) est donnée par un degré de plausibilité h(x,y), x(pX) n'est pas rigoureusement assimilable à un nombre flou, car il n'y a aucune raison pour que �(x) prenne la valeur 1 pour chaque sous-ensemble flou considéré. ti(x) s'interprète plus généralement comme le degré d'appartenance de l'élément x au sous-ensemble flou
x(pX) au sens de ZADEH.
1I.2. Dérivation de la demande floue du bien X
Exemple 2.4. Pour pY = 1, R = 9 et pX variant, on obtient les résultats suivants (figure 5):
Soit R+ l'ensemble des valeurs prises par p.. Etant donné que le prix est considéré ici comme un nombre réel positif ordinaire, on peut écrire:,
13
Dans ces conditions, un point de la demande floue, note
A(pX) , correspondant au prix pX et à la quantité demandée à ce prix est défini par le sous-ensemble flou de N+ x R+ . :
%
Exemple 2.5. Pour pX = 2, les degrés d'appartenance des éléments de A(2) sont donnés dans le tableau ci-dessous:
On vérifie de même que A(4) =
�(1)4)/1)j : : ce point n'est pas flou.
L'ensemble des points déduits de l'exemple 2.4 est reporté sur la figure 6 qui donne une approximation de la demande floue dans le cas continu.
14
On vérifie que la demande de la théorie traditionnelle est un cas particulier de la courbe de la demande floue (la première est obtenue en reliant les éléments dont le degré d'appartenance est égal à 1).