Transferts thermiques instationnaires : vers une optimisation de parois de bâtiments

THESE

en vue de l’obtention du

DOCTORAT DE L’UNIVERSITE DE TOULOUSE

délivré par l’Université Paul Sabatier

Discipline : Energétique et Transferts

présentée et soutenue

par

Vincent SAMBOU

le 05 février 2008

_____________

Transferts thermiques instationnaires :

vers une optimisation de parois de bâtiments

_____________

JURY

M. Stéphane LASSUE

Rapporteur

M.

Guy

LAURIAT

Rapporteur

M.

Mamadou

ADJ

Examinateur

Mme Samira KHERROUF

Examinateur

M. Abdelkader MOJTABI

Examinateur

Mme Françoise STRUB

Invitée

Mme Bérangère LARTIGUE Directrice

de

thèse

Mme Françoise MONCHOUX

Directrice de thèse

Laboratoire PHASE (Physique de l’Homme Appliquée à Son Environnement) 118, route de Narbonne 31062 Toulouse cedex 9

A mes enfants

Séréna,

Samy

et Juliette

et à mon épouse

Jeanne

pour toutes les souffrances endurées

lors de mes absences

A ma mère

Remerciements

Deux sentiments m’animent au moment d’écrire ces mots. Le premier sentiment est l’immense joie d’avoir mené à terme ce travail. Le second sentiment est la peur d’oublier dans ces remerciements quelqu’un qui de près ou de loin a contribué à l’aboutissement de ce projet.

Je tiens à adresser, dans un premier temps, mes vifs remerciements au Professeur Françoise MONCHOUX de m’avoir fait confiance en acceptant de me confier ce sujet. J’espère simplement ne lui avoir pas déçue.

Je voudrais également remercier très sincèrement Madame Bérangère Lartigue, Maître de Conférences au Laboratoire PHASE, qui a dirigé avec rigueur ce travail. Par ses qualités humaines exceptionnelles, elle a su rendre moins difficiles mes séjours à Toulouse. J’espère que la fin de cette thèse n’est que le début d’une collaboration sans cesse grandissante.

Je remercie vivement Monsieur Mamadou ADJ, Professeur à l’Ecole Supérieure Polytechnique de Dakar, pour son soutien infaillible et pour m’avoir fait l’honneur de juger ce travail.

Mes remerciements s’adressent aussi à Monsieur Guy LAURIAT, Professeur au Laboratoire LETHEM de l’Université de Marne-le-Vallée, de m’avoir fait l’honneur d’accepter de rapporter cette thèse.

Je remercie également Monsieur Stéphane LASSUE, Professeur au Laboratoire LAMTI de l’Université d’Artois, pour l’honneur qu’il m’accorde en acceptant d’être rapporteur de ce travail.

Je tiens à remercier Kader MOJTABI, Professeur à l’IMFT de Toulouse, d’avoir accepté de juger ce travail.

J’associe à mes remerciements Mme Françoise STRUB de l’Association Planète Bois, pour l’honneur qu’elle me fait en participant à ce jury.

Je remercie également Madame Samira KHERROUF de l’ADEME d’avoir accepté de juger ce travail.

Mes vifs remerciements vont vers le Professeur Vincent GIBIAT, Directeur du Laboratoire PHASE, laboratoire dans lequel je ne me suis jamais senti étranger.

Je n’oublie pas dans ces remerciements mon voisin de bureau Jean Louis Breton, Professeur émérite au Laboratoire PHASE, qui a accepté de corriger ce document.

Je remercie également les deux Pierre du Laboratoire (TELLA et De GUIBERT), pierres sur lesquelles j’ai bâti la partie expérimentale et de simulation de cette thèse. Je n’oublie pas Marc

BEGUE et Fabien NOUGAROLLES, tous deux techniciens à l’INSA de Toulouse pour l’aide précieuse qu’ils m’ont apporté pendant la partie expérimentale de cette thèse.

Mes pensées vont vers Isabelle MINIER, secrétaire du Laboratoire PHASE, à qui j’adresse mes sincères remerciements. Je lui souhaite un prompt rétablissement.

J’associe à ces remerciements Monsieur Alain TROMBE, Professeur à l’INSA, pour le soutien qu’il m’a apporté lors de la phase expérimentale de cette thèse.

Je tiens également à remercier Madame Françoise TELLIER, Professeur au Laboratoire PHASE. J’espère pouvoir un jour travailler avec elle sur la qualité des ambiances.

Lors de cette aventure toulousaine, j’ai côtoyé des personnes admirables. Il s’agit, dans le désordre, de : Sandra, Valérie, Estelle, Benjamin, Sébastien, Pascal, … A tous je dis simplement merci pour tout.

Je ne saurai terminer ces remerciements sans associés les autorités de mon établissement. Au Directeur de l’Ecole Supérieure Polytechnique j’adresse mes sincères remerciements pour le soutien qu’il m’a accordé tout au long de cette thèse.

Ces remerciements s’adressent aussi à toutes les personnes qui, de près ou de loin, m’ont soutenu. Je pense particulièrement à mon collègue et ami Cheikh M. Fadel KEBE du CIFRES (Centre International de Formation et de Recherche en Energie Solaire).

Table des matières

Remerciements...i

Table des matières ...iii

Nomenclature ...vii

Liste des figures ...xi

Liste des tableaux ... xvii

Introduction générale... 1

Chapitre I Méthodes d’analyse ... 3

I-1 Introduction ... 3

I-2 La méthode des quadripôles... 3

I-2-1 Principe de la méthode : résolution de l’équation de la chaleur en régime variable ... 4

I-2-2 Résolution de l’équation de la chaleur monodimensionnelle en régime périodique établi .... 7

I-2-3 Caractéristiques dynamiques d’une paroi soumise à des sollicitations sinusoïdales ... 16

I-3 Optimisation par algorithme génétique ... 24

I-4 Conclusion ... 25

Chapitre II Optimisation thermique et étude thermodynamique d’une paroi de bâtiment... 27

II-1 Introduction ... 27

II-2 Revue bibliographique ... 28

II-3 Optimisation d’une paroi multicouche par rapport à l’isolation thermique et l’inertie thermique ... 33

II-3-1 Recherche d’une paroi idéale ... 33

II-3-2 Optimisation d’une paroi réelle ... 37

II-3-3 Conclusions ... 45

II-4 Etude thermodynamique d’une paroi ... 46

II-4-1 Méthode de calcul de la production d’entropie ... 46

II-4-2 Production d’entropie d’une paroi monocouche ... 48

II-4-3 Relation entre minimum de production d’entropie et inertie thermique... 50

II-4-4 Production d’entropie d’une paroi multicouche ... 52

II-4-5 Production d’entropie d’une paroi soumise à des conditions aux limites de type Neumann ... 55

II-4-6 Conséquence énergétique de la production d’entropie... 57

II-4-7 Conclusions ... 59

Chapitre III Transferts thermiques à travers une cavité partitionnée en régime permanent ... 61

III-2 Etude expérimentale de la cavité partitionnée ... 64

III-2-1 Description ... 64

III-2-2 Validation du caractère bidimensionnel ... 68

III-3 Etude numérique de la cavité partitionnée... 70

III-3-1 Description de la cavité partitionnée... 70

III-3-2 Modélisation numérique de la cavité partitionnée... 71

III-3-3 Résultats numériques et analyse... 76

III-4 Modèle simplifié 1D des transferts thermiques à travers la cavité partitionnée ... 87

III-4-1 Description du modèle ... 87

III-4-2 Validation du modèle simplifié 1D ... 91

III-4-3 Sensibilité de la résistance thermique à certains paramètres ... 95

III-4 Conclusions ... 103

Chapitre IV Transferts thermiques à travers une cavité partitionnée en régime variable... 105

IV-1 Introduction ... 105

IV-2 Revue bibliographique ... 105

IV-3 Etude expérimentale ... 107

IV-3-1 Description du protocole expérimental ... 107

IV-3-2 Détermination expérimentale de la capacité thermique ... 113

IV-3-3 Résultats expérimentaux et analyse... 114

IV-4 Etude numérique de la cavité partitionnée en régime variable ... 128

IV-4-1 Présentation du modèle ... 128

IV-4-2 Comparaison des résultats expérimentaux et numériques ... 131

IV-4-3 Analyse des phénomènes de transferts thermiques ... 136

IV-4-4 Conclusions... 141

Chapitre V Conception d’un élément alvéolaire de paroi du bâtiment ... 143

V-1- Introduction... 143

V-2 Modèle simplifié 1D des transferts thermiques à travers la cavité partitionnée en régime variable... 143

V-2-1 Présentation du modèle simplifié 1D ... 143

V-2-2 Validation expérimentale du modèle simplifié 1D... 144

V-2-3 Validation numérique du modèle simplifié 1D ... 146

V-3 Evaluation de la capacité thermique d’une cavité partitionnée ... 155

V-3-1 Influence du nombre de cloisons ... 155

V-3-2 Influence de l’épaisseur des parois extérieures... 156

V-3-3 Influence de l’épaisseur des cloisons... 157

V-4-1 Les objectifs et les contraintes de l’optimisation ... 159 V-4-2 Résultats de l’optimisation... 160 V-5 Conclusions ... 164 Conclusion et perspectives ... 165 Annexe 1 ... 169 Annexe 2 ... 173 Annexe 3 ... 173 Annexe 4 ... 175 Annexe 5 ... 179 Annexe 6 ... 183 Références bibliographiques ... 187

Nomenclature

Symbole Signification unité

a Diffusivité thermique [m2.s-1]

A Rapport d’allongement

(A, B, C, D) Eléments de la matrice de transfert inverse

Am Facteur d’amortissement

C Capacité calorifique massique [J.kg-1.K-1] Cp Capacité calorifique massique à pression constante [J.kg-1.K-1] Cth Capacité calorifique surfacique [J.m-2.K-1]

d profondeur [m] e Epaisseur [m] g Accélération de la pesanteur [m.s-2] H Hauteur [m] I Luminance directionnelle [W.m-2] I* Luminance adimensionnelle J Flux d’entropie [W.m-2.K-1] kr Rapport de conductivités L Largeur [m] M Nombre d’alvéoles N Nombre de cloisons Nr Nombre de radiations Nu Nombre de Nusselt p Pression [Pa] P Pression adimensionnelle P Période [s] Pr Nombre de Prandtl

r Résistance thermique pour une unité de surface [m2.K.W-1]

R Résistance thermique [K.W-1]

S Surface [m2]

t Temps [s]

T Température moyenne [°C]

(u, v, w) Composantes de la vitesse [m]

(U, V, W) Composantes adimensionnelles de la vitesse

u Transmittance cyclique [W.K-1.m-2]

(x, y, z) Variables d’espace [m]

(X, Y, Z) Variables adimensionnelles d’espace

y Admittance [W.K-1.m-2]

Z Impédance [m2.K.W-1]

Lettres grecques

Symbole Signification unité

β Coefficient de compressibilité [K-1]

δ profondeur [m]

∆Τ Amplitude des variations de la température [°C]

∆Sirr Production d’entropie [J.m

-2 .K-1]

ε Emissivité

φ Flux [W]

φ Flux complexe

Φ Transformée de Laplace du flux

ϕ Densité de flux [W.m-2]

λ Conductivité thermique [W.m-1.K-1]

Λ Longueur d’onde de propagation thermique [m]

µ Viscosité dynamique [Pa.s]

ν Viscosité cinématique [m2.s-1]

θ Température adimensionnée

θ Température complexe

Θ Transformée de Laplace de la température

ρ Masse volumique [kg.m-3]

σ Constante de Stefan-Boltzmann [W.m-2.K-4]

τ Temps adimensionné

ω pulsation [rad.s-1] Ω Angle solide [Sr] Indice a air C chaud cd conductif cv convectif e entrée ext extérieur F froid G global int intérieur m moyenne p partition rad radiatif s solide s sortie se surface extérieure si surface intérieure e t transversal tot total w paroi extérieure

Liste des figures

Fig. I-1 : Schéma de la paroi monocouche 4

Fig. I-2 : Quadripôle représentatif d’un mur 6

Fig. I-3 : Représentation d’un mur par des impédances en « Π » 7

Fig. I-4 : Schéma de la paroi monocouche 12

Fig. I-5 : Schéma d’une paroi bicouche et la paroi monocouche équivalente 13 Fig. I-6 : Représentation en « Π » d’une paroi avec les différents flux 17 Fig. I-7 : Variation de l’impédance transversale complexe en fonction de l’épaisseur 18 Fig. I-8 : Variation de l’impédance Z2 complexe en fonction de l’épaisseur 19 Fig. I-9 : Variation de la capacité thermique en fonction de l’épaisseur 20 Fig. I-10 : Variation de la capacité thermique en fonction de l’effusivité thermique 22 Fig. I-11 : Variation de la capacité thermique en fonction de l’épaisseur de la couche 1 23 Fig. II-1 : comparaison des variations de la température intérieure obtenue

numériquement et par le modèle de la capacité effective [ANT. 2000]

29

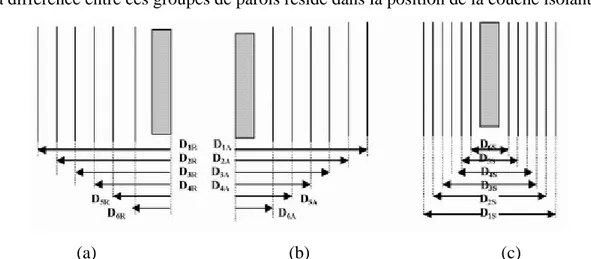
Fig. II-2 : Parois multicouches avec la couche isolante située respectivement (a) du côté intérieur, (b) du côté extérieur et (c) au milieu de la paroi [TSI. 2006b].

30

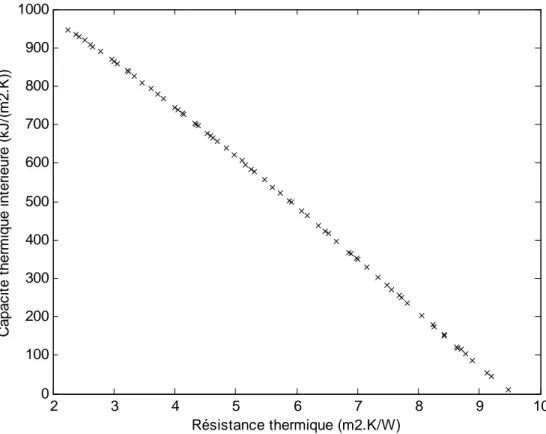
Fig. II-3 : La capacité thermique effective (trait continu) and la constante de temps thermique (pointillés) en fonction de la résistance thermique [TSI. 2006b].

31

Fig. II-4 : Configuration des parois étudiées par [KOS. 2002] 32 Fig. II-5 : Capacité thermique en fonction de la résistance thermique des parois

optimales

35

Fig. II-6 : Capacité thermique en fonction de la résistance thermique des parois optimales

39

Fig. II-7 : Schéma de la composition des parois A à G 40 Fig. II-8 : Capacité thermique en fonction de la résistance thermiques des parois

optimales

42

Fig. II-9 : Capacité thermique en fonction de la résistance thermique des parois optimales

43

Fig. II-10 : Schéma de la composition des parois A à G 44 Fig. II-11 : Système thermodynamique étudié avec ses conditions aux limites 48

Fig. II-12 : Production d’entropie journalière en fonction de l’épaisseur réduite (T_si =20 C° et T_se

( )

t 10 10 sin 2 t 86400 π ⎛ ⎞ = + _{⎜ ⎟} ⎝ ⎠) 49

Fig. II-13 : Production d’entropie journalière en fonction de l’épaisseur réduite (T_si = ° et 0 C T (t)_se 10sin 2 t 86400 π ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠) 49

Fig. II-14 : Minimum de production d’entropie en fonction de l’inverse de la partie réelle de l’impédance transversale (T_si = ° et 0 C T (t)_se 10sin 2 t

86400 π ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠) 51

Fig. II-15 : Minimum de production d’entropie en fonction de l’effusivité thermique (T_si = ° 0 C

52

Fig. II-16 : Minimum de production d’entropie en fonction de la capacité thermique (T_si = ° et 0 C T (t)_se 10sin 2 t 86400 π ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠) 52

Fig. II-17 : Configurations étudiées 53

Fig. II-18 : production d’entropie en fonction de l’épaisseur de la couche massive d’une paroi dans la configuration 1 (T_si = ° et 0 C T (t)_se 10 sin 2 t

86400 π ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠) 54

Fig. II-19 : production d’entropie en fonction de l’épaisseur de la couche massive d’une paroi dans la configuration 2 (T_si = ° et 0 C T (t)_se 10 sin 2 t

86400 π ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠) 55

Fig. II-20 : Production d’entropie journalière en fonction de l’épaisseur réduite d’une paroi (T_int =20 C° et T (t)_ext 10 10 sin 2 t

86400 π ⎛ ⎞ = + _{⎜ ⎟} ⎝ ⎠) 56

Fig. II-21 : Production d’entropie journalière en fonction de l’épaisseur pour une paroi (T_int = ° et 0 C T (t)_ext 10sin 2 t

86400 π ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠) 57

Fig. II-22 : Evolution temporelle de la température intérieure 58 Fig. III-1 : Photo de la maquette de la cavité partitionnée. 64 Fig. III-2 : Positions des thermocouples sur une paroi d’alvéole 65

Fig. III-3 : Dispositif expérimental 66

Fig. III-5 : Stratification des températures expérimentales pour différents nombres de cloisons

68

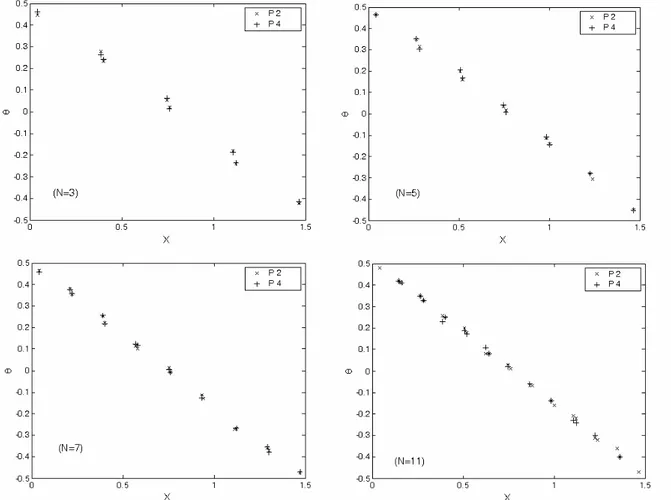
Fig. III-6 : Comparaison des températures expérimentales des points P2 et P4 pour différents nombres de cloisons

69

Fig. III-7 : Schéma de la cavité partitionnée 70

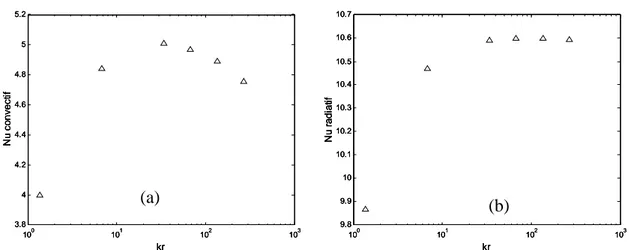
Fig. III-8 : Champ thermique les différentes configurations 77 Fig. III-9 : Lignes de courant dans les différentes configurations 78 Fig. III-10 : Nombres de Nusselt en fonction du nombre de cloisons 79 Fig. III-11 : Champ thermique d’une cavité pour différents ε 80 Fig. III-12 : Lignes de courant d’une cavité pour différents ε 80 Fig. III-13 : Nu en fonction de l’émissivité thermique 81 Fig. III-14 : Champ thermique d’une cavité pour différents kr 82 Fig. III-15 : Lignes de courant d’une cavité pour différents kr 82 Fig. III-16 : Nombres de Nusselt en fonction de la conductivité thermique relative kr 83 Fig. III-17 : Nombre de Nusselt convectif en fonction de la conductivité thermique

relative [KAN. 1991]

83

Fig. III-18 : Champ thermique d’une cavité pour différents nombres de radiation Nr 85 Fig. III-19 : Lignes de courant d’une cavité pour différents nombres de radiation Nr 85 Fig. III-20 : Nu en fonction du nombre de radiation 86 Fig. III-21 : schéma de l’alvéole i 88 Fig. III-22 : Comparaison des températures adimensionnelles expérimentales et

analytiques pour différentes configurations

91

Fig. III-23 : Comparaison des températures adimensionnelles numériques et analytiques pour différentes configurations

92

Fig. III-24 : Variation de la résistance thermique en fonction du nombre de cloisons 95 Fig. III-25 : Variation de la résistance thermique en fonction du nombre de cloisons

(paramètre : C F m T T T 2 + = ) 96

Fig. III-26 : Variation de la résistance thermique en fonction du nombre de cloisons (paramètre : TC-TF)

97

Fig. III-27 : Variation de la résistance thermique en fonction du nombre de cloisons (paramètres : émissivité ε)

Fig. III-28 : Variation de la résistance thermique en fonction du nombre de cloisons (paramètre : la conductivité relative s

r a k = λ

λ )

99

Fig. III-29 : Variation de la résistance thermique en fonction du nombre de cloisons (paramètre : épaisseur des cloisons ep)

100

Fig. III-30 : Variation de la résistance thermique en fonction du nombre de cloisons (paramètre : épaisseur des parois verticales extérieures)

101

Fig. III-31 : Variation de la résistance thermique en fonction du nombre de cloisons (paramètre : épaisseur des parois horizontales)

102

Fig. III-32 : Variation de la résistance thermique en fonction du nombre de cloisons (paramètre : k)

103

Fig. IV-1 : Dispositif expérimental 108

Fig. IV-2 : Position des thermocouples : (a) coupe verticale de la cavité, (b) vue de face d’une cloison

109

Fig. IV-3 : Schéma des configurations étudiées avec différents N 110 Fig. IV-4 : Schéma des configurations étudiées avec des cloisons de différentes

épaisseurs

111

Fig. IV-5 : Schéma des configurations étudiées avec des parois extérieures verticales de différentes épaisseurs

113

Fig. IV-6 : Cavité partitionnée étudiée 115

Fig. IV-7 : Mise en évidence de l’absence de la 3e dimension 116 Fig. IV-8 : Variation temporelle des températures des points P1, P2, P3 et P4 sur

différentes faces

117

Fig. IV-9 : Matérialisation des instants où les températures sont sur (a) un maximum, (b) un minimum, (c) une marche descendante et (d) une marche ascendante

118

Fig. IV-10 : Niveau de stratification sur la face froide de l’alvéole 2 lorsque les températures sont sur (a) un minimum, (b) un maximum, (c) une marche descendante et (d) une marche ascendante

119

Fig. IV-11 : Evolution de Rai dans les alvéoles 120

Fig. IV-12 : Variations de la température moyenne en fonction du temps pour des cavités partitionnées avec différents nombres de cloisons

121

Fig. IV-14 : Variation du facteur d’amortissement dans la cavité partitionnée pour différents nombres de partitions

123

Fig. IV-15 : Variation de la capacité thermique de la demi-cavité en fonction du nombre de cloisons

123

Fig. IV-16 : Variations de la température moyenne en fonction du temps pour des cavités partitionnées avec des cloisons de différente épaisseur

124

Fig. IV-17 : Variation du facteur d’amortissement dans la cavité partitionnée pour différentes épaisseurs de cloisons

125

Fig. IV-18 : Variations de la température moyenne en fonction du temps pour des cavités partitionnées avec des parois extérieures verticales de différente épaisseur

126

Fig. IV-19 : Variation du facteur d’amortissement dans la cavité partitionnée pour différentes épaisseurs des parois extérieures verticales

127

Fig. IV-20 : Variation de la capacité thermique de la demi-cavité en fonction de l’épaisseur des parois extérieures verticales.

128

Fig. IV-21 : Températures expérimentale et numérique sur la face froide de l’alvéole 4 132 Fig. IV-22 : Températures expérimentale et numérique sur la face chaude de l’alvéole 4 132 Fig. IV-23 : Températures expérimentale et numérique sur la face froide de l’alvéole 3 133 Fig. IV-24 : Températures expérimentale et numérique sur la face chaude de l’alvéole 3 133 Fig. IV-25 : Températures expérimentale et numérique sur la face froide de l’alvéole 2 134 Fig. IV-26 : Températures expérimentale et numérique sur la face chaude de l’alvéole 2 134 Fig. IV-27 : Températures expérimentale et numérique sur la face froide de l’alvéole 1 135 Fig. IV-28 : Températures expérimentale et numérique sur la face chaude de l’alvéole 1 135 Fig. IV-29 : Nombres de Nusselt convectif et radiatif sur les faces des alvéoles 1 et 2 137 Fig. IV-30 : Nombres de Nusselt convectif et radiatif sur les faces des alvéoles 3et 4 137 Fig. IV-31 : Nombres de Nusselt convectif et radiatif sur les faces des alvéoles 1 et 2 138 Fig. IV-32 : Nombres de Nusselt convectif et radiatif sur les faces des alvéoles 3 et 4 139 Fig. IV-33 Amplitude des nombres de Nusselt convectifs sur les faces d’alvéoles en

fonction de la période

140

Fig. IV-34 Amplitude des nombres de Nusselt radiatifs sur les faces d’alvéoles en fonction de la période

141

Fig. V-1 : Températures du modèle 1D et expérimentale sur les faces des alvéoles 1 et 2 145 Fig. V-2 : Températures du modèle 1D et expérimentale sur les faces des alvéoles 3 et 4 145

Fig. V-3 : Températures du modèle 1D et du modèle 2D les faces des alvéoles 1 et 2 147 Fig. V-4 : Températures du modèle 1D et du modèle 2D les faces des alvéoles 3 et 4 147 Fig. V-5 : Températures du modèle 1D et expérimentale sur les faces des alvéoles 1 et 2 148 Fig. V-6 : Températures du modèle 1D et expérimentale sur les faces des alvéoles 3 et 4 148 Fig. V-7 : Températures expérimentales et numériques sur la face chaude de l’alvéole 1 149 Fig. V-8 : Températures expérimentales et numériques sur la face froide de l’alvéole 1 149 Fig. V-9 : Températures expérimentales et numériques sur la face chaude de l’alvéole 2 150 Fig. V-10 : Températures expérimentales et numériques sur la face froide de l’alvéole 2 150 Fig. V-11 : Températures expérimentales et numériques sur la face chaude de l’alvéole 3 151 Fig. V-12 : Températures expérimentales et numériques sur la face froide de l’alvéole 3 151 Fig. V-13 : Températures expérimentales et numériques sur la face chaude de l’alvéole 4 152 Fig. V-14 : Températures expérimentales et numériques sur la face froide de l’alvéole 4 152 Fig. V-15 : Comparaison des températures sur les faces des alvéoles 1 et 2 154 Fig. V-16 : Comparaison des températures sur les faces des alvéoles 3 et 4 154

Fig. V-17 : Schéma de la cavité étudiée 155

Fig. V-18 : Capacité thermique d’une cavité partitionnée en fonction du nombre de cloisons (ew=8mm ; ep=3mm)

156

Fig. V-19 : Capacité thermique d’une cavité partitionnée en fonction de l’épaisseur des parois extérieures (N=3, ep=3mm)

157

Fig. V-20 : Capacité thermique d’une cavité partitionnée en fonction de l’épaisseur des cloisons (N=3, ew=8mm)

157

Fig. V-21 : Exemple de cavité partitionnée 160

Fig. V-22 : Front des cavités Pareto-optimales pour de faibles nombres d’alvéoles 161 Fig. V-23 : Composition des cavités à 5 alvéoles sélectionnées (épaisseurs en mm) 161 Fig. V-24 : Composition des cavités à 10 alvéoles sélectionnées (épaisseurs en mm) 161 Fig. V-25 : Front des cavités Pareto-optimales pour de grands nombres d’alvéoles 162 Fig. V-26 : Composition des cavités à 20 alvéoles sélectionnées sur le front de Pareto

(épaisseurs en mm)

163

Fig. IV-27 : Composition des cavités à 30 alvéoles sélectionnées sur le front de Pareto (épaisseurs en mm)

Liste des tableaux

Tab. I-1 : Paramètres thermophysiques de quelques matériaux de construction 21 Tab. II-1 : Détails des parois sélectionnées sur le front de Pareto 36

Tab. II-2 : Matériaux composant une paroi idéale 37

Tab. II-3 : Composition des parois A à G 41

Tab. II-4 : Composition des parois A à G 44

Tab. III-1 : Caractéristiques des configurations de la cavité partitionnée expérimentées 67 Tab. III-2 : Comparaison des nombres de Nusselt pour une cavité carrée (Ra=106) 76 Tab. III-3 : Nombres de Nusselt dans les alvéoles pour la configuration à N=11 93 Tab. III-4 : Nombres de Nusselt dans les alvéoles pour la configuration à N=7 93 Tab. III-5 : Nombres de Nusselt dans les alvéoles pour la configuration à N=5 93 Tab. III-6 : Nombres de Nusselt dans les alvéoles pour la configuration à N=3 94 Tab. IV-1 : Configurations étudiées pour la mise en évidence de l’influence de N 110 Tab. IV-2 : Configurations étudiées pour la mise en évidence de l’influence de ep 112 Tab. IV-3 : Configurations étudiées pour la mise en évidence de l’influence de ew 112 Tab. IV-4 : Caractéristiques de la cavité partitionnée étudiée 115

Introduction générale

Le contexte actuel de l’énergie est marqué par le prix sans cesse croissant du prix du baril de pétrole et de l’énergie en général. Cette situation a pour conséquence une augmentation du déficit de la balance commerciale des pays non producteurs de pétrole. Outre ce problème économique, les prévisions les plus optimistes prédisent la fin des stocks de pétrole fossile dans les quarante prochaines années. Il se posera donc pour les générations futures un problème d’approvisionnement énergétique.

L’autre problème majeur posé par la consommation actuelle d’énergie est d’ordre environnemental. Un groupe international d’experts, le GIEC (Groupement Intergouvernemental d’Etude du Climat), a produit des données incontestables sur la réalité des changements climatiques. Ces changements climatiques ont pour origine l’activité humaine qui disperse dans l’atmosphère des quantités croissantes de gaz à effets de serre (GES), essentiellement du dioxyde de carbone CO2. Le protocole de Kyoto engage les pays industrialisés à réduire l’émission des GES avec un objectif de réduction globale de 5.2 % des émissions du CO2 en 2012 par rapport aux émissions de 1992.

La consommation énergétique du secteur du bâtiment résidentiel et tertiaire qui a progressé de 25% ces dernières 25 années constitue le premier consommateur d'énergie finale en France. Ce secteur représente, à lui seul, 46% de la consommation totale d’énergie. Les émissions de GES correspondant à ce secteur représentent près de 25% des émissions totales. Pour respecter les engagements de Kyoto, des efforts doivent donc être faits dans ce secteur. C’est dans ce cadre qu’il faut situer les réglementations thermiques, notamment la RT 2005 qui a succédé le 1er septembre 2006 à la RT 2000. Les aspects majeurs de cette nouvelle réglementation sont :

− l'expression de la consommation conventionnelle d'énergie d'un bâtiment pour le chauffage, la ventilation, le refroidissement, la production d'eau chaude sanitaire et l'éclairage sous la forme d'un coefficient Cep exprimé en kWh/m² d'énergie primaire ; − l'introduction d'une limite Cepmax de consommation d'énergie primaire ;

− le renforcement de l'isolation thermique ;

− le renforcement des performances des équipements ; − la bonification à l’utilisation de l'eau chaude sanitaire ; − la valorisation de la conception bioclimatique ;

− la fourniture obligatoire à la fin des travaux d'une synthèse de l'étude thermique. Cependant, une forte isolation, si elle limite la consommation d'hiver liée au chauffage, induit de fortes surchauffes lors de la saison chaude. Afin de lutter contre ce phénomène, diverses méthodes sont possibles, comme la surventilation nocturne [PFA. 2003], [FLO. 1998], les méthodes architecturales [GIV. 1978], ou l'inertie thermique [ANT. 2001], [TSI. 2003]. C’est cette dernière qui nous intéresse ici. L’inertie thermique peut être définie comme la capacité d’un bâtiment à emmagasiner de la chaleur (ou de la fraîcheur). Un bâtiment à forte inertie thermique a la propriété de conserver une température stable et de se réchauffer ou se refroidir très lentement, alors qu’un bâtiment à faible inertie suit sans amortissement ni retard les fluctuations de la température extérieure. L’inertie thermique présente deux enjeux : un enjeu d’amélioration du confort thermique d’été et un enjeu d’économie d’énergie de chauffage d’hiver par le stockage des apports solaires transmis par les vitrages.

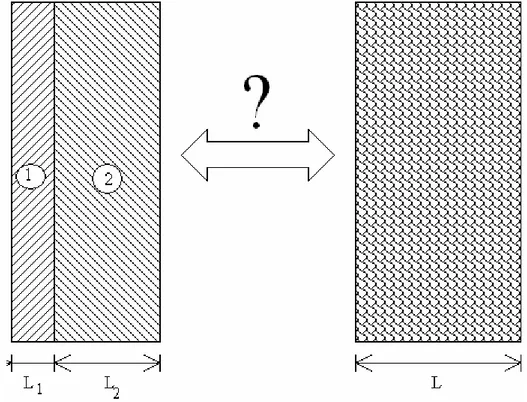
Notre étude consiste à étudier le transfert thermique à travers des parois ou des éléments de parois. Deux types de parois sont étudiés :

− des parois constituées de couches pleines homogènes et parallèles,

− des éléments de parois alvéolaires modélisés par des cavités partitionnées.

L’objectif visé dans cette étude est l’optimisation simultanée de l’isolation thermique et de l’inertie thermique à l’échelle de la paroi ou de l’élément de la paroi.

Pour atteindre cet objectif, nous avons d’abord présenté dans le chapitre I la méthode des quadripôles utilisée pour l’étude des transferts thermiques ainsi que l’outil d’optimisation par algorithme génétique que nous avons adopté. Dans le second chapitre, nous avons fait l’optimisation de la résistance et de la capacité thermique d’une paroi multicouche de bâtiment. Dans ce chapitre, nous avons également étudié la production d’entropie irréversible d’une paroi.

Une cavité partitionnée matérialisant un élément de paroi alvéolaire a été étudiée théoriquement et expérimentalement dans les chapitres III et IV respectivement en régime permanent et en régime variable. Le dernier chapitre aborde l’optimisation de la cavité partitionnée par rapport à l’isolation thermique et l’inertie thermique.

Chapitre I

Méthodes d’analyse

I-1 Introduction

Les parois dont nous allons analyser le comportement thermique peuvent être classées en deux types : les parois constituées de couches homogènes matérielles ou considérées comme telles, et les parois alvéolaires constituées de couches matérielles et de cavités d’air.

On considérera à plusieurs reprises le cas du « mur » monodimensionnel, bien que cette hypothèse simplificatrice ne soit pas toujours de règle dans le bâtiment.

Différentes méthodes d’analyse vont être utilisées, selon le but recherché. Il s’agit :

9 de la méthode des quadripôles pour la caractérisation dynamique des parois afin de déterminer un paramètre pertinent caractérisant l’inertie thermique ;

9 d’un algorithme génétique pour l’optimisation d’une paroi par rapport à l’isolation thermique et à l’inertie thermique ;

9 d’une approche numérique modélisant le transfert thermique à travers des cavités partitionnées ;

9 d’une approche expérimentale pour ces mêmes cavités.

I-2 La méthode des quadripôles

Le transfert thermique conductif à travers un milieu solide est régi par l’équation de diffusion thermique. La résolution de cette équation en régime variable dans les milieux hétérogènes continue de préoccuper la communauté scientifique. En effet, les systèmes avec des parois hétérogènes sont présents dans un grand nombre d’applications techniques, notamment dans le secteur du bâtiment. Les murs d’un bâtiment sont en général composés de couches de matériaux avec des propriétés thermophysiques données. Les calculs de la charge thermique de chauffage et/ou de climatisation d’un bâtiment nécessitent une description précise du comportement thermique en régime variable des parois car les conditions extérieures (température sèche,

rayonnement solaire, …) sont variables, tandis que celles intérieures sont maintenues relativement constantes pour les besoins de confort.

Plusieurs travaux concernant la résolution analytique de l’équation de la chaleur monodimensionnelle en régime variable existent dans la littérature. Diverses méthodes ont été répertoriées par F. de Monte [MON. 2000]. La méthode des quadripôles présentée ci-après est issue de travaux antérieurs [MAI. 2000]. Elle est basée sur l’utilisation de la transformée de Laplace pour résoudre analytiquement l’équation de la chaleur monodimensionnelle en régime variable. Nous nous sommes appuyés dessus pour en extraire les variables pertinentes pour notre étude.

I-2-1 Principe de la méthode : résolution de l’équation de la chaleur en

régime variable

Pour expliciter la méthode des quadripôles, considérons un mur monocouche d’épaisseur L sans source interne et en équilibre thermique à l’instant initial à la température T0. Ce mur soumis à des conditions aux limites de Dirichlet est schématisé par la figure Fig. I-1. On suppose que les propriétés thermophysiques de ce mur sont constantes.

Fig. I-1 : Schéma de la paroi monocouche Ce mur est régi par le système d’équation suivant :

2 2 i T T a pour 0 < x < L t x T(x, 0) T ⎧∂ ₌ ∂ ⎪ ∂ ∂ ⎨ ⎪ ₌ ⎩ (I-1)

où : T est la température,

a est la diffusivité thermique

En faisant un changement de variable (θ = − ), le système d’équation devient : T Ti 2 2 a pour 0 < x < L t x (x, 0) 0 ⎧∂θ₌ ∂ θ ⎪ ∂ ∂ ⎨ ⎪θ = ⎩ (I-2)

Soit Θ la transformée de Laplace de la température θ donnée par :

( )

( )

(

)

0

x, p x, t exp p t dt ∞

Θ = θ

∫

− (I-3)

où p est le paramètre de Laplace.

Dans l’espace de Laplace, la première équation du système (I-2) devient : 2 2 d p a dx Θ Θ = (I-4)

La solution de cette équation différentielle est :

( )

( )

1 2 (x, p) K sh x K ch x Θ = β + β (I-5) où 2 p a

β = , K1 et K2 sont des constantes.

Le flux thermique en un point d’abscisse x est donné par : S

x ∂θ φ = −λ

∂ (I-6)

λ est la conductivité thermique du mur, S est la surface du mur normale à la direction x. La transformée de Laplace du flux thermique notée Φ est donnée par :

( )

( )

(

)

0

x, p x, t exp p t dt ∞

Φ = φ

_∫

− (I-7)

En calculant la dérivée de l’expression (I-5), le flux thermique dans l’espace de Laplace, devient :

( )

( )

(

1 2

)

(x) S S K ch x K sh x x ∂Θ Φ = −λ = −λ β β + β ∂ (I-8)

Notons Θ1 et Θ2 les transformées de Laplace des températures θ = − et ₁ T₁ T_i θ =₂ T₂− T_i respectivement à l’entrée (x=0) et à la sortie (x=L) du mur et Φ1 et Φ2 les transformées des flux

thermiques φ1 et φ2 respectivement à l’entrée et à la sortie. Le système constitué par le mur étant linéaire, il existe une relation linéaire entre les grandeurs d’entrée et les grandeurs de sortie. On a : 1 2 2 1 2 2 A B C D Θ = Θ + Φ ⎧ ⎨Φ = Θ + Φ ⎩ (I-9) La matrice A B C D ⎡ ⎤ ⎢ ⎥

⎣ ⎦ constitue la matrice de transfert inverse du quadripôle associé au mur. Pour déterminer les composantes de cette matrice, il suffit de résoudre le système d’équations suivant :

(

)

(

)

1 2 1 x 0 2 x L x 0 x L S x S x = = ⎧Θ = Θ = ⎪ Θ = Θ = ⎪ ⎪⎪_{Φ = −λ} ∂Θ ⎨ ∂ ⎪ ⎪ _∂Θ ⎪Φ = −λ ∂ ⎪⎩ (I-10)

Il vient de ces relations :

( )

( )

( )

( )

1 2 2 1 2 2 1 ch L sh L S Ssh L ch L ⎧Θ = β Θ + β Φ ⎪ _λβ ⎨ ⎪Φ = λβ β Θ + β Φ ⎩ (I-11) et donc

( )

( )

( )

A D ch L 1 B sh L S C S sh L ⎧ = = β ⎪ ⎪ = β ⎨ _λβ ⎪ ⎪ = λβ β ⎩ (I-12)

Le mur monocouche étant symétrique, les éléments A, B, C et D obéissent à la relation suivante :

AD BC− =1 (I-13)

Ce mur peut être représenté selon l’analogie électrique par le quadripôle suivant :

Comme en électricité, un tel quadripôle peut être représenté par trois impédances complexes associées en « T » ou en « Π ». Nous utiliserons dans la suite la représentation en « Π » suivante :

Fig. I-3 : Représentation d’un mur par des impédances en « Π » Les impédances complexes Z1, Zt et Z2 sont données par :

1 t 2 B Z impédance d'entrée D 1 Z B impédance transversale B Z impédance de sortie A 1 ⎧ = ⎪ ₋ ⎪ = ⎨ ⎪ ⎪ = ⎩ − (I-14)

Cette méthode analytique assez simple permet de lier à travers une relation matricielle les transformées de Laplace des températures et des flux aux bornes du mur. Cette relation intrinsèque est indépendante des conditions aux limites. Cette méthode peut être étendue aisément aux régimes périodiques.

I-2-2 Résolution de l’équation de la chaleur monodimensionnelle en

régime périodique établi

Les sollicitations thermiques que subit une paroi de bâtiment ont le plus souvent un caractère périodique. Le rayonnement solaire et la température sèche par exemple suivent une variation journalière. Lorsqu’un mur est soumis à des sollicitations périodiques suffisamment longtemps, la température T(x,t) en un point d’abscisse x de ce mur varie selon un régime périodique établi. Dans ce cas, la méthode harmonique peut être utilisée à la place de la transformée de Laplace.

On considère une paroi monocouche de paramètres thermophysiques constants soumise à des sollicitations sinusoïdales. Lorsqu’un régime sinusoïdal établi est atteint, la température T(x,t) en un point d’abscisse x du mur est donnée par :

( )

(

)

T x, t =T (x)+ ∆T(x) sin ω + ϕt (x) (I-15)

avec

T(x) = température moyenne en un point x du mur

∆T(x) = amplitude de la variation de température en un point x ω = pulsation du signal

ϕ(x) = phase du signal en un point x. On pose :

(

)

(x, t) T(x) sin t (x)

θ = ∆ ω + ϕ (I-16)

L’équation de la chaleur régissant le comportement thermique du mur étant linéaire, on a alors :

( )

( )

2 2 2 2 T(x) 0 x x, t x, t a t x ⎧∂ ₌ ⎪⎪ ∂ ⎨ ∂θ ∂ θ ⎪ ₌ ⎪ _{∂ ∂} ⎩ (I-17)

La solution de la première équation est évidente :

1 2

T(x)=C x+C (I-18)

Les constantes C1 et C2 sont à déterminer en appliquant les conditions aux limites du régime permanent.

Pour résoudre la deuxième équation du système (I-17), il suffit de remarquer que la fonction sinus est la partie imaginaire d’un nombre complexe :

( )

(

j t ( x )

)

(

)

(

j t

)

(x, t) T e ω +ϕ (x, t) (x) eω θ = ℑ ∆ = ℑ θ = ℑ θ (I-19) avec _{( )} j ( x ) j t ( x )

(x) T(x)e : amplitude complexe de la température (x, t) T(x)e : température complexe

ϕ ω +ϕ ⎧θ = ∆ ⎪ ⎨ θ = ∆ ⎪⎩

On introduit une transformation qui, lorsqu’elle est appliquée à une fonction sinusoïdale, la transforme en une fonction complexe dont la partie imaginaire est la fonction sinusoïdale.

Ainsi, en appliquant la deuxième équation du système (I-17) à la température complexe ainsi obtenue, nous avons :

2 2 d j a dx θ ωθ = (I-20)

L’équation (I-20) est similaire à l’équation (I-4) à condition de remplacer le paramètre de Laplace p par jω. La solution de cette équation est donc :

( )

( )

1 2 (x) K sh x K ch x θ = β + β (I-21) avec β = + α

(

1 j

)

où 2a ω α =

K1 et K2 sont des constantes à déterminer.

La solution générale de l’équation de Fourier est donc :

( )

( )

( )

1 2 (x, t) K sh x K ch x exp j t θ =⎡_⎣ β + β ⎤_⎦ ω (I-22) ou encore :

(

)

(

)

(

(

)

)

( )

' ' 1 2

(x, t) ⎡K exp 1 j x K exp 1 j x ⎤exp j t

θ =_⎣ − + α + + α _⎦ ω (I-23)

I-2-2-1 Cas d’un mur semi-infini

Considérons dans un premier temps une paroi semi-infinie, soumise en x=0 à une température sinusoïdale dont la transformée dans l’espace complexe est θ₀

( )

x, t = ∆T e₀ j tω .

La solution devient :

( )

x, t T exp0

(

(

1 j

)

x exp j t

)

( )

θ = ∆ − + α ω (I-24)

NB : θ doit être une quantité finie, ce qui implique que le coefficient K’2 est nul. La solution peut être réécrite sous la forme suivante :

( )

0 x t x x, t T exp 2 exp j2 T ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ θ = ∆ _⎜− π _{⎟ ⎜} π_⎜ − _⎟⎟ Λ Λ ⎝ ⎠ ⎝ ⎝ ⎠⎠ (I-25)

Cette expression met en évidence une périodicité dans l’espace dont la grandeur caractéristique est la longueur d’onde Λ =2π

α . C’est un paramètre intrinsèque au matériau de la paroi par rapport à la fréquence du signal auquel il est soumis. On remarquera que lorsque x=Λ, l’amplitude de la température est fortement atténuée (∆ =T 1.87 10⋅ −3∆ ). T₀

I-2-2-2 Cas d’un mur monocouche d’épaisseur finie

Les parois de bâtiment ont le plus souvent une épaisseur finie L très faible devant les autres dimensions de la paroi (c’est une des bases justificatives du modèle 1D du transfert thermique). Dans ce cas, le modèle du mur semi infini n’est plus applicable. Cependant, les températures et les flux aux deux surfaces du mur sont liés par une relation matricielle similaire à l’équation (I-9) : 1 2 ₂ 2 1 2 A B C D θ = θ + φ ⎧⎪ ⎨φ = θ + φ ⎪⎩ (I-26)

Le mur monocouche est donc caractérisé par un quadripôle dont les éléments de la matrice caractéristique A B C D ⎡ ⎤ ⎢ ⎥ ⎣ ⎦ sont :

(

)

(

)

(

)

(

)

(

)

L A D ch 2 1 j R L B sh 2 1 j L 2 1 j L 2 1 j L C sh 2 1 j R ⎧ ⎪ ⎪ _{⎛ ⎞} = = π + ⎪ ⎜_{⎝ Λ}⎟_⎠ ⎪ ⎪⎪ ₌ ⎛ _{π +} ⎞ ⎨ ⎜_{⎝ Λ}⎟_⎠ ⎪ π + Λ ⎪ ⎪ π + ⎪ _{⎛ ⎞} Λ ⎪ = _⎜ π + _⎟ Λ ⎪ ⎝ ⎠ ⎩ (I-27) L R S =

λ est la résistance thermique du mur.

Ces équations font apparaître un nouveau paramètre adimensionnel L

Λ. Les éléments de la matrice dépendent uniquement de deux caractéristiques : R et L

Λ.

Les impédances complexes Z1, Zt et Z2 de la représentation en « Π » du quadripôle sont données par :

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

1 t 2 L sh 2 1 j B R Z L L D 1 2 1 j ch 2 1 j 1 R L Z B sh 2 1 j L 2 1 j L sh 2 1 j B R Z L L A 1 2 1 j ch 2 1 j 1 ⎧ _{⎛ ⎞} ⎛ _{π +} ⎞ ⎜ ⎟ ⎪ _{⎜ ⎟ ⎝ Λ⎠} ⎪ = _{= ⎜ ⎟} − ⎛ ⎞ ⎪ _{⎜ π + ⎟ π + −} ⎜ ⎟ ⎪ _{⎝ Λ ⎠ ⎝ Λ⎠} ⎪ ⎛ ⎞ ⎪ ⎜ ⎟ ⎪ _{= =} ⎛ _{π +} ⎞ ⎨ ⎜ ⎟ ⎜ _Λ⎟ ⎝ ⎠ ⎪ ⎜ π + ⎟ ⎝ Λ ⎠ ⎪ ⎪ _{⎛ ⎞} ⎛ ⎞ ⎪ _{⎜ ⎟ ⎜} π + _⎟ Λ ⎝ ⎠ ⎪ _{= = ⎜ ⎟} ⎪ _{− ⎜ ⎟ ⎛ ⎞} π + π + − ⎪ _{⎝ Λ ⎠} ⎜_{⎝ Λ}⎟_⎠ ⎩ (I-28)

Une paroi est donc complètement caractérisée par seulement trois paramètres complexes : Z1 : l’impédance complexe d’entrée

Zt : la transmittance complexe Z2 : l’impédance complexe de sortie Lorsque L <<1

Λ , c’est-à-dire que la paroi est mince, on a alors : t 1 2 m Z R 1 Z Z C j 2 ≈ ⎧ ⎪⎪ ⎨ = ≈ ⎪ _ω ⎪⎩ (I-29)

On remarquera que les impédances Z1 et Z2 sont purement capacitives, tandis que l’impédance transversale Zt est simplement une résistance.

I-2-2-3 Cas d’un mur multicouche soumis à des sollicitations sinusoïdales

On considère une paroi constituée de N couches i d’épaisseur Li représentée schématiquement sur la figure Fig. I-4.

Fig. I-4 : Schéma d’une paroi multicouche

On suppose chaque couche homogène avec des paramètres thermophysiques λi, ρi et Ci constants. Chaque couche est caractérisée par la matrice i i

i i

A B

C D

⎡ ⎤

⎢ ⎥

⎣ ⎦dont les éléments sont donnés

par :

(

)

(

)

(

)

(

)

(

)

i i i i i i i i i i i i i i i i L A D ch 2 1 j R L B sh 2 1 j L 2 1 j L 2 1 j L C sh 2 1 j R ⎧ ⎪ ⎪ _{⎛ ⎞} ⎪ _{= = ⎜ π + ⎟} ⎪ _⎝ Λ _⎠ ⎪ ⎛ ⎞ ⎪ = π + ⎨ ⎜ _Λ ⎟ ⎝ ⎠ ⎪ π + Λ ⎪ ⎪ ⎪ π + ⎛ ⎞ Λ ⎪ = _⎜ π + _⎟ ⎪ _Λ ⎝ ⎠ ⎩ (I-30)

Dans un premier temps, on suppose que les couches sont en contact parfait. Ainsi, si _1,i

1,i et

θ φ sont respectivement la température et le flux à l’entrée de la couche i et

2,i et _2,i

θ φ ceux à la sortie, on a alors la relation matricielle suivante :

1,i _{i i} 2,i i i 1,i 2,i A B C D θ _{⎡ ⎤} θ = ⎢ ⎥ φ _{⎣ ⎦} φ (I-31)

Sachant que 2,i 1 1,i 2,i 1 1,i pour i=2...N − − θ = θ ⎧⎪ ⎨φ = φ ⎪⎩ (I-32)

La relation matricielle liant les conditions d’entrée du mur multicouche à celles de sortie est la suivante : g g 1 1 1 2 2 N 1 N 1 N N 2 2 1 1 2 2 N 1 N 1 N N g g 1 2 2 A B A B A B A B A B ... C D C D C D C D C D − − − − θ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ θ ⎡ ⎤θ =_{⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ = ⎢ ⎥} φ _{⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦} φ _{⎢⎣ ⎥⎦}φ (I-33) g g g g A B C D ⎡ ⎤ ⎢ ⎥ ⎢ ⎥

⎣ ⎦est la matrice globale du mur multicouche. Le déterminant de cette matrice est toujours égal à l’unité.

Ainsi le mur multicouche, tout comme le monocouche, est caractérisé par une matrice obtenue par la multiplication des matrices des différentes couches. Dès lors se pose une question intéressante, à savoir s’il existe une paroi monocouche équivalente à une paroi multicouche. Pour répondre à cette question, considérons une paroi à deux couches schématisée sur la figure suivante.

Fig. I-5 : Schéma d’une paroi bicouche et la paroi monocouche équivalente

(

)

(

)

(

)

(

)

(

)

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 L A D ch 2 1 j R L B sh 2 1 j L 2 1 j L 2 1 j L C sh 2 1 j R ⎧ ⎪ ⎪ _{⎛ ⎞} ⎪ _{= = ⎜ π + ⎟} ⎪ _⎝ Λ _⎠ ⎪ ⎛ ⎞ ⎪ = π + ⎨ ⎜ _Λ ⎟ ⎝ ⎠ ⎪ π + Λ ⎪ ⎪ ⎪ _{π +} ⎛ ⎞ Λ ⎪ = _⎜ π + _⎟ ⎪ _Λ ⎝ ⎠ ⎩ et

(

)

(

)

(

)

(

)

(

)

2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 L A D ch 2 1 j R L B sh 2 1 j L 2 1 j L 2 1 j L C sh 2 1 j R ⎧ ⎪ ⎪ _{⎛ ⎞} ⎪ _{= = ⎜ π + ⎟} ⎪ _⎝ Λ _⎠ ⎪ ⎛ ⎞ ⎪ _{= π +} ⎨ ⎜ _Λ ⎟ ⎝ ⎠ ⎪ π + Λ ⎪ ⎪ ⎪ _{π +} ⎛ ⎞ Λ ⎪ _{= π +} ⎜ ⎟ ⎪ _Λ ⎝ ⎠ ⎩ (I-34)

La matrice globale du mur bicouche est donnée par :

g g 1 1 2 2 1 2 1 2 1 2 1 2 g g 1 1 2 2 1 2 1 2 1 2 1 2 A B A B A B A A B C A B B D C D C D C D C A D C C B D D ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎡ + + ⎤ = = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ _{+ +} ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ (I-35)

On démontre que les éléments de la matrice globale sont obtenus par les expressions suivantes :

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

1 2 1 2 1 2 1 2 g 2 1 2 1 1 2 1 2 1 2 1 2 g 1 2 1 2 1 2 1 2 1 2 1 2 g 1 2 1 2 1 2 2 1 1 2 2 1 g 1 2 1 2 ch R ch R A 1 1 2 R 2 R sh R R sh R R B 2 2 sh sh C 2 R R 2 R R ch R ch R D 1 1 2 R 2 R χ + χ ⎛ χ ⎞ χ − χ ⎛ χ ⎞ = _⎜ + _⎟+ _⎜ − _⎟ χ χ ⎝ ⎠ ⎝ ⎠ χ + χ ⎛ ⎞ χ − χ ⎛ ⎞ = _⎜ + _⎟+ _⎜ − _⎟ χ χ χ χ ⎝ ⎠ ⎝ ⎠ χ + χ ⎛χ χ ⎞ χ − χ ⎛χ χ ⎞ = _⎜ + _⎟+ _⎜ − _⎟ ⎝ ⎠ ⎝ ⎠ χ + χ ⎛ χ ⎞ χ − χ ⎛ χ = _⎜ + _⎟+ − χ χ ⎝ ⎠ ⎝ ⎧ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎞ ⎪ ⎜ ⎟ ⎪ ⎠ ⎩ (I-36) avec

(

)

i i i L 2 1 j pour i=1 ou 2 χ = π + Λ

Pour que ces éléments soient identiques à ceux d’un monocouche il faut que A_g =D_g. Pour que cette condition nécessaire soit réalisée, il faut avoir :

2 2 1 1 L 1 2 1 2 1 2 L 2 2 1 1 R L R 1 b b R L R Λ Λ Λ _{= ⇔ = ⇔ =} Λ (I-37)

où bi est l’effusivité de la couche i.

L’effusivité thermique peut être définie comme la capacité calorifique d’un matériau d’épaisseur égale à l’épaisseur concernée par la propagation d’un phénomène thermique d’une durée de 1 s. Le système (I-36) s’écrit plus simplement :

(

)

(

)

(

)

(

)

(

)

(

)

1 2 g 1 2 1 2 1 2 g 1 2 1 2 1 2 1 2 1 2 1 2 g 1 2 1 2 1 2 g 1 2 L L A ch 2 1 j R R L L B sh 2 1 j L L 2 1 j L L 2 1 j L L C sh 2 1 j R R L L D ch 2 1 j ⎧ ⎛ ⎛ ⎞⎞ = π + + ⎪ ⎜_⎜ ⎜_{Λ Λ} ⎟⎟_⎟ ⎝ ⎠ ⎪ ⎝ ⎠ ⎪ _{⎛ ⎞} ⎛ ⎞ + ⎪ _{= ⎜ π + ⎜ + ⎟⎟} ⎜ ⎟ ⎪ _{⎛ ⎞ ⎝ ⎝Λ Λ ⎠⎠} π + + ⎪ _{⎜ ⎟} Λ Λ ⎪ ⎝ ⎠ ⎨ ⎛ ⎞ ⎪ _{π + +} ⎜ ⎟ ⎪ _{⎝Λ Λ ⎠ ⎛ ⎛ ⎞⎞} ⎪ = _⎜⎜ π + _⎜ + _⎟⎟⎟ + Λ Λ ⎪ ⎝ ⎝ ⎠⎠ ⎪ ⎛ ⎛ ⎞⎞ ⎪ _{= π + +} ⎜ ⎜ ⎟⎟ ⎪ ⎜ _{⎝Λ Λ ⎠}⎟ ⎝ ⎠ ⎩ (I-38) Les caractéristiques R et L

Λ du matériau équivalent sont simplement la somme de celles des couches : 1 2 1 2 1 2 R R R L L L = + ⎧ ⎪ ⎨ = + ⎪Λ Λ Λ ⎩ (I-39)

Ce résultat montre qu’on ne peut pas trouver un matériau équivalent à une paroi constituée d’une couche massive associée à une couche isolante, les effusivités de ces couches étant en général très différentes.

Dans le cas d’un contact non parfait modélisé par une résistance de contact Rci,i+1 entre les couches i et i+1 du mur, on introduit à cette interface la matrice de contact 1 Rci,i 1

0 1

+

⎡ ⎤

⎢ ⎥

⎣ ⎦. Ainsi, la

matrice globale du mur multicouche est donnée par :

g g 1 1 1,2 2 2 2,3 N 1 N 1 N 1,N N N g g 1 1 2 2 N 1 N 1 N N A B A B 1 Rc A B 1 Rc A B 1 Rc A B ... C D C D 0 1 C D 0 1 C D 0 1 C D − − − − − ⎡ ⎤ ⎡ ⎤⎡ ⎤⎡ ⎤⎡ ⎤ ⎡ ⎤⎡ ⎤⎡ ⎤ = ⎢ ⎥ ⎢ ⎥⎢ ⎥⎢ ⎥⎢ ⎥ ⎢ ⎥⎢ ⎥⎢ ⎥ ⎢ ⎥ ⎣ ⎦⎣ ⎦⎣ ⎦⎣ ⎦ ⎣ ⎦⎣ ⎦⎣ ⎦ ⎣ ⎦

Comme pour le mur monocouche, le multicouche peut être représenté par trois impédances Z1, Zt et Z2 associées en « Π ». Ces impédances sont données par :

g 1 g t g g 2 g B Z D 1 Z B B Z A 1 ⎧ = ⎪ − ⎪ ⎪ = ⎨ ⎪ ⎪ ₌ ⎪ ₋ ⎩ (I-41)

Le comportement dynamique d’une paroi monocouche ou multicouche est déterminé soit par la matrice de transfert ou par les trois impédances. Il est intéressant de déterminer les paramètres dynamiques qui permettent de caractériser l’inertie de la paroi.

I-2-3 Caractéristiques dynamiques d’une paroi soumise à des

sollicitations sinusoïdales

L’inertie thermique d’une paroi est sa capacité à stocker et à restituer une grande quantité d’énergie thermique. L’inertie joue deux rôles :

9 elle permet d’améliorer le confort thermique en été par l’amortissement des variations de température intérieure du bâtiment ;

9 elle permet également de réaliser des économies d’énergie notamment en hiver grâce au stockage des apports solaires gratuits transmis par les vitrages.

Davies [DAV. 2004] propose d’utiliser deux paramètres thermiques dynamiques pour caractériser la paroi : la transmittance cyclique u et deux admittances y1 et y2.

Pour bien illustrer ces paramètres, on considère le mur monocouche de la figure Fig. I-1 en ayant en mémoire les éléments de la matrice de transfert donnés par le système (I-27).

La transmittance cyclique u est le rapport entre le flux complexe quittant la surface 2 et la température complexe à la surface 1 lorsque la température complexe à la surface 2 est nulle.

2 2 1 0 1 u B θ = ⎛φ ⎞ =_{⎜ ⎟} = θ ⎝ ⎠ (I-42)

L’admittance yi est le rapport entre le flux complexe absorbé par la paroi à la surface i sur la

température complexe à cette surface lorsque la température à l’autre surface de la paroi est nulle. 2 1 1 1 1 0 2 2 2 ₀ D y B A y B θ = θ = ⎧ _{= −}⎛ φ ⎞ ₌ ⎪ ⎜ ⎟ θ ⎝ ⎠ ⎪ ⎨ ⎛ φ ⎞ ⎪ = −_{⎜ ⎟} = ⎪ _θ ⎝ ⎠ ⎩ (I-43)

Parmi ces admittances, seule celle située du côté intérieur du bâtiment est intéressante.

Les paramètres u et y bien qu’ils soient très attrayants ont été déterminés en posant des conditions difficiles à réaliser. En effet, dans le bâtiment en fonctionnement, il est pratiquement impossible d’imposer une température constante sur les surfaces de parois.

Il nous parait plus judicieux d’utiliser les impédances complexes de la représentation en « Π » du mur. Pour bien illustrer nos propos, reprenons le schéma de la figure I-3 représentant une paroi monocouche soumise à des sollicitations sinusoïdales.

Fig. I-6 : Représentation en « Π » d’une paroi avec les différents flux

Cette représentation présente l’avantage de faire apparaître trois flux supplémentaires : φ’1, φ’2 et φt. Le flux φt met en évidence le rôle de l’impédance transversale Zt qui se trouve être l’inverse de la transmittance cyclique u. Les flux φ’1, φ’2 sont les flux absorbés par la paroi et qui sont susceptibles d’être restitués si la température change de signe. Les impédances Z1 et Z2 jouent un rôle d’accumulateur d’énergie thermique. Dans le cas d’une paroi monocouche, Z1=Z2. Ces impédances sont les paramètres thermiques les plus indiqués pour caractériser l’inertie d’une paroi. Pour illustrer le comportement des impédances Zt et Z2, considérons une paroi monocouche d’épaisseur variable et de paramètres thermophysiques suivants :

1 1 -3 -1 -1

1.5 W m− K ; =2200 kg m et C=1000 J kg− K

λ = ⋅ ⋅ ρ ⋅ ⋅ ⋅

La longueur d’onde de ce matériau pour une période de 24h est de 86 cm.

Traçons les composantes de Zt en fonction de l’épaisseur de la paroi monocouche (Fig. I-7). Lorsque l’épaisseur L du mur est très faible devant Λ, Zt se comporte comme une résistance pure. La partie réelle de Zt augmente avec L pour atteindre sa valeur maximale lorsque L

4 Λ = , puis elle décroît pour devenir négative. La partie imaginaire de Zt est positive lorsque l’épaisseur

est inférieure à 2 Λ

pouvant faire penser à un comportement inductif de la paroi. En effet, la phase de Zt est positive dans cet intervalle.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -5 0 5 10 15 Epaisseur de la paroi (m) P a rt ie ré el le de Z t (m 2 .K /W) 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -15 -10 -5 0 5 Epaisseur de la paroi (m) P a rt ie ima g in a ir e d e Z t ( m 2 .K /W )

Fig. I-7 : Variation de l’impédance transversale complexe en fonction de l’épaisseur

Nous présentons sur la figure Fig. I-8, les éléments de l’impédance Z2 en fonction de l’épaisseur du mur. La partie réelle de Z2 est toujours positive et se comporte comme une résistance de fuite. La partie imaginaire est toujours négative, c’est donc une réactance capacitive XC. On peut donc déduire de cette réactance la valeur de la capacité thermique :

C th th C 1 1 X C C X = − ⇔ = − ω ω (I-44)

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0 0.01 0.02 0.03 0.04 0.05 P a rt ie ré el le de Z 2 (m 2. K /W) 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -1.5 -1 -0.5 0 Epaisseur de la paroi (m) P a rt ie ima g in a ir e d e Z 2 ( m 2 .K /W )

Fig. I-8 : Variation de l’impédance Z2 complexe en fonction de l’épaisseur

En analysant la variation de Cth en fonction de l’épaisseur de la paroi (Fig. I-9), on remarque que cette dernière croît de manière quasi linéaire aux faibles valeurs de l’épaisseur ( L

4 Λ < ) et sa valeur se confond à C L 2 ρ

. Cth atteint sa valeur maximale lorsque L 2 Λ

= . Au-delà de cette valeur, Cth décroit asymptotiquement vers sa valeur à L= Λ . Il est donc inutile du point de vue de la capacité thermique d’avoir une épaisseur supérieure à

2 Λ

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0 50 100 150 200 250 300 350 Epaisseur de la paroi (m) C a pa c it é t h erm iqu e d e l a p a ro i (k J /(m 2. K ))

Fig. I-9 : Variation de la capacité thermique en fonction de l’épaisseur

Nous pensons que la capacité thermique Cth est le paramètre le plus indiqué pour caractériser l’inertie thermique d’une paroi. Pour démontrer cette assertion, nous allons dans ce qui suit déterminer la relation qui existe entre l’effusivité thermique et la capacité thermique. L’effusivité thermique détermine la capacité d’un matériau à accumuler de la chaleur et est le paramètre utilisé pour caractériser l’inertie d’un matériau. Nous allons calculer la capacité thermique d’une paroi de résistance thermique constante (Rth=3 m2.K.W-1) constituée d’un matériau se trouvant dans le tableau Tab. I-1. La figure Fig. I-10 montre une corrélation linéaire entre la capacité thermique et l’effusivité thermique.

Tab. I-1 : Paramètres thermophysiques de quelques matériaux de construction

Matériau ρ (kg/m3) Cp (J/(kg.K)) λ (W/(m.K)) b (J/(m2.K. s0.5))

Béton de granulats plein 2300 936 1.75 1941.0

1650 864 1.15 1280.4 Béton de granulats caverneux

2100 864 1.4 1593.8

Mortier 1950 846 1.15 1377.4

Brique de terre cuite 1900 864 1.15 1374.0

Pierre lourde 2600 702 3 2340.0

Pierre de calcaire 2450 720 2.4 2057.6

Meulière lourde 2200 756 1.8 1730.2

Brique de terre crue 1800 846 1.1 1294.2

Béton de laitier plein 2300 882 1.4 1685.2

Béton de laitier caverneux 1800 882 0.7 1054.2

1000 864 0.35 549.9 Béton de pouzzolane 1650 864 0.52 861.0 400 882 0.16 237.6 Béton cellulaire 800 882 0.33 482.5 Plâtre courant 900 1080 0.35 583.3 Bois lourd 650 2394 0.23 598.2 Bois léger 400 2718 0.12 361.2 Panneau de particules 600 2300 0.14 439.6 Laine minérale 15 840 0.04 22.4 Polystyrène 18 1380 0.04 31.5

0 500 1000 1500 2000 2500 0 50 100 150 200 250 300 350 400

Effusivité thermique (unité SI)

Capac ité ther m ique de la pa ro i ( k J /( m 2 .K) ) 0 500 1000 1500 2000 2500 0 50 100 150 200 250 300 350 400

Effusivité thermique (unité SI)

Capac ité ther m ique de la pa ro i ( k J /( m 2 .K) )

Fig. I-10 : Variation de la capacité thermique en fonction de l’effusivité thermique

Les développements faits plus haut sur la capacité thermique Cth concernent une paroi monocouche. Qu’en est-il pour les parois multicouches ? Pour bien illustrer nos propos, considérons une paroi d’épaisseur fixe L constituée de 2 couches d’épaisseur variable (Fig. I-5). Les deux couches ont les propriétés thermophysiques suivantes :

1 1 -3 -1 -1 1 1 1 1 1 -3 -1 -1 2 2 2 0.03 W m K ; =32 kg m et C =840 J kg K 1.5 W m K ; =2200 kg m et C =1000 J kg K − − − − ⎧λ = ⋅ ⋅ ρ ⋅ ⋅ ⋅ ⎪ ⎨ λ = ⋅ ⋅ ρ ⋅ ⋅ ⋅ ⎪⎩

Les effusivités des deux couches sont très différentes, il n’existe donc pas de paroi homogène équivalente à cette paroi bicouche.

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0 50 100 150 200 250 300 350

Epaisseur de la couche isolante (m)

C a pa c it é t h erm iqu e C th (k J /(m 2. K )) Cth1 Cth2

Fig. I-11 : Variation de la capacité thermique en fonction de l’épaisseur de la couche 1

La variation des capacités thermiques Cth1 et Cth2 en fonction de l’épaisseur L1 de la couche 1 est montrée sur la figure Fig. I-10. Aux très faibles épaisseurs de la couche 1, les deux capacités thermiques sont identiques. La couche 1 se comporte comme une simple résistance. L’énergie thermique est stockée dans la couche 2. Lorsque L1 augmente, la capacité thermique Cth1 se dégrade très rapidement et tend asymptotiquement vers une valeur très faible (celle d’un mur monocouche constitué de cet isolant). Par contre, la capacité thermique Cth2 varie très légèrement aux faibles valeurs L1 (donc aux grandes valeurs de l’épaisseur de la couche 2). C’est le comportement de la capacité thermique d’une paroi monocouche lorsque son épaisseur est supérieure à

2 Λ

. Cth2 atteint cette fois sa valeur maximale à L₂ 4 Λ = au lieu de 2 Λ pour la paroi monocouche. L’épaisseur utile de la couche d’une paroi bicouche est la moitié de celle d’une paroi monocouche. Cela s’explique par le fait qu’une couche d’une paroi bicouche contribue uniquement dans la capacité thermique d’un côté. Ce résultat est important car il montre qu’il est inutile du point de vue de la capacité thermique d’avoir une couche d’épaisseur supérieure à

4 Λ

I-3 Optimisation par algorithme génétique

Un des objectifs de notre travail consiste à optimiser l’isolation thermique et l’inertie thermique d’une paroi. Nous allons utiliser un algorithme génétique pour faire cette optimisation multi-objectif.

Les algorithmes génétiques sont des méthodes stochastiques de recherche qui imitent l’évolution biologique de la nature [GOL. 1994]. Ces algorithmes opèrent sur une population de solutions potentielles d’un problème en appliquant le principe de survie des plus adaptées qui produisent par croisement de meilleures solutions au problème.

Une description du fonctionnement d’un algorithme génétique est faite en annexe 1.

Nous présentons dans ce qui suit en détails un algorithme évolutionnaire développé par G. Leyland [LEY. 2002] et A. Molyneaux [MOL. 2002] au Laboratoire d’Energétique Industrielle (LENI) de l’Ecole Polytechnique Fédérale de Lausanne (EPFL). Cet outil a été conçu pour l’optimisation des systèmes énergétiques qui sont le plus souvent non-linéaires, discontinus, disjoints et multimodaux. Les objectifs fixés dans le cahier de charges pour le développement de l’outil MOO sont entre autres :

- l’algorithme doit être multi-objectif pour permettre une optimisation multicritère sans recourir au regroupement des critères ;

- l’algorithme doit rechercher les optima locaux et globaux, car dans un problème multimodal certains optima locaux peuvent être intéressants à prospecter ;

- l’algorithme doit, après un nombre limité d’évaluations de la fonction objectif, converger rapidement vers les optima locaux et globaux.

Ces objectifs ont été atteints par l’outil MOO. En effet, MOO est un algorithme évolutionnaire multi-objectif et multimodal qui utilise une technique statistique de groupement des individus sur la base des variables indépendantes (création de familles évoluant de manière indépendantes). Cette méthode présente l’avantage de maintenir la diversité de la population et de faire converger l’algorithme vers les optima même difficiles à trouver. Pour éviter que la population soit trop importante et ralentir la convergence de l’algorithme, un choix judicieux d’individus à supprimer est opéré. Dans un problème d’optimisation multicritère, il existe un équilibre tel que l’on ne peut pas améliorer un critère sans détériorer au moins un des autres critères. Cet équilibre est appelé optimum de Pareto. Un point est Pareto-optimal s’il n’est dominé par aucun autre. La

dominance au sens de Pareto dans un problème de minimisation par exemple peut être mathématiquement définie comme suit :

i i i i i, f (x) f (x ') x domine x' i tel que f (x) f (x ') ∀ ≤ ⎧ ⇔ ⎨_{∃ <} ⎩ (I-45)

les fi sont les critères du problème.

L’algorithme MOO préserve les individus situés dans les régions limites de l’espace de recherche et permet ainsi d’explorer l’ensemble des zones optimales du problème.

L’outil MOO est utilisé dans l’optimisation des systèmes énergétiques au laboratoire LENI [PAL. 2007] et ailleurs [BUT. 2007]. Nous utiliserons cet outil dans nos études d’optimisation de parois multicouches et des cavités partitionnées.

I-4 Conclusion

Nous avons montré que la capacité thermique déduite de la représentation en quadripôle d’une paroi peut caractériser l’inertie thermique de cette paroi. Dans le chapitre suivant, nous allons appliquer l’algorithme génétique MOO pour optimiser des parois multicouches par rapport à l’isolation thermique caractérisée par la résistance thermique et par rapport à l’inertie thermique caractérisée par la capacité thermique issue de la représentation quadripôlaire.