Faculté des Sciences, 4 Avenue Ibn Battouta B.P. 1014 RP, Rabat-Maroc Tel +212 (0) 37 77 18 34/35/38, Fax: +212 (0) 37 77 42 61, http:/www.fsr.ac.ma
THÉSE DE DOCTORAT
Présentée par :
Nabila MAMOUNI
Discipline :
Physique Informatique
Spécialité :
Matière condensée et modélisation des systémes
Titre :
Etude ab initio des propriétés magnétiques
et optiques des semi-conducteurs magnétiques
dilués ZnO, GaN, MgO et TiO
2
Soutenue le 16/04/ 2016, Devant le jury :
Président :
Youssef EL AMRAOUI : PES, Faculté des Sciences de Rabat
Examinateurs :
Abdelmajid AINANE : PES, Faculté des Sciences de Meknés
Abdelilah BENYOUSSEF : Professeur, Membre résident, Académie Hassan II, des Sciences Techniques
Mohamed BENAISSA : PES, Faculté des Sciences de Rabat Abdallah EL KENZ : PES, Faculté des Sciences de Rabat Hamid EZ-ZAHRAOUY : PES, Faculté des Sciences de Rabat Mohammed LOULIDI : PES, Faculté des Sciences de Rabat
El Kebir HLIL : Professeur, Institut NEEL, CNRS, Grenoble, France
Remerciements
Les travaux de recherches développés dans cette thèse ont été réalisés au sein du Laboratoire de Magnétisme et Physique des Hautes Energies de l’Université Mohammed V, RABAT, Faculté des Sciences, sous la direction des Professeurs Abdallah EL KENZ et Abdelilah BENYOUSSEF
Je tiens tout particulièrement à remercier mon directeur de thèse, Monsieur Abdallah EL KENZ, Professeur à l’Université Mohammed V, RABAT, Faculté des Sciences. Avec qui j’ai eu le plaisir préparer et obtenir mon DESA. Nos discussions, toujours très fructueuses, ont beaucoup compté dans l’orientation de mes recherches. Encore merci, pour sa disponibilité, son soutien, les coups de main. Il a pris le temps de m’écouter et de discuter avec moi les détails de mes recherches. Ses remarques m’ont permis d’envisager mon travail sous un autre angle. Pour tout cela je le remercie.
Je tiens à remercier très chaleureusement, Monsieur Abdelilah BENYOUSSEF, Professeur à l’Université Mohammed V, RABAT, Faculté des Sciences, pour m’avoir donné la possibilité de réaliser cette thèse, à qui je dois le bien plus que ne saurais exprimer en quelques mots: qu’il trouve ici l’expression de ma profonde gratitude pour avoir assuré la direction de mes recherches. Un grand merci pour votre grande gentillesse et votre disponibilité. Vos conseils étaient, sont et seront toujours les bienvenus.
Je tiens à remercier vivement Monsieur Youssef EL AMRAOUI, Professeur à la Faculté des Sciences de Rabat,qui a bien voulu accepter de présider le jury de cette thèse.
Je remercie vivement à Monsieur Hamid EZ-ZAHRAOUY, Professeur à la Faculté des Sciences de Rabat, d’avoir accepté d’être parmi les membres du jury de ma thèse. Ses remarques et conseils, tous très constructifs, m’ont beaucoup aidé.
Je souhaite également remercier Monsieur Mohammed LOULIDI, Professeur à la Faculté des Sciences de Rabat, pour le partage de ses connaissances scientifiques.
Je suis très reconnaissante à Monsieur Mohammed BENAISSA, Professeur à la Faculté des Sciences de Rabat, d’avoir participé à mon jury de ma thèse et merci pour votre sympathie et votre bonne humeur.
Je suis très reconnaissante à Monsieur Abdelmajid AINANE, Professeur à la Faculté des Sciences de Meknés, qui a accepté d’être le rapporteur de cette thèse et d’avoir participé à mon jury et merci pour votre sympathie et votre bonne humeur.
Je voudrais aussi remercier à Monsieur El Kebir HLIL, professeur de l’Institut Néel, C.N.R.S, FRANCE, qui a accepté d’être le rapporteur de cette thèse. Et aussi, pour ses conseils lors des deux premières années de thèse.
J'ai eu le plaisir de travailler avec à Monsieur Mohammed BOUDINA, Professeur à l’Université BAHRAIN, qui a suivi mes travaux à distance, pendant ces trois années de thèse. Merci pour son soutien durant la période de rédaction de ce manuscript, sa patience pour ses discussions scientifiques (et toutes les autres) ainsi que pour sa gentillesse.
Je remercie également mes collègues de Laboratoire de Magnétisme et Physique des Hautes Energies pour l’ambiance qui règne dans le labo, pour toutes les discussions que nous avons eues et pour leurs soutiens et leurs disponibilités. Je profite aussi de cet espace pour exprimer mes remerciements à toutes les personnes qui ont contribué, de près ou de loin, à l’accomplissement de cette thèse.
Je tiens à exprimer mes remerciements les plus sincères à Mme Houda BIYADE pour ses encouragements et son aide précieuse lors de la relecture de ce manuscrit.
Finalement, un grand merci à mes parents pour m’avoir toujours encouragée et soutenue durant mes études et à mon frère Mohammed qui n’a jamais économisé son temps ni son énergie pour me m’aider. J'ai également une pensée affectueuse pour mes frères et mes sœurs.
Résumé
Ce travail de thèse est dédié à l’étude des effets des métaux de transition sur les comportements magnétique et optique des semi-conducteurs. Les matériaux (MgO, ZnO, GaN et TiO2) ont des propriétés magnétiques qui sont dues aux paramètres liés à la structure et aux paramètres magnétiques de chacun des matériaux. Nous avons comparé nos résultats avec d’autres résultats théoriques et expérimentaux, sachons que la modélisation peut s'établir comme étant un outil performant à mettre en œuvre en parallèle avec l'étude expérimentale. Nous avons utilisé plusieurs méthodes de calculs : Théorie du champ effectif et les méthodes ab initio qui sont devenues aujourd’hui un outil de base pour le calcul des propriétés électroniques et structurales, leur algorithme est basé sur la méthode de la DFT. Puisque, les calculs DFT sur les composés semi-conducteurs peuvent être effectués à l'aide de la fonctionnelle LDA ainsi que par différentes fonctionnelles GGA.
De façon générale, l’étude des propriétés magnétiques et optiques des systèmes (MgO, ZnO, GaN et TiO2) étant donné leur importance dans des applications technologique et l’obtention des semi-conducteurs ferromagnétiques à température ambiante. Ainsi, nous avons montré la nature des interactions magnétiques dans les systèmes (MgO, ZnO, GaN et TiO2) étant essentiellement le super-échange, le double échange de Zener et l’interaction Ruderman-Kittel-Kasuya-Yoshida (RKKY).
Mots-clefs : Oxyde de zinc ; Semi-conducteurs magnétiques ; Spintronique ; Calculs ab initio ; Structure électronique ; Champ effectif ; Méthode de KKR-CPA ; VSM.
Abstract
The effect of transition metals behavior on the magnetic and optical behavior of semi-conductors was investigated in this study. (MgO, ZnO, GaN and TiO2) compounds show magnetic properties due to the structure parameters and to the magnetic parameters of each material. Furthermore, the results of this study and other theoretical and experimental results were comparatively studied, considering that the modeling method has established itself as a very efficient tool to implement in parallel with the experimental study. Several calculation methods were used: the effective field theory and the ab intio methods which have became a basic tool for the electronic and structural calculation and whose algorithm is based on the DFT method. The DFT calculations on the semi-conductors can be performed using the functional LDA and various functional GGA.
En general, this study consisted in the investigation of magnetic and optical properties of (MgO, ZnO, GaN and TiO2) compounds, given their importance in the technological applications and obtaining ferromagnetic semi-conductors at room temperature. Finally, the nature of the magnetic interactions in the (MgO, ZnO, GaN and TiO2) systems is revealed to be essentially super-exchange, the Zener double exchange and the Ruderman-Kittel-Kasuya-Yoshida interaction (RKKY).
Keywords: Zinc oxide; Magnetic semi-conductors; Spintronic; Ab initio calculation; electronic structure; Effective field; KKR-CPA method; VSM.
Liste des publications:
1- N. Mamouni, A. Benyoussef, A. El Kenz, H. Ez-Zahraouy, M. Bououdina Electronic
Structure and Magnetic Properties of Zinc-Blende Co-Doped GaN with N Vacancies. J Supercond Nov Magn (2013) 26:663–667.
2- N. Mamouni , A. Benyoussef , A. El Kenz ,H. Ez-Zahraouy , M. Loulidi , E.H. Saidi ,M.
Bououdina A Comparative First-Principles Study of Fe, Co and FeCo-Doped ZnO with Wurtzite and Zinc Blende Structures. J Supercond Nov Magn (2012) 25:1579–1587.
3- N. Mamouni, A. Benyoussef, A. El Kenz, H. Ez-Zahraouy, M. Loulidi Ab initio and Effective
field Study of V doped TiO2 .M. J. condensed matter volume 14, number 1 march 2012.
4- N. Mamouni, M. Belaiche, A. Benyoussef, A. El Kenz , H. Ez-Zahraouy , M. Loulidi ,
E. H. Saidi and E.K.Hlil Electronic and magnetic structures of V-doped zinc blende Zn 1 − xV xN y O 1 − y and Zn 1 − xVxP y O 1 – y .Chin. Phys. B Vol. 20, No. 8 (2011) 087504.
5- M. Bououdina, N. Mamouni, O.M. Lemine, A. Al-Saie, A. Jaafar, B. Ouladdiaf, A. El Kenz,
A. Benyoussef,E.K. Hlil Neutron diffraction study and ab-initio calculations of nanostructured doped ZnO.Journal of Alloys and Compounds 536 (2012) 66–72.
6- N. Mamouni, A. El Kenz, H. Ez-Zahraouy, M. Loulidi, A. Benyoussef, M. Bououdina
Stabilization of ferromagnetism in (Cr, V) co-doped ZnO diluted magnetic semiconductors. Journal of Magnetism and Magnetic Materials 340 (2013) 86–90.
7- S. Azzazaa, M. El-Hilo, S. Narayanan,J. Judith Vijaya, N. Mamouni, A. Benyoussef,A. El
Ken, M. Bououdina Structural, optical and magnetic characterizations of Mn-doped MgO nanoparticles.Materials Chemistry and Physics 143 (2014) 1500e1507.
Liste des abbreviations
FM : Ferromagnetique AFM : Antiferromagnétique
CPA-KKR : Approximation du potentiel cohérent de Korringa-Kohn-Rostoker DFT : Théorie de la fonctionnelle de la densité
KS : Kohn-Sham
DMS : Semi-conducteurs magnétiques dilués DOS : Densités d’états
BC : Bande de conduction BV : Bande de valence DRX : diffraction de rayons X
GGA : Approximation du gradient généralisée LDA : Approximation de la densité locale GMR : Magnétorésistance géante
J : Couplage d’échange magnétique MT : Métaux de transition
RKKY : Couplage RKKY (Ruderman- Kittel-Kasuya-Yoshida) Tc : Température de Curie
TMR : Magnétorésistance tunnel
VSM : Magnétomètre à échantillon vibrant PL : Spectroscopie de Photoluminescence DLM : Moment local désordonné
RTFM : Ferromagnétisme à température ambiante
Table des matières
Introduction générale ... 1
Chapitre I : Cadre théorique ... 6
I.1 Introduction ... 7
I.2 Equation de Schrödinger à un electron ... 7
I.3 La Théorie de la Fonctionnelle de la Densité (DFT) ... 9
I.3.1 Approximation locale de la densité (LDA) ... 11
I.3.2 Approximation des gradients généralisés (GGA) ... 12
I.4 La méthode de KKR-CPA... 12
I.4.1 Le principe de la méthode ... 12
I.4.2 La diffusion par un seul site ... 13
I.4.3 La diffusion multiple ... 15
I.4.4 La dépendance de la fonction de Green en l’énergie ... 16
I.5 Méthode du champ effectif ... 18
I.5.1 L’approximation du champ effectif ... 18
Chapitre II : Les Semi-conducteurs magnétiques dilués (DMS) ... 20
II.1 Introduction ... 21
II.2 Les différents types de semi-conducteurs ... 21
II.2 .2 Structure de bandes ... 22
II.2 .3 Caractéristiques en optique ... 23
II.3 Interactions magnétiques ... 24
II.3.1 Interaction de super-échange ... 24
II.3.2 Interaction de double échange ... 25
II.3.3 Couplage RKKY (Ruderman, Kittel, Kasuya et Yoshida) ... 26
II.3.4 Le modèle des polarons magnétiques de Coey et al ... 27
Chapitre III : Techniques expérimentales et de caractérisation ... 29
III.1 Diffraction des rayons X ... 30
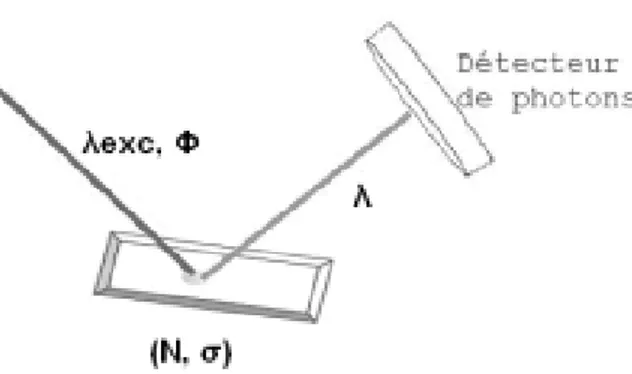
III.2 Spectroscopie de Photoluminescence (PL) ... 30
III.2.1 Diffraction de neutrons ... 31
III.3 Etude des propriétés optiques et des propriétés magnétiques de Zn1-x MTxO ... 32
III.3 .1 Matériels et méthodes ... 32
III.3 .2 Diffraction de neutrons ... 32
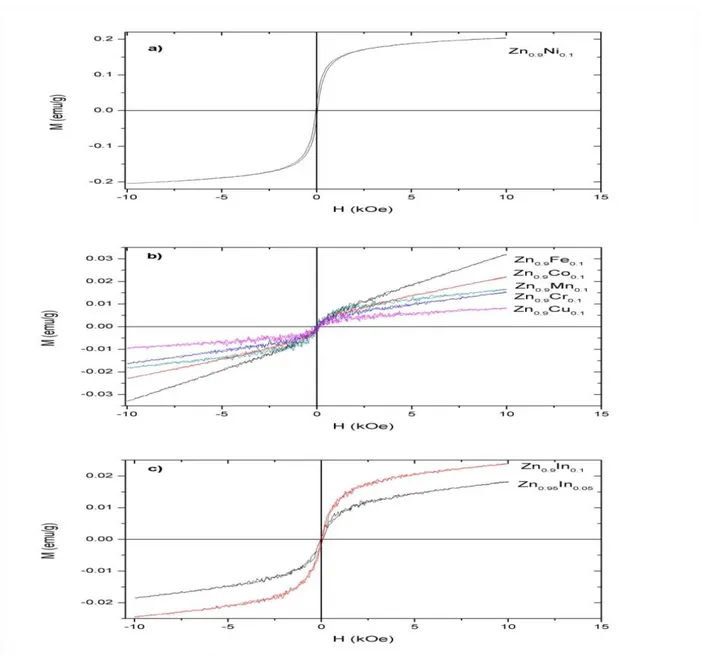
III.3 .3 Propriétés Magnétiques ... 34
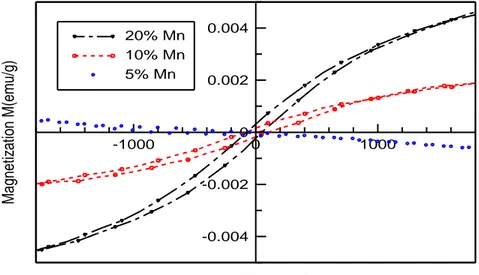
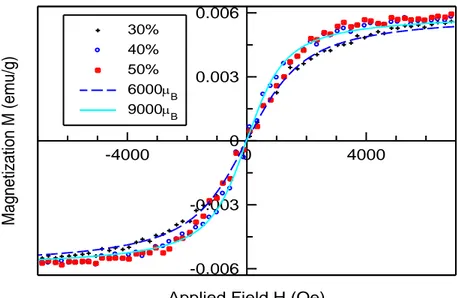
III.4 Etude des propriétés optiques et des propriétés magnétiques de Mg1-x MnxO ... 37
III.4 .1 Matériels et méthodes ... 37
III.4 .2 Caractérisations ... 37
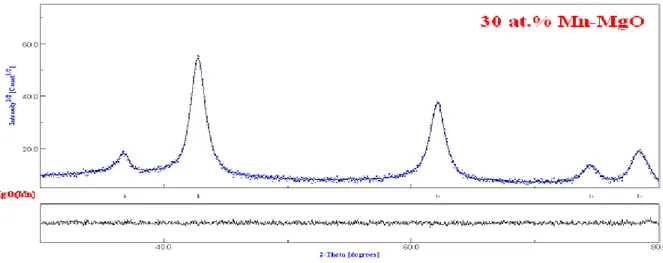
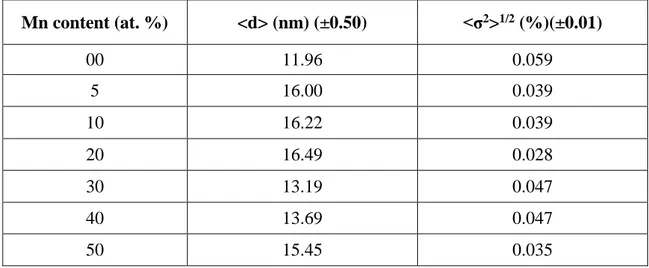
III.4 .3 Analyse de la diffraction des rayons X ... 38
III.5 Propriétés optiques ... 40
III.5.1 Etudes optiques (spectroscopie de réflectance diffuse) ... 40
III.5.2 Etudes de Photoluminescence (PL) ... 41
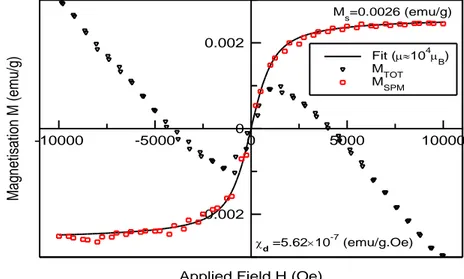
III.5.3 Mesures magnétiques ... 42
CHAPITRE IV : ZnO dopé aux différents métaux de transition ... 48
IV-Introduction ... 49
IV.1 Structure cristalline ... 49
IV.1 .1 Structure Zinc Blende ... 50
IV.1 .2 Structure hexagonale (wurtzite) ... 51
IV.2 Méthodes de calcul ... 51
IV.3 Structure électronique et magnétique du zinc blende dopé au vanaduim (Zn1−xVxNyO1−y et Zn1−xVxPyO1−y)... 52
IV.3 .1 Résultats et discussion ... 52
IV.4 Etude comparative des premiers principes de ZnO dopé par Fe, Co et codopage de (Fe, Co) avec les structures Wurtzite et Zinc Blende ... 57
IV.4.1 Quelques propriétés du système Zn1-xMxO (avec M= Fe, Co et Fe-Co) ... 57
IV.4.2 ZnO dopé avec Fe des structures Zinc-Blende et Wurzite ... 59
IV.4.3 ZnO Zinc-Blende et Wurzite dopé avec Co ... 59
IV.4.4 ZnO Wurzite co-dopé avec Fe-Co ... 60
IV.4.5 ZnO Zinc-Blende co-dopé par Fe-Co ... 62
IV.5 Stabilisation du ferromagnétisme dans les semi-conducteurs magnétiques dilués de ZnO co-dopé avec (Cr, V) ... 64
IV.6 Etude par diffraction des neutrons et des calculs ab-initio de ZnO dopé avec du métaux de transition ... 68
IV.6 .1 Etude du semi-conducteur ferromagnétique Zn1-xMxO ... 68
IV.7 Conclusion ... 71
Chapitre V : Structure électronique et propriétés magnétiques de GaN Zinc-Blende dopé par Co avec les sites vacants de N ... 75
V.1 Introduction... 76
V.2 Propriétés électroniques et magnétiques de Ga1-xCoxN et Ga1−xCoxVcyN1−y ... 76
V.3 Conclusion ... 80
Chapitre VI : Caractérisations structurelles, optiques et magnétiques des nanoparticules MgO dopées avec Mn ... 82
VI .1 Introduction ... 83
VI .2 Structure cristalline ... 84
VI .3 Résultats et discussion ... 84
VI .4 Conclusion ... 90
Chapitre VII : Ab initio et l’étude du champ effectif du TiO2 dopé au vanadium ... 92
VII .1 Introduction ... 93
VII .2 Phase Rutile... 93
VII .3 Calculs d’ab-initio ... 94
VII .4 TiO2 dopé au vanadium... 96
VII .5 Conclusion ... 101
1
2
Les semi-conducteurs sont très utilisés dans différents domaines de l’industrie : électronique, optique, magnéto-optique, magnétique, etc. les technologies de pointe se basent sur les performances et les capacités des composants électriques et optoélectroniques tout en exigeant une production des semi-conducteurs contrôlés au niveau atomique. Ainsi, la fabrication des supports d’enregistrement tels que les disques durs et les souples par exemple, demande des caractéristiques magnétiques, chimiques et mécaniques bien spécifiques. Ces propriétés dépendent des matériaux utilisés et de leurs microstructures. Les chercheurs expérimentateurs s’intéressent donc à la qualité des couches minces en caractérisant leurs microstructures. Ils ont utilisé différentes techniques : La diffusion des neutrons est à l’heure actuelle l’un des outils les mieux appropriés pour étudier les propriétés magnétiques au niveau microscopiques de la matière. D’ailleurs, l’utilisation de la diffraction des neutrons permet une mesure directe des caractéristiques physiques microscopiques à l’échelle des familles de plans inter-réticulaires en position de diffraction. La première utilisation du neutron dans une expérience de diffusion pour étudier la matière date de 1946. Elle s’avère être quasiment indispensable après caractérisation des composés par des mesures macroscopiques telles que la chaleur spécifique et la susceptibilité. Ainsi, Canham et al. ont découvert d’une intense photoluminescence (PL) du silicium poreux dans le domaine visible en 1990, l’intérêt de la recherche en optoélectronique pour l’émission optique des matériaux à base de silicium s’est fortement développé, elle consiste à mesurer un signal de photoluminescence à une longueur d’onde donnée pour différentes valeurs de la longueur d’onde excitatrice. D’autre part, la diffraction des rayons X est une technique d'analyse qui peut fournir des informations sur les caractéristiques structurelles des matériaux à partir de la largeur et l'intensité des pics de diffraction en fonction de la déformation du réseau, la taille des cristallites, ainsi que d'autres imperfections telles que des défauts d'empilement. Actuellement, les besoins croissants dans le domaine de l’informatique, d’accéder rapidement aux données enregistrées et de disposer d’une grande capacité de stockage, ont amené de nombreux chercheurs à déployer leurs efforts pour tenter d’améliorer l’enregistrement magnétique par passage du mode longitudinal, universellement utilisé dans toutes les applications actuelles, à un autre mode d’enregistrement auquel les technologies des multicouches et super-réseaux peuvent apporter une contribution considérable. Parmi les applications technologiques des semi-conducteurs on peut citer l’utilisation de matériaux qui doivent avoir la polarisation la plus grande possible afin d'avoir la magnétorésistance tunnel (TMR) la plus élevée possible. Puisqu'ils possèdent une polarisation de 100%, les matériaux les plus intéressants pour la fabrication de supports d’enregistrement magnétiques à très forte densité de lecture et d’écriture très performants sont donc les matériaux
3
demi-métalliques. Aujourd'hui les études se concentrent préférentiellement sur les propriétés magnétiques, électriques et optiques. Puisque les différents composés semi-conducteurs suscitent un grand intérêt, en premier lieu, les semi-conducteurs à large bande interdite (GaN, AlN, SiC, ZnO, Diamant, etc.) font l’objet d’étude depuis plusieurs années, dans un contexte technologique très compétitif. Tout d’abord, l’ordre ferromagnétique de ces composés réside dans la compétition entre l’interaction ferromagnétique de double échange et l’interaction antiferromagnétique de super-échange. Puisque, l’explication réside dans la structure électronique. A cause du décalage en énergie des états électroniques des deux directions de spin dans le métal ferromagnétique, leur raccordement avec les états électroniques de l’impureté peut être très différent selon la direction de spin considérée, ce qui se traduit par une forte asymétrie en spin de la section efficace de diffusion par l’impureté. Parmi les effets magnétiques très intéressants, l’étude des ordres magnétiques induits sous champ dans des systèmes de spins présentant un gap d’énergie et l’étude des plateaux d’aimantation sont deux exemples de sujets de très grand intérêt dans le domaine de la physique de la matière condensée. Ce qui est remarquable est que l’application d’un champ magnétique permet d’induire un ordre magnétique dans le système et ainsi de modifier complètement ses propriétés magnétiques. Ces phénomènes induits par un paramètre extérieur au système (champ magnétique ou pression par exemple) font partie du domaine très fascinant et très actif qu’est l’étude des transitions de phases. Donc, il est devenu nécessaire d’étudier les transitions de phases magnétiques par des méthodes d’approximation : la méthode du champ moyen. C’est la plus simple des approximations. Elle consiste à considérer un seul spin en remplaçant les interactions avec le reste du système. Et la méthode de l’amas fini basée sur l’idée du champ effectif. C’est une méthode qui a constitué le point de départ pour plusieurs méthodes de calcul des transitions telles, la méthode de l’amas fini proposée par Boccara [14] et développée par Bocarra et benyoussef [15], ou la méthode de l’opérateur différentiel (théorie du champ effectif) proposée par honmura et kaneyoshi [16-17]. Le but de l'étude menée au cours de cette thèse est d’analyser les propriétés électroniques, magnétiques, optiques et le mécanisme d'échange qui correspond au ferromagnétisme dans les quatre systèmes ZnO, MgO, GaN et TiO2. Nous ne pouvons parler d’outils de simulation sans évoquer l’intérêt particulier porté aux méthodes dites ab initio. En plus, nous avons calculé la température de curie en utilisant la théorie du champ moyen. Les chapitres qui suivent présentent les résultats théoriques et des résultats expérimentaux plus précis sur les quatre systèmes qui seront l'objet de la modélisation présentée dans cette thèse.
4
Dans le premier chapitre les méthodes ab initio permettent de décrire le comportement énergétique des matériaux à partir des premiers principes et de connaître la composition des matériaux pour pouvoir les simuler à partir de la résolution des équations de la mécanique quantique. Ensuite, une introduction à la théorie de la fonctionnelle de la densité (DFT) est effectuée. Cette théorie reformule les problèmes à N-corps corrélés en un système d’équations indépendantes se résolvant de façon itérative. Pour pouvoir faire le calcul nous utilisons différentes approximations dont GGA (Approximation des gradients généralisés) et LDA (Approximation locale de la densité).
Le deuxième chapitre constitue une introduction aux semi-conducteurs dopés par des impuretés magnétiques. Il décrit les différents types d’interactions magnétiques existants dans les DMS qui seront exprimées et analysées.
Le troisième chapitre fera l’objet des résultats expérimentaux obtenus avec leurs interprétations. Il comporte deux parties : une première partie portera sur les résultats obtenus par diffraction de neutrons et la caractérisation de Zn1-xMTxO. La deuxième partie de ce chapitre présentera les propriétés optiques et macroscopiques de Mg1-x MnxO, telles que la susceptibilité magnétique et la courbe d’aimantation qui ont été étudiées pour différents pourcentages de Mn.
Dans le quatrième chapitre, on a étudié le comportement magnétique du système (Zn, TM) O. On constate que le magnétisme provient de la polarisation de spin. De plus, le comportement de magnétisme obtenu dans cette étude provient également de l'hybridation des orbitales p de O et des orbitales 3d de MT. En effet, le co-dopage de la structure de wurtzite et Zn-blende avec MT provoque la formation de structures électroniques demi-métalliques. En comparant, les résultats obtenus dans cette étude et les résultats expérimentaux rapportés dans la littérature des systèmes similaires montrent un très bon accord.
Dans le cinquième chapitre, nous avons étudié l’effet des sites vacants N sur les propriétés structurales et magnétiques des systèmes de GaN. La modification du niveau de Fermi due aux sites vacants N a également été signalée.
Dans le sixième chapitre, On a étudié, à la température ambiante, les propriétés optiques et magnétiques des nanoparticules MgO dopées avec des fractions de Mn (5-50 %). Les résultats obtenus suggèrent que les dopants Mn et les sites vacants d'oxygène jouent un rôle important dans le développement du ferromagnétisme à la température ambiante.
5
Dans le dernier chapitre, on présente les résultats de la théorie du champ effectif basés sur le couplage magnétique, et déduits des premiers principaux calculs utilisant KKR-CPA avec l’étude de la corrélation sur les propriétés magnétiques du TiO2 rutile dopé au vanadium.
Le code utilisé dans cette thèse est KKR-CPA. De ce fait, le code MACHIKANEYAMA développé par le professeur Akai est basé sur la méthode de korringa-Kohn-Rostoker (KKR) avec l’approximation du potentiel cohérent (CPA) et amélioré par le professeur Toyoda à travers l’utilisation de l’approximation d’autocorrection (SIC) pour la prise en compte de l’effet de corrélation.
6
7
I.1 Introduction
La théorie de la fonctionnelle de densité (DFT) développée en 1964 et 1965 par Hohenberg, Kohn et Sham [1,2] présente la réduction du problème à plusieurs corps en un problème à un corps dans un champ effectif. Elle fournit une des bases théoriques pour le calcul de structure de bande et la structure électronique. Son idée fondamentale est que, les propriétés exactes de l’état fondamental d’un système fermé formé de noyaux positionnés sur des sites fixes et d’électrons qui les entourent, (c’est-à-dire qu’il ne sera pas question de réactions chimiques), sont des fonctionnelles de la seule densité électronique. Cette idée de l’utilisation de la densité électronique comme variable fondamentale pour décrire les propriétés du système a toujours existé en leitmotiv depuis les premières approches de la structure électronique de la matière (approche de Thomas-Fermi [3-4]) mais n’a obtenu de preuve que par la démonstration des deux théorèmes de Kohn et Sham [2] en 1965. On notera qu’il est relativement aisé d’utiliser la densité électronique qui ne dépend que de 3 coordonnées spatiales pour décrire un système d’électrons ou, à la limite, de 6 coordonnées si l’on considère deux populations de spins (↑et↓) pour décrire les systèmes magnétiques.
I.2 Equation de Schrödinger à un electron
Lorsqu’ on veut étudier la matière, on se base sur le calcul de mécanique quantique pour calculer toutes les propriétés d’un ensemble d’atomes à l’aide de l’équation de Schrödinger (I.1)
Ĥ ᴪ = E ᴪ I.1
Ou Ĥ est l’Hamiltonien du système, ᴪ est la fonction d’onde et E est l’énergie du système. La résolution de cette équation permet de déterminer ᴪ ainsi que la valeur de son énergie or, pour resoudre cette équation, il est nécessaire d’introduire différentes approximation.
L’approximation Bon Oppenheimer [5] se base sur le fait que la masse d’un noyau quelconque est nettement supérieure à celle de l’électron. En d’autres termes, le mouvement des noyaux par rapport aux électrons peut être négligé. C’est -à- dire que les noyaux seront considérés comme figés. Après l’application Bon Oppenheimer, on est ramené à un problème de N électrons en interaction soumis à un champ externe créé par les noyaux, ce problème électronique est toujours trop difficile à cause de la complexité des interactions e-e, c’est pourquoi cette dernière est très couplée à l’approximation de Harter [6], qui considère les électrons comme indépendants, chaque deux évoluant dans le champ créé par tous les autres. A chaque électron correspond une orbitale et des fonctions d’onde à une particule orthogonales entre elles :
8
I.2
L’énergie totale du système est définie comme une fonctionnelle de la fonction d’onde : I.3
La fonction d’onde (1.2) est incompatible avec le principe de Pauli qui stipule que le signe de ᴪ doit changer si l’on permute deux de ses arguments. Ce problème est levé par la description de la fonction d’onde comme un déterminant de Slater [7].
On obtient alors une équation de Schrödinger pour chaque fonction d’onde (orbitale) ᴪi I.4
Ce sont les équations de Hartree, et Ԑi représente le niveau électronique correspondant à ᴪi(r). Le premier terme est l’énergie cinétique de l’électron et le deuxième terme exprime le potentiel
effectif que subit l’électron sous l’influence du noyau ainsi que celle des autres électrons. Ce dernier doit prendre en compte l’interaction électron-noyau décrite par l’équation 1.4 :
I.5
Pour l’interaction électron-électron, on considère que l’électron se déplace dans un potentiel qui s’exprime par :
I.6
Ce potentiel décrit l’interaction d’un électron soumis aux autres électrons représentés par une densité de charge .Ainsi l’électron est soumis à ces deux contributions :
I.7
La somme des deux termes VH +VN constitue un potentiel effectif Veff qu’on peut qualifier de local, car il ne dépend que de r.
Les fonctions propres de la solution de l’équation I.3 permettent de calculer la nouvelle densité électronique :
I.8
L’équation (1.9) exprime l’équation de Poisson qui permet de faire le lien entre le potentiel de Hartree VH et la densité électronique.
RI , ri
ψ1
r1 ...ψNe
rNe
ψ
r i ψ i ε (r) i ψ eff v (r) i ψ 2 m 2 2 h
R 2 N R r 1 Ze r V
r VH
´ r r 1 ´ r d r ρ e r VH ' 3
r
r V r V r Veff H N
r *ψi
r i ψi r ρ N 1 i εi E9
I.9
Nous allons voir maintenant l’approche de Hartree-Fock qui ajoute une correction supplémentaire à l’approche de Hartree.
L’approximation de Hartree –Fock [8] prend en compte un élément important : le principe de Pauli, ce dernier nous amène à considérer l’antisymétrie de la fonction d’onde l’un système électronique quantique tel que :
I.10 On obtient ainsi les équations de Hartree –Fock :
I.11
Dans la méthode Hartree-fock, l’énergie totale du système est définie comme une fonctionnelle
de la fonction d’onde. Cette méthode prend l’échange électronique mais ignore la corrélation existante entre le mouvement d’un électron et le mouvement des autres électrons. Les méthodes dérivées de l’approximation de Hartree-Fock ne tiennent compte que d’une partie de l’énergie de corrélation et s’adressent à des petits systèmes. Pour les molécules de taille plus importante ou pour les solides, la méthode utilisée est la théorie de la fonctionnelle de la densité (DFT).
I.3 La Théorie de la Fonctionnelle de la Densité (DFT)
Les méthodes basées sur la DFT sont classifiées selon les représentations utilisées pour la densité, le potentiel et les orbitales de Kohn-sham. L’idée fondamentale de la DFT est que, les propriétés d’un système électronique sont déterminées à partir de la densité électronique, elle repose sur deux théorèmes fondamentaux, démontrés par Hohenberge et kohn [1].
-L’énergie de l’état fondamental est une fonctionnelle unique de la densité électronique ρ(r)
I.12 -le minimum de l’énergie totale du système correspond à la densité exacte de l’état fondamental.
I.13
Cette densité était exactement celle de l’état fondamental à une particule : I.14
ρ0: est la densité de l’état fondamentale.
r1...,ra ....rN
ψ
r1...,ra....rN
ψ
r Ψ
r Ψ
r εψ
r Ψ r r dr d (r) ψ v (r) ψ m 2 h i i j j ' i * j ' ' 3 i eff i 2 2
r 4πρ
r H ΔV
ρ E E
E E0 min
0 0 E E 10
En suite Kohan et sham [9] ont proposé une méthode pratique pour calculer la densité ρ en passant par des orbitales, comme en Hartree-Fock, mais avec un nouveau potentiel effectif, appelé Vks l’équation d’onde des fonctions nano-électroniques est alors décrite par l’expression :
I.15 Dans laquelle le potentiel effectif Vks est exprimé par :
I.16
Le potentiel d’échange corrélation est donné par la fonctionnelle dérivée :
I.17 L’équation de kohn-sham (KS) est résolue d’une manière itérative selon un schéma proposé
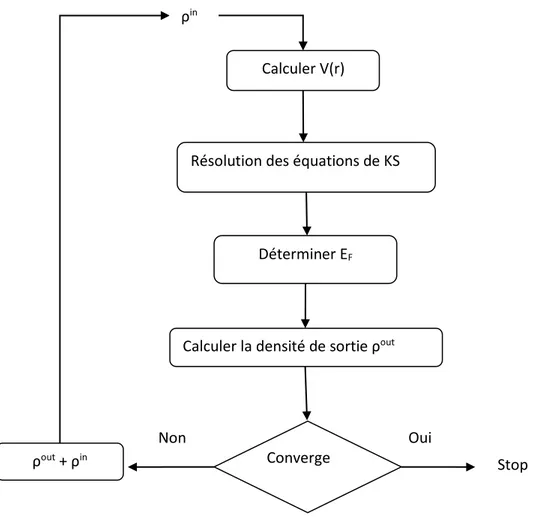
ci-dessous. Le potentiel effectif (KS) dépend de la densité des particules qui elle-même dépend de l’état d’une particule, on arrive à un problème dit auto-cohérent ou self consistent. Le cycle self-consistent commence par l’introduction d’une densité de départ ρin(r) qui permet de calculer le potentiel Vks(r ) après la résolution de l’Hamiltonien obtenu . On obtient l’énergie et les vecteurs propres correspondants à ces valeurs propres permettent de recalculer une nouvelle densité de sortie qui doit être testée suivant les conditions de convergence. Alors, si la densité de sortie obéit à ces conditions, on s’arrête sinon, on mélange la densité de sortie et d’entrée de la manière suivante :
I.18
α est le paramètre de mixage et l’indice i représente le nombre de l’interaction, le processus se répète jusqu’à ce que la convergence soit atteinte.
0 2 2 r r m h i i ks
ν
r r r r ρ r d r ν r ν ' xc ' ' ext ks
i out i in 1 i in 1 α ρ αρ ρ
r δρ ρ , ρ δE V XC xc 11
Figure -1 : Processus itératif pour la résolution des équations de Kohn-Sham
Le terme d’échange et de corrélation résulte de l’interaction électron-électron. Puis, le calcul de l’énergie et du potentiel d’échange-corrélation repose sur un certain nombre d’approximations.
I.3.1 Approximation locale de la densité (LDA)
L’approximation la plus répandue pour calculer le terme d’échange et corrélation est l’Approximation Locale de la Densité, ou LDA. Cette approximation fait l’hypothèse que la densité fluctue assez lentement. Elle remplace donc le potentiel d’échange et corrélation en chaque point de l’espace par celui d’un gaz uniforme d’électrons qui interagissent. Le gaz d’électrons est pris de la même densité que la densité au point calculé. Dans une densité électronique variant”lentement”, Kohn et Sham ont proposé un développement pour l’énergie d’échange-corrélation
I.19 Le terme en gradient au premier ordre ainsi que ceux d’ordres supérieurs sont alors omis,
conduisant à la formule (I.19) : I.20
Calculer V(r)
Résolution des équations de KS
Déterminer EF
Calculer la densité de sortie ρout
Converge ρout + ρin Stop Oui Non ρin
ρ r
d rρε
r Exc
3 xc
ρ(
r
)
ρε
r
d
r
ρ
ε
r
d
r
E
xc
xc
3
2 xc
3
12
I.3.2 Approximation des gradients généralisés (GGA)
La manière la plus naturelle d’améliorer la LDA est de tenir compte de l’inhomogénéité de la densité électronique en introduisant dans l’énergie d’échange et corrélation des termes dépendant du gradient de la densité. La GGA (generalized gradient approximation) [10-12] permet d’introduire une combinaison entre les termes locaux et des termes dépendant du gradient. La solution consiste alors à réécrire l’expression d’échange-corrélation sous une forme similaire à la LDA :
I.21
I.22 est la densité d’énergie d’échange-corrélation. La difficulté réside dès lors dans la
recherche d’expressions analytiques de
I.4 La méthode de KKR-CPA
I.4.1 Le principe de la méthode
La méthode de Kohn-Korringa-Rostoker (KKR) [13] pour le calcul de la structure de bande électronique est une méthode utilisant la théorie de la diffusion multiple reformulée par la technique des fonctions de Green pour résoudre l’équation de Schrödinger sans avoir recours aux fonctions d’onde ni aux valeurs propres de l’Hamiltonien du système. Dans cette approche, les propriétés de la diffusion par chaque centre de diffusion (atome) sont décrites par une matrice de diffusion, alors que la diffusion multiple par tous les atomes dans le réseau est déterminée par le fait que l’onde incidente à chaque centre est la somme des ondes sortantes des autres centres de diffusion.
La fonction de Green et l’équation de Schrödinger :
La fonction de Green G (r, r’, E) associée à l’équation de Schrödinger
I.23 Est définie comme étant la solution de l’équation :
I.24
La signification physique de la fonction de Green :
G (r, r’, E) décrit le mouvement de propagation de la particule libre de r à r’ avec l’énergie E.
ρ(r)
ρε
r d r
ε
r d r Exc xc 3 ρ 2 xc 3
ρ(r) ε
ρ, ρ dr Exc GGAxc GGA xc GGA xc ψ(r) V(r) ψ(r) E) 2 ( ) r' δ(r E) , r' G(r, E) V(r) 2 ( 13 Utilité des fonctions de Green :
La fonction de Green du système est la quantité la plus importante pour le calcul des quantités physiques, à partir de sa détermination toutes les quantités telles que la densité des états, la densité de charge, et par conséquent l’énergie totale ou les moments magnétiques peuvent être extraits. D’autre part, la fonction de Green du cristal parfait (sans défauts) peut être utilisée pour calculer la fonction de Green d’une impureté dans un système avec des défauts via l’équation de Dyson. Les systèmes chimiquement désordonnés peuvent aussi être traités par la méthode KKR dans le cadre de l’approximation du potentiel cohérent CPA (Coherent Potential Ap-proximation).
La résolution de l’équation de Schrödinger :
La résolution de l’équation de Shrödinger (I.23) revient à la résolution de l’équation (I.24) en déterminant la fonction de Green au lieu de la fonction d’onde. L’équation (I.24) possède deux solutions linéairement indépendantes ; une régulière à l’origine, c’est pour cette raison dite solution régulière JL(r). L’autre, la solution non régulière HL(r), présente un comportement singulier pour r→0. La fonction de Green s’écrit en termes de ces deux solutions RL(r) et HL(r). Le potentiel est non nul seulement dans une sphère de rayon rs. Dans le cas de ce potentiel sphérique, la différence dans le comportement asymptotique des solutions, dans et en dehors de la sphère, est déterminée seulement par un déphasage. A l’intérieur de la région du potentiel, les solutions sont différentes des solutions en dehors de cette région. La résolution se fait selon la région du potentiel où on se présente.
I.4.2 La diffusion par un seul site
La fonction de Green pour une particule libre V(r) = 0 a une certaine distance du centre de diffusion, la particule ne ressent pas l’effet du potentiel, elle bouge librement et l’Hamiltonien ne contient que le terme de l’énergie cinétique. L’onde peut être alors décrite comme une onde plane φ(r) = exp(ikr) qui est solution de l’équation de Schrödinger homogène décrivant le mouvement libre de la particule. La fonction de Green G0 (r ; r’ ; E) correspondant à l’opérateur (2 + k2) avec k2 = E satisfait l’équation suivante :
(2 + k2) G0(r; r’;E) = - (r – r’) I.25
Dont la solution est la fonction de Green pour une particule libre :
I.26 G (r,r',E) ik h (kr )jL(kr )
L L
14
r > et r < dénotent respectivement la plus grande et la petite valeur de r et r’. jL(kr) est la fonction sphérique de Bessel définie quand r→0, et hL(kr) est la fonction sphérique de Hunckel qui diverge quand r→0.
La fonction de Green pour une particule diffusée : La solution dans ce cas est déduite du cas libre
via l’équation de Lippmann- Schwinger :
I.27 La solution régulière en présence d’un potentiel de diffusion s’écrit :
I.28 Cette expression décrit physiquement la diffusion de l’onde entrante (r) = jL(kr<) par le potentiel V(r) s’écrit autrement :
I.29 Avec la matrice tl donné par :
I.30
La matrice t porte des informations sur le potentiel. C’est un opérateur de transition entre les ondes planes entrantes et les ondes diffusées. La matrice t peut donc être utilisée pour lier les fonctions d’onde dans, en dehors du potentiel et à sa frontière. Rl (r ; E) est une solution de
l’équation de Schrödinger radiale :
I.31
L’étude du comportement asymptotique de la fonction d’onde radiale RL(r ; E) quand r→
permet d’obtenir : I.32
La fonction de Green pour un seul site de diffusion peut être développée en fonction des solutions régulières et non régulières de la même façon que la fonction de Green pour une particule libre : dr' ) ψ(r' ) V(r' E) , r' (r, G (r) ψ(r) 0
dr' ) ψ(r' ) V(r' E) , r' (r, G ) (kr j (r) RL L
0 ) (kr h (E) t ik ) (kr j (r) RL L
L l L dr' ) (r' J ) V(r' ) (kr j (E) tl
L L 0 E) (r, R E] V(r) r 1) l(l r r r 1 [ 2 2 l 2 (E) sinδ e r E 1 (E) t l (E) iδ l l 15 I.33 Sachant que : I.34 Et I.35
Ainsi, la fonction de Green pour une particule libre s’écrit comme produit de deux solutions linéairement indépendantes. La matrice t est liée à la fonction de Green libre G0 par la relation : t =V+VG0t
La fonction de Green pour un système avec un seul diffuseur s’écrit en termes de la fonction de Green G0 pour une particule libre avec la matrice t représentant la diffusion par un seul site sous la forme : G=G0+G0tG0 : (Fig 2)
Figure-2 : Diffusion par un seul site.
I.4.3 La diffusion multiple
On souhaite étudier un système périodique parfait sans défauts en présence de plusieurs diffuseurs (voir Fig.3). On a besoin d’étendre la diffusion par un seul site à la diffusion multiple. Pour ceci, on définit la matrice T de diffusion pour le système entier :
T = V + VG0T.
Dans le cas d’un seul potentiel, l’opérateur T se réduit à la matrice t définie pour un seul diffuseur. ) (kr H ) (kr R ik E) , r' G(r, L L L
) (kr h (E) ikt ) (kr j RL L l L ) (kr h (E) ikt ) (kr j HL L l L 16
Figure-3 : Electron en mouvement entre atomes.
Chaque atome est un centre de diffusion et le potentiel est constant dans la zone interstitielle (propagation libre) et sur la sphère atomique, le potentiel est sphérique (Muffin-Tin). La fonction de Green G pour le système entier est liée à la matrice T par la relation : G = G0 +G0 TG0. L’électron peut se déplacer directement du site n au site n’, soit après avoir être diffusé par un seul site quelconque, soit par deux sites ou trois, etc. (Voir Fig. 4).
T = t + t G0 t + t G0 t G0 t + . . . = t + t G0(t + t G0 t + . . .) = t + t G0T I.36 Ce qui entraîne : T = (t-1 - G0)-1. Les états stationnaires du système sont donnés par les pôles de T comme fonction de E, ces pôles sont obtenus à partir des zéros du déterminant : det(t-1 - G0)-1 =0. C’est cette équation qui est à la base de la méthode KKR.
I.4.4 La dépendance de la fonction de Green en l’énergie
On peut réécrire la fonction de Green autrement en fonction de l’énergie E, ceci est vrai dans la mesure où la fonction de Green est la solution de l’équation (I.24).
17
Cette équation correspond au problème spectral :
I.37 La fonction de Green de l’énergie s’écrit :
I.38
Ici,
est un nombre réel positif avec
→0, ce qui assure la convergence définissant la transformée de Fourier de la fonction de Green. La fonction de Green peut s’écrire en représentation spectrale sous la forme :I.39
On prend la trace de la fonction de Green, Tr G (r, r’ ; E) = G(r, r ; E) et en tenant compte des propriétés de (r), on obtient après avoir intégré sur r, l’équation suivante :
I.40 On obtient :
I.41 La densité d’état n(E) localisée sur un atome est donnée par :
I.42 La densité de charge (r) localisée sur un atome est donnée par :
I.43
D’une manière générale, à partir de la représentation spectrale, il s’ensuit que la valeur de toute observable physique, représentée par un opérateur A, peut être calculée par la relation :
I.44
Par conséquent, la fonction de Green contient toute information donnée par les fonctions propres. Une fois la fonction de Green est déterminée, toutes les propriétés physiques peuvent alors être trouvées.
(r)
ψ
V(r)
(r)
ψ
E)
(
2
n
n iε H E 1 G(E)
n E En iε ) (r' * n ψ (r) n ψ 0 εlim
E)
r'
G(r;
n iε n E E 1 0 εlim dr E) r, G(r; n n ) E δ(E E) r, drG(r, Im π 1 Im G(r,r,E)dr π 1 n(E) Im EFG(r,r,E)dE π 1 ρ(E)
F E dE E)] r, T[AG(r, Im π 1 A18
I.5 Méthode du champ effectif
La théorie du champ effectif qui a constitué le point de départ pour plusieurs méthodes de calcul des transitions telles, la méthode de l’amas fini proposée par Boccara [14] et développée par Bocarra et benyoussef [15], ou la méthode de l’opérateur différentiel proposée par honmura et kaneyoshi [16-17].Cette méthode qui a la simplicité du champ moyen donne de meilleurs résultats qualitatifs et quantitatifs. Elle ne s’applique qu’à des systèmes dont le désordre est décrit par des variables discrètes. Elle consiste à prendre un spin central et calculer sa valeur moyenne en fixant tous les autres spins du réseau. La valeur moyenne sur toutes les configurations donne l’équation d’état du système qui permet de déterminer la température de transition et d’autres propriétés.
I.5.1 L’approximation du champ effectif
L’Hamiltonien du système est : I.45
La première sommation porte sur les sites où il y a l’impureté et la deuxième sommation est portée sur les voisins jusqu’à une portée donnée. ni est une variable aléatoire prenant la valeur 0 ou 1 selon que le site i est occupé par l’impureté magnétique avec la probabilité p ou non avec la probabilité (1-p). Jij est l’interaction d’échange.
On a : 0 x D σ n J n i i σ e F(x) n pm i j i ij i I.46 Et 0 x D σ n J n 2 i i σ e G(x) n pq i j i ij i I.47
Avec F(x) et G(x) sont des fonctions qui dépendent de l’état du spin S, par exemple pour un spin S=1 :
x 1 cosh 2 x sinh 2 F(X) Et
1 x cosh 2 x cos 2 G(X) I.48On utilise l’opérateur différentiel défini par : e f(x) x 0 f(a)
Da I.49
j i, ij i j i jS
S
n
n
J
H
19
On peut calculer l’aimantation m :
1
1
01
1 cosh sinh ...1 cosh sinh
1 1 X Z i i i i Z X F J m J p p J m J p p m i I.50 Avec :
1
1
0 1 1 2 sinh cosh 1 ... sinh cosh 1 1 X Z i i i i Z X G J m J p p J m J p p q i I.51 zi et le nombre de i énièmes voisin, pi est la probabilité d’occupation du i énièmes voisin.On obtient deux équations couplées de m et q :
i im A ... m A m A m 1 3 3 I.52 j j 2 2 0 A m ... Am A q I.53
Où les coefficients A0, A1, A2, A3, A4, A5… Ai, sont des fonctions des concentrations, de la température T, du paramètre ƞ, de l'interaction d'échange Jij, de p1, pi et ainsi que de la température de curie Tc , pour un modèle d’Ising dilué sur une structure donnée et pour un état de spin S peut être déterminé en résolvant numériquement les équations couplées (I.52)-(I.53).
20
Chapitre II : Les Semi-conducteurs
magnétiques dilués (DMS)
21
II.1 Introduction
Dans un matériau ferromagnétique, les électrons des deux directions de spin conduisent le courant en parallèle avec des mobilités qui peuvent être très différentes. Ce phénomène est à la base des effets et dispositifs d’électronique de spin (ou Spintronique) [18]. La magnétorésistance géante des multicouches magnétiques est un premier exemple d’effet d’électronique de spin et il est aujourd’hui utilisé pour la lecture des disques durs ou bandes magnétiques. L’étude des phénomènes d’électronique de spin s’est depuis étendue à divers types de nanostructures magnétiques qui associent des matériaux ferromagnétiques avec des métaux, des isolants ou des semi-conducteurs. Les jonctions tunnel magnétiques sont aujourd’hui particulièrement étudiées avec des perspectives importantes d’applications dans le domaine des mémoires non volatiles. La possibilité de doper des semi-conducteurs avec des éléments magnétiques a permis de créer une nouvelle catégorie de matériaux appelés les semi-conducteurs magnétiques dilués (DMS) [19]. Une des particularités des DMS est l’apparition de moments magnétiques localisés générés par le couplage électron-trou. Ceci mène à des propriétés intéressantes comme, par exemple, l’augmentation des porteurs de charge ou à des excitations nouvelles, comme les polarons magnétiques. Mais le ferromagnétisme est rarement observé dans les semi-conducteurs à cause de la faible densité des porteurs et aussi à cause de la prédominance du super-échange entre les moments magnétiques locaux. Dans la plupart des cas, les semi-conducteurs magnétiques ont des températures de Curie basses.
II.2 Les différents types de semi-conducteurs
Parmi les semi-conducteurs on distingue deux grandes catégories : les semi-conducteurs intrinsèques et les semi-conducteurs extrinsèques.
Un semi-conducteur est intrinsèque lorsqu’il ne possède aucun défaut physique, ni défaut chimique. La structure ne présente aucune lacune, il n’y a aucune impureté dans le réseau .Ce type de semi- conducteur, les porteurs de charges ne peuvent être fournis que par les atomes du réseau.
Un semi-conducteur extrinsèque est obtenu grâce à l’introduction d’impuretés, par dopage n ou p, ce qui augmente considérablement la conductivité des semi-conducteurs intrinsèques.
Les éléments chimiques choisis comme dopant présentent une valence différente de celle du semi-conducteur. Ils se positionnent dans son réseau en site substitutionnel, c’est-à-dire en remplacement de certains atomes. Si, après le dopage, la concentration en électrons est supérieure à celle des trous, on qualifiera le semi-conducteur de type n. Dans le cas contraire, on parlera de semi-conducteur de type p.
22
On peut distinguer trois types de semi-conducteur : les semi-conducteurs non magnétiques, constitués de cations et d’anions diamagnétiques (spin nul S=0), les semi-conducteurs magnétiques, dans lesquels les cations diamagnétiques ont été remplacés pardes cations magnétiques (spin non nul S ≠ 0), et enfin les DMS, encore appelés conducteurs semi-magnétiques, dans lesquels une fraction seulement des cations diamagnétiques est remplacée par des cations magnétiques de façon aléatoire (Fig 1). On peut considérer le semi-conducteur comme un ensemble de deux systèmes électroniques, l’un contenant des électrons délocalisés (bande de valence et bande de conduction) et l’autre contenant les électrons des impuretés magnétiques avec un moment magnétique localisé.
Figure- 1 : Représentation schématique de trois types de semi-conducteurs
II.2 .1-Origine du ferromagnétique Les semi-conducteurs ferromagnétiques peuvent être
II.2 .2 Structure de bandes
Pour déterminer les propriétés des métaux et isolants, il faut donner les définitions d’un certain nombre de termes indispensables de l’atome. Les électrons sont répartis en orbitales autour du noyau atomique ; on peut ainsi déterminer des niveaux d’énergie : les électrons les plus "proches" du noyau sont ceux dont l’énergie est la plus faible, et les plus "éloignés" sont ceux dont l’énergie est plus élevée. Les électrons exécutent ainsi des "sauts" d’un niveau d’énergie à un autre lorsque l’atome acquiert ou perd de l’énergie. Il existe plusieurs niveaux d’énergie contenant des électrons de valence (respectivement de conduction), on parle de bandes de valence (respectivement de conduction) Fig 2. Chaque bande (chaque niveau d’énergie) peut contenir jusqu’à deux électrons ; on peut ainsi parler de bande vide (aucun électron dans la bande), de bande à moitié pleine (un électron) ou de bande pleine (deux électrons dans la bande). Entre les bandes de valence et celles de conduction, il peut exister une fourchette d’énergies dans laquelle il n’y a pas de niveaux : on parle alors de bande interdite (ou gap) ; aucun électron ne peut se trouver dans cette gamme d’énergies. Enfin, on remplit les diverses bandes avec les
(a) éléments magnétiques formant un réseau périodique, (b) semi-conducteurs sans éléments
23
électrons disponibles dans le matériau, en commençant par les plus basses énergies puis et en complétant par les bandes supérieures avec les électrons restant ; cela donne la configuration électronique de plus basse énergie, celle que le matériau possède au zéro absolu (0 Kelvin) : on parle d’état fondamental. A partir de cet état fondamental, on peut estimer l’énergie maximale que peut avoir un électron : c’est l’énergie de Fermi (on parle aussi de niveau de Fermi). Lorsque des électrons de la bande de valence partent sur la bande de conduction, il y a création d’états vacants dans cette bande de valence, qui devient presque pleine seulement. Les propriétés des états vacants dans une bande presque pleine sont très importantes dans la physique des semi-conducteurs. Et aussi, ces états vacants sont appelés trous. Lorsqu’on applique un champ électrique ou magnétique au matériau, un trou réagit comme s’il était porteur d’une charge.
Figure-2 : Schéma des niveaux d’énergie
II.2 .3 Caractéristiques en optique
Les propriétés optiques des semi-conducteurs sont extrêmement liées à leur structure électronique, sachons que les propriétés optiques se manifeste sous forme d’interaction du rayonnement avec les électrons.
• Absorption :
L’absorption de lumière par un semi-conducteur a lieu à partir d’un seuil : le photon doit avoir une énergie E > Eg pour pouvoir être absorbé. Le semi-conducteur peut donc être vu comme un filtre passe-bas en énergie (passe-haut en longueur d’onde). L’absorption étant très efficace, la totalité de la lumière incidente est généralement absorbée par un échantillon d’épaisseur classique (≈ 0,5 mm.)
24
• Emission :
L’émission, par contre, est résonante : elle a lieu à E ≈ Eg. On peut l’observer dans une diode électroluminescente (DEL, ou LED en anglais). L’injection de porteurs est alors produite par l’alimentation électrique.
II.3 Interactions magnétiques
Les couplages d’échange peuvent être de plusieurs types :
-Couplage direct entre spins appartenant à des orbitales d’atomes voisins, et qui se recouvrent. -Couplage indirect entre deux spins, via un atome intermédiaire non magnétique, ou par l’intermédiaire d’un gaz d’électron (RKKY).
Les principales interactions sont le super-échange, le double échange et l’interaction RKKY (Ruderman, Kittel, Kasuya et Yoshida).
II.3.1 Interaction de super-échange
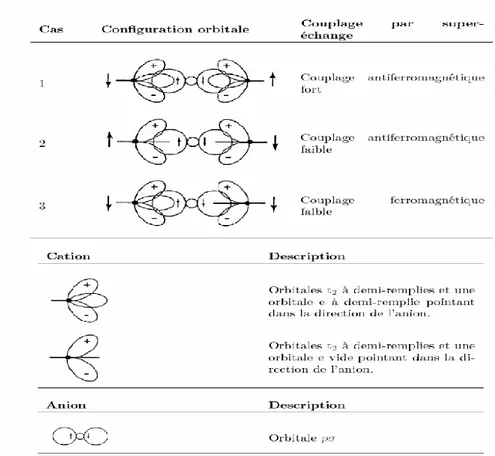
Le super-échange est une interaction indirecte qui se produit entre les impuretés magnétiques par l’intermédiaire des atomes non magnétiques, comme dans le cas des oxydes de métaux de transition ou des composés de structure pérovskite. Dans ce type d’échange, les charges sont localisées et l’interaction dépend fortement des configurations des orbitales, ce qui donne lieu souvent à un couplage antiferromagnétique qui suit les règles de Goodenough-Kanamori-Anderson [20,21,22]. Pour ce couplage antiferromagnétique apparait, il faut que les orbitales cationiques et anioniques soient alignées, c’est –à-dire que l’angle de la liaison métal-oxygène-métal sera fixé à 180°, afin d’obtenir un ordre magnétique. La Fig 5 montre un schéma qui donne les différentes configurations cation-anion-cation à 180°. Dans le cas où les deux cations ont une orbitale eg à moitié pleine pointant dans la direction de l’anion, le couplage est directe par les règles de Hund et donne de l’antiferromagnétisme fort (cas 1 dans la Fig 3). Le cas où les deux orbitales eg sont vides (cas 2 dans la Fig 3) donne également de l’antiferromagnétisme, mais faible. Si le recouvrement d’orbitales est suffisamment fort, c’est –à-dire, que les orbitales des deux cations sont suffisamment remplies, chaque spin de l’orbitale px va interagir avec l’électron de l’orbitale du cation adjacent en le forçant à lui être antiparallèle. Par conséquent, les spins de deux atomes des métaux de transition auront une configuration antiparallèle. Un tel mécanisme conduit à un couplage antiferromagnétique fort, c’est le super-échange. Mais au contraire, si le recouvrement d’orbitales est très faible ou nul, les deux cations auront des spins parallèle ce qui conduit à un couplage ferromagnétique.
25
Dans le cas des semi-conducteurs magnétiques dilués, les mêmes mécanismes peuvent être appliqués pour déterminer l’ordre magnétique dans ces composés. Le super-échange peut-être décrite par un hamiltonien d’Heinsenberg. Dans lequel le signe de couplage est déterminé par l’angle de lien métal –intermédiaire –métal et la configuration de l’électron d des métaux de transition.
Figure -3 : Ordre magnétique en fonction du type d’orbitale des cations avoisinants.
II.3.2 Interaction de double échange
L’interaction de double échange est une interaction ferromagnétique qui correspond à l’interaction entre les cations d’une même espèce et de valences différentes, avec échange d’un électron de couche 3d via un atome non magnétique, par exemple entre Mn4+ et Mn3+ séparés par un ion oxygène. Elle permet au système de gagner de l’énergie en délocalisant l’électron e↑
g de l’ion Mn3+ sur les deux ions Mn, par rapport à une configuration ou l’ion Mn3+ garde son électron e↑g. Le saut est facilité si les moments magnétiques des manganèses voisins sont alignés car le saut peut se faire sans émission d’excitations magnétiques .Ainsi ,La première étude faite sur les manganites à structure pérovskite date depuis 1951 quand C. Zener a introduit le modèle de double échange [23,24] pour expliquer les propriétés de transport et de
26
magnétisme, dont la résistance et la polarisation en spin. Ce modèle fait intervenir les ions d’oxygène pour assurer le transport des électrons entre les cations manganèse d’états de charges différents (charges (III) et (IV)), qui sont séparés par une distance trop grande et pour lesquels l'échange direct (cation-cation) est nul.
Figure- 4 : Mécanisme du double échange.
II.3.3 Couplage RKKY (Ruderman, Kittel, Kasuya et Yoshida)
Le mécanisme RKKY a été introduit pour expliquer le ferromagnétique dans les terres rares [25,26,27].Ainsi que c’est une interaction d’échange indirecte très forte entre les moments localisés portés par les orbitales 4f des terres rares, réalisée par l’intermédiaire des électrons de conductions. La théorie RKKY avait en effet prédit l’oscillation entre les états ferromagnétiques-antiferromagnétiques d’une multicouche formée de deux matériaux magnétiques séparés par un métal non magnétique, oscillation dépendante de la distance entre les couches. Contrairement à l’interaction d’échange directe qui nécessite le recouvrement des fonctions d’ondes électroniques des deux moments magnétiques locaux, l’interaction RKKY ne requière pas ce recouvrement. C’est parce qu’elle utilise la médiation des électrons de conduction qu’elle est susceptible de s’opérer entre deux spins même très éloignés et qu’elle est dominante dans les alliages magnétiques dilués. Dans le système des tri-couches (F1/NM/F2), les électrons de la couche non-magnétique acquièrent une polarisation au contact des deux couches ferromagnétiques. Cette polarisation décroit tout en s’éloignant de l’ion magnétique d’une manière oscillatoire, qui s’explique par la nature ondulatoire de ces électrons de conduction. Selon l’épaisseur de la couche séparatrice (NM), l’interaction RKKY entre les deux couches magnétiques peut passer d’un couplage ferromagnétique à un coulage antiferromagnétique.
27
Figure- 5 : Couplage d’échange indirect RKKY.
II.3.4 Le modèle des polarons magnétiques de Coey et al
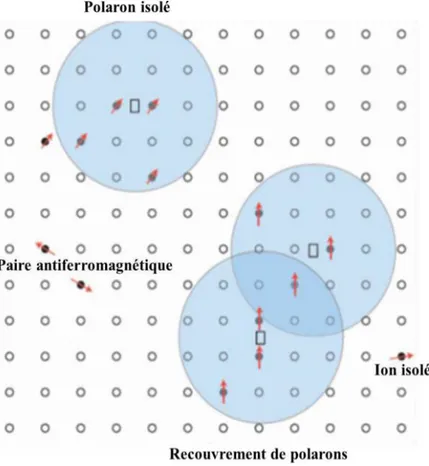
Dans le cas des semi-conducteurs magnétiques dilués (DMS), si la concentration de trous est très faible comparativement à la densité d’ions magnétiques, un polaron magnétique est formé d’un trou localisé et d’un grand nombre d’impuretés magnétiques autour de ce trou (fig. 6). D'ailleurs, le ferromagnétisme observé dans ces systèmes ne peut pas être expliqué par les différentes interactions d’échange présenté ci-dessus. Récemment, Coey et al [28] ont proposé un modèle basé sur les propriétés des polarons magnétiques afin d’expliquer le ferromagnétisme dans le système de ZnO dopé au cobal (due par exemple aux lacunes d’oxygène ou aux sites interstitiels de Zn). Quand la concentration en électrons des niveaux donneurs augmente, ces orbitales vont se chevaucher pour créer une bande appelée bande d’impuretés. La présence de cette bande proche de la bande de conduction et des niveaux 3d de Co (ou autres ions TM) est responsable de la formation de polarons dont le rayon est assez grand pour permettre leur percolation. Par conséquent, les moments magnétiques des ions Co s’alignent dans la direction du champ magnétique dû à ces polarons magnétiques, ce qui donne naissance à un couplage ferromagnétique.
28
Figure -6 : Polarons magnétiques. L’électron forme une orbite hydrogènoide et se couple avec
29