Dynamique des ondes de Rossby dans un jet parabolique

par

Gilben Brunet

Cette thèse est présentée à la Faculté de recherche et des études graduées comme exigence partielle du Doctorat en Philosophie (Météorologie).

Département de météorologie

Université McGill

Montréal, Québec

(

Cette thèse est essentiellement consacrée au problème aux conditions initiales pour l'équation du tourbillon barotrope dans le plan bêta linéarisée autour d'un état de base zonal. Le vent zonal employé dans cette étude est un jet parabolique dans le plan infini, soit V ( Y )

=

Uo + V' Y + V" Y 2/2 . Il est montré que l'équation non dimensionnelle de ce problème ne dépend que d'un paramètre a

= -

2 ( ~ - V" ) / V". L'équation de Raylelgh-Kuo associée a pour tout" a Il un spectre continu de

modes singuliers et pour a

< -

.25 il existe une infinité de modes discrets de Rossby.

Da 1S l'espace de Fourier le problème a une formulation lagrangienne, ce qui permet

une discussion qualitative simple de l'énergétique reliée

à

l'interaction du jet avec la perturbation. De plus, nous avons obtenu de nouvelles lois de conservation qui éclairent grandement la dynamique du jet. Ces résultats montrent qu'il existe des différences importantes entre un jet de vent d'Est et d'Ouest.

En utilisant la théorie des groupes de Lie nous avons obtenu pour a ;;:: - .25 et dans le contexte de l'approximation de l'onde longue des séparations des variables qui

nous permettent de résoudre complètement le problème aux conditions initiales. De plus nous avons obtenu des solutions invariantes localisées en y. Ces solutions invariantes sont pour certaines valeurs de I l a Il analytiquement simples et permettent une comparaison

avec les résultats que l'on retrouve dans la littérature à propos d'un vent zonal linéaire. En particulier pour certaines conditions initiales nous obtenons des phénomènes d'amplifications temporaires comme pour le vent zonal linéaire et qui dépendent de " a ".

Il est montré que pour une condition initiale arbitraire avec une petite amphtude (de l'ordre de e) l'évolution linéaire n'est plus valide après un temps de l'ordre de E - 1 pour

-,

une largeur de l'ordre de E 1/2 • Nous avons obtenu les équations gouvernant l'évolution non linéaire de la perturbation .

(

(

Abstract

'The thesis is mainly concemed with the initial-value problem for barotropic RO'isby waves linearized arol.rld a parabolic zonal flow. U ( y ) = Ua + U' y

+ U"

y

2/2.

It is shown that the non-dlmensional cqual10n for the perturhatIOn depends on only one es~entlal parameter, a

= -

2 (

P -

V")

1

U". The a~sociated Rayleigh-Kuo equation has a continuous spectrum of ~ingu)ar modes for ail values of .. a " and an infinite number of dlscrete Rossby waves for a < - .25.

In Founer space the prohlem ha~ a Lagrangian formulation whlch perr11lts a Simple qualitative di~cussion concerl1lng the nature of the IIlteraction between the perturbatIOn and the zonal flow. Wc have found new con\crvatlOn laws that give 1!l~ight into the dynanllc~ of the jet. These rcsults show a significant difference between the dynamic'i of ea~terhes and westerhes.

Using results From the theory of Lie groups wc have obtained a number of distinct separation of variables for a ~ - .25 in the long wave approximation This allows the initial value problem to be completely solved and also provides a number of exact solutions whlch are localized In

y.

For certain values of .. a " these have a simple analytical fonn that pern1its a comparison with previous results for a linear zonal wind. As in the uniform shear case wc observe a temporary amplification for certain initial conditions, whose nature now depends on " a ".

We have shown that for an arbitrary initial condition of small amplitude ( of order

E ), the linearity hypothesis is invahdated when a« 1 after a time of the order of E - 1 in a criticallayer of wldth of order El/2 centered at the jet extremum. We have also obtained the goveming cquations for the nonlinear evolutIOn stage, which have a striking similarity with those for a forced Rossby wave on a linear wind profile.

J{!;'lm:I\'lt'l1ll'nt::.

En pn:nuer heu, J'allneral" r~mcn .. 'lcr mon lhrc(!cur de th~,>c. Prnfc~"cllr T, Wam, pour m'avOir "lIIVI Clln\OCIKll'lI"cml'nt tout :tu long dl" ma Ihè'''l'' Son "l'Il~ critique ct ~e., COIlI1aI"'>'II1l'C'> ,Il'ad~!llllllle" onl pernm ulle Coll,lhorallon pl;lI"antl' rt de~ plu,> frl1ctucu~c"

au L'OUf" dl' Ille" etudc\

Je voudrai'> rl'mcrCler p.lrllllJ!J~rl'll1l'nl J:vrlync. ma l'lllllp,lgne. pour ,>cs ~nc()lIragcmelll~ ÇpIlIIJllI' .. el pour avoir \lI creer ulle ,lInbl.lllL'~ f.ltlllhak agréahk avec me ... dCllx enfant... Ilugo cl Jc.tn-l-rall\;ol'"

Je

vouùral" également rcmerClcr Je ,1/1-( id le,> el LOIJ .une. IIlC'> p.lrrnl\. Cl (oute ma

falmlle pour \"llde CI le ... encour,lgcmcnh r~,I1'>. hnalcment. JC remcrcle Il' (\)J)~cil de

Recherche en SClencc\ ct Génlc du Canada. le SCI\'ICC d'EnVIlOnnCIl1l'llt AIlllO\phénquc du Canada et le Départemcnt dc Météorologlc dl' l'UI1IVCr\llé Mdilll pour Icur ~ul nort

{

Résumé Abstract Remerciements Table des matières Liste des figures

Déclaration d'originalité

CHAPITRE 1 INTRODUCTION.

Table des matières

CHAPITRE II EQUATION DU TOURBILLON BAROTROPE.

2.1 Equation du tourbillon non linéaire.

2.2 Equation du tourbillon Jinéansée autour d'un état de base zonal. 2.3 Problèmes aux condItions mitIales.

2.3.1 Symétries et résultats analytiques.

Page

Hi

IV V viiI ix

9

9 14

20

20

2.3.2 Modes normaux: solutions spéciales du problème aux conditions initiales,

du problème forcé ou du problème marginalement stable. 23

2.3.3 Modes normaux: Représentation pour une condition initiale arbitratre. 26 2.3.4 Problème aux conditions initiales pour un vent linéaire. 32

2.3.5 Remarques générales. 38

2.4 Théorie du trajet des rayons. 40

CHAPITRE III PROBLEMES AUX CONDITIONS INITIALES DANS UN JET PARABOLIQUE 1 : THEORIE DU TRAJET DES RAYONS ET LOIS

DE CONSERV ATrON. 46

3.1 Présentation du modèle.

3.2 Théorie du trajet des rayons et le jet parabolique.

3.3

Lois de conservation et symétries. 3.3.1 Introduction.

46 51

57 57

3.3.2 FomlUlution lagrangIenne ct le th~orèl11c de Noethcr. 3.3.3 NOllvcllc!\ lOI, de con,ervalJon.

3,4

Nouvclle,> 101' de l'Oll"er vatlOn d.lm l'apprO\imallOn d'onde longuc. 3.t 1 l.0I' de l'on'lerv.ltlOn

3.4 2 RC1l1.lrqllc'l ~lIr J'.lpproxlIl1alllln d'onde longue. ~ .t. -' Le l'

.1"

a 2 - ) / ...

3.t .. Le ça" a < - 1 /4.

CIIAPn'RE IV PROBLFMES AUX CONDITIONS INITIALES DANS UN

JET

Il : 57

59

62

62

63 64

66

SEPARATIONS DES VARIABLES ET SOLUTIONS EXACTES. 69 4.1 Ca~ de l'approxIIl1allOn dc l'onde longue et a ~ - 1 /.t , 69

4.1.1 Exemple ~lInple d'un problème à plll~ieurs séparations des variahles. 69 4.1.2 Syll1étnc~ dc (4.1.1) ct "éparation de~ villlables. 71

4.1.3 Fonction., propres pour a ;Z 3/4. 74

4.1.4 Fonctions propres pour a ;Z - 1/4. 77

4.1.5 Développements asymptotiques et rcmarquc~ sur le~ base~ TAI,

T_n3,

4.2 Commentaires sur l'approxllnatIon de l'onde longue.

4.3

Discussion des solutions invariante~.

4.3.1 Résultats analytIques pour les solutions invariantes (4.2,1), 4.3.2 Conditions initIales avec décrobsance monotonc dc l'énergie. 4.3.3 Conditions IIlJtiales avec amplification de Orr.

4.4

Energétique et taux de crois~ance des solutions invariantes. 4.4.1 Energétiques des solutions invariantes.

4.4.2 Taux de croissance des solutions invariantes.

4.5

Cas a« - 1 : l'approximation de WKB et le spectre discret.

CHAPITRE V LE JET PARABOLIQUE LORSQUE 1 al « 1.

1'1..

2 ct

79

X3

X5

85

X8

101

103

103

108

110

113

(

(

5.1 Evolution linéaire du problème aux conditions initiales avec 1 a 1« 1. 5.2 Evolution non lInéaire du jet parabolique lorsque a

=

O.

CHAPITRE VI CONCLUSION.

6.1

Conclusion.

6.2

Nouvelles avenues de recherches.

APPENDICE A Symétries de l'équation du tourbillon barotrope dans le plan bêta. A.I PrélIminaires.

A.2 Equation non linéaire. A.3 Equation linéaire.

APPENDICE B Symétnes et lois de conservation. B.1 Nouvelles lois de conservation.

B.2 Nouvelle loi de conservation dans l'approximation d'onde longue. APPENDICE C Résultats asymptotiques pour les fonctions hypergéométriques. BIBLIOGRAPHlE.

113

116

121

121

123

126 126 128 129

133

133 135 136 139

.:""

I"jste des

fi~ures

'",

Figure

Page

1.1

Graphe spatial instantané cle la fonction courant

q> (

x. y ) ct

du tourbillon V::!

4>

de la perturbation.

6

2.1

Contribuuons

à

la

tran"f()nn~

inverse LIe Laplace.

29

2.2

Courbes de /11vcau de

(1)

pour U ( y )

= y.

44

3.1

Le ~pectre

du Jet parabohq

lie

en fonctIon de

!3

ct

LJ"(

en

nr 1 çl).

49

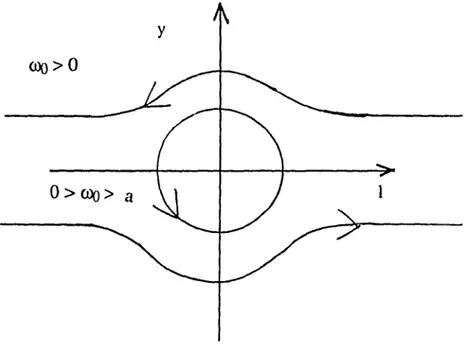
3.2

Courbe~

de niveau de

(1)

pour a

po~itlf.

52

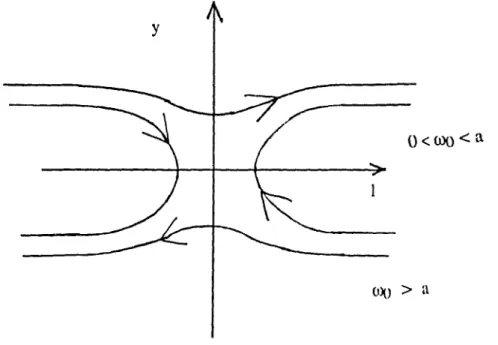
3.3

Courbes de niveau de

(1) pour

a négatif.

53

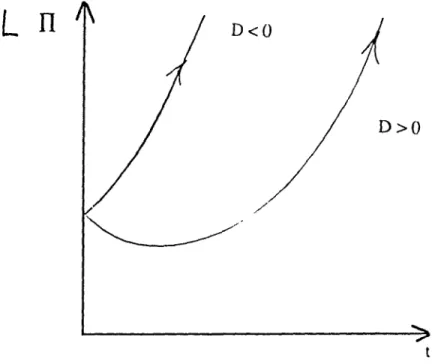
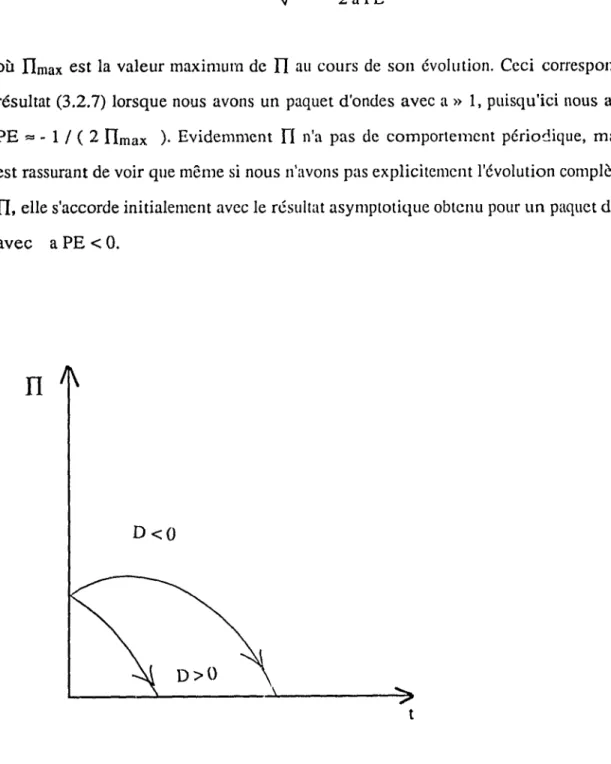
3.4

Evolution de

n

lor~que

a

~

-

1 /4.

65

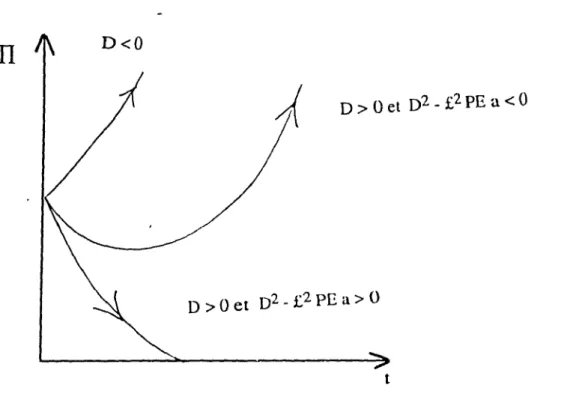
3.5

Evolution de

n

lorsque a

< -

1/4

et

il

PE

>

O.

67

3.6

Evolution de

n

lorsque a

< -

1 /4

et a PE < O.

68

4.1

Le paramètre

~

en fonction de a.

78

4.2

Les cas n

=

1,2. 3

et 4 en fonction de

P

et

U"(

en

nr 1 s-I).

87

4.3

Tourbillon absolu pour n

==

3 et

E

=

1 / 3 .

~O

4.4

Tourbillon absolu pour n

=

3

et e

=

1 .

91

4.5

Tourbillon absolu pour n

=

3

et

ê

=

3 .

92

4.6

Tourbillon pour n

=

3 et

E ==

3 .

93

4.7

Tourbillon absolu obtenu par Held & l'hillips

(1987) .

94

4.8

Tourbillon absolu pour n

=

1 et

ê

=

1/3.

95

4.9

Tourbillon absolu pour n

=

1 et

E

=

1.

96

4.10

Tourbillon absolu pour n

=

1 et e

=

3 .

97

4.11

Tourbillon absolu non centré à l'origine initialement pour n

=

3 et

E

=

1.

98

4.12

Fonction courant non centrée

à

l'origine pour n =

3 et

E ==

1.

99

4.13

Evolution de la densité de l'énergie E ( l,

t)

pour un vent linéaire.

105

4.14

Evolution de la densité de l'énergie pour un jet parabolique.

106

~"

Déclaration d'originalité

L'originalité de cette thèse consiste dans l'utilisation de différentes théories de l'analyse mathématique pour obtenir des résultats analytiques concernant la dynamique des ondes de Rossby dans un jet parabolique. Ces différentes approches à notre problème ont permis une compréhension presque complète de la dynamique linéaire des ondes de Rossby dans un jet et une compréhension partielle de certaines questions de la dynamique non linéaire de ces ondes. Voici une liste des résultats originaux se trouvant dans cette thèse:

i) Une classification complète des symétries de Lie classiques de l'équation du tourbillon barotrope dans le plan bêta linéarisée autour d'un état de base zonal quelconque va être donnée à l"appendice A incluant le cas hydrodynamique, ~

=

O.

ii) La théorie des groupes de Lie est employée pour obtenir des 'ois de conservation et des solutions exactes spécifiques aux ondes de Rossby dans le jet parabolique au Chapitre 3 et 4 respectivement. Ceci permet de comprendre les différences fondamentales entre le profil linéaire et le profil parabolique. Ce dernier pouvant être considéré comme un cas générique d'un vent avec un point d'extremum.

iii) Nous montrons à la Section 4.1.5 que le développement asymptotique, t» 1, obtenu par Brown & Stewartson (1980) pour le spectre continu apparait encore, mais n'est pas uniformément valide pour le jet parabolique. Nous obtientlrons une développement uniformément valide pour certaines solutions.

iv) Nous montrons au cours de cette thèse l'importance cruciale du paramètre géométrique a

= -

2 ( ~ - U" ) / U" pour le jet parabolique. Nous argumentons au Chapitre 6 que si ce paramètre est négatif et grand, il est un critère linéaire pour le développement de grandes échelles méridionales et d'amplification pour des ondes de

Rossby barotropes sur un jet. Cela a des implications intéressantes pour différencier la dynamique barotrope des jets aux latitudes moyennes et des jets de vent d'Est.

v) Nous obtenons au Chapitre 5 un problème

à

couche critique non linéaire qui a été excitée par une condition initiale arbitraire sur le jet parabolique avec

f3 -

U" = O.

(

(

Chapitre 1

Introduction

La rotation terrestre est sans contredit un élément important de la structure atmosphérique aux grandes échelles spatiales. En fait, elle domine les effets de stratification verticale lorsque les échelles spatiales sont plus petites que le rayon barocline de déformation de Rossby dans un contexte quasi géostrophique. De plus, quoique 1'atmosphère est un fluide stratifié, l'approximation d'une atmosphère barotrope peut s'avérer utile pour la compréhension qualitative de certains phénomènes atmosphériques. Alors nous allons supposer que la propagation dans la haute troposphère d'ondes synoptiques qui sont initialement générées par des processus baroclines dans la basse troposphère et aux latitudes moyennes peuvent être adéquatement simulées par un modèle barotrope et quasi géostrophique. De plus, Charney (1963) a montré à partir d'une analyse d'échelles que le modèle barotrope non divergent est adéquat aux tropiques lorsqu'il n'y a pas de phénomènes de condensation.

Un autre élément de la structure atmosphérique aux grandes échelles qui retient l'attentior. est la composante quasi stationnaire de l'écoulement sur laquelle se propagent des pel turbations transitoires. Comprendre la dynamIque de l'interactIon de ces perturbations transitoires avec un écoulement est une question de première importance en météorologie. Les tennes d'advection non linéaires sont une des difficultés principales qui empêchent l'obtention d'une réponse satisfaisante à cette question. Alors un modèle simplifié barotrope qui négligerait les termes d'interactions de la perturbation avec elle-même, mais qui garderait les tennes d'interactions non linéaires entre la perturbation et un écoulement zonal pourrait être utile.

Cette thèse sera en grande partie consacrée à l'étude des interactions d'ondes de Rossby barotropes avec un écoulement zonal. Par exemple, nous sommes intéressés par les mécanismes où une telle onde puisse amplifier, décroître ou rester neutre. Nous allons aborder cette question du point de vue d'un problème aux conditions mitiales non forcé, ce qui exclut à priori les problèmes avec couche critique tels qu'étudiés par Dickinson (1970) et Warn & Warn (1976, 1978). De plus, nous allons étudier des écoulements zonaux qui satisfont le critère linéaire de stabilité de Rayleigh-Kuo. Nous sommes particulièrement motivés à trouver des mécanismes d'amplification pour les ondes de Ros5by autres que ceux qui ont été tradItionnellement employés pour les écoulements barotropes linéairement instables avec modes exponentiels (modes normaux instables).

Il existe plusIeurs problèmes où l'on cherche à exciter des perturbations en choisissant des écoulements ayant des modes normaux instables. Par exemple, des modes instables sont obtenus pour le modèle de Eady, (Pedlosky 1979, Section 7.7 ), dans le contexte d'instabilité barocline. Mais FaITel (1988 a, b) a argumenté que l'étude de certains problèmes aux conditions iniuales montre qu'il existe d'autres mécanismes baroclines d'amplification non négligeables.

Les perturbations dans les jets de vent d'Est sont un autre exemple. En général, on considère qu'il existe deux origines possibles pour le développement des perturb:ttions équatoriales: l'instabilité barotrope et l'instabilité conditionnelle de la seconde espèce, CISK, reliée à des processus de condensation, voir Holton (1979). Nitta, Tsuyoshi & Yanai (1969) proposent des ondes de Rossby non divergentes avec modes normaux instables comme explication possible pour l'amplification de perturbation dans les alizés. Shapiro (1977) a argumenté que l'approche reliée aux modes instables n'était pas valide puisque l'amplitude initiale de la perturbation était en général du même ordre que le vent zonal. Mais ce même auteur argumente qu'initialement la fonction courant et le tourbillon de la perturbation sont quasi parallèles, ce qui entraîne une annulation fortuite des termes

non linéaires. Alors il propose un critère pour le mécanisme de déclenchement d'une tempête tropicale, "triggering mechanism": lorsque cette annulation ne se produit plus, il

conclut en se basant sur une analyse d'échelles et une analyse climatologique que c'est

à

ce moment que la structure géornétnque de la penurbation favonse une transition de l'onde

à

une tempête tropicale. De plus, ShapIro (1980) faH appel

à

la structure non homogène de l'écoulement dans la dIreCtIOn zonale pour permetrre une telle condition initiale d'induire le

"triggering mechanism". Nous verrons au Chapitre 6 qu'il peut y avoir d'autres façons d'initier le "triggering mechanism" que celles qui ont été proposées par Shapiro (1977) ou Nitta, Tsuyoshi & Yanai (1969). En fdit, nous velTons que les mêmes mécanismes d'amplification employés par Farrel (1988 a, b) peuvent être efficaces dans les jets de vent d'Est.

Il existe un autre domaine actif de recherche où l'interaction d'ondes de Rossby avec un écoulement zonal est d'une grande importance. C'est l'étude à l'échelle synoptique des systèmes atmosphériques transitoires qui montre l'importance des interactIons non linéaires et le côté aléatoire de leurs évolutions. Une formulation phénoménologique d'un modèle turbulent isotrope, homogène et bidImensionnel du problème a été développée par Batchelor

(1953, 1969),

Kraichnan

(1967)

et Leith (1968). Cette théorie permet d'expliquer certaines caractéristiques des systèmes synoptiques transitoires cemme l'ont montré Chen

&

Wiin-Nielsen (1978) et Boer & Shepherd (1983)

à

partir de données atmosphériques. Un des résultats importants de cette approche est qu'une cascade d'énergie vers les grandes échelles est accompagnée d'une cascade de l'enstrophie vers les petites échelles. Shepherd (1987) fait la remarque que cette phénoménologie semble réaliste pour expliquer l'interaction des systèmes transitoires entre eux à l'échelle où le flot peut être considéré comme homogène, mais elle n'explique pas adéquatement les interactions entre la composante zonale quasi stationnaire et ces systèmes transitoires tels qu'observés dans l'atmosphère puisqu'il y a une anisotropie zonale dans le spectre aux grandes

échelles, (Boer & Shepherd, 1983). En d'autres mots, d'un point de vue spectral, si la théorie turbulente est satisfaIsante pour simuler l'interaction non linéaire des petites échelles entre elles, il n'en va pas de même pour l'interaction des petites échelles avec les plus grandes échelles stationnaires. Shepherd (1987 a, b) propose sous certaines approximations. quant à lui, un modèle barotrope linéaire d'interaction entre la composante zonale et la composante transitoire qUI retient pour être réalIste: que l'enstrophie de la perturbation transitoire est conservée et que l'énergie de la perturbation n'est pas conservée en général, cette dernière pouvant amplifier ou diminuer selon la situation.

Des amplifications transitoires de l'énergie avec conservation de l'enstrophie sont observées dans le problème aux conditlons initiales d'une perturbation arbitrairement petite superposée sur un vent zonal linéaire, voir Yamagata (1976), Farrel (1982), Tung (1983) et Boyd (1983). Remarquons qu'un profil linéaire n'a aucune instabIlité exponentielle. En général, les résultats de ces auteurs sont qualitativement semblables

à

ceux qui ont été obtenus au début du siècle en mécanique des fluides, sans effet bêta, par Thomson (1887) et Orr (1907). C'est le cisaIllement dû au vent zonal qui induit ces amplifications temporaires ayant des taux de croissances qui se comparent assez bien avec ceux trouvés pour des écoulements avec modes normaux instables, (Farrel, 1987). Nous nommerons ce phénomène d'amplification: amplification ou effet de Orr. Dans le contexte d'une approximation WKB, l'amplification de Orr se produit au point de rebroussement de la position méridionale du paquet d'ondes pour un vent linéaire.

Nous pouvons constater

à

la Figure 1.1 une illustration d'un problème aux conditions initiales avec un état de base zonal illustrant ce type d'interaction dans le contexte de l'équation du tourbillon barotrope, (Shepherd, 1987 b). Cette FIgure 1.1 montre l'intégration numérique de l'évolution linéaire de la fonction courant et du tourbillon de la perturbation

à

la colonne gauche et droite respectivement. Chaque colonne illustre trois temps successifs où la première figure (b) montre aussi le jet zonal superposé.

(

(

La condition initiale, voir (a) et (b), est homogène et isotrope dans l'espace des nombres d'ondes. Nous pouvons voir à la figure Cc)

à

gauche, une amplification de la fonction courant, effet de Orr, accompagnée d'échelles méridionales grandes. Mais éventuellement la fonction courant décroît

à

la figure Ce). Tandis qlle ie t':iUrblllon de la perturbation est simplement cisaillé par le jet et aucune amplification importante est observée.

Il est important d'Insister sur le point SUIvant: l'amplification de

arr

est une amplification de l'énergie de la perturbation. Le concept d'amplIfication dépend de la norme employée, par exemple pour le profil linéaire l'enstrophie est conservée, donc il n'y aura pas d'amplificatIon du tourbillon. L'énergie est une norme intéressante physiquement puisque qu'elle donne une mesure des vents. Nous verrons dans cette thèse que de telles amplifications de Orr semblent être sensibles

à

la géométrie du profil zonal, par exemple lorsqu'Il y a un point d'extremum dans le vent zonal. Alors il serait intéressant d'obtenir des résultats analytiques pour d'autres vents zonaux différents du profIl linéaire pour compléter nos connaissances actuelles sur ce problème.

En général, l'obtention de résultats analytiques spécifiques pour une équation aux dérivées partielles est relié aux symétries de l'équation étudiée. Nous entendons par symétrie, toute transformation de variables laissant invariante la forme de l'équation aux dérivées partielles étudiée. Une étude systématique de ces symétries a été développée

par

Sophus Lie

à

la fin du 19 Ièmc siècle pour les équations aux dérivées partielles. Presque toutes les solutions spéciales, les lois de conservation, les séparations des variables connues d'une équation aux dérivées partielles sont reliées directement ou indirectement à ces symétries.

---1

y

x

Figure 1.1 Graphe spatial instantané de la fonction courant <p ( x,

y )

et du tourbillon V2 <j> de la perturbation. Les traits solides sont des valeurs po~itives. (a)

<P.

t

=

0; (b) \72 <p, t

=

0; (c)

<p,

t = 1; (ci) V2

<P,

t = 1; (e)

<p,

t = 4, (f) V2

<p,

(

Dans cette thèse, nous allons étudier principalement l'équation du tourbillon barotrope dans le plan bêta pour une perturbation arbitrairement petite évoluant sur un vent zonal. Nous allons aborder cette équation en faisant une classification complète de ces symétries de Lie classique pour un vent zonal U ( y), VOIr l'Appendice A. Nous emploierons au cours de cette thèse ces symétries pour obtenir des résultats analytiques qui vent nous permettre d'applOfondir nos connaissances sur l'interactIOn des ondes de Rossby avec un écoulement zonal. Ces résultats vont nous permettre en particulier de mieux comprendre la dynamIque d'une perturbation sur un Jet parabolique. En fait, le jet parabolique et le profil linéaIre sont les seuls écoulements qui pennettent des symétries autres que celles que nous avons pour un profil arbItraire lorsque ~;f:. O. Le jet parabolique est certainement un profil très intéressant à étudier puisque des écoulements avec extremum sont assez communs dans les tropiques et aux latItudes moyennes.

Nous allons au Chapitre 2 faire un survol de la recherche passée et présente du problème aux conditions initiales et des solutions spéciales de l'équation du tourbillon barotrope dans le plan bêta. Notre recherche systématique des symétries de l'équation du tourbillon lInéarisée autour d'un état de base zonal va nous indiquer que le jet parabolique est le seul candidat intéressant qui n'a pas été étudié exhaustivement. Alors nous allons étudier à la Section 3.1 les propriétés générales du jet parabolique. La Section 3.2 sera consacrée à l'évolution d'un paquet d'ondes dans un jet parabolique. Nous allons obtenir des nouvelles lois de conservation

à

la Section 3.3, 3.4 et commenter leurs interprétations physiques.

Le problème aux conditions initiales et l'obtention de solutions exactes pour le jet parabolique sous différentes approximations seront traités au Chapitre 4. Nous allons à la Section 4.1 montrer que sous certaines conditions, dont l'approximation d'onde longue, le problème aux conditions initiales peut être résolu complètement pour le jet parabolique et

du même coup obtenir des solutions exactes. Nous allons discuter graphiquement plusieurs de ces solutions exactes

à

la Section 4.3. Nous allons étudier d'un point de vue énergétique des exemples d'amplifications de Orr pour certaines de ces solutions exactes à la Section

4.4.

Nous allons montrer finalement à la Section 5.1 un cas spécial du jet parabolique,

~ - D"

=

0, dont le problème aux conditions initiales peut être résolu complètement sans aucune approximation. Il sera montré que l'évolution de la perturbation deVIendra nOI1 linéaire après un grand laps de temps pour une condition initiale arbitraire. La Section 5.2 sera consacrée à l'évolution non linéaire de ce cas spécial et nous obtiendrons des équations qui régissent l'évolution non linéaire de la perturbation.

(

(

Chapitre TI

Equation du tourbillon barotrope

Section 2.1 Equation du tourbillon non linéaire.

Les ondes de Rossby non linéaires que nous nous proposons d'étudier dans cette thèse sont gouvernées par l'équation barotrope non-divergente dans le plan bêta

(2.1.1)

où 'P est la fonction courant et J ( , ) est l'opérateur non linéaire jacobien. 'P est reliée aux champs de vitesse par les relations suivantes: u =

-o'Play ,

v

=

i1'P/i1x

où u et v sont respectivement la composante zonale et la composante longitudinale du vent et ~ est le gradient du tourbillon planétaire. Cette équation est obtenue dans le contexte de la théorie quasi géostrophique et peut être généralisée

à

l'espace tridimensionnel avec des situations où une topographie et un mIlieu stratifié sont présents, voir Pedlosky (1979, Chap. 6).

MalS dans cette thèse nous allons nous limiter

à

la version dans le plan. Qüoique cette

version est davantage simplifiée dans le but de simuler l'atmosphère, elle retient quand même beaucoup des propriétés dynamiques de l'atmosphère réelle, voir Hohon (1979). L'utilisation de (2.1.1) avec des échelles spatiales et temporelles différentes dans un contexte océanographique est aussi fréquente comme en fait foi Gill (1982, Chap. 12).

Les conditions aux frontières dans un domaine fini que doit satisfaire le vent dans le cas d'un fluide non visqueux sont que la composante normale de la vitesse

à

une frontière rigide soit nulle sur cette même frontière. Nous allons employer dans cette thèse un domaine infini dans la direction méridionale et un domaine périodique ou infini en x.

De plus, lorsque nous étudierons une perturbation superposée sur un écoulement zonal nous exigerons que la perturbation de la fonction courant soit localisée en

y.

Ce qui d'un point de vue pratique nous amènera

à

étudier les perturbations de carré sommable en x et

y,

qui sont des éléments de l'espace d'Hilbert L2 ( S X R ) où S est la longueur du domaine en x.

L'équation du tourbillon barotrope non linéaire a la propriété d'avoir des quantités scalaires qui sont conservées au cours de l'évolution temporelle, ce qui veut dire qu'elles ne dépendent pas du temps. L'énergie est donnée par

(2.1.2)

et l'impulsion par

(2.1.3)

où

(f)

=

f f

f dx dy . A

Remarquons que la contribution d'une perturbation appartenant

à

L2 ( R

X

S )

à

l'impulsion est tout simplement nulle. En général, pour un fluide ayant une densité non constante, l'impulsion ne sera pas nulle. L'impulsion a été obtenue Ici à partir des équations primitives. Si J'on emplOIe (2.1.1) pour l'obtenir nous devons ajouter à la droite des égalités de (2.1.3) une fonction arbitraire en t. Cette fonction ne doit pas dépendre de t, si l'on veut que (2.1.1) soit compatible avec les équations primitives.

De plus, si cette fonction dépend de t l'unicité de la solution de (2.1.1) pour un problème aux conditions initiales n'est pas garantie. Par exemple, nous avons montré que dans un canal avec un domaine périodique en x si nous avons une solution

'V (

x,

y,

t ),

(

alors nous pouvons générer une nouvelle solution

'1' (

x - s,

y ,

t) - ds/dt y où s ( t) est une fonction arbitraire du temps, voir Appendice A. Cette nouvelle solution satisfait les conditions aux frontières (par exemple périodique en x tt v

=

0 aux murs). Ces deux solutions satisfont les mêmes conditions initiales si s = ds / dt = 0

à

t = 0, mais avec s ( t ) ~ 0 Ils ont des évolutions différentes. Il est aisé de voir que la solution n'est pas une solution acceptable des équations primitives, puisque nous obtenons un champ de pression p non périodique. Cet exemple nous rappelle que lorsque nous avons obtenu (2.l.1) en différenciant les équations primitives, il faut toujours s'assurer que les solutions de (2.1.1) sont compatibles avec l'équation originale.

Il existe UI autre loi de conservation générée par une fonction arbitraire F du

tourbillon absolu, soit

(2.1.4)

Nous pouvons obtenir de (2.1.3) et de (2.1.4) lorsque F est une fonction quadratique une quantité conservée qui se nomme l'enstrophie,

(2.1.5)

La preuve que ces scalaires sont des constantes est donnée dans n'importe quel texte académique traitant ce sujet. Il est bon de remarquer que ces lois de conservation pour l'énergie et l'impulsion sont liées aux symétries de translations dans le temps et l'espace de (2.1.1) respectivement. Lorsque nOlis sommes dans un domaine fini la symétrie de translation spatiale peut être brisée par l'imposition d'une frontière, alors il est possible que l'enstrophie et l'impulsion ne soient plus conservées. Cette situation peut

survenir dans un contexte océanographique comme dans l'exemple simple d'une onde de Rossby réfléchie par une frontière, voir Pedlosky (1979, Chap. 3 ).

La recherche de toutes les lois de conservation d'une équation donnée est une entreprise difficile. Une approche systématique de la question lorsque l'équation a une formulation variationnelle dans l'espace fonctionnel des solutions a été fJrmulée au début du siècle en termes des symétries de l'équation, Noether (1918). Un exposé approfondi du sujet avec exemples tirés de la physique théorique et de la mécanique des fluides se trouve dans Anderson & Ibragimov (1979) ou Olver (1986) . Des résultats en dynamique des atmosphères ont été obtenus par Mclntyre & Shepherd (1987) pour l'équation du tourbillon barotrope et pour des ondes d'eaux sur une surface libre par Benjamin & Olver (1982).

L'étude en général des solutions d'amplitude finie de (2.1.1) est à priori hors de portée en ce qui concerne les méthodes analytiques présentement disponibles. Cette équation permet d'obtenir certaines solutions spéciales dues à la présence de symétries de translation dans le temps et dans les variables spatiales. Les solutions spéciales les plus utilisées en dynamique des atmosphères sont celles qui sont associées aux solutions stationnaires, donc reliées à la symétrie de translation dans le temps de (2.1.1). L'équation peut dans ce cas être réduite au problème

(2.1.6)

où G est une fonction arbitraire. Pour d'autres exemples de solutions spéciales générées par les symétries de (2.1.1) ou d'autres équations de la météorologie, le lecteur est référé

à

Katkov (1965 a, b) et Rokotyian (1968).

L'étude de la stabilité des solutions de (2.1.6) et l'étude de l'évolution d'une perturbation autour de cet état de base sont des questions primordiales en dynamique des

l

(

atmosphères comme en fait foi l'importante littérature scientifique qui y est consacrée, voir

par

exemple Mitchell & Derome (1983) pour l'étude de l'équation du tourbillon potentiel quasi-géostrophique. Nous pouvon~ séparer les états de bases stationnaires en deux classes, soit ceux qUI dépendent de x et y appelés non-homogènes et les écoulements dits de types zonaux, qui ne dépendent pas de x. Les premiers sont définitivement plus pertinents d'un point de vue synoptique comme le font remarquer Pierrehumbert (1983) dans des situations de cyclogénèse, ainsi que Shapiro (1980) dans le développement d'ondes barotropes dans les alizés.

L'étude de la stabilité des écoulements avec états de base non homogènes est souvent numérique, mais certains résultats analytiques ont été obtenus comme par exemple des limites supérieures pour le tat;x de croissance de l'énergie de la perturbation par Pierrehumbert (1983). Une approche variationnelle dans l'espace fonctionnel des solutions, Arnold (1965,1966), a pennis amsi l'obtentIOn d'un critère de stabilité pour des écoulements non homogènes et une amplitude finie. Les travaux de Arnold ont inspiré Dikii (1965), Blumen (1968) et McIntyre & Shepherd (1987) dans l'obtention de résultats similaires dans le contexte météorologique. Mais en général l'étude analytique des écoulements non homogènes est une entreprise difficile comparativement à l'étude des écoulements zonaux. L'étude des flots zonaux perturbés est certainement une question d'intérêt en dynamique des atmosphères autant du point de vue énergétique que du point de vue d'un problème aux condItions mitiales. Un écoulement zonal barotrope avec une perturbation arbi trmrement petlte est définitivement le problème le plus facile à étudier par des méthodes analytiques. Cette thèse y sera principalement consacrée et nous allons dans le reste de ce chapitre faire l'historique du sujet.

r,

l'

Section 2.2 Equation du tourbillon linéarisée autour d'un état de base zonal.

L'approche habituelle pour étudier (2.1.1) est de diviser la fonction courant en deux parties , soit un vent zonal et une perturbation", ( x, y, t )

y

'Y (

X,

y,

t )

= -

f

ds U (

s )

+

E '" (

x,

Y, t )

o

(2.2.1 )

OÙ E est une mesure non dimensionnelle de l'amplitude. Alors (2.1.1) peut être réécrite comme une équation d'évolution non linéaire pour la perturbation

(2.2.2)

De plus, nous obtenons en intégrant sur un domaine périodique en

x ,

une équation pour la moyenne zonale du vent

aïi

d

-- = -- -- ( u v ) où

at

dy

S

f=;

f

dxf

'Vf.

o

(2.2.3)

Un résultat similaire peut être obtenu pour une fonction de carré sommable sur l'axe infini x en omettant la division par S dans (2.2.3).

L'approche préconisée en premier lieu dans ce

travail

sera de négliger les termes non linéaires en supposant qu'initialement la perturbation 'l'est suffisamment petite et d'étudier seulement la dynamique de la partie linéaire dans le contexte d'un problème aux conditions initiales. Soit (2.2.2) avec e

=

0;

(

(

+.

(2.2.4)

avec la condition initiale

(2.2.5)

Nous supposerons en général que

'l'O

est arbitraire et non singulière. Eventuellement, l'évolution de cette perturbation pourra développer, dans certaines régions ou dans le domaine au complet, des instabilités dynamiques qui permettront aux termes non linéaires d'n, oir des contributions non négligeables. Il arrive souvent que l'on puisse dans certains cas, par des méthodes asymptotiques, simplifier la résolution du problème non IméaIre. La premièIe étape de l'évolution est appelée l'évolution linéaire transitoire de l'onde et la seconde étape, s'il y en a une, est appelée l'évolution non linéaire de l'onde. Nous obtiendrons au Chapitre 5 des exemples concrets d'évolutions non linéaires pour des vents zonaux particuliers.

Les lois de conservation de l'énergie et de l'impulsion , définies

à

(2.1.2) et (2.1.3), génèrent

à

chaque ordre des lois de conservation pour la perturbation superposée sur un écoulement zonal arbitraire. Il est aisé de les obtenir en insérant le développement suivant de la perturbation

dans les expressions pour l'impulsion et l'énergie. Alors, l'on obtient des lois de conservation

à

chaque ordre,

(2.2.6)

Donc, si nous avons initialement

<

u! U

>

=

<

u 1

>

=

0, ils seront nuls pour tout temps. Il nous reste

à

résoudre U2 en fonction de la contribution au premier ordre et alors nous aurons des quantités scalaires conservées pour Ut. Ce qui semble

à

première vue une entreprise difficile, peut être finalement résolu en multipliant (2.2.4) par

ç},

en intégrant sur la variable zonale et en employant (2.2.3) pour obtenir,

(2.2.7)

Ce remarquable résultat obtenu par Andrews & McIntyre (1976), McIntyre

&

Weissman (1978) sans effet bêta, peut être substitué dans (2.2.6). En dérivant par rapport à t cette expression et en remarquant que

<

u} > est conservé, voir (2.2.6), nous obtenons les deux lois de conservation suivantes

2 )

J

U

Çl

---"-- = 0 et 2(P-U") (2.2.8)

~

P

Çl

=0

( <

2

)J

dt

P-U"

.

(2.2.9)

L'opérateur P indique que nous devons prendre la valeur principale de l'intégrale lorsque

(

c p

f

f ( Y ) dy

=

lim cS~o a

( y:

(y) dy

+

J

f (y) dy

J .

l

a b + Ô (2.2.10)

Remarquons que ces lois sont valides pour un nombre d'onde zonal fixé. En plus, il peut être montré que les expressions (2.2.8) et (2.2.9) sont valides sur un domaine infini en x.

II est intéressant d'ajouter aussi que nous avons montré que la loi de conservation (2.2.9) peut être généralisée

à

deux solutions Ça et

Sb

(2.2.11)

Ce résultat peut être démontré directement de (2.2.4) et nous allons l'employer explicitp-ment à l'Appendice B pour construire une infinité de lois de conservation.

La première de ces lois avec l'effet bêta a été obtenue dans un contexte plus général pour les écoulements non homogènes par Blumen (1968) et dans un problème différent par Andrews (1983) et comme nous l'avons vu cette loi est une conséquence directe de la conservation de l'énergie. Alors pour un écoulement zonal stationnaire la loi de conservation de l'énergie au premier ordre est la loi de conservation de la pseudoénergie. Dans un contexte plus général, il se peut que ces deux quantités soient différentes en vertu de la discussion de McIntyre

&

Shepherd (1987,Sec.7). La deuxième loi est une conséquence directe de loi de conservation de l'impulsion et elle est nommée loi de conservation de la pseudoimpulsion, voir Reld (1985). La loi de conservation de la pseudoénergie nous indique clairement qu'il peut y avoir un échange d'énergie entre la composante zonale de l'écoulement et la perturbation. Mais il est important de remarquer que l'énergie de la perturbation transmise

à

la composante zonale du vent est associée

à

une

"

correction du second ordre pour U, puisque que UI est nul et que la prochaine contribution est due

à

U2.

Il est intéressant de remarquer que les lois de conservation (2.2.11), de la pseudoénereie et de la pseudoimpulsion peuvent générer une infinitc! de nouvelles lois de conservation. Il s'agit de remarquer que si D ( a fax, a fat) est un opérateur différentiel arbitraire de type polynomial, alors si

'JI

est solution de (2.2.4) alors

i + J

2:

a

'JI

D'JI

=

d.

l, J ':'1 l ':'1 J l, J oX ut (2.2.12)

est aussi une solution de l'équation où les coefficients dl, J sont des constantes. Ceci est tout simplement relié au fait que l'équation est linéaire et ne dépend pas de x et t explicitement. Puisque les lois de conservation sont valides pour toute solution de l'équation, alors

D 'JI

satisfait les lois de conservation et ceci implique que nom, avons une infinité de lois de conservation. Ces lois de conservation sont les mêmes que Held (1987) a obtenues, quoiqu'ici notre méthode permet une dérivation qui est définitivement plus directe et simple. Ce résultat peut être expliqué dans le contexte des symétries généralisées d'une équation aux dérivées partielles linéaire, voir Olver (1986, Section 5.2) ou plus simplement par les remarques de l'Appendice B. Remarquons qu'une approche similaire peut être employée pour les écoulements non homogènes, mais l'opérateur D doit dépendre que des dérivées en t. Loin d'être une curiosité mathématique, ce résultat sera employé explicitement afin d'obtenir des nouvelles lois de conservation pour le jet parabolique au Chapitre 3.

Lorsque la pseudoénergie est définie positive, nous pouvons obtenir une limite supérieure sur l'énergie de la perturbation. Dans ces situations, nous saurons que toute

(

amplification de la perturbation sera limitée. C'est une version du théorème de Fj~rtoft, voir Drazin & Reid (1981), pour la stabilité des modes normaux.

De même, la loi de conservation de la pseudoimpulsion est une nonne positive pour le tourbillon de la perturbation lorsque

y

=

P -

U" ne change pas de signe dans le domaine. Alors comme pour la pseudoénergie, ceci nous pennet de conclure qu'il ne peut pas y aVOl! de modes nornlaux avec croissances exponentielles lorsque la pseudoimpulsion est définie positive, ce qui est tout simplement le théorème de Rayleigh-Kuo. Nous pouvons employer cette norme lorsqu'elle est définie positive pour définir un produit scalaire avec la fonction poids appropriée

y -

1 dans l'espace fonctionnel des solutions pour le tourbillon. Alors fmmellement nous pouvons construire une base orthonomlée

à

partir des modes normaux pour le tourbillon et ainsi résoudre en prillcipe le problème aux conditions iniuales assocIé à l'écoulement U, voir Held (1985). La loi de conservation de la pseudoimpulsion nous mdique la voie naturelle à employer pour analyser l'évolution linéaire des perturbatIOns et elle a donné ses fruits dans l'analyse numérique de l'équation du tourbillon barotrope linéaire Held (1985) et non linéaire sur la sphère Held & Phillips (1987) pour un jet avec stabilité barotrope.

De plus nous avons une expression pour la tendance de l'énergie

a

El =

<

u ( y )

a

U

1

VI)

at

ay

(2.2.13)

qui nous permet d'obtenir un critère pour l'amplification de l'énergie. Après quelques manipulations de l'intégrale de droite, cette condition revient

à

dire dans l'espace réel que la pente des lignes de phase constante de la perturbation soit de signe opposé

à

celui du

cisaillement dans tout le domaine en moyenne. De (2.2.13) nous pouvons aussi obtenir des limites supérieures sur les taux de croissance de l'énergie, par exemple Farrel (1987) a montré que

aE

_ _ 1 <V' E

a

t - 1 (2.2.14)

pour un vent zonal linéaire.

Section 2.3 Problèmes aux conditions initIales.

2.3.1 Symétries et résultats analytiques.

En général, tous les résultats analytiques d'une certaine importance concernant notre problème aux conditions initiales sont reliés aux symétries continues de l'équation (2.2.4). Nous entendons par symétrie continue tout changement de variables qui laisse inchangé la forme de l'équation étudiée. Par exemple, les symétries continues de rranslations dans le temps et de la variable x

x' = x

+

gt et t' = t

+

g2 '

(2.3.1)

laissent (2.2.4) inchangée ou invariante comme peut le vérifier aisément le lecteur pour tout gl et g2. Nous disons symétries continues parce que les transformations (2.3.1) dépendent des paramètres gl, g2 d'une façon continue. La pseudoénergie est associée à la symétrie de translation dans le temps et la pseudoimpulsion est associée

à

la translation en

x.

Un exemple particulier est l'existence pour le vent zonal linéaire dans le plan infini d'un changement de variables pour l'équation (2.2.4) qui permet une séparation des

(

«

variables, voir Tung (1983), et du même coup la résolution du problème aux conditions initiales dans le plan infini. De plus, ce changement de variables permet d'obtenir une solution particulière qui a été analysée et étudiée sous tous ses angles par Yamagata (1976), FaITel (1982),Tung (1983), Boyd (1983) et Shepherd (1985). Un tel changement de variable en présence d'un vent lInéaire est possible parce qu'il existe une symétrie non évidente

à

(2.2.4), quoique cette symétrie continue n'est pas explicitement mentionnée dans la littérature. La symétrie implicitement employée par Tung (1983) pour un vent linéaire est tout simplement

x' = x

+

g3 O't

et y' = y

+

g3 pour tout g .

3 (2.3.2)

A la fin du 19 ièrnc siècle une étude exhaustive de ce type de symétries pour les

équaùons aux dérivées partielles a été entreprise par Sophus Lie. Nous avons obtenu toutes les symétries disponibles dans le contexte des groupes de symétries continues de Lie classiques pour (2.2.4) et (2.1.1)

à

l'Appendice A. Alors tout en respectant le plus possible la chronologie historique des travaux reliés à (2.2.4), nous les situerons dans le contexte de ces symétries continues au cours de cette these. Une étude exhaustive des symétries de l'équation du tourbillon barotrope linéarisée dans le plan bêta n'a jamais été produite

à

la connaissance de l'auteur, quoique systématIquement elles ont été presque toutes employées dans la littérature scientifique d'une manière explicite ou parfois implicite. La présence de symétries pour une équation aux dérivées partielles permet d'utiliser des techniques extrêmement puissantes pour la résoudre. Comme exemples convaincants nous pouvons citer les techniques de séparations de.:; variables, Miller (1977), ou les réductions qui sont des possibilités d'utiliser une symétrie pour obtenir des solutions spéciales de l'équation qui ne dépendront que de " n - l " varÏ'lbles s'ils en avaient fi n If au départ, Oiver (1986, Chap.3). Un exemple évident d'une réduction sont

qui ne dépendent que de deux variables, soit x - c t et y. L'équation que satisfont les solutions stationnaires est appelée normalement en théorie des symétries l'équation réduite et les solutions spéciales sont appelées les solutions invariantes.

Bien qu'en physique-mathématiques cette approche d'une équation aux dérivées partielles est fréquente, nous avons préféré pour cette thèse éviter tout exposé trop technique sur le sujet. Alors nous avons présenté à l'Appendice A tous les résultats et les références qui nous ont permIS d'obtenir les ~ymétnes de notre équation linéarisée pour tout écoulement

U.

Mais il est important de comprendre que la théorie des groupes est en fait une théorie qui génère des résultats analytiques qUI peuvent être vérifiés (tprès coups par les méthodes usuelles. Par exemple, la théorie nous indique qu'il existen des solutions de (2.2.4) dépendantes des variables x - c t et y, alors un lecteur peut le vénfier. C'est pourquoi dans cette thèse nous allons donner les résultats analytiques obtenus de la théorie des groupes et le lecteur pourra toujours les vérifier par les méthodes usuelles et dans certains cas nous expliciterons les étapes importantes de la preuve.

Lorsque nous sommes en présence d'un vent zonal arbitraire les seules symétries disponibles de (2.2.4) sont celles associées

à

une translation en t et x. Ces symétries évidentes ont été historiquement les première~ à être utilisées et les solutions invariantes sont tout simplement les modes normaux. L'équation réduite qu'elles satisfont est l'équation de Rayleigh-Kuo. Il n'existe que deux vents zonaux qui permettent d'obtenir des symétries additionnelles lorsque

13

~ 0; le profil lInéaire et le profil quadratique. Lorsque ~ = 0 nous avons en plus des symétries pour des profils exponentiels, logarithmiques et pour une puissance de y arbitraire, voir Appendice A. Mais au cours de cette thèse nous allons nous concentrer plutôt sur le cas météorologique

13:f.

O. Les symétries additionnelles du jet parabolique vont nous pennettre d'obtenir au Chapitre 3 des lois de conservation spécifiques à ce jet. De plus, au Chapitre 4 nous obtiendrons des séparations des variables et des solutions invariantes associées

à

ces symétries.

(

te

L'obtention de symétries pour ce profil justifie par elle-même une étude approfondie, mais nous verrons qu'en situant ce profil parabolique dans le contexte actuel de la recherche il

est également pertinent d'un point de vue météorologique.

2.3.2 Modes normaux: solutions spéciales du problème aux conditions initiales. du problème forcé ou du problème marginalement stable.

Nous allons, dans ce qui suit, commenter brièvement les modes normaux de l'équation linéarisée qui sont associés aux symétnes (2.3.1) et de leurs différentes utilisations dans la littérature passée comme solutions spéciales. Pour un vent zonal

u (

y) arbitraire, il n'existe qu'une réduction connue de (2.2.4) à une équation différentielle ordinaire. Cette réduction est obtenue en substituant dans (2.2.4) le mode normal suivant

lk(x-ct)

\If ( x, y, t )

=

e <1> ( y ) (2.3.3)

et on obtient alors l'équation de Rayleigh-Kuo

[ 2 ]

-ct -k 2 A -tJ V"

2 <1>+

<1>=0

dy U( y) - c (2.3.4)

Nous employons exceptionnellement un intervalle fini en y, parce qu'historiquement, c'est la façon dont ce problème a généralement été introduit. Mais le formalisme introduit dans cette section peut être étendu

à

un domaine infini sans aucune difficulté. La vitesse de phase est une constante complexe, c = Cr + i Cl , et lorsque Ci

>

exponentiellement lorsque Cl

<

0 . Cette équation a une solution de Frobenius avec une

singularité logarithmique, s'il existe un point Yc satisfaisant l'équation suivante

U(y

_c )-c=O.

En ce point singulier si Cl # 0, il existe une continuation analytique entre les deux régions y

>

Yc et y

<

Yc . Le choix de la branche de la singularité logarithmique pose certains problèmes lorsque 1 CI 1 40 pour la contmuation analytique de la solution, mais

historiquement l'ambiguïté a été contournée si l'on exige que la solution obtenue soit une limite asymptotlque de l'équation de arr-Sommerfeld. Cette demière équation est similaire à celle de Rayleigh-Kuo, mais elle tient compte de la vIscosité. Si 1 Cl 1 « l, alors dans une couche critique autour du point Yc la viscosité devient importante. On peut relier la solution de la ré(~ion non visqueuse extérieure à la solutIon de la 1 églon interne visqueuse,

la couche critIque, par la méthode de raccord des développements asymptotiques et ainsi éliminer la singularité logarithmique. Il peut être montré également que le choix de branche pour la singularité logarithmique dans ce cas est le même que l'on obtient ~i l'on prend la continuation analytique de Cl> 0 avec Cl ~ 0 +, soit

log ( Y - Y c )

=

log

1

y - y c

1-

i 1t pour 0

>

y - y (. et

log ( _{Y - Yc ) =} log 1 y - y c 1 po r u y - Yc

> ()

,

lorsque le point singuher est au dessus de l'axe réel et l'on en cond ut qu'il y a un changement de phase de -1t entre les deux régions extérieures, voir Lin (1955, Chap. 8).

Cette phase étant proportionnelle au saut dans la tension de Reynolds, ü \ Ï , il e~t possible de montrer que l'interprétation physique de la discontinuité dans la divergence de la tension de Reynolds est la suivante: une valeur négative du saut indique que la couche critique et la région de l'écoulement se trouvant de l'autre côté de celle-ci absorbe la plus grande partie de l'énergie de la perturbation.

!f

t

Lorsque la viscosité tend vers zéro Benney

&

Bergeron (1969) ont montré que les termes non linéai.res peuvent dominer dans la couche critique et que le raccord avec les régions extérieures donnait un changement de phase nul, ce qui représente une couche critique qui réfléchit l'énergie de la perturbation. Habennan (1972) a étudié la dépendance de cette phase pour différents pOlds des termes non linéaIres et visqueux. Il reste

à

savoir s'il est possible d'exciter ce type de solutions dans l'atmosphère. Dickinson (1970) a montré que l'on pouvait exciter ce type d'onde de Rossby dans un vent zonal linéaire en forçant à une latitude se trouvant au Nord de la singularité pendant une période de temps assez grande. Les termes non linéaires ne sont plus négligeables après t -

e-

1_{/2 dans la}

couche critique 1 y - yc 1 - e1!2 où E est arbitrairement petit et proportionnel

à

l'amplitude forcée, Warn & Warn (1976). L'évolution non linémre de cette couche critique et de la région extérieure a été étudiée analytIquement par Warn

&

Warn (1978), Stewartson (1978) et avec de la viscosité par Brown & Stewartson (1978) . L'évolution obtenue dans le contexte de l'approxImation de l'onde longue pour la couche critique est que la fonction courant prend une configuration appelée en anglais Il Kelvin's cat's-eye "

et que le champ de tourbillon absolu est défonné par l'advection du vent pour former une structure en spirale. La tension de Reynolds oscille dans le temps pour finalement se stabIliser sur sa vrtleur nulle, pour faire ainsi de la couche critique un parfait réflecteur. Ce résultat asymptotIque devant être interprété avec prudence puisque cette solution a des instabilités hydrodynamiques, Killworth & McIntyre (1985). Quoique brève, cette courte discussion illustre bien le type de questions qui se posent dans le contexte des problèmes aux couches critiques et pour une actualisation du sujet nous référons les lecteurs

à

Maslowe (1986).

Lorsque Ci > 0 et CI -

0 (

1 ) l'hypothèse de linéarisation sera invalide dans un

court laps de temps et dû

à

la croissance exponentielle de l'amplitude du mode normal, il est actuellement impossible de suivre l'évolution non linéaire de la perturbation de façon

analytique. Alors il semble

à

première vue que l'étude d'un écoulement instable ne peut être abordée par des méthodes d'analyse linéaire. Une façon élégante de contourner cette difficulté est d'étudier un écoulement zonaI qui a un Cl arbitrairement petit, ce qui permet de

tempérer suffisamment la crois~ance exponentielle pour nous pennettre d'inclure sur un même pied les effets non linéaires et visqueux. Ces écoulements appelés marginalement stables ont été traités pour

f3

= 0 et pour ~ "#

0 ,

voir par exemple Stewartson (1981) et Burns & Maslowe (1983) respectivement, le dernier ayant certa1I1o,!s similitudes avec les impressionnantes instabilités que nous retrouvons dans les écoulements atmosphériques joviens.

Nous dirons que nous avons une onde de Rossby neutre lorsque Ci

=

0 et une condition suffisante pour qu'il n'existe que des ondes neutres, comme nous l'avons mentionné dans la section précédente; c'est que dans le domaine d'intégration

~ - U" -:;: 0

(2.3.5)

Rayleigh (1880) et Kuo (1949). (2.3.5) donne une condition (suffisante) de stabilité linéaire barotrope. Lorsque (2.3.5) n'est pas satisfaite c'est une condition nécessaire pOUf obtenir un mode avec croissance exponentielle. C'est le théorème du point d'inflexion de Rayleigh-Kuo, Rayleigh l'ayant démontré pour ~

=

O. Nous référons les lecteurs

à

Kuo (1973) et Tung (1981) 1--'our une actualisation de la stabilité ou instabilité linéaire des écoulements barotropes.

2.3.3 Modes nonnaux : Représentation pour une condniQn initiale arbitraire.

Nous avons précédemment discuté plusieurs aspects phy~iques des modes normaux de Rossby, mais nous verrons qu'ils peuvent être employés pour résoudre fonnellement le problème aux conditions initiales (2.2.4) et (2.2.5). La principale difficulté

(

provient de la présence possible d'un spectre continu. Les modes associés au spectre continu étant singuliers comme nous l'avons mentionné dans la section précédente et il est difficile a priori d'interpréter leur signiflcation dans le contexte d'un problème aux conditions initiales. Case (1960), Dlkii (1960) ont montré que ces modes singuliers doivent être employés dans une représentation intégrale si nous vouhns obtenir une base complète pour notre problème aux conditions initiales. L'approche employée est essentiellemeN la suivante: nous prenons la transformée de Laplace de (2.2.4) pour un mode zonal k fixe, ce qui nous donne l'équation suivante

(

d2 2

J3 -

U" ( y)

J

ç

(y)

-dy-2 -k - P

+

ik U ( y) <Pk P =

-p-+~~'---:U'-'(-y-)

(2.3.6)

où

'1'

(x, y, t)

=

e 1 k x <1> k (

y,

t) et <P k P (

y)

est la transformée de Laplace: 00

<Pk P ( y )

=

J

e -

p t <Pk ( y, t ) dt

o

(2.3.7)

Ço

est le tourbillon initial. Alors nous avons à résoudre une équation non homogène, ce qui peut être accompli en introduisant la fonction de Green associée

à

(2.3.6), G (

y,

YO). La fonction de Green nous pennet d'inverser (2.3.6) et ainsi obtenir <P k P en terme de

SQ,

voir Stakgold (1967). Explicitement. si nous prenons les conventions de Dikii (1960)

1

où (2.3.8)

La fonction D ( p ) est le Wronskien des deux solutions et elle définit la relation de dispersion pour ce problème. Pour le choix de conditions à la frontière que nous avons choisies, nous avons D ( P )

=

<l> k pl ( Y2 ). Les zéros de D ( p ) génèrent le spectre discret du problème de Rayleigh-Kuo (2.3.4). Par exemple, pour un écoulement avec stabilité barotrope D a seulement des zéros simples sur l'axe imaginaire qui sont associés au spectre discret neutre. Finalement, nous pouvons retrouver Q> k en employant la transformée inverse de Laplace et nous obtenons fomlellement dans le plan infini

(2.3.9)

où C est une droite parallèle à l'axe imaginaire et elle est à la droite de toutes les singularités de l'intégrant. Alors les contributions des différentes singularités à cette intégrale sont obtenues en déformant le contour C vers le demi-plan

à

gauche de l'axe imaginaire.

Nous devons expliciter la continuation analytique de l'intégrant dans ce domaine et puisqu'il existe des points de branche nous aurons

à

choisir des coupures de branche. Il existe plusieurs choix de coupures qui sont associées à différentes représentations équivalentes de la solution finale. Si nous choisissons une coupure qui soit symétrique par rapport à l'axe imaginaire. ce qui est toujours possible pour ce problème comme le fait remarquer

Briggs,

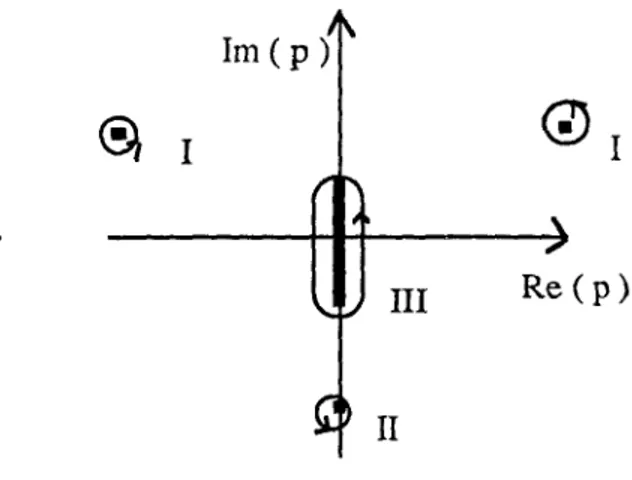
Daugherty & Levy (1970), alors en déformant le contour C vers la gauche nous obtenons une contribution due aux pôles simples de G qui génèrent des ondes

(

«

de Rossby discrètes. Notre choix de coupure symétrique implique que les singularités avec

Cl

*

0 doivent apparaître par paires, voir 1 à la Figure 2.1. Nous avons aussi illustré la

contribution d'un mode discret neutre II

à

la Figure 2.1. Un aut!e type de contribution sont les singularités dues aux points de branche qui se trouvept sur l'axe imaginaire, ce sont les singularités logarithmiques que nous avons déjà commentées pour l'équation de Rayleigh-Kuo (2.3.4). C'est tout simplement la contribution du spectre continu singulier de (2.3.4) et il peut être montré que la coupure symétrique choisie sera sur l'axe imaginaire entre la valeur maximum et minimum de D, voir III à la Figure 2.1.

1

III

Re (p)

II

Figure 2.1 Contributions à la transformée inverse de Laplace. 1 est la contribution d'une paire de modes normaux avec Cl ~ O. II est associé

à

un mode normal neutre.

III

est

la contribution des modes normaux singuliers neutres.

.

[~

-) kCn!

'V

=

e

1 k x ~An <Pk n ( y )

e

+

max ( U )

f

A (

c ) <P ( y ) e - ) k c t dc kc mm(U)

J

+

C.C. (2.3.10)

où An et A ( c ) sont reliés aux conditions initiales. Nous nommerons cette solution la représentation des modes normaux, parce qu'elle utilise explicitement les modes nonnaux associés au spectre continu et discret de 1'équation de Rayleigh-Kuo.

La discussion précédente est une discussion fonnelIe pour un écoulement arbitraire, mais il reste encore à expliciter les propriétés analytiques de A ( c ) en fonction des conditions initiales et de 1'écoulement choisi. Il faut aussi faire l'évaluation de l'intégrale (2.3.9) dans le plan complexe si nous voulons connaître explicitement la continuation analytique des modes normaux des deux côtés du point singulIer. Ce travail n'est possible que pour certains écoulements où il existe des résultats analytique ... , en particulier le profil linéaire. Ces résultats sont nécessaires si nous voulons répondre à une importante question: Quelle est l'évolution asymptotique, pour un grand temps, de la perturbation pour une condition initiale arbitraire? Evidemment, le spectre discret ne pose aucune difficulté, mais l'évolution asymptotique de l'intégrale associée au spectre continu est difficile à analyser. Si difficile, que ces analyses ont été responsables de plusieurs erreurs dans la littérature passée. La rénonse correcte pour le comportement asymptotique dans le cas d'un vent linéaire sans effet bêta a été donnée par Brown & Stewartson (1980) et elle est pour un mode avec un nombre d'onde zonal k fixé

(

(

'V

= H ( Y ) exp

i

k (

x -

U ( y ) t)

+

0 (t -3 )

t2

(2.3.11)

où H ( Y ) est une fonction analytique reliée à la condition initiale et 1 « t . Il est aisé de généraliser formellement cette série asymptotique par inspection pour la composante du spectre continu d'un vent zonal arbitraire en substituant ce premier terme du développement dans l'équation (2.2A) et nous avons obtenu

(

H (y) Hl (y)

'1'

= exp i k ( x -U ( y ) t ) 2

+

3

t t

où Hl est donné par

H 1 = 1 . (

U ' (

y )

H' ( Y ) -

y

H ( Y ) )

k U' (y) 2

(2.3.12)

(2.3.13)

Il n'existe aucune difficulté pour obtenir les autres termes de la série, car ils sont obtenus par des manipulations algébriques seulement. Le seul problème qui se pose est que la série asymptotique n'est valide que pour un écoulement n'ayant pas d'extremum, car s'il existe un point d'extremum

Yc

tel que

U' (

Ye)

=

0

la série devient désordonnée comme en fait foi (2.3.13).

Le résultat (2.3.13) se déduit aisément pour un vent linéaire avec effet bêta

à

partir des résultats analytiques que Tung (1983) a obtenus, mais pour un écoulement général monotone il n'a pas été démontré rigoureusement que toute évolution du spectre continu d'une perturbation initiale génère asymptotiquement la série (2.3.12). Mais puisque cette série asymptotIque est bien ordonnée lorsque nous n'avons pas de point d'extremum, nous supposerons qu'elle est vraisemblablement le comportement asymptotique du spectre continu pour un écoulement zonal monotone dans le plan bêta. Nous verrons au Chapitre 4 pour un jeL parabolique que cette série de Brown

&

Stewartson apparaît encore, mais