Optimisations des structures mécaniques.Forme optimale d'un composant

RÉPUBLIQUE ALGÉRIENNE DÉMOCRATIQUE ET POPULAIRE

MINISTÈRE DE L’ENSEIGNEMENT SUPÉRIEUR ET DE LA RECHERCHE SCIENTIFIQUE UNIVERSITÉ MENTOURI - CONSTANTINE

FACULTÉ DES SCIENCES DE L'INGÉNIEUR DÉPARTEMENT DE GÉNIE MÉCANIQUE

Mémoire :

Présenté en vu d’obtention du Diplôme de Magister en Génie Mécanique

Option :

Mécanique appliquée en engineering

THÈME :

THÈME :

THÈME :

THÈME :

OPTIMIS

OPTIMIS

OPTIMIS

OPTIMISATION DE

ATION DE

ATION DES

ATION DE

S

S

S

STRUCTURES MÉCANIQUES

STRUCTURES MÉCANIQUES

STRUCTURES MÉCANIQUES

STRUCTURES MÉCANIQUES

Forme optimale d’un composant

Forme optimale d’un composant

Forme optimale d’un composant

Forme optimale d’un composant

Par :

KHALFI Mehdi

Soutenu le : 08/07/2009. Devant les membres de jury :

• Président Mr. MILI Fayçal Prof. Université Mentouri Constantine • Rapporteur Mr. CHOUITER Yacine M.C. Université Mentouri Constantine • Examinateurs Mr. BENISAAD Smail M.C. Université Mentouri Constantine Mme. LABED Zohra M.C. Université Mentouri Constantine

Juillet 2009 N° d’ordre : 266 / MAG / 2009

A

VANT PROPOS

Ce mémoire est le résultat d'un travail qui a pu naître et se dérouler grâce à la confiance que mon encadreur, Mr. Chouiter Yacine a eue en moi. Je tiens à lui remercier vivement pour son appui et ses conseils donnés tout le long de ce travail, pour sa compréhension et sa patience, et pour son soutien constant tout au long de ce mémoire.

Je remercie Mr. Mili Fayçal qui m'a fait l'honneur d’avoir accepté de présider le jury. Mes remerciements s'adressent également à Mr. Benisaad Smail et Mme. Labed Zohra qui m'ont fait l'honneur d'accepter d'être examinateurs de ce travail. Je leur exprime, ainsi qu'à Mr. Mili ma profonde gratitude pour leurs commentaires sur mon mémoire.

J’adresse ma reconnaissance également à Mr. Boughouas Hamlaoui pour ses précieux conseils ainsi que pour son encouragement.

Mes remerciements s'adressent aussi à Mr. Benchaker Yacine, Mr. Djilali et Mr. Nacer pour leur aide considérable dans différents sujets.

Je dédie ce mémoire à mes chers parents qui ont toujours été à mes côtés avec leur soutien et leurs encouragements. Il est aussi dédié à mes frères, ma sœur et son époux, ma famille, ainsi qu'à mes amis les plus proches.

R

ÉSUMÉ

Le mémoire porte sur l'optimisation de la forme de la trochoïde d'un engrenage cylindrique à dentures droites. Il commence par une présentation des techniques d'optimisation de structures mécaniques et plus particulièrement son outil incontournable : le calcul des variations.

L'objectif de ce travail est de chercher une forme optimisée de la trochoïde pour laquelle la contrainte maximale due à la flexion au niveau du pied de la dent sera diminuée afin de réduire le risque de rupture par fatigue des dents de l'engrenage.

Les calculs sont effectués sur la base d'une formule exprimant la contrainte maximale au niveau de la trochoïde obtenu analytiquement par une étude récente. La trochoïde est considérée de forme semi-circulaire et le rayon optimal pour lequel la contrainte a était le plus bas possible est déterminé.

Les résultats montrent qu'on peut aller jusqu'à 14% de réduction de la contrainte maximale.

Mots clés : Optimisation de forme, Calcul des variations, Trochoïde, Engrenages à denture droite.

A

BSTRACT

Optimization of mechanical structures: optimal shape of a component.

This work relates to the trochoid shape optimization of a cylindrical straight teeth gear. It starts with a presentation of the optimization techniques of mechanical structures and more particularly its essential tool: the calculus of variations.

The objective of this work is to seek the optimized shape of the trochoid for which the maximum constraint due to the bending on the root of the tooth will be decreased in order to reduce the risk of rupture by tiredness of the gear teeth.

Calculations are carried out on the basis of a formula expressing the maximum constraint on the root of the tooth obtained analytically by a recent work. The trochoid is considered of semicircular form and the optimal ray for which the constraint was low as possible as we can is deduced.

The results show that we can go up to 14 percent of reduction of the maximum constraint.

ﺺﺨﻠﻣ

ﺔﻴﻜﻴﻨﺎﻜﻴﻤﻝﺍ ﺕﺎﺌﺸﻨﻤﻝﺍ ﻥﻴﺴﺤﺘ

:

ﺎﻤ ﺔﻌﻁﻘﻝ لﻜﺸ ﻥﺴﺤﺃ

.

ﺒ ﻡﺘﻬﺘ ﺓﺭﻜﺫﻤﻝﺍ ﻩﺫﻫ

ﻥﻴﺴﺤﺘ

ﺔﻤﻴﻘﺘﺴﻤﻝﺍ ﻥﺎﻨﺴﻷﺍ ﺕﺍﺫ ﺔﻴﻨﺍﻭﻁﺴﻷﺍ ﺕﺎﻨﻨﺴﻤﻝﺍ ﻥﺎﻨﺴﺃ لﻜﺸ

ﻭ

ﻥﺎﻨﺴﻷﺍ ﺭﻭﺫﺠ ﻯﻭﺘﺴﻤ ﻰﻠﻋ ﺍﺫﻫ

.

ﺕﺎﻴﻨﻘﺘﻝ ﻡﻴﺩﻘﺘﺒ ﺃﺩﺒﺘ ﺓﺭﻜﺫﻤﻝﺍ

ﻥﻴﺴﺤﺘ

ﺕﺎﺌﺸﻨﻤﻝﺍ

ﺔﻴﻜﻴﻨﺎﻜﻴﻤﻝﺍ

ﺍ ﺏﺎﺴﺤ ﻲﻓ ﺔﻠﺜﻤﺘﻤﻝﺍ ﻭ ﺔﻴﺴﺎﺴﻷﺍ ﻪﺘﺍﺩﺃ ﺎﺼﻭﺼﺨ ﻭ

ﺕﺍﺭﻴﻐﺘﻝ

.

ﻥﺎﻨﺴﻷﺍ ﺭﺫﺠﻝ ﻥﺴﺤﻤ لﻜﺸ ﻥﻋ ﺙﺤﺒﻝﺍ ﻭﻫ لﻤﻌﻝﺍ ﺍﺫﻫ ﻥﻤ ﻑﺩﻬﻝﺍ

ﺔﻤﻴﻘﺘﺴﻤﻝﺍ ﺕﺎﻨﻨﺴﻤﻠﻝ

ﻥﺎﻨﺴﻷﺍ

ﺀﺍﻭﺘﻝﻻﺍ ﻥﻋ ﺞﺘﺎﻨﻝﺍ ﻰﺼﻗﻷﺍ ﺩﺎﻬﺠﻹﺍ ﺔﻤﻴﻘﻝ ﺽﻴﻔﺨﺘ ﻙﻝﺫ ﻥﻋ ﺞﺘﻨﻴ ﺙﻴﺤﺒ

ﺔﻴﻐﺒ

ﺇ ﺭﻁﺨ ﺹﻴﻠﻘﺘ

ﺭﺎﺴﻜﻨ

ﺏﻌﺘﻝﺍ ﺔﺠﻴﺘﻨ ﻥﻨﺴﻤﻝﺍ ﻥﺎﻨﺴﺃ

.

ﻝﺍ

ﺤ

ﺕﻤﺘ ﺕﺎﺒﺎﺴ

ﺍﺩﺎﻨﺘﺴﺍ

ﺔﻝﺩﺎﻌﻤ ﻰﻝﺇ

ﻰﻠﻋ ﻰﺼﻗﻷﺍ ﺩﺎﻬﺠﻹﺍ ﻲﻁﻌﺘ

ﻥﺎﻨﺴﻷﺍ ﺭﺫﺠ ﻯﻭﺘﺴﻤ

ﺔﺜﻴﺩﺤ ﺔﺴﺍﺭﺩ لﻼﺨ ﻥﻤ ﺎﻴﻠﻴﻠﺤﺘ ﺎﻬﻴﻠﻋ لﻭﺼﺤﻝﺍ ﻡﺘ

.

ﻱﺭﺌﺍﺩ ﻑﺼﻨ لﻜﺸ ﻭﺫ ﺭﺫﺠﻝﺍ ﺭﺎﺒﺘﻋﺍ ﻡﺘ

ﻰﻨﺩﻷﺍ ﺎﻫﺩﺤ ﻲﻓ ﺩﺎﻬﺠﻹﺍ ﺔﻤﻴﻗ ﻥﻭﻜﺘ ﻪﻠﺠﺃ ﻥﻤ ﻱﺫﻝﺍ ﺭﻁﻘﻝﺍ ﻑﺼﻨ ﺩﻴﺩﺤﺘﺒ ﺎﻨﻤﻗ ﻡﺜ

.

ﺩﻭﺩﺤ ﻰﻝﺇ ﻰﺼﻗﻷﺍ ﺩﺎﻬﺠﻹﺍ ﺔﻤﻴﻗ ﺹﻴﻠﻘﺘ ﻊﻴﻁﺘﺴﻨ ﺎﻨﻨﺃ ﻥﻴﺒﺘ ﺞﺌﺎﺘﻨﻝﺍ

14

.%

ﺔﻴﺤﺎﺘﻔﻤﻝﺍ ﺕﺎﻤﻠﻜﻝﺍ : ﺤﺘ ﻥﻴﺴ ﺕﺎﺌﺸﻨﻤﻝﺍ ﺔﻴﻜﻴﻨﺎﻜﻴﻤﻝﺍ , ﺕﺍﺭﻴﻐﺘﻝﺍ ﺏﺎﺴﺤ , ﺍ ﺔﻤﻴﻘﺘﺴﻤﻝﺍ ﻥﺎﻨﺴﻷﺍ ﺕﺍﺫ ﺕﺎﻨﻨﺴﻤﻝ .

T

ABLE DES MATIÈRES

AVANT PROPOS...i

RÉSUMÉ...ii INTRODUCTION GÉNÉRALE... 1 Chapitre I INTRODUCTION À L’OPTIMISATION I.1. Historique...5 I.2. Généralités ...5

I.3. Types d’optimisation ...6

I.3.1. Optimisation paramétrique...6

I.3.2. Optimisation géométrique...8

I.3.3. Optimisation topologique...10

I.4. Ingrédients d'un problème d'optimisation ...11

I.4.1. Modélisation ...11

I.4.2. Critères d’optimisation...12

I.4.3. L'ensemble de formes admissibles...14

I.5. Processus d’optimisation ...14

I.6. Applications ...16

Chapitre II CALCUL DES VARIATIONS II.1. Introduction...19

II.2. Fonctionnelle ...20

II.2.1. Définition ...20

II.2.2. Résultats concernant les fonctionnelles ...21

II.3. Problèmes types du calcul des variations...22

II.3.1. Problème de Lagrange ...23

II.3.2. Problème de Bolza ...23

II.3.3. Problème de Mayer ...23

II.5. Équation d'Euler-Lagrange ...25

II.5.1. Multiplicateurs de Lagrange ...25

II.5.2. Équation d'Euler-Lagrange ...27

II.5.3. Cas particuliers...28

II.6. Quelques exemples ...29

II.6.1. Principe de la moindre action de Hamilton...29

II.6.2. Problème de la brachistochrone ...29

II.7. Problème d'optimisation à limites variables ...30

Chapitre III FORMULATION DU PROBLÈME III.1. Introduction...35

III.2. But de l'étude ...36

III.3. Bibliographie ...36

III.4. La dent d'engrenage ...42

III.4.1. Géométrie...42

III.4.2. Résistance à la flexion ...43

III.5. Hypothèses et contraintes ...46

III.5.1. Intérêt des profils en développante de cercle ...46

III.5.2. Symétrie des dents ...46

III.5.3. Profil de la trochoïde...46

III.6. Détermination de la contrainte en fonction du rayon...47

III.7. Condition de résistance ...50

Chapitre IV CALCULS, RÉSULTATS ET DISCUSSIONS IV.1. Introduction...53

IV.2. Calcul du rayon optimum ...54

IV.2.1 L'algorithme ...54

IV.2.2. Le rayon optimum...55

IV.3. La différence entre les profils des engrenages ...55

IV.4. Analyse des contraintes ...56

IV.5. Résultats et discussions...57

CONCLUSION GÉNÉRALE... 62

ANNEXES A. Rayon du congé au niveau du pied de la dent...65

B. Coefficient de forme de Lewis Y...66

C. Coefficient de forme de l'AGMA ...66

D. Facteur dynamique...67

E. Facteur de surcharge ...67

F. Facteur de taille...68

G. Facteur de distribution de la charge ...68

H. Profil en développante de cercle ...68

I

I

N

N

T

T

R

R

O

O

D

D

U

U

C

C

T

T

I

I

O

O

N

N

G

G

É

_É

N

_N

É

_É

R

_R

A

_A

L

_L

E

_E

INTRODUCTION

INTRODUCTION

INTRODUCTION

INTRODUCTION

GÉNÉRALE

GÉNÉRALE

GÉNÉRALE

GÉNÉRALE

La perception du calcul numérique par les industriels a évolué très fortement ces dernières décennies. En effet, il y a seulement une quinzaine d’années, les calculs par éléments finis étaient le plus souvent dédiés à la vérification d’hypothèses concernant le comportement d’une structure à partir d’une conception donnée ou bien comme moyen d’expertise en cas de problème. De plus, ces simulations étaient le plus souvent réalisées dans un cadre élastique et en petites déformations. Le développement des méthodes de calcul (éléments finis, techniques de résolution et de discrétisation) associé à l’efficacité croissante des moyens informatiques permettent à l’aide d’investissements relativement modestes de simuler le comportement de structures industrielles dans des conditions générales de sollicitations ou de déformation. De plus, ces outils constituent maintenant un moyen efficace de conception en s’appuyant sur des procédures d’optimisation et évitent la réalisation de conceptions ou de maquettes intermédiaires toujours très coûteuses.

D’autre part, le fait de concevoir et de réaliser n'est plus une "fin en soi" d'un point de vue industriel. À une concurrence très ardue entre industriels, il faut faire face, également, à des contraintes de fiabilité et d'esthétique où tout producteur de composants ou d’ensembles mécaniques de nos jours fait face à une question omniprésente : Quel est le meilleur produit possible à obtenir ?

Par "meilleur", on entend non seulement le moindre coût mais aussi, "le plus résistant", "le plus léger", "le plus durable". C'est à ces questions que l'optimisation des structures mécaniques doit apporter les réponses adéquates.

Dans le présent travail, on abordera, en premier lieu, tous ce qui concerne l’optimisation de structures mécaniques à savoir son historique, ses types, outils, techniques, etc.…, en donnant plus d’intérêt à la théorie mathématique du calcul des variances qui représente l'outil incontournable à utiliser en optimisation de structures mécaniques.

Deux chapitres seront consacrés à ce qui à était dit ci-dessus : le premier qui est une "Introduction à l’optimisation", consiste en une étude bibliographique sur l’optimisation des structures mécaniques. Après un bref historique, les concepts généraux de l’optimisation serrant signaler dans ce chapitre ainsi que ses types, sa procédure et plus.

Le "Calcul des variations" représente un outil incontournable dans le processus d'optimisation, c'est pour cela que le second chapitre sera consacré a sa présentation, ses problèmes typiques, ses techniques, ainsi que quelque exemple de calcul de variations.

Une application dans le domaine industriel occupera le reste de ce mémoire, elle est comprend deux chapitres. Le premier, qui est le chapitre N° III, consiste en une formalisation du problème à étudier, ce dernier vise l'optimisation de la forme de la trochoïde dans un engrenage à denture droite.

Dans ce chapitre, une revue des travaux effectués dans le sens de la détermination des contraintes engendrer par les charges agissant sur les dent d'un engrenage sera effectuée, ainsi que les travaux visant l'optimisation de la forme de la trochoïde. Quelques rappels de mécanique relative à l’étude tel que la résistance des dents à la flexion et leur dimensionnement seront aussi réunis dans ce chapitre qui mettra fin à l’étude bibliographique.

Le dernier chapitre comprend les calculs effectuer pour déterminer la forme optimisée. Une analyse de contraintes sera effectuée à l'aide d'un software de simulation afin de valider les résultats obtenus permettant ainsi leur discussion.

Une conclusion générale réunira les résultats obtenus et mettra fin à ce travail.

I

I

N

N

T

T

R

R

O

O

D

D

U

U

C

C

T

T

I

I

O

O

N

N

À

À

L

L

’

’

O

O

P

P

T

T

I

I

M

M

I

I

S

S

A

A

T

T

I

I

O

O

N

N

Sommaire du chapitre :

I.1. Historique... 5 I.2. Généralités... 5

I.3. Types d’optimisation... 6

I.3.1. Optimisation paramétrique... 6

I.3.2. Optimisation géométrique... 8

I.3.3. Optimisation topologique... 10

I.4. Ingrédients d'un problème d'optimisation... 11

I.4.1. Modélisation... 11

I.4.2. Critères d’optimisation... 12

I.4.3. L'ensemble de formes admissibles... 14

I.5. Processus d’optimisation... 14

I.6. Applications... 16

Chapitre

INTRODUCTION

INTRODUCTION

INTRODUCTION

INTRODUCTION

À

À

À

À

L’OPTIMISATION

L’OPTIMISATION

L’OPTIMISATION

L’OPTIMISATION

I.1.

H

ISTORIQUE

L'histoire raconte qu’en 814 avant Jésus-Christ, la reine Didon fuyant les Assyriens accosta sur les rives de l’actuelle Tunisie. Souhaitant s’y installer et fonder une ville (la future Carthage), Didon demanda au chef de la tribu qui occupait les lieux l’autorisation de disposer d’un territoire. Celui-ci lui tendit alors une peau de bœuf en lui disant d’un air goguenard : "Le territoire que vous arriverez à couvrir avec cette peau est à vous !". Didon découpa la peau en une très fine lanière et se trouva alors confrontée au problème suivant : disposant d’une lanière de longueur donnée, comment enclore un territoire de surface maximale ? L’optimisation de forme était née ! [1].

I.2.

G

ÉNÉRALITÉS

Vu la concurrence accrue entre les industriels, l’optimisation de formes est devenue indispensable dans la conception des nouveaux produits, elle intervient dans presque tous les domaines des sciences de l’ingénieur. Elle a par exemple pour cadre soit l’amélioration de l’existant par modification des paramètres vis à vis de nouveaux objectifs ou limitations, soit l’émergence de nouvelles conceptions par l’optimisation topologique. Autrement dit, elle consiste à déterminer la meilleure forme, les meilleures propriétés internes et/ou meilleures conditions de travail d’une structure obéissant à des contraintes connues, produisant ainsi un extremum (soit minimum ou maximum) d’une quantité choisi caractérisant la structure [2].

Dans les problèmes d'optimisation simples, la solution (l'optimum) est la plupart du temps obtenue en cherchant les zéros de la dérivée de la fonction à optimiser, ou de son gradient dans les cas de dimension supérieure. Ceci fournit dans la plupart des cas des optima locaux, parmi lesquels on doit trouver le vrai optimum.

Le choix d’une forme estimée est essentiel pour l’analyse ainsi que l’optimisation d’une structure mécanique. L’optimisation est donc possible sont établir une étude préliminaire des hypothèses mises à propos des aspects de la réponse de la structure, soit réelle ou imaginée.

I.3.

T

YPES D

’

OPTIMISATION

Parmi les problèmes d’optimisation de formes on peut distinguer trois grandes catégories, du plus facile au plus difficile :

I.3.1.

_{Optimisation paramétrique}

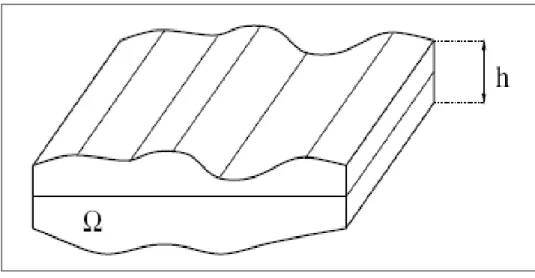
Dans ce type d’optimisation de formes, les formes sont paramétrées par un nombre réduit de variables (par exemple, une épaisseur, un diamètre, des dimensions), ce qui limite considérablement la variété des formes possibles (ou admissibles). L’exemple le plus simple de cette optimisation est l’optimisation de l’épaisseur d’une membrane.

On considère une membrane élastique qui, au repos, occupe un domaine plan Ω, et que l’on suppose tendue et fixée sur son contour. Lorsqu’elle est soumise à un chargement ou force verticale f, elle se déforme en dehors de son plan d’équilibre. Dans le cadre d’une théorie mécanique de petits déplacements et de petites déformations, et si l’on ne considère que des efforts de membranes (en négligeant ceux de flexion), la déformation de cette membrane est modélisé par son déplacement vertical u(x) : Ω → IR , solution de l’équation aux dérivées partielles suivante, dite modèle de membrane :

(

)

Ω ∂ Ω    = = ∇ − sur dans 0 u f u A div (I-1)

où A(x) est le coefficient (en toute généralité le tenseur) qui représente les propriétés de résistance mécanique en x. Ce coefficient varie en espace, reflétant ainsi une variation de l’épaisseur de la membrane ou bien un changement de matériau élastique. Nous supposons ici que le matériau est homogène isotrope, mais que l’épaisseur peut varier d’un point à un autre (voir Fig. I-1). Dans ce cas le coefficient A est relié à l’épaisseur h par la formule :

( )

x h

( )

x I

A =

µ

où I est le tenseur identité, et µ > 0 est le module de Young du matériau.

D’un point de vue pratique l’épaisseur est limitée par des valeurs minimale et maximale : 0 < hmin ≤ h(x) ≤ hmax < +∞. L’épaisseur h sera notre variable

d’optimisation.

Il reste à définir de manière plus précise l’ensemble des épaisseurs admissibles en tenant compte d’éventuelles contraintes de ressource ou de faisabilité pratique ; contrainte sur le poids par exemple. Dans un tel cas on obtient :

( )

{

:Ω telque _min ( ) _max et

∫

( ) ₀

}

Ω = Ω ≤ ≤ → = h x R h h x h h x dx h U_ad (I-2)

où h0 est une épaisseur moyenne imposée.

Figure I-1 : Membrane d’épaisseur variable.

Il ne reste maintenant que préciser le dernier ingrédient d’un problème d’optimisation, à savoir le critère d’optimisation. En général, on cherche à optimiser

une propriété mécanique de la membrane qui est évaluée à l’aide du déplacement u, solution de (I-1). Un critère assez général est donc :

∫

Ω

= j u dx

h

J( ) ( ) (I-3)

où u dépend bien sûr de h à travers l’équation (I-1), et j(u) prend différentes forme selon besoins, par exemple j(u) = fu si en jouer sur la rigidité d’une structure à savoir quelle est souvent mesurée par le travail des forces extérieures (moins la structure travaille, plus elle est rigide). Un autre exemple consiste à obtenir (ou du moins s’approcher) d’un déplacement cible u0(x), ainsi, on aura : j(u) = |u − u0|².

On retrouve bien dans ce problème les trois ingrédients essentiels de tout problème d’optimisation de structures : un modèle (1-1), un ensemble admissible (1-2) et un critère (1-3).

I.3.2.

_{Optimisation géométrique}

L’idée principale en optimisation géométrique est de faire varier la position des frontières d’une forme, sans toutefois changer sa topologie (c’est-à-dire le nombre de trous en 2D) qui reste la même que celle de la forme initiale.

Par rapport à l’optimisation paramétrique, un certain nombre de difficultés nouvelles se présentent. En particulier, se posent les questions de la représentation mathématique des formes et des variations de formes. Par exemple, on peut représenter une forme par la fonction caractéristique de son domaine (qui vaut 1 à l’intérieur et 0 à l’extérieur) ; mais dans ce cas, comment faire des variations de forme ? En effet, une combinaison linéaire de fonctions caractéristiques n’est pas, en général, une fonction caractéristique. On ne peut donc pas faire de "calcul des variations" dans l’espace des fonctions caractéristiques, et calculer un gradient. Il s’agit d’une difficulté typique de l’optimisation de formes géométrique qu’il est important de contourner pour des raisons théoriques tout autant que numériques.

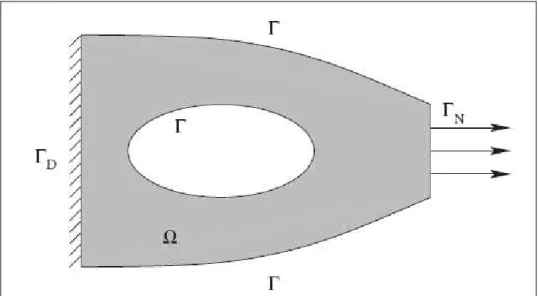
Un exemple d’optimisation géométrique est l’optimisation de la forme d’une membrane, mais cette fois-ci à frontières variable ; l’épaisseur est considérée constante, c’est la forme de la membrane qui est la variable d’optimisation.

Un domaine de référence de la membrane est noté Ω, et son bord est divisé en trois parties disjointes ∂Ω=Γ∪ΓN ∪ΓD, où Γ est la partie variable de la frontière, ΓD

et ΓN sont des parties fixe de la frontière (condition aux limites).

Figure I-2 : Membrane à frontières variables.

On suppose que la partie variable Γ de la frontière est libre de tout effort, autrement dit, le déplacement vertical u est solution du modèle de membrane suivant :

       = ∂ ∂ = ∂ ∂ = Ω = ∆ − sur 0 sur sur 0 dans 0 Γ n u Γ g n u Γ u u N D (I-4)

On rajoutant une contrainte sur le poids ou la masse de la membrane qui est proportionnel au volume de Ω, l’ensemble des formes admissibles sera donc :

{

Ω RN telque et

∫

₀

}

Ω∂ = Ω ∂ ⊂ ⊂ = Γ Γ x V U_{ad D} U _{N (I-5)}

où V0 est un volume imposé.

Il ne manque que le critère d’optimisation pour définir complètement ce problème, celui-ci peut être la compliance qu’on peut formuler comme suite :

∫

= Ω N Γ gudx J( ) . (I-6)

ou un déplacement cible u0 (x) pour lequel :

∫

Ω −

=

Ω u u dx

J( ) ₀ 2 (I-7)

I.3.3.

_{Optimisation topologique}

Dans l’optimisation de formes topologique on cherche, sans aucune restriction explicite ou implicite, la meilleure forme possible quitte à changer de topologie. Ce dernier type d’optimisation est, bien sûr, le plus général mais aussi le plus difficile.

Notons que, si la définition de la topologie d’une forme est assez simple en dimension deux d’espace (nombre de composantes connexes de son bord ou de trous), elle est nettement plus compliquée en dimension trois où ce qui compte n’est pas seulement le nombre de composantes connexes du bord de la forme, mais aussi, son nombre d’anses ou de boucles (une boule ≠ un tore ≠ un bretzel, etc.).

Figure I-3 : Formes de topologie déférentes.

On peut dire que deux formes ont la même topologie si on peut passer de l’une à l’autre par une déformation continue.

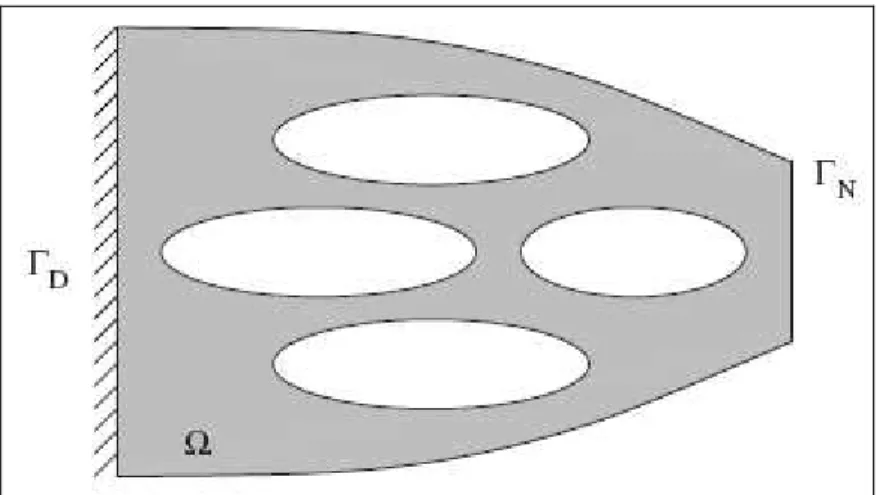
Si l’on considère l’exemple précédent, le but de l’optimisation topologique est donc d’optimiser aussi la topologie de la forme Ω (comparer les Figures 1-2 et 1-4). Pour cela, il ne faut pas représenter une forme par la position de sa frontière, mais plutôt par une fonction indicatrice ou densité de matériau qui vaut 1 si l’on se trouve à l’intérieur de la forme et 0 à l’extérieur.

Il faudra aussi tenir compte de la présence de “trous” minuscules qui permettent d’améliorer les performances de la structure et considérer donc une classe plus large de formes admissibles qui pourront être des matériaux composites de type milieux poreux microperforés.

Figure I-4 : Structure à trous en optimisation topologique.

I.4.

I

NGRÉDIENTS D

'

UN PROBLÈME D

'

OPTIMISATION

Afin de résoudre un problème d'optimisation de structures en mécanique, le mathématicien ou le numéricien travaille à partir de trois ingrédients essentiels pour concevoir une méthode ou un algorithme de résolution du problème.

Ces ingrédients sont :

• Un modèle (typiquement une équation aux dérivées partielles) qui permet d’analyser le comportement mécanique d’une structure,

• Un critère que l’on cherche à minimiser ou maximiser, et éventuellement plusieurs critères (on parle aussi de fonction objective ou coût),

• Un ensemble admissible de variables d’optimisation qui tient compte d’éventuelles contraintes que l’on impose aux variables [3].

Cependant, il faut garder à l’esprit qu’en pratique, les choses sont beaucoup plus compliquées. En effet, le choix de ces trois ingrédients est rarement évident et “naturel” et constitue une partie non négligeable du travail de l’optimisation. Jamais le vieil adage "Bien poser le problème, c’est le résoudre à moitié" n’a été aussi vrai !

I.4.1.

_{Modélisation}

Le choix du modèle doit être un compromis entre un modèle précis, mais certainement coûteux en temps de calcul, et un modèle plus grossier, mais plus économique du point de vue du calcul. Un tel compromis s’impose car la résolution

numérique de problèmes d’optimisation de formes est fondamentalement itérative et nécessite donc de nombreuses évaluations du modèle. On améliore une succession de formes et pour chacune d’entre elles on calcule sa performance en résolvant le modèle. Nous identifierons toujours un modèle à une équation aux dérivées partielles (ou une discrétisation de celle-ci). C’est en quelque sorte le cas idéal, et le plus fréquent, où l’on dispose d’une modélisation précise, ou "exacte", de la réalité. Néanmoins, il peut arriver dans certaines situations très complexes qu’un tel modèle soit inutilisable car trop coûteux, voire impossible, à évaluer.

C’est particulièrement vrai en optimisation multidisciplinaire où l’on considère en fait plusieurs modèles concurremment : par exemple, un avion dont on optimise les propriétés aérodynamiques, acoustiques, structurelles et électromagnétiques (signature radar). Dans une telle éventualité une approche populaire est d’utiliser un modèle de substitution.

L’idée est de remplacer le modèle exact par un modèle très simplifié (typiquement un polynôme des variables d’optimisation) dont les paramètres sont ajustés afin de minimiser l’erreur d’approximation. On parle aussi de méthode de surfaces de réponse.

La conception optimale a lieu alors en deux étapes : premièrement, un certain nombre d’évaluations du modèle exact permet d’établir un modèle de substitution; deuxièmement, on optimise la structure à l’aide de ce modèle simplifié. En général, la seconde étape ne pose pas de problèmes, et toutes les difficultés sont concentrées dans la première [3].

I.4.2.

_{Critères d’optimisation}

Le choix du critère n’est pas plus simple. Il existe des facteurs de performance non quantifiables mathématiquement (par exemple, la beauté, le plaisir, ou tout ce qui est du ressort des sensations). Sans même en arriver à ces extrémités, certains critères physiques ou mécaniques sont difficilement traduisibles en termes mathématiques. Parexemple, si l’on veut minimiser le risque de ruine d’une structure, il est difficile de

trouver un critère absolu car les origines de la rupture sont nombreuses (endommagement, plasticité, fissuration, etc.) [3].

Bien que le critère d’optimisation qu’on a vu dans la sous-section I.3.1, concernant l’exemple de l’optimisation de l’épaisseur d’une membrane, ait l’air assez général, il n’en est rien : de très nombreux critères essentiels du point de vue des applications ne se mettent pas sous la forme (I-3).

Ceci va nous permettre de faire quelques remarques sur les critères d’optimisation, valables aussi pour la plupart des autres modèles en optimisation.

En premier lieu, il est possible de faire dépendre le critère, non seulement du déplacement u, mais aussi de ses dérivées. Par exemple, il est courant d’utiliser des critères portant sur le vecteur des contraintes, défini par :

σ

(x)=

µ

.h(x)∇u(x)

Un critère classique pour éviter l’endommagement ou la rupture est le maximum des contraintes :

( )

x h J x

σ

sup ) ( Ω ∈ = (I-8)

où l’on a utilisé la norme du vecteur σ (en élasticité on utilise plutôt la contrainte équivalente de Von Mises). La difficulté avec ce critère est sa non-différentiabilité, on lui préfère souvent le critère plus régulier suivant :

(

∂

)

≤ ≤+∞

=

_∫

Ω x p

h

J( )

σ

p 1p avec 1 (I-9)

Ce dernier redonne à la limite p → +∞ le critère sur le maximum des contraintes. Les critères précédents correspondent à des chargements stationnaires en temps. En pratique de nombreuses structures sont soumises à des chargements cycliques ou à des vibrations.

C’est pourquoi un autre critère très utilisé en pratique consiste à optimiser des fréquences propres de vibration ω. En général, pour maximiser la rigidité des structures vibrantes on maximise la première fréquence propre, c’est-à-dire qu’on choisit de minimiser le critère :

( )

2 1

)

(h ω

On peut aussi avoir plusieurs critères différents à optimiser, on parle alors d’optimisation multicritères. Par exemple, on peut vouloir minimiser à la fois la compliance et le maximum des contraintes d’une membrane. On peut, soit agréger ces deux critères en une seule combinaison linéaire, soit imposer une valeur maximale à un premier critère et optimiser sous contrainte le deuxième, soit chercher un optimum au sens de Pareto, c’est-à-dire une solution telle que l’on ne peut pas améliorer un critère sans en détériorer un autre.

Il est assez rare qu’une structure ne soit soumise en permanence qu’à un seul chargement, c’est-à-dire une seule force f, ou bien que les forces auxquelles elle est soumise soient uniques et bien déterminées. On préfère donc parfois pratiquer une optimisation multi-chargements.

I.4.3.

_{L'ensemble de formes admissibles}

La définition d’un ensemble de formes admissibles est plus délicate. Très souvent, on doit imposer des contraintes de "faisabilité", difficiles à quantifier précisément, ou bien on doit tenir compte de limitations imposées par d’autres phénomènes physiques. Ainsi, minimiser la traînée d’un profil d’aile (à portance fixée) n’a pas de sens si on oublie que l’aile doit supporter des contraintes mécaniques en liaison avec le reste de l’avion [3].

I.5.

P

ROCESSUS D

’

OPTIMISATION

Le dimensionnement classique dans un bureau d’études repose souvent sur une approche essais-erreurs, c’est à dire, pour réaliser un composant, le concepteur doit :

• Réaliser un modèle initial à partir d’un cahier des charges, de son expérience et de l’environnement général où se situe sa pièce ;

• Réaliser ensuite des modélisations (statique, dynamique, etc.) permettant de vérifier les critères de dimensionnement ;

• Itérer en modifiant sa conception de manière à respecter son cahier des charges.

Divers logiciels d’optimisation d’usage industriel existent actuellement sur le marché, on peut citer parmi eux : Optistruct, ANSYS DesignSpace, Genesis, MSC-Nastran, Tosca, devDept, etc. Leurs principe de base est de pouvoir reproduire de façon automatique ce qu’un concepteur réalisait auparavant manuellement, en y ajoutant :

• La possibilité de balayer un espace de conception plus large ; • Les calculs automatiques ;

• Les possibilités de réaliser des plans d’expériences et de créer ainsi des fonctions d’approximation.

• L’atteinte d’optimum grâce à des algorithmes de plus en plus performants Pour le concepteur, les étapes-clefs en optimisation de forme sont donc :

• La réalisation du modèle de CAO paramétrée ;

• La détermination des analyses à effectuer (statique, dynamique, etc.) ;

• La réalisation d’un modèle paramétré éléments finis et associé à la géométrie ; • La définition des critères de dimensionnement associés à la pièce (contraintes maximales, plage de fréquence interdite, masse, déplacements maximaux, etc.).

Le logiciel d’optimisation va être chargé de reconnaître et de gérer ces modèles (Éléments Finis, CAO, etc.), de permettre à l’utilisateur d’identifier les paramètres sensibles, de piloter automatiquement le processus complet de calcul et de traiter les résultats en fonction des paramètres.

Modèle CAO paramétré Maillage paramétré Résultats

Le plan d’expériences se contentera de permettre la création de fonction d’approximation des fonctions (mais possibilités d’erreurs importante entre la fonction estimée et les points réels), tandis que l’optimisation directe utilisera les valeurs réelles des fonctions et les sensibilités pour atteindre des valeurs optimales [4].

I.6.

A

PPLICATIONS

Concernant ses applications, l’optimisation de formes intervient dans presque tous les domaines des sciences de l’ingénieur ; il pourra s’agir de cristaux photoniques (optique), conception d’antennes ou de composants (électromagnétisme, électronique), panneaux anti-bruit (acoustique), chercher la meilleure aile d’avion (aéronautique), le meilleur pare-brise,…, etc.

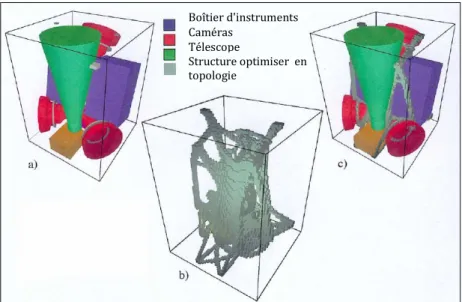
Par exemple, les astronomes danois se sont lancés dernièrement dans la réalisation d’un petit satellite capable de détecter des sources de rayon gamma en provenance de galaxies lointaines. Ce satellite est équipé de quatre caméras (situées à chaque angle) et de divers autres instruments. Les différents instruments sont présentés sur la Figure I-6. La taille du satellite est limitée à 60×60×80 cm3 et le poids à 80 kg.

Figure I-6 : Optimisation d’un satellite. a) Région de dessin et instrumentation.

b) Structure obtenue par optimisation topologique. c) Structure optimisée avec les instruments.

Boîtier d'instruments Caméras

Télescope

Structure optimiser en topologie

La question posée était de trouver la structure permettant d’accrocher ensemble ces divers instruments avec le minimum de poids et une résistance suffisante, compte tenu des efforts mécaniques endurés par le satellite lors du décollage.

C’est typiquement une question à laquelle l’optimisation topologique apporte une très bonne réponse. La Figure I-5b représente le domaine optimal avant post-traitement et la Figure I-5c la structure avec les instruments.

Ce type de calcul tridimensionnel peut prendre plusieurs jours sur une machine très puissante [1].

C

C

A

A

L

L

C

C

U

U

L

L

D

D

E

E

S

S

V

V

A

_A

R

_R

I

_I

A

_A

T

_T

I

_I

O

_O

N

_N

S

_S

Sommaire du chapitre :

II.1. Introduction... 19 II.2. Fonctionnelle... 20 II.2.1. Définition... 20

II.2.2. Résultats concernant les fonctionnelles... 21

II.3. Problèmes types du calcul des variations... 22

II.3.1. Problème de Lagrange... 23

II.3.2. Problème de Bolza... 23

II.3.3. Problème de Mayer... 23

II.4. Première et second variations... 23

II.5. Équation d'Euler-Lagrange... 25

II.5.1. Multiplicateurs de Lagrange... 25

II.5.2. Équation d'Euler-Lagrange... 27

II.5.3. Cas particuliers... 28

II.6. Quelques exemples... 29

II.6.1. Principe de la moindre action de Hamilton... 29

II.6.2. Problème de la brachistochrone... 29

II.7. Problème d'optimisation à limites variables... 30

Chapitre

CALCUL

CALCUL

CALCUL

CALCUL

DES

DES

DES

DES

VARIATIONS

VARIATIONS

VARIATIONS

VARIATIONS

II.1. I

NTRODUCTION

Le présent chapitre est consacré au calcul des variations qui est l'un des sujets classiques des mathématiques. Il a attiré un grand nombre de mathématiciens célèbres, en mathématiques, en physique, dans les sciences de l'ingénieur ou même en économie ou en écologie.

Comme définition, on peu dire que l'étude d'une fonction à valeurs réelles comporte en particulier la détermination de ses extremums. Ceci est l'un des objets du calcul différentiel classique lorsque la source de cette fonction est un espace numérique ; lorsque cette source est un espace fonctionnel, c'est l'objet de ce qu'Euler a appelé le calcul des variations.

De nombreux problèmes de la physique peuvent être posés sous ce que l'on appelle une formulation variationnelle, c'est à dire comme la recherche d'un optimum parmi une famille de solutions possibles. C'est notamment le cas de la mécanique de Hamilton (principe de moindre action), mais aussi du principe de Fermat en optique et de multiples autres exemples [5].

On rencontre déjà dans la plus haute antiquité des problèmes d'une telle nature, mais ; ce n'est qu'au XVIIIe siècle, à la suite de l'essor du calcul infinitésimal, qu'Euler et Lagrange établirent les fondements du calcul des variations et donnèrent une première condition d'extremum. Cette équation d'Euler-Lagrange allait jouer un rôle très important, surtout en physique, où elle justifiait les principes variationnels : principe de Fermat pour la propagation de la lumière dans les milieux différemment

réfringents ; principe de moindre action de Maupertuis et Hamilton pour la détermination des mouvements en mécanique analytique [6].

Dans les problèmes d'optimisation, les modèles sont souvent exprimés en termes d'un principe de minimalité ou de maximalité qui est précisément la question centrale du calcul des variations.

Par exemple, en mathématiques, on peut être intéressé à trouver, sous certaines contraintes, une courbe de longueur minimale ou une surface d'aire minimale. En physique, un exemple typique est le principe de moindre action.

Par ailleurs, les lois de conservation, qui correspondent mathématiquement à des équations différentielles, sont souvent dérivées à partir d'un principe variationnel. Les solutions du problème variationnel sont alors des solutions d’équations différentielles associées [7].

II.2. F

ONCTIONNELLE

II.2.1. Définition

Une fonctionnelle J est une loi de correspondance qui, à chaque fonction d’une certaine classe, fait correspondre un nombre réel.

Soit par exemple la fonctionnelle J défini par : =

∫

1

( )

0y² xdx

J . Si on substitue à

y(x) diverses fonctions, J prendra différentes valeurs numériques. • Pour y =x²; =

∫

1 0 4 dx x J ;

[ ]

10 5 5 / x J = ; J =0,2. • Pour 3 x y = ; =

∫

1 0 6 dx x J ;

[

]

10 7 7 / x J = ; J =0,143. • Pour y=sinx; =

∫

1 0sin²xdx J ;

[

2 sin2

]

1₀ 4 1 x x J = − ; J =0,273.

D’une certaine façon, on peut dire qu’une fonctionnelle est une fonction de fonction [8].

II.2.2. Résultats concernant les fonctionnelles

∗ Argument d’une fonctionnelle

Soit par exemple la fonctionnelle J donnée par :

(

)

∫

′ = 2 1 , , x x F x y y dx J (II-1)

La fonction y = y(x) est appelée argument de la fonctionnelle. ∗ Variation de l’argument d’une fonctionnelle

L’accroissement de l’argument d’une fonctionnelle est la différence de deux fonctions (voir Fig. II-1).

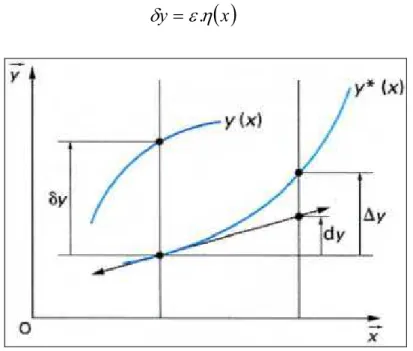
On le note δy = δy(x).

δy = y(x) – y*(x) (II-2)

Il y a une différence essentielle entre δy et dy qui sont toutes deux des variations infinitésimales de y ; dy provient d’une variation de la fonction donnée par une variation infinitésimale de x, le temps que δy est un changement infinitésimal de y causé par une nouvelle fonction. Généralement, on prend la variation δy(x) sous la forme :

( )

x

y εη

δ = . (II-3)

∗ Variation de la dérivée

( )

( )

( )

( )

( )

[

]

( )

x y dx d x y x y dx d x y x y x y δ δ = − = ′ − ′ = ′ * *

La variation de la dérivée est égale à la dérivée de la variation. ∗ Variation de l’intégrale

( )

( )

( )

( )

∫

∫

∫

∫

= − = 2 1 2 1 2 1 2 1 * x x x x x x x x dx x y dx x y dx x y dx x y δ δ

La variation de l’intégrale est égale à l’intégrale de la variation. ∗ Lemme fondamental du calcul des variations

Si l’intégrale

∫

2

( ) ( )

1

.

x

x f x g x dx est nulle quelle que soit la fonction f(x) continue

pour x ∈ [x1, x2] et nulle pour x = x1 et x = x2, et si g(x) est une fonction continue, alors

la fonction g(x) est nulle.

II.3. P

ROBLÈMES TYPES DU CALCUL DES VARIATIONS

Dans le cas général du calcul des variations le problème consiste à trouver la courbe y = y(x) où y(x1) = y1, y(x2) = y2 tels que pour une certaine fonction donnée

F(x, y, y’), l'intégral

(

)

∫

2 ′ 1 , , x x F x y y dx

est un extremum (maximum ou un minimum), également appelé valeur stationnaire. Une courbe qui satisfait cette propriété s’appelle une extrémale.

Les problèmes d’optimisation par le calcul des variations peuvent être ramenés à trois types classiques.

II.3.1. Problème de Lagrange

Il s’agit de minimiser ou de maximiser une fonctionnelle avec des conditions aux limites et des conditions de contraintes, J étant de la forme :

( )

[

]

=

_∫

2

(

′

)

1 , , x x F x y y dx x y J (II-4)

x étant la variable indépendante, y = y(x) et y' =dy/dx.

Par exemple, si F est le lagrangien, on a la fonctionnelle =

∫

2

(

′

)

1 , , t t L x qi qi dt S dite action hamiltonnienne.

II.3.2. Problème de Bolza

Il s’agit de minimiser ou de maximiser une fonctionnelle avec des conditions aux limites et des conditions de contraintes, J étant de la forme :

( )

[

]

=

[

( )

( )

]

+

_∫

2

(

′

)

1 , , , , , _{1 2 2} 1 x x F x y y dx x y x x y x G x y J (II-5)

II.3.3. Problème de Mayer

C’est un problème de Bolza pour lequel F(x,y,y') = 0.

Le problème de Bolza englobe les problèmes de Lagrange et de Mayer, et peut être ramené à un problème de Lagrange.

II.4. P

REMIÈRE ET SECOND VARIATIONS

Soit la fonctionnelle J exprimer par l'équation (II.4) et y*(x) la courbe qui rend cette fonctionnelle extrémale, c'est-à-dire que y*(x) est la solution rechercher [9].

Pour déterminer cette solution, on définit une variation ε.η(x) telle que :

( )

x y

( )

x

( )

x

y = * +ε.η (II-6)

ε étant un réel indépendant de x avec −δ ≤ε ≤δet δ petit.

η(x) est définit comme étant non nulle, sauf aux bornes d’intégrations x1 et x2. De

Figure II-2 : Variables courbes admissible (en haut) et courbe arbitraire η qui s'annule au borne de l'intervalle [x1,x2] (en bas).

On calcule la dérivée en ε de l’intégrale, ce qui donne [10]:

(

)

(

)

(

)

(

)

∫

∫

∫

∫

      + ∂ ∂ + + ∂ ∂ =       ∂ ∂ + ∂ ∂ + ∂ ∂ = ′ = ′ = 2 1 2 1 2 1 2 1 ' *' ' * ' ' , , , , x x x x x x x x dx y d d y F y d d y F dx d dy y F d dy y F d dx x F dx y y x F d d dx y y x F d d d dJ εη ε εη ε ε ε ε ε ε ε alors :

( )

∫

_      ∂ ∂ + ∂ ∂ = 2 1 ' ' ' x x _y dx F y F J ε η η (II-7) On intégrant le terme ' 'η y F ∂ ∂

par parties, on obtient :

∫

∫

 − __∂∂ _      ∂ ∂ = ∂ ∂ 2 1 2 1 2 1 . ' ' ' ' x x x x x x _y dx F dx d y F dx y F η η η donc :

( )

∫

∫

_      ∂ ∂ − ∂ ∂ + ∂ ∂ = 2 1 2 1 2 1 . ' ' . ' x x x x x x _y dx F dx d y F dx y F J ε η η η (II-8) y*(x) x y y1 y2 x1 x2 x η x1 x2

Comme η

( ) ( )

x₁ = xη ₂ =0, le terme η ' y F ∂ ∂

évalué de x1 à x2 sera nul, et on aura :

( )

_∫

_∫

_      ∂ ∂ − ∂ ∂ = 2 1 2 1 . ' . ' x x x x _y dx F dx d dx y F J ε η η

( )

_∫

_            ∂ ∂ − ∂ ∂ = 2 1 ' ' x x _y dx F dx d y F J ε η η

( )

_∫

_            ∂ ∂ − ∂ ∂ = 2 1 . ' ' x x _y dx F dx d y F J ε η (II-9)

C'est la dérivée première de la fonctionnelle.

De l'équation (II-7) et par une deuxième dérivation on obtient la dérivée second :

( )

_∫

_      ∂ ∂ + ∂ ∂ ∂ + ∂ ∂ = 2 1 2 2 2 2 2 2 2 ' ' ' ' " x x _y dx F y y F y F J ε η ηη η (II-10)

II.5. É

QUATION D

'E

ULER

-L

AGRANGE

II.5.1. Multiplicateurs de Lagrange

Pour comprendre l’intérêt des multiplicateurs de Lagrange, considérons une fonction f :

( )

x y f

( )

x y R U f , , : a →

U est un ouvert de R². f est supposée continue et admettant des dérivées première et seconde continues sur U.

dy y f dx x f df ∂ ∂ + ∂ ∂ = (II-11)

Si en (x0, y0), on a ∂f (x0, y0)/∂x = 0 et ∂f (x0, y0)/∂y = 0 alors (x0, y0) est un

extremum de f. La nature de cet extremum dépend des dérivées d’ordres supérieurs. Que se passe-t-il si (x, y) au lieu de parcourir tout U, se déplace sur une trajectoire g(x, y) = Cte et g une fonction de classe C² sur U? [11].

Soit par exemple g(x, y) = x² + y². On peut exprime une variable par rapport à l’autre (y= 1 x− ²) et on résout df /dx=0.

Cette méthode se révèle peu praticable pour les fonctions de plus de deux variables. Par contre, l'utilisation des multiplicateurs de Lagrange est plus pratique.

Partons de : dy y f dx x f df ∂ ∂ + ∂ ∂ =

Si dx et dy sont indépendants, alors : df = 0⇒ =0 ∂ ∂ x f et =0 ∂ ∂ y f

Mais ici, ce n’est pas le cas puisque dx et dy sont reliés par la relation g(x, y) = Cte. dy y g dx x g dy y g dx x g dg ∂ ∂ − = ∂ ∂ ⇒ = ∂ ∂ + ∂ ∂ = 0

Donc, en supposant que ≠0 ∂ ∂ y g , on a : dx y g x g y f x f df                     ∂ ∂       ∂ ∂ ∂ ∂ − ∂ ∂ =

On cherche les points (x, y) de la trajectoire autorisée (g(x, y) = Cte) pour lesquels df = 0. λ = ∂ ∂ ∂ ∂ = ∂ ∂∂ ∂ ⇒                     ∂ ∂       ∂ ∂ ∂ ∂ = ∂ ∂ ⇒ = y g y f x g x f y g x g y f x f df 0

λ est appelé multiplicateur de Lagrange. Aux points recherchés, ∇f

r

et ∇g r

doivent être colinéaires pour que f soit extrémale sur le chemin défini par g ; on a alors :

0 = ∂ ∂ − ∂ ∂ x g x f λ (II-12) 0 = ∂ ∂ − ∂ ∂ y g y f λ (II-13)

Ce système donne (x, y) en fonction de λ. En réinjectant x(λ) et y(λ) dans g(x, y) = Cte, on trouve les valeurs possibles de λ et les éventuelles solutions du problème.

II.5.2. Équation d'Euler-Lagrange

L'équation (II-9) exprime la dérivée première de la fonctionnelle J ayant comme argument y

( )

x = y*

( )

x +ε.η

( )

x . Puisque y*(x) rend la fonctionnelle J extrémale, alors ; pour ε = 0 on aura y

( )

x = y*

( )

x et la valeur de la dérivée première doit être nulle pour cette valeur de ε [9]. Ainsi on aura :

( )

. 0 ' 0 ' 2 1 =             ∂ ∂ − ∂ ∂ =

_∫

x x _y dx F dx d y F J η (II-14)

Puisque η est non nulle entre x1 et x2, il faut alors que son facteur soit nul, donc :

0 '_=     ∂ ∂ − ∂ ∂ y F dx d y F (II-15)

c'est l'équation d'Euler–Lagrange. La résolution de cette équation donnera la fonction y(x) pour laquelle la fonctionnelle J sera stationnaire.

L'équation d'Euler–Lagrange peut être écrite aussi sous la forme :

x F y y F F dx d ∂ ∂ =       ∂ ∂ − ' ' (II-16)

ou bien, en développant (II-15), sous la forme :

0 ' ' ' " ' 2 2 2 2 = ∂ ∂ − ∂ ∂ ∂ + ∂ ∂ ∂ + ∂ ∂ y F x y F y y y F y y F (II-17)

qui est une équation différentielle du second ordre non linéaire. Sa solution dépend de deux constantes arbitraires qui se déterminent par les conditions aux limites.

La valeur de la dérivée seconde pour ε = 0 est :

( )

_∫

_      ∂ ∂ + ∂ ∂ ∂ + ∂ ∂ = 2 1 2 2 2 2 2 2 2 ' ' ' ' 0 " x x _y dx F y y F y F J η ηη η (II-18)

II.5.3. Cas particuliers

∗ Si F ne dépend pas de x :

Dans ce cas, on cherche à minimiser l'intégrale :

∫

2

(

′

)

1

,

x

x F y y dx

L'équation d'Euler–Lagrange (II-16) devient ainsi :

0 ' ' _=     ∂ ∂ − y y F F dx d (II-19) donc : y C y F F = ∂ ∂ − ' ' (II-20)

et qui est une équation différentielle du premier ordre (C est une constante). ∗ Si F ne dépend pas de y :

L'intégrale à minimiser est :

∫

2

(

′

)

1

,

x

x F x y dx

L'équation d'Euler–Lagrange (II-15) devient dans ce cas :

0 '_=     ∂ ∂ y F dx d (II-21) donc : C y F = ∂ ∂ ' (II-22)

C'est une équation différentielle du premier ordre (C est une constante). ∗ Si F ne dépend pas de y' :

L'équation d'Euler–Lagrange (II-15) devient :

0 = ∂ ∂ y F (II-23)

II.6. Q

UELQUES EXEMPLES

II.6.1. Principe de la moindre action de Hamilton

La mécanique Hamiltonnienne est l'exemple le plus classique d'application du calcul variationnel. Cherchant à calquer la mécanique sur l’optique géométrique, Hamilton a observé que le mouvement d’un point matériel dans un champ de potentiel est solution d’un problème variationnel lagrangien.

Considérons un point matériel de masse m se déplaçant sur l’axe des x dans un potentiel V(x). Soit xA, la position de la particule en t = tA et xB, la position de la

particule en t = tB. Quelle va être la trajectoire x(t) de cette particule ?

On considère la fonctionnelle S, l’action qui associe à une trajectoire x(t) le nombre

( )

∫

      ₋ = B A t t mx V x dt S 2 2 1 _& (II-24)

La quantité mx&2 /2−V

( )

x est le Lagrangien, égal à la différence entre l'énergie cinétique et l'énergie potentielle et qui est en fait une fonctionnelle, qui dépend de la trajectoire suivie.

La trajectoire effectivement suivie est celle qui minimise l’action. C'est ce que l'on appelle le principe de moindre action.

II.6.2. Problème de la brachistochrone

Le problème de la brachistochrone fut soumis par Jean Bernoulli à ses contemporains en 1696 et donna naissance au calcul des variations. Leibniz, Newton, de l’Hôpital ainsi que son frère Jacques Bernoulli trouvèrent la solution : il s’agit d’un arc de cycloïde [12].

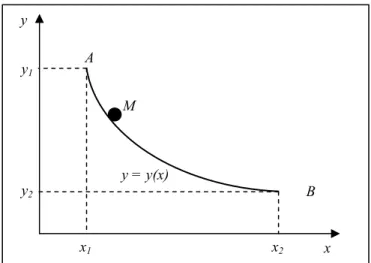
Étant donné deux points A et B de hauteurs différentes, non situés sur une même verticale, il s'agit de rechercher la trajectoire permettant la descente la plus rapide de A à B d'un point M, de masse m, soumis seulement à la pesanteur. L'objectif est d'évaluer le temps de descente et de le minimiser.

Figure II-3 : Problème de la brachistochrone.

En admettant que sa solution soit une courbe plane ayant une équation de la forme y = y(x), on peut en donner la formulation analytique suivante : Déterminer la fonction continûment dérivable y = y(x) vérifiant les conditions y(x1) = y1 et y(x2) = y2

qui minimise l'intégrale suivante [13] :

(

)

∫

+ ₋′ = 2 1 1 2 2 1 x x _{g y y} dx y T (II-25)

II.7. P

ROBLÈME D

'

OPTIMISATION À LIMITES VARIABLES

Nous n'avons considéré auparavant que les problèmes d'optimisation dans lesquels la forme à optimiser est bornée par deux points limites, connus et fixes.

Cependant, la plupart des problèmes d'optimisation consiste en une optimisation d'une forme dont l'une ou les deux extrémités sont variables (voir Fig. II-4).

Ainsi, nous allons étudier dans cette section le cas général d'un problème d'optimisation de forme. Pour cela, considérons le problème qui consiste à rendre extrémale la fonctionnelle [8,9] :

(

)

∫

′ = 2 1 , , x x F x y y dx J (II-26)

dont la solution est une courbe :

( )

_{1 2}

: y x x x x

y ≤ ≤

où x1 et x2 peuvent variés en satisfaisant :

( )

x =Y

( )

x i=1,2 y _{i i i} (II-27) M y = y(x) B A x y y1 y2 x1 x2

Ceci est un problème d'optimisation avec Y1(x) comme étant la courbe de

frontière gauche et Y2(x) celle de droite.

Figure II-4 : Problème générale d'optimisation. Soit la famille des courbes :

( )

ε y*

( )

x ε.η

( )

x x₁

( )

ε x x₂

( )

ε

y = + ≤ ≤ (II-28)

avec y* solution du problème, η courbe arbitraire et – δ < ε < δ (δ petit).

Afin que chaque courbe de la famille des courbes (II-28) satisfait (II-27) on doit avoir :

( )

(

)

.

(

( )

)

(

( )

)

1,2

* x + x =Y x i=

y _i ε εη _i ε _{i i} ε (II-29)

En dérivant par rapport à ε et pour une valeur nulle de ε on obtient :

( )

(

0

) ( )

0

(

( )

0

)

(

( )

0

)

1,2 *' + = i= d x dY x d dx x y i i i i i ε η ε (II-30)

L'équation (II-30) donne une relation entre

( )

ε η

d dx_i 0

, aux points limites de la

courbe solution y* et

( )

ε

d dY_i 0

des courbes de frontières.

On admettant la notation x =_i* x_i

( )

0 pour les points limites de y*, on a :

( )

* =

( )

0 − *'

( ) ( )

* 0 i=1,2 d dx x y d dY x i i i i _{ε ε} η (II-31)

Se sont les seules courbes η(x) qui peuvent être utilisées dans ce problème et les seules créant la famille des courbes (II-28) satisfaisant (II-27). On appel ces courbes les η(x) admissibles.

Pour ces courbes η(x), on a :

( )

(

)

( ) ( )

∫

+ + = ε ε εη εη ε 2 1 ' *' , * , x x F x y y dx J (II-32) alors :

( )

∫

_{( )}( )

( )

(

)

(

)

_      + ∂ ∂ + + ∂ ∂ + ∂ ∂ = ε ε ε ε εη ε εη ε ε 2 1 . ' *' ' * ' x x _d y dx d y F y d d y F d dx x F J

Suivant les mêmes étapes de la section II.4 et d'après l'équation (II-9) on obtient :

( )

( ) ( ) ( ) ( )

( )

( ) ( )ε ε ε ε ε ε ε ε η η ε 2 1 2 1 2 1 . ' . ' ' x x x x x x _d dx F y F dx y F dx d y F J + ∂ ∂ +             ∂ ∂ − ∂ ∂ =

_∫

(II-33)

Comme précédemment, on doit avoir J'

( )

ε nulle pour y*, ainsi, une évaluation pour ε = 0 donne :

( )

.

( )

0 0 ' . ' 0 ' * * * * 2 1 2 1 =       + ∂ ∂ +             ∂ ∂ − ∂ ∂ =

_∫

x x x x _d dx F y F dx y F dx d y F J ε η η (II-34)

Si la courbe y* est une extrémale pour le problème à limite fixes, c’est aussi une extrémale pour le problème à limites variables dont le point terminal serait (x2*, y2*).

On a donc nécessairement : 0 * ' * =       ∂ ∂ −       ∂ ∂ y F dx d y F (II-35)

qui est bien sûr l'équation d'Euler tirer du premier terme

∫

_

           ∂ ∂ − ∂ ∂ 2 1 * * _' . x x _y dx F dx d y F _η .

Remarque : la notation ( )....*signifie que le terme est évaluer le long de la courbe solution y*,

c'est-à-dire : ( ) y y y x F y F ∂ ∂ =       ∂ ∂ * , *, *' _et ( ) ' *' *, , * ' y y y x F y F ∂ ∂ =       ∂ ∂ _.

En plus, le terme restant dans l’expression (II-34) doit être nul, donc :

( )

0 0 . * * '_ × + =     ∂ ∂ ε η d dx F y F (II-36)

Remplaçons maintenant η par sa valeur exprimée en (II-31), on obtient :

( )

_{( ) ( )}

( )

1,2 0 0 * 0 * *' 0 * ' _* + *× = =    ₋ ×       ∂ ∂ = = i d dx F d dx x y d dY y F _i x x i i i x x i i ε ε ε

( )

_{( )}

( )

1,2 0 0 * ' * *' * * ' 0 * * * = =               ∂ ∂ − +       ∂ ∂ = = = i d dx y F x y F y F d dY _i x x i x x x x i i i i ε ε

( )

(

)

_{( )}

( )

1,2 0 0 * ' * *' * * ' 0 * * * = =               ∂ ∂ − +       ∂ ∂ = = = i d dx y F x y F y F dx x dY _i x x i x x x x i i i i i i ε Finalement :

(

( )

)

( )

0 1,2 * ' * *' 0 * * *  = =      ∂ ∂       − + = = i y F x y dx x dY F i i x x i i i i x x (II-37)

Cette relation est dite Condition de transversalité ; elle remplace les conditions aux limites. Si cette condition est satisfaite, la courbe y* rencontrera orthogonalement les courbes de frontière ; d'où vient le vocable condition de transversalité [8].

Remarque : la notation ( )....*x=xi*signifie que le terme est évaluer le long de la courbe solution

y* pour x = xi*, c'est-à-dire : F_x*_x* F(x_i*,y*( )x_i*,y*'( )x_i*) i = = et ( ( ) ( )) ' * *' , * * *, * ' _* y x y x y x F y F i i i x x i ∂ ∂ =       ∂ ∂ = .

F

F

O

O

R

R

M

M

U

U

L

L

A

A

T

T

I

I

O

O

N

N

D

D

U

_U

P

_P

R

_R

O

_O

B

_B

L

_L

È

_È

M

_M

E

_E

Sommaire du chapitre :

III.1. Introduction... 35 III.2. But de l'étude... 36 III.3. Bibliographie... 36 III.4. La dent d'engrenage... 42 III.4.1.Géométrie... 42 III.4.2.Résistance à la flexion... 43 III.5. Hypothèses et contraintes... 46 III.5.1.Intérêt des profils en développante de cercle... 46 III.5.2.Symétrie des dents... 46 III.5.3.Profil de la trochoïde... 46 III.6. Détermination de la contrainte en fonction du rayon... 47 III.7. Condition de résistance... 50

Chapitre

FORMULATION

FORMULATION

FORMULATION

FORMULATION

DU

DU

DU

DU

PROBLÈME

PROBLÈME

PROBLÈME

PROBLÈME

III.1. I

NTRODUCTION

Nous allons dans ce chapitre étudier un problème d'optimisation dans lequel on utilisera la théorie et les techniques d'optimisation présentés dans les chapitres précédents.

Aujourd'hui les engrenages occupent une place spéciale dans les systèmes mécaniques. C'est la façon la plus économique pour transmettre de la puissance et un mouvement de rotation dans des conditions uniformes. L'importance de l'engrenage, comme élément mécanique nécessaire et idéal, revient de leurs avantages, à savoir : un excellent rendement et un encombrement plutôt faible pour un prix de revient modéré. Le développement des nouvelles technologies, comme l'électronique, a remplacé quelques applications des engrenages, mais ils restent toujours un élément mécanique dont l'utilisation croît continuellement dans toutes les industries.

D'autre part, les avaries mécaniques du fonctionnement des engrenages résultent en général de deux causes principales : soit d’une pression de contact élevée entre les dents, soit d’une fissuration au niveau du pied de dent par fatigue en flexion. La figure III-1 qui représente une dent en photoélasticité montre clairement les deux types de sollicitations agissant sur une dent.

Le contour d’une dent d’engrenage cylindrique à denture droite comporte deux parties : la partie engrènement définie par une développante de cercle pour des raisons cinématiques et la base de la dent de forme trochoïdale ; puisque cette dernière ne

participe pas à "l’engrènement" proprement dit, on n’est pas obliger à la respecter si l’on conserve la forme en développante de cercle.

Figure III-1 : Contraintes agissant sur les dents d'un engrenage [14].

La possibilité de varier la forme au niveau du pied de la dent a ouvert la porte devant la recherche de la meilleure forme parmi les formes possibles, envisageant une amélioration des performances des engrenages, à savoir : une durée de vie plus longue, un allégement, une diminution des contraintes de flexion, … etc.

III.2. B

UT DE L

'

ÉTUDE

Mettant en considération ce qui a était dit à la section précédente, il est possible donc d'avoir des dents ayant une forme de la base des dents autre que la forme habituelle. Si l'on cherche une forme pour laquelle la concentration des contraintes est limitée à cet endroit (dents de forme plus résistante et éventuellement de moindre volume), on est ainsi conduit à un problème d’optimisation de la forme de la base des dents.

III.3. B

IBLIOGRAPHIE

La conception d'un engrenage comprend des calculs mathématiques, l'aspect géométrique, la détérioration, les matériaux, la fabrication et la vérification. Parmi tous ces paramètres, il est essentiel de connaître avec précision les contraintes se trouvant dans la dent d'engrenage pour prévenir les risques de rupture. Par conséquent, plusieurs méthodes théoriques et expérimentales ont été développées afin de déterminer ces contraintes [15].

C'est Lewis (1893), qui a analysé les dentures droites symétriques par la théorie des poutres, il considère la dent comme étant une poutre en porte-à-faux sollicitée par une force normale à son axe de symétrie. Suite à cette hypothèse, la contrainte en tension se calcule comme pour une poutre en flexion, avec un encastrement à la section critique.

Un autre moyen d'étude des contraintes dans les engrenages est la photoélasticité, elle permet une étude détaillée des régions chargées. On y observe les zones d’isocontraintes ainsi que leur progression. Cette méthode est très efficace pour l’étude des concentrations de contraintes. Pour modéliser l’objet de l’étude, on utilise une matière plastique transparente. Un système optique spécial (polariscope) permet d’observer les variations de contraintes avec les modifications de couleurs de la pièce.

Ci-dessous, un exemple d’une visualisation des contraintes au niveau du contact entre deux dents d’un engrenage : les zones très colorées subissent les contraintes les plus élevées.

Figure III-2 : Visualisation par photoélasticité des contraintes au niveau du contact entre deux dents d’un engrenage.

Au moyen de la photoélasticité, Timoshenko et Baud (1926) en mesuré les contraintes et ils ont obtenus des valeurs deux fois plus grandes que celles calculées