HAL Id: tel-01303456
https://hal.archives-ouvertes.fr/tel-01303456
Submitted on 18 Apr 2016HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
ULTRASONORES. APPLICATION AU CONTRÔLE
NON DESTRUCTIF DES SOUDURES EN ACIER
INOXYDABLE AUSTÉNITIQUE
Marie-Aude Ploix
To cite this version:
Marie-Aude Ploix. ÉTUDE DE L’ATTÉNUATION DES ONDES ULTRASONORES.
APPLI-CATION AU CONTRÔLE NON DESTRUCTIF DES SOUDURES EN ACIER INOXYDABLE AUSTÉNITIQUE. Acoustique [physics.class-ph]. INSA de Lyon (France), 2006. Français. �tel-01303456�
Thèse
ETUDE DE L’ATTENUATION DES ONDES ULTRASONORES.
APPLICATION AU CONTROLE NON DESTRUCTIF DES
SOUDURES EN ACIER INOXYDABLE AUSTENITIQUE
présentée devant
L’Institut National des Sciences Appliquées de Lyon
pour obtenir
le grade de docteur
Ecole doctorale : MEGA
par
Marie-Aude PLOIX
Soutenue le 20 décembre 2006 devant la Commission d’examen
Jury
CONOIR Jean-Marc Directeur de recherche CNRS, LAUE Rapporteur ELGUERJOUMA Rachid Professeur, LAUM Directeur de thèse GUY Philippe Maître de conférence, GEMPPM
LHEMERY Alain HDR, Ingénieur de recherche, CEA Rapporteur
MOYSAN Joseph HDR, LCND
ROYER Daniel Professeur, LOA Président du jury
Membres invités :
CHASSIGNOLE Bertrand Ingénieur de recherche, EDF R&D
3
SOMMAIRE
Introduction générale... 11
CHAPITRE 1
P
ROBLEMATIQUE DU CONTROLE NON DESTRUCTIF DES SOUDURES ANISOTROPES HETEROGENES... 15
1.1. Contexte de l’étude... 16
1.1.1. Métallurgie des soudures en acier inoxydable austénitique ... 16
1.1.2. Le contrôle non destructif par ultrasons ... 18
1.1.3. Modélisation des soudures : approximation en sous-domaines homogènes... 21
1.2. Propagation ultrasonore à travers un milieu homogène anisotrope ... 24
1.2.1. Equation de Christoffel ... 24
1.2.2. Courbes des lenteurs : généralités et exemples ... 26
1.2.3. Coefficients de transmission en incidence quelconque ... 28
1.3. Atténuation et bruit de structure... 34
1.3.1. Généralités et définition de l’atténuation... 34
1.3.2. Modèles théoriques de l'atténuation dans les matériaux polycristallins ... 37
1.3.3. Méthodes de mesure de l'atténuation ultrasonore ... 46
1.4. Description des échantillons étudiés ... 51
1.4.1. Découpe... 51
1.4.2. Propriétés élastiques ... 52
1.5. Synthèse et objectifs ... 55
CHAPITRE 2
M
ETHODE CLASSIQUE DE MESURE DE L’
ATTENUATION EN TRANSMISSION... 57
4
2.2. Mesure de la vitesse de phase ... 61
2.2.1. Dispersion de vitesse : méthode de déroulement de phase ... 61
2.2.2. Calcul d'incertitude ... 64
2.2.3. Méthodes d'intercorrélation et de Hilbert... 65
2.2.4. Résultats et comparaison ... 68
2.3. Mesure de la dispersion d'atténuation ... 70
2.3.1. Méthode de calcul ... 70
2.3.2. Calcul d'incertitude ... 71
2.3.3. Résultats de mesure en fonction de la fréquence ... 72
2.3.4. Evolution de l’atténuation en fonction de l’orientation des grains ... 78
2.4. Synthèse et discussion ... 82
CHAPITRE 3
M
ESURE DE L'
ATTENUATION PAR DECOMPOSITION DU FAISCEAU EN SPECTRE D’
ONDES PLANES... 85
3.1. Dispositif expérimental et principe général ... 86
3.2. Mesures point par point... 88
3.2.1. Principe ... 88
3.2.2. Cartographies du faisceau ultrasonore... 89
3.3. Décomposition en spectre angulaire d'ondes planes ... 92
3.3.1. Cartographie spectrale ... 92
3.3.2. Spectre d'ondes planes ... 93
3.4. Application des coefficients de transmission ... 95
3.4.1. Calcul des coefficients de transmission ... 95
3.4.2. Comparaison des résultats ... 100
3.5. Calcul de l'atténuation... 102
3.5.1. Formulation... 102
3.5.2. Résultats expérimentaux... 103
5
CHAPITRE 4
D
ISCUSSION ET EXPLOITATION DES RESULTATS... 109
4.1. Synthèse des travaux expérimentaux ... 110
4.1.1. Technique classique de mesure de la vitesse et de l’atténuation ... 110
4.1.2. Estimation de l’atténuation avec décomposition des faisceaux ... 110
4.2. Intégration de l'atténuation dans le code de calcul ATHENA ... 111
4.2.1. Le code ATHENA [FOU 03, TSO 99]... 111
4.2.2. Modélisation à l'échelle du grain [SCH 06] ... 113
4.2.3. Intégration de l'atténuation par diffusion à ATHENA [DUW 06] ... 114
4.2.4. Résultats de simulation et comparaison... 116
4.2.5. Conclusions ... 120
Conclusion générale et perspectives ... 121
Références bibliographiques ... 125
Annexe 1 : Résolution de l'équation de Christoffel... 131
Annexe 2 : Rotation d'un tenseur orthotrope autour de l'axe 2... 135
Annexe 3 : Mesures d'atténuation en ondes transversales... 137
Annexe 4 : Détermination de la taille et de l'orientation des grains ... 139
Annexe 5 : Etablissement des matrices permettant le calcul des coefficients de réflexion et transmission... 141
7
LISTE DES FIGURES
Figure 1.1 : Circuit primaire des réacteurs à eau pressurisée. ... 16
Figure 1.2 : Macrographie d'une soudure multipasses en acier inoxydable austénitique... 17
Figure 1.3 : Propagation et polarisation des ondes longitudinales (a) et transversales (b)... 18
Figure 1.4 : Définition de la vitesse de phase et de la vitesse d'énergie... 19
Figure 1.5 : Propagation d'un faisceau émis par une source de dimensions finies... 20
Figure 1.6 : Déviation théorique ∆ du faisceau en fonction de l'angle θ formé par le faisceau et l'orientation des grains dans du métal soudé austénitique [EDE 86]. ... 21
Figure 1.7 : Variations de la largeur du faisceau dues à l'effet de déviation [EDE 86]... 21
Figure 1.8 : Exemple de microstructure des soudures étudiées : (a) Macrographie – (b) et (c) Description en sous-domaines homogènes orthotropes – (d) Simulation de la propagation. ... 22
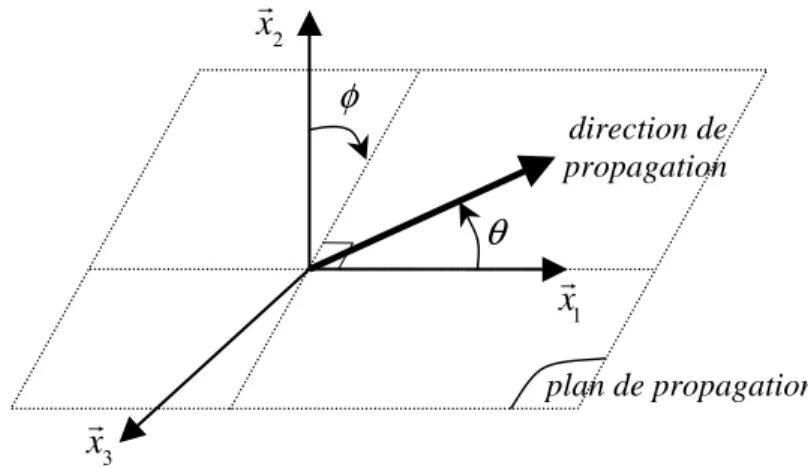
Figure 1.9 : Schéma des angles définissant la direction de propagation dans le matériau. ... 26
Figure 1.10 : Courbes des lenteurs (grains: 0°, plan: 0) avec les directions de polarisation. ... 27
Figure 1.11 : Courbes des lenteurs (grains: 45°, plan: 30) : absence de symétrie. ... 27
Figure 1.12 : Incidence quelconque à une interface liquide/solide : loi de Snell-Descartes. ... 29
Figure 1.13 : Visualisation des six solutions mathématiques sur les courbes des lenteurs. ... 30
Figure 1.14 : Trois cas de choix des solutions physiquement admissibles... 32
Figure 1.15 : Décroissance exponentielle des échos en négligeant la diffraction [GOE 80]. ... 35
Figure 1.16 : Diffusion par une hétérogénéité... 36
Figure 1.17 : Schéma du principe de la diffusion multiple. ... 37
Figure 1.18 : Vitesse de phase normalisée des (a) OL, (b) OTH, (c) OTV, en fonction de la direction de propagation par rapport à l’axe d’orientation des grains [HIR 86]. ... 40
Figure 1.19 : Coefficient de diffusion normalisé des (a) OL, (b) OTH, (c) OTV, en fonction de la direction de propagation par rapport à l’axe d’orientation des grains [HIR 86]... 40
Figure 1.20 : Coefficient d'atténuation normalisé des (a) OL, (b) OT, dans un aluminium polycristallin, en fonction de la fréquence normalisée [STA 84]. ... 42
Figure 1.21 : Coefficient d'atténuation normalisé des (a) OL, (b) OTH, (c) OTV, en fonction de la direction de propagation, pour différentes fréquences normalisées [TUR 99]. ... 43
Figure 1.22 : Coefficient d'atténuation normalisé des OL (a) en fonction de la fréquence normalisée, (b) en fonction de la direction de propagation [AHM 92]. ... 45
Figure 1.23 : Coefficient d'atténuation normalisé des OTH (a) en fonction de la fréquence normalisée, (b) en fonction de la direction de propagation [AHM 92]. ... 45
Figure 1.24 : Principe de la mesure au contact, en mode réflexion... 48
Figure 1.25 : Exemples de dispositifs en immersion : (a) réflexion avec échos successifs [KUM 96, BAD 03], (b) transmission avec mesure de référence [JEO 95, WAN 01]. ... 50
Figure 1.26 : Schéma de la découpe des échantillons. ... 52
Figure 1.27 : Figures de pôle : (a) principe et (b) figure de pôle {100} expérimentale. ... 53
Figure 1.28 : Repère associé à la description élastique du Tableau 1.4. ... 54
Figure 2.1 : Schéma du dispositif expérimental. ... 59
Figure 2.2 : Réglages du dispositif... 59
Figure 2.3 : Recalage des signaux pour calculer la différence de phase. ... 63
Figure 2.4 : Exemple de parties linéaire et dispersive de la phase. ... 63
Figure 2.5 : Incertitude de la vitesse dans l'eau en fonction de la température. ... 64
Figure 2.6 : Fonction d'intercorrélation de deux signaux. ... 67
8
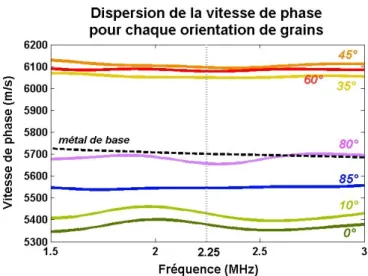
Figure 2.8 : Courbes de dispersion de la vitesse de phase pour chaque échantillon. ... 69
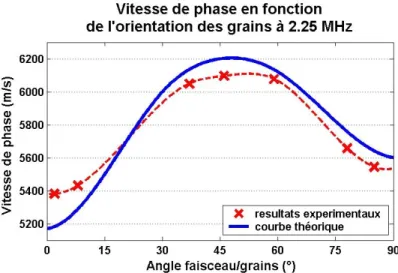
Figure 2.9 : Courbes théorique et expérimentale de la vitesse de phase en fonction de l’angle faisceau/grains à 2,25 MHz. ... 70
Figure 2.10 : Courbes de dispersion de l’atténuation pour chaque échantillon... 72
Figure 2.11 : Filtrage d'un signal par une fenêtre rectangulaire (a) et de Hanning (b)... 73
Figure 2.12 : Courbes de dispersion de l’atténuation après filtrage des signaux. ... 74
Figure 2.13 : Pression normalisée sur l'axe d’un émetteur de diamètre 0,5" à 2,25 MHz... 74
Figure 2.14 : Raccordement des courbes de dispersion de l’atténuation de 1,5 à 10 MHz... 76
Figure 2.15 : Lois d'atténuation de différents échantillons de soudure et du métal de base... 76
Figure 2.16 : Courbe de l’atténuation en fonction de l’orientation des grains à 2,25 MHz. ... 78
Figure 2.17 : Courbes de vitesse et de déviation des ondes longitudinales : comparaison entre la soudure de notre étude et la soudure étudiée par Seldis. ... 79
Figure 2.18 : Atténuation en fonction de l'orientation des grains : comparaison avec les valeurs mesurées par Seldis [SEL 00]... 80
Figure 2.19 : Atténuation à 2,25 MHz en fonction de l'orientation des grains : résultats du modèle d'Ahmed pour différentes valeurs de (d;h), avec d/h=0.05... 80
Figure 3.1 : Dispositif expérimental... 86
Figure 3.2 : Visualisation du faisceau en fonction de la distance à l'émetteur. ... 87
Figure 3.3 : Vues de dessus (a) et de face (b) des zones scannées par le récepteur. ... 88
Figure 3.4 : Exemples de variations d’amplitude en fonction de la distance entre l’échantillon et le récepteur (échantillons : 10 et 85°). ... 89
Figure 3.5 : Image du faisceau incident... 90
Figure 3.6 : Image du faisceau transmis à travers l'échantillon de métal de base. ... 90
Figure 3.7 : Images du faisceau transmis à travers chaque échantillon de soudure. ... 91
Figure 3.8 : Diagramme de rayonnement d’un émetteur circulaire en champ lointain : schéma de la décomposition d'un faisceau en somme d'ondes planes... 92
Figure 3.9 : Schéma du principe de calcul du spectre d'ondes planes. ... 92
Figure 3.10 : Cartographie spectrale en amplitude du faisceau incident à 2,25 MHz... 93
Figure 3.11 : Spectre d'ondes planes du faisceau incident à 2,25 MHz : cartographie (a) et coupe horizontale, à k3 = 0 (b)... 94
Figure 3.12 : Spectre d'ondes planes du faisceau incident : tracé sous forme angulaire. ... 94
Figure 3.13 : Diagramme de rayonnement expérimental du faisceau. ... 95
Figure 3.14 : Repère de travail pour le calcul des coefficients de transmission... 96
Figure 3.15 : Conversions de mode dans un plan non principal... 97
Figure 3.16 : Détermination des ondes réfléchies en deuxième interface. ... 98
Figure 3.17 : Amplitude des coefficients de transmission globale pour une orientation de grains de 10° : cartographie (a) et coupe dans le plan φ=0° (b). ... 100
Figure 3.18 : Comparaison des cartographies spectrales "théoriques" et expérimentales en amplitude à 2,25 MHz, pour chaque orientation de grain (échelle de couleur en dB). ... 101
Figure 3.19 : Atténuation mesurée en fonction de l’orientation des grains, à 2,25 MHz, avec l’hydrophone en réception. ... 103
Figure 3.20 : Atténuation globale en fonction de l’orientation des grains à 2,25 MHz avec le capteur de 0,5" en réception. ... 104
Figure 3.21 : Atténuation globale en fonction de l’orientation des grains à 2,25 MHz en tenant compte de la désorientation des grains de 5° dans le sens de soudage (rouge). ... 105
Figure 3.22 : Atténuation locale pour (k2 = 0;k3 = 0) en fonction de l’orientation des grains à 2,25 MHz comparée aux résultats de la méthode classique (petites croix bleues). ... 105
9
Figure 3.23 : Transmission totale des modes longitudinal et transversal, pour des grains orientés à 0°
(a) et à 35° (b). ... 106
Figure 4.1 : Exemple de simulation de la propagation d'un faisceau ultrasonore (b) à partir de la description en sous-domaines orthotropes de la soudure (a). ... 112
Figure 4.2 : Exemple d'une soudure décrite à l'échelle des grains [SCH 06]. ... 114
Figure 4.3 : Vitesses (m/s) des OL (gauche) et des OT (droite) en fonction de l'orientation des grains : données expérimentales (trait plein) et calage (pointillés)... 116
Figure 4.4 : Atténuations (Np/m) des OL (gauche) et des OT (droite) en fonction de l'orientation des grains : données expérimentales (trait plein) et calage (pointillés)... 116
Figure 4.5 : Atténuations (Np/m) des OL (gauche) et des OT (droite) en fonction de l'orientation des grains : données expérimentales (trait plein) et calage (pointillés)... 117
Figure 4.6 : Schéma de la structure de la soudure D704. ... 117
Figure 4.7 : Structure de la soudure D717B [CHA 00]... 118
Figure 4.8 : Configuration de contrôle pour la soudure D704... 118
Figure 4.9 : Exemple de représentation de type B pour le contrôle en L60 de la soudure D704. ... 119
10
LISTE DES TABLEAUX
Tableau 1.1 : Composition du métal d'apport des soudures industrielles... 17
Tableau 1.2 : Définition des trois régions de diffusion. ... 37
Tableau 1.3 : Composition du métal d'apport de la soudure-école (D704). ... 52
Tableau 1.4 : Constantes d'élasticité de la soudure d'étude D704 (en GPa) [CHA 00]... 53
Tableau 2.1 : Incertitudes sur les mesures de vitesse à 2,25 MHz. ... 65
Tableau 2.2 : Comparaison des valeurs des vitesses de phase obtenues par les trois méthodes pour chaque échantillon (m/s)... 68
Tableau 2.3 : Incertitudes sur les mesures d'atténuation à 2,25 MHz. ... 72
Tableau 2.4 : Comparaison des valeurs de constantes d’élasticité avec celles des échantillons de Seldis [SEL 00] (GPa). ... 79
11
I
NTRODUCTION GENERALE
Les tuyauteries des circuits primaires des centrales nucléaires sont soumises à de fortes contraintes dues au fonctionnement à haute température et à haute pression. C’est pourquoi elles sont réalisées en acier inoxydable austénitique, qui présente de nombreux avantages en termes de résistance à la corrosion et d’utilisation aux températures élevées. Par ailleurs, ces tuyauteries sont assemblées par soudage, et le contrôle de l’intégrité des soudures est donc indispensable. Ainsi, le contrôle non destructif est utilisé pour détecter d’éventuels défauts et les caractériser de manière à évaluer leur nocivité.
Les techniques ultrasonores s’avèrent efficaces, en complément de la radiographie, pour la localisation en profondeur et le dimensionnement des défauts. Mais les soudures austénitiques, élaborées par dépôt de passes successives du métal d’apport, possèdent une structure fortement anisotrope et hétérogène. La forte anisotropie est causée par la croissance cristalline, selon le gradient thermique local, qui se développe lors de la solidification du métal déposé. L’hétérogénéité vient du fait que les grains présentent des directions de croissance différentes selon les passes et leur enchaînement. Ces deux caractéristiques perturbent la propagation des ondes ultrasonores : le faisceau peut subir des déformations (déviation, division…) et une diminution d’amplitude due à la diffusion aux joints des grains. La contrôlabilité du composant peut alors, dans certains cas, présenter des difficultés importantes.
Il est donc essentiel de bien comprendre comment se propagent les ondes ultrasonores dans ce type de soudure, afin de pouvoir émettre un jugement fiable quant à l’état de santé du composant contrôlé. Pour cela, un code de calcul, appelé ATHENA, a été développé par EDF R&D et l’INRIA. Il modélise la propagation des ultrasons dans les structures anisotropes hétérogènes à partir de la description élastique de chaque sous-domaine homogène de la structure. Par ailleurs, depuis une dizaine d’années, différentes études ont été menées pour mieux appréhender les phénomènes de propagation et améliorer leur modélisation. Une première thèse a permis de valider l’hypothèse d’une décomposition des soudures multipasses
12
en zones anisotropes homogènes [CHA 00], et un second travail a abouti à l’élaboration d’un modèle, appelé MINA, qui prédit de manière non destructive les orientations des grains dans une soudure donnée [APF 05a]. Ces études ont notamment permis une meilleure compréhension des phénomènes de déviation du faisceau. Par contre les phénomènes liés à la diffusion aux joints des grains, se manifestant par une atténuation et un bruit de structure, n’ont été que partiellement étudiés et n’ont pas été intégrés dans le code de simulation. En effet, ces phénomènes de diffusion sont difficiles à prévoir car ils dépendent de l’orientation, de la géométrie et des propriétés élastiques des grains.
Nous nous intéressons plus particulièrement ici à l’atténuation par diffusion. La bibliographie menée a montré la complexité de ce phénomène, tant pour le modéliser que pour le mesurer, en particulier dans les structures anisotropes hétérogènes telles que les soudures multi-passes en acier inoxydable austénitique. Le travail exposé dans ce manuscrit a pour but d’apporter des réponses à ce problème, d’étudier et de quantifier l’atténuation ultrasonore par diffusion en fonction de l’orientation des grains, afin de fournir des valeurs fiables au modèle de propagation.
Nous commençons dans le premier chapitre par détailler le contexte de l’étude, en insistant sur l’aspect métallurgique, et les conséquences pour le contrôle ultrasonore. Puis la théorie générale de la propagation ultrasonore à travers un matériau de structure hétérogène et anisotrope est développée et appliquée aux soudures. Nous expliquons ensuite le phénomène d’atténuation, intimement lié au bruit de structure, et présentons quelques modèles théoriques et méthodes de mesure expérimentales permettant d’accéder à l’atténuation par diffusion dans les milieux anisotropes homogènes. Cela nous conduit d’une part à identifier le modèle théorique correspondant le mieux à notre étude, afin d’effectuer une comparaison avec les mesures, et d’autre part à choisir une première méthode de mesure que nous développons dans le chapitre suivant.
Le second chapitre expose donc la première technique expérimentale de mesure de l’atténuation des ondes longitudinales. C’est la technique la plus couramment utilisée pour la caractérisation des matériaux. Elle s’effectue en immersion, en transmission et en incidence normale, et est basée sur la comparaison entre le faisceau propagé dans l’eau et le faisceau ayant traversé l’échantillon inséré entre l’émetteur et le récepteur. Nous présentons la méthode de calcul de la vitesse de phase et de l’atténuation à partir de ces deux mesures. Puis
13
les résultats sont analysés, en les comparant aux résultats expérimentaux et théoriques de la littérature. Nous montrons que la méthode de mesure a ses limites, dont la principale est la non prise en compte des effets de l’ouverture angulaire du faisceau, particulièrement sensible pour un matériau anisotrope. C’est pourquoi une seconde approche, plus précise, est alors étudiée.
Cette seconde voie de travail, exposée dans le troisième chapitre, repose sur la mesure point par point des faisceaux et la modélisation de la transmission du faisceau incident à travers les échantillons. Les réalités physiques du faisceau (en particulier son ouverture) et du matériau (son anisotropie) peuvent alors être prises en compte, par le biais de la décomposition des faisceaux en spectres angulaires d’ondes planes, et l’application des coefficients de transmission en incidence quelconque à chaque composante en onde plane du faisceau incident. Nous montrons que cette méthode donne de meilleurs résultats.
Le dernier chapitre vise à exploiter ces résultats en les intégrant au code de calcul ATHENA. Nous commençons ce chapitre en effectuant une synthèse des différents résultats de mesure. Puis le principe de fonctionnement du code ATHENA est exposé, pour expliquer la manière dont l’atténuation a pu être intégrée. Les confrontations des simulations aux expériences mettent en évidence l’importance de la prise en compte de l’atténuation. Par ailleurs, la bonne cohérence entre simulations et essais ultrasonores valide les valeurs d’atténuation mesurées expérimentalement.
La conclusion rappelle la difficulté d’estimer avec précision l’atténuation par diffusion, mais montre que la méthode basée sur la mesure point par point donne de très bons résultats. Elle est plus précise que la méthode classique utilisée a priori. Elle permet en effet de prendre en compte la réalité du faisceau ultrasonore et l’anisotropie du matériau. Nous proposons finalement des perspectives à ce travail, notamment la mesure précise de l’atténuation des ondes transversales.
15
1. P
ROBLEMATIQUE DU CONTROLE NON
DESTRUCTIF DES SOUDURES ANISOTROPES
HETEROGENES
1.1. Contexte de l’étude... 16
1.1.1. Métallurgie des soudures en acier inoxydable austénitique ... 16
1.1.2. Le contrôle non destructif par ultrasons... 18
1.1.2.1. Généralités...18
1.1.2.2. Le contrôle des soudures austénitiques ...20
1.1.3. Modélisation des soudures : approximation en sous-domaines homogènes... 21
1.1.3.1. Description de la soudure...22
1.1.3.2. Simulation de la propagation ultrasonore...23
1.2. Propagation ultrasonore à travers un milieu homogène anisotrope ... 24
1.2.1. Equation de Christoffel ... 24
1.2.2. Courbes des lenteurs : généralités et exemples ... 26
1.2.3. Coefficients de transmission en incidence quelconque... 28
1.2.3.1. Equation et résolution ...28
1.2.3.2. Détermination des trois solutions physiquement admissibles ...29
1.2.3.3. Calcul des coefficients de réflexion et de transmission ...33
1.3. Atténuation et bruit de structure... 34
1.3.1. Généralités et définition de l’atténuation ... 34
1.3.2. Modèles théoriques de l'atténuation dans les matériaux polycristallins... 37
1.3.2.1. Description de quelques modèles ... 37
1.3.2.2. Synthèse ... 45
1.3.3. Méthodes de mesure de l'atténuation ultrasonore ... 46
1.3.3.1. Méthodes au contact ...47
1.3.3.2. Méthodes sans contact...49
1.3.3.3. Méthodes en immersion ...49
1.3.3.4. Choix de la méthode de mesure : immersion et transmission...51
1.4. Description des échantillons étudiés ... 51
1.4.1. Découpe... 51
1.4.2. Propriétés élastiques... 52
16
Ce chapitre expose la problématique liée au contrôle non destructif par ultrasons des matériaux anisotropes hétérogènes tels que les soudures multipasses en acier inoxydable austénitique. Le contexte de l'étude est d'abord présenté via les aspects métallurgique et ultrasonore. Puis la théorie liée au problème de la propagation des ondes et à leur transmission à travers un milieu anisotrope est étudiée. Une étude bibliographique sur les travaux théoriques et expérimentaux concernant l'atténuation est ensuite réalisée. Une fois la première technique expérimentale choisie pour les mesures, les échantillons étudiés seront alors décrits.
1.1. Contexte de l’étude
1.1.1. Métallurgie des soudures en acier inoxydable austénitique
Les aciers inoxydables austénitiques sont fréquemment utilisés pour leurs propriétés de grande résistance à la corrosion et de bonne performance mécanique aux températures élevées. En effet, ils conservent leur structure austénitique aussi bien à température ambiante qu'aux hautes températures. L'acier AISI 316L (Dénomination AFNOR : Z2CND17-13) est en particulier utilisé en raison de sa composition présentant un faible pourcentage de ferrite δ qui permet de dissoudre en grande partie les impuretés et donc de minimiser la formation de microségrégations, qui peuvent être des points de départ de fissures sous l'effet des contraintes thermiques [BAI 77]. Du fait de ces propriétés, l’acier 316L est utilisé comme métal d’apport pour de nombreuses soudures du circuit primaire des centrales nucléaires à réacteurs à eau pressurisée (Figure 1.1). Ces soudures étant de taille importante, elles sont élaborées par superposition de passes (ou cordons) successives (Figure 1.2).
17
Figure 1.2 : Macrographie d'une soudure multipasses en acier inoxydable austénitique.
La composition du métal d’apport des soudures industrielles en acier 316L est détaillée dans le Tableau 1.1. Par ailleurs, l’étude porte sur des soudures réalisées par procédé manuel à l'électrode enrobée. Elles présentent une microstructure texturée induite par la croissance des grains lors du procédé de soudage et de la solidification. En effet, les grains sont allongés (en forme de "cigare") selon un axe cristallographique <100>.
Elément Cr Ni Mo Mn Si C P S
Teneur (%) 19 12.5 2.3 1.6 0.5 0.03 0.016 0.01
Tableau 1.1 : Composition du métal d'apport des soudures industrielles.
Plusieurs facteurs entrent en jeu lors de la croissance des grains : la direction du gradient thermique et les phénomènes de croissance par épitaxie et de croissance sélective. La direction locale de croissance des grains aura tendance à suivre la direction du gradient thermique local. Ce dernier est notamment influencé par la position de soudage (soudure à plat, verticale, plafond…) et par l'ordre d'enchaînement des passes. Le phénomène d'épitaxie signifie que les cristaux d'une passe qui vient d'être déposée vont adopter l'orientation des cristaux sur lesquels ils reposent. D'autre part, la croissance sélective implique que les grains colonnaires dont l'axe cristallographique <100> coïncide le mieux avec la direction du gradient thermique auront tendance à croître préférentiellement par rapport aux autres grains. En effet, la croissance des grains le long du gradient thermique est plus rapide dans la direction de l'axe cristallographique <100>, et les grains dont l'orientation est défavorable finissent par disparaître [TOM 80]. Les grains peuvent alors atteindre plusieurs millimètres de longueur. 1 cm 1 2 3 4 5 6 7 8 9 10 11 12 14 13 15 16 17 18 19 20 21 22 23 24 25 ordre d'enchaînement des passes
18
En conclusion, les soudures présentent à la fois un caractère anisotrope (croissance des grains selon une direction cristallographique privilégiée) et hétérogène (l’orientation des grains varie d’une zone à l’autre de la soudure).
1.1.2. Le contrôle non destructif par ultrasons 1.1.2.1. Généralités
Les méthodes de contrôle non destructif sont nombreuses. Le contrôle par ultrasons est fréquemment utilisé car il présente de nombreux avantages : facilité de mise en œuvre, possibilité de travailler sur une seule face de la pièce à contrôler (pas besoin d'un accès à la deuxième face), et capacité à traverser d'importantes épaisseurs de matière en fonction de la fréquence de travail. De plus, l'existence de relations entre la propagation des ultrasons et les caractéristiques du matériau permet sa caractérisation. L'utilisation des ultrasons offre donc la possibilité, sans aucune détérioration, d'une part de caractériser des matériaux afin d'en connaître les propriétés élastiques, et d'autre part de contrôler des pièces pour vérifier leur intégrité et repérer d'éventuels défauts d'élaboration (inclusions, soufflures, défauts de collage…) ou d'endommagement dû aux sollicitations (fissures…).
Les ondes ultrasonores les plus couramment utilisées pour la caractérisation et le contrôle sont les ondes de volume longitudinales (ou de compression) et transversales (ou de cisaillement). Une onde longitudinale (resp. transversale) a la direction de vibration des particules (appelée polarisation) parallèle (resp. perpendiculaire) à sa direction de propagation (Figure 1.3).
Figure 1.3 : Propagation et polarisation des ondes longitudinales (a) et transversales (b).
La propagation des ondes dépend directement des propriétés élastiques du milieu traversé. Comme nous le verrons dans le paragraphe 1.2, la résolution de l’équation de Christoffel donne les vitesses et les directions de polarisation des ondes pouvant se propager dans une direction donnée. Elles sont définies par leur direction de propagation nG, leur nombre d'onde
V
k = ω (ω : pulsation, V : vitesse de propagation), et leur vecteur de polarisation PG. Direction de propagation Vibration des particules a) b)
19
Dans le cas général d'un milieu anisotrope, on trouve trois ondes de vitesses différentes et de directions de polarisation perpendiculaires entre elles. L'une de ces ondes a sa direction de polarisation proche de sa direction de propagation : c'est l'onde quasi-longitudinale, notée L. Les deux autres sont des ondes dites quasi-transversales. L'une sera dite horizontale, et l'autre, verticale, par rapport au plan de propagation considéré, notées TH et TV respectivement. La connaissance de ces éléments permet de prévoir la façon de se propager des ondes ultrasonores et donc de détecter d'éventuels défauts dans les pièces contrôlées.
D'autre part, dans les matériaux anisotropes, il faut distinguer la vitesse de phase et la vitesse d'énergie (ou vitesse de groupe). En effet, ces deux vecteurs ne coïncident pas forcément du fait de la déviation de l'énergie causée par l'anisotropie du matériau traversé (Figure 1.4). La vitesse de phase désigne la vitesse du front d'onde. Le vecteur vitesse de phase est donc perpendiculaire au front d'onde. En revanche, la vitesse d'énergie représente la vitesse de propagation de l'énergie, dans la direction du flux d'énergie. Ces deux vitesses sont liés par la relation suivante : Vphase = Vénergie cos
α
, oùα
est l'angle que forment les deux vecteurs. La théorie fait en général intervenir la vitesse de phase dans les équations. Nous rentrerons plus en détail dans la théorie de la propagation dans les milieux anisotropes dans le paragraphe 1.2.Figure 1.4 : Définition de la vitesse de phase et de la vitesse d'énergie.
Le phénomène de diffraction d'un faisceau d’ultrasons est également important à prendre en compte. En effet, les dimensions finies de la source utilisée pour générer les ultrasons implique un phénomène de diffraction (ou divergence) du champ ultrasonore émis. Dans le cas d'une source circulaire de diamètre D , l'ouverture du faisceau peut être calculée par le biais de la formule : sinδ = 1.22λ D, où λ est la longueur d'onde. Le faisceau sera donc
plus ou moins ouvert selon la taille de la source, la fréquence de travail et le milieu de propagation (Figure 1.5). On distingue alors deux zones de propagation : le champ proche, où le faisceau est droit et où l'amplitude oscille, et le champ lointain, où le faisceau est ouvert mais où l'amplitude décroît de façon monotone. La limite entre ces deux zones, appelée limite
vitesse de phase ⊥ front d'onde vitesse d'énergie // flux d'énergie
matériau anisotrope émetteur
20
de champ proche, se situe à la distance D2 4λ de la source. C'est une caractéristique très importante en contrôle non destructif.
Figure 1.5 : Propagation d'un faisceau émis par une source de dimensions finies.
1.1.2.2. Le contrôle des soudures austénitiques
La propagation ultrasonore dans les milieux anisotropes hétérogènes tels que les soudures étudiées est complexe. L'orientation des grains peut varier de façon très importante d'un point à l'autre de la soudure. Un faisceau traversant ce type de soudure pourra alors subir des déviations, des divisions, ainsi qu’une forte atténuation par la microstructure. Ces phénomènes dépendent directement de la direction de propagation des ondes par rapport à l'orientation des grains.
En effet, dans les matériaux anisotropes comme les soudures, la vitesse d'énergie subit une déviation par rapport à la vitesse de phase. Cette déviation dépend de l'angle entre la direction de propagation et l'axe d'orientation des grains. La Figure 1.6 montre l'angle de déviation de la vitesse d'énergie par rapport à la vitesse de phase, pour chaque mode de propagation : L, TH et TV. Les trois courbes sont tracées en fonction de l'angle entre la vitesse de phase et l'axe d'élongation des grains, pour du métal soudé austénitique [EDE 86].
La déviation des ondes ultrasonores en fonction de l'orientation des grains implique une déformation du faisceau qui traverse une soudure austénitique. En effet, comme nous l’avons vu précédemment, un faisceau d'ultrasons n'est pas parfaitement cylindrique, mais il présente une certaine ouverture en fonction du diamètre du transducteur et de la distance au transducteur. Dans le cas des ondes longitudinales, pour des grains orientés à 0° par rapport à l'incidence des ondes, le faisceau aura tendance à fortement diverger (Figure 1.7, schéma de
gauche), alors que pour des grains à 45°, sa divergence sera la plus faible (Figure 1.7, schéma de droite). source circulaire générant le faisceau ouverture du faisceau δ D
21
Figure 1.6 : Déviation théorique ∆ du faisceau en fonction de l'angle θ formé par le faisceau et l'orientation des grains dans du métal soudé austénitique [EDE 86].
Figure 1.7 : Variations de la largeur du faisceau dues à l'effet de déviation [EDE 86].
Il est donc essentiel de bien connaître la structure de la soudure contrôlée afin de prévoir la propagation des ondes ultrasonores, et ainsi pouvoir localiser un éventuel défaut et estimer sa taille.
1.1.3. Modélisation des soudures : approximation en sous-domaines homogènes
Les outils de simulation sont des outils essentiels permettant d’aider à la compréhension de la propagation des ondes dans ce type de structure. Ils permettent par ailleurs de réaliser des études paramétriques et d'analyser l'influence de la configuration de contrôle (matériau
5°
5° 5° 5° 5° 5°
ϕ
Angle du faisceau par
rapport aux grains (ϕ) 0° 24° 48°
Angle de déviation 0° 12° 0°
Divergence du faisceau Elevée Moyenne Faible
Vitesse de propagation Faible Moyenne Elevée
22
insonifié, type et position d’un défaut, type d'onde…) sur la propagation des ondes. La simulation est divisée en deux grandes étapes : la description de la soudure qui sera introduite dans le modèle, puis la simulation de la propagation ultrasonore dans cette soudure.
1.1.3.1. Description de la soudure
Une précédente étude [CHA 99, CHA 00] a proposé un modèle de description de la microstructure des soudures. La soudure est divisée en sous-domaines homogènes orthotropes. Le nombre de sous-domaines est fonction du degré d'hétérogénéité de la soudure. Dans chacun de ces domaines, une orientation particulière des grains (notée ω dans le tableau de la Figure 1.8.b) est déterminée par le biais de méthodes numériques d'analyse d'image à partir de la macrographie de la soudure étudiée (Figure 1.8.a). Les valeurs des constantes d’élasticité, liées au repère défini par la structure locale (angle ω), sont supposées invariantes d’un sous-domaine à l’autre. Les sous-domaines sont donc simplement désorientés les uns par rapport aux autres.
Figure 1.8 : Exemple de microstructure des soudures étudiées : (a) Macrographie – (b) et (c) Description en sous-domaines homogènes orthotropes – (d) Simulation de la propagation.
Une autre étude [MOY 03, APF 05b] a été réalisée, visant à simuler la microstructure à partir des données caractéristiques du soudage multipasses. Le modèle développé, appelé MINA
b)
c) d)
23
(Modelling anIsotropy from Notebook of Arc welding), prend en compte deux types de paramètres :
des paramètres propres au procédé de soudage : refusion entre passes, inclinaison des passes et paramètre traduisant les phénomènes de croissance sélective et de croissance par épitaxie ;
des paramètres propres à la soudure spécifiquement étudiée et susceptibles d’être mentionnés dans le cahier de soudage : géométrie du chanfrein, diamètre des électrodes utilisées par le soudeur ainsi que le nombre et l'ordre d'enchaînement des passes.
Au final, la description obtenue est un maillage régulier de sous-domaines homogènes orthotropes (Figure 1.8.c). Ce modèle permet d’estimer l’orientation des grains et ainsi de s’affranchir d’une analyse métallographique.
1.1.3.2. Simulation de la propagation ultrasonore
La description de la soudure est introduite dans le code ATHENA développé par EDF et l'INRIA. C'est un modèle 2D qui résout les équations de l'élastodynamique exprimées en terme de contraintes et de vitesses particulaires par une méthode d'éléments finis. Les éléments sont des carrés de côté égal à 1/15 de la longueur d'onde. ATHENA simule la propagation des ondes ultrasonores dans un plan de symétrie de matériaux hétérogènes anisotropes complexes, en particulier dans les soudures étudiées [CHA 01]. Le code est basé sur l'hypothèse que le milieu peut être décrit par un nombre fini de domaines homogènes anisotropes. Il prend également en compte les interactions entre le faisceau et des défauts pouvant avoir des géométries complexes. Le modèle sera expliqué plus en détail dans le quatrième chapitre.
La simulation fournit une très bonne prédiction des déviations et des divisions du faisceau (Figure 1.8.d), ainsi que des temps de vol [CHA 00]. En revanche, les amplitudes obtenues ne sont pas représentatives des amplitudes réelles pouvant être recueillies in situ [APF 05a, CHA 04]. En effet, le modèle actuel simule les effets de divergence du faisceau et de diffusion aux frontières des différents domaines en raison des sauts de propriétés élastiques. Par contre, il ne prend pas en compte la diffusion aux joints des grains à l'intérieur de chaque domaine du matériau traversé.
24
1.2. Propagation ultrasonore à travers un milieu homogène anisotrope
La propagation des ondes élastiques dans les milieux homogènes élastiques est régie par l’équation de Christoffel. Sa résolution donne accès, pour une direction de propagation donnée, à la vitesse et à la polarisation des trois modes susceptibles de se propager [AUL 73, DIE 74].1.2.1. Equation de Christoffel
On considère un matériau homogène élastique soumis à une perturbation ultrasonore. Sous l'hypothèse d'un comportement élastique linéaire, la relation entre le tenseur des contraintes T et le tenseur des déformations ε est donnée par la loi de Hooke :
kl ijkl
ij
C
T
=
ε
(1.1)où Cijkl sont les composantes du tenseur d'ordre 4 des constantes d'élasticité du matériau.
Les tenseurs des contraintes et des déformations étant symétriques, le tenseur d'élasticité C
est donc symétrique également.
Le tenseur des déformations s'exprime en fonction du vecteur de déplacement uG par :
⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ = k l l k kl x u x u 2 1
ε
(1.2)D'autre part, ρ étant la masse volumique du milieu soumis à la perturbation, le principe fondamental de la dynamique conduit à :
j ij i
x
T
t
u
∂
∂
=
∂
∂
2 2ρ
(1.3)La combinaison de ces trois équations donne les équations de propagation pour les composantes du déplacement uG :
(1.4)
La solution recherchée est classiquement une onde plane progressive monochromatique de pulsation ω , et dont le champ de déplacement, en un point défini par le vecteur position rG à l'instant t , est de la forme :
k j l ijkl i
x
x
u
C
t
u
∂
∂
∂
=
∂
∂
2 2 2ρ
25
(1.5)
où A est l'amplitude initiale de l'onde, PG (unitaire) sa polarisation et kG son vecteur d'onde : n
V
kG = ω G où nG est le vecteur unitaire normal au plan d'onde et V est la vitesse de phase.
NB: La présence d'atténuation s'exprime dans la partie imaginaire du vecteur d'onde, en
posant j n V ' k j k kG G G ⎟⎟ G ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = − = ∗ α ω
, où α est le coefficient d'atténuation (avec α >0).
La substitution de l'expression dans l'équation (1.4) permet d’aboutir au système d'équations de Christoffel :
(1.6)
où l'on a posé Γil = Cijklnjnk, appelé tenseur de Christoffel. C'est un tenseur d'ordre 2, symétrique en raison des propriétés de symétrie du tenseur élastique.
Pour un matériau de symétrie quelconque (i.e. avec 21 constantes d'élasticité indépendantes), les expressions explicites des Γ s'écrivent : il
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
23 32 13 31 12 21 3 2 44 23 3 1 45 36 2 1 25 46 2 3 34 2 2 24 2 1 56 23 3 2 45 36 3 1 55 13 2 1 56 14 2 3 35 2 2 46 2 1 15 13 3 2 25 46 3 1 56 14 2 1 66 12 2 3 45 2 2 26 2 1 16 12 3 2 34 3 1 35 2 1 45 2 3 33 2 2 44 2 1 55 33 3 2 24 3 1 46 2 1 26 2 3 44 2 2 22 2 1 66 22 3 2 56 3 1 15 2 1 16 2 3 55 2 2 66 2 1 11 11 2 2 2 2 2 2 2 2 2 Γ = Γ Γ = Γ Γ = Γ + + + + + + + + = Γ + + + + + + + + = Γ + + + + + + + + = Γ + + + + + = Γ + + + + + = Γ + + + + + = Γ , , n n C C n n C C n n C C n C n C n C n n C C n n C C n n C C n C n C n C n n C C n n C C n n C C n C n C n C n n C n n C n n C n C n C n C n n C n n C n n C n C n C n C n n C n n C n n C n C n C n C (1.7)Les solutions recherchées par la résolution du système d'équations sont les vitesses V et les
polarisations PG associées à chacun des trois modes de propagation : longitudinal, transversal horizontal et transversal vertical. Elles s'obtiennent en cherchant les valeurs propres et les vecteurs propres du tenseur de Christoffel, qui sont respectivement ρV2 et uG. Les vecteurs de
polarisation se calculent en normalisant les vecteurs de déplacement uG.
( )
r,t APexp(
j(
t k r)
)
uG G = G ω − G⋅G0
2=
−
Γ
ilu
lρ
V
u
i26 1.2.2. Courbes des lenteurs : généralités et exemples
La résolution de l'équation , par la recherche des valeurs propres et vecteurs propres, permet de calculer, pour une direction donnée de propagation, les vitesses et les polarisations de chaque mode susceptible de se propager dans le matériau. Nous avons appliqué cette équation dans le cas de sous-domaines de soudure supposés homogènes orthotropes.
Le calcul a été effectué pour chaque direction de propagation, définie par l'angle θ , dans différents plans de propagation contenant le vecteur xG1 du repère (xG1,xG2,xG3), et repérés par
l'angle φ (Figure 1.9). Cela nous permet de tracer les courbes des lenteurs (mG = nG V) de
chacun de nos échantillons, et donc de mieux comprendre comment se propage une onde plane quelconque dans le matériau.
Figure 1.9 : Schéma des angles définissant la direction de propagation dans le matériau.
Dans le cas de modes de propagation purs, chaque couple {vitesse ; polarisation} est classiquement associé à un mode de la façon suivante :
mode longitudinal : le vecteur de polarisation est colinéaire à la direction de propagation, mode transversal horizontal : le vecteur de polarisation est normal au plan de propagation, mode transversal vertical : il correspond au dernier vecteur de polarisation, normal aux deux autres, et qui est donc dans le plan de propagation.
Un exemple de courbes de lenteurs avec la visualisation des directions de polarisation est donné sur la Figure 1.10. Elles ont été tracées dans un plan principal du matériau orthotrope. Les modes propagés sont donc des modes purs. Comme on peut le voir sur la figure, les ondes longitudinales sont les plus rapides (i.e. lenteurs les plus faibles). D'autre part, la direction de
1 xG 2 xG 3 xG direction de propagation θ φ plan de propagation
27
polarisation des ondes transversales horizontales est perpendiculaire au plan de la feuille. On peut également remarquer que les trois courbes sont symétriques par rapport à xG1 et à xG2.
Figure 1.10 : Courbes des lenteurs (grains: 0°, plan: 0) avec les directions de polarisation.
En dehors des plans principaux, les modes générés ne sont pas purs. Les trois modes de propagation sont dits quasi-longitudinal, quasi-transversal vertical et quasi-transversal horizontal.Il devient alors difficile de classer les modes transversaux en deux catégories, l'une verticale et l'autre horizontale. C’est pourquoi nous choisissons de caractériser les modes transversaux plutôt sur un critère de vitesse, en les attribuant à un mode transversal rapide et un mode transversal lent [LAN 98]. D'autre part, on peut également remarquer qu'en dehors des plans principaux, la symétrie des courbes des lenteurs par rapport à xG1 disparaît (Figure 1.11).
Figure 1.11 : Courbes des lenteurs (grains: 45°, plan: 30) : absence de symétrie.
1 xG 2 xG 1 xG
28
1.2.3. Coefficients de transmission en incidence quelconque
Nous avons vu qu'un faisceau ultrasonore présente une certaine ouverture. Or comme nous l'expliquerons plus loin, nous avons choisi d'effectuer les mesures expérimentales en immersion et en transmission sur des échantillons sous forme de lames à faces parallèles. Le faisceau traversera alors une interface eau/solide et une interface solide/eau. La description complète du faisceau et de sa propagation dans le solide nécessite la connaissance des coefficients de réflexion et de transmission théoriques pour une incidence quelconque.
1.2.3.1. Equation et résolution
L'équation de Christoffel est utilisée lorsque la direction de propagation dans le matériau est donnée. Dans le cas d'une onde plane arrivant à la surface d'un matériau, l'incidence dans l'eau est connue, et on cherche les directions de propagation dans le matériau de chaque mode transmis, ainsi que leur vitesse et leur polarisation.
Pour cela, on travaille sur une autre forme de l'équation de Christoffel [HOS 91] :
(1.8)
où ω est la pulsation, et où l'on a posé Λil = Cijklkjkk. Le tenseur Λ présente les mêmes propriétés que le tenseur de Christoffel Γ , et ses expressions explicites sont les mêmes que celles de Γ , en remplaçant les n par i k . i
L'idée est de calculer la direction de propagation, la vitesse de propagation et la polarisation de chaque mode. Les inconnues sont donc les composantes des vecteurs d'onde k pour avoir i
les directions et les vitesses de propagation, et les composantes des vecteurs de déplacement
i
u pour avoir les polarisations. Or les lois de Snell-Descartes établissent que les vecteurs
d'onde des ondes incidentes, réfléchies et réfractées dans le matériau sont contenus dans le même plan, et que tous ces vecteurs admettent la même projection sur l'interface (Figure
1.12). Les deux composantes k et 2 k du vecteur d'onde de chaque mode généré sont donc 3
égales aux composantes k et 2 k de l'onde incidente. Les solutions recherchées sont alors la 3
composante normale à l'interface k du vecteur d'onde de chaque mode, ainsi que leur vecteur 1
de déplacement.
0
2
=
−
29
Figure 1.12 : Incidence quelconque à une interface liquide/solide : loi de Snell-Descartes.
On recherche dans un premier temps les inconnues k . Pour cela, il faut résoudre l'équation 1
suivante :
(1.9) où I est la matrice identité.
L'annulation de ce déterminant donne un polynôme d'ordre 6 en k (détails de calcul en 1
Annexe1). On obtient donc 6 solutions mathématiques pour k , dont 3 sont physiquement 1
admissibles. Nous verrons dans le paragraphe suivant comment sélectionner les solutions physiquement admissibles.
Le vecteur de polarisation PG associé à chaque solution est ensuite déterminé en normalisant le vecteur v colinéaire au déplacement, de composantes v , 1 v et 2 v telles que : 3
(
)
(
)
[
]
(
12 2 13 3)
11 1 3 2 12 22 11 23 11 13 12 2 3 1 Π Π − Π − = Π − Π Π Π Π − Π Π = = v v v v v v (1.10)où l'on a préalablement posé Π= Λ − ρω2I.
1.2.3.2. Détermination des trois solutions physiquement admissibles
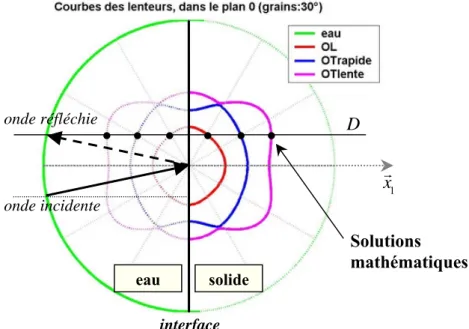
Les six solutions mathématiques obtenues par la résolution de l'équation vérifient toutes la loi de Snell-Descartes. C'est-à-dire qu'elles correspondent à des vecteurs d'onde dont la composante parallèle à l'interface est égale à celle du vecteur d'onde de l’onde incidente. Les six vecteurs d'onde solutions ont donc leur extrémité sur la droite D de la Figure 1.13.
solide anisotrope onde incidente onde réfléchie liquide ondes transmises interface inc kG réfl kG 1 xG L kG kGT1 kGT2 D L k1 k1T1 k1T2
(
Λ− 2I)
=0 det ρω30
Figure 1.13 : Visualisation des six solutions mathématiques sur les courbes des lenteurs.
Cas d'un solide orthotrope :
Dans le cas orthotrope, du fait de la symétrie des courbes des lenteurs par rapport au plan de l'interface, les solutions k sont opposées deux à deux. On retrouve cela analytiquement : 1
l'annulation du déterminant donne un polynôme du troisième ordre en
( )
k1 2. On devra doncchoisir une solution dans chaque couple de solutions k opposées. D'autre part, les solutions 1
sont soit réelles soit imaginaires pures. Les solutions réelles correspondent au régime sous-critique d'un mode, pour lequel une onde de volume est propagée vers l'intérieur du matériau. Les solutions imaginaires pures correspondent au régime hypercritique, pour lequel il existe des ondes dites hétérogènes qui se propagent parallèlement à la surface et dont l'amplitude décroît exponentiellement avec la profondeur [HOS 91]. Cela se traduit graphiquement par l’absence d’intersection entre la courbe des lenteurs d’un mode et la droite D . Ces deux régimes sont classiquement définis à l'aide de l'angle critique de chaque mode, donné par :
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
− e mod / solide liquide cV
V
sin
1θ
(1.11)On distingue donc les deux cas suivants :
Le couple de solutions est réel :
La solution physiquement admissible est sélectionnée à l'aide du vecteur de flux d'énergie EG de chacune de ces solutions [ROK 86a, ROK 86b, RIB 92, LAN 93]. Ce vecteur est en tout
1 xG D interface eau solide onde incidente onde réfléchie Solutions mathématiques
31
point normal à la surface des lenteurs, et sa composante suivant xG1 (direction de l'épaisseur du
solide) doit être positive pour que l'onde propage de l'énergie dans le matériau (Figure
1.14.a). Pour une onde hétérogène, cette composante sera nulle, ce qui signifie que l'onde ne
propage pas d'énergie vers l'intérieur du matériau.
La composante suivant xG1 de l’énergie, que l’on note E1, peut s'écrire :
(
∗ ∗ ∗)
+ = A Cijkl PjPkml PjPkml E1 2 2 4 1ω
(1.12)où A est l'amplitude de l'onde, P la ii ème composante du vecteur de polarisation, m la ii ème
composante du vecteur lenteur (mG =kGω), et Z∗ désigne le conjugué de la grandeur
complexe Z .
Ainsi, une onde dont le vecteur d'onde est dirigé vers le liquide pourra quand même être retenue comme solution si sa composante E est positive, puisque cela signifie que le flux 1
d'énergie est dirigé vers l'intérieur du solide (Figure 1.14.c). A l’inverse, une onde dont le vecteur d’onde est dirigé vers l’intérieur du matériau ne sera pas systématiquement une solution admissible.
Le couple de solutions est imaginaire pur (Figure 1.14.b) :
La solution physiquement admissible parmi les deux est la solution négative. Ainsi, l'onde correspondante, dite hétérogène, s'atténue exponentiellement dans la direction xG1 de la
profondeur du matériau [NAY 95].
Dans la plupart des cas, lorsque l'angle d'incidence augmente, on passe du régime sous-critique au régime hypersous-critique. Autrement dit, au-delà de l'angle sous-critique, l'onde de volume n'existe plus et cède sa place à une onde hétérogène. Or dans certains cas, on note la "réapparition" d’une onde de volume lorsque l'angle d'incidence augmente même après l'angle critique. Ce phénomène est illustré sur la Figure 1.14.c : l'angle critique de l'onde longitudinale est dépassé, donc il ne devrait rester que deux ondes de volume, mais on en observe une troisième.
32
En effet, pour une certaine plage angulaire d’incidence, la courbe des lenteurs des ondes transversales lentes présente deux points d’intersections avec la droite D . Lanceleur [LAN 92] définit alors la notion d’angle critique comme l’angle pour lequel la direction de propagation de l’énergie devient parallèle à l’interface.
Figure 1.14 : Trois cas de choix des solutions physiquement admissibles.
Cas général :
Dans le cas général, étant donné l’absence de symétrie des courbes de lenteurs par rapport au plan de l’interface eau/solide, les solutions mathématiques sont totalement distinctes. D’autre part, les solutions peuvent être complexes avec partie réelle non nulle. En effet, le point d'une courbe des lenteurs pour lequel le flux d'énergie devient parallèle à l'interface ne se situe pas forcément sur l'interface, ce qui signifie que la partie réelle de la composante du vecteur d'onde suivant xG1 n'est pas nulle. Le critère de sélection des solutions reste comme
précédemment la direction du vecteur de flux d’énergie, ainsi que le signe de la partie imaginaire de k pour les solutions complexes. 1
On retiendra que le choix des trois solutions physiquement admissibles se base sur le flux d'énergie de chacune des six solutions. Ce flux d’énergie doit être dirigé vers l'intérieur du matériau et le signe négatif de la partie imaginaire de k . Ainsi, les ondes correspondant aux 1
Solutions physiquement admissibles Solutions physiquement non admissibles Vecteur de flux d'énergie onde incidente dans l'eau a)
D
couple de solutions imaginaires pures b)D
c)D
33
solutions choisies se propagent dans le matériau, et s’atténuent dans la direction de la profondeur de l’échantillon pour les ondes hétérogènes.
1.2.3.3. Calcul des coefficients de réflexion et de transmission
Les coefficients de réflexion et de transmission à travers une interface sont obtenus en établissant les conditions aux limites de continuité des contraintes et des déplacements, appliquées aux trois ondes planes solutions de l'équation et physiquement admissibles pour une onde incidente donnée.
Pour établir les conditions aux limites à une interface, on utilise les expressions des contraintes et des déformations, données dans le cas général par :
⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ + + + + + = + + + + + = + + + + + = = 6 56 5 55 4 45 3 35 2 25 1 15 13 6 66 5 56 4 46 3 36 2 26 1 16 12 6 16 5 15 4 14 3 13 2 12 1 11 11 ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε C C C C C C T C C C C C C T C C C C C C T TG et ⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ = i j j i ij x u x u 2 1 ε , où j( t k1x1 k2x2 k3x3) i i APe u = ω− − − (1.13) ⇒
(
)
( 11 2 2 33) 2 1 j t kx k x kx i j j i ij jA Pk P k e − − − + − = ω ε avec la convention : εi = εii , i = 1à3, et ε4 = 2ε23 , ε5 = 2ε13, ε6 = 2ε12 , et où CIJ est la notation contractée de Cijkl.A chaque interface, on établit quatre équations qui permettent de déterminer à chaque fois les quatre inconnues :
Un coefficient de réflexion et trois coefficients de transmission à une interface eau/solide. En effet, une seule est réfléchie car seules les ondes longitudinales se propagent dans l'eau. En revanche, trois modes peuvent se propager dans le solide anisotrope.
Un coefficient de transmission et trois coefficients de réflexion à une interface solide/eau pour chaque mode incident, pour les mêmes raisons que précédemment.
Les quatre équations des conditions aux limites sont les suivantes : 1. Continuité de la contrainte normale à l'interface :
p
34
où p désigne la pression dans le fluide et le signe dépend du repère et de l'interface considérée.
2 & 3. Annulation des contraintes tangentielles : 0
13 =
T et T12 = 0 (1.15)
4. Continuité de la composante normale à l'interface du champ de déplacement des particules :
1 ) ( 1 ) ( 1 ) (inc uréfl utransm u +
∑
=∑
(1.16)Le développement et la résolution de ce système de quatre équations fournit les coefficients de réflexion et de transmission à une interface entre l'eau et un solide anisotrope pour une incidence quelconque. Les calculs seront étudiés plus en détail dans le troisième chapitre.
1.3. Atténuation et bruit de structure
L’un des problèmes pratiques rencontrés lors de l'inspection des soudures austénitiques est la diffusion des ondes ultrasonores par la structure. Cette diffusion conduit à une atténuation ainsi qu’à une éventuelle rétrodiffusion des ondes vers le transducteur (phénomène communément appelé bruit de structure). Ces deux phénomènes sont intimement liés [SAN 88], et varient selon la direction de propagation par rapport à l’orientation des grains. De plus, ils induisent un faible ratio du signal sur bruit [EDE 86, NEU 89]. Ils peuvent alors fausser le diagnostic d’un contrôle en masquant la manifestation d’un défaut par exemple. La propagation des ondes dans les milieux anisotropes a donc beaucoup été étudiée. Des modèles relativement simples permettent de comprendre le comportement des ondes en terme de vitesse et de direction de propagation. En revanche, l'atténuation et le bruit de structure sont deux phénomènes plus complexes, moins étudiés.
1.3.1. Généralités et définition de l’atténuation
Une onde ultrasonore perd de l'énergie lors de sa propagation dans un milieu réel. Cette observation expérimentale immédiate constitue une caractéristique importante de la propagation. Dans un matériau homogène et à faces parallèles par exemple, on observe cette perte d’énergie en enregistrant les échos successifs par une mesure en écho. L'enveloppe d'une séquence d'échos de fond de pièce présente alors une décroissance exponentielle de
35
l'amplitude de la forme exp
(
−α x)
, en négligeant les effets de la diffraction du faisceau[GOE 80] (Figure 1.15).
Figure 1.15 : Décroissance exponentielle des échos en négligeant la diffraction [GOE 80].
La notion d'"atténuation intrinsèque" que nous étudions désigne la perte d'énergie due exclusivement aux interactions entre la microstructure du milieu et l'onde. Elle ne dépend ni de la géométrie de la pièce, ni de la méthode et de la configuration de mesure. Autrement dit, tous les phénomènes extérieurs ne peuvent être assimilés à l'atténuation intrinsèque du milieu traversé. Ces phénomènes peuvent être la réflexion/transmission aux interfaces entre l'échantillon et le milieu extérieur, ou encore la divergence du faisceau, propre à la propagation de tout faisceau de section limitée.
L'atténuation intrinsèque est causée par deux catégories de phénomènes : L'absorption :
Elle résulte de la conversion de l'énergie mécanique vibratoire en chaleur. Ce type d'atténuation intrinsèque est lié à la viscosité du matériau contrôlé. La dissipation de l'énergie sous forme de chaleur est due d'une part à des pertes thermoélastiques résultant du déphasage entre contrainte et déformation, et d'autre part à la non linéarité entre la contrainte et le déplacement atomique. Certains défauts cristallins comme les dislocations peuvent contribuer à l'atténuation par absorption.
L'objet de notre étude concerne un matériau métallique polycristallin fortement texturé. L'atténuation par absorption est négligeable dans les métaux polycristallins [BAI 77, EDE 86]. Nous nous intéresserons donc plus particulièrement à l'atténuation par diffusion.
enveloppe ~ exp(−α x) amplitude distance échos de fond impulsion envoyée transducteur échantillon
36 La diffusion :
Dans le cas de la diffusion (aussi appelée dispersion), une fraction de l'onde est déviée ou réfléchie lors de la rencontre de discontinuités d'impédance acoustique (Figure 1.16). Ces hétérogénéités acoustiques peuvent être des porosités, des précipités, des inclusions, des joints de grains, ou encore des défauts… Ici, une partie de l'énergie "quitte" le trajet rectiligne prévu par la théorie.
Figure 1.16 : Diffusion par une hétérogénéité.
Dans notre étude, nous nous intéressons plus particulièrement à la diffusion aux joints de grains qui est due à la différence d’impédance acoustique d’un grain à l’autre résultant de leurs orientations cristallographiques différentes.
Dans un milieu statistiquement isotrope, l'atténuation par diffusion est indépendante de la direction de propagation des ondes. C’est le cas du métal de base de part et d’autre des soudures, qui est constitué de grains aléatoirement orientés. Elle dépend de la taille, de la forme et de l'orientation des grains, et également du type d'ondes propagé : la diffusion est plus forte en mode transversal qu'en mode longitudinal [EDE 86].
En revanche, dans un milieu anisotrope tel qu’une soudure en acier inoxydable austénitique, l’atténuation est également fonction de la direction de propagation [AHM 92]. L'analyse de l'atténuation par diffusion dans le cas anisotrope est donc plus compliquée que dans le cas isotrope.
On distingue classiquement trois domaines de diffusion, selon le rapport de la longueur d'onde sur la taille moyenne des grains [PAP 65]. Chaque domaine est associé à une loi théorique du coefficient d'atténuation par diffusion αd. Elles sont données dans le Tableau 1.2, où λ est la longueur d'onde, d est la taille moyenne des grains, et f est la fréquence. On peut remarquer que lorsque les grains sont très grands par rapport à la longueur d'onde, c'est-à-dire dans le domaine géométrique, l'atténuation ne dépend plus de la fréquence.
onde incidente onde transmise
37
Domaine λ d Loi de αd
Rayleigh >>1 ∝ d3f4
Stochastique ≅1 ∝ d f2
Géométrique << 1 ∝ 1 d
Tableau 1.2 : Définition des trois régions de diffusion.
La notion de taille moyenne des grains est à prendre avec précaution. En effet, dans le cas des métaux, selon le procédé de fabrication, la distribution des tailles de grains autour de la valeur moyenne peut être plus ou moins dispersée. D'autre part, la taille à prendre en compte est la dimension "vue" par les ondes. Pour un même matériau, elle dépend donc de la direction de propagation.
1.3.2. Modèles théoriques de l'atténuation dans les matériaux polycristallins
Les chercheurs se sont intéressés à l'atténuation ultrasonore par diffusion depuis les années 50, et ont proposé des modèles théoriques visant à prévoir la valeur du coefficient d'atténuation des ondes longitudinales et transversales à partir des caractéristiques du matériau étudié.
1.3.2.1. Description de quelques modèles
On peut distinguer deux types d'hypothèse de départ : la diffusion simple et la diffusion multiple. L'hypothèse de diffusion simple considère que chaque grain diffuse les ondes incidentes indépendamment des autres grains, alors que la diffusion multiple prend en compte le fait que l'onde arrivant sur un grain a déjà été diffusée par d'autres grains (Figure 1.17). La diffusion simple est donc une approximation afin de simplifier le problème. Prendre en compte la diffusion multiple permet de se rapprocher de la réalité. Nous présentons ici les principaux modèles théoriques de la littérature ainsi que leurs résultats.
Figure 1.17 : Schéma du principe de la diffusion multiple.
transducteur
![Figure 1.7 : Variations de la largeur du faisceau dues à l'effet de déviation [EDE 86]](https://thumb-eu.123doks.com/thumbv2/123doknet/14719861.750942/22.892.132.784.440.829/figure-variations-largeur-faisceau-dues-effet-déviation-ede.webp)


![Figure 1.20 : Coefficient d'atténuation normalisé des (a) OL, (b) OT, dans un aluminium polycristallin, en fonction de la fréquence normalisée [STA 84]](https://thumb-eu.123doks.com/thumbv2/123doknet/14719861.750942/43.892.161.734.593.926/coefficient-atténuation-normalisé-aluminium-polycristallin-fonction-fréquence-normalisée.webp)