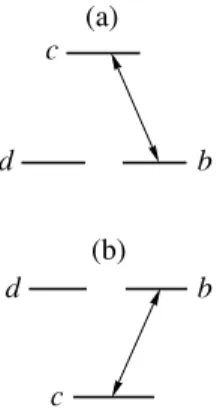Dark and bright states of the coherently excited three level atom

(1)

Publisher’s version / Version de l'éditeur:

Laser Physics (International Journal), 14, 1, pp. 39-50, 2004

READ THESE TERMS AND CONDITIONS CAREFULLY BEFORE USING THIS WEBSITE.

https://nrc-publications.canada.ca/eng/copyright

Vous avez des questions? Nous pouvons vous aider. Pour communiquer directement avec un auteur, consultez la

première page de la revue dans laquelle son article a été publié afin de trouver ses coordonnées. Si vous n’arrivez pas à les repérer, communiquez avec nous à PublicationsArchive-ArchivesPublications@nrc-cnrc.gc.ca.

Questions? Contact the NRC Publications Archive team at

PublicationsArchive-ArchivesPublications@nrc-cnrc.gc.ca. If you wish to email the authors directly, please see the first page of the publication for their contact information.

NRC Publications Archive

Archives des publications du CNRC

This publication could be one of several versions: author’s original, accepted manuscript or the publisher’s version. / La version de cette publication peut être l’une des suivantes : la version prépublication de l’auteur, la version acceptée du manuscrit ou la version de l’éditeur.

Access and use of this website and the material on it are subject to the Terms and Conditions set forth at

Dark and bright states of the coherently excited three level atom

Shakhmuratov, R. N.; Odeurs, J.; Coussement, R.; Szabo, Alexander

https://publications-cnrc.canada.ca/fra/droits

L’accès à ce site Web et l’utilisation de son contenu sont assujettis aux conditions présentées dans le site LISEZ CES CONDITIONS ATTENTIVEMENT AVANT D’UTILISER CE SITE WEB.

NRC Publications Record / Notice d'Archives des publications de CNRC: https://nrc-publications.canada.ca/eng/view/object/?id=01c77669-c5cb-4a8f-8518-7d5973aeacfd https://publications-cnrc.canada.ca/fra/voir/objet/?id=01c77669-c5cb-4a8f-8518-7d5973aeacfd

(2)

Laser Physics, Vol. 14, No. 1, 2004, pp. 39–50.

1. INTRODUCTION

In the past decade, there was a considerable growth in the interest in the multifrequency excitation of atoms, molecules, and impurity-doped crystals with more than two levels involved [1, 2]. Population trap-ping, adiabatic population transfer, electromagnetically induced transparency, lasing without inversion, and optical bistability are examples (this is even an incom-plete list) of when the multilevel structure of the medium and the simultaneous or pulse delayed excita-tion of several transiexcita-tions play a crucial role.

The description of these phenomena is mostly based on the density matrix formalism. The number of equa-tions for the density matrix (Liouville equation) is much larger than one obtains from the Schrödinger equation for the wavefunction. However, the Liouville equation allows an easy introduction of the decay parameters resulting in the master equations. A disad-vantage of the more complex density matrix formalism is the difficulty with the interpretation of the results. For example, the simplest way to illustrate the phenom-enon of coherent population trapping is to present the numerical solution for the steady-state values of the density matrix equations [3–5].

For the two-level system, the Bloch-vector model was introduced to simplify the description and under-standing of a large variety of coherent phenomena [6]. This success of the density-matrix SU(2) coherence-vector theory was a good motivation to find something similar for the three-level system. Some attempts were undertaken to introduce the generalization of the Liou-ville equation for the N-level system using the SU(N) coherence-vector theory [7–9]. The unambiguous suc-cess of this approach was the prediction of the stimu-lated Raman adiabatic passage (STIRAP) and the coun-terintuitive Raman pulse sequence [9]. However, a sim-ple explanation of the STIRAP was found later for the

intuitive and counterintuitive sequences within the wavefunction formalism (see, for example, [10–12]).

In this paper, we summarize the previous results obtained in the cited references and introduce a further simplification using the formalism of the Schrödinger equation. The simplification is based on the use of the bright and dark states, or the so-called coupled and non-coupled states [2]. It helps to reduce the analysis to the consideration of a two-level system interacting with a single effective field. Then, the Bloch-vector model is introduced, which helps to understand the manipulation of quantum states by the bichromatic field.

In Section 2, we consider the Hamiltonian of the resonant interaction of the three-level atom with two coherent fields. The transformation to the basis of the bright and dark states is derived. It is shown that the system evolves between two states, i.e., “bright” and “common” (they are specified in this section).

In Section 3, we consider the time evolution of the atomic state vector for the Λ scheme of the excitation. Bloch-like equations are derived. Nonadiabatic popula-tion transfer, populapopula-tion trapping, and low-frequency coherence excitation clearly follow from this approach. In Section 4, we consider the V scheme of the exci-tation. It is shown that population trapping does not take place in this case. The low-frequency coherence excitation is considered for atoms with different relax-ation constants.

2. THREE-LEVEL ATOM INTERACTING WITH TWO RESONANT FIELDS.

GENERAL FORMALISM

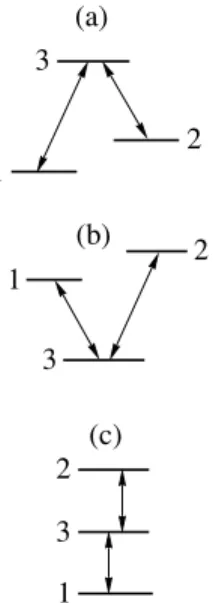
We consider the three-level atoms shown in Figs. 1a–1c. The arrows indicate the transitions induced by the coherent fields. By convention, these excitation schemes are classified as Λ, V, and the ladder (Ξ) schemes (Figs. 1a, 1b, 1c, respectively). We define

INTERACTION OF LASER RADIATION

WITH MATTER

Dark and Bright States of the Coherently Excited

Three-Level Atom

R. N. Shakhmuratov

1, 3

_{, J. Odeurs}

1

_{, R. Coussement}

1

_{, and A. Szabo}

2

1_{Instituut voor Kern- en Stralingsfysica, Katholieke Universiteit Leuven, Celestijnenlaan 200 D, B–3001 Leuven, Belgium} e-mail: Rustem.Shakhmuratov@fys.kuleuven.ac.be

2_{Institute for Microstructural Sciences, National Research Council of Canada, Ottawa, K1A 0R6 Canada} 3_{Kazan Physicotechnical Institute, Russian Academy of Sciences, ul. Sibirsky Trakt 10/7, Kazan, 420029 Russia}

Received February 3, 2003

Abstract—The dynamical evolution of the three-level atom under the influence of a bichromatic excitation is studied in the basis of the dark and bright states. With the help of these states, the analysis can be reduced to the consideration of a two-level system interacting with one effective field. Then, a simple Bloch-vector model is applied to describe the evolution of the initially complicated system. Special attention is paid to the low fre-quency coherence excitation, nonadiabatic population transfer, and population trapping.

(3)

40

LASER PHYSICS Vol. 14 No. 1 2004 SHAKHMURATOV et al.

the level that is common for both transitions as 3. The others are designated by the numbers 1 and 2, the level 2 being of higher energy than 1. The latter condition is taken only to simplify the notations. The dynamical part of the Hamiltonians of these three-level atoms, excited by two resonant fields E1(t) = E1cosΩ1t and

E2(t) = E2cosΩ2t, are

(1)

(2)

(3)

where the subscript of the Hamiltonian specifies the excitation scheme and ω_n is the energy of the state n. Planck’s constant is set equal to one (ប_{= 1) for} simplic-ity. The operators are defined as follows:

(4) where 〈n| and |m〉 are bra and ket vectors of the states n

and m in the Schrödinger representation. The interac-tion constant Bn = (dn3 · En)/2 = (d3n · En)/2 depends on the dipole-transition matrix elements dn3 = d3n and the

H_Λ ωnPˆnn n=1 3

∑

B1 Pˆ13e iΩ1t Pˆ31e–iΩ1t + ( ) – = – B₂ Pˆ23eiΩ2t Pˆ32e–iΩ2t + ( ), HV ωnPˆnn n=1 3

∑

B₁ Pˆ13e–iΩ1t Pˆ31eiΩ1t + ( ) – = – B₂(Pˆ23e–iΩ2t+Pˆ32eiΩ2t), HΞ ωnPˆnn n=1 3

∑

B1 Pˆ13e iΩ₁t Pˆ31e–iΩ1t + ( ) – = – B2 Pˆ23e iΩ2t – Pˆ32eiΩ2t + ( ), Pˆmn Pˆmn = | 〉 nm 〈 |,

field amplitude En. The rotating wave approximation is taken into account.

If the fields E1(t) and E2(t) are in exact resonance

with the relevant transitions, the Hamiltonians, Eqs. (1)–(3), can be made time-independent by trans-forming them into the interaction representation (IR). This representation is defined by a canonical transfor-mation by means of the unitary operator

(5) The wavefunction of the atom in the IR is defined by

(6) where |Ψ(t)〉 is the wavefunction in the Schrödinger representation; |Φ(t)〉 satisfies the Schrödinger equation with the effective Hamiltonian [13]

(7) This Hamiltonian has the explicit form

(8) The operators are defined for the vectors |m〉 and 〈n| of the interaction representation. In Eqs. (7) and (8), we have dropped the subscript of the Hamiltonian, specifying the excitation scheme, since the transformed Hamiltonians have the same form.

First, we consider the case B1 = B2 = B. The

Hamil-tonian, Eqs. (8), is diagonalized by a unitary transfor-mation,

(9) where

(10)

The new ket vectors are related to the former ones |n〉, defined in the interaction representation, as follows:

(11) The explicit relation is

(4)

The basis , where the Hamiltonian is diagonal, is called the basis of the quasi-energy states [14]. It coin-cides with the basis of the dressed states if the limit of the classical field is taken for the latter.

The states and are mixtures of all unper-turbed states |1〉, |2〉, and |3〉, whereas the state does not contain the common state |3〉. For the Λ scheme (see Fig. 1a), this point is very important. If the atom is in the state , a mixture of the ground-state sublevels 1 and 2, the atom does not leave this state since the latter is an eigenstate of the interaction Hamiltonian, Eq. (9). The bichromatic field E(t) = E₁(t) + E₂(t) does not inter-act with such an atom, and consequently it is not excited. Therefore, we call this state a dark state and designate it |d〉. This state was introduced for the first time by Arimondo in [2], who called this state a non-coupled state. He introduced the non-coupled state as well, which interacts with the bichromatic field E(t). Follow-ing Arimondo, we define the state

, (15)

which is orthogonal to the dark state. We call this state a bright state, since for the Λ scheme, if the atom is in this state, it is excited by the bichromatic field and then the luminescence from the state |3〉 may follow. The excitation can take place because the bright state is not an eigenstate of the interaction Hamiltonian, Eq. (9).

The states |d〉, |b〉, and |3〉 are mutually orthogonal and can be chosen as a new basis. We call this basis dbc, designating the state |3〉 by the letter |c〉, since it is com-mon for the induced transitions. Because we will often refer to these states, they are presented below in a com-mon set of equations to simplify further citation:

(16) (17) (18) The interaction Hamiltonian, Eq. (8), is transformed in this basis as follows:

(19) where the unitary operator of the canonical transforma-tion is

(20) We call this basis the dbc representation.

The states b and c are not eigenstates of the interac-tion Hamiltonian. Therefore, the bichromatic field induces transitions between them, as shown in Figs. 2a

n | 〉 1 | 〉 | 〉3 2 | 〉 2 | 〉 b | 〉 1 2 --- 1(| 〉+| 〉2 ) = d | 〉 1 2 --- 1(| 〉 2–| 〉), = b | 〉 1 2 --- 1(| 〉+| 〉2 ), = c | 〉 = | 〉.3

Ᏼ

_dbc ₌ _S

Ᏼ

_S–1 ₌ _– _{2B P}₍ˆ_bc₊_Pˆ_cb_), S 1 2 --- P(ˆd1+Pˆb1–Pˆd2+Pˆb2) Pˆ+ c3. =

and 2b. The energy of the b and c states is not defined in the dbc representation because the Hamiltonian

Ᏼ

dbc is not diagonal. To present schematically the dbc states and the transitions between them, we choose the state population before the excitation for their relative posi-tion in the diagram. So, the vertical scale in Figs. 2a and 2b (counted from the top to the bottom) is not the energy but the initial population of the state. Figure 2a presents the Λ and ladder schemes of the excitation in the dbc basis. For these schemes, the states d and b are populated before the excitation and c is not. Therefore, the first two are put at the bottom and the last at the top. Figure 2b presents the V scheme of the excitation in the

dbc basis. For this scheme, only state c is populated before the excitation, and, therefore, c is put at the bot-tom.

The Hamiltonian in the dbc basis, Eq. (19), resem-bles the interaction Hamiltonian of the two-level sys-tem bc, excited by one resonant field with an effective interaction constant . The dynamical evolution of the atom is described by the Schrödinger equation with this Hamiltonian, which contains only the transition operators between the states b and c.

To reveal the main physical processes in the atom evolution, we consider Λ and V excitation schemes sep-arately. We have to emphasize that the ladder and Λ schemes have many common features and can be con-sidered together. For example, to obtain the dynamic evolution in the ladder scheme, one can take the results for the Λ scheme with initial condition |Ψ(0)〉 = |1〉. If relaxation processes are involved, these schemes require separate treatment. However, the physical pro-cesses in both models are still similar. We make a spe-cial remark in the text clarifying the difference between these schemes when we consider the case of different field amplitudes related to electromagnetically induced transparency. 2B (a) (b) b c d b d c

Fig. 2. The excitation scheme of the atom in the dbc basis.

Diagram (a) shows how the Λ and Ξ schemes are trans-formed in this basis. Diagram (b) shows the former V scheme. The vertical scale represents the initial population of the level before the excitation. The higher populated level is put at the bottom, and the lower or unpopulated level is at the top.

(5)

42

LASER PHYSICS Vol. 14 No. 1 2004 SHAKHMURATOV et al.

3. Λ SCHEME

3.1. Time Evolution of the State Vector

In this scheme, the states 1 and 2 are the ground-state sublevels. For example, in solids, they may repre-sent the electron or nuclear spin splittings. The state vector of the atom, being initially (before the excita-tion) in the state |1〉 or |2〉, is

(21) where the sign (+) corresponds to the initial state |1〉 and the sign (–) to the initial state |2〉. The Rabi frequency χ = is defined as a double interaction constant in the Hamiltonian, Eq. (19), according to the conven-tional definition adopted for the two-level system [6].

Suppose that the pulse duration of the bichromatic field, tπ, is chosen such that the effective two-level

sys-tem bc experiences a so called π pulse; i.e., χtπ = π.

Then, the population of the level b is completely trans-ferred to the state c. After this pulse, the state vector is (22) Equation (22) shows that, for both initial conditions, i.e., independent of the sign in this expression, the same low-frequency coherence of the states 1 and 2 appears. We describe the state coherence by the nondiagonal elements of the density matrix,

(23) in the interaction representation, where Cm and Cn are the coefficients of the state vector development in the ket vectors of the interaction representation:

. (24)

According to this definition, the low-frequency coher-ence after the π pulse is σ12 = –1/4 or, in terms of the

Bloch-vector components [6],

(25) (26) we have u12(tπ) = –1/2 and v12(tπ) = 0.

So, the π pulse of the bichromatic field E(t) induces the low-frequency coherence u₁₂ = –1/2 in the ensemble of the atoms, even in the case of initially equal popula-tions of the levels 1 and 2. If these levels are spin com-ponents of the ground-state atom, then the creation of the coherence u12 = –1/2 corresponds to the appearance

of giant spin magnetization oscillating with a frequency ω21 = ω2 – ω1. This is a remarkable way to induce the

spin coherence because, for example, direct, resonant excitation of the nuclear spin states by an RF pulse cre-ates a magnetization which is a million times smaller in amplitude at room temperature [13].

Φbc(t,±) | 〉 = 1 2 --- χt 2 ---⎝ ⎠ ⎛ ⎞ b|〉 cos i χt 2 ---⎝ ⎠ ⎛ ⎞ c|〉 sin ±| 〉d + ⎩ ⎭ ⎨ ⎬ ⎧ ⎫ , 2 2B Φbc(tπ,±) | 〉 1 2 --- i c( | 〉±| 〉d ). = σmn = CmCn*, Φ | 〉 = C₁| 〉 C1 + ₂| 〉 C2 + ₃| 〉3 u12 = σ12+σ21, v 12 = –i(σ12–σ21),

The low-frequency coherence appears due to the dark state since it is a coherent mixture of the states |1〉 and |2〉 [see Eq. (16)]. The dark-state mixture has a neg-ative coherence (u12)d = –1 according to the definition given in Eqs. (23)–(25). The bright state is also a coher-ent state with a positive coherence (u12)b = 1 [see Eq. (17)]. Both states have a zero imaginary part of the coherence; i.e., (v₁₂)_b_{, d} = 0.

Before the excitation, the low-frequency coherence was zero because the dark-state coherence was com-pensated by the bright-state coherence. This compensa-tion simply follows from the definicompensa-tion, and one can find that each nonperturbed state is an equal mixture of the dark and bright states; i.e.,

(27) (28) The bichromatic π pulse removes the population of the bright component, and the balance between the coher-ences is broken. The presence of the dark component in each pure ground state 1 and 2 makes also impossible the complete transfer of the ground-state population to the state c. Only 1/2 of the atomic population can be excited.

Suppose that the pulse lasts two times longer than tπ.

Then, the two-level system bc experiences a so-called 2π pulse; i.e., χ2tπ = 2π. During the second half of the

pulse, the population of the excited state c comes back to the ground state b. The state vector of the atom at the end of the pulse is

(29) Equation (29) shows that the atom, being initially in the state 1 (2), is transferred to the state 2 (1) after the 2π pulse. This is a purely coherent effect, since it origi-nates directly from the π phase shift of the state b. Usu-ally, for the simple two-level atom, the π phase shift of the ground state after a 2π pulse is not revealed in the observables. In our case, apart from the two levels b and

c, we have the third level d, whose phase is well defined with respect to the phase of the state b. The phase defi-nition is determined by the phase relation of the com-ponents of the bichromatic field (see below). If the phase of the state b is changed by the field and the phase of the state d is not, then the ground state population is changed [see Eqs. (27), (28)].

The population transfer 1 2 is nonadiabatic since the state vector is far from a pure eigenstate dur-ing the excitation. However, the maximum population of the state c is two times smaller than the value one would have for a consequent train of π pulses of the fields E1(t) and E2(t), inducing the transitions 1 c

and c 2 separately, one after another. That is, the 1 | 〉 1 2 --- b(| 〉+| 〉d ), = 2 | 〉 1 2 --- b(| 〉 d–| 〉). = Φbc(2tπ,±) | 〉 1 2 ---(–| 〉b ±| 〉d ). =

(6)

maximum value of the population of the level c during the bichromatic 2π-pulse excitation is 1/2, while for the latter case it is 1.

To have a closed cycle and bring the atom back to the initial state 1, one has to apply a 4π pulse with dura-tion 4tπ [see Eq. (21)]. During this cycle, the order in

which the absorption and emission follow each other is different for the fields E₁(t) and E₂(t). Part of the time the field E1(t) is absorbed and the field E2(t) is

ampli-fied, and part of the time the process is reversed. There-fore, one can say that the energy is transferred from one field to the other. To describe this process, we transform the state vector Φbc(t, ±), Eq. (21), to the interaction representation by applying the inverse transformation

S–1_{[see Eq. (20)]. The result is}

(30)

The equation describing the electromagnetic wave evolution in the matter contains the density matrix com-ponents [6]

(31) (32) where the values v13 and v23 are the matter response on

the fields E1(t) and E2(t), respectively. The time

depen-dence of these components simply follows from the state vector, Eq. (30), and the definition, Eq. (23), i.e.,

(33)

(34) Figure 3 shows the time evolution of the v13 component

(thin line) and of the v23 component (dashed line) if the

initial state 1 is chosen. The field E_n(t) is absorbed (amplified) by the system if the value of the corre-sponding component v_n₃ is negative (positive), where

n = 1, 2. During the first part of the cycle (0 < χt < 2π),

the field E₁(t) is absorbed by the atoms and the field E2(t) is amplified (see Fig. 3). During the next half of

the cycle (2π < χt < 4π), the first field E1(t) takes back

the energy from the atoms and the second field E₂(t) puts in energy. The interplay of these processes limits the maximum population of the state 3 to 1/2.

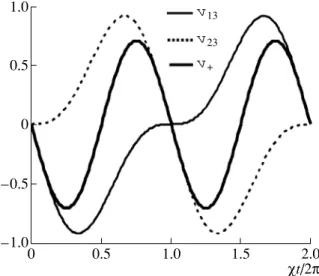
The maximum absorption of the first field takes place if χt = 2π/3, whereas the maximum amplification of the second field occurs at χt = 4π/3. Both functions oscillate with a period Tosc = 4π/χ, which is consistent

with the 4π cycle discussed above. The bold line in Φ t ±( , ) 1 2 --- χt 2 ---⎝ ⎠ ⎛ ⎞ cos ±1 | 〉1 = +1 2 --- χt 2 ---⎝ ⎠ ⎛ ⎞ cos +−1 | 〉2 i 2 --- χt 2 ---⎝ ⎠ ⎛ ⎞ 3|〉. sin + v 13 = –i(σ13–σ31), v 23 = –i(σ23–σ32), v 13( )t 1 2 --- χt 2 ---⎝ ⎠ ⎛ ⎞ cos ±1 χt 2 ---⎝ ⎠ ⎛ ⎞ , sin – = v 23( )t 1 2 --- χt 2 ---⎝ ⎠ ⎛ ⎞ cos ₊₋1 χt 2 ---⎝ ⎠ ⎛ ⎞ . sin – =

Fig. 3 shows the evolution of the sum of the v13 and v23

components, i.e.,

(35) It oscillates with a period 2π/χ. The 2π cycle originates from the atom evolution between the states b and c since v+ is proportional to the vbc component of the two-level system bc, as shown below. It is interesting to notice that the evolution of the v+ component is the

same whatever the initial state of the atom, 1 or 2.

3.2. Bloch-Vector Model

Because the atom evolves only between the two states b and c, one can apply the Bloch-vector model valid for the two-level system. We define the following components of the Bloch-vector for the Λ scheme:

(36) (37) where ρbc, ρcc, and ρbb are the elements of the density matrix ρ in the dbc basis. One can derive the Bloch equations for these components using the Liouville equation for the density matrix ρ with the Hamiltonian, Eq. (19). They have a standard form

(38) (39) and their solution is

(40) v +( )t v13( ) vt + 23( )t χt ( ) sin 2 ---. – = = v_bc = –i(ρ_bc–ρ_cb), wbc = ρcc–ρbb, v˙_bc = χw_bc, w˙bc = –χvbc, v bc( )t χt ( ) sin 2 ---, – = 1.0 0.5 0 –0.5 –1.0 0 0.5 1.0 1.5 2.0 χt/2π v₁₃ v₂₃ v₊

Fig. 3. The evolution in time of the v₁₃ component (thin line), of the v₂₃ component (dashed line), and of the v₊ component (bold line). Initially, at t = 0, the atom is in the state |1〉.

(7)

44

(41) where it is assumed that the atom was in the pure state |1〉 or |2〉 at t = 0. This solution is also valid if, initially, the ensemble of atoms is in an incoherent mixture of the ground states 1 and 2, i.e., if each atom of the ensemble populates any combination of the states |1〉 and |2〉, but where the net coherence of the ensemble is zero.

The relation between the Bloch-vector components, defined in the dbc basis, and the density matrix ele-ments, defined in the interaction representation, can be found from the S transformation

(42) The explicit relation is

(43) (44) where vbc is smaller than v+ by a factor of . This

relation remarkably resembles the substitution pro-posed by Brewer and Hahn [15] to reduce the Liouville equation for the three-level system excited by a bichro-matic field to the so called three-level Bloch equations. Our approach shows that this intuitively found substitu-tion has a physical base because of the existence of the dark state.

The Bloch equations (38) and (39) simplify the cal-culation of the main characteristics of the atom for any initial condition. The time evolution of v13(t) + v23(t)

follows from the v_bc-component time evolution. The

wbc( )t χt ( ) cos 2 ---, – = ρ = SσS–1. v_bc 1 2 --- v₁₃ v 23 + ( ), = wbc σ33 1 2 ---(σ₁₁+σ₂₂+u12), – = 2

time dependence of the excited-state population σ33(t),

of the low frequency coherence u₁₂(t), and of the sum of the ground-state populations

(45) can be calculated from the equations

(46) These values are simply the constituting parts of the Bloch-vector component wbc. Therefore, they evolve according to the bc-system evolution. The general solu-tion of Eq. (46) is

(47)

(48)

(49) where vbc(τ) is a solution of the Bloch equations. The plots of these functions, Eqs. (47)–(49), for the initial conditions u12(0) = σ33(0) = 0 and n12(0) = 1 are shown

in Fig. 4. The functions have the same period of oscil-lation as the vbc component.

The Bloch equations, together with Eqs. (47)–(49), do not describe the evolution of the other components which contain information about the coherence between the state |d〉 and the states |b〉, |c〉. Some of these components can be incorporated into two combi-nations of physical interest, i.e.,

(50) (51) where the coherence v_dc is defined in a similar way as the coherence vbc [see Eq. (36)]. The first equation describes the population difference of the ground-state sublevels (for example, of spin sublevels). The second equation describes the coherence between d and c states, which is proportional to the difference in the absorption/emission of the fields E1(t) and E2(t). The

combinations w₁₂ and v_dc satisfy the independent set of equations (52) (53) n12 = σ11+σ22 u˙₁₂ n˙₁₂ –σ˙33 χ 2 ---vbc. = = = u₁₂( )t u₁₂( ) χ0 2 --- vbc( ) τ,τ d 0 t

∫

+ = n₁₂( )t n₁₂( ) χ0 2 --- vbc( ) τ,τ d 0 t

∫

+ = σ33( )t σ33( ) χ0 ₂--- vbc( ) τ,τ d 0 t

∫

– = w₁₂ = σ₂₂–σ₁₁, v – = v13–v23 = 2vdc, w˙₁₂ χ 2 ---vdb, – = v˙ dc χ 2 ---w₁₂, = 1.0 0.5 0 –0.5 0 0.2 0.4 0.6 0.8 1.0 χt/2π σ33 n12 u12

Fig. 4. The time dependence of the excited- state population

σ33(t) (thin line), of the sum of the population of

ground-state levels n₁₂(t) (dashed line), and of the low-frequency coherence u₁₂(t) (bold line) for the initial condition σ₃₃(0) = u₁₂(0) and n₁₂(0) = 1.

(8)

which can be reduced to a single, oscillator-type equa-tion

(54) The solution of Eqs. (52) and (53) for the initial condi-tion v_–(0) = 0 is

(55) (56) These combinations oscillate with a period which is two times longer than the period of oscillation of the Bloch equation solution. So, to reverse the population of the ground-state sublevels, one has to apply a 2π pulse. Only a 4π pulse leaves this population unchanged. The increase in the period or the decrease in the frequency simply follows from the state vector development:

where the coefficients C_b, C_c, and C_d are defined in Eq. (21). One can find that the coherence between the states |b〉 and |c〉,

is composed of the product of the two periodic func-tions having the same period, i.e., the sine (or cosine) and cosine (or sine) functions. The coherence between the states |d〉 and |b〉 or |c〉 contains only one periodic function, i.e., the sine or cosine function, since the coef-ficient Cd of the ket vector |d〉 in the development of |Φbc(t, ±)〉 is constant. Therefore, the coherence b – c oscillates with a frequency χ and the coherences d – b and d – c oscillate with a frequency χ/2.

3.3. Population Trapping

The dynamical evolution between the bright (b) and common (c) states is disturbed by different relaxation processes. One of them is spontaneous emission. This process can be described if one considers the general Hamiltonian, which contains three parts. They are the atom Hamiltonian, the vacuum field Hamiltonian, and the interaction between the vacuum fluctuations and the atom. The last term can be expressed in the Schrödinger representation as follows:

(57) where Ank is the interaction constant (n = 1, 2) and and are the creation operators of the photons with

w˙˙12 χ 2 ---⎝ ⎠ ⎛ ⎞2_w 12 + = 0. w₁₂( )t w₁₂( )0 χt 2 ---⎝ ⎠ ⎛ ⎞ , cos = v dc( )t w12( )0 χt 2 ---⎝ ⎠ ⎛ ⎞ . sin = Φbc(t,±) | 〉 = Cb| 〉 Cb + c| 〉 Cc + d| 〉,d ρbc = CbCc*, Hsp A1kak + Pˆ13 A2kbk + Pˆ23 + ( ) k

∑

+h.c., = ak + bk +

wave vectors k, which can be different from the wave vectors of the bichromatic field. In the dbc basis, the Hamiltonian of the interaction with the vacuum modes is

(58)

If the events A1 (emission of the ω31 photon) and A2

(emission of the ω32 photon) are independent, then one

can find that the atom spontaneously decays to the bright and dark states with equal probability:

(59) where the coefficient of proportionality is not explicitly shown and the densities of the vacuum modes of the frequencies ω31 and ω32 are assumed equal.

After several excitation cycles (only the bright state is excited) and spontaneous decay into both states, b and d, the atom ends up in the dark state with its high inherent coherence. If the ground levels are spin levels, this coherence results in giant spin polarization oscillat-ing with the frequency ω21. Spin coherence is also

affected by relaxation processes. Spin phase relaxation induces transitions between the dark and bright compo-nents, destroying the phase order. The relaxation pro-cesses mentioned above and the coherent pump in the

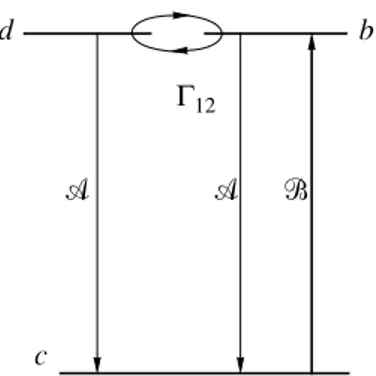
dbc basis are shown in Fig. 5. The bichromatic field E(t) pumps the system to the level c at the rate

Ꮾ

₌

4B2/Γ, where Γ is the decay rate of the optical

coher-ences σ13 and σ23. The spontaneous emission populates

the levels b and d at the rate

Ꮽ

_{. The phase relaxation of}

the low-frequency coherence σ12 equalizes the

popula-tion of the levels b and d with the rate Γ12. If

Ꮾ

Ⰷ Γ12

Ᏼ

_sp ₌ _{ST H}_sp_T–1_S–1 = 1 2 --- A_1kak + e–iω31t A_2kbk + e–iω32t – ( )Pˆdc { k

∑

+ A_1kak + e–iω31t A2kbk + e–iω32t + ( )Pˆbc} h.c.+ Wc→b Wc→d

Ꮽ

ⵒ 1 2 --- A1k 2 A2k 2 + ( ), k

∑

= = c d b Γ12 Ꮽ Ꮾ Ꮽ

Fig. 5. The relaxation processes and the pump in the dbc

basis. Ꮽ is the spontaneous decay rate of the population of the state c. Ꮾ is the pump rate of the state c. Γ12 is the decay

rate of the low-frequency coherence σ12 in the interaction

representation. This last process induces transitions b d and d b in the dbc basis.

(9)

46

and

Ꮽ

_Ⰷ_Γ

12, the levels b and c become essentially

empty and the atom is trapped in the dark state d. One can prove these empirical speculations by solv-ing the Bloch equations with the relaxation terms included. The latter can be derived by applying the

S-transformation to the master equations well known for the three-level atom in the interaction representa-tion. The result is

(60) (61) Since the relaxation terms bring additional components not included in the dynamical part, we have to complete the system by adding two other equations,

(72) (73) where α = B1/B2. Then, the unitary operator S of the

canonical transformation to the dbc basis modifies as

(74)

The Hamiltonian of the atom interaction with the bichromatic field in the dbc-basis again has a simple form, but with a different interaction constant,

(75) where χ = .

One can easily find the state vector of the atom that starts its evolution from the level 1

(76) where 1 stands for the initial state |1〉, i.e.,

(77) The initial condition implies the absence of the low-fre-quency coherence u₁₂ at t = 0. After the π pulse, the bright component is depopulated,

(78) and the coherence appears. Since the phases ϕ1 and ϕ2

of the bichromatic field components are different, we redefine the low-frequency coherence as follows:

(79) Its value after the π-pulse is

(80)

Ᏼ

Ᏼ

(10)

where 1 again stands for the initial state 1. The u12

com-ponent has an extremum (–3 /8 ≈ –0.65) if B1/B2 =

1/ ≈ 0.577 (see Fig. 6). Figure 6 shows also the dependence of the low-frequency coherence on the ratio of the interaction amplitudes B1/B2 after the 2π

pulse:

(81) This coherence is zero if B1 = B2. One can show that this

condition is the only one if the population is completely transferred from the state 1 to the state 2 after the 2π pulse. The evolution of the level 2 population is described by the equation

(82) It has an absolute maximum 1 if χt = 2π and B1 = B2.

Therefore, complete population transfer 1 2 takes place only for equal interaction constants and after the 2π pulse.

The low-frequency coherence has two extrema ±1 after the 2π pulse if

(83) These extrema, u12(2tπ, 1) = ±1, are the largest

coher-ences available for the ground-state atom when it is in 3 3 u₁₂(2t_π,1) 4B₁B₂ B1 2 B2 2 – B₁2+B₂2 ( )2 ---. = σ22(t,1) B₁2B₂2 B1 2 B2 2 + ( )2 --- 1 χt 2 ---⎝ ⎠ ⎛ ⎞ cos – 2 . = B1 B2 --- 3±2 2 2.4 0.4 ⎩ ⎭ ⎨ ⎬ ⎧ ⎫ . ≈ =

the equal coherent superposition (mixture) of the states |1〉 and |2〉 and the state |3〉 is not excited.

The time evolution of the low-frequency coherence during the excitation simply follows from Eq. (76):

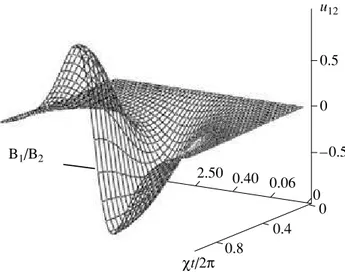
(84)

A 3D plot of this function versus the pulse area and the ratio of the interaction amplitudes is presented in Fig. 7. One could expect that, by playing with the pulse duration and the ratio of the field amplitudes, it would be possible to create a giant spin coherence u12(2tπ, 1) =

–1, which corresponds to the dark state for the case of equal field amplitudes. So, the fast change of the ratio of the field interaction constants from the value B₁/B₂ = 0.4 to B₁/B₂ = 1 at the appropriate time could bring a self-induced transparency. However, this is only possi-ble if all the atoms are initially in the state 1. If half of them are in the state 1 and the other half in the state 2, then simultaneous transfer of all of them to the state having the same maximal coherence (–1) is impossible. This can be shown if one calculates the state vector of the atom initially in the state |2〉:

(85) u12(t,1) = 2B1B2 3 B1 2 B2 2 + ( )2 --- 1 B1 2 B₂2 --- χt 2 ---⎝ ⎠ ⎛ ⎞ cos + χt 2 ---⎝ ⎠ ⎛ ⎞ cos –1 . Φbc(t,2) e iϕ2 – α χt 2 ---⎝ ⎠ ⎛ ⎞ b|〉 cos i χt 2 ---⎝ ⎠ ⎛ ⎞ c|〉 sin + cos = – eiϕ1sinα d| 〉. 1.0 0.5 0 –0.5 –1.0 10 1 0.1 0.01 100 B1/B2 u12(tπ) u12(2tπ)

Fig. 6. The dependence of the low-frequency coherence u₁₂

on the ratio of the B₂ and B₁ constants of the interaction with the spectral components of the bichromatic field. The solid line corresponds to the π pulse, and the dashed line corresponds to the 2π pulse. The B₁/B₂ ratio is on a logarith-mic scale. The initial state of the atom is |1〉.

0.5 0 –0.5 0 0 0.4 0.8 0.40 0.06 2.50 B1/B2 u12 χt/2π

Fig. 7. 3D plot of the low frequency coherence versus pulse

area (in the units of the 2π cycle) and the ratio of the inter-action constants of the bichromatic field components. The scale of the latter is logarithmic. The initial state of the atom is |1〉.

(11)

48

For this case, the low-frequency coherence is

(86)

The low-frequency coherence of the ensemble of atoms is (87) which, with Eqs. (84) and (86), can be written as

(88) Finally, we see that the module of the average coher-ence cannot be larger than 1/2 and this extremum takes place if B₁ = B₂ and χt = π.

The Bloch-vector model is also applicable for the case of different field amplitudes, since the atom again evolves only between the two states b and c [see the Hamiltonian

Ᏼ

dbc, Eq. (75)]. According to Eqs. (42) and (74), the Bloch-vector components are related to the density matrix elements of the interaction represen-tation as follows:

(89) (90) Here, because of the different phases of the field com-ponents, the combinations v13 and v23 are redefined as

follows:

(91) where n = 1 or 2 and the u12 component is redefined in

Eq. (79).

In the case of different phases and amplitudes, the Bloch equations are almost the same as those derived in subsection 3.3 for equal interaction amplitudes [see Eqs. (60), (61)], except for the dissipative terms in Eq. (61). The relaxation process of the population exchange between the states |1〉 and |2〉 gives an addi-tional nonzero contribution in this case, and this increases the number of density matrix components that need to be taken into account.

The dynamical evolution of the atom on a time scale much shorter than any relaxation time can still be described by simple Bloch equations, Eqs (38) and (39). The population evolution of the level 3, σ33 and

the time dependence of the sum of the ground-state sub-levels 1 and 2, n12 also satisfy Eq. (46), and its general

solution, Eqs. (48) and (49), is still applicable. Mean-while, the equation for the low-frequency coherence,

u12, modifies as follows: (92) u12(t,2) = 2B1 3 B₂ B₁2+B₂2 ( )2 --- 1 B2 2 B₁2 --- χt 2 ---⎝ ⎠ ⎛ ⎞ cos + χt 2 ---⎝ ⎠ ⎛ ⎞ cos –1 . u12( )t 〈 〉en 1 2 --- u[ ₁₂(t,1) u+ 12(t,2)], = u₁₂( )t 〈 〉en B1B2 – 2 B1 2 B2 2 + ( ) --- 1[ –cos( )χt ]. = v_bc v 13sinα+v23cosα, = wbc σ33 σ22cos α 2 – –σ₁₁sin2α 1 2 ---u₁₂sin2α. – = v_n 3 i σn3e iϕn – σ3ne iϕn – ( ), – = u˙₁₂ χ 2 ---V , =

where a new combination of the density matrix compo-nents appears

(93) This new variable V satisfies the equation

(94) It is quite simple to find the solution of the system of equations (38), (39), (46), (92), and (94) for any initial condition.

Population trapping also takes place in the case of different field amplitudes if the level 2 is initially empty and the condition B₂ Ⰷ B₁ is satisfied. Because of the imposed condition (empty state 2), the Λ and Ξ schemes are indistinguishable. To describe the trapping process, one has to consider master equations similar to Eqs. (60)–(63). However, there is a difference in the structure of these equations. The decay rate Γ12/2 in

Eq. (61) has to be replaced by Γ12sinαcosα and the

variable u₁₂ is coupled to the new component V [see Eqs. (92), (94)]. The decay terms in Eqs. (92) and (94) are –Γ12u12 and –ΓV, respectively. With this

modifica-tion, one can find that, if the condition Ⰷ ΓΓ₁₂ is sat-isfied, under cw excitation the population of the level 3 is reduced from 2 /Γ2_{to 2(B}

1/B2)2Γ12/Γ and the

absorption of the field B1 is also reduced by the same

factor of ΓΓ12/ . This effect of the driving field

influ-ence on the absorption of the probe becomes easy to implement if the decay rate Γ12 of the coherence 1–2 is

much smaller than the decay rate Γ of the coherence 1–3. Then, the decrease in the absorption of the probe B1

takes place at quite moderate amplitudes of the field B₂. The absorption is reduced because of population trap-ping in the dark state with its inherent coherence u₁₂ = –2B1/B2. This coherence is created because of

popula-tion of the state 2: σ22⯝ , which can be much larger than the population of the common level 3 if Γ12 Ⰶ Γ.

4. V SCHEME

For the V scheme, the atom evolution starts from the state |3〉. Therefore, the state vector is

(95) neglecting all relaxation. The low-frequency coherence appears in the excited-state sublevels 1 and 2 due to the population of the bright state b:

(96) V v 13cosα+v23sinα = = vbcsin2α+vdccos2α. V˙ χ 2α σ₃₃ n12 2 ---– ⎝ ⎠ ⎛ ⎞ sin χ 2 ---u₁₂. – = B₂2 B₁2 B2 2 B1 2 /B2 2 Φbc(t,3) | 〉 χt 2 ---⎝ ⎠ ⎛ ⎞ 3|〉 cos i χt 2 ---⎝ ⎠ ⎛ ⎞ b|〉, sin + = u₁₂( )t 1 2 --- 1( –cosχt), =

(12)

where u12(t) is defined in expression (25). The creation

of coherence in the excited-state spin sublevels is important from the viewpoint of excited-state spectros-copy in solids (see, for example, [16]). To describe the cw excitation of the spin coherence, one can use the Bloch-vector model. Because the order of the energy levels is different in the V scheme, we introduce new combinations of the density matrix elements to obtain a correspondence between the sign of the v component and the absorption/amplification of the relevant field component:

(97) (98) (99) Then, the Bloch equations with a dissipative part are

(100) (101) where Γ12 is caused, for example, by the magnetic

dipole interaction of the atom with the neighbors, i.e., by the impurity ion interaction with the host ions, and

Ꮽ

_{is the relaxation rate due to spontaneous emission.}

Due to the relaxation processes, extra components are introduced, satisfying the equations

(102) (103) The stationary solution of these equations is

(104)

(105) It follows from this solution that the population trap-ping is impossible for the V scheme. For example, if

Ꮾ

Ꮾ

---+ + ---, = = ρdd ( )_st Γ12 2

Ꮽ

--- u( ₁₂)_st. =

the relaxation and pump rates in the V scheme, one can never trap the population in any particular state (see Fig. 8). However, it is possible to create an appreciably large spin coherence (u₁₂ ~ 1/2) in the excited state if the spontaneous decay is faster than the spin coherence decay. This cw coherence is only two times smaller than the value induced by the pulse of duration tp if χtp = π [see also Eq. (96)].

5. CONCLUSIONS

The introduction of the basis of the dark and bright states facilitates the understanding of the physical pro-cesses in the three-level atom excited by a bichromatic field. The dynamical evolution of the atom between the dark, bright, and common states is as simple as the dynamics of the two-level atom excited by one field. This is because the evolution of the three-level atom can be effectively reduced to the evolution between two states, i.e., the bright and common states. The excita-tion of the low-frequency coherence, which is impor-tant for the spectroscopy of the spin splittings in the excited and ground states of optical transitions, clearly follows from this model. The reduction of the three-level model to the two-three-level one allows also the appli-cation of the Bloch-vector model and Bloch equations for the treatment of the three-level atom excitation by the bichromatic field. This approach allows an easy introduction of the relaxation processes as well. Then, the phenomenon of population trapping in the dark state has a simple interpretation and the condition for its existence becomes trivial. The dynamical evolution of the three-level atom excited by a sequence of pulses can be described using simple algebra. The nonadia-batic population transfer has a nice interpretation in terms of dark, bright, and common states. This simpli-fied algebra could prove useful for the description of atom-state manipulation by coherent fields.

c

d b

Γ12

Ꮽ Ꮽ Ꮾ

Fig. 8. The relaxation processes and the pump for the V

scheme in the dbc basis. Ꮽ is the spontaneous decay rate of the population of the dark and bright states to the state c. Ꮾ is the pump rate from the state c to the state b. Γ₁₂ is the decay rate of the coherence of states 1 and 2. This decay process induces transitions between dark and bright states.

(13)

50

ACKNOWLEDGMENTS

This work was supported by the Fonds voor Weten-schappelijk Onderzoek Vlaanderen and by the Russian Foundation for Basic Research, the UIAP programme of the Belgian government.

REFERENCES

1. The amount of work already published is far too vast to cite. To simplify the problem, we cite a review, Ref. [2], and from time to time we will cite some particular papers, apologizing to authors of other papers on a sim-ilar topic.

2. E. Arimondo, in Progress in Optics, Ed. by E. Wolf (Elsevier, Amsterdam, 1996), Vol. 25, p. 257.

3. E. Arimondo and G. Orriols, Nuovo Cimento Lett. 17, 333 (1976).

4. H. R. Gray, R. M. Whitley, and C. R. Stroud, Jr., Opt. Lett. 3, 218 (1978).

5. G. Orriols, Nuovo Cimento B 53, 1 (1979).

6. L. Allen and J. H. Eberly, Optical Resonance and

Two-Level Atoms (Wiley, New York, 1975).

7. F. T. Hioe and J. H. Eberly, Phys. Rev. Lett. 47, 838 (1981).

8. F. T. Hioe, Phys. Rev. A 28, 879 (1983); Phys. Rev. A 29, 3434 (1984); Phys. Rev. A 30, 3097 (1984).

9. J. Oreg, F. T. Hioe, and J. H. Eberly, Phys. Rev. A 29, 690 (1984).

10. J. R. Kuklinsky, U. Gaubatz, F. T. Hioe, and K. Berg-mann, Phys. Rev. A 40, 6741 (1989).

11. F. T. Hioe and C. E. Carroll, Phys. Rev. A 37, 3000 (1988).

12. C. E. Carroll and F. T. Hioe, Phys. Rev. A 42, 1522 (1990).

13. A. Abragam, The Principles of Nuclear Magnetism (Clarendon Press, Oxford, 1961).

14. Ya. B. Zeldovich, Usp. Fiz. Nauk 110, 139 (1973). 15. R. Brewer and E. L. Hahn, Phys. Rev. A 11, 1641 (1975). 16. T. Blasberg and D. Suter, Phys. Rev. B 51, 6309 (1995).

View publication stats View publication stats