Réduction du bruit et tomographie quantique d'un faisceau laser interagissant avec des atomes froids : théorie et expériences

HAL Id: tel-00011915

https://tel.archives-ouvertes.fr/tel-00011915

Submitted on 10 Mar 2006

HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

Réduction du bruit et tomographie quantique d’un

faisceau laser interagissant avec des atomes froids :

théorie et expériences

Thomas Coudreau

To cite this version:

Thomas Coudreau. Réduction du bruit et tomographie quantique d’un faisceau laser interagissant avec des atomes froids : théorie et expériences. Physique Atomique [physics.atom-ph]. Université Pierre et Marie Curie - Paris VI, 1997. Français. �tel-00011915�

KASTLER BROSSEL

Thèse

de doctorat de

l’Université Paris 6

Spécialité :

Lasers

et

Matière

présentée

par

Thomas

Coudreau

Pour obtenir le

_grade

de

DOCTEUR

de

l’UNIVERSITE

PARIS

6

Sujet :

Réduction du

bruit

et

_tomographie

_quantique

d’un

faisceau

laser

_{interagissant}

avec

des

atomes

froids:

théorie

et

_{expériences.}

Soutenue le 17 décembre 1997 devant le

_jury

_composé

de :

M. C. FABRE Président

Mme. E. GIACOBINO Directeur de thèse M. P. GRANGIER

_Rapporteur

M. A. LEVENSON

M. L. LUGIATO

A

mes

grands-pères,

de conditions de recherche

_{exceptionnelle.}

Je tiens à remercier

_Jacques

Bauche

_grâce

à

_qui

j’ai

pu

bénéficier

d’une allocation de recherche du Ministère de

l’Enseignement Supérieur

et

de la Recherche. Je veux

_également

remercier MM. Gouédard et Ben

_Kelfat

de m’avoir

permis

d’effectuer

des vacations durant cette thèse.

_{Enfin, je}

suis très reconnaissant à

Jacqueline

Gouzerh

_qui

m’a

_permis

d’obtenir un _poste d’A.T.E.R. à l’Université

_paris

VII et

ainsi de terminer cette thèse dans de bonnes conditions.

Elisabeth Giacobino a encadré ce travail. Je la remercie de la

_{confiance qu’elle}

m’a

accordée _{ainsi que} de ses nombreux conseils et _{encouragements} au cours de cette thèse. Je la remercie

_également

de l’attention

_qu’elle

a

portée

à la correction de ce mémoire.

A mon arrivée au

Laboratoire, j’ai

eu le

plaisir

de travailler avec Astrid Lambrecht et

Aephraim Steinberg.

Je remercie Astrid Lambrecht de

_{m’avoir fait profiter}

de sa

grande

connaissance de

_{l’expérience.}

Je suis

_également

reconnaissant à

_Aephraim

_Steinberg

d’avoir

guidé

mes

_premiers

_pas sur

l’expérience

et de m’avoir aidé à

_m’y

retrouver sur une table de

manip’ bien

encombrée.

J’ai eu la

grande

chance et le

_{grand plaisir}

de travailler

_pendant

un an et demi avec

Antonio

_{Zelaquett-Khoury}

en

_séjour

_{post-doctoral.}

Je le remercie car ce travail lui doit

beaucoup.

Paulo

_Nussenzveig

a

_passé

un mois sur

l’expérience

et a

beaucoup

contribué à la

stabilisation du

_système.

Je tiens à le remercier de son aide

_précieuse.

Gerd Breitenbach de l’Université de Constance a

passé

une semaine au laboratoire _pour nous aider à réaliser les

_premières

mesures de

tomographie,

il nous a

aussi fourni

son

programme de calcul de la

fonction

de

Wigner

et de la matrice densité. Je le _{remercie pour} sa

disponibilité

autant lors de son

séjour

_{que par courrier}

électronique

interposé.

Merci

également

à M.

_Raymer

et A. Faridani de l’Université

_d’Oregon

de nous

avoir fourni

le

programme initial pour le calcul de la

fonction

de

Wigner

par

transformée

de Radon inverse

et à A. Zucchetti et W.

_Vogel

de l’Université de Rostock _{pour le calcul de} la matrice densité dans la base de Fock à

_partir

de nos données

expérimentales.

Laurent Vernac a commencé sa thèse sur cette

_expérience.

J’ai eu

beaucoup

de

_plaisir

à

travailler avec lui

_{et je}

tiens à le remercier pour ses lectures nombreuses et attentives de ce

mémoire.

Je voudrais

_également

remercier ici toutes les _personnes

_qui

m’ont aidé au cours de cette

thèse et

_qui

_{n’ont jamais}

hésité à

_répondre

à mes

_questions

même durant les moments les

moins _opportuns

_(qui

sont

_toujours

les moments où les

_problèmes

se

_{posent) :}

Antoine Heidmann _pour m’avoir aidé à résoudre de nombreux

_problèmes

de

_physique

mais aussi

_{d’informatique}

et

_{d’électronique qui}

se sont

_posés

au cours de ce travail. Il a

toujours

montré une bonne humeur et une

disponibilité qui

ne se

sont jamais

démenties.

Michel _{Pinard pour m’avoir}

_expliqué

les

_mystères

_{du pompage}

_optique

et _{pour avoir}

répondu

dans le détail à toutes les

_questions

_{que j’ai}

pu lui poser,

François

Biraben et

_François

_Nez

_qui

ont

_passé

de

_longs

moments à

_{m’expliquer}

_par

l’exemple

le

_{fonctionnement}

du laser

_{Titane:Saphir}

et dont la

_patience

et le savoir me

furent

précieux,

Jean-Michel

_Courty

_{pour m’avoir}

_expliqué

les nombreux

_points

de

_{physique atomique qui}

m’échappaient

ainsi que pour les moments

_qu’il

a

passé

à m’aider à

régler

le laser

Catherine Schwob et Yassine

_Hadjar

_pour les nombreuses discussions _que nous avons eu

et toutes les

_pièces

et

_{appareils qu’ils}

m’ont

_prêtés

au cours de cette

_thèse,

Francesca Grassia _pour ses _{encouragements} constants tout au

_long

de cette

_thèse,

Agnès

Maitre pour ses

_précieux

conseils _pour mes diverses

_{présentations}

orales et nos

nombreuses

discussions,

tous les

thésards,

stagiaires

et _visiteurs, Cédric

_Bégon,

Nicolas

_Borghini,

Alberto Bramati,

Hichem

Eleuch,

Jean-Pierre

Hermier,

Valéry

Jost,

Katsuyuki

Kasai, Gaétan Messin et

Matthias

_{Vaupel qui font}

du bureau dans

_lequel

nous travaillons un endroit vivant, convivial

et stimulant même

_quand

on n’aime pas

le football,

Pierre-François

Cohadon _pour sa relecture du

manuscrit,

Benoît Grémaud _pour sa

_patience

à

_{m’expliquer}

LaTeX et

_PostScript,

tous ceux _que

_je

n’ai pas remercié

_jusqu’ici

et

_{qui font}

de ce laboratoire un lieu de travail

particulièrement agréable.

Ce travail a aussi été rendu

possible

_par le

personnel

des ateliers du laboratoire. Pour

cela,

mes remerciements vont donc à

Francis Tréhin

_qui

_{ne fut jamais}

à court d’idée _pour résoudre les divers

_problèmes

rencontrés

_pendant

cette

_thèse,

Bernard

_{Rodriguez qui}

a

toujours accepté

avec

philosophie

et bonne humeur mes

modifications après

coup sur les

_{pièces mécanique}

qu’il

m’avait fabriqué,

Alexis Poizat

qui

a de

nombreuses fois accepté

avec de traiter des

pièces

en _urgence,

Sylvain

Pledel _pour son

efficacité

et sa

rapidité

au

_magasin

de

mécanique

de Paris

VI,

Jean-Claude Bernard

_qui

a _conçu de nombreux _montages

_{électroniques qui}

ont été réalisés

par

Philippe

Pace et Jean-Pierre

_Okpisz,

Jean-Pierre Plaut _pour son aide _pour résoudre les nombreux

_{problèmes informatiques,}

Karine Gautier et Blandine _{Moutiers pour m’avoir} aidé _{pour les}

_différentes

démarches

nécessaires au bon déroulement d’une thèse.

Je remercie tout

_{particulièrement}

Claude Fabre _{pour avoir}

_accepté

de

_présider

ce

jury

mais aussi pour ses

_{explications patientes}

et

_répétées

des divers

_{problèmes d’optique}

quantique qui

m’ont troublé durant cette thèse. Je tiens

_également

à remercier

_Philippe

Grangier

et Pierre Pillet d’avoir

_accepté

d’être les _rapporteurs de cette thèse

_malgré

les

courts délais _que nous leur avons laissé. Je suis

également

reconnaissant à Ariel Levenson et

Luigi Lugiato

pour l’intérêt

qu’ils

ont

_manifesté

_pour ce travail en _acceptant

de faire

_partie

du jury.

Enfin, je

veux remercier mes amis et

_{ma famille}

_pour leurs _{encouragements} au cours de cette thèse. Un immense _{merci pour terminer à}

_Sylvie

sans

qui

ce travail n’aurait

Table des

matières

1 Introduction 5

2 Introduction au bruit

quantique -

Réduction du bruit _par effet Kerr 9

2.1 Introduction ... 9

2.2

_{Quantification}

du

_champ

_{électromagnétique}

... 9

2.2.1

_Composantes

de

_quadrature

... 12

2.2.2

_{Représentation}

dans

_l’espace

des

_phases

... 14

2.2.3 Choix d’un ordre ... 15

2.2.4

_Statistique

du

_rayonnement

... 16

2.3

_{Représentation}

des états du

_champ

... 22

2.3.1 Introduction ... 22

2.3.2

_{Représentation}

P ... 22

2.3.3

_{Représentation}

de

_Wigner

... 23

2.4 Réalisation

_{expérimentale}

d’états

_comprimés

du

_{rayonnement...}

24

2.4.1 Introduction ... 24

2.4.2 Réduction du bruit dans un milieu

~

(2)

... 25

2.4.3 Réduction du bruit _par effet Kerr ... 26

3 Présentation du

_{montage expérimental}

31 3.1 Introduction ... 31

3.2 Les sources lasers ... 31

3.2.1 La diode laser de _repompage ... 31

3.2.2 Le laser

_{Titane:Saphir}

... 33

3.3 Le

_{piège magnéto-optique}

... 37

3.3.1

_Principe

... 37

3.3.2 Mise en oeuvre

expérimentale

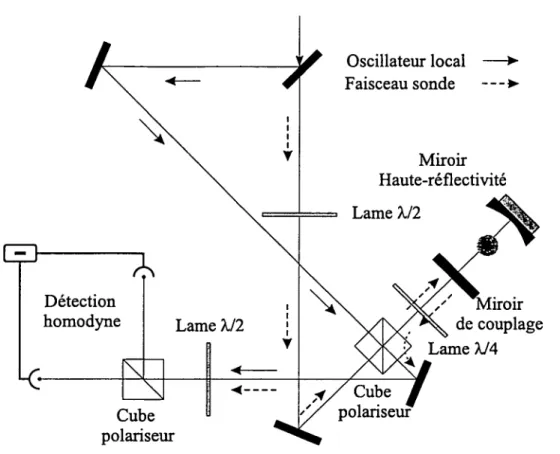
... 38

3.4 La cavité d’interaction ... 40

3.4.1

_{Montage expérimental}

... 40

3.5 La détection

_homodyne

... 42

3.5.1

_Principe

de la détection

_homodyne

... 42

3.5.2 Détection des fluctuations

_quantiques

... 42

3.5.3

_{Représentation}

dans

_l’espace

des

_phases

... 45

3.5.4 Influence de la

_dépendance

_spatiale

des modes ... 45

3.6 Améliorations du

_{montage ...}

47

3.6.1 Amélioration du

_montage

de la cavité d’interaction ... 47

3.6.2 Amélioration de la détection ... 49

4 Etude

_théorique

de la réduction de bruit avec des atomes froids. 55 4.1 Introduction ... 55

4.2 Méthode des forces de

_{Langevin ...}

56

2

4.2.2 Méthodes des forces de

_Langevin

en

_{optique quantique ...}

57

4.3 Calcul des

_spectres

de bruit ... 59

4.3.1 Présentation du modèle ... 59

4.3.2 Article "A three level

_approach

to

_squeezing

with cold atoms" .. 61

4.4 Prédictions

_{théoriques -}

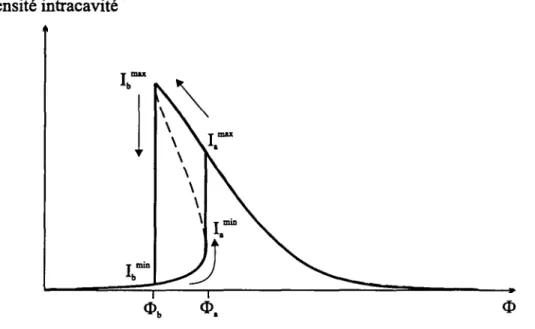
conclusions ... 86

4.4.1 Allure de la courbe de transmission de la cavité ... 86

4.4.2 Etude du

_spectre

de la réduction de bruit ... 87

4.4.3

_Balayage

de la

_longueur

de la cavité ... 87

4.4.4 Etude en fonction de la

puissance

des faisceaux

pièges ...

88

4.4.5 Etude en fonction de la

puissance

du _repompeur ... 88

4.4.6 Etude en fonction de la

_puissance

de la sonde ... 89

4.4.7 Conclusions ... 91

5 Mesure de la réduction de bruit 93 5.1 Introduction ... 93 5.2 Conditions

expérimentales ...

93 5.2.1 Le faisceau sonde ... 93 5.2.2 Le

_{piège magnéto-optique}

... 95 5.3 Résultats

_{expérimentaux ...}

99 5.3.1 Procédure de mesure ... 99

5.3.2 Courbes de réduction de bruit ... 100

5.4

_{Comparaison théorie-expérience}

... 101

5.4.1 Introduction ... 101

5.4.2 Cas des faisceaux

_pièges

_peu intenses ... 103

5.4.3 Cas des faisceaux

_pièges

intenses ... 103

5.5 Conclusions ... 105

6

_{Tomographie Quantique : Principes}

et mise en oeuvre

expérimentale107

6.1 Introduction ... 107

6.2

_Tomographie

médicale ... 108

6.2.1 Introduction ... 108

6.2.2

_Tomographie

de transmission:

_principes

... 108

6.2.3

_{Rétroprojection}

_simple

... 109

6.2.4 Reconstruction bidimensionnelle de Fourier ... 111

6.2.5

_Filtrage

de Fourier - Transformée de Radon inverse ... 113

6.2.6 Mise en 0153uvre

expérimentale

... 114

6.3

_Tomographie

_quantique

... 114

6.3.1 Bases de la

_tomographie

_quantique

... 114

6.3.2

_Filtrage

de Fourier ... 116

6.3.3 Calcul par

régularisation quadratique

... 116

6.3.4 Reconstruction directe de la matrice densité ... 117

6.4 Résultats

_{expérimentaux ...}

121

6.4.1 Procédure de mesure ... 121

6.4.3

_{Représentation}

de la matrice densité dans la base de Fock .... 126

6.5 Conclusion ... 129

Conclusions 131

Appendice

133

5

1

Introduction

L’étude des fluctuations

_quantiques

du

_champ

_{électromagnétique}

a commencé à se

développer

de manière

_{spectaculaire}

à

_partir

des années 1960 mais il fallu attendre la fin des années 1970 _pour

_{qu’apparaissent}

les

_{premières propositions}

visant à contourner

la "limite

_quantique

standard" venant des

_{inégalités d’Heisenberg.}

En

_effet,

_{l’inégalité}

d’Heisenberg n’impose

une condition _{que pour} le

produit

des variances des deux

ob-servables

_conjuguées

_qui

décrivent le

_champ

_{électromagnétique}

_quantifié.

Un état du

champ possédant

des fluctuations sur une

_composante

au-dessous du bruit

_quantique

standard est dit

_comprimé.

L’intérêt d’utiliser un état

comprimé apparaît

dans les mesures de très

grande

précision.

Les mesures d’intensité ou de

phase

sont limitées de manière ultime _par le bruit

_quantique

standard du

_champ.

Il est donc intéressant d’obtenir

_{expérimentalement}

des états dont les fluctuations soient

_comprimées

en

am-plitude

ou en

phase.

Dans le cas d’une mesure de

spectroscopie

_par

absorption,

on

pourra utiliser avec

profit

des états

comprimés

en

amplitude

_pour

_augmenter

la

sen-sibilité. De

_même,

dans le cas de mesures

interférométriques

comme celles visant à

détecter des ondes

_{gravitationnelles,}

il sera intéressant d’utiliser des états

_comprimés

en

phase

_pour améliorer le

_rapport

signal

à bruit de la mesure.

Depuis

une dizaine d’années de nombreuses méthodes ont été mises au

_point

_pour

créer et étudier ces états

comprimés.

On

_peut

classer ces méthodes en deux

_types.

Le

premier

type

de méthode consiste à

_appliquer

un

principe

dit de

"pompe

régulière"

dans un laser

[Golubev

84].

Selon ce

principe,

la

statistique

de la _pompe est

_reproduite

sur

la

_statistique

de la lumière émise _par le laser. Cette méthode a été utilisée de manière

très convaincante dans le cas des diodes lasers où des

_compressions

des fluctuations

jusqu’à

70%

ont été obtenues _pour des faisceaux utilisables

_{[Kilper 96].}

L’autre

_type

de méthode est basée sur une interaction entre un faisceau laser et un milieu

non-linéaire. De nombreuses études

_théoriques

ont été menées _pour identifier les milieux favorables à la réduction du bruit. Ces non-linéarités sont

_typiquement

_~

₍₂₎

ou

~

(3)

.

La

_première

_expérience

a été réalisée en 1985 en utilisant une interaction avec un

milieu

_{atomique présentant}

une non-linéarité

~

(3)

[Slusher 85].

L’effet non linéaire était

augmenté

par la

proximité

d’une résonance

atomique.

On a _par la suite cherché à utiliser

des non-linéarités

_{paramétriques}

_pour

_lesquelles

les sources de bruit sont faibles

_(a

_priori

elles ne sont _pas liées à la non-linéarité mais à des effets

_parasites).

Ces interactions

paramétriques

ont été

_{principalement}

réalisées dans des cristaux

_présentant

une

génération paramétrique

ou la

génération

de

second-harmonique.

Ces

expériences

ont

conduit à de fortes réductions de bruit

_pouvant

aller

_jusqu’à

_{90%[Mertz 91].}

Les milieux

_présentant

une non-linéarité de

_type

Kerr

(~

(3)

)

sont eux aussi de

bons candidats pour la réduction de bruit. Il est bien connu _que ce

_type

de milieu est

à

_l’origine

d’un

_phénomène

de bistabilité

_optique

_[Gibbs

_76]:

la courbe de résonance

en

présence

d’un milieu Kerr n’est

plus

une fonction

d’Airy

mais

_peut

_posséder,

_pour une valeur donnée de la

longueur

de la

cavité,

trois

points

de fonctionnements dont

deux seulement sont stables. De nombreux travaux

_théoriques

ont montré _{que cet} effet

purement

classique

est à même de réduire le bruit _pour une

_composante

du

champ

[Reynaud

89].

Deux

_types

de milieu

_~

₍₃₎

ont été utilisés avec succès _pour réduire les

fluctuations

_quantiques

du

_rayonnement,

les fibres

_optiques

_{[Shelby 86][Shirasaki 90]}

et les milieux

_{atomiques. L’expérience}

étudiée au cours de ce travail utilise un milieu

atomique.

En

_{première approximation,}

on

_peut

interpréter

la non-linéarité comme une

variation de l’indice

_optique

avec la

puissance

ce

qui

est

équivalent

à une non-linéarité

de

_type

Kerr. Nous allons voir maintenant les conditions nécessaires à la réduction de bruit dans un milieu

atomique.

La non-linéarité dans ces milieux

provient

de la

proximité

d’une résonance. Cette

résonance est à

_l’origine

d’un excès de bruit à cause de

l’absorption

et de l’émission

spontanée

dans le mode _pour

_lequel

est

_prédite

la réduction de bruit. Afin d’éviter

cet excès de

_bruit,

on

s’éloigne

de la résonance. L’effet

Doppler

est alors un obstacle

à la

_compression

des fluctuations

_{puisqu’il élargit}

les résonances. Des

_expériences

ont

été réalisées dans une _vapeur

atomique

mais ont donné des résultats très inférieurs à

des

_{prédictions théoriques}

ne

_prenant

_pas en

_compte

l’effet

Doppler

[Maeda 87].

La

première

solution _{retenue pour} éliminer l’effet

_Doppler

est le

_{jet atomique.}

Pour un

jet

bien

_collimaté,

l’effet

_Doppler

est

_négligeable

dans la direction transverse. Des effets de réduction de bruit ont été observés dans ces conditions

[Orozco 87][Hope 92].

Cepen-dant,

les résultats obtenus étaient

_toujours

inférieurs aux

prédictions

théoriques.

Afin

de mieux contrôler les conditions

_{expérimentales,}

il est intéressant d’utiliser les atomes

refroidis et

_piégés

_par laser comme milieu non-linéaire. Une

expérience

a commencée

dans ce sens dans notre laboratoire en 1989. Les

premières

observations de bistabilité

ont été faites _{par L.} Hilico au cours de sa thèse

[Hilico 92a].

Dans les mesures de

bruit effectuées _par la

_suite,

l’effet

_perturbateur

des faisceaux

_pièges

s’est révélé très

important.

En

_particulier,

avec les faisceaux

_pièges

à leur

_{pleine puissance,}

il est

possi-ble d’observer un

phénomène

d’émission laser

[Hilico

92c].

Ce laser a des fluctuations

propres

qui

détruisent la réduction de bruit. Il est donc nécessaire de s’affranchir des

faisceaux

_pièges.

La

_première

solution

_développée

_par A. Lambrecht a été d’éteindre

les faisceaux

_pièges

_{[Lambrecht 96a].}

_Quelques

millisecondes

_après

la _coupure, il reste

encore suffisament d’atomes _pour avoir une non-linéarité

importante

et la mesure de

bruit est affranchie de l’effet des faisceaux

_pièges.

La réduction de bruit observée dans

ces conditions est de l’ordre de

40%.

Cette réduction de bruit n’est _que transitoire

(quelques

millisecondes).

Afin

_{d’augmenter}

le

_temps

_{pendant lequel}

elle est

_observée,

on

_peut

mesurer la modification des fluctuations

_quantiques

sur une transition non

perturbée

par les faisceaux

pièges.

Ceci a été réalisé dans

l’équipe

de P.

Grangier

à

7

Orsay

dans le cadre de mesures

quantiques

non-destructrices

[Roch 97],

[Sinatra 98]

pour

lesquelles

deux faisceaux sont

nécessaires,

un faisceau

signal

intense et un faisceau mesure faible. Cette solution n’est _pas

envisageable

dans une mesure de réduction de

bruit où on ne

dispose

_que d’un faisceau. Dans ce _cas, on

_peut

utiliser des faisceaux

pièges

atténués.

_Cependant,

dans ces

conditions,

un modèle

atomique

à deux niveaux

n’est

_plus

valable.

_{Jusqu’alors,}

un modèle

théorique

d’atomes à deux niveaux était

sat-isfaisant

_puisque

les faisceaux

_pièges

étaient absents lors de la mesure de la réduction

de bruit. La validité de cette

_approche

était confirmée _par le fait que les

prédictions

théoriques

étaient en bon accord avec les mesures

expérimentales.

En

_présence

des fais-ceaux

pièges,

ce modèle n’est

plus

valable et doit

prendre

en

_compte

les autres niveaux intervenant dans le mécanisme de

_piégeage.

Nous avons

développé

un modèle basé sur un ensemble d’atomes à trois niveaux. Pour

cela,

nous avons résolu

analytiquement

les

_équations

_{d’Heisenberg-Langevin}

_qui

_régissent

l’évolution du

_{système composé}

du faisceau laser

_sonde,

des faisceaux

_pièges,

de _repompage et des atomes

_supposés

im-mobiles. Nous avons alors _pu calculer

analytiquement

les

expressions

des fonctions de

corrélation _pour le

_champ

mesurées

_{expérimentalement.}

Nous avons

comparé

les

pré-dictions

_théoriques

aux résultats

expérimentaux

dans

plusieurs

régimes

de

paramètres

différents et obtenu un excellent accord.

L’expérience

sera

présentée

dans le second

chapitre

tandis _que les calculs

_théoriques

feront

_l’objet

de notre troisième

_chapitre.

Enfin,

le

_{quatrième chapitre}

sera consacré à la

comparaison

des

prédictions

théoriques

et des résultats

_{expérimentaux.}

Indépendamment,

nous avons

appliqué

la méthode dite de

tomographie

quantique

du

_champ

_{électromagnétique.}

Les

_champs

_{électromagnétiques}

sont souvent

_{représentés}

par leur matrice densité. Cette matrice densité

développée

dans une base

quelconque

peut

être mesurée

_{expérimentalement :}

on mesure _par

exemple

la fonction de

_Wigner

qui

est une distribution de

quasiprobabilités

qu’on

_peut

relier à la matrice densité

[Wigner 32].

L’intérêt de ces mesures est de donner accès non seulement à la valeur

moyenne et à la variance du

champ

mais aussi à toute sa

_statistique.

Nous avons ainsi

obtenu les

_premières

mesures de la fonction de

Wigner

d’un état _pour

lequel

les

fluc-tuations

_prédites

_{théoriquement}

sont non minimales. Nous avons ainsi _pu vérifier _que

la

_statistique

de ces états obéit à une loi

gaussienne.

La

présentation

de la

tomogra-phie quantique

et les mesures _que nous avons faites sont détaillées dans le

_cinquième

2

Introduction

au

bruit

quantique

-Réduction

du

bruit

_par

effet

Kerr

2.1

Introduction

Comme nous l’avons mentionné dans l’introduction de ce

mémoire,

il _est

pos-sible de réduire les fluctuations

_quantiques

du

_champ

_{électromagnétique}

au-dessous d’une certaine valeur

_appelée

limite

_quantique

standard. L’existence de fluctuations du

_{champ électromagnétique}

découle de sa nature

_quantique,

nature

_qui

a été mise en évidence lors de l’étude des

propriétés

_statistiques

de la lumière. Nous allons donc

rappeler

brièvement les méthodes utilisées _pour décrire le

_champ

_{électromagnétique}

quantifié

ainsi que les

_{propriétés statistiques qui}

s’en déduisent. La

_{première partie}

sera consacrée à un

rappel

des

propriétés

du

champ quantifié

puis

la deuxième

par-tie détaillera les différentes

_{représentations}

utilisées _pour le décrire.

_Finalement,

nous

montrerons comment un milieu dont l’indice

optique dépend

de l’intensité incidente

(milieu Kerr)

est

_susceptible

de modifier les fluctuations

_quantiques

du

_rayonnement

et

nous décrirons dans

_quels

conditions on

_peut

considérer

qu’un

_nuage d’atomes refroidis

par laser est un milieu Kerr favorable à la réduction du bruit.

2.2

_{Quantification}

du

_{champ électromagnétique}

La

_{quantification}

du

_{champ électromagnétique}

est _apparue nécessaire dès le début du siècle : le

_spectre

de

_rayonnement

du _corps noir ne

_peut

être

interprété qu’en

consid-érant une

description quantifiée

du

champ.

Cette

quantification implique

_que

_l’énergie

du

_champ

_{électromagnétique}

n’est

_plus

continue comme on le

croyait jusqu’alors

mais

composée

de

_quanta

_{(individuels)}

_{d’énergie :}

les

_photons.

Les

_{propriétés statistiques}

d’un faisceau lumineux sont étroitement liées à ce

_concept.

Si on

considère,

_par

ex-emple,

un faisceau laser dans

_lequel

on

néglige

toutes les sources de bruits extérieures

arrivant sur un détecteur

_parfait,

on

_peut

montrer

(voir

2.2.4.2)

_que les

_temps

d’arrivée

des

_photons

sur le détecteur sont

_répartis

selon une

statistique

particulière :

une

statis-tique poissonienne.

Pour étudier ces

propriétés statistiques,

nous allons d’abord

10

Pour

_quantifier

le

_{champ électromagnétique,}

on utilise une

analogie

entre les

équations classiques qui

lient les différentes

_composantes

du

_{champ électromagnétique}

et les

_{équations quantiques}

d’évolution d’un oscillateur

_harmonique.

Dans une boîte de

dimensions L x L x

L,

on

_peut

décomposer

le

champ

en modes caractérisés _par une

fréquence

03C9i, un vecteur d’onde

k

i

, 203C0 L)

z

, 203C0 L, n

y

203C0 L, n

xi

(n

et une

polarisation

03B5

i

.

On

_peut

montrer

_qu’un

mode est entièrement caractérisé par un vecteur

_03B1

_i

(k

i

,

t)

donné _par la relation

_{(Cohen-Tannoudji 87] :}

où 03B5

i

(k, t) et

B

i

_(k

_i

_{, t)}

désignent

les transformées de Fourier

_spatiales

du

_champ

élec-trique

et

du

_champ

_magnétique.

Pour un

champ

quelconque,

l’énergie

du

champ

_peut

s’écrire en utilisant la

décomposition

en modes :

De

_plus,

l’évolution de

_a

_i

(k, t)

_peut

se déduire des

équations

de Maxwell et on

obtient _pour un

champ

se

_propageant

dans le vide :

Les

_équations

2.2 et 2.3 sont

_identiques

à celles

_qui

_gouvernent

l’évolution d’un oscillateur

_harmonique.

La

_{quantification}

d’un oscillateur

_harmonique

étant bien

con-nue, il est

possible

de

quantifier

le

champ

électromagnétique

d’une

façon

similaire.

Par

_analogie,

on associe aux

grandeurs

classiques

03B1 et 03B1* les

_opérateurs

bien connus

de création et d’annihilation d’un

_quantum

_d’énergie

dans un mode

i,

â

i

et

â

~

i

.

Ces

opérateurs

sont

_hermitiques

_{conjugués. L’énergie}

du

_champ

s’écrira alors :

On a des relations de commutation

générales

entre les

opérateurs

création et

où

_03B4

_i,j

_représente

le

_symbole

de Kronecker.

En

_{représentation}

de

_{Schrödinger,}

les

_{opérateurs champs}

s’écrivent en fonction des

opérateurs

création et annihilation :

avec

B

03C9i

=

1 cE

03C9i

.

E

03C9i

correspond

au

champ

d’un seul

photon.

Dans le

_point

de vue de

Schrödinger,

on utilise des

opérateurs

qui

agissent

sur des

vecteurs d’états

_dépendant

du

_temps,

_|03C8

_{S (t)).}

En

_{optique quantique,}

on utilise

plus

fréquemment

le

_point

de vue

d’Heisenberg.

Cette

représentation

consiste à

appliquer

à

|03C8

S

(t)>

une transformation

unitaire, U,

de telle sorte _que U

|03C8

S

(t))

soit

indépendant

du

_temps.

On a donc :

Cette relation

_permet

d’introduire le vecteur d’état en

représentation

d’Heisenberg :

Afin de conserver les

prédictions

de la

mécanique quantique,

il est nécessaire

d’appliquer

aux

opérateurs

dépendant

du

_temps

une transformation similaire. Dans la

représentation

d’Heisenberg,

un

opérateur

s’écrit alors :

12

L’expression

des

_champs

_{électromagnétiques}

en

représentation

d’Heisenberg

est :

L’intérêt de la

_{représentation}

_{d’Heisenberg}

est de conduire à des

_équations

d’évolution

analogues

à celles obtenues dans la théorie

_classique

dans

_lesquelles

on

remplace

les

grandeurs

classiques

par des

opérateurs.

On

peut

aussi calculer des moyennes à deux

temps

du

_type

_<03C8

_{|F(t)G(t’)|03C8>.}

Ces moyennes à deux

temps

interviennent,

par

ex-emple,

dans le calcul des corrélations entre les

_temps

d’arrivée des

_photons.

Il est

intéressant de _{noter que} dans le cas d’un

champ libre,

i

â

(t)

et

â

~

i

_(t)

sont

_{indépendants}

du

_{temps :}

toute la

_dépendance

_temporelle

est

_regroupée

dans le terme

e

±i03C9

i

t

.

2.2.1

_Composantes

de

_quadrature

On

_peut

aussi

_décomposer

le

_champ

en

composantes

de

quadrature,

Ê

Pi

et

Ê

Qi

:

avec

et

On

_peut

déduire de la relation 2.5a une relation de commutation _pour les

{â

Pi

,â

Qi

} :

Le commutateur de

_â

_Pi

et

_â

_Qi

étant un

_imaginaire

_pur non

nul,

les fluctuations de ces

grandeurs

sont liées _par une

inégalité

de

Heisenberg :

où

0394Â désigne

l’écart

_quadratique

_moyen de  : 0394Â

= <Â

2

- <Â>

2

>.

On a aussi :

E

2

03C9i

apparaît

ici comme une limite

imposée

_par la nature

_quantique

du

_champ.

Elle est

appelée

limite

_quantique

standard. Si on fait

plusieurs

mesures de

Ê

Pi

,

les résultats

obtenus

_présentent

en

général

une

dispersion.

Cette

dispersion

est caractérisée _par un

écart

_quadratique

_moyen,

0394Ê

Pi

,

non nul.

L’équation

2.19 _{montre que} le

_produit

des

dispersions

Pi

0394Ê

et

0394Ê

Qi

est borné inférieurement _par

_.

_E

_03C9i

₂

On ne

_peut

_pas mesurer

simultanément les deux

_composantes

de

_quadratures

avec une

précision

infinie.

Néan-moins,

il n’existe _pas de limite fondamentale à la mesure d’une seule de ces

_grandeurs.

Ainsi,

il est

_{envisageable d’augmenter}

la

_précision

sur la mesure d’une des deux

com-posantes

du

_champ,

c’est à dire de diminuer ses

fluctuations,

au

prix

bien entendu d’une

augmentation

des fluctuations sur la

_composante

conjuguée.

On _pourra donc

_augmenter

la

_précision

d’une _mesure, la seule limite étant de nature

_technique.

Des états

_ayant

des fluctuations inférieures à la limite

_quantique

standard sur une

quadrature

sont dits

comprimés.

On définit de manière

_générale

un état minimal comme un état vérifiant

l’égalité :

Enfin,

remarquons

qu’un

terme de

phase

dans

l’équation

2.13b ne modifie _pas les

propriétés

du

_champ,

la

_{représentation}

en

quadratures

n’est donc _pas

unique. Ainsi,

la

14

2.2.2

_{Représentation}

dans

_l’espace

des

_phases

On utilise couramment une illustration

graphique

des

propriétés

du

champ :

on

représente

le

_champ

dans

_l’espace

des

_phases,

c’est à dire le

_plan

(Ê

P

,

Ê

Q

).

Dans

_l’espace

des

_phases,

le

_champ

_{électrique classique}

est

_représenté

_par un

vecteur tournant à la

_fréquence

03C9. Si on considère le

champ

quantifié,

toute mesure du

champ

est entachée d’un bruit. On

_peut

_représenter

ces fluctuations _par une surface

centrée à l’extrémité du

_champ

_électrique

_moyen. La

_projection

de cette surface sur une droite faisant avec l’axe

Ê

P

un

angle 03B8

correspond

à la variance de la

_quadrature

considérée

_(voir

_figure

_1).

Fig.

1:

_{Représentation}

dans _l’espace des _phases de la surface des fluctuations.

Les fluctuations dans l’axe du

_champ

_{électrique correspondent}

aux fluctuations

d’amplitude

alors _que les fluctuations

_{perpendiculaires}

_{correspondent}

aux fluctuations

de

_phase.

On

_peut

montrer

_qu’un

état

_cohérent,

c’est à dire un état _propre de

â,

est un état

minimal

_qui

ne

possède

_pas de

quadrature

privilégiée.

Sa

représentation

dans

l’espace

des

_phases

est donc un cercle

correspondant

à des fluctuations

égales

à la limite

quan-tique

standard sur toutes les

quadratures.

Dans le cas des

petites

fluctuations

(c’est

à

dire de fluctuations faibles devant la valeur _moyenne du

_champ),

un état

comprimé

est

Fig.

2: _{Représentation} dans _l’espace des _phases d’un état cohérent et d’un état _comprimé.

2.2.3

Choix

d’un ordre

En

_{représentation}

_{d’Heisenberg,}

l’évolution d’un

_système

est donnée _par un

ensem-ble

_{d’équations}

_pour les

_{opérateurs dépendants}

du

_temps.

Afin de résoudre ce

système,

on cherche souvent à _passer à un

système

d’équations

_pour des variables

_{complexes qui}

"correspondent

aux

opérateurs".

Il existe

cependant

une différence

importante

entre

les variables

_complexes

et les

_{opérateurs. L’algèbre}

_gouvernant

les

_opérateurs

est non

commutative alors _que les variables

_complexes

commutent. Si on considère une fonction

F

_(a,

_a

_~

₎

_qui

_peut

se

développer

en

série,

on a :

où _{p1, p2,} ..., sont np des entiers

positifs.

Il est

toujours

possible

d’utiliser les relations de

commutation entre â et

â

~

_pour les

_réarranger

entre eux. Cela va conduire à différentes

expressions

pour F

(â, â

~

)

qui

seront toutes

égales.

16

Ce classement des

_opérateurs

avec les â à droite des

â

~

est dit "ordre normal".

L’origine

de cette

_désignation

de normal réside dans le fait _que c’est l’ordre

_qui

_apparaît

lors de la

_{photodétection}

_{[Glauber 63a].}

L’ordre antinormal

_correspond

à _{arranger F}

en classant les â à

_gauche

des

â

~

.

On a alors :

On

_peut

introduire un troisième

ordre,

l’ordre dit

symétrique dqui

fait intervenir

toutes les combinaisons des

_produits

_{d’opérateurs}

_(voir

_{[Mandel 95],}

_p.

_541).

De manière

_générale,

on

f

(A)

rs

~

f

(N)

rs

bien

qu’on

ait :

Le classement en ordre

normal,

anti-normal ou

symétrique

étant

_unique,

il est

pos-sible d’établir une

correspondance

unique

entre les fonctions des

opérateurs

F

(N)

(â, â

~

)

et

F

(A)

_{(â, â}

_~

₎

d’une

_part

et les fonctions de la variable

_complexe

_03B1,

F

(N)

_{(03B1, 03B1*)}

et

F

(A)

_(03B1,

_03B1*)

d’autre

_part.

Cette

_{correspondance}

est

_simplement

faite en

remplaçant

dans les

_expressions

ordonnées 2.22 et 2.23 â _par 03B1 et

â

~

_{par 03B1*.}

Dans nos calculs de la réduction du bruit _par des

_atomes,

nous avons choisi l’ordre

normal. C’est l’ordre le

_plus

couramment utilisé _par de nombreux auteurs _pour les calculs

_{d’optique quantique.}

2.2.4

_Statistique

du

_rayonnement

Nous allons étudier les différents

_types

d’états

_{qui apparaissent}

le

_plus

couramment

en

optique quantique

et voir

_quelles

sont leurs

_propriétés

_{statistiques.}

2.2.4.1 Etat de Fock

Comme nous l’avons

déjà

indiqué,

l’hamiltonien du

champ électromagnétique

se

est la somme des

â

~

k

â

k

qui

représentent

le nombre de

_photons

dans le mode k

multiplié

par

l’énergie

d’un

photon, 03C9

k

et d’une

énergie

correspondant

aux fluctuations

du vide.

Les états _propres de cet hamiltonien sont

_appelés

états de Fock ou états nombres.

On les notera

_|n

_k

_>.

Ces états forment une base

complète

et

_orthogonale

de

_l’espace

des états.

Ces états

_possèdent

un nombre de

photons

_parfaitement

_déterminé et n’ont donc

pas de fluctuations

d’amplitude.

Par

contre,

l’inégalité

de

_Heisenberg

_impose

des fluc-tuations de

_phases

infinies. Dans

_l’espace

des

_phases,

les états de Fock sont

_{représentés}

par un anneau

(figure 3).

Fig.

3: _{Représentation} de Fresnel d’un état de Fock

Ces états sont difficiles à créer

_{expérimentalement.}

Si on sait maintenant

produire

des états contenant un seul

photon

ou deux

photons

dans deux modes

différents,

il

est

_{beaucoup plus}

difficile d’obtenir

_{expérimentalement}

des états à

_{plusieurs photons.}

Les états à

_grands

nombres de

_photons

_que nous considérerons dans la suite sont

généralement

des

_{superpositions}

d’états de Fock.

2.2.4.2 Etats cohérents

Les états cohérents sont les états _propres de

_{l’opérateur}

â. Ils

_peuvent

être obtenus

18

où D

_(03B1)

=

exp

(03B1â

+

-

03B1*â)

et 03B1 est un nombre

complexe

quelconque.

On montre facilement _que le

_{développement}

d’un état cohérent dans la base des états de Fock est de la forme :

Cette

_statistique

est celle d’événements

_{indépendants}

_(comme

l’arrivée des

_photons

sur un

détecteur).

Supposons

_que la

probabilité

de détecter un

photon

pendant

un

intervalle 0394t ne

dépende

_que de la

longueur

de cet intervalle

_(selon

une loi

linéaire) :

où 03BA est une constante. On a alors :

A la limite 0394t ~

_0,

on a :

On introduit alors la fonction

_{génératrice :}

d’où :

Si on _suppose

qu’aucun photon

n’est arrivé à t =

0,

_{on a} P

(0, 0)

= 1 et P

(n, 0)

= 0

~n ~ 1,

d’où

_{G (s, 0)}

= 1. On en tire

Ceci montre _que la

_{statistique correspondante}

est une

statistique

poissonienne.

Par

_ailleurs,

on a :

03BAt

_correspond

donc au nombre _moyen de

_photons

détectés durant le

_temps

t noté

N.

On

_peut

donc écrire de manière

_{générale :}

Les états cohérents sont

_{particulièrement}

utiles car ils

correspondent

dans une

bonne

_{approximation}

au

_rayonnement

émis _par un laser très stable fonctionnant très

au-dessus du seuil.

2.2.4.3 Etats

_comprimés

Nous ne

parlerons

ici _que des états minimaux c’est à dire ceux _pour

lesquels

le

produit

des

_dispersions

est

_égal

à la valeur minimale :

Les états

_comprimés

sont

_générés

à

_partir

d’un

_opérateur

unitaire de

_compression

20

où 03B5 =

re

2i~

.

Si on considère le cas

où ~

=

0,

_on obtient :

où les variances sont évaluées dans l’état

_|03B5>

= (03B5)

_|0>.

L’état obtenu _par

_{l’opérateur}

de

_compression

est un état minimal. La surface d’incertitude a une dimension minimale

dans la direction de

_Ê

_p

_(dans

le cas où r est

positif)

et maximale dans la direction

orthogonale.

Dans le cas

où ~ ~

_0,

on _passe dans la base des

quadratures

(Ê

P,03B8

,

Ê

Q,03B8

)

définies

par

Ê

P,03B8

+

iÊ

Q,03B8

=

(Ê

P

+

iÊ

Q

)

e

-i~

.

On a alors:

Les variances sont alors:

L’état

_produit

dans ce cas est un état minimal dont l’axe de

compression

est

maintenant

_Ê

_P,03B8

_(toujours

dans le cas où r est

positif).

2.2.4.4 Etat _propre de la base

_{d’amplitude}

du

_champ

La base

_{d’amplitude}

du

_champ

a été introduite _par W.

Vogel

et al

_[Schubert

78][Vogel 90].

Elle

_correspond

à la base définie par les états propres de

l’opérateur

où

_{g (r)}

décrit la structure

_spatiale

du

_{champ :}

_{g(r) = |g(r)|e}

_i~g

_.

Les états _propres sont donnés _par la relation :

Ces états _propres sont des états

_{parfaitement comprimés}

sur une

quadrature.

En

effet,

si on _{pose ~g} = 0

(ce

qui

est

_toujours

_possible

en

changeant

les

_composantes

de

quadrature),

on a :

donc

_|E

_(r))

est un état _propre de

Ê

Q

et on

_peut

écrire :

Si on choisit la base des états de

Fock,

|E (r))

s’écrit :

où

H

n

est le

_polynôme

d’Hermite d’ordre

n

1

.

En

_fait,

Ê

est

_l’analogue

_pour un

champ

électrique

à

l’opérateur

_pour un

oscil-lateur

_harmonique.

En

_particulier,

_{l’expression}

de

_|E

_(r))

en fonction de

|n>

(2.47)

est

identique

à celle

_qui

relie

_|x>,

vecteur _propre

de

à

_|~

_n

_>,

vecteur _propre de

_{l’opérateur}

nombre de l’oscillateur

_harmonique

_{[Cohen-Tannoudji 77] :}

où

1

22

2.3

_{Représentation}

des états

du

_champ

2.3.1

Introduction

Comme nous l’avons

mentionné,

la

représentation

dans la base de Fock n’est _pas

commode à

_appliquer

aux

champs

_que nous considérons

puisque

ceux-ci sont

générale-ment des

_mélanges

d’états cohérents. Afin d’étudier les

_mélanges

d’états

_cohérents,

on

utilise le formalisme de la matrice

_densité,

_p. On définit de manière

_générale

la fonction

W(03C9,s) :

où C

_{(~, s)}

est la fonction

_{caractéristique :}

Les différentes

_{représentations}

du

_champ

habituellement utilisées sont des cas

par-ticuliers de la fonction W

_(03B1,

_s)

pour

lesquelles

on fixe une valeur du

paramètre

s. Selon

la valeur de s et pour certains états du

champ,

la fonction W

_peut

ne _pas être définie

pour tout 03B1. Ces

propriétés

sont

rappelées

sur la

figure

4.

Fig.

4: _Propriétés de W

_{(03B1, s)}

en fonction de s.

Comme nous le verrons _par la

suite,

la fonction W

(03B1, s)

est reliée à la

distribu-tion de

_probabilité

sur une

quadrature, P

03B8

(Ê

Q,03B8

)

[Vogel

89].

C’est cette

propriété

fondamentale

_qui

sera utilisée _pour la mesure

expérimentale

de la matrice densité

(voir

chapitre

5).

2.3.2

_{Représentation}

P

La

_{représentation}

P

_correspond

au cas s = +1.

On

_peut

par ailleurs montrer que la

représentation

P est

_simplement

le

Cette base étant

_{surcomplète,}

on

_peut

décomposer

la matrice densité

uniquement

sur

les

_projecteurs

_{diagonaux :}

La

_{représentation}

P est commode _pour l’évaluation de

_{produit d’opérateurs}

dans l’ordre

normal

2

:

On

_peut

ainsi

_interpréter

la fonction de corrélation au second ordre

g

(2)

(0)

en

fonction de P

_{(03B1) :}

où

_<|03B1|

₂

_>

₌

P

_(03B1)

_|03B1|

₂

d

2

03B1.

L’inconvénient de la

_{représentation}

P vient du fait _que la base des états cohérents

est

_{surcomplète :}

deux états cohérents ne sont _pas

orthogonaux

dans le cas

général.

La

représentation

P

_peut

donc être

_singulière.

Par

_exemple,

on voit immédiatement _que

la

_{représentation}

P d’un état cohérent est une fonction de Dirac. On utilise souvent la

représentation

de

_Wigner

_qui

ne

possède

_pas de

singularité.

2.3.3

_{Représentation}

de

_Wigner

C’est la

_première

des distributions de

_{quasi-probabilités}

à avoir été introduite en

mécanique quantique

[Wigner 32].

Elle

_correspond

au cas s = 0. Cette fonction est

toujours

définie mais pas

toujours positive,

c’est

_pourquoi

on

parle

de distribution de

quasi-probabilité.

Cependant,

dans le cas des états cohérents ou dans celui des états

comprimés monomodes,

la fonction de

_Wigner

est

_{toujours positive}

et bornée _par une

gaussienne

[Lütkenhaus 95].

Le théorème

d’Hadamard

3

_s’applique

alors et la fonction de

_{Wigner correspondante}

est nécessairement une

_gaussienne.

Pour un état cohérent

minimal,

la fonction de

_Wigner

est une

_gaussienne

de révolution centrée autour de la

valeur moyenne du

champ.

La fonction de

Wigner

d’un état

comprimé

minimal est une

2 _Cette

propriété est _{parfois appelée} Théorème _{d’Equivalence Optique}

_{[Mandel 95][Davidovich 96].}

3

L’énoncé de ce théorème est le suivant .

Toute fonction

_{f (z)}

_analytique sur tout le plan complexe

(c’est

à dire développable en série

entière),

qui n’a aucun zéro et dont le carré du module est borné par la fonction exp

(-|z|

2

)

est nécessairement

24

gaussienne

avec des

_largeurs

à mi-hauteur différentes suivant les directions et

_toujours

centrée autour de la valeur moyenne du

champ.

L’intérêt de la fonction de

_Wigner

est de faciliter le calcul des moyennes de

produits

dans l’ordre

_symétrique.

La fonction de

_Wigner

est reliée

_simplement

à la surface d’incertitude dont nous avons

parlé

précédemment. Ainsi,

on a :

avec

<03B1

+

_03B1*>

₌

_(03B1’

+

_03B1’*)

W

_(03B1’)

d

2

03B1’.

Dans le cas d’un état cohérent ou d’un état

comprimé minimal, l’équation

2.54b montre _que la surface d’incertitude

_peut

être vue comme le contour de la fonction de

_Wigner

à

_1/e.

Par

_ailleurs,

la fonction de

_Wigner

est

reliée de manière

_simple

aux distributions de

probabilité

des

_composantes

de

quadra-tures

_{[Kühn 94] :}

où P

03B8

(Ê

Q,03B8

)

désigne

la distribution de

_probabilité

de la

_quadrature

Ê

Q,03B8

et

2.4

Réalisation

_{expérimentale}

d’états

_comprimés

du

_rayonnement.

2.4.1

Introduction

Depuis plus

d’une dizaine

_d’années,

de nombreuses

_expériences

visant à obtenir

expérimentalement

des états

_comprimés

ont été réalisées. On

_peut

classer ces méthodes en

plusieurs

familles:

- méthodes basées

sur le _pompage

régulier

d’un laser:

lorsqu’on

_pompe un laser de

manière

_régulière,

la

_statistique

des

_photons

émis

_peut

être

_{sub-poissonienne}

_[Golubev

84].

En alimentant une diode laser avec un courant

régulier,

on

_peut

donc obtenir un

faisceau

_comprimé

_{[Machida 88].}

- méthodes basées

sur une interaction non-linéaire de

_type

~

(2)

.

- méthodes basées

sur une interaction non-linéaire de

_type

~

(3)

.

Nous mentionnerons brièvement la méthode de réduction de bruit _par

interac-tion non-linéaire de

_type

_~

₍₂₎

_.

_Ensuite,

nous montrerons comment un

milieu ~

(3)

est