Description analytique des phénomènes acoustophorétiques, en solutions et suspensions

HAL Id: tel-01408678

https://tel.archives-ouvertes.fr/tel-01408678

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

Description analytique des phénomènes

acoustophorétiques, en solutions et suspensions

Simon Gourdin

To cite this version:

Simon Gourdin. Description analytique des phénomènes acoustophorétiques, en solutions et suspen-sions. Chimie-Physique [physics.chem-ph]. Université Pierre et Marie Curie - Paris VI, 2015. Français. �NNT : 2015PA066720�. �tel-01408678�

Thèse de doctorat

Pour l’obtention du grade de docteur

de l’Université Pierre et Marie Curie

École doctorale de Chimie Physique et Chimie Analytique

Description analytique des phénomènes acoustophorétiques

en solutions et suspensions.

Simon Gourdin

Directeur de thèse : Olivier Bernard

Soutenue le 21 septembre 2015 devant un jury composé de :

M. Dick Bedeaux . . . Rapporteur M. Werner Kunz . . . Rapporteur Mme Claire Chassagne . . . Examinateur M. Jean-François Dufrêche . . . Examinateur M. Emmanuel Maisonhaute . . . Examinateur M. Thomas Zemb. . . Examinateur Mme Marie Jardat . . . Co-encadrant de thèse M. Olivier Bernard . . . Directeur de thèse

Table des matières

I

Introduction générale

3

II

Historique des approches existantes et bibliographie

cri-tique

9

1 1933 : Prédiction de l’acoustophorèse par P. Debye 10

1.1 Résumé de l’article de P. Debye . . . 10

1.1.1 Description qualitative . . . 10

1.1.2 Equations à résoudre . . . 11

1.1.3 Résolution des équations . . . 12

1.1.4 Ordres de grandeur . . . 14

1.1.5 Réécritures de l’expression de Debye . . . 15

1.2 Discussion physique du phénomène . . . 16

1.2.1 Démonstration de l’expression de Debye en terme de courants . . 16

1.2.2 Dépendance du signal en concentration . . . 19

Etablissement des limites . . . 19

Limite des hautes concentrations . . . 20

Limite des basses concentrations. . . 21

1.3 Conclusion sur l’article de Debye . . . 21

2 Développements de l’acoustophorèse jusqu’aux années 1990 22 2.1 Inclusion des corrections dépendant de la concentration par Oka . . . . 22

2.1.1 Principe de la modification . . . 22

2.1.2 Force électrophorétique . . . 23

2.1.3 Force de relaxation électrique . . . 24

2.1.4 Pertinence de la démarche d’Oka . . . 25

2.2 Introduction des forces de pression et de diffusion par Hermans . . . 27

2.2.1 Résumé de l’article . . . 27

2.2.2 La force de pression . . . 28

Expression de la force de pression . . . 28

Argument qualitatif pour son inclusion . . . 28

Effet de la force de pression sur l’expression de Debye . . . 29

2.3 Unification du jeu de forces par Bugosh, Yegear et Hovorka . . . 29

2.4 Utilisation de ce jeu de forces par Zana et Yeager . . . 30

2.4.1 Obtention "douteuse" de l’expression d’Hermans . . . 30

2.4.2 La question du volume des ions . . . 31 iii

TABLE DES MATIÈRES iv

3 1995 : Théorie moderne des forces correctives, développée au

labora-toire PHENIX 32

3.1 Contexte et introduction . . . 32

3.2 Cas de la force de pression . . . 33

3.3 Approche proposée pour le calcul des forces correctives . . . 34

3.3.1 Force de relaxation électrique . . . 34

3.3.2 Force hydrodynamique . . . 35

3.3.3 Théorie MSA . . . 37

3.3.4 Accord entre théorie et expérience . . . 38

4 Développement d’un nouvel appareil au laboratoire PHENIX 39 4.1 Contexte . . . 39

4.2 Description sommaire de l’appareil . . . 40

4.3 Phase du signal mesuré . . . 40

4.4 Comparaison avec la mesure de la conductivité . . . 41

5 Bilan des approches précédentes 43

III

Nouvelle approche pour l’acoustophorèse des solutions

d’électrolytes

47

6.1.1 Réponse aux objections de Durand-Vidal . . . 49

6.1.2 La force de pression est nécessaire pour rendre compte des résultats expérimentaux . . . 52

6.2 Absence d’effet de la relaxation électrique . . . 55

6.2.1 Approche qualitative . . . 55

6.2.2 Modification des équations de Durand-Vidal . . . 56

6.2.3 Ordres de grandeur . . . 56

6.3 Absence des forces de diffusion . . . 57

6.4 Calcul et effets de la correction hydrodynamique . . . 59

6.4.1 Calcul de la correction hydrodynamique . . . 59

Modification de la correction hydrodynamique . . . 59

Modification plus rigoureuse de la correction hydrodynamique . . 60

6.4.2 Effet de la correction hydrodynamique sur l’amplitude du signal . . 61

6.4.3 Evolution du potentiel à haute concentration . . . 63

6.5 Calcul approché de la correction hydrodynamique . . . 67

6.5.1 Théories analytiques . . . 67

6.5.2 Convention sur les rayons . . . 68

6.5.3 Comparaison entre théorie et expérience . . . 68

6.5.4 Méthode semi-numérique . . . 70

v TABLE DES MATIÈRES

7 Résultats nouveaux sur les systèmes à trois espèces ioniques 72

7.1 Jeu de forces considéré . . . 73

7.1.1 Correction hydrodynamique . . . 74

7.1.2 Force de relaxation électrique . . . 74

7.1.3 En résumé . . . 84

7.2 Formulation auto-cohérente des forces correctives . . . 85

7.2.1 Principe de la procédure de bouclage . . . 85

7.2.2 Effet de la procédure . . . 87

7.3 Exemple d’un nano-colloïde : le dodécatungstosilicate de potassium . . . 90

7.3.1 Comportement sans les corrections . . . 90

7.3.2 Effet des corrections . . . 92

8 Application de l’acoustophorèse à d’autres systèmes 96 8.1 Acoustophorèse des liquides ioniques . . . 96

8.1.1 Théorie . . . 96

Equations du mouvement et résolution . . . 97

Sens physique de la formule établie . . . 99

8.1.2 Expériences et interprétation d’icelles . . . 100

Renormalisation des données. . . 100

8.2 Acoustophorèse des surfactants . . . 101

8.2.1 Bibliographie . . . 102

8.2.2 Un modèle simple . . . 102

8.2.3 Prédiction du signal d’acoustophorèse . . . 104

IV

Passage des théories des électrolytes aux théories des

col-loïdes

111

9.1.1 Validité du modèle primitif . . . 112

9.1.2 La théorie MSA . . . 113

Approximation HNC . . . 114

Approximation de Percus-Yevick . . . 114

Approximation MSA . . . 115

Approximation de Debye-Hückel . . . 116

Approximation de Debye-Hückel étendu . . . 117

MSA : une synthèse de Percus-Yevick et de Debye-Hückel. . . 117

9.1.3 Qualités et limites de l’approximation dans le calcul du potentiel acoustophorétique . . . 118

Nano-colloïde et ses contre-ions . . . 118

Nano-colloïde en solution d’électrolyte . . . 120

Lien entre les fonctions de corrélation totale HNC et MSA . . . 121

Comparaison entre des simulations et MSA. . . 122

TABLE DES MATIÈRES vi

Mobilités électriques . . . 122

Potentiel acoustophorétique . . . 124

Conductivité . . . 125

Rayons utilisés . . . 125

Validité de la version simplifiée de MSA pour le chlorure de baryum126 9.2 Validité de l’équation différentielle décrivant la relaxation . . . 127

9.2.1 Vitesse hydrodynamique locale . . . 128

9.2.2 Densité locale en ions . . . 129

10 Différences principales entre les ions et colloïdes 131 10.1 Brève bibliographie sur les colloïdes . . . 131

10.1.1 La question de la mobilité électrique . . . 131

10.1.2 La mesure de phénomènes électroacoustiques . . . 132

10.1.3 Les théories dynamiques des phénomènes électroacoustiques . . . 132

10.2 Ions et colloïdes à l’équilibre . . . 133

10.2.1 Ion idéal . . . 133

10.2.2 Ion quasi-idéal . . . 134

10.2.3 Colloïde idéal . . . 134

10.3 Ions et colloïdes sous un champ électrique . . . 135

10.3.1 Ion idéal . . . 136

10.3.2 Ion quasi-idéal . . . 136

10.3.3 Colloïde idéal . . . 137

Mobilité des colloïdes idéaux . . . 137

Tentative d’extension de la théorie vers les ions . . . 138

Conductivité des colloïdes idéaux . . . 141

Différence entre potentiel ζ fixé et charge fixée . . . 143

10.4 Potentiel de sédimentation . . . 143

10.4.1 Courant mécanique de sédimentation pour les ions idéaux. . . 144

10.4.2 Courant mécanique de sédimentation pour les colloïdes idéaux . . 145

10.5 Conclusion . . . 145

11 Calcul direct du potentiel de sédimentation dans la limite de Smolu-chowski 147 11.1 Calcul direct du courant mécanique . . . 147

11.2 Approche basée sur le calcul du dipôle créé . . . 149

11.2.1 Somme des dipôles à l’aide du théorème de Gauss . . . 151

11.2.2 Une autre manière de sommer les dipôles . . . 151

11.3 Origine de la différences entre les deux résultats . . . 152

V

Relations de réciprocité d’Onsager

155

vii TABLE DES MATIÈRES

13 Compatibilité des approches mécaniques avec les relations d’Onsager 166

13.1 Jeu de forces de Hermans . . . 166

13.2 Jeu de forces quelconque . . . 170

13.3 Jeu de forces d’Oka . . . 172

13.4 Jeu de forces proposé dans ce travail . . . 173

13.4.1 Cas particulier sans la relaxation électrique . . . 173

13.4.2 Cas où la relaxation électrique est prise en compte. . . 178

13.4.3 Cas où trois espèces ioniques sont présentes . . . 182

VI

Lien entre l’acoustophorèse, l’amplitude électrosonique,

et l’électrophorèse

184

14.1.1 Description qualitative . . . 186

14.1.2 Description quantitative . . . 187

15 Lien entre le flux de masse et la mobilité 190 15.1 Flux de masse, mobilités et masses volumiques . . . 190

15.1.1 Mobilité dans le référentiel des volumes . . . 191

15.1.2 Mobilité dans le référentiel de l’eau . . . 192

15.1.3 Mobilité dans le référentiel barycentrique . . . 192

15.2 Lien entre les mobilités pour des suspensions simples . . . 194

15.2.1 La mobilité dans le référentiel de la solution ne dépend pas des conditions de flux . . . 194

15.2.2 Lien entre mobilités et conditions de flux . . . 195

15.3 Application à l’acoustophorèse et à l’amplitude électrosonique des suspen-sions simples . . . 197

15.3.1 Acoustophorèse des suspensions simples . . . 198

15.3.2 Amplitude électrosonique des suspensions simples . . . 199

15.4 Formule générale pour l’acoustophorèse . . . 199

VII

Conclusion générale

203

VIII

Annexes

207

A.1.1 Equations générales et conditions aux limites . . . 209

A.1.2 Différence entre ce jeu d’équations et celui des ions . . . 210

A.1.3 Domaine de validité des solutions analytiques . . . 211

A.2 Conductivité électrique des suspensions colloïdales . . . 211

A.2.1 Relation de "continuité du courant électrique" . . . 212

TABLE DES MATIÈRES viii A.3 Vitesse et potentiel de sédimentation. . . 214 A.4 Potentiel de vibration des colloïdes et potentiel de vibration des ions en

suspension colloïdales diluées . . . 217

B Programme pour le calcul du potentiel acoustophorétique et de la

conduc-tivité 219

Table des figures

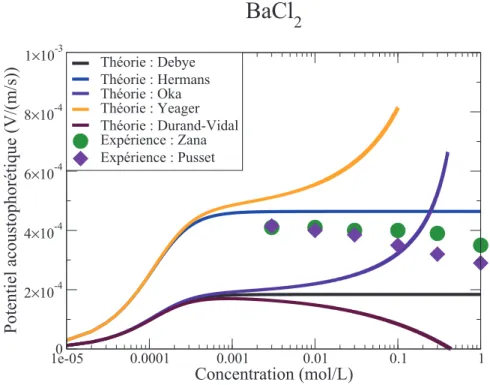
5.1 Potentiel acoustophorétique de BaCl2, théories et expériences. . . 44

6.1 Potentiel acoustophorétique des chlorures alcalins . . . 53

6.2 Potentiel acoustophorétique des chlorures alcalino-terreux . . . 54

6.3 Potentiel acoustophorétique des nitrates alcalino-terreux . . . 54

6.4 Evolution du potentiel acoustophorétique de CsCl avec la concentration . 65 6.5 Evolution du potentiel acoustophorétique de BaCl2 avec la concentration 65 6.6 Evolution du potentiel acoustophorétique de Mg(ClO4)2 avec la concentration 66 6.7 Potentiel acoustophorétique de BaCl2, théories et expériences. . . 69

7.1 Conductivité du chlorure de baryum, lin-lin . . . 88

7.2 Potentiel acoustophorétique du chlorure de baryum, lin-log . . . 89

7.3 Potentiel acoustophorétique du Keggin en solution de KCl, avec et sans corrections, lin-lin . . . 92

7.4 Différentes contributions au numérateur, lin-lin . . . 93

7.5 Répartition de la contribution du Keggin, lin-lin . . . 95

8.1 Courant mécanique du DTAB (unité arbitraires) en fonction de la concen-tration, données de Takata [1], lin-lin. . . 103

8.2 Conductivité des divers surfactants, calculée selon les hypothèses précitées, lin-lin. . . 106

8.3 Potentiel acoustophorétique de divers surfactants, calculé selon les hypo-thèses précitées, lin-log.. . . 106

8.4 Potentiel acoustophorétique de divers surfactants, calculé selon les hypo-thèses précitées, lin-log.. . . 108

8.5 Potentiel acoustophorétique de divers surfactants, calculé selon les hypo-thèses précitées, lin-lin. . . 108

9.1 Distributions des ions dans une solution de Keggin avec ses contre-ions. . . 121

9.2 Mobilités électriques calculées du chlorure et du baryum, en fonction de la concentration en chlorure de baryum . . . 123

9.3 Potentiel acoustophorétique calculé du chlorure de baryum, en fonction de la concentration. . . 124

9.4 Conductivité calculée du chlorure de baryum, en fonction de la concentration.126 9.5 Conductivité calculée du chlorure de baryum en fonction de la concentration, avec divers rayons. . . 127

Première partie

Introduction générale

4 Les suspensions colloïdales correspondent à un état dispersé de la matière, dans lequel des particules solides, les colloïdes, sont suspendues dans un milieu liquide. Les colloïdes sont des particules trop grandes pour être appelées ions, et trop petites pour sédimenter complètement. Ainsi, les colloïdes ont une taille comprise entre un et mille nanomètres.

Ils suscitent un fort intérêt, tant en milieu académique qu’industriel. C’est notamment par l’étude de suspensions colloïdales, avec les profils de sédimentation et le mouvement brownien, que Jean Perrin [2] a montré la validité de l’hypothèse atomique. Réaliser une suspension colloïdale est une méthode pour obtenir un liquide avec des propriétés classiquement réservées aux solides, comme c’est le cas pour les ferrofluides par exemple. L’intérêt industriel pour ces milieux vient des nombreuses applications des colloïdes, soit comme agent de charge, par exemple pour épaissir une peinture, soit comme état de base d’un produit courant, par exemple le ciment ou les eaux usées, soit comme une manière d’augmenter la surface spécifique, dans le cas de la catalyse. Des recherches sont également en cours sur la façon d’utiliser des colloïdes dans des dispositifs médicaux, notamment pour créer une hyperthermie locale [3].

Pour ces diverses applications, un point essentiel est la stabilité des suspensions. En effet, si un colloïde est trop petit pour sédimenter complètement, plusieurs colloïdes peuvent s’associer ensemble, formant ainsi un objet plus gros qui peut sédimenter. Cette association est dûe aux forces d’attraction de Van der Waals : la matière tend à s’attirer à courte portée, à l’échelle moléculaire, avec une énergie variant en l’inverse de la puissance sixième de la distance. Ainsi, quand deux colloïdes se heurtent en suspension, ils devraient rester associés ensuite. Cependant, les colloïdes sont généralement chargés, et comme deux objets de même charge se repoussent, les colloïdes assez chargés ne s’associent pas ensemble. Si des colloïdes sont gênants et doivent être éliminés, comme dans le cas des eaux usées, l’ajout de floculant permet entre autres de rendre les colloïdes neutres et leur permet de s’associer, de floculer, pour pouvoir être éliminés par sédimentation ou décantation. Le critère "assez chargé" est déterminé par le potentiel électrique ζ, ou potentiel zêta près de la surface du colloïde, plus précisément là où le liquide n’est plus fixé au colloïde : si le potentiel ζ est petit devant le potentiel électrique correspondant à l’énergie thermique, 25 mV à température ambiante, les colloïdes vont s’associer rapidement ; s’il est grand devant 25 mV, la suspension sera stable.

Pour caractériser les colloïdes, il faut donc, en plus de leurs tailles, de leurs densités et de leurs fractions volumiques, déterminer leurs potentiels de surface, ou leurs charges, les deux étant liés. Une des méthodes les plus efficaces pour cela est l’électrophorèse : un champ électrique E est appliqué, les colloïdes se déplacent à une vitesse v, une mobilité électrique µ = v/E en est déduite et cette mobilité est, dans les cas les plus simples, proportionnelle au potentiel électrique ζ : µ = ǫ0ǫr

η ζ, avec ǫ0ǫr la permittivité électrique du

milieu, et η la viscosité. Pour appliquer un champ électrique, il faut un milieu qui ne soit pas trop conducteur, sinon le courant électrique est important et le milieu s’échauffe. Pour déterminer la vitesse, les méthodes les plus courantes sont le suivi par laser et l’observation

5

visuelle sous microscope. Ces deux méthodes supposent que la solution soit assez diluée, sous peine de réflexions lumineuses multiples, et qu’elle soit transparente, sous peine de ne rien voir.

Pour l’étude de la peinture, du ciment, des ferrofluides ou des eaux usées, la méthode d’électrophorèse ne fonctionne donc pas. Une autre méthode existe, basée sur le couplage entre onde acoustique et champ électrique. Au début des années 30, Debye a proposé, pour déterminer les masses des ions, d’appliquer une onde sonore à une solution d’électrolyte. Si le milieu accélère vers la droite, et que le cation est lourd, comme dans le chlorure de césium, il reste en retard, donc vers la gauche, et crée un champ électrique vers la droite. Ainsi, un couplage existe entre onde sonore et champ électrique. Ce couplage permet la technique expérimentale appelée dans la littérature UVP, IVP, CVP, TVP et acoustophorèse, les sigles signifiants dans l’ordre potentiel de vibration ultrasonique, potentiel de vibration des ions, potentiel de vibration des colloïdes et potentiel de vibration total. Le potentiel électrique créé est appelé potentiel acoustophorétique. Le couplage peut aussi être vu ainsi : quand le milieu accélère vers la droite, le lourd cation se déplace vers l’arrière, par rapport à l’eau. Il y a donc un courant électrique allant vers la gauche. Il y a donc un couplage entre onde acoustique et courant électrique. Ce phénomène est appelé dans la littérature IVI, CVI et TVI, les sigles signifiant dans l’ordre intensité de vibration des ions , intensité de vibration des colloïdes et intensité de vibration totale. Un appareil commercial, le DT-1200, basé sur ce phénomène, est vendu par l’entreprise Dispersion Technology pour caractériser les colloïdes. Enfin, si un couplage existe entre onde de pression et champ électrique, un couplage inverse doit exister, la création d’une onde sonore par un champ électrique. Ce phénomène est appelé ESA, pour amplitude électro-sonique. Un appareil commercial basé sur ce couplage est vendu sous le nom d’Acoustosizer par l’entreprise Colloidal Dynamics et sert également à caractériser les colloïdes. Ces phénomènes de couplages électro-acoustiques pour l’études des ions et colloïdes ont suscité un fort intérêt au laboratoire PHENIX (PHysicochimie des Electrolytes et Nano-systèmes Interfaciaux). Ainsi, une thèse [4] portant notamment sur l’acoustophorèse des ions a été soutenue par Durand-Vidal en 1995, et le DT-1200 a été acheté pour caractériser les colloïdes fabriqués au laboratoire.

Ces deux appareils commerciaux présentent néanmoins divers défauts pour un usage de recherche. Le volume de l’échantillon est grand, de 50 à 120 mL, ce qui est gênant pour des suspensions coûteuses. Les suspensions doivent être assez concentrées, à au moins 1% massique. De plus, les appareils sont des "boîtes noires", ne donnant pas accès au signal brut. Et comme ils ont été conçus pour être utilisés sur des suspensions colloïdales, les résultats qu’ils donnent ne sont pas exploitables pour des solutions d’électrolytes, qui ne sont pas caractérisées par des particules de fraction volumique, de densité et de taille connues. Les théories sous-jacentes à ces appareils ont été publiées par morceaux, et leur compréhension en est ardue. Enfin, il faut noter que les résultats fournis par ces deux

6 appareils, le DT1200 et l’Acoustosizer, sont très différents pour un même échantillon.1 Enfin, un doute subsiste sur la quantité mesurée par chaque appareil, qui peut être affichée comme une mobilité électrique : est-ce la même mobilité pour les deux ?

Ces divers défauts, et la nécessité de caractériser les colloïdes dans les milieux opaques, ont conduit au financement d’une thèse CIFRE, financée par Cordouan, une PME bor-delaise spécialisée dans les appareils de caractérisation des colloïdes, et effectuée au laboratoire PHENIX par Raphaël Pusset. Sa thèse, soutenue en 2013, porte sur la mise au point d’un nouvel appareil de mesure du couplage acoustophorétique, qui utilise un faible volume (4 mL) de solution ou suspension, fonctionne sur des suspensions plus diluées, donne accès au signal brut et permet d’étudier ainsi des solutions d’électrolytes. Une qualité particulière de cet appareil est qu’il donne une valeur absolue du couplage acoustophorétique, et non une valeur relative de type "six fois la suspension de référence".

Dans ce contexte, l’objectif de ma thèse, commencée en 2012, est d’effectuer un travail théorique permettant la prédiction, la compréhension et l’interprétation du couplage acoustophorétique pour les solutions d’électrolytes et les suspensions colloïdales. La prédiction du signal sur des systèmes déterminés est en effet indispensable pour valider l’appareil de Pusset. Cet appareil affiche une valeur absolue, et non une valeur relative. Il faut donc trouver des systèmes pour lesquel la valeur absolue est connue, et non susceptible de dévier. La comparaison entre le signal théorique et le signal expérimental peut permettre de valider l’expérience pour les systèmes simples. Une fois l’appareil validé, il peut être utilisé sur des systèmes plus complexes pour valider d’autres aspects de la théorie. La prédiction quantitative du signal peut permettre également une compréhension qualitative de certains phénomènes. La compréhension est aussi indispensable, et peut porter sur les hypothèses de base, sur les intermédiaires de calcul, sur les approximations faites, ou encore sur les résultats obtenus. Il faut en effet comprendre pourquoi une hypothèse est posée, ou quel est le modèle sous-jacent, en lisant un article. Un calcul peut être mené d’une certaine manière pour des raisons physiques (ce terme représente un effet) ou mathématiques (si ce terme reste, aucun résultat ne peut être obtenu, donc il doit être retiré). Les approximations peuvent être plus ou moins pertinentes selon les cas, et il faut déterminer leurs implications physiques pour pouvoir soit les utiliser quand elles sont acceptables, soit constater qu’un résultat peut être plus ou moins fiable théoriquement, et pour savoir lesquelles peuvent être supprimées et lesquelles constituent des écueils. Un résultat numérique obtenu peut avoir une signification physique, et cette signification physique suppose une compréhension en profondeur du phénomène. L’interprétation est la reformulation d’un résultat en fonction de grandeurs connues dans la littérature, pour permettre une comparaison. En particulier, il faut déterminer le lien entre couplage acoustophorétique et mobilité électrique.

1. La conclusion d’une comparaison entre les deux appareils et les données de la littérature, faite par Pusset [5] dans sa thèse réalisée à PHENIX, est "si ce que fait l’Acoustosizer n’est pas totalement clair, ce que fait le DT1200 est incompréhensible".

7

La première partie de ce manuscrit consiste en une bibliographie commentée des théories dynamiques de l’acoustophorèse des solutions d’électrolytes. Cette étape de bibliographie est nécessaire pour comprendre qualitativement le phénomène et pour poser les bases d’une nouvelle théorie. Le chapitre 1porte sur l’article fondateur de Debye, qui est la prédiction de l’existence du couplage acoustophorétique et sa première tentative de prédiction quantitative, en utilisant des forces d’inertie, électrique et de friction des ions sur l’eau. Le commentaire que j’apporte permet une meilleure compréhension de l’article et du phénomène. Le chapitre 2 résume les modèles proposés à la suite de Debye, jusqu’aux années 90. Les divers modèles sont des extensions du modèle de Debye, avec la prise en compte de nouvelles forces, notamment de pression et des "corrections" liées à la concentration, comme en théorie classique des électrolytes. Le chapitre 3 présente les résultats obtenus par Durand-Vidal durant sa thèse, avec sa façon judicieuse d’écrire les corrections à l’idéalité, et son omission de la force de pression, sans aller au delà. Enfin, le chapitre4 décrit l’appareil mis au point par Pusset, et donne une interprétation expérimentale de la phase du signal, ainsi qu’une comparaison qualitative entre les techniques d’acoustophorèse et de conductivité.

Dans la deuxième partie je propose une nouvelle théorie dynamique de l’acoustophorèse des ions, qui consiste en l’assemblage des meilleurs éléments des théories précédentes : à savoir les forces inertielles, de pression, électrostatique et de friction sur l’eau, ainsi que les corrections à l’idéalité faites par Durand-Vidal. Dans le chapitre6, portant sur les sels simples, les forces précédentes sont discutées en détail, notamment la question du sens physique de la force de pression, l’existence ou non d’une diffusion induite par une onde acoustique, et l’absence d’effet d’une partie des corrections, ainsi que l’effet de la force de pression sur les corrections. Les implications de la nouvelle théorie sont présentées, notamment l’évolution du potentiel acoustophorétique en fonction de la concentration, qualitativement et quantitativement, et les éléments permettant de le calculer. Dans le chapitre7, je calcule les expressions des forces de corrections à utiliser pour l’acoustophorèse dans une solution contenant trois espèces différentes d’ions, en étendant les calculs faits au laboratoire sur la conductivité électrique. Une discussion physique du lien entre les différentes corrections existantes est menée, et permet d’affiner les calculs de conductivité comme d’acoustophorèse. Enfin, dans le chapitre 8, l’approche dynamique permet de proposer une méthode de détermination du volume des ions dans les liquides ioniques, et de prédire le potentiel acoustophorétique obtenu dans le cas de solutions micellaires.

La troisième partie vise à l’extension des théories des électrolytes vers les colloïdes. Dans le chapitre 9, j’étudie précisément le domaine de validité des calculs analytiques proposés dans la partie précédente par comparaison avec des méthodes numériques, pour conclure que la nouvelle théorie ne peut pas être "simplement" étendue aux colloïdes. Les chapitres suivants reprennent certains points de la littérature sur l’électrophorèse des colloïdes. J’insiste sur les différences fondamentales entre colloïdes et électrolytes au chapitre 10 puis redémontre l’expression du potentiel de sédimentation des colloïdes

8 idéaux. L’approche suivie a été développée de manière indépendante de la littérature, et permet une meilleure compréhension de l’effet de la polarisation interne des colloïdes. Un point bibliographique est fait en annexe A sur un auteur de référence en terme de colloïdes, Ohshima, et une erreur de raisonnement est mise à jour2

.

La quatrième partie est basée sur une approche complètement différente de l’élec-troacoustique : la thermodynamique irréversible et les relations de réciprocité d’Onsager. L’écriture de la création d’entropie dans les cas de la sédimentation et de l’acoustophorèse, présente dans la littérature, est rappelée au chapitre 12. Cela permet de montrer que l’acoustophorèse est bien une méthode apparentée à l’étude du potentiel créé par la sédimentation. Dans le chapitre 13, les différentes théories existant pour l’acoustophorèse des ions sont passées au crible des relations d’Onsager, ce qui n’avait pas été réalisé jusque là.

La cinquième partie, explicite les liens entre les diverses techniques expérimentales. Le chapitre 14 explicite le lien entre l’ESA et l’acoustophorèse, et propose un modèle simple du phénomène ESA, modèle sous-entendu et non explicité dans la littérature. Le chapitre 15 offre une interprétation de l’acoustophorèse en terme de mobilité électrique, et dissipe les zones d’ombres sur les référentiels. Il se termine par la proposition d’une procédure expérimentale de séparation du signal des ions et des colloïdes pour les suspensions.

Deuxième partie

Historique des approches existantes

et bibliographie critique

Chapitre

1

1933 : Prédiction de l’acoustophorèse

par P. Debye

En 1933, P. Debye [6] écrivit un article, dans le premier numéro du Journal of

Chemical Physics, dont le titre se traduit par "une méthode pour déterminer les masses

des électrolytes". Cet article, clair et bien écrit, présente les bases de l’acoustophorèse. L’article est en quatre parties : une description qualitative, les équations à résoudre, leurs résolutions et un ordre de grandeur. Dans ce qui suit, je commence par résumer l’article puis propose quelques commentaires.

1.1

|

Résumé de l’article de P. Debye

Dans un souci de clarté, les notations sont adaptées, en effet plusieurs conventions ont changé depuis 1933. Comme cet article fonde un domaine, il est sans bibliographie. Sa lecture est indispensable pour tout lecteur intéressé par le sujet.

1.1.1

|

Description qualitative

Debye commence par noter que, pour les électrolytes, l’inertie1 _{est le plus souvent} négligeable. En effet, les ions sont très petits, et donc ont un temps inertiel très petit, de l’ordre de 10−14_{s à 10}−13_{s, ce qui signifie que le mouvement de l’ion est en régime}

sur-amorti pour les excitations à des fréquences inférieures à celle de l’infrarouge. Si les ions avaient une masse rigoureusement nulle, ils suivraient parfaitement le liquide quand une onde acoustique est appliquée à une solution électrolytique. Cependant, les ions ayant une masse non-nulle, ils ne suivent que quasi-parfaitement le liquide. Si les ions positifs sont plus lourds que les ions négatifs, ils vont tendre à "rester en arrière" par rapport aux ions négatifs et vont donc créer un champ électrique. Debye affirme qu’ "il est bien évident que si cet effet est détectable et mesurable, il permettra d’avoir des certitudes sur la masse des ions, et ainsi de déterminer le nombre de molécules de solvant qui y sont liées".

1. Au sens d’existence d’un régime balistique pour le mouvement des ions.

11 1933 : Prédiction de l’acoustophorèse par P. Debye

1.1.2

|

Equations à résoudre

Les équations impliquées sont celles de Newton, de Maxwell-Gauss et de continuité, ou de conservation de la matière. Toutes les grandeurs, sauf mention contraire, dépendent de l’espace et du temps. La vitesse de l’eau, considérée comme très proche de celle de la solution, est imposée par l’onde acoustique. Ainsi, veau est une fonction sinusoïdale du

temps en tout point, et le mouvement des ions ne la modifie pas. Toutes les équations, sauf mention contraire, sont écrites dans le référentiel du laboratoire, supposé galiléen. L’équation de Newton, ou équation fondamentale de la dynamique, établit que la dérivée de la quantité de mouvement par rapport au temps est égale à la somme des forces extérieures, dans un référentiel galiléen :

mi

∂v_i ∂t =

Ø

F_iext (1.1)

avec mi la masse de l’ion i, et vi sa vitesse. Debye considère les forces de friction Ff ric et

électrostatique Felec_{. Pour un ion, elles s’écrivent :}

F_if ric = −kBT D0 i (v_i− v_eau) (1.2) et Felec = eiE (1.3)

avec kB la constante de Boltzmann, T la température en Kelvin, E le champ électrique. La

relation de fluctuation-dissipation a été utilisée pour écrire eq.1.2, avec D0

i le coefficient de

diffusion à dilution infinie. Le signe "-" signifie que quand un ion se déplace par rapport à l’eau, la friction s’oppose à ce mouvement. L’équation est écrite en fonction de la différence de vitesse entre l’ion et l’eau, elle pourrait également l’être entre l’ion et la solution. Les deux reviennent au même si la solution est diluée2

. ei est la charge de l’ion i, et peut

s’écrire ei = ezi, avec e la charge élémentaire et zi la valence de l’ion. L’équation de la

dynamique s’écrit donc :

mi ∂v_i ∂t = − kBT D0 i (vi− veau) + eiE (1.4)

Il n’y a pas de champ électrique imposé, le champ électrique est créé par l’accumulation locale d’ions. Le lien entre charge électrique locale et champ électrique est l’équation de Maxwell-Gauss : ∇_{· E =} ρelec ǫ0ǫr (1.5) = q iniezi ǫ0ǫr (1.6)

1933 : Prédiction de l’acoustophorèse par P. Debye 12 avec ρelec la charge électrique par unité de volume, en C.m−3, ǫ0 la permittivité électrique

absolue du vide, et ǫr la permittivité électrique relative du milieu. Et avec ni la

concentra-tion numérique en ions i. Cette concentraconcentra-tion numérique est égale à la concentraconcentra-tion en mol/L, multipliée par mille et par la constante d’Avogadro. L’unité est le m−3_.

Enfin, le dernier ensemble d’équations est la conservation de la matière, ou équation de continuité :

∂ni

∂t + ∇ · ji = 0 (1.7)

j_i est le flux numérique en espèce i. Son unité est m−2s−1, car ji = nivi.

S’il y a n espèces ioniques, il y a donc 2n+1 équations et 2n+1 inconnues (l’ensemble des concentrations ioniques, l’ensemble des vitesses des ions, le champ électrique) : il faut maintenant résoudre ce système d’équations.

1.1.3

|

Résolution des équations

Une hypothèse utile et courante est l’approximation des ondes planes progressives sinusoïdales. Cela permet de remplacer l’opérateur ∇ par uz_∂z∂ , avec uz le vecteur-unité

selon l’axe z, et de passer dans le domaine de Fourier, et de remplacer ∂

∂t par iω, avec

i2 _{= −1 et ω la pulsation.}3

La dérivée spatiale par rapport à la direction du problème,

u_z∂z∂ , devient alors une multiplication par −iq, avec q le vecteur d’onde4

. Les grandeurs dans les espaces réels et de Fourier sont notées de la même manière, afin de limiter le nombre de notations différentes, bien que Debye les ait très soigneusement distinguées. L’équation de la dynamique (eq.1.4) s’écrit alors :

(iωmi+ kBT D0 i )vi = kBT D0 i veau+ eiE (1.8) comme iωmi << k_DB0T

i , i.e. le temps inertiel est très petit comparé à la fréquence, la vitesse peut s’écrire : v_i = veau− iωmiDi0 kBT v_eau+ eiD 0 i kBT E (1.9)

Comme le temps inertiel est petit comparé à la fréquence, les ions sont en régime suramorti, et ont donc une vitesse en phase avec les forces appliquées, inertielles ou électrique.

Pour quelques lignes, la notation suivante est adoptée : ni = neqi + δni, avec neqi la

concentration à l’équilibre et δni la modification de la concentration induite par l’onde

acoustique. L’électroneutralité s’écrit alors q_ineq_i ei = 0. L’équation de Maxwell-Gauss

3. La notation i n’est pas parfaite. Elle ne désignera jamais un courant électrique. Quand une somme est faite sur i,q_i, c’est une somme sur les espèces présentes, et un facteur i dans la somme désigne

i2_{= −1, et peut donc toujours être sorti de la somme.}

13 1933 : Prédiction de l’acoustophorèse par P. Debye devient : − iq · E = q iδniei ǫ0ǫr (1.10) et l’équation de continuité :

iωδni− iq · ((neqi + δni)(vi− veau+ veau)) = 0 (1.11)

Elle peut être développée en :

iωδni = ineqi q· veau+ ineqi q· (vi− veau) + iq · (δni(vi− veau)) + iq · (δniveau) (1.12)

Le terme iq · (δni(vi− veau)) est négligé, car il est incompatible avec la réponse linéaire (il

dépend de manière quadratique de l’onde acoustique). Le dernier terme iq · (δniveau) est

petit. En effet, [iq · (δniveau)]/[iωδni] est de l’ordre de qveau/ω, autrement dit de l’ordre

du rapport de la vitesse du liquide veau sur la vitesse du son cs = ω/q . Pour une onde

acoustique d’une pression d’environ une atmosphère, le liquide se déplace à une vitesse de quelques cm/s, à comparer au km/s de l’onde acoustique. Ce terme est donc négligeable, de cinq ordres de grandeur. L’équation de continuité se simplifie alors en :

iωδni = ineqi q· veau+ ineqi q· (vi− veau) (1.13)

Pour relier les équations de Maxwell-Gauss et de continuité, il faut dériver l’équation de Maxwell-Gauss par rapport au temps (donc la multiplier par iω) :

− iqiωǫ0ǫr· E =

Ø

i

ei(iωδni) (1.14)

et y insérer l’équation de continuité :

−iqiωǫ0ǫr· E =

Ø

i

ei(ineqi q· veau+ ineqi q· (vi− veau)) (1.15)

Le termeq_iei(ineqi q· veau) est nul, du fait de l’électroneutralité. L’équation est simplifiée

de −iq5 : iωǫ0ǫrE = − Ø i neq_i ei(vi− veau) (1.16)

Cette équation sera commentée ultérieurement.Notons dès à présent que les δni ne servaient

qu’à l’établir. Pour la suite, la notation neq

i est aussi abandonnée, les ni désignant la

1933 : Prédiction de l’acoustophorèse par P. Debye 14 concentration locale qui est très proche, en valeur numérique, de la concentration moyenne

neq_i .

En insérant l’équation de Newton eq.1.9 dans l’équation précédente :

iωǫ0ǫrE = Ø i niei( iωmiDi0 kBT veau− eiDi0 kBT E) (1.17)

En mettant à gauche tous les termes en E (Ø

i

ni

eiD0i

kBT

+ iωǫ0ǫr)E = iωveau

Ø i nimi eiDi0 kBT (1.18) le champ électrique est obtenu :

E = iωveau q inimi eiD0i kBT iωǫ0ǫr+qinieieiD 0 i kBT (1.19) C’est l’expression de base du champ électrique créé par l’application d’une onde acoustique sur une solution d’électrolyte. Elle peut être réécrite en :

E = iωveau q inimiµ0i iωǫ0ǫr+q_inieiµ0i (1.20) avec µ0 i = eiDi0

kBT la mobilité électrique dite idéale.

1.1.4

|

Ordres de grandeur

Pour qu’une théorie soit utilisable, elle doit être reliée à l’expérience et à des grandeurs mesurables. Le plus simple est de mesurer un potentiel électrique. Le champ électrique est l’opposé du gradient du potentiel électrique Ψ

E= iqΨ (1.21)

En combinant avec l’expression de Debye : Ψ = ω qveau q inimiµ0i iωǫ0ǫr+qinieiµ0i (1.22) en notant que ω

qveau est le produit de la vitesse du son cs par l’amplitude de vitesse de

l’eau veau Ψ = csveau q inimiµ0i iωǫ0ǫr+q_inieiµ0i (1.23)

15 1933 : Prédiction de l’acoustophorèse par P. Debye En ordre de grandeur, l’équation précédente donne :

Ψ = csveau

m

e (1.24)

avec m une masse typique des ions, par exemple (10 − 100)g/mol, e étant la charge élémentaire, de l’ordre de 105_C/mol

Ψ veau = cs m e ≈ (10 −3_{− 10}−4_{)V /(m/s) (1.25)}

Le potentiel électrique par unité de vitesse de l’eau est donc de l’ordre de (1−10).10−4_{V /(m/s),}

ou, pour reprendre des notations plus anciennes, (1 − 10)µV/(cm/s). Pour une onde acous-tique avec une pression de l’ordre de l’atmosphère, le potentiel électrique créé a une amplitude de l’ordre de quelques microvolts, ce qui est mesurable.

1.1.5

|

Réécritures de l’expression de Debye

Ces réécritures ne sont techniquement pas de Debye, mais sont présentes dans la littérature depuis les début des années 30. L’équation 1.20 donne le lien entre champ électrique mesuré et accélération de l’eau sous l’effet d’une onde acoustique.

E = iωveau

q

inimiµ0i

iωǫ0ǫr+qinieiµ0i

(1.26) A la fin du manuscrit, des aspects thermodynamiques seront étudiés, et il faudra pour cela travailler en gradient de pression. L’équation de l’acoustique, ou équation de Newton, s’écrit, dans le référentiel du laboratoire, pour une solution diluée :

ρ∂veau

∂t = −∇P (1.27)

avec P la pression et ρ la masse volumique de la solution ou de l’eau, qui sont proches. L’expression de Debye devient :

E = −∇P ρ q inimiµ0i iωǫ0ǫr+qinieiµ0i (1.28) En notant que E = −∇Ψ, cela donne :

Ψ = P ρ q inimiµ0i iωǫ0ǫr+q_inieiµ0i (1.29) Cette écriture est utilisée au laboratoire, car l’amplitude de pression est connue et l’amplitude de potentiel électrique mesurée. Les deux doivent être exprimées de la même manière, crête-crête, base-crête ou valeur quadratique moyenne.

1933 : Prédiction de l’acoustophorèse par P. Debye 16 Enfin, le lien peut être fait entre amplitude de potentiel électrique et amplitude de vitesse, pour retrouver les formalismes utilisés depuis Debye jusqu’à l’an 2000 [7] [8], comme à l’équation1.22 Ψ = csveau q inimiµ0i iωǫ0ǫr+q_inieiµ0i (1.30) Les quatre formules précédentes peuvent être écrites en ne conservant que les modules, car le module donne l’amplitude du signal final, qui est la donnée la plus facile à mesurer. Pour la dernière, par exemple :

|Ψ| = csveau --q_inimiµ0i --iωǫ0ǫr+qinieiµ0i -- (1.31) = csveau --q_inimiµ0i -ð (ωǫ0ǫr)2+ (q_inieiµ0i)2 (1.32) Ces différentes formules peuvent être plus ou moins adaptées à la théorie ou à l’expé-rience. La première version 1.26 est pédagogique, la deuxième 1.28 utile en thermodyna-mique, la troisième1.29est proche de celles utilisées par les colloïdistes et la quatrième 1.30 est utilisée depuis Debye pour les solutions ioniques. Tout potentiel ou champ électrique, dû à une vitesse, accélération ou pression de l’eau sera appelé "potentiel acoustophorétique" ou "signal".

1.2

|

Discussion physique du phénomène

Pour aller au delà des travaux de Debye, il est utile d’interpréter l’expression obtenue et d’en extraire le sens physique. En démontrant cette formule autrement, l’interprétation est simplifiée. Les interprétations qui suivent ne figuraient pas dans l’article original de Debye, et elles ont été principalement faites durant la thèse, de manière indépendante. Comme elles aident à comprendre le phénomène, je les rapporte ici et non dans une partie séparée.

1.2.1

|

Démonstration de l’expression de Debye en terme de

courants

L’équation de Maxwell-Gauss (1.5) peut être combinée directement à l’équation de conservation de la charge électrique. Soit Maxwell-Gauss

∇_{· E =} ρelec ǫ0ǫr

17 1933 : Prédiction de l’acoustophorèse par P. Debye L’équation est dérivée par rapport au temps, et les dérivées sont permutées :

∇_·∂E ∂t = 1 ǫ0ǫr ∂ρelec ∂t (1.34)

Soit l’équation de conservation de la charge :

∂ρelec

∂t + ∇ · I = 0 (1.35)

avec I le courant électrique volumique, en C.m−2_.s−1_.

En combinant les deux équations précédentes :

∇_·∂E ∂t = −

1

ǫ0ǫr

∇_{· I} (1.36)

L’opérateur divergence peut être enlevé, le phénomène est unidimensionnel. La différence entre deux vecteurs ayant une même divergence est un vecteur constant, qui est nul grâce aux symétries du problème. On a donc :

ǫ0ǫr

∂E

∂t = −I (1.37)

En notant que le courant électrique est la somme des déplacements de charges :

I = Ø i n_ieivi (1.38) = Ø i n_iei(vi− veau) (1.39)

l’équation1.16 est retrouvée.

Le courant électrique I a deux origines physiques : une origine mécanique et une origine électrique. I = Ielec+ Iméca. L’origine électrique correspond simplement à la loi

d’Ohm, qui s’écrit :

I_elec = KE (1.40)

avec K la conductivité. Dans le modèle de Debye, la conductivité s’écrit :

K =Ø

i

nieiµ0i (1.41)

L’origine mécanique correspond au mouvement relatif des ions les uns par rapport aux autres. Par exemple, un ion très lourd tend à rester immobile, i.e. en retard, quand l’eau accélère. L’équation décrivant cela peut être obtenue dans le référentiel de l’eau. En effet, dans le référentiel de l’eau, les ions subissent une force d’inertie d’entraînement de valeur −mi∂v_∂teau i.e. −iωmiveau dans nos notations. Cette force d’inertie d’entraînement induit

1933 : Prédiction de l’acoustophorèse par P. Debye 18 une vitesse relative de l’ion par rapport à l’eau de −iω Di

kBTmiveau. La différence de vitesse entre les ions crée un courant électrique noté Iméca.

I_méca = Ø i niei(vi− veau)E=0 (1.42) = Ø i nimi(− ∂veau ∂t )ei Di kBT (1.43) = −∂veau ∂t Ø i nimiµ0i (1.44)

La notation "indice E = 0" signifie "avec un champ électrique nul". Le terme ǫ0ǫr∂E_∂t

de l’équation1.37 peut aussi être vu comme un courant : c’est le courant de déplacement de Maxwell. Ce courant est très largement dû à la polarisation de l’eau, la permittivité électrique de l’eau étant grande devant celle du vide. Ce courant est noté Idepl, ce qui

permet de réécrire l’équation 1.37 :

I_depl+ I = 0 (1.45)

Idepl+ Ielec+ Iméca= 0 (1.46)

C’est une sorte de relation de courant nul, bien que la vraie condition de courant nul soit

I = 0. En effet, Idepl n’est pas un courant électrique au sens strict du terme.

Dans le domaine de Fourier, le courant de déplacement devient :

I_depl= iωǫ0ǫrE (1.47)

Il peut être combiné au courant d’origine électrique :

I_depl+ Ielec = (iωǫ0ǫr+

Ø

i

nimiµ0i)E (1.48)

= (iωǫ0ǫr+ K)E (1.49)

= K∗E (1.50)

K∗ _{est la conductivité complexe, et est la somme de la conductivité réelle et d’une}

"conductivité de polarisation" : K∗ _{= K + iωǫ}

0ǫr. Cette conductivité complexe ne signifie

pas que les ions ne suivent pas le champ électrique. C’est une manière d’inclure dans la conductivité les termes de polarisation.

Le champ électrique vaut donc, sous l’effet d’une onde acoustique, d’après eq.1.46 et eq.1.50 :

E = −Iméca

19 1933 : Prédiction de l’acoustophorèse par P. Debye Cette équation est identique à l’équation 1.20, dite expression de Debye, si les expres-sions de Iméca et de K∗ y sont injectées. L’équation est ici en fait plus générale que le

modèle de Debye.

1.2.2

|

Dépendance du signal en concentration

Dans cette partie, je discute de l’évolution du champ électrique créé par l’onde acoustique en fonction de la concentraiton en électrolyte et je propose une interprétation de la conductivité complexe en terme de temps de Maxwell-Wagner. L’aspect dépendance en concentration est connue depuis les années 30 mais l’interprétation que je propose est nouvelle.

Etablissement des limites

Le courant Iméca est proportionnel à la concentration en ions. Si la concentration

en ions double, le nombre d’ions double et leurs vitesses relatives restent les mêmes, le courant double donc. L’équation 1.44 est rappelée :

Iméca = − ∂veau ∂t Ø i nimiµ0i (1.52)

La conductivité réelle K est aussi proportionnelle à la concentration en ions.

K =Ø

i

nieiµ0i (1.53)

La "conductivité de déplacement" vaut iωǫ0ǫr, et ne dépend donc pas de la concentration.

Le module de la conductivité complexe |K∗_{| =}ð_K2_{+ (ωǫ}

0ǫr)2 est donc une constante à

basse concentration, une fonction linéaire de la concentration à haute concentration, avec une fonction de raccordement entre les deux.

En reprenant l’équation 1.51 :

E = −Iméca

K∗ (1.54)

On constate que :

– A basse concentration, le numérateur est proportionnel à la concentration et le dénominateur en est indépendant : le champ électrique est proportionnel à la concentration, à onde acoustique donnée.

– A haute concentration, le numérateur est proportionnel à la concentration, et le dénominateur l’est également. Le rapport des deux est donc constant, et le champ électrique obtenu ne dépend pas de la concentration, à haute concentration. Il y

1933 : Prédiction de l’acoustophorèse par P. Debye 20 a un "plateau" pour le champ électrique en fonction de la concentration, à haute concentration.

Que signifient haute et basse concentrations ? La limite entre les deux est la concentra-tion telle que les parties réelles et imaginaires de la conductivité complexe sont égales :

ωǫ0ǫr = Ø i nieiµ0i (1.55) autrement écrit, ωǫ0ǫr K = 1 (1.56) or ǫ0ǫr

K = τM W est le temps de Maxwell-Wagner. Le temps de Maxwell-Wagner est le

temps associé à la dissipation des charges électriques dans un conducteur. Il s’obtient classiquement en combinant les équations de Maxwell-Gauss, de conservation de la charge et d’Ohm : ∂ρelec ∂t = − K ǫ0ǫr ρelec (1.57)

Ce temps est inversement proportionnel à la concentration. A haute concentration, le produit ωτM W est petit. La haute concentration est donc équivalente à une basse

fréquence, du point de vue électrique. De même, a basse concentration est équivalente à une haute fréquence, du point de vue électrique. Dans les expériences faites au laboratoire, la fréquence est de 1MHz. La limite entre haute et basse concentration est ainsi de l’ordre de 0,4 mM pour le chlorure de potassium, et de 0,25 mM pour du chlorure de baryum. Limite des hautes concentrations

Comme la haute concentration est équivalente à une basse fréquence, une condition de courant nul I = 0 s’applique. En effet, à basse fréquence, si le courant n’est pas nul, les charges s’accumulent, et leur accumulation crée un champ électrique qui en est proportionnel et donc très important, ce qui est non physique. Cela peut également être vu comme l’interdiction d’avoir une accumulation de charge dans un conducteur en situation quasi-statique, elle doit se disperser sous l’effet de son propre champ électrique. Le courant d’origine mécanique Iméca est donc complètement compensé par le courant Ielec. Cela est

bien équivalent à avoir Idepl << Ielec dans l’équation 1.46. Pour fixer les idées, faisons

l’hypothèse "le cation est nettement plus lourd que l’anion, les deux ayant des mobilités semblables". Cela correspond par exemple au cas du chlorure de césium. Dans ce cas, si le liquide accélère vers la droite, les cations vont, relativement aux anions, vers la gauche, car ils sont plus lourds. Le courant électrique résultant Iméca est donc vers la gauche.

Pour compenser Iméca, Ielec est dirigé vers la droite. Le champ électrique créant ce dernier

21 1933 : Prédiction de l’acoustophorèse par P. Debye l’équation1.20, le résultat est retrouvé :

E = iωveau q inimiµ0i q inieiµ0i (1.58) avec q_inimiµ0i ≥ 0 et iωveau l’accélération de l’eau (la dérivée temporelle étant, par

convention, la multiplication par +iω). Limite des basses concentrations

Comme la basse concentration est équivalente à une haute fréquence, le système n’a pas le temps de réagir électriquement. Pour être précis, les charges transportées n’ont pas le temps d’être dispersées par le champ électrique qu’elles créent et donc Idepl >> Ielec . Si

une surface fictive, orthogonale à l’onde acoustique est considérée, tant que Iméca est vers

la droite, de plus en plus de charges positives vont vers la droite et le champ électrique est de plus en plus intense vers la gauche. C’est lorsque le courant électrique Iméca s’annule,

après avoir été vers la droite, que le champ électrique a la plus grande valeur et est dirigé vers la gauche. Cela signifie que le champ électrique a 90◦_{, ou π/2, d’avance sur}

le courant mécanique. Dans le cas du chlorure de césium, le courant mécanique étant en opposition de phase avec l’accélération, le champ électrique a alors 90◦_{, ou π/2, de retard}

sur l’accélération. En reprenant l’équation 1.20, le résultat de proportionalité du champ créé et de la concentration est retrouvé :

E = iωveau q inimiµ0i iωǫ0ǫr (1.59) avecq_inimiµ0i ≥ 0

1.3

|

Conclusion sur l’article de Debye

Les travaux fondateurs de Debye permettent de comprendre le phénomène d’acousto-phorèse, qui est la création d’un champ électrique par une onde sonore. Ce phénomène peut être décrit comme la solution des équations du mouvement pour les ions, couplées aux équations de continuité et de Maxwell-Gauss. Il peut être interprété comme l’effet de la création d’un courant électrique par l’onde acoustique, avec la réaction de la solution au courant électrique créé. Ce courant vient des différences de masses entre les ions, qui donne des différences de forces inertielles et donc de vitesses. Le signal dépend linéairement de la concentration à grande dilution, et en est indépendant à moyenne et faible dilution. Améliorer la théorie de Debye peut se faire de deux manières : en décrivant mieux la mise en mouvement des ions par une onde acoustique d’une part, et en tenant compte des interactions entre les ions d’autre part. Ces deux axes ont été explorés dans la littérature au cours des années 30, mais aussi plus récemment.

Chapitre

2

Développements de l’acoustophorèse

jusqu’aux années 1990

Le premier développement théorique de l’acoustophorèse a eu lieu dans les années 30. Suite à l’article de Debye de 1933, Oka [9] propose, pour l’acoustophorèse des ions, d’inclure des forces correctives dépendant de la concentration, les forces de relaxation électrique et hydrodynamique. Hermans [10], en 1938, considère que ces forces sont justifiées mais petites, qu’il est aussi possible d’inclure la force de diffusion et qu’il faut surtout inclure la force de pression, pour l’acoustophorèse des colloïdes. En 1947, Bugosh, Yeager et Hovorka [11] combinent les suggestions de Hermans et d’Oka, et ajoutent également la force de pression pour les ions. Ils tentent de mesurer le potentiel acoustophorétique pour divers sels, de manière peu convaincante [12], montrant néanmoins l’existence d’un effet dépendant du sel utilisé et peu de sa concentration. Enfin, Yeager et Zana [7], identifient le volume impliqué dans la force de pression au volume molaire partiel, et font une série de mesures du potentiel acoustophorétique de bonne qualité, avec un bruit inférieur au signal d’intérêt, et en utilisant diverses astuces expérimentales. Le plan de ce chapitre est chronologique, et seuls les aspects théoriques sont décrits (le chapitre 3 de la thèse de Pusset [5] contient un historique expérimental).

2.1

|

Inclusion des corrections dépendant de la

concentration par Oka

2.1.1

|

Principe de la modification

Dans cet article, très clair, "Fortpflanzung der ultrakurzen Schallwellen durch einen Elektrolyten" [9], compréhensible par un non germanophone, Oka inclut des forces correc-tives s’exerçant sur les ions en plus des forces déjà utilisées par Debye. Les forces de Debye étaient la friction, la force électrostatique et l’inertie. Oka rajoute deux forces, la force hydrodynamique, ou électrophorétique et la force de relaxation électrique. Le nouveau jeu

23 Développements de l’acoustophorèse jusqu’aux années 1990 de forces s’écrit donc :

mi ∂veau ∂t = eiE− kBT D0 i

(vi− veau) + δFihyd+ δFirel (2.1)

Les forces hydrodynamique et de relaxation électrique dépendent a priori linéairement du champ électrique et de l’accélération :

δF_ihyd= αhyd_i E− β_ihyd∂veau

∂t (2.2)

et

δF_irel = αrel_i E− β_irel∂veau

∂t (2.3)

Quelles sont ces deux forces ? Pourquoi vouloir les ajouter, et est-ce judicieux ?

Dans un article [13] fondateur de la théorie du transport dans les électrolytes, Onsager1 a proposé, en 1932, pour rendre compte de l’évolution de diverses grandeurs avec la concentration, de prendre en compte l’influence des couplages hydrodynamiques (force électrophorétique) et des interactions électrostatiques (force de relaxation électrique) sur le déplacement des ions. Cet article d’une centaine de pages traitait de la conductivité électrique, de la viscosité et de la diffusion. Si certains passages sont clairs, d’autres sont particulièrement ardus. Une explication qualitative de l’origine des deux forces, et des ordres de grandeur, sont repris ici. Pour le calcul précis de ces forces correctives, un développement sera fait dans le chapitre 9. Le livre de Fuoss et Accassina [17], contenant beaucoup de calculs mais moins que les articles d’Onsager, développe les arguments présentés ici.

2.1.2

|

Force électrophorétique

La force électrophorétique, ou hydrodynamique, est assez intuitive. Tout ion est entouré d’une atmosphère ionique. Dans de l’eau salée, autour d’un sodium, il y a en moyenne une charge négative. Cette charge négative vient aussi bien d’un excès local de chlorure que d’un défaut local de sodium. Suivant les travaux de Debye et Hückel [16], cette atmosphère ionique, correspondant à la compensation de la charge, est à une distance κ−1 _{de l’ion}

central supposé ponctuel, avec κ−1 _{la longueur de Debye :}

κ2 = e 2 ǫ0ǫrkBT Ø i nizi2 (2.4)

1. Cet article en anglais est une extension d’un double article, publié en allemand en 1926 [14] et 1927 [15]. Dans ce double article, Onsager traitait de la conductivité des sels simples. Ce double article est une amélioration de la théorie de Debye-Hückel [16] sur la conductivité des électrolytes, publiée sous le même titre, et notamment sur la façon d’écrire l’équation différentielle régissant la relaxation électrique. L’erreur de Debye dans l’article [16] a été de considérer que la déformation de l’atmosphère ionique de l’ion i est indépendante de la déformation de l’atmosphère ionique de l’ion j, alors que l’atmosphère ionique de i contient j et que celle de j contient i.

Développements de l’acoustophorèse jusqu’aux années 1990 24 Quand un ion subit un champ électrique, son atmosphère ionique le subit aussi. L’atmo-sphère ionique se comporte, qualitativement, comme une boule de charge opposée à l’ion central, donc de charge -e, et de rayon κ−1_{. Elle se déplace, d’après la loi de Stokes, à une}

vitesse δvhyd

+ :

6πηκ−1δvhyd₊ ≈ −eE (2.5) Cette vitesse est retrouvée quand un calcul plus rigoureux est fait, en utilisant la fonction de corrélation totale de Debye et Hückel, comme dans l’article de 1932 d’Onsager, qui reprend aussi un article de Debye. Cette vitesse correspond plus précisément à la vitesse de l’eau, à l’emplacement de l’ion central, sous l’effet de l’atmosphère ionique.

Cette vitesse δvhyd _{peut être transformée formellement en force :}

δF₊hyd = kBT

D0 +

δv₊hyd (2.6)

Cette force, qui traduit l’incrément de vitesse du solvant du fait du mouvement de l’atmosphère ionique, est la force électrophorétique ou hydrodynamique. En combinant les équations précédentes, elle est proportionnelle à l’inverse de la longueur de Debye, donc à la racine carrée de la concentration. Plus précisément, le rapport de la force hydrodynamique avec la force l’ayant créée (ici, δFhyd

+ /(eE)) est de l’ordre de κaStokes,

avec aStokes le rayon de Stokes de l’ion central.

2.1.3

|

Force de relaxation électrique

La force de relaxation électrique est aussi assez intuitive. Un ion, par exemple sodium, est toujours entouré d’une atmosphère ionique. Si l’ion sodium est tiré vers l’avant, l’atmosphère ionique met un certain temps à suivre. Pour être précis, l’atmosphère ionique a un retard temporel de l’ordre du temps de Debye τD. Le temps de Debye2 est le temps

de diffusion sur la longueur de Debye, et est donc :

τD ≈

κ−2

D0 (2.7)

Si l’atmosphère ionique a un retard temporel de l’ordre du temps de Debye, elle a un décalage spatial δz de l’ordre du produit de la différence de vitesse entre l’ion et son contre ion par le temps de Debye :

δz ≈ τD(v−− v+) (2.8)

Si les vitesses ne sont dues qu’à un champ électrique appliqué, comme en conductivité :

δz ≈ τD(−2

D0_eE

kBT

) (2.9)

2. Le temps de Debye est ici égal au temps de Maxwell-Wagner, c’est un heureux hasard et non un résultat physiquement intéressant.

25 Développements de l’acoustophorèse jusqu’aux années 1990 L’atmosphère ionique n’étant plus centrée sur le sodium, le sodium ressent un champ électrique local δE, qui est de l’ordre du produit du décalage spatial par le gradient de champ électrique ∇Eatm _{au centre de l’atmosphère ionique. Ce champ électrique est créé}

seulement par l’atmosphère ionique.

δE ≈ −δz∇Eatm (2.10)

Ce gradient de champ électrique est, en prenant une loi de Coulomb avec la longueur de Debye comme longueur caractéristique :

∇_Eatm_{≈ −} κ

3_e

4πǫ0ǫr

(2.11) Le champ électrique lié à la relaxation, ressenti par l’ion central, vaut donc :

δE ≈ κ 3_e 4πǫ0ǫr (−2D 0_eE kBT )κ −2 D0 (2.12)

et la force ressentie par l’ion central :

δF₊rel ≈ −κe 2₍₂D0_eE kBT ) 4πǫ0ǫrD0 (2.13) ≈ −2κLBeE (2.14)

Cette force, dite de relaxation électrique, car elle vient du champ électrique dû à la relaxation de l’atmosphère ionique, est aussi en racine carrée de la concentration. Elle est proportionnelle au rapport entre longueur de Bjerrum LB et longueur de Debye, et est

aussi proportionnelle aux forces l’ayant créée. Ce sont ces deux forces, hydrodynamique et relaxation, qui expliquent la décroissance en racine carrée de la concentration de la conductivité molaire (loi de Kohlrausch). Comme la longueur de Bjerrum est du même ordre de grandeur que le rayon de Stokes, les deux forces correctives sont du même ordre du grandeur. Onsager a réussi à calculer le coefficient de la loi de Kohlrausch grâce à ces deux forces, après que Debye [16] en ait fait l’interprétation qualitative.

2.1.4

|

Pertinence de la démarche d’Oka

La suggestion d’Oka n’est pas pertinente pour deux raisons, de natures différentes. D’abord, les forces précédentes ont été calculées à partir de la fonction de corrélation totale de Debye-Hückel, laquelle est grossièrement fausse dès que la solution est concentrée. En effet, la longueur de Debye tend vers zéro quand la concentration augmente, ce qui donne des corrections trop importantes. Ainsi, la conductivité3

devient négative entre 0,1 3. La conductivité peut s’écrire comme la sommeq_inieiµi. Des corrections excessives peuvent rendre