Evaluations des propriétés mécaniques effectives des composites à matrice organique par la théorie de la micromécanique

ةيبعشلا ةيطارقميدلا ةيرئازجلا ةيروهمجلا La République Algérienne Démocratique et Populaire

يملعلا ثحبلاو يلاعلا ميلعتلا ةرازو

Ministère de l'Enseignement Supérieur et de la Recherche Scientifique سيداب نب ديمحلا دبع ةعماج

– مناغتسم

Université Abdel Hamid Ben Badis - Mostaganem ايجولونكتلاو مولعلا ةيلك

Faculté des Sciences et de la Technologie ةيكيناكيملا ةسدنهلا مسق

Département Génie Mécanique

N d’ordre : M……..../GM/2020

MEMOIRE DE FIN D’ETUDE

MASTER ACADEMIQUE

Filière : Génie Mécanique

Spécialité : Construction Mécanique

Thème

Présenté Par:

 HOUNA Ismail  GHOUL Sara

Soutenu le 30/06/2020 devant le jury composé de :

Président Dr. SAHNOUN Mohammed Université de Mostaganem UMAB Examinateur Dr. BENKABOUCHE Sallah Eddine Université de Mostaganem UMAB Encadreur Dr. KHIAT Med Amine Université de Mostaganem UMAB

Evaluations des propriétés mécaniques effectives des

composites à matrice organique par la théorie de la

Remerciement

Je remercier mon Dieu de m’avoir donné la patience et le courage et la volonté pour réaliser ce travail.

Je tiens à remercier mon encadreur Dr. KHIAT pour avoir proposé et dirigé mes travaux de recherche et son encouragement pendant l’accomplissement de ce travail.

Mes remerciements s’adressent également au membre du jury qui ont bien voulu accepter de juger ce travail.

Résumé

La méthode généralisée de cellules (GMC) de la micromécanique est employée dans cette étude pour la prédiction des modules effectifs des composites fibreux et périodiques en divisant la cellule unitaire répétitive (RUC) en un certain nombre de sous-cellules dans lesquelles les propriétés des matériaux sont attribuées et les résultats sont donnés.

L'objectif principal de cette étude est d'évaluer l'applicabilité du GMC à la prédiction du comportement thermoélastique des composites et il consiste en des équations analytiques capables de traiter à la fois le processus d'homogénéisation et de localisation des matériaux composites de manière très efficace numériquement. Un milieu continu approprié a également été intégré à la micro-échelle. Pour les simulations de stratifiés composites, GMC a été intégré dans la théorie des stratifiés, qui est utilisée pour modéliser le stratifié en tant que modèle à l'échelle globale ou structurelle. Dans ces simulations, GMC opère à la méso-échelle, entre l'échelle globale du stratifié et la micro-échelle des phases individuelles du composite. L'analyse GMC représente le comportement du matériau composite aux points d'intégration dans chaque couche du stratifié. L'approche est entièrement couplée en ce que l'analyse sur chaque échelle affecte les autres échelles car la localisation et l'homogénéisation se produisent à plusieurs reprises tout au long de l'application de la charge appliquée simulée.

Plusieurs équations de modélisation de la réponse des matériaux composites et des stratifiés composites ont été présentées, basées sur le modèle micromécanique analytique GMC, qui fournit des équations constitutives de forme fermée pour les matériaux composites ainsi que les champs de contrainte et de déformation à micro-échelle dans les phases du composite.

Pour fournir un cadre pour GMC, un code appelé MAC/GMC est utilisé, à travers lequel diverses charges thermiques, mécaniques et thermomécaniques sont imposées, de nombreuses architectures de fibres différentes sont utilisées et les résultats sont sortis et discutés via la génération de fichiers de sortie contenant des colonnes de paires X-Y, qui sont tracées à l'aide d'un programme graphique distinct.

Abstract

The micromechanical generalized method of cells (GMC) is employed in this study for the prediction of the effective moduli of the fibrous and periodic composites by dividing the repeating unit cell (RUC) into a number of subcells, in which material properties are assigned, and results are given.

The primary objective of this study is to assess the applicability of GMC in predicting the thermoelastic behavior of composites and it consists of analytical equations that are able to deal with both the homogenization and localization process for composite materials in very numerically efficient way. An appropriate continuum was incorporated on the micro scale as well.

For simulations of composite laminates, GMC has been embedded within lamination theory, which is used to model the laminate as a global or structural scale model. In these simulations, GMC operates on the meso scale, between the global scale of the laminate and the micro scale of the individual phases in the composite. The GMC analysis represents the behavior of the composite material at the integration points within each layer of the laminate. The approach is fully coupled in that the analysis on each scale affects the other scales as localization and homogenization occur repeatedly throughout the application of the simulated applied loading.

A multiple equations to modeling the response of composite materials and composite laminates has been presented. It is based on the analytical GMC micromechanics model, which provides closed-form constitutive equations for composite materials as well as the micro scale stress and strain fields in the composite phases.

To provide a framework for GMC, a code referred to as MAC/GMC is utilized, through it various thermal, mechanical and thermomechanical load histories are imposed, many different fiber architectures are utilized and results are output and discussed through the generation of output files containing columns of X-Y pairs, which are plotted using a separate graphing program.

صخلملا

متي يف هذه ةساردلا مادختسا ةقيرطلا ةيكيناكيموركيملا ةممعملا ايلاخلل ؤبنتلل تادحولاب ةلاعفلا تابكرملل ةيفيللا ةيرودلاو نع قيرط ميسقت ةيلخ ةدحولا ملا ت ةررك ىلإ ددع نم ايلاخلا ةيعرفلا يتلا متي اهيف نييعت صئاصخ داوملا و متي ءاطعإ جئاتنلا . فدهلا يساسلأا نم هذه ةساردلا وه مييقت ةيلباق قيبطت يج مأ يس ؤبنتلل كولسلاب نرملا يرارحلا تابكرملل تو نوكت نم تلاداعم ةيليلحت ةرداق ىلع لماعتلا عم لك نم ةيلمع سناجتلا زكرمتلاو داوملل ةبكرملا ةقيرطب ةلاعف نم ةيحانلا ةيددعلا ، مت نيمضت ةلسلس ةلصتم ةبسانم ىلع سايقملا ريغصلا اًضيأ . وأ ماع سايقم جذومنك حئافصلا ةجذمنل مدختست يتلاو ةيقبطلا حئافصلا ةيرظن يف يس مأ يج نيمضت مت ةبكرملا حئافصلا ةاكاحمل ، يلكيه ةيدرفلا لحارملل ريغصلا سايقملاو حئافصلل ماعلا سايقملا نيب ، طسوتملا سايقملا ىلع يس مأ يج لمعت ةاكاحملا هذه يف بكرملا يف يف اًمامت جهنلا اذه نرتقي حئافصلا نم ةقبط لك لخاد لماكتلا طاقن دنع ةبكرملا ةداملا كولس يس مأ يج ليلحت لثمي ، ؤي سايقم لك ىلع ليلحتلا نأ ثدحي ثيح ىرخلأا سيياقملا ىلع رث سناجتلا زكرمتلاو قبطملا ليمحتلا قيبطت لاوط رركتم لكشب .يكاحملا مت ضرع تلاداعم ةددعتم ةجذمنل ةباجتسا داوملا ةبكرملا حئافصلاو ةبكرملا ثيح دنتست ىلإ جذومن اكيناكيملا ةقيقدلا يج مأ يس يليلحتلا ، يذلا رفوي تلاداعم ةينيوكت ةقلغم داوملل ةبكرملا كلذكو تلااجم دهجلا طغضلاو ىلع سايقملا ريغصلا يف لحارملا بكرملل . ريفوتل راطإ لمع يجـل مأ يس متي مادختسا زمر راشي هيلإ كامـب يج مأ يس ، نم هللاخ متي قيبطت تلايمحت ةيرارح ةيكيناكيمو ةيكيناكيمو ةيرارح ةفلتخم ، متي مادختسا ديدعلا نم تاططخم فايللأا ةفلتخملا و متي جارخإ جئاتنلا اهتشقانمو نم للاخ ءاشنإ تافلم جارخلإا يتلا يوتحت ىلع ةدمعأ جاوزأ يتلاو متي اهمسر مادختساب جمانرب موسر ةينايب لصفنم . تاملكلا ةلادلا : تابكرملا ، اكيناكيملا ةقيقدلا ، ةقيرطلا ةممعملا ايلاخلل ، صاوخلا ةيكيناكيملا ، ةينبلا ةيرهجملا .

Sommaire

Sommaire

Introduction Générale………...1

Chapitre I : Principes fondamentaux I.1. Les matériaux composites………2

I.2. Modélisation des composites………3

I.3. Échelles et homogénéisation/localisation………...4

I.4. Macromécanique versus Micromécanique………...5

I.5. Élément de volume représentatif (RVE) et cellule unitaires répétitive (RUC)………....6

Chapitre II : La méthode généralisée de cellules (GMC) et la théorie des stratifiés II.1. Géométrie et relations de base………..8

II.2. Continuité interfaciale des déplacements………...10

II.3. Continuité interfaciale des tractions………...12

II.4. Loi de comportement thermomécanique globale………...12

II.5. Conductivités thermiques………...14

II.6. Modèle constitutif………...15

II.6.1. La loi de Hooke pour les matériaux isotropes……….15

II.6.2. Transversalement isotrope dans les coordonnées globales……….15

II.7. Théorie des stratifiés………...16

II.8. Conclusion………..21

Chapitre III : Résultats et discussions Exemple 1……….22 Exemple 2……….25 Exemple 3……….30 Exemple 4……….34 Exemple 5……….38 Conclusion générale………...43 Références bibliographiques………..44

Liste des figures

Liste des figures

Figure I.1 : Systèmes de composites………3

Figure I.2 : Illustration des niveaux d'échelle pertinents pour l'analyse multi-échelle de composites.4 Figure I.3 : Diagramme en arbre multi-échelle mettant en relation les constituants et les structures..5

Figure I.4 : Relations entre les échelles d'un RVE, d'un RUC et d'une structure …...………...6

Figure II.1 :Géométrie RUC de GMC-3D………...9

Figure II.2 : Définition de la convention de numérotation des cellules unitaires voisines………….10

Figure II.3 : Cellule unitaire répétitive (RUC) de GMC doublement périodique………..14

Figure II.4 :Théorie des stratifiés multi-échelles disponible en MAC/GMC..………..17

Figure II.5 :Diagramme d'arbre au niveau du stratifié [0°/90°] pour la théorie des stratifiés multi-échelles………...17

Figure III.1 : Approximation de fibre circulaire 7×7, paquet rectangulaire de cellules unitaires répétitives………...23

Figure III.2 : Tracé de la réponse simulée de la contrainte en fonction de la force appliquée pour le composite graphite/époxy………...25

Figure III.3 : RUC de fibre carrée, paquet diagonal carré………..26

Figure III.4 : Tracé de la contrainte simulée en fonction du temps pour le composite…………...28

Figure III.5 : Tracé de la déformation simulée en fonction du temps………28

Figure III.6 : Tracé de la réponse longitudinale et transversale simulée de la déformation en fonction de la température du composite ……….29

Figure III.7 : Géométrie générale du stratifié et système de coordonnées utilisé dans MAC/GMC 4.0………..….31

Figure III.8 : Tracé de la réponse de la force résultante de traction globale en fonction de la déformation du plan moyen du stratifié à 150 °C avec un angle variable d'orientation des fibres....32

Figure III.9 : RUC d’approximation de fibre circulaire 26×26, paquet rectangulaire………...34

Figure III.10 : Tracé de la réponse de la force résultante de traction globale en fonction de la déformation du plan moyen (𝑁𝑥𝑥− 𝜀𝑥𝑥0 ) pour les stratifiés graphite/époxy à couches croisés et quasi-isotropes à 150 °C………...36

Liste des figures

Figure III.12 : Réponse 𝑀𝑖𝑗 − 𝐾𝑖𝑗 d'un stratifié graphite/époxy quasi-isotrope à fraction volumique

de fibres de 0.60 aux courbures appliquées à 150 °C………...37

Figure III.13 : RUC de fibres courtes en réseau diagonal (RUC triplement périodique)……...38

Figure III.14 : RUC de fibres courtes en réseau carré (RUC triplement périodique)………38

Figure III.15 : RUC de matériau monolithique………...39

Figure III.16 : Tracé de la réponse de la force résultante globale Nij pour un stratifié SiC/époxy asymétrique à 23 °C à une déformation du plan moyen 𝜀_𝑥𝑥0 appliquée……….40

Liste des tableaux

Liste des tableaux

Tableau III.1 : Propriétés mécaniques de graphite [Dvorak et al. (1973)] et d’époxyde [Aboudi (1991)] à 23 °C………...22 Tableau III.2 : Propriétés effectives calculées par le MAC/GMC de l’exemple 1……….24 Tableau III.3 : Propriétés mécaniques de graphite [Dvorak et al. (1973)] et d’époxyde [Aboudi (1991)] à 23 °C et 150 °C………...26 Tableau III.4 : Propriétés effectives calculées par le MAC/GMC de l’exemple 2……….27 Tableau III.5 : Propriétés élastiques dépendantes de la température pour la fibre SCS-6 (Bednarcyk et Arnold, 2000a)………30 Tableau III.6 : Les propriétés effectives à 150 °C pour la couche 0° de l’exemple 3………32 Tableau III.7 : Résultats de rigidité et de constantes d'ingénierie effectives pour les stratifiés

analysés………...36 Tableau III.8 : Résultats de rigidité et de constantes d'ingénierie effectives pour le stratifié

Nomenclature

Nomenclature

v_𝑓 : Fraction volumique de fibres v𝑚 : Fraction volumique de la matrice 𝑠_𝑢 : Champ de déplacement appliqué 𝑠_𝜎 : Champ de contrainte appliqué RVE : Elément de volume représentatif RUC : Cellules unitaires répétitives 𝑑 : La taille microstructurale 𝐷 : La taille du RVE

𝐿 : Longueur caractéristique du composant ou de la structure composée du matériau hétérogène 𝑑_∝ℎ_𝛽𝑙_𝛾 : Volume de chacune des sous-cellules

𝑑ℎ𝑙 : Le volume total du RUC

𝑤_𝑖(∝𝛽𝛾)(x) : Les composantes de déplacement au centre de chaque sous-cellule

𝜒_𝑖(∝𝛽𝛾), 𝜙_𝑖(∝𝛽𝛾), 𝜓_𝑖(∝𝛽𝛾) : Micro-variables qui caractérisent la dépendance linéaire des déplacements 𝑢_𝑖(∝𝛽𝛾) : Déplacements de la sous-cellule

𝜀̅𝑖𝑗 : Déformation moyenne du composite 𝜎̅𝑖𝑗 : Contrainte moyenne dans le composite

ε̅𝐼 _{: Tenseur de déformation inélastique du composite}

ε̅𝑇 : Tenseur de déformation thermique moyen du composite 𝜀_𝑖𝑗(∝𝛽𝛾) : La déformation totale dans la sous-cellule

𝜎_𝑖𝑗(𝛼𝛽𝛾) : La contrainte totale dans la sous-cellule 𝜀_𝑖𝑗𝐼(𝛼𝛽𝛾) : Déformation inélastique de la sous-cellule 𝜀_𝑖𝑗𝑇(𝛼𝛽𝛾) : Déformation thermique de la sous-cellule

𝛼_𝑖𝑗(𝛼𝛽𝛾) : Le tenseur de coefficient de dilatation thermique (CTE) ∆𝑇 : L'écart de température = 𝑇 − 𝑇𝑅

Nomenclature

𝐶_{𝑖𝑗𝑘𝑙}(𝛼𝛽𝛾) : Tenseur de rigidité élastique du matériau

A_𝑀 : Matrice implique les propriétés élastiques du matériau dans la sous-cellule A : Matrice de concentration mécanique

C∗ : Tenseur de rigidité élastique effectif du composite C(𝛼𝛽𝛾) : Tenseur de rigidité élastique de chaque sous-cellule

𝛼∗ _{: Vecteur de coefficient de dilatation thermique (CTE) effectif du composite} 𝑘_𝑖(𝛼𝛽𝛾) : Conductivité thermique du matériau

𝑘_𝑖∗ : Conductivité thermique du composite

𝐶𝑖𝑗𝑘𝑙 : Les composantes de tenseur de rigidité élastique du matériau 𝐸_𝐴 : Module d'élasticité axial

𝐸_𝑇 : Module d'élasticité transversal 𝜈_𝐴 : Coefficient de Poisson axial 𝜈𝑇 : Coefficient de Poisson transversal 𝐺_𝐴 : Module de cisaillement axial

𝜎₁, 𝜎₂ et 𝜏₁₂ : Les composantes de contrainte dans les coordonnées locales 𝜎𝑥, 𝜎𝑦 et 𝜏𝑥𝑦 : Les composantes de contrainte dans les coordonnées globales 𝜀₁, 𝜀₂, et 𝛾₁₂ : Les composantes de déformation dans les coordonnées locales 𝜀_𝑥, 𝜀_𝑦, et 𝛾_𝑥𝑦 : Les composantes de déformation dans les coordonnées globales 𝑄_𝑖𝑗𝑘 : Les composantes de la matrice de rigidité réduite pour la 𝑘ième couche 𝜃 : L'angle de la couche

𝑢₀, 𝑣₀ et 𝑤₀ : Les déplacements du plan moyen 𝜀_𝑥0, 𝜀_𝑦0 et 𝛾_𝑥𝑦0 : Les déformations du plan moyen 𝑘_𝑥, 𝑘_𝑦, 𝑘_𝑥𝑦 : Les courbures du plan moyen

𝑁𝑥, 𝑁𝑦 et 𝑁𝑥𝑦 : Les forces résultantes du stratifié par unité de longueur 𝑀_𝑥, 𝑀_𝑦 et 𝑀_𝑥𝑦 : Les moments par unité de longueur

𝐻 : L'épaisseur du stratifié

𝑁𝑇 : Le vecteur thermique de force 𝑀𝑇 _{: Le vecteur thermique de moment}

Nomenclature

*CONSTITUENTS : Paramètres des constituants du composite

NMATS : Nombre de matériaux constitutifs spécifiés

M : Numéro de matériau numéroté séquentiellement

CMOD : Numéro d'identification du modèle constitutif

EL : Propriétés du matériau

EA : Module d'élasticité axial

ET : Module d'élasticité transversal

NUA : Coefficient de Poisson axial

NUT : Coefficient de Poisson transversal GA : Module de cisaillement axial

ALPA : CTE axial

ALPT : CTE transversal TEM : Température

K : Conductivités thermiques locales

*RUC : Paramètres de l’architecture des fibres

MOD : Identifiant du modèle de matériau périodique

ARCHID : Numéro d'identification de l'architecture RUC

VF : Fraction volumique de fibre

R : Rapport de forme du RUC = L/H (voir figure II.1)

F : Numéro de matériau de la fibre (sa numérotation est déterminée dans *CONSTITUENTS)

M : Numéro de matériau de la matrice (sa numérotation est déterminée dans *CONSTITUENTS)

ASP1 : Rapport de forme de la fibre courte (longueur de la fibre / diamètre de la fibre)

ASP2 : Rapport de forme du RUC = l/h (voir figure II.3)

*MECH : Paramètres de chargement mécanique

LOP : Option de chargement

NPT : Nombre de points de temps

TI : Points de temps

MAG : Points de magnitude de la charge

MODE : Mode de chargement appliqué pendant l'étape de chargement

*THERM : Paramètres de température

NPT : Nombre de points de temps

Nomenclature

TEMP : Points de température

*LAMINATE : Paramètres de stratifié

NLY : Nombre de couches (plis) constituant le stratifié

LY : Numéro de couche

THK : Épaisseur de couche

ANG : Angle hors axe de la couche (voir figure III.7)

*SOLVER : Algorithmes d'intégration

NPT : Nombre de points de temps

TI : Points de temps

STP : Taille des pas de temps

*PRINT : Niveau d'impression globale de sortie pour le fichier de sortie

NPL : Spécificateur de niveau d'impression pour le fichier de sortie MAC/GMC 4.0

*XYPLOT : Sortie de tracé X-Y

FREQ : Fréquence des pas de temps pour écrire la sortie

MACRO : Nombre de fichiers de tracé macro (niveau RUC)

NAME : Nom du fichier de tracé

LAMINATE : Nombre de fichiers de tracé au niveau du stratifié

Introduction générale

Introduction générale

Les matériaux composites étant de plus en plus utilisés, le besoin de modèles analytiques et de codes informatiques pour prédire les propriétés et la réponse thermomécanique des matériaux et structures composites s'est considérablement accru. En outre, les modèles analytiques qui prédisent le comportement effectif des composites sont utilisés non seulement par les ingénieurs qui effectuent l'analyse structurelle des composants composites à grande échelle, mais aussi par les scientifiques des matériaux pour développer de nouveaux systèmes de matériaux. Pour qu'un modèle analytique puisse remplir ces deux fonctions distinctes, il doit être basé sur une approche micromécanique qui utilise des modèles constitutifs de déformation basés sur la physique et génère la réponse moyenne (macro) d'un matériau composite compte tenu des propriétés des constituants individuels et de leur disposition géométrique [1,9].

L'objectif principal de cette étude est d'évaluer l'applicabilité de GMC dans la prédiction du comportement thermoélastique des composites renforcés de fibres qui sont influencés par divers paramètres caractéristiques tels que les arrangements de fibres, la fraction volumique de fibres, les rapports de forme des fibres, les rapports de rigidité entre les fibres et la matrice et le type de renfort [2]. Le GMC est entièrement capable de modéliser des architectures de composites multiphasés arbitraires et permet une analyse précise et efficace de l'impact des matériaux, des charges, de la forme et de la disposition des fibres sur la réponse macroscopique du composite [4,6,9], comme l'ont démontré Arnold et al. (1996) et consiste en des équations analytiques [10] capables de traiter à la fois le processus d'homogénéisation et de localisation des matériaux composites d'une manière très efficace sur le plan numérique [2], la capacité prédictive de la méthode dans diverses applications a été récemment résumée par Aboudi (1996).

La relation entre les variables locales et globales est fournie par l'utilisation des tenseurs de concentration de déformation et de contrainte de Hill (1963) qui définissent la réponse macroscopique instantanée le long du chemin de chargement [14].

Le MAC/GMC 4.0 utilisé dans cette étude est un logiciel développé par le centre de recherche Glenn de NASA, basé sur la méthode généralisée de cellules (GMC) et couplé avec la théorie classique des stratifiés [3,11].

 Le première chapitre présente des informations de base sur le matériau composite et sa modélisation.

 En deuxième chapitre, description mathématique du GMC et de la théorie des stratifiés et des lois constitutives sont décrites.

 En troisième chapitre, différentes applications sont traitées et prédictions numériques des matériaux composites sont obtenues à partir du logiciel MAC/GMC 4.0.

Chapitre I

Chapitre I Principes fondamentaux L’approche d'analyse multi-échelles généralisée est le fruit du développement, de la mise en œuvre et de l'application des théories de la micromécanique pour les composites [13]. L'objectif de ce chapitre est de placer ces théories dans leur contexte, de fournir leurs fondements théoriques de manière claire et concise, et d'illustrer leur utilité pour la conception et l'analyse des composites. Ce chapitre fournit des informations fondamentales sur les composites et se concentre ensuite sur la modélisation des composites, en particulier la micromécanique et la modélisation multi-échelles.

I.1 Les matériaux composites

Les scientifiques et les ingénieurs ont développé des moyens de représenter les matériaux à travers les propriétés qui décrivent comment le matériau se comporte à un point dans un corps, comme le module de Young, la conductivité thermique, la densité, le coefficient de Poisson et le coefficient de dilatation thermique [21]. Le corps lui-même, d'autre part, est une structure. Le matériau est un milieu continu, ce qui signifie qu'il est continu et remplit complètement la région de l'espace qu'il occupe [24].

Dans son contexte le plus large, un composite est tout ce qui est composé de deux ou plusieurs matériaux ayant une interface reconnaissable entre eux. Comme il s'agit d'un matériau, il n'a pas de limites extérieures ; une fois qu'une limite extérieure est introduite, il devient une structure composée de matériaux composites. Il est clair, cependant, qu'un matériau composite a des limites internes distinctes. Si ces limites internes sont ignorées, la mécanique des milieux continus peut être utilisée pour modéliser les matériaux composites en tant que matériaux anisotropes pseudo-homogènes avec des propriétés de matériaux "effectives", "homogénéisées" ou "étalées" dépendantes de la direction. En micromécanique, les matériaux individuels (généralement appelés constituants ou phases) qui composent un composite sont chacun traités comme des liaisons continues par la mécanique des milieux continus, leurs propriétés représentatives individuelles et leur disposition dictent le comportement global du matériau composite [1,9].

Dans de nombreux cas, en particulier avec les matériaux composites utilisés dans l'ingénierie des structures, la disposition géométrique d'une phase est continue et sert à maintenir ensemble l’autre ou les autres constituants. Ce constituant est appelé matériau de matrice. Alors que l’autre ou les autres constituants, souvent appelés inclusion(s) et/ou renfort(s), sont des matériaux qui peuvent être continus ou discontinus et qui sont maintenus ensemble par la matrice. Un descripteur fondamental des composites qui doit toujours être indiqué lorsqu'on désigne un système donné (car il influence fortement le comportement effectif) est la fraction volumique des phases présentes. En général, seule la phase de renfort est indiquée, sauf si plusieurs phases sont présentes, car la somme de toutes les phases doit être égale à 100%, par exemple, dans un composite à deux phases renforcé de fibres, v𝑓 est la fraction volumique de fibres et v_𝑚 = 1 − v_𝑓est celle de la matrice. [23]

Les composites sont classés au niveau de la forme du renfort en fibres discontinues, fibres continues ou tissées (textile) Figure I.1 [25].

Les composites, en particulier les composites à matrice polymère (PMC), sont souvent fabriqués sous la forme d’un assemblage de couches minces réunies pour former un stratifié (voir figure I.1(b)). Chaque couche est appelée "pli" [25]. En orientant la direction de renfort de chaque couche, les propriétés et le comportement du stratifié résultant peuvent être contrôlés [22].

Chapitre I Principes fondamentaux

3

Sans différences de propriétés entre les constituants, un composite cesserait d'être un composite. C'est-à-dire que c'est la différence de propriétés entre les constituants qui fait qu'un composite se comporte différemment d'un matériau monolithique et permet son adaptation à des fins spécifiques.

Figure I.1 : Systèmes de composites : (a) Types de renfort. (b) Constructions de stratifié et de tissu

[25].

I.2 Modélisation des composites

L’expression «modélisation des composites» vise à faire référence à la simulation ou à l’analyse du comportement d’un matériau ou d’une structure composite entièrement consolidée. Dans ce contexte, il existe deux approches de base pour la modélisation des composites: l'approche macromécanique et l'approche micromécanique. L'approche macromécanique implique la construction de modèles strictement à l'échelle macro/globale (voir figure I.2), dans laquelle le composite est considéré comme un matériau anisotrope et les détails de l'arrangement sous-jacent des matériaux constitutifs sont ignorés [13].

L'approche micromécanique de la modélisation des composites considère explicitement les matériaux constitutifs et la façon dont ils sont disposés pour former le composite. L'objectif de la micromécanique est de prédire le comportement effectif d'un matériau hétérogène basé sur le comportement des matériaux constitutifs et de leur agencement géométrique. En déterminant le comportement effectif d'un composite via la micromécanique, il peut ensuite être traité comme un matériau dans des analyses à plus grande échelle (similaire à l'approche macromécanique). Par exemple, les propriétés effectives du composite déterminées par la micromécanique peuvent être utilisées dans une analyse de stratifié pour représenter les matériaux des couches. Un avantage de la micromécanique est que les propriétés du composite peuvent être déterminées, dans n'importe quelle direction, pour n'importe quelle fraction volumique de fibres ou architecture de renfort, même si le

Chapitre I Principes fondamentaux composite n'a jamais été fabriqué. Il peut donc aider à concevoir les matériaux composites eux-mêmes ainsi que les structures qui les composent.

I.3 Échelles et homogénéisation/localisation

La modélisation multi-échelles des composites fait référence à la simulation de leur comportement à travers plusieurs échelles de temps ou de longueur [20]. Bien que la nomenclature dans la littérature varie, une analyse de modélisation multi-échelles suivra généralement les échelles de longueur illustrées à la figure I.2 pour la modélisation basée sur le milieu continu. Ces échelles, progressant de gauche à droite sur la figure I.2, sont la micro-échelle (au niveau des constituants: fibre, matrice), la méso-échelle (composite, stratifié), la macro-échelle et l'échelle globale/structurelle. Traditionnellement, on traverse (transcende (se déplace à droite) ou descend (se déplace à gauche)) ces échelles via des techniques d'homogénéisation et de localisation, respectivement (figures I.7 et I.8), une technique d'homogénéisation fournit les propriétés ou la réponse d'une «structure» (niveau supérieur) compte tenu des propriétés ou de la réponse des «constituants» de la structure (échelle inférieure). Inversement, les techniques de localisation fournissent la réponse des constituants étant donné la réponse de la structure. La figure I.3 illustre l'interaction des techniques d'homogénéisation et de localisation en ce que, lors d'une analyse multi-échelles, une étape particulière de la procédure d'analyse peut fonctionner simultanément sur les deux niveaux. Par exemple, pendant le processus d'homogénéisation des étapes représentées par X et Y, pour obtenir les propriétés de l'étape représentée par V, X et Y doivent être considérées comme le niveau des constituants, tandis que V est au niveau de la structure. Cependant, pendant le processus d'homogénéisation de V et W pour obtenir les propriétés de U, V est maintenant au niveau des constituants (tout comme W). De toute évidence, la capacité d'homogénéiser et de localiser avec précision nécessite une théorie sophistiquée qui relie les caractéristiques géométriques et matérielles de la structure et des constituants [13].

Figure I.2 : Illustration des niveaux d'échelle pertinents pour l'analyse multi-échelle de composites

Chapitre I Principes fondamentaux

5

Figure I.3 : Diagramme en arbre multi-échelle mettant en relation les constituants et les structures

[13].

Si un matériau monolithique est chargé uniaxialement, le champ de contrainte interne est constant et uniaxial. Dans un composite, même s'il est chargé uniaxialement, le mésappariement des propriétés des constituants dans les différentes directions crée des champs de contrainte multiaxiales dans chaqueconstituant. Lorsque la non-linéarité du matériau est présente dans les constituants, comme le composite est chargé de façon monotone, la redistribution des contraintes se produit en interne entre les constituants - et même au sein des constituants - parce que les régions de contraintes plus élevées du composite se comportent différemment des régions de contraintes plus faibles. Il en résulte une non-proportionnalité locale car chaque point de chaque constituant affecte la réponse de chaque autre point de ce type. Le déchargement local peut souvent se produire même si la charge monotone globale sur le composite continue [13].

I.4 Macromécanique versus Micromécanique

La caractéristique distinctive entre les approches micromécaniques et macromécaniques est leur point de départ relatif, dans lequel le premier commence à la micro-échelle (c'est-à-dire au niveau des constituants) [1,9] et le second au niveau de l'élément matériel homogénéisé à l'échelle globale. Chaque approche a des besoins uniques en termes de caractérisation et de vérification expérimentales. Dans l'approche à micro-échelle, les modèles des constituants sont utilisés en conjonction avec l'homogénéisation pour prédire le comportement du composite. L'approche à macro-échelle traite le composite comme un matériau anisotrope, avec ses propres propriétés. Par conséquent, le matériau lui-même effectue la procédure d'homogénéisation de la micro-échelle à l'échelle globale.

L'approche macromécanique n'est pas universellement applicable pour l'analyse structurale des matériaux multiphasés car sa validité dépend des dimensions structurales caractéristiques, de la gravité des gradients (contrainte, température, etc.) dans la structure et de la taille (taille de cellules) de la texture interne du matériau (voir la figure I.4 et Aboudi, 1993; Liu, 1988; et Onat et Wright, 1991).

La supériorité de l'approche à micro-échelle ou à macro-échelle reste discutable par rapport à l'objectif principal de développer des outils d'analyse précis, efficaces sur le plan des calculs et validés expérimentalement. Il est clair que chaque approche a son domaine d'applicabilité avec des forces et des faiblesses évidentes [4,6,9].

Chapitre I Principes fondamentaux

Figure I.4 : Relations entre les échelles d'un RVE, d'un RUC et d'une structure; 𝑠_𝑢 = champ de déplacement appliqué, 𝑠𝜎 = champ de contrainte appliqué [24].

Par exemple, l'approche à micro-échelle (micromécanique) est considérée comme la plus adaptée aux applications impliquant la fabrication et le développement de matériaux, où une évaluation précise des micro-contraintes et des déformations est critique, cependant, ces informations détaillées ont souvent un coût de calcul élevé, ce qui est souvent peu pratique et prohibitif pour la conception et l'analyse des composants structurels. En revanche, l'approche à macro-échelle (macromécanique) est clairement la plus efficace sur le plan des calculs, ce qui facilite son utilisation dans la conception et l'analyse de composants à grande échelle; cependant, cette efficacité peut se faire au détriment de la précision par rapport à son homologue à micro-échelle plus intense sur le plan des calculs, en particulier lorsque le comportement très localisé, non-uniforme par rapport à l'élément de volume représentatif (RVE) domine. Par conséquent, compte tenu de ces considérations, une variété d'approches théoriques à micro-échelle et à macro-échelle continuent d'être poursuivies et affinées dans la littérature dans le but ultime de développer une approche qui soit à la fois efficace sur le plan des calculs et précise pour l'analyse sous des charges multiaxiales [6].

I.5 Élément de volume représentatif (RVE) et cellule unitaire répétitive (RUC)

La mécanique des milieux continus est basée sur le concept d'un milieu continu homogène, qui peut être subdivisé à plusieurs reprises en sous-volumes infinitésimaux, chacun d'entre eux conserve les propriétés du matériau en vrac [16]. Cependant, à une certaine échelle, tous les matériaux réels sont hétérogènes. L'objectif de la micromécanique est de rendre compte explicitement de la microstructure hétérogène d'un matériau tout en permettant de le traiter comme un milieu continu effectif (pseudo-homogène) à une échelle de longueur plus élevée (par exemple, au sein d'une structure). Pour tenir compte de cette microstructure, la micromécanique s'appuie sur un élément de volume représentatif (RVE) ou sur une cellule unitaire répétitive (RUC) [24].

Un RVE est un volume d'un matériau dont le comportement effectif est représentatif (et indiscernable) de celui du matériau dans son ensemble. Pour un matériau fictif parfaitement homogène, le RVE serait infiniment petit. Pour tous les matériaux réels, qui contiennent une microstructure, le RVE doit contenir un volume suffisamment important pour qu'il capte l'essence de la microstructure d'un point de vue statistique.

Chapitre I Principes fondamentaux

7

pour générer la microstructure globale [1,9]. Des conditions de périodicité sont appliquées aux limites du RUC pour imposer la nature répétitive du RUC. Il est souvent difficile de garantir qu'un volume d'analyse choisi est bien un RVE; par conséquent, l'approche RUC/périodicité est généralement utilisée. Drago et Pindera (2007) fournissent une discussion approfondie des concepts RVE et RUC dans le contexte de la micromécanique de composites.

L'interaction entre les échelles d'un RVE, d'un RUC et d'une structure est illustrée à la figure I.4. Ici, 𝑑 représente la taille microstructurale (un RUC fibre/matrice du composite dans cette illustration), 𝐷 est la taille du RVE et 𝐿 est une longueur caractéristique du composant ou de la structure composée du matériau hétérogène. Si les rapports de ces dimensions (𝑑 𝐷⁄ et 𝐷 𝐿⁄ ) sont bien inférieurs à 1, alors le RVE doit inclure un nombre suffisant d'unités microstructurales pour permettre (statistiquement) la nature hétérogène du matériau à homogénéiser [24]. En d'autres termes, le RVE du matériau est tel que (a) il est entièrement typique du composite en vrac en moyenne [16] et (b) il contient un nombre suffisant de phases de matériau et est donc grand par rapport aux échelles de microstructure, mais reste petite par rapport à l'ensemble du corps [24].

Chapitre II

La méthode généralisée de

cellules (GMC) et la théorie des

stratifiés

Chapitre II La méthode généralisée de cellules et la théorie des stratifiés

8

Récemment, une technique de micromécanique appelée la méthode généralisée de cellules (GMC) [6] a été développée par Paley et Aboudi (1991, 1995) [5,6,9], dans laquelle la microstructure d'un matériau périodique est représentée par une cellule unitaire répétitive rectangulaire constituée d'un nombre arbitraire de sous-cellules rectangulaires, dont chacune peut être un matériau distinct. Il s'agit d'un modèle micromécanique analytique basé sur le milieu continu qui fournit des équations constitutives multiaxiales de forme pseudo fermée pour les matériaux [10] et fournit le comportement global (réponse macroscopique) et la capacité de simuler une charge thermomécanique générale de composites multiphasiques continus [9] et discontinus (à fibres courtes) [4] avec microstructures et forme de renfort périodiques arbitraires à partir de la connaissance des propriétés, de la taille, de la forme, de la distribution et de la réponse des constituants ou des phases individuels qui composent le matériau [2]. La nature périodique des composites permet généralement d'identifier une cellule unitaire répétitive qui peut être utilisée comme bloc de construction pour construire le composite entier. Les propriétés de cette cellule unitaire sont donc représentatives des propriétés de l'ensemble complet. Les champs de contraintes et de déformations internes dans les constituants individuels sont exprimés en termes de contraintes et déformations appliquées macroscopiquement via des facteurs de concentration de déformation ou de contrainte [4,9]. GMC représente le composite comme un milieu continu sans aucune frontière et peut être intégré de manière transparente dans une analyse structurelle à plus grande échelle. La mécanique des milieux continus, qui permet de décrire (sur un élément de volume représentatif approprié) les microprocédés hétérogènes impliqués lors de la déformation des matériaux et des structures à l'échelle macroscopique. La cellule unitaire est divisée en un nombre arbitraire de sous-cellules et c’est la plus petite section du composite pour laquelle la réponse peut être considérée comme représentative du composite dans son ensemble.

Les contraintes et déformations macroscopiques sont ensuite définies en termes de contraintes et déformations microscopiques (sous-cellules), et les équations constitutives macroscopiques globales du composite peuvent être déterminées.

La méthode GMC suppose un champ de déplacement linéaire dans chaque sous-cellule et impose une continuité des composantes de traction et de déplacement entre les sous-cellules dans un sens moyen (Aboudi, 1995) [4]. Cette procédure aboutit à un système d'équations linéaires.

Pour l'analyse du stratifié, pour modéliser le comportement du stratifié composite, la théorie classique des stratifiés (Jones (1975) et Herakovich (1998)) est utilisée comme modèle à l'échelle globale ou structurelle, tandis que GMC est intégré pour fonctionner à la méso-échelle pour simuler le comportement du matériau composite au sein de chaque couche du stratifié. Les équations de la théorie des stratifiés homogénéisent ensuite les déformations du composite pour donner la force et le moment résultants de l'échelle requise du stratifié. La théorie micro/macro actuelle est maintenue aussi générale que possible afin de maximiser son applicabilité.

II.1 Géométrie et relations de base

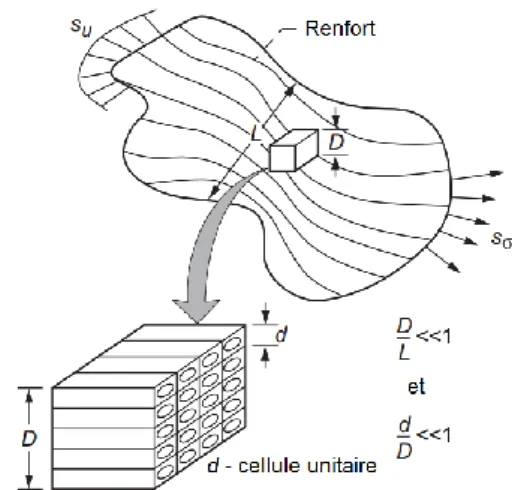
Considérons un matériau composite à microstructure périodique dont le RUC est constitué de sous-cellules parallélépipédiques rectangulaires 𝑁𝛼× 𝑁𝛽× 𝑁𝛾. Le volume de chacune des sous-cellules est 𝑑_∝ℎ_𝛽𝑙_𝛾, où ∝, 𝛽 et 𝛾 sont des indices courants: ∝= 1,…,𝑁_∝; 𝛽 = 1,…,𝑁_𝛽; et 𝛾 = 1,…,𝑁_𝛾, dans les directions orthogonales 𝑥1, 𝑥2, et 𝑥3, respectivement [15]. Le volume total du RUC est 𝑑ℎ𝑙 où 𝑑 = ∑𝑁∝=1∝ 𝑑∝, ℎ = ∑ ℎ𝛽

𝑁𝛽

𝛽=1 , 𝑙 = ∑ 𝑙𝛾 𝑁𝛾

𝛾=1 . Dans la figure II.1, un exemple est montré pour un élément de volume représentatif (RVE) avec 𝑁_𝛼 = 3, 𝑁_𝛽 = 4, et 𝑁_𝛾= 2 [4].

Chapitre II La méthode généralisée de cellules et la théorie des stratifiés Chacune des sous-cellules peut être remplie par un matériau. En sélectionnant de manière appropriée les dimensions géométriques des sous-cellules et en remplissant les sous-cellules de manière appropriée, divers types de composites peuvent être envisagés tels que les composites unidirectionnels à fibres longues, les composites à fibres courtes et les matériaux en couches.

Figure II.1 :Géométrie RUC de GMC-3D [4].

Compte tenu des interactions détaillées des sous-cellules de la RUC, des relations constitutives globales, qui régissent le comportement effectif du composite multiphasé, peuvent être établies. Cette analyse semi-analytique repose sur les exigences selon lesquelles l'équilibre statique des matériaux dans les différentes sous-cellules est assuré et que la continuité des déplacements et des tractions entre les sous-cellules voisines au sein du RUC, ainsi qu'entre les RUC voisins, est satisfaite en moyenne. Pour ce faire, des coordonnées locales 𝑥̅₁(∝), 𝑥̅₂(𝛽), et 𝑥̅₃(𝛾) sont introduites, dont l'origine se situe au centre de chaque sous-cellule (∝ 𝛽𝛾). Ces coordonnées locales sont représentées sur la figure II.2 pour la sous-cellule (∝ 𝛽𝛾) et la voisine (∝̂ 𝛽𝛾) dans la direction 𝑥₁, où ∝̂ est défini pour avoir la forme :

∝̂= {∝ +1 ∝< 𝑁∝ 1 ∝= 𝑁_∝

Cette définition garantit que pour ∝< 𝑁∝ la sous-cellule voisine dans la direction 𝑥1 est celle étiquetée par (∝ +1,𝛽,𝛾) dans le RUC, tandis que pour ∝= 𝑁_∝ la sous-cellule voisine est dans le RUC suivant dont la première sous-cellule est (1𝛽𝛾). De même, 𝛽̂ et 𝛾̂ sont définis par :

𝛽̂ = {𝛽 + 1 𝛽 < 𝑁𝛽 1 𝛽 = 𝑁_𝛽 𝛾̂ = {𝛾 + 1_{1 𝛾 = 𝑁}𝛾 < 𝑁𝛾 𝛾

Chapitre II La méthode généralisée de cellules et la théorie des stratifiés

10

Figure II.2 : Définition de la convention de numérotation des cellules unitaires voisines.

Le GMC considère une théorie du premier ordre dans laquelle les déplacements 𝑢_𝑖(∝𝛽𝛾) dans chaque sous-cellule sont étendus linéairement en termes de distances par rapport au centre de la sous-cellule; c'est-à-dire, en termes de coordonnées locales 𝑥̅₁(∝), 𝑥̅₂(𝛽), et 𝑥̅₃(𝛾). Ainsi, l'expansion de premier ordre suivante dans la sous-cellule (∝ 𝛽𝛾) est représentée par :

𝑢_𝑖(∝𝛽𝛾) = 𝑤_𝑖(∝𝛽𝛾)(x) + 𝑥̅₁(∝)𝜒_𝑖(∝𝛽𝛾)+ 𝑥̅₂(𝛽)𝜙_𝑖(∝𝛽𝛾)+ 𝑥̅₃(𝛾)𝜓_𝑖(∝𝛽𝛾) 𝑖 = 1,2,3 (1)

où 𝑤_𝑖(∝𝛽𝛾)(x) sont les composantes de déplacement au centre de chaque sous-cellule, et 𝜒_𝑖(∝𝛽𝛾), 𝜙_𝑖(∝𝛽𝛾), et 𝜓_𝑖(∝𝛽𝛾) sont des micro-variables qui caractérisent la dépendance linéaire des déplacements 𝑢_𝑖(∝𝛽𝛾) sur les coordonnées locales 𝑥̅₁(∝), 𝑥̅₂(𝛽), et 𝑥̅₃(𝛾). Le vecteur x = (𝑥1,𝑥2,𝑥3) indique la position du centre de la sous-cellule par rapport au système de coordonnées global fixe (voir figure II.1). Il convient de souligner que la coordonnée x est constante au niveau de la sous-cellule, où les positions sont décrites en termes de coordonnées locales. Dans l'équation (1) et dans tout ce qui suit, les lettres grecques répétées n'impliquent pas de sommation. Notez qu'en raison de la linéarité de l'équation (1), l'équilibre statique du matériau à l'intérieur de la sous-cellule (∝ 𝛽𝛾) est assuré.

II.2 Continuité interfaciale des déplacements

A tout instant, les composantes de déplacement doivent être continues aux différentes interfaces du RUC et aux interfaces entre les cellules unitaires voisines.

Les composantes de déformation totale de la sous-cellule sont indépendantes de 𝑥̅₁(∝), 𝑥̅₂(𝛽), et 𝑥̅₃(𝛾) et sont donc constantes dans une sous-cellule donnée. Étant donné que les CTE sont constants dans une sous-cellule donnée, les composantes de déformation thermique 𝜀_𝑖𝑗𝑇 sont également constantes dans une sous-cellule donnée. Le fait que les composantes de déformation totale et de déformation thermique de sous-cellule soient constantes dans une sous-cellule donnée nécessitent que les composantes de contrainte de sous-cellule soient constantes dans une sous-cellule donnée, à condition que la sous-cellule se déforme élastiquement. Ces arguments montrent que les champs moyens et les champs ponctuels au sein des sous-cellules sont identiques. Soit,

Chapitre II La méthode généralisée de cellules et la théorie des stratifiés 𝜎̅_𝑖𝑗(∝𝛽𝛾) = 𝜎_𝑖𝑗(∝𝛽𝛾), 𝜀̅_𝑖𝑗(∝𝛽𝛾) = 𝜀_𝑖𝑗(∝𝛽𝛾), 𝜀̅_𝑖𝑗𝑇(∝𝛽𝛾)= 𝜀_𝑖𝑗𝑇(∝𝛽𝛾), 𝜀̅_𝑖𝑗𝐼(∝𝛽𝛾)= 𝜀_𝑖𝑗𝐼(∝𝛽𝛾)

Les déformations moyennes du composite, 𝜀̅𝑖𝑗 sont 𝜀̅𝑖𝑗 = 1 2( 𝜕𝑤_𝑖 𝜕𝑥𝑗 +𝜕𝑤𝑗 𝜕𝑥𝑖 ) Les déformations dans la sous-cellule 𝜀_𝑖𝑗(∝𝛽𝛾) sont données par

∑ 𝑑𝛼 𝑁𝛼 𝛼=1 𝜀₁₁(∝𝛽𝛾)= ∑ 𝑑𝛼 𝑁𝛼 𝛼=1 𝜒₁(∝𝛽𝛾) = 𝑑𝜀̅11= 𝑑 𝜕 𝜕𝑥1 𝑤1 𝛽 = 1, … , 𝑁𝛽 𝛾 = 1, … , 𝑁𝛾 ∑ ℎ𝛽 𝑁𝛽 𝛽=1 𝜀₂₂(∝𝛽𝛾)= ∑ ℎ𝛽 𝑁𝛽 𝛽=1 𝜙₂(∝𝛽𝛾) = ℎ𝜀̅22= ℎ 𝜕 𝜕𝑥2 𝑤2 𝛼 = 1, … , 𝑁𝛼 𝛾 = 1, … , 𝑁𝛾 ∑ 𝑙𝛾 𝑁_𝛾 𝛾=1 𝜀₃₃(∝𝛽𝛾) = ∑ 𝑙𝛾 𝑁_𝛾 𝛾=1 𝜓₃(∝𝛽𝛾)= 𝑙𝜀̅33= 𝑙 𝜕 𝜕𝑥3 𝑤3 𝛼 = 1, … , 𝑁𝛼 𝛽 = 1, … , 𝑁𝛽 2 ∑ ∑ ℎ𝛽 𝑁𝛾 𝛾=1 𝑙𝛾 𝑁_𝛽 𝛽=1 𝜀₂₃(∝𝛽𝛾)= ∑ ∑ ℎ𝛽 𝑁𝛾 𝛾=1 𝑙𝛾 𝑁_𝛽 𝛽=1 (𝜙₃(∝𝛽𝛾)+ 𝜓₂(∝𝛽𝛾)) = 2ℎ𝑙𝜀̅23= ℎ𝑙 ( 𝜕𝑤2 𝜕𝑥3 +𝜕𝑤3 𝜕𝑥2 ) 𝛼 = 1, … , 𝑁𝛼 2 ∑ ∑ 𝑑𝛼 𝑁_𝛾 𝛾=1 𝑙𝛾 𝑁𝛼 𝛼=1 𝜀₁₃(∝𝛽𝛾)= ∑ ∑ 𝑑𝛼 𝑁_𝛾 𝛾=1 𝑙𝛾 𝑁𝛼 𝛼=1 (𝜓₁(∝𝛽𝛾)+ 𝜒₃(∝𝛽𝛾)) = 2𝑑𝑙𝜀̅13= 𝑑𝑙 ( 𝜕𝑤1 𝜕𝑥3 +𝜕𝑤3 𝜕𝑥1 ) 𝛽 = 1, … , 𝑁𝛽 2 ∑ ∑ 𝑑𝛼 𝑁𝛽 𝛽=1 ℎ𝛽 𝑁_𝛼 𝛼=1 𝜀₁₂(∝𝛽𝛾)= ∑ ∑ 𝑑𝛼 𝑁𝛽 𝛽=1 ℎ𝛽 𝑁_𝛼 𝛼=1 (𝜙₁(∝𝛽𝛾)+ 𝜒₂(∝𝛽𝛾)) = 2𝑑ℎ𝜀̅12= 𝑑ℎ ( 𝜕𝑤1 𝜕𝑥2 +𝜕𝑤2 𝜕𝑥1 ) 𝛾 = 1, … , 𝑁𝛾

Ces dernières relations de la déformation de sous-cellule peuvent s'écrire sous forme matricielle comme suit :

A𝐺ε𝑠 = Jε̅

où le vecteur de déformation moyenne du sixième ordre est défini par ε̅ = (𝜀̅₁₁, 𝜀̅₂₂, 𝜀̅₃₃, 2𝜀̅₂₃, 2𝜀̅₁₃, 2𝜀̅₁₂) (2) et le vecteur de déformation de sous-cellule ε_𝑠 d'ordre 6𝑁_𝛼𝑁_𝛽𝑁_𝛾 est défini par

ε𝑠 = (𝜀(111),…,𝜀(𝑁𝛼𝑁𝛽𝑁𝛾))

où les six composantes du vecteur 𝜀_𝑖𝑗(𝛼𝛽𝛾) sont disposées comme dans l'équation (2). Il est à noter que la matrice A_𝐺 n'implique que les dimensions géométriques de la cellule répétitive.

Les déformations moyennes dans le composite sont exprimées comme suit :

𝜀̅_𝑖𝑗 = 1 𝑑ℎ𝑙∑ ∑ ∑ 𝑑𝛼ℎ𝛽𝑙𝛾 𝑁𝛾 𝛾=1 𝜀_𝑖𝑗(𝛼𝛽𝛾) 𝑁𝛽 𝛽=1 𝑁𝛼 𝛼=1

Chapitre II La méthode généralisée de cellules et la théorie des stratifiés 12 𝜎̅_𝑖𝑗 = 1 𝑑ℎ𝑙∑ ∑ ∑ 𝑑𝛼ℎ𝛽𝑙𝛾 𝑁𝛾 𝛾=1 𝜎_𝑖𝑗(𝛼𝛽𝛾) 𝑁𝛽 𝛽=1 𝑁𝛼 𝛼=1 (3)

Ces équations établissent des relations entre les déformations moyennes et les contraintes moyennes du composite et des microvariables dans les sous-cellules du RVE.

L'équation constitutive du matériau élastique-viscoplastique dépendant de la température qui occupe la sous-cellule (𝛼𝛽𝛾) est exprimée comme une relation entre la contrainte 𝜎_𝑖𝑗(𝛼𝛽𝛾), la déformation totale 𝜀_𝑖𝑗(𝛼𝛽𝛾), la déformation inélastique 𝜀_𝑖𝑗𝐼(𝛼𝛽𝛾), et la déformation thermique 𝜀_𝑖𝑗𝑇(𝛼𝛽𝛾) = 𝛼_𝑖𝑗(𝛼𝛽𝛾)∆𝑇 (où 𝛼_𝑖𝑗(𝛼𝛽𝛾) est le tenseur CTE, et ∆𝑇 est l'écart de température 𝑇 − 𝑇𝑅 par rapport à une température de référence 𝑇𝑅) :

𝜎_𝑖𝑗(𝛼𝛽𝛾) = 𝐶_{𝑖𝑗𝑘𝑙}(𝛼𝛽𝛾)(𝜀_𝑘𝑙(𝛼𝛽𝛾)− 𝜀_𝑘𝑙𝐼(𝛼𝛽𝛾)− 𝜀_𝑘𝑙𝑇(𝛼𝛽𝛾)) où 𝐶_{𝑖𝑗𝑘𝑙}(𝛼𝛽𝛾) est le tenseur de rigidité élastique du matériau.

Il a été démontré ([Paley et Aboudi (1992)] et [Aboudi (1995)]) qu'en employant les conditions de continuité de déplacement et de traction aux interfaces entre les sous-cellules de l'élément de volume répétitif et aux interfaces entre les éléments de volume répétitifs voisins, il est possible d'éliminer les microvariables et d'obtenir, via une opération de lissage (homogénéisation), un ensemble d'équations de milieu continu qui modélisent le comportement global du composite à fibres courtes polyphasique [1,9]. Ceci a été réalisé en établissant des relations qui connectent les microdéformations au niveau des sous-cellules aux macrodéformations globales totales dans le composite via les tenseurs de concentration appropriés, A et D [4,9].

II.3 Continuité interfaciale des tractions

Les tractions doivent être continues aux interfaces entre les sous-cellules des cellules répétitives et aux interfaces entre les cellules répétitives voisines.

A_𝑀(ε𝑠− ε𝑠𝐼 − ε𝑠𝑇) = 0

où la matrice A_𝑀 implique les propriétés élastiques C(𝛼𝛽𝛾) du matériau dans la sous-cellule [6] et ε_𝑠𝐼 _{= (𝜀}𝐼(111)_,…,𝜀𝐼(𝑁𝛼𝑁𝛽𝑁𝛾)₎

ε_𝑠𝑇 _{= (𝜀}𝑇(111)_,…,𝜀𝑇(𝑁𝛼𝑁𝛽𝑁𝛾)₎

II.4 Loi de comportement thermomécanique globale

ε_𝑠 = Aε̅ + D(ε_𝑠𝐼 + ε_𝑠𝑇) (4) A = [A_A𝑀 𝐺] −1 [0_J] D = [A_A𝑀 𝐺] −1 [A𝑀 0 ]

Rend la matrice de concentration mécanique A divisée en sous-matrices carrées de sixième ordre 𝑁𝛼𝑁𝛽𝑁𝛾 sous la forme [4,9] A = [ A(111) ⋮ A(𝑁𝛼𝑁𝛽𝑁𝛾) ]

Chapitre II La méthode généralisée de cellules et la théorie des stratifiés D = [ D(111) ⋮ D(𝑁𝛼𝑁𝛽𝑁𝛾) ] Il résulte de l'équation (4) que

ε(𝛼𝛽𝛾) = A(𝛼𝛽𝛾)ε̅ + D(𝛼𝛽𝛾)(ε_𝑠𝐼 _{+ ε} 𝑠

𝑇_{) (5)}

où A(𝛼𝛽𝛾) et D(𝛼𝛽𝛾) sont des matrices carrées d'ordre 6𝑁_𝛼𝑁_𝛽𝑁_𝛾 et A_𝑀 implique les propriétés élastiques C(𝛼𝛽𝛾) du matériau de la sous-cellule, A_𝐺 les dimensions géométriques de la cellule répétitive uniquement, et J est une matrice contenant les déformations moyennes imposées (composite) [6].

L'équation (5) exprime les composantes de la déformation dans chaque sous-cellule en termes de déformation globale uniforme ε̅ (la macrodéformation appliquée) et les déformations inélastiques et thermiques de la sous-cellule, via les matrices de concentration A et D. Ces tenseurs de concentration mécanique et de déformation propre dépendent des modules élastiques locaux et de la forme et de la fraction volumique des phases et sont donc constants. [7,8]

𝜎(𝛼𝛽𝛾) = C(𝛼𝛽𝛾)[A(𝛼𝛽𝛾)ε̅ + D(𝛼𝛽𝛾)(ε𝑠𝐼 + ε𝑠𝑇) − (ε𝐼(𝛼𝛽𝛾)+ ε𝑇(𝛼𝛽𝛾))]

Par conséquent, en conjonction avec l'équation (3), la loi thermomécanique élastoplastique effective suivante du composite peut être établie [1,9]

𝜎̅ = C∗_{(ε̅ − ε̅}𝐼_{− ε̅}𝑇₎

où le tenseur de rigidité élastique effectif C∗ _{du composite est donné par}

C∗ ₌ 1 𝑑ℎ𝑙∑ ∑ ∑ 𝑑𝛼ℎ𝛽𝑙𝛾 𝑁𝛾 𝛾=1 C(𝛼𝛽𝛾)A(𝛼𝛽𝛾) 𝑁𝛽 𝛽=1 𝑁𝛼 𝛼=1 (6)

où C(𝛼𝛽𝛾) est le tenseur de rigidité élastique de chaque sous-cellule [6], et le tenseur de déformation inélastique du composite est défini comme suit

ε̅𝐼 =−C ∗−1 𝑑ℎ𝑙 ∑ ∑ ∑ 𝑑𝛼ℎ𝛽𝑙𝛾 𝑁𝛾 𝛾=1 C(𝛼𝛽𝛾)(D(𝛼𝛽𝛾)ε_𝑠𝐼 − ε𝐼(𝛼𝛽𝛾)) 𝑁𝛽 𝛽=1 𝑁𝛼 𝛼=1

et le tenseur de déformation thermique moyen est donné par

ε̅𝑇 ₌−C ∗−1 𝑑ℎ𝑙 ∑ ∑ ∑ 𝑑𝛼ℎ𝛽𝑙𝛾 𝑁𝛾 𝛾=1 C(𝛼𝛽𝛾)(D(𝛼𝛽𝛾)ε_𝑠𝑇_{− ε}𝑇(𝛼𝛽𝛾)₎ 𝑁𝛽 𝛽=1 𝑁𝛼 𝛼=1 (7)

Le vecteur du coefficient de dilatation thermique (CTE) effectif, 𝛼∗ du composite est donné par 𝛼∗ = ε̅𝑇⁄∆𝑇

Dans le cas de renforts continus avec 𝑁_𝛼× 𝑁_𝛽 nombre de sous-cellules, les équations (6), (7) se réduisent comme suit :

𝑁𝛾

Chapitre II La méthode généralisée de cellules et la théorie des stratifiés 14 ε̅𝑇 ₌−C ∗−1 ℎ𝑙 ∑ ∑ ℎ𝛽𝑙𝛾 𝑁𝛾 𝛾=1 C(𝛽𝛾)(D(𝛽𝛾)ε_𝑠𝑇_{− ε}𝑇(𝛽𝛾)₎ 𝑁𝛽 𝛽=1

où les six composantes des vecteurs ε𝑠𝑇 et ε𝑇(𝛼𝛽𝛾) sont disposées comme dans l'équation (2).

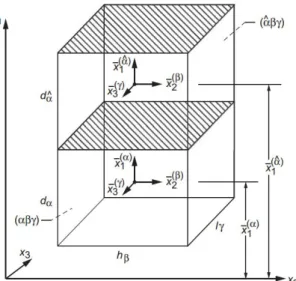
Figure II.3 : Cellule unitaire répétitive (RUC) de GMC doublement périodique [11].

La loi de comportement GMC établie est basée sur les principes de la mécanique des milieux continus où le micro-équilibre et la continuité des déplacements et des tractions aux différentes interfaces sont assurés dans un sens moyen.

Parmi les nombreux avantages qui peuvent être énoncés en ce qui concerne la loi de comportement macro/micro de GMC, se trouve le fait que tout type de chargement simple ou combiné (état de contrainte multiaxiale) peut être appliqué indépendamment de l'existence ou non d'une symétrie, ainsi que sans recourir à différentes stratégies d'application des conditions aux limites et on peut obtenir le même niveau de précision globale en évitant un nombre important d'éléments finis dans une cellule répétitive donnée. [1,9]

II.5 Conductivités thermiques

𝑘₁∗ ₌ 𝑑 ℎ𝑙 ∑ ℎ𝛽𝑙𝛾 2 𝛽,𝛾=1 ( 𝑑1 𝑘₁(1𝛽𝛾)+ 𝑑2 𝑘₁(2𝛽𝛾)) −1 𝑘₂∗ ₌ ℎ 𝑑𝑙 ∑ 𝑑𝛼𝑙𝛾 2 𝛼,𝛾=1 ( ℎ1 𝑘₂(𝛼1𝛾)+ ℎ2 𝑘₂(𝛼2𝛾)) −1 𝑘₃∗ = 𝑙 𝑑ℎ ∑ 𝑑𝛼ℎ𝛽 2 𝛼,𝛽=1 ( 𝑙1 𝑘₃(𝛼𝛽1)+ 𝑙2 𝑘₃(𝛼𝛽2)) −1

Chapitre II La méthode généralisée de cellules et la théorie des stratifiés

II.6 Modèle constitutif

II.6.1 La loi de Hooke pour les matériaux isotropes

La loi de Hooke pour un matériau thermoélastique est donnée par : 𝜎𝑖𝑗 = 𝐶𝑖𝑗𝑘𝑙(𝜀𝑖𝑗− 𝛼𝑖𝑗∆𝑇)

où 𝜎_𝑖𝑗 et 𝜀_𝑖𝑗 sont respectivement les composantes de contrainte et de déformation, 𝐶_{𝑖𝑗𝑘𝑙} sont les composantes du tenseur de rigidité élastique, 𝛼𝑖𝑗 sont les CTEs, ∆𝑇 est le changement de température par rapport à une température de référence, et la déformation thermique est donnée par 𝜀_𝑖𝑗𝑡ℎ = 𝛼_𝑖𝑗∆𝑇 Sous forme matricielle, la loi de Hooke de matériau isotrope peut s'écrire comme suit :

[ 𝜎₁₁ 𝜎₂₂ 𝜎₃₃ 𝜎₂₃ 𝜎₁₃ 𝜎12] = [ 𝐶11 𝐶12 𝐶12 0 0 0 𝐶₁₂ 𝐶₁₁ 𝐶₁₂ 0 0 0 𝐶₁₂ 𝐶₁₂ 𝐶₁₁ 0 0 0 0 0 0 (𝐶11− 𝐶12) 2 0 0 0 0 0 0 (𝐶11− 𝐶12) 2 0 0 0 0 0 0 (𝐶11− 𝐶12) 2 ] × ([ 𝜀₁₁ 𝜀₂₂ 𝜀₃₃ 𝛾₂₃ 𝛾13 𝛾12] − [ 𝛼∆𝑇 𝛼∆𝑇 𝛼∆𝑇 0 0 0 ])

où 𝜎_𝑖𝑗 et 𝜀_𝑖𝑗 sont respectivement les composantes de contrainte et de déformation où les composantes de rigidité

𝐶11=

𝐸(1 − 𝜈) (1 + 𝜈)(1 − 2𝜈)

𝐶₁₂= 𝐸𝜈

(1 + 𝜈)(1 − 2𝜈)

sont écrites en fonction de deux constantes indépendantes d'ingénierie des matériaux, 𝐸 et 𝑣. Notez que 𝛾_𝑖𝑗 𝑖 ≠ 𝑗, sont les composantes d'ingénierie de la déformation de cisaillement et sont liées aux composantes de la déformation de cisaillement tensorielle par 𝛾_𝑖𝑗 = 2𝜀_𝑖𝑗 , 𝑖 ≠ 𝑗. Le comportement normal et de cisaillement des matériaux isotropes n'est pas couplé, c'est-à-dire que l'imposition d'une contrainte ou d'une déformation normale n'entraîne aucune contrainte ou déformation de cisaillement, et vice versa.

Un seul CTE est nécessaire pour un matériau isotrope : 𝛼_𝑖𝑗 = 𝛼 for 𝑖 = 𝑗 𝛼𝑖𝑗 = 0 for 𝑖 ≠ 𝑗

II.6.2 Transversalement isotrope dans les coordonnées globales

La loi de Hooke pour un matériau transversalement isotrope, avec un plan d'isotropie 𝑥2-𝑥3, [6] est donnée par :

Chapitre II La méthode généralisée de cellules et la théorie des stratifiés 16 [ 𝜎11 𝜎22 𝜎₃₃ 𝜎₂₃ 𝜎₁₃ 𝜎₁₂] = [ 𝐶11 𝐶12 𝐶12 0 0 0 𝐶₁₂ 𝐶₂₂ 𝐶₂₃ 0 0 0 𝐶12 𝐶23 𝐶22 0 0 0 0 0 0 (𝐶22− 𝐶23) 2 0 0 0 0 0 0 𝐶₆₆ 0 0 0 0 0 0 𝐶₆₆] × ([ 𝜀11 𝜀22 𝜀₃₃ 𝛾₂₃ 𝛾₁₃ 𝛾₁₂] − [ 𝛼𝐿∆𝑇 𝛼_𝑇∆𝑇 𝛼𝑇∆𝑇 0 0 0 ])

où les composantes de rigidité peuvent être exprimées en termes de cinq constantes indépendantes : 𝐸𝐴, 𝐸𝑇, 𝜈𝐴, 𝜈𝑇, 𝐺𝐴

où les indices 𝐴 et 𝑇 se réfèrent respectivement aux propriétés axiales et transversales, et 𝐺 est le module de cisaillement. Les composantes de rigidité sont :

𝐶11 = 𝐸𝐴+ 4𝜒𝜈𝐴2 𝐺₁₂ = 2𝜒𝜈_𝐴 𝐶₂₂ = 𝜒 + 0.5𝐸𝑇 (1 + 𝜈_𝑇) 𝐶23 = 𝜒 − 0.5𝐸_𝐴 (1 + 𝜈𝑇) 𝐶66 = 𝐺𝐴 avec 𝜒 = 0.25𝐸𝐴 [0.5(1 − 𝜈_𝑇) (𝐸𝐴 𝐸_𝑇) − 𝜈𝐴2]

Les matériaux transversalement isotropes conservent un comportement normal et de cisaillement non couplé. [6]

II.7 Théorie des stratifiés

Le code MAC/GMC comprend un module de théorie des stratifiés classique multi-échelles qui est capable d'analyser des stratifiés composites généraux (symétriques et non symétriques) [12], dans lequel les théories de la micromécanique d'Aboudi sont utilisées à chaque point d'intégration dans chaque couche (voir figure II.4). Ainsi, une fois que la théorie des stratifiés localise la charge au niveau du stratifié appliquée de manière incrémentielle à la couche puis au point d'intégration à travers l'épaisseur, ces contraintes et déformations locales sont appliquées au RUC par GMC. Ces théories de la micromécanique se localisent au niveau de la sous-cellule et les modèles de déformation non linéaire de MAC/GMC pour les constituants sont appliqués. Les effets de ces mécanismes locaux sur le stratifié sont ensuite captés par homogénéisation aux niveaux de la couche et du stratifié. La figure II.5 illustre un diagramme d'arbre du stratifié [0/90] spécifique où le niveau 1 est associé aux constituants de la fibre (F) et de la matrice (M); le niveau 2 est le RUC qui opère aux points d'intégration dans la couche; et le niveau 3 est la réponse réelle du stratifié composite lui-même [20]. Un examen des équations de la théorie classique des stratifiés, y compris les déformations thermiques

Chapitre II La méthode généralisée de cellules et la théorie des stratifiés et inélastiques, qui est utilisée pour effectuer l'homogénéisation/localisation entre les niveaux 2 et 3, est donné ci-dessous.

La figure II.4 illustre la géométrie de la théorie des stratifiés. Les coordonnées 1, 2 se réfèrent aux coordonnées principales du matériau d'un stratifié (couche), et les coordonnées x, y se réfèrent au stratifié.

Figure II.4 :Théorie des stratifiés multi-échelles disponible en MAC/GMC, où 𝑘 est le numéro de couche [12].

Figure II.5 :Diagramme d'arbre au niveau du stratifié [0°/90°] pour la théorie des stratifiés multi-échelles [20].

En supposant une contrainte plane, les équations constitutives pour un stratifié en présence de déformations inélastiques sont [17] :

[ 𝜎1 𝜎2 𝜏₁₂] = [ 𝑄₁₁𝑘 𝑄₁₂𝑘 0 𝑄₁₂𝑘 𝑄₂₂𝑘 0 0 0 𝑄₆₆𝑘 ] [ 𝜀₁− 𝜀₁𝐼 − 𝛼₁𝑘∆𝑇 𝜀₂− 𝜀₂𝐼 _{− 𝛼} 2𝑘∆𝑇 𝛾₁₂− 𝛾₁₂𝐼 ]

où 𝜎₁, 𝜎₂ et 𝜏₁₂ sont les composantes de contrainte dans le plan et 𝜀₁, 𝜀₂ et 𝛾₁₂ sont les composantes de déformation dans le plan (la note 𝛾 fait toujours référence à la déformation de cisaillement technique). De plus, 𝑄_𝑖𝑗𝑘 sont les composantes de la matrice de rigidité réduite pour la 𝑘ième couche:

𝑄₁₁𝑘 = 𝐸1 𝑘 1 − 𝜈₁₂𝑘𝜈₂₁𝑘 𝑄12 𝑘 ₌ 𝜈12 𝑘 _𝐸 2𝑘 1 − 𝜈₁₂𝑘𝜈₂₁𝑘 𝑄22 𝑘 ₌ 𝐸2 𝑘 1 − 𝜈₁₂𝑘𝜈₂₁𝑘 𝑄66 𝑘 _{= 𝐺} 12𝑘

Chapitre II La méthode généralisée de cellules et la théorie des stratifiés

18

les composantes de la déformation inélastique [17]. Notez que dans le contexte de la théorie des stratifiés multi-échelles, les contraintes, les déformations et les propriétés des matériaux dans les équations ci-dessus (applicables à une couche) sont les quantités moyennes effectives de cellule unitaire dans la théorie de la micromécanique (GMC). Les propriétés des constituants sont utilisées pour déterminer les propriétés effectives des couches (homogénéisation) à utiliser dans les équations de la théorie des stratifiés, tandis que les contraintes et les déformations des couches sont utilisées pour déterminer les contraintes et les déformations locales des sous-cellules (localisation).

Les équations de transformation des coordonnées sont utilisées pour transformer les composantes de contrainte, déformation, CTE et de rigidité réduite entre le système de coordonnées principal du matériau (1,2) de chaque couche et le système de coordonnées global (x,y) [18]. Ceux-ci sont données par [ 𝜎₁ 𝜎₂ 𝜏₁₂] = T1[ 𝜎_𝑥 𝜎_𝑦 𝜏_𝑥𝑦] [ 𝜀₁ 𝜀₂ 𝛾₁₂] = T2[ 𝜀_𝑥 𝜀_𝑦 𝛾_𝑥𝑦] (8) où T₁ = [

cos2_{𝜃 sin}2_{𝜃 2 cos 𝜃 sin 𝜃} sin2𝜃 cos2𝜃 −2 cos 𝜃 sin 𝜃 − cos 𝜃 sin 𝜃 cos 𝜃 sin 𝜃 cos2𝜃 − sin2𝜃 ]

T₂ = [

cos2_{𝜃 sin}2_{𝜃 cos 𝜃 sin 𝜃} sin2_{𝜃 cos}2_{𝜃 − cos 𝜃 sin 𝜃} −2 cos 𝜃 sin 𝜃 2 cos 𝜃 sin 𝜃 cos2_{𝜃 − sin}2_𝜃

]

et 𝜃 est l'angle de la couche. L'équation de transformation des coordonnées pour les matrices de rigidité réduites est donnée par

Q

̅_{𝑘 = T1}−1_Q 𝑘T2

où Q̅_𝑘 est la matrice de rigidité réduite tournée. Notez que les déformations inélastiques et les CTE se transforment selon les équations de transformation des déformations EQ. (8). Après transformation, les équations constitutives du pli dans le système de coordonnées du stratifié sont données par [18] [ 𝜎_𝑥 𝜎_𝑦 𝜏_𝑥𝑦] = [ Q̅₁₁𝑘 Q̅₁₂𝑘 Q̅₁₆𝑘 Q̅₁₂𝑘 _Q̅ 22 𝑘 _Q̅ 26 𝑘 Q̅₁₆𝑘 Q̅𝑘₂₆ Q̅𝑘₆₆ ] [ 𝜀_𝑥− 𝛼_𝑥𝑘_{∆𝑇 − 𝜀} 𝑥 𝑝 𝜀_𝑦− 𝛼_𝑦𝑘∆𝑇 − 𝜀_𝑦𝑝 𝛾_𝑥𝑦− 𝛼_𝑥𝑦𝑘 ∆𝑇 − 𝛾_𝑥𝑦𝑝 ] (9)

Selon l'hypothèse de Kirchhoff-Love pour les plaques, une section transversale plane qui est à l'origine perpendiculaire au plan moyen du stratifié (un plan x, y) reste plane et perpendiculaire au plan moyen lorsque le stratifié est soumis à la flexion et à l'extension. Cette hypothèse conduit aux expressions suivantes pour les composantes de déplacement dans le plan, 𝑢 et 𝑣 :

𝑢 = 𝑢₀− 𝑧𝜕𝑤0

𝜕𝑥 𝑣 = 𝑣0− 𝑧 𝜕𝑤0

𝜕𝑦 où 𝑢₀, 𝑣₀ et 𝑤₀ sont les déplacements du plan moyen.