Etude des propriétés structurales et électroniques de l'alliage InxGa1-x Sb par la méthode ab-initio FP-LMTO

Université Djilali LIABES

FACULTE DES SCIENSES EXACTES

SIDI BEL-ABBES

Mémoire DE MAGISTER

Présenté par

M

elle

_{MOUSSALI Amel}

Spécialité : physique

Option : Physique et chimie des Matériaux

Intitulé

Etude des propriétés structurales et électroniques de

l'alliage In

x

Ga

1-x

Sb

par la méthode ab-initio

FP-LMTO

Soutenue le :

Devant le Jury composé de :

Président Mr_{. MOULAY Noureddine MCA UDL-SBA-}

Examinateurs Mr_{. BENSAID Dlillali M. Ab MCA CU Ain temouchent} Directeur de mémoire Mr_{. AMERI Mohammed Pr UDL-SBA Rabah}

KHENATTA Pr

Dédicaces

Je dédie le fruit de mon travail à : Ma très chère mère Mon très cher père Mon cher frère Mes chères sœurs Mon cher fiancé Toutes mes amies

AMEL

[Tapez un texte] Page i

Nomenclature: les notations utilisées dans ce mémoire sont listées ci-dessous :

𝑯 Hamiltonien d’un système. 𝑻𝑬 Energie cinétique des électrons.

𝑻𝒏 Energie cinétique des noyaux.

𝑽 Energie potentiel Muffin-tin.

𝑽_𝒏𝒏 Energie potentielle d’interaction entre les noyaux. 𝑽𝒆𝒆 Energie potentielle de répulsion entre les électrons.

𝑽_𝒏𝒆 Energie potentielle d’attraction noyaux-électrons. 𝑽𝒆𝒇𝒇 Potentiel extérieur effectif.

𝑽_{𝑯𝒂𝒓𝒕𝒓𝒆𝒆} Potentiel de Hartree

𝑽𝑿𝑪 Potentiel d’échange et corrélation.

𝑽𝑿𝒂 Potentiel local.

W Interaction coulombienne de l’électron avec tous les noyaux du cristal.

𝑼_𝒊 Répulsion coulombienne exercée sur l’électron i par tous les autres électrons j≠i. 𝑭_𝑯−𝑲 Fonctionnelle de Hohenberg et Kohn.

𝜳 Fonction d’onde exacte d’un système à N particules.

𝝍 Fonction d’onde indépendante du temps d’un système à N particules.

𝝋𝒋 Fonction d’onde mono-particulaire relative à la particule j (orbitale de

Kohn-Scham).

𝝆𝒇𝒐𝒏𝒅 Densité électronique de l’état fondamental.

𝜵 _{Opérateur gradient}𝛿 𝛿𝑥𝑖 +

𝛿 𝛿𝑦𝑗 +

𝛿

𝛿𝑧𝑘 (en coordonnées cartésiennes).

Δ _{Opérateur Laplacien} 𝛿2

𝛿𝑥2𝑖 +

𝛿2

𝛿𝑦2𝑗 +

𝛿2

𝛿𝑧2𝑘 (en coordonnées cartésiennes).

𝛉_𝐃 Température de Debye 𝐍𝐀 Le nombre d’Avogadro. M La masse molaire

𝛒 La densité

[Tapez un texte] Page i

Quelques constantes

h Constante de Planck : 6,626 18(4).10−34 J.s ℏ=𝒉/𝟐

𝒎_𝒆 Masse d’électron : 9,109 53(5).10−31kg

e Charge élémentaire : 1,602 189 (5).10−19 Coulomb 𝒂𝟎 Rayon de Bohr : 0,529 177 1(5).10−10m

c Vitesse de la lumière dans le vide : 2,997 927 58(1) m.s-1 Kb Constante de Boltzmann (1.38´ 10-23 J.K-1)

Indices et exposants

fond Relatif à l’état fondamental. MT Muffin-Tin.

F Relatif à un vecteur d’onde ou une énergie de Fermi. H.K Relatif à la théorie de Hohenberg et Kohn.

K .S Relatif à la théorie de Kohn et Sham. DFT Théorie de la fonctionnelle de la densité. LDA Approximation de la densité local. GGA Approximation du gradient généralisé.

Figure Titre Page

Figure I.1 Le schéma du calcul self consistant de la fonctionnelle de densité. 14

Figure II.1: Figure II.2

Potentiel Muffin-tin.

Comparaison des fonctions de Hankel standard et lisse.

17 22

Figure III.1 Extrait de la classification périodique des éléments. 33

Figure III.2 L'Indium. 33

Figure III.3 Le Gallium. 35

Figure III.4 L'Antimoine 37

Figure III.5 Structure cristalline de InSb. 38

Figure: III.6 Structure cristalline de GaSb. 39

Figure IV.1 Variation l’énergie totale de InSb (zinc-blende) en fonction du volume

en utilisant la LDA.

44

Figure IV.2 Variation l’énergie totale de GaSb (zinc-blende) en fonction du

volume en utilisant la LDA.

44

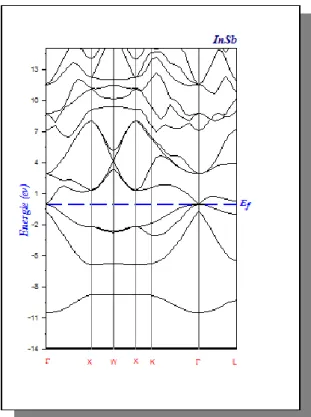
Figure IV.3 Structure de bandes de InSb en LDA 46

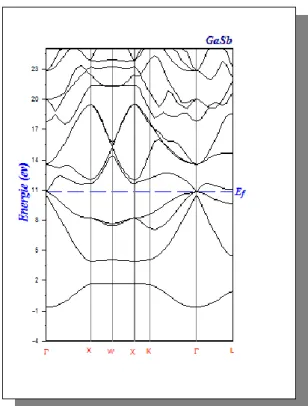
Figure IV.4 Structure de bandes de GaSb en LDA 47

Figure IV.5 Variation de l’énergie totale de In0, 25Ga0, 75Sb en fonction du volume

pour la LDA .

50

Figure IV.6 Variation de l’énergie totale de In0, 5Ga0, 5Sb en fonction du volume

pour la LDA .

51

Figure IV.7 Variation de l’énergie totale de In0, 75Ga0,75Sb en fonction du volume

pour la LDA .

52

Figure IV.8 Variation du paramètre du réseau calculé en fonction de la

concentration, en LDA, comparés à la loi du Vegard (InxGa1-x Sb).

Figure IV.9 Variation du module de compressibilité calculé en fonction de la

concentration, pour le ternaire InxGa1-x Sb en LDA, comparés à la loi du

Vegard.

55

Figure IV.10 Structure de bande du In0.25Ga.75 Sb (zinc-blende) pour la LDA. 56

Figure IV.11 Structure de bande du In0.5Ga.5 Sb (zinc-blende) pour la LDA. 56

Figure IV.12 Structure de bande du In0.75Ga.25 Sb (zinc-blende) pour la LDA 57

Figure IV.13 Paramètre du courbure en fonction de la concentration x de l'alliage

InxGa1-x Sb

59

Tableau Titre Page

Tableau IV.1 Paramètres constitutifs de InSb et GaSb utilisés dans nos calculs

effectués par la méthode FP-LMTO

43

Tableau IV.2 propriétés structurales (paramètre du réseau 𝑎₀, module de

compressibilité 𝐵₀ et sa dérivée 𝐵′₀) des composés binaires InSb et GaSb

45

Tableau IV.3 Energies des gaps des composés InSb et GaSb 48

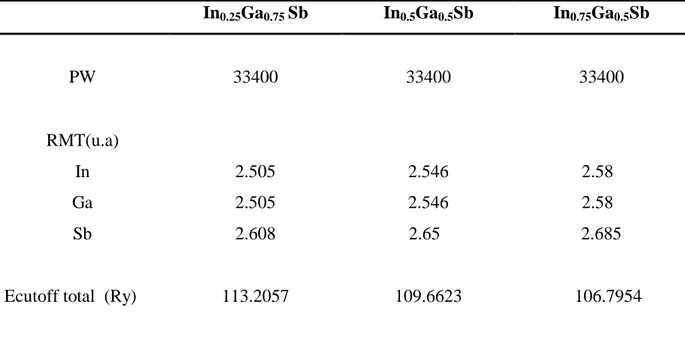
Tableau IV.4 Paramètres constitutifs de l’alliage InxGa1-x Sb utilisés dans nos

calculs par la méthode FP-LMTO

50

Tableau IV.5 Propriétés structurales de l’alliage InxGa1-x Sb (paramètre du réseau

a, module de compressibilité B0 et sa dérivée B’0) pour les

concentrations x=0.25, x=0.5 et x et 0.75.

53

Tableau IV.6 Energie de gap de l’alliage InxGa1-x Sb (phase zinc-blende) pour les

concentrations x=0.25, x=0.5 et x et 0.75.

58

Tableau IV.7 Décomposition du bowing optique des gaps de l’alliage InxGa1-x Sb

(x=0.25, x=0.5 et x et 0.75) Déformation du volume (VD),échange de charge (CE) et relaxation structurale (SR).

Introduction Générale

Introduction générale……….………... Références bibliographiques...

Chapitre I : Théorie de la fonctionnelle de densité

I.1. Introduction……….………...

I.2. Equation de Schrödinger………..…………...07

I.3. Approximation de Born-Oppenheimer……….………...08

I.4. Approximation de Hartree (des électrons libres)………..………...08

I.5. Théorie de la Fonctionnelle de la Densité……….………..………...09

I.5.1. Théorèmes de Hohenberg-Kohn……….……….….……...10

I.5.2. Les équations de Kohn-Sham……….…………..………….……...11

I.5.3. Traitement de terme d’échange et corrélation………...………...13

I.5.3.a Approximation de la densité locale (LDA) ………...13

I.5.3.b Approximation du gradient généralisé (GGA)………...15

I.5.4 Résolution des équations de Kohn-Sham……….…………......6

Références bibliographiques………...…..18

Chapitre II : La méthode de la FPLMTO II.1. Introduction…………..……….………...……20

II.2. Approximation Muffin-tin... II.3. Instruction de base………..……….……….22

II.3..1 Fonctions de base………..…...22

01 03 03 03 04 05 06 06 07 16 16 17 18 09 09 11 12 14

II.5. Fonctions lisses de Hankel (Smooth Hankel functions)………...25

II.5.1. Propriétés de base………..……..……..…...26

II.5.2 Formalisme des fonctions de Hankel lissées…….………..…..………...27

II.5.3 Les avantages des fonctions enveloppes lisses de Hankel……….……...28

II.6. Matrices du chevauchement et Hamiltonien………..………...31

II.7. Contribution d’échange et de corrélation………...…...32

II.8. Les fonctions d’onde……….………...33

II.9. Calcul de la densité de charge………...3

II.10. Harmonie sphérique... II.11. Augmentation LAPW et LMTO……….……….……..35

II.12. Avantages et inconvénients de la méthode (LMTO)………….…...………36

Références bibliographique……….………...…...39 62 Chapitre III: Généralité sur les alliage et présentation des matériaux

III.1. Introduction...

III.1. Les alliages semi-conducteurs... III.2. présentation des matériaux... III.2.1. L'indium... III.2.2. Le Gallium... III.2.3. L'Antimoine... III.3. Présentation des alliages binaires InSb et GaSb... Références bibliographiques... 21 21 22 24 25 26 26 27 28 28 29 31 32 32 32 33 35 37 38 40

VI.1. Introduction………...………...67

VI.1.1. Détail de calcul………..…...6.7

VI.2. Propriétés structurale, électroniques et optiques des composés binaires InSb et

GaSb……….………...68

VI.2.1. propriétés structurales des composés binaire InSb et GaSb………...……...

VI.2.2. Propriétés électronique des composés binaires InSb et GaSb...

VI.3. Propriétés structurales et électroniques de l'alliage ternaire InxGa1-x Sb... VI.3.1. Méthode de calcul...

VI.3.2. Propriétés structurales de l'alliage InxGa1-x Sb :……….…...7.3. VI.3.3. Propriétés électroniques de l'alliage InxGa1-x Sb...

VI.3.3.1. Structure de bande...

Références bibliographiques………...………..135 Conclusion générale Conclusions générales……….………....139 41 41 41 42 45 48 48 50 52 55 55 62 61

1

De nos jours, les matériaux évoluent beaucoup plus vite qu’a tout autre moment de leur histoire. La recherche de nouveaux matériaux aux propriétés physiques et/ou chimiques spécifiques est un enjeu majeur de l’industrie actuelle, et quels que soient les domaines d’applications considérés (matériaux émergents, micro-électronique, environnement, biomatériaux, énergie etc.) la physique des matériaux joue un rôle de plus en plus important dans les applications technologiques, et ce rôle ne fera que progresser dans beaucoup des domaines en modélisant des milliers des matériaux avec des caractéristiques spécifiques qui répondent aux besoins d’une industrie en pleine expansion.

Avant d’employer les matériaux dans l’industrie, il faut s’assurer de la qualité de leurs propriétés structurales, électroniques, mécaniques…etc. La compréhension des propriétés physique d’un matériau nécessite la connaissance fondamentale de sa structure, sa stabilité de phases et de ses diverses propriétés structurales, électroniques. Cette science a connu de nombreuses réussites dans le domaine de la modélisation et la prédiction des propriétés des matériaux, notamment de leurs propriétés électroniques et optiques. Le cout exorbitant lors de la fabrication de nouveaux composants a poussé les chercheurs a utilisé la simulation pour mieux comprendre les phénomènes physiques et pour proposer des pistes d’améliorations des structures et de nouvelles architectures de dispositifs à moindre cout. Des logiciels de simulation sont utilisés pour résoudre numériquement les systèmes d’équations obtenues par les lois de la physique qui sont difficiles à résoudre analytiquement. Avant la fabrication d’un nouveau matériau , les chercheurs procède la simulation qui est définit dans le cas général comme une technique permettant de reproduire de façon virtuelle le comportement d'un phénomène réel, et dans ce cas, les résultats obtenus sont très satisfaisantes, car la simulation gagne en terme de cout et de temps par rapport à la fabrication et elle peut même remplacer l’expérience qui est parfois coûteuse, dangereuse où même inaccessible au laboratoire. Les techniques de calcul de la structure électronique mises au point au cours des dernières décennies sont nombreuses, et en particulier, les méthodes ab-initio (méthode de premier principe) utilisant seulement les constantes atomiques comme données pour la résolution l’équation de Schrödinger qui sont devenues aujourd’hui un outil de base pour le calcul des propriétés électroniques et structurales des systèmes les plus complexes ainsi leur propriétés physique [1]. Parmi ces méthodes ab-initio, la méthode des ondes planes augmentées

linéarisées (FP-LMTO) est l’une des plus précises méthodes de calcul actuellement [2] . Les semi conducteurs antimoniures III-Sb sont des composés formés a partir d'éléments de la

2

3 eme colonne de la classification périodique des éléments et l'élément de la 5eme colonne qui est l'Antimoine (Sb) .Ces matériaux cristallisent dans la phase cubique Zinc-blende qui se constitue de deux sous-réseaux cubique a face centré (cfc) décalé par rapport de l'autre de 1/4 de la diagonal du cube [3] .

L’objectif de ce travail est l’étude des propriétés structurales, électroniques et le calcul du coefficient de désordre par l'approche de Zunger de l'alliage ternaire InxGa1-xSb (0 ≤ x ≤1) des

composés binaire InSb et GaSb dont l'énergie de gap à 0K° varie de 0.812 ev pour le GaSb et 0.23 ev pour le InSb[4]. Ces matériaux ont une grande importance dans les applications optoélectronique et en particulier dans la réalisation des diodes laser ou diodes électroluminescentes[5].

Le travail que nous présentons dans ce mémoire comprend quatre parties :

Dans la première partie, nous rappelons le principe de la densité fonctionnelle de la théorie (DFT) qui considère la densité électronique comme variable fondamentale et toutes les propriétés physiques, notamment l’énergie totale du système d’électrons, peuvent être exprimés comme une fonction de celle-ci. Cette densité peut être obtenue par la résolution des équations de Kohn et Sham [6].

Dans la partie qui suit, nous détaillons la méthode de calcul FP-LMTO , utilisée tout au long de notre travail.

Dans la troisième partie, nous présentons les matériaux utilisé dans notre travail.

La dernière partie est destinée à l’exploitation des différents résultats obtenus par notre simulation.

En dernier lieu, une conclusion générale suivit par des perspectives pour résumer l’essentiel des points abordés et énumérer les résultats les plus intéressants, tout en proposant des voies d’explorations futures.

Chapitre I:

Théorie de la fonctionnel de densité

I.1 Introduction.

I.2 Equation de Schrödinger.

I.3 Approximation de Born-Oppenheimer.

I.4. Approximation de Hartree (des électrons libres). I.5. Théorie de la Fonctionnelle de la Densité. I.5.1 Théorèmes de Hohenberg-Kohn. I.5.2 Les équations de Kohn-Sham.

I.5.3 Traitement de terme d’échange et corrélation. I.5.3.a Approximation de la densité locale (LDA). I.5.3.b Approximation du gradient généralisé (GGA). I.5.4 Résolution des équations de Kohn-Sham.

Références bibliographiques.

4 I.1 Introduction

La connaissance de la structure électronique a un rôle déterminant dans la compréhension des propriétés physiques et chimiques des matériaux. Le calcul de la structure électronique d'un cristal revient à résoudre le problème des interaction entre un grand nombre de noyaux et d'électrons, ce qui rend la résolution de l'équation de Schrödinger impossible.

Du côté théorique, plusieurs méthodes ont été utilisées au cours des dernière décennies pour calculer la structure électronique, La Théorie de la Fonctionnelle de la Densité ou DFT (Density Functional Theory) [1] développé en 1964-1965 par Hohenberg, khon et Sham constitue actuellement l'une des méthodes les plus utilisées dans les calculs quantiques de la structure électronique de la matière. Elle permets de réduire le problème à plusieurs corps en un problème à un corps.

Dans ce chapitre nous allons présenter la théorie de la fonctionnelle de la densité (DFT),cette méthode fait partie des méthodes ab-initio qui constituent un outil puissant pour prédire les propriétés structurales et électroniques des matériaux et donne dans une grande majorité de cas, des résultats satisfaisants . Elle est basée principalement sur la résolution des équations de la mécanique quantique et en particulier l'Equation de Schrödinger. La résolution de cette dernière équation reste très difficile, ce qui conduit à présenter de multiples approximations de manière à rendre la résolution de cette équation maitresse plus facile.

I.2 Equation de Schrödinger

Les solides sont constitués par une association de particules élémentaires: les noyaux et les électrons en interaction . Le problème théorique fondamental de la physique des solides est de comprendre l'organisation de ces particules a l'origine de leurs propriétés. Mais dans ce cas, la mécanique classique s'avère être très insuffisante et il faut faire appel a la mécanique quantique dont la base est la résolution de l'équation de Schrödinger [2] proposé par le physicien Autrichien Erwin Schrödinger en 1926 qui décrit toutes ces interactions :

𝑯 𝜓 = 𝐸𝜓 (I.1)

ou:

𝑬: Energie totale du système.

5

𝑯 : L'opérateur Hamiltonien donné par la relation suivante [3] :

𝑯 = 𝑻 _𝒏+ 𝑻_𝒆+ 𝑽_𝒆−𝒆 + 𝑽_𝒆−𝒏 + 𝑽_𝒏−𝒏 (I.2)

Avec :

 𝑻𝒏 : L’énergie cinétique des noyaux.

 𝑽_𝒏𝒏 : terme d’interaction noyaux- noyaux.

 𝑽_𝒆𝒏 : terme d’interaction électrons-noyaux.

 𝑽_𝒆𝒆 : terme d’interaction électron-électron.

 𝑻_𝒆 : terme d’énergie cinétique des électrons.

En détail, le développement de l’Hamiltonien 𝑯 du système s’écrit:

𝑯 = _{𝟒𝝅 𝜺}𝒆𝟐 𝟎+ − ℏ𝟐 𝐦𝐢 𝐢 𝚫_𝟐𝐢 + 𝒆 𝟐 𝟒𝝅 𝜺𝟎 −𝒁𝒌 𝒓𝒊 _ 𝑹𝒌 𝒊,𝒌 + 𝒆 𝟐 𝟒𝝅 𝜺𝟎 −𝟏 𝒓𝒊 _ 𝒓𝒋 𝒊 ≠𝒋 + − ℏ 𝟐 𝐦𝐢 𝐢 𝚫_𝟐𝐢 (I.3)

Les termes contenant 𝚫_𝐢 représentent l’énergie cinétique respectivement de l’électron et du noyau. Les trois derniers termes décrivent respectivement les interactions électrostatiques électrons- électrons, noyaux-noyaux et noyaux-électron. En appliquant l’approximation de Born-Oppenheimer qui permet de négliger l’énergie cinétique des noyaux, l’équation de Schrödinger peut s’exprimer pour un ensemble de positions fixées des noyaux. On a alors à résoudre l’Hamiltonien électronique suivant :

𝑯 = 𝑻 𝒆+ 𝑽𝒆𝒆+ 𝑽𝒆𝒏 (I.4)

Le problème de la résolution de l’équation de Schrödinger se réduit à celui du comportement des électron , mais il reste encore très complexe à cause de l’existence du terme d’interaction électron-électron( dernier terme de l’équation ).Cette difficulté à décrire les électron en interaction oblige à passer par des approximation pour résoudre ce problème, comme l’approximation de Hartree [4] et la Théorie de la Fonctionnelle de la Densité (DFT) que nous exposons ci-dessous.

I.3 Approximation de Born-Oppenheimer

Suivant Born et Oppenheimer [5], on commence par négliger le mouvement des noyaux par rapport à celui des électrons. Elle est justifiée par le fait que la masse des noyaux est plus de

6

trois ordres de grandeur supérieure à celle des électrons. Alors les électrons se déplacent donc plus rapidement que les noyaux atomiques. On néglige ainsi l’énergie cinétique 𝑻_𝒏 des

noyaux et l’énergie potentielle noyaux-noyaux 𝑉 _𝑛𝑛 devient une constante qu’on peut choisir comme la nouvelle origine des énergies. L’Hamiltonien total peut alors être remplacé par l’Hamiltonien électronique suivant [5] :

𝑯 = 𝑻 _𝒆+ 𝑽_𝒆𝒆+ 𝑽_𝒆𝒏 ( I.5)

L’équation de Schrödinger est donc réécrite de la façon suivante :

𝑯 𝝍_𝒆 = 𝑬 𝝍_𝒆 (I.6)

Avec 𝛹𝑒 𝑒𝑡 𝐸𝑒 : l’état propre et l’énergie propre du système de 𝑁𝑒 électrons.

𝐸𝑇𝑂𝑇𝐴𝐿𝐸 L’énergie totale du système est alors donnée par:

𝑬_{𝑻𝑶𝑻𝑨𝑳𝑬} = 𝑬_𝒆+ 𝑬_𝒏𝒐𝒚 (I.7)

Bien que le problème soit grandement simplifie, la résolution exacte de l'équation (I.6) est toujours impossible. Cependant il est possible d’accéder à l’état fondamental du système, l’énergie associée répondant à un principe variationnel. En effet l’état fondamental du système de Ne électrons est par définition l’état qui minimise l’énergie Ee. C’est dans la

recherche de minimum d’énergies que les techniques ab-initio vont intervenir.

I.4. Approximation de Hartree (des électrons libres):

L’approximation de Hartree [6] consiste à chercher les fonctions propres de l’Hamiltonien 𝑯

sous la forme approchée :

𝝍_{𝒂𝒑𝒑𝒓𝒐𝒄𝒉é𝒆} = 𝝍_𝟏 𝒓_𝟏 + 𝝍_𝟐 𝒓_𝟐 + ⋯ 𝝍_𝒏 𝒓_𝒏 (I.8)

Cette approximation est basée sur l’hypothèse des électrons libres ce qui revient à ne pas tenir compte des interactions entre les électrons et des états de spin. Ceci a deux conséquences importantes :

La répulsion coulombienne totale du système électronique est surestimée. Le principe d’exclusion de Pauli n’est pas pris en compte.

7 I.5 Théorie de la Fonctionnelle de la Densité

Parmi les méthodes ab initio, La Théorie de la fonctionnelle de la densité (Density Functional Theory, DFT), [7,8] est une méthode de calcul de structure électronique dans laquelle la densité électronique n (⃗r) occupe la place centrale, au lieu de la fonction d'onde à N corps Ψ(⃗𝑟 ⃗, ⃗ 𝑟1 ⃗, ..., ⃗ 𝑟2 ⃗) comme c'est le cas pour la méthode Hartree-Fock. Elle trouve ses origines 𝑁

dans le modèle développé par Thomas et Fermi à la fin des années 1920 mais ce n'est qu'au milieu des années 1960 que les contributions de P. Hohenberg et W.Kohn [7] d'une part et W. Kohn et L.J. Sham [8] d'autre part permettent d'établir le formalisme théorique sur lequel repose la méthode actuelle. Il s'agit d'une théorie exacte dans son principe qui permet de calculer toutes les propriétés de l'état fondamental dont l'énergie. Alors que la fonction d'onde multiélectronique dépend de 3N variables, la densité est seulement fonction de trois variables, ce qui réduit considérablement les temps de calculs et permet d'étudier des systèmes de grandes tailles hors de portée des autres méthodes basées sur la fonction d'onde

I.5.1 Théorèmes de Hohenberg-Kohn

Le formalisme de base de la DFT est basé sur le théorème de Hohenberg-Kohn (1964) [9].

Cette approche s’applique pour tout système à plusieurs particules en interaction évoluant dans un potentiel externe. Elle repose sur deux théorèmes :

Premièrement Hohenberg et Kohn ont montré que l'énergie totale d'un gaz d'électrons en présence d'un potentiel extérieure set une fonctionnelle unique de la densité électronique ρ(r):

𝑬 = 𝑬[𝝆_𝒓] (I.9)

Deuxièmes Hohenberg et Kohn montre que la valeur minimale de cette fonctionnelle est l'energie exacte de l'état fondamental, et que la densité qui conduit à cette 'énergie est la densité exacte de l'état fondamental sont aussi fonctionnelles de cette densité.

𝑬 𝝆_𝟎 = 𝒎𝒊𝒏 𝑬(𝝆 ) (I.10)

𝜌₀: la densité de l'état fondamental.

La fonctionnelle de l'énergie totale de l'état fondamental s'écrit comme suit :

8

ou:

𝑭[𝝆𝒓] = 𝝍 𝑻 + 𝑽 𝝍 (I.12)

La fonctionnelle 𝑭[𝝆_𝒓] est universelle pou n'importe quel systéme à plusieurs électrons. Si la fonctionnelle 𝑭[𝝆𝒓] est connue, alors, il sera relativement facile d'utiliser le principe

vibrationnel pour déterminer l'énergie totale et la densité électronique de l'état fondamental pour un potentiel extérieur donné. Malheureusement, le théorème de Hohenberg et Kohn ne donne aucune indication de la forme de 𝑭[𝝆𝒓]

I.5.2. Les équations de Kohn-Sham

Kohn et Sham [10] ont écrit la densité électronique comme étant la somme des densités des particules libres. Ils ont utilisé le principe variationnel pour obtenir l'énergie de l'état fondamental et la densité donnant la fonctionnelle 𝑬 [𝝆𝒓] s'écrit sous la forme :

𝑬_𝒆𝒙𝒕 𝝆 = 𝑻_𝟎 𝝆 + 𝑽_𝑯 𝝆 + 𝑽_𝑿𝑪 𝝆 + 𝑽_𝒆𝒙𝒕[𝝆] (I.13)

Ou

𝑇₀: est l'energie cinétique du systéme sans intéraction

𝑉𝐻:désigne le termr de Hartree (l'intéraction de Coulomb classique entre les électrons)

𝑉_𝑋𝐶: le term qui comprend les effets d'échange et de corrélation

𝑉_𝑒𝑥𝑡: inclut l'intéraction coulombienne des électrons avec les noyaux et celle des noyaux entre eux.

Le terme de Hartree et celui de l'energie cinétique jouent un role important dans la description des états des électrons libres.

En 1965 Walter Kohn et Lu Sham [10] proposaient une méthode pratique permettant d’utiliser la théorie de la fonctionnelle de la densité. Tout d’abord ils supposent qu’il existe un système fictif de N électrons indépendants ayant la densité dans son état fondamental

𝜌

_{𝑓𝑜𝑛𝑑}

𝑟

. L’intérêt vient du fait que les expressions de l’énergie cinétique et de l’énergie potentiel pour ce système fictif sont connues. Puis, ils montrent que pour qu’il en soit ainsi, ces électrons

9

doivent être plongés dans un potentiel extérieur effectif, c’est la première équation de Kohn-Sham (K.S)

V

_eff

ρ(r)

:

𝑽𝒆𝒇𝒇 𝝆(𝒓) ⃗ = 𝑽𝒆𝒏(𝒓) ⃗ + 𝑽𝑯𝒂𝒕𝒓𝒆𝒆 (𝒓) ⃗ + 𝑽𝒙𝒄 𝝆 (𝒓) ⃗ (I.14)

Avec

𝑉

_{𝐻𝑎𝑡𝑟𝑒𝑒}

(𝑟)

⃗ le potentiel de Hartree qui définie par : 𝑽_{𝑯𝒂𝒕𝒓𝒆𝒆} (𝒓) ⃗ = 𝝆 (𝒓′) ⃗ 𝒅𝒓′

𝒓′_−𝒓 (I.15)

Et

𝑉

_𝑥𝑐

𝜌 (𝑟)

⃗

le potentiel d’échange et corrélation :

𝑉_𝑥𝑐 𝜌 (𝑟) ⃗ =𝛿𝐸𝑥𝑐 𝜌

𝛿𝜌 (𝑟) ⃗ (I.16)

Dans cette expression (I.16) 𝐸𝑋𝐶 est l’énergie d’échange-corrélation, qui regroupe tout ce qui

n’est pas connu dans le système, à savoir les effets de corrélations dues à la nature quantique des électrons. Ce terme définie par :

𝐸_{𝑥𝑐 𝜌} =

𝐹

_𝐻𝐾

𝜌

_8𝜋𝜀𝑒2 0

𝑑

3

_𝑟

_′𝜌 𝑟 ⃗ ′ 𝜌(𝑟) ⃗ 𝑟

⃗−𝑟 ⃗ ′

− 𝑇

𝑓𝑜𝑛𝑑

𝜌

(I.10)

𝑇₀ [ρ] est l’énergie cinétique des électrons de Kohn-Sham et le second terme le terme électrostatique de Hartree.

Pour calculer la densité électronique 𝜌𝑓𝑜𝑛𝑑 et l’énergie E du système, ils ont ainsi remplacé le

problème de départ : E 𝑯𝝍𝒋 = 𝑬𝝍𝒋 𝝆_{𝒇𝒐𝒏𝒅} (𝒓) ⃗ = 𝐝𝟑𝐫_𝟐 … … … … 𝐝 𝟑_𝐫 𝐍 𝝍𝒇𝒐𝒏𝒅 𝒓 ⃗, 𝒓 ⃗ … … … . 𝒓𝟐 ⃗ 𝒏 𝟐 (I.18)

Par le problème plus simple.

E’ 𝑯𝑲𝑺𝝋𝒋(𝒓) ⃗ = 𝜺𝑱𝝋𝒋(𝒓) ⃗ ⇔ −ℏ𝟐𝛁𝟐

𝟐𝒎 +𝑽𝒆𝒇𝒇 𝝋𝒋 𝒓 ⃗ = 𝜺𝑱𝝋𝒋(𝒓) ⃗

𝝆𝒇𝒐𝒏𝒅 (𝒓) ⃗ = 𝝋𝑵𝒋=𝟏 𝒋(𝒓) ⃗

𝟐 (I.19)

Le problème E’ est plus simple que le problème E car :

 On résoud une équation de Schrödinger à une seule particule (mono-électronique) utilisant le potentiel 𝑽𝒆𝒇𝒇 qui permet d’obtenir la seconde équation de Kohn-Sham à

Ne états 𝜑𝑗 .

 On donne l’expression de la densité électronique en fonction des 𝑁𝑒 fonctions d’onde

10

Ces trois équations interdépendantes doivent être résolues de manière auto-cohérente afin de trouver la densité de l’état fondamental. Tous les calculs de type DFT sont basées sur la résolution itérative de ces équations. Notons que pour la DFT, seules

l’énergie totale, l’énergie de fermi et la densité électronique ont un sens physique. Les états et les énergies de Kohn-Sham ne sont que des intermédiaires de calcul. Néanmoins, ils sont utilisés dans de nombreux travaux scientifiques, pour calculer certaines grandeurs comme les structures de bande.

I.5.3 Traitement de terme d’échange et corrélation:

La théorie de la fonctionnelle de la densité appliquée dans le cadre de l’approche orbitalaire de Kohn-Sham demeure exacte dans son formalise. Progressivement, la partie inconnue dans la fonctionnelle E[ρ] a été réduite à une fonctionnelle universelle 𝑭𝑯𝑲 [ρ] et

finalement à une énergie d’échange et corrélation 𝑬_𝑿𝑪 [ρ]. A ce stade, il est nécessaire d’approcher l’expression de cette fonctionnelle d’échange et corrélation qui repose sur un certain nombre d’approximations :

I.5.3.a Approximation de la densité locale (LDA):

L’approximation de la densité local ou LDA [11] considère le potentiel d’échange et

corrélation comme une quantité locale, définie en un point r, dépendant faiblement des variations de la densité autour de ce point r [12 ,13]. Ainsi, en un point r auquel correspond

une densité ρ(r), il sera associé un potentiel d’échange et corrélation comparable à celui d’un gaz homogène d’électrons de même densité ρ(r). L’énergie d’échange et corrélation 𝑬𝒙𝒄 𝑳𝑫𝑨 𝝆

s’exprime alors de la manière suivant [14] :

𝑬_𝒙𝒄 𝑳𝑫𝑨 𝝆 = 𝝆 𝒓 𝜺_𝒙𝒄𝝆 𝒓 ⃗ 𝒅𝒓 ⃗ (I.21)

Où :

𝜀

_𝑥𝑐 représente l’énergie d’échange et corrélation pour une particule d’un gaz homogène

d’électrons de densité ρ. Elle peut-être considérer comme la somme d’une contribution d’échange et corrélation :

𝑬_𝒙𝒄 = 𝜺_𝒙 𝝆 + 𝜺_𝒄 𝝆 (I.22)

Le terme d’échange

𝜀

𝑥

𝜌

, appelé échange de Dirac [15], est connu exactement par la

relation suivante :

𝑬𝒙𝒄 = −𝟑_{𝟒 𝝅}𝟑𝝆 𝒓 ⃗

𝟑 𝟒

11

La partie corrélation

𝜀

_𝑐

(𝜌)

ne peut être exprimée de manière exacte. L’approximation de ce terme est basée sur l’interpolation de résultats de calculs Monte-Carlo quantique de Ceperley et Alder (1980) [16]. Aujourd’hui, il existe dans la littérature des paramétrisations, numériques ou analytiques de

𝜀

_𝑐

(𝜌)

comme celle de Hedin et Lundqvist (1971) [17] ou Perdew et al [18].

En utilisant la LDA pour une molécule ou un solide on suppose implicitement que l’on peut obtenir l’énergie d’échange-corrélation pour un système inhomogène en considérant le gaz d’électrons comme homogène dans des portions infinitésimales de celui-ci. On peut alors appliquer localement à ces régions les résultats du gaz homogène et la sommation de ces contributions individuelles

𝜌 𝑟 𝜀

_𝑥𝑐

𝜌(𝑟⃗) 𝑑𝑟⃗

donne une valeur

approchée de l’échange-corrélation du système inhomogène.

Il va de soi que la validité de LDA suppose des systèmes où la densité électronique ne varie pas trop rapidement. L’efficacité de cette approximation est apparue à partir des années 1977 avec les travaux de Zunger et Freeman [19,20], ainsi que ceux de Moruzzi et al (1978) [21].

Enfin, notons qu’un précurseur de la LDA a été introduit par Slater en 1951 [22] où il proposa la méthode Xα comme une simplification de la méthode Hartree-Fock. Cette simplification aboutit à l’équation suivante :

(−ℏ

𝟐

𝐦𝐢𝛁𝐣

𝟐_{+ 𝐕}

𝐞𝐧+ 𝐕𝐇𝐚𝐫𝐭𝐫𝐞𝐞 𝐫⃗ + 𝐕𝐱𝛂𝐋𝐃𝐀 𝐫⃗ )𝝋𝒋(𝒓) ⃗ = 𝜺𝒋𝝋𝒋(𝒓) ⃗ (I.23)

Avec le potentiel local 𝑽𝑿𝜶 :

𝑽𝒙𝒄 𝝆 = −𝟑_𝟒𝛂 _𝝅𝟑𝝆 𝒓 ⃗

𝟏 𝟑

(I.24)

α désigne un paramètre qui a été initialement pris comme étant égal à 1. Par la suite il a été évalué pour tous les atomes neutres par Schwarz [23]. Il faut aussi noter que Kohn et Sham ont réalisé que l’équation 𝑿𝜶 était équivalente à la LDA, si la corrélation était

ignorée et si en plus α=2/3. La méthode 𝑿𝜶 peut donc être considérée comme un

formalisme de fonctionnelle de densité, qui néglige la corrélation et dont l’énergie est donnée par

𝑬_𝒙 𝑳𝑫𝑨 𝝆 = −𝟗_𝟖𝛂 𝟑_𝟒

𝟏 𝟑

12

La plus grande source d’erreur de la LDA provient de l’énergie d’échange qui est souvent sous-estimée tandis que l’énergie de corrélation est souvent surestimée même.

Si, en valeur absolue, sa contribution à l’énergie totale est plus petite. Ces deux erreurs ont tendance à s’annuler. Pour améliorer la précision des calculs DFT, nous avons besoin de meilleures approximations pour la fonctionnelle d’échange-corrélation. Certains auteurs ont eu l'idée de définir une fonctionnelle de la densité qu'ils ont associée à ses dérivées propres dans le but de prendre en compte l’inhomogénéité du système. Dans un premier temps, la LDA fut traitée comme le premier terme d’un développement en série de Taylor :

𝑬𝒙𝒄 𝑮𝑨𝑬 𝝆 = 𝜺𝒙𝒄𝑮𝑬𝑨 𝝆 𝒓 𝝆 𝒓 𝒅𝒓 + 𝑪𝒙𝒄 𝝆 𝒓 𝛁𝝆 𝒓

𝝆𝟑𝟒 𝒓 𝒅𝒓 + ⋯ (I.26)

Cette forme de fonctionnelle est l’approximation du gradient (GEA ou Gradient Expansion Approximation en anglais). Malheureusement, ceci donne de plus mauvais résultats que la LDA. En effet, le trou d’échange-corrélation ne satisfait plus les conditions qui assuraient à la LDA un certain sens physique. Afin de corriger ces problèmes, la fonctionnelle ci-dessus a été modifiée pour la forcer à respecter les principales conditions aux limites. Nous obtenons alors l’approximation du gradient généralisé (GGA ou Generalized Gradient Approximation en anglais) à l’origine du succès de la DFT :

𝑬_𝒙𝒄 𝑮𝑮𝑨[𝝆; 𝛁𝝆] = 𝜺_𝒙𝑮𝑮𝑨(𝝆, 𝛁𝝆)+𝜺_𝒄𝑮𝑮𝑨(𝝆, 𝛁𝝆) (I.27)

Le problème majeur de la LDA provenant de l’échange, une attention toute particulière fut portée sur le développement de cette partie :

𝑬𝒙𝒄 𝑮𝑮𝑨 𝝆; 𝛁𝝆 = 𝜺𝒙𝑳𝑫𝑨− 𝑭(𝒔(𝒓)) 𝝆𝟑/𝟒(𝒓)𝒅𝒓 (I.28)

Où F est une fonction du gradient de densité réduite (sans dimension) :

𝒔 𝒓 =_𝝆 𝛁 ⃗𝝆 𝒓 _{𝟑/𝟒(𝒓)} (I.29)

En revanche, il existe plusieurs façons d’inclure le gradient de la densité [24, 25]. Dans

ce travail, on a systématiquement préféré la formulation de Perdew, Burke et Ernzerhof (PBE) [26] de la construction est transparente et libre de paramètres.

13 I.5.4. Résolution des équations de Kohn-Sham

La résolution des équations de Kohn-Sham (I.18) nécessite le choix d'une base pour les fonctions d'onde que l'on peut prendre comme une combinaison linéaire d'orbitales appelées orbitales de Kohn-Sham écrites sous fourme:

𝝍_𝒋 𝒓 ⃗ = 𝑪_𝒋𝜶𝝋_𝜶 (I.30)

Où: les 𝜑_𝑗

(𝑟)

⃗ sont les fonctions de base et les 𝐶𝑗𝛼sont les fonctions de l'expansion.

Puisque l'énergie totale est variationelle dans la DFT, la solution auto-cohérente des équations de KS revient à déterminer les 𝐶_𝑗𝛼 pour les orbitales occupées qui minimisent l'énergie totale. La résolution des équations de KS pour les points de symétrie dans la première zone de Brillouin permet de simplifier les calculs. Cette résolution se fait d'une manière itérative en utilisant un cycle d'itération auto-cohérent [27]. On commence par

injecter la densité de charge initiale 𝜌_𝑖𝑛 pour diagonaliser l'équation séculaire: Avec :

𝑯 − 𝜺_𝒋𝑺 𝑪_𝒋= 𝟎 (I.31)

H: représente la matrice Hamiltonienne et S: la matrice de recouvrement.

Ensuite, la nouvelle densité de charge 𝜌𝑜𝑢𝑡 est construite avec les vecteurs propres de cette

équation séculaire en utilisant la densité de charge totale qui peut être obtenue par une sommation sur toutes les orbitales occupées.

Si les calculs ne concordent pas, on mélange les deux densités 𝜌_𝑖𝑛 et 𝜌_𝑜𝑢𝑡de la manière suivante:

𝝆_𝒊𝒏𝒋+𝟏= 𝟏 + 𝜶 𝝆_𝒊𝒏𝒋 + 𝜶_𝒐𝒖𝒕𝒋 (I.32)

j représente la jéme itération et 𝛼 un paramètre de mixage. Ainsi la procédure itérative

14

14

[1] C. FRAYRET, « Thèse de doctorat », Université de Bordeaux I, Bordeaux, France, (2004).

[2] E.Shrodinger, The Energy- impulse Hypothesis of Material Waves » , Ann. Phys. (Lei

(Leipzig) 82 : 265, (1927).

[3] E. Schrödinger, Ann. Phys., 79, 489, (1926) ; E. Schrödinger, Ann. Phys., 79, (1926) 361.

[4] R. Parr & W. Yang, in Density Functional Theory of Atoms and Molecules (Oxford University Press, New York, (1989).

[5] M. Born, R. Oppenheimer, Ann. Physik., 84, 457, (1927).

[6] D. R. Hartree, Proc. Combridge Philos. Soc. 24, 89, (1928).

[7] P. Hohenberg and W. Kohn. Phys. Rev., 136 (3B) : B864_B871, 11, 15, 19, (1964).

[8] W. Kohn and L. J. Sham. Phys. Rev., 140(4A):A1133_A1138, 11, 16, 20, (1965).

[9] P. Hohenberg and W. Kohn, Phys. Rev. 136, B864, (1964).

[10] W. Kohn, L. Sham, Phys. Rev, A1133, 140, (1965).

[11] R. M. Dreizler and J. da Provincia, Density Functional Methods in Physics, (Plenum, NewYork), (1985).

[12] A. D. Becke, Phys. Rev. A 38, 3098, (1988).

[13] J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Peederson, D. J. Singh and C. Fiolhais, Phys. Rev. B 46, 6671, (1992).

[14] L.J.Sham, W.Kohn, Phys. Rev. 145, 56, (1966) .

[15] P. A. M. Dirac, Proc. Cam. Phil. Soc. 23, 542, (1927).

[16] D. M. Ceperley and B. J. Alder, Phys. Rev. Lett. 45, 566, (1980).

[17] L. Hedin and B. I. Lundqvist, Explicit local exchange- correlation potential, J. Phys. C 4, 2064, (1971).

[18] J. P. Perdew and Wang, Accurate and simple analytic representation of the electron- gaz correlation energy, Phys. Rev. B 45, 13244, (1992).

15 [19] A. Zunger and A. J.freeman, Phys. Rev. B 16, 2901, (1977).

[20] A. Zunger and A. J.freeman, Phys. Rev. B 16, 4716, (1977).

[21] V. L. Moruzzi, J. F. Janak, and A. R. William, Calculated Electronic Properties of Metal, Pergamon, New York, (1978).

[22] J. C. Slater, Phys. Rev. 81, 385, (1951).

[23] C. Fiolhais, F. Nogeria and M. Marque. A premire in Densty Fonctinnele Théorei. Spring, (2003).

[24] J. P. Perdew, Phys. Rev. Lett. 55, 1665–1668, (1985).

[25] J. P. Perdew, Physica B 1, 172, (1991).

[26] J. P. Perdew, K. Burke, and M. Ernzerhof, Phys. Rev. Lett. 77, 3865, (1996).

Chapitre II:

Chapitre II : La méthode de la FPLMTO

II.1. Introduction. II.2. Instruction de bas. II.3. Fonctions de base. II.3.1. Sphères muffin-tin.

II.4. Fonctions lisses de Hankel (Smooth Hankel functions). II.4.1. Propriétés de base.

II.4.2. Formalisme des fonctions de Hankel lissées.

II.4.3 Les avantages des fonctions enveloppes lisses de Hankel. II.5. Matrices du chevauchement et Hamiltonien.

II.6. La contribution d’échange et de corrélation. II.7. Les fonctions d’onde.

II.8. Calcul de la densité de charge. II.9. Augmentation LAPW et LMTO.

II.12. Avantages et inconvénients de la méthode (LMTO). Références bibliographiques.

16 II.1. Introduction:

La détermination des caractéristiques structurales et électroniques des matériaux a savoir, le paramètre de réseau le module de compressibilité, les structures de bandes l'énergie de cohésion, la densité de charge...ect. est l'un des problèmes les plus difficiles qui préoccupe les scientifiques. Cependant, plusieurs réflexions ont été faites dans ce domaine afin d'obtenir une meilleur précision de ces propriétés. Plusieurs méthodes ont été développées dans le but de mieux comprendre certains phénomènes qui se manifestent dans les matériaux. Cela a permis l'apparition de quelques approches, parmi elles, une des plus importantes approches qui fournissent des informations utiles sur les matériaux: c'est la méthode LMTO (linear muffin-tin orbital) qui sera utilisée dans notre travail.

Cette méthode est parmi les techniques qui jouent un rôle important pour résoudre les équations de la fonctionnelle de la densité [1] pour un système de matière condensée. Cette approche est caractérisée par deux point :

- L’utilisation des fonctions de base de l’atome centré, qui sont définies par le moment angulaire, construites en dehors des fonctions de Hankel.

- L’utilisation de l’augmentation pour introduire les détails atomiques dans les fonctions de base à proximité de chaque noyau.

De façon générale, le raisonnement de cette approche est de construire les fonctions de base qui ressemblent beaucoup aux fonctions d’ondes du début.

Pour la méthode (LMTO), l'équilibre n'est aucun doute positif si1'approximation de la sphère atomique est employée. Methfessel [2] a développé la méthode (FP-LMTO), en considérant un lissage des fonctions de Hankel (Augmented Smooth Hankel functions) qui jouent le rôle des fonctions enveloppes de la méthode (LMTO). De façon générale, ces critères sont utilisés afin d’améliorer et développer la méthode (LMTO).

II.2. Approximation Muffin-Tin (MT) :

L’approximation Muffin-Tin consiste à découpler le cristal en deux régions :

 Des sphères appelées sphère Muffin-Tin [3], englobent chaque atome où le potentiel est supposé à symétrie sphérique comme le montre la figure (II.1).

17

Figure II.1: Potentiel Muffin-Tin [3]

II.3. Instruction de base:

On suppose que l’espace cristallin soit divisé en sphères d’atome centré et la région restante constitue la région interstitielle. La densité de charge et le potentiel effectif sont augmentés par des harmoniques sphériques à l’intérieur des sphères :

 

 

l

 

L L L

r

r i Y

r

   









_(II.1)

 

 

l

 

L L L

V

_

r

_





V

_

r i Y

_

r

_(II.2)

L’équation de Schrödinger est résolue en termes du principe variationnel :





2

0

k k

V

E

_



_

  



(II.3)

 

k k

 

k Lk lk Lk

r

A



r

   









_(II.4)

Et l’équation de la valeur propre est donnée par:

2 ' ' ' ' ' '

0

k k k k L k Lk k L k Lk Lk Lk

V

E

A

       



 













(II.5)

18 II.3.1 Fonctions de base:

L’espace est divisé en sphères nids d’abeilles (muffin-tin) non chevauchées (ou légèrement chevauchées) SR entourant chaque atome et la région restante est la région interstitielle int.

A l’intérieur des sphères, les fonctions de base sont représentées en termes de solutions numériques de l’équation de Schrödinger radiale pour la partie sphérique du potentiel multiplié par des harmoniques sphériques ainsi que leurs dérivés d’énergie prises à un certain niveau d’énergie.

Dans la région interstitielle, où le potentiel est essentiellement constant, la fonctions de base sont des ondes sphériques prises des solutions de l’équation de Helmholtz :



2



 

, 0

f r

 

   avec une certaine valeur fixe de l’énergie cinétique moyenne



_



k

_2

. En particulier, dans la méthode (LMTO) standard utilisant l’approximation de la sphère atomique (A.S.A), la valeur choisie est de

k

_2



0

.

k

_2



0

. Dans les développements de la méthode (LMTO) pour un potentiel de la forme arbitraire (Full Potential), plusieurs ensembles de base (kappa) sont normalement utilisés afin d’augmenter la liberté variationnel des fonctions de base tandis que les développements récents d’une nouvelle technique (LMTO) évite ce problème.

La stratégie générale pour inclure les termes du potentiel total dans le calcul est l’utilisation du principe variationnel. Quelques différentes techniques ont été développées pour tenir compte des corrections non sphériques dans le cadre de la méthode (LMTO). Elles incluent les transformées de Fourier dans la région interstitielle, les développements des harmoniques sphériques à un centre dans les cellules atomiques, les interpolations en termes de fonctions de Hankel aussi bien que des calculs directs de la densité de charge dans la représentation Tight-Binding. Dans les deux arrangements, le traitement des structures ouvertes, par exemple, la structure diamant est compliquée et les sphères interstitielles sont habituellement placées entre les sphères atomiques.

De ce fait, est développée la technique (Linear-response LMTO) en utilisant la représentation des ondes planes de Fourier. Les ondes planes partielles ou les orbitales muffin-tin sont définies dans l’espace entier :

 

 

H

Lk

r

 Lk

r



19 et



Lk

 

r

 HLk

 

r

 r S (II.7) Où:

 

H Lk r

 est construite à partir de la combinaison linéaire



 et





_ avec la condition de l’augmentation du lissage de la sphère.

II.4. Sphères muffin-tin:

Les fonctions de base de la méthode (LMTO) s’obtiennent à partir de la somme de BLOCH de ces ondes partielles :

 





 

'





k lkR H ikR Lk Lk Lk Lk R R

r

e

r R

r

e

H

r R

     









   









 



_II.8)

L’utilisation du théorème d’addition permet d’avoir la relation suivante :





' '

 

' ' ' '

 

' ikR k Lk L k l L L R L

e

H

_

r



R





 

J

_

r

_



_

S

_{ }

k





(II.9)

Pour que les constantes de la structure S_Lk_{' ' L}

 

k se stabilisent et la valeur de





' ' 1 2 1 l S l      on obtient:

 

'

 

' ' '

 

' ' ' ' '

 

' k H k Lk Lk L k l L L L r r J r S k          



 









(II.10)

L’utilisation de l’augmentation à l’intérieur de la sphère muffin-tin montre que:

 

J

 

Lk Lk

J _ r_   _ r_

Où JLk

 

r est une combinaison linéaire de



 et





 , avec la condition d’augmentation

20

Alors, les fonctions de base dans la sphère muffin-tin sont réécrites sous la forme suivante :

 

'

 

' ' '

 

' ' ' ' '

 

' k H k Lk Lk L k l L L L

r

r

r

S

k

         



 











_(II.11)

Dans la région interstitielle les fonctions de base sont définies comme suit :

 

'

 

' ' '

 

' ' ' ' '

 

' k k Lk Lk L k l L L L

r

H

r

J

r

S

k

         













_(II.12)

Les fonctions radiales numériques sont données par:

 



,





,



k H H Lk

r



a

lk



Lk

r E

 

b

lk



Lk

r E

 









(II.13) Où (II.14) (II.15) (II.16) (II.17) Avec Wfg S2



f 'g fg '



et les coefficients

a

lk et

b

lk fournissent un lissage

similaire avec



lk .

Les propriétés d’ortho normalisation sont par les relations suivantes:

 



.



2 2 0

1

S lk

r r dr

W

lk lk         













(II.18)

21

 

 

. 2 0

0

S lk

r

lk

r

r dr

        









(II.19)

II.5. Fonctions lisses de Hankel (Smooth Hankel functions):

La fonction enveloppe de la méthode (LMTO) standard est une fonction de Hankel dont le paramètre d’énergie est nul ou négatif, multiplié par une harmonique sphérique. Cette fonction est désignée comme (fonction de Hankel du solide). La résolution de l’équation de Schrödinger pour un potentiel constant décroît exponentiellement à des grandes distances si le paramètre est négatif multiplié par une harmonique sphérique et a une singularité à l’emplacement où il est centré. L’essentiel de la modification est d’enlever la singularité. La fonction de Hankel est lisse et analytique dans toutes les parties de l’espace. Quand une telle fonction est utilisée pour construire la base, les paramètres peuvent (où doivent) être choisis de sorte que les fonctions deviennent des variantes non lisses en dehors de la sphère atomique centrale. Ceci accélère le calcul pour deux raisons :

1. La base peut être plus petite.

2. L’intégrale numérique peut être faite en utilisant une maille plus brute.

II.5.1. Propriétés de base:

Dans le contexte de l’établissement ou du fonctionnement du calcul, l’information appropriée au sujet des fonctions lissées de Hankel [4,5] peut être prise de la figure (II.2). Pour des grands rayons, la fonction lissée à chaque moment angulaire est égale à la fonction de Hankel standard correspondante, qui montre une décroissance exponentielle proportionnelle à exp (-ikr) spécifiée par le paramètre d’énergie négatif  = -k2.

Pour des petits rayons, la fonction est courbée et le dépasse graduellement jusqu’à ce qu’elle approche finalement rl près de r = 0. Une fois multiplié par l’harmonique sphérique Y_L r



     , le résultat est analytique dans toutes les parties de l’espace. De même importance est Rsm,

désigné comme le rayon lisse associé à la fonction. Il s’avère que la fonction standard de Hankel et sa variante lisse sont égales quant le gaussien [exp (-r2/R2sm)] est négligeable, c'est-à-dire pour r3Rsm. Quand Rsm est croissant, la dérivation à partir de la fonction standard

22

De façon générale, deux paramètres distincts déterminent la forme de chaque fonction.

L’énergie donne une décroissante à des grands rayons et le rayon lissé détermine comment la fonction est fortement lissée. Pour optimiser la base pour un type d’atome donné, les deux paramètres devraient être ajustés. Comme un ensemble de base, ces fonctions combinent plusieurs avantages des fonctions de Hankel et gaussiennes. Grâce au comportement de la fonction d’onde exponentielle à de grande valeur de r, leurs utilisations montrent que les calculs sont plus stables que ceux qui emploient les fonctions gaussiennes. Près de l’origine, elle a une forme non singulière lissée. Plusieurs quantités importantes peuvent être évaluées analytiquement pour ces fonctions.

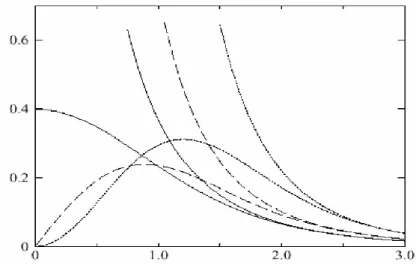
Figure II.2 Comparaison des fonctions de Hankel standard et lisse pour l = 0 (lignes

continues), l = 1 (tiret) et l = 2 (lignes pointillées). L’énergie  = -1 et le rayon lisse Rsm = 1.0.

Pour des grands rayons, les fonctions lisses et standard coïncident. Près de l’origine, la fonction lisse se courbe graduellement en se comportant comme rl tandis que la fonction

standard a une singularité proportionnelle à 1/rl+1 [4-5-8-9] .

II.5.2. Formalisme des fonctions de Hankel lissées:

On définit les fonctions de Hankel lissées comme suite : La fonction de Hankel, habituellement pour le moment angulaire nul, est h0(r) = e-kr/r où k définit la décroissance à

des grands rayons. Comme une fonction de r  r dans l’espace tridimensionnel, h0 satisfait

l’équation :

23

Où  = -k2 est l’énergie liée à la fonction, la valeur étant toujours prise pour être négative. Ainsi, la valeur (+) appliquée à h0, est partout nulle excepté à r = 0, où la fonction  résulte

d’une singularité (1/r) de h0. Exprimée différemment, h0(r) est la réponse de l’opérateur (+)

pour un terme de source spécifique, à savoir une fonction. Pour changer cette fonction standard de Hankel en fonction de Hankel lissée, la forme de la fonction de  est infiniment pointue et prend, en dehors, la forme d’une Gaussienne :



 



  

h0 r  4



g0

 

r (II.21)

Une normalisation convenable est donnée par g0(r) = C exp (r2/R2sm).

La fonction de Hankel lissée s’approche alors de la fonction standard pour une grande valeur de r. Pour r plus petit, elle atteint la rangée où g0(r) est non négligeable, la fonction se courbe

plus lissement et se comporte comme une constante rl pour r0.

Les fonctions lissées de Hankel sont aussi utilisées pour des moments angulaires élevés afin de construire des fonctions de base des états : s, p, d et cetera. Ceux-ci peuvent être obtenus immédiatement en appliquant un opérateur différentiel Y_L

 

 , défini comme suit. Le polynôme harmonique sphérique y(r)=rlYL est un polynôme en x, y, et z, par exemple

C(x2 – y2). En substituant les dérivées partielles



x ,



y et



z pour x, y, et z

respectivement, l’opérateur recherché est obtenu d’une manière directe. L’application de cet opérateur à la fonction delta donne un dipôle, quadripôle ainsi de suite, en l’appliquant aussi à g0(r) donne des courbes en dehors de la forme gaussiennes. Ainsi, les fonctions lissées de

Hankel d’ordre L sont

H r

L

 



y

L

   



h r

0 et satisfont l’équation différentielle :



 





H

L

 

4



G

L

 

r

 

4



y

L

   



g

0

r

(II.22)

Plusieurs quantités importantes peuvent être calculées analytiquement pour ces fonctions, telle que l’intégrale du chevauchement et la valeur de la probabilité de l’énergie cinétique entre deux fonctions quelconques. Elles peuvent être également augmentées autour d’un certain point dans la cellule unité [5].

24 II.5.3. Les avantages des fonctions enveloppes lisses de Hankel:

Les avantages de définir les fonctions de base de la méthode LMTO comme des fonctions de Hankel augmentées ne sont pad évidentes. Cela mène à un formalisme compliqué et un grand effort de programmation. D’où l’avantage de la méthode LMTO.

Les fonctions LMTO sont construites pour être semblables aux véritables fonctions d’onde du cristal. En fait, si le potentiel cristallin est approximé par la forme muffin-tin, c'est-à-dire, sphérique à l’intérieur et constant à l’extérieur, la véritable fonction d’onde du cristal devient une somme finie des fonctions LMTO.

Une conséquence de la petite taille de base, les calculs devraient être rapides. Plus précisément, la réduction de la base par la moitié qui peut sauver un sept-huitième du temps machine.

Une autre conséquence de la petite taille de la base est la réduction de la mémoire demandée, qui peut être également importante en économisant le temps machine quand on calcule les grands systèmes.

Les fonctions enveloppes de la méthode LMTO, c'est-à-dire, les fonctions de Hankel solide, sont plus simples analytiquement. Ceci aide à performer les différentes étapes qui doivent être faites. Finalement, beaucoup de propriétés utiles surviennent parce que ces fonctions sont des fonctions propres de l’opérateur de l’énergie cinétique.

ΔHL(r) = ε HL(r) où ε =-k2 est une énergie qui caractérise la localisation de la fonction.

En choisissant l’ensemble de base pour un système spécifique. L’intuition chimique peut être utilisée. La base peut être conçue en fonction du problème, elle peut être choisie pour chaque atome séparément, parfois les résultats peuvent être interprétés plus simplement dus aux fonctions de base atome-orienté.

Parmi les caractéristiques partagées par la méthode LAPW sont :

Le premier avantage est la stabilité numérique dans le contexte de résoudre l’équation de Schrödinger. En plus, parce que chaque fonction séparée est déjà une solution de l’équation. L’ensemble de base de la méthode LMTO peut être également bien appliqué à tous les atomes dans la table périodique. En incluant un nouveau type d’atome, aucun effort n’est nécessaire pour construire et examiner un pseudo potentiel approprié.

Comme dans d’autre méthodes de tout-électron, les donnés concernant les états du cœur sont valides qui ne peuvent être directement fourni dans une formulation pseudo potentielle. es quantités relatives sont la densité au noyau et le gradient du champ électrique. En élevant un électron du cœur, les énergies du niveau liaison-cœur peuvent être directement calculées