Analyse des plaques orthotropes minces sous l'effet des conditions exterieures

REPUBLIQUE ALGERIENNE DEMOCRATIQUE ET POPULAIRE Ministère de L’Enseignement Supérieur Et De La Recherche Scientifique

UNIVERSITE MENTOURI CONSTANTINE Faculté des Sciences de l’Ingénieur DEPARTEMENT DE GENIE MECANIQUE

Ecole Nationale Doctorale de la Mécanique de Construction

MEMOIRE

Présenté pour obtenir le Diplôme de Magister en Génie Mécanique

Option : CONSTRUCTION MECANIQUE

« Mécanique Appliquée en Engineering »

Intitulé :

ANALYSE DES PLAQUES ORTHOTROPES

MINCES SOUS L’EFFET DES CONDITIONS

EXTERIEURES

Présentée par:

SOFIANE CHORFI

Soutenu Le : …..Mai 2010, Devant le Jury :

Président : Mr. A.BOUCHOUCHA Prof. Université Mentouri Constantine Rapporteur : Mr. B.NECIB Prof. Université Mentouri Constantine Examinateur : Mr. A. BELLAOUAR Prof. Université Mentouri Constantine Mme. Z. LABED M.C. Université Mentouri Constantine

Mai 2010

N° d’ordre : ….. /…… / 2010 Série : ……. / GM / 2010

A la mémoire de ma mère, et de mon père

J’espère qu’ils reposent en paix à jamais.

Faible témoignage de ma reconnaissance infinie

A ma petite famille :

« Ma femme et ma petite fille JOMANA RAWANE »

A ma grande famille :

« Mes frère et mes sœurs et leurs petites familles »

A Ma belle famille,

Et a Tous mes amis,

iv

Remerciement

Je tiens à exprimer nos sincères remerciements à toute personne qui a contribué de prés ou de loin a l’accomplissement de ce travail.

Je tiens tout d’abord à remercier Mr. Brahim NECIB, Professeur au département de génie mécanique, Université Mentouri Constantine, encadreur de mon mémoire de magister, pour la confiance qu’il m’a accordé en me proposant ce mémoire. De plus, son enthousiasme et sa confiance qui m’ont donné les motivations nécessaires pour réaliser ce travail. Je n’oublierai pas la grande humanité dont il m’a fait preuve. Son encouragement, son entière disponibilité au cours de ce mémoire et ses judicieux conseils.

Je tiens particulièrement à remercier le ¨Professeur Mr. BOUCHOUCHA Ali de l’Université Mentouri Constantine de m’avoir fait l’honneur de présider le jury de ce mémoire.

Je tiens aussi à remercier les autres membres de jury Monsieur le professeur Mr. Ahmed BELLAOUAR et Docteur Mm ZOHRA LABED qui m'ont fait l'honneur d'accepter d'être les examinateurs de mon travail et pour le temps qu'ils ont consacré à l'examen de ce mémoire.

Je n’oubli pas aussi de remercier tous les enseignants de l’école national doctorale qui ont contribués à ma formation et spécialement monsieur le responsable du pole de Constantine Mr. Professeur NECIB BRAHIM et le Directeur de l’Ecole Mr. Toufik BOUKHAROUBA, Professeur à l’USTHB de Bab Ezouar - Alger.

Je tiens remercier Mr. Ismail BEN YASAAD chef de département de Génie mécanique Je tiens enfin à remercier également tous mes collègues et amis pour leur soutien, conseil et aide.

v

« ANALYSE DES PLAQUES ORTHOTROPES MINCES SOUS L’EFFET DES CONDITIONS EXTERIEURES »

Les matériaux orthotropes présentent un intérêt très important dans le domaine des applications industriels modernes tels que : la mécanique, l’aéronautique, le génie civil et la biomécanique vu leur dureté leur légèreté et leur super élasticité. Durant leur fonctionnement et sous l’effet des efforts extérieurs, ces matériaux peuvent subir des fissurations ou des ruptures qui peuvent provoquer le désastre de la structure. Afin d’éviter ces types de problèmes, l’analyse de ces matériaux est nécessaire afin de prédire leur caractéristiques mécaniques et ainsi d’augmenter leur durée de vie. Cette analyse repose essentiellement sur la structure interne du matériau, sa géométrie, ses conditions aux limites et les conditions extérieures appliquées.

Notre travail consiste en l’analyse du comportement statique et dynamique des plaques orthotropes minces bi dimensionnelle sous l’effet des efforts extérieurs utilisant les méthodes numériques et de modélisations en se basant sur la méthode des éléments finis. Les contraintes et les déformations à n’importe quel noeud de la plaque orthotrope ont été déterminées pour différents types de chargement (aléatoires et harmoniques), avec et sans amortissement comparativement avec celles d’une plaque isotrope de même dimension. Et de bonnes efficacités et fiabilités des propriétés mécaniques de la plaque orthotrope ont été observées que celles du matériau isotrope.

vi

Abstract:

«ANALYZIS OF THIN ORTHOTROPIC PLATES UNDER THE EXTERNAL CONDITION EFFECTS »

The orthotropic materials are of a great importance and interest in the field of the modern industrial technologies applications such as: mechanics, aeronautics, civil engineering and biomechanics due to their hardness, their lightness and their super elasticity. During their working operation and under the effect of the external efforts, these materials can be submitted to cracks or ruptures which can cause the disaster of their structure. In order to avoid these types of problems, the analysis of these materials is necessary in order to predict their mechanical characteristics and thus to augment their lifespan. This analysis is based essentially on the internal structure of material, its geometry, its boundary conditions and the external applied conditions.

Our work consists of the analysis of the static and dynamic behaviour of thin orthotropic bi- dimensional plates under the effect of external efforts using the numerical methods and of modulating based on the finite element methods. The strain and stress in any node of the orthotropic plate have been found for various types of loading (random and harmonic), with and without damping comparatively with those of an isotropic plate of the same dimension. And good effectiveness and reliabilities of the mechanical properties of the orthotropic plate were observed compared to those of orthotropic one.

Key words: Orthotropic plate, finites elements, numerical simulation, vibration, stress and Strain.

vii

صيخلت

:

ا

تيػإصٌا ثاميبطخٌا يف تيىل تحٍصِ اهٌ شياغخٌا ةذِاؼخٌّا تيبوشحىحسولأا داىٌّ

ًٌإ شظٌٕاب هٌر و تيىيحٌا اىئاىيٌّاو تئذٌّا تسذٕهٌاو ءاضفٌاو تيىئاىيٌّا ًثِ تثيذحٌا

، تيجساخٌا يىمٌا جحح شيثأخٌا تجيخٔ اهٌاّؼخسإ يلاخ ِٓ تبلاصٌا و تفخٌا ،تيىمٌا تٔوشِ

ًىيهٌٍ تثساو ببسح ْأ ٓىّي يخٌا سىسىٌا وأ شيسىخٌ غضخح داىٌّا ٖزهٌ ٓىّي

.

ٖزهٌ ابٕجح و

ةدايص ًجأ ِٓ اهيف شظٌٕا ُح ذل و داىٌّا ٖزهٌ ًيٌاحح ءاشجإ ٓىّي ،ًواشٌّا ِٓ عاىٔلأا

تيىئاىيٌّا اهصئاصخو اهشّػ

.

ةداٌٍّ تيٍخاذٌا تيٕبٌا ًٍػ يولأا َامٌّا يف ذٕخسح ًيٌاحخٌا ٖزه

يىمٌا وأ ياّحلأا كيبطح تيفيوو اهدوذح فوشظو ، تسذٕهٌا يف ،

.

تيبوشحىحسولأا تميلشٌا حئافصٌٍ يىيِإيذٌا و يىيحاخسٌا نىٍسٌا ًيٍحح إٍّػ ّٓضخيو

ًٍػ ءإب تجزٌّٕا و تيّلشٌا قشطٌا َاذخخساب تيجساخٌا يىمٌا شيثأح جحح داؼبلأا تيئإث

تيهخٌّٕا شصإؼٌا تميشط

.

داهجلإا

ُح تيبوشحىحسولأا حئافصٌا ِٓ ةذمػ ًو يف ثاشحىخٌاو

ًيّحح ِٓ تفٍخخِ عاىٔلأ اهيٍػ ًصحخٌا وأ اهذيذحح

(

تيسود و ةشباػ ،ُغإح

)

ْوذبو غِ ،

لإا حئافصٌا غِ هٌر تٔسامِو ذِاخح

وشحوضي

جٌ تيب

أ

تيىئاىيٌّا صئاصخٌا تيٌاؼف و تيحلاص ذيو

تيبوشحىحسولأا تميلشٌا حئافصٌٍ

.

ةحتافملا تاملكلا

:

تيهخٌّٕا شصإؼٌا ،تيبوشحىحسولأا داىٌّا

،

ةاكاحملا

،

ثلاامخٔلإا ىحاداهجلإا ،صاضخهلإا،تجزٌّٕا

viii

La nomenclature

L’insigne Désignation

Cijkl Tenseur d’élasticité (ou de rigidité)

Sijkl Tenseur de souplesse

ij Tenseur de déformation

E Module de Young

Cij Coefficient d’élasticité

h Epaisseur

Dij Coefficient qui caractérise la matrice de rigidité

x,y,z Cordonnée principale 1,2,3 Cordonnée global D66, Dxy Rigidité à la torsion

s La lure de l’ondulation

l Longueur de l’arc d’une demi onde f Epaisseur d’onde

E’ Module de Young des renforts

I Moment d’inertie

Dx, Dy, D Moment d’inertie suivant l’axe Y

Kx, Ky, Kxy Courbure de flexion et de torsion qui caractérise les déformations angulaires p Vecteur de force de volumique de l’élément

Fd Vecteur de force volumique d’intensité (correspond à la résistance linéaire) [] Déplacement généralisé

f(t) Vecteur des force appliqué u(t) Vecteur de position de la masse) T Energie cinétique total du système

v Energie potentielle du système (déformation + force conservatives extérieurs) wnc

Travail effectué par les forces non conservatives agissant sur le système (amortissement + autre charge extérieur)

 Variation subie pendant l’intervalle du temps {ü} Vecteur d’accélération

ix

,  Coefficient de New mark ou Constante d’amortissement de Rayleigh

t Pas de temps

G Coefficient de coulomb

a, b Espacement des renforts dans la direction x, y respectivement G12 Module de cisaillement

 Coefficient de poisson

El Module de Young dans le sens de fibre

Et Module de Young dans le sens transverse

Fx, Fy, Fz Composantes de la force volumique suivant x, y, et z M Moment de la force

U Déplacement suivant x V Déplacement suivant y

ij Distorsion ou déformation angulaire

 Densité ou masse volumique

 la viscosité

x , y Rotation autour de l’axe x et y respectivement

{U} , {} Vecteur de déplacement {P} Vecteur de charge [K] Matrice de rigidité [m] Matrice de masses [C] Matrice de l’amortissement Qi Travail interne .Qe Travail externe t Temps (s) ζ Contrainte ζii Contrainte de traction ηij Contrainte de Cisaillement δ L’allongement А Section

x

Table des matières

Dédicace………...

iii

Remerciement………..

iv

La nomenclature………..

v

Table des matières………...

vi

Table des figures………..

vii

Introduction

1

1. Introduction aux matériaux orthotropes...

2

2. Application des matériaux orthotropes ………...

3

a. Application dans l’industrie aérospatiale ………... 3

b. Application dans l’industrie mécanique……….. 4

c. Application dans le domaine de la biomécanique ……….. 5

d. Application dans le domaine des sports et de loisir ………... 5

3. Modélisation numérique par la méthode des éléments finis ……...

6

3.1. Introduction………. 6

3.2. Avantage de la M.E.F……….. 8

3.3. Autres types de modélisation……….. 8

3.3.1. Modélisation par ANSYS……… 8

3.3.2. Modélisation par SAP2000 ………. 8

4. Objectif de l’étude ………..

10

Chapitre I Théorie d’élasticité linéaire des plaques

orthotropes

12

1.1 Introduction………

13

1.1.1 Théorie des Plaques……….. 13

1.1.1 Historique ……… 13

1.1.1.2. Démarche ………... 13

1.1.1.3. Démarche pour l'étude des plaques ……… 14

1.1.1.4. Définitions et hypothèses ……….. 14

1.2. les Milieux Continue………..

15

1.2.1. Définition……….… 15

1.2.2. Milieu homogène……… 15

1.3. Loi de Hooke Généralisée ………

15

1.4. les Différents Types des Matériaux………...

15

1.4.1. Les matériaux anisotropes……… 15

xi

1.4.5. Matériaux quasi isotropes transverses………. 19

1.4.6. Matériaux quasi isotropes……… 19

1.4.7. Matériaux isotropes………. 19

1.5. Cas des Plaques Orthotropes………..

22

1.5.1. Différentes Formes des Plaques Orthotropes……….. 23

1.5.1.1. Plaque ondulée……….. 25

1.5.1.2. Plaque renforcée……… 25

1.5.1.3. Plaque composite……….. 27

1.5.1.4. Plaque stratifiée………. 28

Chapitre II Analyse des plaques orthotropes

29

2.1. Introduction………...

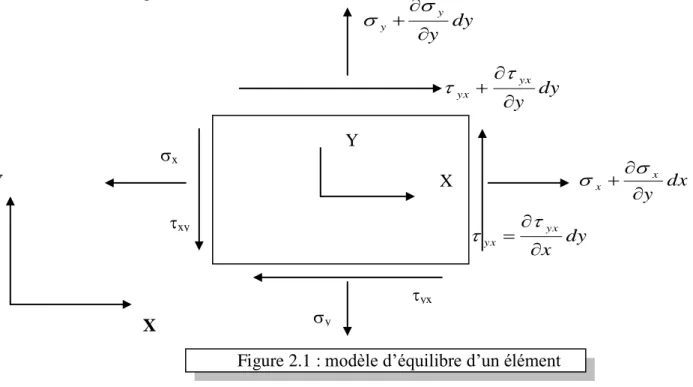
30

2.2. Equations d'équilibres ………..

30

2.2.1. Equilibre des contraintes……….. 30

2.2.2. Equilibre des forces……….. 31

2.3. Types de forces appliquées sur la plaque ……….

32

2.3.1. Forces extérieures………. 32

2.3.1.1. Forces volumiques………... 32

2.3.1.2. Forces surfaciques……… 32

2.3.2. Contraintes………... 32

2.4. Forces et Moments Résultants………..

33

2.4.1. Moments fléchissant ……….. 33

2.4.2. Moments de torsion……… 34

2.4.3. Efforts tranchants ………... 34

2.4.4. Particularités des plaques orthotropes………. 35

2.5. Equation Différentielles de Déplacements………

36

2.5.1. Validité des théories de la plaque………. 36

2.5.2. Plaque mince………... 37

2.5.3. Théorie des Plaque épaisse ……….. 40

Chapitre III Analyse des plaques orthotropes par

méthodes des éléments finis

44

3.1. Introduction

………

45

3.2. Formulation d’un Elément………

45

3.2.l. Méthode directe……….. 46

3.2.2. Méthode des résidus pendérés………. 46

3.2.3. Méthode variationnelle………... 46

3.3. Formulation de la Matrice de Rigidité de la Plaque………..

46

3.4. La Méthode de l'Energie Potentielle……….

51

xii

Chapitre IV Etude dynamique de la plaque orthotrope

par la méthode de New Mark

53

4.1. Introduction………...

54

4.2. Formulation des Equations du Mouvement………..

54

4.2.1. Ecriture directe de l'équilibre dynamique par le principe d’Alembert……….. 54

4.2.2. Principe des déplacements virtuels……….. 55

4.2.3. Principe de Hamilton………... 55

4.3. Choix des degrés de liberté………...

55

4.4. Expression d'Equilibre Dynamique………...

56

4.5. Différents Types de Chargement………..

56

4.5.1. Chargement Harmonique……….. 57

4.5.2. Chargement périodique………. 57

4.5.3. Chargement par impulsion……… 58

4.5.3.1. Impulsion sinusoïde……… 58

4.5.3.2. Impulsion rectangulaire……….. 58

4.6. L'Amortissement des Vibrations………...

59

4.7. Détermination de l'Amortissement………

59

4.8. Résolution Numérique par la Méthode de NEW MARK….

59

Chapitre V Analyse des plaques orthotropes par

modélisation numériques

65

5.1. Introduction………...

66

5.2. Calculs Numériques et Modélisation ………...

66

5.3. Organisation du Programme de Fortran……….

67

5.3.1. Introduction des données………. 67

5.3.2. Construction des matrices [K], [M] et F……….. 67

5.3.3. Résolution du système d'équation [K] U = F………….. 67

5.3.4 Impression des résultats……… 67

5.3.5. L'enchaînement de ces différents blocs……… 67

5.4 Organisation du Programmation avec ANSYS……….

68

5.4.1. Organisation de logiciel d'ANSYS……….. 68

5.4.2. les Procédés d’analyse……….. 68

5.4.2.1. Établissez le modèle……… 69

5.4.2.2. Choisissez le type d'analyse & Options.. 69

5.4.2.3 Résultats de revue……… 69

5.5. Organisation du Programmation avec le SAP2000………..

69

5.5.1. Dispositifs d'analyse………. 70

5.6. Modèle d’application : Caractéristiques des plaques considérée ………

71

5.6.1. Méthode utilisant le programme Fortran 77 ……….. 71

xiii

5.8. Conclusion ………

₁₀₆

Conclusion Générale ………...

107

Bibliographie ………...

110

Annexes

113

Annexe 1 : Programme Fortran……….

114

Annexe 2 : Aide d’utilisation « ANSYS, SAP2000 » ……..

128

Annexe 3 : Résultat du programme Fortran………..

143

xiv

Table des figures

Figure 1.1 : organigramme du démarche de l’étude de la plaque. Figure 1.2 : matériau orthotrope.

Figure 1.3 : Déformation d'une plaque mince avec mise en évidence du déplacement d'un

élément de matière, de son feuillet moyen (rouge) et de sa fibre normale (bleue)

Figure 1.4 : Déplacement du feuillet moyen (gauche) et d'une fibre normale (droite) Figure1.5 : plaque ondulée

Figure 1.6 : plaque renforcée par deux séries équidistantes de renforts Figure 1.7 : plaque renforcée par une série de nervures équidistantes Figure 1.8 : plaque composite

Figure 1.9 : plaque stratifiée

Figure 2.1 : modèle d’équilibre d’un élément Figure 2.2 : Moments fléchissant et contraintes Figure 2.3 : Moments de torsion et scission Figure 2.4 : Efforts tranchants et scission

Figure 2.5 : déformation de la plaque du point A au point A’

Figure 3.1 : illustration déplacement et rotation d’un élément rectangulaire a 4 noeud Figure 3.2 : illustration effort tranchant et moment d’un élément rectangulaire a 4 Figure 4.1 : chargement harmonique

Figure 4.2 : chargement périodique Figure 4.3 : Impulsion sinusoïde Figure 4.4 : Impulsion rectangulaire

xv

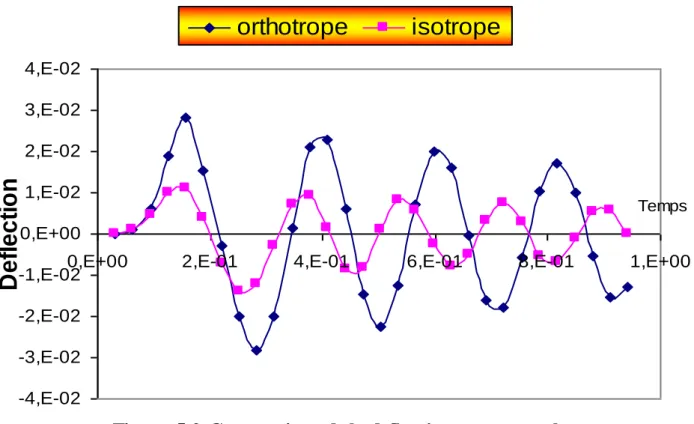
Figure 5.2 : Comparaison entre déflection d’une plaque orthotrope et isotrope avec

amortissement facteur d’amortissement 2%

Figure 5.3 : Comparaison entre déflection d’une plaque orthotrope et isotrope avec

amortissement facteur d’amortissement 5%

Figure 5.4 : l’influence du coefficient de New Mark Alpha sur l’amortissement (plaque

orthotrope)

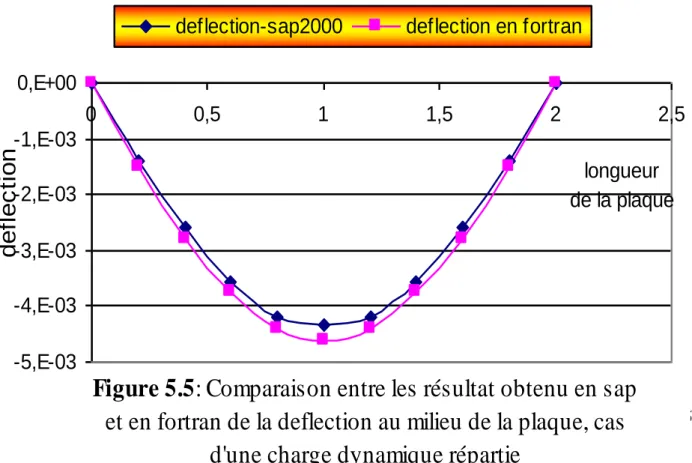
Figure 5.5 : comparaison entre les résultats obtenus en SAP2000 et en Fortran de déflection au

milieu de la plaque

Figure 5.6 : comparaison entre les contraintes suivant la direction x et y sans amortissement

pour une plaque orthotrope

Figure 5.7 : comparaison entre les contraintes suivant la direction x et y avec amortissement

pour une plaque orthotrope

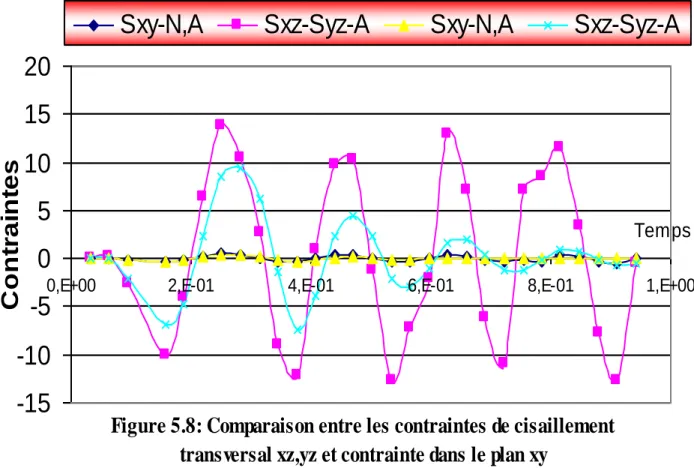
Figure 5.8 : comparaison entre les contraintes de cisaillement transversale xz,yz et contrainte

dans le plan xy avec et sans amortissement pour une plaque isotrope

Figure 5.9 : comparaison entre les contraintes de cisaillement transversale xz,yz et contrainte

dans le plan xy avec et sans amortissement pour une plaque orthotrope

Figure 5.10 : variation du déplacement en fonction d’épaisseur. Figure 5.11 : Amplitude modale des déplacements et des contraintes.

Figure 5.12 : variation des déplacements en fonction d’épaisseur pour une plaque orthotrope

« nœud 14 ».

Figure 5.13 : variation de fréquence fondamentale en fonction de nombre des nœuds.

Figure 5.14 : variation de fréquence fondamentale en fonction d’épaisseur pour plaque isotrope. Figure 5.15 : variation de fréquence fondamentale en fonction d’épaisseur pour plaque

xvi

Figure 5.17 : Effet du bêta atténuation sur la constante d'amortissement (atténuation d'alpha

ignorée).

Figure 5.18 : Comment rapprocher des constantes d'amortissement de Rayleigh.

Figure 5.19 : Déflection Ux et Uy en fonction de la fréquence pour une plaque isotrope Figure 5.20 : Déflection Ux, Uy, et Uz en fonction de la fréquence pour une plaque isotrope. Figure 5.21 : Déflection, vitesse, et accélération suivant y ou x en fonction de la fréquence

plaque isotrope.

Figure 5.22 : Déflection, vitesse, et accélération suivant z en fonction de la fréquence plaque

isotrope.

Figure 5.23 : Contrainte suivant x et y en fonction de la fréquence plaque isotrope. Figure 5.24 : Contrainte suivant z en fonction de la fréquence plaque isotrope.

Figure 5.25 : Contrainte suivant xy, yz et xz en fonction de la fréquence plaque isotrope. Figure 5.26 : Contrainte suivant xz et yz en fonction de la fréquence plaque isotrope. Figure 5.27 : Contrainte équivalent VM en fonction de la fréquence plaque isotrope.

Figure 5.28 : Contrainte suivant x, y, z et contrainte équivalent VM en fonction de la fréquence

Chargé nœud 408 plaques isotropes.

Figure 5.29 : Déflection Uz en fonction du temps Chargé Transitoire nœud 408 plaque isotrope. Figure 5.30 : Déflection Ux et Uy en fonction du temps Chargé Transitoire nœud 408 plaque

isotrope.

Figure 5.31 : Déflection, vitesse et accélération suivant x en Fct temps. Chargé Transitoire

nœud 408 plaque isotrope.

Figure 5.32 : Déflection, vitesse et accélération suivant y en Fct temps. Chargé Transitoire

xvii

Figure 5.34 : Contrainte suivant x en Fonction du temps. Chargé Transitoire nœud 408 plaque

isotrope.

Figure 5.35 : Contrainte suivant z en Fonction du temps. Chargé Transitoire nœud 408 plaque

isotrope.

Figure 5.36 : Contrainte suivant x, y, et z en Fonction du temps. Chargé Transitoire nœud 408

plaque isotrope.

Figure 5.37 : Contrainte suivant xy, yz, et xz en Fonction du temps. Chargé Transitoire nœud

408 plaque isotrope.

Figure 5.38 : Déflection Ux et Uy en fonction du temps Charge Harmonique nœud 408 plaque

orthotrope.

Figure 5.39 : Déflection Uz en fonction du temps Charge Harmonique nœud 408 plaque

orthotrope.

Figure 5.40 : Contrainte suivant x en Fonction du temps. Charge Harmonique nœud 408

plaques orthotropes.

Figure 5.41 : Contrainte suivant z en Fonction du temps. Charge Harmonique nœud 408

plaques orthotropes.

Figure 5.42 : Contrainte suivant xy en Fonction du temps. Charge Harmonique nœud 408

plaques orthotropes.

Figure 5.43 : Contrainte suivant yz en Fonction du temps. Charge Harmonique nœud 408

plaques orthotropes.

Figure 5.44 : Contrainte suivant xz en Fonction du temps. Charge Harmonique nœud 408

plaques orthotropes.

Figure 5.45 : Contrainte équivalent Vm Fonction du temps. Charge Harmonique nœud 408

xviii orthotrope.

Figure 5.47 : Déflection Uy en fonction du temps Charge transitoire nœud 408 plaque

orthotrope.

Figure 5.48 : Déflection Uz en fonction du temps Charge transitoire nœud 408 plaque

orthotrope.

Figure 5.49 : Déflection, vitesse et accélération suivant x en fonction du temps Charge

transitoire nœud 408 plaque orthotrope.

Figure 5.50 : Déflection, vitesse et accélération suivant y en fonction du temps Charge

transitoire nœud 408 plaque orthotrope.

Figure 5.51 : Déflection, vitesse et accélération suivant z en fonction du temps Charge

transitoire nœud 408 plaque orthotrope

Figure 5.52 : Contrainte suivant x en fonction du temps Charge transitoire nœud 408 plaques

orthotropes.

Figure 5.46 : Déflection Ux en fonction du temps Charge transitoire nœud 408 plaques

orthotropes.

Figure 5. 47 : Déflection Uz en fonction du temps Charge transitoire nœud 408 plaques

orthotropes.

Figure 5.48 : Déflection, vitesse et accélération suivant x en fonction du temps Charge

transitoire nœud 408 plaques orthotropes.

Figure 5.49: Déflection, vitesse et accélération suivant y en fonction du temps Charge

transitoire nœud 408 plaques orthotropes.

Figure 5.50 : Déflection, vitesse et accélération suivant z en fonction du temps Charge

transitoire nœud 408 plaques orthotropes.

Figure 5.51 : Contrainte suivant x en fonction du temps Charge transitoire nœud 408 plaques

xix

Figure 5.53 : Contrainte suivant z en fonction du temps Charge transitoire nœud 408 plaques

orthotropes.

Figure 5.54 : Contrainte suivant xy, yz et xz en fonction du temps Charge transitoire nœud

1

2 Les matériaux orthotropes présentent actuellement un intérêt important dans le domaine des applications industriels modernes tels que : le domaine de la mécanique, de l’aéronautique, du génie civil et de la biomécanique vu leur dureté leur légèreté, leur super élasticité et leur durée de vie. Ces matériaux sont des matériaux anisotropes à caractère structural inhomogène et complexes utilisés pour la réalisation des pièces ou des corps légers de haute fiabilité et résistance mécanique. Cependant durant leur fonctionnement et leur mode de vie, ces matériaux peuvent subir des fissurations sous l’effet des efforts extérieurs provoquant leur rupture et leur désastre [1]. En conséquence les charges limites à leur rupture de ces matériaux doivent être déterminées à l’état statique comme à l’état dynamique.

En effet, les matériaux orthotropes sont des matériaux anisotropes ayant des différentes propriétés mécaniques suivant leurs trois directions orthogonales. Parmi ces matériaux on rencontre souvent : les matériaux composites, les matériaux ondulés, les matériaux sandwiches, les matériaux renforcés, etc...

Afin de répondre aux besoins des compagnies aéronautiques, pour la réalisation d’appareils plus légers et moins polluants, les prochaines générations d’avions civils intégreront de nombreuses structures primaires en matériaux orthotropes, telles que le caisson central, le fuselage ou les ailes. La réalisation de ce type des matériaux, jouant un rôle clé dans la tenue de l’avion, nécessite un haut niveau de confiance dans les méthodes de dimensionnement. D’un point de vue académique, de nombreuses méthodes d’analyse des plaques ont été proposées dans la littérature. Toutefois, ces approches avancées sont relativement complexes à mettre en œuvre dans un bureau d’étude et les coûts de calculs associés à ces méthodes restent très élevés pour traiter des structures aéronautiques. D’un point de vue industriel, des méthodes simplifiées d’analyse de la tenue de matériaux orthotropes, sont couramment utilisées. Toutefois, le calcul de pièces aéronautiques nécessite l’établissement de valeurs de calculs massivement recalées sur les données expérimentales disponibles. Actuellement, l’identification des paramètres constitutifs de matériaux à partir d’un nombre réduit d’essais mécaniques et exploitant les mesures de champs cinématiques ou thermiques constituent un fort courant de recherche. Les techniques d’identification développées exploitent la richesse des mesures de champs sur des essais qui sont généralement analysés à partir de modèle analytique. (Chalal, 2005) (Meuwissen et al. 1998) (Gavrus et al. 1999) (Forestier, 2003)[2-3-4-5], l’identification des paramètres du

3 comportement orthotrope est conduite selon une technique inverse fondée sur une approche variationnelle. Celle-ci est basée sur la minimisation d’une norme énergétique formulée par l’erreur en relation de comportement (Bonnet et al. 2003), (Constantinescu, 1995) [6-7]. Cette erreur est traduite en fonction de l’écart entre les déformations théoriques et les champs de déformations expérimentales obtenues par des techniques de mesure de champs cinématiques. L’identification des paramètres du comportement est effectuée par la minimisation de ce problème inverse. L’utilisation de cette méthode de résolution nécessite le calcul de la matrice de sensibilité. Dans la littérature, il existe plusieurs méthodes de construction de cet opérateur de sensibilité. (Gavrus et al. 1999) [3] utilisent des méthodes analytiques directes tandis que (Tortorelli et al. 1994) [8] le font par la méthode adjointe. (Forestier et al. 2003) [4] proposent une technique mixte basée sur les méthodes semi analytique utilisant conjointement la méthode des différences finies pour la différentiation numérique et un calcul analytique. Dans le présent travail, le choix s’est porté sur la méthode semi analytique combinant les avantages de la méthode analytique directe et la méthode des différences finies pour le calcul du gradient et construire ainsi la matrice de sensibilité. La dérivation numérique a été faite par la méthode de différences finies. Cette méthode tout en étant relativement stable, permet au modèle inverse d’évoluer avec le code du modèle direct. (M.E.F) est utilisé pour résoudre le problème direct. La mise en oeuvre d'une telle approche nécessite alors un choix pertinent de géométrie d'éprouvette, de méthode de mesure de champs cinématiques ainsi que d'une stratégie d'identification. Ce code permet de développer la robustesse de la technique de calcul pour différentes configurations d’essais. Le choix de ces essais mécanique permet de générer des champs hétérogènes de contrainte/déformation dans les zones d’étude. Cette technique est utilisée pour tester des corps bruités par simulation des erreurs [39].

2. Application des matériaux orthotropes :

Les matériaux orthotropes ont une grande application dans le domaine de l’ingénierie et de la biomécanique essentiellement :

a. Application dans l’industrie aérospatiale :

En aéronautique, les matériaux orthotropes ont connus des applications courantes surtout dans la construction des pièces de structures primaires, les gouvernes et l’habillage extérieur ainsi de l’intérieur de l’aéronef. L’utilisation des matériaux orthotropes dans les constructions aéronautiques entraînes un gain de poids substantiel dont les gains de masse varient de 10 à 20 %, le poids de l’avion moyen-courrier Bœing 767 a été réduit, par l’emploi

4 de poids sont déterminants pour optimiser la consommation de carburant d’appareils soumis a des cycles quotidiens élevés de décollages et d’atterrissages. Un gain de masse d’1Kg, sur la structure de l’avion 120 litre/année d’exploitation et une augmentation du rayon d’action de l’appareil d’un mile nautique ainsi sa vitesse de croisière. Par l’introduction des matériaux orthotropes dans la construction du gros porteur TRISTAR, la société LOCKHEED a effectué une réduction importante du nombre d’éléments assemblés par rivets de 175 éléments assemblés par 40000 rivets pour une masse totale au décollage de 363 tonnes à 18 éléments assemblés par 5000 rivets pour une masse de 245 tonnes au décollage 5000 rivets et obtenir par conséquent des surfaces lisses entraînant de meilleures performances. Les matériaux orthotropes sont aussi utilisés dans la construction spatiale (lanceurs, navettes et satellites) à cause de leurs propriétés remarquables dont la haute résistance à l’élévation de la température. Surtout ceux a fibres de carbone (dilatation nulle jusqu’à 600°c) et l’allégement. Les preuves sont les coûts minimisés de 30000$ pour chaque Kg gagné dans la réalisation du lanceur de la fusée européennes ARIANE E.S.A de plus, les matériaux orthotrope sont essentiellement utilisés dans la réalisation de propulseurs de poudre des lanceurs de satellites et de leurs tuyères d’éjection des gaz de propulsion [13].

b. Application dans l’industrie mécanique :

L’intégration des matériaux orthotropes dans l’industrie mécanique, de l’automobile et des transports terrestres a pu réduire substantiellement la consommation de carburant au moyen de l’économie du poids obtenu. Les applications sont très nombreuses dans les domaines des transports, même ferroviaires. Avec la fabrication de nombreux éléments de carrosserie et des boucliers amortisseurs de choc placés à l’avant de motrices de T.G.V. et qui présentent des performances supérieures en matière d’absorption d’énergie [9]. La société LOHEAC de transports routiers a pu réduire substantiellement sa consommation de carburant grâce à l’économie du poids obtenue en remplaçant les cabines conventionnelles de ses tracteurs par de nouveaux éléments moulés en une seule pièce. Cette innovation a permis de réduire le poids de la cabine de 875 Kg équipée en acier à 455 Kg seulement et de présenter une plus grande solidité et une meilleure résistance aux dégâts. Le saut technologique, réalisé grâce à l’introduction des matériaux orthotropes dans la construction traditionnelle en bois.

L’adoption de tels matériaux dans la construction des coques des bateaux a permis de procurer à la structure une haute résistance à l’usure et aux chocs répétés dans les vagues et

5 (composites, tels que ceux renforcés par la fibre aramide kevlar 49 associée à la fibre de verre-E) conduisant à des propriétés mécaniques supérieures, a permis de diminuer le poids des structures de bateaux rapides (patrouilleurs, bateaux d’intervention ou de service) tout en ayant une résistance suffisante affin d’avoir pour résultat soit un augmentation de la vitesse pour une puissance donnée, soit une meilleure rentabilité pour la même vitesse ou soit l’utilisation d’une motorisation moins puissante.

c. Application dans le domaine de la biomécanique :

En biomécanique, les matériaux orthotropes ont connus des applications courantes surtout dans la construction des biomatériaux. Les biomatériaux sont des matériaux non vivants utilisés dans des dispositifs médicaux, prévus pour interagir avec le système biologique dans le cadre d’un acte thérapeutique à savoir :

- implants, plaques et vis d’ostéosynthèse….etc.

- appareils de circulation extracorporelle (dialyseurs…etc.) - instruments chirurgicaux (seringue….etc.)[11].

Dans ce domaine les matériaux orthotropes sont des matériaux synthétiques (métaux, polymères, céramiques, composites,…..etc.). La particularité de ces matériaux c’est que ces derniers sont biocompatibles c-a-d ils n’entraînent aucune réponse inflammatoire de l’hôte au niveau des site où ils sont appliqués [10].

d. Application dans le domaine des sports et de loisir :

De par leur légèreté. Leur bonne tenue à la fatigue statique est dynamique et leur stabilité dimensionnelle, les matériaux orthotropes sont des matériaux idéaux pour la fabrication et la conception de très nombreux d’articles de sport et de loisirs tels que les skis et les bâtons, les planches à voiles, des instruments de musique…. Etc.

Des nombreux résultats d’études confirment le haut degré d’amortissement des vibrations des skis sur neige qui confère au skieur le confort tout en conservant au produit ses caractéristiques essentielles. De plus, les matériaux orthotrope permettent de concevoir de raquettes légères, très rigides et excellentes en fatigue dynamique qui confèrent au joueur une moindre sollicitation des muscles du bras et donc de moindre fatigue et plus de confort [12].

6

3.1. Introduction

L'utilisation très répondue de structures en plaques orthotropes exige une investigation afin de développer une conception précise et confiante. Dans ce domaine, d'un point de vu engineering, la méthode des éléments finis (MEF) donne une solution complète au problème d'évaluation des modes de vibrations et les réponses dynamiques d'une plaque orthotrope lorsque les propriétés des matériaux et les conditions limites sont connues.

Cependant au cours des premières étapes pendant l'élaboration et la conception du projet, où la tache essentielle consiste à sélectionner les dimensions et les propriétés des matériaux constitutifs doivent être sélectionnés, de même que lorsqu'on applique les contrôles de qualités pour la précision de la conception au moyen de calcul par la (MEF), dans ce cas il est très utile d'avoir une méthode simplifiée pour calculer les fréquences modales des plaques orthotropes rectangulaires [18]. On dit qu’une structure est complexe si toute solution analytique de celle-ci est impossible ou est obtenue après des calculs délicats. Cette définition s’applique aux structures en plaques. Et on dit aussi qu’une telle méthode est équivalente si elle nous permet de calculer une structure avec des méthodes approchées tout en respectant un seuil d’erreur à ne pas dépasser. Nous allons utiliser donc ces méthodes équivalentes pour trouver les solutions des structures en plaques en vibration libre [17]. Concept La méthode de l'analyse par éléments finis (MEF), à l'origine présentée par Turner et autres (1956), est une technique informatique puissante pour les solutions approximatives aux une série de " ; vrai world" ; les problèmes de technologie ayant des domaines complexes sous réserve des conditions générales de frontière. MEF est devenu étape essentielle dans la conception ou la modélisation d'un phénomène physique dans diverses disciplines de technologie. Un phénomène physique se produit habituellement dans a le continuum de matière (solide, liquide, ou gaz) impliquant plusieurs mettent en place des variables. Les variables de champ varient de point par point, de ce fait possédant un nombre infini de solutions dans le domaine. Dans la portée de ce livre, a le continuum avec une frontière connue s'appelle un domaine [16]. La base de MEF se fonde sur la décomposition du domaine dans un nombre fini de subdomains (les éléments) pour lesquels les systématiques rapprochent la solution est construite en appliquant les méthodes résiduelles variationnelles ou pesées. En effet, FEA ramène le problème à celui d'un nombre fini d'inconnus en divisant le domaine en éléments et par l'expression la variable inconnue de champ en termes de rapprocher assumé fonctionne

7 dans chaque élément. Ces fonctions (également appelées les fonctions d'interpolation) sont définies en termes de valeurs des variables de champ aux points spécifiques, visées comme noeuds. Des noeuds sont habituellement situés le long des frontières d'élément, et ils relient les éléments adjacents

La capacité de discrétiser les domaines irréguliers avec les éléments finis fait à la méthode un valable et l'outil d'analyse pratique pour la solution de la frontière, de l'initiale, et des problèmes de valeur propre surgissant dans la diverse technologie discipline. Depuis son commencement, beaucoup d'exposés techniques et de livres sont apparus sur le développement et l'application de MEF. Les livres par Desai et Abel (1971), Oden (1972), Gallagher (1975) [17-19], Huebner (1975) [17-19], se baignent et Wilson (1976), Ziekiewicz (1977), cuisinier (1981), et se baignent (1996) ont influencé état actuel de FEA. Problèmes communs de technologie de représentant et leurs discrétisations correspondantes de MEF sont illustrées dans figure suivante :

La méthode d'analyse par éléments finis exige les étapes principales suivantes [27] : • Discrétisation du domaine dans un nombre fini de subdomains (éléments). • Choix des fonctions d'interpolation.

• Développement de la matrice d'élément pour le subdomain (élément).

• Assemblée des matrices d'élément pour que chaque subdomain obtienne la matrice globale pour le domaine entier,

• Imposition des conditions de frontière. • Solution des équations.

• Calculs additionnels (si désiré) [16].

8 - on peut représenter un grand nombre de formes de structures à l’aide de modèle

analytique générales communes.

- La faculté de définir des maillages très irréguliers et depuis l’origine un des grands avantage de la M.E.F

- Peut accepter des loi complexes de propriétés intrinsèque de matériaux si on compare aux possibilité des méthodes classiques de résolution, et offrent plus vastes perspectives en analyse non linaire [18].

3.3. Autres types de modélisation

3.3.1. Modélisation par ANSYS:

ANSYS, est l'un des plus grands développeur et fournisseur de logiciels de simulation

numérique au monde. Ses produits majeurs sont des logiciels qui mettent en œuvre la méthode des éléments finis, afin de résoudre des modèles discrétisés [27].

Ce produit permet d'effectuer des simulations mécaniques. Ses principales capacités sont : (1) l'analyse statique.

(2) l'analyse modale

(3) l'analyse harmonique (réponse forcée) (4) l'analyse temporelle ou transitoire

(5) la gestion de différentes situations non linéaires (contacts, plasticité des matériaux, grands déplacements ou grandes déformations

(6) simulations en matière de mécanique des fluides

(7) permet de résoudre des modélisations mettant en jeu des phénomènes électromagnétiques.

3.3.2. Modélisation par SAP2000 :

Est un progiciel à partir de Computers et Structures, pour l'analyse structurale et de signe. Chaque paquet est un système entièrement intégré pour la modélisation, l'analyse, concevoir, et les structures de linéarisation d'un détail type :

 SAP2000 pour général structure, y compris des ponts, des stades, tours, ensembles industriels, structures en mer, systèmes sifflants, bâtiments, barrages, sols, machine pièces et beaucoup d'autres.

9 Au coeur de chacun de ces progiciels est un moteur commun d'analyse, désigné par dehors ce manuel sous le nom de SAP2000. Ce moteur est le plus tardif et les la plupart version puissante de la série bien connue de SAP de programmes d'analyse structurale.

Le but de ce manuel est à de scribe les dispositifs du moteur de l'analyse SAP2000. Par dehors ce manuel le moteur d'analyse désigné sous le nom de SAP2000. Non tous les dispositifs de tracés réellement soient disponibles dans chaque niveau de chaque

programme.

Leur moteur d’analyse offre les dispositifs suivants : • Analyse statique et dynamique.

• Oreille de Lin et analyse non linéaire.

• Analyse séismique dynamique et analyse statique de facilité. • Analyse de vivre charge de véhicule pour des ponts.

• Non linéarité géométrique, y compris des effets de grand déplacement. • Construction (par accroissement) étagée.

• Fluage, rétrécissement, et effets de vieillissement. • Analyse de boucle.

• Analyse équilibrée et de puissance spectral densité.

• Éléments structuraux de vue et de coquille, y compris la colonne de faisceau, la botte, la membrane, et le comportement de plat.

• Avion bidimensionnel et éléments pleins axisymétriques. • Éléments pleins tridimensionnels.

• Éléments non linéaires de lien et de soutien.

• Propriétés liées à la fréquence de lien et de soutien. • Systèmes du même rang multiples.

• Beaucoup de types de contraintes.

• Une large variété d'options de chargement. • Alpha numérique marque.

• Grande capacité.

10 Notre travail consiste en l’analyse du comportement statique et dynamique des plaques orthotropes minces bi dimensionnelle sous l’effet des efforts extérieurs utilisant les méthodes numériques et de modélisations en se basant sur la méthode des éléments finis. La méthode des éléments finis (M.E.F) est très répandue de structures en plaques orthotropes exige une investigation afin de développer une conception précise et confiante. Elle donne une solution complète aux problèmes statique et dynamique afin d'évaluer les modes de vibrations et les réponses dynamiques d'une plaque orthotrope lorsque les propriétés des matériaux et les conditions limites sont connues. Au cours des premières étapes de l'élaboration de cette étude, notre tache essentielle consiste à sélectionner les dimensions et les propriétés des matériaux constitutifs doivent être sélectionnés, de même que lorsqu'on applique les contrôles de qualités pour la précision de la conception au moyen de calcul par la (MEF), dans ce cas il est très utile d'avoir une méthode simplifiée pour calculer les fréquences modales des plaques orthotropes rectangulaires. Les contraintes et les déformations en chaque noeud de la plaque orthotrope ont été déterminées pour différents types de chargement (aléatoires, harmoniques et transitoire) avec et sans amortissement comparativement avec celles d’une plaque isotrope.

L’étude des vibrations ou l’analyse des plaques mince orthotropes et isotrope soumise a des effort à l’aides de la méthode M.E.F

Pour atteindre ce but on va suivre les étapes suivantes : - présenter l’élasticité linéaire et l’orthotropie de la plaque. - Présenter les équations de base d’une plaque orthotrope - Réaliser le traitement numérique correspondant (New Mark)

- Présenter le code de calcul des plaques orthotropes et isotropes [27].

Le mémoire de magistère comprend essentiellement cinq chapitres en plus d’une introduction et conclusion et des références bibliographiques. Le premier chapitre est consacré à la théorie d’élasticité linéaire des plaques orthotropes ou on a présenter la loi de Hooke généralisé et les différents types des matériaux et plaques orthotropes, on a développé au second chapitre l’analyse des plaques orthotropes ou on peut voir l’équation d’équilibre et les différents types de forces appliquées et après l’équation différentielle de la plaque orthotrope. Le troisième chapitre aborde l’analyse des plaques orthotropes par la méthode des éléments finis ou on peut montrer la formulation de la matrice de rigidité de la plaque à l’aide de plusieurs méthodes. Le quatrième chapitre abord l’étude dynamique des plaques orthotropes par la méthode de New Mark ou on peut voir équation de mouvement des différents types de charge,

11 le problème d’amortissement et la résolution numérique de New Mark. Dans le dernier chapitre on informatisé les différentes étapes de calcules des plaques orthotropes pour effectuer une étude comparative de leurs comportement mécaniques en utilisant plusieurs types de programmation « fortran, ANSYS, et SAP200 ». En fin l’analyse des différents résultats obtenus va nous permettre d’établir une conclusion qui met au point la fiabilité et l’efficacité des plaques orthotropes.

12

I

Chapitre I : Théorie

d’élasticité linéaire des plaque

orthotropes

Chapitre I : Théorie d’élasticité des plaques orthotropes

1.1 Introduction:

Les matériaux anisotropes selon leur modèle de fabrication et leurs structures internes à l’état macroscopique dépendent essentiellement de l'orientation de leurs fibres et des efforts internes existant durant leur fabrication.

Dans ce chapitre on va montrer la théorie des plaques ainsi les matériaux orthotropes et isotropes, les constantes mécaniques qui les caractérisent et les différents types des plaques orthotropes.

1.1.1 Théorie des Plaques

La théorie des plaques est une théorie permettant de calculer les déformations et les contraintes dans une plaque soumise à des charges. Elle s'inspire de la théorie des poutres.

13

1.1.1.1. Historique

En 1888, Love utilise les hypothèses de Gustav Kirchhoff, elles-mêmes inspirées des hypothèses d'Euler Bernoulli pour les poutres, pour fonder une théorie des plaques minces1. La théorie des plaques épaisses a été consolidée par Mindlin2 à partir des travaux de Rayleigh (1877), Timoshenko (1921), Reissner (1945) et Uflyand (1948) [25-26-22-15-37].

1.1.1.2. Démarche

Comme pour l'étude des poutres, on met en relation

 la forme finale de la plaque, c'est-à-dire le champ des déplacements, avec le champ de tenseur des déformations ;

 les efforts de cohésion avec les efforts extérieurs ;

 les efforts de cohésion avec le tenseur des contraintes, grâce au principe d'équivalence ;

 et le tenseur des contraintes avec le tenseur des déformations, grâce à la loi de Hooke généralisée.

1.1.1.3. Démarche pour l'étude des plaques :

Efforts Extérieur Champ de Tenseur Des Contraintes Principe D’équivalence Champ De Tenseur DesDéformations Loi de Hooke Généralisé

ε

_ij Champ de Déplacement ui(xi) Dérivation/ Intégration

Figure 1.1 Organigramme de démarche de l’étude de laplaque [30]. [15].

14

1.1.4. Définitions et Hypothèses

Une plaque est un solide délimitée par deux plans parallèles, les faces, et un cylindre au sens large (de section quelconque et pas nécessairement circulaire) dont l'axe est perpendiculaire aux faces. On définit :

 le plan moyen, ou plan médian : plan situé à équidistance entre les faces (c'est l'équivalent de la courbe moyenne des poutres) ;

 le feuillet neutre : élément de matière d'épaisseur infinitésimale situé autour du plan moyen (c'est l'équivalent de la fibre neutre des poutres) ; c'est le plan (O, x, y), d'équation z = 0 ;

 une fibre normale : ensemble des points situés sur une normale au plan médian, à un endroit (x, y) donné ; elle a pour direction z.

On appelle h l'épaisseur de la plaque ; le plan inférieur est donc le plan z = -h/2 et le plan supérieur est le plan z = h/2.

On se place dans le cas d'un matériau continu, élastique, homogène et isotrope. Si les faces ne sont pas planes, on parle de coque.

On sépare l'étude en deux parties : pour l'étude de la flexion, on considère que les charges sont perpendiculaires aux faces, donc que les forces sont de la forme

Et que les couples sont de la forme

.

Pour les charges situées dans le plan des faces, on parle de voile ou de membrane.

1.2. Les Milieux Continue:

1.2.1 Définition:

C'est un domaine qui ne présente aucune rupture dans le temps et dans l'espace occupé par un solide dont la répartition de la matière elle se caractérise par des fonctions continues et dérivables sur les trois coordonnées [37].

15

 

1

.

2

12 31 23 33 22 11 66 56 55 46 45 44 36 35 34 33 26 25 24 23 22 16 15 14 13 12 11 12 31 23 33 22 11





















































































































































C

C

C

sym

C

C

C

C

C

C

C

C

C

C

C

C

C

C

C

C

C

C

1.2.2. Milieu homogène:

Est un corps où un milieu dont la composition uniforme

1.3. Loi de Hooke Généralisée :

Est une loi de dépendance entre les contrainte et les déformation donc c’est une proportionnalité entre les déplacements élastique d’un corps et les efforts aux quels il est soumis.

1.4. Les différents Types des matériaux

1.4.1. Les matériaux anisotropes:

Sont des matériaux dont ses propriétés varient selon une direction considérée mais ils ne présentent pas de plans de symétrie. La loi de Hooke peut être exprimée par:

ij = Cijklkl i,j,k,l = 1,2,3

ij = Sijklkl i,j,k,l = 1,2,3

Cijkl = Tenseur d'élasticité (ou de rigidité)

Sijkl = Tenseur de souplesse

ij = Tenseur de déformation

ij = tenseur de contrainte

Le tenseur de rigidité en a 81 coefficients de même pour le tenseur de souplesse, pour raison de la symétrie des contraintes ij et de déformation, il y a une réduction des cœfficients a 36

parmi ces derniers, 21 sont indépendants. Les distorsions angulaires sont exprimées en fonction des déplacements :

23= 223

13= 213

12= 212

On écrit (1.2) sous la forme matricielle

16

 

1

.

3

12 31 23 33 22 11 66 56 55 46 45 44 36 35 34 33 26 25 24 23 22 16 15 14 13 12 11 12 31 23 33 22 11





















































































































































S

S

S

sym

S

S

S

S

S

S

S

S

S

S

S

S

S

S

S

S

S

S

) 4 . 1 ( 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 12 31 23 33 22 11 66 36 26 16 55 45 45 44 36 33 23 13 26 23 22 12 16 13 12 11 12 31 23 33 22 11                                                                           C C C C C C C C C C C C C C C C C C C C En inversant (1.2), on obtient : 1.4.2. Matériaux monocliniques:

Si le matériau a un plan de symétrie, monoclinique, quelques constantes sont zéro et le comportement peut être décrit avec 13 constants:

1.4.3. Matériaux orthotropes:

Sont des matériaux qui possèdent 3 plans de symétrie orthogonaux, ces derniers ont les mêmes propriétés ou caractéristiques mécanique.

Ce qui réduit le nombre des coefficients indépendants à 9 (Fig.1.2)

Donc :

Y X Z

17

 

1

.

6

0

0

0

0

0

0

0

0

0

0

0

0

12 31 23 33 22 11 66 55 44 33 23 22 13 12 11 12 31 23 33 22 11





















































































































































S

S

sym

S

S

S

S

S

S

S

) 5 . 1 ( 0 0 0 0 0 0 0 0 0 0 0 0 12 31 23 33 22 11 66 55 44 33 23 22 13 12 11 12 31 23 33 22 11                                                                           C C sym C C C C C C C

En inversant le système (1.5) on obtient

Le coefficients de souplesse sont définis par:

1 11 1 E S  ; 2 22 1 E S  ; 3 33 1 E S  ; 4 44 1 E S  13 55 1 G S  ; 2 21 12 E S   ; 3 32 23 E S   ; 3 31 13 E S   ; 12 66 1 G S  Avec :

 E_ijet Gijsont le module d’Young et Coulomb respectivement.

 _ij est le coefficient de Poisson A cause de la symétrie:  11 12 22 21 E E     11 13 33 31 E E   

18



33 22 E

E 

1.4.4. Matériaux transversalement isotropes:

Figure 1.3 : Matériau transversalement isotrope

Un matériau isotrope transverse est un matériau orthotrope qui comporte un axe ou un plan d'isotropie.

Les propriétés suivant les axes 2 et 3 sont identiques, donc:

 C22 C33  C12 C13  C55 C66

Le nombre de coefficients indépendants se réduit à 5 coefficients. La loi de comportement s'écrit:

                                                              12 31 23 33 22 11 66 66 23 22 22 23 22 12 12 11 12 31 23 33 22 11 0 0 0 2 0 0 0 0 0 0 0 0 0             C C sym C C C C C C C C (‎I)

1.4.5. Matériaux quasi isotropes transverses:

Le nombre de coefficients indépendants se réduit à 6 coefficients. Et la loi de comportement s'écrit:

3

1

19                                                              12 31 23 33 22 11 66 44 44 33 13 11 13 12 11 12 31 23 33 22 11 0 0 0 0 0 0 0 0 0 0 0 0             C C sym C C C C C C C (1.8)

1.4.6. Matériaux quasi isotropes:

Le nombre de coefficients indépendants se réduit à 3 coefficients. La loi de comportement s'écrit:

) 9 . 1 ( 0 0 0 0 0 0 0 0 0 0 0 0 12 31 23 33 22 11 44 44 44 11 12 11 12 12 11 12 31 23 33 22 11                                                                           C C sym C C C C C C C 1.4.7. Matériaux isotropes:

Matériaux dont les propriétés physiques ou mécaniques sont identiques dans toutes les directions : El =E2=E3=E

12 = 13 = 23 =  (1.10)

G12=G13=G23 =G

Ce qui réduit le nombre des coefficients élastiques indépendants à 2 (C11, C12).

) 11 . 1 ( 2 0 2 0 0 2 0 0 0 0 0 0 0 0 0 12 31 23 33 22 11 12 11 12 11 12 11 11 12 11 12 12 11 12 31 23 33 22 11                                                                                  C C C C sym C C C C C C C C

20                                                                          12 31 23 3 2 1 12 31 23 3 2 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0                 G G G E E E E E E E E E (1.12) Avec:

_

_

   1 2 E G

Théorie des plaques minces

La théorie des plaques minces, ou théorie de Love Kirchhoff, suppose que

 le plan moyen (équivalent de la courbe moyenne des poutres) est initialement plan ;

 le feuillet moyen (équivalent de la fibre neutre des poutres) ne subit pas de déformation dans son plan ; on ne considère que le déplacement transversal w des points du feuillet moyen ;

 modèle de Kirchhoff : les sections normales au feuillet moyen restent normales lors de la déformation ; en conséquence, on peut négliger le cisaillement ;

 l'épaisseur est faible ; en conséquence, les contraintes dans le sens de l'épaisseur sont supposées nulles ;

 elle reste une petite déformation [25].

Déplacement

Figure 1.3 : Déformation d'une plaque mince avec mise en évidence du déplacement d'un élément de matière, de son feuillet moyen (rouge) et de sa fibre normale (bleue) [30].

21 Soit un point M(x, y, z) de la plaque au repos. À l'instant t, sa position est M’, et l'on définit le vecteur déplacement

.

Pour une plaque à un instant donné, les déplacements sur les axes u, v et w sont en fonction du point M, donc de ses coordonnées (x, y, z), et de l'instant t.

Par hypothèse, les déplacements verticaux sont les mêmes pour tous les points d'une même fibre normale, on a donc : w(x, y, z, t) = w(x, y, t) [30].

La fibre normale en (x, y) tourne d'un angle θx autour de l'axe x et d'un angle θy autour de l'axe

y. Comme on est en petite déformation, l'arc de cercle décrit par un point lors de la rotation de

la fibre normale est assimilable à un segment de droite, et l'on a :

u(x, y, z, t) ≃ z·θy(x, y, t) ; v(x, y, z, t) ≃ -z·θx(x, y, t) ;

Ou encore

Les angles θx et θy représentant aussi la pente que prend le feuillet moyen, on a donc

également :

Déformation

D'après la définition du tenseur des déformations, on a : (1.13)

22

 

1

.

15

0

66 22 12 12 11

































































xy yy xx xy yy xx

S

S

S

S

S













x E S11 1 y yx x xy E E S₁₂   y E S22  1

 

1

.

16

0

66 22 12 12 11

































































xy yy xx xy yy xx

C

C

C

C

C













xy G S₆₆  1 .

1.5 Cas des Plaques Orthotropes:

Une plaque orthotrope possède des paramètres de rigidité différents selon deux axes perpendiculaires, cesaxes étant dans notre problème parallèle aux bords de laplaque.Il existe plusieurs types d’orthotropie :

- une orthotropie de géométrie où la géométrie de la plaque entraîne l’orthotropie à module d’Young constant,- une orthotropie de matériau où la plaque possède deux modules d’Young différents selon les deux directions. Les plaques orthotropes en flexion présentent une coïncidence entre les axes d'orthotropie et les directions principales x , y.

Pour un état de contrainte plane

zz =yz =xz= 0

La relation entre le tenseur de déformation et le tenseur de contrainte sous forme matricielle est la suivante :

Avec :

Pour obtenir la relation des contraintes en fonction des déformations on peut inverser la relation précédente qui donne