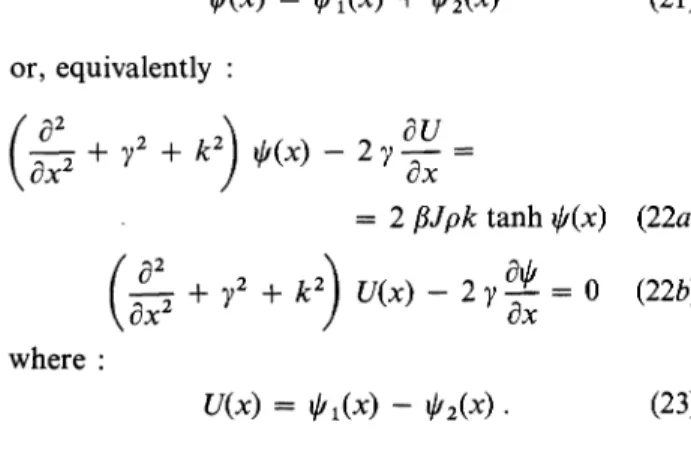Non-homogeneous mean field picture for spin-glasses

HAL Id: jpa-00231877

https://hal.archives-ouvertes.fr/jpa-00231877

Submitted on 1 Jan 1981

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

teaching and research institutions in France or

abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

recherche français ou étrangers, des laboratoires

publics ou privés.

Non-homogeneous mean field picture for spin-glasses

Henri Orland, C. de Dominicis, T. Garel

To cite this version:

Henri Orland, C. de Dominicis, T. Garel. Non-homogeneous mean field picture for spin-glasses.

Journal de Physique Lettres, Edp sciences, 1981, 42, pp.73-77. �10.1051/jphyslet:0198100420407300�.

�jpa-00231877�

L-73

Non-homogeneous

mean

field

picture

for

_spin-glasses

H.

Orland,

C. de Dominicis and T. Garel

_(*)

DPh-T, CEN _Saclay, B.P. n° 2, 91190 Gif sur _Yvette, France

(Reçu le 14 octobre _1980, revise le 16 decembre, accepte le 22 decembre 1980)

Résumé. 2014 Dans

cette lettre, nous _{calculons la moyenne gelée (sans répliques) pour} des verres de _spin avec désordre local. Ceci _permet une définition naturelle du _champ moyen. On montre que les champs moyens décrivant les

verres de _spin sont du _type instanton. Abstract. 2014 In this letter _we

perform quenched averages (without

replicas)

for spin-glass systems with local

disorder. This allows a natural definition of a mean field _theory. The mean fields relevant to _spin-glasses are shown

to be instantons.

LE

JOURNAL

DE

_{PHYSIQUE - LETTRES}

J. _Physique - LETTRES 42 (1981) L-73 - L-77 15 FÉVRIER 1981, I Classification Physics Abstracts 61.40D 1. Introduction. - In order

to

_explain

the

_puzzling

experimental properties

of

_spin-glasses

_[1],

_many

ingredients

are

likely

to be _necessary. On the theore-tical side

_[2],

there is wide _agreement on the minimum

input

needed to understand

_{qualitatively}

such proper-ties.

_Namely,

one should consider models with

com-peting

magnetic

interactions

_{(frustration)}

and

quench-ed disorder. Most theoretical models thus

_replace

the

original problem (randomly

located

_{spins) by}

a lattice

problem

with random

_couplings.

Along

these

lines,

there have been

_mainly

two _ways

of

_approaching

the delicate

_{spin-glass problem.}

On the one

_hand,

a mean field

theory

has been

proposed

by Sherrington

and

_Kirkpatrick

_(SK)

[3],

for a

model with

_long-range

interactions;

such a model

displays

a

_phase

transition towards a

spin-glass

phase,

but the presence of a

quenched

disorder has

made so far the low

_temperature

phase

difficult to

study

(and

to

_{understand) [4].}

Moreover, due to its

mean field

character,

the SK model washes out all

spatial

correlations,

and its results are

expected

to be relevant

_only

for dimensions

_greater

than six. On the other

_hand,

_computer

studies for «more realistic

models »

_(e.g.

three-dimensional systems with nearest

neighbour

interactions)

have shown that

spatial

correlations are

_important

indeed

[5]

and some

expe-rimental results have been

_{successfully explained}

in

terms of a cluster

_picture

_[6].

This cluster

interpre-tation is somewhat reminiscent of the Néel’s

theory

of «

grains

fins »

[7],

but it seems difficult to

_bridge

the _gap between the

_phase

transition

_approach,

where one _expects a collective behaviour of the

_spins,

and the cluster

approach

with _strong intracluster

couplings

and weak intercluster

_couplings.

In this _note, we wish to

_study

a class of

spin

_systems,

with

_purely

local disorder. For such _systems, we

perform

in section

2,

the

_quenched

_average and calculate the free _energy

_(without

_replicas).

A

quench-ed

_partition

function is defined

_{(section 3)}

whose

leading

term is a mean

density quenched

free _energy. Mean field

_theory

follows from a saddle

point

treat-ment of the

_leading

term

_only.

In section

_4,

we consider

two

_simple

one-dimensional

_examples,

_namely

ran-domly

located

_{spins interacting}

via

_long-range

oscil-latory

interactions. The salient features of such models is the existence of

_{non-homogeneous}

mean field

solu-tions. The first

_example

_[8]

_{displays oscillatory}

solu-tions,

and is

_unlikely

to

_depict

a

_spin-glass

_phase

whereas in the second one, clusters of

spins

(or

instan-tons)

show _up below the transition _temperature.

2.

Quenched

averages. - We consider

a model

with local disorder : N

_{magnetic impurities}

are

located at random sites of a D-dimensional lattice.

Any

of the Q sites of the lattice can be

occupied by

0 or 1

_impurity.

A

_{given configuration}

of

_impurities

is defined

_{by occupation}

numbers

_n.,

_taking

the value 0 or

_1,

with the constraint :

L-74 JOURNAL DE PHYSIQUE - LETTRES

The

_partition

function for such a

_{configuration}

reads :

where the summation runs over all

_{possible spin configurations,}

_{and Jjl}

denotes the

_exchange

interaction between

spins

at

_{sites y}

and l

_(for

a realistic _system,

_J1

can be

_thought

of as the RKKY

interaction).

The

_quenched

free energy for such a _system is defined

by :

]

For

_{Ising spins,}

for

_instance,

₍₂₎

can be rewritten :

The

_quenched

free _energy

F

is thus

_replaced

_{by :}

Since Ln

_{Z({ nj })}

behaves at most

_(for

a

_{given configuration)}

like

N2,

we _may

_compute

_{(5) by}

saddle

_point

expansion

on a, _{Vj’ nj} around the saddle

point

value :

i.e.

The

_quenched

free _energy

_averaged

over

disorder,

is thus

_{given by :}

where the first term is a mean

_{density quenched}

free _energy and L1 stands for all corrections to this saddle

_point

result.

This is to be contrasted with the annealed case where one is

averaging

the

partition

function Z

{

n~ }

(instead

of the free

_energy).

In that case the

_partition

function enters the saddle

_point

_equations

and

_(6b)

is to be

_replaced

by :

-leading

to a solution distinct from

(7).

for the corrections to the mean

_density

_quenched

free _energy,

This

_expression

includes fluctuation effects around _p and is valid as

_0,

N -~ oo with

N/D

=- _p. Here the

average >p

means that one uses a

_density

matrix exp L

_{

_ni =

p }

_as

appearing

in

(4)

with nj

=

p.

3. Mean field

_theory.

- In the

following

we shall

be interested in _systems with

_large

effective number of

_{interacting neighbours,}

a case relevant for «

long-range » forces

(or high dimensionality).

In such

circumstances a _very

good approximation

is

provided

by

the mean field

_theory

that

_replaces

a

_density

matrix

proportional

to _exp

_L(p)

as in

₍₄₎

_by

a

_separable

one

]t exp

L/p) :

j

Here

_{4> j}

is chosen self

_consistently

as the best

_possible

mean

_field,

and this is

_provided

_by

the saddle

_point

equation

on

_{L(p) :}

yielding

It is of interest

to

notice that in this mean field

approximation

all corrections L1 to the mean

density

quenched

free

energy vanish :

Furthermore it can be shown that L1 does not either affect

_stability

boundaries of the mean field

approxi-mation.

4.

_Examples.

- To work out

examples

convenient-ly,

we _go to the continuous limit _~2, N -~ oo and

4.1 SEPARABLE INTERACTION. - We consider

a

one-dimensional model with :

This model has been

_previously

considered

_[8].

The

mean field

approximation

is exact and shows a

_phase

transition. Below

_{7~ (7~}

=

JI2),

equation

(13)

yields :

where :

The

_periodic

solution

_displayed

in

_{equation (16)}

does not seem to

_correspond

to _any realistic

spin-glass

model

_(existence

of

_{long-range order).}

4.2 NON-SEPARABLE INTERACTION. - We

now

consider a one-dimensional model with :

where _y k

_(which

means that the oscillation

period

is small

_compared

to the interaction

_range).

Even

_though

this model is

_unlikely

to show a

_phase

transition in one

_dimension,

mean field

theory

pro-vides,

as

_usual,

a

qualitative

understanding

of the low _temperature

_phase

in

_higher

dimensions.

The Fourier transform of

_{J(x, y)}

can be

split

into two terms

where :

L-76 JOURNAL DE _{PHYSIQUE -} LETTRES

equation (13)

becomes :

or,

_{equivalently :}

where ;

In the

_{long-range approximation (y}

_k),

equa-tion

_(22b)

shows that

_U(x)

is of order y.

Neglecting

terms of

_{order y2}

in

_(22a),

we

replace

equations

(22)

by :

Note

that,

since the function

_tf¡(x)

is

_only

defined

on the

_length

0, the above results were obtained

with the

_underlying

_assumption

that

_~(x)

is

_{periodic :}

Equation (24a)

is

_equivalent

to the motion of a

classical

_particle

of mass

_unity

in the

_{potential :}

A

_phase

transition _appears when the curvature of the

_{potential at t/1 =}

0,

changes

sign

(Fig.

1),

namely,

at a

_{temperature :}

Fig. 1. - Schematic

potential ~).

At T >

_7c,

the

_simplest

solution to

_{equations (24)}

is ~

=

0,

namely

a

_paramagnetic

_phase.

Below

_Tc,

two _types of solution _{appear :}

-

Homogeneous : they correspond

to the two

ferromagnetic phases l/J ==

±

l/J 0’

and to the

parama-gnetic one ~

= 0.

-

Non-homogeneous :

in the

_{thermodynamic}

limit

(~2 -~

+

_oo),

new _types of mean field are to be

consi-dered, namely

those

_{corresponding}

to motions close

to zero _energy

(instantons) [9].

A

_{simple study}

of the

_stability

of the solutions shows that

_homogeneous

solutions are unstable

below

_Tc

and that

_only

_{inhomogeneous}

solutions

of the instanton

_type

_may survive.

The

_{physical picture arising}

below

_Tc

is that of a gas of instantons. These instantons can be

_thought

of as coherent

spin

clusters,

with _up or down

magne-tization. The finite size of these clusters

_(increasing

with _temperature and

_diverging

at

_7c)

and the

exis-tence of a zero

magnetization region

between two

such clusters

_(Fig.

₂₎

are due to the frustration effect.

Fig. 2. - Instanton-anti-instanton classical solution.

One must

_keep

in mind that these instantons are

completely

delocalized in space,

yielding

the

picture

of a

_paramagnetic

_gas of clusters

(1).

In this

_approach,

the EA order parameter, which builds up below

T~,

measures the

_{magnetization}

carried

_by

one instanton.

Note that in the mean field

_{approximation}

used

here,

7~

scales like _p. However it is clear that for

short-range

interaction and small

_enough

_density

(p

pp

percolation threshold)

the

system

will be

paramagnetic

at all

_{temperatures.}

This

_phenomenon

appears

through

the corrections to mean field.

For

_spin-glasses

that do not have

_long-ranged

interactions like

_{insulating spin-glasses}

the above

picture

of an instanton _gas should remain useful for

densities

_sufficiently

_larger

than _pp.

Acknowledgments.

- We would like to thank

E.

Brezin,

C.

_Itzykson,

J.

Lebowitz,

H. J. Schulz and R. E. Peierls for

_helpful

discussion at various

stages

of this work.

(1) In mean field theory, the instanton _gas is non-interacting,

References

[1] JOFFRIN, J., in the Ill-condensed matter, R. Balian et al. eds. (North-Holland, New _{York) 1979, p. 68.}

[2] ANDERSON, P. _{W., ibidem, p. 214.}

[3] SHERRINGTON, D., KIRKPATRICK, S., Phys. Rev. Lett. 35 ₍₁₉₇₅₎ 1792.

[4] THOULESS, D. J., ANDERSON, P. _W., PALMER, R. G., Philos.

Mag. 35 ₍₁₉₇₇₎ 593.

KIRKPATRICK, S., SHERRINGTON, D., Phys. Rev. B 17 ₍₁₉₇₈₎ 4384.

PARISI, G., Philos. _Mag. B 41 (1980) 677.

[5] BINDER, K., J. _{Physique Colloq.} 39 (1978) C6-1527 and refe-rences therein.

[6] LEVIN, K., SOUKOULIS, C. M., GREST, G. S., J. Appl. Phys. 50 (1979) 1695 and references therein.

[7] THOLENCE, J. L., TOURNIER, R., J. _{Physique Colloq.} 35 ₍₁₉₇₄₎ C4-229.

[8] FERNANDEZ, J. F., SHERRINGTON, D., Phys. Rev. B 18 ₍₁₉₇₈₎ 6270.

[9] COLEMAN, S., The Uses _of Instantons, Int. Summer School of Subnuclear Physics, Ettore Majorana Erice _(1977).