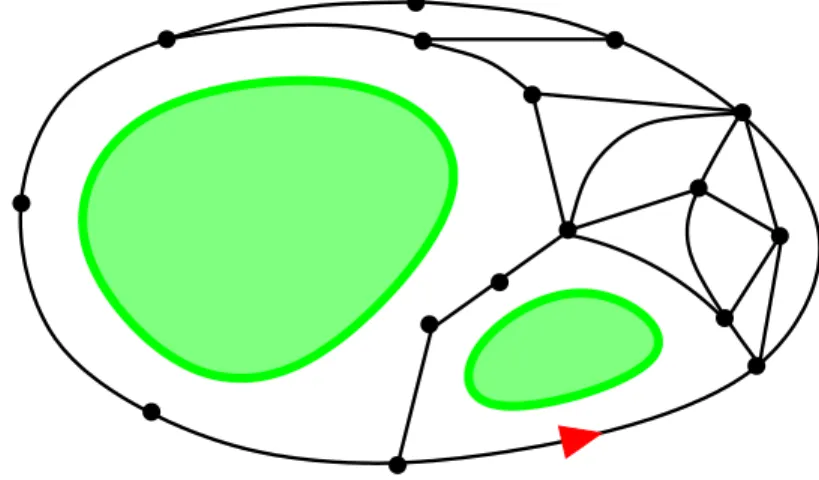
Nesting statistics in the $O(n)$ loop model on random planar maps
Texte intégral
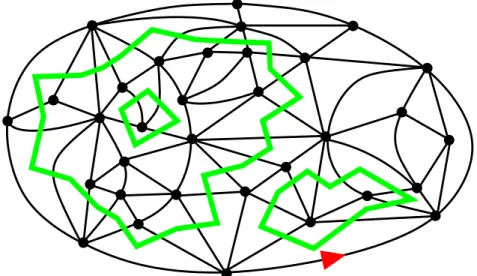
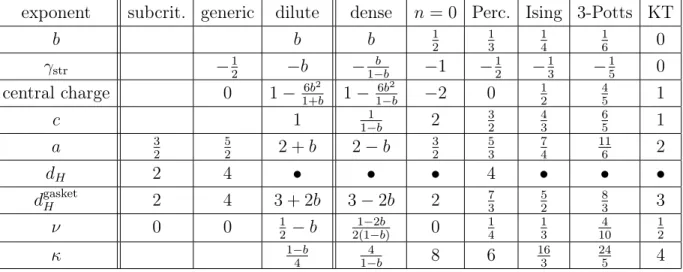
Figure


Documents relatifs
• A random map hosen in some lass of planar maps with `size' n (e.g. a map whose n faes are all of degree 4 ), whose edge-lengths are properly resaled, should onverge in distribution
Assume A is a family of connected planar graphs that satisfies the previous condition, and let X n denote the number of connected components that belong to A in a random planar
In the first case, this edge carries more than one mark : during its two visits by the exploration at time at steps 3 and 9, we will face Case 1 of the algorithm (i.e. discovery of
Proof. The claim is proved by induction. Then, at step i < θ , the distribution of the map filling-in the hole of ¯ e i follows from the spatial Markov property of the
The diameter of a random connected labelled planar graph with n vertices and bµnc edges is in the interval (n 1/4− , n 1/4+ ) a.a.s.. with
As a prime example, it allows to establish the following result left as an open question in [CK14], saying that the Brownian CRT is the scaling limit of looptrees associated
A way to generate random bipartite pointed Boltzmann planar maps consists in constructing it as previously, starting from a random forest. Furthermore, easy calculations show that µ
Marckert and Miermont (2006) show that similar results as in Chassaing and Schaeffer (2004); Le Gall (2006); Marckert and Mokkadem (2006) hold for rooted and pointed bipartite