Formulation et estimation des modèles ARCH et GARCH avec application à l'analyse de la volatilité des séries économiques

Faculté d' Administration Université de Sherbrooke

FORMULATION ET ESTIMATION DES MODÈLES ARCHET GARCH AVEC APPLICATION À L'ANALYSE DE LA VOLATILITÉ DES SÉRIES

ÉCONOMIQUES

Par

GABIN OTHA-NDOUMBA J

D\1�----Bachelier ès sciences (économique)

de l'université de Sherbrooke

MÉMOIRE PRÉSENTÉ

pour obtenir

LA MAîTRISE ÈS SCIENCES (ÉCONOMIQUE)

SHERBROOKE

JUIN 2004

Je tiens d'abord à exprimer toute ma reconnaissance à mon directeur M. Gérald ROY pour ses conseils et le soutien dont il a fait preuve tout au long de cette recherche, qui ont suscité en moi le désir d'apprendre.

Également, je tiens à remercier les membres de mon comité de lecture, M. Pene

KALULUMIA et M. Mario FORTIN pour leur appui.

Je tiens enfin à exprimer ma profonde reconnaissance à mes parents, ma

fiancée, mon fils, et à tous ceux que ma réussite importe.

TABLE DES MATIÈRES

REMERCIEMENTS 1

TABLE DES MATIÈRES II

LISTE DES FIGURES IV

LISTE DES TABLEAUX V

INTRODUCTION GÉNÉRALE 1

CHAPITRE 1 4

FORMULATION 4

1.1 Introduction 4

1.2 La famille des modèles ARCH 4

1.2.1 Le modèle A RCH (q) 6

1.2.2 Le modèle GARCH (p,q) 8

1.2.3 Propriétés des modèles (G)A RCH 10

1.2.3.1 Propriétés sur la loi de distribution normale 11

1.2.3.2 Loi des erreurs 16

ESTIMATION ET TEST 20

2.1 Introduction 20

2.2.1 La méthode d'estimation du maximum de vraisemblance (MV) 21

2.2.2 Estimation des modèles ARCH et GARCH 36

2.2.3 Les dérivées de la log-vraisemblance d'un modèle ARCH(l) 39

2.2.4 Les dérivées de la log-vraisemblance d'un modèle GARCH(1,1) 41

2.3 Test d'homoscédasticité : test ARCH 44

2.4 Tests D'ASYMÉTRIE ET d'aplatissement 45

CHAPITRES 51

APPLICATION EMPIRIQUE SUR LES RENDEMENTS BOURSIERS 51

3.1 Introduction 51

3.2.1 Approche descriptive 52

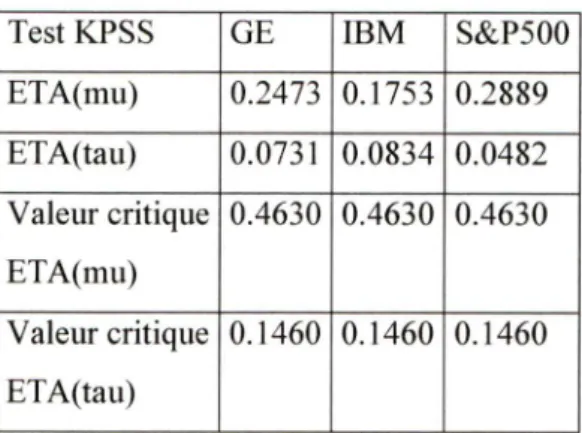
3.2.2 Test de stationnarité : Test de KPSS 59

3.2.3 Test d'homoscédasticité 61

3.2.4 Test de normalité 63

3.3 LA DEUXIÈME PARTIE : ESTIMATION ET SPÉCIFICATION 65

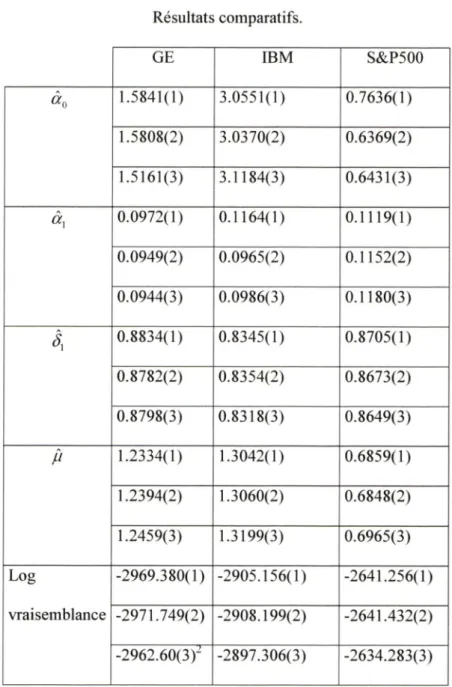
3.3.1 Estimation de modèles (G)ARCH 66

3.3.2 Estimation de modèles (G)ARCH : Comparaison des résultats de plusieurs logiciels

(ECTS, RATS et EVIEWS) 73

CONCLUSION 76

ANNEXE 78

Programmes ECTS 78

Programmes RATS 89

DOCUMENTS DE TRAVAIL ET ARTICLES TROUVÉS SUR INTERNET 95

LISTE

DES

FIGURES

f

3.1 Evolution temporelle des titres 54

3.2 Y, vsY,.i 56

3.3 Fonctions de répartitions empiriques et théoriques 58

3.4 Corrélogrammes des séries 60

3.1 Statistiques descriptives des séries mensuelles 55

3.2 Test de stationnarité 62

3.3 Statistiques du test d'homoscédasticité 63

3.4 Corrélogrammes des résidus au carré 63

3.5 Résultats du test de normalité 65

3.6 Test d'autocorrélation résiduelle 69

3.7 Résultats de la régression OPG 70

3.8 Diagnostic de corrélation sérielle 73

Le développement des modèles ARCH se place dans le contexte et la lignée des

modèles traditionnels de séries chronologiques. Ces modèles pour séries

temporelles ont été développés dans une perspective de description, de

désaisonnalisation, de prévision ou de contrôle de systèmes. L'âge d'or de cette

modélisation se situe dans les années soixante-dix, qui ont vu le développement des modèles autorégressifs à moyennes mobiles (ARMA) et leur généralisation. Ces modèles sont fondés sur une approximation linéaire de la valeur présente d'une série en fonction linéaire de ses valeurs passées et de la valeur présente d'un bruit blanc (BB), s'interprétant comme l'innovation de la série. Plus précisément, on dit qu'un processus stationnaire X, suit un ARMA(p,q) s'il vérifie la relation suivante :

= £,-Oe,-x

où les coefficients <z>(/ =

l,...,p) et ej{j =

\,...,q) sont des réels et

£, ~ 55(0, <j^ ). Cette formulation présente cependant quelques inconvénients. Elle

est linéaire, ce qui restreint sa généralité. En outre, sa mise en œuvre impose peu de contraintes sur les paramètres autorégressifs, ce qui nuit à des interprétations

plus structurelles des problèmes étudiés.

Panni les domaines d'application où la fonnulation ARMA classique se révèle

insuffisante figurent les problèmes financiers et monétaires. Les séries financières

observables en pratique présentent d'abord certaines caractéristiques de dynamique non linéaire, dont la plus importante est le fait que la variabilité instantanée de la série (ou volatilité) dépend de façon importante du passé. Par

d'équilibre et de comportements rationnels des agents intervenant sur le marché qui conduisent naturellement à introduire et à tester des contraintes structurelles

sur les paramètres.

Les modèles ARCH (Autoregressive Conditional Heteroskedasticity) fournissent un cadre mieux adapté à ce genre de situation. Et depuis leur introduction, de

nombreuses publications s'y rapportent. Cet engouement reflète l'importance accordée par la communauté scientifique à ce type de modèle, tant au point de vue

statistique que financier.

Si l'on se place d'un point de vue statistique, les modèles ARCH constituent une

classe spécifique de modèles non linéaires pour laquelle on peut mener une étude complète en abordant un certain nombre de problèmes classiques (test de marche

aléatoire, loi des erreurs, calcul des moments, etc.).

D'un point de vue fmancier, la mise en œuvre de modèles où la dépendance

temporelle de la volatilité joue un rôle fondamental conduit à repenser la théorie dans le même contexte. Parallèlement au développement des modèles ARCH, on

assiste donc à la réécriture des modèles structurels concernant les déterminations

de portefeuilles optimaux, les évaluations de prix des options, les liens entre des

actifs de base et rendement du portefeuille de marché, etc.

Un survol de la littérature nous pennet de constater que l'utilisation des modèles

ARCH ne se limite plus à la théorie financière, car ils sont de plus en plus utilisés

dans des buts décisionnels.

Ce mémoire est consacré à l'étude des modèles ARCH. Nous nous attarderons

principalement sur les difficultés posées par l'estimation de ces modèles, qui selon

l'estimation. Dans le chapitre I, nous présentons la formulation de ces modèles, ainsi que leurs propriétés. Puis brièvement, nous énumérons les différentes

extensions de ces modèles.

Dans le chapitre II, nous abordons l'estimation des modèles ARCH par la méthode du maximum de vraisemblance. De nombreuses questions y sont particulièrement examinées : la difficulté posée par l'estimation de tels modèles, le calcul de dérivées analytiques nécessaires à l'estimation, la façon de mettre en œuvre des tests simples d'homoscédasticité, d'asymétrie et d'aplatissement.

Enfin, nous présentons au chapitre III un exemple simple d'application de la méthodologie ARCH à la modélisation des séries de rendements boursiers. Nous comparons ainsi les résultats obtenus par approches analytique et numérique. Les différentes étapes de la modélisation sont présentées en détail et illustrées à l'aide des logiciels ECTS, RATS et EVIEWS.

Formulation

1.1 Introduction

Dans ce chapitre, nous nous proposons de décrire les principales formulations des modèles avec hétéroscédasticité conditionnelle qui ont été proposés dans la

littérature.

Nous commençons d'abord par présenter le modèle ARCH dans son ensemble et,

brièvement, nous énumérerons les différentes extensions qui ont été faites sur ce modèle. Puis, nous étudierons les propriétés de ce modèle.

1.2 La famille des modèles ARCH

Les différentes études empiriques concernant les séries temporelles macro économiques et financières ont montré que celles-ci étaient caractérisées par une distribution leptokurtique, une hétéroscédasticité corrélée à son passé. La spécification correcte de la variance conditionnelle est importante pour au moins deux raisons. D'une part, dans les études empiriques financières, l'aspect incertain des changements de prix est souvent mesuré par celle-ci; il est important pour les investisseurs de saisir le degré de risque puisque les agents ont une aversion face au risque et exigent, généralement, un rendement espéré supérieur en compensation d'un plus grand risque. D'autre part, les changements de la variance inter-temporelle ont d'importantes conséquences sur l'efficacité des estimateurs des

information importante mais aussi leur volatilité, comme pour l'établissement du prix des options, et peut affecter le commerce international, voir F. Klaassen

(1998).

Pourtant, les modèles économétriques conventionnels ne se concentrent pas sur les premiers moments (c'est le cas des modèles ARMA), et ignorent une quelconque dépendance de ceux plus élevés et supposent une variance constante.

Le processus ARCH, Autoregressive Conditional Heteroskedasticity, introduit par R.F. Engle (1982), permet à la variance conditionnelle de fluctuer dans le temps et d'être fonction du passé des erreurs tout en maintenant une variance inconditionnelle (globale) constante. Il apporte une meilleure description des mouvements de rendement des titres et d'autres séries macro-économiques et

financières.

Ces dernières années, les modèles ARCH ont fait l'objet de beaucoup de discussions. Des publications telles que celle de T. Bollerslev, R.F. Engle et D.B. Nelson (1993) et A.K. Bera et M.L. Higgins (1993) présentent les différents avancements observés et suggèrent divers modèles et tests.

Selon la notation de T. Bollerslev, R.Y. Chou et K.F. Kroner (1992), le modèle

ARCH se réfère à tous les processus temporels discrets {«,} de la forme u, = eih,

où £,iid,E(£,) = 0,var(f,)= 1,

avec h, une fonction de variance (scédastique), indépendante de .

T. Bollerslev, R.F. Engle et D.B. Nelson (1993) présentent quelques applications de ces modèles en finance où les rendements d'actifs tendent à être leptokurtiques ;

volatilité, c'est-à-dire, les fortes (faibles variations de prix qui sont suivies par d'autres fortes (faibles) variations de prix, mais dont le signe n'est pas prévisible, voir B. Mandelbrot (1963).

1.2.1 Le modèle ARCH

(q)

Le modèle ARCH a été introduit dans le but de mieux analyser la dynamique des actifs financiers. L'article de base est celui de R.F. Engle (1982) qui fut le premier à proposer une paramétrisation possible de la variance. L'idée de base, ici, est que la variance du terme d'erreur à la période t dépend des valeurs réalisées du carré des erreurs dans les périodes précédentes.

Cette paramétrisation de la fonction de variance, ht, s'exprime comme suit :

a; = E{II^\ Q,_,) = /?, =

«■„ +

a, - «o + «(!)«/_,

(1.9)

avec «0 > 0 et «, >0,L représentant l'opérateur retard. Ce modèle est coimu

sous le

nom de modèle ARCH(q). L'intérêt de cette approche réside dans l'introduction d'une dynamique endogène au niveau de la définition de la variance. Il fournit une spécification originale de l'hétéroscédasticité dont les causes sont inconnues. L'ensemble de l'information disponible à la date (t - 1) est :

(Q, = })

La variance conditionnelle à

notée crf, varie au cours du temps; elle est

non corrélés : E(u,u,_j )= )) = 0.

Il existe donc une quantité d'informations entre l'indépendance et la non-corrélation, qui peut être exploitée.

Par un raisonnement analogue, nous pouvons montrer que £(m,Mj)=0 pour tout s <t. Ceci implique qu'il y a seulement présence d'hétéroscédasticité dans le processus ARCH, mais pas de corrélation sérielle.

Si le modèle ARCH est stationnaire, alors la variance non conditionnelle des

innovations, notée cr^, qui est l'espérance non conditionnelle de uf est

indépendante du temps. Sous l'hypothèse de stationnarité, l'espérance non conditionnelle de l'équation (1.9) nous donne :

■y 7

cr = a, + cr2„^jûr,

Donc,

— (1-10)

Elle est positive si a, > O,pour z =0,l,---q', et stationnaire si or, < 1. Ce sont

les contraintes de positivité.

La variance est estimée comme une moyenne mobile des carrés des innovations. Contrairement aux solutions traditionnelles qui spécifient le modèle uniquement en fonction des variables observables, les modèles ARCH prennent en compte directement la variation temporelle de la variance conditionnelle du processus du phénomène étudié dans l'estimation des paramètres d'intérêts.

En pratique, plusieurs séries financières présentent de la volatilité fluctuante dans le temps, mais avec une corrélation faible entre des valeurs de uf. Pour satisfaire ces deux caractéristiques, il devient nécessaire d'avoir im paramètre q élevé. Dans

ce cas, il faut estimer plusieurs paramètres et la contrainte de positivité n'est pas

toujours respectée.

1.2.2 Le modèle GARCH

(p,q)

Pour pallier aux inconvénients ci-dessus, T. Bollerslev (1986) introduit le modèle

GARCH (Generalized Autoregressive Conditional Heteroskedasticity), une généralisation du modèle ARCH dans laquelle sont ajoutés p retards de la variance

conditionnelle h,. Ce modèle permet une plus grande flexibilité dans la structure des retards. Il s'agit d'une extension du processus ARCH, et constitue un modèle ARMA de la variance conditionnelle alors que ARCH est un modèle AR de cette

même variance. Toutefois, R.F. Engle (1995) observe que le modèle ARCH est une moyenne mobile puisque la variance conditionnelle est moyenne mobile des

résidus au carré.

Le modèle GARCH (p,q) est tel que

A, = of = «0 + XL + X/=1

= <^o+a(L)ulj+S(L)h,^i, (1.11)

ou encore :

[1 -

S{L)}], = «0 + oc{L)u]_^

0(L)y, = y + ©(/,)£•,

Tous les coefficients a, et ôj doivent être positifs et «o > 0- Pour que le modèle

<7, = Go + 0!iUi^\ + (1.12)

Sous l'hypothèse de stationnarité, la variance non conditionnelle, peut être trouvée en prenant l'espérance non conditionnelle de (1.12). Nous obtenons :

<7^ = Uo +

+ ô^a^.

Donc,

<^=,

•

(1-13)

Pour que cette variance existe et qu'elle soit positive, il faut que a^+S^< 1, et

«0 >0.

Puisque le modèle GARCH (p,q) correspond à un modèle ARCH de dimension

infinie ARCH (0°), la plupart du temps un modèle GARCH (1,1), GARCH

(1,2)

ou GARCH (2,1) est employé. T. Bollerslev, R.Y. Chou et K.F. Kroner (1992) notent qu'un modèle GARCH (p,q) avec p et q petits peut approcher un modèle ARCH (q) où q est grand et modéliser les dynamiques de la variance sur de longues périodes.

Différentes extensions ont été proposées à ces modèles. Dans le modèle ARCH-M de Engle, Lilien et Robins (1987), la moyenne conditionnelle est fonction de la variance conditionnelle, voir T. Bollerslev, R.F. Engle et D.B. Nelson (1993). Le modèle E-GARCH introduit par D.B. Nelson (1991) modélise le log de la variance conditionnelle. Il se distingue des modèles (G)ARCH usuels par le fait qu'il rejette l'hypothèse de symétrie liée à la spécification quadratique de la variance conditionnelle. Face à la persistance de la volatilité, Engle et Bollerslev (1986) ont

proposé le modèle GARCH intégré, IGARCH, pour incorporer les résultats

empiriques â+ est comprise entre 0.9 et 1, dans le cas d'un GARCH

(1,1).

On retrouve aussi des modèles (G)ARCH multivariés. En effet, dans la plupart des cas, l'évaluation des actifs ou la décision d'allocation des portefeuilles doit être étudiée dans un contexte multivarié pour être significative. Ainsi u, désignera maintenant un processus stochastique vectoriel. La notion de modèle ARCH est élargie à une représentation de la forme:

Uf = e,T,'

Eiiid E(£,) = 0 Variée,) = I

OÙ la matrice NxN de la variance covariance r, est définie positive et mesurable par rapport à l'ensemble de l'information de la date t- 1. La défmition générale des processus multivariés définis par les deux équations ci-dessus autorise une grande variété de représentations possibles, mais peu d'entre elles sont utiles. Dans la représentation ARCH(^) multivariée proposée par Kraft et Engle (1983) r, est une fonction linéaire des produits matriciels des carrés des erreurs passées. Ce modèle a été généralisé par la suite au modèle GARCH(/j,^) par Bollerslev, Engle et Wooldridge (1988).

1.2.3 Propriétés des modèles

(G)ARCH

Dans les sous-sections précédentes, nous avons brièvement évoqué certaines

Dans ce qui suit, nous allons étudier plus en détail les propriétés portant sur les

moments de ces modèles.

1.2.3.1 Propriétés sur la loi de distribution normale

La fonction de densité d'une distribution normale centrée réduite est notée

<t>{x) = /( Jr) = (2 exj^ ~ 2

(^-14)

Une propriété fondamentale d'une variable aléatoire (v.a) X est son espérance mathématique qui est définie par

E{X) = ^ x(l){x)dx.

(1-15)

Lorsque l'on parle d'espérance mathématique d'une v.a, on se réfère souvent à son premier moment. Les moments d'ordre supérieur, s'ils existent, sont aussi les espérances mathématiques de la v.a élevée à une certaine puissance. Ainsi, le second moment de la v.a X est l'espérance mathématique de , le 3'™' moment est l'espérance de , ainsi de suite. De manière générale, le k'""' moment d'une variable aléatoire, X, continue est donnée par

mk{X)=t x''f(x)dx.

(L16)

m oo

Afin de mieux saisir les propriétés ci-dessus, calculons les deux premiers moments

de la distribution normale.

Les dérivées première et seconde de (1.14), par apport à x, sont respectivement :

^'(x) = -(2;r) 2-exp|^--AT"

ou encore :

x<l){x)=-(l)\x), (1.18)

et

0"{x) = -^'{x) + x{27ty^'^2^xQXT^-^x^

=

-0{x)

+ x'<l){x).

(1.19)

Ainsi, le premier moment de la distribution est égal à :

'n\(X) = iJ=^ (2;r) "^Arexp^-—

^x)dx.

fà" oo

= - ^\x)dx = = 0, à cause de la symétrie de la loi normale

par rapport à 0.

Et par intégration par parties, c'est-à-dire :

^iidv= ^udv- Jvr/w

-2^ , ( ^2\ . . (

X

OU M = jc,i/v= xexp

, Jrfv = -exp "Y L e/j vdu= Jexp --y

2 j' J J 2

le deuxième moment (la variance) est égal à :

dx.

m2(x)=/i2 = r x^f{x)dx- {2ïï) f x^exp(-—)f3&c

2 2

= (2;r)'"^(-xexp(-Y))

expt-Y^*.

le membre de gauche, de l'expression ci-dessus, est égal à 0, nous obtenons alors

nt^ix)

= //, = (2;r)""^ r exp{-^)dx^-r^

2 V2;r

Ces deux résultats caractérisent les deux premiers moments d'une distribution

normale centrée réduite. Dans cet exemple, nous avons constaté que le 1^'' moment est égal à 0, alors que le 2® moment est égal à 1. Ces résultats résultent du fait que.

par symétrie de la loi, les moments impairs sont nuls et les moments pairs sont non nuls. Vérifions cette propriété. Pour cela, nous utilisons l'expression (1.14).

Ainsi, pour les moment d'ordre pair, nous avons n, un entier naturel, 2n est pair. Soit un moment d'ordre pair. Par définition :

= r x^"(l){x)dx ={2/1)'^'^ r x^"QXD{-—)dx.

Soit M{t), la fonction génératrice des moments. Elle est définie par

2

M(r)= (2;r)""^ r exp(/x)exp(-—

Vre de l'ensemble des réels, exp(ix)exp(-—)=

„| —;x"exp(—

2 ! 2

converge uniformément en x.

Nous avons alors :

"<'>■11-, S"

Ainsi, le moment //„ est le coefficient de — dans exp(-1 ), et_{n\ 2}

__LiM n

~ 2" ni

(1-20)

À partir de l'expression (1.20), nous pouvons, par exemple, tirer le 4" moment de

la distribution,

w = 2.

Il vient alors :

1 (2x2)! 1 4x3x2! _

Dans le cas où, le 2^ moment est égal à a\ l'expression (1,20) s'écrit : (2n)\

Il s'agit de la généralisation de l'expression (1.20), avec fonction de densité ^{x)

définie comme suit ;

Pour les moments d'ordre impair, nous posons :

A2n+1

Montrons que cette intégrale est égale à 0. Pour ce faire, posons :

F„(x) = -x<'"^'>)exp(-Y).

Étudions la parité de F„{x), c'est-à-dire :

F„ (-X) = -x^'"^' ') exp(-<- Y

f

)

= (-if

)

exp(-Y )•

= -x''""")exp(-Y) = -F(x).

La fonction est alors dite impaire.

Donc,

rF„(x)dx = 0

Nous pouvons donc déduire que les moments d'ordre impair, d'une distribution

normale, sont nuls. Par exemple le 3^ moment, où « = 1, est détenniné comme suit

Nous avons montré que les moments d'ordre pair d'une distribution normale sont tirés de l'expression (1.21).

Cette expression est équivalente à n;

,(27-1).

Montrons que :

1 (2w)! j—rn

Utilisons un raisonnement par induction sur n.

Pour « = 1, vérifions l'égalité (1.22).

2' ,

et

f|'.^j(27-l) = 2xl-l=l.

L'égalité est vérifiée au rang m = 1,

Hypothèse d'induction :

Supposons que ^

= n/=i(2y-

U-Vérifions que cette égalité est vraie au rang w +1.

Nous avons alors ;

(2(77 + 1))! (2w + 2)(2» + 1X2/7)! 2"'""'(77+1)! ~ 2"2(77+ 1)77 ! (277)1 (277+ 2X2/7+ 1) (2/7)1

•2;!" 2(„+l)

= n".i<2-'-l)x(2n-.l).

nn+1

Donc V77,nous avons :

(2/7)1

Nous pouvons donc conclure que le moment d'une distribution normale centrée réduite est égale à

(1.23)

Ces résultats intermédiaires vont maintenant nous servir à caractériser la

distribution des erreurs dans les modèles G(ARCH).

1.2.3.2 Loi des erreurs

Dans le cas d'un processus ARMA, la distribution non conditionnelle de u, est habituellement normale, en autant que e, soit bruit blanc. Mais lorsque les erreurs sont de type (G)ARCH, ceci n'est pas valide. Comme nous le verrons, la distribution statiomiaire des modèles (G)ARCH n'est pas normale, et les moments d'ordre 1 et 2 peuvent ne pas exister.

Afin de déterminer les deuxième et quatrième moments de ces processus, nous allons d'abord porter notre attention sur le modèle ARCH(l).

Pour un processus ARCH(l) dont les innovations sont nonnalement distribuées et

suivent un bruit blanc, la distribution de u, conditionnellement à Q, est normale.

Comme la variance stationnaire de cette distribution est égale à , les deuxième

et quatrième moments valent respectivement

et la*, = aQ+

. Donc.

£(«? |n,_i) = cr = «0 + •

et

Si nous supposons que les deuxième et quatrième moments non conditionnels existent et nous notons le quatrième moment en prenant l'espérance non

conditionnelle des deux relations ci-dessus, nous obtenons

a'=7^

(1.24)

et

2 ôa^a, 2

OT4 = Soo +—"—'■ + Scri mA, 1- «I

OÙ nous avons utilisé le résultat de la première équation, celle du 2'""' moment, pour déduire la 2'""" équation. En résolvant cette équation par rapport à W4 nous

obtenons

Ces résultat ne sont valides que si «i <1 et Sa, <1. En effet, si ces conditions ne sont pas satisfaites, les 2'™^ et 4'™'' moments n'existent pas.

Engle (1982) a introduit son modèle en supposant un processus u, avec une

distribution conditionnellement normale :

«,|£Vi =A^(0;^).

(1.26)

Il est clair que ce processus conditionnellement gaussien n'est pas marginalement gaussien; en effet si c'était le cas, la variance conditionnelle devrait être indépendante des valeurs passées, condition non réalisée.

Des résultats plus précis peuvent être obtenus concernant l'aspect non gaussien de la distribution marginale de u,.

En effet, d'après les résultats (1.25) et (1.26), nous pouvons déduire que le coefficient d'aplatissement, kurtosis, associé à la distribution marginale vaut

(1.27)

E(u]) (l-a,)(l-3or,-) «5 (l-3or,^)

Ce coefficient d'aplatissement est toujours supérieur à 3, valeur correspondant à la loi normale. Pour cette raison, la loi des erreurs est dite leptokurtique.

Dans le cas d'un GARCH (1,1), la fonction scédastique est

(^1 = ocq + cC]tî^-] +

(1.28)

La variance stationnaire vérifie l'équation = Uq +(ûr, + Ôx)g^ .

CCfx

Soit m4 l'espérance non conditionnelle de at- Nous avons alors :

/W4 — E{^OCq + -i- .

=

^^/-i ^ ^/-i 2ûfo(

+ Si ojLi )+2 ûj

o^-\ J.

Or E(aj^i) = E((/) = Ei(Ti) = m4.

Comme m, = aie, avec e, = A^(0,l), on a que m,!, = of.isf.i et uf_i =

Donc,

= 3/7/4 et = W4.

Les espérances non conditionnelles de //,i, et sont a^. Alors /W4 = 3af /W4 +S^m4 + 2aiSi + + 2aro(<^i + Si )a^.

et

Or •; f—-, ce qui nous donne \-a\- Si

/W4(l-3a? -S\ - lUiSi = «0 + 2oro —

=> W4(l-(ai +ôif - 2af) = al '"'""1+^ ^

-(1 + a, +

On a vu que le 4^ moment non conditionnel de u, est 3m4. Nous avons alors

p, 4 , af,(\+ a,^S,)(l-a,-ô,)

Pour que ces moments existent, il faut que le dénominateur de l'équation de m^ soit positif. Si ^ = 0, cette condition devient

l-af -2a? = l-3a? >0,

ce qui équivaut à la condition 3

a? <1, qui est la condition d'existence du 4^

moment non conditionnel d'un ARCH(l).

Une fois de plus, on déduit que la loi marginale de u, a des queues plus lourdes qu'une loi normale. Nous voyons qu'il y a accroissement de l'aplatissement lorsqu'on passe des lois conditionnelles aux lois non conditionnelles.

CHAPITRE

2

Estimation et test

2.1 Introduction

Les modèles introduits dans le chapitre précédent reposent sur des formulations des moyermes et des variances conditionnelles. En pratique, celles-ci sont souvent exprimées de façon à ce qu'elles apparaissent comme des fonctions de paramètres incoimus et des valeurs passées du processus. La coimaissance de ces moments ne suffit cependant pas, sans l'hypothèse supplémentaire de la forme de la distribution, à caractériser la loi conditionnelle du processus. Le maximum de

vraisemblance (MV) sera la méthode d'estimation utilisée dans ce mémoire.

Dans cette partie, nous nous attacherons à présenter les notions statistiques nécessaires à l'estimation et aux tests. Nous présenterons, en effet, les éléments requis à l'estimation de ces modèles.

De façon à ne pas compliquer la présentation et parce que les résultats ne sont pas spécifiques aux modèles ARCH-GARCH, nous n'insisterons pas sur les démonstrations de certaines propriétés asymptotiques, ni sur le conditions de régularité sous lesquelles elles sont valides.

2.2.1 La méthode d'estimation du maximum de vraisemblance

(MV)

L'idée fondamentale de l'estimation par maximum de vraisemblance est, comme le nom l'indique, de trouver un ensemble d'estimations de paramètres tel que la vraisemblance d'avoir obtenu l'échantillon que nous utilisons soit maximisée. Nous

signifions par là que la fonction de densité jointe (FDC) pour le modèle que l'on

estime est évaluée aux valeurs observées de la (des) variable(s) et traitée(s) comme une fonction de paramètres du modèle. Si on peut simuler la variable dépendante, cela signifie que la FDC doit être connue, à la fois pour chaque observation comme variable scalaire aléatoire, et pour l'ensemble de l'échantillon comme un

vecteur de variables aléatoires.

Comme d'habitude, nous décrivons la variable dépendante par un vecteur y. Pour un vecteur Adonné de paramètres û, la fonction de densité conjointe de y s'écrit f(y,9). Cette FDC constitue la spécification du modèle. Puisqu'une fonction de densité de probabilité fournit un contenu ambigu pour la simulation, il suffit, dans ce cas, de spécifier le vecteur e afin de donner la caractérisation complète du processus générateur des données (PGD). Il y aussi une relation de correspondance biunivoque entre les PGDs du modèle et les vecteurs de paramètres admissibles. L'estimation par maximum de vraisemblance est basée sur la spécification du modèle à travers la fonction de densité conjointe Quand e est fixé, la fonction f{.,G) de y est interprétée comme la fonction de densité de y. Mais si f(y, 0) est plutôt évaluée par le vecteur y trouvé dans un ensemble de données, la fonction f(y,.) des paramètres du modèle ne peut plus être, alors interprétée

comme ime FDC. Cela renvoie plutôt à une fonction de vraisemblance du modèle pour l'ensemble des données spécifiées. L'estimation par maximum de

vraisemblance (MV) revient alors à maximiser la fonction de vraisemblance. Le

vecteur de paramètres e auquel la vraisemblance atteint sa valeur maximale est appelé estimateur du maximum de vraisemblance ou EMV, des paramètres.

Dans bien des cas, les observations successives d'un échantillon sont autre que le

produit des densités des observations individuelles. Posons f{y,,6) la FDC d'une

observation, y,.

La densité jointe de tout l'échantillon y s'écrit alors :

fiy,e)=YÏ,^,f(y,.0)

(2.1)

supposées être statistiquement indépendantes. Dans ce cas, la densité jointe de

l'échantillon n'est nul

Dans le cas d'échantillons de grande taille, (2.1) peut devenir extrêmement importante ou extrêmement petite, et prendre des valeurs qui sont bien au-delà des capacités des ordinateurs. Pour cette raison, parmi d'autres, il est d'usage de maximiser le logarithme de la fonction de vraisemblance plutôt que la fonction de vraisemblance elle-même. Bien évidemment, nous obtiendrons la même réponse en procédant ainsi, car la fonction logvraisemblance est une transformation

monotone de la fonction de vraisemblance. Nous écrivons alors :

/(>-, 6) ^ \ogf{y, d) = {y,, 01 (2.2)

OÙ li{y,,0X la contribution à la fonction logvraisemblance faite par chaque observation est égale au log/,(y,,0).

La manière la plus simple de saisir l'idée fondamentale de l'estimation par MV est de considérer un exemple simple. Supposons que chaque observation y, soit générée par la fonction de densité

f{y,,0)=Oe''^\

y,>0, 0>O

(2.3)

et soit indépendante de toutes les autres y,. Il s'agit de la fonction de densité de la distribution exponentielle. Il y a un seul paramètre inconnu 0 que nous désirons estimer, et nous disposons de « observations avec lesquelles nous allons travailler.

Comme les y, sont indépendantes, leur densité jointe est simplement le produit de

leurs densités marginales. La fonction de vraisemblance s'écrit alors

= (2.4)

La fonction de logvraisemblance correspondant à (2.4) est

Ky, e) = " iog{^)- (2.5)

La maximisation de la fonction de logvraisemblance par rapport au seul paramètre inconnu 0, est une procédure directe. Différencier l'expression plus à droite de (2.5) par rapport à 0 et poser la dérivée à zéro donne la condition de premier ordre

(CPO)

(2.6)

et nous trouvons que l'estimateur MV 0 est

^ =

^

(2-7)

Dans ce cas, il n'est pas nécessaire de se soucier des multiples solutions de (2.6). La dérivée seconde de (2.7) est toujours négative, ce qui nous permet de conclure

toujours le cas; pour certains problèmes les CPO peuvent mener à des solutions

simples.

Après cet exemple, nous poursuivons notre présentation sur la méthode d'estimation par maximum de vraisemblance.

Lorsque la fonction de vraisemblance ne peut pas s'écrire sous la forme de (2.1), il est toujours possible, en théorie, de factoriser /(>>, 6) en une série de contributions, chacune provenant d'une seule observation.

Supposons que les observations individuelles y,,t = \ «, soient ordonnées d'une

certaine manière, comme dans le cas des séries temporelles où les observations sont dépendantes. Or cette factorisation peut être accomplie comme suit. Nous commençons par la densité marginale de la première observation > que l'on peut appeler ^(vi), en supprimant la dépendance par rapport à d pour le moment, et ce dans le but d'alléger l'écriture. Puis la densité conjointe des deux premières observations peut être écrite comme le produit de la densité de yi

conditionnellement à >'i, et nous la notons fi](y2\y\)- Si maintenant, nous prenons

les trois premières observations ensemble, leur densité jointe est le produit de la densité conditionnelle des deux premières prises simultanément, par la densité de la troisième conditionnellement aux deux premières, et ainsi de suite. Le résultat

pour l'échantillon entier des observations est

f(y) =/iCfi )My2\y\ l/sCrsh.Vi)-

■■/«0'nk-i,.j'i)

= = Y\^,^JAy,\yi-\...y\).)

(2.8)

Notons que ce résultat (2.8) est parfaitement général et peut être appliqué à n'importe quelle densité ou fonction de vraisemblance. L'ordre des observations est

habituellement l'ordre naturel, comme pour les séries temporelles, mais même si aucun ordre naturel n'existe, l'équation (2.8) demeure vraie pour un classement

arbitraire.

Comme nous l'avons précisé précédemment, dans la pratique on utilise la fonction de logvraisemblance Ky,0) plutôt que la fonction de vraisemblance f(y.e). La décomposition de Ky,0) en contributions provenant d'observations individuelles résulte de l'équation (2.8). Elle peut être écrite comme suit, en supprimant la dépendance par rapport à d pour alléger les notations :

Ky)=^iiiy\yi-\^--.y\\

(2.9)

où lAyi\yi-\,-

= ^ogfi{y\yi_],...,y^), comme précédemment.

Nous pouvons dès à présent doimer la définition de l'estimation par maximum de

vraisemblance. Nous disons que h est une estimation par MV,

pour les doimées y

si

l(y,0)>l{y,0) V6'€0, (2.10)

0 étant un espace paramétrique dans lequel 0 prend ses valeurs.

Si l'inégalité est stricte, alors h est l'unique EMV, comme ce fut le cas

précédemment dans notre exemple.

Il est souvent plus commode d'utiliser une autre défmition de l'estimation par MV, qui n'est pas équivalente en général. Si la fonction de vraisemblance atteint un maximum intérieur à l'espace paramétrique, alors elle, ou de façon équivalente la fonction de logvraisemblance, doit satisfaire les CPO pour un maximum. Ainsi une estimation par MV peut se définir comme une solution aux équations de vraisemblance, qui correspondent précisément aux CPO suivantes:

g(j'/d)^o,

(2.11)

où g(y, 6) est le vecteur gradient, ou le vecteur score, dont les éléments sont :

Comme nous l'avons signalé antérieurement, il peut arriver que plus d'une valeur de 0 satisfasse les équations de vraisemblance (2.11), la définition nécessite par ailleurs que l'estimation 0 soit associée à un maximum local de I{y. 0) et que

p {n'^Ky, 0)) > p (n'^Ky, 0* »,

OÙ 0' est n'importe quelle autre solution des équations de vraisemblance. Cette

seconde définition de l'estimation par MV est souvent associée à Cramér, (Cramér,

1946). Dans la pratique, la nécessité que p\im{n~^l{y, 0~))> p\\m{n'^l{y,0')) est

impossible à vérifier en général. Le problème vient du fait que l'on ne connaît pas

le PGD et que par conséquent, le calcul analytique des limites de probabilité est

impossible. Si pour un échantillon donné il existe deux racines ou plus aux

équations de vraisemblance, celle qui associée à la valeur la plus haute de l{y, 0) pour cet échantillon peut ne pas converger vers celle qui est associée à la valeur la

plus haute asymptotiquement. Dans la pratique, il existe plus d'une solution pour

les équations de vraisemblance, l'on sélectionne celle qui est associé à la valeur la plus haute de la fonction de logvraisemblance.

Nous insistons sur le fait que ces deux définitions de l'estimation par MV ne sont pas équivalentes. En conséquence, il est parfois nécessaire de parler des estimations par MV du type 1 quand nous faisons référence à celles obtenues par la maximisation de /(>>, 0) sur 0, et des estimations par MV de type 2 quand nous faisons référence à celles obtenues comme solutions des équations de

Par le terme estimateur du maximum de vraisemblance nous désignerons la variable aléatoire qui associe à chaque occurrence aléatoire possible y l'estimation par MV correspondante. Avant de poursuivre, rappelons la distinction entre une estimation et un estimateur. Nous pouvons rappeler qu'un estimateur, une variable aléatoire (v.a.), est représenté comme une fonction des ensembles possibles d'observations, alors qu'une estimation est une valeur que peut prendre cette fonction pour un ensemble d'observations bien spécifié.

Tout comme il existe deux définitions possibles des estimations MV, il existe également deux définitions possibles d'un estimateur MV. Les définitions suivantes montrent clairement que l'estimateur est une v.a. qui dépend des valeurs observées de l'échantillon y. L'estimateur de type 1, correspondant à la définition

standard (2.10) de l'estimation MV,

est è(y) défini par

Ky, ky))

> Ky, G)

€ 0

tel que d ^ ky).

(2.13)

L'estimateur de type 2, correspondant à la définition (2.11) de Cramér, est d{y) défini par :

g{y,ky)) = 0,

(2.14)

où è{y) dorme le maximum local de /, et

p linî„_.„ («"'/(v, ^)))

> p\\m„^^{n'''^l{y,e\y)))

(2.15)

pour n'importe quelle autre solution 6* (y) des équations de vraisemblance.

Nous concluons cette sous-section par une variété de définitions importantes pour la méthode d'estimation par MV. En utilisant la décomposition (2.9) de la fonction de logvraisemblance /(>>, 6*), nous pouvons définir une matrice G(y,^) de

(2.16)

Étant donné que gjCy, <9) = ^"

^ G„(j,0). Nous appellerons G(y,0) la matrice des

contributions au gradient, ou matrice CG tout simplement. Cette matrice est

intimement reliée au vecteur gradient g, qui est égale à G^l, où / désigne un

vecteur de taille n constitué de 1 seulement et l'on note G^ la transposée de G. La

r'™""ligne de G, qui mesure la contribution au gradient de la /"'"''observation, sera

notée G,.

La matrice Hessienne associée à la fonction de logvraisemblance l(y,0) est la matrice Ho .é») de dimension k x k dont l'élément type est

(2.17)

Nous définissons la matrice Hessienne asymptotique, si elle existe, comme

K(0) = pl\mg -HCy.é»)

n

Cette quantité, qui est une matrice symétrique, et en général semi-définie négative, apparaît souvent dans la théorie asymptotique de l'estimation par MV.

Nous définissons l'information contenue dans l'observation / par 1,(0), la matrice de dimension k x k dont l'élément type est

(2.18)

La notation "Eg", ici, signifie que l'espérance a été prise sous le PGD caractérisée par 0. Le fait que 1,(0) soit une matrice symétrique, en général semi-définie positive, et qu'elle soit définie positive à condition qu'il existe une relation linéaire entre les composantes du vecteur aléatoire Gt est une conséquence immédiate de

cette définition. Nous pouvons alors définir la matrice d'information \{d), comme

la matrice l(<9) est symétrique et semi-définie positive.

La matrice d'information asymptotiqne, si elle existe, est définie par

J(e) = p\ïme -I((9). (2.19)

La matrice l,{0) mesure la quantité espérée d'information contenue dans la t'""' observation. La matrice d'information J est, cormne I, symétrique et en général semi-définie positive.

Il existe une relation très importante entre la Hessieime asymptotiqne (H(0)) et la matrice d'information asymptotiqne (J(^))- Cette relation nous donne la matrice de covariance asymptotiqne, aussi appelée égalité de la matrice d'information,

et nous la notons

K((9) = -y(0). (2.20)

Littéralement, la matrice Hessierme asymptotiqne est l'opposé de la matrice d'information asymptotiqne. Formellement, nous pouvons donc dire que la matrice de covariance asymptotiqne de l'estimateur MV est donnée par

Var(h)=-¥r\e).

(2.21)

ou par

Var{e)=J~\ff). (2.22)

L'obtention, à l'aide de (2.21) ou de (2.22), de Varih) est parfois chose difficile

permet d'obtenir l'estimateur de la matrice de covariance asymptotique. Il s'agit de l'estimateur OPG (Produit-extérieur-du-gradient). Il est basé sur la définition

ou 00 est un vecteur paramétrique associé au PGD.

Nous pouvons donc, logiquement, estimer w~'l(0o) par n~^G^{è)G{6). L'estimateur

OPG est alors

VaroPG(e)=i.G''{d)Gm-' (2.23)

C'est un estimateur que l'on calcule facilement. Et contrairement à la Hessienne empirique (2.21), il dépend seulement des dérivées premières. Et par rapport à (2.22), il ne nécessite pas de calculs théoriques. Toutefois, en échantillons fmis, il

est moins fiable que les deux autres.

Explicitons un peu plus la régression OPG, de laquelle découle l'estimateur OPG. La régression OPG peut être utilisée pour n'importe quel modèle estimé par MV. Elle a été utilisée premièrement comme un moyen de calcul des statistiques de test par Godfrey et Wickens (1981). Il s'agit d'une régression artificielle qui permet de vérifier les CPO pour la fonction de logvraisemblance, l'estimation de la matrice

de covariance, et ainsi de suite.

Supposons un modèle paramétré défini par la logvraisemblance (2.2). Soit G(0)la matrice CG associée à la fonction de logvraisemblance (2.2), avec comme élément

type

G„(0)=-^;

t = \ «, i = \,...,k,

où k est le nombre d'éléments dans le vecteur paramétrique 0. La régression OPG associée au modèle (2.2) peut alors être écrite comme

l = G{6)c + résidus (2.24)

Ici, i désigne encore un vecteur de taille n dans lequel chaque élément est unitaire et c est vecteur de dimension k des paramètres artificiels. Le produit de la

matrice des régresseurs avec le régressé (0 est le gradient g{e)=G^i0)i. La

matrice des sommes des carrés et les produits croisés des régresseurs, G^{0)G{0),

lorsqu'elle est divisée par n, estime de manière convergente la matrice d'information J(0). Ces deux caractéristiques sont essentiellement tout ce qu'il faut pour que (2.24) soit une régression valide. Comme dans le cas d'une régression Gauss-Newton, les régresseurs de la régression OPG dépendent du vecteur 0. Par conséquent, avant d'effectuer la régression artificielle, ces régresseurs doivent être évalués pour im vecteur paramétrique spécifique.

Un choix possible pour ce vecteur paramétrique est 0 l'estimateur MV du modèle (2.2). Dans ce cas, la matrice du régresseur est G = G{0) et les estimations paramétriques artificielles, qui sont désignées par c, sont identiquement égales à

zéro :

c =

{G^Ôy'G^i =

(G^G)-'g =

0.

Comme ici g est le gradient évalué en 0 de la fonction logvraisemblance, la demière égalité ci-dessus est une conséquence des CPO pour le maximum de vraisemblance. La mise en marche de la régression OPG avec 0= 0 fournit, alors, une manière simple de tester comment, en fait, sont satisfaites les CPO par une série d'estimations calculées au moyen d'un certain programme infonnatique. Comme les estimations c de la régression (2.24) valent zéro lorsque les régresseurs sont G, ces régresseurs n'ont aucun pouvoir explicatif sur /. et la

somme des résidus au carré (SSR) est alors égale au total de la somme des carrés.

Cette dernière vaut

Z»

et l'estimation MV de la variance des résidus dans (2.24) est juste l'unité

1 1 T 1

-SSR=- r i=-n = \.

n n n

L'estimation de la matrice de covariance pour le vecteur c de (2.24) est alors (G^G)"'.

C'est cette expression qui dorme à la régression OPG son nom.

L'estimateur OPG a été préconisé par Brendt, Hall, Hall et Hausman (1974) et on

s'y réfère sous le nom de l'estimateur BHHH.

Afin de nous aider à mieux comprendre les résultats théoriques énumérés ci-dessus, sur la méthode d'estimation MV, voyons un exemple. Cet exercice présente

un intérêt. Tout d'abord, il foumit une illustration concrète de la manière d'utiliser

la méthode MV. Deuxièmement, il foumit une matrice de covariance asymptotique pour les estimations de p et a conjointement.

Considérons un modèle linéaire classique

y = XP + u i/ = Af(0,c7^/). (2.25)

Dans ce modèle, la matrice des variables explicatives, X, est supposée être exogène. Le vecteur paramétrique P est supposé être de longueur k, ce qui implique qu'il y a A: +1 paramètres à estimer, dont les k premiers sont les éléments

du vecteur y? , et le dernier est celui de o. Les éléments u, du vecteur u sont

La fonction de densité de u, est

1 1

Afin de construire la fonction de vraisemblance, nous avons besoin de la fonction

de densité de y, plutôt que celle de u,. La fonction qui relie u, à y, est

u, =y,- Xfi (2.26)

La FDC de y, s'écrit ainsi,

La contribution à la fonction de logvraisemblance apportée par la t""" observation

est le logarithme de (2.27). Comme loger = -^log£r^, nous obtenons

, A (T) = -^ log 2;r - ^ log -

"^

(V» - X,pf.

Comme toutes les observations sont indépendantes, la fonction logvraisemblance elle-même correspond précisément à la somme des contributions A cr) sur tout

t, ou

/{j,;ff,CT) = --^log2;r-jlogo^

(y,-Xpf.

(2.28)

= --^\og2?v-^\og(/-:^(y-XP)'{y,-Xp).

Pour trouver l'estimateur MV, nous devons maximiser (2.28) par rapport aux

paramètres inconnus p et a.

Pour le modèle de régression (2.25), le vecteur paramétrique 6 est le vecteur [5: cr]. Nous calculons à présent la matrice d'infonnation asymptotique J{p, a) en

utilisant la méthode basée sur la matrice CG, qui ne nécessite que les dérivées

premières.

La dérivée première de /,(>>„>9, cr) par rapport à est

G,AP,(T)=-^=-p{y,-X,P)X, = -^^X„, i =

(2.29)

La dérivée première l,{yi,p, a) par rapport à a est

= (2.30)

Les expressions (2.29) et (2.30) sont tout ce dont nous avons besoin pour calculer la matrice d'infonnation en utilisant la matrice CG. La colonne de cette matrice qui correspond o aura l'élément type (2.30), tandis que les k colonnes restantes, qui correspondent aux y?,, auront l'élément type (2.29).

Pour i,j = \,...,k, le ij""" élément de G^G est

Zn 1 5

Ainsi, l'élément J{p, a) correspondant à p, et pj est

JiPuPj )

= p ("^Z"=i

Comme uf a une espérance de

sous le PGD caractérisé par (P,o) et est

indépendant de X, nous pouvons le remplacer ici par pour obtenir

JiPi^Pj )

=

Z=i

Ainsi, nous voyons que le bloc entier (J3,P) de la matrice d'information asymptotique est

p\\m„^S^X^X\.

L'élément de a) correspondant à <7 est

(

l x~'"

1 w!* 2uf

J(cT,a) =

1 ^ M 3«<y 2w(T^

(2.31)

(2.32)

Ici, nous avons utilisé les faits que, sous le PGD caractérisé par E{u,) = a^

et E(u*)=3a'^, la demière égalité étant une propriété bien connue de la distribution

normale (voir chapitre 1).

Le (/,A:+l)'™' élément de (G^G) est

Z" , ï 1 2 ^ ^

= -Z"=, -^«'^" + 21=1

(2-33)

Finalement, l'élément de J(P, a) correspondant à et a est

(2.34)

= 0.

Les éléments sont nuls parce que, sous le PGD caractérisé par {fi, a) et u, est indépendant de X, et le fait que les aléas soient normalement distribués implique

que E(u,)= Eu,) = 0.

En regroupant les résultats (2.31), 2.32) et (2.34), nous obtenons

Dans la pratique, naturellement, nous sommes intéressés par p et a. Ainsi, au lieu

d'utiliser (2.35), nous devrions en fait réaliser des inférences basées sur la matrice

de covariance estimée. Cette dernière est obtenue en multipliant l'inverse de (2.35)

par w"' et en remplaçant a par b. D'où

Var{0)= Var^P, b) = cr{X^X)^^ 0

0^ (tV2«. (2.36)

2.2.2 Estimation des modèles ARCH et GARCH

Dans le chapitre 1, nous avons vu que l'équation de la variance conditionnelle (fonction de variance) d'un modèle GARCH(1,1) dépend des carré des résidus

retardés, qui à leur tour dépendent des estimations de la fonction de régression.

Pour cette raison, l'estimation de la fonction de régression ainsi que la fonction de

variance doivent être faites ensemble. L'estimation simultanée ces deux fonctions

en même temps s'avère plus efficace qu'estimer l'une conditionnellement à l'autre, conune c'est le cas lorsqu'on utilise les moindres carrés généralisés (MCG); voir

Engle(1982).

La manière recommandée, pour estimer les modèles avec erreurs GARCH est de

supposer que les termes d'erreur sont normalement distribués et d'estimer ensuite

les fonctions du modèle par MV.

Supposons un modèle de régression linéaire, où les erreurs suivent un processus

GARCH et les iimovations sont normalement distribuées y, =X,P + u,,

où e, ~ N(0,l), et Q,_, dénote l'ensemble de l'information disponible jusqu'à t-l. L'équation de la régression linéaire peut se réécrire, comme

OÙ y, est la variable dépendante, x, est un vecteur d'exogène ou de régresseurs prédéterminés, et fi est un vecteur des paramètres de la régression. La fonction

(jfifi, 6) est défmie pour un choix particulier de retards p Qi q par l'équation (2.37)

où u, est remplacé par y, -X,fi. Elle dépend donc de fi mais aussi de a, et ôj que

nous avons regroupé dans un seul vecteur, d.

La densité de y, conditionnelle à s'écrit alors

(2.39)

a,(fi,ff)\p(fi,e))

où (!>{•) dénote la densité normale standard. Et le premier facteur de (2.39) est le facteur Jacobien qui reflète le fait que la dérivée de e, par rapport à y, vaut

of {fi, d)\ voir Davidson et MacKinnon (1999).

En prenant le logarithme de l'équation (2.39), nous obtenons la contribution à la fonction logvraisemblance faite par la t'™" observation, c'est-à-dire

/,(A 0

= {log2;r \o%{a;{fi,d))-\

n

(2.40)

Malheureusement, (2.40) ne peut pas être évaluée directement, à cause de la

fonction skédastique aXfi- f') qui est définie implicitement par l'équation récursive

(2.37). Cette récursion ne constitue pas une définition complète parce qu'elle ne foumit pas les valeurs de départ requises pour débuter la récursion. En cherchant

les valeurs de départ appropriées, nous faisons face à la difficulté qu'il n'existe pas de solution analytique pour la densité d'un GARCH stationnaire.

Dans le cas d'un ARCH(^), nous pouvons éviter ce problème en traitant les q premières observations comme valeurs initiales, car dans ce cas, la fonction de variance est complètement déterminée par les q décalages des carrés des résidus. Il n'y a donc pas d'information manquante pour les ^ + 1 observations jusqu'à n. Nous pouvons donc sommer les contributions (2.40), juste pour ces observations. Mais une telle approche fonctionne uniquement avec des modèles ARCH, et dans la pratique ces modèles sont moins employés dans la modélisation des rendements

financiers.

Avec un modèle GARCH(jt7,ç), les p valeurs de départ de a} sont requises en plus

des q -p valeurs de départ des carrés des résidus pour pouvoir débuter la récursion (2.37). Il est donc nécessaire de recourir à une sorte de procédé ad hoc pour spécifier les valeurs de départ. Une possibilité non intéressante serait de les poser à zéro. Une meilleure idée est de les remplacer par une estimation moyenne. Pour ce faire, il existe au moins deux manières différentes de procéder.

La première consiste à remplacer l'espérance non conditionnelle par la fonction des paramètres 6', ceci conduit à prendre <7^ =

1 dans le cas d'un

GARCH(1,1).

La seconde consiste à utiliser la somme des carrés des résidus des estimations

MCO divisé par n.

Une autre approche est de considérer les valeurs de départ inconnues comme des paramètres supplémentaires, et de maximiser la fonction logvraisemblance par

rapport à ces paramètres p qX 6 conjointement. Dans tous les échantillons, sauf pour des grands échantillons, le choix des valeurs de départ peut avoir des effets

significatifs sur les estimations des paramètres. Ceci implique que l'utilisation de

programmes différents pour l'estimation des GARCH peut produire des résultats

très différents. Brooks et Persand (2001) ont développé une argumentation

convaincante sur cette problématique.

Peu importe le choix des valeurs de départ, la maximisation de la fonction de

logvraisemblance obtenue par l'addition des contributions n'est pas chose facile,

surtout lorsqu'il s'agit de modèles GARCH.

Il est essentiel d'utiliser, autant que possible, les dérivées analytiques, plutôt que

numériques, voir à ce sujet Fiorentini, Calzolari et Panattoni (1996).

Par ailleurs, selon McCullough et Renfro (1999) et Brooks, Burke et Persand

(2001) tous les logiciels ne fournissent pas des estimations et des écarts types

fiables. Par conséquent, il est vivement recommandé d'estimer ce type de modèle plus d'une fois en utilisant des options différentes et des programmes différents.

2.2.3 Les dérivées de la log-vraisemblance d'un modèle ARCH(l)

Dans la sous-section précédente, nous nous sommes aperçus que l'estimation par MV requiert des calculs de dérivées afin de déterminer le(s) estimateur(s) qui maximise(nt) la fonction de vraisemblance ou la fonction de logvraisemblance. Ainsi, dans la présente sous-partie et la suivante, nous allons calculer les dérivées nécessaires à l'estimation par MV des modèles ARCH-GARCH.

y,=x,p+u, (2.41)

nous supposons que les innovations suivent un processus ARCH(l) :

M, =cr,v,;(7,^ =cir+

Nous avons vu que la contribution de l'observation t à la fonction de la logvraisemblance a la fonne

I 2ct,

où u,(J})=y,-X,p

Nous pouvons dès lors déterminer les dérivées analytiques de /, par rapport aux différents paramètres p, a et y.

Nous avons tout d'abord :

dl, _ u, dl, _ ufcrf

du, <rf '

daf a*

daf

Ainsi, par rapport aux paramètres, nous avons donc _ A. - n

^--2»

A-Il vient alors :

dl, _ dl, du, ^ dl, daf ^u,X,

ôf, dl, d(7^ u} - (7;

da ddj da 2àj

dl, dl, da} u} - a} 2

' — ' = ' ' tt

dy daf dy 2 o]'.■T "'-1

Ces dérivées peuvent se généraliser dans le cas d'un ARCH(q). Toutefois, leurs

calculs demeurent fastidieux.

2.2.4 Les dérivées de la log-vraisemblance d'un modèle

GARCH(1,1)

On maintient le modèle (2.41), mais on suppose que les aléas du modèle suivent

un processus GARCH( 1,1).

La caractérisation formelle du processus est alors :

Ui = aiV,\a} = or +

(2.42)

OÙ V, est BB normal à variance 1.

La contribution à la fonction de log-vraisemblance est toujours de la forme

/,(«,;0,r,^) = -|log(2;rof)--^^

OÙ -X,p

Afin de rendre le calcul des dérivées plus sympathique, on va supposer que la

première observation porte l'indice 0 plutôt que 1, et nous allons définir la

convolution de deux séries.

conv{x,y), = x,y,_,. On a alors (?/, u, dl, u} - qf du, of '2of 2(7^ <?!/, 1^, ^ du, „ (?«,

dp^~ ''da^ '" dy^ ^dS^

Nous constatons que les dérivées et sont inchangées par rapportau

processus ARCH(1)=GARCH(1,0), de même que les dérivées de u, par rapport aux paramètres. Par contre, il faut détenniner à nouveau les dérivées de (jj.

Pour ce faire, nous réécrivons, après manipulation de (2.42), l'équation (2.42) afin d'éliminer le terme constant a. Pour ce faire, on pose

sj = af -

%-s), et nous obtenons

qui est une équation de récurrence.

Cette récurrence conduit aux équations suivantes :

^2 + jUi,sl = s'^s^ + ôyux + yil

si = + ô^yi^ + Sytl + yu] et ainsi de suite.

-r-l

L'expression de s} pour tout t est donc sj = S' ^sl + y^^^ S''ul_

sf = S'~^sl + ]Conv(â,u^)i_j

(2.43)

OÙ nous notons le vecteur dont l'élément est uf, et ô le vecteur dont l'élément t

Nous pouvons donc ainsi calculer la variance non conditionnelle du processus

GARCH( 1,1 ) en utilisant la récurrence dans l'équation (2.42).

En notant cette variance <to •. nous remarquons que les espérances marginales de af

et de uf sont égales à al nous avons alors : al =a+ yal + ôal , d'où

^2 _ «

® ~ _\-y-ô1 s'

Par conséquent.

si = ol -

l-S

Pour initialiser la récurrence et rendre opérationnelle l'équation (2.43), nous

supposons que = ^. 11 vient alors

ayiô' '

2 a ayô' ' „ 2

Ainsi, pour tout r =1, la valeur de la convolution est nulle. Dès lors, les dérivées nécessaires à l'évaluation de la logvraisemblance sont déterminées comme suit

dal

1

yô'~^

da "\-ô^ (1- 7-^x1- ^

ddl aô''^ , „ 2

+

dy (\-y-S) conv(S,u ),_!

Étant donné que l'élément t du vecteur S est S'~\ nous constatons que l'élément t

du vecteur

est

De même, l'élément t du vecteur {dldfi)u^ est

-llÀ,X,. Nous aboutissons alors aux expressions

ô?, du, dl, ôcP; u,X, - <7^

an

'

of

la;

dl, dl, ôaj

- df 1

yô''^

da 8d\ da Ic^ I-^^(1-x-«^Xl-^)

dl, dl, da} u}- a} , a

ay8~^' "

a}8'~'(2- y-28)

n/ ^ ,

d8~da}d8~ 2&} ^(1-^)2

Cormne nous l'avons souligné précédemment, nous constatons bel et bien que la maximisation de la vraisemblance s'avère délicate, compte tenu de l'augmentation

du nombre de dérivées à calculer. L'estimation des modèles ARCH-GARCH, requiert dans un premier temps la présence d'hétéroscédasticité conditionnelle dans les aléas du modèle spécifié. Pour ce faire, nous avons alors recours à un test ARCH, dont nous exposons la théorie dans la section suivante.

2.3 Test d'homoscédasticité : test ARCH

Considérons le modèle de régression linéaire avec erreur ARCH(q) défini par

(2.41), c'est-à-dire :

y, =x,p + u,

£(«/k-i)=o

u,=(y,v,y{u\^_^ )= a} =h, = a+ y^u}.^ + y2ih-2+- + Yq«f-q

Comme Engle (1982) l'a montré le premier, il est facile de tester cette hypothèse

en exécutant la régression :

ùj = fl +

+ C2M?_2+...+CçW,_ç + résidu,

(2.44)

OÙ û, désigne un résidu provenant de l'estimation par moindres carrés du modèle

de régression auquel sont associés les u,. Nous calculons ensuite un test F

ordinaire (ou simplement n fois le centré) pour les hypothèses de nullité des paramètres ci à c,. Il ne s'agit nul autre que d'une régression artificielle où les régresseurs sont des résidus au carré retardés. Ainsi, pour tout modèle de

régression estimé à l'aide de séries temporelles, il est très facile de tester

l'hypothèse nulle d'homoscédasticité contre l'hypothèse alternative que les erreurs suivent un processus ARCH(q). Il s'agit simplement d'un test LM pour

l'hétéroscédasticité conditioimelle en termes de régression artificielle.

2.4 Tests d'asymétrie et d'aplatissement

Bien qu'il soit correct d'utiliser les MCO chaque fois que les aléas associés à une fonction de régression sont d'espérance nulle et ont une matrice de covariance qui satisfait des conditions de régularité assez faibles, les moindres carrés conduisent à un estimateur optimal seulement dans des circonstances particulières. Ainsi, l'information sur les seconds moments des aléas conduira, en général, à un gain d'efficacité dans l'estimation des paramètres de la fonction de régression. C'est aussi le cas pour les moments des aléas d'ordre supérieur. Par exemple, si les aléas sont très leptokurtiques, c'est-à-dire si leur distribution possède des queues très épaisses, les MCO peuvent se révéler très inefficaces par rapport à un autre estimateur qui prend en compte la leptokurticité. Par analogie, les aléas sont

asymétriques, il sera possible de trouver mieux que les MCO en utilisant un estimateur qui reconnaît la présence d'asymétrie.

Tout cela suggère qu'il est généralement prudent de tester l'hypothèse que les aléas sont nonnalement distribués. Dans la pratique, nous calculons rarement des moments au-delà du troisième ou du quatrième; ceci signifie que l'on teste l'asymétrie ou l'excès du kurtosis (aplatissement). Dans une section antérieure,

nous avons vu que pour une distribution normale de variance le troisième

moment centré, qui détermine l'asymétrie, est nul, tandis que le quatrième moment

centré, qui détennine l'excès du kurtosis. est 3(t^. Si le troisième moment n'est pas

nul, la distribution est dite asymétrique. Si le quatrième moment centré est

supérieur à 3

a'*, la distribution est dite leptokurtique alors que si le quatrième

moment centré est inférieur à 3 a'*, la distribution est dite platykurtique. Dans la

pratique, les résidus sont fréquemment leptokurtiques et rarement platykurtiques.

On rencontre souvent l'asymétrie et l'excès de kurtosis dans les doimées de

rendements financiers, et surtout lorsque ces rendements sont mesurés sur de courtes périodes. Un bon modèle devrait éliminer, ou au moins réduire sensiblement, l'asymétrie et l'excès de kurtosis qui sont généralement présents dans

des données quotidiennes, hebdomadaires et, moindrement, dans les rendements

mensuels.

Un moyen simple pour tester si les aléas sont normalement distribués est

d'imaginer un test sur la régression OPG (voir Russell Davidson et James G. Mackinnon, 1999, chapitre 13).

Supposons que le modèle de régression linéaire à tester soit

l'ajout d'une constante ou l'équivalent dans les régresseurs ne modifie pas les

résultats. La régression OPG correspondant à ce modèle s'écrit

/ = Ui(fi)X,b + b(, ' + résidu (2-46)

OÙ /, une fois de plus, est un vecteur unitaire et nous avons posé u, ^y,-X,p, et sous l'hypothèse que les aléas sont normalement distribués, il y a ni asymétrie ni excès de kurtosis. Si nous voulons tester l'hypothèse nulle que les aléas sont symétriques, contre l'hypothèse alternative que les aléas sont asymétriques, le

régresseur naturel approprié à ajouter à (2.46) est u]{j}).

L'estimation par MCO de (2.45) nous fournit p et =SSR/n. Ainsi, la régression OPG associée à cette équation s'écrit

/

Ui(P)X,b + b„

^

+ eu, (P)+résidu

(2.47)

La statistique de test sera simplement le t de Student associé à ce régresseur, c'est-à-dire qu'on teste si c = 0.

La régression (2.47) n'est pas nécessairement compliquée. Car sous l'hypothèse nulle, le régresseur de test est déjà asymptotiquement orthogonal au second régresseur (c'est celui qui correspond au paramètre o). Pour s'en rendre compte, évaluons les régresseurs par rapport au vrai paramètre A) au lieu de p. Les résidus u, (Pq ) correspondent alors aux aléas u, et nous constatons que

1

1 tr -o 3 0

Ce résultat est obtenu en utilisant la loi des grands nombres et l'hypothèse que les aléas (u,) sont normalement distribués, ce qui implique que les moments impairs

sont nuls (£(«,')= £(m,^) = 0. Donc, même si nous omettons le régresseur

correspondant à a, dans (2.47), le /-test de c = 0 reste asymptotiquement inchangé. Rappelons que cette statistique de test restera inchangée, même dans un échantillon fini, si nous ajoutons à n'importe quelle combinaison linéaire de régresseurs correspondant à p. Nous faisons référence ici au théorème FWL. Comme nous avons supposé qu'il y a un terme constant dans la régression, la

statistique de test restera inchangée si nous remplaçons u\p) par u^(P)-3(/u,(P).

En procédant ainsi, ce nouveau régresseur est asymptotiquement orthogonal à tous les régresseurs correspondant p, comme nous pouvons le constater par le calcul

suivant :

XiU,{i4 = X,E(u'j -3ct^uJ) = 0.

Sous l'hypothèse de normalité de u,, E(uj) = 3</. D'où le résultat de la deuxième

égalité ci-dessus. Par conséquent, il n'y a aucune différence asymptotiquement si nous omettons les régresseurs qui correspondent à p.

Les arguments ci-dessus impliquent que nous pouvons obtenir un test valide simplement en employant le /-test de la régression suivante

I = c{u^{ p~)

-3c^UiiP)) + résidu,

(2.48)

ce qui est numériquement identique au /-test de la moyerme d'un échantillon dont le modèle comprend un seul régresseur. Coimne la p lim de la variance des erreurs vaut 1, et que les régresseurs et les régressés sont asymptotiquement orthogonaux, les deux /-tests sont alors asymptotiquement équivalents à

' (2.49)

où û, = UiCp). Puisque les résidus de la régression par MCO comportent une somme

constante égale à zéro et que sous Hq = = cr^, le numérateur de (2.49) vaut alors

^1/2^-3

sixième moment de la distribution normale vaut alors 15 et la

p\im du dénominateur est égale à la racine carré de E{u, - ) = <7^15 -18+ 9) = 6o\

Sous l'hypothèse que les résidus sont normalisés, il vient alors, en remplaçant u, par e, et o par 1, que la statistique de test pour l'asymétrie est

(2.50)

Il s'en suit que la variance de = vaut 6a®. Alors que la variance de

= qui est égale à la variance de vaut I5cr®. Nous constatons une

inexactitude dans ces deux résultats, qui peut être due au fait que les résidus

normalisés sont calculés à l'aide d'estimation de l'espérance et de l'écart type.

Par analogie, pour tester l'hypothèse que les aléas ont un quatrième moment égal à

3(7*, le régresseur naturel à ajouter à (2.46) est u^-3a*. Il est facile de constater

que ce nouveau régresseur est asymptotiquement orthogonal à tous les autres régresseurs de l'équation (2.46) et que le /-test reste inchangé même si nous

ajoutons 6(/ fois le régresseur correspondant à ct, nous obtenons alors

u* -6a^i^ +3a*. Puis nous divisons cette expression par a*, le /-test n'est toujours

pas affecté, et nous obtenons la régression OPG correspondant à ce test

/ = c{e* -6e," + 3)+ résidu,

(2.51)

SOUS l'hypothèse que les résidus sont normalisés. La statistique de test associée à ce test est asymptotiquement équivalente à

t,^(24n)-^'j;je:-3)

(2.52)

Tout comme est asymptotiquement distribuée selon A'(0,1) sous l'hypothèse

nulle de nonnalité. Leurs carrés seront asymptotiquement distribués selon une ^*(1). De plus, puisque ces deux statistiques sont indépendantes, la somme de leurs

carrés sera asymptotiquement distribuée selon une z^i2). Nous écrivons alors

(2.53)