Spectroscopie infrarouge de fils et boîtes quantiques d'InAs/InAlAs/InP(001)

HAL Id: tel-00002702

https://tel.archives-ouvertes.fr/tel-00002702

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

d’InAs/InAlAs/InP(001)

Frédéric Fossard

To cite this version:

Frédéric Fossard. Spectroscopie infrarouge de fils et boîtes quantiques d’InAs/InAlAs/InP(001). Physique [physics]. Université Paris Sud - Paris XI, 2002. Français. �tel-00002702�

ORSAY

N° d’ordre : 7010

UNIVERSITE DE PARIS-SUD

UFR SCIENTIFIQUE D’ORSAY

THESE

présentée pour obtenir

le grade de

DOCTEUR EN SCIENCES

DE L'UNIVERSITE PARIS XI ORSAY

PAR

Frédéric FOSSARD

SUJET :

Spectroscopie infrarouge des fils et boîtes quantiques

d'InAs/InAlAs/InP(001)

Thèse soutenue le 22 octobre 2002 devant la commission d’examen : M. G. Fishman

M. M. Gendry

M. J. M. Gérard Rapporteur

M. Y. Guldner

M. F. H. Julien Directeur de Thèse

M. P. Lefebvre Rapporteur

FOSSARD

Et je dois suivre, si je le puis La poursuivant d'un pied las,

Jusqu'à ce quelle rencontre quelque voie plus large Où maints sentiers et courses se rencontrent. Et où alors? Je ne saurais le dire.

J.R.R. Tolkien (Le Seigneur des Anneaux)

Cette thèse ne s'est heureusement pas restreinte pas à maudire le spectromètre ou à interagir, de façon plus ou moins violente, avec ma station de travail. Au cours de ces trois années, j'ai rencontré de nombreuses personnes qui ont participé, directement ou non, à ce travail. Si écrire cette page est un exercice traditionnel en ouverture du manuscrit, que les personnes citées sachent que mes remerciements sont sincères. Je tiens à remercier :

Claire DUPAS de m'avoir accueilli, il y a trois ans, à l'Institut d'Electronique Fondamentale. Jean-Michel LOURTIOZ, son successeur, pour son soutien inconditionnel durant ce travail. Yves GULDNER qui m'a fait l'honneur de présider mon jury de thèse.

Pierre LEFEBVRE et Jean-Michel GERARD d'avoir accepté d'être rapporteur de ce travail. Leurs remarques éclairées ont permis d'améliorer le manuscrit.

François JULIEN, directeur de thèse d'une disponibilité rare, de m'avoir considéré comme un collègue malgré mes lacunes en optique et en bricolage. Il a été, à la fois très motivant et très enrichissant de travailler avec quelqu'un dont la culture scientifique n'a d'égale que l'enthousiasme.

Michel GENDRY d'avoir fournit la matière première de cette thèse. Je n'oublierai pas nos discussions sur l'épitaxie et ses "paramètres cachés" qui ont rendu cette collaboration aussi conviviale que scientifique.

Guy FISHMAN pour le soutien philosophique (comprenez théorique) lorsque j'ai essayé de modéliser les objets étudiés dans ce manuscrit. Sans son aide, je n'aurais pas vu le petit bout de la queue du chat.

Antigoni ALEXANDROU, pour sa compétence en spectroscopie femtoseconde et sa bonne humeur. Eliezer FINKMAN et Shmuel SCHACHAM du Technion pour les expériences de photoconduction et surtout leurs interprétations.

Gérald BASTARD, Robson FERREIRA et Jean-Pierre LEBURTON pour les discussions théoriques sur les boîtes quantiques et leurs propriétés.

Julien BRAULT et Emmanuel PERONNE qui ont rédigé les deux premiers tomes de cette trilogie des nanostructures InAs/InAlAs.

Olivier GAUTHIER-LAFAYE et Sebastian ROWSON pour le soutien technique au cours des premiers mois de thèse.

Alain LUSSON, Khalid MOUMANIS, Maria TCHERNYCHEVA et Elias WARDE pour leur implication dans l'action Opto GaN.

Les orfèvres Stéphane CABARET et Flavien DELGEHIER pour la réalisation de ces petits bijoux qui font que nos manipes sont à la fois uniques et performantes.

Benjamin DAMILANO, Sergei DANILOV, Bruno DAUDIN, Emmanuelle DELEPORTE, Nicolas GRANDJEAN, Daniel LE SI DANG, Jean MASSIES et Isabelle PREVOT qui ont élargi mon horizon à travers l'étude de systèmes différents.

Claudine NOGUERA pour son précieux conseil.

Je veux également associer à ce manuscrit ceux qui m'ont mis le pied à l'étrier, il y a quelques années : William "Bill" SHEPARD, qui m'a appris tant de choses sur les cristaux, le rayonnement synchrotron et les whiskys écossais...

Gérard KRILL, qui m'a fait confiance en me prenant en stage.

France CHEVRIER et Eddy FOY qui m'ont initié à l'épitaxie par jets moléculaires de la façon la plus sympathique qui soit.

La proximité de la machine à café a autorisé les conversations les plus scientifiques ou les plus débridées avec tous les personnels de CROQ qui sont bien trop nombreux à citer. Je tiens cependant à remercier tout particulièrement les CROQuettes, CROQuants et "assimilé(e)s" que j’ai le plaisir de compter parmis mes amis : Moustapha EL KURDI, Frédérique GADOT, Laurent JOULAUD, Vinh LE THANH, Jérôme LOPEZ, Juliette MANGENEY, Cécile MAUNOURY, Florian MONSEF et Vy YAM.

Remerciements très spéciaux à :

Nicolas CAVASSILAS pour les photos du mariage (reconnaissance éternelle).

Anne Lise COUTROT pour les milliers de km parcourus en métro à supporter mon analyse techniquo-tactique des matches du dimanche.

Cornelia CUISIN pour m'avoir fait goûter au stress de la soutenance, avec un an d'avance...

Sylvain DAVID, binôme de thèse, avec lequel j'ai échangé balles jaunes et balles ovales, partagé bières et boutades dans la neige, le sable, la boue et la joie...

Ana HELMAN, pour son aide inestimable lors de la dernière année de thèse et toutes ces petites choses qui ont contribué à une ambiance sympathique et spectroscopique. Hvala sto si samnom dijelila sobu 38 i bezbrojne lude smjehove (merci à Ana PERSIC pour la traduction).

Merci au Dr Serge HERMAN pour avoir réalisé la plus belle manipe de ces 3 années.

Merci à ma famille de m'avoir laissé mûrir pendant de si longues années : le fruit est entre vos mains. Merci à celui qui m’a encouragé de la-haut.

Merci à ma belle-famille pour son soutien et ses bons conseils.

Et enfin MERCI à ma moitié, Kareen FOSSARD, qui supporte mes doutes, mes certitudes, mes bleus au corps et à l'âme et auprès de laquelle je trouve toujours sagesse et réconfort.

Introduction

Chapitre I : Propriétés intersousbandes de nanostructures

semiconductrices

I Structure de bande d'un semiconducteur 5

I.1 Structure et fonction d'onde 5

I.2 Origine de la bande interdite 8

I.3 La masse effective 11

I.4 Densité d'états 13

II Hétérostructures semiconductrices 14

II.1 L'hétérojonction 15

II.2 Le formalisme de la fonction enveloppe 17

II.3 Le puits quantique 21

II.4 Structure électronique des fils et des boîtes quantiques 25

II.5 Interactions électrons phonons dans les nanostructures 31

III Propriétés optiques des hétérostructures semiconductrices 35

III.1 Transitions optiques 35

III.2 Le coefficient d'absorption 39

III.3 Force d'oscillateur et section efficace 42

IV Etat de l'art des transitions intrabandes 44

IV.1 Dispositifs de détection 45

IV.2 Dispositifs d'émission intersousbande 52

IV.3 Autres dispositifs optoélectroniques 56

Chapitre II : Croissance des îlots d'InAs sur InAlAs/InP(001)

I Epitaxie 57

I.1 Généralités sur l'épitaxie 57

I.2 L'épitaxie par jets moléculaires 59

II.1 Désaccord de maille 62

II.2 Energie de contrainte et épaisseur critique 63

II.3 Bilan énergétique 63

II.4 Le rôle des conditions de croissance 65

III Les îlots InAs/In0.52Al0.48As sur InP(001) 66

III.1 Protocole standard de croissance 67

III.2 Contrôle de la forme des nanostructures 67

III.3 Suppression de l'anisotropie 70

III.4 Echantillons étudiés 72

IV L'auto-organisation verticale 72

IV.1 Microscopie à force atomique (AFM) 73

IV.2 Microscopie électronique en transmission (TEM) 74

V Conclusion 76

Chapitre III : Spectroscopie infrarouge

I Photoluminescence 77

I.1 Principe 77

I.2 Montage expérimental 79

II Spectroscopie à transformée de Fourier 81

II.1 Le spectromètre (FTIR) 81

II.2 Montage expérimental 84

II.3 La référence 87

II.4 Spectroscopie d'absorption photo-induite (PIA) 88

Chapitre IV : Caractérisation optique des nanostructures

InAs/InAlAs/InP(001)

Préambule : le point de départ 93

I Spectroscopie des fils quantiques 97

I.1 Spectroscopie interbande 97

I.2 Spectroscopie intrabande 98

I.3 Etude en fonction du dopage 99

I.4 Photoconduction 104

II Spectroscopie de boîtes quantiques 116

II.1 Spectroscopie interbande 116

II.2 Spectroscopie intrabande 122

II.3 Spectroscopie de photocourant et structure énergétique 135

II.4 Spectroscopie des boîtes isotropes 137

III Conclusion 139

Chapitre V : Modélisation

I La théorie k.p 142

I.1 Principe 142

I.2 Résolution du Hamiltonien k.p 143

II Construction du Hamiltonien à 8 bandes 144

II.1 La plus petite base : la masse effective 144

II.2 Hamiltonien à deux bandes : la philosophie générale 146

II.3 Le Hamiltonien de Pidgeon et Brown 148

II.4 Le Hamiltonien ramené à 2 bandes 152

III Le modèle 154

III.1 La base du modèle 154

III.2 La procédure de calcul 158

III.3 Modélisation d'un fil quantique 160

III.4 Résultats 163

Conclusion générale et perspectives

Bibliographie

Introduction

Le développement des hétérostructures de matériaux semiconducteurs a donné des illustrations claires de certains concepts de la mécanique quantique comme le confinement ou la quantification des niveaux d'énergie. Une nouvelle génération de dispositifs optoélectroniques a été développée mettant à profit ces effets quantiques. Pour la majeure partie de ces dispositifs, l'interaction entre la lumière et le matériau implique des transitions entre la bande de conduction et la bande de valence. Plus récemment, des applications concernant la détection, la modulation optique ou l'émission laser impliquent des transitions intersousbandes, c'est-à-dire entre niveaux confinés d'une même bande. Les progrès accomplis dans les techniques de croissance ont permis de réaliser différentes formes de nanostructures semiconductrices (puits, fils et boîtes quantiques) de manière à confiner les porteurs dans une, deux ou trois directions de l'espace.

Des études montrent les avantages tirés de l'utilisation de photodétecteurs à fils et à boîtes quantiques plutôt que de celle de photodétecteurs à puits quantiques. Les deux principaux atouts sont la possibilité d'absorption intrabande à incidence normale, interdite dans les puits quantiques. C'est aussi diminuer le bruit de génération-recombinaison grâce à un ralentissement du temps de capture des électrons. Ces nanostructures présentent également un grand intérêt pour la réalisation de sources unipolaires dans le moyen infrarouge (lasers à cascade quantique). L'étude des transitions intersousbandes dans ces structures est l'objet de cette thèse.

Dans le premier chapitre, j'introduirai les concepts de base de la physique des semiconducteurs. Ensuite, je décrirai les propriétés électroniques et optiques particulières des puits, fils et boîtes quantiques. Les transitions intersousbande dans ces structures seront

particulièrement discutées. L'intérêt de ces transitions pour l'optique infrarouge est illustré par l'état de l'art des dispositifs intrabandes.

Le chapitre II concerne l'élaboration par épitaxie par jets moléculaires des structures réalisée par J. Brault et M. Gendry au LEOM. Je synthétiserai les résultats obtenus par J. Brault au cours de sa thèse.

Je montrerai comment le désaccord de maille entre l'InAs et l'InAlAs/InP(001) permet de fabriquer, en jouant sur les paramètres de croissance, des fils, des boîtes allongées ou des boîtes isotropes par auto-organisation selon le mode croissance Stranski-Krastanov. La caractérisation de ces structures par microscopie à force atomique est présentée et montre les différentes formes d'objets obtenus ainsi que leur dispersion en taille. L'étude en microscopie électronique en transmission de l'empilement de ces structures est réalisée et montre une anti-corrélation entre deux plans successifs lorsque l'épaisseur de la barrière est faible.

Le troisième chapitre porte sur la description concise des différentes techniques spectroscopiques que j'ai mises en œuvre au laboratoire. Je mettrai l'accent sur la spectroscopie infrarouge à transformée de Fourier qui constitue la base de notre étude des propriétés optiques intrabandes dans les fils et boîtes quantiques d'InAs/InAlAs/InP(001). Je présenterai la spectroscopie d'absorption photo-induite, technique très sensible développée au laboratoire qui permet de mesurer des absorptions différentielles inférieures à 10-5

.

Le chapitre IV est consacré à l'étude expérimentale des fils, boîtes allongées et boîtes isotropes d'InAs/InAlAs/InP(001) présentées au chapitre II. L'étude systématique de ces structures nous fait distinguer 4 comportements : des fils et des chapelets de boîtes allongées dans lesquels une seule direction de confinement est observée, des boîtes allongées isolées présentant un confinement dans les deux directions du plan et enfin des boîtes plus isotropes. Je montrerai que ces structures présentent de fortes résonances intersousbandes polarisées dans le plan des couches. Ces absorptions géantes atteignent 26 % à incidence normale pour

10 plans de boîtes allongées dopées n à 1012

cm-2

. Je présenterai également les résultats obtenus en photoconduction par E. Finkman au Technion et en spectroscopie femtoseconde par E. Péronne et A. Alexandrou au LOA. À partir de la synthèse des résultats obtenus avec les différentes spectroscopies réalisées, je reconstruirai le diagramme énergétique des fils et des boîtes allongées.

Je présenterai dans le chapitre V mes résultats de simulations de la structure énergétique des fils dans une théorie k.p à 8 bandes. Je montrerai qu'un modèle simple réduit à deux bandes permet de décrire avec une excellente précision la dispersion en bande de conduction. Je confronterai les résultats de nos simulations aux valeurs des différentes transitions intrabandes observées tant en spectroscopie de photoconduction qu'en spectroscopie infrarouge.

Chapitre I :Propriétés intersousbandes

de nanostructures semiconductrices

L'objectif de ce chapitre est d'introduire les propriétés spécifiques des transitions intersousbandes dans les nanostructures semiconductrices. Je commencerai par un rappel des concepts essentiels à la compréhension de la physique des semiconducteurs. Puis, je montrerai les propriétés particulières générées par le confinement des porteurs dans une, deux puis trois directions de l'espace. Les propriétés intersousbandes de ces nanostructures seront discutées afin de comprendre l'intérêt de ces systèmes pour l'optoélectronique. Enfin, j'illustrerai ces propriétés en faisant un état de l'art des dispositifs dont le fonctionnement repose sur les transitions optiques intersousbandes.

I Structure de bande d'un semiconducteur

I.1 Structure et fonction d'onde

Les semiconducteurs sont des solides cristallins. La plupart s'ordonne selon un réseau cubique à faces centrées (cfc). Chaque nœud du réseau porte un motif constitué de deux atomes A et B. Si ces deux atomes sont semblables, cette structure est celle du diamant (Ge, Si). Dans le cas contraire, elle est nommée blende de zinc (GaAs, InSb).

Figure I.1 : Structure cristallographique de la Blende de Zinc : les atomes A et B sont disposés sur deux réseaux cfc décalés d'un quart de la diagonale du cube. Chaque atome A (B) est au centre d'un tétraèdre régulier formé par 4 atomes B (A).

D'autres semiconducteurs comme le GaN ou ZnO cristallisent selon un réseau hexagonal compact : la Wurzite. Les matériaux cristallisant dans ce système présentent des propriétés différentes des semiconducteurs à structure cubique et en particulier une polarisation spontanée (effet ferroélectrique). Cette propriété vient de la symétrie particulière de la structure et des propriétés tensorielles associées à cette structure.

Figure I.2 : Structure cristallographique de la structure Wurzite : les atomes A et B sont disposés sur deux réseaux hexagonaux décalés de à peu près 3/8 de la hauteur. À l'instar de la structure Blende de Zinc, les atomes d'un élément sont au centre d'un tétraèdre formé par 4 atomes de l'autre élément.

Le nombre gigantesque d'électrons dans un solide (1022

cm-3

) rend la résolution de l'équation de Schrödinger insoluble. La physique du solide montre qu'en tenant compte de la structure cristalline du matériau, ce problème est grandement simplifié. Le Hamiltonien décrivant l'interaction entre électrons ainsi qu'entre les électrons et les atomes du cristal est complexe, mais ces interactions peuvent souvent être ramenées à un potentiel effectif V(r). L'Hamiltonien décrivant un électron dans la structure périodique est:

H V cristal i i m = p +

∑

où p est la quantité de mouvement de l'électron et m sa masse. Les ri sont les positions des

nœuds du réseau. En tenant compte de la périodicité du cristal, on peut écrire :

H cristal m U = p + r 2 2 ( ) (I.2)

où U(r) est le nouveau potentiel vu par les électrons. Ce potentiel qui possède la périodicité du cristal nous permet donc de restreindre la somme des interactions à traiter. Dans le vide, les solutions du Hamiltonien H=p2/2m, sont des ondes planes eik.r. Dans le cristal, les solutions de l'équation de Schrödinger Ψ sont les fonctions de Bloch, produit d'ondes planes par des fonctions périodiques un,k(r) :

Ψ_{n,k( )r =un,k( )r e}ik.r

(I.3) La structure périodique du réseau réciproque permet de replier l'espace des k et de restreindre le vecteur d'onde à une cellule primitive : la première zone de Brillouin. Cette cellule élémentaire du réseau réciproque possède plusieurs directions de haute symétrie. Dans la plupart des semiconducteurs, les directions étudiées sont les directions ΓL [111] et ΓX [100] qui représentent les directions de l'espace réciproques. Le voisinage de Γ décrit le centre

Figure I.3 : Première zone de Brillouin d'un réseau à cubique face centrée. Les directions ΓX et ΓL sont des directions de haute symétrie

I. 2 Origine de la bande interdite

On peut, à l'aide d'un modèle chimique simpliste, comprendre l'origine de l'énergie de bande interdite dans un matériau semiconducteur. La liaison chimique entre 2 atomes crée des niveaux liants et antiliants. La construction de ces niveaux et leur remplissage par les électrons va donner directement la nature métallique ou isolante du matériau.

Figure I.4 : Remplissage des couches d'une liaison chimique entre 2 atomes identiques ayant chacun 4 électrons de valence. La structure énergétique de la liaison dépend du couplage entre les atomes. Le nombre entre parenthèse indique le nombre d'états disponibles dans la couche.

Lorsque le dernier niveau occupé n'est que partiellement rempli, le matériau se comporte comme un métal. Dans le cas contraire, le matériau est isolant. Parmi ces isolants, les matériaux semiconducteurs se répartissent en trois familles, suivant la position dans le tableau périodique, des deux atomes impliqués dans la liaison : les semiconducteurs IV-IV (Si, Ge), III-V (GaAs, AlSb), II-VI (CdTe). Dans chaque cas, on dénombre huit électrons de valence impliqués dans la liaison chimique. Les 8 électrons vont remplir les 2 premières couches et laisser les deux autres vides.

Nous allons nous intéresser au dernier niveau occupé que nous appellerons niveau de valence (dégénéré trois fois) que l'on assimile à un moment orbital L=1 (fonction de type X, Y, Z), et au premier niveau vide : le niveau de conduction associé à un moment orbital L=0 (fonction de type S). La dégénérescence du niveau de valence va être partiellement levée par l'interaction spin-orbite qui permet de construire deux états J=L+S. On crée donc des niveaux J=1/2 et J=3/2.

Dans le solide, le nombre important d'atomes induit une dégénérescence des niveaux liants et antiliants donnant ainsi naissance à des bandes [Pankove 1971]. Dès lors, la dernière bande occupée sera la bande de valence (quatre fois dégénérée : Γ₈) et la première bande non occupée (une fois dégénérée : Γ6) sera la première bande de conduction. L'écart d'énergie

entre ces deux bandes Γ est l'énergie de bande interdite EG*. L'écart d'énergie entre la bande

de valence et la bande Γ7 (plus profonde) vient de l'interaction spin-orbite et est notée ∆SO.

Figure I.5 : Origine de la bande de valence et de la bande de conduction dans un semiconducteur. Les notations des bandes sont issues de la théorie des groupes

Nous avons vu précédemment que la périodicité du cristal permettait de restreindre k à la première zone de Brillouin. On peut donc tracer la structure de bande d'un matériau en reliant les points de haute symétrie de la zone de Brillouin.

On peut distinguer deux types de bande interdite. Dans le premier cas, le sommet de la bande de valence et le bas de la bande de conduction se situe au même endroit de la zone de Brillouin et nous verrons par la suite que cela autorise des transitions optiques sans modification du vecteur d'onde à k=0. Une telle bande interdite est dite "directe". Dans le deuxième cas, les extrema de bande ne se font pas face et les transitions ne se font pas à k constant. La bande interdite est, par opposition au cas précédent, "indirecte".

Figure I.6 : Diagramme de bande d'un semiconducteur à bande interdite indirecte (type Si) et directe (InAs).

I. 3 la masse effective

L’approximation de masse effective (théorie k.p à 1 bande) dans les semiconducteurs permet de tenir compte au premier ordre des interactions entre les différentes bandes d’énergies. Ce formalisme simple fournit essentiellement des informations qualitatives. En effet, les bandes ne sont paraboliques qu’au voisinage du centre de zone. La validité de ce modèle est ainsi limitée à une fraction de la zone de Brillouin (quelques pour cent) dans certains matériaux tels qu’InAs ou InSb [Boujdaria 2001]. Nous verrons dans le chapitre modélisation comment traiter la non-parabolicité à l’aide de la théorie k.p à un ordre supérieur.

I. 3. 1 Description classique de la masse effective

Nous allons définir la notion de masse effective de façon classique en tenant compte des interactions entre l’électron et son environnement. Soit une particule évoluant dans un cristal de dimension finie. Elle est soumise à :

• F : la force extérieure appliquée ;

• Fi : la résultante de toutes les forces d'interaction entre la particule et la structure.

Si m0 est la masse de la particule, la mécanique classique donne :

F+ =F_i m₀γ (I.4) donc F=m − Fi    0 _γ γ et F=m*γ (I.5) et (I.6)

On introduit une particule fictive de masse m* (seule intervient la force extérieure) dont l'état est identique à celui de la particule réelle (accélération, énergie).

Dans le cristal, on redéfinit la masse de l'électron par :

1 2

2

mi j, E/ k ki j

= h

∂ ∂ ∂ (I.7)

Dans le cas d'un cristal tridimensionnel, le résultat n'est plus trivial et se présente sous la forme d'un tenseur à neuf composantes [Wang 1994]. m* est constante si E(k) est parabolique. Elle sera notée me pour une particule de charge négative (électron), mh pour une

particule de charge positive (trou) que nous définirons par la suite. Les surfaces d'énergies constantes sont ainsi des ellipsoïdes centrés sur les extrêma de zone.

Figure I.7 : Surfaces d'énergie constante dans un semiconducteur. A gauche, la masse est anisotrope (Si), à droite, la masse est isotrope (GaAs)

Dans le cas d'un semiconducteur à gap direct (GaAs), la masse effective est isotrope. Dans le cas d'un semiconducteur à gap indirect (Si ou Ge), on peut définir des masses longitudinales et transverses dans certaines directions de l'espace.

I. 3. 2 Masse du trou

Supposons que la bande de valence soit entièrement remplie. Il n'y a pas de transport possible. Si maintenant il manque un seul électron, la conduction résultante du mouvement des N-1 électrons est équivalente à celle d'une seule particule positive (trou) dont la vitesse est celle de l'électron manquant. La masse effective du trou est : m_h = −m_e.

I. 4 Densité d'états

Avant de présenter les particularités des nanostructures semiconductrices, il est intéressant de voir la relation qu'il existe entre la densité d'état dans une bande et l'énergie. Prenons l'exemple d'un semiconducteur à bande interdite directe. L'énergie d’un électron dans une bande n s'écrit :

E k E m k k k E k m n( ) n x y z n * * , , = ₀ + 2

(

)

ρ

π

( )k = V

8 3 (I.9)

Pour relier ρ(k) à ρ(E), on somme sur tous les états de l'espace des k. Nous devons, bien

entendu, retrouver le même résultat en sommant sur toutes les énergies :

La surface d'énergie constante étant une sphère, la variation infinitésimale de volume peut s'écrire :

d k3 =4πk dk2 (I.11)

Nous avons alors tous les termes qui permettent de calculer ρ(E) :

k2 = 2m₂* (E E− _n,0) h (I.12) et dE dk k m m m E E m E E n n = h = h − = − h h 2 2 2 0 0 2 2 * * * _{( )} * ( ) , , (I.13)

En tenant compte des deux états de spin, on en déduit l'expression de la densité d'état en fonction de l'énergie : ρ π ( ) * ( ) / , / E = V  m E E_n   − 2 2 2 2 3 2 0 1 2 h (I.14)

Le résultat important est que la densité d'état varie comme la racine carrée de l'énergie. Nous verrons que le confinement des porteurs induit un comportement différent dans les puits, fils et boîtes quantiques.

II Hétérostructures semiconductrices

Le confinement des porteurs va permettre d'obtenir une structure énergétique discrète dans une ou plusieurs directions de l'espace. Nous verrons qu'il est ainsi possible de concevoir de nouveaux matériaux ayant une structure énergétique bien déterminée.

II. 1 L'hétérojonction

On obtient une hétérojonction en faisant croître une couche d'un semiconducteur B de bande interdite Eg

B

sur un autre semiconducteur A de bande interdite Eg A . Arbitrairement, on posera Eg A > Eg B .

Avec l'essor des différentes techniques d'épitaxie (jets moléculaires : MBE [Gossard 1986], organo-métalliques : MOCVD [Breiland 1999], phase gazeuse : CVD [Tong Lee 1999]), il est possible de créer des interfaces abruptes entre ces deux matériaux dont la rugosité est de l'ordre de la couche atomique. L'intérêt d'une telle structure réside dans la création d'un décalage entre les bandes d'énergie permises des deux semiconducteurs. Les énergies de bande interdite des deux matériaux A et B n'étant pas égales, il y a création de discontinuités en bandes de conduction ∆Ec et de valence ∆Ev à l'interface. En fonction de la position des bandes interdites, l'hétérojonction peut être de trois types différents :

• type I : la bande interdite Eg B

est entièrement dans Eg A

. • type II : Une des discontinuités est plus grande que Eg

A - Eg B mais inférieure à Eg A . • type III : une des discontinuités est supérieure à Eg

A

.

Figure I.8 : Les trois types d'hétérojonctions entre deux semiconducteurs A et B ayant des énergies de bande interdite EgA et EgB. Ec et Ev désignent la bande de conduction et la bande de valence. ∆Ec et ∆Ev sont les

Pour les porteurs (électrons ou trous), la discontinuité de bande se présente comme une discontinuité de l'énergie potentielle. Il est donc possible en alternant les couches de semiconducteurs différents de construire un profil de potentiel déterminé. Il existe cependant certaines limites à cette technique. Pour avoir une hétérojonction de grande qualité, il faut que les paramètres de maille des deux matériaux soient proches assurant ainsi une structure cristalline parfaite. Si le désaccord de maille est trop important, l'énergie élastique emmagasinée par le dépôt va conduire à la formation de dislocations ou, comme nous le verrons plus tard, de structures tridimensionnelles à la surface. Nous verrons que l'usage d'alliages ternaires ou quaternaires permet dans la plupart des cas d'obtenir des hétérojonctions adaptées en maille.

Figure I.9 : Energie de bande interdite et paramètre de maille de semiconducteur. Les courbes reliant les différents semiconducteurs représentent les alliages ternaires.

Si les énergies de bandes interdites et les masses effectives des porteurs sont bien connues et accessibles par des expériences d'optique ou de résonance cyclotron, il reste cependant un paramètre crucial à éclaircir. La différence d'énergie de bande interdite ∆Eg des matériaux constituant l'hétérostructure se répartit entre bande de conduction (∆Ec) et bande de

valence (∆Ev). La manière dont se fait cette répartition est d'une importance particulière car

décalage de bande sont basées sur la différence des affinités électroniques qui donne le décalage en bande de conduction [Casey 1978]. D'autre part, des modèles atomiques sont également capables de prédire le décalage avec une précision de quelques dizaines de meV [Vagos 1994].

Figure I.10 : Décalage de bande de conduction (cercle plein) et de valence (cercle vide) pour les 12 semiconducteurs binaires III-V. Le trait plein correspond à l’énergie de bande interdite en centre de zone. Le décalage de bande de conduction (valence) entre deux semiconducteurs distincts, est donné par la différence d’énergie entre les positions des bandes de conduction (valence) dans l’échelle absolue de la figure [Vurgaftman Meyer200].

II.2 Le formalisme de la fonction enveloppe

II.2.1 Hypothèse de départ

Les fonctions d'onde à un électron dans une hétérostructure se décrivent par le formalisme de la fonction enveloppe. Pour cela, nous supposons que le matériau A et le matériau B ont un paramètre de maille identique et qu'ils cristallisent dans la même structure. A partir de ces deux hypothèses, on peut déduire un certain nombre de relations concernant les fonctions d’onde :

i) Dans chaque couche, la fonction d'onde est développée sur la partie périodique des fonctions de Bloch :

ψ( )r fn( )A ( )r u( )n kA, ( )r n

=

∑

Si r correspond au matériau A et,

ψ( )r fn( )( )r u( ), ( )r B n k B n =

∑

si r correspond au matériau B. les fonctions un sont les parties périodiques des fonctions de

Bloch qui varient rapidement à l'échelle de la maille. Les fn sont les fonctions enveloppes

variant lentement à cette échelle.

On peut restreindre le modèle à un nombre de bandes fini n au voisinage d'un point de haute symétrie k0 de la zone de Brillouin (Γ, L, X). Cela revient à dire que les vecteurs kA et kB

sont très proches de ce k0. Toutefois, la fonction enveloppe ne permet pas de décrire les états

conjuguant différents extrema de bandes [Bastard 1992].

ii) La partie périodique des fonctions de Bloch est la même dans les deux couches constituant l'hétérostructure : ψ( )r fn( , )( )r u , ( )r A B n k n =

∑

Il découle de cette équation, une relation de continuité de la fonction d'onde à l'interface z=z0

entre les deux matériaux :

f_n( )A( , )r z_{⊥ 0} = f_n( )B ( , )r z_{⊥ 0} (I.18) Les paramètres structuraux des deux matériaux étant semblables dans le plan, on a une invariance de la structure par translation dans le plan qui suggère la factorisation de la fonction enveloppe en un produit d'une onde plane dans le plan des couches par une fonction lentement variable en z : f r z S e z n( , )A B( , )⊥ = ik r⊥ ⊥ n( , )A B( ) 1 _χ (I.19)

II.2.2 Validités du modèle

Pour simplifier le problème, on aimerait pouvoir simplifier la fonction d’onde et ainsi résoudre l’équation de Schrödinger. A partir des hypothèses précédentes, on peut écrire que :

f r u r dr( ) ( ) f r dr( ) u r( ) dr −∞ +∞ −∞ +∞

∫

∫

∫

avec Ω, volume de la cellule périodique de la fonction périodique u(r). Cette approximation

permet de laisser la partie périodique de la fonction d’onde et de s’intéresser uniquement à la fonction enveloppe.

Cependant, avant d’aller plus loin, il faut noter que l’approximation I.20 n’est vraie que dans la mesure où les fonctions f(r) et u(r) varient à des échelles bien différentes. Prenons un exemple, à une dimension, dans lequel les deux parties de la fonction d’onde sont définies par : f x e x b ( )= − et u x a x a ( )= 1 cos (2 π ) (I.21)

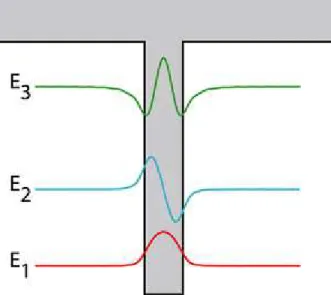
Fonction enveloppe d'une impureté de type donneur

Les deux paramètres a et b correspondent respectivement à la période de la fonction de Bloch et à l'extension spatiale de la fonction d'onde du donneur. Nous posons b=n.a et nous obtenons : A f x u x dx b n = = + + −∞ +∞

∫

∫

∫

On en déduit la relation donnant l’erreur commise par l’approximation.:

A

Aƒ − =1 + n

1

Si b=a, l’erreur est égale à 2,5% Si b=5*a, l’erreur est de 0,1%

Figure I.11 : Représentation de la fonction d’onde (trait fin) et de la fonction enveloppe (trait gras) du cas i). A gauche b=5*a, à droite b=a.

La figure I.11 illustre bien l'approximation réalisée dans le cadre de la fonction enveloppe. L'extensions spatiale de la fonction f(r) étant la plupart du temps très supérieure à la période de la fonction de Bloch, cette approximation est justifiée.

II.2.3 La fonction enveloppe dans l’hétérojonction (modèle de Ben Daniel-Duke) [Ben Daniel 1966]

Dans ce qui suit, nous nous limiterons au modèle à une bande dans le cadre de la masse effective. On résout l'équation de Schrödinger qui a été modifiée de manière à assurer l'hermiticité du Hamiltonien : − ∇ ∇ +       = h2 2 1 r r m* ( )z V z f r( ) ( ) Ef r( ) (I.24)

En reportant l'équation I.19 dans l'équation I.24 on obtient :

− _ _ _ _{ +} +       = ⊥ h2 h2 2 2 1 2 ∂ ∂ ∂ ∂ χ χ z m z z V z k m z z E z * ( ) ( ) * ( ) ( ) ( ) (I.25)

Nous pouvons noter que la fonction χ doit être dérivable une fois en tout point. Cette

restriction impose donc des conditions de raccordement aux interfaces entre les deux matériaux car il faut assurer la continuité de χ(z) et de (1/m*)χ'(z).

Nous pouvons faire plusieurs remarques :

• Lorsque la fonction enveloppe varie à une échelle proche de celle de la fonction

périodique, les variations lentes de la fonction d'onde ne sont pas bien approchée par la fonction enveloppe. On peut alors penser que ce formalisme n’est pas adapté à des objets de dimension atomique. Cependant, lorsque l’extension spatiale de f(r) devient proche du paramètre de maille, la dispersion E(k) n’est plus parabolique pour les k considérés. Ce qui veut dire que la masse effective ne permet plus de décrire la bande. On est alors obligé de prendre le Hamiltonien qui tient compte de la vraie dispersion des bandes :

E k_c( )+V z f r( ) ( ) Ef r( )

[

]

• Si l’épaisseur du puits devient fine, le niveau d’énergie est repoussé vers le haut du puits

et la fonction d’onde s’étend d’autant plus dans la barrière. Alors l’extension spatiale de la fonction enveloppe redevient grande devant la maille et l’on retrouve les résultats précédents. Toutefois, si les deux matériaux formant le puits sont de masses très différentes et présente une forte discontinuité de bande (en admettant que la structure soit réalisable), on peut alors avoir une fonction d’onde extrêmement localisée dans le puits ce qui rend du coup le modèle de masse effective également inapproprié.

II.3 Le puits quantique

En utilisant deux hétérojonctions, il est possible de donner un profil au potentiel pour les porteurs correspondant à un puits quantique. La superposition des matériaux impose

naturellement, aux électrons ou aux trous, un puits le long de l’axe de croissance. Celui-ci va permettre de confiner les porteurs.

Figure I.12 : Profil de potentiel dans un puits quantique de type I : les électrons et les trous sont confinés dans le même matériau. Dans le cas d’un puits quantique de type II, les électrons et les trous sont séparés spatialement.

II.3.1 Calcul des niveaux d’énergies

Par la suite, nous prendrons l’exemple d’un puits simple en bande de conduction. Pour des raisons de commodités, l’origine des énergies sera prise au fond du puits. On pose donc Vc le profil de potentiel en bande de conduction un puits quantique :

V E z L z L c c = > <        ∆ 2 0 2 (I.27)

Nous appellerons le matériau à grande bande interdite : matériau barrière et le matériau à petite bande interdite : matériau puits. Si on considère que dans chaque matériau, la masse effective est constante, l'équation I.25 devient une simple équation de propagation. Les solutions dans le puits sont des combinaisons linéaires d'ondes planes :

χ( )z =Aeikz+Be−ikz (I.28) Dans la barrière, la fonction d’onde est évanescente, les solutions de l’équation de Schrödinger donne des exponentielles décroissantes.

Figure I.13 : Fonctions d'ondes dans la bande de conduction d'un puits quantique

Pour déterminer les énergies solutions du Hamiltonien, nous devons au préalable vérifier la continuité de la fonction d’onde et du courant de probabilité à l’interface :

χ₊( L )=χ₋( L ) 2 2 (I.29) 1 2 1 2 m z L m z L *₊ +( ) *₋ −( )   ∂∂ χ =   ∂ ∂ χ (I.30)

En résolvant ce système, qui devient un système de deux équations à deux inconnues, on trouve les solutions de l'équation.

Toutefois, les sousbandes d'énergies ne peuvent pas être exprimées analytiquement. Il est cependant possible de résoudre graphiquement ou numériquement ces équations pour obtenir l’énergie de confinement des niveaux à partir des k, solutions de ces deux équations.

0 100 200 300 400 500 600 0 50 100 150 200 E nerg ie d e co nfinem ent (m eV ) largeur du puits (Å) E₂ E₁ E₃ E₄ E₅

Figure I.14 : Energies de confinement calculées dans un puits quantique InAs/In52Al48As dans un modèle non-parabolique. Les énergies de liaison supérieures à 660 meV n'ont pas été représentées car elles ne correspondent pas à des états liés [Yu Cardona 95].

II.3.2 Densité d’états à deux dimensions

À l'instar de la relation calculée dans le I.4, nous allons voir l’allure particulière de la densité d’états en fonction de l’énergie. Le calcul est sensiblement le même, mais la courbe d’énergie constante n’est plus une sphère mais un cercle. Les différentes grandeurs vues dans le cas du volume deviennent :

• Densité d’états en fonction de k : ρ

π

( )k = S

4 2 (I.31)

• Élément d’intégration : d k2 =2πk dkxy xy (I.32)

• Dérivée de l’énergie : dE dk k m xy xy = h 2 * (I.32)

En appliquant un calcul semblable à (21) pour le volume, on obtient alors, pour chaque sousbande n :

ρ π n E Sm ( )= * h2 (I.33)

La densité d’états dans une sousbande n est constante et donc indépendante de E. Pour avoir la dispersion dans toute la bande, on fait simplement la somme sur toutes les sousbandes. Ainsi, la densité d’états à un profil en escalier :

ρ ρ π ( )E _n( )E Sm* E E n n n =

∑

∑

(

)

Où Y(E-En) est la fonction de Heavyside qui vaut 0 pour E<En et 1 pour E>En.

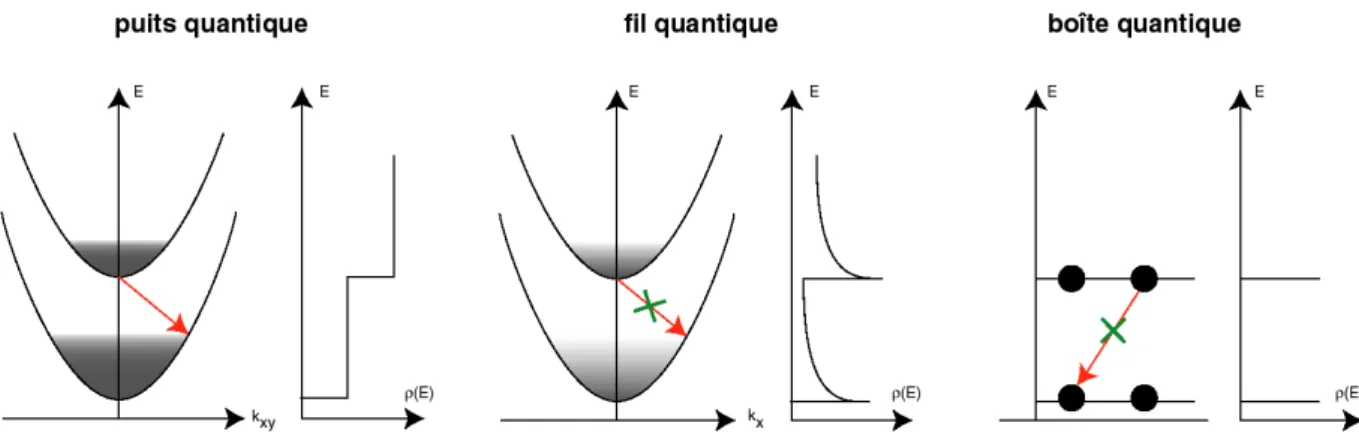
Figure I.15 : Structure énergétique, relation de dispersion dans le plan et densité d’états d’un puits quantique

II.4 Structure électronique des fils et des boîtes quantiques

Dans un premier temps, nous allons voir l'influence du confinement dans le plan sur la structure électronique et des propriétés électroniques comme la relation de dispersion E(k) ou la densité d'états ρ(E). La partie suivante montrera l'importance de ces grandeurs pour

II.4.1 Confiner dans le plan.

Dans les paragraphes précédents, nous avons vu que pour confiner les porteurs dans une direction de l’espace (la direction de croissance), il suffisait d’alterner les couches de semiconducteurs. Pour confiner les porteurs dans le plan des couches, il existe plusieurs méthodes :

• Optique : Par gravure lithographique, on peut découper latéralement un puits quantique.

L’avantage de cette technique étant de permettre la fabrication "sur mesure" par plusieurs procédés. Cependant, sa résolution est limitée par la longueur d'onde du faisceau de gravure [Quate 1997].

• Electrique : Par application d'une tension négative sur des contacts métalliques qui sont

séparés d'une très courte distance. En augmentant le potentiel électrostatique sous les contacts, on crée dans le puis quantique une zone désertée sauf sous l'ouverture entre les contacts. Selon la tension appliquée, la taille latérale peut être diminuée jusqu'au pincement du canal [Rosencher 1998].

Figure I.16 : Deux méthodes de fabrication d'un fil quantique. A droite : définition d'un mesa très fin par lithogravure. A gauche : désertion latérale par application d'un potentiel sur les contacts métalliques.

• Technologique : La croissance du matériau puits sur un substrat recouvert d'un masque

permet de créer artificiellement des motifs sur la surface. Cependant, les étapes technologiques nécessaires sont importantes [Finnie 1995]. Il est également possible de déposer les atomes du matériau puits sur une surface ayant subie au préalable une étape technologique in situ [Ishikawa 2000], [Lüscher 2002].

Les fils en V sont obtenus par dépôt d'une couche de GaAs entre deux couches d'AlAs sur des sillons en forme de V gravés par une attaque chimique sur un substrat de GaAs [Kapon 1989].

Figure I.17 : Section d'un fil quantique GaAs/AlGaAs en forme de V

D'autre part, on peut citer les fils en T. Pour réaliser ces structures, un puits quantique est déposé sur un substrat plan. L'échantillon est ensuite clivé perpendiculairement au plan du premier puits et un deuxième puits est déposé sur le plan de clivage. L'intersection des deux puits correspond alors à une région de plus faible confinement [Goñi 1992].

Figure I.18 : Section d'une structure en T fabriquée sur une face clivée

• Thermodynamique : En jouant sur la désorientation du substrat, il se forme un réseau

de marches atomiques (surfaces vicinales). La croissance est alors réalisée dans des conditions telles que la mobilité des atomes est supérieure à la longueur des marches. L'incorporation des atomes a alors lieu sur le site le plus favorable énergétiquement, en bord de marche [Nakashima 1998].

Il est également possible de confiner dans le plan en déposant un matériau puits sur un substrat, ayant un paramètre de maille légèrement différent. On peut obtenir des fils ou des boîtes auto-assemblées sous l’effet du relâchement de la contrainte élastique [Goldstein 1985].

Nous traiterons de façon plus approfondie cette dernière technique, utilisée pour obtenir les nanostructures étudiées dans les chapitres suivants.

II.4.2 Le fil quantique

Dans son principe, la description du fil quantique n'est pas très différente de celle des boîtes. Le Hamiltonien à résoudre est de la forme :

H_fil =H3D +V x z( , ) (I.35) Si on considère que le fil est orienté le long de l'axe y. On va pouvoir quantifier les niveaux d'énergie dans les deux directions de confinement. La dispersion E(k) sera désormais une parabole dans la seule direction libre pour chaque sousbande n issue du confinement des porteurs. E k E k m n y ( ) * = + h 2 2 2 (I.36)

De la même façon qu'au II.3.2, en introduisant la longueur du fil L, on trouve la densité d'états pour chaque sousbande n :

ρ π n n E L m E E ( ) * ( ) = − h 2 (I.37)

ρn(E) n'est plus une constante de l'énergie, mais elle évolue avec l'inverse de la racine carrée de l'énergie. Ce résultat se traduit par une décroissance rapide du nombre d'états dans une sousbande lorsque l'on s'éloigne du centre de zone. Pour obtenir la densité d'états totale, on fait la somme sur toutes les sousbandes n :

ρ ρ π fil n n n n n E E L m E E E E ( ) ( ) * ( ) = = −

(

)

∑

∑

En admettant que l'on peut séparer les deux variables dans l'expression de l'énergie de confinement :

E_n =E_nx +E_ny (I.39)

On peut distinguer les contributions des énergies de confinement. Sachant que cette énergie est, au premier ordre, inversement proportionnelle au carré de l'épaisseur du puits, si la largeur du fil devient grande devant sa hauteur, on doit retrouver un comportement de type puits quantique en marche d'escalier. Si ces deux dimensions sont proches, il n'est pas possible de différencier les deux contributions.

Figure I.19 : Courbe de dispersion E(ky) le long du fil et densité d'état ρ(E)

II.4.3 La boîte quantique

A l'instar du fil quantique, les propriétés électroniques du semiconducteur sont considérablement altérées par le confinement tridimensionnel des porteurs. Le Hamiltonien se déduit donc de celui du fil en rajoutant un profil de potentiel en y :

H_boîte = H3_D +V x y z( , , ) (I.40)

Les porteurs étant confinés dans les trois directions de l'espace, il n'y a plus de courbe de dispersion parabolique mais une discrétisation des niveaux d'énergies à l'image des niveaux dans un atome. On parle alors d'atome artificiel :

E k( )=E_{n x y z}( , , ) (I.41)

On en déduit immédiatement la densité d'état semblable à celle d'un atome puisque deux porteurs seulement peuvent peupler un niveau discret. ρ(E) est alors un peigne de Dirac.

ρboîte ρn δ

n n

n

E E E E

( )=

∑

∑

(

)

De la même façon que dans le fil, l'énergie de confinement dans une boîte est très dépendante des dimensions. De plus, l'absence de dispersion des énergies implique qu'il n'y a pas de Hamiltonien de masse effective contrairement à ce qui se passe dans les semiconducteurs 3D,

2D ou 1D. Cela implique que le problème est plus compliqué que dans les autres cas et qu'il faudra faire plus d'approximations.

Figure I. 20 : Courbe de dispersion E(k) et densité d'état ρ(E) pour une boîte quantique. Les cercles ouverts, représentent les deux états libres par niveaux issus de la dégénérescence de spin.

II.5 Interactions électron-phonon dans les nanostructures

Dans cette partie, nous allons voir brièvement, l'importance du couplage entre les porteurs confinés et les vibrations du réseau. Dans un premier temps, nous verrons comment les phonons optiques participent, avec une grande efficacité, à la relaxation non-radiative des porteurs. Ensuite, nous discuterons du couplage entre les électrons peuplant la boîte et les phonons.

II.5.1 Relaxation non radiative

Contrairement à la bande interdite comprise entre la bande de valence et la bande de conduction dans les semiconducteurs massifs, il n'existe pas d'énergies interdites entre deux sousbandes dans un puits quantique. De ce fait, il existe un continuum d'états entre le niveau fondamental et le niveau excité ce qui permet d'obtenir des mécanismes de relaxation intersousbandes sans émission de photons. La dispersion d'énergie de chaque sousbande est un paraboloïde et, compte tenu de la dispersion quasi-nulle (quelques meV) des modes de

phonons optiques, il existe un très grand nombre de chemins de relaxation possibles pour les porteurs excités.

Figure I.21 : Relaxation par phonon optique dans un puits quantique. Le transfert d'une sousbande à l'autre s'effectue avec émission d'un phonon LO conservant ainsi l'énergie et l'impulsion.

On s'attend à ce que ces phénomènes de relaxation soient moins efficaces dans les nanostructures à une ou zéro dimension. En effet, on parle d'effet "phonon bottleneck" dans ces structures à fils et boîtes quantiques [Benisty 1991]. Cet effet est surtout dû à la singularité de la densité d'états dans ces structures.

Dans les boîtes quantiques, le confinement des porteurs dans les trois directions forme un spectre d'énergie discret. La séparation en énergie entre les niveaux créés ne s'accorde pas avec l'énergie du phonon optique (sauf cas particulier) ce qui empêche la relaxation intersousbande [Bockelmann 1990]. Dans les fils quantiques, il subsiste une direction de dispersion parabolique dans laquelle il peut y avoir émission/absorption de phonons optiques. Mais la densité d'états très piquée sur le centre de zone ne favorise pas la probabilité d'avoir un porteur chaud sur la sousbande fondamentale.

Il est également possible pour un électron de se coupler à un phonon acoustique. Ce processus est très peu efficace dans les boîtes quantiques. L'électron ne peut se désexciter qu'en impliquant plusieurs phonons acoustiques de basses énergies [Inoshita 1996].

Figure I.22 : Courbe de dispersion et densité d'états représentant le mécanisme de relaxation assisté par des phonons dans les nanostructures 2D (puits), 1D (fil) et OD (boîte).

II.5.2 Polarons

Nous venons de voir l'importance des phonons optiques dans la dynamique des porteurs. Cependant, dans les boîtes quantiques, l'interaction entre ces deux entités va engendrer un couplage important. Des expériences de photo-absorption sous champ magnétique ont montré le couplage fort entre phonons LO et électrons confinés dans des boîtes InAs/GaAs.

Un état purement électronique υ est représenté par υ avec une énergie E_υ. Dans le matériau massif, υ ≡k (vecteur d'onde de l'électron), tandis que dans υ ≡

{

}

{ }

Ces modes optiques du cristal sont dus aux vibrations en opposition de phase des deux atomes qui constituent le motif de chacune des cellules élémentaires du cristal (In et As). La

liaison étant légèrement polaire, elle engendre un dipôle élémentaire oscillant à l'intérieur de chaque cellule unitaire. Une particule chargée (ici l'électron de la boîte) interagit alors avec le champ induit par tous les dipôles associés aux modes longitudinaux optiques de la vibration.

Dans un semiconducteur massif, la fréquence d'oscillation des dipôles dépend du vecteur d'onde q de la vibration optique, mais la dispersion est très faible. En ce qui concerne les états électroniques, on a affaire à un continuum d'états propagatifs très large. Ainsi l'ensemble d'états forme un continuum très large essentiellement à cause du continuum électronique. Dans une boîte quantique, les premiers niveaux électroniques sont discrets et séparés par une distance énergétique bien plus grande que la largeur du continuum de phonons. Les états non perturbés du système {électron + vibration LO} forment alors des continuums étroits attachés à chaque niveau électronique discret. Ceci a des conséquences profondes sur le couplage électron-phonon dans les boîtes quantiques [Bastard 2002].

Figure I.23 : Représentation schématique de la variation avec le champ magnétique des niveaux non perturbés des boîtes. L'épaisseur de certains niveaux vient du couplage entre un niveau électronique discret et un continuum étroit de phonons LO.

Les expériences de magnétospectroscopie de boîtes quantiques InAs/GaAs montrent que ces niveaux sont fortement couplés et que les états propres du système sont des

1S ⊗ 0_ph 1P− ⊗ 0_ph 1P− ⊗ 1_ph 1S ⊗ 1_ph 1S ⊗ 2_ph 1P+ ⊗ 0_ph B E hω_LO

combinaisons linéaires des états non perturbés [Hameau 1999]. Ces états intriqués sont les états polarons, pour lesquels un découplage du type état électronique ⊗ mode de vibration est donc a priori impossible.

III Propriétés optiques des hétérostructures semiconductrices

Les propriétés électroniques engendrées par le confinement quantique des porteurs ont permis de créer de nouveaux dispositifs pour l'optoélectronique, s'appuyant sur la possibilité de créer un matériau avec une structure de bande "sur mesure". L'objectif de cette partie est de décrire, dans le modèle présenté précédemment, les propriétés optiques intersousbandes de ces nanostructures. Le calcul de l'élément de matrice optique dipolaire permettra d'indiquer les règles de sélections de ces transitions et de calculer le coefficient d'absorption.

III.1 Transitions optiques

III.1.1 Interaction rayonnement/matière

Considérons l'interaction d'une onde électromagnétique avec un électron confiné dans un puits quantique. Dans ce qui suit, nous considérerons que l'onde est plane, le vecteur champ électrique εrF de l'onde est constant (onde plane) et que son potentiel vecteur est

r A : r r r r r r r A r t cF i e e i t q r i t q r ( , )= − ε

{

}

La longueur d'onde des transitions optiques étudiées est de l'ordre de quelques microns. Or l'échelle caractéristique des nanostructures utilisées est nanométrique. Le potentiel vecteur est donc lentement variable devant la taille du système. On peut alors négliger le terme dépendant de la position. En présence du potentiel vecteur, le Hamiltonien de l'électron est donné par la relation au premier ordre :

H H e m c p A A p = ₀+ + 2 * ( . . ) r r r r (I.44) Le second terme de l'équation peut être traité en perturbation pour des petites intensités. De plus, on peut prendre

[ ]

m c A p

( , )

* .

r r r

= .

La probabilité d'obtenir une transition optique entre deux états (i) et (f) est donnée par la règle d'or de Fermi : ƒ _{( )} P_i→f = 2π f W i 2δ E_f − −E_i ω h h (I.45) Avec f W i ieF m f p i = 2 *ω ε. r r (I.46) On extrait donc l'élément de matrice optique dipolaire f εr r.p i qui va donner naissance aux règles de sélection sur la polarisation de l'onde.

III.1.2 Elément de matrice dipolaire

Nous allons maintenant développer cet élément de matrice dans le cadre de la fonction enveloppe. Nous rappelons que la fonction d'onde d'un électron dans un état i d'une bande n

s'écrit : ψ_{i ν}

i i u f

= . De manière générale, on peut écrire l'élément de matrice entre deux

sousbandes n'appartenant pas forcément à la même bande : ψ ε ψ_f r r.p _i . Après développement, on obtient la somme de deux termes :

u_νf εr r.p u_νi f f_{f i} + u_νf u_νi f_f εr r.p f_i (I.47)

Les fonctions de Bloch forment une base orthogonale donc u_νf u_νi =δ_{m n,} . L'équation précédente peut être réécrite comme une somme de deux intégrales :

r r r r r r

ε.pif =ε. u_νf p u_νi

∫

∫

3 3

Ω Ω

Les deux termes de l'équation précédente font apparaître les deux types de transitions optiques possibles dans l'hétérostructures :

* Les transitions interbandes, définies uniquement par le premier terme car la bande

initiale et la bande finale ne sont pas les mêmes : δ_{m n,} =0. Les règles de sélection sont alors imposées par le recouvrement des fonctions enveloppes : f f_{f i} et par le dipôle atomique. La contrainte sur les fonctions enveloppes explique pourquoi les transitions optiques En-HHm

ou En-LHm les plus observées, dans les puits de type I, sont celles qui vérifient n=m.

Toutefois, il est possible d'obtenir les transitions E1-HH3 [Miller 1984]. En fait, le

recouvrement de deux fonctions d'onde est nul dans le cas ou n et m sont de parité différente. Cependant, cette restriction peut être partiellement levée dans un puits fortement asymétrique (effet Stark) ou encore dans le cas d'un puits de type II dans lequel électrons et trous sont séparés spatialement.

* Les transitions intrabandes, définies par le deuxième. Contrairement aux transitions

interbandes, ces transitions ne mettent en jeu qu'un seul type de porteur : les électrons ou les trous. On les appelle transitions unipolaires. Dans un puits quantique, on peut décomposer le terme intrabande sous la forme d'une composante parallèle à la direction de croissance et d'une composante perpendiculaire :

f_f εr r.p f_i = eik f r⊥ . χ ε_{f ⊥ ⊥}p +ε_{z z}p eik i r⊥. χ_i (I.49) En posant p i r = −h ∂ ∂ , on obtient en développant : f_f εr r.p f_i =hε_{⊥ ⊥}k δ_{k i k f i f,} δ _, +ε δ_{z k i k f,} χ_f p_z χ_i ⊥ ⊥ ⊥ ⊥ (I.50)

De nouveau, chaque terme correspond à un type de transition dans la bande :

• En regardant le premier terme de plus près, on peut voir que le deuxième symbole de Kronecker montre que la transition a lieu dans la même sousbande : c'est le terme

intrasousbande. Ce terme traduit, en quelque sorte, un terme d'absorption porteur libre à deux dimensions. Cependant, en tenant compte de l'allure de la courbe de dispersion, il ne peut pas y avoir, en principe, de transition optique à k constant dans une sousbande. En effet, il va falloir ajouter une autre particule comme un phonon ou une impureté pour conserver l'énergie et surtout apporter le moment nécessaire pour permettre la transition [Spector 1983].

• Le deuxième terme traduit la transition verticale entre deux sousbandes différentes : il s'agit du terme intersousbande. La polarisation de l'onde électromagnétique est alors orientée le long de l'axe de croissance et implique donc une propagation de l'onde dans le plan des couches. De plus, l'opérateur pz étant impair, l'élément de matrice χ_f p_z χ_i sera non nul si

les deux états impliqués dans la transition sont de parité opposée.

Polarisation

ε

ε

ε

Propagation parallèle à z interdite interdite impossible Propagation parallèle à y interdite impossible permise Propagation parallèle à x impossible interdite permise

Règles de sélection pour les transitions intersousbandes dans un puits quantique

À l'instar des transitions interbandes, lorsque le puits présente une forte asymétrie, l'élément de matrice devient non nul et toutes les transitions intersousbandes deviennent possibles.

Dans le cas d'un fil ou d'une boîte quantique, le confinement latéral des porteurs donne naissance à des niveaux d'énergies. Il est alors possible d'effectuer des transitions entre ces niveaux. Le dipôle de ces transitions n'est plus perpendiculaire mais parallèle au plan. Les règles de sélection vues auparavant sont alors modifiées. Nous verrons plus loin, la portée de cette propriété des nanostructures 1D et 0D sur l'absorption dans le moyen infrarouge.

III.2 Le coefficient d'absorption

Le calcul du coefficient d'absorption pour une transition intersousbande dans un puits quantique vient illustrer le calcul de l'élément de matrice dipolaire. Pour ce calcul, nous nous placerons dans un modèle à un électron.

Le coefficient d'absorption d'une transition dans un puits quantique, est la perte d'énergie par unité de temps P(ω) et de volume divisée par l'intensité incidente :

α ω ω ε ρ ρ ( ) ( ) , , = 1

∑

∑

Avec Ω : le volume du matériau d'indice n, ε0 : la constante diélectrique du vide, c : la vitesse de la lumière et F : l'amplitude du champ électrique de l'onde incidente de pulsation ω. La

sommation porte sur toutes les valeurs du moment des électrons dans le plan des couches pour les niveaux i (ki_ρ) et f (k_ρf). Le moment porté par le photon ne distingue pas ki_ρ de k_ρf donc il

est très acceptable de ne sommer que sur k_ρ.

On peut calculer cette puissance P(ω) à partir de la probabilité d'avoir l'onde absorbée

par le matériau. Cette probabilité s'obtient à partir de l'élément de matrice dipolaire introduit dans la règle d'or de Fermi comme perturbation dépendante du temps W :

ƒ ( ) ( ) P_i→f ω = 2π f W i 2δ E_f − −E_i ω h h (I.52) avec : W ieF m p = 2 ₀ω ε r r . (I.53)

Nous pouvons développer l'équation (I.52) et ne laisser dans la valeur absolue que le terme

ε.p qui nous donne le dipôle de la transition i→f :

ƒ ( ) . ( ) P eF m f p i E E i→f = f i     − − ω π ω ε δ ω 2 2 ₀ 2 2 h r r h (I.54)

Considérons que la polarisation de l'onde fait un angle θ avec la direction de croissance (et de quantification), nous pouvons alors écrire εr r.p=p_zcosθ. En introduisant le dipôle µ_if de la transition i→f : f p i m E E i e i f if r r h ε. = * ( − ) cosθ µ (I.55) on obtient : ƒ ( ) cos ( ) P_i→f ω = π F E

(

)

Cependant, cette équation ne tient pas compte des populations dans les deux états pris en compte. Il faut donc pondérer (71) par la probabilité d'avoir un porteur dans l'état i et une place libre dans l'état f :

P_i→f =2Pƒ_{i→f FDi}f

( )

[

( )

]

Où fFD(E) est la fonction de Fermi-Dirac. Le facteur 2 vient de la dégénérescence de spin.

Notons qu'il est également possible d'obtenir un photon à partir de la transition stimulée f→i. Nous en tiendrons compte dans le calcul de la puissance totale absorbée :

P_i→f −P_f→i =2 ƒP_i→f

[

( )

( )

]