Ecoulement dans les talus intertidaux

HAL Id: hal-01006763

https://hal.archives-ouvertes.fr/hal-01006763

Submitted on 8 Apr 2017

HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

Public Domain

Ecoulement dans les talus intertidaux

Aïssa Rezzoug, Alain Alexis, Pierre Thomas

To cite this version:

Aïssa Rezzoug, Alain Alexis, Pierre Thomas. Ecoulement dans les talus intertidaux. Journal de Recherche Océanographique., 1994, 19 (3-4), pp.125-136. �hal-01006763�

ECOULEMENT DANS LES TALUS INTERTIDAUX

Aïssa REZZOUG, Alain ALEXIS, Pierre THOMAS,

Laboratoire de Génie Civil E.C.N. BP420, I.U.T.

44606 ST-NAZAIRE Cedex

FLOW IN INTERTIDAL SLOPES

Key-words: tide, slope, cyclic flow in JX>rous medium, analytic. Abstract

Estuarian or coast al areas general/y undergo the influence of tide, which generales cyclic stresses disturbing the stability of banks (slopes,flats. beaches) and harbour buildings (dykes, wharfs). Tide induces also flow phenomenons through soUs, which are pervious media, disrurbed by the flow velocities. Srability of banks and structures can be also highly modified and phenomenons of slopefai-lures or slope toe scouring can appear. During a rida/ cycle. bank alternative/y fills and emplies. Thefree surface of flow, water-air interface in the soi/, undergoes the atmospheric pressure and oscillates with the tide period.

We propose a modelisation of this phenomenon, using main/y soi/ permeability and tide characteristics.The resolution is difficult, be cau-se of the flow equation non-linearity, and the shape of the boundary condition on the interface ground-water.

We propose he re an original analytical method of resolution which gives basis data about the free surface flow in sloping banks indu-ced by oscillation of the tide. This method is based on ajustified linearization, and on an iterative process of differentiai equations inte-gration. According to tidal cycle the final solution shows thefree surface flow oscillation in the po rous media ofintertidal slopes. This research can be appliedfor determining the stabiliry of natural or harbour si opes in intertidal areas.

Mots-clés : marée, talus, écoulement cyclique dans un milieu poreux, analytique.

INTRODUCTION

Dans les zones littorales soumises à de fortes marées, il est appa-ru de nombreuses perturbations ou appa-ruines d'ouvrages sous l'ac-tion de contraintes océaniques périodiques.

Dans Je but d'estimer 1' impact des actions hydrauliques cycliques dues à la marée sur le comJX)rtement des talus estuariens et sur les ouvrages portuaires en général, tels que les quais et les digues en terre, nous cherchons à identifier le phénomène de 1 'écoule-ment à caractère dynamique de ces types d'ouvrages; car le pro-blème s'est JX)Sé concrètement sur les côtes à forte marée. Une meîlleure connaissance des problèmes hydrauliques des écoulement internes tels que :

-le niveau d'eau dans l'ouvrage, ou à quelque distance, à chaque moment du marnage ;

-les limites de la zone de perturbation par les fluctuations du niveau de la nappe dues à la marée ;

-les vitesses résultantes du débit, de J'écoulement, entrant et sortant par l'effet de la marée;

permet de mieux appréhender l'étude des problèmes de génie civil tels que :

-l'effet de la surpression hydrostatique dans le massif (ou remblais) de l'ouvrage. Cette surpression est due à la forte dénivellation du niveau d'eau à la basse mer. Elle introduit des poussées hydrostatiques de la nappe sur les murs des quais;

- l'effet de la perturbation sur les caractéristiques physiques du sol en place ;

-l'effet dynamique de changement de vitesse. A la basse mer la vitesse de 1 'écoulement sortant est très importante. Localement au pied du talus le matériaux risque d'être entraîné (affouille-ment et érosion). Globale(affouille-ment, il y a naissance d'une force de

poussée globale dans le sens de 1 'écoulement en raison des varia-tions instantanées de vitesse. Un talus de pente ou un quai ver-tical risque ainsi une rupture par glissement.

Les problèmes d'écoulements transitoires dus à la marée dans les talus portuaires, sont abordés par une approche mathéma-tique relative à l'étude d'oscillations des nappes libres dans un milieu poreux. Celle approche est fondée sur la physique des transferts d'eau depuis la mer jusqu'à la nappe. Sa théorie repose sur une hypothèse restrictive imJX)nante qui revient à réduire l'écoulement à la seule zone saturée limitée à sa surface supérieure par la sur-face libre de la nappe.

Cette idéalisation s'appuie principalement sur 1 'hypothèse de Dupuit et la loi de Darcy dans un milieu poreux supposé indé-formable. Pratiquement toutes les solutions publiées en hydro-dynamique des nappes à surface libre reposent sur celle hypo-thèse, considérée comme une approche traditionnelle (Vauclin 1975). Boussinesq 1904, a proposé une linéarisation simple dont la solution analytique est publiée par plusieurs auteurs (Rat et Vau trin 1973 ; Razack et al. 1980 : Marino 1973). Nous avons déjà démontré pour un cas du massif vertical (Rezzoug et Alexis 1992), que cette linéarisation ne donne pas une meilleure solution analytique JX>Ur ce type de problème.

Nous traitons dans cet anicle l'approche traditionnelle, unidi-mensionnelle de 1 'écoulement transitoire à travers les talus d'es-tran soumis à la marée et nous proposons une méthode analy-tique qui nous semble plus simple.

NOTATIONS

a (t) la fonction de translation horizontale de DXz par rapJX)rt à Oxz.

A amplitude de la marée

c consLante intermédiaire (c=k12n) C consLante intermédiaire (C=2cHm) C' _{,C" .C 1.}

c

₂ consLantes d'intégration. D consl.ante intermédiaire (D=A(J)!P)

G fonction intermédiaire par changement de variable G (X,I )=h2 (X,l)

h la charge hydraulique

hauteur moyenne de la marée mesurée à partir du substratum

le nombre imaginaire pur (P=-1)

j l'ordre d'itération

k perméabilité du sol du talus

K ~·" matrice des coefficients complexes de Fourier d'ordre m,n à l'itération")" du processus itératif

9tK m,n la partie réelle et de K "'·"

:!>Km,n la partie imaginaire de K,.,,

Ln coefficients complexes de Fourier dans le cas du m.n

n Ne

Oxz

développement de la condition au limite. entiers relatifs variant de -oo à +oo

porosité efficace du sol

niveau de la nappe dans le talus du coté terre, (niveau d'équilibre)

surélévation du niveau d'équilibre (Ne-Hm) repère absolu fixe lié à la ba<;e du substratum pente du talus d'angle (}, (P=tan9) pente limite (minimale)

coefficient complexe multiplicateur période de la marée

z cote d'un point mesurée à partir du substratum

z=h(x,t) équation de la hauteur de la surface libre au point d'abscisse x et à l'insLant t

(ù

nxz

sa pulsation (ro=2TCIT) repère relatif mobile ({Jm,n argument de K m,n

À,.,,. racine de in(JJ/C dont la partie réelle est positive ô symbole de Kroneker ( + 1 ou -1)

MODELISATION DU PROBLEME PHYSIQUE

1. Surface libre et transfert dans un massif

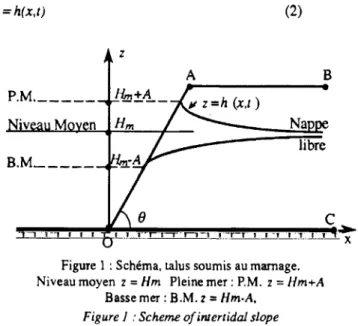
La figure ci-dessous schématise un talus, ou un massif (selon la grandeur de la pente), constitué d'un matériaux poreux, per-méable, homogène et indéformable. Il repose sur une couche imperméable et est sollicité par des oscillations du niveau d'eau dues à la marée sur sa pente OA. Nous appellerons le domaine [OABC] massif vertical si ()

=

TCI2 et talus (de pente P= tanO) si 0< 9<7rl2. Cette excitation du niveau d'eau hors le domaine [OABC] oscille donc selon une fonction sinusoïdale directe de période T et de pulsation

w,

autour d'un niveau moyen Il,. consLant.

z =h(x,t)

=

H,.+ A sinCùl avec:w

=

2TCIJ (1) H,. est la hauteur moyenne de la marée et A son amplitude.

Nous cherchons donc, l'équation de la ligne oscillatoire de la surface libre dans le domaine [OABC]

z

=

h(x,l) (2) z B B.M ____ _

c

L.L.X.~:r .. r-r· ·11--l-•.:::.~.r-r 1 _!...: .. I~.t~::L. ... .L_t.:__ ~ Figure 1 : Schéma, talus soumis au marnage.

Niveau moyen z =Hm Pleine mer: P. M. z = Jim+A Basse mer: B.M. z =Hm-A,

Figure 1 : Scheme ofinJertidal slope

où x est la disLance au rivage, comptée positive du côté terre et négative du côté mer. Sa courbe fluctue sous 1' influence du mou-vement de la marée sur la pente OA.

2. Equation de Dupuit en transitoire

Polubarinova 1962, a démontré que 1 'équation de la surface libre dans le matériau à l'intérieur du domaine [OABC] est solution de l'équation dite de "Dupuit" en transitoire pour un écoulement unidimensionnel

(3) c

=

kl2n : désigne une constante dépendante des caractéristiques hydrauliques du matériau constin.uuule talus (ou le massif), carac-térisé par sa perméabilité k et sa la porosité n.

3. Conditions aux limites et sur le temps

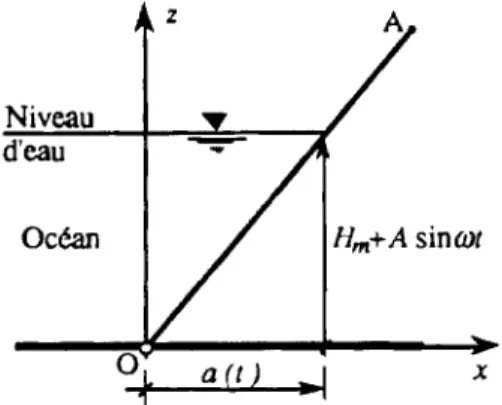
-L'agitation de la marée sur la penteOA, Fig. 2, c'est à dire pour toute P

*

0, l'abscisse du niveau d'eau et sa hauteur sur la fron-tière OA sont respectivement décrites par:

p

=

tan () = If m + A sin

wt

a(t)

z

=

h (x= a (t ), t) =Il,.+ A sin Cùl

(4) (5)

- le talus est illimité du côté BC, fig.l, alors que le niveau de la surface libre ici tend vers un niveau d'équilibre constant, que nous désignerons par Ne, inconnu. En passage à la limite, on peut écrire

h(x ~ oo,t) =Ne ₍₆₎

-la surface libre est périodique de période T, d'où une condi-tion sur le temps :

z

Niveau d'eau

Océan

a(t) .. 1 x Figure 2: Modélisation de la condition sur la pente

Figure 2: Mode ling of the slope boundary condition

RÉSOLUTION

1. Transformations analytiques

Il s'agit de résoudre analytiquement le système composé des équations (3), (5), (6) et (7). La non linéarité de l'équation (3) pose des difficultés de résolutions analytiques, sauf dans le cas spé-cifique de linéarisation sous certaines hypol.hèscs physiques sim-plificatrices. Pour permettre quelques développements analy-tiques, nous sommes amenés à opérer une linéarisation sous réserve d'une hypol.hèse : les variations spatiales, de la côte de la surface libre, oscillent autour d'une hauteur moyenne Hm, dont l'amplitude des oscillations du niveau piézométriquc est petit devant l'épaisseur de la nappe. L'équation (3) peut devenir alors:

dh2(x,t) _ C d2h2(x,t)

=

0

dl dx2 _{avec C}

₌

_{2cllm (8)}

Cette linéarisation en h2 a une précision et un domaine d' appli-cabilité meilleurs que la linéarisation classique en h, notamment pour les forts rabattements (Josseaumc 1970). Elle permet éga-lement de retrouver la formule de Dupuit pour les nappes libres en régime permanenl

De même, la dépendance des variables dans la condition (5) ne fait que compliquer le problème. Pour revenir à une condition plus simple aux variables indépendantes, nous posons le changement de variables suivant:

X= x- a (t )

G (X ,t ) =h2 (x,t ) (9)

Cc changement signifie la recherche d'une fonction comme z=G (X,t ) dans le repère relatif (.QXz ). Celle-ci est décrite dans le repère absolu (Oxz) par z = h2 (x,t ). Ici a (t) désigne la fonction du mouvement de translation sinusoïdal, horizontale, du repère relatif dans le repère absolu fixe (Fig.3.).

J z

a ( t)

0

x

x

Figure 3 : Repère relatif par rapport au repère absolu

Figure 3: Relative reference and absolwe reference

Compte tenu de (9), (8) change sa forme pour devenir :

aG(X ,1) _ C d2G(X,t) _ D dG(X,t)

dl d2

x -

cos wt dX

(10) avec D=A(JiP. La condition (5) devient aussi

G(X=O.t) = (H,+Asinwt)2 (11)

Donc finalement le problème se ramène au système (12) dG(X,t) -C d2G(X,t) _ D dG(X,t) j J ₂ - COSW/ at oX dX G(X = 0,1) =(Hm+ A sin wt)2 (CLI) G(X ~ oo,t) = Ne2 (CL2) G(X,t+T)=G(X,t) (C3) ₍₁₂₎

La résolution de cc système se simplifie beaucoup, si nous adop-tons les notions complexes de Fresnel ct le développement en termes de série de Fourier. Ce mode de calcul est employé cnte autre par les électriciens pour l'étude des courants alternatifs. La condition (11) peul donc être écrite en série finie de termes com-plexes de coefficients Ln : +2 G(X = 0,1) =(Hm+ A sin W/)2 =

L

L,.ei"".r 11=-2 (13) soit 2. Résolution générale 2.1. Processus itératif

Nous proposons ici une mél.hode analytique, qui s'appuie sur un processus itératif de résolution d'équations différentielles. Elle permet par un développement en série de Fourier aux termes complexes, d'approcher de mieux en mieux à la solution. A un stade "j" donné du processus itératif. nous supposons connaître l'expression de Gj.₁(X,t) que nous devons injecter dans le second membre de l'équation:

ac.

d2_G

ac

1 ::..:::..J.._ C~= Dcoswt_J::_

dt dX

ax

(14)

Nous généralisons le processus et nous supposons que Gj.₁ (X ,t ) est la fonction de donnée, connue (d'entrée). G/X ,t) est la fonc-tion solufonc-tion (sonie), dans le circuit du processus itératif d'ordre La solution GiX,t) compte tenu des conditions (CLl, CL2, C3) devra être aussi réinjectée dans le second membre de (14), ct ain-si de suite.

L'équation de la premier itération "j=l" sera alors

dG d2G dG

- -1- C - -1 = Dcosmt--0

On initialise Je processus itératif par : t1Go =0

iJX (16)

puisque H'" est constant ( 14) reprend donc une forme plus simple,

acl -ca

2

c

1

=O

at

ax

2

(17)

Cette équation avec les conditions (CL 1, CL2, C3), décrit le cas du massif venical ( 8=n:!2 => D:::() ). Nous retrouvons ici une

for-me différentielle appelée "équation de la chaleur". Elle peut se résoudre simplement pour obtenir une solution réelle dont 1 'écri-ture en termes complexes est :

avec

"-n2

= in(J){C, met n entiers relatifs négatifs ou positifs, (Rezzoug et Alexis 1992).

En deuxième itération nous injectons à nouveau G ₁ dans le second membre de (14) puis nous cherchons la solution de l'équation complète, et ainsi de suite. Le processus itératif continue jusqu'à obtention d'une solution suffisamment proche de la fonction injectée (comme donnée).

Théoriquement J'existence d'une solution comme (18) dans le cas particulier de pente infinie confirme 1 'existence de la solution générale du système (12). Celte solution générale correspondra à une forme étendue de l'équation (18), pouvant satisfaire les conditions aux limites et la condition de périodicité sur le temps.

La solution que nous cherchons existe et peut être écrite sous une forme plus générale, en sommes de termes complexes en série de Fourier:

G;(X,t)

=

L,k~ (X) einwt

n (19)

avec

_'"

m, n sont des entiers relatifs variant de -oo à +oo, et K ~-" est un élément de la matrice des constantes complexes d'intégration relative à 1' itération "j".

D'une manière générale, connaissant le second membre de (14):

ac

.

₁ Dcoswt--1_--

=

a

x

_ D).,.. """'<KJ-1 KJ-1 ) -.l..,X ùwJI 2 ~ ~ '"·"-! + '"·"+t e e Il ' " (20) nous cherchons alors une solution réelle dont l'écriture complexe est une forme plus générale (19). Remplaçons (20) et (19) dans J'équation (14) en simplifiant ei"QN, nous obtenons l'équation différentielle suivante :

(21) 2.2. Résolution de l'équation différentielle

L'équation différentielle (21) est du second ordre, linéaire, non homogène et aux coefficients constants. Selon les valeurs des paramètres m et n, les solutions générales et particulières sont différentes.

·cas n = 0,

n =0 est un cas particulier, l'équation (21) change de forme et devient:

(22) Intégrons (22) directement pour tout m entier relatif. C' et C" sont des constantes d'intégration,

k (X)="" _E_(KJ-t + KJ-t )e-.l..,X + C X+ C"

0 ~ _2C). m,-1 m,l

'""0 m

(23) Solution ~énérale de 1 'é{Juatjon différentielle homo~ène ·cas n ;t 0

Sans second membre, l'équation (21) a une solution générale:

(24) avec C1 et C2 constantes d'intégration.

Solution oaniculière de 1 'équation non homogène Nous distinguons deux cas :

-casm

=

n

Dans ce cas nous avons en particulier:

K0 •. 1+K0,1

=

L_1+L1

=

iAH,..+(-iAH,..)

=

0

(25)

Par récurrence nous montrons à l'aide de

(26)

que: Kn,n-1 + Kn,n+l

=

0 (27)

Donc dans le cas m =n le second membre de (21) est toujours nul. Cette équation devient alors homogène.

·cas où m ;t n

*Sim= 0, pour tout n entier relatif non nul, (21) est homogène car

..'.c=O.

*Sim ;t 0, la solution particulière par identification des facteurs

La solution complète du système ( 12) est la somme des solutions partielles (23), (24) et (28), reponée dans (19).

2.3. Solution du système (13)

Compte tenu des conditions aux limites (CLl), (CL2) et (12), la solution de l'équation (14) pour un ordre d'itération "j" don-né, peut s'écrire en fonction des coefficients de la fonction (19), de donnée d'ordre "j-1".

G/X.t)

=

I[<L"-

I',R"'·"(K~~~-I

+

K~~~+l

))e-;,.x

"

"'

(29) avec:

R - D)."'

"'·" - 2C(Â~ - ;.; ) _{V m;t:n (30)}

Nous pouvons expliciter encore le facteur R"'·"' il devient:

. A

~!miro

R"'·" = (z-

8) 2P(n-

m) 2C

(31) où 8=1 pour m ~ et 8=-1 pour m <0 V m ;t:n,

car selon la condition (CL2), la partie réelle de Â,. doit être posi-tive.

Si nous réécrivons la fonction (29) sous la forme (19), les for-mules de pao;sage de Gi·l (X ,t) fonction de donnée à Gi(X,t) fonc-tion résultat, sont :

(32) Ki - L -"" R (Ki-l Ki-l ) "·" - " .(... "'•" m,11-l + M,fl+l

"'

ou encore:

K~,,.

=

L,.-

I',K~,It(M

.. It)

"'

(33)

Retour aux variables réelles :

L'écriture de la solution en série de termes complexes est choi-sie de manière à simplifier la recherche et à éviter les calculs

tri-gonométriques fastidieux.

La

solution physique existe, donc la solu-tion mathématique doit être réelle. Nous pouvons l'exprimer de la façon suivante:

1

-G(X,t)

=

Ï(G(X,t)+ G(X,t))

(34) la barre désigne la fonction conjuguée. Nous noterons par la

sui-te les sui-termes complexes par leur partie réelle et imaginaire:

K

=

9\ K + i ::3 K, et  = 9\  + i ::3 Â,

Si nous écrivons G sous la forme :

G( X /)="" ""(9\K + ::.:JK )e-91)..,Xei(ll(a-!:J)..X) ' .(... .(... "'·" l "'·"

"

"'

(35)

sa conjuguée aura la forme:

"

"'

(36)

finalement son écriture réelle dans le repère relatif est:

"

"'

avec: IK,.,,.I

=

~(9\K,.,,.)2

+ (::3K,..,,.)2

;JK,..,.

tan

cp,.._,.=

9tK ·

"'·"

9\).

=~!miro

"' 2C ;j).m

=

9\)."' si m 2:0

::3).,.

= -9\Â,. sim <0 (37)

Nous rappelons que x est l'abscisse réelle dans le repère absolu correspondant à la pénétration horizontale (fig.!) dans le mas-sif; d'après (4) et (9),

Hm+Asinrot ()

X=x-

=x-at

p ₍₃₈₎

La cote physique de la surface libre de l'eau dans le talus, est définie par ( 1) qui peut être exprimée aussi explicitement par son carré défini en (9) et (37):

fi " '

cos(nrot-::3 Â,..

(x- a(t ))

+ (/),.,") (39) Tous les paramètres sont déjà définis auparavant, Km.n est une matrice carrée de centre (m,n )= (0,0). Nous choisissons les valeurs entières extrêmes positives et négatives demet den, qui sont fonction de l'ordre d'itération "j".

max(m )

=

max(n )

=

j + 1

min(m) =min (n)

=

-(j +1) (40)

(j =5), par exemple,la matrice finale Km.n utilisée pour le calcul de la fonction (39) doit être définie par m et n balayant l'inter-valle des entiers relatifs

r

-6, +6].

3. Applications 3.1. Calcul manuel

En pratique les calculs se font sur un tableau de valeurs K "'·"

centré en n=O et m=O, dont m est le nombre de lignes, et n le

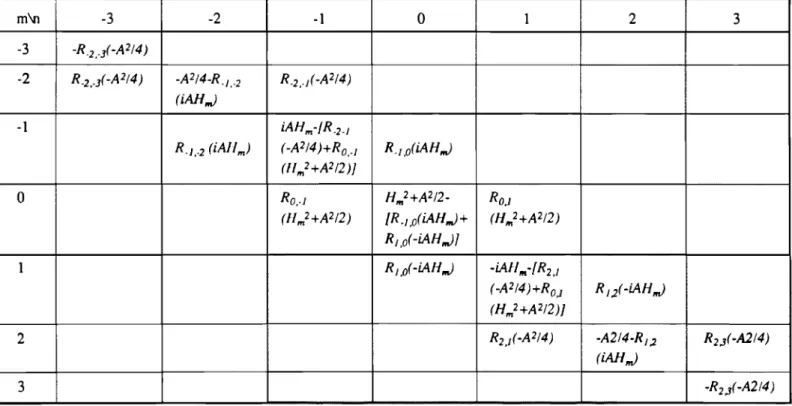
nombre de colonnes, (Tableau 1 et II). A l'a.idede la formule (32) on peut remplir une case autre que la diagonale du tableau. Par exemple pour remplir une case dans une ligne, on somme les deux cases voisines de la même ligne en multipliant Je résultat Tableau 1. Calcul de KI"'·"

m\n -2 -1 -2 -A2f4 -1 iAii, ... 0 1 2

Tableau II. Calcul de

1(1,_,.

m\n -3 -2 -1

-3 -R_₂_.₃(-A 214)

-2 _{R.2,.j(-A214)} -A2!4-R .1 .. 2 R.2 .. j(-A2f4)

(iAH,)

-1 iAH,.-/R._{2_1}

R._{1,.2 (iAll,)} ( -A2f4 )+Ro.-J

(11,2+A2f2)] 0 Ro,-J (lfw,2+A2/2) 1 2 3 Tableau III.

par le facteur R,,, décrit en (31 ). Sur la diagonale du tableau

on fait appel à la formule (33) qui utilise la somme des éléments des colonnes déjà calculées.

Tableau 1 et Tableau II montrent le mécanisme de calcul respec-tivement pour la première et la deuxième itération.

A une itération "j" donnée, l'expression littérale de chaque case

prend la Conne d'un polynôme en (

2

~ ~

2":: ) avec des

coeffi-cienLo; qui varient peu, de signes quelconques, et décroissent en fonction de l'augmentation du nombre d'itérations "j".

0 1 2 H,2+A2f2 -iAH.,. -A214 0 1 2 3 R.₁,o(iAH,) H,2+A2f2- _Ro.J [R .1 ,o(iAH,)+ (JI,2+A212) R _{1 ,0(} -iAII ,)/ R 1 ,0( -iAii,) -iAII.,.-[R2,1 (-A2f4)+Ro,J R ₁ ,2( -iAH,) (H,,,2+A2f2)]

R2,j(-A2f4) -A214-R1;;. R2.3(-A214)

(iAH,)

-R₂,J(-A214)

Type de sol Porositén Perméabilité k (m/s) Rappon kin (m/s)

Sables _{0,30 0,45} 1 w-2 5 w-5 3,33

w-

2 1,11

w-4

Limon-sableux _{0,35 0,45} 5w-5 3 w-6 _{t.43 104} 0,6610"5

Limons _{0,35 0,50} 1 w-5 5

w-

7 2,86 w-5 t,oo w-6

D'après Je critère de convergence de d'Alembert pour les séries aw: termes réels, ce processus itératif de calcul des coefficients

K ,.,,. ne converge que si :

(41)

d'où finalement une condition sur la pente P, pour une convergence assurée des calculs, en fonction des paramètres A,

w.

li,.. n, k. car:

C=kll,.ln, (Rezzoug 1990).

(42)

Cette condition n'est pas toujours nécessaire mais elle est suffi-sante. PL est la pente limite.

10.00 9.00 8.00 7.00 Cl) 6.00

...

·-

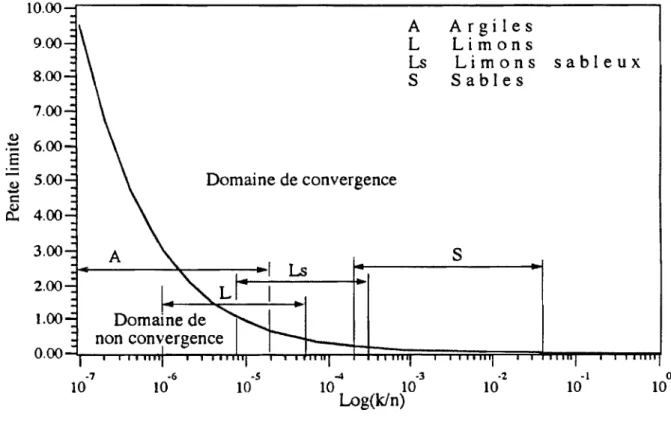
E

gramme délimité par une courbe qui représente la variation de la pente limite (minimale) en fonction du rapport (k.Jn) caracté-risant le type de sol. Le tableau III représente une étendue des caractéristiques hydrauliques des sols, (Alexis 1987).

Nous pouvons alors tracer la pente limite en fonction de Log( kin) de manière à faire apparaître les différents types de sol (fig. 4). La validité et la commodité de cette méthode est remar-quable pour les graviers et les sables. Dans ces types de sols, cet-te méthode ne cesse pas d'être précise et complècet-te pour la recherche d'allures de surface libre de la nappe, lors des diffé-rents cycles du marnage, et pour n'importe quelle pente non pra

-tiquement nulle. Alors que les problèmes de stabilité des calculs des coefficients K,.,,. se posent pour les sols fins. La convergen

-ce ne peut être atteinte qu'avec une pente égale au moins 1 dans le cas de l'argile.

3.2. Calcul numérique

Le calcul manuel des coefficients Ki"'·"' dans des expressions analytiques, est long et fastidieux. Un programme de calcul, ité-ratif simple, sur tableaux, est nécessaire. Pour procéder à ce

cal-A

Argiles

L

Limons

Ls

Limons sableux

s

Sables

-

....

Cl) 5.00

Dom ai ne de convergence

c Cl) 4.00 0.. 3.00

s

Ls

2.00 1.00 0.00 -7 -6 -5 -4 -3 -2 -1 0 10 10 10 10 10 10 10 10

Log(k/n)

Figure 4: PL pente limite du domaine de convergence en fonction du rapport (kin) pour A= 2 m; Hm= 8 m.

Figure 4: Limit slope of convergence field (PL) versus the ralio (kin) for A= 2 m; Hm= 8 m.

A.N.

Pour A =2m et li,. =6m : P >0,47 Pour A =2m etH,. =8m : P >0,41 Pour A =4m et H,. =8m : P >0,85

Ces valeurs sont prises pour le cas d'un sol de référence de per-méabilité k

=

0,0792m!h et de porosité n

=

0,4.

La pulsation de la marée est

w

=

!!.

rd/Il.

6

Nous avons explicité le domaine de convergence par un

dia-cul, chaque tableau est déduit du tableau précédant par des opé-rations simples. Nous définissons une précision suffisante de l'ordre du millimètre à l'échelle des talus naturels. Cette préci-sion ne demande que quelques itérations, citons par exemple, un massif de limon sableux de pente unité ne demande que 6 itéra-tions sur les coefficients K,.,,. pour qu'une précision suffisante soit atteinte.

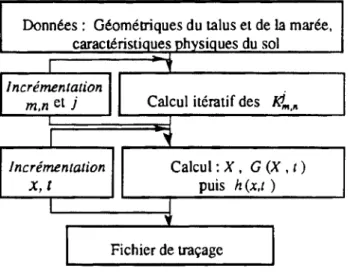
La figure 5 donne l'algorithme généralisé du programme de cal-culs depuis l'introduction des données jusqu 'au traçage des pro-fils de surface libre dans le talus.

Données : Géométriques du talus et de la marée, caractéristiQues physiques du sol

1

'

Jncrémentation

Td,..,,.

m,n et

i

Calcul itératif des

1

1

Incrémenta/ion Calcul: X, G (X, t)

x,

t puis h (x.t ) 1 1 1 'f Fichier de traçage

Figure 5: Algorithme de résolution

Figure 5: Resolution algorythm

4. Cas particulier d'un massif vertical 4.1. Calcul du niveau d'équilibre

1

Nous soulignons que pour le cas d'un massif vertical quand

8 ~ 1r

1

2 ==> D ~ 0 et R,..,,. ~ 0, quelque soit m;tn; la fonnu-le de passage sc réduit alors, quelque soit l'ordre d'itérations, à

K,..,,.

=

0 si m~n

et K,.,,. = L,. si m=n (43)

L'expression (37) sc ramène alors à l'équation (18). Sa partie réelle tend vers lf2,..+A2f2 quand x~ oo. La racine de cette

valeur exprimée en (6), définit physiquement le niveau d'équi-libre qui s'établit au fond du massif sur la limite infinie du coté terre (en "BC" sur fig. 1 ).

(44)

4.2. Validation de la linéart~tation

Le passage de l'équation de Dupuit (3) à l'équation de Boussinesq est assuré par la linéarisation en carré (8) rarement utilisée dans la littérature des écoulements périodiques dans les sols. Si l'équa-tion (3) non linéaire pose d'énonnes difficultés de résolul'équa-tion ana-lytique, elle pourra sûrement nous donner au moins la possibili-té de prévoir Je niveau d'équilibre Ne défini auparavant. Ce dernier peut êl.re un moyen suffisant pour justifier le choix de cette linéarisation si nous pouvons retrouver ( 44) à partir de (3 ). Nous avons indiqué en (7) que la fonction h (x,t) est périodique, soit T cette période. Nous pouvons écrire autour d'un instant t₀

donné

J

to +T ()h(x t) h(x,t0+T)-h(x,t0)=

a'

dt=O to t (45) d'après (3), (46) c'est à dire (47) C1 et C2 sont les constantes d'intégration. C1=0 d'après (CL2) du (12), ainsi que (9). Dans le cas d'un massif vertical, pourtout x, nous avons

Puisque l'intégrale est indépendante de la variable x, elle pour-ra donc nous aider à évaluer la moyenne quadpour-ratique pour un cycle de marée autour de 1 'instantto en x =0 et x ~ 00

•

(49) d'où

Le niveau d'équilibre est alors bien celui trouvé en (44), après la procédure de linéarisation au carré. Nous vérifions ainsi la validité du modèle proposé dans ce ca.~ particulier simple. (39) est alors une solution générale complète pour tous les cas de pentes naturelles.

S. Résultats de la modélisation

Nous avons choisi de représenter quelques exemples des résul-tats, de manière à pouvoir appréhender les divers aspects du phé-nomène.

La figure 6 représente la convergence de la hauteur libre en fonc-tion du nombre d'itérafonc-tions à mi-flot pour une pente unité. Pour un nombre d'itérations inférieur à 6, la hauteur oscille autour de la position stable, obtenue à partir de 1 'itération 6. Les courbes sont 1.racées à mi-flot, pour une pente unité composée d'un limon sableux de référence : k

=

2,2 10-s m/s et n

=

0,4 ; marée :A

=

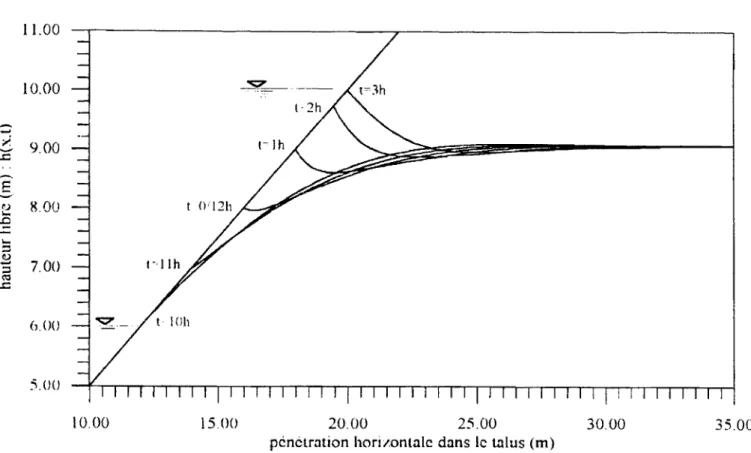
2 m,ll,.= 8 m.

La figure 7 mon1.re la montée de la surface libre dans un talus de pente P= 0,5 lors du flot. Le talus simule une rive d'inclinaison 26° composée d'un limon de pennéabilité 2,2 1()-5 rn/set de poro-sité0,3 ; sur lequel agit une marée de période de 12 heures, d'am-plitude 2

rn

et de niveau moyen compté à partir du subsl.ratum impennéable de 8 m. Les courbes sont représentées à toutes les heures du flot, de la basse mer (B.M.) à la pleine mer (P.M.). Elles correspondent aux instants: t

=

10, 11, 12 heures du cycle, et t

=

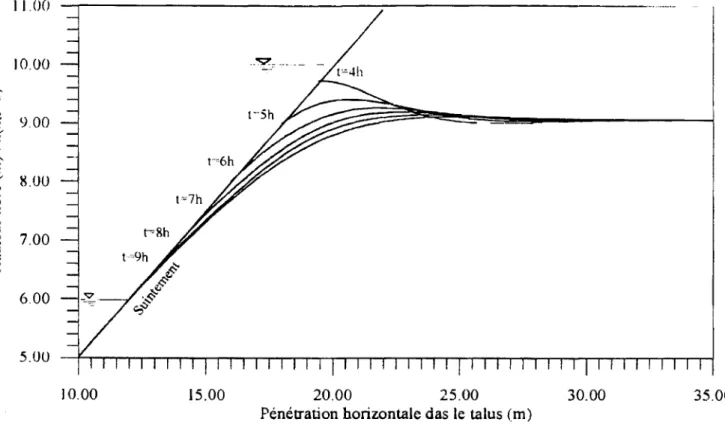
0, l, 2, 3 du cycle suivant. Elles tendent vers un niveau d'équilibre Ne= 9,06m, alors que Je niveau moyen de la marée n'est que li,.. =8m.

De même, la figure 8 montre, pendant le jusant la descente pro-gressive du niveau de la mer sur le même talus. Les profils cor-respondent respectivement du haut vers le bas aux instants t = 4, 5, 6, 7, 8 et 9 heures du cycle. La question du suintement ne fait pas 1 'objet de cette étude. la hauteur de suintement fait partie de la ligne de surface libre ; analytiquement dit : la courbe repré-sentant la ligne de saturation est continue et dérivable du point,

11.00 1 O. 00 .:::;, l!. ; 9.00 :E .-. E -- 8.00 2 .D

-

._ :::1 8 7.00 :::::; t';!

:r::

·

-

_. ;

-..c

-

E

0

....

,e

.... :::1 ~ :::1 C':l ..c

(,.oo

5.00 11.00 10.00 9.00 H.OO 7.00 6. ()() 5.00 5.00 10.00 -~--11cration (,cl 1.~ 1t::rat1on ·l 10.00 15.00 20.00 25.00 30.00

Pénétration horizontale das le talus (rn)

Figure 6 : Convergence de la hauteur libre en fonction du nombre d'itérations.

Figure 6: Free leve! convergence versus !'Wmber of iterations.

:s?.'-=.- ·

-15.00 20.00 25.00 30.00 35.00

pénétration horizontale dans le talus (rn)

Figure 7. Surface libre d'écoulement dans un talus de pente= 0,5 lors du flot.

Figure 6 : Free surface of flow in bank with slope = 0.5 during flood.

(sur l'interface eau-sol), de la hauteur libre de la nappe extérieure

à la pénétration horizontale infinie dans le talus. Le suintement est défini, donc, par le rapprochement de la ligne de saturation à

la ligne de pente, (Fig. 8. etFig.9)

appelons l'ensemble de cette surface, représentée par les courbes enveloppes, et la surface juste au-dessous jusqu 'au substratum par la "zone battue". Dans cene zone des phénomènes cycliques lents se produisent et peuvent occasionner des altérations des caractéristiques du matériau. Nous convenons de définir sa lon-gueur horizontale par la dislanee à l'intérieur du talus où l'amplitude Pour le même talus, nous avons représenté sur la figure 9, les

1 1. ()() 10.00 __ 'ÇI'c ---

-~

_{...: tJ.OO} :E ,-._ _,... c

-

8.00 ~ .J::l

...

:::: ~ 7.00 ::; C":l

::r:

6.00 5.00 10.00 15.00 20.00 25.00 30.00 35.00

Pénétration horizontale das le talus (rn)

Figure 8: Surface libre d'écoulement dans un talus de pente= O,Siors du jusant.

Figure 8: Free surface of flow in bank wùh slope

=

0,5 during ebb.

de propagation de la nappe libre n'est plus que 10% de l'ampli-tude de la marée. Verticalement, elles' étend du substratum jus-qu'au niveau supérieur de la nappe.

tude A= 2m, niveau moyen H,. =Sm et un rapport. de perméabi-lité kin variable en fonction du type de sol.

Si le cas du limon permet de comprendre les phénomènes, il

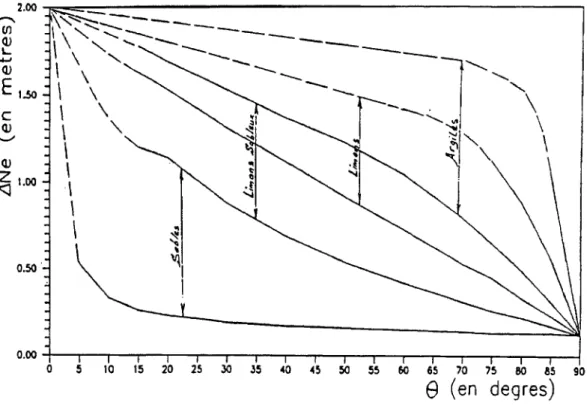
semble indispensable de les quantifier pour les différents types de sols. La figure 10 montre la surélévation du niveau d'équi-libre Ne en fonction de 1 'inclinaison du talus, pour une

ampli-11.00 10.00 ."8'. -~

....

>[ 9.00

-..c

-

E

--

~ 8.00 :-9

...

:::: .B _7.00 "Zone Battue" ::; C":l ..c 6.00 5.00 10.00 15.00 20.00

Les parùes interrompues des courbes représentent la continuité probable, (où les calculs divergent), pour les sols très fins et les petites pentes, alors que les cow-bes continues proviennent des résul-tats de cette méthode .

25.00 30.00 35.00

Pénétration horizontale dans le talus (rn)

Figure 9. Diagramme enveloppe des lignes de surface d'écoulementdans un talus de pente= 0,5

Deux points remarquables sont à noter. Le point de coordonnées

(0°, 2m) ne peut jamais être atteint En effet dans le cas où la

pen-tc est pratiquement nulle, Je point sur la pente relatif au nive<~u P. M. est à 1' infini. Par conséquent le temps du marnage n'est pas

suf-fi sant pour permettre à 1 'e<~u de parcourir une distance infinie sur

le sol. Alors on voit qu'il n'y a pas de contact périodique complet e<~u-sol. Le point (90°, 0,12m) montre que pour un massif droit

venical, la surélévation de l'e<~u au dessus du nive<~u moyen de

la marée est LlNe = 12,4cm, et indépendante du type de sol.

(1J

~

1.00

0.50.

J. Chapon, 1966, dans son ouvrage "Travaux maritimes". a

étu-dié le bilan des poussées qui peuvent solliciter un ouvrage

por-tuaire à écran tel que les bassins ct les ouvrages d'accostages. Il

reconnaît que le nive<~u de la nappe dans le sol à quelque

distan-ce de l'ouvrage est généralement un peu supérieur au niveau moyen de la mer. La surpression hydrostatique est importante ct transmise directement à l'ouvrage par l'intcrmédiaircdes remblais.

Il est donc prudent d'admettre dans le cas d'un marnage

impor-tant de 4m une pression hydrostatique correspondant à une

sur-0 5 10 15 20 25 JO 35 40 45 50 55 60 65 70 75 BO 85 90

e

(en degres)

Figure 10. Surélévation du niveau d'équilibre en fonction de l'inclinaison du talus pour différents types de sols, &Ve =Ne-Hm·

Figure JO. Raising versus inclination of slope for different types of soils, &Je =Ne- Il m·

6. Comparaison avec les observations en nature et conclu-sion

Ces différent résultats théoriques et numériques apportent des

informations originales sur 1' écoulement dans les talus portuaires.

Ce phénomène n'avait pas été jusqu'alors étudier de façon

quan-titative. Il avait, toutefois, été observé par De Cazenave (1971 ),

et analysé qualitativement par Chapon ( 1966).

De Cazenave 1971, a constaté ce qu'il définit par la dissymétrie des marées d'estuaire :

-à marée haute, grande hauteur noyée, l'onde va vite très

loin,

- à marée basse, le vidage de la nappe est lent;

- d'où marée montante rapide, marée descendante lente,

longue étale de pleine mer, brève étale de basse mer; et nive<~u

moyen au-dessus du nive<~u moyen de la mer (un peu au-des-sus si le substratum est très en dessous des basses mers, très

au-dessus si Je substratum est découvert à marée basse).

D'après cet auteur,Ies nappes libres communiquant avec la mer, la pente du rivage d'une part son colmatage d'autre part, peu-vent accentuer J'effet d'estuaire, ou Je diminuer: à marée haute l'eau s'infiltre par une plus grande surface, mais la vase est

pla-quée contre les ouvenures du sol à marée basse, la pente du sol

freine l'écoulement, mais des résurgences peuvent se faire jour

à travers la vase.

charge hydrostatique d'au moins 1 m.

Les observations en nature et les analyses qualitatives de ces

deux auteurs valident cette étude et mettent en relief 1 'intérêt de

ses résultats originaux : modélisation et quantification du pro-cessus d'écoulement dans les talus. Le présent article permet ain-si de donner une justification théorique à ces observations en nature, ct constitue la base de nos futurs travaux de recherche,

qui seront étendus à d'autres domaines scientifiques, en

parti-culier à l'étude du suintement.

RÉFÉRENCES BIBLIOGRAPHIQUES

ALEXIS, A., (1987). "Etude géotechnique et sédimento-logiquc

de souilles et chenaux de la rade de Lorient. Contribution à la

stabilité des sols immergés", Thèse de Docteur ingénieur,

EN.S.M. Nantes, 260 p.

BOUSSINESQ, J .• (1904). "Recherches théo-riques sur

l'écou-lement des nappes d'eau infilt-rées dans le sol et sur le débit des

sources". Journal de mathématiques appliqués,fasc. 1,

Gauthier-Villars.

CHAPON, J., ( 1966). "Travaux maritimes" - Tome 2 -Edition

Eyrolles.

DE CAZENOVE, E., (1971). "Ondes phréaùques sinusoïdales",

JOSSEAUtvŒ, H., (1970). "Essai de pompage hydraulique des soJs". B ul/etin des Laboratoires routiers. Avril 1970, pp. 39-55. MARINO, M.A., (1973). "Water table fluctuation in semiper-vious steam-unconfined aquifer systems". Journal of Hydrology

19, pp. 43-52.

POLUBARINOVA, P.Y.A., (1962). "Theory of ground water movement". Princeton Ed., 613 p.

RAT, M. et VAUTRIN, J., ( 1973). "Détermination des caracté-ristiques hydrauliques des sols à partir des variations piézomé-triques". Bull. LL.P.C. 1280, pp. 103-119.

RAZACK, M., DROGUE, C., ROMARIZ, C. & ALMEIDA, C., (1980). "Etude de 1 'effet de la marée océanique sur un aquifère carlxmaté côtier", Journal of Hydrology 45, pp. 57-69.

REZZOUG, A., (1990). "Résolution de l'équation de la surface libre de l'écoulementdans un talus soumis au marnage". Mémoire

de D.E.A., E.N.S.M. Nantes. 118

p.

REZZOUG, A. & ALEXIS, A., (1992). "Impact d'un écoule-ment cyclique sur un ouvrage semi-émcrgé". Journées natio-nales de Génie Côtier-Génie Civil, 26-28 février Nantes, pp. 222-231.

VAUCLIN, M.,(1975). "Etude expépimentale et numérique du drainage de nappes à surface libre influence de la zone non satu· rée". Thèse de Doctorat ès-sciences physiques. Université de Grenoble. p.196.