La rente de Thünen retrouvée (quelques réflexions en histoire de la pensée spatiale)

HAL Id: hal-01539098

https://hal.archives-ouvertes.fr/hal-01539098

Submitted on 14 Jun 2017

HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de

La rente de Thünen retrouvée (quelques réflexions en

histoire de la pensée spatiale)

Jean-Marie Huriot

To cite this version:

Jean-Marie Huriot. La rente de Thünen retrouvée (quelques réflexions en histoire de la pensée spatiale). [Rapport de recherche] Laboratoire d’analyse et de techniques économiques(LATEC). 1989, 29 p., ref. bib. : 2 p. �hal-01539098�

EQUIPE DE RECHERCHE ASSOCIEE AU C.N.R.S.

DOCUMENT DE TRAVAIL

INSTITUT DE MATHEMATIQUES ECONOMIQUES

UNIVERSITE DE DIJON

FACULTE DE SCIENCE ECON OMIQUE ET DE GESTION 4, BOULEVARD GABRIEL - 21000 DIJON

LA RENTE DE THUNEN RETROUVEE

Qu e l q u e s r é f l e x io n s e n h is t o ir e de l a p e n s é e s p a t i a l e

Résumé.

Le but de ce papier est de faire mieux comprendre la pensée de von Thünen sur la rente, qui a été trop souvent abusivement simplifiée par les auteurs qui s ’en réclament. A partir d ’une lecture du texte original, on propose une reformulation mathématique qui montre à la fois la richesse, les curiosités et les limites de l’analyse de Thünen. Aucune des fonctions de rente q u’utilise Thünen n ’est linéaire, et le modèle ne garantit pas leur décroissance avec la distance au centre.

Abstract.

Von Thünen’s thought about land rent has often been oversimplified by modern economists: the aim of this paper is to analyse the properties of the original rent function of The Isolated State. We give a mathematical reformulation of Thünen’s reasoning and we show its richness, its curiosities and olso its limits. None of the Thünen’s rent functions is linear, and the original model is anable to assure that they are decreasing with distance to the center.

Mots-clés : Histoire de l’analyse économique spatiale, théorie de la rente.

LA RENTE DE THÜNEN RETROUVEE

Quelques réflexions en histoire de la pensée spatiale

Jean-Marie Huriot, Institut de Mathématiques Economiques, Université de Bourgogne.

Si j e juge les deux hommes exclusivement d ’après le degré de compétence de nature purement théorique qui apparaît dans leurs oeuvres, alors, je pense, Thünen doit être placé au-dessus de Ricardo ou en fait de n ’ importe quel économiste de la période, sauf peut-être de Cournot.

(Schumpeter, 1954, traduction, 1983, II, 123).

1. QUELQUES REPERES.

1826: J.-H. von Thünen publie le premier volume de l’"Etat Isolé", après de nombreuses années passées à recueillir des données chiffrées et à concevoir son schéma théorique des cercles de culture. C ’est la naissance du premier

modèle

spatial. La construction de Thünen est géniale, non seulement parce q u’elle est en avance sur son temps, mais parce q u’elle marque encore fortement la pensée des chercheurs contemporains en analyse spatiale, par exemple dans le domaine de la "Nouvelle Economie Urbaine". Un tel succès est le fait d ’une idée simple, la plus simple dont peut partir l’analyse spatiale: la structure spatiale s ’explique entièrement par l’action d ’un centre d ’attraction unique.

Abstrait et général, le modèle de Thünen se prête facilement, comme celui de Ricardo, à des récritures plus ou moins formalisées, à des simplifications ou à des généralisations. Il s ’écoule cependant plus d ’un siècle avant que n ’apparaissent les premières suites

théoriques sérieuses (Lösch, 1940). Dès lors, l’analyse spatiale de Thünen est reformulée, simplifiée, généralisée, transposée; elle est interprétée, trahie, louée ou attaquée, et engendre une littérature suffisamment vaste pour qu’on puisse parler du paradigme thünenien. Le texte qui suit en étudie un seul aspect: les fonctions de rente utilisées explicitement ou implicitement par Thünen. Il s ’insère dans un projet de recherche sur l’ensemble des aspects du paradigme. Les reformulations actuelles, issues de celle de Lösch, sont pour la plupart abusivement simplificatrices en ce qui concerne les fonctions de rente. La quasi totalité des auteurs contemporains représentent la rente de Thünen par une fonction affine décroissante de la distance au centre de marché. L ’analyse de Thünen n ’est ni aussi simple, ni aussi naïve. Aucune des fonctions de rente qu ’il utilise ne peut être représentée par une droite, et certaines sont croissantes: pourquoi? Une nouvelle formulation mathématique, plus proche du raisonnement de Thünen lui-même, peut en révéler les causes: il s ’agit principalement de propriétés particulières, parfois curieuses, que Thünen inclut dans ses coûts de transport et dans ses coûts de production, mais il s ’agit aussi de l’application des premiers éléments de l’analyse marginaliste. On a trop longtemps oublié cette richesse analytique de Thünen. Cette reformulation permet, en outre, d ’analyser rigoureusement la nature et les propriétés des fonctions de rente de Thünen. Des résultats approchants peuvent être trouvés ailleurs, par exemple dans Kellerman (1983a,1989), et dans Jones et a l . (1978); l’analyse qui suit est plus générale.

Pour mieux comprendre la pensée de Thünen sur la rente, nous présentons dans cette section une version simplifiée de la rente thünenienne*.Ensuite nous verrons quelle est la véritable nature de la rente dans l’"Etat Isolé", d ’abord en fixant les rendements de tous les facteurs dans la section deux, puis en rendant variable le rendement de la terre (fertilité) ou celui des autres facteurs (ce qui revient à faire varier l’intensité de culture), dans la section trois.

Dans tout ce document, nous utiliserons des expressions comme "rente thünenienne" ou "modèle thünenien" pour désigner des concepts ou des analyses développés à la suite de Thünen.

1.1. Les hypothèses thüneniennes.

Sous une forme simplifiée, le modèle thünenien obéit au corps d ’hypothèses suivant, plus lourd que celui de Thünen lui-même.

L ’espace: c ’est cette plaine uniforme entourée d ’un désert que Thünen nomme "Etat Isolé". Dans cette plaine existe un centre de marché unique, la ville, représentée par un point, où sont effectuées toutes les transactions. Chaque lieu de cette plaine est identifié par sa distance x à la ville.

La production: elle est réalisée sur des terres de qualité (fertilité) homogène, avec un seul autre facteur de production (le travail, ou bien un facteur composite) dont toutes les unités sont identiques. Chaque processus de production est représenté par une fonction de production du type:

Q = Q(T,L), (1)

où Q est le produit brut total obtenu en utilisant une quantité de travail L sur une surface de terre T. On suppose que la fonction (1) est homogène du premier degré et, provisoirement, que les deux facteurs sont non substituables, ce qui implique que:

- la quantité produite (ou produit brut) par unité de surface, q = ^ , est fixe, ainsi que la quantité de travail utilisée par unité

L de surface, 1 =

- le coût de production par unité de surface, c, est fixe également; il est égal à wl, si w est le taux de salaire (ces grandeurs sont indépendantes de la localisation par rapport au centre).

Le seul coût de transport supporté est celui du produit, du lieu de production à la ville. Ce coût est proportionnel à la distance parcourue et à la quantité de produit transportée: le taux de transport, par unité de distance et par unité de produit est t. Il est le même à partir de tous les lieux et dans toutes les directions (propriété d ’isotropie)

Le prix du produit, pv , est fixé par le marché, à la ville, indépendamment du lieu de production.

La rente foncière est définie comme un surplus différentiel. La rente en un lieu quelconque et pour un processus donné de production est l’économie réalisée par rapport au lieu où les conditions de production sont les plus mauvaises, c ’est-à-dire, selon les hypothèses précédentes, au lieu le plus éloigné de la ville.

1.2. La rente thiinenienne.

Dans ces conditions, la rente foncière par unité de surface, p, est définie comme une fonction affine de la distance à la ville, x:

p(x) = pvq - c - xqx (2)

où pv> q, c, r sont pour l’instant des paramètres fixes pour un processus productif donné. De fait, la fonction de rente thiinenienne est le plus souvent représentée par une droite décroissante avec la distance (figure la). Cependant, cette courbe simple subit des déformations si l’on assouplit les hypothèses de départ relatives aux rendements et aux coûts de transport.

Figure 1: fonctions de rente thiinenienne.

Si l’on abandonne l’hypothèse des rendements constants, la courbe de rente n ’est plus une droite, et peut alors avoir n ’importe quelle configuration (Dunn, 1954). Néanmoins, des rendements marginaux du travail décroissants déterminent généralement une fonction de rente convexe (Beckmann, 1972; Saive, 1981; Huriot, 1988; infra, section 3), illustée sur la figure lb.

Si maintenant on abandonne l’hypothèse du coût de transport proportionnel, on doit remplacer la fonction de coût t x par une

fonction plus générale de la distance: t(x). Si on admet que ce coût s ’accroît moins vite que la distance (hypothèse souvent faite en économie des transports), alors la fonction t(x) est concave:

t’ (x) >0 , et t” (x) <0. (3) La fonction de rente (2) devient:

p(x) = pvq-c-qt(x). (4)

Alors, p ’(x) = -q t’ (x) <0 , et p ’’(x) = -q t’’(x) >0 ,

et la rente est à nouveau une fonction décroissante et convexe de la distance.

On peut montrer que cette propriété est conservée si l’on a

à la

fols

des rendements décroissants et une fonction de coûts de transport concave (Huriot, 1988). D ’autres complications pourraient être introduites, par exemple l’existence d ’ un second marché d ’écoulement du produit ou d ’approvisionnement. Si la ville de Thünen n ’est plus le seul marché, la rente n ’est plus forcément décroissante quand on s ’en éloigne. Cependant nous nous limiterons dans la suite à l’examen des propriétés de la fonction de rente dans le cas d ’un seul centre de marché.

2. LA VERITABLE FONCTION DE RENTE DE THÜNEN.

Il se trouve que, pour des raisons différentes des précédentes, la rente de Thünen n ’est pas une fonction affine et n ’est pas forcément décroissante avec la distance à la ville. Il suffit de reporter sur un graphique les valeurs que donne Thünen pour différentes distances relativement à l’un ou l’autre des processus de production étudiés

2

pour obtenir une courbe convexe (Thünen,I,36; 1,173; 1,179; 1,184) . Dans la plupart des les cas, on observe que la fonction de rente de Thünen est de la forme générale:

3L"**bX

p(x) = , avec a,b,c >0. (5)

Cette fonction correspond à une courbe décroissante et convexe. On vérifie aisément que p ’(x) <0, et que p ’’(x) >0 .

Cependant il nous faut comprendre pourquoi il en est ainsi. Pour celà, il faut reprendre la démarche de Thünen. Suivons le raisonnement mené pour le seigle (Thünen, 1,5-12 et 36).

Le calcul des coûts de transport semble à la fois complexe et démodé. Thünen prend en compte trois formes de dépenses de transport. La première est la source d ’une variation du prix à la production, ou

2

L ’"Etat Isolé" comprend plusieurs volumes publiés en allemand respectivement en 1826, 1850, et après la mort de Thünen, en 1863. Nos références renvoient aux traductions françaises de Laverrière et Volkoff du premier volume et de la première section du second volume,qui contiennent l’essentiel de ce qui nous intéresse ici

prix à la ferme, avec la distance à la ville. Elle provient de la nécessité, lors du transport d ’un produit à la ville, de transporter simultanément la source d ’énergie du transport, en l’occurrence la nourriture que consomment les animaux de trait durant le trajet, à l’époque. Cette charge supplémentaire est bien-sûr propotionnelle à la distance à parcourir

et

à la charge

totale

à transporter. S ’ajoute à celà le coût du transport proprement-dit, indépendamment de l’énergie consommée, qui se décompose en coût supporté en grain et coût supporté en monnaie, tous deux également proportionnels à la distance et à la quantité totale transportée.

2.1. Le prix du grain à la ferme.

Pour porter sur le marché la quantité de grain q (en poids) produite à la distance x, il faut transporter une quantité supplémentaire a (source d ’énergie, en poids également) proportionnelle à la quantité totale à transporter , q+a=q, et à la distance à parcourir. Soit a la part de la charge totale de départ consommée par unité de distance ; a et q sont liés par la relation:

a = a(q+a)x = aqx .

On tire: a =

1-ax ’

et: q = — = _{ax 1-ax}q . (6)

Supposons que le coût de transport proprement-dit soit défini par les taux suivants: pour transporter une unité de poids sur une unité de distance, il en coûte t en grain et r en monnaie. La livraison au

g m

marché de la quantité q coûte donc, en monnaie: x

t qx = r q ---- ,_{m m l-otx}

et le gain monétaire net (recette de la vente au marché moins frais monétaires de transport) est:

Pvq 1-ax

Pour porter la quantité q de grain au marché, il faut produire, en plus de cette quantité, celle qui sert à payer le coût de transport, soit au total:

q + r q x = q + r q — —

g g 1-ax

Le prix du grain à la ferme est égal au gain net moyen, soit:

X X p q - _vn t q ---- _{mn 1-ax} p - t ----_{v m 1-ax} pf ( x ) --- : --- ^---;--- x— <7) q + t q ; --- _{g 1-ax} 1 + t_{g 1-ax} ---p - (t +a---p ) x * v m v 1 + ( t - a ) x g (8)

Ce prix est une fonction décroissante de la distance x, dont la convexité dépend des paramètres relatifs au coût réel de transport. En effet: P T _{v g} + T_m p ’ (x) = --- -— < 0 , car p ,x ,x >0 , (9) f r-. . _{[l + (x -a)x]}

t

\

v g m g et p ” (x) = - (PvTg+xm ) 2(t -a)(l-ax+T x) g g {l+(x -a)x}^ g avec p _{v g m}t +x >0 ,

1-ax >0 puisque, par définition, ax est la

part

du chargement total consommée pour le transport durant le trajet, si bien que ax <1, donc 1—ax+T x >0 ;

g

le signe de la dérivée seconde dépend donc de celui de ( t - a ) , et g

on a: > >

p ” (x) = 0 ssi (Tg"a ) | 0 • ( 10) La fonction p^-(x) est donc concave si (r^-a) <0

convexe si (r -a) >0 . g

x et a sont des taux sans dimension, exprimant des rapports en g

poids/poids, et sont tous deux inférieurs à 1. Mais le signe de (t -a) g est a priori indéterminé.

Les chiffres utilisés par Thünen sont tels que cette expression est positive, et sa fonction p^-(x) est

convexe.

Sa spécification est

(Thünen, I, 10):

, * 273-5.5x ___

= 182+x < U )

2.2. La fonction de coût de transport.

La logique demande habituellement que l'on commence par établir une fonction de transport et que l'on détermine seulement ensuite le prix à la ferme. Mais l'inversion de la démarche est conforme à

l’

exposé de Thünen et permet de mieux appréhender sa construction

théorique.

Le coût de transport supporté pour livrer à la ville une quantité

q de grain produite à la distance x, c’

est-à-dire pour transporter une

quantité totale q, se monte à:

t

qx , en monnaie, et

_m

T qx , en grain, ce qui vaut x qxp-(x) en monnaie;

g

8

Donc le coût de transport de cette quantité q s’

élève à:

t qx + x qxp_(x) =

_m

_g

_f

t

_ni*

q r2— + t q

₁

_-ax

_g

7₁

^— Px-(x) ,

_-ax

d ’

après (

6

), soit, pour chaque unité de poids de grain à porter au

marché:

t(x) =

t

_m

~ — + x ■

”—

Pr ( x )

.

(12)

1

-ax

g

1

-ax f

On vérifie évidemment que ce coût de transport par unité de

produit est égal à la différence entre le prix à la ville et le prix à

la ferme:

t(x) = py - pf (x) .

(13)

Les propriétés de t(x) dépendent donc de celles de p^.(x).

Ainsi, t’

(x) = -p^.(x) >0 , puisque p^.(x) <0 . De plus:

t” (x) = -p” (x) ;

or, le signe de p ” (x) dépend de la comparaison de x^ et de a; de la

condition (

1 0

) ci-dessus on déduit donc que:

t’’(x) =

0

ssi (r -a) =

0

.

(14)

>

g

<

Celà entraîne que la fonction de coût de transport de Thünen est

croissante, et qu’

elle est concave si et seulement si (x -a)

>0

g

(figure

2

a), et convexe si et seulement si (x -a)

<0

(figure

2

b).

g

Figure 2 : fonction de transport de Thünen.

t(x)

t(x)

constitutifs:

(1)- une partie de la charge qui part du lieu de production disparaît pendant le transport, parce q u ’il faut transporter la nourriture consommée par les animaux durant le trajet: on peut dire q u ’il y a "fonte" de la charge durant le transport . C ’est là un élément très archaïque, lié à la lente traction animale, à moins q u ’on le traduise en termes d ’énergie, auquel cas il peut jouer un rôle non négligeable dans certains transports à longue distance, aériens en particulier. On peut rapprocher ce phénomène de la "fonte" décrite dans le "modèle de l’iceberg" utilisé par Samuelson (1983). La "fonte" de Thünen est linéaire puisqu’elle est proportionnelle à la charge de départ: d ’après (6), on a q = q(l-ax); la "fonte" de 1’"iceberg" est exponentielle puisqu’elle est à chaque instant proportionnelle à la

"“(XX

charge restante: on a alors q = qe . Samuelson semble avoir négligé cette différence.

(2)- Un paiement en nature (en grain) est effectué, proportionnellement à la distance et à la charge totale à transporter. Si on suppose que ce grain est destiné à nourrir les hommes qui assurent le transport, on peut se demander pourquoi il n ’est pas transporté, ou pourquoi son transport n ’est pas pris en compte. Ici apparaît encore une curiosité du modèle de Thünen: ce paiement en nature croît avec la distance, d ’autant plus qu’il se proportionne à une charge de départ qui elle-même croît avec la distance à parcourir; mais il est évalué en termes d ’un prix à la production qui décroît avec la distance. Le résultat est indéterminé.

(3)- Un coût monétaire de transport respectant la même double proportionnalité.

Seul le troisième élément est retenu dans les versions modernes. Il faut alors introduire une non proportionnalité pour obtenir une fonction de transport concave, donc une fonction de rente convexe. Thünen obtient ce résultat avec les trois éléments ci-dessus et avec des taux de transport

constants:

les valeurs empiriques q u ’il donne aux paramètres conduisent effectivement à la fonction croissante et concave (Thünen, I, 11):

199.5x , (15)

182+x

ce qui est la conséquence des propriétés de décroissance et de convexité de la fonction de prix à la ferme (11).

Il est possible de modifier la formulation précédente des équations (6) à (14) en éliminant l’un des éléments "curieux" de Thünen. On remarque alors que:

- si on abandonne la "fonte" de la charge en cours de transport, la fonction de coût de transport devient:

(

P “ T X \

T “I--- » (1®)

g

fonction

toujours croissante et concave, de même forme générale que

celle de la figure (2a);

- si on abandonne la partie du coût en nature, la fonction de coût de transport devient:

t

-r—

, (17)

m 1-ax

fonction croissante et convexe, comme celle de la figure (2b).

Cela montre que la concavité de la fonction utilisée par Thünen est probablement due, comme l’intuition le suggère, à la baisse du prix du grain lorsque la distance s ’accroît. Cette baisse a un effet de freinage sur la croissance du coût de transport avec la distance qui domine l’effet d ’accélération entraîné par la "fonte" de la charge.

2.3. La fonction de rente.

Nous nous intéressons à un processus productif donné, pour lequel le produit brut par unité de surface, q, est donné (la fertilité de la terre est fixe, pour l’instant).

Thünen soustrait de la valeur du produit brut à la ville le coût de transport et les "frais de production" pour obtenir la rente foncière, selon une formule implicite apparentée à l’expression (2):

p(x) = pvq - c - t(x)q . (18) Les frais de production se répartissent en deux catégories (Thünen, I, 19-26):

- les frais proportionnels à la surface exploitée: frais de semailles et de préparation;

- les frais proportionnels au montant de la récolte: frais de récolte, frais généraux.

Ainsi le coût réel, en grain, par unité de surface serait de la forme:

c = c + c q_{o 1}

A fertilité donnée, le produit brut q est fixé et le coût réel par

10

unité de surface est constant.

Une autre curiosité de Thünen apparaît alors: la double évaluation des coûts de production (Thünen, I, 24-26): seule une partie des frais est supportée en grain: c ; l’autre partie est supportée en monnaie:

8

c . Thünen suppose que le rapport entre ces deux parties est fixe m

(trois quarts-un quart). Ainsi le coût est défini par les deux éléments: (c , c ), et son évaluation monétaire dépend du prix du

g m

grain à la ferme, qui décroît avec la distance à la ville . Alors: c = p_(x)c + c . _{1 g m} (19) L ’hypothèse d ’un rapport fixe entre les deux parties du coût est assez curieuse: elle ne peut être tenue que pour x donné. Thünen établit ce rapport fixe entre les deux parties du coût mesurées en monnaie (Thünen, I, 26), or la valeur de la partie payée en grain varie avec la distance, donc le rapport entre les deux parties est variable avec la distance.

Le produit brut q est facile à évaluer dans le cas d ’un système de culture unique. Dans le cas d ’un système d ’ assolement comme celui q u’étudie Thünen, le produit brut est composé de plusieurs biens différents. Il est alors entièrement converti en termes de grain sur la base du rapport existant entre les prix des différents produits, ce rapport étant supposé fixe (Thünen, I, 23-24).

Avec ce que nous savons maintenant, la fonction de rente (18) peut être récrite de façon plus précise:

p(x) = p q-p (x)c -c -t(x)q . _{v i g m} (20) Deux cas sont alors à considérer.

(a) Dans le cas de la culture du

grain,

ou d ’un assolement avec

grain,

on a:

p(x) = [py-t(x)]q-cgpf (x)-cm

= p_(x)(q-c )-c . _{i g m} (21) q, c et c sont des paramètres fixes. p(x) a donc les mêmes _{g m} propriétés (9) et (10) que pf (x) si et seulement si:

q - c >0 . (22)

o

Cette condition est

toujours vérifiée:

elle signifie que le coût de production en grain n'est pas supérieur au produit brut en grain, ce qui est une condition de fonctionnement du processus de production. Ainsi, la fonction de rente relative à la production de grain est

décroissante; elle est concave ssi (r -a) <0 (figure 3f), 8

convexe ssi (r -a) >0 (figure 3e). g

Puisque Thünen utilise une fonction Pj.(x) décroissante et convexe, sa fonction de rente, par exemple pour le système "pastoral", est décroissante et convexe; son expression est (Thünen, I, 36):

202 202-7065X

182+x '

( J

(b) Si le produit n ’est ni du grain , ni exprimable en grain (c’est le cas général), utilisons pour le désigner l’indice i; la fonction de rente s ’écrit alors:

V * ’ * pv i V ' >f (x)og r c. i - t(x)<:' i ■ (24)

qui ne peut être réduite comme dans le cas du grain.

Si le coût de transport par unité de poids est indépendant du bien à transporter, on peut cependant écrire, d ’après (13):

V x) = pv i V cm r pf (x)cgi'1Pv"Pf (,!)lqi

= pv l V ° m 1-pv V pf (x)(V cg i ) • (25) qui est encore une transformation affine de la fonction p^(x), et en garde donc les propriétés si et seulement si:

(qi"cg i } >0 •

Cependant, cette condition n ’est plus vérifiée naturellement, q^ est maintenant le produit brut, en poids, du bien i considéré (par exemple la pomme de terre), et c ^ est le coût de production,

en

grain,

du bien i. Donc rien ne garantit a priori que la condition (26 )

soit réalisée. On peut noter que les conditions (22 ) et (2 6 ) sont équivalentes aux conditions de décroissance de la rente obtenues par Jones et al. (1978). Leur modélisation est indépendante de celle que nous proposons ici. Elle n ’intègre pas le phénomène de "fonte" de la charge durant le transport, ce qui simplifie les résultats, mais ne permet pas de saisir toutes les propriétés de la fonction de rente de Thünen. Ces propriétés sont rassemblées, pour plus de clarté, dans l’encadré de la page 13 ainsi que sur la figure 3.

Les résultats numériques de Thünen peuvent facilement être retrouvés, par exemple dans le cas de la sylviculture (Thünen, I, 157-159, et 172-173), où l’on a:

(qi"cg i } >0 ‘ (26)

’1(X) ° ( 33Î 8^ x ° ' 6X ) 250 ■ (27)

fonction décroissante et convexe.

Propriétés de la fonction de rente de Thünen.

1er cas: ^ i -cgi^ toujours vrai dans la production de grain; non garanti ailleurs, mais supposé par Thünen.

(t -a) >0 : vrai si le phénomène de "fonte" est absent 8

ou relativement faible par rapport au coût de transport en grain; supposé par Thünen. Alors, la fonction de rente est DECROISSANTE ET CONVEXE.

2ème cas: >

(t - a) <0: vrai si la "fonte" est relativement forte g

ou si le coût de transport en grain est nul. Alors, la fonction de rente est DECROISSANTE ET CONCAVE.

3ème cas: <<-l: possible dans les productions autres que le grain;

(t - a) >0. g

Alors, la fonction de rente est CROISSANTE ET CONCAVE.

4ème cas: (q.-c .) <0 ; --- i gi

(t - a) <0 . g

Alors, la fonction de rente est CROISSANTE ET CONVEXE.

Thünen se limite au premier cas, mais son modèle est compatible avec les trois autres.

Figure 3: prix à la ferme, coût de transport et rente.

Ainsi on peut attribuer la forme spécifique des courbes de rente de Thünen à une fonction de coût de transport concave et à une fonction de prix du grain à la ferme décroissante et convexe. Toutefois, décroissance et convexité de la rente ne sont vraies que pour certaines spécifications numériques de Thünen; elles ne sont garanties par aucune propriété intrinsèque du modèle, en d ’autres termes elles ne sont pas endogènes au modèle. La fonction de rente de Thünen peut très bien être

croissante

avec la distance.

Dans le cas plus général où les coûts de transport du produit cultivé et du grain sont différents, une croissance de la rente peut d ’autant plus survenir. La fonction (24) s’écrit alors:

p

4

(x) - V p vr t

1

<,

01

-ogiIpv"t(,<)1"o»i

,

avec pt(x) = c jt’(x)-q^t^(x)

° g i t i ( x )

< 0 ssl <¡7" < t’ (x) ' l26’ ’ Cette condition se ramène aux conditions (22) et (26) si t^(x) = t(x). Sa réalisation n ’est pas plus garantie.

Les conditions (22), (26) et (26’) assurent la fermeture du système spatial, c ’est-à-dire l’existence d ’une limite spatiale absolue à la production d ’un bien, définie par la distance à laquelle la rente s ’annule. Mais l’analyse de Thünen ne fait aucune référence à de telles conditions. La possibilité d ’une rente croissante dans le cadre analytique de Thünen est mentionnée par d ’autres commentateurs, notamment Artle et Varaiya (1974), Jones et al. (1978), Kellerman

(1983a, 1983b). Cependant tous semblent oublier que Thünen lui-même a construit des fonctions de rente en partie

croissantes,

pour l’industrie du bétail c ’est-à-dire la production de beurre (Thünen, I, 200-227). Il n ’a pas explicité ces fonctions, se limitant à en donner des évaluations pour quelques distances. Si l’on suppose que le prix du beurre est de 0,118 thalers la livre (Thünen, I, 210) et q u ’il faut 2 acres de sol par vache (Morgan, 1973, p.307), on peut, après les conversions d ’unités appropriées, établir l’expression analytique suivante:

^ -677,04+29,68x-0,0?88x2j (28)

proximité du marché; elle est ensuite décroissante, ce que Thtinen n ’a pas remarqué parce que celà se produit largement en dehors de l’espace utile de l’étude. Cependant, il considère que cette expression de la rente n ’est valide que jusqu’à une certaine distance, que nous désignerons par x , correspondant à la limite du cercle où la culture

S

du grain donne une rente positive. Au-delà, le grain est encore cultivé, non pour le marché, mais pour couvrir les frais de production du beurre: il est uniquement auto-consommé, et son prix reste fixe, égal à p f (x )=0,45 thalers l’unité de poids, indépendamment de la distance au marché (Thünen, I, 207). Pour cette zone, 11 est aisé d ’établir que la rente a la forme affine décroissante suivante:

270(2,895-0,0588x) , (29)

et q u ’elle s ’annule pour x=50 milles: la fermeture du système spatial est donc réalisée. On a ainsi la configuration de la figure 4.

Fleure 4 : la rente pour la production de beurre.

Il est très important de remarquer que Thünen a parfaitement expliqué la croissance de la rente avec la distance:

...à mesure que la distance de la ville augmente, les frais de production du beurre diminuent plus fortement, à cause de la baisse du prix du grain, que ne croissent les frais de transport du beurre. ( Thünen, I, 220).

Une rente croissante peut exister dans d ’autres conditions que celles de Thünen, que nous avons strictement respectées ju s q u’ici, et en particulier avec une autre fonction de coût de transport (Artle et Varaiya, 1978).

A partir de l’analyse précédente, nous pouvons modifier la

fonction de transport "à la carte" et en déduire immédiatement la forme de la courbe de rente correspondante.

Supposons d ’abord que le phénomène de "fonte" n ’existe pas, c ’est-à-dire que le paramètre a est nul. La fonction de coût de transport prend alors la forme donnée par (16), et la fonction de prix du grain à la ferme devient:

p - t x v m

p_(x) = --- , (30)

1 + t x

g

et les fonctions de rente sont toujours données par (21) et (25), où p^.(x) prend la forme (30) ci-dessus. On se trouve alors dans le cas où (t -a) >0, et, d ’après ce qui précède (cas 1 et 3 de l’encadré), la

g

rente est décroissante si (q.-c .) >0 et croissante sinon. i gi

Supposons maintenant que le coût de transport en nature disparaisse, c ’est-à-dire que = 0 . La fonction de coût de

transport prend la forme donnée par (17) et la fonction de prix du grain à la ferme devient:

pf M ' pv-Tm( ] • (31)

alors les fonctions de rente sont données par (21) et (25) où p^.(x) prend cette nouvelle forme (31). t = 0 implique (t - a) <0, et nous

g g

sommes dans le cas 2 ou le cas 4 de l’encadré: la fonction de rente est encore décroissante si (q,-c ) >0, et croissante sinon.

1 gl

Enfin, retenons une fonction de transport de forme moderne, sans "fonte" et sans paiement en nature, donc uniquement monétaire. On se trouve alors dans le cas 3 avec a = 0 et z = O.Dans les fonctions de

g

rente (21) et (25), le prix du grain à la ferme est donné par:

P f (x) = Pv -Tmx > (32) fonction affine décroissante. Les propriétés du paragraphe précédent sont encore vérifiées, et ceci reste vrai pour toute fonction de transport t(x) croissante:

Pour toute fonction de transport croissante, la rente de Thvlnen est une fonction décroissante de la distance si et seulement si:

< v V >0

-Plus généralement, une fonction de rente comportant un coût de production qui décroît quand on s ’éloigne du centre peut être

croissante en partie ou totalement.

2.4. Prix central et prix local.

Revenons sur la définition du prix à la ferme. Pour le grain, Thünen postule la relation (13):

pf (x) = pv - t(x) ,

et l’utilise implicitement pour évaluer tous les coûts en grain, quel que soit le bien produit. Celà mérite une réflexion plus approfondie.

La relation (13) signifie que le grain est évalué à la ferme à sa valeur avant transport à la ville, c ’est-à-dire à son coût d ’opportunité : le gain net q u ’aurait le fermier qui irait le vendre à la ville au prix pv et devrait déduire le coût de transport t(x). Mais ce calcul n ’est valide que s ’il s ’agit d ’une autoconsommation. Tout se passe donc pour Thünen comme si le grain utilisé pour payer une partie des coûts de production et de transport était disponible sur place, à la ferme; celà revient à supposer que le grain est produit partout, ou q u ’il est disponible partout sans avoir à être transporté. Celà entre en contradiction avec le modèle même des cercles de culture qui est bâti sur cette théorie de la rente. Chaque cercle est spécialisé dans la culture d ’un bien déterminé, et le seul lieu où l’on peut se procurer les autres biens est la ville centrale. La relation (13) est donc correcte lorsqu’on désire évaluer le grain qui est utilisé pour payer les frais de production ou de transport du grain. Elle ne l’est plus quand on évalue le grain utilisé pour payer les frais relatifs à un autre bien.

Thünen n ’est pas conscient de cette incohérence, pourtant il traite tout-à-fait correctement le cas d ’un autre bien intermédiaire, l’engrais, dans le cas de la production de pommes de terre, par exemple (Thünen, I, 178-181). L ’engrais (fumier) peut être produit sur place ou bien acheté à la ville. Dans ce dernier cas, il faut évidemment ajouter les frais de transport de l’engrais à son prix à la ville pour obtenir la dépense totale en engrais (Thünen, I, 181). On a donc, pour l’engrais, e:

p_ (x) = p _{fe ve} + t (x) , _e (33) où t (x) est calculé en tenant compte du nécessaire retour des moyens

e

de transport qui vont livrer le produit brut à la ville. (33) est la relation correcte à utiliser pour toute dépense qui ne porte pas sur

une autoconsommation, tant que la ville est le seul lieu où l ’on peut se procurer les biens qui ne sont pas produits sur place. Nous avons utilisé une relation semblable dans une récente extension du modèle de

localisation de Thlinen (Huriot, 1987).

3. RENTE, FERTILITE ET INTENSITE.

Nous avons raisonné jusqu’ici (section 2) à fertilité donnée (mesurée par le produit brut q) et en supposant que chaque bien est produit selon une technique, ou combinaison de facteurs, unique, c ’est-à-dire avec une intensité de culture unique (mesurée ici par la quantité de travail par unité de surface, 1). Thünen revient séparément sur ces deux hypothèses. En fait, il s ’agit d ’un seul et même problème lorsque q et 1 sont liés par une fonction de production néoclassique .

3.1. Rente et fertilité.

Une partie des frais de la production des grains est proportionnelle à l’étendue cultivée, une autre partie à la grandeur des récoltes. (Thünen, I, 32).

Plus la fertilité du sol diminue, plus la production du grain coûte cher, et l’on ne peut s ’y livrer sur les terrains de fertilité minime que lorsque le prix des grains atteind un chiffre élevé. (Thünen, I, 29).

La première citation signifie que toute partie du coût de production doit prendre la forme suivante, déjà rencontrée au paragraphe 2.3. :

c = c q + c q , (34)

La seconde citation signifie d ’abord que le coût moyen de production du grain augmente quand la fertilité diminue, c ’est-à-dire quand le produit brut par unité de surface, q, diminue. C ’est une conséquence immédiate de l’expression (34), et ne nécessite pas la longue et fastidieuse justification numérique q u ’en donne Thünen.

Elle signifie ensuite que la culture du grain sur des terrains moins fertiles exige un prix du grain plus élevé, ce qui est intuitivement immédiat puisque le coût moyen est plus élevé. Thünen donne de cette proposition une démonstration algébrique (Thünen, I, 33-35) reprise notamment par Ponsard (1955, 1958), qui peut être

remplacée par la suivante, plus rapide.

Partons de l'expression (21) de la rente pour la culture du grain: p(x) = pf (x)(q-c )-cm ,

où chaque partie du coût se décompose selon (34); pour une distance

donnée x q et pour une fertilité variable, on peut écrire:

p(xo.q) = Pf <x0 ><i-cgo-cgiq>-CB -ciiq . (35)

Le prix à la ferme qui maintient la rente constante égale à p

lorsque la fertilité varie est tel que:

c +c a-p -c c -c +c c -c p

mo miM K mi go mo mo gi g r Pf (V q) = q-c -c q ’_{go giH} aVeC P f ' V " 1 --- ; _(q-cgQ-Cgiq)^

Or, Thünen suppose une proportionnalité entre les coûts en monnaie et les coûts en grain qui est vraie, on l'a vu, pour une distance donnée; alors: c c ml S 1 --- = --- , donc: c c = c c , et p' (x , q) <0 ; (36) c c mi go mo gi ' * 1 o M mo go &

le prix du blé à la ferme doit bien varier en sens inverse du produit brut, c'est-à-dire de la fertilité, toutes choses égales d ’ailleurs.

Toujours à une distance déterminée, quel est l'effet de la fertilité sur la rente? De l'expression (35) de la rente, on tire:

p' (x , q) = p _(x ) ( 1 —c ) —c o ^ f o gi mi Cette expression est positive si et seulement si:

Cmi

w > — • (37)

gl

Dans le cas général (production d'un bien quelconque) l'expression de la rente (25), modifiée par la relation (34), à une distance x q et pour une fertilité variable, devient:

p i (V q) ■ P v i V W ^ i . V W P f ' V ' V V o - V i V • avec: p i (v q ) ” pv r cm i r v pf (ito ) ( 1 -cg i , ) >0 ssl

~pvi+cmii+pv

p f (V " --- • (38)

gil

Puisque p^-(x) est une fonction décroissante de x, les conditions (37) et (38) signifient que, lorsque la fertilité s ’accroît, la rente augmente à proximité du centre et diminue dans les lieux plus

éloignés, toutes choses égales d ’ailleurs.

3.2. Rente et intensité.

Il existe actuellement deux approches pour le modèle thünenien d ’intensité (Kellerman, 1983a, 1983b, 1989); l’une, dite classique, est une analyse discontinue; l’autre, dite néoclassique, est continue. La première est développée par Thünen lui-même, puis reprise récemment notamment par Scott (1979, 1980) et par Huriot (1981, 1986, 1987). la seconde, seulement suggérée par Thünen, est plus largement développée aujourd’hui. Nous présentons ici une formulation critique de l’analyse de Thünen. L ’approche néoclassique est utilisée dans le prochain paragraphe pour faire une synthèse des problèmes de fertilité et d ’intensité.

L ’approche classique consiste à supposer que la production d ’un bien déterminé peut se faire selon un nombre fini de techniques, chacune étant décrite par un vecteur de coefficients de production fixes. Thünen compare deux systèmes de culture du grain, auxquels sont associés deux vecteurs (q, c , c ) fixes: un système d ’assolement de

g m

sept ans dit "pastoral", qui est le plus intensif, et un système d ’assolement triennal. En chaque lieu, on doit préférer le système qui dégage la plus forte rente. Thünen conclut:

Il ne peut donc exister aucune préférence absolue pour l’un des deux assolements; l’avantage de l’un ou de l’autre n ’est déterminé que par le prix des grains. Des prix inférieurs font adopter l’assolement triennal, des prix élevés, au contraire, l’assolement pastoral. (Thünen, I, 108).

(Par "prix des grains", il faut entendre "prix à la ferme"). Ces lignes de Thünen sont la première expression de la loi thünenienne d ’intensité, selon laquelle, pour la production d ’ un bien déterminé,

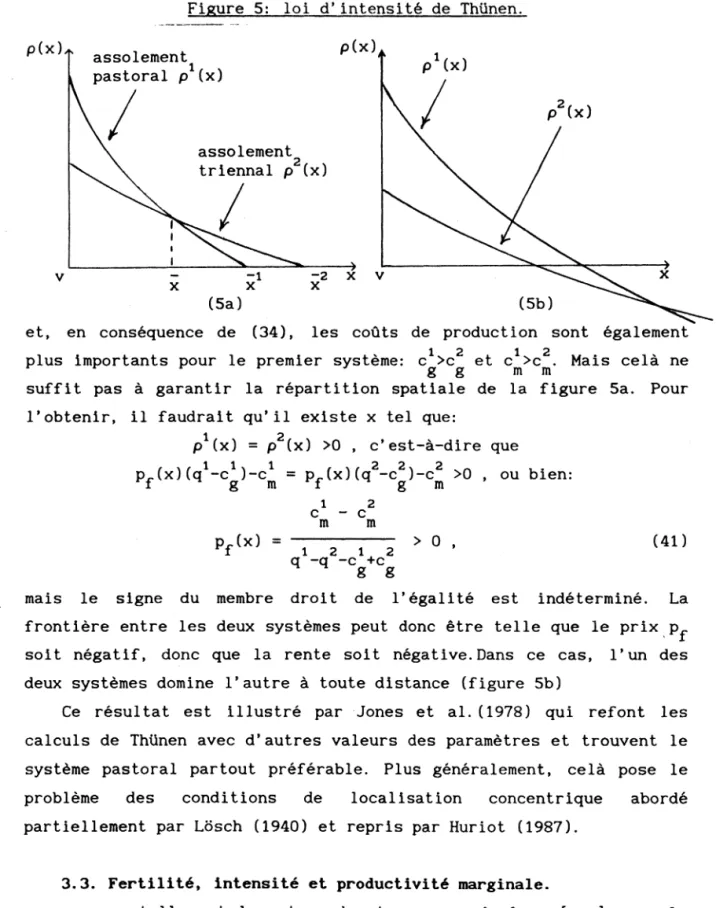
l’intensité de culture est d ’autant plus forte q u ’on est près de la ville centrale. Cependant, ce résultat, illusté sur la figure 5a, dépend des valeurs particulières des paramètres.

D ’après (21), les fonctions de rente du système pastoral et du système triennal s ’écrivent respectivement:

p*(x) = p (x)(q1-c1)-c1 , (39)

f g m

p 2(x) = p (x)(q2-c2 )-c2 ; (40)

f g m

Thünen utilise des données telles que le produit brut, en grain, 1 2 par unité de surface, est plus grand pour le premier système: q >q

p(x)

assolement^ pastoral p (x)

Figure 5: loi d ’intensité de Thünen p(x) assolement 2/ \ p (x) triennal p (x) (5a) (5b)

et, en conséquence de (34), les coûts de production sont également

1 2 1 2

plus importants pour le premier système: Cg >Cg cm >cm* ne suffit pas à garantir la répartition spatiale de la figure 5a. Pour l’obtenir, il faudrait q u ’il existe x tel que:

1 2 p (x) = p (x) >0 , c ’est-à-dire que 1 1 1 2 2 2 p_(x)(q -c )—c = p_(x)(q -c )-c >0 , ou bien: _{f g m *1} p m Pf (x) = 1 2 C ~ C m m 1 2 1 2 q -q -c +c g g > 0

(41)

mais le signe du membre droit de l’égalité est indéterminé. La frontière entre les deux systèmes peut donc être telle que le prix p^. soit négatif, donc que la rente soit négative.Dans ce cas, l’un des deux systèmes domine l’autre à toute distance (figure 5b)

Ce résultat est illustré par Jones et a l . (1978) qui refont les calculs de Thünen avec d ’autres valeurs des paramètres et trouvent le système pastoral partout préférable. Plus généralement, celà pose le problème des conditions de localisation concentrique abordé partiellement par Losch (1940) et repris par Huriot (1987).

3.3. Fertilité, intensité et productivité marginale.

... telle est la nature des travaux agricoles, [...], que le surcroît du rendement n ’augmente pas dans le même rapport avec le nombre des ouvriers ajoutés, mais que chaque ouvrier, placé en dernier lieu, produit moins que celui placé précédemment; (Thünen,

II, 22)

Dans une exploitation rationnelle, l’augmentation des familles de journaliers doit être continuée jusqu’à ce que l’accroissement du rendement fourni par le dernier ouvrier ajouté soit égal en

valeur au salaire obtenu par l’ouvrier. (Thünen, II, 21).

Ces lignes font de Thünen certainement le plus grand précurseur de la théorie de la productivité marginale. Elles expriment d ’une part la loi des rendements marginaux décroissants, d ’autre part le critère de rationalité constitué par l’égalité du prix d ’un facteur et de la valeur de sa productivité marginale. Il ne nous faut rien de plus pour fonder une approche néoclassique .

La fonction de production (1) admet maintenant la substituabilité des facteurs. Elle est toujours homogène du premier degré: elle admet donc des rendements d ’échelle constants; supposons en outre que les rendements marginaux du travail sont décroissants; on peut écrire:

^ = Q(l,!p) ,ou

q = q(l) , avec q ’ (1) = >0 , et q ” (1) = <0 . (42) dl

Le produit brut q dépend maintenant de la quantité de travail 1 qui, en toute généralité, varie selon les lieux, si bien que:

q = q [1(x)] .

D ’après l’hypothèse néoclassique de Thünen, le producteur rationnel égalise la valeur du produit marginal du travail et son coût marginal. Ici, compte tenu des frais de transport (Beckmann, 1972):

(pv~rx)q’(1) = w , (43)

où w est constant, et (p -tx) décroissant avec la distance x. Donc v

q ’[l(x)] est croissant avec x, c ’est-à-dire: ^ = q ” (1) 1’ (x) >0 ,

avec q ’’(l) <0 , donc 1’(x) <0 . (44) Ainsi, l’intensité de la production, mesurée par 1, est décroissante de façon continue , pour un bien déterminé, du centre vers la périphérie.

Comment varie alors la rente p avec la distance x ?

p(x) = pvq[l(x)]-wl(x)-Tq[l(x)]x . (45) On montre facilement que, étant donné (43),

p ’ (x) = -xq <0 , puisque x,q >0, et

p ’’(x) = -x q ’(1) 1’(x) >0 , d ’après (42) et (44).

Ainsi, dans les conditions définies ci-dessus, la rente est une fonction décroissante et strictement convexe de la distance: figure

lb (dans le cas d'une fonction de Cobb-Douglas: Saive, 1981; dans un cas plus général: Huriot,1988). Cette fonction de rente intègre les rendements marginaux décroissants du travail et les variations spatiales de l'intensité qui résultent de la rationalité des producteurs. Kellerman (1983a, 1983b, 1989) représente une fonction semblable par une "courbe d ’intensité" et la compare à la "courbe de rente" qui néglige ces éléments. L ’analyse comparative qui suit est sensiblement différente. Elle porte sur les fondements des analyses classique et néoclassique issues de Thünen, et elle est conduite en deux temps.

3.3.1. Rente de localisation et rente intensive.

Il est intéressant de comparer les fonctions de rente obtenues dans le cas classique et dans le cas néoclassique. Dans le premier cas, le producteur est passif et subit un produit brut et une intensité de production fixes; il n ’a aucune marge de manoeuvre dans la détermination du surplus représenté par la rente. La fonction (2) peut s* écrire:

p(x) = p q -wl -xq . (46)

K *vMo o o

Dans le second cas le producteur est actif et choisit produit brut et intensité (liés par la fonction de production) en chaque lieu de manière à maximiser le surplus. La fonction de rente p(x) est alors donnée par (45), avec les propriétés correspondantes.

Les pentes des courbes correspondantes sont respectivement égales à:

p ’ (x) = ~T(ïo P* = “TCl •

Supposons que qQ et 1q sont des valeurs particulières compatibles avec la fonction de production q=q(l), c ’est-à-dire telles que qo=q(lo ). Soit la distance x q à laquelle l'intensité 1 est optimale: 1 =l(x ). A cette distance, on a simultanément:

° o

p(xo) = p(x0)

et p’ (xq) = p* (xq) = -xqo ,

ce qui signifie que les deux courbes sont tangentes en l'abscisse xq,

avec 0 ^ x q î x (figure 6b). Pour toute distance x * xq , on a p > p, ce qui veut dire que p comprend, outre une pure rente de localisation représentée par p, un supplément que l'on peut appeler rente intensive. A une distance x quelconque, elle est égale à:

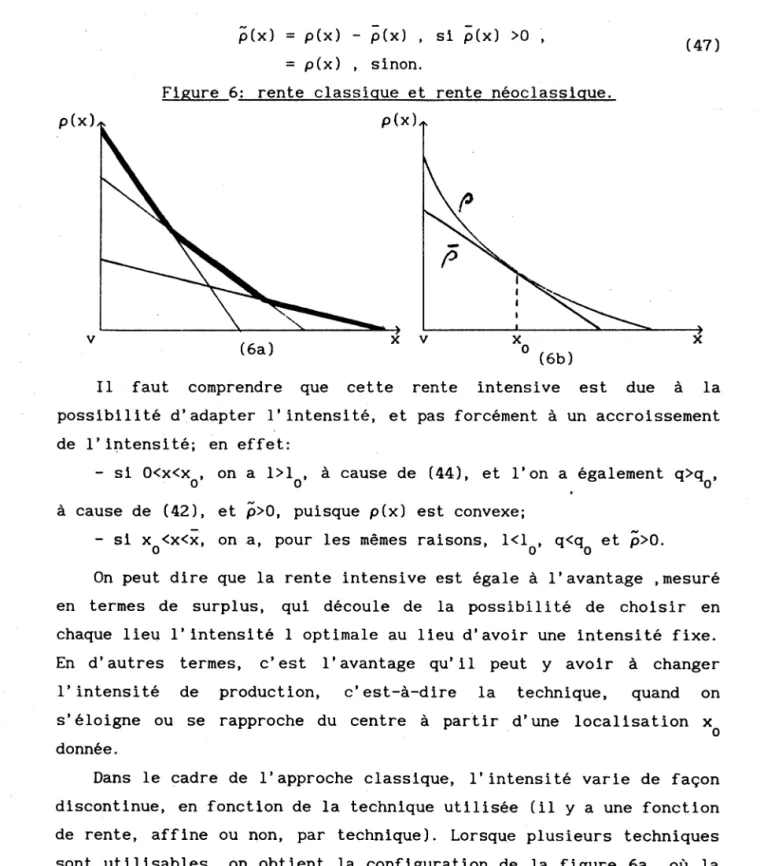
p(x) = p(x) - p(x) , si p(x) >0 , = p(x) , sinon.

Figure 6 : rente classique et rente néoclassique.

possibilité d ’adapter l’intensité, et pas forcément à un accroissement de l’intensité; en effet:

- si 0<x<xq, on a 1> 1Q» à cause de (44), et l’on a également ÇI^q» à cause de (42), et p>0, puisque p(x) est convexe;

- si x q<x<x, on a, pour les mêmes raisons, 1<10» (ï<cï0 P>0.

On peut dire que la rente intensive est égale à l’avantage .mesuré en termes de surplus, qui découle de la possibilité de choisir en chaque lieu l’intensité 1 optimale au lieu d ’avoir une intensité fixe. En d ’autres termes, c ’est l’avantage q u ’il peut y avoir à changer l’intensité de production, c ’est-à-dire la technique, quand on s ’éloigne ou se rapproche du centre à partir d ’une localisation x q donnée.

Dans le cadre de l’approche classique, l’intensité varie de façon discontinue, en fonction de la technique utilisée (il y a une fonction de rente, affine ou non, par technique). Lorsque plusieurs techniques sont utilisables, on obtient la configuration de la figure 6a, où la ligne brisée en trait gras, enveloppe supérieure des courbes de rente à intensité fixe, représente une approximation discontinue de la fonction de rente néoclassique à intensité variable. Cette approximation est d ’autant plus exacte que le nombre de techniques fixes augmente. A partir de cette nouvelle fonction de rente, on peut procéder comme précédemment à une décomposition en rente de localisation et rente intensive; celle-ci mesure toujours, en termes

de surplus, l’avantage du choix de la meilleure technique en chaque lieu. Trois remarques s ’imposent à ce stade.

(a) La décomposition de la rente en rente de localisation et rente intensive est dans une certaine mesure arbitraire, p u i s q u ’elle dépend de l’intensité fixe qui sert de référence.

(b) Si l’on dérive la fonction de rente (45) par rapport à q, on obtient:

P ’ (q) = Pv “w l > (q)“TX »

expression nulle car équivalente à la condition de rationalité (43). Dans le cas d ’une intensité variable, une variation de la fertilité n ’a aucun effet sur la rente, simplement parce que l ’adaptation optimale de l’intensité compense l’influence de la fertilité.

(c) Dans la fonction de rente néoclassique, la fertilité, mesurée par q, et l’intensité, mesurée par 1, sont liées techniquement par une fonction de production et au niveau des comportements par une règle de rationalité (sans laquelle la fonction de rente serait indéterminée). La fertilité perd donc son caractère purement naturel et exogène et devient le résultat d ’un choix technologique. Cela est déjà vrai chez Thünen qui fait varier les frais de production en raison directe de la fertilité (citation en tête du paragraphe 3.2., et relation (34)).

3.3.2. La loi d ’intensité inversée.

Dans la fonction générale de rente (45), nous avons supposé fixe le taux de salaire w. Si l’on abandonne cette hypothèse, la loi d ’intensité décroissante peut être remise en cause, ainsi que, encore une fois, la décroissance de la rente. Supposons que, pour des causes exogènes au modèle, le taux de salaire décroît quand on s ’éloigne du centre'*:

3

La décroissance du taux de salaire peut être due à une évolution des rapports de force défavorable aux salariés, à une diminution des besoins jugés vitaux ou à toute autre cause liée à 1’éloignement du centre, mais exogène c ’est-à-dire indépendante des autres variables du modèle, q et 1. On pourrait bien sûr penser que la variation de w dans l’espace est liée à celle de l’intensité 1; l’inélasticité de l ’offre de travail impliquerait w = w(l), avec w ’(l)>0; alors w(x) = w[l(x)], et w ’(x) = w ’(l)l’(x). La détermination du sens de variation de l’intensité, c ’est-à-dire du signe de 1’(x), serait alors triviale si on spécifiait le sens de variation du taux de salaire, c ’est-à-dire le signe de w ’(x) , et impossible sinon. Mais si la variation de w était endogène, 11 serait impossible de fixer ce signe a priori.

w = w(x) , avec w ’(x) <0 . La fonction (45) devient alors:

p(x) = pvq[l(x)]-w(x)l(x)-Tq[l(x)]x . (48) En chaque lieu la condition de rationalité par rapport à 1 est satisfaite:

(pv -rx)q’(1) = w(x) . (49)

En posant Pv-t x = p^-(x) et en dérivant par rapport à x on obtient: p^(x)q’(l)+pf (x)q’’(l)l’(x)=w’, ou

w ’(x)-p^.(x)q’(1) r ( x ) = p f (x)q’ ’ (1) :

puisque w ’ (x)<0, p^.(x)<0, q ’ (1)>0, p^.(x)>0 et q ’’(l)<0, le signe de q* (1) est indéterminé; toutefois on peut dire que si la décroissance du taux de salaire est relativement faible par rapport à celle du prix à la ferme, c ’est-à-dire par rapport à la croissance du coût de transport, on aura 1* (x)<0; dans le cas contraire, 1* (x)>0.

L ’ intensité de production 1 est décroissante avec la distance au centre si et seulement si la décroissance du taux de salaire est relativement faible; avec un taux de salaire fortement décroissant, elle est croissante.

Si l ’on dérive la fonction de rente, compte tenu de la relation (49) on trouve:

p ’(x) = - w ’(x)l(x)-xq[l(x)] , où w ’(x) <0 .

Ainsi, pour un taux de salaire fortement décroissant, la rente peut à nouveau être croissante avec la distance. Encore une fois, les conditions de fermeture du système spatial sont défaillantes.

4. Conclusion.

Ce papier avait pour but de réviser l’idée déformée q u ’on a généralement de la pensée de Thlinen, 1’*'inventeur" de la fonction de rente spatiale. Nous avons réalisé une formulation mathématique aussi proche que possible de sa propre démarche et de ses suggestions. Nous avons constaté que sa conception de la rente n ’est pas aussi simple

que ce qui est passé à travers le filtre des années et nous avons établi les limites de sa validité, en précisant les propriétés des fonctions de rente et les conditions de leur réalisation. Les exemples de Thünen ont le mérite d ’être pris dans la réalité, mais ils sont dépendants de conditions historiques et locales. Malgré sa richesse souvent ignorée, son analyse théorique n ’atteint pas le degré de généralité q u ’il souhaite lui-même... Est-il atteint aujourd’hui?

Août 1989.

BIBLIOGRAPHIE.

Artie R. , Varaiya P. , 1974, On the existence of positive rent gradients in Thünen models, Memorendum E.R.L.-M459, Electronic Research Laboratory-College of Engineering, University of California, Berkeley. Beckmann M . J . , 1972, Von Thünen revisited: a neoclassical land use model, Swedish Journal of Economics. 74, 1-7.

Huriot J.-M., 1981, Rente foncière et modèle de production, Environment and Planning. A ,13, 1125-1149.

Huriot J.-M., 1986, Taille des firmes et distance au centre ville: une reformulation théorique, in: Problèmes de développement macroéconomique et régional. Akademia Economiczna w Poznaniu, Zeszyty Nankowe, Séria 1, Zeszyt 147, Poznan, 55-66.

Huriot J.-M., 1987, Land rent, production and land use, Sistemi Urbani. 2/3, 167-192.

Huriot J.-M., 1988, L ’espace de production et la rente foncière, in: Ponsard C. , éd., Analyse économique spatiale. Paris, P . U .F . , coll. Economie, 23-57.

Jones A.P., McGuire W.J., Witte A., 1978, A reexamination of some aspects of von Thünen’s model of spatial location, Journal of Regional Science. 18, april, 1-15.

Kellerman A. , 1983a, Agricultural location theory: a review and bibliography of theory and applications, Regional Science Research

Institute, Discussion Paper n°129, Peace Dale, december.

Kellerman A., 1983b, Economic and spatial aspects of von Thü ne n ’s

factor intensity theory, Environment and Planning. A, 15, 1521-1530. Kellerman A . , 1989, Agricultural location theory, 1 & 2, Environment and Planning A . à paraître.

Lösch A. , 1940, Die Räumliche Ordnung der Wirtschaft. Jena, G. Fischer. Rééditions: 1944, 1962.

Traduction anglaise par Woglom W. H. et Stolper W . F . , 1954, The Economics of Location. New Haven, Yale University Press.

Morgan W.B . , 1973, The doctrine of the rings, Geography. 58, 301-312. Ponsard C., 1955, Economie et espace. Paris, S.E.D.E.S.

Ponsard C. , 1958, Histoire des théories économiques spatiales. Paris, Armand Colin.

Traduction anglaise par Stevens B.H., Chevaillier M., Pujol J.P. , 1983, History of spatial economic theory. Berlin, Springer-Verlag. Saive M. A . , 1981, Le modèle de von Thünen et la localisation agricole,

in: Analyse spatiale et utilisation du sol, actes du colloque 1980 de l’A.S.R.D.L.F. , Dijon, L ’Economie du Centre-Est. 23-1, 117-139.

Samuelson P .A. , 1983, Thünen at two hundred, Journal of Economic Literature. XXI, december, 1468-1488.

Schumpeter J. , 1954, History of Economic Analysis. London, Allen & Unwin.

Traduction française sous la dir. de Casanova J.C., 1983, Histoire de L ’analyse économique. Paris, Gallimard, 3 vol.

Scott A.J., 1979, Commodity production and the dynamics of land use, Urban Studies. 16, 95-104.

Scott A . J . , 1980, The urban land nexus and the state. London, Pion. Thünen von- J.H. , 1826-1863, Der Isolierte Staat ln Beziehung auf Landwirtschaft und Nationalöconomie.

Vol. I, 1826, Hamburg, Perthes. Traduction française par Laverrière J. ,1851, Recherches sur l’influence que le prix des grains la richesse du sol et les impôts exercent sur les systèmes de culture. Paris, Guillaumin.

Vol. II, Section 1, 1850, Rostock, Leopold. Traduction française par Volkoff M. , 1857, Le salaire naturel et son rapport au taux de

1’intérêt. Paris, Guillaumin.

Vol. II, Section 2 et Vol. III, éd. posthume par Schumacher H . , 1863, Rostock, Hinstorff.

LISTE DES DOCUMENTS DEJA PUBLIES

n* 1

Michel PREVOT

: Théorème du point fixe. Une étude topologique

génrérale (juin 1974).

n* 2

Daniel LEBLANC

: L ’introduction des consommations intermédiai­

res dans le modèle de LEFEBER (juin 1974).

n*

3

Colette BOUMON

: Spatial equilibrium of the sector in quasi­

perfect competition (September 1974).

n* 4

Claude PONSARD

: L ’imprécision et son traitement en analyse

économique (septembre 1974).

n*

5

Claude PONSARD

: Economie urbaine et espaces métriques (sep­

tembre 1974).

n*

6

Michel PREVOT

: Convexité (mars 1975).

n* 7

Claude PONSARD

: Contribution à une théorie des espaces écono­

miques imprécis (avril 1975).

n* 8

Aimé VOGT

: Analyse factorielle en composantes principales

d ’un caractère de dimension n (juin 1975).

n*

9

Jacques THISSE et Jacky PERREUR

: Relation between the point

of maximum profit and the point of minimum total transportation cost : a restatement July 1975).

n*

10

Bernard FUSTIER

: L ’attraction des points de vente dans des

espaces précis et imprécis (juillet 1975).

n*

11

Régis DELOCHE

: Théorie des sous-ensembles flous et classifi­

cation en analyse économique spatiale (juillet 1975).

n' 12

Gérard LASSIBILLE et Catherine PARRON

: Analyse multicritère

dans un contexte imprécis (juillet 1975).

n' 13

Claude PONSARD

: On the axiomatization of fuzzy subsets theory

(July 1975).

n' 14

Michel PREVOT

Probability calculation and fuzzy subsets

theory (August 1975).

n* 15

Claude PONSARD

: Hiérarchie des places centrales et graphes

flous (avril 1976).

n ’

16

Jean-Paul AURAY et Gérard DURU

. : Introduction à la théorie

des espaces multiflous (avril 1976).

n* 17

Roland LANTNER, Bernard PETITJEAN et Marie-Claude PICHERY :

n* 18

Claude PONSARD

: Esquisse de simulation d ’une économie régio­ nale : l’apport de la théorie des systèmes flous (septembre 1976).

n* 19

Marie-Claude PICHERY

: Les systèmes complets de fonctions de

demande (avril 1977).

n* 20

Gérard LASSIBILLE et Alain HINGAT

: L ’estimation de modèles à

variation dépendante dichotomique. La sélection universitaire et la réussite en première année d ’économie (avril 1977).

n* 21

Claude PONSARD

: La région en analyse spatiale (mai 1977).

n* 22

Dan RALESCU

: Abstract models for systems identification (June

1977).

n*

23

Jean MARCHAL et Frédéric P0UL0N

: Multiplicateur, graphes et

chaînes de Markov (décembre 1977).

n' 24

Pietro BALESTRA

: Déterminant and inverse of a sum of matrices

with applications in économies and statistics (avril 1978).

n'

25

Bernard FUSTIER

: Etude empirique sur la notion de région

homogène (avril 1978).

n* 26

Claude PONSARD

: On the imprécision of consumer’s spatial pre-

ferences (April 1978).

n*

27

Roland LANTNER

: L ’apport de la théorie des graphes aux repré­

sentations de l’espace économique (avril 1978).

n* 28

Emmanuel JOLLES

: La théorie des sous-ensembles flous au ser­

vice de la décision : deux exemples d ’application (mai 1978).

n ’

29

Michel

PREVOT : Algorithme pour la résolution des systèmes

flous (mal 1978).

n ’

30

Bernard FUSTIER

: Contribution à l’analyse spatiale de l’at­

traction imprécise (juin 1978).

n* 31

Phuoc TRANQUI

: Régionalisation de l ’économie française par

une méthode de taxinomie numérique floue (juin 1978).

n ’ 32

Louis de MESNARD

: La dominance régionale et son imprécision, traitement dans le type général de structure (juin 1978).

n ’ 33

Max PINHAS

: Investissement et taux d ’intérêt. U n modèle stochastique d ’analyse conjoncturelle (octobre 1978).

n* 34

Bernard FUSTIER et Bernard ROUGET

: La nouvelle théorie du

consommateur est-elle testable ? janvier 1979).

n*

35

Didier DUBOIS

: Notes sur 1’intérêt des sous-ensembles flous