Approche combinatoire des modèles minimaux en théorie des champs conformes : connexion avec les chemins sur réseau demi-entier

OLIVIER BLONDEAU-FOURNIER

Approche combinatoire des modèles minimaux en

théorie des champs conformes

Connexion avec les chemins sur réseau demi-entier

Mémoire présenté

à la Faculté des études supérieures de l'Université Laval dans le cadre du programme de maîtrise en physique pour l'obtention du grade de Maître es sciences (M.Sc.)

FACULTÉ DES SCIENCES ET DE GÉNIE UNIVERSITÉ LAVAL

QUÉBEC

2010

Une description des états Virasoro dans les modules irréductibles de plus haut poids des modèles minimaux À4(p,p') en théorie des champs conformes est fournie par les chemins RSOS. Ces chemins sont issus des configurations des hauteurs sur une rangée du réseau des modèles statistiques exactement résolubles RSOS lors de l'évaluation de la probabilité locale d'une hauteur dans le régime III. Une seconde catégorie de chemins, définis sur un réseau demi-entier, a été proposée et élevée au rang de conjecture comme une description alternative des états Virasoro pour les modèles À4(p, 2p + 1). L'avantage de cette seconde catégorie de chemins réside dans la formulation du poids qui ne dépend plus de la hauteur. L'analyse combinatoire de ces derniers est suffisamment simple pour permettre d'obtenir leurs fonctions génératrices qui sont, en vertu de la conjecture, équivalentes aux formules de caractères pour ces modèles minimaux. En nous intéressant davantage à ces chemins sur réseau demi-entier, nous avons découvert qu'il est également possible de les utiliser pour décrire les états Virasoro des modèles Ai(p + 1.2p+ 1). Nous présentons l'analyse combinatoire pour cette nouvelle classe ainsi que la dérivation des fonctions génératrices. Nous montrons également comment relier les chemins sur réseau demi-entier aux chemins RSOS au moyen d'une bijection qui préserve le poids. Par conséquent, nous validons la conjecture sur l'équivalence des chemins sur réseau demi-entier et des états Virasoro pour tous les modèles minimaux M ( p + e,2p-rl), e = 0,1.

Avant-propos

Je tiens à remercier particulièrement le professeur Pierre Mathieu, mon directeur de recherche, pour sa grande compréhension, son enthousiasme et sa patience. Il m'a donné le privilège de pouvoir effectuer mon travail de recherche dans un environnement sans contrainte et sans pression. Sa grande disponibilité et ses conseils avisés m'ont permis de progresser dans mes travaux tout en évitant les embûches. Il m'a également donné l'opportunité de voyager à l'étranger pour assister à des conférences et à des colloques dans le but d'apprendre, dans une large mesure, sur des sujets connexes au mien.

Un merci spécial à Trevor Welsh, chercheur post-doctoral à l'Université de Toronto et (maintenant) à l'Université Laval pour sa collaboration. Les bijections présentées aux chapitres 4 et 5 ont également été indépendamment découvertes par ce chercheur. Notre collaboration a mené à une publication sur la bijection du chapitre 4.

Je ne voudrais pas oublier de remercier ma conjointe Lison pour son soutien constant, par temps clair comme par temps couvert, et ce malgré son travail très prenant. Merci à ma famille et à mon très bon ami Benoît pour avoir su me changer les idées lorsque j'en ai eu besoin.

Au coeur de l'hiver, j'ai finalement appris qu'en moi existe un été invincible.

Table des matières

Résumé ii Avant-propos iii

Table des matières v Table des figures vii

Introduction 1 1 L'algèbre de Virasoro 6

2 Les chemins RSOS 12

2.1 Définition 16 2.1.1 Le poids 17 2.2 Les caractères de l'algèbre de Virasoro 20

2.3 Deux classes particulières 21 3 Les chemins sur réseau demi-entier 23

3.1 Définition 25 3.1.1 Le poids 26 3.1.2 La charge 27 3.2 Les caractères de l'algèbre de Virasoro 29

3.3 Les fonctions génératrices des 1ip(X 29

3.3.1 Configuration de poids minimal 30 3.3.2 Configuration générique à charge totale fixe 33

3.3.3 Fonction génératrice pour tous les modules 36

3.3.4 Vers les caractères M [p + 1, 2p + 1 ) 39 3.4 Les fonctions génératrices des chemins duaux 41

3.4.1 Lien avec les partitions dentelées restreintes 46 4 Bijection entre les chemins pour les modèles M{p.2p+ 1) 51

4.1 Introduction 52 4.1.1 Les opérateurs {c, c*,d} 52

4.1.2 Les opérateurs {c,c*,d} 55 4.2 Description de la bijection 57 5 Bijection entre les chemins pour les modèles M ( p + l , 2 p + 1) 61

5.1 Introduction 62 5.2 Description de la bijection 63

5.3 Retrait des paires de vertex N 67 5.4 Inversion du chemin compressé 68 5.5 Ajout de pics de charge 1/2 70

5.6 Creusage des vallées 72 5.7 Tout ensemble maintenant 75

Conclusion 77 A Notation 79

A.l Fonction génératrice 79

A.2 Partitions 80 B Partitions dentelées 85

Table des figures

2 . 1 Pour une face i, j , m , n du réseau, on identifie une h a u t e u r à chaque site conformément à (2.1) et à la condition (2.2) qui implique que l'on doit avoir |/$ — lj\ = \lj — ln\ =

\lm — ln\ = I'm — h\ = 1- Un poids (non-nul) W ( l i , l j \ l m A n ) est ensuite associé à

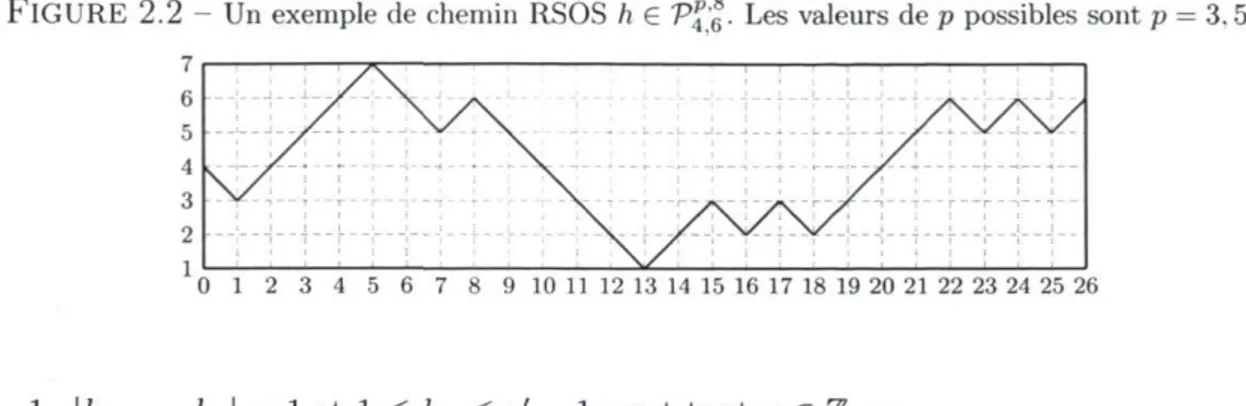
chaque face du réseau d é p e n d a m m e n t des valeurs des h a u t e u r s 1 3 2 . 2 Un exemple de chemin RSOS h e V%'6 ■ Les valeurs de p possibles sont p = 3,5,7. . 17

2 . 3 Le même chemin q u ' à la FlG. 2.2 avec p = 3 et la s t r u c t u r e de bande correspondante. Seulement les vertex indiqués avec un cercle (vide ou plein) contribuent au poids. Les vertex avec un cercle vide ont un poids Ui et ceux avec un cercle plein, un poids Vi

(ces valeurs é t a n t définies en (2.16)) 19 2 . 4 Un exemple de chemin a p p a r t e n a n t à l'ensemble V \ -i. Les cercles vides indiquent

les vertex S-montant, ayant un poids ux, et les cercles pleins indiquent les vertex

^-descendant, ayant un poids vx. Leurs valeurs sont spécifiées à l'équation (2.16). . 2 2

2 . 5 Un exemple de chemin a p p a r t e n a n t à l'ensemble Vf 2- Les cercles vides indiquent les vertex S-montant, ayant un poids ux, et les cercles pleins indiquent les vertex

S-descendant, ayant un poids vx. Leurs valeurs sont spécifiées à l'équation (2.16). . 2 2

3 . 1 Un exemple de chemin a p p a r t e n a n t à l'ensemble H Q i 2 5 3 . 2 Un exemple de chemin a p p a r t e n a n t à l'ensemble H A 1 26

2 ' 2

3 . 3 Exemple de deux chemins fondamentaux pour les ensembles r l J s (à gauche) et % , .

2 ' 2 2 ' 2

(à droite) 2 7 3 . 4 Un exemple de configuration de poids minimal pour un chemin r l \ t avec n i /2 =

2 ' 2

n5/2 = 1 et n i = n3/2 = n2 — 2 3 0

3 . 5 Exemple d ' u n e séquence de déplacements d'un pic de charge 1/2 vers la gauche, traversant un pic de charge 5 / 2 . Le pic de charge 1/2 traverse le pic de charge 5/2 en 4 étapes où chaque é t a p e augmente le poids de un. A u t r e m e n t dit, si la première

configuration a un poids de g, alors la configuration finale a un poids de g + 4. . . 3 4 3 . 6 Un chemin générique (e) s'obtient de sa configuration de poids minimal (a), avec

n5/2 = n2 = 1, n-.$/2 = n\ = 2 et n i /2 = 5, par les déplacements de ses pics : u '2 ) = (1),

^(3/2) _ ( 2 , i )j / z( i ) = (4.2) et /i(1/2> = ( 1 2 , 1 0 . 8 . 5 . 3 ) m o n t r é s respectivement en (b),

3.7 Modification de la configuration de poids minimal lorsque les conditions initiales et finales a.b varient. Ces deux effets peuvent être traités indépendamment. Le chemin

du haut correspond à a = 1/2 —> 5/2 et pour le chemin du bas, b = 1/2 —> 5/2. . . 38 3.8 Exemple de chemin h G ^3/2 (a) et le chemin fondamental /icf correspondant (b). 42 3.9 Chemin de Bressoud restreint B2 5 correspondant au chemin de la FlG. 3.8(a). . . 49 4.1 Action des opérateurs cx, c* et bx sur une portion de chemin purement oscillante

entre les hauteurs / et l + 1. Les cercles (pleins ou vides) indiquent le type de vertex qui est généré suite à l'action de l'opérateur. L'opérateur d peut agir sur un creux (c)

ou sur un pic (d) 53 4.2 Action des opérateurs dx, cx et c* sur une portion de chemin oscillant entre les

hauteurs l et l - 1/2, où Z e Z. Les points noirs indiquent la position des vertex qui

sont des montées ou des descentes générés par l'action des opérateurs 56 5.1 Le chemin hc o m p obtenu à partir du chemin h de la FlG. 2.5 en retirant les K = 7

paires de vertex N . On a M = 16, un poids de wt(/icomp) = 97 et une longueur V = 38 — 2(7) = 24. On a également ajouté le segment pré-initial et le segment

post-final 66 5.2 Le chemin compact hc o m p sur le réseau demi-entier obtenu à partir de hc o m p de la

FlG. 5.1 en le renversant (en le lisant depuis la droite) et en creusant chacune des vallées. On a un poids de wt(hc o m p) = 97 et une longueur Ï = 24/2 + (5 - 1) = 16. On a également ajouté le segment pré-initial et le segment post-final. Les vallées sont

numérotées de gauche à droite (débutant avec la vallée à gauche du premier pic). . 66 5.3 Le chemin h^ obtenu depuis la FlG. 5.2 en creusant les vallées 5 et 3. Les numéros

indiquent les positions (représentées par un cercle vide avec une croix à l'intérieur) de gauche à droite où il est possible d'insérer une séquence de liens NE-SE (un pic de

charge \ ) 67 5.4 Exemple d'un déplacement d'une vallée, identifiée par le point noir, partant d'entre

le premier et deuxième pic à la position entre le deuxième et troisième pic 73 5.5 Deux exemples de transformations d'un pic de charge i , identifié par un point noir,

en une vallée à la position # 1, également identifiée par un point noir 74 A . l Les 10 configurations différentes des chemins entre les points (0.0) et (2.3) 84

A.2 Les 10 partitions associées aux chemins de la FlG. A.l 84 B . l Exemple d'un chemin de Bressoud restreint, h S BJ avec n\ = 4 et n.2 = TI3 = 1. . 88

Introduction

Les modèles statistiques exactement résolubles [5] permettent de modéliser et de décrire les transitions de phases. Typiquement, ce sont des réseaux rectangulaires (ré-guliers) où chaque site est occupé par une certaine valeur (spin ou hauteur) et un poids (ou énergie) y est associé dépendamment des valeurs de ses plus proches voisins. L'ana-lyse de ces modèles consiste à utiliser les outils de la physique statistique : à partir des interactions locales entre plus proches voisins peut se déduire un comportement global (macroscopique) du système. Par le calcul de la fonction de partition, il est possible d'obtenir par la suite des quantités physiques telles l'énergie libre ou encore la chaleur spécifique.l En prenant la limite thermodynamique, i.e. le nombre de sites du réseau devenant infini, on détermine les exposants critiques qui décrivent le comportement du point critique associé au modèle statistique.2 Un des premiers modèles à avoir été considéré, et sans doute l'un des plus connus, est le modèle d'Ising : chaque site prend une valeur de spin soit de +1/2 ou de —1/2. Onsager, en 1944, solutionne ce modèle et donne le calcul de l'énergie libre. Une expression pour la magnétisation spontanée est trouvée un peu plus tard par Yang en 1952. Ce modèle permet de décrire la transition ferromagnétique à anti-ferromagnétique d'un métal.

Une propriété déterminante pour de tels modèles est l'intégrabilité. Cela signifie que

1. La fonction de partition est une somme sur toutes les configurations (avec l'énergie de la configu-ration associée) du réseau Z = ^2exp[-E/kT] où k est la constante de Boltzmann et T la température. L'énergie libre est donnée par F = — kTln Z.

2. Soit N, le nombre de sites du réseau. En s'intéressant à la limite / = lim/v^œ N ~lF , un exemple d'exposant critique pour la chaleur spécifique c est le suivant :

c = - d r T2d r [ f / T } ~ [(T - Tr) / T , ] -a lorsque T -> T+

où Tc est la température du point critique et a l'exposant critique. D'autres exposants critiques parmi les principaux sont les suivants (avec t = (T - Tc)/Tc) :

Magnétisation spontanée : A/o ~ (—t) lorsque t —» 0~ Susceptibilité magnétique : \ ~ ( t ) " lorsque t —> 0+.

l'on peut obtenir de manière exacte, i.e. sans approximation, la fonction de partition. Il s'agit d'une condition très importante pour tous modèles statistiques décrivant les transitions de phases. Cette condition est motivée par la raison suivante. Si l'on définit une longueur de corrélation entre deux hauteurs sur le réseau, celle-ci deviendra infi-nie au point critique.3 Cela implique que des régions éloignées du réseau deviennent soudainement fortement intriquées. En outre, si l'on fait quelques approximations, on néglige des termes correspondant aux interactions de longues portées qui se révèlent essentielles pour décrire le comportement au point critique. Il est donc crucial de pou-voir résoudre exactement le modèle statistique. Après le travail d'Onsager sur le modèle d'Ising, d'autres modèles statistiques importants seront résolus. Parmi ceux-ci, il y a le modèle à 6 vertex (Lieb, 1967), à 8 vertex (Sutherland, 1970), le modèle des hexagones durs (Baxter, 1981) et les modèles de type RSOS, restricted s olid-on-s olid, (Andrews, Baxter et Forrester, 1984). Ce dernier sera central pour ce mémoire.

Baxter [33] synthétise cette question d'intégrabilité. Il montre qu'une paramétri-sation particulière des poids de Boltzmann (via des fonctions elliptiques) assurant la validité d'une symétrie locale, soit la relation triangle-étoile (ou Yang-Baxter), permet de résoudre exactement le modèle statistique. Plus précisément, cette relation implique que les matrices de transferts commutent. La fonction de partition dans la limite ther-modynamique s'obtient ainsi à partir de la (plus grande) valeur propre associée à ces matrices.4 En plus, Baxter découvre une technique révolutionnaire permettant d'obte-nir une expression explicite pour la probabilité d'une hauteur sur le réseau, ainsi que pour les exposants critiques, sans le calcul direct de la fonction de partition : c'est la technique des matrices de transferts de coins, MTC (le chapitre 13 de son livre [5] en est le sujet principal; voir aussi [6] pour une introduction).

Une seconde approche dans l'étude des transitions de phases est amorcée en 1984 par la découverte de la théorie des champs conformes (TCC) par Belavin, Polyakov et Zamolodchikov [8]. L'idée est que l'invariance d'échelle, qui est une signature d'un point critique, est élevée à l'invariance conforme, soit le groupe de symétrie fondamental de la TCC. L'application majeure de la TCC devient alors l'étude des transitions de phases et permet le calcul des fonctions de corrélations ainsi que des exposants critiques via les dimensions conformes des champs primaires. Par la suite, il est remarqué par Huse [24] (pour le cas unitaire) et plus tard par Riggs [35] (pour le cas général) que les dimensions conformes pour les modèles minimaux M.(p,p') sont les mêmes que

3. Remarquons que la divergence de la longueur de corrélation est une signature d'un point critique. 4. Les matrices de transferts furent utilisées dans la solution du modèle d'Ising par Onsager. Il s'agit de décomposer la fonction de partition en un produit de matrices. La fonction de partition correspond à la trace de ce produit. Conceptuellement. ces matrices de transferts agissent une à la suite de l'autre pour reconstruire le réseau, diagonale par diagonale.

Introduction

les exposants critiques des modèles statistiques RSOS.5 Par conséquent, les modèles minimaux en TCC sont associés à la limite d'échelle des mdèles RSOS.

Mais il y a plus encore. Le calcul de la probabilité d'une hauteur dans le réseau pour les modèles statistiques RSOS [3, 23] dans le régime III, par la méthode des MTC, mène à l'évaluation d'une sommation sur des configurations de séquences d'entiers. Ces configurations peuvent être interprétées comme des chemins dans le plan x-y.6 Chaque chemin possède un poids qui peut être calculé directement depuis sa représentation graphique. En calculant les fonctions génératrices des chemins RSOS dans la limite de longueur infinie, on obtient que celles-ci sont égales aux formules de caractères des modules irréductibles des représentations de plus haut poids pour tous les modèles minimaux M.(p,p') en TCC. Autrement dit, pour un module irréductible quelconque, chaque état Virasoro peut être représenté par un chemin RSOS de poids égal au ni-veau où il se situe dans le module. Deux types de fonctions génératrices sont possibles. Lorsqu'elles sont obtenues via des relations de récurrences, elles sont généralement sous la forme de séries alternées que l'on nomme forme bosonique. Par opposition, une véri-table analyse combinatoire des chemins par des méthodes constructives conduit à une expression sous la forme de séries définies positivement, de forme fermionique. Bien qu'il soit relativement assez simple d'obtenir des expressions de formes bosoniques pour les fonctions génératrices des chemins RSOS, obtenir des expressions de formes fermio-niques par des méthodes constructives se révèle particulièrement compliqué. La raison provient du fait que le poids des chemins RSOS dépend, dans la plupart des cas, de la hauteur du chemin.

Toutefois, une nouvelle catégorie de chemins a été proposée récemment [27], dé-finie sur les positions entières et demi-entières du plan x-y et pouvant décrire les états Virasoro pour une classe spécifique de modèles minimaux en TCC : les modèles M{p,2p + l ) .7 Ces chemins ont été introduits comme la version duale (q —» g"1) des chemins décrivant les partitions dentelées (2p—2)-restreintes [19, 20, 30] , base décrivant les parafermions gradués [13, 25, 26]. L'avantage qu'ils possèdent est que l'expression du poids ne dépend plus de la hauteur, rendant par conséquent l'analyse combinatoire très simple. Le désavantage est que ces chemins ne découlent pas d'un modèle physique relié à la TCC. Ainsi, les auteurs de [27] ont fait la conjecture suivante : les fonctions génératrices des chemins sur réseau demi-entier dans la limite de longueur infinie sont égales aux formules de caractères pour les modèles M(p, 2p + 1).

5. Les modèles unitaires en TCC sont les modèles minimaux pour lesquels les paramètres p.p' ont une différence de 1 : M ( p . p + 1).

6. Ceux-ci seront d'ailleurs référés comme les chemins RSOS. 7. Ces chemins sont appelés chemins sur réseau demi-entier.

Dans le cadre de mon projet de recherche à la maîtrise, cette conjecture a constitué mon premier sujet d'intérêt. La validation de cette conjecture a pu être démontrée grâce à la construction d'une bijection, une transformation 1—1, reliant l'ensemble des chemins sur réseau demi-entier à l'ensemble des chemins RSOS (associés aux modèles M(p, 2p+ 1)). Puisque les chemins RSOS décrivent les états Virasoro dans les modules irréductibles de plus hauts poids, on obtient par conséquent la confirmation que les chemins sur réseau demi-entier décrivent également les états Virasoro.

En outre, en s'intéressant davantage à cette nouvelle base de chemins sur réseau demi-entier, il a été découvert que celle-ci peut être également utilisée pour décrire les états Virasoro pour les modèles M ( p + 1, 2p+ 1). Par une méthode constructive, l'ana-lyse combinatoire des chemins sur réseau demi-entier a permis d'obtenir les fonctions génératrices sous formes fermioniques. L'expression duale (q —r ç- 1) a été reliée par une transformation, qui ne préserve pas le poids des chemins, aux partitions dentelées (2p — 1)—restreintes. Une seconde conjecture a pu ainsi être formulée : les fonctions génératrices des chemins sur réseau demi-entier dans la limite de longueur infinie sont égales aux formules de caractères pour les modèles M.(p + 1, 2p + 1).

Enfin, cette seconde conjecture a pu être validée par la construction d'une deuxième bijection entre l'ensemble des chemins sur réseau demi-entier et l'ensemble des chemins RSOS (associés à la description des modèles Ai{p + 1, 2p + 1)).

L'organisation de ce mémoire est comme suit. Dans le chapitre 1, on introduit l'al-gèbre de Virasoro ainsi que les modèles minimaux des théories de champs conformes. La structure des modules irréductibles de plus haut poids et les formules de caractères sont présentées.

Dans les chapitres 2 et 3, on définit les deux classes de chemins : les chemins RSOS et les chemins sur réseau demi-entier. On spécifie également les chemins RSOS pour les modèles M ( p + e, 2p + 1), e = 0,1. Une analyse combinatoire pour les chemins sur réseau demi-entier ainsi que les fonctions génératrices pour le nouveau cas (associé à e = 1) sont également présentées. On s'intéresse également à la version duale de ces chemins et l'on indique le lien avec les partitions dentelées.

Le coeur du mémoire, soit les chapitres 4 et 5, relie les chemins RSOS aux chemins sur réseau demi-entier par une bijection qui préserve le poids, démontrant ainsi que la base des chemins sur réseau demi-entier décrit les états Virasoro dans un module de plus haut poids. Dans un premier temps, pour les modèles M.(p, 2p + 1), on introduit une base d'opérateurs qui génère les chemins et qui se transforme d'une classe de chemins à l'autre en préservant le poids. En second lieu, pour les modèles M.{p + l,2p + 1),

Introduction

l'utilisation d'opérateurs se révèle superflue et l'on utilise plutôt une technique similaire à celle de [9] où l'on déconstruit le chemin en le codant avec des partitions que l'on utilise ensuite pour reconstruire le chemin correspondant. Pour les deux bijections, on présente la preuve que celles-ci préservent le poids.

Enfin, deux annexes ont été ajoutées pour compléter certains sujets traités dans ce mémoire et peuvent être consultées indépendamment des chapitres. Toutefois, il est recommandé de consulter l'annexe A pour la notation utilisée tout au long de ce mémoire.

L'algèbre de Virasoro

L'algèbre de Virasoro est une algèbre de Lie affine (de dimension infinie) avec une extension centrale, construite à partir de l'algèbre décrivant les sy-métries conformes du plan : translation, rotation, inversion et dilatation (i.e. l'ensemble des transformations qui préservent les angles entre deux droites). Cette algèbre est entre autres essentielle en théorie des champs conformes pour la classification des champs quantiques et l'analyse des représentations irréductibles de plus haut poids.

La majeure partie des notions de la théorie des champs conformes n'étant pas nécessaire dans ce mémoire, par conséquent, seulement les notions requises seront introduites.

L'algèbre de Virasoro [22, §12] est un espace vectoriel de dimension infinie dont les générateurs sont :

Vir = (Ln , n G 1 ) . (1.1)

La règle de produit entre les générateurs est définie via le crochet de Lie (qui est l'opérateur bilinéaire antisymétrique) :

[Ln , Lm] = (n - m ) Ln + m + y xn( "2 - l)<Wm,o K, [Ln . K] = 0. (1.2)

K est l'élément central et le crochet de Lie sera pris comme le commutateur usuel, i.e. [Ln. Lm] = LnLm — LmLn.] Le générateur LQ est l'opérateur diagonal, c'est-à-dire pour

1. Les opérateurs de l'algèbre sont quasi-hermitiques, i.e. L]n = L_m. Le produit (intérieur) entre deux états est défini comme :

( a L „ K P Li nV ) = aif3L-.nLm(V,V') pour o,/? des constantes.

Chapitre 1. L'algèbre de Virasoro

TABLE 1.1 - Premiers états Virasoro descendant d'un plus haut poids.

£

m

r

_LU,

LU,

un état (ou vecteur) V, on obtient :

L0 V = v V, (1.3)

où v est la valeur propre de L0 associée au vecteur V. Les autres générateurs sont des opérateurs d'échelle. Suite à l'application d'un générateur Ln, la valeur propre est changée comme suit :

L0 LnV = (LnL0 - n Ln) V = (v - n) LnV, (1.4)

où l'on a utilisé la relation (1.2) pour changer l'ordre des opérateurs. Si n est positif (négatif), la valeur propre est donc diminuée (augmentée) par n; c'est ce qui définit le changement de niveau de l'état (ou vecteur). Plus généralement, un état générique W = L_niL_n. L-nkV aura une valeur propre associée de

L0 W = (v + A£)W (1.5)

avec Ai = 2~2ni et l'on dira que l'état W est au niveau A£ relativement à l'état V. Pour un état de plus haut poids h, définit par :

Ln>o h — 0, (1.6)

le niveau sera par définition £ = 0. À partir d'un état de plus haut poids h, on peut identifier niveau par niveau les différents états pouvant être obtenus à partir de celui-ci suite à l'application successive des modes de Virasoro, L_n iL_„2... L^nkh. On obtient ainsi typiquement un module de Verma. Le tableau (1.1) montre les premiers états possibles (partant d'un état de plus haut poids). La valeur d(£) est par définition le nombre d'états Virasoro au niveau £ dans un module de plus haut poids h. 2 On re-marque qu'il y a un nombre infini de niveaux, mais à chaque niveau, un nombre fini

(dénombrable) d'états. On appelle le caractère, x/i, la fonction génératrice qui exprime le nombre d'états, partant d'un plus haut poids h, à chaque niveau. Typiquement, cette fonction est choisie comme une simple série de puissance où chaque coefficient indique le nombre d'états correspondant au niveau indiqué par la puissance de la variable de sommation :

X/,(<7) := $ > W < 7n, (1.7)

n>0

avec d(0) = 1 et où la variable q est une variable auxiliaire (sans signification). Pour un module de Verma, (TAB.1.1) on compte évidemment le nombre p(n) de partitions A := (Ai,..., Xm) de n = ^ Ai avec Ai > . . . Am > 0 avec l'équivalence triviale :

(Ai,...,Am) o L_Al . ..L_A m/i.

Par exemple, il y a 5 partitions de 4 : (4), (3,1), (2,2), (2,1,1), (1,1,1,1) chacune cor­ respondant à un état listé dans le tableau ci­haut. Donc, pour le module de Verma, on a :

d(n) =p{n),

et la fonction génératrice des partitions de n est un résultat bien connu, dû à Euler [1] :

E ^

= è ■

(i­8)

n > 0 (<?)c

Le cas du module de Verma est donc Xh{o) = ( Q ) ^ ­ P1U S loin, les modules de plus haut poids que l'on considère contiennent des vecteurs singuliers que l'on doit retirer et par conséquent, les formules de caractères ne sont pas aussi simples.

L'algèbre de Virasoro joue un rôle essentiel en théorie des champs conformes. Grâce à la correspondance champs­états, elle permet de classifier les champs par famille ou par module de plus haut poids. Les générateurs de l'algèbre apparaissent dans le déve­ loppement en série de Laurent du tenseur énergie­impulsion, celui­ci étant responsable des transformations conformes.

La théorie des champs conformes, dénotée TCC, est une théorie des champs quan­ tiques en deux dimensions avec la propriété d'invariance conforme [8, 15]. (Voir aussi les références [34, 14, 41] pour une introduction plus pédagogique. La référence [34] est celle sur laquelle se base majoritairement les notions de la TCC présentées dans ce chapitre.

avec (1.2) :

soit une combinaison linéaire de deux états déjà comptés. En fait, par convention, on prend n\ > n2 > . . . > Tifc pour l'état L_r i lL_„2 .. .L­„kh . On ne compte pas non plus par exemple l'état L\L_2 au niveau (. = 1 pour la même raison. On prend alors également n^ > 0.

Chapitre 1. L'algèbre de Virasoro 9

La référence [21] fait l'historique des avancées majeures depuis les 25 dernières années). Typiquement, les transformations conformes incluent les rotations, translations, inver­ sions et dilatations. En deux dimensions, en travaillant dans le plan complexe avec les coordonnées z = x + iy et z = x — iy, les transformations conformes sont les fonc­ tions analytiques z —> w(z) et anti­analytiques z —»■ w(z). Avec ce nombre infini de contraintes pour les transformations conformes, il est possible de déterminer la forme des fonctions de corrélations entre les champs quantiques.

Un rôle important est joué par le tenseur énergie­impulsion. Lorsque l'action est invariante sous translation et rotation, on obtient que le tenseur énergie­impulsion est conservé. En plus, si l'action est aussi invariante sous une transformation d'échelle (ou dilatation), la trace de ce tenseur est nulle. Par conséquent (en deux dimensions), les seules composantes non­nulles sont :

­2TTT,,2 = T(z) et ­2­nT­z­z = T ( z ) (1.9) où les deux secteurs sont appelés holomorphe et anti­holomorphe respectivement. En

fait, cette séparation apporte une simplification supplémentaire en TCC puisque un problème en deux dimensions se ramène en une analyse de deux problèmes (indépen­ dants dans une large mesure) d'une dimension. Les générateurs de l'algèbre de Virasoro sont les modes de Laurent du tenseur énergie­impulsion :

T(z) = Y

L

z­

­

. (1.10)

nez

En TCC, il y a une infinité de champs quantiques. Ceux­ci peuvent se regrouper en famille comme suit. Chaque famille est caractérisée par un champ primaire (ph qui se transforme rph(z) —> 4>'h(w) sous une transformation conforme z —» w(z) telle que :

<j>'h{w){dw)h = 4>h{z){dz)h (1.11) où h est appelé la dimension conforme. Les autres champs quantiques (dans la même

famille) s'obtiennent soit par des dérivés de rfrh ou encore par des combinaisons de T(z) avec 0/,. Il y a une infinité de champs quantiques dans une famille. Il existe une correspondance très utile entre champs quantiques et états Virasoro. Cela permet de représenter une famille (de champs quantiques) caractérisée par un champ primaire directement par les états Virasoro descendants d'un état de plus haut poids. À un champ primaire, on associe un état de plus haut poids de l'algèbre de Virasoro :3

<t>h^\h) (1.12) 3. On utilise maintenant la notation bra­ket pour un état Virasoro (ou un veteur) associé à un

avec Ln>(j\ h ) = 0. On obtient les champs secondaires en correspondance avec les états

descendants du module généré par ce plus haut poids, i.e. L_n i . . . L _nJ / i ) comme

introduit précédemment. Par exemple, l'état L_i| h ) correspond à dz(ph(z).

Pour un choix de deux entiers p , p ' qui sont relativement premiers et avec 1 < p < p', l'élément central K de l'algèbre de Virasoro sera donné par la valeur de c suivante (K s c) :

c = 1

_!^Xrt!. (,

13

)

pfp

Pour une valeur de c fixée par les conditions ci-haut, on appelle les théories des champs conformes correspondantes les modèles minimaux et que l'on dénotera par M.(p,p').

Pour un modèle M.(p,p'), il existe un total de (p— 1) x (p' — 1) modules irréductibles de plus haut poids. Chacun des états de plus haut poids, dénoté par :

\hrt 8) avec 1 < r < p - 1, 1 < s < p ' - 1 , (1.14)

a une dimension conforme donnée par :

(p'r - ps)2 - (p' - p)2

hr,s = — . (1.15)

ip'p

Pour un module de plus haut poids identifié par (r, s) d'un modèle minimal A4(p,p'), le module de Verma généré à partir de | / ir s ) est typiquement réductible : il contient des

vecteurs singuliers que l'on doit retirer pour obtenir une représentation irréductible. Un vecteur singulier (ou null state) est un état qui est descendant et satisfait les conditions de plus haut poids. Dénotons par | rji ) un tel état qui se trouve au niveau /. Alors, cet état est un descendant de | h ) :

\V l) = Y/^ L .X l. . . L ^ J h ) , (1.16)

A h /

où la somme est sur toute les partitions A de / et où les A\ sont des constantes. Il est également plus haut poids, ce qui implique :

Ln > 0\ n , ) = Q. (1.17)

Le module de Verma généré par ce vecteur singulier doit être retiré. Pour le module de plus haut poids (r, s), un vecteur singulier se trouve au niveau rs. Par exemple, pour le module (r,s) = (1,1), le vecteur singulier au niveau 1 est

Chapitre 1. L'algèbre de Virasoro 11

et il est facile de vérifier que :

L1\ nl) = LiL-i\ hl A ) = (L.aLj + 2L0)\ hh l ) = 0, (1.19)

puisque | /il t l ) est un plus haut poids et est nul lorsque l'on agit avec L\ et la valeur

propre associée à l'application de L0 est h\A = 0. Il est facile de vérifier que l'application

des Ln >i conduit au même résultat. Un autre vecteur singulier (plus intéressant) est :

l%> = (L- * - 4 ^ 2L- i ) l/ li . 2 > - C1-20)

Le caractère obtenu plus haut pour un module de Verma doit maintenant tenir compte du module retiré dû au vecteur singulier au niveau r s :

1 qTS

n --nr-

(L21)

(9)00 (9)00

En regardant l'expression (1.15) pour les dimensions conformes, on déduit la relation suivante :

" r , s r^p—r,p'—s- y l . ^ Z J

Cela implique également qu'il existe un vecteur singulier au niveau (p — r)(p' — s). La formule de caractère se voit ainsi corrigée par le retrait de ce (second) module :

1 qr s n(p-r)(p'-s)

(9)00 (9)00 (q)r

(1.23) Mais, en fait, les modules générés par les deux vecteurs singuliers s'avèrent être très intriqués. Parmi les vecteurs singuliers retirés générés par le module de Verma du vecteur singulier au niveau r s , se trouvent deux modules qui seront retirés avec le retrait du module de Verma dû au vecteur singulier au niveau (p — r)(p' — s). On doit donc rajouter ces deux modules. En faisant cela, on ajoute trop et il faut soustraire à nouveau d'autres sous-modules. Ce processus se continue indéfiniment : le caractère pour le module irréductible est ainsi construit par un principe d'inclusion-exclusion,

1 fr s n( p - r ) ( p ' - s ) nrs+{p+r)(p'-s) n(p-r)(p'-s)+r(2p'-s)

(ÇJoo (Ç)oc {Q)co (Ç)OO (9)oo

où maintenant on note par \r's Ie caractère du module irréductible de plus haut poids

(r, s) du modèle minimal Ai{p,p'). Une expression générale, dite de Rocha-Caridi [36], existe d'ailleurs pour tous les modules des modèles minimaux. Elle est :

\p'p'(q) = — \ ^ (qk2PP,+k(p'r-Ps> — q(kP+r)(kp'+••»)) (1.25)

' ^ /tez

On remarque que cette expression s'écrit comme la différence de deux g-séries. Une formule de caractère écrite sous cette forme est qualifiée de bosonique.

Les chemins RSOS

L'origine des chemins RSOS est issue de l'expression de la probabilité d'une hauteur en terme d'une somme sur des configurations pour les modèles sta-tistiques RSOS dans le régime III. Dans la limite de longueur infinie de ces chemins, leurs fonctions génératrices reproduisent les formules de caractères de l'algèbre de Virasoro pour les modules irréductibles de plus haut poids en théorie des champs conformes.

Dans ce chapitre, l'origine de ces chemins en physique statistique sera retra-cée brièvement et plus précisément dans le cadre de l'analyse des transitions de phases par des réseaux en deux dimensions. En terminant, deux classes particulières de chemins RSOS seront introduites dont nous nous servirons plus tard.

Les modèles statistiques exactement résolubles RSOS (pour restricted solid-on-solid) ont été introduits par Andrews, Baxter et Forrester en [3] et généralisés ensuite par Forrester et Baxter dans [23]. Les modèles RSOS sont une généralisation du modèle des hexagones durs de Baxter (voir par exemple [5, §14] pour une présentation de ce modèle).

Les modèles RSOS sont des modèles statistiques dits de face (qui est différent d'un modèle de vertex) définis sur un réseau rectangulaire. Une hauteur l{ est associée à chaque site i du réseau et est restreinte par :l

h e n , o<k<p'. (2.i)

1. La notation utilisée dans la définition des modèles RSOS. différente de l'article original [3], a été choisie pour être cohérente avec celle utilisée dans ce mémoire.

Chapitre 2. Les chemins RSOS 13

FIGURE 2.1 Pour une face i . j , m. n du réseau, on identifie une hauteur à chaque site conformément à (2.1) et à la condition (2.2) qui implique que l'on doit avoir |/,-Zj| = \lj — ln\ = \lm— ln\ = \lm — U\ = 1. Un poids (non-nul) W(li,lj\lm,ln) est ensuite associé à chaque face du réseau dépendamment des valeurs des hauteurs.

m n

VV ( l i , l j \ l m i ' n /

De plus, les hauteurs adjacentes sur le réseau doivent différer par 1 :

\ l i - l j \ = l, (2.2)

pour (i,j), des sites plus proches voisins. Pour chaque face du réseau (ou plaquette) i,j,m,n où les hauteurs satisfont ces conditions (voir FlG. 2.1), il y est associé un poids (de Boltzmann) W(li,lj\lm,ln) qui dépend des valeurs des hauteurs. Il existe six configurations possibles. 2 Très brièvement, les différents poids sont parametrises par des fonctions elliptiques et satisfont la relation triangle-étoile (ou Yang-Baxter). Un rôle crucial est joué par un paramètre, que l'on nommera n (qui provient du modèle à 8-vertex), utilisé comme argument dans les formules de poids. Il prend la valeur suivante :

V = ( P - P ) ^ , (2-3) p1

où K est une constante liée au modèle et p < p' sont des entiers relativement premiers. Le poids total du réseau est le produit de tous les poids associés à chacune des faces. La fonction de partition est :

Z = Y . HWiliJjlln.lm).

Configurations Faces

(2.4)

Les auteurs de [3] s'intéressent aux cas p = p' — 1 avec p' > 3 (le cas p' = 5 est une réduction particulière du modèle à 8-vertex : le modèle des hexagones durs) et calculent les valeurs des exposants critiques associés aux différentes transitions de phases du sys-tème (dans la limite de taille infinie du réseau des modèles RSOS). Parmi les quatre

2. Celles-ci sont W(l,l + l \ l - 1,1) W ( l - l , l \ l , l + l ) W ( l , l - 1|/ + 1./) W(l + l . l \ l . l + l ) W ( l + l . l \ l . l W ( l - l , l \ l , l 1) 1)

régimes inhérents aux modèles RSOS, nous allons nous concentrer sur la transition entre les régimes III et IV (la raison, en lien avec la T C C , deviendra évidente bientôt). Lors de cette transition, p' — 2 phases coexistantes deviennent instantanément indiscernables. Une observation non­triviale faite par Huse [24] montre que les exposants critiques (is­ sus de la transition entre les régimes III et IV) de ces modèles RSOS sont les mêmes que ceux prédits par la théorie des champs conformes et plus précisément par ceux des modèles minimaux unitaires M ( p ' — \ , p ' ) ­ Ainsi, par un argument d'universalité, on peut comprendre les modèles minimaux M ( p ' — l , p ' ) comme étant la limite d'échelle des modèles RSOS avec n = K j p ' . Par exemple, p ' = 4 correspond au modèle d'Ising. Au point critique, on a 4 — 2 = 2 phases indiscernables (qui sont bien sûr la phase ferro­ magnétique et la phase anti­ferromagnétique). Andrews, Baxter et Forrester obtiennent une valeur de /3 = 1/8 pour l'exposant critique de la magnétisation spontanée. Cela est égal à 2/i1>2, la dimension d'échelle associée à l'opérateur spin dans A4(3,4).

Dans un second temps, les auteurs de [23] considèrent le modèle général avec le paramètre n donné en (2.3) où p , p ' sont relativement premiers (i.e. qui n'ont pas de facteurs communs) et avec p < p'. Comme précédemment, ils calculent les valeurs des exposants critiques et pour le régime III, ceux­ci sont reliés [35] aux théories des champs conformes, i.e. les modèles minimaux AA{p,p').

En plus des exposants critiques, il existe une connexion encore plus incroyable entre les modèles RSOS et les modèles minimaux. Conceptuellement, cette relation n'est pas bien comprise encore à ce jour.

Pour les modèles statistiques RSOS, introduisons la probabilité Pa d'une hauteur

égale à a dans un réseau de taille infinie et lorsque le modèle est dans une phase identifiée par b et c. Considérons pour débuter un réseau de taille finie mesurée par m' avec des conditions frontières fixées par les indices b, c = bdz 1 de l'état fondamental3 et

choisissons le site 1 au centre. La probabilité Pa( m ' ) que le site 1 ait une hauteur fixe l\ =

a est obtenue en sommant sur toutes les configurations (avec leur poids de Boltzmann associé) pour lesquelles li = a, normalisé par le nombre total de configurations (avec

3. L'état fondamental (ou ground­state) est le réseau identifié par la configuration où tous les sites impairs ont une hauteur 6 et tous les sites pairs ont une hauteur c = b ± 1. Par exemple, pour Ising (p' = 4), les états fondamentaux sont :

1 ■1 _{1 2 1 3 2 3 2 3} 2 1 2 1 2 2 3 2 3 2

1 2 1 2 1 3 2 3 2 3 2 1 2 1 2 2 3 2 3 2

Chapitre 2. Les chemins RSOS 15

leur poids de Boltzmann respectif) :

Pa(m') = Z"1 J 2 < ^ 'G) I l W{li,li\lm,ln). (2.5)

Configurations Faces

En prenant la limite lim^i'^oo Pa{rn'), on obtient Pa. Cette probabilité, qui est manifes-tement une somme sur des configurations en deux dimensions, peut être ramenée en une sommation sur des configurations d'une dimension en utilisant une technique puissante introduite par Baxter : les matrices de transfert de coin (voir [5, 6]). L'évaluation de cette probabilité requiert alors le calcul de :

Ym.(a,b,c;q) := J ] q"{l\ (2.6)

h,-,lm.

avec

UJ(1) = H(h,l2, l3) + 2H(l2, l3, U) + ... + m'H(lm., lm'+i,lm'+2) (2.7) où l = {/i,/2i • • • J lm'+2] est un ensemble d'entiers satisfaisant :

l < / i < p ' - l , | /î + 1- /2| = l (2.8) pour i > 1. La sommation dans (2.6) est sur les hauteurs l2,... ,lm' qui correspondent

aux configurations possibles sur la ligne du réseau des modèles RSOS, partant du site 1 au centre (de hauteur égale à a) jusqu'à la frontière (de droite) fixée par les hauteurs de l'état fondamental (b, c),

h = a, lm'+i = b, lm'+2 = c. (2.9)

La fonction H(i,j, k) est définie par [23, §1.6] :

H ( l ? l , l , l ± l ) = \

In (2-10)

H ( l , l ^ l , l ) = K

où [/J désigne le plus grand entier inférieur ou égal à / . Andrews, Baxter et Forrester [3] parviennent (pour p = p' — 1) à obtenir une expression explicite (une différence de deux fonctions thêta) par un argument de récurrence pour Ym>(a, b, c: q). Forrester et Baxter [23| généralisent ce résultat par la suite. Toujours pour le régime III, si l'on définit :

X{a,b,c:q):= lim q-AYm>(a,b,c;q) (2.11)

m'—¥oc

avec A, une constante donnée par [17, §A] :

où le signe + est choisi si c = b + 1 et le signe — est choisi si c = b — 1, on obtient la relation étonnante :

X(a,b,c;q) = X p r^(q), (2.13)

avec r' = [pc/p' J + (b — c -f l ) / 2 . X(a, b, c; q) représente ainsi un caractère de l'algèbre de Virasoro pour le module irréductible (r',a) du modèle minimal M.(p,p'). Ceci est obtenu sans jamais avoir considéré la théorie des représentations des modules de plus haut poids comme au chapitre 1.

Warnaar [37, 38] est le premier à proposer un argument purement constructif pour l'analyse de la fonction génératrice des configurations l = { l \ , . . . , lm'+2] pour le cas

K / n = p' (et pour le régime III). Le contour d'une configuration / s'interprète natu-rellement en terme d'un chemin dans le plan x-y avec des conditions frontières a, b, c fixes. Chaque chemin est associé à un poids, défini par l'expression u(l) à l'équation (2.7). Notons que dans ce cas, une simplification considérable survient dans la fonction H ( l , l =F 1,/) en (2.10) ; puisque chaque hauteur est toujours inférieure à p', voir (2.8), on obtient H{1,1 T L O = 0. Par une analyse combinatoire de ces chemins, Warnaar parvient à calculer les fonctions génératrices pour (2.6) et ensuite en prenant la limite de longueur infinie des chemins, les formules de caractères xf{,+2-i)/2a(9) ^e s modèles

minimaux unitaires. Toutefois, les formules de caractères obtenues suite à son analyse diffèrent largement de toutes celles précédemment obtenues. Celles-ci ne s'expriment pas comme une différence de deux g-séries (reflétant un principe d'inclusion-exclusion), mais plutôt comme une série définie positivement, i.e. sans soustraction de termes. De telles formules sont dites fermioniques [31, 32]. Cette construction indique qu'il existe une base génératrice permettant d'engendrer toutes les configurations (ou états) sans sous-traction. La même approche est ensuite utilisée pour le cas général [18, 17, 32, 40, 39].

Le reste de ce chapitre s'organise comme suit. Tout d'abord, on définit formellement les chemins RSOS dans le plan x-y. On décrit ensuite une méthode pour déterminer le poids (relatif) d'un chemin. En faisant l'inventaire du nombre de chemins ayant un poids fixe, on indique que ceci permet de compter les états Virasoro (et mène aux formules de caractères des TCC). Enfin, on spécifie deux classes précises de chemins RSOS qui seront utilisées dans le reste de ce mémoire.

2.1 Définition

Soit la séquence non négative h := (ho, h^, /i2....) avec /i, G Z>o- Soit p < p' deux

entiers qui ne possèdent pas de diviseurs communs. On dira que la séquence h appartient à l'ensemble Vpa\ , noté h E Vvap , si et seulement si :

Chapitre 2. Les chemins RSOS 17

FIGURE 2.2 - Un exemple de chemin RSOS h e V%'%. Les valeurs de p possibles sont p = 3.5.7

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

1. \hx+ï — hx\ = 1 et 1 < hx < p1 — 1 pout tout x € Z>0 ; 2. h0 = a et /ix E {b,b — 1} pour tout x > N > 0.

En reliant les points (0, h0), (1, /ij), (2, /i2),... dans le plan x-y, on obtient une repré-sentation graphique de la séquence h qu'on appelle ainsi le chemin (associé à h). Deux points consécutifs (x, hx), (x + 1, hx +i) seront reliés soit par un lien sud-est (SE) ou soit par un lien nord-est (NE). Pour chaque x > 0, la position (x,hx) sur le chemin h sera appelée un vertex. La forme d'un vertex peut être soit un sommet (ou pic), une vallée, une montée ou une descente dépendamment si les segments d'une part et d'autre du vertex sont soit NE-SE, SE-NE, NE-NE ou SE-SE respectivement. La FlG. 2.2 présente un exemple de chemin appartenant à Pfg.

Souvent, il sera nécessaire de considérer la position (0, h0) comme un vertex, et d'avoir sa forme prédéterminée. Lorsque requis, cela sera fait en spécifiant la valeur de /i_i comme étant égal à ho ± 1. On aura alors un segment pré-initial au chemin. De plus, pour un chemin infini, on introduira (parfois) la notion de longueur efficace finie L. Pour ces chemins tronqués à une longueur L, on spécifiera également un segment post-final en fixant la valeur hL + ï égale à h i ± 1.

Les chemins V^\ sont appelés les chemins RSOS puisque que ceux-ci découlent des configurations de la probabilité d'une hauteur locale à un site dans le cadre des modèles statistiques sur réseau RSOS [3, 23]. D'après la définition des chemins RSOS, on remarque que le paramètre p n'intervient pas. En fait, il est seulement requis pour le calcul du poids du chemin que nous allons maintenant définir.

2.1.1 Le poids

À un chemin RSOS h G Vvap est associé un poids, wt(/i), qu'on obtient comme suit.4 Dans la portion du plan x-y qui définit le chemin RSOS, on appelle la A:-ième

4. La définition du poids présentée ici est celle de [17]. Elle diffère considérablement de la définition originelle que nous avons brièvement mentionnée au début de ce chapitre. Pour un chemin h € Vva\ , on

bande (avec 1 < k < p' — 2), la région incluse entre les hauteurs y = k et y = k + 1. On colore ensuite p — 1 bandes (en gris par exemple) sur le réseau RSOS. Les numéros de ces bandes sont donnés par l'indice k suivant :

k = { [ t p ' / p \ , l < t < p - l } . (2.14) Souvent, on appellera une bande colorée, une bande foncée. Les bandes qui ne sont pas

foncées sont appelées les bandes claires. Pour le chemin h G V%'6 à la FlG. 2.2 avec p = 3, on obtient les numéros suivants des bandes que l'on doit colorer :

k = {2, 5}, (2.15) ce qui donne la FlG. 2.3.

Les vertex qui sont soit une montée/descente avec leur segment de droite à l'intérieur d'une bande foncée ou soit un pic/vallée avec leur segment de droite dans une bande claire seront référés comme des vertex de type S (pour scoring). Tous les vertex qui ne sont pas de type S sont de type N (pour non-scoring). Les vertex de type S (ou simplement vertex S) peuvent se séparer en deux catégories : les S'-montant si leur

associe un poids (local) Wj à chaque vertex (i, ht) du chemin. Ce poids local est défini par la fonction Lui = H(hi_i,hi,hi+i) donnée à l'équation (2.10), mais avec un décalage puisque la configuration commence à ho = a. Rappelons que la définition de cette fonction dépend des paramètres p,p' :

H ( h ^ l , h , h ± l ) = ] - H(h,h^l,h) = ± h(p'-p)

Le poids total w du chemin est donné par la somme w = 5Zi>o*Wi- Toutefois, le poids sera toujours calculé relativement à un chemin fondamental. Le chemin fondamental est défini comme étant le chemin de poids minimal parmi tous les chemins de Vp'p . Le poids (relatif) du chemin h est alors :

fond

A u j ( h ) = ui — u)

où a/ond désigne le poids du chemin fondamental. Notons que la soustraction du poids du chemin fon-damental est équivalente à la soustraction de la constante A (définie plus haut) à chaque configuration de Ym'(a,b,c;q). Par exemple, prenons le chemin à la FlG. 2.2 où on a a = 4, b = 6, c = 5, L = 26 et fixons p = 3. Le chemin fondamental est (4, 5.6,5.6,5,6,5,6,5,6,5,6,...) et le calcul du poids donne : Acj(h) = | l ( 2 ) + 2* + 3± + 4± + 5(-3) + 6^ + 7(3) + 8(-3) + 9± + 10± + 11± + 12± + 13(1) + ...

+ 2 0 | + 21^ + 22(-3) + 23(3) + 24(-3) + 25(3) + 26(-3)} - { l | + [2 + 4 + 6 + 8 + 1 0 + ... + 22 + 24 + 26](-3) + [3 + 5 + 7 + 9 + 1 1 + ... + 23 + 25](3)|

= i ( - 2 7 + 95) = 34.

La seconde définition, celle que nous utiliserons par la suite, est une simplification drastique de la première ci-haut. Elle rend le poids local indépendant de p en introduisant un réseau avec une structure de bandes (qui, elle, dépend de p). De plus, seulement un certain nombres de vertex contribuent au poids (au lieu de tous les vertex du chemin) et le chemin fondamental acquiert un poids nul.

Chapitre 2. Les chemins RSOS 1!)

FIGURE 2.3 - Le même chemin qu'à la FlG. 2.2 avec p = 3 et la structure de bande correspondante. Seulement les vertex indiqués avec un cercle (vide ou plein) contribuent au poids. Les vertex avec un cercle vide ont un poids Ui et ceux avec un cercle plein, un poids V{ (ces valeurs étant définies en (2-16)).

o i 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

segment de gauche est un lien NE ou les S-descendant si leur segment de gauche est un lien SE. Sur la représentation graphique du chemin, on identifie (souvent) les vertex S-montant par un cercle vide et les vertex S-descendant par un cercle plein. Cela a été fait à la FlG. 2.3.

Enfin, en introduisant les deux valeurs :

ux = - { x - hx + o) vx = -{x + hx - a), le poids wt(/i) d'un chemin h est défini par5 :

wt(/i) = y^w

,

5. Il est facile de vérifier que le poids d'un chemin RSOS est toujours entier en montrant que les valeurs (2.16) donnent toujours un poids (local) entier. Considérons un chemin débutant à (0, a) et où il y a un vertex de type S à (x, hx). Décomposons le chemin comme suit : partant de (0, a) à {x, hx), le chemin est composé d'abord de m liens SE, suivi de m\ liens NE, suivi de n2 liens SE, etc. On a alors la séquence n \ . m \ , n2, m2. . . . .np.mQ décrivant la portion du chemin jusqu'à (x.hx). Notons que l'on peut avoir ni = 0 si le chemin débute par une série de liens NE. Également, on peut avoir ITIQ = 0 si

le vertex S à (x,hx) est après une série de liens SE. Le calcul des poids ux et vx donnent :

m)

E'

Puisque le vertex (x, hx) est arbitraire, ceci montre que tous les poids ux, vx sont entiers et par consé-quent le poids total wt(ft) aussi. En fait, on observe que le couple (ux,vx) donne les coordonnées du vertex (x, hx) à partir du point initial (0, a) en tournant les axes x-y de 45 degrés dans le sens horaire.

Si nous retournons au chemin h à la FlG. 2.3, on obtient pour le poids :

wt(/i) = -{0 + 2 + 2 + 8 + 10 + 10 + 16 + 20} = 34, (2.19) ce qui est la même valeur qu'avec le définition originelle du poids calculé un peu plus

haut, voir la note (4), comme il se doit.

La condition imposée par le paramètre b sur un chemin RSOS h est que celui-ci, à partir d'une certaine position, doit osciller (à jamais) dans une seule bande. C'est ce qu'on appelle la queue du chemin. La définition (2.17) implique que le poids wt(/i) du chemin peut être soit fini ou infini dépendamment si la queue du chemin est dans une bande foncée ou une bande claire respectivement. Plus loin, on ne considère que les cas où cette bande est foncée.

2.2 Les caractères de l'algèbre de Virasoro

Les chemins RSOS fournissent une description combinatoire des états Virasoro des modules irréductibles de plus haut poids en théorie des champs conformes. En comptant les chemins de l'ensemble Vp'p , on compte les états Virasoro dans le module irréductible de plus haut poids (r, s) pour le modèle minimal Ai(p,p'). Plus précisément, le nombre de chemins h G Vp'p de poids n correspond exactement au nombre d'états de Virasoro, pour un module (r,s), au niveau £ = n. Cela implique que les fonctions génératrices (fonction d'une variable auxilière q qui code le nombres d'éléments par niveau, voir annexe §A) des chemins RSOS sont égales aux formules de caractères de l'algèbre de

Chapitre 2. Les chemins RSOS 21

Virasoro [17, 39], c'est­à­dire6 :

E r*" = x#(«)■

fce^:?

Les indices des modules de plus haut poids (r, s) des ­M(p,p') sont reliés aux conditions de bords des chemins Vp p par les relations :

a = s et b = [ r p ' / p \ + l . (2.21) On remarque que la région entre les hauteurs b et b — 1 est la r­ième bande foncée, ce

qui implique que la queue du chemin doit être dans une bande foncée (et ainsi son poids est fini).

2.3 Deux classes particulières

Plus tard, nous considérons deux classes précises de chemins RSOS. La première est celle des Vp'b p + Ï. La structure de bande de cette série de modèles est la suivante : il y a p bandes claires, séparées l'une de l'autre par une bande foncée (au nombre de p — 1 au total). On utilisera la notation :

■pp — ­p; ,p,2p+l (2.22)

pour indiquer cette classe. La FlG. 2.4 présente un exemple de chemin h G Pf3 de même que la structure typique du réseau pour cette série. Son poids wt(/i) est :

wt(h) = 0 + 0 + 3 + 1 + 1 + 2 + 9 + 9 + 6 + 11 + 11 + 9 + 1 2 = 74. (2.23)

6. Le lien avec les caractères de Virasoro se déduit comme suit. Si l'on considère les chemins RSOS de longueur finie L, on peut déduire une relation de récurrence que doit satisfaire toute fonction génératrice (pour les chemins de longueur L), voir [39, §B]. Il est facile de vérifier que la fonction suivante de type bosonique est une fonction génératrice des chemins h G Vp'p de longueur finie L (avec h i = b et h i+\ = b — 1) :

X

'(L;

) = J2/

"'

"'

­

N­p'e­a

avec N = (L + a — 6)/2 et r = [ b p / p ' \ . Pour 0 < r < p, on prend ensuite la limite de longueur infinie des chemins :

Km Xp p' ( L : q ) = ­ ï ­ W W + < ( P ' « ­ P « ) _ J L y q((v+r)(tP'+a)

= Xrï'iv),

et l'on retombe alors sur les formules de Rocha­Caridi pour les caractères de Virasoro avec les conditions (2.21).

FIGURE 2.4 - Un exemple de chemin appartenant à l'ensemble Vf3. Les cercles vides indiquent les vertex S-montant, ayant un poids ux, et les cercles pleins indiquent les vertex S-descendant, ayant un poids vx. Leurs valeurs sont spécifiées à l'équation (2.16).

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

La seconde classe de chemins est celle des Vp+b ' p + . La structure de bande de ce cas est l'opposé de la précédente : il y a p bandes foncées, séparées l'une de l'autre par une bande claire (au nombre de p — 1 au total). En fait, cela est équivalent à prendre la structure de bande précédente et à échanger les bandes foncées et les bandes claires. Egalement, plus loin, on utilisera la notation :

<pP _ <pp+l,2p+l

ra , b — ra , b (2.24)

La FlG. 2.5 présente un exemple de chemin h G V\2. Son poids wt(/i) est le suivant : wt(/i) = 1 + 4 + 3 + 3 + 3+11 + 12 + 12 + 11 + 13 + 13 + 13 + 17+14 + 18+19= 167. (2.25)

La raison pour laquelle on ne se restreint qu'à ces deux sous-classes va devenir rapidement évidente. En fait, et curieusement, il existe une autre description en terme de chemins. Ce sont les chemins sur réseau demi-entier que nous allons maintenant introduire.

FIGURE 2.5 — Un exemple de chemin appartenant à l'ensemble V \2. Les cercles vides indiquent les vertex S-montant, ayant un poids ux, et les cercles pleins indiquent les vertex S-descendant, ayant un poids vx. Leurs valeurs sont spécifiées à l'équation (2.16).

Chapitre 3

Les chemins sur réseau demi-entier

Une nouvelle classe de chemin est introduite. Ce sont des chemins dans le plan x-y mais où les positions et les hauteurs demi-entières sont permises. Une restriction supplémentaire est imposée quant aux positions des pics. Leur grand avantage est d'avoir une expression simple pour le poids (celui-ci ne dépend plus de la hauteur du chemin). Contrairement aux chemins RSOS, l'analyse combinatoire de cette nouvelle classe de chemins permet d'obtenir leurs fonctions génératrices de manière constructive. Celles-ci, dans la limite de longueur infinie des chemins, peuvent être reliées aux caractères Virasoro des modèles minimaux en TCC (preuve qui sera donnée aux chapitres sub-séquents) .

Les chemins sur réseau demi-entier ont d'abord été introduits comme représenta-tion pour les partireprésenta-tions dentelées K— restreintes [30]. Pour K pair, il s'agit de la base décrivant les parafermions gradués [13, 25]. Dans cette version, le chemin est défini sur les positions et hauteurs entières avec la position des pics à des positions paires. De plus, pour ces chemins, il est possible d'avoir des liens de type plateau sur l'axe des x seulement. En divisant tout le réseau par un facteur de 2 et en éliminant les liens de type plateau, on obtient des chemins qui sont définis dans le plan x-y avec les po-sitions et les hauteurs demi-entières permises (ce qui sera maintenant appelé le réseau demi-entier) avec la restriction que la position des pics doit être entière (une définition plus précise sera présentée à la section suivante). Chaque position des creux et des pics contribue alors au poids du chemin. En cherchant la version duale, soit en assignant maintenant à la position des montées et des descentes un poids, Jacob & Mathieu [27] découvrent que les fonctions génératrices de ces (nouveaux) chemins donnent les carac-tères Virasoro pour les modèles M.(p, 2p + 1). Ils proposent alors la conjecture selon laquelle ces nouvelles formules, sous forme fermionique, sont égales aux formules boso-niques des caractères Virasoro pour les modèles M.(p, 2p+ 1). Dans le chapitre suivant,

on montrera qu'en fait ces chemins peuvent être reliés aux chemins RSOS [9] (et donc aux états Virasoro) et validant par conséquent l'égalité entre les fonctions génératrices et les formules de caractères.

Il s'avère également qu'une extension de ces chemins sur réseau demi-entier permet de formuler une seconde conjecture pour de nouvelles formules de caractères de type fermionique pour tous les modèles M.(p + l , 2 p + 1). L'analyse combinatoire menant à la construction des fonctions génératrices pour cette deuxième classe est l'objet du présent chapitre. Pour y parvenir, on doit décomposer le chemin en un ensemble de sommets avec une charge spécifique. Un peu comme une base de vecteurs qui permet d'engendrer tout l'espace vectoriel, notre base de sommets chargés permettra de générer tous les chemins et ainsi d'obtenir la fonction génératrice.

Pris séparément, ces deux classes de chemins sur réseau demi-entier fournissent des représentations des états Virasoro dans les modules irréductibles de plus haut poids des modèles M.{p+e, 2p+l), e = 0,1. Ces deux modèles sont reliés entre eux par une dualité de type McCoy-Berkovich, i.e. M.(p,p') —> M.(p' — p,p'). Cette dualité s'exprime par une transformation q —> q~l au niveau des formules de caractères obtenues à partir des chemins RSOS de longueur finie. Etrangement, cette propriété n'est pas présente dans le cas des chemins sur réseau demi-entier. Comme mentionné plus haut, la première version de ces chemins (ceux considérés par Jacob & Mathieu) est duale aux caractères des parafermions gradués. Pour la seconde classe des chemins sur réseau demi-entier, il sera indiqué que la version duale mène aux partitions dentelées K— restreintes (avec K impaire) qui eux fournissent une interprétation combinatoire à certains modèles su-perconformes (modèles qui ne seront toutefois pas abordés dans ce mémoire). Signalons aussi que l'équivalence des ces chemins avec une autre construction (les chemins de Bressoud généralisés [29]) conduit à une famille d'identités entre g-séries (sujet qui ne sera pas traité dans ce mémoire).

Curieusement, cette construction plutôt ad hoc des chemins sur réseau demi-entier ne découle pas d'un modèle physique relié aux modèles minimaux comme pour les chemins RSOS. Ainsi, pour démontrer la correspondance avec les TCC, on devra trouver des règles de transformation entre ceux-ci et les chemins RSOS (étape qui sera accomplie aux prochains chapitres). De plus, jusqu'à maintenant, ils correspondent seulement aux classes M.(p + e, 2p+ 1), e = 0,1 des modèles minimaux. Plusieurs généralisations à des réseaux 1 / / en lien avec les modèles M.(p, f p ± 1) ont été explorées, mais sans succès.

Chapitre 3. Les chemins sur réseau demi­entier 25

3.1 Définition

Soit la séquence h := (ho, hi/2, h\, h3/2, ■ ■ • ) avec ht G |Z>o­ Soit t = p + t / 2 , p > 2,

p G Z et e = 0 , 1 . On dira que la séquence h appartient à l'ensemble Tila b, noté h G Hla b,

si et seulement si :

2. ho = a et /ix G {6,6 — | } pour tout x > N > 0, avec 0 < a, b < t — l o ù

L |^x+i/2 — /ii| = 1/2 et 0 < hx < t ­ 1 pour tout x G | Z >0 ;

a, be Z + § ;

3. une configuration de la forme (• • ■ , /ix — 1/2, hx, hx — 1/2, • • • ) n'est possible que

pour i ç Z .

En reliant les points (0, ho), (1/2, /ïi/2), (1, /ii), ­ . . dans le plan x­y, on obtient une représentation graphique de la séquence h qu'on appelle ainsi le chemin (associé à h). Le lien reliant deux positions successives peut être soit selon la direction nord­est (NE) ou soit selon la direction sud­est (SE). Pour chaque x > 0, la position (x, hx) sur le chemin

h sera qualifiée de vertex. La forme du vertex peut être soit un sommet (ou pic), une vallée, une montée ou une descente dépendamment si les segments d'une part et d'autre du vertex sont soit NE­SE, SE­NE, NE­NE ou SE­SE respectivement. Notons que la dernière condition impose que la position x des pics doit être entière. Les FlG. 3.1 et FlG. 3.2 représentent des exemples de chemins sur réseau demi­entier pour un t entier et demi­entier respectivement.

À l'occasion, il sera utile de considérer la position (0, h0) comme un vertex et d'avoir

sa forme prédéterminée. Cela sera fait en spécifiant un segment pré­initial au chemin en fixant la hauteur /i_i/2 = a ± l / 2 (on déterminera la convention aux chapitres ultérieurs). Egalement, pour des chemins de longueur infinie, on utilisera la notion de longueur efficace finie L. Pour ces chemins de longueur finie, un segment post­final sera parfois nécessaire. La forme du vertex final (L, h i ) sera déterminée en fixant /iL+1/2 = / Î L ± 1 / 2 .

FIGURE 3.1 Un exemple de chemin appartenant à l'ensemble Ti^ j .

3

r

1 1

FIGURE 3.2 - Un exemple de chemin appartenant à l'ensemble r i J \ .

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

3.1.1 Le poids

Le poids (absolu) w°(h) d'un chemin h G "Hla b est défini comme la demi-somme des positions des montées et des descentes, ou en équation :

w°(h) 1

2

E

/ îx - l / 2 # ' « x + l / 2

.r. (3-1)

Définissons le chemin fondamental, hcS G "H^fe, comme étant le chemin de poids mi-nimal parmi tous les éléments de Hlab. La FlG. 3.3 montre deux exemples de che-mins fondamentaux. On voit que ce chemin possède une partie oscillante hxf = b et hx { + 1/2 = b — 1/2 pour x G Z>|a_j,|, précédée par un segment droit1 (pour a ^ b) avec hx{ = ( a , a ± 1/2, a ± 1 , . . . , b T 1/2) pour x = (0,1/2,1,..., \a - b\ - 1/2), où le signe du dessus s'applique lorsque b > a et le signe du dessous lorsque b < a.

Le calcul du poids d'un chemin sur réseau demi-entier se fera toujours par rapport à celui du chemin fondamental :

wt(h) = w ° ( h ) - w ° ( hc l) (3-2) Pour le chemin h à la FlG. 3.1, le chemin fondamental est celui avec hcJ = 1 et hct., /0 =

x + l / 2

1/2 pour x G Z>i précédé par hx = (0,1/2) pour x = (0,1/2). Son poids est : wt(/z) = | ( | + l + | + 2 + | + | + 5 + ^ + f + f + 8

+f + f + f + f + ^ + f ) - I ( 0 + I ) = 7 4 . (3-3)

Pour le chemin h à la FlG. 3.2, le chemin fondamental a un poids de 0 et l'on obtient directement :

wt(/i) = | ( | + l + i + | + | + f + 7 + f + 9 + 1 0 + f + f + f + 13

f + 19 + 20 + f + f + 23) = 167. (3-4) 2 + 1 5 + f + f + 1 7 + f + 18 ,

Chapitre 3. Les chemins sur réseau demi-entier 27

FIGURE 3.3 — Exemple de deux chemins fondamentaux pour les ensembles H& 3 (à gauche) et Ti, «

2 ' 2 2 - 2

(à droite).

o i

w°(h«) = I w°(hc{) =

De façon générale, et puisque nous connaissons la forme du chemin fondamental, le calcul de son poids se fait directement et donne :

w ° ( h « ) =l- ( a - b f + \ ( a - b ) . (3.5)

3 . 1 . 2 L a c h a r g e

La notion de charge sera très importante dans le calcul des fonctions génératrices des chemins sur réseau demi-entier. Tout chemin (sur réseau demi-entier) pourra se décomposer en une série de charges associées à chaque sommet. Ces pics chargés seront nos constituants fondamentaux pour l'analyse combinatoire des ces chemins. En fait, dans un premier temps, on s'intéressera aux fonctions génératrices des chemins avec un contenu en charge fixe. En quelque sorte, la charge totale du chemin codera la longueur efficace du chemin.

Tout d'abord, on considère une transformation qui fait correspondre chaque sommet à un couple de coordonnées. La méthode est la suivante [11].

On identifie chaque portion du chemin délimitée par deux points de contact avec l'axe des x ou un point de contact avec l'axe des y. Appelons cette portion du chemin un massif. Un massif peut comporter plusieurs sommets. À l'intérieur de chaque massif, on identifie le sommet d'hauteur maximale le plus à gauche. Pour ce sommet le plus haut et le plus à gauche, la première coordonnée du couple prend la valeur de sa hauteur et la seconde coordonnée, la hauteur minimale parmi tous les vertex à sa gauche (et en restant à l'intérieur du massif).

2'

S'il reste des sommets qui n'ont pas été choisis, on tronque le réseau à la hauteur Cela peut avoir pour effet de séparer les massifs initiaux en de nouveaux massifs

avec maintenant des points de contacts avec la droite x = | . De ces nouveaux massifs, pour lesquels aucun sommet n'a été auparavant choisi, on identifie le sommet d'hauteur maximale le plus à gauche. De cette séquence de nouveaux sommets choisis, on fait correspondre un couple de coordonnées (comme dans le cas précédent) où la première coordonnée est la valeur de sa hauteur et la seconde coordonnée, la hauteur minimale et d'au moins \ parmi tous les vertex à sa gauche (et toujours à l'intérieur du massif). On procède ainsi par récurrence en tronquant le réseau par bonds de \ de bas vers le haut jusqu'à ce que tous les sommets soient représentés par un couple de coordonnées.

Sommets : {(xi,/ii ) , . . . , (xn,/i„)} •-> {{hi, ea ) , . . . , (hn,en)} (3.6) où les e, correspondent aux secondes valeurs des couples de coordonnées associés aux

pics tel que décrit ci-dessus.

La séquence de hauteurs relatives (par rapport à la gauche) des sommets qui com-posent le chemin sera donnée par la différence de chaque couple, i.e. hi — e,-. La charge de chaque sommet est donnée par cette valeur. Par exemple, pour le chemin à la figure 3.1, nous avons les couples de coordonnées associés à chaque pic (de gauche à droite) :

{(3,0), (3, | ) , (2,1), (1, §), (1, \ ) , (1, \ ) , (1, \ ) , (1,0), (1, \ ) , (1, §), ( l , i ) , ( l , 0 ) , ( l , | ) , ( l , 0 ) }

et la charge des pics est (dans le même ordre) :

I l 1 1 1 1 I 1 1 1 1 1 i i i l Ci 8)

l 0 ' 2 ' ' 2 ' 2 ' 2 ' 2 ' ' 2 ' 2 ' 2 ' ' 2 ' J ' \°-°)

Egalement, pour la figure 3.2, on trouve que les différents sommets ont des charges :

lo 1 I I I i I I 2 I ii (Q q)

l ^ i -*•> 2 ' 2 ' 2 ' > 2 ' 2 ' 2 ' 2 ' 2 / " \'J-'JJ

Remarquons que pour des chemins de l'ensemble 'rliab, les charges j possibles des som-mets sont j G {\, 1, | , . . . , t — 1}.

Dénotons par Uj le nombre de pics de charge j dans le chemin. On définit la charge totale m du chemin par :

m := 2_. 3nj - (3.10)

i

2

La charge totale est reliée à la longueur efficace du chemin par L = 2m. + (a — b) + 1/2. Dans ce chapitre, nous aurons souvent à considérer des sommations dont la variable de sommation prend aussi les valeurs demi-entières. Typiquement, les sommations se-ront par bonds de 1/2. On choisira de ne plus écrire explicitement ce type de sommation