Amélioration de la méthode d'échantillonnage en deux cycles et application à l'estimation du total de la population

Amelioration de la m e t h o d e d'echantillonnage e n d e u x cycles et application a l'estimation d u total de la population "

Par

Fatoumata Nene Dicko

Memoire presente au departement de mathematiques e n v u e de l'obtention du grade de maitre es sciences (M.Sc.)

FACULTE DES SCIENCES UNIVERSITE DE SHERBROOKE

1*1

Library and Archives Canada Published Heritage Branch 395 Wellington Street OttawaONK1A0N4 Canada Bibliotheque et Archives Canada Direction du Patrimoine de I'edition 395, rue Wellington Ottawa ON K1A 0N4 Canada

Your file Votre r6f6rence ISBN: 978-0-494-61446-4 Our file Notre reference ISBN: 978-0-494-61446-4

NOTICE: AVIS:

The author has granted a

non-exclusive license allowing Library and Archives Canada to reproduce, publish, archive, preserve, conserve, communicate to the public by

telecommunication or on the Internet, loan, distribute and sell theses

worldwide, for commercial or non-commercial purposes, in microform, paper, electronic and/or any other formats.

L'auteur a accorde une licence non exclusive permettant a la Bibliotheque et Archives Canada de reproduire, publier, archiver, sauvegarder, conserver, transmettre au public par telecommunication ou par I'lnternet, preter, distribuer et vendre des theses partout dans le monde, a des fins commerciales ou autres, sur support microforme, papier, electronique et/ou autres formats.

The author retains copyright ownership and moral rights in this thesis. Neither the thesis nor substantial extracts from it may be printed or otherwise reproduced without the author's permission.

L'auteur conserve la propriete du droit d'auteur et des droits moraux qui protege cette these. Ni la these ni des extraits substantiels de celle-ci ne doivent etre imprimes ou autrement

reproduits sans son autorisation.

In compliance with the Canadian Privacy Act some supporting forms may have been removed from this thesis.

Conformement a la loi canadienne sur la protection de la vie privee, quelques formulaires secondaires ont ete enleves de cette these.

While these forms may be included in the document page count, their removal does not represent any loss of content from the thesis.

Bien que ces formulaires aient inclus dans la pagination, il n'y aura aucun contenu manquant.

1+1

Canada

Le 25 Janvier 2010

lejury a accepte le memoire de Madame Fatoumata Nene Dicko

dans sa version finale.

Membres du jury

Professeur Ernest Monga

Directeur de recherche

Departement de mathematiques

Professeur Bernard Colin

Codirecteur de recherche

Departement de mathematiques

Professeur Jean Cadieux

Membre

Faculte d'administration

Departement de systemes d'information

et methodes quantitatives de gestion

Professeur Jean-Marc Belley

President rapporteur

Departement de mathematiques

Sommaire

L'analyse des donnees dans des populations de tailles finies utilise les methodes d'echantil-lonnage. Lorsque nous sommes en presence de donnees qui sont recueillies a diverses periodes dans le temps, une methode que Ton peut privilegier est la methode d'echantillon-nage en deux cycles.

Ce memoire propose une amelioration de la methode d'echantillonnage en deux cycles basee sur l'exploitation de la technique de selection avec probabilites proportionnelles a la taille.

Apres avoir introduit les methodes classiques d'echantillonnage, nous decrirons en detail le plan d'echantillonnageen deux cycles et nous l'appliquerons a un ensemble de donnees agricoles.

4 S O M M A I R E

Remerciements. Je tiens a remercier tres sincerement :

- Mon directeur de recherches, Monsieur Ernest Monga, du departement de

mathematiques, pour la disponibilite, l'encadrement sans failles, le soutien et l'aide qu'il m'a apportes pour la realisation de ce memoire;

- Mon co-directeur de recherches, Monsieur Bernard Colin, du departement de mathematiques, pour son soutien, sa disponibilite et son enseignement de qualite; - Madame Marie-France Roy, Secretaire de direction, pour son accueil chaleureux et sa

disponibilite;

- La Faculte des sciences pour l'aide financiere qu'elle m'a offerte; - Tous les professeurs de la Faculte des sciences;

- Mon frere Amadou Hussein Dicko, pour son aide et sa disponibilite; - Mes parents, pour leur appui et leur amour durant ces annees d'etude; - Ma tante Fatoumata Salah Dicko;

S O M M A I R E

Dedicace. Je dedie ce memoire a mon frere bien aime El Hadj Seckou Dicko qui nous a quitte le 11 Fevrier 2008.

Table des matieres

Sommaire 3 Table des figures 8

Chapitre 1. Introduction 9 Chapitre 2. Echantillonnage aleatoire simple 11

1. Introduction au PAS 11 2. Le Plan Aleatoire Simple (PAS) 13

Chapitre 3. Echantillonnage stratifie 18 1. Echantillonnage aleatoire stratifie 18 2. Echantillonnage stratifie proportionnel 22 3. Echantillonnage optimal, allocation de Neyman 24

4. Taille de l'echantillon 26 5. Stratification a posteriori 27 Chapitre 4. Echantillonnage avec probabilites egales 29

1. Echantillonnage avec probabilites proportionnelles a la taille et avec remise 29 2. Echantillonnage avec probabilites proportionnelles a la taille et sans remise 31 Chapitre 5. Echantillonnage en deux cycles : Estimation du total de la population 34

1. Plans d'echantillonnage 34 2. Methode d'estimation du total de la population au deuxieme cycle 35

3. Strategies d'echantillonnage 38 4. Strategies proposees 42 5. Strategie 2 .. 48 6. Efficacite 50 7. Exemple de Arnab 51 8. Generalisation , 52 9. Exemple illustratif 54 10. Conclusion 57 Annexe A. Donnees 58 Annexe B. PAS 59 6

TABLE DES M A T I E R E S

Table des figures

1 Plan d'echantillonnage 1 35 2 Plan d'echantillonnage 2 36 3 Generalisation 53 4 Strategic 2 55 5 Strategic 2 56 1 Echantillon 60 2 Strategic 1 61

CHAPITRE 1

Introduction

II apparait tres souvent en statistique. mathematique que nous soyons confronted a un probleme fondamental : l'echantillonnage. II permet de comprendre ce qui se passe dans une population sans avoir a interroger chacun des individus.

L'echantillonnage est aussi bien primordial pour la collecte des donnees que l'analyse et l'interpretation des resultats. Comme l'affirment Miles et Huberman dans [MH94]; page 27 : «peu importe ce que vous ferez, vous ne reussirez jamais a etudier tout le monde partout et dans toutes leurs activites. Les choix que vous faites (les personnes a qui vous parlerez, ou, quand, a quel sujet et pourquoi) sont autant de limites aux conclusions que vous pourrez tirer, a la confiance avec laquelle vous les formulerez et au credit que les autres leur accorderont.»

Afin d'estimer ses caracteristiques en regard des changements qui surviennent dans le temps, une meme population peut etre l'objet d'enquetes realisees a intervalles reguliers. Exemple : l'lndice Harmonise du Prix a la Consommation (IHPC) dont les donnees sont recueillies sur une base mensuelle; le nombre d'immigrants dans un pays sur une annee, et bien d'autres.

Lorsqu'une population est sujette a un echantillonnage successif, les donnees recueillies au premier cycle sont utilisees dans l'elaboration de strategies efficaces en regard des couts et peuvent produire un estimateur sans biais de l'ensemble de la population au cycle present.

Nombreux sont les auteurs qui ont traite ces methodes :

- Avadhani et Sukhatme dans [AS70] ont utilise l'information recueillie au premier cycle comme une mesure de la taille, pour selectionner l'echantillon apparie au deuxieme cycle.

- Arnab dans [Arn91] a utilise les donnees du premier cycle, non seulement comme une variable de stratification mais aussi pour en faire une mesure de la taille de rechantillon au deuxieme cycle;

- Prasad et Graham dans [PG94] en modifiant les methodes de Raj [Raj65] et de Chotai [Cho74], ont pris l'information recueillie au premier cycle comme mesure de la taille de l'echantillon apparie au deuxieme cycle. lis ont ainsi constate que cela donnait de meilleurs resultats que celle de Chotai [Cho74].

10 1. I N T R O D U C T I O N

La problematique de ce memoire est de proposer une strategie d'amelioration de la methode d'echantillonnage en deux cycles en application a l'estimation du total de la population. L'elaboration de la methode d'echantillonnage en deux cycles necessite la tres bonne comprehension des trois plans d'echantillonnage que sont : le plan aleatoire simple, le plan stratifie et les plans d'echantillonnage avec probabilites variables, ainsi que des principaux resultats qui y sont rattaches. Ces resultats concernent notamment le calcul des moments des estimateurs, en particulier l'esperance et la variance.

Pour ce faire, ce document est structure en quatre grands chapitres :

(1) Le premier chapitre detaille les principaux resultats associes a 1'echantillonnage aleatoire simple;

(2) Le deuxieme chapitre decrit 1'echantillonnage stratifie et post-stratifie; (3) Le troisieme chapitre porte sur 1'echantillonnage avec probabilites variables; (4) Le dernier chapitre traite des strategies d'echantillonnage en deux cycles.

CHAPITRE 2

Echantillonnage aleatoire simple

Dans ce chapitre, nous etudierons en detail l'echantillonnage aleatoire simple (PAS), qui se trouve etre le plan le plus utilise dans la theorie de l'echantillonnage. Nous ne considererons que les tirages sans remise (utilises en pratique) car le tirage avec remise n'est utile que pour des raisons theoriques.

1. Introduction au P A S

Un echantillonnage aleatoire simple est une methode d'echantillonnage permettant de choisir n unites parmi les N de la population de facon aleatoire, c'est-a-dire, de sorte que chacun des ( ) echantillons possibles ait la meme probability d'etre selectionne. La combinaison ( ) permet de calculer le nombre d'echantillons qu'il est possible de former a partir de la population totale composee de N individus, chacun des echantillons comportant n individus tires au hasard parmi les N.

, 1.1. La population. La population, encore appelee univers ou population cible est l'ensemble des elements sur lesquels les resultats d'une enquete ou d'un sondage seront etendus. Les individus (unites elementaires, unites statistiques, elements) sont les consti-tuants d'un ensemble representes par leurs caracteristiques.

II arrive souvent que n'ayons pas a notre disposition la liste de toutes les unites statistiques (ex. : liste des menages disponibles alors que l'unite statistique est une personne). Nous noterons par iV le nombre total d'individus et par X, y,... les variables aleatoires qui les caracterisent. On note par Yi la valeur, dans la population, de la variable y pour l'individu i = 1 , . . . ,n.

L'un des principaux objectifs en echantillonnage est de fournir une bonne estimation des parametres (fonctions des valeurs) du caractere observe. Pour une population donnee, chaque parametre est une constante.

Les parametres de la population qui sont a la base inconnus s'ecrivent comme suit : Le total

• N

2. E C H A N T I L L O N N A G E A L E A T O I R E S I M P L E La moyenne La variance La variance corrigee ^ N N N N ^ i=l i=l

(v;

- n

2 2 = 1

La quantite SY peut aussi s'exprimer des manieres suivantes, c'est le lien entre la variance

non corrigee et celle qui est corrigee :

= ^ i E ^ - *

!

)-E£-EE-

_{- ^ ^ i V ( i V - l )}

i=l / t=l z=l j ^ i v ' N „ * Y-N-l L'ecart-type -<Tv oY = ^ (Yj - Yf

\h

N

- '

Le coefficient de variation

CVy = "-L.

Y

Le nombre total d'echantillons de taille n que Ton peut extraire d'une population de taille

N est egal a :

N\ N\ n) n\(N-n)\'

Pour determiner la probabilite d'inclusion d'un element, nous raisonnons a l'aide de l'evenement contraire : il y a ( ~x) echantillons de taille n qui ne contiennent pas Telement

en question, done la probabilite pour qu'il ne soit pas dans l'echantillon est :

N - l \ / ( N \ _ (N-l)\ n\(N-n)\ N-n_ n n ) l \nj n\(N-l-n)\ N\ N • N'

2. LE PLAN A L E A T O I R E S I M P L E (PAS) 13

On en deduit que la probability d'inclusion est egale a n/N. Cette quantite est aussi appelee taux d'echantillonnage.

1.2. L'echantillon. II existe deux sortes d'echantillons : probabiliste ou non proba-biliste. Un echantillon est probabiliste lorsque tout element a une probability (connue) d'appartenir a l'echantillon.

Les echantillons non probabilistes sont utilises en general dans les etudes de marche et enquetes d'opinion car ils sont moins couteux a obtenir. Dans la suite nous ne traiterons que des echantillons probabilistes.

Supposons qu'on ait un echantillon de taille n issu d'une population de iV elements. Les estimes des parametres de la population a partir des caracteristiques equivalentes dans l'echantillon sont : Le total La moyenne La variance corrigee

y =

X >

-i=\

y - Y] — = y/n.

i = l 2

•= = £

(yt -

yf

y ^ n - l

2. Le P l a n Aleatoire Simple (PAS)

2.1. Cas d'une variable quantitative. Nous allons maintenant calculer l'esperance et la variance de y. Pour ce faire, nous utiliserons les variables de CORNFIELD.

Posons :

n N v+

\~^ yi V~^ liH

y = 2^- =

> _ , — '

z—' n *—' n

ou U = 1 si l'individu appartient a l'echantillon et ti = 0 sinon (CORNFIELD). On sait que :

14 2. E C H A N T I L L O N N A G E A L E A T O I R E S I M P L E

C'est ce que nous avons nomme plus haut la probability d'inclusion. Par ailleurs, on a :

P(*i = 1 , ^ = 1) = N\N_{) P °u r ^ 3 On a alors :

mj = £

Var((,) = "( J V-n ) • ' Cow (ti,tj) = iV2 n(N - n) 3' N2(N-1) 2.1.1. Esperance et variance.

P r o p o s i t i o n 2 . 1 . i a quantite y est un estimateur sans biais de Y.

E(y) = Y D E M O N S T R A T I O N . * Y n N XT

E

li —

nN

= 7

a

P r o p o s i t i o n 2.2. La variance de Vestimateur y sous le plan aleatoire simple est

Va

l(S

) - ^ S l

D E M O N S T R A T I O N . On salt que

V a r ( y ) = V a r ( 5 ^ -* i W!

n

l

2. LE PLAN A L E A T O I R E SIMPLE (PAS) 15

En utilisant les formules precedentes de la variance et de la covariance, on obtient :

nN \ ^ N ^>*-<N(N-l)

On sait que : N , ,2 AT AT

« =

E ^ - E E

r

*

1 = 1 2=1 j / i V ' Alors : Var(y) = — - ^ N-n nN - n

ou / = ra/iV est le taux d'echantillonnage. D

P r o p o s i t i o n 2.3. La quantite Sy qui est la variance corrigee dans la population est

estimee sans biais par la variance corrigee dans Vechantillon

16 2. E C H A N T I L L O N N A G E A L E A T O I R E SIMPLE D E M O N S T R A T I O N .

E

(^) =

E

( ^ I ( E ^

2

- ^ )

2

) )

^r(

E

(E^

2

)--

E

(y

2

))

3 i (

E

(|S

2

M -

n

(

Vai

^) + (

E

(y))

2

)

\ 1=1 ^ n n l-^-S2Y + Y2 2 ~2 S£ - nY n 1 / N V = l

^(^(f>?-^)-(^)

2 2

= £

Nous estimons alors Var(y) par :

v{y)=

l

—tsl.

n y

2.1.2. Intervalles de confiance de niveau 1 — a. Pour la moyenne Y :

•

Y e y ± zai2Syyj ——.

Pour le total Y" :

Ye-y±z

a/2

N-^=y/T^J,

ou 2a/2 est le quantile d'ordre 1 — a/2 d'une loi normale.

2.2. C a s d'une proportion. Pour estimer la proportion P d'individus qui possedent un certain caractere A, on associe a chaque individu une variable y telle que :

J 1 si l'individu possede le caractere A I 0 sinon.

2. LE PLAN A L E A T O I R E S I M P L E (PAS)

Et ainsi,

N

Y-P =

yli

Y.

La proportion p = y, observee dans l'echantillon, est un estimateur sans biais de P. En effet,

E(p) = E(y) = Y = P Et

L'estimateur de cette variance est :

v(p) = v(y) = s. 1 - / 2

-s2

pq

n y

ou v(p) = (1 — '/) avec q = 1 — p. Un intervalle de confiance de niveau 1 — a pour P est alors :

Pe

P

±z

a/2x

l(l-f)

pq

n - l

2.3. E s t i m a t i o n de la taille de l'echantillon. Pour avoir une certaine precision

d sur la moyenne de y, la taille minimale de l'echantillon necessaire au niveau 1 — a

s'obtient comme suit : Cas d'une moyenne :

n =

avec

W . 2

Cas d'une proportion :

dy = z

a/2

y s:

1

+ zl/iW/d

2 n = avec 1 + zljjpq/NcP' d-za/2\\ N)n_1

-CHAPITRE 3

Echantillonnage stratifie

Dans ce chapitre, nous allons faire une etude de l'echantillonnage aleatoire stratifie et par la suite, nous discuterons de l'echantillonnage poststratifie.

1. Echantillonnage aleatoire stratifie

Nous avons vu precedemment que lorsqu'il s'agit d'un plan aleatoire simple, l'echantillon est directement extrait en bloc de la population. II n'a pas ete necessaire de subdiviser la population en sous-groupes avant de proceder a l'echantillonnage.

Parfois on divise la population en sous-groupes ou strates et l'echantillonnage se fait separement a l'interieur de chaque strate, c'est le plan stratifie. Si le processus de tirage dans chaque strate correspond a celui du plan aleatoire simple, alors on dit qu'on a un plan aleatoire stratifie. Cependant, il arrive que cet echantillon ne soit pas representatif de la population, ainsi, pour que cela ne se produise pas, on utilise la stratification a

priori ou a la •stratification a posteriori.

La stratification a priori est le fait de diviser la population en strates de telle sorte qu'un individu appartienne a une seule strate. Le critere de stratification est l'homogeneite dans chaque strate et l'heterogeneite entre les strates, le but etant d'y obtenir la plus petite variance.

Dans ce qui va suivre nous dirons simplement plan stratifie ou echantillonnage stratifie (PSTR).

1.1. Quelques notations. Voici quelques notations associees a des caracteristiques dans les strates.

- L designe le nombre de strates

- Nh le nombre total d'individus de la strate h

- Yht la valeur de la variable Y pour la ie observation de la strate h

~ Wh = Nh/N le poids de la strate h

- Yh = Yli=i YhjNh la moyenne de la variable Y pour la strate h

- Syh = ^2i=i JV _i la variance de la variable Y pour la strate h

Leur equivalent dans l'echantillon est

- nh le nombre d'observations dans l'echantillon tire de la strate h

1. E C H A N T I L L O N N A G E A L E A T O I R E S T R A T I F I E 19

- y^ la valeur observee pour la ie observation de l'echantillon de la strate h

- Vh = J 3 2 i yhi/nh la moyenne de l'echantillon tire de la strate h

- sf, = y ^ " \ Vhi y, la variance de l'echantillon tire de la strate h

Puisque le tirage se fait independamment d'une strate a l'autre, le nombre total d'echantillons s'obtient comme suit :

Nx\ /iV2\ /j\rA = - ^ fNh

Ce nombre est toujours inferieur ou egal a ( ) , le nombre total d'echantillons de taille

La probability d'inclusion d'un element dans la strate h est egale a rih/Nh pour 1 < h < L. La stratification est utilisee pour des raisons de representativite, de gains en precision et aussi lorsqu'on veut, dans une enquete globale, faire des inferences particulieres sur des sous-groupes ou des sous-domaines de la population.

L'un des buts de l'echantillonnage stratifie est d'estimer :

N Y

Z^ N

L Nh

^ ^ N Nh

Pour cela, on pose

= Y^W

h

Y

h

Y

= y* = ^2

WhVh =

]v E

NhVh

20 3. E C H A N T I L L O N N A G E STRATIFIE

1.2. C a s d'une variable quantitative.

1.2.1. Esperance et variance de la m,oyenne stratifiee. L'esperance se calcule ainsi :

y

st

) = ElJ2

W

^

\h=l L

= J2

W

»

E

^

h=l L

=£

WhYh

h=l L Nh „ h=l i=l = Y.

Ce qui signifie que yst est un estimateur sans biais de Y.

Calculons maintenant sa variance :

Var(&t) = Var ( ^ Whyh ) = ^ W^Vax{yh).

\h=l J h=l

Puisque Ton effectue des echantillonnages aleatoires simples independamment dans chaque strate.

Var(yh) = —Si ou fh = nh/Nh

Done

Var(f^) = vJj2

W

^j = E wfi^T'

sS

YH-\h=\ / h=l

Un estimateur sans biais de cette variance est donne par :

h=l h

\.1.2. Intervalles de confiance. L'expression za/2 designe le quantile d'ordre 1 — a / 2

d'une loi normale.

L'intervalle de confiance pour la moyenne Y est donnee par :

1. E C H A N T I L L O N N A G E A L E A T O I R E S T R A T I F I E 21

1.3. Cas d'une proportion. Pour estimer la proportion P d'individus qui possedent un certain caractere A, on associe a chaque individu une variable y telle que :

J 1 si l'individu possede le caractere A I 0 sinon. Et ainsi, Posons : L Nh h=l i=l Nh P

_ V^ *

h

* _ v

Ph

-^N~

h

-

Yh nh

E

Vht =Vh-. =Vh-. nh t=\

La proportion P est estimee par :

L

Pst = Yl W

h

p

h

.

On a : h = i E(prt)

= E [Y,W

h

Ph

\h=\ L

= £V

h

E(p„)

fe=i L

= J2

W

^

h=l L

= J2

Wh?h

h=\

= Y = P

3. E C H A N T I L L O N N A G E STRATIF1E et Vai{pst)=Vail^2whph L

= J]) W

2

Var(p,)

L

E

M^PhQh (Nh-nh\ ,

L'estimateur sans biais de cette variance est L

Un intervalle de confiance de niveau 1 — a pour P est alors :

P epst±za/2\/v(pst).

2. Echantillonnage stratifie proportionnel

2.1. Cas d'une variable quantitative. On choisit n/i pour chaque strate de maniere a ce qu'il soit proportionnel a Wh c'est-a-dire : rih =

nWh-Alors,

, nh 1 Nh 1 n

h

=wr

nWh

NT

n

TwrN=

!

-Le taux d'echantillonnage reste inchange dans chaque strate. On estime alors Y par : L ystP = ^2whyh h=l L nh • _

=E^E

!

*"

h=l i = l " n 1 ^ .W f c. h=\ t=l = y iV

2. E C H A N T I L L O N N A G E S T R A T I F I E P R O P O R T I O N N E L 23

Dans ce cas l'echantillonnage est autopondere, car tous les individus ont le meme poids dans l'estimateur de la moyenne. Ce poids est N/n alors que, dans rechantillonnage stratifie ordinaire, le poids N^/uh depend de la strate.

On peut ecrire

L nh

1 - - j Vh

Done la variance se calcule comme suit :

/ L ^ Var(ystp) = Varl ^ Whyh U = i / L h=l

fct

n

»

Vh

= ^Twt

l

~

f

s

2 ^ h nWh m et h=\

pour un estimateur de la variance.

2.2. Cas d'une proportion. On applique le rneme raisonnement pour effectuer un echantillonnage stratifie proportionnel en vue d'estimer la proportion P d'individus ayant un certain caractere A : L L nh h=l . h=\ i=l h. et L nh n h=l i=\ ou

J 1 si l'individu possede le caractere A 0 sinon.

24 3. ECHANTILLONNAGE STRATIFIE

L'estimateur de la variance de pstp sera alors :

• 1 - / • n Wh- l h=l

1 - /

L n i L

E

w

*™« ( r n y *

i ^ I > » » * + — E —

h—\ h=\

En general, on neglige le deuxieme terme; et done : 1 — f *.L -y

v(PstP) ~ y~] Whphqh.

3. Echantillonnage optimal, allocation d e N e y m a n

3.1. Cas d'une variable quantitative. L'allocation optimale est utilisee lorsqu'on veut trouver les rih qui minimisent Var(yst) tout en respectant la relation Y2h n^ = n. On

utilise alors la methode des multiplicateurs de Lagrange, e'est-a-dire qu'on minimise

$(A) =. V-dx{y

st

) + A f ^ n

h

- n J

-EE^-E^^fe-H

h=l h=\ n h=l n \ft=l /

ou A est un multiplicateur de Lagrange.

Les quantites n^ qui minimisent $(A) sont obtenues en derivant <5(A) par rapport a A et par la suite, il faudra annuler cette valeur :

9*(A) = ^ W*S>Yh | A = Q

3. ECHANTILLONNAGE OPTIMAL, ALLOCATION DE NEYMAN 25

Alors en sommant sur toutes les strates, on a : Ylh=i nhV^ = Y2h=i WhSYh et done

nV\ = T,Lh=1WhSYh.

Ainsi est obtenue l'allocation de Neyman en eliminant \/A entre les deux equations precedentes :

WhSYh

nh

Eti^V

La quantite Var(ysto) est la valeur optimale de l'allocation de Neyman. Elle s'obtient en

remplagant dans l'expression de Var(yst) les quantites rih, par l'allocation de Neyman

ci-dessus. 2 1 ~~ Jh C2

Vai(j/

8t

) = £ V ;

h nh ^ h=i n L

= E^(^i)

s

-On obtient alors :

V*r(y

sto

) = Uj2w

h

S

Yh

) - £

\h=l / h=l

wis.

h^Y*

Nh

2

\h=l / h=\

Un estime de cette variance serait :

3.2. Cas d'une proportion. L'objectif reste le meme e'est-a-dire minimiser la va-riance de la proportion empirique en utilisant l'allocation de Neyman, done il faudra determiner la valeur des nh qui minimisent :

Var(

P

,«) = £ Wl

l

-^\P

h

Q, ^ t ^ ^ ' t

W

^

h=l h h=\ h h=\ h

On utilise la methode des multiplicateurs de Lagrange pour minimiser :

•w=t <~ ~ t ^

2

^r

+x

(t*-") •

3. ECHANTILLONNAGE STRATIFIE

On trouve n^ qui minimise cette fonction :

En le remplacant dans l'expression de Var(psi) on obtient l'estime de Var(psto) :

• I (

L

V 1

L

v(Psto) = - ( ^2 Why/p^Th J - — Y^

w

hPhqh-n \h=\ J h=\

4. Taille de l'echantillon

4.1. Cas d'une variable quantitative. On veut une precision absolue D en esti-mant la moyenne de la population grace a un echantillonnage stratifie proportionnel :

Y e y

stp

± D.

L'intervalle de confiance est alors :

d'ou D = za/2^Vnv{ystp). En utilisant on obtient Y e ystp ± za/2\JVar(t/Stp), Var(ystp) = ^ ^ W ^ , h=l

4/2ZL,w

h

sl

2

n =

^ "r JV

Afin de trouver la taille de l'echantillon, il vaut mieux utiliser l'echantillonnage stratifie optimal car cette methode utilise les valeurs de S\ .

4.2. Cas d'une proportion. On veut.estimer une proportion P avec une precision

D, en utilisant un echantillonnage optimal :

P e p

sto

± D,

5. STRATIFICATION A POSTERIORI 27

d'ou D = za/2^Vav(psto).

En utilisant

on obtient :

Et on a

Var(psto) =•- {^Why/P&h\ ~^Y.WhPhQh,

Za/2 1 L»2

[n=

iz l / \ :1 Why/PhQh) j E L ^ ^ O * N n = 5. Stratification a posteriori

C'est vin plan d'echantillonnage qui consiste a selectionner les observations selon le plan aleatoire simple mais avec l'application du plan aleatoire stratifie. IT est utilise lorsqu'on a le poids de chaque strate mais pas la liste des individus appartenant a cette strate.

5.1. Cas d'une variable quantitative. Pour l'estimation de la moyenne de la population, on utilise :

^ L

y = y

P

st = Y2

Wh

-y

h

-h=\

Son esperance est :

L

E{yPst) = Yl WhEnh(Ey(yh\nh)),

h=l

ou Ey(y/i|n/j) est une esperance conditionnelle. Si les nh sont fixes, on a :

Ey{yh\nh) = Yh:

et ainsi :

L -. L

HVpst) = J2

W

^n

h

{Y

h

) ) = ^ E Wk =

Y

-h=l -h=l

Done l'estimateur ypst de Y est sans biais. On calcule la variance de cet estimateur en

3. E C H A N T I L L O N N A G E S T R A T I F I E

Var(yh) = E ^ V a r ^ K ) ) + V&Ynh(E(yh\nh))

= En i, | I J v , ~~ T T ^ V , •

Jnh\ „ I uYh

N^Yh-Pour determiner la valeur de E„h(l/n^) quand rih suit une loi hypergeometrique :

Enjn/O = nWh

On retrouve le calcul en detail dans [Mor93].

Cette valeur est ensuite portee dans l'expression de Var(y/l) = Enh(l/rih) SY — SY /N^

.

v

«<*>=^(ii

+

(

1

-'0^-ivk)-Ainsi on calcule Var(ypst) :

L

Vav(ypst) = ^2w2hVar(yh)

h=l

^ t ^ + ^ D

1

- ^ ,

h=l h=\

On peut maintenant donner l'expression d'un estimateur sans biais de Var(ypst) :

CHAPITRE 4

Echantillonnage avec probabilities egales

Pour selectionner les observations d'un echantillon, il faut que tous les membres de la population aient une chance pas forcement la meme d'etre tires. En general on utilise la taille de chaque unite pour la constitution de l'echantillon si cette information existe et varie selon l'unite, ce qui permet d'accroitre l'emcacite. Rappelons que la taille d'une unite est la valeur prise par une variable positive associee a cette unite. Dans le cas de cette methode, plus la taille de l'unite est grande, plus sa chance d'etre incluse dans l'echantillon est elevee. Cette methode est done appelee echantillonnage avec probability

proportionnelle a la taille (PPT). Dans ce chapitre, nous traiterons de cette methode.

La variable £* = 1 si l'individu appartient a l'echantillon et U = 0 sinon (la variable de CORNFIELD).

Posons : P(£j = 1) = 7IY, 7T, etant la probabilite d'inclusion de l'individu i dans l'echantillon.

V a r ( i j ) = 7Ti(l - TTi) Cov(U,tj) = TTij — TTiTTj

1. Echantillonnage avec probabilities proportionnelles a la taille et avec remise

Cette methode est la plus utilisee (p.p.t), elle a ete etudiee par [HH43]. On associe a chaque unite i sa taille, et Ton pose :

N

nMi Mi

30 4. E C H A N T I L L O N N A G E AVEC P R O B A B I L I T E S EGALES

E

Vi

L'estimateur de Horvitz-Thompson de y donne :

_Vi NTT; 1 n = n ^ NMQ 2=1 i=i

ou a,i est une variable aleatoire multinomiale telle que :

E(a,i) = npi

Var(ai)npi(l - p{) Coy(ai,aj) =-npiPj)

ce qui entraine que :

E(a,i) = npi = iri

E(aj) = npj = TTJ

E(ai, cij) = Cov(a,i, a,-) + E(aj) E(a,j) = n(n — l)piPj = TTJJ.

Enongons quelques resultats importants (de Horvitz Thompson) etablis sur la base d'un echantillonnage avec remise. (A voir les demonstrations detaillees dans le livre [Mor93]).

<3)

V{SHT)

= ^hry(§

(T%)

- "&*)

La variance de l'estimateur de Horvitz-Thompson est obtenue en utilisant le resultat (1) :

ou encore en utilisant le (2) :

1 / N

Var(yppt) = - ^

2. P R O B A B I L I T E S P R O P O R T I O N N E L L E S , SANS REMISE 31

Cette variance est estimee par :

2. Echantillonnage avec probabilites proportionnelles a la taille et sans remise

Son objectif est de proposer des methodes pour tirer les unites avec des probabilites 7r, et TTJ d'inclusion faciles a calculer ou connues a priori. Theoriquement, l'echantillonnage sans remise avec probabilites variables se traite sans trop de difficulte. Cependant, dans la pratique, il arrive que les probabilites d'inclusion deviennent extremement compliquees a exprimer lorsqu'on depasse les premiers tirages.

L a m e t h o d e d e R a o , H a r t l e y , Cochran.

Cette methode est employee pour effectuer un echantillonnage de taille n, sans remise et avec probabilites proportionnelles a la taille. On realise une partition de la population en

n groupes comprenant NX,N2,... ,Nn individus.

On tire ensuite un individu k du groupe g avec probabilites proportionnelles a la taille

ou fc=l On pose : 1 ^ Ml VRHc = ^ ^ y g - w . 3 = 1 y

Les quantites Mg et yg se rapportant a l'unite qui represente le groupe g.

Pour calculer Fesperance de cet estimateur, on considere deux etapes : l'etape 1 de repartition de la population en n groupes et l'etape 2 de selection d'un individu par groupe.

4. E C H A N T I L L O N N A G E AVEC PROBABILITIES EGALES

^(URHC) = Ei( E2( yRHc

-M*s*S'))

ou Ofc = 1 si l'individu k du groupe g est choisi, et dk = 0 sinon.

/ l n ^ Ms \ E(y^c) = EX - £ E n^(E2(afc|l)) \ g=l fc=l fe / (, n N9 \ = E i l v E E F M carE2(af e|l) = Mfc7M09 N = E i ( F )

= r.

3 = 1 fc=l

C'est un estimateur sans biais de la moyenne de la population. Calculons sa variance :

Var(yi?//c) = Ei(V™2(yRHc\l)) + V&ri{EiyRHC\l)).

Le deuxieme terme est nul puisque E^VRHCI^-) — Y.

Quant au premier terme,

2. P R O B A B I L I T E S P R O P O R T I O N N E L L E S , SANS REMISE 33

On utilise alors Var(yppt) :

N9 Ng 2 N T 7 - - T 7 )

_M

_k

_{Mi J \}

M*M> / 1 n / W9 iV9

Var(y«

ffC

) = E

1

Kp £ *° U ^ E £

\i V 9= i \Z i V3 fc=i ¥fc g=l i = l ^ V J / 9=1 »=1 j # i N J f • •

= E ^

(

7v_ i) "

Var

te*)

_ n ( E ^ = i ^ - i v )

N(N-1)

Si iV3 = iV/n, alors : -Var(ypp4) _ . N — n _ V a r ( y ^ c ) = ^ _ 1Var(yB p t), ou encore V a r ^ H c H ^ ^ - ^ — - r j

On remarque que le rapport des variances pour les echantillonnages sans remise et avec remise est (JV — n)/(N — 1), comme pour l'echantillonnage aleatoire simple.

On peut montrer [Coc77] qu'un estimateur sans biais de Var(y^//c) e st :

CHAPITRE 5

0 _ _ '

Echantillonnage en deux cycles : Estimation du total de la

population

Rappelons que notre objectif est d'avoir une estimation du total de la population au deuxieme cycle en regard de l'information recueillie au cycle precedent (premier). Dans ce chapitre deux strategies sont proposees, une qui utilise les donnees du premier cycle seulement comme mesure de la taille de l'echantillon apparie et l'autre comme mesure de la taille et comme variable de stratification. Nous conclurons qu'une des strategies est meilleure que celle de [PG94] qui ont utilise l'information du cycle anterieur seulement comme mesure de la taille de l'echantillon apparie.

Nous examinons une population finie U = (Ui,..., Ui,..., U^).

1. P l a n s d'echantillonnage

Au premier cycle, un echantillon Si de taille n est tire de notre population U avec un certain plan d'echantillonnage que nous nommerons Pi dans un premier temps.

Nous denoterons les donnees issues de ce plan par Yu avec i appartenant a l'echantillon S\; ou Yu represente la valeur de la variable aleatoire a l'etude pour la ie unite. Aussi Y^ est

la valeur de la meme variable etudiee, pour la ie unite au deuxieme cycle.

Au deuxieme cycle, un echantillon apparie aussi appele sous-echantillon Sm de taille m = nX (nombre entier) ou 0 < A < 1 est choisi dans l'echantillon Si du premier cycle

par un plan d'echantillonnage que nous denoterons Pm. Ce dernier sera complete par un

echantillon non apparie Su de taille u = nfi (m = nX ; u = n\i = n — m avec \x = 1 — A)

selon deux cas de figures :

- Soit il est choisi dans l'ensemble de la population U suivant un plan d'echantillonnage

Pu en ayant une partie de Si, voir figure 1.

- Soit parmi U/Si, la serie d'unites qui n'ont pas ete selectionnees au premier cycle par le plan d'echantillonnage Pu. Voir figure 2.

Ainsi les donnees Y2i sont obtenues avec i appartenant a Sm et a Su au deuxieme cycle.

Dans la suite, nous ne considererons que le deuxieme cas. De ce fait, nous savons evidemment que le cout de l'enquete pour la collecte des donnees de l'echantillon apparie est beaucoup moins eleve que celui de l'echantillon non apparie car Sm est tire d'un echantillon deja

2. M E T H O D E DESTIMATION DU TOTAL DE LA P O P U L A T I O N AU D E U X I E M E CYCLE 35

FIGURE 1. Plan d'echantillonnage 1

mis en place (les donnees existent), ce n'est pas le cas de Su; il faudra done faire une

nouvelle enquete. Pour une simplification de l'etude, nous presumerons que le cout des unites reste le meme pour toutes les unites au deuxieme cycle

2. M e t h o d e d'estimation du total de la population au d e u x i e m e cycle Un estimateur sans biais Y^m de Y2, le total de la population au deuxieme cycle, est

determine a partir des donnees de Yu, i appartenant a l'echantillon initial Si et de

Y2i avec i appartenant a l'echantillon apparie Sm en utilisant Yu comme information

auxiliaire. Puisqu'on a besoin d'information auxiliaire pour estimer Y2, l'estimateur Y^m sera habituellement obtenu en utilisant la methode de l'estimation par la difference, par le quotient ou par la regression.

36 5. E C H A N T I L L O N N A G E EN DEUX CYCLES : ESTIMATION DU T O T A L

FIGURE 2. Plan d'echantillonnage 2

Enfin, un estimateur composite (une combinaison) de Y2m et de Y2u est obtenu en utilisant

un poids de (f> avec 0 < </> < 1 :

Y2 = <$>%m + . ( 1 - <t>)%u.

La valeur optimale de (f> = (f>(\) est obtenue en minimisant la valeur de la variance de

Y2 (VarfY2\) par rapport a (f> pour un m fixe (implicitement de A car m = nX). Dans la

suite nous supposerons que Y2m et Y2u sont independantes.

Notons par Vm et Vu les variances de Y2m et F2u de respectivement.

P r o p o s i t i o n 2 . 1. La valeur optimale est donnee par

4>(\)

l Vm V K 1 1

+

_v

_n D E M O N S T R A T I O N . On a % = 0 F2 m + (1 - 4>)Y2u,

2. M E T H O D E DESTIMATION DU T O T A L D E LA P O P U L A T I O N AU D E U X I E M E CYCLE 37

Var(y2|A) = V a r ( #2 m + (1 - cf>)Y2u)

= 02V a r ( y2 m) + (1 - ^ )2V a r ( f2 u) .

Etant donne que y2 m et Y2u sont independantes, leur covariance est done nulle.

Trouvons la valeur de <f> qui minimise Var( Y^AJ :

dVar

° = - *f>

±-—?- = 20Vax(y2 mJ - 2(1 - ^ ) V a r ( y2 uJ = 2</>Var(y2m) + 20Var(F2„) - 2 V a r ( f2 u) ^ 0 ( V a r ( f2 m) + </»Var(F2u)) = Var(y2„) (/-(A) = V a r ( y2 u) / ( V a r ( y2 m) + <£Var(y2u)) = VU/(VU + Vm) = (1/Vm)(l/Vm + 1/Vu)

Verifions les conditions de second ordre. II suffit de verifier que la derivee seconde est positive au point qui annule la derivee premiere. En fait ici, la derivee est toujours positive car :

d2Var(r2|A) / - x

^ '- = 2 V a r ( F2 m) + 2Var(Y2uJ > 0.

P r o p o s i t i o n 2.2. La variance de Y2 etant donne la valeur de A est :

V a r ( y2| A ) = ( l / Km + l / K ) -1.

D E M O N S T R A T I O N . Puisque

<t>{\) = {i/v

m

){i/v

m

+i/v

u

r\

et

Var(r2|A) = Var(</>y2m + (1 - ^)Y2 u)

= 02Var(i>2 m) + (1 - ^ )2V a r ( f2 u)

= 4>2Vm + ( 1 - cj>)2Vuy

5. E C H A N T I L L O N N A G E EN DEUX CYCLES : ESTIMATION DU T O T A L

H^) = {^)

2

^(y^r)

2

^

V^Vm + V^Vu

(v

m

+ v

u

y

VuVmjVu + Vm)

v

u

v

m

v

m

+ v

u 1 l/Vm + l/Vu D

La proportion optimale de l'echantillon apparie A = A0 est determined en reduisant au

maximum la valeur de V a n l ^ A ] par rapport a A. En introduisant cette egalite dans l'expression de Var( V2I.A 1, on obtient la plus petite variance de

% ( V a rm i n( f2) ) = Var(?2|A0)).-.

Rappelons que notre objectif est de trouver des strategies afin cle minimiser Varl Y2\\)

en faisant une combinaison des trois plans Pi, Pm et Ps.

3. Strategies d'echantillonnage

3.1. L'approche de Avadhani et S u k h a t m e . En considerant qu'aucune infor-mation n'est disponible avant la premiere enquete, l'echantillon au premier cycle S\ de taille n est selectionne suivant un echantillonnage aleatoire simple sans remise (PAS). En ce qui concerne l'echantillon apparie, la methode de Rao, Hartley et Cochran, com-munement appelee RHC (1962) propose que les n unites de l'echantillon au premier cycle soient reparties aleatoirement en m groupes, chacun de taille n/m que Ton presume etre un nombre entier. Ainsi dans chacun des groupes, est choisie de facon aleatoire une unite avec une probabilite proportionnelle a la mesure de la taille de l'echantillon. Alors Avadhani et Sukhatme (1970) ont choisi les unites de l'echantillon apparie de taille m selon cette methode RHC.

Par consequent, si la ie unite [/* appartient auje groupe Gj, pour 1 < j; < m, alors la

probabilite de selectionner Ui est egale a q* (i appartenant a Si) avec :

q* = yu

3. S T R A T E G I E S D ' E C H A N T I L L O N N A G E 39

L'echantillon Su a ete preleve de U/S\ par echantillonnage aleatoire simple.

3.2. L'approche de Chotai. Elle utilise la methode de Rao, Hartley, Cochran pour selectionner l'echantillon au premier et au deuxieme cycle.

Pour la selection de l'echantillon S\ de taille n, cet auteur divise la population en n groupes Gj (j = l,...,n) de maniere a obtenir le meme nombre d'individus N/n, un entier, dans chacun de celui-ci. Ensuite il tire un individu dans chaque groupe avec une probability proportionnelle a Zj, Zi represente la mesure de la taille de la ie unite. Cette

mesure est censee etre positive et connue pour chaque i E U. On pose :

z=^2

Zi

P

k = Zk

i

z A

J = y i

Pk-ieu keGj

Ainsi est obtenu l'echantillon Si. - .

Pour la deuxieme etape, c'est-a-dire celle de l'echantillon apparie et non apparie, il precede de la maniere suivante :

Avec le meme principe que precedemment, en supposant que n/m soit un entier, l'echantillon

Sm de taille m a ete selectionne mais cette fois-ci, on utilise A, (le meme precedemment)

pour la ie unite avec i appartenant a l'echantillon Si comme mesure de la taille normee.

ie5i

L'echantillon non apparie Su de taille u a ete egalement preleve avec le meme principe que

l'echantillon Sm avec comme mesure de taille normee pi, pour la ie unite, en supposant

que N/u soit un entier.

Supposons que Pf soit le total des valeurs des A, associees aux unites appartenant au groupe aleatoire duquel la ie unite a ete selectionnee dans Sm. De meme, p't est le total

des valeurs des p, associees aux unites appartenant au groupe aleatoire duquel la ie unite

a ete selectionnee dans Su.

On a :

ieSm iesu

L'estimateur de Y^ s'ecrit :

40 5. E C H A N T I L L O N N A G E EN DEUX CYCLES : ESTIMATION DU T O T A L

ou

7^ Pi \£? Pi ^ Pi I

et * W = 2 —

Vi-iesu p%

On doit choisir 7 de maniere a reduire au minimum la variance de Yim.

Remarque 1. Si les observations demeurent inchangees d'un cycle a l'autre et que Ton pose 7 = 1, on trouve i^m = X^6SX Uu/Pi\, ce qui n'est autre que l'estimateur du total

issu de la methode RHC au premier cycle.

Alors la variance de Y2 que nous allons appeler Variance de Chotai (Vc) s'ecrit comme

suit : ou Vc = Vmin = k(l-f + V T ^ ^ ) a22/2. k = N/n(N - 1) . / = n/N •

Y

t

= ^2vu i = 1,2

5* = Y^Pi(yZi/Pi - Y2)(Vli/Pi ~ Yi)IVl°2

L'expression de cette variance se trouve dans Chotai (1974).

3.3. L'approche de Arnab. L'echantillon Si est construit par la methode de selection avec probability proportionnelle a la taille avec remise, avec comme mesure de taille normee Pi = z,,/Z pour la ie unite choisie. Avec les informations Yu recueillies au

pre-mier cycle avec un plan d'echantillonnage quelconque, Arnab repartit les n unites de l'echantillon Si en L strates Si = UhSih- Soit n^ la taille de l'echantillon Sih de he

strate, on supposera que n est assez grand pour avoir les n^ positifs. Au deuxieme cycle,

Smh de taille nih est selectionne selon un plan d'echantillonnage approprie avec comme

3. S T R A T E G I E S D ' E C H A N T I L L O N N A G E

Quand a l'echantillon non apparie Su, sa selection se fait avec probability proportionnelle

a la taille avec remise, a partir de 1'ensemble de la population U ou z\ designe la mesure de taille.

3.4. L'approche de Prasad et Graham. Prasad et Graham ont procede de la menie facon que Chotai (1974) en utilisant comme mesure de taille normee pi = Zi/Z pour la selection de l'echantillon initial Si. Pour celle de l'echantillon apparie Sm, la

mesure de taille est p* = (yuSi/Pi) / YlieSiiv^i/Pi) Po u r 1& ^ unite selectionnee, avec

i G Si et 5{ = YljeG Pj Po u r le groupe renfermant la ie unite. Ensuite Su est selectionne

dans toute la population comme Chotai (1974) avec l'utilisation de la methode RHC. On presumera que N/n, n/m et N/u sont des nombres entiers.

Supposons que p, soit le total des valeurs de P* associees aux unites appartenant au groupe aleatoire duquel la ie unite a ete selectionnee dans Sm.

L'estimateur de Yi s'ecrit :

Y2 = 4>Y2m + (1 - 4>)Y2u ou y*2i = y2i\/Pi

Y2m = Yl (V2i/Pi)Pi e t ^2« =

J2{y2i/Pi)Pi-De meme, p',- est le total des valeurs des pi associees aux unites appartenant au groupe aleatoire duquel la ie unite a ete selectionnee dans Su.

VPG(Y2) = Vmin = k(l-f + ^C)a22/2 ou al = ^<iAv2ilqi-Y2f qi = yu/Yi k = N/n(N - 1) f = n/N ^t=^2pi(yti/Pi-yt)2 t = i,2 ieu Yt = J^yti t = l,2. ieu

Remarque 2. Avadhani et Sukhatme (1970) proposent une strategic moins exigeante que celle des autres auteurs car elle requiert moins d'information sur les mesures des tailles (les Yu sont utilises comme mesure de la taille). Celle de Chotai(1974) se trouve etre la plus efficace car elle utilise les mesures de taille piy = Zi/Z pour la selection, et les

5. E C H A N T I L L O N N A G E EN DEUX CYCLES : ESTIMATION DU T O T A L

informations Yu obtenues au premier cycle pour Testimation. Par contre, la strategie de Chotai pour le calcul Y2 est plus compliquee a obtenir dans le sens ou il faut estimer les

parametres inconnus 0 , 7 .

La methode utilisee par Prasad et Graham est aussi plus efficace que celle de Chotai de facon empirique. Aussi en pratique, on peut utiliser celle de Prasad et Graham car ici on a un seul parametre <f> a estimer. Arnab (1991) fut le premier a introduire la notion de stratification : il a utilise 1'information Yu pour stratifier et estimer. Elle est done en principe meilleure que toutes les autres. En pratique, on devrait toujours songer a stratifier lorsque les informations sont disponibles.

4. Strategies proposees

Nous allons examiner deux strategies d'echantillormage qui sont des strategies modifiees de celles de Prasad et Graham et de Arnab.

4 . 1 . Strategie 1. Le plan d'echantillonnage est le meme que celui de Prasad et Graham a la seule difference que la mesure de taille initiale de sm a ete modifiee.

Posant :

z* = ZiAi/pi

V\i = V2i&l/Pi

r* = rtAi/pi

n = V2i - @Zi

et s'inspirant de la formule de Chotai (voir (1), page 39) on obtient :

ou Z = Ylieu z* remplace E i£ Si ( y w M )A»

-La constante (3 doit etre choisie avec soin de maniere a minimiser la variance de l2m-Les quantites p*,pi et Aj sont les memes que decrites par Prasad et Graham.

Y2 = 4>Y2m + (1 - 0)>2« avec Y2u = ^ ( y2i M ) P i

Designons par E\ l'esperance mathematique non conditionnelle pour la selection de S\,

Vi la variance, E2 l'esperance mathematique pour Sm et V2 sa variance. On utilisera la

formule de la decomposition de la variance dans la proposition ci-apres :

Var(f4|/?) = EMWJP) + E

2

V

l

(Y*J(3).

4. S T R A T E G I E S P R O P O S E E S 43

Ce resultat se demontre a partir de la proposition ci-apres.

Proposition 4.1. Si X et Y sont deux variables aleatoires alors :

Var(X) = Vax(E(X|y)) + E(Vax(X|Y)).

DEMONSTRATION.

Var(X) •= Var(E(X|y)) + E(Var(X|F))

= (E(E(X\Y))

2

- E(E(X|F))

2

) +

E(E(X2\Y)

- E(X\Y)

2

)

= (E(E(X\Y)

2

) - E(X)

2

) + E(X)

2

- E(E{X\Y)

2

)

= Var(X)

Selon Prasad et Graham, on a :

Var(Y£J/?) = E ^ V ^ J / ? ) ) + E.fv^jP))

ou

E

x

(y

2

(F;

m

|/?)) = haf(p)

E

2

( ^ ( r ; j / ? ) ) = f c ( i - / y

;

N(n - m)

*2 2 fcl =

nm(N - 1)

ieu 5 = C03/C0C3

iesm V * i£sm / \ ^ * iesm /

5. E C H A N T I L L O N N A G E EN DEUX CYCLES : ESTIMATION DU T O T A L avec k = N/n{N - 1) / = n/N

^ = J2fr(yu/Pi-Y

t

)

2

t = l,2

i& d = m(N - 1)/N(m - 1) etqi = yu/Y1.

L'optimum de (5 qui reduit au minimum la variance Var(f2*J/?) s' ecrit :

opt /? = (30 = 5—

En remplacant j3 par /30, on obtient :

Var(y2*J/?) = Var(i>;m|/?0) = fc((l - / ) + (1 - A)C*/A)a22

oil (* = (1 — 52)( et k, f et (, sont obtenus comme precedemment.

On obtient la variance de y2 pour une valeur donnee de A en reduisant la variance de F2

par rapport a cp lorsque opt (3 = (3Q = 6a3/a0 et la variance est

Varo p t(F|A) = ( l / V a r ( y2 m| / 30) ) + l / V a r ( f2 u) ) *

+ — — I

02-k{\ - f) + (1 - A)C/A 02-k{\ -ffi)

Si on reduit au minimum la valeur de Varopt par rapport a A, on obtient :

opt A = A0 = v / C / ( l + y/c)

La variance minimum s'ecrit :

Varm i n(y2) =k(l-f + s / c ) (T\I2 = M1

et Ton peut determiner la valeur minimum de la variance en remplagant A par sa valeur optimale dans la formule de la variance optimum, on a :

/ 1 ' \ - 1

Varo p t(y2|A) =ul

2 \k(l - f) + (1 - A)C/A HI - fp)

Posons \x = 1 — A et AQ =

1 + V C A l o r s l - A0 = l / ( l + V C )

-4. S T R A T E G I E S P R O P O S E E S 45

Var

ODt

(y

2

|A) = a

2

, ( — ^—^

7r

^r +

l o p t

^

2 , / % ;

~ ^ U ( l - / ) + (l-A)C*/A

+

fe(l-/A«)

= o-> T—: s—r.—;=v +

,. i i / a + v ^ )

= CTn — — 7 = +

fc(i - /) + v ^ fc(i - /) + fc/VC/U + VF).

2 i 1 1 N ~*

" °

2 {

k(i - f) + VC

+

k(i - /)(i + VC) + kfVC

fc(i-/) + >/£* k-kf + kV?

= *2 I ~ ^- +

1 1

(To C o

M l - / ) + ^ C k(l-f)+ky/?

2kQ.-f) + (l + k)VC

(k(l-f) + y/?)(k(l-f)+kVF)

\k(l-f) + VF)(k(l-f) + ky/?)'

2(fc(l-/) + (±±VC)) J

= al(k{l-f)+k^)

= Var

min

^F

2

J

Pour simplifier l'equation, Arnab a considere :

1 + k ,

2 ~ *

l + fc«2

Jfc« 1

Cela signifie quo n = 1, co qui n'cst pas tros pertinent, ct nc serait utile que pour de tres

petites tailles d'echantillons.

Remarque 3. On ne peut utiliser l'estimateur de Y^ en pratique que lorsqu'on possede

46 5. E C H A N T I L L O N N A G E EN DEUX CYCLES : ESTIMATION DU T O T A L

utiliser l'estimateur de difference

base sur l'echantillon apparie, alors on aurait :

Var

min

(y

2

) =k(l-f+yj£\ a

22

/2 = M

x

ou

C = {1 + T2 + 2T5)(

T = a0/a3.

4.1.1. Estimation de la variance. L'estimation de la variance est donnee dans les deux resultats ci-apres que Ton peut retrouver dans [Arn98] :

var(f

2m

) = J L (

(y,(VI^/PIWP*

- Yim)

est un estimateur sans biais de Van Y2m) quand (3Q est connu avec k = et

, n — m K2 = •—z r . m(n — 1) R e s u l t a t 2. On peut estimer V \iesm / / N(n — m) nm{N - l)(a2 + a\ - a03) par

~s E (nix - E «/*>)'

i £ sm \ i£sm / ( 2 n — m

avec f* = TiAi/pi et fj = y2i — Zi et cr^al et a03 ont les memes expressions que

4. S T R A T E G I E S P R O P O S E E S

, 2 „2

Les estimateurs sans biais de a^, a\ et a^ sont donnes respectivement par

iGSm \ J 6 s „

Pi

i£sm \ i&s-m J

^03 = d Y^ (

ZX/PX

- H Wi/Pi J (y*/p* ~ H y2iPi/pt J

avec d = m(N - l)/N(m - 1).

4.1.2. Estimateur de Varopt( Y2\\ J. Si ra est fixe, alors

Varo p t(f2|A) = (l/Vm + I / K ) "1

avec

\>m = Var(r2*m|/?0)

et Vu = Va,r(Y2uJ = N _^^2Pi ( W R - Y2u)

4.1.3. Estimateur de Varm;n ( F2) • En introduisant des estimateurs de £*, A et a

Varrain ( ?2) = fc (1 - / + (1 - \)C/\) a\

C * = ( l + f2) c ou r = a0/a3

A = ^/c/(i + c )

obtient

C = aj/a

22

a\ = Aa|(m) + (1 - A)<r22(u)

La quantite a2(m) est un estimateur sans biais base sur 1'echantillon sm.

V a r ( y2 m) = £ {ylAi/tf) Pi/p* - Y2m - Vm. i£Sr,

48 5. E C H A N T I L L O N N A G E EN D E U X CYCLES : ESTIMATION DU T O T A L

La quantite er|(u) est un estimateur sans biais base sur l'echantillon su.

k et f restent inchanges.

Remarque 4. Afin de simplifier l'ecriture de a\, il est estime par <r|, sinon il devrait etre estime par les estimateurs sans biais des variances de l'echantillon de taille m et celui de taille u.

5. S t r a t e g i e 2

Comme dans Arnab (1991), la population est divisee en L strates de taille Nh avec h qui va de 1 a L et la somme des Nh = N, la taille de la population.

L'echantillon Si est construit par la methode de selection avec probability proportionnelle a la taille avec remise (PPT), avec comme mesure de taille normee pi = Zi/Z pour la

ic unite choisie. La quantite n^ represente la taille de s\h de 5i. Designons par yn(h)

et V2i(h) les valeurs observees des variables-aux premiers et deuxiemes cycles pour la ie

unite de la he strate.

Les smh de taille w,h sont construits au deuxieme cycle par la methode de Rao, Hartley,

Cochran (RHC) avec une mesure de taille

* = yih(h)/zj(h) ,

• 9hi Y,iesiyih(h)/Zi{h)

pour la ie unite de la he strate. La selection de l'echantillon non apparie Su se fait avec

la methode RHC a partir de l'ensemble de la population U, avec pi la mesure de taille. Alors les estimateurs de y2m et y2s s'ecrivent comme suit :

n™ = x > ( £ * w * / — 1

iesm \jesmh ' y J /

et

iesu l l

avec Q^ = J2j Qh P°ur le groupe qui contient la he unite de la ie strate construite a

5. STRATEGIE 2 49

Wh =

n

rz(h) = y2i(h) - chyu(h)

Arnab (1991) montre que la variance de Y2m e st donnee par

/ \ Nh V a r ( r2 mJ = / c2^ ^ h j=l P[h) n avec n — m k2 = n Viiih) Qh< = Yi(h)

P(h) = §

Nh

Les Ch sont des constantes. La valeur optimale de Ch qui minimise la variance Var(y2 m)

liee a l'echantillon apparie et la valeur correspondante du minimum de Var(y2m) sont

respectivement donnees par :

Nh a

opt c

h

= c

h

(0) = 5

3h

= 2__,

et

al{\ + (n-m)0/m)

n

50 5. E C H A N T I L L O N N A G E E N D E U X CYCLES : ESTIMATION DU T O T A L avec othj =V2j{h)/qhj ~Y2(h) flhj = Zhjqhj — Zh Nh 2 V ^ 2 J = l Nh

0 = ^(l'Sl)alJp

h

al

Alors 1'estimateur composite pour Y2 s'ecrit :

% = <t>Y

2m

+ (1 - <f>)Y

2u Avec l'optimum Done o p t A = An = 1=—— •

9 + fVdVF-i

V a r ' - ' - ^ A i o - / ) ^

<*H

+ (^o/Vo) V T V ^

M2, ou

Y

2m

= £ «* f E nWQki/nintitP* +

ChJ2

^

Zj{h)

) ,

l£Sm \«€-Smh 3 / etf* = N/(N-l), MO = 1 - A0.

K, / et <J| sont les raemes que dermis dans la section de l'approche de Chotai (section 3.2).

6. Efflcacite

Parmi ces deux strategies, la strategie 1 est plus efficace que la 2 et que celle proposee par Prasad et Graham car la variance est minimale. Pour mesurer son efficacite, il faut

7. E X E M P L E DE ARNAB 51

se referer a 5 (correlation entre y2i/qi et Zi/qi) : quand elle augmente, Tefficacite fait de

meme.

Par ailleurs, son efficacite et celle de Prasad et Graham augmentent a mesure que C, =

G\la\ diminue. Cette strategie est plus utilisee en pratique. Elle est egalement meilleure

que celle de Chotai selon que £* = (1 — 52)( ou 1 — S*2 avec S*2 un coefficient de correlation

entre y2i/pi et yu/pi- Si Z{ sont constantes alors 5* devient un coefficient de correlation entre y2i et yu.

7. E x e m p l e de Arnab

Nous ne disposons pas des donnees numeriques detaillees de cet exemple. Nous sommes en presence de trois populations.

La population 1 a ete etudiee .par Prasad et Graham (1994); elle fait reference a la superficie ensemencee en ble en 1937 (y2) et en 1936 (j/i) ainsi qu'a la superficie en

culture (z) dans un ensemble de 34 villages de l'lnde, selon les donnees compilees par Sukhatme et Sukhatme (1970). Cette population est divisee en deux strates selon que la superficie en ble en 1936 est superieure ou inferieure a 200 acres.

Population 1 : N = 34, Nx = 20, N2 = 14, kd* = 0.7635, S = 0.3638, C = 0.3811,

0 = 0.2436.

La population 2 represente la production de cereales en Amerique du Sud en 1980 (z), 1988 (yi) et 1989 (j/2), selon les donnees compilees dans l'annuaire (1988-1989). Elle est aussi divisee en deux strates selon que la production est superieure ou inferieure a 570 milliers de tonnes metriques. Population 2 : N = 19, Ni = 7, N2 = 12, 5* = —0.6939, 5 = 0.7666, C = 1-1478, 9 = 0.3681.

La population 3 compilee par Singh et Chaudhuri (1986) fait reference a la superficie ensemencee en ble en hectares, en 1979-1980 (y2) et 1978-1979 (yi) et a la superficie

totale en culture en 1978-1979 (z) dans 16 villages du district de Meerut. Population 3 :

N = 16, iVx = 9,N2 = 7, 6* = 0.7729, S = 0.1057, C = 0.3965, 6 = 0.2827.

Posons : E\ = Vc/M\ : Efficacite relative de la strategie 1 par rapport a la strategie de

Chotai E2 = Vc/M2 : Efficacite relative de la strategie 2 par rapport a la strategie de

Chotai £3 = Vc/VpG : Efficacite relative de la strategie de Prasad et Graham par rapport

a la strategie de Chotai

Arnab trouve qu'au regard des donnees de cet exemple, la strategie 2 se trouve etre la plus efficace avec des resultats meilleurs (E2 est toujours plus grande que 1 et plus grande

que les autres). Aussi les deux strategies sont meilleures que celle de Chotai et de Prasad et Graham. Etant donne que pour la population 1, C = 0.3811, cela favorise la strategie de Prasad et Graham. Pour la population 2, £ = 0.3811, ceci est tres eleve et defavorise

52 5. E C H A N T I L L O N N A G E EN DEUX CYCLES : ESTIMATION DU T O T A L

la strategie de Prasad et Graham. Enfin, pour la population 3, £ = 0.3965, cette valeur est bonne pour la strategie de Prasad et Graham.

Selon la methode de Prasad et Srivenkataramana (1980), on pourrait egalement etudier 1'efFet de la deviation par rapport a la valeur optimale de (3 = (30 quand on possede

differentes valeurs provisoire de (1. La variance minimale s'ecrirait :

Varm i n(f2|/5) = k ( l - / + v^C**) o\j2 = M^

Ou $ represente une valeur provisoire de f30 = J3, (** = 1 — (1 — v2)52 et v = 1 — /3/{30.

Alors avec ce raisonnement, la strategie est meilleure de que celle de Prasad et Graham si

\v\ < 1 et pire si \v\ > 1. Elle est superieure a celle de Chotai si v > (1 — 1/<52)(1 — l / £ ) et

inferieure si v < (1 — \/52){\ — 1/C)- La sensibilite de l'emcacite se calcule de la maniere

suivante :

VpC

E* = lf£

8. Generalisation

II y a plusieurs generalisations possibles de la methode d'echantillonnage en deux cycles. Une generalisation naturelle en v cycles necessiterait Testimation additionnelle de v — 1 parametres d'une combinaison convexe de v estimateurs.

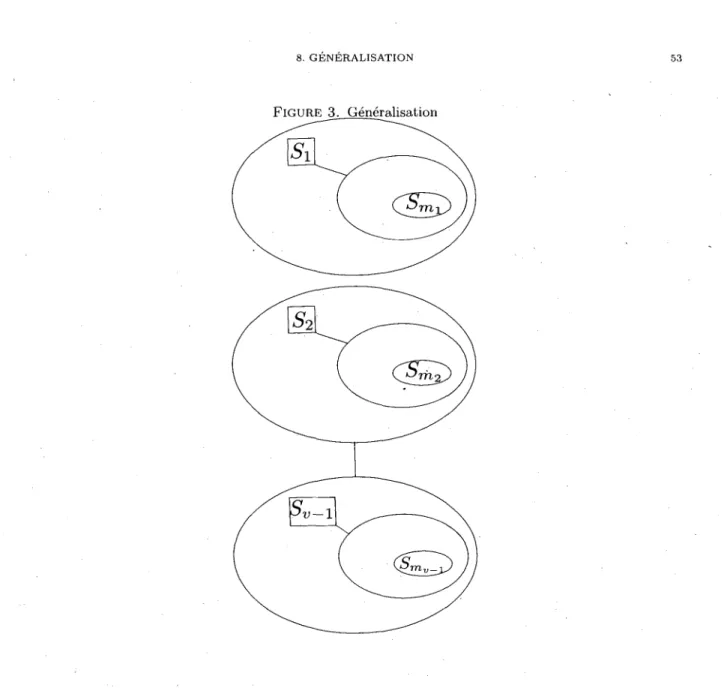
Nous preconisons plutot une generalisation qui conserve ^estimation d'un seul parametre additionnel d'une combinaison convexe telle que nous l'avons presente dans ce travail. Cette generalisation consiste a extraire l'echantillon apparie dans les v — 1 premiers cycles de la maniere indiquee dans la figure ci-dessous :

Alors v—1 v-1 / j—l \ S

m = | J Sj; = ( J I Sj ~ \J Si I

3 = 1 J = l V • i = l / et i - l

S

U

CU\\JSJ

3=1 donc Yv = 4>Yvm + ( 1 - <j>)Yvu.

Les calculs concernant les moments de cet estimateur se feront de la meme maniere que pour les estimateurs proposes dans ce travail, et dependront essentiellement de la methode de tirage des unites et de la fagon de construire les estimateurs Yvm et Yvu.

8. GENERALISATION 53

FIGURE 3. Generalisation

Nous suggerons de maniere generate d'utiliser les methodes RHC pour sm et le plan

d'echantillonnage habituel (plan aleatoire simple, plan stratifie . . . ) pour su.

En particulier, le choix optimal de 4> se fera en minimisant la variance de Yv selon le plan

retenu.

Une autre generalisation necessite le calcul de plusieurs estimateurs intermediaires Yjm.

a chaque cycle. On obtient alors Yvm a l'aide de la formule :