Disjunctive closures for knowledge compilation

To link to this article : DOI :

10.1016/j.artint.2014.07.004

URL :

https://doi.org/10.1016/j.artint.2014.07.004

To cite this version :

Fargier, Hélène and Marquis, Pierre Disjunctive

closures for knowledge compilation. (2014) Artificial Intelligence, vol.

216 (Nov. 2014). pp. 129-162. ISSN 0004-3702

O

pen

A

rchive

T

OULOUSE

A

rchive

O

uverte (

OATAO

)

OATAO is an open access repository that collects the work of Toulouse researchers and

makes it freely available over the web where possible.

This is an author-deposited version published in :

http://oatao.univ-toulouse.fr/

Eprints ID : 16897

Any correspondence concerning this service should be sent to the repository

administrator:

staff-oatao@listes-diff.inp-toulouse.fr

Disjunctive

closures

for

knowledge

compilation

✩

Hélène Fargier

a

,

Pierre Marquis

b,∗

a_{IRIT,CNRS,UniversitéPaulSabatier,Toulouse,France} b_{CRIL,CNRS,Universitéd’Artois,Lens,France}

a b s t r a c t

Keywords:

Knowledgerepresentation Knowledgecompilation Computationalcomplexity

Theknowledgecompilation (KC)map[1] canbeviewed as amulti-criteriaevaluationof a number of target classes of representations for propositional KC. Using this map,the choiceofaclassforagivenapplicationcanbemade,consideringboththespaceefficiency ofit (i.e., its ability to represent information using littlespace), and its time efficiency, i.e., thequeries and transformations which can be achieved in polynomial time, among thoseofinterest for theapplicationunderconsideration.Whenno classofpropositional representationsoffersallthetransformationsonewouldexpect,someofthemcanbeleft implicit.Thisisthekeyideaunderlyingtheconceptofclosure introducedhere:insteadof performingcomputationallyexpensivetransformations,onejustremembersthattheyhave tobedone.Inthispaper,weinvestigatethedisjunctiveclosureprinciples,i.e.,disjunction, existential quantification, and their combinations. We provide several characterization results concerning the corresponding closures. We also extend the KC map with new propositionallanguagesobtainedasdisjunctiveclosuresofseveralincompletepropositional languages, including the well-known KROM (the CNF formulae containing only binary clauses), HORN (the CNF formulae containing only Horn clauses), and AFF (the affine language, which is the setof conjunctionsof XOR-clauses). Each introduced languageis evaluatedalongthelinesoftheKCmap.

1. Introduction

Knowledge compilation(KC) consistsof afamily ofapproacheswhich aimatimproving theefficiencyofsome compu-tational tasks–typically,savingon-line computationtime–viapre-processing. Thepre-processingstepconsistsinturning some piecesofavailableinformationintoacompiledform,duringanoff-linecompilationphase.

KCgathersanumberofresearchlines focusingondifferent problems,[5–12], rangingfromtheoreticalones, wherethe key questionis the compilability issue, i.e., determining whether pre-processing can lower the computationalcomplexity of some tasks, to morepractical ones,especially the design of compilation algorithms forsome specific tasks like clausal entailment. Animportant researchline[13,1] isconcernedwith theissue ofchoosinga target classofrepresentations for KC. In [1], the authors argue that the choice ofa target classfor a compilation purpose mustbe based bothon itstime efficiency, definedasthesetofqueriesand transformations whichcanbeachievedinpolynomialtimewhenthepiecesof data to be exploited are represented in the class, aswell as thespace efficiency of theclass, i.e., its ability to represent data usinglittle space. Thus,theKC map[1] isanevaluation ofa dozenofsignificant propositionalclasses L, alsocalled propositional fragments, w.r.t. several dimensions: the space efficiency (aka succinctness) of the fragment and its time

✩ _{Thispaperisanextendedandrevisedversionof[2,3].Italsoelaboratesonsomeoftheresultspresentedin[4].}

*

Correspondingauthor.

efficiency(akatractability),i.e.,theclassofqueriesandtransformationsitsupports(ornot)inpolynomialtime,oftenunder standard assumptionsfrom complexity theory.The KC mapisintended toserve asaguidefor selectingthe“right” target classgiventherequirementsimposedbytheapplicationunderconsideration.

The KCmapreported in[1] hasalready been extended toother propositional classes,queries and transformations ina number of subsequent papers, including [14–18,2,4,19–21,3,22]. In all those papers,queries and transformations are also viewed as properties ofclasses ofpropositional representations L. One says that L offers or satisfies a given queryor a transformation when there exists a polynomial-time algorithm to achieve it, provided that the input representations are from L.When suchanalgorithmdoesnotexist forsureorunless P₌NP,onesays thatL doesnotofferthequeryorthe transformation.

When no class of propositional representations offers allthe transformations one would expect, an approach consists in leaving some ofthem implicit. This isthe key idea underlying closureprinciples as introduced in this paper: insteadof performingsomecomputationallyexpensivetransformations onrepresentations,onejustremembersintherepresentations that thetransformationshavetobedone.Thisleadstoextend thepreviousclassesto newones, whichareatleast as suc-cinct,andforwhichimplicittransformationsareforfree.Anotherniceeffectofsomeimplicittransformationsonincomplete propositional languagesistorecovercompleteness, i.e.,theabilitytorepresentany Booleanfunction.

Inthispaper,weinvestigate thedisjunctiveclosureprinciples,i.e.,disjunction[_∨],existential quantification[_∃],and their combinations.Thedisjunctionprinciple[_∨]whenappliedtoaclassLofrepresentationsleadstoaclass_L[∨],the disjunc-tion closure of L, which qualifiesdisjunctions of representationsfrom L, whiletheexistential quantificationprinciple [_∃] applied to aclass L leads to aclass _L[∃], the existential closure ofL, which qualifiesexistentially quantified representa-tionsfromL._L[∨,∃],thefulldisjunctiveclosureofL,isobtainedbyapplyingbothdisjunctiveclosureprinciplestoL.We provide a number ofcharacterization results concerning thecorresponding closures. Especially, we show that applying at most once eachdisjunctiveclosure principle on L isenough, inthesense that applyingone ofthem twiceormore leads to classespolynomiallyequivalentto L. Wealsoidentifythequeries andtransformations whicharepreservedbyapplying disjunctiveclosureprinciples.

Inaddition,weextendtheKCmapwithnewclassesofpropositionalrepresentationsobtainedasdisjunctiveclosuresof severalincompletepropositionallanguages,namelythewell-knownKromCNFfragmentKROM(alsoknownasthebijunctive fragment)[23]theHorn CNFfragmentHORN[24],and theaffinefragmentAFF(alsoknownasthebiconditionalfragment)

[25],aswellasK/H(KromorHorn CNFformulae) andrenH, thelanguageofrenamableHorn CNFformulae[26]. Eachof these languages isawell-known polynomial classforthesatisfiability problem sat (i.e., itoffers CO),but none ofthemis fully expressivew.r.t. propositional logic(thereexist propositionalformulaewhich cannotberepresented inany ofthem), which drasticallyrestrictstheirattractiveness fortheKCpurpose.Importantly,switchingfromany ofthoselanguagestoits disjunctionclosureortoitsfulldisjunctiveclosureleadstorecoverafullyexpressivepropositionallanguage.Thisiscrucial formany applications.

The rest of the paper is organized as follows. In Section 2, some formal preliminaries about graph-based, quantified, propositional representations areprovided.In Section 3, wemake precisethequeries and transformationsof interest,and extend thenotions ofexpressiveness, succinctnessand polynomial translations toany subsets of theclassofgraph-based, quantified,propositionalrepresentations.InSection 4,theconceptsofdisjunctiveclosuresofaclassofpropositional repre-sentationsaredefinedandwederiveanumberofcharacterizationresultsaboutthem.InSection5,thedisjunctiveclosures ofKROM,HORN,K/H,renH,andAFFareconsideredandweanalyzethemalongthelines oftheKCmap.Finally,Section6

concludes thepaperbydiscussingtheresults,pointingoutthedisjunctiveclosureswhich appearasthebesttargetclasses fortheKCpurpose;italsogivessomeperspectivesforfurtherresearch.

2. Quantifiedpropositionalrepresentations 2.1. Syntax

In this paper, we consider subsets of the class C -QDAG of quantified propositional representations over a countably infinite setPS ofpropositionalvariables,givenafinitesetC ofpropositionalconnectives.Eachconnectivec_∈C issupposed tohaveafixed,finitearity.LeafnodesofsuchDAGsarelabeledbyliterals,wherealiteral(over V_⊆PS)isanelementx_∈V

(a positive literal) or a negated one _¬x (a negative literal), or aBoolean constant(_⊤ and _⊥). LV is theset ofall literals

over V . Literall isthecomplementary literalofliteral l,so that_{⊤ = ⊥}, _{⊥ = ⊤}, x_{= ¬}x and _¬x₌x.Foraliterall different

fromaBooleanconstant,var(l)denotesthecorrespondingvariable:forx_∈PS,wehave var(x)₌x andvar(_¬x)₌x.

Formally, C -QDAGisgivenby:

Definition1(C -QDAG).C -QDAGistheset ofallfinite,single-rootedDAGs(alsoreferredtoas“representations”)

α

where:

• eachleafnodeof

α

islabeledbyaliterall overPS,

• eachinternal nodeof

α

islabeledbyaconnectivec_∈C andhasasmany childrenasrequiredbyc (it isthencalleda

c-node),orislabeledbyaquantification_∃x or _∀x (where x_∈PS)andhasasinglechild.1

1 _{Eachbinaryconnectivec whichisassociative(like∧,∨,⊕)correspondstoafamilyofconnectives(withthesamenamec)ofarityi withi≥2.For} eachi≥2,theconnectivec ofarityi isdefinedby:foreveryi-tuplehx1,. . . ,xiiofBooleanvalues,c(x1,. . . ,xi)=c(x1,c(x2,c(. . . ,c(xi−1,xi)). . .)).

Fig. 1. A C -QDAGrepresentation with C_{= {∧, ∨, ¬, ⊕}}.

Fig. 2. A C -QDAGformula with C_{= {∧, ∨, ¬, ⊕}}.

Thesize _|

α

_|ofaC -QDAG representation

α

isthenumberofnodesplus thenumberofarcsintheDAG. Var(

α

) denotes the set offree variables of

α

, i.e.,those variables x for which thereexists aleaf node Nx of

α

labelled bya literall such

that var(l)₌x and there is a path from the root of

α

to Nx such that no node from it is labelled by ∃x or ∀x. Clearly

enough, determiningwhetheragiven x_∈PS belongs toVar(

α

) canbedoneintimepolynomialinthesizeof

α

2;similarly, computing Var(

α

)canalsobeachievedintimepolynomialinthesizeof

α

.

Fig. 1presentsaC -QDAGrepresentation

α

with C_{= {∧,∨,¬,⊕}}.Itsset offreevariablesisVar(

α

)_{= {}q,r_}.

As Fig. 1 exemplifies it,a C -QDAG mainlycorresponds to aQuantifiedBoolean Circuit [27]. Abusing words, such DAG-based representationsarealsoreferredto as“formulae”intheKCliterature,and classes ofsuchrepresentationsarecalled “languages”.Inthefollowing,wewillonlyusetheterm“formula”fordesignatingatree-shapedrepresentationofaBoolean function,andtheterm“language”forsetsofformulae.Fig. 2givesa C -QDAGformulawith C_{= {∧,∨,¬,⊕}}.

Many classes of propositional representations considered so far as target classes for KC are subsets of C -QDAG with

C_{= {∧,∨,¬,⊕}}, and typically subsets of C -DAG, the subset of C -QDAG with C_{= {∧,∨,¬,⊕}} where no node labeled by a quantification is allowed.Especially, the propositional DAGs considered in [14] are C -DAG representations with C₌

{∧,∨,¬}, and the classes considered in [1] are subsets of DAG-NNF (the non-quantified DAGs with C_{= {∧,∨}}). Clearly enough,foreachnon-quantifiedrepresentation

α

from C -DAG,Var(

α

) coincideswiththeset ofvariablesoccurringin

α

.

In Fig. 1, the DAG rooted at the _∧ node is a C -DAG representation with C_{= {∧,∨,¬}} and the DAG rooted at the _∨ node isa DAG-NNFrepresentation. DNNFis thesubsetof DAG-NNF consisting ofDAGs where each_∧-node _∧(

α

1,. . . ,

α

k)

is decomposable, which means that _∀i,j_{∈ {}1,. . . ,k_}, if i₆₌ j then Var(

α

i)∩Var(

α

j)= ∅. d-DNNF is the subset of DNNF

whereevery _∨-node_∨(

α

1,. . . ,

α

k) isdeterministic,whichmeans that∀i,j∈ {1,. . . ,k},if i6= j then

α

i∧

α

j isinconsistent.

BDD is thesubset of C -DAG with C_{= {}ite_} which consists of DAGs

α

such that every leaf node islabelled by a Boolean constant, _⊤ or _⊥. ite is aternary connective (“ite”standsfor “if... then... else ...”). Usually,instead oflabeling adecision node N_{= h}x,N₊,N_−iofaBDDformulabythenameoftheconnectiveused(i.e.,“ite”)andconsideringthreechildrenforit

2 _{ThealgorithmconsistsinlabelingeachnodeN ofα byasetofvariables V}

N;thenodesareconsideredininversetopologicalordering,VN=var(l) whenN isaleafnodelabeledbyl,VN=VM\ {x}whenN isaninternalnodelabeledby∃x or∀x andM isthechildofN,VN=SMichild of VNVMi when

(onefor x,oneforN₊ andoneforN₋),N islabelledbyx andhasonlytwochildren(one for N₊andonefor N₋).Givena total, strictordering<over PS,theclassOBDD_< isthesubsetofBDD whichconsistsofDAGs

α

suchthateverypath from therootof

α

toaleafnodeiscompatiblewith<.

As usual,aclause (resp.aterm)isafinitedisjunction(resp.conjunction)ofliterals. CLAUSEisthesubsetofDAG-NNF

consistingofallclauses,andTERMisthesubsetofDAG-NNFconsistingofallterms.NNFisthesubsetofDAG-NNF consist-ingofformulae(i.e.,tree-shapedrepresentations).CNF isthesubsetofNNFconsistingofallconjunctionsofclauses,while

DNF is thesubset of NNF consisting of all disjunctions of terms. PI isthe subset of CNF consisting of prime implicates formulae(alsoknownasBlakeformulae);aPI formulaisaCNFformula,theconjunctionofallclauses fromtheset PI(

α

)

for someC -QDAGrepresentation

α

;PI(

α

)containstheprimeimplicatesof

α

, i.e.,thelogicallystrongestclauses whichare impliedby

α

(onerepresentativeperequivalenceclassisconsidered,only).Anessential primeimplicateof

α

isaprime im-plicateδ of

α

suchthatiftheclauseequivalenttoδ isremovedfromPI(

α

),theconjunctionoftheclausesfromtheresulting set isnolongerequivalentto

α

.Forinstance,if

α

_{= (}p_⇒q)_{∧ (}q_⇒r)_{∧ (}p_{⇒ (}r_∨s)),thenPI(

α

)_{= {¬}p_∨q,_¬q_∨r,_¬p_∨r_}.

¬p_∨q and _¬q_∨r are essentialprime implicates of

α

, while _¬p_∨r isnot. An importantpoint is that any CNF formula equivalenttoapropositionalrepresentation

α

contains(uptologicalequivalence)everyessentialprimeimplicateof

α

.

Forspacereasons,wedonotprovidehereafterthedefinitionsofthepropositionalclassesofrepresentationsDNNFT and

IP (see[1,18]forformaldefinitions).

2.2. Semantics

Let usrecallthat aninterpretation(orworld) over V _⊆PS isamapping

ω

from V to BOOL_{= {}0,1_}. Interpretationsare sometimes viewed assubsets of PS, consisting of allthe variables that are set to 1 by the interpretations. When a total, strictordering< overPS is considered,therestrictionofaninterpretation

ω

over afinitesubset_{x1,. . . ,xn} ofPS canalso

berepresentedasabitvector;forinstance,therestrictionof

ω

over_{a,b,c_}suchthat

ω

(a)=1,

ω

(b)=0,and

ω

(c)=0 can berepresentedas100 whena,b,c aresuchthata<b<c.Foranyx_∈V ,

ω

₋x istheinterpretationover V whichcoincides

with

ω

on everyvariableof V ,exceptonx;formally,

ω

₋x(y)=

ω

(y) if y6=x, =1−

ω

(x) if y=x.

Wearenowreadytodefinethesemantics ofC -QDAGrepresentationsinaninterpretation

ω

over PS:

Definition2(SemanticsofC -QDAGrepresentations).Thesemantics ofaC -QDAGrepresentation

α

inaninterpretation

ω

over

PS is thetruthvalue❏

α

❑(

ω

) fromBOOL definedinductivelyasfollows:

• If

α

_{= ⊤},then❏

α

❑(

ω

)₌1.

• If

α

_{= ⊥},then❏

α

❑(

ω

)₌0.

• If

α

isapositiveliteral x,then❏

α

❑(

ω

)=

ω

(x).

• If

α

isanegativeliteral_¬x,then❏

α

❑(

ω

)=1₋

ω

(x).

• If

α

₌c(β1,. . . ,βn), where c∈C has arity n, then ❏

α

❑(

ω

)= ❏c❑(❏β1❑(

ω

),. . . ,❏βn❑(

ω

)), where ❏c❑ is the Boolean

functionfromBOOLn toBOOL,whichisthesemanticsofc.

• If

α

_{= ∃}x.β,then❏

α

❑(

ω

)₌1 iff❏β❑(

ω

)₌1 or ❏β❑(

ω

₋x)=1.

• If

α

_{= ∀}x.β,then❏

α

❑(

ω

)₌1 iff ❏β❑(

ω

)₌1 and❏β❑(

ω

₋x)=1.

An interpretation

ω

over PS is said to be amodel of

α

_∈C -QDAG, noted

ω

_|H

α

, if and only if ❏

α

❑(

ω

)₌1. If

α

has a model, thenitisconsistent;if everyinterpretation overPS is amodelof

α

,then

α

isvalid. Ifevery modelof

α

isamodel of β_∈C -QDAG, then β is a logicalconsequence of

α

, noted

α

_{|H β}. Mod(

α

) denotes the set of models of

α

over Var(

α

). Furthermore, whenboth

α

|H β and β|H

α

hold,

α

andβ arelogicallyequivalent,noted

α

≡ β.

Forinstance,withC_{= {∧,∨,¬,⊕}},theC -QDAGrepresentationgiveninFig. 1isequivalenttotheC -QDAGformulagiven inFig. 2.

Bystructuralinductiononecaneasilyshowthat thesemanticsofany C -QDAGrepresentation

α

dependsonlyonitsfree variables,in thesense that, foranyinterpretation

ω

′ _{over PS whichcoincideswithagiven interpretation}

_ω

_onallthefree variablesof

α

,

ω

isamodelof

α

ifand onlyif

ω

′ _isamodelof

_α

_{.Accordingly,thesemantics ofaC -QDAGrepresentation}

α

inaninterpretation

ω

overPS isfullydeterminedby

α

andtherestrictionof

ω

overVar(

α

).

Clearlyenough,renamingatthesametimeaquantifiedoccurrenceofavariablex inaquantification_∃x or_∀x occurring

in a C -QDAG formula

α

, and every occurrence ofx in

α

which dependson thequantification leads toa C -QDAGformula equivalentto

α

.Furthermore, sucharenamingprocess canbeachievedintimelinearinthesizeof

α

.

However, things are much more tricky when general C -QDAG representations (not reduced to formulae) are consid-ered. Consider for instance the quantification _∃q occurring in the C -QDAG representation

α

reported at Fig. 1, where

C_{= {∧,∨,¬,⊕}}.Theoccurrenceofvariableq intheleafof

α

labelledwithliteralq dependsonthisquantification. Replac-ingq bythefreshvariables in_∃q andatthisoccurrence wouldnotleadtoarepresentationequivalentto

α

sinces would

be afree variableof theresulting representation. Indeed, thereexist fourpaths fromthe rootof

α

to that leaf,and three of themdonot containany quantifiedoccurrence ofq.Thisissalient onthe C -QDAGformula equivalentto

α

reportedat

Fig. 2,andobtainedby“unfolding”

α

. Thus,whensome variableoccurrencecanbebothfree andbound,renaming quanti-fiedvariableswhilepreservingequivalencecanbeacomputationallydemandingtask(theunfoldingprocessmayeasilylead to anexponential blow-upof theinputrepresentation). Actually, when C_{⊇ {∧,∨}},thepossibility ofhaving some variable

occurrencesbothfreeand bound(ortodependon differentexistentialquantifications)inC -QDAGrepresentationsnot con-taining universal quantifications isenough to simulateuniversal quantifications inthem (see [27]). As a consequence, the correspondingclassofDAGsisstrictlymoresuccinctthanthecorrespondinglanguageofformulae.Ontheotherhand,some problems arecomputationallyeasierwhenformulae(and notDAGs)are considered; forinstance, whenuniversal quantifi-cations aredisabled,themodelchecking problemfor C -QDAG formulaewith C_{⊇ {∧,∨}}is“only” NP-complete, whileitis PSPACE-completewhenthefullclassofC -QDAGrepresentationswithoutuniversalquantificationsisconsidered.

Conventionally, the representation

α

N rooted at a decision node N = hx,N₊,N₋i over x∈PS in the standard

repre-sentation of an ordered binary decision diagram (i.e., an OBDD_< representation) is such that

α

N ≡ite(x,

α

N₊,

α

N₋)≡

(x_∧

α

N₊)∨ (¬x∧

α

N₋).

α

N₊ (resp.

α

N₋), the representation associated with node N₊ (resp. N₋), is the conditioning of

α

byx (resp._¬x),i.e.,therepresentationobtainedbyreplacingeveryoccurrenceofx in

α

N by⊤(resp.⊥).

Finally,weconsiderthefollowingnotations.If

α

∈C -QDAGand X_{= {}x1,. . . ,xn}⊆PS,then∃X.

α

isashortfor

∃

x1

.

¡∃

x2

.(...

∃

xn

.

α

)...

¢

and _∀X.

α

isashortfor

∀

x1

.

¡∀

x2

.(...

∀

xn

.

α

)...

¢

(these notations are well-founded since whatever the chosen ordering on X , the resulting representations are logically equivalent).

2.3. KROM,HORN,AFF,K/H,andrenH

In the following, we will focuson several well-known propositional languages, namelythe Krom CNF language KROM

(alsoknown asthebijunctive fragment)[23],theHorn CNFlanguageHORN [24], andtheaffinelanguageAFF (alsoknown as the biconditionalfragment) [25], as wellas K/H (Krom or Horn CNF formulae) and renH, the language of renamable Horn CNFformulae[26].

ThelanguagesKROM,HORN,AFF, K/H,andrenHareformallydefinedasfollows:

Definition3(KROM,HORN,AFF,K/H,andrenH).

• ThelanguageKROMisthesubsetofallCNFformulaeinwhicheachclauseisbinary,i.e.,itcontainsatmosttwoliterals.

• ThelanguageHORNisthesubsetofallCNFformulaeinwhicheachclauseisHorn, i.e.,itcontainsatmostonepositive literal.

• ThelanguageK/HistheunionofKROMandHORN.

• The language renH is the subset ofall CNF formulae

α

for which there exists a subset V ofVar(

α

) (called aHorn renamingfor

α

) such that the formulanoted V(

α

) obtained bysubstituting in

α

every literal l of LV byits

comple-mentaryliteral¯l isaHORNformula.

• ThelanguageAFF isthesubsetofC -DAG withC_{= {∧,¬,⊕}},consistingofconjunctionsofXOR-clauseswherea XOR-clauseisafiniteXOR-disjunctionofliterals(theXORconnectiveisdenotedby_⊕).

Herearesomeexamplesofformulaefrom KROM,HORN,renH,andAFF:

• (x_∨y)_{∧ (¬}y_∨z)isaKROMformula.

• (¬x_{∨ ¬}y_∨z)_{∧ (¬}y_∨z)isaHORNformula.

• (x_∨y_∨z)_{∧ (¬}x_{∨ ¬}y_∨z)isarenHformula.

V _{= {}x,z_}isaHorn renamingforit.

• (x_{⊕ ¬}y_{⊕ ⊤)∧ (¬}x_⊕y_⊕z) isanAFFformula.

Clearlyenough, determining whether a given C -QDAGrepresentation

α

(for any fixed C ) isa KROM (resp. HORN, K/H,

AFF)formulacanbeeasilyachievedintimepolynomialinthesizeof

α

.Notealsothatthereexistslineartimealgorithms for recognizing renHformulae(see e.g.[28,29]); furthermore,such recognitionalgorithmstypicallygiveaHorn renaming whenitexists.

KROM, HORN, AFF, K/H,and renHare known aspolynomial classes for the sat problem(i.e., therestriction of sat to any ofthemisinpolynomialtime–statedotherwise,eachofthemsatisfiesCO).However,noneofthemisfullyexpressive w.r.t. propositionallogic(thereexistpropositionalformulae,like(x_∨y_∨z)_{∧ (¬}x_{∨ ¬}y_{∨ ¬}z),whichcannotberepresented inanyofthem);thisseverelyrestrictstheirattractiveness fortheKCpurpose.

Interestingly, KROM,HORN,andAFFhavesemanticalcharacterizationsintermsofclosuresofsetsofmodels:

• Aset S ofinterpretations over afinite V _⊆PS istheset ofmodels ofaKROM formula

α

suchthat Var(

α

)₌V if and onlyifitisclosed formajority[30,25],i.e., _∀

ω

1,

ω

2,

ω

3∈S,theinterpretationmaj(

ω

1,

ω

2,

ω

3) over V belongs to S as well.Heremaj(

ω

1,

ω

2,

ω

3)isdefinedby∀x∈V ,maj(

ω

1,

ω

2,

ω

3)(x)=1 ifatleasttwointerpretationsamong

ω

1,

ω

2,

ω

3 givethetruthvalue 1 tox.

• A set S of interpretations over a finite V _⊆PS is the set of models of a HORN formula

α

such that Var(

α

)₌V if

andonly ifitisclosed forthebitwiseANDconnective[31,32],i.e., _∀

ω

1,

ω

2∈S,theinterpretationand(

ω

1,

ω

2) over V belongsto S.Hereand(

ω

1,

ω

2)isdefinedby∀x∈V ,and(

ω

1,

ω

2)(x)=1 if

ω

1(x)=

ω

2(x)=1.

• Aset S ofinterpretations over afinite V _⊆PS isthe set ofmodelsof anAFF formula

α

suchthat Var(

α

)₌V if and onlyif S is closedfor theternary _⊕ connective[30,25],i.e., _∀

ω

1,

ω

2,

ω

3∈S,theinterpretation ⊕(

ω

1,

ω

2,

ω

3) over V belongsto S.Here_⊕(

ω

1,

ω

2,

ω

3) isdefinedby∀x∈V ,⊕(

ω

1,

ω

2,

ω

3)(x)=

ω

1(x)⊕

ω

2(x)⊕

ω

3(x).

Thesecharacterizationresults canbeexploited toshowthat somepropositionalformulaecannotbeexpressedasKROM

(resp.HORN,AFF)formulae.

3. Queries,transformations,expressivenessandsuccinctness

Let usnow briefly recall thesets ofqueries and transformations used for comparing propositionallanguages in [1],as well as thenotions of expressiveness and succinctness; their importance is discussed in depth in [1], so we refrain from recallingithere.

3.1. Queries

Thebasicqueriesconsideredin[1]andsubsequentpapersconcernDAG-NNFrepresentations;theyincludetestsfor con-sistency (CO), validity(VA),clausal entailment(CE),implicants(IM),equivalence (EQ), sententialentailment (SE),counting (CT) and enumerating theorymodels (ME). We extend themto C -QDAG representationsand add to themMC, the model checking query,whichistriviallyofferedbyunquantifiedrepresentations,butnotbyquantifiedrepresentationsinthe gen-eralcase.

Definition4(Queries).LetL denoteanysubsetofC -QDAG.

• LsatisfiesCO,theconsistency query (resp. VA,thevalidity query)ifthereexistsapolynomial-timealgorithmthatmaps everyrepresentation

α

fromLto 1 if

α

isconsistent(resp.valid),andto0 otherwise.

• L satisfies CE, the clausalentailment query, if there exists a polynomial-time algorithm that maps every pair _h

α

,δ_i, where

α

isarepresentationfromL andδ isaclause, to1 if

α

_{|H δ} holds,and to0 otherwise.

• L satisfies EQ,the equivalence query(resp.SE, thesententialentailment query)if there existsa polynomial-time algo-rithmthatmapsevery pair_h

α

,β_iofrepresentationsfromLto1 if

α

_{≡ β} (resp.

α

_{|H β})holds,andto 0 otherwise.

• LsatisfiesIM,theimplicant query,ifthereexistsapolynomial-timealgorithm thatmapsevery pair_h

α

,

γ

_i,where

α

is arepresentationfrom Land

γ

isaterm,to 1 if

γ

_|H

α

holds,andto0 otherwise.

• L satisfiesCT,themodelcounting query, ifthereexists apolynomial-timealgorithm thatmapsevery representation

α

fromLtoanonnegativeintegerthat representsthenumberofmodelsof

α

over Var(

α

) (inbinarynotation).

• LsatisfiesME,themodelenumeration query,ifthereexistsapolynomial p(.,).andanalgorithmthatoutputsallmodels ofanarbitrary representation

α

fromL intime p(n,m), wheren is thesize of

α

and m isthe numberofitsmodels overVar(

α

).

• LsatisfiesMC,themodelchecking query,ifthereexistsapolynomial-timealgorithmthatmapseverypair_h

α

,

ω

_i,where

α

isarepresentationfromLand

ω

isaninterpretationover Var(

α

),to1 if I isamodelof

α

,andto 0 otherwise.

3.2. Transformations

The basic transformations considered in [1] areconditioning (CD), (possibly bounded)closures under theconnectives3

∧,_∨, and_¬ (_∧C, _∧BC,_∨C,_∨BC, _¬C)and (possiblybounded)forgettingwhich canbeviewed asaclosure operationunder existential quantification (FO, SFO).Forgetting isan important transformationas it allowsus to focus/projecta represen-tation on a set of variables, which proves helpful in many applications, including model-based diagnosis [33], reasoning about actions[34],andreasoningunderinconsistency[35,36].Allthosetransformations concernDAG-NNFrepresentations. WeextendthemtoC -QDAGrepresentationsandenrichthelist withtwoadditionaltransformations,whicharedualto(FO,

SFO),namely“ensuring” (EN)and theboundedrestriction ofit(SEN).Ensuring amountsto eliminatinguniversal quantifi-cations and allowsustoproject arepresentation on aset ofvariablesina robustway,i.e., independentlyof thevaluesof theremovedvariables.Thistransformationiscentralindecisionmakingunderuncertaintyandnon-deterministicplanning, seee.g.[37].

Definition5(Transformations).Let Ldenoteany subsetofC -QDAG.

• LsatisfiesCD,theconditioning transformation,ifthereexistsapolynomial-timealgorithmthatmapseverypair_h

α

,

γ

i, where

α

isarepresentationfrom Land

γ

isaconsistentterm, toarepresentationfrom Lthat islogicallyequivalent to_∃Var(

γ

).(

α

_∧

γ

).

• L satisfies FO, theforgetting transformation, if there exists apolynomial-time algorithm that mapsevery pair _h

α

,X_i, where

α

isarepresentationfromLand X isaset ofvariablesfromPS,toarepresentationfromLequivalentto_∃X.

α

. Ifthepropertyholdsforeachsingleton X,wesaythatL satisfiesSFO (singletonforgetting).

• L satisfies EN, the ensuring transformation, if there exists a polynomial-time algorithm that mapsevery pair _h

α

,X_i, where

α

isarepresentation fromLand X isasetofvariablesfromPS,toarepresentation fromLequivalentto_∀X.

α

. Ifthepropertyholdsforeachsingleton X,wesaythatL satisfiesSEN (singletonensuring).

• L satisfies _∧C, the closureunderconjunction transformation (resp. _∨C, the closureunderdisjunction transformation) if thereexistsapolynomial-timealgorithmthatmapseveryfinitesetofrepresentations

α

1,. . . ,

α

nfromL toa

represen-tationofLthat isequivalentto

α

1∧ . . . ∧

α

n (resp.

α

1∨ . . . ∨

α

n).

• L satisfies _∧BC, the boundedclosureunderconjunction transformation (resp. _∨BC, the boundedclosureunderdisjunction

transformation),ifthereexistsapolynomial-timealgorithmthatmapseverypairofrepresentations

α

and β fromLto arepresentationofL thatisequivalentto

α

_{∧ β} (resp.

α

_{∨ β}).

• L satisfies _¬C, the closureundernegation transformation, if thereexists apolynomial-time algorithm that maps every representation

α

fromLtoarepresentationofLwhichisequivalentto_¬

α

.

When

α

isaC -DAG representation(i.e.,anon-quantified representation),theconditioningof

α

by

γ

can bedefined in an equivalent,yet simpler way, astherepresentation

α

_|γ obtained byreplacing in

α

every occurrence ofvariable x by ⊤

(resp. _⊥) when x (resp. _¬x) is a literal of

γ

. Such a characterization cannot be extended to C -QDAG representations in thegeneral case.Especially,consideringonly thosevariablesx occurringfree in

α

ascandidatesfor thereplacementisnot enough. Indeed, since DAG-basedrepresentations are considered,it canbe thecase that in

α

one can finda leafnode N

labeledbyx such thatone pathfromtherootof

α

tothisleafnodedoesnotcontainanynodelabeledbyaquantification on x,whileotherpathsfromtheroottoN contain suchquantifications(see[27]).

3.3. Expressiveness,succinctness,andpolynomialtranslations

Weconsiderthreenotionsoftranslationson classesofpropositionalrepresentations(here,subsets ofC -QDAG),starting fromthelessdemandingone,namelyexpressiveness:

Definition6(Expressiveness). LetL₁ and L₂ betwosubsets ofC -QDAG. L₁ isatleastasexpressiveasL₂,denoted L_1≤eL₂, if foreveryrepresentation

α

_{∈ L}2,thereexistsanequivalentrepresentationβ∈ L1.

A first refinement of sucha notion of translatability consists in considering only polynomial-spacetranslations, i.e., the sizeofthetranslatedrepresentationmustremainpolynomialinthesizeoftheinputrepresentation:

Definition7(Succinctness). Let L₁ and L₂ be two subsets of C -QDAG. L₁ is atleastassuccinctas L₂, denoted L_1≤sL₂, if there existsa polynomial p such that forevery representation

α

_{∈ L}2, thereexists anequivalent representation β∈ L1 where _|β|≤p(_|

α

_|).

Finally,weconsiderstillmoredemandingtranslations,namelypolynomial-timetranslations:

Definition8 (Polynomialtranslation).Let L₁ and L₂ betwo subsets of C -QDAG. L₂ is said to bepolynomiallytranslatable

intoL₁,notedL_1≤pL₂,ifthereexistsa(deterministic)polynomial-time algorithm f suchthat forevery

α

_{∈ L}2,wehave

f(

α

)_{∈ L}1 and f(

α

)≡

α

.Wealsosaythat

α

ispolynomiallytranslatableinto f(

α

).

Clearlyenough, _≤e, ≤s, and ≤p arepre-orders (i.e.,reflexive and transitiverelations)over thesubsets of C -QDAG.

Fur-thermore,wehavetheinclusions:

≤

p

⊂ ≤

s

⊂ ≤

e

For each relation_≤∗ among _≤e, ≤s, and ≤p, therelation ∼_∗ denotes the symmetric partof ≤_∗,defined byL1∼_∗L2 if L_1≤∗L₂ and L_2≤∗L₁. By construction, each_∼∗ is an equivalence relation(i.e., a reflexive,symmetric and transitive relation). On the other hand,the relation <_∗ denotes the asymmetric part of _≤∗, defined by L_1<∗L₂ if L_1≤∗L₂ and

L_2£∗L₁.Byconstruction,each<_∗ isastrictorder(i.e.,anirreflexiveandtransitiverelation).

Inthefollowing,L_1£∗_s L₂means thatL_1£sL₂unlessthepolynomialhierarchy PH collapses(whichisconsideredvery unlikelyincomplexitytheory).

When L_1≤eL₂ holds, every representation fromL₂ can betranslatedinto anequivalentrepresentation from L₁. The minimalelementsw.r.t._≤e(i.e.,themostexpressiveelements)ofthesetofallsubsetsofC -QDAGwhenC isanyfunctionally

complete set of connectives (especially, as soon as C contains _∨ and _∧ since leaf nodes of C -QDAG representations are labeledbyliterals)arecalledcomplete propositionalclasses:theycanprovidearepresentation(uptologicalequivalence)of any Booleanfunction.

WhenL_1∼eL₂(resp.L_1∼sL₂,L_1∼pL₂),L₁and L₂ aresaidtobeequallyexpressive(resp.equallysuccinct, polyno-miallyequivalent).

Whenever L₁ is polynomially translatableinto L₂, every querywhich can beanswered in polynomial timein L₂ can also beanswered in polynomial time in L₁; and conversely, every querywhich cannot beanswered in polynomial time in L₁ unless P₌NP cannotbeanswered in polynomial timein L₂, unless P₌NP.Furthermore, polynomially equivalent classes areequallyefficientinthesensethat theypossessthesameset oftractablequeriesand transformations.

4. Onclosuresofpropositionalrepresentations

Intuitively, aclosureprincipleappliedto aclassLofpropositional representationsdefines anewclass,calledaclosure of L, through the (implicit) application of “operators” (i.e., connectives from C or quantifications) to the representations from L.Formally:

Definition9(Closure).LetL_⊆C -QDAGand _△⊆C_{∪ {∀,∃}}.Theclosure_L[△]ofLby_△isthesubsetofC -QDAGinductively defined asfollows4_:

1. if

α

_{∈ L},then

α

_{∈ L[△]},

2. if c_{∈ △}isan n-ary connectiveand

α

1,. . . ,

α

n areelementsofL[△] suchthat ∀i,j∈ {1,. . . ,n}, ifi6=j then

α

i and

α

j

donotshareanycommon(nonempty) subgraphs,thenc(

α

1,. . . ,

α

n)∈ L[△],

3. if c_{∈ △}isaquantifier, x_∈PS,and

α

_{∈ L[△]},thencx.

α

_{∈ L[△]}.

Each element of _L[△] can be viewed as a“tree” which “internal nodes” are labeled by connectives from C or quan-tifications and its “leaf nodes” correspond to “independent” representations from L. Accordingly, the representations

α

i

consideredinitem2.ofDefinition 9donotshareanycommonsubgraphs.

Clearly,ifthereexistsapolynomial-time algorithmfordeterminingwhetheragiven representation

α

_∈C -QDAGbelongs ornottoL,thentherealsoexistsapolynomial-timealgorithmfordeterminingwhetheragivenrepresentation

α

_∈C -QDAG

belongsornottotheclosure _L[△]ofLby_△.

We have derived the following(easy) proposition, which rulesthe inclusions betweenclosures depending on the way theirsetsofconnectivesarerelated bysetinclusion:

Proposition1.ForeverysubsetL,L′ofC -QDAGandeverysubset_△1,△2ofC∪ {∃,∀},wehave: 0. L_{⊆ L[△1]},andifL_{⊆ L}′_{,thenL[△1]⊆ L}′_[△1].

1. (L_[△1])[△2]⊆ L[△1∪ △2]. 2. (L_[△1])[△1]= L[△1].

3. If_△1⊆ △2thenL[△1]⊆ L[△2].

4. If_△1⊆ △2then(L[△1])[△2]= L[△2]and(L[△2])[△1]= L[△2].

Some additional properties stating how some closures of a class L can be composed, can be derived when bound variablescanbe“freely” renamedintheL representations.Thepropertyofstabilitybyuniformrenaming,given at Defini-tion 10, characterizes thesubsets of C -QDAGfor which, intuitively, thechoiceof variablenames inthe L representations doesnotreallymatter:

Definition10 (Stabilitybyuniformrenaming). Let L beany subsetof C -QDAG. L is stablebyuniformrenaming if for every

α

_{∈ L},for every non-empty subset V of variablesoccurringin

α

,there exist arbitrarilymany distinct bijections ri (i∈ N)

from V to subsets Vi of fresh variables from PS (i.e., for each i,j∈ N with i6= j, we have Vi∩Vj=Vi∩V = ∅) such

that therepresentationri(

α

)obtainedbyreplacingin

α

(inauniformway)everyoccurrence ofx∈V (either quantifiedor

non-quantified)byri(x)belongstoLaswell.

Thiscondition isnotvery demanding:allthe“standard”classes ofpropositional representations(quantified ornot)are stable by uniform renaming (when based on a countably infinite set PS as thisis the case here). Special attention must nevertheless bepaid tothe OBDD_< language, and more generally toevery class basedon an ordered set of propositional

4 _{Inordertoalleviatethenotations,when△= {δ}

Fig. 3. AnOBDD<representation of x0∨x1.

variables.FortheOBDD<casewhere<isastrictandcompleteorderingoverPS wemayassumetheorderedset(PS,<)to beofordertype

η

(

η

istheordertypeofthesetofrationalnumbersequippedwithitsusualordering[38]).Thisrestriction is harmlesssince thesetof variablesoccurringinany OBDD_< representationisfinite.In anutshell,whateverthewaythe variables occurringina given OBDD_< representation

α

areordered w.r.t. <,one mustbe ableto “insert” inthisordering arbitrarily many fresh variables between two variables of

α

while preserving the way other variables are ordered. Order type

η

clearly allows it (between two distinct rational numbers one can find countably many rationals). To make things clearer,letusgiveacounter-example:letPS_{= {}xi|i∈ N}orderedinsuchawaythatforeveryi∈ N,xi<xi+1.Consideran

OBDD_< representationofx0∨x1asgiveninFig. 3.<isnotoftype

η

.Take V = {x0}:x0cannotberenamedintoadifferent variable from PS without questioning the ordering requirement over OBDD_<, which shows that OBDD_< is not stable by uniformrenaminginthiscase.

Straightforwardly,theclosurebyanysetofconnectives/quantifiersofanyclassofpropositionalrepresentations,whichis stablebyuniformrenaming,alsoisstablebyuniformrenaming.

We are now ready to present more specific results. The following polynomial (dual) equivalences, showing that ex-istential quantifications (resp. universal quantifications) when viewed as “operators” “distribute” over disjunctions (resp. conjunctions), arewell-known:

∃

x

.(

α

1

∨ . . . ∨

α

n

)

≡ (∃

x

.

α

1

)

∨ . . . ∨ (∃

x

.

α

n

),

∀

x

.(

α

1

∧ . . . ∧

α

n

)

≡ (∀

x

.

α

1

)

∧ . . . ∧ (∀

x

.

α

n

).

Itcanthenbeshownthat:

Proposition2.LetLbeanysubsetofC -QDAGs.t.Lisstablebyuniformrenaming.Wehave:

• (L[∃])[∨]∼p(L[∨])[∃]∼pL[∨,∃].

• (L[∀])[∧]∼p(L[∧])[∀]∼pL[∧,∀].

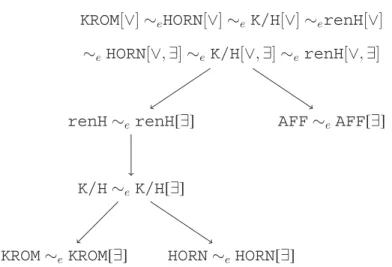
Fig. 4illustratesthepolynomialequivalencesbetweendisjunctiveclosuresgiven atProposition 2.

Proposition 1 and Proposition 2show togetherthat when _{△= {∨,∃}}(resp. _{∧,∀})closing _L[△] bysubsets of _△ inan iterativefashiondoesnotleadtoa“new”class,i.e.,aclasswhichisnotpolynomiallyequivalenttoL.Especially,wehave

¡

L

[∨, ∃]¢[∃] ∼

_p

¡

L

[∨, ∃]¢[∨] ∼

_pL

_{[∨, ∃].}

Thisshows,sotosay,thatthe“sequential”closureofapropositionalclass,stablebyuniformrenaming,byasetofoperators among_{∨,∃}(resp.among_{∧,∀})ispolynomiallyequivalenttoits“parallel”closure.Nosimilarresultcanbesystematically guaranteedforarbitrarychoicesofclassesandoperators.Forinstance,ifListhesetofliteralsoverPS,thenthe“sequential” closure (L_[∨])[∧]istheset ofallCNFformulae,the“sequential” closure(L_[∧])[∨]isthesetofallDNFformulae,andthe “parallel”closure _L[∨,∧]isthesetofallNNFrepresentations.Itiswell-knownthatthosethreelanguagesarenotpairwise polynomiallyequivalent(indeed,wehaveCNF_£sDNF,DNF£sCNF, NNF<sCNF,andNNF<sDNF,seee.g.[39]).Similarly,

ifL_{= CLAUSE},then(L[∧])[∃] and_L[∧,∃]arepolynomiallyequivalenttoCNF_[∃],but(L[∃])[∧]ispolynomiallyequivalent toCNF,whichisnotpolynomiallyequivalenttoCNF_[∃].Indeed,whateverC ,C -DAGispolynomiallytranslatableintoCNF_[∃]

using Tseitin’s extension principle [40], while CNF is not atleast as succinct as C -DAG as soonas C_{⊇ {∧,∨,¬}} (indeed,

CNF isnotatleastassuccinctasthesubsetDNFofNNF,whichisitselfasubsetofC -DAGinthiscase).

We have derived thefollowing proposition, which relates the queries and the transformations offered by L, with the queries and transformations offered by its disjunctive closures _L[∨] (the disjunction closure of L), _L[∃] (theexistential closure ofL),and_L[∨,∃](thefulldisjunctiveclosureofL).

Proposition3.LetLbeanysubsetofC -QDAGs.t.Lisstablebyuniformrenaming.

• IfLsatisfiesCO (resp.CD),then_L[∨],_L[∃]and_L[∨,∃]satisfyCO (resp.CD).

• IfLsatisfiesCO andCD,thenLsatisfiesCE andME.

• IfLsatisfiesCO andCD,thenL,_L[∨],_L[∃]and_L[∨,∃]satisfyMC.

Fig. 4. Polynomial equivalences between disjunctive closures. Therepresentation α at the top of the picture belongs toL[∨,∃]. β1[X,Y,Z,T] and

β2[X,Y,Z,T]denote propositionalrepresentations(not necessarilytree-structured ones)from Lsuchthat Var(β1)=Var(β2)=X∪Y∪Z∪T ,where X ,Y ,Z ,andT arepairwisedisjoint,finitesubsetsofPS.Therepresentationα_∃∨atthebottom,left-handsideofthepictureisan(L_[∨])[∃]representation into whichα canbepolynomiallytranslated.Therepresentationα_∨∃atthebottom, right-handside ofthepictureisan(L[∃])[∨]representationinto whichαcanbepolynomiallytranslated.

• IfLsatisfiesFO (resp.SFO),then_L[∨]satisfiesFO (resp.SFO).

• IfLsatisfies_∧C (resp._∧BC,_∨C,_∨BC),then_L[∃]satisfies_∧C (resp._∧BC,_∨C,_∨BC).

Notethat applyingdisjunctiveclosuresdonotpreserveotherqueriesortransformationsinthegeneral case.Thus:

• If L satisfies VA (resp. IM, CT, EQ,and SE), thenit canbe thecasethat _L[∨] doesnot satisfyit. For instance, TERM

satisfieseachofVA,IM,CT,EQ,and SE,butTERM_{[∨]= DNF}doesnotsatisfyany ofthemunlessP₌NP[1].

• IfLsatisfiesVA (resp.IM,CT,EQ,andSE),thenitcanbethecasethat _L[∃]doesnotsatisfyit.Thus,L_{= CNF}satisfies

VA andIM but CNF_[∃] does not satisfyany of themunless P₌NP; indeed, DNF (whichdoes not offer any ofthem) ispolynomiallytranslatable intoCNF_[∃] usingTseitin’s transformation[40]. Similarly,L_{= HORN} satisfiesbothEQ and SE, but HORN_[∃] does not offer any of them (see Proposition 5). Finally, the subset L_{= d}-DNF of DNF consisting of deterministic DNF formulae (i.e., the DNF formulae

α

₌Wn

i=1

γ

i such that for each i,j∈1,. . . ,n, if i6= j, then the

terms

γ

i and

γ

j aresuchthat

γ

i∧

γ

j isinconsistent)satisfies CT,but d-DNF[∃] doesnot.Indeed, DNFispolynomially

translatable into d-DNF_[∃]: with each DNF formula

α

₌Wn

i=1

γ

i we can associate in polynomial time the equivalent

d-DNF_[∃]formula_∃{y1,. . . ,yn}.Win=1(yi∧Vij−₌11¬yj∧

γ

i),where {y1,. . . ,yn} isasetoffreshvariables(disjoint from

Var(

α

)).

• IfLsatisfies_∧C,thenitcanbethecasethat_L[∨]doesnotsatisfyit.Thus,L_{= TERM}satisfies_∧C,butTERM_{[∨]= DNF}

doesnot,unless P₌NP[1].

• If L satisfies _¬C, then it can be the case that none of _L[∨] and _L[∃] satisfies it. Thus, L_{= OBDD<} satisfies _¬C,

but none of OBDD_<[∨] and OBDD_<[∃] satisfies _¬C unless P₌NP. As to OBDD_<[∨], this comes from the fact that

TERM_≥pOBDD<, which impliesthat DNF≥pOBDD<[∨]. Sinceevery CNF formula

α

is polynomiallytranslatable into thenegation ofa DNF formula β, if OBDD_<[∨]would satisfy _¬C, then theconsistency of

α

could betested in poly-nomialtimebycomputingfirst anOBDD_<[∨]representationequivalenttoβ,then“negating”ittoreachanOBDD_<[∨]

representation equivalent to

α

. Indeed, since OBDD_< satisfies CO, OBDD_<[∨] also satisfies CO (see Proposition 3). As to OBDD_<[∃], we canmake arather similar proofgiven that OBDD_<[∃] also satisfies CO (seeagain Proposition 3).To

gettheproof, itisenoughto showthat OBDD_<[∨]≥pOBDD<[∃]:let

α

=Wni₌1

α

i beanOBDD<[∨]representation;let

y1,. . . ,yn be variablesfrom PS\Var(

α

) suchthat each yi (i∈1,. . . ,n) precedesevery variablefrom Var(

α

).From

α

,

wecangenerateinpolynomialtimetheOBDD_< representation

β

₌

­

y1

,

α

1

,

­

y2

,

α

2

, . . . ,

h

yn

,

α

n

,

⊥, i . . .

®®.

Toconcludetheproofitisenoughtoobservethat

α

isequivalenttotheOBDD_<[∃]representation_∃{y1,. . . ,yn}.β.

• IfLsatisfiesEN,thenitcanbethecasethat_L[∨]doesnotsatisfyit.Thus,L_{= TERM}satisfiesEN,butTERM_{[∨]= DNF}

does not, unless P₌NP, since a DNF formula

α

is valid iff its universal closure _∀Var(

α

).

α

is valid iff _∀Var(

α

).

α

is consistent(since_∀Var(

α

).

α

hasno freevariable,it isequivalentto_⊤ orto _⊥, henceitisconsistent preciselywhenit isvalid),and DNFsatisfiesCO.

• IfLsatisfies EN,thenitcanbethecasethat_L[∃]doesnotsatisfyit.Thus,L_{= CNF}satisfiesEN,but CNF_[∃]doesnot, unless PH collapses.Thiscomeseasily fromthefactthatthevalidityproblemforCNF_[∃]formulaeoftheform_∃X.

α

is

Π₂p-complete.Indeed,_∃X.

α

isvalidiffthe(closed)quantifiedBooleanformula_∀Var(

α

)\X.(∃X.

α

)isvalid.

5. OnthedisjunctiveclosuresofKROM,HORN,AFF,K_/H,andrenH

Letusnowfocuson thedisjunctiveclosuresofKROM,HORN,AFF,K/H,andrenH.

Firstofall,itisobviousthatthefourlanguagesKROM,HORN,K/H,andAFFarestablebyuniformrenaming.Thisisalso thecaseforrenH:ifV isaHornrenamingforarenHformula

α

,andif

α

′

X istheCNFformulaobtainedbysubstitutingin

auniformwayin

α

everyoccurrenceofavariablev from X_⊆PS by thefreshvariable v′_,then

_α

′

X alsoisarenHformula

and V′_{= {v∈Var(}

_α

′_{)|v∈V\X}∪ {v}′_∈Var(

_α

′_{)|v∈V∩X} isaHornrenamingforit.}

Now,thankstoPropositions 1 and 2,itisenoughtoconsiderthethreedisjunctiveclosures_L[∃],_L[∨],and_L[∨,∃]with

L being any on thefiveabove languages. Clearlyenough,the disjunction(resp.existential,full disjunctive)closure ofany languageamong KROM,HORN,K/H,renH,and AFFisalsostablebyuniformrenaming.

Applying thedisjunctiveclosureprinciples _[∨],_[∃],and _[∨,∃] tothe fivelanguagesKROM, HORN,K/H,renH, and AFF

leads toconsiderfifteen additionallanguages.Thefollowingeasyresultshowsthat someoftheresultinglanguagesdonot needtobeconsideredseparately,becausetheyarepolynomiallyequivalent.

Proposition4.

• KROM ∼pKROM[∃].

• KROM[∨]∼pKROM[∨,∃].

• AFF ∼pAFF[∃].

• AFF[∨]∼pAFF[∨,∃].

As adirect consequence, we have that KROM and KROM_[∃] (resp.AFF and AFF_[∃], KROM_[∨] and KROM_[∨,∃], AFF_[∨]

and AFF_[∨,∃])areboth(pairwise) equallysuccinctand equallyexpressive.

Accordingly, we focus in the following on the sixteen languages: KROM, HORN, K/H, renH, AFF, HORN_[∃], K/H_[∃],

renH_[∃],KROM_[∨],HORN_[∨],K/H_[∨],renH_[∨],AFF_[∨],HORN_[∨,∃],K/H_[∨,∃],andrenH_[∨,∃]. FromProposition 1,wegetthat:

KROM

_{⊆ KROM[∨] ⊆ KROM[∨, ∃]}

HORN

_{⊆ HORN[∃] ⊆ HORN[∨, ∃]}

HORN

_{⊆ HORN[∨] ⊆ HORN[∨, ∃]}

K/H

_{⊆ K/H[∃] ⊆ K/H[∨, ∃]}

K

/H

⊆ K/H[∨] ⊆ K/H[∨, ∃]

renH

_{⊆ renH[∃] ⊆ renH[∨, ∃]}

renH

_{⊆ renH[∨] ⊆ renH[∨, ∃]}

AFF

_{⊆ AFF[∨]}

Obviously enough, from the definitions of the languages KROM, HORN, K/H, and renH, we also have the following inclusions:

KROM

_{⊆ K/H}

HORN

_{⊆ K/H}

HORN

_{⊆ renH}

Table 1

KROM, HORN, K/H, AFF, renH, theirdisjunction, existentialand full dis-junctiveclosuresandthecorrespondingpolynomial-timequeries.√means “satisfies”and◦means“doesnotsatisfyunlessP=NP”.

CO VA CE IM EQ SE CT ME MC renH_{[∨, ∃]} √ _◦ √ _{◦ ◦ ◦ ◦} √ √ K/H_{[∨, ∃]} √ _◦ √ _{◦ ◦ ◦ ◦} √ √ HORN_{[∨, ∃]} √ _◦ √ _{◦ ◦ ◦ ◦} √ √ AFF_[∨] √ _◦ √ _{◦ ◦ ◦ ◦} √ √ renH_[∨] √ _◦ √ _{◦ ◦ ◦ ◦} √ √ K/H_[∨] √ _◦ √ _{◦ ◦ ◦ ◦} √ √ HORN_[∨] √ _◦ √ _{◦ ◦ ◦ ◦} √ √ KROM_[∨] √ _◦ √ _{◦ ◦ ◦ ◦} √ √ renH_[∃] √ √ √ √ _{◦ ◦ ◦} √ √ K/H_[∃] √ √ √ √ _{◦ ◦ ◦} √ √ HORN_[∃] √ √ √ √ _{◦ ◦ ◦} √ √ AFF √ √ √ √ √ √ √ √ √ renH √ √ √ √ √ √ _◦ √ √ K/H √ √ √ √ √ √ _◦ √ √ HORN √ √ √ √ √ √ _◦ √ √ KROM √ √ √ √ √ √ _◦ √ √

Fromsuchresults,weimmediatelyderivethat:

KROM

_{[∨] ⊆ K/H[∨]}

HORN

_{[∨] ⊆ K/H[∨]}

HORN

_{[∨] ⊆ renH[∨]}

HORN

_{[∃] ⊆ K/H[∃]}

HORN

_{[∃] ⊆ renH[∃]}

HORN

_{[∨, ∃] ⊆ K/H[∨, ∃]}

HORN

_{[∨, ∃] ⊆ renH[∨, ∃]}

In addition, since every consistent KROM formula is a renH formula5 _{and since KROM satisfies CO, with every K/H}

formulawecanassociateinpolynomialtimeanequivalentrenHformula,i.e.,K/H≥prenH.Asaconsequence,wealsoget

that

K

/H

[∨] ≥

p

renH

[∨]

K

/H

[∃] ≥

p

renH

[∃]

K

/H

_{[∨, ∃] ≥}

p

renH

[∨, ∃]

Finally,sinceforeverysubsetLofC -QDAG,L_{⊆ L[∨]⊆ L[∨,∃]},_⊆isincludedinto_≥p,andboth⊆and≥paretransitive

relations, a number of additional inclusions/polynomial translatability results can be directly obtained from the results above;theywillbeexploitedinsomeforthcomingproofs.

5.1. Queriesandtransformations

Astoqueries,wehaveobtainedthefollowingresults:

Proposition5.TheresultsinTable 1hold.

Astotransformations, wehaveobtainedthefollowingresults:

Proposition6.TheresultsinTable 2hold.

5 _{ThisisadirectconsequenceofthefactthataCNFformulaαisrenamableHornpreciselywhenthereexistsaninterpretationωsuchthatatmostone} literalperclauseofαisfalseinω[26];indeed,whenαisaKROMformula,thislaststatementexactlymeansthatαisconsistent.

Table 2

KROM,HORN,K/H,AFF,renH,theirdisjunction,existentialandfulldisjunctiveclosures and thecorrespondingpolynomial-time transformations. √means“satisfies,”• means “doesnot satisfy,” while ◦means“doesnot satisfyunless P=NP.”! means that the transformationisnotalwaysfeasiblewithinthelanguage.

CD FO SFO EN SEN _∧C _∧BC _∨C _∨BC _¬C renH_{[∨, ∃]} √ √ √ _{◦ ◦ ◦ ◦} √ √ _◦ K/H_{[∨, ∃]} √ √ √ _◦ √ _{◦ ◦} √ √ _◦ HORN_{[∨, ∃]} √ √ √ _◦ √ _◦ √ √ √ _◦ AFF_[∨] √ √ √ _◦ √ _◦ √ √ √ _◦ renH_[∨] √ _• √ _{◦ ◦ ◦ ◦} √ √ _◦ K/H_[∨] √ _• √ _◦ √ _{◦ ◦} √ √ _• HORN_[∨] √ _• √ _◦ √ _◦ √ √ √ _• KROM_[∨] √ √ √ _◦ √ _◦ √ √ √ _• renH_[∃] √ √ √ √ √ _{! ! ! ! !} K/H_[∃] √ √ √ √ √ _{! ! ! ! !} HORN_[∃] √ √ √ √ √ √ √ _{! ! !} AFF √ √ √ √ √ √ √ _{! ! !} renH √ _• √ √ √ _{! ! ! ! !} K/H √ _• √ √ √ _{! ! ! ! !} HORN √ _• √ √ √ √ √ _{! ! !} KROM √ √ √ √ √ √ √ _{! ! !} 5.2. Expressiveness

It is well-known that none of the languages KROM, HORN, K/H, renH, orAFF iscomplete for propositional logic. For instance, there is no formula from any of these languages which is equivalent to the CNF formula (x_∨ y_∨z)_{∧ (¬}x_∨

¬y_{∨ ¬}z).This isproblematicformany applications; indeed,what canbedonewhen theavailableinformation cannotbe represented inthetargeted language?Approximatingitisnotalwaysanoption,especially becausethebest approximation of theavailableinformationcan berough andthemissingpiecesof informationintheapproximation canbecrucial ones forreasoningand/ordecisionmaking.Inthefollowing,wearegoingtoprovethatwhileconsideringtheexistentialclosure ofany ofthoselanguagesdoesnotincreaseitsexpressiveness, switchingtoitsdisjunctionclosure(ortoitsfulldisjunctive closure) is enough to recovera completepropositional language, thus escaping from theabove mentioned expressiveness problem.

Let us start with the existential closures of KROM, HORN, K/H, renH, and AFF. First, since KROM (resp. AFF) is polynomially equivalent to KROM_[∃] (resp. AFF_[∃]), it turns out that those languages are (pairwise) equally expressive:

KROM_[∃]∼eKROM, and AFF[∃]∼eAFF. Similarly, we have derived the following expressiveness results, showing that the

existential closureofanylanguageL amongHORN,K/H,and renHisnotmoreexpressivethanL itself.

Proposition7.

• HORN[∃]∼eHORN.

• K/H[∃]∼eK/H.

• renH[∃]∼erenH.

Now, from the definitions of KROM, HORN, K/H, renH, thefact that K/H_≥prenH, and the fact that x∨y is a KROM

formula,which isnotequivalenttoa HORNone, _¬x_{∨ ¬}y_{∨ ¬}z is aHORNformulawhichisnot equivalenttoaKROM one,

x_∨y_∨z isarenHformulawhichisnotequivalenttoaK/Hone, weeasily getthat:

KROM

£

e

HORN

and

HORN

£

e

KROM

renH

<

e

K/H <

e

HORN

K/H <

e

KROM

In addition, AFF and any of KROM, HORN, K/H, renH are incomparable w.r.t. _≤e. Indeed, there is no renH formula

equivalent to theAFF formulax_⊕y_⊕z. Thiscomes from the factthat every CNF formulaequivalent to x_⊕y_⊕z must

containthefourclausesx_∨y_∨z, _¬x_{∨ ¬}y_∨z,x_{∨ ¬}y_{∨ ¬}z, _¬x_∨y_{∨ ¬}z sincethoseclausesareessentialprimeimplicates ofx_⊕y_⊕z,plusthefactthatbyconstruction,everyCNFformulacontainingtheclausesx_∨y_∨z,_¬x_{∨ ¬}y_∨z,x_{∨ ¬}y_{∨ ¬}z,

¬x_∨y_{∨ ¬}z isnotrenamableHorn(renamingatleasttwovariablesinthefirstclausetomakeitaHornclausealsochanges oneoftheremainingthreeclausesintoanon-Hornone).Conversely,thereisnoAFFformulaequivalentto_¬x_{∨ ¬}y,which isbothinKROMandinHORN.ThisisadirectconsequenceofthesemanticalcharacterizationresultconcerningAFFrecalled in Section2.3:with x<y,

ω

1=00,

ω

2=01, and

ω

3=10 aremodels of¬x∨ ¬y,but ⊕(

ω

1,

ω

2,

ω

3)=11 isnot amodel of_¬x_{∨ ¬}y.

Fig. 5. Theexpressivenesspicturefordisjunctiveclosures.AnarrowfromL₁toL₂meansthatL₁isstrictlymoreexpressivethanL₂,sothatalackof arrowmeansthattheexpressivenessofL₁andtheexpressivenessofL₂areincomparable.

Fig. 6. Thesuccinctnesspictureforincompletelanguages.AnarrowfromL_1toL_2meansthatL_{1isstrictlymoresuccinctthan}L_2,i.e.,L₁<sL2.The arrowisthickinthespecificcasewhenthefactthatL_2£sL_{1comesfromthefactthat}L_2£eL_{1.A lackofarrowmeansthatthesuccinctnessof}L₁ andthesuccinctnessofL_{2areincomparable.}

Let us finallyswitch to the disjunctionclosures and the full disjunctive closures ofKROM, HORN, K/H, renH, or AFF; interestingly, theeightlanguagesdefinedassuchareequally,andfully,expressive:

Proposition8. KROM_[∨], HORN_[∨],K/H_[∨],renH_[∨],AFF_[∨],HORN_[∨,∃],K/H_[∨,∃],renH_[∨,∃] arecompletepropositional languages.

Fig. 5depictstheexpressivenessrelationshipsidentifiedintheabovepropositions.

5.3. Succinctness

As to incomplete languages, since KROM (resp. AFF) is polynomially equivalent to KROM_[∃] (resp. AFF_[∃]), those lan-guages are (pairwise) equally succinct: KROM_[∃]∼sKROM, and AFF[∃]∼sAFF. More interestingly, we have obtained the

following succinctness results, showing that the existential closure of any language L among HORN, K/H, and renH is strictlymoresuccinctthanL itself.

Proposition9.

• HORN[∃]<sHORN.

• K/H[∃]<sK/H.

• renH[∃]<srenH.

• renHandK/H_[∃]areincomparablew.r.t._≤s.

• K/HandHORN_[∃]areincomparablew.r.t._≤s.

Fig. 6 summarizes thesuccinctness relationships among incomplete languages identified in Proposition 9. We observe that itdoesnotcoincidewiththecorrespondingexpressiveness picture,restrictedtoincompletelanguages(seeFig. 5).