Broken Triangles: From Value Merging to a Tractable Class of General-Arity Constraint Satisfaction Problems

To link to this article : DOI :

10.1016/j.artint.2016.02.001

URL : https://doi.org/10.1016/j.artint.2016.02.001

To cite this version :

Cooper, Martin and Duchein, Aymeric and El

Mouelhi, Achref and Escamocher, Guillaume and Terrioux, Cyril and

Zanuttini, Bruno Broken Triangles: From Value Merging to a

Tractable Class of General-Arity Constraint Satisfaction Problems.

(2016) Artificial Intelligence, vol. 234. pp. 196-218. ISSN 0004-3702

O

pen

A

rchive

T

OULOUSE

A

rchive

O

uverte (

OATAO

)

OATAO is an open access repository that collects the work of Toulouse researchers and

makes it freely available over the web where possible.

This is an author-deposited version published in :

http://oatao.univ-toulouse.fr/

Eprints ID : 16973

Any correspondence concerning this service should be sent to the repository

administrator: staff-oatao@listes-diff.inp-toulouse.fr

Broken

triangles:

From

value

merging

to

a

tractable

class

of

general-arity

constraint

satisfaction

problems

Martin

C. Cooper

a,∗

_,

_{Aymeric Duchein}

a

_,

_{Achref El Mouelhi}

b

_,

Guillaume Escamocher

c

,

Cyril Terrioux

b

,

Bruno Zanuttini

d a_{IRIT,UniversitédeToulouse,CNRS,INPT,UPS,UT1,UT2J,France}

b_{Aix-MarseilleUniversité,CNRS,ENSAM,UniversitédeToulon,LSISUMR7296,Marseille,France} c_{INSIGHTCentreforDataAnalytics,UniversityCollegeCork,Cork,Ireland}

d_{GREYC,UMR6072,NormandieUniversité,UNICAEN,CNRS,ENSICAEN,Caen,France}

a b s t r a c t Keywords: CSP Constraintsatisfaction Domainreduction Tractableclass Hybridtractability NP-completeness Globalconstraints

A binary CSP instance satisfying the broken-triangle property (BTP) can be solved in polynomial time.Unfortunately,in practice,few instances satisfythe BTP.We showthat a local version of the BTP allows the merging of domain values in arbitrary instances of binary CSP, thus providing a novel polynomial-time reduction operation. Extensive experimentaltrialsonbenchmarkinstancesdemonstrateasignificantdecreaseininstance size for certain classes of problems. We show that BTP-merging can be generalised to instanceswithconstraintsofarbitraryarityandweinvestigatethetheoreticalrelationship withresolutioninSAT. Adirectionalversionofgeneral-arityBTP-merging thenallowsus toextendtheBTPtractableclasspreviouslydefinedonlyforbinaryCSP.Weinvestigatethe complexityofseveralrelatedproblemsincludingtherecognitionproblemforthe general-arityBTPclasswhenthevariableorderisunknown,findinganoptimalorder inwhichto applyBTPmergesanddetectingBTP-merges inthepresenceofglobalconstraintssuchas AllDifferent.

1. Introduction

Atfirstsightonecouldassumethatthedisciplineofconstraintprogramminghascomeofage.Ontheonehand,efficient solvers are regularly used to solve real-world problems in diverse application domains while, on the other hand, a rich theory has been developed concerning, among other things,globalconstraints, tractableclasses, reduction operations and symmetry.However,thereoftenremainsalargegapbetweentheoryand practice,whichisperhapsmostevidentwhenwe look atthelargenumberofdeep resultsconcerning tractableclasseswhich haveyet to findany practicalapplication.The researchreportedinthispaperispartofalong-termprojecttobridgethegapbetweentheoryandpractice.Ouraimisnot only todevelopnewtoolsbutalsotoexplainwhypresenttoolsworksowell.

Most researchon tractableclasses hasbeen basedon classesdefined byplacingrestrictions eitheronthetypesof con-straints [1,2] or on theconstraint hyper-graphwhose vertices arethe variablesand whose hyper-edgesare theconstraint scopes [3,4]. Anotherway of defining classes of binary CSP instances consistsof imposing conditions on the

microstruc-*

Correspondingauthor.

E-mailaddresses: cooper@irit.fr (M.C. Cooper),Aymeric.Duchein@irit.fr (A. Duchein),achref.elmouelhi@lsis.org (A. El Mouelhi), guillaume.escamocher@insight-centre.org (G. Escamocher),cyril.terrioux@lsis.org (C. Terrioux),bruno.zanuttini@unicaen.fr (B. Zanuttini).

ture, a graph whose vertices are the possible variable-value assignments with an edge linking each pair of compatible assignments [5,6].If each vertexof themicrostructure, correspondingto avariable-value assignmenthx,ai,is labelled(or coloured) bythevariable x,thenthis so-calledcoloured microstructureretains all informationfrom theoriginal instance. The broken-triangle property (BTP) is a simple local condition on the coloured microstructure which defines a tractable class of binaryCSP [7]. The BTP correspondsto forbidding a simple pattern, known asa broken triangle, inthe coloured microstructureforagiven variableorder.InspiredbytheBTP, investigationofother forbiddenpatternsinthecoloured mi-crostructurehasledtothediscoveryofnewtractableclasses [8–10]aswellasnewreductionoperationsbasedon variable orvalue elimination[11,12]. TheBTPitselfhas alsobeen directlygeneralisedinseveraldifferentways. Forexample, ithas been shownthatunderanassumptionofstrongpath consistency,theBTPcanbeconsiderably relaxedsincenotallbroken trianglesneed beforbiddento defineatractableclass [13–15]. Indeed, even withoutany assumptionsof consistency, itis notnecessarytoforbid allbrokentriangles[12].ImposingtheBTPinthedualproblemleadsdirectlytoatractableclassof general-arity CSPs[16].TheBTPhas also beengeneralised totheBroken Angle Propertywhich defines atractableclassof QuantifiedConstraintSatisfactionProblems[17].

Inthispaperweshowthattheabsenceofbrokentrianglesonapairofvaluesinadomainallowsustomergethesetwo valueswhilepreservingthesatisfiabilityoftheinstance.Furthermore,givenasolutiontothereducedinstance,itispossible to find a solution to the original instance in linear time (Section 3). We then investigate the interactions between arc consistency andBTP-merging operations(Section4)and showthat itisNP-hardtofindthebest sequenceofBTP-merging (andarcconsistency)operations(Section5).TheeffectivenessofBTP-merginginreducingdomainsinbinaryCSPbenchmark problemsisinvestigatedinSection6.Inthesecondhalfofthepaperweconsider general-arityCSPs.Section7showshow to generalise BTP-merging to instances containing constraints of any arity (where allconstraints are given in the form of eithertables,listsofcompatibletuplesorlistsofincompatibletuples).Wethengoontoconsiderglobalconstraints,and in particular theAllDifferent constraint,inSection8.Finally, adirectionalversion ofthegeneral-arityBTPallowsustodefine atractableclassofgeneral-arityCSPinstanceswhichisincomparablewiththetractableclassobtainedbydirectlyimposing the BTP in the dual [16] (Section 9). However, on the negative side, we thenshow that it is NP-complete to determine the existence of a variable order for which an instance falls into this tractable class. The results of Sections 3, 7, 9and Sections4,5firstappearedintwoconferencepapers(respectively[18]and [19]).

2. TheConstraintSatisfactionProblem

For simplicity of presentation we use two different representations of constraint satisfaction problems. In the binary case,ournotationisfairlystandard,whereasinthegeneral-aritycaseweuseanotationclosetotherepresentation ofSAT instances.Thisisforpresentationonly,though,andouralgorithmsdonot needinstancestoberepresentedinthismanner.

Definition1. AbinaryCSPinstance I consistsof

• aset X ofn variables,

• adomainD(x) ofpossiblevaluesforeachvariablex∈X ,

• arelation Rxy⊆ D(x)× D(y),for eachpairofdistinctvariables x,y∈X ,which consistsofthesetofcompatible pairs ofvalues(a,b)forvariables(x,y).

Apartialsolution toI onY = {y₁,. . . ,yr}⊆X isaset{hy1,a1i,. . . ,hyr,ari}suchthat∀i,j∈ [1,r],(ai,aj)∈Ryiyj.Asolution

to I isapartialsolutionon X .

Forsimplicityofpresentation,Definition 1assumesthatthereisexactlyoneconstraintrelationforeachpairofvariables. The number of constraints e is the number of pairs of variables x,y such that Rxy6= D(x)× D(y). An instance I is arc

consistent if for each pairof distinct variables x,y∈X , each value a∈ D(x) has an AC-supportat y, i.e.a value b∈ D(y)

suchthat (a,b)∈Rxy.

Inourrepresentationofgeneral-arityCSPinstances,werequirethenotionoftuple whichissimplyasetofvariable-value assignments.Forexample,inthebinarycase,thetuple{hx,ai,hy,bi}iscompatible if(a,b)∈Rxy andincompatible otherwise.

Definition2.A(general-arity)CSPinstance I consists of

• aset X ofn variables,

• adomainD(x) ofpossiblevaluesforeachvariablex∈X , • aset NoGoods(I)consistingofincompatibletuples.

A partialsolution to I on Y = {y₁,. . . ,yr}⊆ X is a tuple t= {hy1,a1i,. . . ,hyr,ari} such that no subset of t belongs to NoGoods(I). Asolution isapartialsolutionon X .

Fig. 1. A broken triangle on two values a,b for a given variable x.

3. ValuemerginginbinaryCSPbasedontheBTP

Inthissectionweconsideramethod,basedon theBTP, forreducingdomainsizewhilepreservingsatisfiability.Instead of eliminatingavalue, asinclassicreductionoperations suchasarcconsistency orneighbourhoodsubstitution,wemerge twovalues.Weshowthattheabsenceofbroken-triangles[7]ontwovaluesforavariablex inabinaryCSPinstanceallows us tomerge these two valuesin thedomainof x whilepreserving satisfiability.This rulegeneralises thenotion ofvirtual interchangeability [20]aswellasneighbourhoodsubstitution[21].

Itisknown thatifforagivenvariablex in anarc-consistentbinaryCSPinstance I,theset of(in)compatibilities(known asa broken-triangle)showninFig. 1occurs forno twovaluesa,b∈ D(x) and no twoassignmentsto two othervariables,

thenthevariablex canbeeliminatedfrom I withoutchangingthesatisfiabilityof I [7,11].Infigures,eachbulletrepresents a variable-valueassignment,assignments to thesamevariableare groupedtogether withinthesameovaland compatible pairs of assignmentsare linkedby solidlines. In Fig. 1 (and inother figuresillustrating forbidden patterns) incompatible pairsofassignmentsarelinkedbybrokenlines. Evenwhenthisvariable-eliminationrulecannotbeapplied,itmaybethe casethatforagivenpairofvaluesa,b∈ D(x),no brokentriangleoccurs.Wewillshowthatifthisisthecase,thenwecan perform adomain-reduction operationwhichconsistsinmergingthevaluesa andb.

Definition3.Merging values a,b∈ D(x) inabinaryCSP consistsinreplacinga,b in D(x) byanewvaluec which is com-patiblewithallvariable-valueassignmentscompatiblewithatleastoneoftheassignmentshx,ai orhx,bi.Avalue-merging condition isapolytime-computablepropertyP(x,a,b)ofassignmentshx,ai,hx,biinabinaryCSPinstanceI suchthatwhen

P(x,a,b) holds,theinstance I′ _{obtainedfrom I bymerginga,b∈ D(x) issatisfiable ifandonlyif I issatisfiable.}

Wenowformallydefinethevalue-mergingcondition basedon theBTP.

Definition4. A brokentriangle on the pairof variable-valueassignments a,b∈ D(x) consists ofa pair ofassignments d∈ D(y),e∈ D(z)todistinctvariables y,z∈X\ {x}suchthat(a,d)∈/Rxy,(b,d)∈Rxy,(a,e)∈Rxz,(b,e)∈/Rxz and(d,e)∈Ryz. Thepairofvaluesa,b∈ D(x) isBT-free ifthereisnobrokentriangleona,b.

Proposition5.In abinaryCSPinstance,beingBT-freeisavalue-mergingcondition.Furthermore,givenasolutiontotheinstance resultingfromthemergingoftwovalues,wecanfindasolutiontotheoriginalinstanceinlineartime.

Proof. Let I betheoriginalinstanceand I′ _{thenewinstanceinwhicha,b havebeenmergedintoanewvaluec.Clearly,if}

I issatisfiablethensoisI′_{.Itsufficestoshowthatif I}′_{hasasolutions whichassignsc tox,thenI hasasolution.Lets}

a,sb

beidenticalto s exceptthatsa assignsa to x andsb assignsb tox.Supposethat neithersa norsb aresolutionsto I.Then, therearevariables y,z∈X\ {x} suchthat ha,s(y)i∈/Rxy andhb,s(z)i∈/Rxz.Bydefinitionofthemergingofa,b toproduce

c,and sinces isasolutionto I′_{containing hx,ci,wemusthave(b,s(y))∈R}

xy and(a,s(z))∈Rxz.Finally,(s(y),s(z))∈Ryz since s isasolutionto I′_{.Hence,hy,s(y)i,hz,s(z)i,hx,ai,hx,biformsabroken-triangle, whichcontradictsourassumption.}

Hence,theabsenceofbrokentrianglesonassignmentshx,ai,hx,bi allowsusto mergetheseassignmentswhilepreserving satisfiability.

Reconstructing a solution to I from a solution s to I′ simply requires checking which of sa or sb is a solution to I. Checking if sa orsb isasolution onlyrequireschecking the(atmost)n−1 binaryconstraintsthat include x.Thusfinding asolutiontotheoriginalinstancecanbeachievedinlineartime. ✷

WecanseethattheBTP-mergingrule,givenbyProposition 5,generalisesneighbourhoodsubstitution[21]:ifb is neigh-bourhood substitutable bya, thenno broken triangle occurson a,b and merginga and b produces aCSP instance which is identical (except for the renaming of the value a as c) to the instance obtained by simply eliminating b from D(x). BTP-mergingalsogeneralisesthemergingruleproposedbyLikitvivatanavongand Yap[20].Thebasicideabehindtheirrule is that ifthe twoassignments hx,ai, hx,bi haveidentical compatibilitieswith allassignmentsto allothervariables except concerningatmostoneothervariable,thenwecanmergea andb.ThisisclearlysubsumedbyBTP-merging.

TheBTP-mergingoperationisnotonlysatisfiability-preservingbut,fromProposition 5,weknowthatwecanalso recon-struct asolution inpolynomialtimetotheoriginalinstance I fromasolutiontoaninstance Im towhich wehaveapplied

Fig. 2. (a)Abrokentriangle(showninbold)existsonvaluesa′_,b′ _{atvariablez.(b)AfterBTP-mergingofvaluesa andb inD(x),thisbrokentrianglehas}

disappeared.

Fig. 3. (a)Thisinstancecontainsnobrokentriangle.(b)AfterBTP-mergingofvaluesa andb inD(x),abrokentriangle(showninbold)hasappearedon valuesa′_,b′_{∈ D(z).}

a sequence ofmerging operationsuntil convergence. It is known that for the weaker operation ofneighbourhood substi-tutability,allsolutionstotheoriginalinstancecanbegeneratedin O(N(de+n2))time,whereN isthenumberofsolutions to theoriginal instance, n is thenumber ofvariables,d the maximum domainsize and e the number ofconstraints [22]. Wenowshowthat asimilarresultalsoholdsforthemoregeneralruleofBTP-merging.

Proposition6.LetI beabinaryCSPinstanceandsupposethatwearegiven

• asequenceofm triplesoftheform(xi,ai,bi)m_i=−₀1,implicitlydefiningasequenceofinstancesI0=I,I1,· · · ,ImsuchthatIi+1is

obtainedfromIibyBTP-mergingvaluesai,biforxi(i=0,. . . ,m−1),

• thesetofallN solutionstotheinstanceIm_.

AllsolutionstoI canthenbeenumeratedwithdelayO(mn)afterapreprocessingstepinO(mnd2)(henceintotaltime O(n2d3+ Nn2d)).

Proof. We start by computing, for each constraint Rxy in the original instance I, its successive versions Rtxy1,. . . ,R

tmxy

xy ,

where t1,. . . ,tmxy ∈ {1,. . . ,m} recordbywhichBTP-mergingoperation thisversion was produced.SinceeachBTP-merging

operationcanchange only O(n) constraints(thoseinvolvingxi),thispreprocessingsteprequirestime O(mnd2).

Nowgivenasolution s to Ii weproceedinductivelyasfollows.Ifi=0 then weoutputs,otherwisewetestwhethersa orsb (orboth) aresolutionsto Ii−1,wheresa (resp.sb)isobtainedfroms bysettingxi toai (resp.tobi),asintheproofof

Proposition 5.Foreachofthemfoundtobeasolutionto Ii−1_{,werecursewithI}i−1_{.Thisrequires O(n)timeperstep,since}

againthereareatmostn−1 constraintstobechecked(thoseinvolvingxi)andthesehavebeenprecomputed.Finally,since ateachstepeithersa orsb isguaranteedtobeasolutionto Ii−1,weindeedgeneratesolutionsto I with delay O(mn). ✷

Theweaker operationofneighbourhood substitutionhas thepropertythattwo differentconvergent sequencesof elim-inations by neighbourhood substitution necessarily produce isomorphic instances Im₁, Im₂ [22]. This is not the case for BTP-merging. Firstly,and perhapsrather surprisingly, BTP-merging canhave asa side-effect to eliminatebroken triangles. Thisisillustratedinthe3-variableinstanceshowninFig. 2.Inordertoavoidclutteringupfigureswithbrokenlineslinking eachpairofincompatibleassignments,inallfiguresillustratingbinaryCSPinstances,weusetheconventionthatthosepairs ofassignmentswhicharenotexplicitlylinkedwithasolidlineareincompatible.TheinstanceinFig. 2(a)containsabroken triangleonvaluesa′_,b′ _{forvariablez,butafterBTP-mergingofvaluesa,b∈ D(x)intoanewvaluec,asshowninFig. 2(b),}

therearenobroken trianglesintheinstance.Secondly,BTP-mergingoftwovaluesinD(x)canintroduceabrokentriangle on avariable z6=x,asillustratedinFig. 3.The instanceinFig. 3(a)containsno brokentriangle,but aftertheBTP-merging ofa,b∈ D(x) intoanewvaluec,abrokentrianglehasbeen createdonvaluesa′,b′∈ D(z).

Fig. 4. (a)AninstanceinwhichapplyingACleadstotheeliminationofallvalues(startingwiththevaluesa andb),butapplyingBTPmergingleadstojust oneelimination,namelythemergingofa withb (withtheresultinginstanceshownin(b)).

4. MixingarcconsistencyandBTP-merging

Giventheomnipresenceofarcconsistencyinconstraintsolvers,itisnaturaltoinvestigateitsrelationshipandinteraction with BTP-merging. Values which can be BTP-merged may or may not be arc consistent. Trivially, two values a,b∈ D(x)

which are compatible with all assignments to all other variables can be BTP-merged, but cannot be eliminated by arc consistency. Conversely, ifa∈ D(x) has no AC-support at y butotherwise is compatible withall assignmentsto all other variables, b∈ D(x) has no AC-support at z6=y but otherwise is compatible with all assignments to all other variables, and Ryz6= ∅, thena,b can both beeliminated by arc consistency but a,b cannot be BTP-merged.Having established the incomparability ofarc consistencyand BTP-merging,wenowinvestigate theirpossibleinteractions.

We have already observed that BTP-merging is a generalisation of neighbourhood substitutability, since if a∈ D(x) is neighbourhood substitutable for b∈ D(x) thena,b can beBTP-merged.The possible interactionsbetween arc consistency (AC)andneighbourhood substitution(NS)arerelativelysimpleandcanbesummarisedasfollows [22]:

1. Thefactthata∈ D(x) isAC-supportedornotatvariable y remainsinvariantaftertheeliminationofanyothervalueb

(inD(x)\ {a}orinthedomainD(z) ofany variablez6=x)byneighbourhoodsubstitution.

2. An arc-consistent value a∈ D(x) that is neighbourhood substitutable remains neighbourhood substitutable after the eliminationofanyothervaluebyarcconsistency.

3. On theotherhand,avaluea∈ D(x)maybecomeneighbourhoodsubstitutableaftertheeliminationofavaluec∈ D(y)

(y6=x)byarcconsistency.

Indeed,ithasbeenshownthatthemaximumcumulatednumberofeliminationsbyarcconsistencyandneighbourhood sub-stitutioncanbeachievedbyfirstestablishingarcconsistencyandthenapplyinganyconvergentsequenceofNSeliminations (i.e.anyvalidsequenceofeliminationsbyneighbourhoodsubstitutionuntilno moreNS eliminationsarepossible) [22].

Theinteractionbetweenarcconsistencyand BTP-mergingisnotsosimpleand canbesummarisedasfollows:

1. Thefact that a∈ D(x) isAC-supported ornot atvariable y remainsinvariant afterthe BTP-mergingofany other pair of other values b,c (in D(x)\ {a} or in the domain D(z) of any variable z6=x). However, after the BTP-merging of two arc-inconsistent values the resulting merged value may be arc consistent. An example is given in Fig. 4(a). In this3-variable instance, the two values a,b∈ D(x) can be eliminated byarc consistency (which in turn leads to the eliminationofallvalues),oralternativelytheycanbeBTP-merged(toproducethenewvaluec)resultingintheinstance showninFig. 4(b)inwhichnomoreeliminationsarepossiblebyACorBTP-merging.

2. AsingleeliminationbyACmaypreventone ormoreBTP-mergings.Anexample isgiveninFig. 5(a).Inthis4-variable instance, if the value b is eliminated by AC, then no other eliminations are possible by AC or BTP-merging in the resulting instance(shown inFig. 5(b)),whereas ifa and b are BTP-merged intoanew valued (as shownin Fig. 5(c)) thisdestroysabrokentrianglethusallowingc tobeBTP-mergedwithd (asshowninFig. 5(d)).

3. Ontheotherhand,twovaluesinthedomainofavariablex maybecomeBTP-mergeableafteraneliminationofavalue

d∈ D(z)(z6=x)byarcconsistency.AnexampleisgiveninFig. 6.Inthis4-variableinstance,initiallya andb cannotbe BTP-merged (Fig. 6(a)), but after valued is eliminated fromD(z) byAC, thebrokentriangle has disappearedand a,b

Fig. 5. (a)AninstanceinwhichapplyingACleadstooneelimination(thevalueb)(asshownin(b)),butapplyingBTPmergingleadstotwoeliminations, namelya withb (shownin(c))andthend withc (shownin(d)).

Fig. 6. (a)Abrokentriangle(showninbold)existsonvalues a,b atvariable x.(b)Afterremovingvalued from D(z)byAC,thisbrokentriangle has disappeared.

5. TheorderofBTP-mergings

WesawinSection 3that BTP-mergingcanbothcreateand destroybrokentriangles.Thisimpliesthat thechoiceofthe orderinwhichBTP-mergingsareappliedmayaffectthetotalnumberofmergesthatcanbeperformed.Unfortunately, max-imisingthetotal numberofmerges inabinaryCSPinstance turnsout tobeNP-hard,even whenbounding themaximum size ofthedomainsd byaconstantassmall as3.For simplicityofpresentation, wefirstprove thisforthecasein which theinstance isnotnecessarilyarc consistent.We willthenprove atighterversion, namelyNP-hardnessofmaximisingthe total numberofmergeseveninarc-consistentinstances.

Theorem7.Theproblemofdeterminingifitispossibletoperformk BTP-mergingsinabooleanbinaryCSPinstanceisNP-complete.

Proof. For a given sequence of k BTP-mergings, verifying if this sequence is correct can be performed in O(kn2d2) time

because lookingforbrokentrianglesforagiven coupleofvalues takesO(n2d2). Aswe canverifyasolution inpolynomial

time, the problem of determining if it is possible to perform k BTP-mergings in a binary CSP instance is in NP. So to completetheproofofNP-completenessitsufficestogiveapolynomial-timereductionfromthewell-known3-SATproblem.

Fig. 7. (a)Representation of thevariable Xi anditsnegation(by thepossibilityofperforming a mergein D(xi j) orD(yi j), respectively,accordingto

rules(1),(2)).(b)Representationoftheclause(Xj∨Xk∨Xl).Pairsofpointsjoinedbyasolidlinearecompatibleandincompatibleotherwise.

Fig. 8. Gadget representing the clause ( Xj∨Xk∨Xl).

Let I3SAT beaninstanceof3-SAT(SATinwhicheachclausecontainsexactly3literals)withvariablesX1,. . . ,XN andclauses

C1,. . . ,CM. Wewillcreatea booleanbinaryCSP instance ICSP which has asequenceofk=3×M mergings if and only if

I3SAT issatisfiable.

For eachvariable Xi of I3SAT,weadd anew variable zi to ICSP. For eachoccurrence of Xi intheclause Cj of I3SAT,we

add two more variablesxi j and yi j to ICSP.Each D(zi) containsonly one value ci and each D(xi j) (resp. D(yi j))contains only twovaluesai andbi (resp.a′_i andb′_i).Therolesofvariablesxi j and yi j arethefollowing:

Xi

=

true

⇔ ∀

j

,

ai

,

bican be merged inD

(

xi j

)

(1)

Xi

=

false

⇔ ∀

j

,

a′_i

,

b′_ican be merged inD

(

yi j

)

(2)

Inordertoprevent thepossibilityofmergingboth(ai,bi)and (a_i′,b′_i),wedefinethefollowingconstraints forzi,xi j and

yi j:∀j Rxi jzi= {(bi,ci)}and Ryi jzi = {(b

′

i,ci)};∀j∀k Rxi jyik= {(ai,a

′

i)}.TheseconstraintsareshowninFig. 7(a)forasingle j (whereapairofpointsnotjoinedbyasolidlineareincompatible). Bythisgadget,wecreateabrokentriangleoneach yi j whenmergingvaluesinthexi j andviceversa.

Theidea isthat BTP-mergingai and bi inanyD(xi j)(1≤j≤N) preventsusfromBTP-merginga′_i and b′_i inany D(yik) (1≤k≤N),thus ensuringthat thevalueof Xi isthesameineachclauseinwhich itoccurs.If Xi ispreventedfrom being assigned eitherfalseortrueaccordingto therules(1) and (2)(becauseoftheclause gadgetsdescribed below),then I3SAT

willbedetectedasunsatisfiablesincethetotal numberofmergeswillbelessthan 3×M.

Foreachclause Ci= (Xj,Xk,Xl),weaddthefollowingconstraints inordertohaveatleastoneoftheliterals Xj, Xk, Xl true: Ryi jyik = {(a ′ j,bk′)}, Ryikyil= {(a ′ k,b′l)}and Ryilyi j = {(a ′

l,b′j)}.Thisconstruction,showninFig. 7(b),issuchthatitallows two mergingson thevariables yi j, yik, yil beforeabroken triangleiscreated.Forexample, merginga′_j,b′_j and thena′_k, b′_k createsabrokentriangleona′

i,b′i.So athirdmergingisnotpossible.

If the clause Ci contains a negated literal Xj instead of Xj, it suffices to replace yi j by xi j. Indeed, Fig. 8 shows the constructionfortheclause( Xj∨Xk∨Xl)togetherwiththegadgetsforeachvariable.

The maximum numberof mergings that can beperformed are one per occurrence ofeach variable ina clause, which isexactly3×M.Givenasequenceof3×M mergingsintheCSPinstance,thereisacorrespondingsolutionto I3SAT given

by(1) and (2).Togiveaconcrete example, considerthegadgetshown inFig. 8 representingtheclause Xj∨Xk∨Xl.This gadgetismadeupofthreetrianglesofthetypeshowninFig. 7(a).Toperformthreemergesinthisgadget,wemustperform exactly one merging in each ofthese triangles.For example, if wemerge the pairsof values (aj,bj), (ak,bk) and (al,bl),

Fig. 9. Ensuring arc consistency between the variables zi, yi j, xi jby addition of new values di.

then thissequence of mergescorresponds to theassignment (Xj,Xk,Xl)= (true,true,true) which satisfies theclause. On the otherhand, the assignment(Xj,Xk,Xl)= (true,false,true),which doesnot satisfy the clause, isimpossibledue to the centraltriangleofvariables(ofthetypeshowninFig. 7(b))whichpreventsusfromsimultaneouslymergingthethreepairs ofvalues(aj,bj),(a′_k,b′_k)and (al,bl).

Theabovereductionallowsustocode I3SAT astheproblemoftestingtheexistenceofasequenceofk=3×M mergings

in thecorrespondinginstance ICSP. Thisreduction being polynomial,we haveproved theNP-completenessof theproblem ofdeterminingwhetherk BTPmergesarepossibleinabooleanbinaryCSPinstance. ✷

Thereduction intheproofofTheorem 7supposesthat noarc-consistencyoperationsareused. Wewillnow showthat itispossibletomodifythereductionso astoprevent theeliminationofany valuesintheinstance ICSP byarc-consistency, even when the maximum size of the domains d is bounded by a constant as small as 3. Recall that an arc-consistent instanceremainsarc-consistentafteranynumberofBTP-mergings.

Theorem8.Theproblemofdeterminingifitispossibletoperformk BTP-mergingsinanarc-consistentbinaryCSPinstanceis NP-complete,evenwhenonlyconsideringbinaryCSPinstanceswherethesizeofthedomainsisboundedby3.

Proof. In ordertoensurearc-consistencyoftheinstance ICSP,weaddanewvaluedi tothedomainofeachofthevariables

xi j, yi j, zi.However, wecannot simplymake di compatible withallvalues inallother domains,becausethiswould allow allvaluestobemergedwithdi,destroyingintheprocessthesemanticsofthereduction.

Inthethreebinaryconstraintsconcerningthetripleofvariablesxi j, yi j,zi,wemakedicompatiblewithallvaluesinthe other twodomainsexcept di.Inotherwords,weaddthefollowingtuplestoconstraintrelations,asillustratedinFig. 9:

• ∀i∀j,(ai,di),(bi,di),(di,ci)∈Rxi jzi • ∀i∀j,(a′

i,di),(b′i,di),(di,ci)∈Ryi jzi

• ∀i∀j,(ai,di),(bi,di),(di,a′_i),(di,b′_i)∈Rxi jyi j

This ensures arc consistency, without creatingnew broken triangleson ai,bi ora′_i,b′_i, while atthe sametime preventing BTP-mergingwiththenewvaluedi.ItisimportanttonotethatevenafterBTP-mergingofoneofthepairsai,bi ora′i,b′i,no BTP-mergingispossiblewithdiinD(xi j),D(yi j)orD(zi)duetothepresenceofbrokentrianglesonthistripleofvariables. For example, the pair ofvalues ai,di∈ D(xi j) belongsto a broken triangleon ci∈ D(zi) and di∈ D(yi j),and thisbroken trianglestillexistsifthevaluesa′_i,b′_i∈ D(yi j) aremerged.

We can thensimply make di compatible with allvalues in thedomain of allvariables outside thistriple of variables. Withtheseconstraints weensurearcconsistencywithoutchanginganyofthepropertiesofICSP usedinthereductionfrom 3-SATdescribedintheproofofTheorem 7.Foreachpairofvaluesai,bi∈ D(xi j) anda′i,bi′∈ D(yi j),nonewbrokentriangle is created since these two values always have the same compatibility with all the new values dk. As we have seen, the constraints showninFig. 9preventanymergingofthenewvaluesdk. ✷

Corollary9.Theproblemofdeterminingifitispossibletoperformk valueeliminationsbyarcconsistencyandBTP-merginginabinary CSPinstanceisNP-complete,evenwhenonlyconsideringbinaryCSPinstanceswherethesizeofthedomainsisboundedby3.

ArelatedquestionconcernsthecomplexityoffindingtheoptimalorderofBTP-mergingswithinthedomainofasingle variable. It turnsout that this toois NP-complete.The proof ofthis theorem [19]is basedon a similartechnique tothat used intheproofofTheorem 7.

Theorem10.Theproblemofdeterminingifitispossibletoperformk BTP-mergingswithinasamedomaininabinaryCSPinstanceis NP-complete.

6. Experimentaltrials

Inthissection,westudyBTP-mergingfromapracticalviewpoint.

6.1. Experimentalprotocol

To test the utility of BTP-merging we performed extensive experimental trials on CSP benchmark instances available fromtheInternationalCP Competition.1Amongthe7272 CSPbenchmarkinstances,weconsideralltheinstancesincluding onlybinaryconstraints(namely3795 instances).Foreachoftheseinstances,weperformedBTP-mergingsuntil convergence withatime-outofonehour.Intotal,weobtainedresultsfor2944 instancesoutof3795 benchmarkinstances.Intheother instances,thesearchforallBTP-mergingsdidnotterminatewithinthetime-out.Notethatsomeoftheconsideredinstances have constraintsdefined bypredicates.Insuchcases,theseconstraints arefirstexpressed inextensionbefore applyingthe BTP-mergingalgorithm.Theruntimeofthistransformationisincludedinthereportedruntime.

BTP-mergingsareperformedbycheckingfirstforvirtualinterchangeability andthenbylookingforBTP-mergeablepairs ofvalues.Thesetwostepsarerepeateduntilafixedpointisreached.Bysodoing,thevirtualinterchangeabilitystepallows ustomergemorequickly somepairsofvaluessincethevirtualinterchangeability ruleiseasiertocheckthantheBTPrule. Ourexperiments(notreportedhere)haveshownthatthisversionofBTP-mergingissignificantlyfasterthan onepresented in[18]whileleading toasimilarnumberofmergings.

FortheBTP-mergingstep,weconsiderthevariablesaccordingtoagivenordering.Amongthedifferentvariableorderings wetried,weoptedinourexperimental trialsforonewhichordersthevariablesaccordingtoincreasingdegree(thedegree of avariablebeing the numberofconstraints whose scope containsthevariable). Notethat thisorderingdiffers from the oneused in[18]whichcorrespondstoalexicographicalordering.Inpractice,weobtainasimilarnumberofmergingswith these two orderings but thealgorithm is significantlyfasterwith the firstone. Ingeneral, weobserved that thedifferent variableorderings wetriedhad moreimpactonruntimethanonthenumberofmergingsperformed.

For agivenvariable x,wecheckforeachpairofvaluesa,b∈D(x) whethera,b areBTP-mergeable.If abrokentriangle on a,b isfound, wesaveitinadatastructure.Thenif, later,wehavetocheck againtheBTP-mergeabilityofa,b,westart withthissavedbrokentriangle.If thistriangleisstillbroken,wecanimmediatelydeduce thata,b arenotBTP-mergeable, thus avoiding some useless checks. On the other hand, if this triangle is no longer broken, we check whether a,b are

BTP-mergeable.Ifnobrokentriangleoccursona,b (thatisa,b areBTP-mergeable),weimmediatelymergea,b.Thisgreedy algorithm isanaturalchoicesincebyTheorem 8itisNP-hardtooptimisetheorderofBTP-merges. Forefficiencyreasons, when merging a,b, we keep one value (assume without loss of generality that a is thisvalue) and delete theother one instead ofcreating anew valuec and removing a and b asevoked inDefinition 3. Thena ismade compatible witheach variable-valueassignmentcompatiblewiththeassignment hx,bi.

We also implemented the deletion of values by neighbourhood substitution, by virtual interchangeability or by arc-consistency (which is enforced by the AC-2001 algorithm [23]). In the remainder of this section, we denote AC+P the application of AC followed by merging according to the property P where P may be BTP-merging, neighbourhood sub-stitution (NS) or virtualinterchangeability (VI). For solving, we use MAC (for Maintaining Arc-Consistency [24]) basedon AC-2001 together with the variable ordering heuristicdom/wdeg [25]. The choice of MAC is a natural choice since most state-of-the-art solversrelyon it.All thealgorithmsareimplementedinC++.

Theexperimentationswereperformedon8DellPowerEdgeM820bladeserverswithtwoprocessors(IntelXeonE5-2609 v22.5GHzand 32GBofmemory)underLinuxUbuntu 14.04.

6.2. ComparisonsbetweenBTP-mergingandAC+BTP-merging

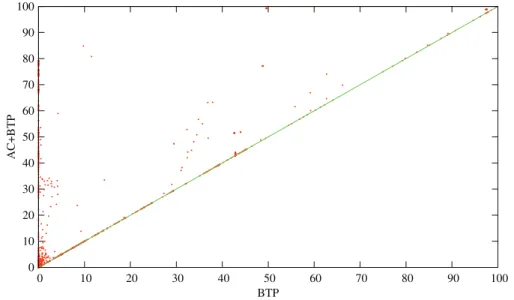
Wecompare inthissubsectiontheresults obtainedbyBTP-mergingand byAC+BTP-merging. First, asshown inFig. 10, AC+BTP-merging is able to process (i.e. find a fixed point in which no more BTP-mergings are possible) more instances withinthetime-out thanBTP-mergingalone.Moreprecisely,AC+BTP-mergingsucceedsinterminating withinthetime-out for 2944 instancesagainst2856 for BTP-merging.In bothcases,formorethanonethirdoftheseinstances,some mergings occur.Fig. 11comparesthepercentagesofvaluesremovedbyBTP-mergingandAC+BTP-mergingfortheinstancesforwhich bothBTP-mergingand AC+BTP-merging terminate.Clearly, AC+BTP-mergingoutperformsBTP-merging sincethepercentage ofvaluesremovedbyAC+BTP-mergingisalwaysgreaterthanorequaltothenumberofvaluesremovedbyBTP-merging.We canseethatforcertaintypesofproblem,(AC+)BTP-mergingisveryeffective(morethan 90%ofdeletedvalues),whereasfor othershardlyanymergingofvaluesoccurred.Inparticular,wehaveobservedthatoftentheinstancesforwhichnomerging ispossiblehavesomedisequalityconstraints(whichmakessense,sinceevenaconjunctionofdisequalityconstraintsas sim-pleas(x6=y)∧ (x6=z)∧ (y6=z) witha,b∈D(x),a∈D(y),b∈D(z),inducesabrokentriangleona,b). Forinstance,forthe graphcolouring instances,(AC+)BTP-mergingsonlyoccurwhentheinstanceshavevariableswithdegree0or1.Incontrast, (AC+)BTP-mergingisveryeffectiveforsomereal-world instancesfromfrequencyassignmentproblems(fapp*,graph*or scen*)or forsome patterned instances(likeBlackHole* oros-taillard*).Note that atbest, BTP-mergingreduces

Fig. 10. Number of instances processed by BTP-merging with and without AC preprocessing depending on the elapsed time (in seconds).

Fig. 11. Percentage of values removed by BTP vs percentage of values removed by AC and BTP-merging (AC+BTP) for each considered instance.

all variabledomainsto singletons (and socannot remove allthevalues inadomain). For example,thisis thecasefor all instances hanoi* which satisfythebroken-triangle property[26].Tables 1 and2 providesome detailedresults for some

selected instances.Theseinstanceshavebeenselectedinsuchawaythatallobservedtrends arerepresented.

Regardingruntime,BTP-mergingand AC+BTP-mergingareoftenclose asshown inFig. 12.However, forafewinstances, suchaslangford-4-14,AC+BTP-merging requiresmoretimethan BTP-merging.Sucharesultisoften explainedbythe

fact thatthevaluesused toquickly findbrokentrianglesinBTP-merginghave beenremovedbyACin AC+BTP-merging.In contrast, in most cases, achievingan AC preprocessing isuseful since itsaves time. Moreover, sometimes, it turnsout to be very useful sinceit makes itpossible to process moreinstances. For example, for the instance fapp25-2230-8, the

values removedbyAC makeitpossiblefortheBTP-mergingsteptoterminate. Finally,wecannotethat alargepartofthe considered instances are processed quickly. Indeed, for about 57% of instances, achieving (AC+)BTP-merging requires less than onesecond.

6.3. Comparisonswithneighbourhoodsubstitutionandvirtualinterchangeability

As shown in Section 3, the BTP-merging rule generalises the notion of neighbourhood substitution as well as virtual interchangeability.Hence,whenwecomparethepercentage ofvalues removedbyBTP-mergingwiththenumberofvalues removed by neighbourhood substitution or virtual interchangeability, BTP-merging is always better than or equivalent to neighbourhoodsubstitutionorvirtualinterchangeability.Thesametrendisobservedwhentheinstancesarepreprocessedby AC.Figs. 13 and14comparethepercentageofvaluesremovedbyBTP-mergingandbyneighbourhoodsubstitutionorvirtual interchangeability after having enforced AC. Nevertheless, even when the percentages are equal, we have no guarantee that BTP-merging removes the same values as neighbourhood substitution or virtual interchangeability. So, in order to

Table 1

Foreachselectedinstance,thenumbern ofvariables,thenumbere ofconstraints,thetotalnumberofvalues,thenumberofvaluesremovedby neighbour-hoodsubstitution(NS)orbyvirtualinterchangeability(VI),thenumberofvaluesremovedbyBTP-merging,thenumberofvaluesforwhichneighbourhood substitutionorvirtualinterchangeabilityholdamongthevaluesremovedbyBTP-mergingandtheruntimeinsecondsofBTP-merging.Adashmeansthat theinformationisunknownbecausetheruntimeofBTP-mergingexceedsthetime-outofonehour.

Instance n e # values NS VI BTP

# del. # del. # del. # NS # VI Time

bqwh-15-106-18_ext 106 597 385 0 0 0 0 0 <0.01 le-450-5a-2-ext 450 5714 900 0 0 0 0 0 0.04 geo50-20-d4-75-100_ext 50 393 1000 0 0 0 0 0 0.05 rand-24-24-276-139-53021_ext 24 276 576 0 0 0 0 0 0.03 langford-4-14 56 1540 3136 0 0 0 0 0 8.18 haystacks-21 441 4430 9261 0 20 20 0 20 6.44 rand-2-40-180-84-900-56_ext 40 84 7200 0 358 358 0 358 23.47 mulsol-i-4-31 185 3946 5735 300 300 300 300 300 8.01 e0ddr2-10-by-5-7 50 265 6215 366 0 366 218 0 224.11 inithx-i-2-28 645 13,979 18,060 2349 2349 2349 2349 2349 220.76 scen1-f9 916 5548 28,596 368 532 1200 251 588 669.72 fapp01-0200-8 200 1108 26,963 0 113 113 0 113 2528.42 ehi-85-297-33_ext 297 4094 2079 0 0 891 0 0 1.18 os-taillard-4-105-5 16 48 2500 812 0 812 406 0 102.73 scen10-w1-f3 680 1138 25,192 893 6626 7419 2411 6770 345.57 BlackHole-4-7-e-0_ext 112 1261 2102 697 887 896 463 887 5.71 BlackHole-4-13-e-1_ext 208 4217 7334 2541 3209 3226 1691 3209 151.31 os-taillard-4-95-7 16 48 2508 1558 0 1573 777 49 123.43 scen4 680 3967 26,856 0 268 3103 214 455 445.89 graph13-w0 916 458 35,176 0 34,260 34,260 17,130 34,260 0.36 large-92-unsat_ext 92 4186 8464 8280 8275 8280 4233 8279 2.83 lard-92-92 92 4186 8556 7163 5303 8347 840 5314 448.00 fapp25-2230-8 2230 11,974 610,084 44,168 – – – – – hanoi-5_ext 30 29 6808 0 27 6778 41 6752 0.45 Table 2

For eachselectedinstance,thetotalnumberofvalues,thenumberofvaluesremoved byAC,byACandneighbourhoodsubstitution(NS)orbyvirtual interchangeability (VI)afterACpreprocessing,thenumberof values removedbyBTP-mergingafterACpreprocessing,thenumber ofvalues forwhich neighbourhoodsubstitutionorvirtualinterchangeabilityholdamongthevaluesremovedbyBTP-mergingandtheruntimeinsecondsofBTP-merging.

Instance # values AC NS VI BTP

# del. # del. # del. # del. # NS # VI Time

bqwh-15-106-18_ext 385 0 0 0 0 0 0 <0.01 le-450-5a-2-ext 900 0 0 0 0 0 0 0.04 geo50-20-d4-75-100_ext 1000 0 0 0 0 0 0 0.05 rand-24-24-276-139-53021_ext 576 0 0 0 0 0 0 0.03 langford-4-14 3136 1428 0 0 0 0 0 35.18 haystacks-21 9261 0 0 20 20 0 20 6.45 rand-2-40-180-84-900-56_ext 7200 0 0 358 358 0 358 23.50 mulsol-i-4-31 5735 0 300 300 300 300 300 7.93 e0ddr2-10-by-5-7 6215 0 366 0 366 218 0 225.09 inithx-i-2-28 18,060 0 2349 2349 2349 2349 2349 225.93 scen1-f9 28,596 7604 0 383 390 168 383 329.40 fapp01-0200-8 26,963 9155 21 159 174 6 159 1003.46 ehi-85-297-33_ext 2079 2 0 0 889 0 0 1.19 os-taillard-4-105-5 2500 287 810 0 818 404 22 102.44 scen10-w1-f3 25,192 5134 0 6321 6808 2138 6451 190.51 BlackHole-4-7-e-0_ext 2102 280 634 802 802 427 802 2.93 BlackHole-4-13-e-1_ext 7334 793 2422 3007 3007 1623 3007 79.57 os-taillard-4-95-7 2508 451 1346 4 1406 656 122 106.43 scen4 26,856 19,534 0 774 2161 406 924 44.44 graph13-w0 35,176 0 0 34,260 34,260 17,130 34,260 0.36 large-92-unsat_ext 8464 0 8280 8275 8280 4233 8279 2.82 lard-92-92 8556 4350 4114 3878 4114 2494 3886 3.93 fapp25-2230-8 610,084 590,850 5294 14,469 16,449 4209 15,840 226.09 hanoi-5_ext 6808 6778 0 0 0 0 0 <0.01

make afiner comparison,wecheck, for eachBTP-mergeablepairofvalues, whetherneighbourhood substitutionorvirtual interchangeability mayalsohold.Table 1givestheseresultsforaselectionoftheconsideredinstances.Forafewinstances, all the values removed by BTP-merging can also be deleted by neighbourhood substitution or virtual interchangeability. In most cases (e.g. for the instances inithx-i-2-28 or mulsol-i-4-31), the removed values belong to domains of

Fig. 12. Runtime of BTP-merging vs runtime of AC+BTP-merging for each considered instance.

Fig. 13. PercentageofvaluesremovedbyACandneighbourhoodsubstitution(AC+NS)vspercentageofvaluesremovedbyACandBTP-merging(AC+BTP) foreachconsideredinstance.

the values removed by BTP-merging can beremoved by neighbourhood substitution orvirtual interchangeability. For the majority ofinstances, BTP-mergingremoves somevalueswhichareremovedneitherbyneighbourhood substitutionnorby virtualinterchangeability.WeobservethesametrendswhentheinstancesarepreprocessedbyAC(Table 2).

6.4. Impactonsolving

Inthissubsection,weinvestigatetheimpactofremovedvaluesonthesolvingperformedbyMAC.Fortheseexperiments, we onlyconsider those828instanceswhich arearc-consistentand forwhich AC+BTP-mergingremoves atleastone value. First, weobserve that MAC with AC+BTP-merging solves697 instances against688 for MAC alone withinthe time-out of onehour.NotethattheruntimeofMACwithAC+BTP-mergingincludestheruntimeofthesolvingandtheAC+BTP-merging. Fig. 15 providesa comparisonof theruntimes ofMAC and MAC with AC+BTP-merging for theselected instances. Clearly, for mostinstances, MAC outperformsMAC with AC+BTP-mergingwith respecttoruntime. Thisresultisclearly due tothe cost ofachievingAC+BTP-merging which sometimesturnsout tobetooexpensive withrespectto theruntimeof solving. However,insomecases,MACwithAC+BTP-mergingisfasterthanMAC aloneand, overall,isabletosolvemoreinstances.

Inordertobetterassesstheimpactonsolving,wenowconsiderthenumberofnodesdevelopedbyMACandMACwith AC+BTP-merging. Wecan seeinFig. 16 thatsolving byMAC withAC+BTP-mergingturns outto bemoreefficientthan we wouldhavethoughtbyjuststudyingthetotalruntime.Indeed,thankstothevaluesremovedbyAC+BTP-merging,MACwith AC+BTP-merging is often able to develop less nodes than MAC alone. The total numberof nodes developed byMAC with AC+BTP-mergingis27%lessthanthetotalnumberofnodesdevelopedbyMAC(32millionscomparedto44millions).These preliminaryresultsconcerningsolvingarepromising.However,inordertomakeMACwithAC+BTP-mergingcompetitive,we have now to look forbetter algorithms for achievingAC+BTP-merging ortechniques for identifyingwhich instances could

Fig. 14. PercentageofvaluesremovedbyACandvirtualinterchangeability(AC+VI)vspercentageofvaluesremovedbyACandBTP-merging(AC+BTP)for eachconsideredinstance.

Fig. 15. Runtime of MAC vs runtime of MAC after BTP-merging. Runtimes are given in seconds.

Fig. 17. A general-arity broken triangle on values a,b∈ D(x).

best profit from BTP-merging during preprocessing. Note that the cost of searching for broken triangles precludes using BTP-mergingduringsearch.

Aninterestingphenomenonwhichisworthyoffurtherinvestigationisthatthenumberofnodesinthesearchtreemay actually increase due to merging (since it tends to make constraints less tight) even though domain size has decreased. Likitvivatanavongand Yap[20]mentionthatsearchruntimemayincreaseafter mergingvirtualinterchangeablevaluesand indeed they observed that the number of instances for which search runtime increased was approximately the same as the numberof instancesin which searchruntimedecreased. An opentheoretical questionconcerning theperformance of MAC withor without BTP-mergingis theexistence of conditions under whichBTP-merging is guaranteednot to increase the numberofnodesin thesearchtree.Similarly, furtherexperimentaltrialswould benecessaryto uncover relationships between theexpected gainbyBTP-mergingand parameterssuchasaveragedomainsize, constraintdensityand constraint tightness.

7. GeneralisingBTP-mergingtoconstraintsofarbitraryarity

In theremainder ofthe paper, weassume that the constraints of ageneral-arity CSP instance I are given inthe form describedinDefinition 2,i.e.asasetofincompatibletuplesNoGoods(I),whereatupleisasetofvariable-valueassignments. For simplicityof presentation,we usethepredicate Good(I,t) which istrueiff thetuplet is apartial solution, i.e.t does

notcontain anypairofdistinctassignmentstothesamevariableand∄t′_{⊆t suchthatt}′_{∈NoGoods(I). Wefirstgeneralise}

thenotionofbrokentriangleandmergingtothegeneral-aritycase,beforeshowingthatabsenceofbrokentrianglesallows merging.

Definition11. A general-aritybrokentriangle (GABT) on values a,b∈ D(x) consists of a pair of tuples t,u (containing no assignmentstovariablex) satisfyingthefollowingconditions:

1. Good(I,t∪u)∧Good(I,t∪ {hx,ai})∧Good(I,u∪ {hx,bi}) 2. t∪ {hx,bi}∈NoGoods(I) ∧u∪ {hx,ai}∈NoGoods(I)

Thepairofvaluesa,b∈ D(x) isGABT-free ifthereisnobrokentriangleona,b.

A general-arity broken triangleis illustrated in Fig. 17. This figure isidentical to Fig. 1 except that Y,Z are now sets of variablesandt,u aretuples.Note that thesets Y and Z mayoverlap. Asin thebinarycase,adashedlinerepresents a nogood(i.e.atuple notintheconstraintrelationonitsvariables).Asolidlinenowrepresentsapartialsolution.

If theconstraintsarerepresented bynogoods,asinourDefinition 2,thentodecide whetherthereisaGABTona,b in

aCSPinstance,onecanusethesecondconditioninDefinition 11andexploreallpairst∪ {hx,bi},u∪ {hx,ai}∈NoGoods(I).

On the other hand, if the constraints are represented as lists of allowed tuples, then one can use the first condition in Definition 11 and explore all pairs t∪ {hx,ai},u∪ {hx,bi} of tuples explicitly allowed by the constraints in I (since the

second condition implies that under thisrepresentation, there isa constraint over thevariables of t and x,and one over the variablesof u and x). Whateverthe representation, apairt,u canbechecked tobea GABTon a,b byevaluatingthe properties ofDefinition 11,allof whichinvolve only constraintchecks.Hence decidingwhether apaira,b isGABT-free is polytimeforconstraints giveninextension(asthesetofsatisfyingassignments)aswellasforthosegivenbynogoods(the set ofassignmentsviolatingtheconstraint).

Definition12.Merging valuesa,b∈ D(x)inageneral-arityCSP instance I consistsofreplacinga,b inD(x) byanewvalue

c which iscompatible withallvariable-valueassignments compatiblewith atleastone oftheassignments hx,ai orhx,bi, thus producinganinstance I′ _{withthenewsetofnogoodsdefinedasfollows:}

NoGoods

(

I′

) = {

t

∈

NoGoods

(

I

) | h

x

,

a

i, h

x

,

b

i /

∈

t

}

∪ {

t

∪ {h

x

,

c

i} |

t

∪ {h

x

,

a

i} ∈

NoGoods

(

I

) ∧

∪ {

t

∪ {h

x

,

c

i} |

t

∪ {h

x

,

b

i} ∈

NoGoods

(

I

) ∧

∃

t′

∈

NoGoods

(

I

)

s

.

t

.

t′

⊆

t

∪ {h

x

,

a

i}}

Avalue-mergingcondition is apolytime-computableproperty P(x,a,b)ofassignmentshx,ai, hx,biinaCSP instance I such

that when P(x,a,b) holds,theinstance I′ _{issatisfiableifand onlyif I issatisfiable.}

Thismergingoperationcanbeperformedinpolynomialtimewhetherconstraintsarerepresentedpositivelyinextension ornegativelyasnogoods.ForrepresentationsusingnogoodsthisisclearfromDefinition 12.Forrepresentationsinextension, simply observethat asinthebinarycase, theoperationamountstogatheringtogether tupleswhich satisfyGood(I,·)and containinghx,aiorhx,bi,andsetting x toc inthem.

Proposition13.Inageneral-arityCSPinstance,beingGABT-freeisavalue-mergingcondition.Furthermore,givenasolutiontothe instanceresultingfromthemergingoftwovalues,wecanfindasolutiontotheoriginalinstanceinlineartime.

Proof. In orderto provethat satisfiabilityispreservedbythismergingoperation, itsufficestoshow that if s isasolution to I′ _{containing hx,ci, then either s}

a= (s\ {hx,ci})∪ {hx,ai} or sb= (s\ {hx,ci})∪ {hx,bi} isa solution to I. Suppose, for a contradiction that this is not the case. Then there are tuples t,u⊆s\ {hx,ci} such that t∪ {hx,bi}∈ NoGoods(I) and u∪ {hx,ai}∈ NoGoods(I). Since t,u are subsets of the solution s to I′ _{and t,u contain no assignments to x, we have}

Good(I,t∪u). Since t∪ {hx,ci} is a subset of the solution s to I′_{, we have t∪ {hx,ci}∈/ NoGoods(I}′_{). By the definition}

of NoGoods(I′_{)given inDefinition 12, and sincet∪ {hx,bi}∈ NoGoods(I), we know that ∄t}′_{∈ NoGoods(I) such that t}′_⊆

t∪ {hx,ai}. ButthenGood(I,t∪ {hx,ai}).By asymmetric argument,we candeduce Good(I,u∪ {hx,bi}). Thisprovidesthe contradiction wewerelookingfor,sincewehaveshownthatageneral-aritybrokentriangleoccursont,u,hx,ai,hx,bi.

Reconstructing a solution to the original instance can be achieved in linear time, since it suffices to verify which (or both) ofsa or sb isasolutionto I. ✷

7.1. RelationshipwithresolutioninSAT

We now show that inthe case ofBoolean domains,there is aclose relationship between merging two values a,b on which no GABT occursand a common preprocessingoperation used by SAT solvers.Givena propositional CNF formula

ϕ

in theform ofasetofclauses (eachclauseCi beingrepresentedasaset ofliterals)and avariablex occurring in

ϕ

,recall that resolution istheprocessofinferringtheclause(C0∪C1)fromthetwoclauses({¯x}∪C0),({x}∪C1).Definetheformula Res(x,

ϕ

) to be the result ofperforming all suchresolutions on

ϕ

, removing all clauses containing x or x,¯ and removing subsumedclauses:

Res

(

x

,

ϕ

) =

min

⊂

({

C

|

C

∈

ϕ

;

x

, ¯

x

∈

/

C

} ∪ {(

C0

∪

C1

) | ({¯

x

} ∪

C0

), ({

x

} ∪

C1

) ∈

ϕ

})

Itisawell-knownfactthatRes(x,

ϕ

) issatisfiable ifandonlyif

ϕ

is.

Eliminatingvariablesinthismannerfrom SATinstances, togetanequisatisfiable formulawith lessvariables, isa com-monpreprocessingstepinSATsolving,andistypicallyperformedprovideditdoesnotincreasethesizeoftheformula[27]. A particularcase iswhen it amountsto simply removing alloccurrences of x,which is thecase,for instance, if x or x is¯

unitorpurein

ϕ

,orifallresolutionson x yieldatautologicalclause.

Definition14.Avariablex issaidtobeerasable fromaCNF

ϕ

if

Res

(

x

,

ϕ

) ⊆ {

C

|

C

∈

ϕ

;

x

, ¯

x

∈

/

C

} ∪ {

C0

| ({¯

x

} ∪

C0

) ∈

ϕ

} ∪ {

C1

| ({

x

} ∪

C1

) ∈

ϕ

}

ACNF

ϕ

canbeseenastheCSPinstance Iϕ on theset X of variablesoccurringin

ϕ

, withD(x)= {⊤,⊥}forallx∈X , and NoGoods(Iϕ)= {C|C∈

ϕ

},where({x1, · · ·xp, ¯xp+1, · · · , ¯xq}) = {hx1,⊥i,. . . ,hxp,⊥i,hxp+1,⊤i,. . . ,hxq,⊤i}.

Proposition15.AssumethatnoGABToccursonvalues⊥,⊤forx inIϕ.Assumemoreoverthatnoclausein

ϕ

issubsumedbyanother

one.2Thenx iserasablefrom

ϕ

.

Proof. Rephrasing Definition 11 (1) in terms of clauses, for any two clauses ({¯x}∪C0),({x}∪C1)∈

ϕ

we have one of (i)∃C∈

ϕ

,C⊆ (C0∪C1),(ii)∃C′_∈

_ϕ

_,C′_{⊆ (C}

0∪ {x}),or(iii) ∃C′′∈

ϕ

,C′′_{⊆ (C}

1∪ {¯x}).Moreover,inCase (ii)C′ _mustcontain

x,forotherwisetheclause({¯x}∪C0)wouldbesubsumedin

ϕ

,contradictingourassumption.Similarly,inCase (iii)C′′_must

contain ¯x.

InCase (i)theresolvent(C₀∪C₁)of({¯x}∪C₀),({x}∪C₁) issubsumedbyC inRes(x,

ϕ

),andhencedoesnotoccurinit.

Similarly, inthesecond case(C0∪C1) issubsumedbythe resolventof({¯x}∪C0) and C′, whichis preciselyC0. Thethird

caseis dual.Wefinallyhave thattheonly resolvents addedareoftheform C₀ (resp.C₁)forsome clause ({¯x}∪C₀) (resp. ({x}∪C₁))of

ϕ

,asrequired. ✷

Wecanshowtheconverseisalsotrueprovidedthataveryreasonablepropertyholds.

Proposition16.Assumethat

ϕ

satisfies:∀({x}∪C)∈

ϕ

,∄C′_{⊆C,({¯x}∪C}′_)∈

_ϕ

_{anddually∀({¯x}∪C)∈}

_ϕ

_,∄C′_{⊆C,({x}∪C}′_)∈

_ϕ

_.

Ifx iserasablefrom

ϕ

,thennoGABToccursonvalues⊥,⊤forx inIϕ.

Proof. Assumefor acontradiction that thereisaGABTon values ⊥,⊤ for x in I_ϕ, lett,u be witnessesto this,and write

t∪ {hx,⊤i}= ({¯x} ∪C0), u∪ {hx,⊥i}= ({x} ∪C1). Then the clause (C0∪C1) is produced by resolution on x. Since x is

erasable,(C0∪C1)isequaltoorsubsumedbyaclause C∈Res(x,

ϕ

),where(applyingDefinition 14 inreverse)eitherC ,or

({x}∪C),or({¯x}∪C) isin

ϕ

.Thefirst casecontradictsGood(Iϕ,t∪u),so assume bysymmetry ({x}∪C)∈

ϕ

. From C∈/

ϕ

and C∈Res(x,

ϕ

)weget∃C′_{⊆C,({¯x}∪C}′_)∈

_ϕ

_{.Butthenthepairofclauses({x}∪C),({¯x}∪C}′_)∈

_ϕ

_{violatestheassumption}

oftheclaim. ✷

8. BTP-merginginthepresenceofglobalconstraints

Global constraints are animportant featureof constraint programming. They not only facilitate modelling of complex problemsbut many globalconstraintsalsohave dedicatedefficientfilteringalgorithms [28].Inthepresenceofglobal con-straints therearespecific questionswhichneedtobeaddressedto knowwhetherBTP-mergingisuseful.Thefirst thingto verifyisthatmergingsarepossibleinthepresenceofoneormoreglobalconstraints.Asecondimportantpointiswhether these BTP-mergingscanbedetectedinpolynomialtime.Athirdpointistodeterminewhetherthesemantics oftheglobal constraint(s) are preserved by the operation of merging two values. For those global constraints that are decomposable into the conjunction of low-arity constraints, we can also ask whether BTP-merging applied to the decomposed version is equivalent to BTP-merging applied to the original global constraint(s). The answers to these questions depend on the global constraints. This section presents results concerning the important global constraint AllDifferent. These results are bothnegativeandpositive.

Proposition17.DeterminingwhethertwovaluescanbeGABTP-mergedinaCSPinstanceconsistingoftwoAllDifferentconstraintsis coNP-complete.

Proof. It suffices to show that the problem of testing the existence of a general-arity broken triangle (GABT) in a CSP

instance consisting of two AllDifferent constraints is NP-complete. We denote this problem by ∃GABT(2AllDiff). Clearly, the validity of a GABT can be checked in polynomial time. Testing the satisfiability of a CSP instance consisting of two AllDifferent constraints (aproblemwhichwe denotebyCSP(2AllDiff))isknown to beNP-complete[29].Thus tocomplete theproofitsufficestoexhibitapolynomialreductionfromCSP(2AllDiff)to∃GABT(2AllDiff).

Let I be an instance, over variables X , consisting of two AllDifferent constraints with scopes S1,S2. Without loss of

generality, we suppose that S1∪S2=X . Let x,y,z be threevariables not in X with domains containing only values not occurring in the domains of the variables in X , including a,b∈ D(x) with a∈ D(y), a∈ D(z)/ , b∈D(z), b∈/D(z). We constructanewinstance I′ withvariables X∪ {x,y,z},withdomainsasin I forvariablesin X andthedomainsofvariables

x,y,z as just described.Theinstance I′ _{has just two constraints: AllDifferentconstraints with scopes S}

1∪ {y,x} and S2∪ {z,x}. We will show that I′ _{has a GABT on a,b∈ D(x) if and only if I has a solution. A GABT on a,b∈ D(x) consists}

of tuples t,u (containing no assignments to variable x) satisfying the following conditions: Good(I′_{,t∪u), Good(I}′_,t∪

{hx,ai}), Good(I′_{,u∪ {hx,bi}), t∪ {hx,bi}∈ NoGoods(I}′_{) and u∪ {hx,ai}∈ NoGoods(I}′_{). Since u∪ {hx,ai}∈ NoGoods(I}′_),

but Good(I′_{,u), we must have hy,ai∈u, since y is the only variable other than x containinga in its domain. Similarly,}

we can deduce that hz,bi∈t. NowGood(I′_{,t∪u) implies that (t\ {hz,bi})∪ (u\ {hy,ai}) isa solution to I. On the other}

hand, suppose that s is a solution to I. Let u = s[S1]∪ {hy,ai} and t = s[S2]∪ {hz,bi} (where s[S] represents the

subsetof s correspondingtoassignmentsto variablesin S).Thenthetuplest and u satisfytheconditions:Good(I′_,t∪u),

Good(I′_{,t∪ {hx,ai}), Good(I}′_{,u∪ {hx,bi}), t∪ {hx,bi}∈NoGoods(I}′_{) andu∪ {hx,ai}∈ NoGoods(I}′_{).Thust,u formaGABT}

on a,b∈ D(x).

Wehaveshown that I′ _{has aGABTona,b∈ D(x) ifand onlyif I hasasolution. Sincethereduction fromCSP(2AllDiff)}

to ∃GABT(2AllDiff) isclearlypolynomial,thiscompletestheproof. ✷

Another problem with merging values in the presence of global constraints is that the global constraint may lose its semanticswhenvaluesaremerged.Togiveanexample,consideraninstanceI inwhichavariablex (withdomainD(x)=A)

occurs in thescope of asingleconstraint, anAllDifferent constraint on variables X . Since thereis only one constrainton variable x,therecanbeno GABTon anypair ofvaluesinD(x).It iseasytoseethat wecan,infact, GABTP-mergeallthe values in D(x). When thedomain of x becomesa singleton, wecan clearly eliminate x.However, theresulting constraint on the variables X\ {x} combines bothan AllDifferent constraint on X\ {x} and a constraint which says that the set of valuesassignedtothese variablesdoesnotcontainallof A.Thisconstraintclearlydoesnothavethesamesemanticsasan