Comportement élastique des articulations flexibles à col elliptique

The International congress for applied mechanics

La mécanique et les matériaux, moteurs du développement durable

du 02 au 04 mai 2012, Marrakech – Maroc

Comportement des articulations flexibles à col elliptique

Debongnie Jean-François

1

1

Université de Liège, dépt. A&M/Méthodes de Fabrication, Belgique, JF.Debongnie@ulg.ac.be

Résumé :

Nous présentons un modèle permettant de déterminer le comportement élastique des cols elliptiques, en flexion et cisaillement dans les deux plans, en extension et en torsion. La démarche utilisée consiste d’abord à établir la solution exacte dans le cadre de la théorie des poutres, à l’aide du changement de variables de Sommerfeld bien connu en lubrification. Nous en déduisons alors la forme asymptotique de la solution pour un col très mince. Enfin, et c’est là notre principale originalité, nous établissons numériquement une correction simple permettant de passer de la solution asymptotique à la solution générale avec une approximation excellente pour tous les cas pratiques. Le modèle ainsi construit est d’une simplicité sans équivalent dans la littérature, ce qui lui confère un très grand intérêt en matière de conception.

Abstract :

We present here a model for the prediction of the elastic behaviour of elliptic notch hinges, including flexure and shear in both planes, stretching and torsion. In a first step, an exact solution is established in the frame of the beam theory, making use of Sommerfeld’s change of variables, which is well known in the lubrication theory. The second step is the deduction of the asymptotic solution for very thin hinges. Finally, and this is the most original part of our presentation, a simple corrective factor is deduced numerically, which enables to pass from the asymptotic solution to the exact one with a very fair approximation in the practical range of thicknesses. The simplicity of the obtained model has no equivalent in the literature, which is specially useful at the design stage.

Introduction

Les articulations flexibles à col constituent une alternative aux articulations classiques présentant les avantages suivants : absence de jeu, absence de frottement et, par conséquent, absence d’hystérésis et de particules d’usure. Tout ceci les rend très attractives en métrologie, en micromécanique et dans les systèmes devant injecter des fluides dans le corps humain. Leur seul inconvénient est l’amplitude limitée des mouvements qu’elles permettent. Du reste, elles peuvent être réalisées de manière efficace par électroérosion à fil.

Pour les concevoir, on a besoin de leurs raideurs sous les diverses sollicitations classiques. Des résultats sont donnés à ce sujet par Henein [3] et par Lobontiu [6] mais soit ils se limitent au cas asymptotique des très faibles épaisseurs de col, soit ils sont d’une complexité incompatible avec une procédure de conception.

Nous proposons dans la présente communication une étude des articulations à col elliptique suivant la démarche que voici, tout entière orientée vers la conception : tout d’abord, nous établissons les formules exactes, puis nous en déduisons leur expression asymptotique pour les cols très minces, puis enfin nous proposons des coefficients approchés simples permettant de corriger la solution asymptotique pour obtenir avec une excellente approximation la solution générale.

1. Paramétisation géométrique

Nous nous proposons dans ce qui suit d’étudier le comportement élastique de cols elliptiques tels que celui de la figure 1. Le col a une épaisseur minimale . Pour l’obtenir, on a découpé d’un bloc rectangulaire, symétriqument de chaque côté, des ellipses de profondeur et de longueur . Il est supposé que le rapport est relativement petit et, en tout cas que , ce qui suffit à tous les besoins pratiques. Nous utiliserons la coordonnée 0 h / a a 5 l 2 h /₀ a , 0 0 ≤ h

xprise suivant l’axe moyen de la pseudo-articulation , avec comme origine, le point le plus étroit du col. Cette coordonnée varie donc entre −l et . L’épaisseur du col perpendiculairement au dessin est notée l b.

Figure 1 – Col elliptique.

Posant φ sin l = x (1) on obtient l’expression suivante de l’épaisseur du col :

φ cos 2 2 ) (x h₀ a a h = + − (2) Ceci peut encore s’écrire

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + = cosφ 2 1 2 ) ( 0 a h a x h

Introduisant alors le paramètre

a h 2 1 1 0 + = ε (3) on obtient ( ) 2 1 cos 2 (1 εcosφ) ε φ ε ⎟⎠= − ⎞ ⎜ ⎝ ⎛ − = a a x h (4)

2.

Sollicitation par un moment de flexion constant dans le plan du dessin

Figure 2 - Moment constant dans le plan du dessin

2.1. Expression générale

Si l’on applique un moment constant Mf dans le col, l’angle de rotation d’extrémité est donné par

∫

− = l l 3 12 h dx Eb Mf α (5)

où Eest le module de Young. Tenant compte de l’expression (4) de l’épaisseur courante, on obtient

) ( 4 ) cos 1 ( cos 4 ) cos 1 ( cos 8 1 2 / 0 3 3 3 3 3 3 2 / 2 / 3 3 3 ε ε φ φ ε φ ε φ ε φ φ ε π π π I a d a d a h dx

∫

∫

∫

= − = − = − − l l l l l avec φ φ ε φ ε π d I

∫

− = 2 / 0 3 1 ) cos 1 ( cos ) ( (6) Ainsi, ) ( 3 1 3 3ε ε α I a Eb Mf l = (7)

2.2. Calcul de l’intégrale I

1

Pour calculer l’intégrale qui apparaît ci-dessus, on peut avantageusement utiliser le changement de variables de Sommerfeld [1,2] ω ε ε ω φ cos 1 cos cos + + = (8) bien connu en théorie de la lubrification. A φ=0 correspond ω=0et à φ =π/2 correspond

) arcos(

* ε

ω = − (9) Le calcul est détaillé dans les références [4,5] et donne

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − = * 2 3 1 2 1 ) 1 ( 1 ) ( 2 2 2 / 5 2 1 ω ε ε ε ε ε I (10)

2.3. Expression asymptotique pour les très faibles épaisseurs de col

Lorsque le rapport h0/aest très petit devant l’unité, on a

π ω ε ε ε ≈ + ≈ , 1− ≈ , *≈ 2 3 2 1 , 1 2 0 2 a h ce qui donne π 2 3 . 2 / 5 0 , 1 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = h a I as (11) et donc, 2 / 5 0 2 9 h a a Eb M as f l π α = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ (12)

Dans le cas d’un col circulaire (l=a), la même expression a été obtenue par Paros et Weisbord [7].

2.4. Expression approchée pour le cas général

La formule (10) est complexe et il existe des compensations entre ses différents termes. Aussi proposons-nous d’écrire ) / ( 1 . 0 1 h a K M M as f f ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = α α (13) 1

K étant un facteur correctif défini par

1 3 2 / 5 0 1 2 3 I h a K ε π ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = (14)

et de chercher par voie numérique une approximations simple de ce facteur. Comme le montre le tableau ci-dessous, l’expression

a h

K1,app =1+0,136 0 (15)

est correcte à moins de 0,08% près pour h0/a≤0,5.

a h /₀ 0,01 0,02 0,05 0,1 0,2 0,5 1 K 1,0012 1,0025 1,0064 1,0129 1,0264 1,0683 app K_1, 1,0014 1,0027 1,0068 1,0136 1,0272 1,0680 % Δ 0,01 0,02 0,04 0,07 0,08 -0,03

3. Sollicitation d’extension

Figure 3 - Extension

3

.

1. Expression générale

Pour une force d’extension N, le déplacement d’extrémité vaut u

∫

− = l lh dx Eb N u (16) On calcule ) ( 1 soit ) ( cos 1 cos 2 2 2 / 0 ε ε φ φ ε φ επ I a Eb N u I a d a h dx l l l l l = = − =

∫

∫

− (17)

3.2. Calcul de l’intégrale I

2

Toujours en faisant usage du changement de variables de Sommerfeld, on obtient [4,5]

2 2 1 * 2 ) ( ε ω π ε − + − = I (17)

3.3. Expression asymptotique

Pour les très faibles valeurs de h /₀ a, l’expression précédente se ramène à

0 , 2 h a I _as =π , ce qui donne 0 1 h a a Eb N u as π l = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ (18)

3.4. Correction pour le cas général

Suivant la même démarche que ci-dessus, nous écrirons

) / ( 1 . 0 2 h a K N u N u as ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = (19)

On peut approcher le facteur K2par l’expression simple a h K _app 0 , 2 =1+0,97 (20)

avec une erreur relative ne dépassant pas 1,62% pour h₀/a≤0,5, comme le montre le tableau suivant :

a h /₀ 0,01 0,02 0,05 0,1 0,2 0,5 2 K 1,085 1,122 1,197 1,287 1,422 1,714 app K2, 1,097 1,137 1,217 1,306 1,434 1,686 % Δ 1,13 1,39 1,62 1,50 0,80 -1,62

4. Sollicitation de torsion

Figure 4 – Torsion

Si G est le module de Coulomb, la rotation d’extrémité ψ due à un moment de torsion constant Mt se calcule par

) ( 4 3 3 3 1 3 3 2 / 2 / 3 2 / 2 / 3 ε ε ψ I a Gb M h dx Gb M dx Gbh M_{t t} l _{t l} l l l = = =

∫

∫

− − (21)

On retrouve donc la même intégrale qu’en flexion, ce qui permet d’écrire directement

1 2 / 5 0 1 . 8 9 K h a a Gb M_t l π ψ ₌ (22)

5. Flexion transverse, sous moment constant

Pour une flexion dans le plan perpendiculaire au dessin, la rotation d’extrémité βse calcule par

∫

− = 2 / 2 / 3 12 l l h dx Eb MfT β (23)

On retrouve donc la même intégrale qu’en extension, ce qui permet d’écrire directement

2 3 1 12 K a Eb M_fT l π β = (24)

6. Raideur en translation latérale pure d’une extrémité dans le plan

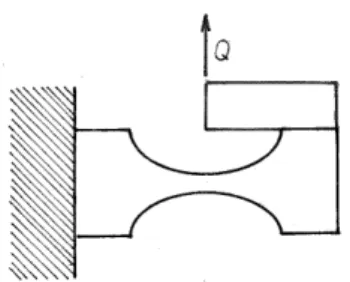
On peut obtenir une translation d’une extrémité sans rotation parasite en applquant une charge latérale Q au droit du col, ce qui se réalise par l’artifice illustré en figure 5. Le moment de flexion a alors pour expression . La déformée inclut un terme de flexion et un terme de cisaillement : .

Qx M_f =− c f v v v= +

Figure 5 – Obtention d’une translation latérale pure d’une extrémité dans le plan

6.1. Contribution de la flexion

La rotation de flexion vérifie l’équation

3 3 12 12 Ebh Qx Ebh M dx dα ₌ f ₌₋ (25) On en déduit le déplacement d’extrémité par

[ ]

) 26 ( ) ( 3 ) cos 1 ( 8 cos sin 12 12 3 3 3 3 2 / 2 / 3 3 3 2 2 3 2 ε ε φ ε ε φ φ φ α α α α π π I a Eb Q a d Eb Q dx h x Eb Q dx dx d x dx dx d x x dx vf l l l l l l l l l l l l l = − = = − = − = =

∫

∫

∫

∫

∫

− − − − − − avec

∫

₋ = 2 / 0 3 2 3 ) cos 1 ( cos sin ) ( π φ φ ε φ φ ε d I (27)

Le calcul de l’intégrale I3 est un peu long et mène au résultat suivant :

( )

⎥⎥_⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ − = 2 2 2 / 3 2 3 1 2 1 * sin * 1 1 2 * 2 sin * 2 1 1 1 ) ( ε ε π ε ε ω ε ω ε ε ε ω ω ε ε ε I (28)

Pour des cols très minces, on obtient l’expression asymptotique suivante :

( )

3/2 0 3 3 2 ⎟⎟_⎠ ⎞ ⎜⎜ ⎝ ⎛ = h a I _as π ε ce qui donne 2 / 3 0 3 2 3 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ h a a Eb Q v as f π l (29)

La solution générale peut en être déduite à l’aide du coefficient correcteur

3 3 2 / 3 0 3 2 I h a K ε π ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = permettant d’écrire 3 1 . K Q v Q v as f f ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = (30)

On peut donner à ce coefficient l’expression approchée suivante

a h K app 0 , 3 =1+1,40 (31)

a h /0 0,01 0,02 0,05 0,1 0,2 0,5 3 K 1,017 1,033 1,078 1,150 1,288 1,696 app K3, 1,014 1,028 1,070 1,140 1,280 1,700 % Δ -0,30 -0,49 -0,79 -0,89 -0,63 0,22 6.

2. Contribution du cisaillement

Le calcul de cette contribution est aisé :

0 2 2 5 6 1 ) ( 5 6 6 5 1 h a a Eb K I a Eb h dx Eb Q v_c l _{l l} l π ε = = =

∫

− (32)

Dans la plupart des cas pratiques, ce terme qui ne contient que la racine carrée de est petit devant le terme de flexion qui en contient la puissance 3/2.

0

/ h

a

7. Raideur en translation latérale pure hors plan

Il s’agit du même genre de sollicitation que ci-dessus, mais dans la direction transversale au plan. La charge appliquée sera ici notée R, et le déplacement w correspondant se décomposera encore en un terme de flexion wf et

un terme de cisaillement wc.

7.1. Contribution de la flexion

Partant de la relation de base donnant la rotation

h Eb Rx h Eb M dx d fT 3 3 12 12 − = = β (33) on procède comme ci-dessus pour obtenir

) 34 ( ) ( 12 ) cos 1 ( 2 cos sin 12 12 4 3 3 2 / 2 / 2 3 3 2 3 ε φ φ ε ε φ φ β π π I a Eb R d a Eb R h dx x Eb R dx dx d x wf l l l l l l = = − = = − =

∫

∫

∫

− − − avec

∫

− = 2 / 0 2 4 cos 1 cos sin ) ( π φ φ ε φ φ ε ε d I (35)

Le calcul exact de l’intégrale I4 donne

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − + − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + + = 2 * 4 1 2 1 1 1 4 ) ( ε α π ε ε ε ε π ε I (36)

Pour de très petites valeurs du rapport h /0 a, on obtient l’expression asymptotique 1,785 4 1 4 ≈ + = π I , ce qui donne ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + = 4 1 12 3 2 , π a Eb R w_{f as l l} (37) Dans le cas général, nous écrirons

4 1 . K R w R w as f f ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = (38)

K4 étant naturellement défini par 4 / 4

4 1 I K ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +

= π . Une bonne approximation de ce coefficient est donnée par l’expression

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + + = a h a h K_4,app 1 1,726 0 1 0 (39)

qui, comme le montre le tableau ci-dessous, conduit à une erreur inférieure à 0,6% pour h0/a≤0,5.

a h /₀ 0,01 0,02 0,05 0,1 0,2 0,5 K4 1,190 1,278 1,468 1,709 2,105 3,094 K4,app 1,190 1,279 1,472 1,718 2,117 3,083 % Δ -0,03 -0,07 0,31 0,53 0,58 -0,35

7.2. Contribution du cisaillement

On a, comme dans le plan,

∫

− = = l l l 0 2 5 6 1 5 6 h a a Eb K h dx Eb R wc π ₍₄₀₎

On remarquera que le rapport entre le terme de cisaillement et le terme de flexion, donné par

0 2 2 4 85 , 17 h a b K K w w f c _⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = l (41)

n’est généralement pas petit devant l’unité.

8. Conclusion

Les résultats précédents permettent d’étudier toutes les sollicitations du col, puisqu’une flexion simple se décompose aisément en une flexion pure (Mf=cte) et une translation pure (Mf linéaire). Pour chaque cas de

sollicitation élémentaire, nous avons établi la solution exacte, malheureusement un peu compliquée. Nous en avons déduit la solution asymptotique, retrouvant certains résultats connus. Enfin, nous avons développé des corrections approchées simples permettant de calculer avec une excellente approximation la solution exacte à partir de la solution asymptotique. Le jeu de formules simples ainsi obtenues constitue un outil très utile au niveau de la conception.

Bibliographie

[1] SOMMERFELD Arnold. Zur hydrodynamische Theorie der Schmiermittelreibung. Z. Math. Physics, vol. 50, 1904.

[2] LELOUP Lucien. Etude de la lubrification et calcul des paliers. 2e édition, Sciences et Lettres, Liège, 1961. [3] HENEIN Simon. Conception des guidages flexibles. Presses polytechniques et universitaires romandes, collection META, 2001.

[4] MERKEN Patrick, DEBONGNIE Jean-François. Le col circulaire comme articulation flexible. 6e congrès national de mécanique théorique et appliquée, Gent, 26-27 mai 2003.

[5] MERKEN Patrick. La fonction guidage en micromécanique. Thèse de DEA, Liège, 2006.

[6] LOBONTIU Nicolae. Compliant mechanisms – Design of flexure hinges. CRC Press, Boca Raton, Florida, 2002.