Thermoélasticité et amortissement par thermoconduction

THERMOELASTICITE ET AMORTISSEMENT

PAR THERMOCONDUCTION

J.F. DEBONGNIE I.C.M.E. (Mécan.), Lg, 1973 Dr. Sc. Appl. 2010

Introduction

Les pages qui suivent constituent un exposé de la thermoélasticité dans le cadre des grands déplacements, avec petites déformations. Il s’agit d’un travail que nous avons entrepris lors d’un séjour à l’E.N.S.M. de Nantes en 1985, puis retravaillé par morceaux depuis lors.

Le premier chapitre rappelle les notions fondamentales de la cinématique et de la statique des milieux continus.

Dans le second chapitre sont traitées les lois constitutives. Adoptant le cadre naturel de la thermodynamique, avec l’hypothèse de l’équilibre local, on obtient simplement les lois de la thermoélasticité, ainsi qu’une série de relations et d’inégalités utiles. Les cas extrêmes de la déformation isotherme et de la déformation isentropique sont pris en considération.

Le troisième chapitre présente une application un peu inattendue de la thermoélasticité, à savoir, l’amortissement par thermoconduction.

Chapitre 1 : Cinématique et statique des milieux continus

1. Cinématique des milieux continus

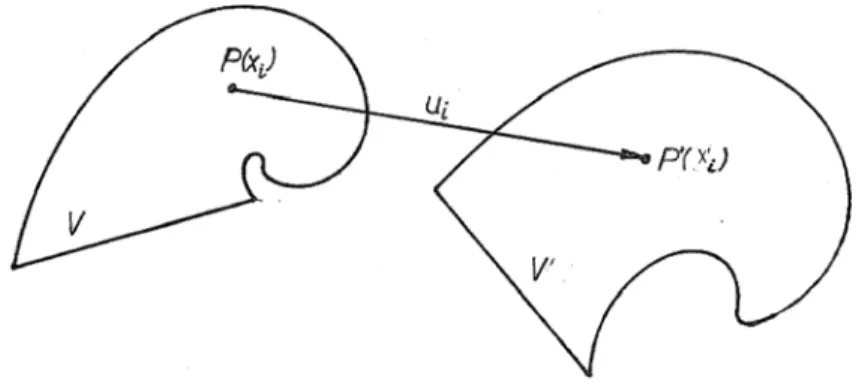
Soit un corps continu déformable. Nous utiliserons une variable d’évolution, que l’on peut assimiler au temps, bien que cela ne soit pas nécessaire. En t =0, le corps occupe un certain volume de l’espace V, où chaque point P peut être repéré par ses coordonnées cartésiennes x . C’est la configuration de référence. A l’instant t, il occupe un volume V’, où i le point P susvisé a pris une nouvelle position P’ de coordonnées x' . C’est la configuration i

réelle ou position déformée (fig. 1).

Figure 1 – Configuration de référence et configuration déformée On appelle déplacement le vecteur

' ( 'x_i x_i)

= − = − _i

u P P e (1)

En mécanique des fluides, il est d’usage courant de considérer u comme une fonction des coordonnées x' , car on s’intéresse le plus souvent à un écoulement dans une zone limitée de i l’espace, avec une entrée et une sortie pour le fluide (fig. 2). C’est la description eulérienne.

Figure 2 – Problème typique d’écoulement

En mécanique des structures, au contraire, il convient de suivre le corps dans sa déformation et c’est la description lagrangienne qui s’impose. On considère donc le déplacement comme une fonction des coordonnées de référence x .

A ces deux points de vue correspondent deux systèmes de coordonnées pour la position réelle. Dans le point de vue eulérien, on repère un point par ses coordonnées

spatiales x' : on a donc _i

'=x'_{i i}

P e (2)

Mais les coordonnées spatiales sont en fait l’inconnue du problème, ce qui rend la description implicite. Tel que le problème se pose, il faut construire une description qui suive la matière. A cette fin, traçons dans la pensée, sur le corps non déformé, un réseau de coordonnées x . Ce _i

réseau, bien qu’il se déforme avec le corps, n’en reste pas moins capable de repérer les points du corps. Il définit dans l’espace occupé par le corps un système de coordonnées curvilignes dont les vecteurs de la base covariante

' i x ∂ = ∂ i P E (3)

ne sont en général ni orthogonaux, ni normés. C’est ce que l’on appelle le système des

coordonnées convectées. Il est bien clair que lors de la déformation, un point donné du corps

conserve toujours la même valeur algébrique des coordonnées convectées qui apparaissent donc comme des coordonnées lagrangiennes. Introduisant la matrice jacobienne

j i ij x J = '_, , (4) on a visiblement

(

)

_, , ' '_j '_{j i ji} i i x x J x ∂ = = = = ∂ i j j j P E e e e (3’)

L’élément de volume de référence construit sur les trois vecteurs élémentaires

, ,

i j k

dP=dxe_i dQ=dy e_j dR=dz e _k

est donné par

k j i ijk k j i kdxdx dz e dxdx dx e dV =(dP×dQ)⋅dR=(e_i×e_j)⋅ = , (4) où e est le symbole alternateur. Dans la configuration réelle, ces trois vecteurs élémentaires _ijk

deviennent (avec dXi =dxi,...)

'=dx'i i =dXi i, '=dYj j, d '=dZk k,

dP e E dQ E R E

et l’élément de volume réel est donc

(

)

' i j k

=J J J_{li mj mk}

(

e_l×e_m

)

⋅e_n dX dY dZi j k =e_lmnJ J J_{li mj nk} dX dY dZi j k

=e J dX dY dZijk i j k,

où J est le jacobien de la transformation. On a donc JdV

dV'= (5)

La conservation de la masse élémentaire s’exprime par la relation ' ' dm=ρ dV =ρ dV , (6) ce qui implique J ' ρ ρ = .

En particulier, comme la masse volumique doit toujours rester strictement positive et finie, on obtient la condition

0 >

J (7)

c’est-à-dire que le jacobien de la transformation x→x' doit être positif. Il en découle notamment que la base covariante

{

E E E₁, ₂, ₃

}

garde nécessairement la même orientation (dextrorsum ou sinistrorsum) que la base

{

e e e₁, ₂, ₃

}

.

2. Tenseur métrique et base contravariante des coordonnées convectées

Dans les coordonnées convectées, un vecteur u défini au point P admet le développement

i

U

= _i

u E , (8)

les Ui étant les composantes contravariantes de ce vecteur ; On peut calculer la norme du vecteur par 2 i j i j ij U U E U U = ⋅ = _i⋅ _j = u u u E E , (9)

où apparaît le tenseur ij

appelé tenseur métrique. Mais si l’on donne le vecteur u, comment déterminer ses composantes contravariantes ? Multipliant scalairement la définition (8) par E , on obtient _j

i i ij U U E ⋅ _j = _i⋅ _j = u E E E (11) Les grandeurs j U = ⋅u E _j (12)

sont appelées composantes covariantes de u. On est donc ramené au système linéaire j

i jiU U

E =

qui admet pour solution j ij i U E U = , (13)

en notant Eij le tenseur inverse de E , appelé tenseur métrique inverse. La relation (11) _ij

entraîne encore, après multiplication par Ejk,

jk i jk i k k ij i E U E E Uδ U ⋅ _j = = = u E , soit k k U = ⋅u E (14)

en introduisant la base contravariante

{ }

Ek définie par k kl

E

= _l

E E . (15)

Il est clair que l’on a k k

U

=

u E . (16)

Il est possible de définir des tenseurs dans le système convecté, mais il faut prendre garde à la position des indices. C’est d’ailleurs ce qui nous a fait écrire, au paragraphe précédent, Xi

pour x_i. La remarque fondamentale est que la contraction d’un vecteur covariant avec un vecteur contravariant donne un scalaire indépendant du système de coordonnées : en effet,

i j j i i

j i j i

U V δ U V U V

⋅ = _i⋅ = =

De même, une grandeur à deux indices est un tenseur covariant contravariant mixte ⎧ ⎫ ⎪ ⎪ ⎨ ⎬ ⎪ ⎪ ⎩ ⎭ et on la note ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ i j ij ij A A A . si l’on a inv V U Aij _{i j} = inv V U A_ij i j = inv V U A_.i_{j i} j =

On notera que la symétrie ne se conçoit que pour les tenseurs covariants ou contravariants. Examinons à présent les relations entre composantes convectées et composantes spatiales. On a

i ji ji j

U = ⋅u E_i = ⋅u J e_j =J u (17.1)

Par ailleurs, comme

ij ki lj k l ki kj E =E E_i⋅ _j =J J e e =J J , on a 1 1 − − = _{il jl} ij J J E et 1 1 1 1 i ij il jl mj il lm il E J J J− − J−δ J− = _j = ⋅ _m = _m = _l E E e e e , (17.2) donc 1 i i il l U = ⋅u E =J u− (17.3)

3. Statique des milieux continus

La statique des milieux continus repose sur la notion de contrainte. Précisons que les contraintes sont toujours définies dans la configuration réelle. Les différentes définitions que nous en donnerons ne diffèrent que par le système d’axes utilisé ou par une petite correction scalaire. Contrairement à une opinion répandue, il n’y a donc pas à proprement parler de contraintes lagrangiennes et de contraintes eulériennes, mais un seul tenseur de contraintes, que l’on peut exprimer dans différentes bases.

Adoptons d’abord le système d’axes spatial

{

e e e₁, ₂, ₃

}

. La force df passant par un élément dS’ de surface réelle est décomposée en

i

df

= _i

df e

On définit alors le vecteur traction de surface

' dS df

t i

i =

Si n' est la normale unitaire à cet élément de surface, on décompose alors t_i en

ji j i n

t = ' τ

où τ_ji sont les contraintes dans le système spatial ou contraintes eulériennes. Au total, l’élément de force s’exprime donc par

'_{j ji} '

n τ dS

= _i

df e (18)

La même décomposition vaut pour les forces intérieures, à condition de faire les coupes nécessaires. Ceci permet de définir les contraintes en tout point du corps.

Pour obtenir les équations d’équilibre, nous partirons du principe des travaux virtuels, qui stipule qu’à l’équilibre, le travail virtuel des forces extérieures (forces de volume et de

surface) égale le travail virtuel des forces intérieures (contraintes).

Soit δ le travail virtuel spécifique (c-à-d par unité de masse) des forces intérieures. w Le travail virtuel de ces forces sera donc

∫

= ' ' ' V dV w W ρ δ δ

On notera que δ est indépendant du système de coordonnées. Les forces massiques sont de w la forme ρ'gdV', et leur travail virtuel est donc

∫

' ' ' V i i u dV g δ ρ

Enfin, les forces de surface ont un travail

' ' ' '_{j ji i} ' S S dS n τ δu dS ⋅ =

∫

dF u

∫

Le principe des travaux virtuels s’exprime donc par

∫

∫

Le dernier terme peut, par le théorème d’Ostrogradski, être mis sous la forme

(

)

∫

∫

+

∫

∂_∂ ∂ ∂ = ∂ ∂ ' ' ' ' ' ' ' ' V V V j i ji i j ji i ji j dV x u dV u x dV u x δ τ δ τ δ τ

On a donc, quel que soit le volume V’ considéré dans le corps continu,

∫

= ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∂ ∂ + ∂ ∂ + + − ' 0 ' ' ' ' ' V j i ji i j ji i i dV x u u x u g w ρ δ τ δ τ δ δ ρ (19) ce qui implique j i ji i j ji i i x u u x u g w ' ' ' ' ∂ ∂ + ∂ ∂ + =ρ δ τ δ τ δ δ ρ (20)

A ce stade, nous ferons appel à un second principe fondamental de la statique, à savoir, que

dans un corps rigide, les forces intérieures ne travaillent pas. Il en découle évidemment que, chaque fois que, dans une partie V’ quelconque du corps, le déplacement virtuel est un mouvement de corps rigide, on doit avoir δw=0 pour cette partie du corps. Les

déplacements de corps rigide peuvent être des translations ou des rotations. Une translation virtuelle de corps rigide est de la forme

cte a ui =δ i =

δ , ce qui implique, par (19),

∫

_⎟⎟ = ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ' 0 ' ' ' V j ji i i dV x g a ρ τ δ

quels que soient V’ et δa_i. On en déduit l’équation locale d’équilibre de translation

0 ' ' + = ∂ ∂ i j ji g x ρ τ (21) qui ramène (19) à

∫

= ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∂ ∂ + − ' 0 ' ' ' V j i ji dV x u w τ δ δ ρ (22) et (20) à ui ji x w ' ' ∂ ∂ =τ δ δ ρ (23)

Une rotation virtuelle d’ensemble est de la forme cte w x e u_i = _ipqδω_{p q} δ _p = δ ' , , ce qui donne p ipj j i _e x u _δω δ ₌ ∂ ∂ ' On déduit donc de (21) ∫ = ' 0 ' V ji p ipj dV e δω τ

quels que soient V’ et δω , soit _p 0

= ji ipj

e τ , (24)

condition qui équivaut à la symétrie du tenseur τ_ij.

Cette description comporte l’avantage de la simplicité de la définition des contraintes. En particulier, les contraintes équivalentes de Von Mises se calculent aisément dans ce système d’axes. Par centre, les équations d’équilibre impliquent la dérivation par rapport aux positions rélles qui sont inconnues a priori. De plus, les directions des axes n’ont rien à voir avec les directions éventuelles d’anisotropie du corps déformé. Enfin, la densité du travail des forces intérieures a pour expression

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ = i j j i ij x u x u w ' ' 2 1 'δ τ δ δ ρ , (25)

mais comme les symboles de variation δ (typiquement lagrangiens !) ne commutent pas avec les dérivées spatiales, la grandeur entre parenthèse n’est pas la variation d’un tenseur simple.

3.2. Les contraintes dans la base convectée

Reprenons la décomposition dans la base convectée. Nous écrirons i

dF

= _i

df E

et définirons les tractions de surface

' dS dF T i i =

Notant alors N ' les composantes covariantes de la normale unitaire, nous écrirons, par _i

analogie avec la décomposition précédente, ji j i T N T = ' ,

ce qui définit les contraintes dans le système convecté T . Au total, l’élément de force ji

s’exprime donc par ' ji '

j N T dS

= _i

df E (26)

Pour trouver la relation entre T et ij τ_ij, exprimons N ' et _j E dans la base spatiale : on _i

obtient, par (3’) et (17.1) ' ji ' kj k li J n T J dS = _l df e ce qui, comparé à (18), '_{k kl} ' n τ dS = _l df e , conduit à ji li kj kl = J J T τ (27)

De la relation (25), on déduit donc

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ = k l l k ij lj ki x u x u T J J w ' ' 'δ δ δ ρ Or, m k ml m k l m l k u J u x x x u , 1 , ' ' δ δ δ ₌ − ∂ ∂ = ∂ ∂ ce qui conduit à

(

ml km mk lm

)

ij lj kiJ T J u J u J w 1 _, 1 _, ' 2ρδ = −δ + −δ

(

ki k j lj li

)

ij u J u J T δ , + δ , =

(

)

(

)

[

ki ki k j lj l j li

]

ij u u u u T δ _, + _, δ _, + δ + _, δ _, =

[

i j ji ki k j k j ki

]

ij u u u u u u T δ _, +δ _, + _,δ _, + _,δ _, =

ij ij T w δγ δ ρ' = , (28)

en introduisant le tenseur de GREEN

(

i j ji ki k j

)

ij u, u , u ,u , 2 1 + + = γ (29)

3.3. Les contraintes de KIRCHHOFF-TREFFTZ

Le travail des forces intérieures a donc pour expression

∫

=

∫

= ' ' ' ' ' V V ij ij V T wdV W ρδ δγ δ δ

On peut également l’exprimer dans la configuration de référence : notant que , ' ' dV dV ρ ρ = on a

∫

= V ij ij dV T W δγ ρ ρ δ '

Ceci suggère l’introduction des grandeurs ij ij T ' ρ ρ σ = (30)

appelées contraintes de Kirchhoff-Trefftz, qui permettent d’écrire

∫

= V ij ij dV W σ δγ δ (31)

On remarquera qu’en pratique, on rencontre essentiellement les deux situations suivantes : a) Les déformations sont petites. Alors, ρ ≈ ρ'

b) Les déformations sont grandes. Cela se produit dans le cas de la plasticité, où ρ ≈ en ρ' négligeant la petite déformation élastique, ainsi que dans le cas des matériaux très déformables comme le caoutchouc, qui sont incompressibles, c’est-à-dire que ρ ≈ . On ρ' constate donc que, dans les situations courantes, on peut pratiquement confondre les contraintes de Kirchhoff-Trefftz avec les contraintes dans la base convectée.

Nous allons montrer que ces nouvelles contraintes admettent une interprétation physique simple. Introduisant

ij ij T σ ρ ρ' = ,

dans la relation (26), on obtient ' '_{j ij} ' N ρ σ dS ρ = _i df E .

Or, le vecteur 'n dS', élément de surface orienté peut s’exprimer comme suit : en un point de la surface réelle, considérons deux vecteurs élémentaires tangents à la surface,

'=dxi _i, '=dy Ej _j

dP E dQ

Ils définissent un élément de surface 'dS'= '× '= _i× _j dx dyi j n dP dQ E E On a donc

(

)

' ' ' ' i j i j k ijk N dS =n dS ⋅E_k = E_i×E_j ⋅E_k dx dx =e J dx dx Il en découle ' q jpq ij J e ρ dx dxρ σ ρ = _i df E

et, comme on a toujours ρ= ρ'J, q jpq ij e dx dxρ σ = _i df E Mais

(

)

)

q jpq j e dx dxρ = dP dQ e× ⋅ =_j n dS

c’est-à-dire la surface orientée de référence, ce qui signifie que j ij

nσ dS

= _i

df E (32)

En d’autres termes, on décompose d’abord df dans la base convectée : i

dF

= _i

puis on définit les tractions de surface par dS dFi

, au moyen de l’élément de surface de

référence. Ensuite, on pose

ji j i n dS dF _σ = (34)

avec la normale unitaire de référence. Cette interprétation est due à Trefftz.

3.4. Equilibre en termes des contraintes de K.T.

Nous appliquerons encore le principe des travaux virtuels. Tout d’abord, le travail des forces intérieures s’écrit

∫

=

∫

= ' ' ' V V dV w dV w W ρδ ρδ δ .

Le travail virtuel des forces massiques a pour expression

∫

=

∫

' ' ' V V i i i i udV g u dV gδ ρ δ ρ

et celui des forces de surface a pour expression j ji surf S nσ δ dS ⋅ = ⋅

∫

δu dF

∫

Ei u et comme , '_{k i k ki k} x u J u δ δ δ ⋅ = = ⋅ i E u on obtient la condition

∫

=

∫

+

∫

V V S k ki ji j i i udV n J u dS g wdV ρ δ σ δ ρδ

qui se ramène aisément à

(

)

_, , 0 i i ji ki _j k ji ki k j V w g u J u J u dV ρ δ ρ δ σ δ σ δ ⎡_{− + + +} ⎤ ₌ ⎣ ⎦

∫

Le raisonnement est le même qu’en axes cartésiens. Tout d’abord, pour une translation de corps rigide, on obtient

(

)

, 0

i i ji ki _j V

x g J dV

ce qui conduit aux équations d’équilibre de Signorini

(

)

0 ,j+ i = ki jiJ ρg σ (35)

Pour une rotation de corps rigide de la forme

q p kpq k e x u δω ' δ = , on a évidemment qj p kpq j k e J u δω δ _, = , ce qui implique 0 = ji qj ki pqk pe J J σ δω ,

c’est-à-dire la symétrie du tenseur

ji ji ki qJ ji ki qJ qk J J J J T r τ ρ ρ ρ ρ σ ' ' = = = ,

ce qui n’a rien de particulièrement étonnant, d’ailleurs. Cette relation, explicitée en ji qi kj ji ki qjJ J J J σ = σ ,

peut être prémultipliée par J_rq−1J_sk−1, ce qui donne

sr rs σ

σ = (36)

L’équilibre de rotation se traduit donc encore par la symétrie des contraintes de Kirchhoff-Trefftz.

4. Interprétation du tenseur de Green

Considérons deux points voisins x et x dx+ . Leur distance dx est donnée par

i idx

dx

dx2 = .

Après déformation, ces points sont transportés en x' et x dx'+ ' et le carré de leur distance est devenu

i idx

dx dx'2 = ' '

Comme

(

ij i j

)

j j j i i x dx u dx dx' = '_, = δ + _, , on a

(

ij i j

)

(

ik ik

)

j k jk j k i i i idx dxdx u u dx dx dx dx dx' '− = δ + _, δ + _, −δ =2γ_jkdx_jdx_k (37)

Il est donc bien clair que le tenseur γjk mesure les variations de distance entre les points et s’annule si et seulement si le mouvement est rigide.

On peut présenter les choses autrement. En effet, on a encore '= _i dx_i dx E , si bien que

(

)

2 2 ' _{ij i j} dx − dx = E Ei⋅ j−δ dx dx , ce qui entraîne

(

ij ij

)

ij E δ γ = − 2 1 (38)

Considérons alors un terme direct, par exemple γ : on a _"

(

1

)

2 1 2 1 11= E − γ

Or, e a une longueur unitaire ; après déformation, sa longueur peut être écrite sous la forme ₁

1 1 ε = + 1 E Il vient alors

(

)

2 1 1 2 1 1 11 2 1 1 2 1 2 1 _{ε ε ε ε} γ = + + − = + (39)

et, si les déformations sont petites,

1 11 ε

γ ≈ (39’)

Passons aux termes croisés. Nous examinerons, pour fixer les idées, γ₁₂. Avant déformation, e et 1 e sont perpendiculaires. Ils cessent de l’être au cours de celle-ci et on a 2

(

)

12 11 22 2 cos , 1 2 1 2 γ γ γ ⋅ = = + + 1 2 1 2 1 2 E E E E E E

La variation α de l’angle entre les deux vecteurs vérifie donc

22 11 12 2 1 2 1 2 sin 2 cos γ γ γ α α π + + = = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −

Pour de petites déformations, on a sinα ≈α et 1+2γ₁₁ ≈1, 1+2γ₂₂ ≈1, ce qui donne

12

2γ α ≈ .

Dans maintes applications, il est utile de calculer la dilatation volumique

' ' ρ ρ = dV dV . Il est bien clair que c’est le jacobien J ; mais on peut encore l’exprimer en termes du tenseur de Green. En effet,

( )

J J dtmE dtm J2 = T = , avec ij ij ij E =δ +2γ

Utilisant le développement classique

(

ij ij

)

I

( )

ij I

( ) ( )

ij I ij dtm2γ −λδ =−λ3+λ₁ 2γ −λ ₂ 2γ + ₃ 2γ

où I1, I2, I3 sont les trois invariants d’un tenseur symétrique, on obtient ici, comme λ =−1,

) 2 ( ) 2 ( ) 2 ( 1 ) (G_ij I_{1 ij} I_{2 ij} I_{3 ij} dtm = + γ + γ + γ =1+2I₁(γ_ij)+4I₂(γ_ij)+8I₃(γ_ij) avec ii ij I₁(γ )=γ

(

ii jj ij ji

)

ij I γ = γ γ −γ γ 2 1 ) ( 2

( )

ij ij dtm I₃(γ )= γ

Dans le cadre des petites déformations, on peut se limiter au premier ordre, ce qui donne

(

)(

)

2 2 2 2 2 ' ' ' ) ( 2 dV dV dV dV dV dV dV dV O ii + − = − = + γ γ dV dV dV dV dV dV dV'− _⋅2 +( '− ) = = − ⋅_⎢⎣⎡ + − _⎥⎦⎤ dV dV dV dV dV dV ' 2 ' soit 0 ) ( 2 ' 2 ' 2 2 = − − − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − _{γ γ} O dV dV dV dV dV dV ii . On en déduit ) ( 2 1 1 ' γ γ2 O dV dV dV ii + + ± − = −

Pour 0γij = , la variation de volume est nulle, ce qui exclut le signe négatif devant le radical. Par conséquent, ) ( ) ( 2 1 1 ' γ γ2 γ γ2 O O dV dV dV ii ii + = + + + − = − .

Chapitre 2 : Lois constitutives

1. Expression eulérienne du premier principe de la thermodynamique

Le premier principe de la thermodynamique stipule que la variation d’énergie interne est égale au travail des forces appliquées augmenté de la chaleur reçue par le corps. La variation d’énergie interne s’écrit

∫

= ' ' ' V dV u U ρδ δ (1)

où δ est la variation d’énergie interne spécifique. A l’équilibre, nous savons que le travail u des forces appliquées s’écrit également

∫

= ' ' ' V dV w W ρδ δ (2)

Il nous reste à calculer la chaleur entrante. A cette fin, on exprime le flux entrant dδQ' par une portion de surface dS' sous la forme

' ' . ' ' q n dS Q dδ =−δ (3) ' q

δ étant la densité de flux de chaleur sortant. Il vient donc

∫

=−

∫

− = ' ' ' ' ' ' S S i in dS q dS n' . δq' dQ δ (4)

En description eulérienne, on a donc, pour tout V’,

∫

=

∫

−

∫

' ' ' ' ' ' ' ' ' ' V V S i in dS q dV w dV u ρδ δ δ ρ soit encore,

∫

∫

−

∫

∂_∂ ∂ ∂ = ' ' ' ' ' ' ' ' ' V V V i i j i ij dV q dV u dV u ξ δ ξ δ σ δ ρ ,

ce qui mène à l’équation locale

i i j i ij q u u ξ δ ξ δ σ δ ρ ∂ ∂ − ∂ ∂ = ' ' (5)

2. Passage à la description lagrangienne

∫

= V dV u U ρδ δ , ainsi que

∫

=

∫

= V V ij ij dV dV w w ρδ σ δγ δ

En ce qui concerne la variation de chaleur, notant que dV'=JdV , on a

∫

∫

− ∂ ∂ − = ∂ ∂ − = V V ji j i i i _{J J dV} x q dV J q Q ' δ ' 1 ξ δ δ

Admettons provisoirement l’identité de JACOBI

( )

1 =0 ∂ ∂ − ji j JJ x (6)

Elle permet d’écrire

(

1

)

, ' ji i i i j V V Q JJ q dV q dV x δ _{= −} ∂ −δ _{= −} δ ∂

∫

∫

,

en définissant le flux lagrangien j ji i JJ q q 1δ ' δ ₌ − (7) qui vérifie visiblement

∫

− = V i indS q Q δ δ (8)

Le premier principe se ramène alors à l’équation locale i i ij ij q u σ δγ δ , ρδ = − (9)

Il nous reste à démontrer l’identité (6). On a

( )

j ji j ji ji j x J J x J J JJ x ∂ ∂ + ∂ ∂ = ∂ ∂ − − −1 1 1 (10) Remarquant que kj lk k lk kl lk kl kl x J JJ x x JJ x J JJ x J J cof x J ∂ ∂ = ∂ ∂ ∂ = ∂ ∂ = ∂ ∂ = ∂ ∂ − − −1 2 1 1 ) ( ξ ,

il découle de l’identité

( )

0 1 1 = ∂ ∂ = ∂ ∂ + ∂ ∂ − − lj l l lk kj l kj lk x x J J x J J δ que l lk kj J x J JJ x J ∂ ∂ − = ∂ ∂ −1 , d’où j ji l lk ik l lk kj ji j ji _x J J x J J x J J JJ x J J ∂ ∂ − = ∂ ∂ = ∂ ∂ = ∂ ∂ − − − − − 1 1 1 1 1 δ ,

c’est-à-dire l’opposé exact du premier terme de (10).

3. Principe d’équilibre local et entropie

A ce stade, il est nécessaire d’introduire le principe d’équilibre local. A priori, un corps continu dans lequel s’écoule de la chaleur n’est pas en équilibre – la température, par exemple, varie d’un point à l’autre. Intuitivement, en découpant le corps en fractions très petites, on verra les différentes propriétés physiques d’un morceau donné varier de moins en moins, et on pourra finalement les considérer comme à peu près uniformes dans ce morceau. Mais pour pouvoir appliquer à un petit morceau de volume dV les relations classiques de la thermodynamique, il faudra que ses dimensions soient encore suffisantes pour pouvoir la considérer comme un système comportant un grand nombre de particules. Cette possibilité fait l’objet d’un postulat, dit principe de l’équilibre local, dont la validité n’est prouvée que par le bon accord avec l’expérience des conclusions qu’on en tire. Pratiquement, l’application de ce principe n’est discutable qu’en présence de quasi-discontinuités comme les ondes de choc, qui se produisent sur une longueur de quelques parcours moyens seulement.

Dans le cadre de cette hypothèse, il est possible de définir localement une entropie

sdV

ρ et une température absolue T telles que

s T w

u _ρδ e _{ρ δ}

ρδ = + , (11)

où δwe représente la partie élastique du travail. La décomposition d

e _w

w

u ρδ ρδ

ρδ = +

en travail élastique et travail dissipatif dépend du phénomène particulier pris en compte : viscosité, plasticité, etc…

i i d _q w s Tδ ρδ δ _, ρ = − (12) 4. Corps thermoélastique

Nous dirons qu’un corps est thermoélastique si le travail dissipatif est nul, 0

= d

w

δ (13)

et s’il existe des relations de la forme

∑

= _ij ij (γ,T ) σ , (14) pouvant s’inverser en ) , ( T ij ij σ γ =Γ (15)

Les relations (14) et (15) se différencient en dT d H dσ_ij = _ijkl γ_kl−β_ij (16) et dT d B dγ_ij = _ijkl σ_kl +α_ij (17)

Ces deux relations ne seront compatibles que si

dT dT H d B H dσ_ij = _{ijkl klmn} σ_mn + _ijklα_kl −β_ij , ce qui implique kl ijkl ij ijkl ijkl H H B = − β = α , 1 (18)

Les grandeurs H sont appelées modules élastiques. Les _ijkl α_ij sont les coefficients de

dilatation thermique et on donne aux (−β_ij) le nom de contraintes de bridage par (degré)

Kelvin.

5. Déformations isothermes et isentropiques

Imaginons une déformation menée à ce point lentement qu’à chaque instant, on laisse au corps le temps d’échanger la chaleur nécessaire pour maintenir sa température constamment égale à celle de l’ambiance. Ces conditions définissent ce que l’on appelle une déformation

kl ijkl ij H δγ

δσ =

et l’énergie libre, définie par ) (u Ts f = ρ − ρ (19) vérifie w T s f σ_ijδγ_ij δ σ_ijδγ_ij ρδ ρδ = − = = (20)

Dans une déformation statique, le travail est donc la différentielle totale de l’énergie libre. Il en découle en particulier klij kl ij ijkl H f H = ∂ ∂ ∂ = γ γ ρ ) ( 2 , (21)

relation qui, ajoutée aux conditions jikl

ijkl H

H = et H_ijkl =H_ijlk (22)

qui découlent naturellement de la symétrie des contraintes et déformations, ramène le nombre de modules différents à 21 au maximum.

Le fait que le travail de déformation soit une différentielle totale porte le nom d’hyperélasticité [5]. Nous venons donc de voir que les déformations isothermes d’un corps thermoélastique sont hyperélastiques.

Il découle de (11) que l’hyperélasticité est également réalisée lors des déformations isentropiques. Les vibrations à relativement haute fréquence des solides peuvent approximativement être considérées comme isentropiques, dans la mesure où la chaleur n’a pas le temps de s’écouler pendant une oscillation. Dans ce cas,

u

dw ρδ

ρ = , (23)

et c’est l’énergie interne qui sert de potentiel. On peut donc définir de nouveaux modules, les

modules adiabatiques, par

kl ij ad ijkl u H γ γ ρ ∂ ∂ ∂ = 2( ) , (24)

à utiliser dans l’étude des vibrations rapides. Pour les obtenir, il suffit d’exprimer dans (16) la variation de température à l’aide de la condition δs=0. Ceci peut être réalisé de deux manières :

T T s s s _ij T ij δ δγ γ δ γ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ = (25)

On remarque d’abord que T

T s T δ γ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂

est la chaleur absorbée par unité de masse à

déformation constante, c_vδT , ce qui donne

T c T s _ν γ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ (26) Pour calculer T ij s ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂

γ , on part du fait que l’énergie libre a pour différentielle

T s f σ_ijδγ_ij ρ δ

ρδ = − , ce qui entraîne la relation

ij ij T ij T s σ _β γ ρ γ + = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ − = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ (27) Il vient donc ij ij T T c s β δγ ρ δ δ ₌ ν ₊ 1 _{, (28)}

ce qui entraîne que, dans une déformation isentropique,

ij ij c T T β δγ ρ δ ν − = (29)

Introduisant cette valeur dans (16), on obtient

kl kl ij ijkl ij c T H β β δγ ρ δσ ν ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ + = soit kl ij ijkl ad ijkl c T H H β β ρ _ν + = (30)

(b) Une seconde approche consiste à considérer l’entropie comme une fonction des contraintes et de la température :

T T s s s _ij T ij δ δσ σ δ σ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ = (31) Ici, la grandeur T T s T δ σ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂

représente la chaleur absorbée par unité de masse à contraintes

constantes, c_pδT , ce qui donne

T c T s _{⎟ =} p ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ σ (32) On calcule T ij s ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂

σ en introduisant l’enthalpie libre

Ts u

g =ρ −σ_ijγ_ij −

ρ (33)

dont la différentielle vaut

T s d g γ_ij σ_ij ρ δ ρδ =− − , ce qui implique ij ij T ij T s γ _α σ ρ σ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ (34) On a donc ij ij p _T T c s α δσ ρ δ δ = + 1 (35)

si bien que, lors d’une déformation isentropique,

ij ij p c T T α δσ ρ δ =− (36)

Introduisant ce résultat dans (17), on obtient

kl kl ij p ijkl ij c T H α α δσ ρ δγ _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = −1 soit

( )

ij kl p ijkl ijkl ad c T H H α α ρ − = − −1 ₁ (37)

6. Relation entre cp et cv pour les solides

Les relations (30) et (37) sont évidemment équivalentes. Or, elles ne sont compatibles que si

( )

klmn im jn ad ad ijkl H H −1 =δ δ , soit, explicitement, jn im mn kl p klmn kl ij ijkl c T H c T H α α δ δ ρ β β ρ _ν ⎟⎟_⎠= ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + −1 , ce qui équivaut à 0 2 2 = − − _{ij mn kl kl} v p mn ij p mn ij v c c T c T c T _{β α β α} ρ α β ρ α β ρ soit à

(

)

1 _⎥=0 ⎦ ⎤ ⎢ ⎣ ⎡ − −c T c c c T kl kl v p mn ij p v α β ρ α β ρ

Ceci n’est possible que moyennant la relation suivante entre les chaleurs spécifiques :

T H c c_{p v ijkl}α_ijα_kl ρ 1 = − (38)

Expérimentalement, il est assez aisé de mesurer le cp des solides. Par contre, la valeur de cv

est pratiquement inaccessible à l’expérience et on ne l’obtient en pratique qu’en faisant usage de la relation ci-dessus.

Le résultat (38) est l’équivalent pour les solides de la relation de Mayer des gaz parfaits

r c c_p − _ν =

Elle implique l’inégalité v

p c

7. Stabilité locale [6]

Une portion infinitésimale du corps sera stable si, plongée dans une enceinte adiabatique, elle conserve son équilibre. Un système adiabatique est en équilibre si son entropie atteint un

maximum. Il faudra donc que δs=0 et δ2s<0, pour des perturbations infinitésimales. Partant de l’équation

s T u σ_ijδγ_ij ρ δ

ρδ = + ,

on constate que les variables sont u,γ_ij,s. Deux de celles-ci peuvent être prises comme variables indépendantes. Nous choisirons u et γ_ij, ce qui implique δ2u=0,δ2γ_ij =0. On a alors ij ij T u T s σ δγ ρ δ δ = 1 − 1 (39) et la condition δs=0 implique ij ij u σ δγ ρδ =

Différenciant (39), on obtient, après multiplication par ρ >0,

ij ij T u T s ρδ δ δ σ δγ ρδ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = 1 1 2

Il nous est à présent loisible d’exprimer les différentielles en termes des variables γ_ij et T : on a successivement • T T T δ δ 1⎟=− 1₂ ⎠ ⎞ ⎜ ⎝ ⎛ • _ij T ij ij ij T _Ts T T s u δγ γ ρ δ ρ δγ σ ρδ γ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + = =σ_ijδγ_ij +ρc_vδT +β_ijTδγ_ij • T T H T T T Tσij σijδ ijklδγkl βijδ δ 1 ⎟=− 1₂ + 1 − 1 ⎠ ⎞ ⎜ ⎝ ⎛ ,

ce qui mène à la condition

( )

2 1 0 2 2 _{=− − <} kl ij ijkl v _H T T T c s ρ δ δγ δγ ρδ (40)

Considérant des variations séparées de la température et des déformations, on obtient les conditions suivantes : 0 > v c (41a) 0 > kl ij ijkl

H δγ δγ (positive définition des modules élastiques) (41b) On notera que les modules adiabatiques vérifient

(

ij ij

)

ijkl ij kl v kl ij ijkl kl ij ad ijkl H C T H H β δγ δγ δγ ρ δγ δγ δγ δγ = + 2 ≥

Ils sont donc eux aussi définis positifs. Enfin, on déduit de (38) et (41b) que 0

> − _v p c

c (42)

8. Petits accroissements de température et déformations Lorsque les déformations sont petites,

1 << ij

γ

et que, de plus, les accroissements de température sont faibles, ,

, _o

o T

T

T = +θ θ <<

on peut développer l’énergie libre d’un corps thermoélastique en série de Taylor limitée au second ordre : θ ρ γ γ ρ ρ ρ o ij o ij o T f f T f f ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + = ( ,0)

(

3 2 2 3

)

2 2 2 2 2 , , , 2 1 2 1 _{γ θ ρ θ γ γ θ γθ θ} γ ρ γ γ γ γ ρ O T f T f f o ij o ij kl ij o kl ij + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ ∂ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ ∂ +

Identifions les dérivées qui apparaissent dans ce développement. Comme

T s f σ_ijδγ_ij δ ρδ = − , on obtient directement o o o ij o ij s T f f _{σ ρ ρ} γ ρ ⎟ =− ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ , .

Les σ sont les contraintes résiduelles, présentes dans le corps dans son état de référence ; _ijo s _o est l’entropie spécifique dans l’état de référence. Pour ce qui est des dérivées secondes,

2 ij o ijkl ij kl _o kl _o f H σ ρ γ γ γ ⎛ ∂ ⎞ ⎛∂ ⎞ = = ⎜ ⎟ ⎜ ⎟ ⎜_{∂ ∂} ⎟ _{⎝∂ ⎠} ⎝ ⎠ 2 ij o ij ij _o o f T T σ ρ β γ ⎛ ∂ ⎞ ₌⎛∂ ⎞ _{= −} ⎜ ⎟ ⎜ ⎟ ⎜_{∂ ∂} ⎟ _{⎝ ∂ ⎠} ⎝ ⎠ o o o o T c T s T f _{ρ ρ ν} ρ ⎟ =− ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ 2 2 Il vient donc

[

ijo ijo

]

ij ijklo ij kl o o v o o s _Tc H T f f ρ ρ θ ρ θ σ β θγ γ γ ρ 2 1 2 1 ) 0 , ( 2 + − + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − − ≈ (43)

Lorsque l’on s’intéresse principalement à l’aspect mécanique, on peut ordonner ces termes d’après leur degré d’homogénéité en les déformations. On écrira alors

), ( ) , ( ) (θ ρ₁ θ γ ρ ₂ γ ρ ρf = f_o + f + f (44) avec ⎪ ⎪ ⎪ ⎩ ⎪⎪ ⎪ ⎨ ⎧ = − = − − = kl ij o ijkl ij o ij o ij o o o o H f f T C s T f f γ γ γ ρ γ θ β σ γ θ ρ θ ρ θ ρ ρ θ ρ ν 2 1 ) ( ) ( ) , ( 2 1 ) , 0 ( ) ( 2 1 2 (45)

Les contraintes s’obtiennent par dérivation :

(

ijo ijo

)

ijklo kl T ij ij H f _{σ β θ γ} γ ρ σ _⎟⎟ = − + ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ = (46)

L’entropie est donnée par

ij o ij o o v o ij T c s T f s ρ ρ ρ θ β γ ρ γ + + = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ − = (47) On a donc

ij o ij o o v o ij o ij o o v o o o T c s T c s T s T Ts ρ θ ρ ρ θ ρ β γ ρθ ρ θ β θγ ρ = + = + + + + 2+ ) ( ,

ce qui entraîne, en notant que u(T_o,0)= f(T_o,0)+T_os_o,

(

ijo ijo o

)

ij ijklo ij kl o o v o v o c _Tc T H T u Ts f u ρ ρ ρ θ ρ θ σ β γ γ γ ρ 2 1 2 1 ) 0 , ( ) ( 2_⎟⎟+ + + ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + + = + = (48)

L’équation linéarisée d’une isentrope (s=s_o) s’obtient à partir de (47)

o T c ij o ij o o vθ +β γ = ρ soit ij o v o o ij c T γ ρ β θ =− (49)

En réintroduisant cette valeur dans (44), on obtient

kl ij o kl o ij vo o o ijkl ij o ij o C T H O T u u β β γ γ ρ γ σ ρ ρ _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + = 2 1 ) , ( ,

où se retrouvent les modules adiabatiques sous forme linéarisée.

9. Milieux élastiquement isotropes

Un milieu est élastiquement isotrope si, en l’absence de contraintes résiduelles et de gradients thermiques, sa densité d’énergie libre a une expression indépendante du système d’axes. Elle ne peut donc dépendre que des trois invariants I₁(γ),I₂(γ),I₃(γ) du tenseur des déformations. En se limitant à une expression quadratique, la seule forme possible est

2 2 1 2 AI BI f = + ρ (50)

ou, ce qui est équivalent,

2 2 1 2 2 2 I GÎ K f = − ρ , (51)

où Î est le second invariant du déviateur ₂ γ_ij γ_ij γ_llδ_ij 3 1 ˆ = −

(

ii jj ij ji

)

ij ij ij ij kk ii I γ γ γ γ γ γ γ γ γ γ 6 1 2 1 ˆ ˆ 2 1 ˆ ˆ ˆ ˆ 2 1 ˆ 2 = − =− =− + (52)

L’avantage de l’expression (52) est que I et 12 (−Iˆ2) peuvent s’annuler séparément, que tous deux sont positifs et qu’en outre, l’annulation simultanée de ces deux grandeurs assure la nullité du tenseur γ_ij. Pour assurer la stabilité locale, il faudra donc que

K >0, G>0 (53) Explicitement, on a donc ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ₊ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = K G _{kk ll} G _{kl kl} f γ γ γ γ ρ 2 3 2 2 1 2 , ce qui entraîne ij ij kk ij K G γ δ Gγ σ 2 3 2 + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = (54) et kl ij jl ik ijkl G K G H δ δ ⎟δ δ ⎠ ⎞ ⎜ ⎝ ⎛ − + = 3 2 2 (55)

Pour chercher la relation inverse de (54), notons d’abord que

kk ll kk ll K G γ Gγ Kγ σ 3 2 3 3 2 _{⋅ + =} ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = (56) ce qui implique ij ij kk ij _K G G K γ δ σ σ 2 3 3 2 + − = et ij ll ij ij kk ij ij K G G KG G K G σ δ σ σ δ σ γ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ − + − − = 9 1 6 1 2 1 6 3 2 2 (57)

L’usage courant des ingénieurs veut que l’on utilise plutôt les modules E et ν , appelés respectivement module de Young et coefficient de Poisson, tels que

ij ll ij ij E E σ δ ν σ ν γ =1+ − , (58)

K G E G E 9 1 6 1 2 1 1+ν ₌ ν _{= −} (59) On en déduit directement K G E E E 9 1 3 1 1 1 + = − + = ν ν (60)

En vertu des conditions (53), le module de Young E est positif. Quant au coefficient de Poisson, il vaut

1 3 2 3 2 1 1 3 1 2 3 9 1 3 1 9 1 6 1 + − = + − = + − = ⋅ = G K G KG K K G K G E E ν ν

C’est donc une fonction croissante du rapport

G K

qui, pour =0

G K

, vaut (-1) et, pour ∞ → G K , tend vers 2 1 . On a donc 2 1 1< < − ν (61)

Les relations (59) s’inversent en

) 2 1 ( 3 ) 1 ( 2 +ν = − ν = E K E G (62) et ν ν ν ν) 2 1 2 2 1 ( 3 6 9 1 6 1 6 3 2 − = − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ = − G E G E K G KG G K , ce qui implique ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + = _{ij ll ij} ij G γ ν _νγ δ σ 2 1 2 (63) Les modules valent donc

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + = _{ik jl ij kl} ijkl G H δ δ ν ν δ δ 2 1 2 (64)

[

ik jl ij kl

]

ijkl E H− = +ν δ δ −νδ δ ) 1 ( 1 1 (65) 10. Isotropie thermoélastique

Nous parlerons d’isotropie thermoélastique si, en plus des conditions précédentes, on a ij

ij αδ

α = , (66)

c’est-à-dire que la dilatation thermique est identique dans toutes les directions. On a alors

ij ij ij kl ijkl ij H αδ Gαδ K G αδ Kαδ β 3 3 3 2 2 ⎟⋅ = ⎠ ⎞ ⎜ ⎝ ⎛ − + = = (67)

Dans ce cas, la relation entre modules adiabatiques et modules isothermes s’écrit à partir de (30) kl ij v ijkl ad ijkl K C T H H α δ δ ρ 2 2 9 ⋅ = − soit ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = = v ad ad C T K K K G G ρ α2 9 1 , (68) A partir de (37), on a

( )

ij kl p ijkl ijkl ad C T H H α δ δ ρ 2 1 1 − = − − − , ce qui donne p ad ad _C T K K G G ρ α2 9 1 1 , 1 1 _{= = −} (69) On déduit alors de (60) p ad C T E E ρ α2 1 1 _{= −} , soit

p ad C T E E E ρ α2 1− = , (70)

formule obtenue par Lord KELVIN en 1878 [8]. On déduit de (59) p ad ad c T E E E ρ α ν ν 2 1 1 1 1 − = = + + et p p p ad c T E c T E C T E ρ α ρ α ν ρ α ν ν ₂ 2 2 1 1 1 1 − + = − − + = (71) Enfin, ρ α α β ρ T K T c c_{p v ij ij} 2 9 1 = = − , (72)

ce qui implique d’ailleurs par (68)

K K c c ad v p ₌ (73)

11. Relations empiriques pour les chaleurs spécifiques [7]

A la suite d’expériences effectuées sur divers métaux, GRÜNEISEN a établi en 1908 la loi approchée suivante : la chaleur spécifique à pression constante c et le coefficient de _p

dilatation thermique varient suivant la même loi. En d’autres termes, le rapport

p c

A= α (74)

est une constante du métal, indépendante de la température. En fonction de la constante de Grüneisen, on obtient

⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ = − − + = − = ρ ρ ρ ν ν ρ ρ T c KA c c T c EA T c EA T c EA E E p v p p p ad 2 2 2 2 2 9 1 1 (75)

Comme K et ρ varient peu avec la température, on peut écrire ,

T BC c

c_p − _v = _p (76)

en considérant B comme constant.

Mais il y a plus. LINDEMANN a montré en 1910 que le produit

M f o

BT

B = (77)

où T est la température de fusion et M, la masse atomique, est approximativement constant _f pour tous les métaux, sa valeur étant

J kg

B_o =5,112.10−6 / (78)

ce qui permet d’écrire

⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ − − − + = − − = = − f p o f p o f p o ad f p o p T T c B T T c B T T c B E E T T c B c c M M M M ad 3 2 1 1 3 2 1 3 2 1 1 2 ν ν ν ν ν ν (79)

ρ

c c c_p − _v

. Ainsi, pour l’aluminium, on a

M = 27 kg, cp = 896 J/kg/K, Tf = 931,2 K, Et, à 293,15 K, K kg J c c_{p v} 34,88 / / 2 , 931 15 , 293 896 27 10 112 , 5 ⋅ 6⋅ ⋅ 2⋅ = = − − et 039 , 1 , 10 893 , 3 ⋅ 2 = = = − ₋ v p ad p v p C C K K c c c

Par la formule exacte (72), on aurait trouvé

040 , 1 , 10 . 027 , 4 , / / 08 , 36 − = 2 = = − − K K c c c K kg J c c ad p p p ν ν

La différence des modules de Young est encore plus faible : le calcul donne 004 , 1 = E E_ad .

12. Lois d’écoulement thermique

En description eulérienne, la loi de Fourier s’écrit

j ij i T q ξ λ ∂ ∂ − = ' ' & ,

où q'& sont les densités de flux par unité de temps. On passe aisément à la description _i lagrangienne en s’aidant de la définition (7), transformée ici en

k ik i JJ q q& = −1 &' . On a donc l kj lj ik l j l kj ik i T JJ J T x JJ q , 1 1 1 ' , ' λ ξ λ − − − ₌₋ ∂ ∂ = &

j ij i T q& =−λ , (80) à condition de poser kl jl ik ij JJ J ' 1 1 λ λ ₌ − − (81) La transformation inverse s’écrit

kl jl ik ij J J J λ λ' = 1 (82)

Pour autant que les déformations soient petites, il est raisonnable de supposer la constance des λ_ij lors de la déformation. La variation subséquente des λ'_ij exprime alors la variation des axes d’anisotropie. Dans le cas isotrope, on a

ij ij λδ λ = et λ λ λ_{ij ik jk} G_ij J J J J 1 1 ' = = ,

avec, pour de petites déformations, ),J =1+γ_ii +O(γ2 G_ij =δ_ij +2γ_ij, soit

))λ'_ij=λδ_ij(1+O(γ .

13. Positive définition des coefficients de conductivité thermique La variation d’entropie s’écrit

∫

∫

∫

∫

∫

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = − = = V V V S V i i i i i i i i _dV T q dS T n q dV T q dV T q dV s S , , , 1 & & & & & & ρ

Le premier terme du dernier membre représente le flux d’entropie entrant par unité de temps dans le corps. Le second terme est donc la production d’entropie, nécessairement positive dans tout volume :

∫

⎟ =−

∫

> ⎠ ⎞ ⎜ ⎝ ⎛ = V V i i i i dV T T q dV T q 1 ₂, 0, , & & P

ce qui implique par (80) , , , 2 2 1 0 i i ij i j q T T T T T λ − & = > , (83)

quel que soit le gradient non nul de température. Cette condition ne sera vérifiée que si la matrice d’éléments λ_ij est définie positive. Notons qu’elle est symétrique en vertu du principe de réciprocité d’ONSAGER [6,9].

14. Bilan thermique

Les contraintes étant élastiques, on déduit de (12) et (80)

( )

ij j _i i i T q s T , , , λ ρ _{&= &}− = (84)

Tenant compte de la différentielle (28) de l’entropie, on obtient

( )

ij j _i ij ij vT T T c , , λ γ β ρ &+ _& = (85)

On constate donc que le champ des températures dépend de la déformation. D’une façon équivalente, on peut développer l’entropie en termes de la température et des contraintes, ce qui donne

( )

ij j _i ij ij pT T T c , , λ σ α ρ &+ _& = (86)

Dans le problème du calcul des contraintes thermiques d’une structure, les conditions aux limites thermiques sont données. Il s’agit de calculer le champ des températures et les contraintes qui en résultent. En imaginant le corps parfaitement bridé, on aura γ_ij =0 et

( )

ij j _i vT T c , , λ ρ &=

A l’autre extrême, si les déformations étaient parfaitement libres et compatibles, on aurait 0 = ij σ et

(

ij j

)

_i pT T c , , λ ρ &=

La solution exacte est intermédiaire. Comme C_ρ ≈C_v, on voit que l’on peut, dans ce problème, négliger le couplage.

Mais le couplage est responsable d’un certain nombre de phénomènes secondaires, parmi lesquels l’amortissement par thermoconduction, qui fera l’objet du chapitre 3.

3. AMORTISSEMENT PAR THERMOCONDUCTION

1. Introduction

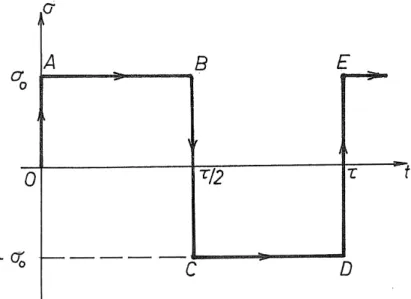
L’existence d’échanges de chaleur a notamment pour effet d’introduire un certain amortissement structural, même si les contraintes sont élastiques. Pour faire comprendre le phénomène, considérons un système unidimensionnel soumis à un cycle de contraintes rectangulaire de période longue (fig. 3).

Figure 3 – Sollicitation en escalier à longs paliers

La variation de contrainte étant instantanée, elle sera isentrope. Dès lors, la température variera, diminuant lors de l’extension et augmentant lors de la compression. Les paliers sont supposés suffisamment longs pour que l’équilibre thermique puisse se réaliser. Examinons ce qui se passe sur le diagramme (σ,γ) (fig. 4).