Analogical proportions: From equality to inequality

Any correspondence concerning this service should be sent

to the repository administrator:

tech-oatao@listes-diff.inp-toulouse.fr

This is an author’s version published in:

http://oatao.univ-toulouse.fr/24804

To cite this version:

Prade, Henri and Richard, Gilles

Analogical proportions: From equality to inequality. (2018)

International Journal of Approximate Reasoning, 101. 234-254.

ISSN 0888-613X

Official URL

DOI :

https://doi.org/10.1016/j.ijar.2018.07.005

Open Archive Toulouse Archive Ouverte

OATAO is an open access repository that collects the work of Toulouse

researchers and makes it freely available over the web where possible

Analogical

proportions:

From

equality

to

inequality

✩

Henri

Prade

a,b,∗

,

Gilles

Richard

a

a _{IRIT,CNRS&UniversitéPaulSabatier,118routedeNarbonne,31062ToulouseCedex09,France} b _{QCIS,UniversityofTechnology,Sydney,Australia}

a b s t r a c t

Keywords:

Analogicalproportion Similarity Dissimilarity Booleanlogic Multiple-valuedlogic

Algorithmiccomplexity

Analogical proportions are statements ofthe form a is to b as c is tod. Such expressions compare the pair (a, b)with the pair (c, d). Previouspapers have developed logical modelings ofsuch proportions bothinBooleanandinmultiple-valuedsettings.They emphasizeareadingoftheproportionas“theway a and b differ is the same as c and d differ”. The ambition of this paper is twofold. The paper first provides a deeper understanding and further justificationsof theBoolean modeling, beforeintroducing analogicalinequalities,where “as” isreplacedby “asmuchas” inthecomparisonof two pairs. Froman abstract viewpoint, analogical proportions are supposed to obey at least three postulates expressing reflexivity, symmetry, and stability under central permutation. Nevertheless these postulates are not enoughtodetermineasinglemodel andaminimalityconditionhastobeaddedasshowninthispaper. These models areorganizedina completelatticebased onset inclusion.This leads us todiscuss lower and upper approximations of the minimal model. Apart from being minimal, this model can also be evaluated in terms of Kolmogorov complexity via an expression reflecting the intended meaning of analogy. We showthat thesix Boolean patternsof the minimalmodel thatmakeBoolean analogy true minimize this expression. Besides, analogical proportions extend to 4-tuples of Boolean vectors. This enablesustoexplain whyanalogicalproportionsalsoreadsintermsofsimilarity(ratherthandifference, i.e., dissimilarity): a and d share the same presence or absence of features as b and c. Moreover, we establish a link between analogical proportion and Hamming distances between components of the proportion. We also emphasize that analogical proportions are pervasive in any comparison of two vectors a and d that implicitly inducethe existence of “intermediary” vectors b and c forming together suchaproportion.Thesimilarityreading andthedissimilarityreadingofaBooleananalogicalproportion are no longer equivalent in the multiple-valued setting, where they give birth to two distinct options that are recalled. These options are also discussed with respect to their capability to handle so-called “continuous”logicalproportionsoftheforma istob asb istoc involvingsomeideaof “betweenness”.In allthepreviouslyinvestigated issues,thepairsinvolvedinthe4-tuples werecompared viaequalitiesof similarities or equalities ofdissimilarities. This observation suggests to also consider statements of the form “a isto b atleast as muchas c is to d”, leading tothe concept of“analogical inequalities”. Thus, instead of expressing equality between differences or similarities, as it is the case for analogical proportions, it is also interesting to express inequalities between such differences or similarities. Starting from the modeling ofanalogical proportions,we investigate thelogical modeling of analogical inequalities, both in the Boolean and in the multiple-valued cases, and discuss their potential use in relation with some recent related work in computer vision.

✩ ThispaperispartoftheVirtualspecialissueonthe14thEuropeanConferenceonSymbolicandQuantitativeApproachestoReasoningwithUncertainty

(ECSQARU2017),EditedbyAlessandroAntonucci,LaurenceCholvyandOdilePapini.

*

Correspondingauthorat:IRIT,CNRS&UniversitéPaulSabatier,118routedeNarbonne,31062ToulouseCedex09,France. E-mailaddresses:prade@irit.fr(H. Prade),richard@irit.fr(G. Richard).

1. Introduction

Comparative thinking plays a key role inour assessment of reality. This has been recognized for a long time. Making comparisoniscloselyrelatedtosimilarityjudgment[45] andanalogymaking[12,17].Analogicalproportions,i.e.,statements of the form a is to b as c isto d,usually denoted a:b::c:d,provides a well-known way for expressing a comparative judgment betweentwopairs(a,b) and(c,d);see,e.g.,[14,15].Suchastatementsuggeststhatthecomparison(intermsof similarity and dissimilarity)ofthe elementsofpair (a,b) yields thesamekind ofresultaswhen comparingtheelements ofpair(c,d)[39].

Analogicalproportionsconstitute akeynotionforformalizinganalogicalinferencebyrelyingonthefollowingprinciple: if such proportionshold on anoticeable subsetofknown features used for describingthefour items,theproportion may still hold onother features aswell,which mayhelp guessing theunknown values ofd onthese otherfeatures from their values on a, b, and c. The interest of such inference mechanism has been recently pointed out in machine learning for classification problems [2,28,4], and in visual multiple-class categorization tasks for handling pieces of knowledge about semantic relationships between classes. More precisely in thislatter case, analogical proportions are used for expressing analogies between pairs of concrete objects in the same semantic universe and with similar abstraction level, and then this gives birth to constraints that serve regularization purposes [18]. Besides, the power of analogical proportion-based inferencehas beenalsoillustratedonthesolvingofIQtests[6].

Different formal modelings of analogicalproportions have been proposed in thelast decades. Quite early, a theory of analogical reasoning,where elements arerepresented aspointsin multidimensionalEuclideanspaces, and analogical pro-portions are represented byparallelograms insuch spaces, has been proposed in [41]. This geometric view is atwork in the above-mentioned reference invisual categorization.An empiricalmodeling ofanalogy making,where thefourth term d of an analogical proportion a:b::c:d to be completed is obtained by minimization of the difference of changes be-tween a and b and between c and d is atwork in the programs ANALOGY [10] and COPYCAT [16]. Later on, a machine learning-oriented view where analogical proportions are represented in terms ofKolmogorov algorithmic complexity has been presentedin [5].Asimilar,butsimplified modeling,stillexpressingthata andb differasc andd differ,canbefound in[1],wherethecomplexitiesofthetargetandsourceuniverseshavenottobetaken intoaccount, sincetheyareidentical inthislattercase.Quitemorerecently,asetofvariousalgebraicmodelingsofanalogicalproportionshavebeen introduced and discussedin[25,29,30,46].Followingtheseworks,alogical modelinghasbeen proposed[31,32].This logicalmodeling makesclear that theanalogicalproportion holdsifand only ifa differs fromb asc differsfrom d andvice-versa. Thisfits quite well with what issuggested by theusual reading of theproportion that states that “a is to b as c is to d”, where “a is to b”(resp. “c istod”) refers toan implicitpairwisecomparison,and the central“as”to anidentity.This leadsto a Booleantruthtablefora:b::c:d which makestheexpressiontrueforsixpatternsofvaluesofthe4-tuplea,b,c,d among 24=16 possiblepatterns. Itcaneasilybecheckedthat theexpected postulates(reflexivity, symmetry,formalpermutation) aresatisfiedbythemodeling.However,onemaywonderifothermodelingswouldmakesenseforananalogicalproportion, and ifotherjustificationscouldbefoundfortheabove-mentionedmodeling.Thisisoneofthegoalsofthispaper.

Thepaperfirst investigatesnewjustifications oftheBooleanexpressionofananalogicalproportion. First, startingfrom the core postulates supposed to be satisfied by an analogical proportion, and agreed by everybody for a long time, we exhibit alltheBoolean modelscompatible withthem. Thereareseveral ones, butthesmallest modelis thebasicBoolean expressionofananalogicalproportionpreviouslyproposed.Thissmallestmodelisindeedcharacterizedbythesixexpected Booleanpatterns.Anotherunderstandingofanalogicalproportion,intermsofsimilarity,canbestatedas“whata andd have incommon(positivelyandnegatively),b andc haveitalso”.ItcorrespondstoaBooleanformulathatturnstobeequivalent to the one inducedbythedifference-based reading,since thesametruth-table is obtainedin bothcases, asobservedfor about tenyearsnow[32].Wealsoprovideadirectproofand anintuitiveexplanationofthisfact.

Moreover,wetrytoevaluatethecognitivesignificanceoftheproposedBooleanmodelingofananalogicalproportionin termsofalgorithmiccomplexity (i.e.,Kolmogorovcomplexity)and showthatitisalsominimalamong allBooleanpatterns withrespecttoanalgorithmiccomplexity-baseddefinitionofananalogicalproportion.Indeed algorithmiccomplexity mea-suresakindofuniversalinformationcontentofaBooleanstring.Despiteitsinherentuncomputability,thereexist powerful tools forcomputing goodapproximations.Kolmogorovcomplexity hasbeen provedtobeofgreatvalue indiverse applica-tions: for example, indistance measures [3] and classificationmethods, plagiarism detection,network intrusion detection [13],andinnumerousotherapplications[27].

As already said, analogical proportions express the identity of the results of the comparisons of two pairs. We may wonder if an inequalityinstead of anequality would make sense as welland wouldbe useful for expressing constraints of the form “a is to b as much asc is to d”. In fact, constraints ofthe samekind, but stated interms of distances, have been shown to beusefulfor categorization tasksin computer vision for representing pieces ofknowledge stating relative comparisons between quadruplets of images, feature by feature [23,24]. Interestingly enough, it has been also recently

noticed thatsimilarrelationsintermsofcomparisonofpairswerealsopresent inmultiplecriteriaanalysisforexpressing, for instance,thatthe“difference”betweentwoevaluationvectorson acriterionissmallerthan(i.e.,doesnotcompensate) the “difference” between thevectors on the restof the criteria [34]. This recent emergence of theinterest for inequality constraints between pairs of items motivates the introduction of the notion of “analogical inequalities” and their formal study,inrelationwiththeBooleanaswellasthemultiple-valuedmodelingofanalogicalproportions.

2. Summary

Thepaperisbasedontwoconferencepapers[37,38] dealingrespectively:

– on theonehand, withlogicalandalgorithmiccomplexityjustifications fortheBooleanmodelingofanalogical propor-tions,and

– ontheotherhand, withthenotionof“analogicalinequalities”.

Thepapergathersthismaterialinaunifiedway.Italsosubstantiallyextendsitinvariousdirectionsinparticular regard-ingdiverseaspectsofBooleanproportionsnotpreviouslyconsidered:i)directproofoftheequivalencebetweenthe2basic expressions ofanalogical proportions (Subsection 3.4); ii)Investigation of thevalidity of thevectorial extension for these formulas (Subsection5.1);iii)Operationalexplanationoftheequivalencebetweenthese formulas(Subsection 5.2); iv)Link betweenanalogicalproportionsand Hammingdistance(Subsection5.3);v)Emergenceofanalogicalproportionsfromitems comparison (Subsection 5.4); vi) Formaldiscussion ofthe modelingof continuous analogicalproportions (Subsection 6.2). Moreover, thepresentationoftheresults oftheconferencepaperhas beensomehowimprovedbygivingmoredetailsand providingextensivediscussionsofrelatedworks.

We now describethe general organization and contents of the article. We first start in Section 3with the postulates governing analogical proportions and study the Boolean modelings of analogy1 compatible with them. This investigation lays barealattice ofBoolean modelsforanalogicalproportions, whichincludesaminimalmodelcorrespondingtotheone introducedin[31] andsubsequentlydeveloped,aswellasanothermodelofparticularinterestproposedalongtimeagoby Klein [20,21].Whiletheminimalmodelmakestheproportiontrueforsixinput patterns,Klein’soperator istrueforeight. Wealsostudylowerapproximationsoftheminimalmodelwhicharetrueforfourinputpatternsonlyandwhichonlysatisfy apartofthepostulates.TheminimalmodelcanbenaturallyassociatedwithasyntacticBooleanformulaexpressingexactly that the difference ofa withb is thesameasthedifference of c withd and vice-versa.We investigate otherremarkable, logically equivalent,expressions oftheanalogicalproportion.Inparticular, weestablish thattheanalogicalproportion also fitswiththestatementthat“whata andd haveincommon(positivelyandnegatively),b andc haveitalso”.Thediscussion ofthemeaningfulsyntacticforms isimportantfordetermining theformsthatare appropriatefor anextension to Boolean vectors, andthentomultiple-valuedlogic.

In Section 4, we first briefly review the main definition and theorems of Kolmogorov complexity. Once we have the maintools,weareinapositiontogiveaKolmogorovcomplexity-based definitionofanalogyand toexperimentinorderto empirically validatetheminimalmodel-based definition.Section 5isdevotedto analogicalproportion definedfor Boolean vectors. This setting makes easierthe understanding of theequivalence between the difference-based and the similarity-basedreadingsofanalogy.Moreover,weestablishlinksbetweenvectorialanalogicalproportionandconstraintsexpressedin termsofHammingdistancesbetweencomponentsoftheproportion.Wealsopointoutthatanalogicalproportionsare per-vasiveinanycomparisonoftwovectors, saya andd,thatimplicitlyinducetheexistenceof“intermediary”vectors b andc formingtogetheraproportiona:b::c:d.InSection6,twomeaningfulextensionsofBooleandefinitionstomultiple-valued proportions, agreeingrespectively withthedifference-basedand the similarity-basedreadings ofanalogy, arerecalledand putintheperspective oftheprevioussections.Thencontinuousanalogicalproportions,i.e.,statements oftheform“a isto b as b istoc” whicharetrivializedintheBooleansetting,but makessense formultiple-valuedproportions,arediscussed. With all thisnecessary background on Boolean and multiple-valued proportions, we are equipped for finallyintroducing “analogical inequalities” inSection 7, intheBoolean and then inthemultiple-valued settings. Inboth cases,weestablish some expected properties,includingtransitivity. Finally, wediscuss thepotential interestofsuch inequalities,on thebasis ofsomerecentrelatedworks.

3. Booleananalogicalproportions

At the time of Aristotle, the idea of analogicalproportion originated from the notion of numerical proportion. In that respect,thearithmetic proportionbetween4integers a,b,c,d,whichholdsiffa−b=c−d,isagood prototypeoftheidea of analogicalproportion, sincewecanread itas“a differsfromb as c differsfromd”, whichperfectly fitswith “a isto b asc is tod”. Thisarithmeticproportioncanbeeasily extendedover avectorspacelikeRn bykeepingthesamedefinition. It simply means the proportion holds in Rn iff the points a,b,c,d are the vertices of a parallelogram in a plan. In the following, we denote an analogical proportion between four ordered elements a,b,c,d as a:b::c:d. When considering Boolean interpretation wherea,b,c,d∈ {0,1},it is tempting tocarry on with the samedefinition as{0,1}_{⊂ R}, withthe inevitable drawback that difference is not aninternal operator in B= {0,1}.Nevertheless, if we drawthe truthtable (16 lines) correspondingtothisdefinition,wegetTable1highlightingthatonly 6among24=16 linesarevalidproportions.

Table 1

Booleanvaluationsfora:b::c:d.

a b c d a:b::c:d a b c d a:b::c:d 0 0 0 0 1 1 0 0 0 0 0 0 0 1 0 1 0 0 1 0 0 0 1 0 0 1 0 1 0 1 0 0 1 1 1 1 0 1 1 0 0 1 0 0 0 1 1 0 0 1 0 1 0 1 1 1 1 0 1 0 0 1 1 0 0 1 1 1 0 0 0 1 1 1 0 1 1 1 1 1 3.1. Postulateperspective

Taking inspiration from numericalproportions and froman abstractviewpoint, analogycan beviewed asaquaternary relation R,supposedobeyingthefollowingthree postulates (e.g.,[25,29]):

1. ∀a,b,R(a,b,a,b) (reflexivity);

2. ∀a,b,c,d,R(a,b,c,d)→R(c,d,a,b) (symmetry);

3. ∀a,b,c,d,R(a,b,c,d)→R(a,c,b,d) (centralpermutation).

Some basicpropertiescanbededucedbyproperapplicationsofsymmetryand centralpermutation:

• ∀a,b,R(a,a,b,b) (identity);

• ∀a,b,c,d,R(a,b,c,d)→R(b,a,d,c) (insidepairreversing);

• ∀a,b,c,d,R(a,b,c,d)→R(d,b,c,a) (extreme permutation).

Infact,anotherlessstandardaxiomexpected fromanatural analogyis:

∀

a

,

b

,

x

,

R

(

a

,

a

,

b

,

x

) → (

x

=

b

) (

unicit y

)

All these propertiesfitwith theintuitionofwhatmaybeananalogicalproportion.Itcan bealsoeasilycheckedthat they aresatisfiedbythearithmeticproportiona−b=c−d (aswellaswiththegeometricproportion a_b =c_d).

Ifwenowfocuson_B= {0,1}asinterpretationdomain, R shouldbeinterpretedasasubsetof_B4_{.Removingtheempty}

set,leaves216−1 candidatemodels.Itisstraightforwardtogetabasicmodel:

• Byapplyingreflexivity,weseethat 0101,1010 shouldbelongtotherelationand0000,1111 aswellsincewemayhave a=b,and

• Centralpermutationthenleadstoadd0011 and1100.

Thus, we getthemodel Ä0= {0000,1111,0101,1010,0011,1100}, which isalsostable undersymmetry. ObviouslyÄ0 is thesmallest Booleanmodelforanalogyasevery modelshouldincludeitasasubset.

3.2. LatticeofBooleanmodels

Infact,thereismorethanonemodelofanalogyinaBooleaninterpretation.Wehavethefollowingresult:

Property1.Thereareexactly8modelsofanalogy(i.e.,satisfyingthethreefirstpostulates)overB.Thereareexactly2modelsof analogysatisfyingthethreefirstpostulatesplusunicity.

Proof. Any model shouldinclude Ä0.Let us notethat a biggermodel shouldnecessarily havean even cardinality due to thefollowingfacts:

– Tobebiggerthan Ä0,itshouldcontainastrings containingboth0and 1.

– Thankstosymmetryorcentralpermutationaxioms,itshouldcontainthesymmetric cdab ofs=abcd andthecentral permutationacbd ofs:necessarily,oneofthese2stringsisdifferentfroms (otherwise,wegeta=b=c=d).

Sowehavetolookformodelsofcardinality8,10,12,14and16. Obviously_B4 _{ofcardinality 16isamodel,thebiggest}

one. Due totheaxioms, we haveto add toÄ0 subsets ofB4 that are stablew.r.t.symmetry and central permutation.We haveexactly:

– onesubsetwith2elements: S2= {1001,0110}

Fig. 1. The lattice of Boolean models of analogy.

i) S3= {1110,1101,1011,0111};

ii) S4= {0001,0010,0100,1000}.

SinceeverymodelhastobebuiltbyaddingtoÄ0 oneoftheprevioussubsets,wegetthefollowingmodelsforanalogy in_B:

1) one modelwith6elements:Ä0 (thesmallestone), 2) one modelwith8elements:

K l= Ä0∪S2= {0000,1111,0101,1010,0011,1100,0110,1001}

Aspreviouslymentioned,thismodelisduetoS.Klein[20]. 3) twomodelswith10elements:

– M3= Ä0∪S3= {0000,1111,0101,1010,0011,1100,1110,1101,1011,0111},

– M4= Ä0∪S4= {0000,1111,0101,1010,0011,1100,0001,0010,0100,1000},

4) twomodelswith12elements:

– M5=M3∪S2= {0000,1111,0101,1010,0011,1100,1110,1101,1011,0111,0110,1001},

– M6=M4∪S2= {0000,1111,0101,1010,0011,1100,0001,0010,0100,1000,0110,1001},

5) one modelwith14elements:

– M7=M3∪S4=M4∪S3= Ä0∪S3∪S4= {0000,1111,0101,1010,0011,1100,1110,1101,1011,0111,0001,0010,0100,

1000},

6) one modelwithexactly16elements:Ä= Ä0∪S2∪S3∪S4= B.

FinallyÄ0andK l satisfyunicitybutM3(containing1100and1101)andM4(containing0000and0001)donotsatisfy it.

Thisachievestheproof. ✷

Theset ofmodelsisalattice withbottomelement Ä0 andtopelement B,seeFig.1.As canbeseen,8modelsfitwith theaxiomsintheBooleancase,includingthe6-patternsmodelÄ0 andthe8-patternsmodelK l duetoKlein.However,itis natural toprivilege thesmallestmodel, theminimalone thatjust accountsfortheaxiomsand nothingmore.Besides,itis worthnoticingthat 4modelsarecodeindependent,whichmeans thattheyarestableif0and1areexchanged.Foragiven model M,thisisformallyexpressedas:

(

a

,

b

,

c

,

d

) ∈

M

=⇒ (¬

a

, ¬

b

, ¬

c

, ¬

d

) ∈

M

.

TheyareÄ0,K l,M7andÄ.Althoughcodeindependencyisnotapostulate,itseemstobeadesirablepropertyforanalogical

proportionsincetheencodingby0or1isamatterofconvention(dependingonif oneprivilegesapropertyoritsopposite).

3.3. Upperandlowerapproximationsofanalogicalproportions

As canbe seen, Klein’s model can beconsidered as anupper bound of Ä0. It was thefirst logical view proposed for analogicalproportion [20].S.Kleinsuggestedthat ananalogicalproportionwould holdassoonasa,b,c arecompletedby d takenasd=c≡ (a≡b).This amountsto defineitas AK(a,b,c,d), (a≡b)≡ (c≡d). Then0:1::1:0 and 1:0::0:1

suchpatterns maybeadvocatedon thebasisofafunctionalviewofanalogywherea: f(a)::b: f(b)soundsindeed valid, taking the negation in _B for f . But, this is debatable since then AK(a,b,c,d)↔AK(b,a,c,d) (which does not fit with

intuition).Itturnsoutthat a:b::c:d→AK(a,b,c,d).

While AK(a,b,c,d)isanupperapproximationofa:b::c:d truefor8patterns,onemaylookforlowerapproximations

that aretrue for4 patterns only(taking intoaccount code independency). There are3 suchapproximations,given below, followed bythepatternstheyvalidate2:

• (a≡b)∧ (c≡d) 1 1 1 1 0 0 0 0 1 1 0 0 0 0 1 1 ; • (a≡c)∧ (b≡d) 1 1 1 1 0 0 0 0 1 0 1 0 0 1 0 1 ; • (a6≡d)∧ (b6≡c) 1 1 0 0 0 0 1 1 1 0 1 0 0 1 0 1 .

Obviously,these lowerapproximationsthat aremissingtwo ofthepatterns oftheminimalmodel Ä0,whilepreserving code independency,obeyonly asubsetof thethreepostulates.All aresymmetrical. Onlythethirdapproximation satisfies central permutation,butmisses to satisfy“a istoa as a isto a”(aspecial caseofreflexivityand identity,satisfiedbythe firsttwo approximations).

Wehave seen thattheanalysisoftheBoolean modelsthat arecompatible withthepostulatesofanalogicalproportion offers a kind of intrinsic justification that only the minimal model true for 6 patterns (and false for the 10 others) is reasonable. Before providing another justification in terms of algorithmic complexity in the next section, we revisit and discuss differentsyntacticpropositionalformsthat aretrueforthesepatternsonly,andthat laybarevariousaspectsofthe meaningofBooleananalogicalproportion.

3.4. Booleanformulasforanalogicalproportion

Instead of relying on the “arithmetical” definition of analogy (a−b=c−d), we may look for a propositional logic definition of a:b::c:d. Since analogy is a matter of comparison, it is natural to use basic comparative indicators as buildingblocks,asdonein[35,36].Theseindicatorsarenaturallyassociated toanypairofBooleanvariables(a,b):

– a∧b and¬a∧ ¬b arepositivesimilarity andnegativesimilarity indicators respectively:a∧b (resp. ¬a∧ ¬b)istrueiff only botha andb are true(resp.false);

– a∧ ¬b and¬a∧b are dissimilarity indicators:a∧ ¬b (resp.¬a∧b)istrueiffonlya (resp.b) istrueandb (resp.a)is false.

Thenanalogicalproportiona:b::c:d couldbedefinedbyformula(1) [32] asbelow:

a

:

b

::

c

:

d

=

de f

(

a

∧ ¬

b

≡

c

∧ ¬

d

) ∧ (¬

a

∧

b

≡ ¬

c

∧

d

)

(1)

This formula reads “a differs from b as c differs from d and b differs from a as d differs from c”, which fits with the expected meaningofanalogy.Formula(1) isobviouslystablew.r.t.negation,namely

a

:

b

::

c

:

d

→ ¬

a

: ¬

b

:: ¬

c

: ¬

d

making clearthecodeindependencyofanalogicalproportion.Ascanbenoticed,thepresenceofdissimilarity indicatorsin (1) exactlyfitswithpatterns1010and0101,whilethefourotherpatternscoverthecaseofnodifferencebetweena andb and betweenc and d.

Taking inspirationofawell-known propertyofarithmeticalproportions:a−b=c−d isequivalenttoa+d=b+c (or fromasimilarpropertyforgeometricproportion: a_b=_dc equivalenttoad=bc fornon-zero numbers),onecouldaskifthere

2 _{Thereare3companionapproximationsthatinvolvethetwoadditionalpatternsofA}

K (a≡d) ∧ (b≡c) 1 1 1 1 0 0 0 0 1 0 0 1 0 1 1 0 ; (a6≡b) ∧ (c6≡d) 1 0 0 1 0 1 1 0 1 0 1 0 0 1 0 1 ; (a6≡c) ∧ (b6≡d) 1 1 0 0 0 0 1 1 1 0 0 1 0 1 1 0 .

would beacounterpart inBoolean logic,involvinga and d onone side and b andc on theother side. Thisisindeed the case:thefollowingtwo formulas,whichareclearlyequivalent(thefirstone(1) exhibitingonlycomparisonindicators,while formula(2) has nonegation),havethesametruthtables[32] asformula(1).

(

a

∧

d

≡

b

∧

c

) ∧ (¬

a

∧ ¬

d

≡ ¬

b

∧ ¬

c

) (

A

) ; (

a

∧

d

≡

b

∧

c

) ∧ (

a

∨

d

≡

b

∨

c

) (

B

)

(2) Notethat codeindependencyisobviouson(1),aswellasthe3postulatesofanalogyonthetwoexpressions.

Formulas(1) and(2) providetwocompletelydifferentviewsoftheideaofanalogy,respectivelyintermsofdissimilarity and in terms of similarity. Their logical equivalence is far from being obvious at first glance, without resorting to truth tables,asoftendone.Thisiswhy, wegivebelowasimpleproofinsyntacticterms,usingseveralsteps.

Property2.((a∧ ¬b≡c∧ ¬d)∧ (¬a∧b≡ ¬c∧d))≡ ((a∧d≡b∧c) ∧ (a∨d≡b∨c))isatautology.

Proof.

i) (1) impliesa→ (b∨c).

Since (1) holds, the first equivalence in (1) a∧ ¬b≡c∧ ¬d holds. Thus (a∧ ¬b)→c holds, which is equivalent to a→ (b∨c).Thisgivestheresult.

ii) (2) implies(a∧ ¬b≡c∧ ¬d).

Starting from (2), wesuppose a∧ ¬b holds. Consideringthe firstequivalence inexpression (2): for thisequivalence to hold, we needd notto hold, i.e., ¬d to hold.Considering now thesecond equivalencein expression(2), sinceb does not hold, we needc to hold.Then we havew implies (a∧ ¬b→c∧ ¬d).Proving that (2) implies (c∧ ¬d→a∧ ¬b) isdone similarly.

iii) (1) implies(2).

(1) implies(d→ (b∨c))comesfromextremepermutationpropertyandstatementi).Then(1) implies((a∨d)→ (b∨c)). Codeindependencyof(1) andDeMorganlawsensurethat(1) implies((b∧c)→ (a∧d))aswell.Observingthatexchanging a andc ontheone handandb andd ontheotherhandleave(1) unchangedthankstosymmetrypostulate,itmakesclear that (1) implies((a∧d)≡ (b∧c))and ((a∨d)≡ (b∨c)).Thisistheexpectedresult.

iv) (2) implies(1).

Westartfromstatementii).Codeindependencyappliedtoexpression(2) showsthat (2) implies (¬a∧b≡ ¬c∧d) and wearedone. ✷

In light of expression (2), “a isto b as c is to d” can now beread “what a and d have in common, b and c have it also(both positivelyandnegatively)”,which,however, isaless straightforwardreadingoftheidea ofanalogythan theone associated withexpression(1).

As said above, expression (2) can also be viewed as the logical counterpart of a well-known propertyof geometrical proportions:theproductofthemeans isequaltotheproductoftheextremes.Interestinglyenough,Piaget[33,pp.35–37] named logicalproportion anylogical expression betweenfour propositional formulas a,b,c,d forwhich (2) is true. Appar-ently,and strangelyenough,Piagetneverrelatedthisexpressiontotheideaofanalogy.

Besides, by observingthe truth table ofthe minimal model ofanalogical proportion, it iseasy to check that formulas other than (1) or (2) can be obtained by combining lower approximations by means of disjunction. Three options are possible, whichyieldnoticeable,equivalent,disjunctiveexpressionsoftheanalogicalproportion:

Property3.The3followingformulasareequivalenttoformula(1) (andthen(2) aswell):

((

a

6≡

d

) ∧ (

b

6≡

c

)) ∨ ((

a

≡

b

) ∧ (

c

≡

d

))

((

a

≡

b

) ∧ (

c

≡

d

)) ∨ ((

a

≡

c

) ∧ (

b

≡

d

))

((

a

≡

c

∧

b

≡

d

)) ∨ ((

a

6≡

d

) ∧ (

b

6≡

c

))

Nevertheless,weshallseeinSection5thattheseformulas,involvingdisjunctionastopconnectorinsteadofconjunction, are not really suitable to model analogy in higher dimension when considering analogy between 4-tuples of vectors of Boolean features.

We now investigate if another justification in favor of the minimal model Ä0 could be obtained. Instead of focusing on the word“minimal” interms ofsize, itcould behelpfultoconsider theword “minimal” inthecontext ofinformation theory. Weinvestigatethisoptioninthefollowingsection.

4. Complexity-basedjustificationoftheBooleanmodel

Asfarasweknow,theworkof[5] wasthefirsttoestablishalinkbetweenanalogicalinferenceandinformationtheory, starting from a machine learning perspective. The aim was to integrate analogical reasoning in the global landscape of predictingvaluesfromobservableexamples.Acleardefinitionof“informationcontent”comesfromKolmogorovcomplexity

theory,alsoknownasAlgorithmicComplexityTheory.Kolmogorovcomplexityisnotanewconceptandthetheoryhasbeen designedmany yearsago:seeforinstance[27] foranin-depthstudy.Let usbrieflyrecallthemainideasofthistheory. 4.1. Kolmogorovcomplexityasastartingpoint

We needthehelp of auniversal Turing machinedenoted U .Then p denotes aprogram runningon U .Two situations can happen: i)either p doesnot stopfor the input x,or ii) p stops for theinput x andoutputs a finitestring y. Inthat case,wewriteU(p,x)=y.TheKolmogorovcomplexity[27] of y w.r.t.x isthendefined as:

KU

(

y

/

x

) =

min

{|

p

|,

U

(

p

,

x

) =

y

}.

KU(y/x) isthesizeoftheshortestprogramabletoreconstruct y withthehelp ofx.TheKolmogorovcomplexity [27] of y

isjustobtainedwiththeemptystring

ǫ

: KU

(

y

) =

min

{|

p

|,

U

(

p

,

ǫ

) =

y

}.

Given a string s, KU(s) is an integer which, in some sense, is a measure of the information content of s: instead of

sending s to somebody,wecansend p from which s canbe recoveredassoonas thissomebodyhas themachine U . KU

enjoys alot ofproperties among which isa kindof universality: thiscomplexity isindependent oftheunderlying Turing machineaswehavetheinvariancetheorem[27]:

Property 4. If U 1 and U 2 are two universal Turing machines, there exists a constant cU 1U 2 such that for all strings s:

|KU 1(s)−KU 2(s)|<cU 1U 2,whereKU 1(s)andKU 2(s)denotethealgorithmiccomplexityofs w.r.t.U 1 andU 2 respectively.

This theorem guarantees that complexity values may only diverge by aconstant c (e.g. the length of a compileror a translation program) and for hugecomplexity strings, we can denote K without specifying the Turing machine U . It can alsobeshownthat[27]:

Property5.∀x,y,K(xy)=K(x)+K(y/x)+ O(1).

Unfortunately K has been proved as a non-computable function [27]. But in fact, K or an upper bound of K can be estimatedindiversewaysthatweinvestigatenow.

4.2. Complexityestimation

Thefirstwellknownoptionavailabletoestimate K isvialosslesscompressionalgorithm.Forinstancebzip approximates better than gzip,and the P A Q familyisstillbetterthan bzip2.Dueto theinvariancetheorem, whenthesizeof s ishuge, using compression will provide a relatively stable approximation as the constant c in the theorem can be considered as negligible.Itisobviouslynotthecasewhenthesizeofs becomessmall.When s isshort,compression isnotavalidoption. On another side, the constant c canprevent from providing stableapproximations of K(s). Luckily, theworks of [7,8,43] givemeansofprovidingsensiblevaluesforthecomplexityofshortstrings(i.e.lessthan10bits).Thisjobhasbeendoneby the Algorithmic Nature Group (https://algorithmicnature.org/). They have developed a tool OACC for Online Algorithmic Complexity Calculator (http://www.complexitycalculator.com/) allowing to estimate the complexity of short strings. The authors derived their approach from a Levin’s theorem [26,8] establishing the exact connection between m(s) and K(s), wherem(s)isasemi-measureknownastheUniversal Distributiondefined asfollows[44]:m(s)= 6p:U(p,ǫ)=s2−|p|.

Property6.Thereexistsaconstantc dependingonlyonthe underlyingTuringmachinesuchthat:∀s,|−log2(m(s))−K(s)|<c. Rewritingtheformula as K(s)= −log2(m(s))+ O(1), showsthat estimating K couldalsobedone viaestimatingm(s). Estimatingm(s) becomesrealistic whens isshort aswehaveto estimatetheprobabilityfor s to betheoutputofashort program. Considering simple Turing machines asdescribed in[43],over aBoolean alphabet {0,1} and a finite numbern of states {1,. . . ,n} plus a special Halt state denoted 0, there are exactly (4n+2)2n such Turing machines. Using clever optimizations [43],running these machines forn=4 andn=5 becomesrealistic and providesan estimationofm(s) and ultimatelyof K(s).Inthefollowing,wedenote K′(s)thisOACCestimationofK(s).

4.3. Shortchainscomplexityestimation

Somepropertiesareexpectedfromacomplexitycalculatormachinerytobeinaccordancewithacognitiveprocess: 1. Thereisnowaytodistinguishstringsoflength1and itisabsolutelyclearthat K(0)=K(1) shouldholdwhateverthe

Table 2

Complexityof1bitand2bitschainswithOACC. x K(x) 0 3.5473880692782100 1 3.5473880692782100 x1x2 K(x1x2) 00 5.4141012345247104=a 01 5.4141040197301500=b 10 5.4141040197301500=b 11 5.4141012345247104=a

2. An important point is to be able to distinguishthe 4 stringsof length 2: 00,11,10,01 and we expectthe following properties:K(00)=K(11)<K(01)=K(10);

3. Intermsofn bitsstrings,weexpect0. . .0 and1. . .1 tobethesimplestonesand tohavethesamecomplexity. Observingthetablesin[8],itappearsthatthepropertiesabovearesatisfied,namely:

– Whateverthenumberofstatesofa2-symbolsTuringmachine,K′(0)=K′(1).

– Whateverthenumberofstatesofa2-symbolsTuringmachine,K′(00)=K′(11)=a, K′(01)=K′(10)=b anda<b. – Whateverthenumberofstatesofa2-symbolsTuringmachine,andforstringsoflengthlessthanorequalto10(short strings) K′(0. . .0)=K′(1. . .1)=a anda istheminimumvalueamongthesetofvalues.

Then the estimation of K via K′ comingfrom the OACC estimator isa suitable candidatefor our purpose. But before going further, wehave firstto check that OACCvalidate the aboveconditions. As we cancheck byexamining Table2 and column4ofthefinaltableinSection4.5,thesebasiccognitiveevidencesareconfirmedwiththeOACCtool.Sowecanstart fromOACCtocheckthepropertiesrequiredtovalidatetheanalogicalhypothesisthatweproposeinthenextsection. 4.4. AKolmogorovformulatomeasurethequalityofananalogy

When stated with a machine learning perspective, the problem of analogical inference is as follows: for a given x3,

predict x4 suchthat thetarget pair(x3,x4) isinthesame relation thatanother given source pair(x1,x2) consideredasan

example. Thepair(x3,x4)isthetargetpairwhichispartiallyknown.Inthecaseofclassificationwherethe2ndelementin apairisthelabel,itamountstopredictthelabelofx3 havingonlyoneclassified example(x1,x2)athand.

Afunctional view amountsto considering ahidden function f such that x2= f(x1) and we have to guess x4= f(x3).

Thisfunctional viewistheonedevelopedin[5]: theproblemofanalogicalinferencestrictlyfitswitharegressionproblem but with only one example. Ruling out any statistical models, this approach needs a brand new formalization that the authors extractfromalgorithmic complexitytheory.Insteadoftrying tofind regularitiesamong alargesetofobservations (statistical approach),theyconsider theverymeaningofeachofthe3observablesx1,x2=f(x1)and x3.Westartfromthis

philosophy,but wedepartfromitasbelow:

– Wefocuson theBooleancasewherethe3objectsunderconsiderationareBooleanvectors. Sowedonothavetocare about the change between the source domain representation and thetarget domainrepresentation: these 2domains are identical. Thecostofthisrepresentationchangeisnullintermsofalgorithmiccomplexity.

– Tobeinlinewiththemachinelearningminimalassumptionthatthereexists someunknownprobability distribution P fromwhich thedata are drawn, wedo not consider that x2 isa (hidden)functionof x1. We just have aprobability of

observing x2 havingalready observedx1 whichismoregeneralthanassociatingafixedx2 witheverygiven x1.Itcouldbe

thecasethatforanotherx′₂westillhave x1:x′₂::x3:x4.

Asaconsequence,westartfromthefollowingintuitions:

1. For x1:x2::x3:x4 to be accepted as a valid analogy, it is clear that the way we go from x1 to x2 should not be

very differentfrom theway wego from x3 to x4 (butit has not tobe afunctional link).We suggestto measure this

expectedproximitywiththedifference|K(x2/x1)−K(x4/x3)|.ConsideringK(x2/x1)asthedifficulty tobuildx2fromx1,

thepreviousexpression|K(x2/x1)−K(x4/x3)|,whensmall,tellsusthatitisnotmoredifficulttobuildx4 fromx3 than

tobuildx2 fromx1,and viceversa.Thisiswhatwecalltheatomicviewofanalogy.Butthisisobviouslynotenough.

2. In fact, the previous formula does not tell anything about the link between the pair (x1,x2) and the pair (x3,x4). For x1:x2::x3:x4 to beaccepted asa valid analogy, the difficulty toapprehend the string x1x2 from the string x3x4

shouldbeclose tothedifficultytoapprehendx3x4from x1x2.Wesuggesttomeasure thisexpectedproximitywiththe

difference |K(x1x2/x3x4)−K(x3x4/x1x2)|. This difference isobviously symmetric and islinkedto thesymmetry ofan

analogy.

3. Above all, the global picture has to be “simple” i.e. telling that x1:x2::x3:x4 is a valid analogy should not be too

disturbing, at least from a cognitive viewpoint. This means that the occurrence of the string x1x2x3x4 in this order

shouldbehighlyplausible.We suggestto measure thisplausibilitywith K(x1x2x3x4) whichisthesize oftheshortest

programproducingthebinarystring x1x2x3x4fromauniversalTuringmachine.

Followingtheideasof[5],weusethesumasaggregatoroperatoranddenotek(x1x2x3x4)thefollowingformulameasuring,

insomesense, thequalityofananalogy:

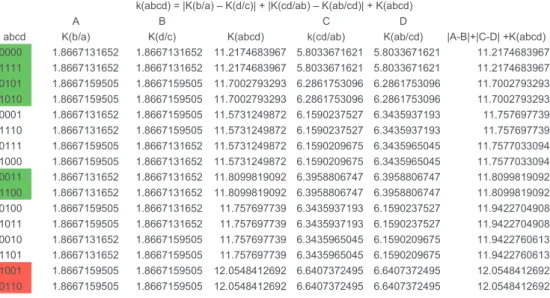
Fig. 2. OACC estimations.

This leads us to postulate that the “best” x4 we are looking for to build a valid analogy x1:x2::x3:x4 is the one

minimizing thisexpression.So,wehave: x4

=

argminuk

(

x1x2x3u

)

Let usseeif wecan, atleast fromanempiricalviewpoint,validate thismodel.Letusnotethatwecanhaveseveral values minimizing suchanexpression.

4.5. ValidationintheBooleansetting

As wearenotin apositiontoprove somethingatthisstage,letusjust investigatenow theempiricalevidence forour formula. One pointto startwithis to checkif thisformula holdsinthe very basic Booleancase. Considering x1,x2,x3,x4

as Boolean values, we have to check how the 6 cases of valid analogical proportions actually behave w.r.t. the formula k(x1x2x3x4).Thus, wehave toestimateformulak(x1x2x3x4) forevery x1x2x3x4∈ B4.The pointisthat ourstringsarevery

short:only4bits.So,asexplainedinSections4.2and4.3,wehavetorelyonOACCinsteadofacompression estimation. Ontopofthat,wehavetoconsider,notonlypureKolmogorovcomplexity K butalsocomplexityw.r.t.agivenstringas in K(x3x4/x1x2). Generally,itisquite clearthat K(xy)≤K(x)+K(y/x):roughly speaking,wecanbuild aprogramwhose

output is xy byconcatenating aprogramwhose outputis x to a programtaking x asinput and providing y as output.It ismoredifficultto getamoreprecisebound.Thanks toTheorem2: K(xy)=K(x)+K(y/x)+ O(1),whichshowsthat we can approximate K(y/x)with K(xy)−K(x).As wenow haveallthetoolsneeded toapproximate formulak, itremainsto use OACC to computethe estimation. Fig. 2reports the results of thiscomputation. As can be seen for the6 patterns of the modelÄ0 ofanalogicalproportion, theuniquesolution ofequation a:b::c:x alwayscorrespondsto astringabcx that minimizes expression k w.r.t. theother option abcx (where x= ¬x), e.g. k(1111)<k(1110). Besides 0101 is simplerthan 0110 despitethefactthat inthesecondcasethereisalsoanunderlying functionsuchthat x2= f(x1) and x4= f(x3):the

negation. Note that 0110 and 1001 exhibit the highest complexity asestimated byOACC. It eliminates K l. As there isno knownconvergenceresultregardingK andthatwecannotestimatetheconstantintheformulaK(s)= −log2(m(s))+ O(1), these experiencesshouldonlybeconsideredasaddingabit ofcredibility tothesmallestmodel.

Nevertheless,inreallifeapplication,attributesorfeaturesarenotnecessarilyBooleanandagradedextensionof analog-icalexpressionisneeded. Thisistheobjectofthenextsectiontoinvestigatehow toextendtheseformulas.

5. ExtensiontoBooleanvectors

RepresentingobjectswithasingleBooleanvalueisnotgenerallysufficienttohandlerealsituations,anditemsareusually represented byvectors ofBoolean values,eachcomponent being thevalue ofabinaryattribute. Sowe haveto extendthe Boolean caseto Booleanvectors.Thiscan bedonecomponentwise, asillustratedbythefollowingexample “acalf( A) isto a cow (B) asa foal (C ) is toa mare (D)”.3 The attributeshave been chosen in order toexhibit (vertically) eachof the6 patternsthat makeananalogicalproportiontrue.

mammal young equine adult female bovine adult male

A: calf 1 1 0 0 1 0

B: cow 1 0 0 1 1 0

C : foal 1 1 1 0 0 0

D: mare 1 0 1 1 0 0

5.1. Analogicalproportionsbetweenvectors

Awaytomoveto Booleanvectors wouldbetoextend theoperators ofBooleancalculusto vectorsand toconsider the derived definitions.Withthat perspective,wehavein_Bn:

• ¬Ea=de f (¬a1,. . . ,¬an)

• Ea∨ Eb=de f (a1∨b1,. . . ,an∨bn)

• Ea∧ Eb=de f (a1∧b1,. . . ,an∧bn)

• Ea≡ Eb=de f (a1≡b1,. . . ,an≡bn)

The truthvalueofaBoolean vectorEa isjust Vn

i=1ai.As aconsequence,Ea: Eb:: Ec: Ed hasatruthvaluewhichisjust Vni=1ai:

bi::ci:di. Itis quiteeasyto seethat thethreepostulatesof analogyarestill valid withthisvectorial definition.It isalso

thecaseforcodeindependency.Moreovertheequivalencebetween

(E

a

∧ ¬E

b

≡ E

c

∧ ¬E

d

) ∧ (¬E

a

∧ E

b

≡ ¬E

c

∧ E

d

)

and

(E

a

∧ E

d

≡ E

b

∧ E

c

) ∧ (E

a

∨ E

d

≡ E

b

∨ E

c

)

isstillvalid.Butifweconsiderthevectorialversionof

((

a

≡

b

) ∧ (

c

≡

d

)) ∨ ((

a

≡

c

) ∧ (

b

≡

d

)),

coming from Property 3 where ∨ is the top operator, it is definitely not equivalent to aE: Eb:: Ec: Ed. Let us start from an example togetthepicture.With:

E

a

= (

0

,

1

,

0

), E

b

= (

1

,

1

,

0

), E

c

= (

0

,

1

,

1

), E

d

= (

1

,

1

,

1

),

wehaveaE: Eb:: Ec: Ed (whichisbettervisualizedinTable3)despitethefactthat ((Ea≡ Eb)∧ (Ec≡ Ed))∨ ((Ea≡ Ec)∧ (Eb≡ Ed))does nothold.Thiscomes fromthefactthat thetopoperator ∨intheformuladoesnotcommutewiththe∧operator involved inthetruthvaluedefinitioni.e.:

n

^

i=1

((

ai

≡

bi

) ∧ (

ci

≡

di

)) ∨ ((

ai

≡

ci

) ∧ (

bi

≡

di

)) =⇒

/

(

n

^

i=1

(

ai

≡

bi

) ∧

n

^

i=1

(

ci

≡

di

)) ∨ (

n

^

i=1

(

ai

≡

ci

) ∧

n

^

i=1

(

bi

≡

di

))

whichistheexactdefinitionof:

((E

a

≡ E

b

) ∧ (E

c

≡ E

d

)) ∨ ((E

a

≡ E

c

) ∧ (E

b

≡ E

d

))

As a consequence, wewill not considerthe equivalencesshown in Property 3asvalid candidatesfor any extension of analogicalproportion.

Thisleads to restonthe initialequivalent expressions(1) and(2) as being themostsuitable one to accuratelycapture theintuitivemeaningofanalogicalproportion.

Table 3

AnalogicalproportionEa: Eb:: Ec: Ed be-tweenvectors. E a 0 1 0 E b 1 1 0 E c 0 1 1 E d 1 1 1

Table 4

Pairingpairs(Ea,Eb)and(Ec,Ed).

A₁ ... A_i−1 A_i ... A_j−1 A_j ... A_k−1 A_k ... A_r−1 A_r ... A_s−1 A_s ... A_n E a 1 ... 1 0 ... 0 1 ... 1 0 ... 0 1 ... 1 0 ... 0 E b 1 ... 1 0 ... 0 1 ... 1 0 ... 0 0 ... 0 1 ... 1 E c 1 ... 1 0 ... 0 0 ... 0 1 ... 1 1 ... 1 0 ... 0 E d 1 ... 1 0 ... 0 0 ... 0 1 ... 1 0 ... 0 1 ... 1 Table 5 Pairing(Ea,dE)and(Eb,Ec). A₁ ... A_i−1 A_i ... A_j−1 A_j ... A_k−1 A_k ... A_r−1 A_r ... A_s−1 A_s ... A_n E a 1 ... 1 0 ... 0 1 ... 1 0 ... 0 1 ... 1 0 ... 0 E d 1 ... 1 0 ... 0 0 ... 0 1 ... 1 0 ... 0 1 ... 1 E b 1 ... 1 0 ... 0 1 ... 1 0 ... 0 0 ... 0 1 ... 1 E c 1 ... 1 0 ... 0 0 ... 0 1 ... 1 1 ... 1 0 ... 0

5.2. Playingwithanalogicalproportionsbetweenvectors

Itisimportantto noticethatthefourvectors inananalogicalproportionareofthesamenature,sincetheyrefertothe same set offeatures.Then symmetry just means that comparing theresults ofthe comparisonsofthe two vectorsinside each pair of vectors (Ea,bE) and (Ec,dE) does not depend on the ordering of the two pairs. Thus the repeated applications of symmetry followed by centralpermutation yield8 equivalentforms ofthe analogicalproportion:(Ea: Eb:: Ec: Ed)= (Ec: Ed:: E

a: Eb)=(Ec: Ea:: Ed: Eb)=(Ed: Eb:: Ec: Ea) = (Ed: Ec:: Eb: Ea)= (Eb: Ea:: Ed: Ec)= (Eb: Ed:: Ea: Ec)= (Ea: Ec:: Eb: Ed).Table4picturesthesituation, where thecomponentsof thevectorshave beensuitablyreordered insuchawaythat theattributesforwhich oneofthe 6patternscharacterizingtheanalogicalproportionisobserved,havebeengathered,e.g.,attributesA₁ toA_i−1 exhibitsthe pattern 1111.Inthegeneralcase,someofthepatternsmaybeabsent.

Table 4 shows that building the analogical proportion aE: Eb:: Ec: Ed is a matter of pairing the pair (Ea,bE) with the pair

(Ec,Ed). More precisely, on attributes A₁ to A_j−1, the four vectors are equal; on attributes A_j to A_r−1, Ea= Eb and Ec= Ed, but (Ea,bE)6= (Ec,dE);on attributesA_r to A_n, Ea= Ec,bE= Ed,and Ea6= Eb.Inotherwords, onattributes A₁ toA_r−1 Ea andb agreeE and Ec and Ed agreeaswell.This contrastswithattributesA_r to A_n,forwhich wecanseethata differsE fromEb asEc differs from d (andE vice-versa). We recognize the meaning ofthe formal definition of theanalogical proportion as described by expression (1).

Let us now pair the vectors differently, namely considering pair (Ea,dE) and pair (Eb,Ec), asin Table 5. First, we can see that Ea: Ed:: Eb: Ec doesnothold due to attributesA_s to A_n. Obviously, wecontinue to have aE= Eb= Ec= Ed for attributesA₁

to A_j−1, whileon therestoftheattributesthevaluesinside eachpairdiffer(inthefourpossible differentways). Thenit shouldnotcomeasasurprisethat werecover,inthevectorialcase,expression(2),sincetheexpressionholdseitherwhen a=d=b=c,orwhena6=d andb6=c:

((

a

∧

d

) ≡ (

b

∧

c

))∧((

a

∨

d

) ≡ (

b

∨

c

))

(

2

)

5.3. LinkwithHammingdistance

Sincewe havearelation betweenelements of_Bn_{, namelytheanalogicalproportion, itisquitenatural toconsider this}

relationwithregardtostandardmetricon Bn.AclassicaloneoverBn isHammingdistancedefinedasfollows: Hn

(E

x

, E

y

) = |{

i

∈ [

1

,

n

] :

xi

6=

yi

}|

Note thatthisdistancesatisfies:

Hn+1

(E

x

, E

y

) =

Hn

(E

x

/

n

, E

y

/

n

) +

H1

(

xn+1

,

yn+1

)

where Ex/n denotestheprojectionof Ex over _Bn_{. Wewrite H whenthereis noambiguity about thedimension.Afirst link}

betweenanalogicalproportionandHammingdistancecanbeeasilychecked:

Property7.∀Ea,Eb,Ec,Ed_{∈ B}nsuch thataE: Eb:: Ec: Ed,wehave: H(Ea,Eb)=H(Ec,Ed),H(Ea,Ec)=H(Eb,Ed),H(Ea,dE)=H(Eb,Ec).

Proof. We provethefirst equality H(Ea,bE)=H(Ec,dE) byinductionover n.The equalityisobviouslysatisfiedforn=1.Now wehavetonotethat,due tothedefinitionofanalogyon _Bn+1,given Ea,bE,Ec,Ed_{∈ B}n+1,

E

Theinductionhypothesisleadsto:

H

(E

a

/

n

, E

b

/

n

) =

H

(E

c

/

n

, E

d

/

n

)

and H

(

an+1

,

bn+1

) =

H

(

cn+1

,

dn+1

)

Addingthese2equationsleadstotheexpectedresult.Thesamereasoningappliestotheremaining2equalities. ✷

The reverse property does not hold in general: for instance 0:1::1:0 does not hold. This comes from the fact that Hamming distance issymmetric but analogy does not allowto reverse only one side ofthe proportion:when aE: Eb:: Ec: Ed holds,itisunlikelythatbE: Ea:: Ec: Ed holds.Obviously,Property7doesnotholdin_RnwhenequippedwithEuclideandistance: a parallelogramEa,Eb,Ec,d doesE not alwayssatisfyd(Ea,dE)=d(Eb,Ec) where d istheEuclideandistance. Asecond linkcan still beestablished:

Property8.∀Ea,Eb,Ec,dE,such thataE: Eb:: Ec: Ed,wehave:

H(Ea,Eb)+H(Ea,Ec)=H(Ea,dE)andsimilarly:H(Ed,Ec)+H(Ed,bE)=H(Ed,aE).

Proof. Thefirstequalitycanbeeasilyprovedbyinductionovern.Thepropertyistrueforn=1.Sincewehave

E

a

: E

b

:: E

c

: E

d iffa

E

/

n

: E

b

/

n

:: E

c

/

n

: E

d

/

n and an+1

:

bn+1

::

cn+1

:

dn+1

wecanapplytheinductionhypothesistoget H(Ea/n,bE/n)+H(Ea/n,Ec/n)=H(Ea/n,Ed/n) and H(an+1,bn+1)+H(an+1,cn+1)= H(an+1,dn+1). And wearedone byaddingthese 2equations.Then thesecondequality isjust deduced fromthefirst one usingProperty7. ✷

Theseresultsstrengthenthegeometricalinterpretationofanalogicalproportionasaparallelograminthesuitablevector space,viewinga,b,c,d aspointsin_Rn _{andvectors definedbypairs(a,b),(a,c),(a,d),etc.}

5.4. Equationsandtheinductionofanalogicalproportionsbycomparingtwoitems

Itisalsointerestingtoconsider analogicalproportionsfromanequationalpoint ofview, asdonebyS. Klein[20] inhis pioneering work. Hewas thefirst to propose awayto solvethe equationbetween Boolean vectorsaE: Eb:: Ec: Ex where Ex is unknown.

InB,theequationa:b::c:x hasauniquesolutionx=c≡ (a≡b) providedthat(a≡b)∨ (a≡c) holds.Indeedneither 0:1::1:0 nor 1:0::0:1 holds true in the minimal model of analogy, departing from Klein’s model with which the equation has always a solution. This process can be extended componentwise to vectors. In that case, for instance, the following equation 010:100:011: Ex has for unique solution the vector (1,0,1) which is not among the three previous vectors (0,1,0),(1,0,0),(0,1,1). We can also observe in Table 1 that analogical proportions for vectors are creative (an informalqualityusuallyassociated withtheidea ofanalogy)astheymayinvolve4distinctvectors. Namely,onemayhave

E

a,b,E Ec alldifferentwhile∀i∈ [1,n],di=ci≡ (ai≡bi) and∃idi6=ai,∃jdj6=bj,and∃kdk6=ck.Forinstance,inTable1,we

cantake(d1,d2)= (0,0),with(a1,a2)= (1,1),(b1,b2)= (1,0),(c1,c2)= (0,1).

Another equation of interest is aE: Ex:: Ey: Ed where Ex and Ey are unknown. As we shall see, starting from two Boolean vectors Ea and d,E one can find two “intermediary” vectors such that the equation holds. This shows how pervasive the concept ofanalogical proportion is,since itis implicitlypresent as soonas wecompare two vectors a andE d.E Let us first consider theequation in theBoolean set _B. As soonaswe gettwo elementsa,d_{∈ B}, itis obviousthat wecan find two other elements (not necessarily distinct) such that a:b::c:d, thepair (b,c) establishing a bridge between a and d. For instance tobridge0 and1 wecanstill use0 and1 tobuild0:0::1:1 or1 and0 tobuild0:1::0:1.

Considernow twodistinct Boolean vectorsEa andEd in_Bn _{(ifaE= Ed,thesolutionistriviallyEx= Ey= Ea).Itisthenpossible}

tofindtwoothervectorsb andE Ec suchthataE: Eb:: Ec: Ed.BeyondtheeasysolutionsEx= Ea andEy= Ed (orEx= Ed and Ey= Ea),itis generally possibletofindtwo distinctvectorsEb andEc,themselvesbeing distinctfromEa andd,E suchthat Ea: Eb:: Ec: Ed holds.

Indeed, let Agr(Ea,dE) betheset of indiceswherea andE d agreeE and Dis(Ea,dE) theset of indiceswherethe two vectors differ. Namely Agr(Ea,dE)= {i | ai=di} and Dis(Ea,Ed)= {i | ai6=di}. Clearly, the two solution vectors b andE Ec of equation

E

a: Eb:: Ec: Ed shouldbesuchthat

∀

i

∈

Agr

(E

a

, E

d

),

ai

=

bi

=

ci

=

di

(allequalto1orallequalto0).ForthecomponentsinDis(Ea,dE)wehavetwooptionsforpreservingananalogicalproportion componentwise

∀

i

∈

Dis

(E

a

, E

d

)(

bi

=

aiand ci

=

di

)

or

(

bi

= ¬

aiand ci

= ¬

di

).

For instance, takeEa= (0,1,1,0),dE= (0,0,1,1).We have Agr(Ea,dE)= {1,3} and Dis(Ea,dE)= {2,4}. ThenbE= (0,1,1,1) and

E

Property9.Assoonas Di f(Ea,dE) containsatleasttwoindices,therearesolutionsofequationaE: Ex:: Ey: Ed wherethefour vectors

E

a,Ex,Ey,Ed aredistinct.

This isexemplified by theabove example. The creation of (Eb,cE) from a andE d hasE been recently illustratedin [19] on images,usinganon-Boolean logicapproach.Theirworkdealswiththetransferofvariousvisualattributeslikecolor,texture, style, etc.,fromoneimagea toanotherimaged.Usinganalogicalproportions,theauthorsarethefirsttosuggestageneral method ableto dealwith any typeofattributes.Totransfer attributesfromanimagea to animaged,theirsolution isto formulate the mapping asa problemof building ananalogicalproportion between images a:b::c:d,where b and c are unknown andhaveto beestimated.Theassumptionisthatb= φ(a)and d= φ(c).Toestimatetheoperator φ,theauthors consider thefeatures extracted from severalconvolutional neural networks. Atthe endoftheprocess, theoperator φ will beappliedtoc inordertogetd.

Some well-known apps or services like Prisma (https://prisma-ai.com/), Google Deep Style (http://www. deepstylegenerator.com/), Ostagram (https://www.ostagram.me/) are able to transform photos and videos into works of art using the styles of famous artists like Van Gogh or Picasso. They mainly use amix ofclassical AI withconvolutional neural networks[11].

In comparison,the analogicalapproach of[19] is capableof higher qualitycontent-specific stylizationthat better pre-servesstructures.

6. Multiple-valuedanalogicalproportions:Arefresher

The aim of this section is mainly to provide the necessary background for thenext section on analogical inequalities sincetheyareweakenedformsofBooleanormultiple-valuedanalogicalproportions. Itisanopportunity toemphasizethe influence ofthetwo equivalentsyntacticforms ofanalogicalproportion foundmeaningfulin theBooleancase whichlead to two multiple-valued extensions that are no longer equivalent. It is also the occasion to discuss the particular case of continuous analogicalproportions,wherethetwocentralelementsareequal,whicharenotoften considered.

Weassumethatattributesarenowvaluedin[0,1],possiblyafterrenormalization,ratherthaninB.Thenweexpectthat thegradedextensionofa:b::c:d fromB4 to [0,1]4 _{takesintermediaryvaluesbetween 0 and1 (e.g.,0.9:0::1:0 canbe}

neither1 nor0,butshouldratherhaveahighvaluesince0.9 iscloseto1.Forsimplicity,inthesequel,asymbola denotes bothavariableanditstruth-value.Note thatusingasimple differenceisnotasatisfactoryoptionsince[0,1]isnotclosed underthedifference operator.Usingabsolutevalueofdifference willnotsolvetheproblem;indeed welosethe orientation partoftheinformation,since|a−b|= |c−d|doesnotentaila−b=c−d.SincetheBooleanmodelÄ0 istheonethatwe chooseforanalogicalproportion,wecanconsider thattheBooleanformulas (1) and(2) given insubsection3.4 areagood starting pointto beextendedovergradedtruthvalues usingmultiple-valuedconnectives. Letusrecallthese twoformulas below:

(

a

∧ ¬

b

≡

c

∧ ¬

d

) ∧ (¬

a

∧

b

≡ ¬

c

∧

d

)

(1)

(

a

∧

d

≡

b

∧

c

) ∧ (

a

∨

d

≡

b

∨

c

)

(2)

6.1. Conservativeandliberalextensions

Despite the factthat (1) and (2) are equivalentin Boolean logic,it willappear that thisisnot thecase in a multiple-valued framework. The multiple-valued logic extension of the two formulas requires the choice of connectives for the external conjunction and the two equivalences. As described in [40,35,9], extending these formulas can be done in the followingway:

i) thecentral,externalconjunction∧istakenasequaltotheminimumforsimplicity.

ii) s≡t is taken as min(s→Lt,t→Ls) where →L isŁukasiewicz implication, defined by s→Lt=de f min(1,1−s+t),

forL= [0,1]and thus s≡t=de f 1− |s−t|.Therearetwoargumentsinfavorofthischoice.First, withthisdefinition,

s≡t takesthetruthvalue 1 ifand onlyif s=t,whichisfullyin thespiritofexactcomparisons; moreoverthisindex isexplicitly relatedto theusualdistance betweennumericalvalues (expressedbytheabsolutevalue ofthedifference betweens andt).

iii) replacing thefour expressions ofthe form s∧ ¬t by thebounded difference max(0,s−t)=de f 1− (s→Łt),which is

associatedtoŁukasiewiczimplication,using1− (·)asnegation.

Thisbeingsaid,wecannowextendthetwoformulas(1) and(2).Westartwiththelastone.

A straightforward extension of expression (2) is obtained by also taking minimum for the internal conjunction and maximum fortheinternal disjunction[35].Thisis referredtoastheconservative extension [9].For instancea∧d leads to min(a,d)and (a∧d≡b∧c)to1− |min(a,d)−min(b,c)|.Globally,thisyields: