Estimation de modèles à volatilité stochastique avec applications dans la couverture de fonds distincts

ESTIMATION DE MODÈLES À VOLATILITÉ STOCHASTIQUE AVEC APPLICATIONS DANS LA COUVERTURE DE FONDS DISTINCTS

MÉMOIRE PRÉSENTÉ

COMME EXIGENCE PARTIELLE DE LA MAÎTRISE EN MATHÉMATIQUES

PAR

JONATHAN GRÉGOIRE

Avertissement

La diffusion de ce mémoire se fait dans le respect des droits de son auteur, qui a signé le formulaire Autorisation de reproduire et de diffuser un travail de recherche de cycles supérieurs (SDU-522 - Rév.1 0-2015). Cette autorisation stipule que <<conformément à l'article 11 du Règlement no 8 des études de cycles supérieurs, [l'auteur] concède à l'Université du Québec à Montréal une licence non exclusive d'utilisation et de publication de la totalité ou d'une partie importante de [son] travail de recherche pour des fins pédagogiques et non commerciales. Plus précisément, [l'auteur] autorise l'Université du Québec à Montréal à reproduire, diffuser, prêter, distribuer ou vendre des copies de [son] travail de recherche à des fins non commerciales sur quelque support que ce soit, y compris l'Internet. Cette licence et cette autorisation n'entraînent pas une renonciation de [la] part [de l'auteur] à [ses] droits moraux ni à [ses] droits de propriété intellectuelle. Sauf entente contraire, [l'auteur] conserve la liberté de diffuser et de commercialiser ou non ce travail dont [il] possède un exemplaire.»

Je remercie mon superviseur de mémoire Mathieu Boudreault qui est professeur au Département de mathématiques à l'UQAM. Tout au long du processus, il a démontré une grande implication dans ce projet. Il m'a permis d'acquérir des no-tions très approfondies lors de nos nombreuses rencontres et discussions. Je suis très impressionné par toutes ses réalisations et ses qualités (rigueur, générosité, attention, dévouement, etc). Il est sans aucun doute un exemple à suivre. Sans son soutien, sa confiance et son transfert de connaissances, ma réussite n'aurait pas été envisageable.

Je tiens également à remercier l'Autorité des marchés financiers (AMF) pour son soutien financier. Également, cette organisation m'a permis d'effectuer un stage pratique dans le contexte des fonds distincts. En plus de cette opportunité, mon superviseur de stage, Emmanuel Hamel, m'a permis d'acquérir des connaissances pratiques utiles pour les applications du mémoire.

Sur le plan personnel, il y a beaucoup de gens qui ont cru en moi. Je tiens à manifester ma gratitude envers mes parents (Manon et Jean-François) qui m'ont donné un support inconditionnel me permettant de réaliser tout ce dont j'avais envie. Ma partenaire de vie, Carol-Anne, a nécessairement été LA ressource indis-pensable lors de cette aventure.

Une dernière reconnaissance pour Maciej Augustyniak pour son aide quant à l'es-timation du modèle MS-GARCH et pour ses autres conseils.

LISTE DES TABLEAUX vii

LISTE DES FIGURES . 1x

RÉSUMÉ . . . xi

INTRODUCTION 1

CHAPITRE I

ESTIMATION DU MODÈLE À VOLATILITÉ STOCHASTIQUE EN TEMPS

DISCRET . . . . . 7

1.1 Le modèle SVOL . . . . . . . . . . . . 8 1.1.1 Autres cas particuliers dans la littérature .

1.2 Synthèse des procédures d'estimation dans la littérature 1.2.1 Estimation basée sur une linéarisation du modèle 1.2.2 Estimation basée sur le vrai modèle . .. . 1.3 Méthodes d'estimation utilisées dans ce mémoire

1.3.1 Filtre non-linéaire discret (DNF) 1.3.2 Filtre à particules (PF)

1.4 Étude Monte Carlo . . . . .

9 14 15 17 19 21 26 33 1.4.1 Étude de la fonction de vraisemblance 34 1.4.2 Étude Monte Carlo sur les propriétés statistiques du DNF 40

1.4.3 Conclusion 43

1.5 Exemple empirique

1.5.1 Comparaison entre des variantes du SVOL

1.5.2 Comparaison avec des modèles financiers populaires . CHAPITRE II

ESTIMATION DU MODÈLE À VOLATILITÉ STOCHASTIQUE EN TEMPS 43 44

47

2.1 Le modèle à volatilité stochastique (temps continu) . . . 2.1.1 Le modèle de Heston sous la mesure de probabilité Q 2.2 Synthèse des techniques d'estimation

2.2.1 Calibration . . . . 2.2.2 Estimation statistique 2.3 Simulation du modèle de Heston .

2.3.1 Discrétisation selon les schémas d'Euler . 2.3.2 Discrétisation selon les schémas de Milstein 2.3.3 La méthode exacte . . . . . . . . . . . . 2.4 Méthode proposée pour l'estimation du modèle de Heston

2.4.1 Quelques ajustements aux méthodes proposées . 2.5 Étude Monte Carlo . . . .

52 53 54 55 58 63 65 66 67 67 69 70 2.5.1 Étude de la fonction de vraisemblance 70 2.5.2 Étude Monte Carlo sur les propriétés statistiques du DNF 75

2.5.3 Conclusion 76

2.6 Exemple empirique CHAPITRE III

EFFICACITÉ DE STRATÉGIES DE COUVERTURE 3.1 Construction du marché dans un fonds distinct

3.1.1 Dynamique du sous-jacent . . . .

3.1.2 Dynamique de la valeur du fonds d'investissement 3.1.3 Autres hypothèses de marchés

3.1.4 Le double risque du marché .

3.2 Les prestations garanties offertes par l'assureur

3.2.1 Prestation minimale garantie à l'échéance ou au décès. 3.2.2 Dynamique de la valeur garantie Gt .

3.3 Efficacité des stratégies de couverture . . . .

77 81 82 82 82 83 84 84 84 85 87

3.3.1 Modèle sous la mesure de probabilité neutre au risque Q . . . 88 3.3.2 Couverture delta d'une garantie minimale à l'échéance (GMMB)

avec une prime unique 3.3.3 Résultats numériques . CONCLUSION . . . . APPENDICE A

RÉSULTATS DU MAXIMUM DE VRAISEMBLANCE RÉFÉRENCES . . . . . . . . . . . . . . . . . . . . . . . 89 93 97 99 103

Tableau Page 1.1 Quantiles empiriques des erreurs relatives absolues ~abs-rei (%)

se-lon les 50 000 jeux de paramètres et trajectoires aléatoires. . . . . 38 1.2 Quantiles empiriques des erreurs relatives absolues ~abs-rei (%) des

quatre groupes en fonction des coefficients de variation selon les intervalles de 1 'équation ( 1. 50). . . . . . . . . . . . . . . . . 39 1.3 Résultats numériques de l'étude de la convergence du DNF (1ère

partie : p = 0 et p = -0.3) où le biais moyen est répertorié ainsi que l'écart-type entre parenthèse. . . . . . . . . . . . 41 1.4 Résultats numériques de l'étude de la convergence du DNF (2e

partie : p

=

-0.5 et p

=

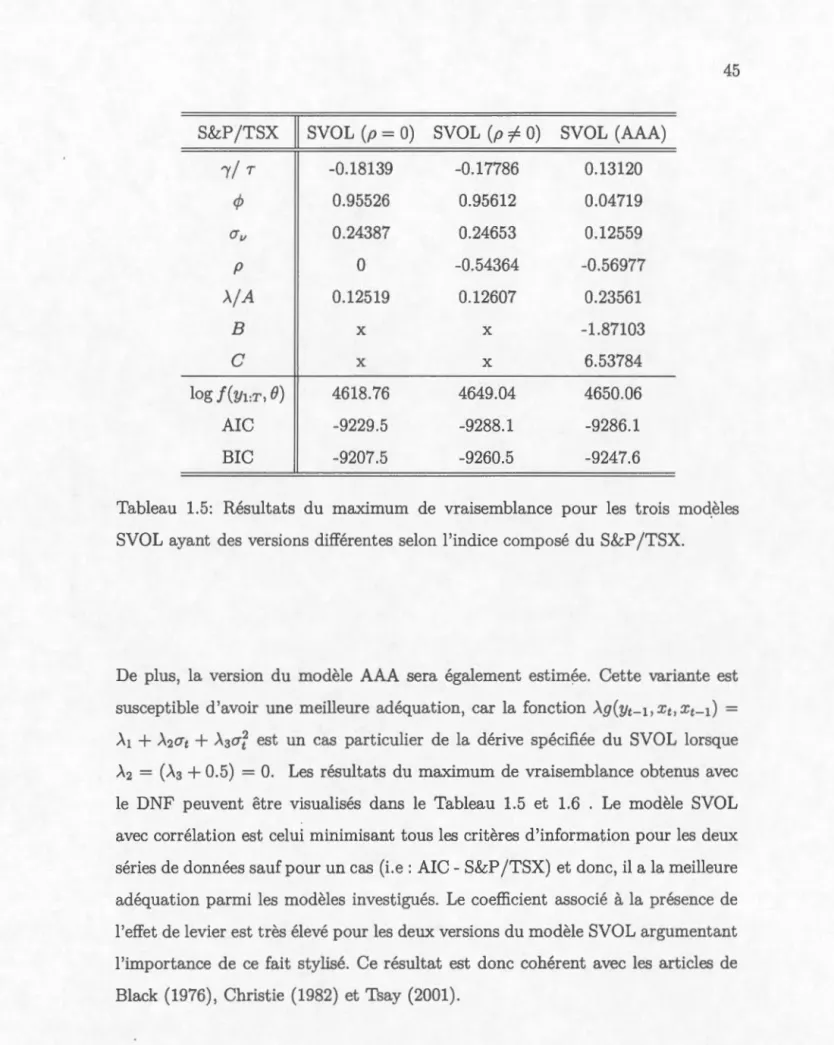
-0. 7) où le biais moyen est répertorié ainsi que l'écart-type entre parenthèse. . . . . . . . . . 42 1.5 Résultats du maximum de vraisemblance pour les trois modèles

SVOL ayant des versions différentes selon l'indice composé du S&P /TSX. 45 1.6 Résultats du maximum de vraisemblance pour les trois modèles

SVOL ayant des versions différentes selon l'indice composé du S&P500. 46 1.7 Résultats du maximum de vraisemblance pour les cinq modèles

stochastiques selon les indices composés du S&P /TSX et S&P500. Pour les détails sur les paramètres, se référer au tableau A.l dans l'annexe.

2.1 Quantiles empiriques des erreurs relatives absolues ~abs-rei (%) se-49

lon les 50 000 jeux de paramètres et trajectoires aléatoires. . . . . 7 4 2.2 Résultats numériques de l'étude des propriétés asymptotiques du

DNF dans le modèle de Heston. Le biais sur les paramètres et l'écart-type entre parenthèses y sont inscrit. . . . . . . . . . . . . 77 2.3 Résultats du maximum de vraisemblance pour les trois modèles

3.1 Résultats de la perte non-couverte de la garantie GMMB. La co-lonne de gauche représente les résultats selon les paramètres du S&P /TSX tandis que celle de droite est selon l'indice du S&P500. 93 3.2 Résultats des erreurs de réplications Err(r) de la garantie GMMB

où la fréquence de re-balancement est mensuelle. La colonne de gauche représente les résultats selon les paramètres du S&P /TSX tandis que celle de droite est selon l'indice du S&P500. . . . . . . 94 3.3 Résultats des erreurs de réplications Err(r) de la garantie GMMB

où la fréquence de re-balancement est hebdomadaire. La colonne de gauche représente les résultats selon les paramètres du S&P /TSX tandis que celle de droite est selon l'indice du S&P500. . . . . 94 3.4 Résultats des erreurs de réplications Err(T) de la garantie GMMB

où la fréquence de re-balancement est journalière. La colonne de gauche représente les résultats selon les paramètres du S&P /TSX tandis que celle de droite est selon l'indice du S&P500. . . . . . . 95 3.5 La prime unique 1r et la volatilité implicite utilisée dans le modèle

de Black-Scholes sous la mesure

Q

lors des résultats des erreurs de couverture du GMMB. . . . . . . . . . . . . . . . . . . . . . 95 A.1 Résultats du maximum de vraisemblance pour les quatre modèles

stochastiques selon les indices composés du S&P /TSX et S&P500. 100 A.2 Résultats du maximum de vraisemblance pour le modèle MS-GARCH

selon les indices composés du S&P /TSX et S&P500. . . . . . . . . 101 A.3 Résultats du maximum de vraisemblance pour les cinq modèles

Figure

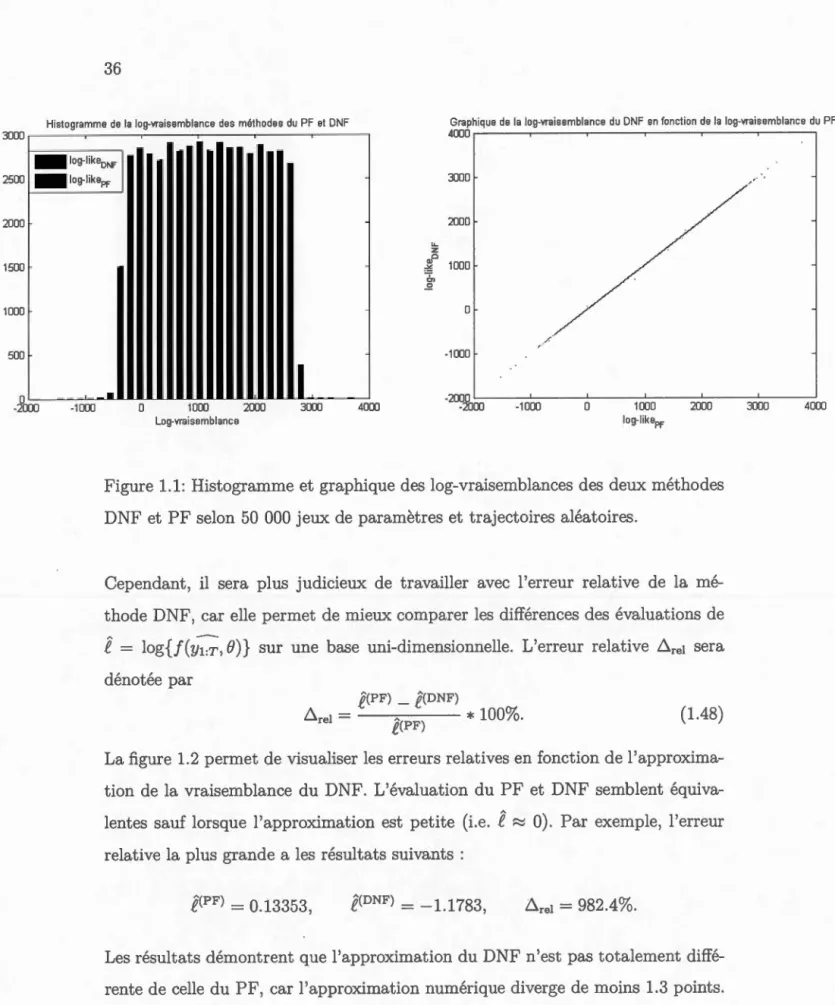
1.1 Histogramme et graphique des log-vraisemblances des deux mé-thodes DNF et PF selon 50 000 jeux de paramètres et trajectoires

Page

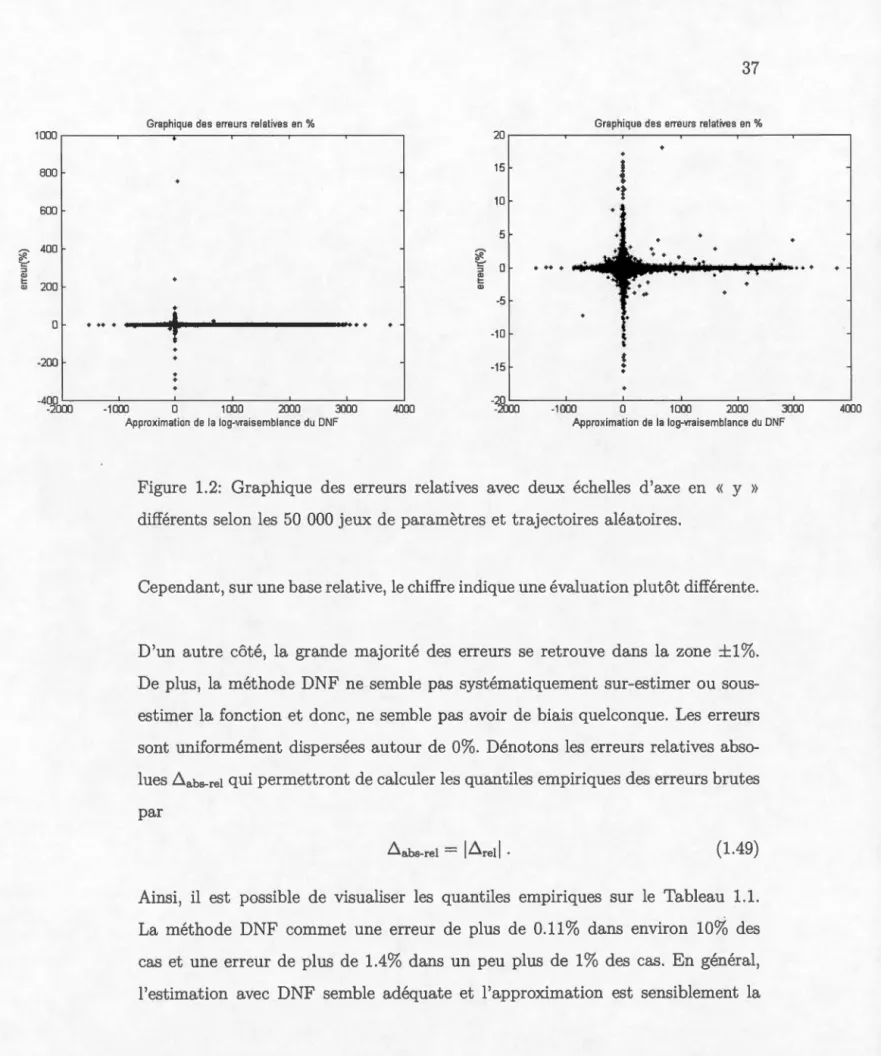
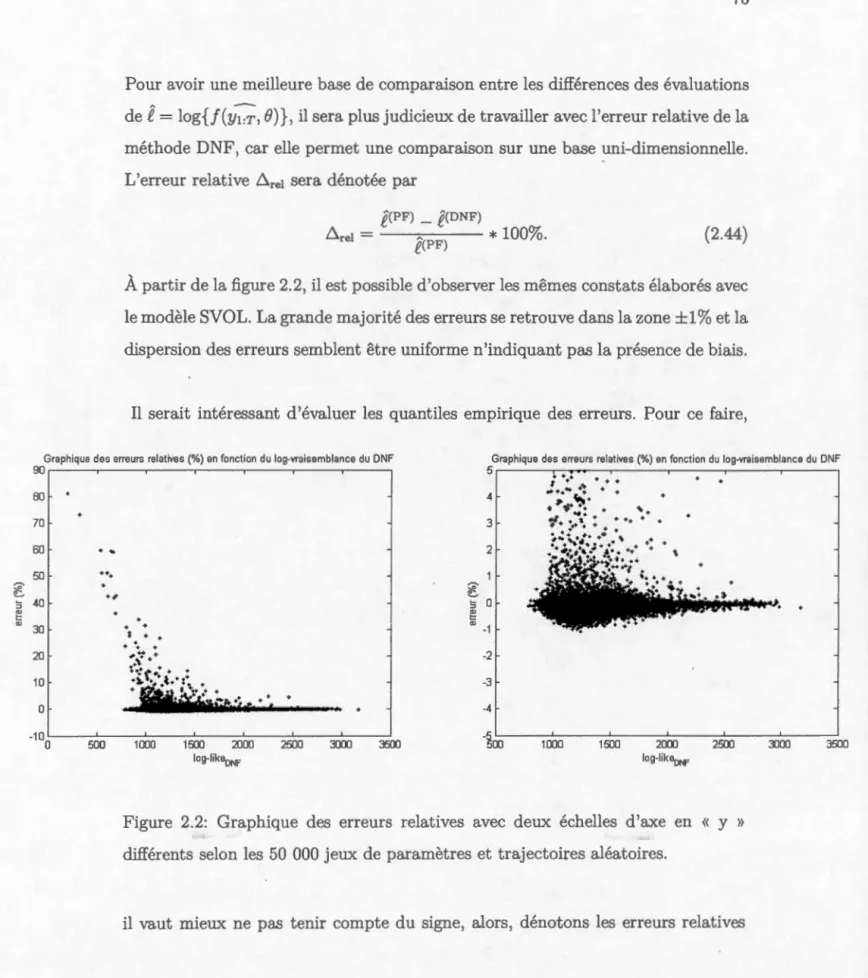
aléatoires. . . . . . . . . . . . . . . . . . . . . . . . . 36 1.2 Graphique des erreurs relatives avec deux échelles d'axe en « y »

différents selon les 50 000 jeux de paramètres et trajectoires aléatoires. 37 2.1 Histogramme et graphique des log-vraisemblances des deux

mé-thodes DNF et PF selon 50 000 jeux de paramètres et trajectoires aléatoires. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72 2.2 Graphique des erreurs relatives avec deux échelles d'axe en « y »

différents selon les 50 000 jeux de paramètres et trajectoires aléatoires. 73 2.3 Graphique des erreurs relatives en fonction de la condition de Feller

Le modèle à volatilité stochastique, qu'il soit défini en temps discret (comme Taylor (1986)) ou en temps continu (comme Heston (1993)), est un modèle très populaire pour représenter l'évolution temporelle du prix d'actifs financiers. Cette popularité provient du fait que ce modèle incorpore plusieurs faits stylisés et p er-met de générer des rendements asymétriques avec des queues de distribution plus lourdes que le modèle de Black-Scholes. Toutefois, l'estimation par maximum de vraisemblance du modèle à l'aide d'une seule série temporelle financière est com-pliquée par le fait que la volatilité n'est pas observable. Ce mémoire analyse nu-mériquement la méthode de filtrage par chaîne de Markov cachée proposée par MacDonald & Zucchini (1997) sur le modèle à volatilité stochastique à temps dis-cret et propose une extension pour estimer le modèle de Heston à temps continu. Cette dernière sera également étudiée numériquement. Pour ces deux modèles, nous comparerons l'approximation par chaîne de Markov cachée avec les filtres à particules. Dans une étude empirique réalisée sur les rendements d'actifs financiers, l'adéquation des modèles à volatilité stochastique est supérieure à plusieurs mo-dèles populaires. Par conséquent, ces modèles sont des alternatives intéressantes pour les assureurs modélisant des fonds distincts en comparaison à d'autres mo-dèles souvent utilisés dans la pratique (par exemple : log-normal à changements de régimes (RSLN)). Finalement, en utilisant les paramètres trouvés précédemment et en comparant avec des modèles populaires, ce mémoire analyse l'efficacité de la stratégie de couverture delta neutre déterminé avec Black-Scholes lorsque le modèle de marché est inconnu. L'idée de l'application est d'analyser la taille de l'erreur de couverture dans un contexte de gestion des fonds distincts venant à échéance à très long terme.

Mots clés : volatilité stochastique, Heston, fonds distincts, stratégie de couver-ture, méthode de filtrage, maximum de vraisemblance.

Les fonds distincts sont des produits jumelant les caractéristiques d'un fonds com-mun de placement et d'une assurance vie. Dans un fonds commun de placement, l'investisseur paie une prime périodique en échange d'une gestion efficiente de son fonds d'investissement. Un fonds distinct permet également à un assuré d'investir dans les marchés financiers comme le fonds commun de placement tout en ayant une forme de protection quelconque lors des rendements défavorables du marché.

La protection prend la forme soit d'une rente périodique minimale ou d'une ga -rantie sur la valeur du fonds à l'échéance effective. Comme l'assurance vie, les protections s'appliquent lors d'événements en lien avec le décès ou la survie de l'assuré. Ce produit incorpore donc des caractéristiques actuarielles ainsi que fi-nancières.

Les fonds distincts sont une alternative visant à compléter les produits conven-tionnels d'assurance vie. Plusieurs avenants aux contrats permettent d'avoir un produit attrayant se distinguant d'un assureur à l'autre. Cela permet aux princi-paux intéressés de s'exposer à long terme aux rendements des marchés financiers et de planifier leur retraite en offrant plus de flexibilité. Par conséquent, les per-sonnes visées par les assureurs sont les gens avers au risque de marché approchant la retraite (âgés de 40 à 55 ans).

Généralement, l'assuré choisit le gestionnaire de son fonds en fonction de son profil de risque (i.e. : un fonds en capital actions, obligations, diversifié, etc.). Par

la suite, l'assureur s'engage à remplir les obligations dictées au contrat. Pour le reste du document, il sera supposé que l'assuré choisit d'investir tout son capital dans un fonds d'investissement qui réplique parfaitement les rendements des in-dices du S&P /TSX ou du S&P500.

Dans l'assurance traditionnelle, la mortalité est le principal et unique risque. Ce risque est généralement supposé comme étant diversifiable car les compagnies d'as-surance ont suffisamment d'assurés. Par conséquent, la théorie des grands nombres s'applique. Donc, les hypothèses actuarielles vont être quantifiées comme étant dé-terministes.

Contrairement à l'assurance traditionnelle, les fonds distincts font face au risque de marché qui est un risque non-diversifiable. Lors de rendements défavorables sur les marchés, tous les contrats vont être affectés négativement. Ainsi, les com-pagnies d'assurance doivent élaborer une gestion active de ce risque. L'idée est de créer des stratégies pour répliquer les garanties offertes. Donc, ils vont prendre des positions dans des instruments transigés sur le marché de sorte à contrebalancer leurs obligations.

Pour comprendre comment gérer le passif actuariel lié aux fonds distincts, il faut en connaître la distribution des résultats. Il est donc nécessaire d'élaborer un gé-nérateur de scénarios économiques. Ainsi, l'assureur pourra évaluer la différence entre son passif et son actif sur chacun des scénarios en supposant une stratégie de couverture. Cela va permettre de fixer la prime du contrat en fonction du risque résiduel et de la profitabilité visée.

À ce jour, il existe plusieurs modèles réalistes pour générer les prix d'un indice financier mais aucun qui ne soit parfaitement valable. Généralement, les modèles

les plus sophistiqués améliorent la qualité de l'adéquation mais sont également plus difficiles à estimer. Ainsi, l'actuaire doit choisir entre un modèle bien estimé à l'adéquation insuffisante ou un modèle sophistiqué mal estimé.

La création de modèles financiers se base principalement sur l'observation de faits stylisés des rendements financiers. Par exemple, une volatilité stochastique, des changements de régimes, des sauts, un effet de levier entre la volatilité sont des exemples de faits stylisés qui ont influencé certains auteurs à proposer un nou-veau modèle dans la littérature financière. Le but est de représenter les rendements boursiers avec un modèle suffisamment sophistiqué captant plusieurs faits stylisés.

Un modèle populaire au Canada pour la tarification des fonds distincts est le modèle lognormal à changements de régimes (RSLN). Une alternative intéres-sante est la classe de modèles incorporant une volatilité stochastique et latente. Parmi cette classe, on retrouve le modèle à volatilité stochastique à temps discret (SVOL) et le modèle de Heston à temps continu. Également, dans un rapport pu-blié en 2005 par l'American Academy of Actuaries (AAA), ce groupe recommande fortement l'utilisation d'un modèle à volatilité stochastique pour la tarifcation des fonds distincts. Cependant, tous ces modèles nécessitent des méthodes numériques exigeantes en temps de calcul pour en estimer les paramètres. Le principal objec-tif de ce mémoire est d'analyser l'estimation par maximum de vraisemblance de divers modèles à volatilité stochastique avec l'objectif que ces modèles puissent être utilisés dans la gestion des risques liés aux fonds distincts.

Après avoir fait une revue exhaustive de la littérature, nous appliquerons tout d'abord la méthode des chaînes de Markov cachée de Zucchini & McDonald (1997) et Clements et al. (2004) à l'estimation de différents modèles à volatilité stochas-tique en temps discret. Ensuite, nous proposerons une extension de la méthode

pour estimer le modèle à temps continu de Heston. Au meilleur de nos connais-sances, il n'existe pas de méthode efficiente d'estimation du modèle de Heston basée sur le maximum de vraisemblance qui utilise seulement les prix d'une ac -tion. Finalement, nous présenterons une brève application à l'analyse de l'efficacité de la couverture de fonds distincts. La structure du mémoire est présentée ci-bas.

Premièrement, le chapitre 1 présente une revue de la littérature concernant les modèles SVOL à temps discret ainsi que les différentes méthodes d'estimation. La section 1.3 approfondit deux techniques d'estimation soit les chaînes de Mar -kov cachées et les filtres à particules. Par la suite, la section 1.4 sert à vérifier le comportement numérique de ces deux techniques d'estimation pour valider leur utilisation. Finalement, la section 1.5 permet de comparer l'adéquation de mo-dèles à volatilité stochastique par rapport à certains autres modèles populaires de la littérature.

Deuxièmement, la construction du chapitre 2 est très similaire au chapitre 1 mais porte sur le modèle de Heston à temps continu. Encore une fois, une revue de la littérature concernant les méthodes d'estimation de ce modèle y est présentée. Les deux mêmes techniques présentées plus tôt y sont appliquées. Les sections 2.3 et 2.4 proposent l'adaptation nécessaire pour permettre l'estimation de ce modèle. Dans un premier temps, il y aura une discrétisation du modèle continu vers un mo-dèle à temps discret. Ensuite, nous proposerons des modifications à la technique d'estimation pour qu'elle demeure valide. La section 2.5 est similaire à la section 1.4 et permet l'analyse de l'efficacité des techniques d'estimation avec le modèle de Heston. La section 2.6 est une extension de la section 1.5 où la comparaison est étendue en incluant le modèle de Heston.

de modèle dans l'efficacité de stratégies de couverture pour la gestion de fonds distincts. Tous les modèles présentés précédemment sont estimés sur deux bases de données (S&P500 et S&P /TSX). Dans la section 3.3, la stratégie de couverture delta neutre dans le modèle de Black-Scholes est analysée lorsque le modèle de marché y est inconnu (SVOL, Heston, RSLN, etc). Ce chapitre est davantage une application numérique simple pour recréer les risques attachés aux fonds distincts.

ESTIMATION DU MODÈLE À VOLATILITÉ STOCHASTIQUE EN TEMPS DISCRET

1.1 Le modèle SVOL

Le modèle à volatilité stochastique (SVOL) à temps discret a été introduit par Taylor (1986). Plusieurs formes sont apparues dans la littérature financière et peuvent être pratiquement toutes écrites comme :

Yt = >.g(Yt-1, Xt, Xt-d

+

<JtEt

(1.1) Xt

= /

+

cPXt-1

+

bp(Yt-1, Xt-1)

+

<Jvllt

où <Jt

=

exp(xt/2) et { /, cfy, <Jv, À, 6) sont des paramètres. Dans cette représenta-tion, les log-rendements Yt sont considérés comme étant observés 1 _{tandis que la} log-variance Xt est supposée latente, non-observée. Une hypothèse simpliste serait de considérer Et et lit comme étant des bruits gaussiens indépendants. Cependant, dans le but de représenter l'effet de levier observé sur les marchés financiers, il vaut mieux considérer Et et lit comme des variables corrélées mais la paire (Et, lit) comme étant i.i.d. dans le temps. Cela est possible lorsque lE[Et · lit] = p. Il est également possible d'y inclure une certaine « corrélation » en incluant un « threshold » dans l'équation de Xt avec la fonction 6p(yt_1, Xt-1 ) comme dans les modèles classiques EGARCH, NGARCH, GJR-GARCH2

. Par exemple, en lien avec le modèle EGARCH, il serait possible de supposer 6p(Yt-l, Xt-1 ) 61(IEt-1l - lE[IEt-11])

+

b2Et-1 qui captera en quelque sorte l'asymétrie des ren-dements.

1. Le log-rendement Yt peut être obtenu comme Yt = log ( ss~1) où St est le prix d'un actif financier.

2. Bollerslev (1986) a introduit le modèle GARCH ( Generalized Autoregressive Conditional Heteroskedasticity). Plusieurs extensions de ce modèle ont été proposées par la suite comme les modèles EGARCH (exponential GARCH) par Nelson (1991), le GJR-GARCH par Glosten, Jagannathan et Runkle (1993) puis le NGARCH (non-linear GARCH) par Engle et Ng (1993).

La fonction >.g(Yt-1, Xt, Xt-1) sert à spécifier la dérive du processus de Yt· Le cas

le plus simple serait tout simplement de poser Àg(Yt-₁, Xt, .'Et-d

=

À

=

p, une constante fixant la moyenne des rendements. Toutefois, la fonction permet d'être

un peu plus flexible. Comme le modèle « GARCH in mean, GARCH-M »,elle pe r-met une portion auto-régressive sur les rendements ainsi que l'ajout d'un terme

hétéroscédastique en fonction de CJZ = exp(xt)· Alors, un autre choix serait de

poser Àg(Yt-1, Xt, Xt-1) = À1 + À2Yt-1

+

À₃r:Jf, Dans la littérature, l'estimation du modèle se fait généralement en fixant Àg(Yt-₁, Xt, Xt-1 ) = 0 tout en utilisant une base de données où la moyenne est soustraite ainsi que les autres composantes auto-régressives et saisonnières.

1.1.1 Autres cas particuliers dans la littérature

1.1.1.1 Version la plus répandue

Plusieurs cas particuliers du modèle (1.1) sont apparus dans la littérature. Par

exemple, la version la plus simple s'écrivant :

Yt = r:Jtét

(1.2) Xt = /

+

cPXt-1

+

fJvVt

où 1E[ét · vt] = Àg(Yt-1, Xt, Xt- d = !ip(Yt-1, Xt-d =O. En supposant des perturba

-tions gaussiennes, les travaux de Melino & Turnbull (1990), Duffi.e & Singleton (1993), Jacquier et al. (1994), Danielsson & Richard (1993) et Shephard (1993)

ont investigué ce modèle. Il y a eu également les travaux de Nelson (1988), Harvey et al. (1994), Kim et al. (1998), Singleton (2001) et Knight et al. (2002) mais dans

une version linéarisée (voir l'équation (1.8)).

1.1.1.2 Version avec des bruits non-gaussiens

Certains auteurs ont permis l'extension du modèle avec des bruits ayant des queues

puisque le but ultimement de ce mémoire est d'utiliser une transformation du processus de Yt (i.e. : St)· Très souvent, dans les contrats de type fonds distinct, il faut calculer des valeurs d'options (ou primes) mais également des mesures de risques (VaR, TVaR, ... ) pour déduire ces primes. Une condition nécessaire pour avoir des prix d'options C(t, St) avec une variance finie (i.e. : carré intégrable), il est requis que

lE[SzJ

< oo

.

Donc, il est préférable d'avoir des perturbations venant de lois gaussiennes, car

l'exponentielle d'une Student, par exemple, ne sera pas toujours de carré inté-grable.

1.1.1.3 Extensions pour une meilleure adéquation

D'autres variantes du modèle de l'équation (1.2) sont apparues pour mieux cap-ter la moyenne de Yt et l'adéquation de la variable latente Xt. Geweke (1994) propose d'inclure des variables exogènes dans l'équation de Yt qui se résume à poser Àg(Yt-l, Xt, X t-l)

=

X

Zt où Zt est un vecteur de variables exogènes et

X

un vecteur de paramètres. Fridman & Harris (1998) ont proposé quelques variantes du modèle dont la plus générale avec un GARCH dans la moyenne et un ajustement dans l'adéquation de la variable latente se résumant à po-ser Àg(Yt-l, Xt, Xt-l)

=

Àcr~ et 6p(Yt-l, Xt-l)

=

61Yt-ll· Dans la même optique, Watanabe (1999) propose de mieux· prédire la moyenne en fixant la dérive par

Àg(Yt-l, Xt, Xt-l)

=

Ào

+

À1Yt-1

+

À2Yt-2

+

À3CT~

+

À4Dt et de rajouter des termes dans l'équation de Xt en fixant 6p(Yt- 1,Xt-l)

=

61Dt

+

62Et-l

+

63IEt-1l où Dt est une variable indicatrice saisonnière (fin de semaine). Évidemment, ces exemples sont seulement quelques cas particuliers parmi ceux proposés dans la littérature financière.

1.1.1.4 Présence de l'effet de levier

Une extension intéressante du modèle SVOL consiste à incorporer un effet de levier entre les rendements et la log-variance. Cependant, les premiers travaux se basaient surtout sur la version transformée (basée sur log yi) et l'information relative à la corrélation entre les processus Yt et Xt est perdue. Pour pallier à ce problème, Harvey et Shephard (1996) ont démontré comment il était possible de retrouver cette information en conditionnant sur le signe (st) de Yt· Cela n'altère pas la distribution du bruit du logEZ et il en résulte ce modèle :

log

yz

=

xt

+

logEZ

(1.3)

Xt

=

r/JXt-1

+

Ast +Dt,

où A = 0.7979pav, B = 1.1061pav, et lE[logEz ·

vt]

= Est. Sachant que Et et Vt sont des normales bivariées où lE[Et · vt] = p, il est possible d'en déduire que JE[vtiEt]

=

pavEt· En dénotant l'espérance conditionnelle sachant que Et est positif par JE+, les constantes A et B proviennent des relations suivantes :

A JE+[vt] ·= pavJE+kt] = pav/iFr

B cov+[vt ·logEz]= pavlE[IEtllogEz]-AlE[logEz].

Cependant, la nouvelle distribution conditionnellement sur le signe St du bruit Dt n'est plus normalement distribuée et causera une perte d'efficacité lors de l'esti-mation du modèle via le filtre de Kalman. En effet, les filtres de Kalman supposent des perturbations gaussiennes. Ce modèle a également été analysé par Sandmann

& Koopman (1998) permettant de capter l'effet de levier, mais avec une autre technique d'estimation.

Par la suite, MacDonald et al. (1997) et Jacquier et al. (2004) ont proposé une

-méthode d'estimation sur le modèle suivant :

Yt

=

O"tEt

(1.4) .'Et= / + cPXt- 1

+

0",_,1/t

où E[Et •1/t] = p, Àg(Yt- 1, Xt, Xt-1)

=

0 et op(Yt-1, Xt-1)

=o. L

a différence parmi les autres modèles est que l'effet de levier est directement modélisé sans avoir recours à des transformations au sein de l'équation de la variable latente.

Également pour capter l'effet de levier, un modèle SVOL avec un «threshold» permettant des paramètres variant dans le temps a été proposé par So et al. (2003) s'écrivant :

où E[Et · vt]

= 0

, St est la variable indicatrice 1l.{yt<O} et

/o

+

St-1/1,

f3st-J

=

f3o

+

St-1f31 cPst-J =cf;o+St- 1cP1

(1.5)

Ce modèle peut pratiquement être écrit sous la forme proposé par l'équation (1.1) en fixant Àg(Yt-1, Xt, Xt- 1)

=

P,o

+

St-1f.11

+

f3oYt- 1

+

St-1f31Yt-1 et Op(Yt-1, Xt-1)

=

St-1{1

+

St_1cj;1xt-l mais n'incorpora pas la portion reliée au coefficient O"~,st_

1

• Cependant, les méthodes proposées dans le mémoire pourraient être adaptées avec quelques légères modifications pour prendre en compte cette portion. De plus, Smith (2009) a proposé une extension du modèle (1.5) pour améliorer l'aspect général de l'effet de levier en rajoutant également une corrélation entre les bruits

1.1.1.5 Cas répandu dans la pratique

Un autre modèle espace-état avec une définition légèrement différente pour la variable latente est celui proposé par l'American Academy of Actuaries (AAA,

2005) pour de la modélisation des rendements mensuels (.6.t = 1/12) dans le

contexte des fonds distincts. Ce modèle s'écrit :

Yt

=

(A+ BO"t

+

CO"z).6.t

+

j"i:;O"tEt

(1.6)

où lE[ Et

:

vt]

=

p. Ils présentent ce modèle avec deux restrictions sur la log-volatilité.

Ce sont des bornes x+ et x- représentant respectivement le maximum et minimum que peut prendre la log-volatilité donc,

À noter que, hormis les deux restrictions, ce modèle pourra être estimé avec les

méthodes présentées plus bas en modifiant légèrement les densités conditionnelles

de Yt et Xt.

Bref, le modèle proposé permet d'englober un vaste nombre de modèles sans avoir recours à des transformations supplémentaires. Son utilisation peut être appliquée

dans plusieurs contextes financiers (taux de change, rendements boursiers, taux d'intérêt, etc.) en incorporant facilement diverses facettes connues de la littérature

selon la représentation de Yt· Par exemple, il pourrait être intéressant d'avoir une

auto-corrélation sur la valeur absolue des rendements qui est facilement intégrable dans la fonction >.g(Yt-1, Xt, Xt-d

=

À1

1Yt-

1

1.

Contrairement à certaines méthodes d'estimation dans la littérature, les méthodes présentées plus bas permettront d'avoiJ; des estimés sur tous les paramètres en une seule maximisation.

1.2 Synthèse des procédures d'estimation dans la littérature

Cette partie analysera principalement les procédures dont l'objet est la mmci-misation de la fonction de vraisemblance. Dans lE! cas du modèle SVOL, il est

impossible d'écrire cette fonction de manière analytique. Pour une série de don-nées Y1:T

=

{y1, . . . , Yr} et de variables d'état Xo:r

=

{x0 , . . . , xr} où x0 est la

variable d'état initiale, la vraisemblance du modèle SVOL s'écrit :

OÙ 8 = {/,4J,Œv,À,6,p} est Un vecteur de paramètres.

Dans une représentation générale des modèles sous la forme espace-état, il est

possible de résoudre ces intégrales avec des filtres de Kalman (KF) si les pertur-bations du systèmes sont gaussiennes et que le lien entre l'équation d'observation et l'équation de la variable latente est linéaire. Sinon, il faut des filtres de Kalman plus sophistiqués (filtre de Kalman étendu (EKF, Extended KF) ou filtre de Kal-man inodore (UKF, Unscented KF)) lorsque le lien n'est pas linéaire.

Dans le cas du modèle SVOL, les perturbations de l'équation d'observation ne sont pas gaussiennes et le lien entre Yt et Xt n'est pas linéaire. Alors, le problème

demeure dans la résolution de cette intégrale de T

+

1 dimensions. Dans un contexte de maximum de vraisemblance, il vaut mieux travailler avec la log-vraisemblance car numériquement la maximisation de la vraisemblance n'est pas envisageable.

Cela engendre l'équation suivante

1.2.1 Estimation basée sur une linéarisation du modèle

Dans la littérature, une des premières approches pour estimer le modèle a été de linéariser le système venant de l'équation (1.1). En prenant le log du carré de Yt., il en résulte un modèle SVOL transformé s'écrivant :

(1.8)

où Àg(yt,-1, Xt, Xt- 1) = 5p(Yt-1, Xt-1) = p = 0 et log( Et) correspond au log d'une

variable aléatoire distribuée selon la loi du chi-carré (X2) avec un degré de liberté. Suite à cette transformation, le système (1.8) est linéaire et additif. Cependant, un nouveau problème survient. Les perturbations de l'équation d'observation ne sont

plus gaussiennes et ne peuvent être approximées par les méthodes traditionnelles de filtrage.

Nelson (1988) et Harvey et al. (1994) ont proposé de façon indépendante d'ap-proximer la distribution du log( X2) par une loi normale de moyenne égale à

'!j;(1/2) - log(1/2) et de variance 1r2 /2 où 'lj; est la fonction digamma. À partir du système (1.8) et de cette hypothèse, l'équation (1.7) peut être calculé avec un filtre de Kalman traditionnel.

Dans la littérature du SVOL, cette méthode est souvent référencée sous le nom de « Quasi-Maximum Likelihood » (QML). Harvey et al. (1994) et Ruiz (1994) remarquent que l'approximation du bruit non-gaussien par un bruit gaussien est adéquat seulement lorsque Œv est grand. En effet, la composante systémique de Xt

dans l'équation d'observation doit dominer le terme d'erreur du log

Et.

Une autre approche a été introduite par Kim et al. (1998) pour régler ce problème. Ils ont approximé le bruit non-gaussien par un mélange de variables normales

jumelé à une procédure bayésienne de re-pondération pour corriger l'erreur de

linéarisation. Cependant, les méthodes « Monte Carlo Markov Chain » (MCMC) ·

sont reconnues exigeantes en termes de calculs. Ainsi, Sandmann & Koopman (1998) ont développé une technique basée sur la simulation pour approximer la log-vraisemblance du bruit non-gaussien. Cette technique « Monte Carlo like

li-hood » (MCL) peut être représentée par cette équation générale

1

(

1

)

_[

ftrue(log X

2

IB)l

log .L(y B) =log .Le y() +log lEe fe (log X2

IB)

(1.9) .

où G signifie la provenance du modèle transformé avec l'approximation gaus-sienne tandis que « true » provient de la vraie distribution du log X2. Or, la log-vraisemblance du modèle peut être vue comme étant celle du modèle QML ad

-ditionnée d'un terme de correction basé sur la densité d'importance fe(log X2

IB).

Contrairement à la méthode MCMC, Sandmann & Koopman mentionnent qu'il

est possible d'être précis seulement avec cinq simulations (N = 5) rendant la

pro-cédure plus rapide.

Singleton (2001) et Knight et al. (2002) ont proposé une approche complètement différente basée sur la fonction caractéristique. Le but sera d'égaliser la fonction

cumulative théorique du modèle transformé à la fonction caractéristique empirique

(ECF). Ainsi, l'estimation reposera sur un critère de minimisation de la distance

entre ces deux fonctions.

Ces différentes approches permettent de simplifier la résolution de l'intégrale (1. 7)

mais rendent pl us difficile l'ajout de faits stylisés des marchés financiers (variables

exogènes, auto-régression, effet de levier, etc). En effet, il faut souvent considérer Àg(Yt-1 , Xt, Xt_ 1 ) = 0 pour que la transformation soit possible et maintenir un

système linéaire. Ainsi, l'estimation du modèle se fera en deux temps. Il faudra

sein de la fonction .>.g(Yt-1, Xt, Xt_1 ). Par la suite, la base de données sera modi-fiée en enlevant ces composantes précédemment estimées. Finalement, l'estimation des autres paramètres se fera avec une méthode quelconque sur la nouvelle base de données. De plus, l'effet de levier peut être incorporé en utilisant l'astuce de Harvey et Shephard (1996) mais nécessite des hypothèses supplémentaires. En général, cette transformation résout un peu la problématique de l'équation (1.7) mais le modèle devient beaucoup moins flexible.

1.2.2 Estimation basée sur le vrai modèle

D'autres approches d'estimation ont été proposées après Nelson (1988) qui ne reposent pas sur des transformations du modèle. Les deux problèmes de l'équation

(1.7) vont être résolus en gardant les propriétés et l'écriture du modèle. 1.2.2.1 Méthodes des moments

Les premiers travaux furent basés sur des méthodes des moments (MM). Cela permet d'ignorer la résolution de la fonction de vraisemblance et de résoudre un système d'équations avec autant d'inconnues. Melino & Turnbull (1990) proposent d'estimer les paramètres via une méthode des moments généralisés (GMM) tan-dis que Duffie & Singleton (1993) proposent une méthode des moments simulés (SMM). Ces méthodes sont très simples et requièrent peu de calculs informatiques. Cependant, l'efficacité de ces méthodes n'est pas optimale en les comparant à des méthodes bayésiennes ou de maximum de vraisemblance (ML). Tel que démontré dans les articles de Jacquier et al. (1994) et (2004), ces méthodes sont imprécises quant à l'estimation de O"v surtout lorsque l'estimation de ljJ ~ 1. Les résultats sont

encore moins concluant lorsque le coefficient de variation modifié défini comme étant

est petit. C'est également le cas pour les techniques basées sur QML. Il est im-portant de noter que MM et QML ne sont pas des techniques appropriées car tel que démontré par Jacquier et al. (1994), en économétrie financière le paramètre

<P est près de 1 et le CV est petit.

1.2.2.2 Maximum de vraisemblance

Plusieurs travaux sur les méthodes numériques de filtrage ont permis l'approxi-mation de l'équation (1.7). En ce sens, Danielsson

&

Richard (1993) proposent une méthode générale pour estimer les modèles à variables latentes. En prenant N échantillons d'une distribution spécifique p(B), l'approximation de l'équation ( 1. 7) devient

~

( 1 ) - 1

~

(i)

L Y1, ... , Yr 8 - N L... P ( 8). i=l

(1.11)

Ainsi, l'application de la méthode du maximum de vraisemblance simulé (SML) a été appliquée au modèle SVOL par Danielsson (1994). Le problème demeure de trouver l'échantillonneur optimal qui permet de bien approximer la fonction

p(B). Très souvent, cela requière un algorithme d'optimisation exigeant en calcul informatique.

Deux méthodes plus rapides ont été proposées par Fridman & Harris (1998) et Watanabe (1999) toutes les deux basées sur la méthode d'intégration numérique récursive suggérée par Kitagawa (1987). En utilisant les densités conditionnelles de Yt et Xt, il est possible de construire un filtre récursif dans l'optique d'évaluer l'équation (1. 7) en calculant successivement plusieurs intégrales par morceaux. La différence est dans la résolution des intégrales par morceaux. Kitawaga (1987) a suggéré de résoudre ces intégrales en approximant certaines densités par plusieurs fonctions linéaires. Fridman & Harris (1998) réclame que la méthode d'intégration Gauss-Legendre est plus efficiente. D'un autre côté, Watanabe (1999) propose de

résoudre ces intégrales en discrétisant la variable latente et en résolvant les inté-grales par morceaux avec une méthode trapézoïdale. Ces méthodes ont pour but de maximiser l'équation (1.7) pour approximer l'estimateur de

e.

1.2.2.3 Méthodes bayésiennes

Une approche totalement différente serait d'utiliser des algorithmes bayésiens. Les

premiers algorithmes bayésiens ont été proposés par Shephard (1993) et Jacquier

et et al. (1994) suivis de Geweke (1994). Le but est de créer une chaîne de Markov

récursive basée sur une méthode d'échantillonnage qui finira par converger vers la

densité a posteriori. Ainsi, les paramètres

e

seront approximés lorsque la

conver-gence de cette densité sera atteinte. Il existe une très grande littérature au sujet de

ces méthodes qui est judicieusement abrégée dans l'article de Jacquier et & (2004).

En général, les méthodes bayésiennes et de maximum de vraisemblance sont très

souvent perçues dans la littérature comme étant équivalentes au niveau

compu-tationnelle. De plus, ces deux méthodes sont très souvent exigeantes au niveau

informatique en raison des problèmes de convergence pour les méthodes bayé-siennes ou en raison de la résolution d'intégrale numériques pour les méthodes maximum de vraisemblance.

1.3 Méthodes d'estimation utilisées dans ce mémoire

Le double objectif est de proposer des méthodes accommodant tous les faits

sty-lisés du modèle (1.1) tout en étant efficace (sans biais et rapide). Deux méthodes seront décrites soit celle du filtre non-linéaire discret (D F) proposée par Mac-Donald et al. (1997) et repris par Clement et al. (2004a et 2004b) puis celle d'un filtre à particules (PF).

Ces méthodes requièrent uniquement les densités conditionnelles de Yt et Xt qui

serviront essentiellement à appliquer des techniques de filtrage lors de la résolution des intégrales de l'équation (1.7). En appliquant la décomposition de Cholesky et en introduisant un bruitE; indépendant de Vt, le système (1.1) se réécrit

Et

=

PVt

+ji-

p2E:

Vt

=

Xt

-'Y- c/JXt-1- bp(Yt-1, Xt-1)

Cl v

( ) 1\ iA ( / ) ( Xt- 'Y - c/J.'Et-1 - bp(Yt-1, .'Et-1)

V

2

*

)

Yt

=

Àg Yt-1,Xt,Xt-1 Dt+ ylltexp Xt 2 p · Clv

+

1-PEt

(1.12) où lE[vt · E;] = O. Cela engendre les distributions conditionnelles suivantes :

où flt représente la fréquence d'observation annuelle et

_ \ ( ) 1\ iAexp(xt/2)p (xt- 'Y-c/Jxt-1- bp(Yt-1, Xt-1))

f..Lt - /\g Yt-1' Xt, Xt-1 Dt+

v

Dt .

Cl v

Ces distributions sont déduites avec l'hypothèse que Et et Vt sont des bruits

gaus-siens mais il est aussi possible de faire l'extension avec des bruits ayant des queues plus lourdes.

Les mêmes démarches peuvent être effectuées pour accommoder certaines va-riantes de processus à volatilité stochastique dont celle du modèle de AAA référée par l'équation (1.6). Pour ce modèle, les densités conditionnelles de Yt et Xt en ne

considérant pas les restrictions sont :

(1.14) où

[A B ( ) C ( )] " iAexp(xt)P(Xt- (1- </J).'Et-1- </Jlogr)

f-Lt

=

+

exp Xt

+

exp 2xt u.t

+

y u.t .

CT v

Dans les deux prochaines sous-sections, les méthodes DNF et PF seront présentées

et feront référence à l'écriture de ces deux densités conditionnelles.

1.3.1 Filtre non-linéaire discret (DNF)

Cette méthode a été proposée par MacDonald et al. (1997) et elle permet d'ob-tenir les paramètres du modèle (1.1) en maximisant l'équation (1.7). Le principal avantage de cette méthode est qu'elle permet d'évaluer directement les intégrales (intégrales doubles lorsqu'on inclut l'effet de levier) dans les filtres non-linéaires pour différentes dynamiques de processus à variables latentes. Ceci est possible en discrétisant le domaine de la variable latente en N intervalles adjacents et en supposant des transitions similaires à une chaine de Markov. En opposition, Ki-tawaga (1987), Fridman et al. (1998) et Watanabe (1999) utilisent des techniques d'intégrations différentes pour résoudre le filtre non-linéaire récursif.

1.3.1.1 Trois étapes du filtre non-linéaire

Ces étapes sont grandement inspirées du filtre de Kitawaga (1987) avec quelques modifications. En effet, lors de l'introduction de l'effet de levier, la distribution marginale de Yt ne dépend plus seulement de Xt mais également de .'Et-1 et nécessi-tera une intégration supplémentaire par rapport à Xt_1 . Les étapes feront référence

aux densités écrites à l'équation (1.13).

L'étape de prédiction devient :

(1.15)

et l'étape de mise à jour de Xt conditionnellement à l'information au temps t

est donnée par :

f(xt.iYt, e) = ;_: f(xt, Xt-11Yt, B)dxt-1 f~oo f(xt, Xt-1, YtiYt-1, B)dXt-1

f(YtiYt~1, B)

f~oo r(YtiXt, Xt-1, Yt-1, B)f(xt, Xt-11Yt-1> B)dxt-1 f(YtiYt-b B)

(1.16)

Or, il ne reste plus qu'à déduire la fonction de vraisemblance de Yt qui s'écrit :

f(YtiYt-1, e)

= ;_

:

;_

:

f(Yt, Xt, Xt-11Yt-1, B)dxtdXt-1

= ;_

:

;_

:

r(YtiXt, Xt-1, Yt-1, B)f(xt, Xt-11Yt-1, B)dxtdXt-1·

(1.17)

L'utilité de la méthode DNF est d'approximer numériquement l'intégrale double

de l'équation (1.17) via une technique simple. Ceci va être possible en discrétisant

la variable latente et en l'évaluant de la même manière qu'un processus markovien (HMM) d'une série temporelle discrète. L'adaptation du filtre de Smith (2009) est

très similaire à celle décrite plus haut sauf que la méthode d'intégration utilisée

va dans le sens de celle proposée par Fridman et al. (1998).

1.3.1.2 Discrétisation de la variable latente

L'évaluation du filtre repose sur la discrétisation de la variable latente. Notons X le vecteur représentant les N points uniformément dispersés sur l'intervalle

23 suivant :

(1.18)

où E0 et

Va

signifient respectivement l'espérance et la variance du processus sta-tionnaire de la variable latente 3. La distance ~x engendrée entre chaque points x(k) sera de

(1.19) La fonction 5x(N) sert à assurer la convergence du filtre et elle devra respecter les deux conditions suivantes :

1. lim bx(N) -t 00 N--'too . bx(N) 2. hm - N -t O. N--'too (1.20)

La première condition assure la couverture éventuelle du processus de x1 tan-dis que la deuxième condition sert à créer un raffinement dans la partition. Il existe une multitude de fonctions 5x(N) satisfaisant les deux conditions dont 5x(N) = 5

+

log(N). Évidemment, la spécification de cette fonction devra être cohérente avec la distribution de x1 surtout lorsque 5p(Yt-1, x1_1) =1= O. Le but est de couvrir le plus efficacement le domaine de x1. Cette spécification sera utilisée pour le reste du document et celle-ci n'est pas nécessairement plus valide qu'une autre.

La distribution de la variable latente est continue et devra être découpée en plu-sieurs intervalles centrés sur chaque x(k). À partir des points X, il sera possible de

3. Advenant le cas où op(Yt-1, Xt-1) = 0, il est possible de conclure que limk-->oo lE[Xt+k] =

"Y/(1- cf;) tandis que limk-->oo Var[Xt+k] = a~/(1 - 4;2

). Dans le cas contraire, il faudra adapter

construire N sous-intervalles C (.) comme étant : x(k)

+

x(k-l) c(k)

=

2 , k

=

2, ... N c(1) = -oo, c(N

+

1)

=

oo C(k) = [c(k), c(k

+

1)], k= 1, ... N, (1.21)

où les bornes c(1) et c(N

+

1) assurent que l'entièreté de la distribution est c

ou-verte et donc, la sommation des probabilités se~a toujours égale à un. Ainsi, l'idée

de cette construction est que le point x(k) représente toutes les valeurs possibles

de l'intervalle C(k). Donc, plus N sera grand, plus l'intervalle sera petit et plus l'approximation sera valide.

Dénotons la matrice (t ,j) Vi, j = 1, ... N représentant les probabilités du pro

-cessus Xt de transiter à partir de l'intervalle centré sur xU) au temps t - 1 vers

l'intervalle C(i) au temps t par

q

fi,j)

=

q(xt E C(i)lxt-1 E C(j),Yt-l,e)

l

c(i+l) ( .) ~ q(xt!Xt~l> Yt-l, e)dxt. c(i) (1.22)

Cette matrice N x N sera invariante lorsque 6(Yt-l, Xt-l) n'est pas fonction de Yt-l· Il est possible de con.sidérer un vecteur X qui tient compte de Yt-l pour mieux

cibler le domaine de la distribution de Xt mais la construction de l'intervalle devrait pouvoir capter toutes les valeurs lorsque N -t oo. Par conséquent, la distribution

conditionnelle de Yt sachant Xt E C(i) et Xt-l E C(j) pourra être discrétisée par

f~i,j) ~ r(yt!Xt E C(i), Xt-l E C(j), Yt-l, e)

(1.23)

1.3.1.3 Algorithme

L'algorithme suppose un vecteur X fixe et ce dernier s'ajuste facilement dans le cas contraire.

Initialisation (t = 0)

- Création du vecteur X selon l'équation (1.18)

- Calcul du vecteur de probabilités d'observer x(i) E C(i) à partir de la distribu-tion incondidistribu-tionnelle comme étant :

. 1c(i+1)

U~

=

q(xol11)dxo,

c(i)

i

=

1, ... ,N. Boucle pour t = 1, ... , T

- Construction de la matrice ct·j) à partir de l'équation (1.22) si op(Yt-1, Xt-1) -=!= 0

sinon cette étape se fait dans la partie initialisation parce que la matrice sera invariante.

- Calcul de la matrice (N x N) des probabilités prédictives jointes d'observer

x~i) E C(i) et x~~\ E C(j) comme étant :

pt(i,j)

=

p(x~i), x~~11Yt-1, 11)

( i) (j) (j)

= q(xt lxt.-l> Yt-1, 11)p(xt-11Yt-1, 11) (1.24)

~ qA(i,j) u<j)

~ t 0

t-1·

- Calcul de la mise à jour du vecteur de probabilité x~i) E C(i) comme étant :

ut(i) = p(x~i) IYt, 11)

" N ( 1 (i) (j) Ll) ( (i) (j) 1 11) ~ uj=1 r Yt Xt , xt-1, Yt-1, o P Xt , xt-1 Yt-1, ~ P(YtiYt-1, 11) " N A(i,j) p(i,j) _ uj=l rt · t f(YtiYt-1, 11)

- Calcul de la vraisemblance d'observer Yt comme étant :

T

f(YLT, 11)

=

f(y1, 11)

II

f(YtiYl:t-1, 11) t=2 T ~ f(yl, 11)

II

f(YtiYt-l, 11) t=2 (1.25) (1.26)

où

N N

(i) (j) (i) (j)

f(YtiYt-I,e) ~ LLr(vtlxt ,xt-l,Yt-l,e)p(xt ,xt-1IYt-1,e) i=l j=l N N - " " " " "';(i..i) p(i,j) - 0 0rt · t i=l j=l et N N

f(yl, e) ~

L L

rii,j) · P1(i,j). i=l j=l

Finalement, l'estimateur

e

sera trouvé en résolvant l'équation suivante :

ê

=

argmax log f(Yl:T, B).

eEe 1.3.2 Filtre à particules (PF)

(1.27)

(1.28)

Les filtres à particules (ou méthodes Monte Carlo séquentielles) sont des procé-dures ayant comme objectif d'obtenir la densité filtrée f (x0,riY1:r) de la variable

latente. Ces méthodes sont principalement basées sur la simulation et convergeront lorsque le nombre de simulations sera infiniment grand. Les propriétés théoriques des PF ont été grandement analysées depuis les travaux de Del Moral (1996). C'est ce dernier qui donna la première preuve robuste du premier filtre à particules de Gordon et al. (1993). Il existe plusieurs excellentes références à ces procédures pour une variété de systèmes à espace-état où la vraisemblance ne peut être écrite de manière analytique. Les références classiques sont Doucet et al. (2001), Aru

-lampalam et al. (2002) et Creai (2012). Récemment, Pitt et al.(2014) ont permis l'estimation de plusieurs modèles à volatilité stochastique avec le filtre à particules dont le modèle SVOL avec des sauts dans l'équation des rendements.

1.3.2.1 Échantillonnage d'importance bayésien (BIS)

L'intuition du filtre à particules est de calculer des quantités du type lE[h(::r0,r)

ly

1,r], une espérance d'une fonction des variables d'état conditionnelle aux observations.

Par définition, cette espérance s'écrit :

(1.29)

et correspond à une intégrale de T

+

1 dimensions. En général, il est difficile

de simuler à partir de la densité filtrée f(xo,riYl:T) puisqu'elle n'est pas dis po-nible pour tous les systèmes à espace-état. Alors, il faudra utiliser la technique

de l'échantillonnage d'importance qui consiste à introduire une densité alte rna-tive f*(x₀,_rly1,r) avec l'objectif de pouvoir simuler à partir de celle-ci. À l'aide de quelques manipulations, l'équation (1.29) se réécrit comme étant :

E[h(xo:T) IYl:T]

=

j

h(xo,r )f(xo,riYl:T )dxo:T

J

)

f(xo,riYLT) *(

=

h(xo:T !*(

l

)

f Xo,riYl:T )dxo,r

Xo:T YI:T

J

f (Yl:T lxo:T) f ( Xo:T) *

=

h(xo,r)f*(

l

)J( )f (.7.:o,riYI:T)dxo,r

Xo:T YI:T Yl:T

(1.30)

=

J(y~

,

r)

j

h(xo,r )wr(xo:T )j*(xo,riYl:T )dx0,r

où le poids non-normalisé wr et la fonction de vraisemblance f(y 1,r) sont :

( ) f (Yl:T lxo:T) f ( Xo:T)

WT Xo·T

=

· f*(xo,riYI:T)

f(Yl:T)

=

j

wr(xo:T )J*(xo,riYI:T )dxo:T·

(1.31)

En décomposant f*(.7.:o:riYI:T) par

!*( Xo:T l Yl:T ) = f*(Yl:rl!x* ( o_Yl:T _:)J*(_T ) xo:T) (1.32)

permet à l'équation (1.31) d'être calculable. Par conséquent, lQ[h(

)l

]-

f h(xo,r)wr(

xo,r)J*(xo,riYI:T)dx0,r ID xo

_·

·T Y1·

_·

T -

_J

( ) (

l )

wr Xo:T !* Xo:T YI:T dxo:T

E*[h(xo:T )wr(xo:T) IYl:T] (1.33) E* [wr(xo:T) IY1:rl

où E* signifie l'espérance prise par rapport à J* et cette espérance sera approximée en simulant N* réalisations de x₀,r appelées particules. L'estimateur Monte Carlo

de cette espérance est calculé comme étant : N* A 1 " (i) -(i) lE[h(xo:r)JYl:T] ~ N* L...,h(xo:r)wr i=l ( i) (i) -(i) Wr (xo:r) Wy

=

1 " N• (i)( (i) ) . N• L...i=l Wy Xo:T (1.34)

Cet algorithme permet de calculer une espérance échantillonnée ajustée en s

imu-lant à partir de

f*

plutôt que de

f.

Toutefois, cet algorithme est impraticable en

raison de la dimension du problème et la prochaine section présentera une façon

de rendre cet algorithme applicable en pratique.

1.3.2.2 Échantillonnage d'importance séquentiel (SIS)

L'échantillonnage d'importance séquentiel sert à réduire la dimension de BIS tout

en conservant les fondements de cette procédure. Pour ce faire, trois hypothèses

devront être postulées qui sont :

1. les observations courantes et passées de la densité alternative

f*

ne dé

-pendent pas des observations futures;

2. l'évolution temporelle des états est markovienne sachant l'information passée

Ft-1

=

{y1, ... , Yt-1};

3. les observations, sachant les états et l'information passée, sont conditionnel

Après quelques manipulations, la densité alternative filtrée devient f*(xo:riYl:r) = f*(xr, Xo:r-liFr)

= f*(xrlxo:r-l, Fr)f*(xo:r-liFr)

= f*(xrlxo:r-l,Fr)f*(xo:r-liFr-d (*)

= f*(xrlxo:r-l, Fr )j*(xr-llxo,r-2, Fr-df*(xo:r-21Ft-d (1.35)

r

=

f(.To)

II

f*(xtiXo:t-l, Ft)·

t=l

où la ligne ( *) est justifiée par l'hypothèse #1. Selon le théorème de Bayes, le numérateur de l'équation (1.31) se réécrit comme

(1.36) et avec quelques manipulation, on obtient

f(Y1:r,Xo:r)

=

f(Yl:r-1,Xo:r-1,Xr,Yr)

= f(xr, YriY1:r-1, Xo:r-l)f(Yl:r-1, Xo:r-1)

= f(Yrlxr, Xo:r-1, Fr-1)f(xrlxo:r-1, Fr-l)f(Yl:r-1, Xo:r-l)

=

f(Yrlxo,r, Fr-l)f(xrlxo:r-1, Fr-df(YI:r-2, Xo:r-2, Xr-l, Yr-l) r

=

II

f(Ytlxo:t, Ft-I)f(xtlxo:t-1, Ft-d· t=l

(1.37)

À l'aide des égalités précédentes, cela permet une écriture récursive du poids de

l'équation (1.31) comme étant :

Tif

=l

f(Ytlxo:t, Ft-df(xtlxo:t-1, Ft-l)

wr

=

r

Tit

=

l

f*(xtlxo:t-l, Ft)

=

Tif

=1

1 f(Yti.To:t, Ft-1)f(xtlxo:t-1, Ft-d { f(Yri.To:r, Fr-l)f(.Trlxo:r-1, Fr-d}

TI[

==ï_

1 _{f*(xtlxo:t-1, Ft) f*(xrlxo:r-l, Fr)}

=

Wr-l f(Yrlxo:r, Fr-1)f(xri.To:r-1, Fr-l) f*(xrlxo:r-l, Fr)

Cependant, cet algorithme souffre d'un problème de dégénérescence des poids ( weight degeneracy), car le SIS simplifie l'expression du poids en une équation récursive. Chopin (2004) a démontré que la variance des poids d'importance du SIS croit de manière exponentielle. Après quelques itérations de l'algorithme, une

faible minorité de particules auront des poids élevés et le SIS sera ultimement une

fonction d'une seule particule.

1.3.2.3 Échantillonnage d'importance séquentiel avec ré-échantillonnage (SISR)

Dans le but de pallier au problème de dégénérescence des poids, une stratégie serait d'appliquer une étape supplémentaire, un ré-échantillonnage ( resampling) des particules. L'idée consiste à tirer aléatoirement (avec remise) des particules parmi les N* couples (x~i), Wt(i)) où

w?)

est le poids normalisé d'une certaine particule se dénotant par

(1.39)

À chaque itération, un nouvel échantillon sera composé en multipliant les parti-cules probables et en éliminant les particules improbables. Cependant, cette stra-tégie introduit un nouveau problème qui est l'appauvrissement de l'échantillon ( sample impoverishment). En effet, certaines particules auront des poids élevés et se feront tirer plus fréquemment composant en majorité le nouvel échantillon.

Pour solutionner le problème de l'appauvrissement de l'échantillon, les nouvelles particules devront être tirées aléatoirement au sein d'une distribution continue. Par exemple, un ré-échantillonnage continu basé sur une densité à noyau (ker-neZ smoothing) ou le ré-échantillonnage proposé par Pitt (2002) et Malik & Pitt (2011) sont envisageables. Ainsi, à chaque étape de l'algorithme, la distribution de la variable d'état sera représentée par N* particules différentes. ayant des poids normalisés tous significatifs.

1.3.2.4 Choix de la densité alternative filtrée

Selon l'hypothèse #2, la densité

f*

est choisie de sorte qu'elle ne dépend que de

Xr- 1 et Fr_{- 1} ce qui en résulte l'équation du poids suivante :

f(Yrlxo:r, Fr-1)f(xrlxr-1, Fr-1)

WT = WT-1

f*(xrlxr-1, Fr-d _(1.40)

= wr-1 f(Yrl:ro:r, Fr-d·

Ce choix est connu comme étant le « Bootstrap ?article Filter » (BPF) et permet de simplifier l'écriture du poids. En lien avec l'hypothèse #3 et des densités de

l'équation (1.13), le poids wr correspond à

wr

=

wr-1 f(Yrlxo:r, Fr-d

(1.41)

= Wr-1 r(yrlxr, Xr-1, Yr-d

et le choix de la densité candidate est tout simplement

(1.42)

Il est également possible d'améliorer la distribution des particules à chaque étape en utilisant l'information venant de la distribution de f(x~~~IYu). En effet, cela

permet d'améliorer la prédiction de la particule Xt conditionnellement à la nouvelle

information venant de Yt· L'intuition est d'incorporer les fondements des filtres

de Kalman en utilisant une étape supplémentaire de mise à jour. Cette étape

supplémentaire ne sera pas utilisée car cette amélioration devient négligeable en utilisant N* suffisamment grand.

1.3.2.5 Algorithme

L'algorithme décrit est celui du filtre à particules avec ré-échantillonnage (SISR)

basé sur une densité à noyau gaussien. À noter qu'il existe d'autres méthodes de ré-échantillonnage plus efficace dans la littérature.

Initialisation ( t=O)

- Simulation de xg) "' q(x0JB), 2 inconditionnelle 4.

1, ... , N* particules à partir de la densité

Boucle pour t= 1, ... , T

- Simulation de x~i) "' q(xtlx~~

1

, Yt-1 , B), 'i = 1, .. . , N* particules à partir de la densité candidate.

Calcul des poids comme étant :

(i) (i) (i) (i)

wt =wt-lr(vtlxt ,xt-I,Yt-I,e)

(1.43)

où le signe proportionnel est valable seulement lorsqu'il y a un ré-échantillonnage

à chaque étape. Suite au ré-échantillonnage, le poids de toutes les particules

de-vient w~i) =

1/

N*.

- Ré-échantillonnage en deux étapes à partir des N* couples (x~i),

w?l)

où Wt(i) est le poids normalisé de chaque particule selon l'équation (1.39).

1. Ré-échantillonnage avec remise selon une distribution multinomiale et for-mation de N* nouveaux couples où le nouveau poids normalisé sera

1/

N* pour toutes les particules.

2. Ré-échantillonnage selon une distribution à noyaux gaussiens à partir des nouveaux couples. Le paramètre de lissage h ( bandwidth) est

h =

(~)1/

5

3N*

où s est l'écart-type de l'échantillon des x~i) à l'étape (1). Il peut être démontré que cette fenêtre h est celle minimisant le critère de « mean

integrated squared error » (MISE).

4. L'initialisation de la volatilité pourrait être fixée à une valeur pré-déterminée telle que

Posons les nouveaux N* couples comme étant :

où x~i) est la nouvelle particule ré-échantillonnée à partir de la distribution à

noyaux gaussiens.

Fonction de vraisemblance du SISR

La dernière étape consiste à écrire la fonction de vraisemblance. Hürzeler &

Künsch (2001) démontrent qu'un estimateur sans biais de la fonction de

vrai-semblance est

T

](y1,r,

e)

=

II

wt

t=l

(1.44)

où wii) est le poids avant l'étape de ré-échantillonnage. Par la suite, l'estimateur

e

sera trouvé en résolvant l'équation suivante :

1.4 Étude Monte Carlo

ê

=

argmax log ](Yl:T, 8).

0E8

(1.45)

Les deux méthodes de la section 1.3 servent à approximer numériquement la fonc-tion de vraisemblance. Le but de cette section est de valider (ou d'invalider) que la

méthode DNF est une approximation robuste pour la fonction de vraisemblance. La qualité de l'approximation sera analysée de deux façons. Premièrement, la qua

-lité de la fonction de vraisemblance approximée sera vérifiée en plusieurs points

aléatoires. La base de comparaison sera le filtre à particules avec un très grand nombre de particules. Deuxièmement, les propriétés statistiques asymptotiques

1.4.1 Étude de la fonction de vraisemblance

Plusieurs applications sur les filtres à particules démontrent leurs propriétés

asymp-totiques lorsque N*

---+

oo et c'est pourquoi il est possible de considérer l'évaluation

de la vraisemblance selon la méthode du PF comme étant « exacte ». Ces a

pplica-tions ont été réalisées par plusieurs auteurs dont Del Moral (1996), Doucet et al.

(2001), Doucet & Johansen (2008) et Creal (2012). Ainsi, il sera possible de com -parer l'approximation du DNF versus PF selon un jeu de paramètres

e

et d'une

série d'observations y1,y. Alors, plusieurs évaluations de la fonction f(YLr, B) p

er-mettront de conclure, s'il existe, un potentiel biais sur la fonction.

L'étude se basera sur 50 000 jeux de paramètres tirés aléatoirement sur le

do-maine plausible de B. De plus, le modèle étudié est

(1.46)

où Àg(Yt-1? Xt, Xt-1)

=

0, 6p(Yt-1, Xt-1)

=

0, lE[ Et . Vt]

=

p. Le domaine de

e

sera

sélectionné pour valider la méthode DNF en économétrie financière. En ce sens,

il vaut mieux utiliser une transformation du paramètre '"Y pour représenter la

moyenne à long terme du processus de la variable latente. Alors, en posant u

comme étant la moyenne à long terme

u

=

lim E[xt+k] = '"Y/(1-<P),

k--too

l'équation de la variable latente devient

Selon cette écriture, le paramètre u représente la moyenne du processus de l

domaine suivant :

log(0.0012) :::;

u:::;

log(0.52); 0.01 :::;

cp:::;

0.99;

0.01 :::; O"v :::; 1; -0.99 :::;

p:::;

0.99.

(1.47)

où le domaine de

cp

est nécessaire pour avoir un processus stationnaire tandis que le domaine de a-v et p est plutôt usuel. Les bornes de u sont choisies de sorte de représenter une pseudo-volatilité d'un sous-jacent incorporant une fréquence journalière, hebdomadaire, mensuelle ou annuelle. Évidemment, il est possible de transformer le paramètre u vers Î pour avoir l'écriture conventionnelle lorsque

e

est fixé.

Dénotons par g(Jl, j = 1, ... , 50000, le jeu de paramètres tiré aléatoirement sur le

domaine de l'équation (1.47) et par

f(yi{f,,

e(j)) la trajectoire simulée par ce jeu de paramètre. Il est possible de générer 50 000 trajectoires du processus SVOL

chacune ayant 500 observations. Ainsi, il suffit d'évaluer chacune des

approxi-mations (DNF et PF) de la fonction de vraisemblance f(y~~~

00

, g(Jl) pour vérifier la présence de biais. Pour négliger les effets liés aux différentes approximations,

le nombre de particules et la longueur du vecteur X seront fixés à N* = 25000

et N = 150. Néanmoins, il y aura toujours de légères différences entre les deux méthodes même si ces deux paramètres sont très grands, car ce sont des approxi-mations numériques.

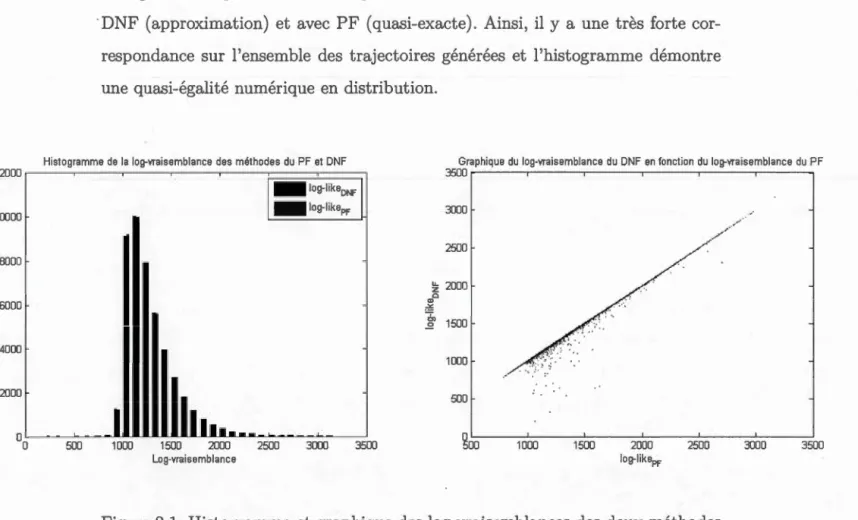
La figure 1.1 représente la correspondance entre la vraisemblance évaluée avec

DNF (approximation) et avec PF (quasi-exacte). Ainsi, sur le graphique, il y a une très forte correspondance sur l'ensemble des trajectoires générées et l