Capital productif, incertitudes et profitabilité

HAL Id: hal-01541929

https://hal.archives-ouvertes.fr/hal-01541929

Submitted on 19 Jun 2017

HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

Capital productif, incertitudes et profitabilité

Edmond Malinvaud

To cite this version:

Edmond Malinvaud. Capital productif, incertitudes et profitabilité. [Rapport de recherche] Institut de mathématiques économiques (IME). 1986, 57 p., ref. bib. : 1 p. �hal-01541929�

DOCUMENT DE TRAVAIL

INSTITUT DE MATHEMATIQUES ECONOMIQUES

UNIVERSITE DE DIJON

FACULTE DE SCIENCE ECON OMIQUE ET DE GESTION

n° 93

CAPITAL PRODUCTIF, INCERTITUDES ET PROFITABILITE Edmond MALINVAUD

1. Introduction

Les économistes historiens comme les experts en gestion des entreprises considèrent depuis longtemps que la profitabilité des opérations productives constitue le stimulant essentiel de l'investissement. Jusqu'à une époque récente la théorie économique formalisée n'en faisait pas cas, sans doute parce que la profitabilité est un concept de "déséquilibre" et ne trouvait donc pas sa place dans une réflexion concentrée sur le fonctionnement d'économies de marché où offres et demandes sont censées s'équilibrer.

C'est James Tobin (1969) qui a le premier corrigé cette lacune en introduisant son rapport q qui doit effectivement mesurer la profitabilité des investissements productifs. Mais il l'a fait, presque en incidente de ses travaux sur la gestion des portefeuilles, par une argumentation non intégrée dans la théorie des décisions réelles des entreprises. L'intégration a été réalisée récemment, mais d'une manière qui me paraît insuffisante (voir H. Yoshikai/ua, 1980, et F. Hayashi, 1982). Ce serait les coûts d'ajustement qui expliqueraient pourquoi l'investissement réagit aux variations de la profitabilité. L'argument est certes valable pour les variations à court terme. Mais il a peu de force quand il s'agit de comparer les caractéristiques de la croissance économique dans deux pays distincts ou à deux époques dans un même pays.

- 2

-Si la demande de capital productif est sensible à la profitabilité c'est surtout en raison des incertitudes affectant les opérations productives et de l'irréversibilité des décisions d'investissement. La théorie devrait dont considérer prioritairement cet aspect des choses, qui va justement être examiné de près ici (1).

L'objet de l'article est donc d'étudier pourquoi et comment, dans une pespective à moyen terme, la profitabilité constitue l'un des déterminants fondamentaux de l'équipement en capital productif d'un pays. Cette étude vise à doter la théorie macroéconomique d'un des fondements qui semblent aujourd'hui lui manquer pour la discussion des problèmes de notre temps.

Plus précisément, je me propose d'étudier de façon approfondie un modèle que j'estime approprié. Ce modèle traite des décisions d'une firme, donc uniquement d'un "équilibre partiel" et sans considération des effets que l'agrégation peut entraîner. Il repose aussi sur diverses autres simplifications. C'est pourquoi, après qu'il ait été étudié de près, les dernières sections de cet article seront consacrées à l'examen séparée de diverses complications.

Cependant, une formalisation purement statique sera retenue tout au long de l'article (2). Le souci est évidemment de réduire la modélisation à ses éléments essentiels de façon à pouvoir pousser loin

(1) Cet article reprend et complète une note de travail non publiée, à laquelle je me suis souvent référé dans le passé (E. Malinvaud, 1983). (2) La modélisation intertemporelle généralisant la spécification statique de cet article a été étudiée par P. Artus (1984).

l'étude des propriétés de statique comparée qui jouent le rôle principal dans une perspective à moyen terme. On peut encore dire que l ’objet de l'article réside dans la détermination du capital productif désiré. Une théorie complète de l ’investissement suppose encore que soient précisés

les déterminants de la vitesse d ’adaptation du capital effectif au capital désiré. L ’aisance du financement à chaque moment doit alors intervenir. Mais l ’étude peut suivre une démarche familière q u ’il est inutile de discuter ici.

2. Fonction de production (1)

L ’irréversibilité du capital productif a deux dimensions. Au moment où le capital est installé, sont choisies non seulement les techniques de fabrication, mais aussi la taille de la capacité de production. Une fois l ’installation faite, les degrés de liberté sont fortement réduits, q u ’il s ’agisse de la combinaison des facteurs mobiles de production ou du niveau de la production. Ces deux dimensions vont être représentées de la manière la plus simple possible, qui conduit à la version statique de ce q u ’il est habituel d ’appeler aujourd’hui la fonction de production ”putty-clay”.

Raisonnant sur le cas d ’un seul bien produit, nous pouvons représenter la capacité de production par une variable numérique y

S ’en tenant aux seules substitutions techniques entre capital et travail, admettant de plus la constance des rendements d ’échelle, nous pouvons caractériser 1 ’intensité capitalistique par une autre variable numérique k, égale par définition au rapport entre le volume du capital K et la capacité de production.

(1) La spécification est fondamentalement la même que celle retenue par L. Johansen (1972).

- 4

-ci) k =

-4-ÿ

La quantité de travail L à mettre en oeuvre à un moment donné pour 1 1 utilisation de ce capital sera proportionnelle à la production y à réaliser, dans la limite de la capacité de production, le coefficient de proportionnalité étant d'autant plus faible que l'intensité capitalistique est plus élevée. Désignons par g(k) ce coefficient, la fonction g étant donc décroissante. Pour des valeurs données de y et k, la fonction de production à court terme est définie par les deux contraintes suivantes sur y et L :

(2) L = yg(k) y^ÿ

Ainsi, une fois le capital installé, la quantité de travail par unité produite est strictement déterminée. En ce sens on peut dire que capital et travail sont complémentaires à court terme.

On peut encore définir une fonction de production à long terme s'appliquant avant le choix du capital et sous l'hypothèse d'une pleine utilisation de la capacité de production. Déterminant y=y comme fonction de K et de L, elle résulte de l'élimination de k des équations (1) et (2). Elle a alors toutes les caractéristiques familières des fonctions de production à rendements d'échelle constants, bien que la spécification :

(3) L = yg {-y-)

soient moins usuelle que la spécification équivalente :

L'équation (3) montre immédiatement que le taux marginal de substitution ex ante entre capital et travail est égal à -g'(k), donc à l'opposé de la dérivée de la fonction g. L'élasticité de ce taux marginal de substitution par rapport à k est kg"/g'. Par ailleurs le rapport L/K caractérisant la combinaison des facteurs vaut g(k)/k ; son élasticité par rapport à k est donc (kg' - g)/g. Egale par définition au rapport entre cette élasticité et celle du taux marginal de substitution, l'élasticité marginale de substitution ex ante est donc donc donnée par :

-g' [g-kg1]

Capital et travail sont ainsi substituables à long terme.

3. Fonction de demande

En vue de donner la forme la plus simple possible aux décions à court terme, le modèle central retenu ici suppose une forme extrême de la "fonction de demande coudée". Plus précisément l'entreprise est censée n'avoir d'action ni sur le prix de son produit ni sur les coûts des facteurs de production. C'est donc un "price taker". Mais contrairement à ce qu'impliquerait l'hypothèse de concurrence parfaite, la quantité de produit que l'entreprise peut écouler est limitée à une borne supérieure d fixée par la demande, donc exogène. En conséquence la décision à court terme de l'entreprise est représentée par (2) et :

(6) y = Min {y, d }

Cette égalité suppose en fait deux choses. D'une part l'entreprise n'est sujette à aucune autre contrainte que celle de ses débouchés ; en particulier elle peut disposer de la quantité de

- 6

-travail L impliquée par (2) et (6). L'attention est ainsi concentrée sur les situations où l'offre de travail serait excédentaire, ou au moins suffisante. D'autre part les coûts ne sont pas tels que l'entreprise ait intérêt à ne pas satisfaire, dans la limite de sa capacité de production, la demande qui s'adresse à elle. Avec la spécification retenue, seul intervient à court terme le coût réel du travail, rapport entre le coût d'une unité de travail et le prix d'une unité de produit. Soit w ce coût réel. La condition retenue est alors y - wLè 0, soit, compte tenu de (2) :

!

(7) wg(k)Sl

Implicitement il est aussi admis que, si le capital (y et k) est parfaitement fixe et rigide à court terme, le travail est parfaitement mobile, de sorte que le coût du travail est strictement proportionnel à la production ; c'est évidemment une hypothèse simplificatrice, dont il faudra se souvenir au moment de toute transposition du modèle à la réalité.

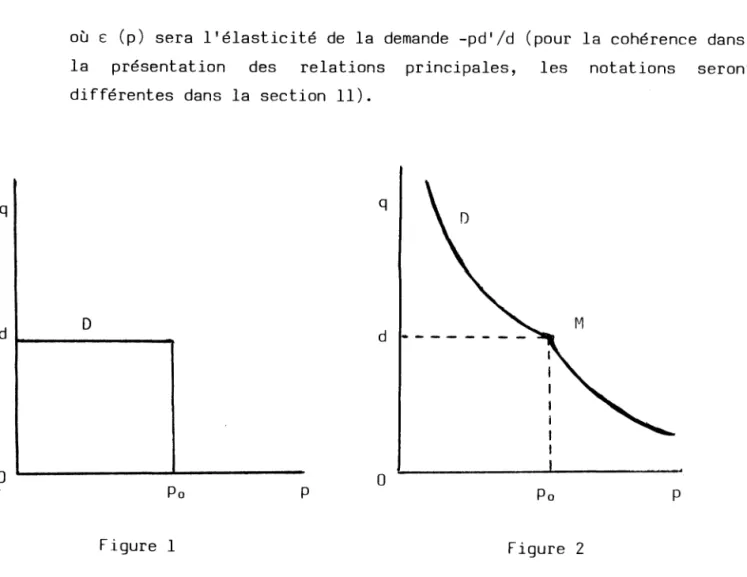
Une brève discussion du choix de cette fonction de demande s'impose sans doute, bien qu'il s'explique d'abord évidemment par un souci de simplicité. Les économistes ne peuvent qu'être conscients de l'allure caricaturale de la courbe de demande qui est ainsi retenue (voir figure 1, où dans le plan prix-quantité (p,q) cette "courbe" à la forme d'une marche d'escalier définie par l'horizontale q=d correspondant au niveau de la demande et la verticale p = p 0 correspondant au prix exogène du produit). Une hypothèse moins sévère, retenant le contexte de la concurrence monopolistique, sera d'ailleurs étudiée dans la section 11. On admettra alors l'existence d'une fonction de demande d(p) familière. Dans ses décisions de court terme l'entreprise, prenant pour donné le coût unitaire nominal du travail s et maximisant son profit, choisira alors un niveau de production tel que :

(8) — g(k) = 1 - 1

e(p)

où e (p) sera l'élasticité de la demande -pd'/d (pour la cohérence dans la présentation des relations principales, les notations seront différentes dans la section 11).

Figure 1 Figure 2

Pour rattacher l'hypothèse retenue dans le modèle principal à cette formulation plus familière, il suffit de remarquer que la forme extrême de la figure 1 ne s'impose pas. Toutes les conclusions du modèle sont encore valables avec une fonction de demande coudée du type de celle de la figure 2, dès lors que la condition (7) est remplacée par la condition plus stricte :

- 8

-(9) 1 - - J- S wg(k) —

d g

w étant le coût réel du travail s/p0 au point M, tandis que et sont respectivement les élasticités de la demande à gauche et à droite du coude. Les inégalités (9) remplacent en effet alors l'équation (8) pour garantir que M corresponde à l'équiibre à court terme de l'entreprise placée en position de monopole face à la demande qui s'adresse à elle.

Fondamentalement est donc en cause l'hypothèse d'une fonction de demande coudée et non la forme extrême donnée ici à cette hypothèse. Le modèle principal peut fournir une approximation admissible si on a des raisons de penser que l'élasticité de la demande est perçue par les entreprises comme devant être nettement plus faible pour les baisses de prix que pour les hausses de prix : il y a beaucoup plus de clients à perdre en élevant son prix au dessus du prix normal p 0 qu'il n'y en a à gagner en baissant son prix au dessous.

Cette hypothèse a été discutée à maintes reprises depuis qu'elle a été introduite explicitement par P. Sweezy (1939) (pour une discussion, voir par exemple T. Negishi (1979); chap. 6 et 7). Récemment J. Drèze (1979) a fait valoir que les entreprises connaissent mal l'élasticité de la demande s'adressant à elles. Cette incertitude, jointe à leur aversion vis-à-vis du risque, les conduit à se comporter comme si elles étaient confrontées à une fonction de demande certaine déformée par rapport à leur espérance mathématique de la demande incertaine, la déformation se traduisant par une diminution de l'élasticité aux prix bas et par une augmentation aux prix élevés.

Il faut surtout retenir l'intuition de Sweezy : la réalité ne se conforme pas strictement au modèle de la concurrence monopolistique ; elle est souvent beaucoup plus oligopolistique. Or l'étude théorique de l'oligopole conduit à attribuer de plus en plus de rôle à 1'"équilibre de Bertrand" où chaque entreprise, ayant à annoncer à l'avance son prix, choisit un prix systématiquement proche de celui de la concurrence, en vue de ne pas perdre sa clientèle (voir par exemple H. Dixon, 1986). De même la recherche de la continuité des relations avec la clientèle, qui s'explique par les économies de publicité et autres en résultant, exige la confiance qu'un juste prix est pratiqué et que les relèvements de tarifs sont motivés par des exigences de coûts s'appliquant à tous les producteurs.

Quoi qu'il en soit de ces justifications fondamentales, la demande d est traité comme exogène et comme connue par l'entreprise au moment de ses décisions de production. En revanche ex ante, au moment du choix de l'équipement, les prévisions de l'entreprise sur la demande d sont affectées d'aléas ; seule est donc connue à ce moment une loi de probabilité de la demande.

Cette loi de probabilité, qui va jouer un rôle essentiel dans le modèle, est représentée par une fonction F où interviennent deux paramètres E et a caractérisant respectivement la tendance centrale et la dispersion de la variable aléatoire d :

(10) Prob {d^a} = F (-■_{l j} —-■_a --)

Bien que la chose ne s'impose pas, on parlera de E comme de l'espérance mathématique de la demande. Ce qui importe vraiment est l'exogénéité de E, de a et évidemment de la spécification précise de la fonction F. On admettra que F est dérivable et l'on notera sa

- 10

-dérivée, la densité de probabilité de d étant donc f/a.

On remarque que la loi de comportement à court terme (6) permet le calcul direct de la probabilité que la capacité de production soit suffisante, ainsi que l ’espérance mathématique du taux d'utilisation de cette capacité y/y. On notera l'une P(y) et l'autre T(y)

; mais il faudra se rappeler qu'elles dépendent non seulement du niveau y de la capacité de production, mais aussi de E et a.

(11) P(ÿ) = F

(12) T(y ) = l-P(ÿ) + G(ÿ)

où par définition :

y

(13) G(ÿ) =

J

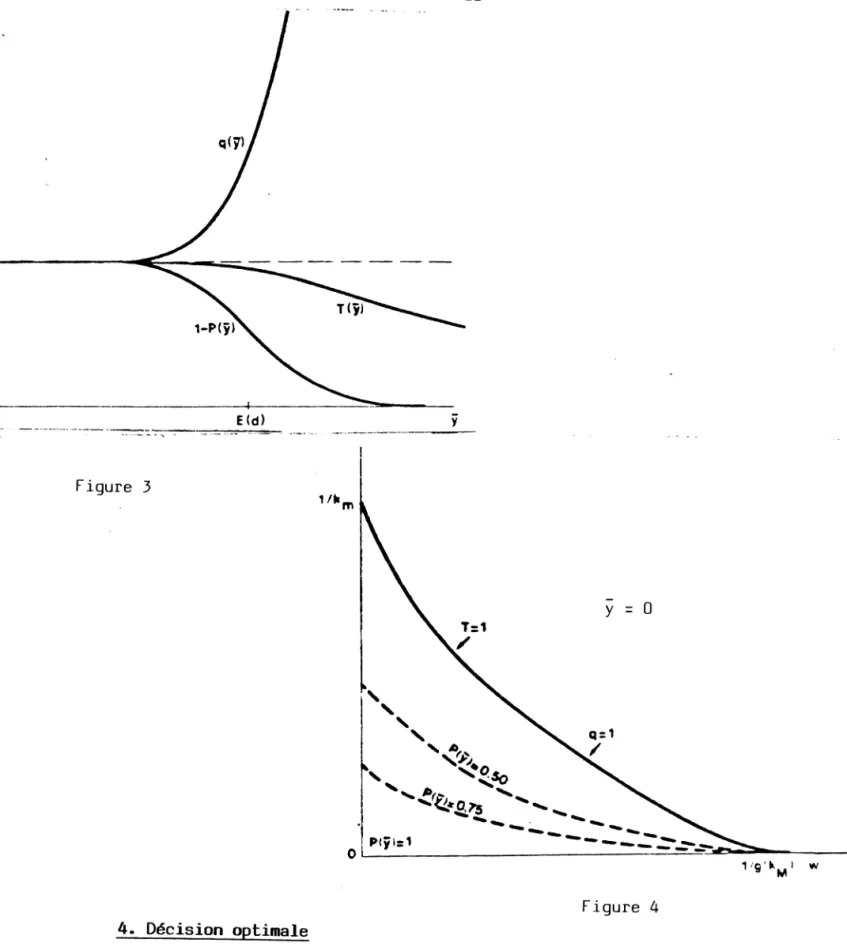
u f (---§--E ) du Y ° o

A titre d'illustration, la figure 3 représente ce que seraient les variations des deux fonctions P et T pour une distribution F à allure normale. La figure comporte aussi la représentation d'un indicateur q(y) qui servira par la suite et est défini par :

Figure 4 4. Décision optimale

Pour le choix de la capacité de production ÿ et de l'intensité capitalistique k l'objectif de l'entreprise, confrontée à une demande incertaine, est supposée être la maximization de l'espérance du profit. A nouveau c'est un souci de simplicité qui explique la présence de cet objectif dans le modèle principal. L'alternative d'un objectif reconnaissant l'existence d'une aversion vis-à-vis du risque sera étudiée dans la section 12.

- 12

-Pour la simplicité des notations, mais sans que ceci change fondamentalement les résultats dès lors que les prix sont exogènes, on retiendra l'espérance du profit réel plutôt que celle du profit nominal. Le coût unitaire réel du capital étant dénoté par r, le profit réel est :

(15) tt = y - wL - rK

ou encore, compte tenu de (2) :

(16) tt = [l - wg(k) ] y - rky

L'incertitude concernant le profit provient surtout de l'incertitude sur la production, laquelle reflète l'incertitude sur la demande en raison de l'égalité (6). Elle peut provenir aussi de l'incertitude sur les coûts des facteurs w et r. Mais cette seconde source d'aléa n'importe pas vraiment si coûts des facteurs et demande sont indépendants en probabilité. En effet, l'expression (16) étant linéaire par rapport à w et r, l'espérance mathématique du profit ne fait alors intervenir que les espérances mathématiques de w et r. Sous l'hypothèse d'indépendance des aléas, on ne perd donc pas en généralité à traiter les coûts w et r comme connus exactement. C'est ce qui sera fait ici.

Le critère à maximiser peut dès lors s'écrire :

(17) W = {[l - wg(k)] T (y) - rk}ÿ

où il est tenu compte de ce que, par définition :

(18) Ey = ÿ T(ÿ)

Le choix optimal de (y, k) est ainsi obtenu par la maximization de W, les grandeurs w, r, E et a étant alors prises pour données. Ce choix optimal peut être caractérisé aisément grâce à l ’étude des conditions du premier et du second ordre.

On note sur les équations (12) et (13) que la dérivée de yT(y) par rapport à y est égale à l-P(y). En conséquence, on écrit directement les deux équations suivantes :

n q ) <std [l - wg(k)] [l-P(ÿ) ] -rk <5y' “

(20) ^ = ~[wg' (k) T(ÿ) + r ]ÿ

Les équations du premier ordre de la maximisation s'écrivent donc :

(21) [l - P (y ) ] [l - wg(k)] = rk

(22) -T(ÿ) g 1(k) = — w

Ces deux équations jouent un rôle fondamental. Leur interprétation économique est simple. La première signifie que le cout réel du capital pour une unité de capacité doit être exactement couvert par le produit entre la probabilité de pleine utilisation de la capacité et le taux de marge brute rapporté par cette utilisation. La seconde signifie que le taux marginal de substitution ex ante entre le capital et le travail, corrigé de l'espérance du taux d'utilisation de la capacité, doit être égal au coût relatif du capital par rapport au travail.

- 14

-L'étude des conditions du second ordre suppose celle des valeurs prises par la matrice H des dérivées secondes de W lorsque les conditions du premier ordre sont satisfaites. Tenant compte des équations (19) à (22) on calcule :

(1-iA/g) m/g ' G

(23) H =

-i/v/g" y 7

où les arguments des fonctions n'ont pas été répétés pour la simplicité de l'écriture. Tous les termes de la matrice H sont négatifs. Pour qu'elle soit négative définie, comme l'exigent les conditions du second ordre, il faut que le déterminant de la matrice soit positif. Tenant compte de ce que 1 - w g = rk/(l-P) et -i/vg' = r/T on peut écrire ce déterminant sous la forme :

(24) r2 A - r2 _{r û - r |^a(1_p)} _____- ¿ 1_{_gI}

Il est effectivement positif si la densité de probabilité de la demande, au niveau de la capacité de production, n'est pas trop faible ; plus précisément si :

(2 5) ïf-... > G - g 1

U } a(l-P) t2 k g 11

Nous reviendrons ultérieurement sur cette condition du second ordre ainsi que sur l'éventualité où, malgré la satisfaction des conditions (21), (22) et (25), le maximum local de l'objectif W ne serait pas un maximum global. Pour le moment nous allons admettre que la solution du système (21)-(22) maximise effectivement W.

Il est instructif de considérer la figure 2 qui illustre la relation entre la capacité de production optimale y et les coûts réels unitaires des facteurs w et r. On note tout d'abord que les valeurs trop élevées de w et r ne sont compatibles qu'avec une capacité de production nulle. Quand le couple (w,r) se situe en un point de la courbe en trait plein, la capacité de production est telle que sa pleine utilisation est garantie 1 - P (y ) = T(y) = q(y) = 1. On peut appeler cette courbe frontière du coût des facteurs. Au fur et à mesure que le couple (w,r) se déplace vers le bas par rapport à elle, la capacité de production croît et la probabilité que la demande ne l'excède pas croît aussi.

Notons au passage que, sur la figure 4, la frontière du coût des facteurs rencontre les axes. Mais il n'est pas indispensable qu'il en soit ainsi. L'hypothèse a été faite que la substituabilité ex ante ne pouvait intervenir que sur un intervalle (k , k^), de valeur de l'intensité capitalistique, entre un minimum k^ pour lequel le taux marginal de substitution serait infini et un maximum k^ pour lequel ce taux de substitution est nul. Quoi qu'il en soit, nous nous trouvons devant une situation théorique atypique où, dans le modèle le plus agrégé qu'il se puisse, avec rendements d'échelle constants, les conditions d'équilibre de la production laissent subsister deux degrés de liberté pour le système des prix.

5. Ratio de Tobin et capacité

L'équation (21) implique une relation très simple entre la capacité de production et un indicateur de la profitabilité des opérations productives, le ratio q introduit par J. Tobin (1969).

Plus précisément ce ratio sera défini ici comme le rapport entre la valeur actualisée de l'espérance des profits et la valeur de remplacement du capital. (La définition initiale de Tobin prenait pour numérateur la valeur boursière de l'entreprise ; on s'en tient ici à une définition qui ne préjuge pas de l'exactitude de cette évaluation).

Dans le modèle statique considéré ici, la valeur actualisée de l'espérance des profits s'interprète comme E(y-wL)/r tandis que la valeur de remplacement du capital est simplement K. En vertu des égalités (2) et (18) on peut écrire :

(26) „ - E(y-wL) _ [ 1 - wg (k)] T(y)

H rk rk

où E est l'opérateur usuel d'espérance mathématique. L'équation (21) implique alors :

(27) q(ÿ) = --- = q 1 - P(ÿ)

où la définition (14) de q(y) reçoit son interprétation.

Ainsi la courbe supérieure de la figure 3 peut maintenant être comprise comme illustrant la relation d'équilibre entre la profitabilité et la capacité de production. A un ratio q proche de 1 correspond une faible capacité de production et un taux espéré d'utilisation de cette capacité lui aussi proche de 1. Au contraire une large capacité de production suppose une valeur élevée de l'indicateur de Tobin.

La simplicité de cette relation conduit à privilégier le ratio de Tobin comme mesure de la profitabilité par rapport à un autre indicateur auquel on se réfère également souvent : 1'espérance du taux

pur du profit. Avec nos notations ce dernier serait W/K ; il vaudrait donc (q-l)r.

Il faut toutefois se garder de donner une interprétation causale directe à l'équation (27). Celle-ci ne détermine pas la capacité de production y à partir de la valeur du ratio q. Ce ratio est lui-même une variable endogène du modèle, ainsi qu'on le voit bien sur l'équation

(26). Nous verrons néanmoins que, moyennant des définitions adéquates, pour les études de statique comparée, une relation directe, au moins approximative, peut être établie entre l'impact des variables de coût sur la profitabilité et les variations correspondantes de la capacité de production.

6. Cas de la loi normale

L'étude des relations de statique comparée partira de la différentiation du système (21)-(22). Elle fera apparaître des expressions, telles celle du déterminant A définie par l'équation (24), où les ordres de grandeur des divers termes ne sont pas a priori familiers. Or tenir compte des ordres de grandeur conduira à des relations approchées intéressantes. En vue de se faire une idée à cet égard, il est utile de considérer des spécifications particulières de la distribution de probabilité F de la demande.

On s'en tiendra ici au cas d'une loi normale, le cas d'une loi uniforme ayant été aussi considéré dans E. Malinvaud (1983). A strictement parler cette loi ne serait pas admissible puisque des valeurs négatives de la demande d sont exclues. Mais cette particularité n'a aucune incidence pratique puisque, pour l'étude d'une firme représentative, on ne fait évidemment intervenir que des cas où

- 18

-espérance mathématique et variance sont telles que la loi normale attribue une probabilité infime aux valeurs négatives.

Si, selon l'usage, on retient $ et cp pour désigner respectivement la distribution cumulée et la densité de la loi normale centrée réduite, on peut directement écrire :

(28) P(ÿ) = $ ( - ^ - ) f = cp ( - ^ - )

On calcule aussi sans difficulté l'expression (13) :

(29) G(ÿ) = -4- $ ( - ¿ ^ ) - -2- cp ( - ^ - )

y ÿ

et par suite aussi l'espérance T(y) du taux d'utilisation de la capacité donnée par l'équation (12).

Ces diverses expressions font intervenir non seulement la valeur y de la capacité, mais aussi les valeurs des deux paramètres E et a. Il est clair que 1 'écart-type a de la loi de probabilité de la demande ne doit être qu'une fraction de l'espérance de cette demande. Pour fixer les idées, on peut examiner en particulier les valeurs obtenues quand a est le cinquième de E et quand ÿ prend les valeurs suivantes : E - a, E, E + a, E + 2a. Les tables numériques usuelles de la loi normale permettent les calculs. Le tableau 1 donne les valeurs de diverses expressions que cette étude amène à considérer.

On peut porter plus particulièrement l'attention sur les deux cas ÿ=E et ÿ = E+a impliquant une probabilité de demande excédentaire respectivement de 50 % et 16 %. Le taux espéré d'utilisation de la capacité se trouve être de 92 % ou de 82 %, correspondant à des valeurs du ratio q de 1,8 ou de 5. On note en particulier que le membre de gauche de la condition du second ordre (25) vaut 4 ou 9 tandis que, dans

2

2

de substitution ex ante considérable pour que la condition du second ordre ne soit pas satisfaite.

Tableau 1

F est la loi normale ; E = 5 g

ÿ E-a E E+a E+2a

l-P(y) 0,84 0,50 0,16 0,023 G(ÿ) 0,14 0,42 0,66 0,69 T(ÿ) 0,98 0,92 0,82 0,71 q(ÿ) 1,17 1,84 5,1 31 G/T 0,14 0,46 0,80 0,97 f 0,24 0,40 0,24 0,05 a = ÿf/a(l-P) 1,2 4,0 9,0 16,4 (l-P)/aT 0,71 0,14 0,02 0,002 7. Hypothèses de régularité

Nous admettrons donc par la suite que cette condition du second ordre est satisfaite. Pour certains raisonneniènts il importe de plus que la fonction q(ÿ) soit croissante ainsi qu'il est supposé sur la figure 3. Numérateur et dénominateur de la fraction (14) définissant cette fonction sont décroissants. Pour que le numérateur décroisse moins vite que le dénominateur il faut et il suffit que :

Nous supposerons aussi que cette condition est satisfaite, le tableau 1 montrant d failleurs qu'elle l fest très largement dans le cas particulier considéré.

Les inégalités (25) et (30) définissent ainsi les ’’conditions de régularité" retenues dans cet article. On n'étudiera pas ici ce qui pourrait se passer si elles n'étaient pas satisfaites. L'étude a été faite dans E. Malinvaud (1983) où ont été examinés en particulier deux cas extrêmes, fort peu vraisemblables : celui d'une élasticité de substitution ex ante infinie, celui où le support de la loi de probabilité de la demande consisterait en deux intervalles disjoints, la densité de probabilité étant nulle dans l'intervalle intermédiaire. Ces cas extrêmes font apparaître la possibilité théorique que, pour certaines valeurs des variables exogènes, la solution (y,k) du système (21)-(22) soit multiple et/ou que le couple des valeurs optimales (y,k) connaisse une ou des discontinuités dans ses variations en fonction des variables exogènes. L'essentiel est d'avoir vérifié que ces éventualités sont effectivement trop peu vraisemblables pour devoir retenir l'attention.

8, Relations de statique comparée

Sous les hypothèses de régularité la différentiation des équations (21) et (22) fait apparaître quelles variations ôÿ et 6k résultent de variations infiniment petites apportées aux variables exogènes : w, r, E et a.

Pour la clarté de l'interprétation, il y a d'ailleurs avantage à ne pas prendre pour variations exogènes indépendantes Siai, ôr, 6E,6a eux

mêmes, mais plutôt quatre variations qui, prises individuellement, sont plus significatives. S'agissant des variations du système des prix, il est naturel de distinguer leurs impacts sur les coûts relatifs et sur la profitabilité :

(3 1) 6c _ 6r 6w

c ~ r iAi

(-5 9) ^ ^ r _ iA/q # 6w

q r 1-iA/g w

Notons en particulier que (32) définit la variation relative du ratio q de Tobin, comme le montre l'équation (26). Mais cette variation concerne uniquement l'impact des variations de prix, comme si y et k étaient maintenus fixes. C'est en vue de rappeler cette convention de définition qu'une notation un peu particulière est introduite dans le membre de gauche de (32). Sans doute n'est-il pas inutile d'attirer ici l'attention sur le caractère naturel de la convention dans la théorie du capital. On connait en effet une source de confusion qui a compliqué les débats auxquels cette théorie a donné lieu : l'intuition suggère qu'un renforcement de l'intensité capitalistique s ’accompagne d'une baisse du taux de profit marginal ; toutefois, même acceptant de se limiter aux cas dans lesquels l'intuition peut être validée, encore faut-il que la variation de la quantité du capital, ou de la période de production, soit définie de façon adéquate, notamment en maintenant conventionnellement fixes les

prix relatifs ; Wicksell lui-même, et bien d'autres après lui, se heurtèrent à d'inutiles difficultés faute d'avoir introduit la convention. La situation est ici symétrique.

S'agissant des modifications affectant la demande on prendra pour variations relatives indépendantes celles de l'espérance E et du coefficient de variation h :

En d'autres termes, quand on étudiera l'effet propre des variations de l'espérance de la demande, on admettra que son écart-type varie simultanément proportionnellement. Au contraire quand on étudiera l'effet propre du degré d'incertitude, on admettra que l'espérance mathématique reste fixe.

Pour les écritures il est enfin commode d'introduire la notation a pour désigner le membre de gauche des inégalités (25) et (30)

(33) h a_E

(34) a

De même, on désignera par e la quantité :

(35) e = d a W = I [ i + rk

]

«Sÿ G Ôk ¿g 6E /, E^ (36) a

- 1— + ■

_T

=■

— r = — a + a —_{k " q °} F _{E T} + a ( l ---) 6h_h

y

y

G ôÿ ôk <5c G ÔE /G E P N ôh (37) T - + e ~ k = - — +

T

" T * (T - -7> “h

y

yT

La solution de ces équations conduit à :

ôÿ ôq ôc ÔE ôh (38) — = a —L + a + + a, ---q c r- n , y H q c E h (39) _ü< = 3 + Bc _ôc + e 6h h k c h

où les six coefficients à ont des expressions intéressantes à considérer :

-

24-(42) cl = 1 - — [ l - ± 7— ( 1 - T ) ]

ÿ T A

(43) . 6h = a(l-T)E ATÿ

où A, déterminant des coefficients du membre de gauche de (36)—(37), a été défini par l'équation (24) et est positif en raison de l'inégalité (25).

On s'intéresse aussi aux variations des espérances de la production Ey et de la demande de travail EL. Il est facile de les calculer à partir des équations précédentes et de :

(44) ¿(Ey) _ô£ _6T ¿(EL) _ 6(Ey) t kg'. 6k

Ey y T EL Ey g k (45) _6T _ _ G . ¿x + Ç 6 E + ( G _ E P ) ¿h T T ÿ T E T ÿ T h On trouve ainsi : (46) _—¿(EL) _{s y _ Ü + Y _}¿q ¿c _{+ _}¿E _{+ Y _}¿h EL ^ q c c E h ou (47) y = [(1-P) e + ] q TA wg T

(48) y = — [(1-P) - + — a ]

c TA T wg

(49) yh = 1 — — { 1 - [(1-P) - + — a ]}

yT T A T wg

Les conclusions suivantes de statique comparée peuvent dès lors être énoncées.

Une modification des coûts qui améliore la profitabilité (Sq > 0) tout en laissant inchangé le coût relatif du travail par rapport au capital a un effet favorable sur la capacité de production et la demande de travail (a et y sont positifs), un effet défavorable sur

q

q

K

l'intensité capitalistique (6^ < 0).

Un relèvement du coût du capital, compensé par une baisse du coût du travail (ôc >0, 6^ = 0), provoque une augmentation de la capacité de production et de la demande de travail (otc > 0, y^ >0) mais une diminution de l'intensité capitalistique (6^ < 0).

Un accroissement de l'espérance mathématique de la demande, accompagné d'un accroissement proportionnel de sa dispersion (ôh = 0), provoque une augmentation exactement proportionnelle de la capacité de production et de l'espérance mathématique de la demande de travail. Il n'a en revanche aucun effet sur l'intensité capitalistique.

Un accroissement de l'incertitude de la demande, qui ne comporte aucune modification de l'espérance de cette demande et qui n'est accompagné d'aucun changement des coûts, a des effets complexes.

26

-Retenant le cas dans lequel la capacité y est supérieure à E et où

G ( 1—T ) est inférieur à T2^, nous voyons sur l'équation (42) que la capacité de production doit augmenter. L'équation (45) montre que simultanément le taux d'utilisation de cette capacité doit diminuer, aussi bien du fait de l'augmentation de la capacité que de celui de l'effet propre du terme en

ôh

(on peut en effet admettre que EP > y G, une inégalité qui est nécessaire si la loi de probabilité est symétrique autour de E, car alors l'intégrale de (u-E)f entre 0 et y est négative si P(y)< 1). La diminution du taux d'utilisation implique une élévation du coût du capital par unité produite r/T, d'où une diminution de l'intensité capitalistique (3^ < 0). Le sens de l'effet de toutes ces variations sur la demande est cependant ambigu, comme l'expression (49) de Ie montre.

9. Lois approchées

Les relations de statique comparée peuvent ainsi être exprimées par les équations (38), (39) et (46). Une discussion des ordres de grandeur des coefficients est cependant intéressante. Elle permet de préciser les résultats de trois manières.

Puisqu'il s'agit d'ordre de grandeur, on peut se satisfaire d'approximations. Celles qui vont être considérées ici partent de l'hypothèse que G/T est négligeable relativement à e . Sur le tableau 1 par exemple a est environ dix fois plus grand gue G/T. Dans l'expression définissant e le crochet est supérieur à 1 ; tant gue l'élasticité de substitution entre capital et travail ne dépasse pas 1, e est lui aussi supérieur à 1.

En premier lieu, notons que l'approximation proposée simplifie les relations, car elle conduit à considérer comme négligeables l'effet des coûts relatifs sur la capacitéde production et l'effet de la profitabilité sur l'intensité capitalistique. En effet si G/T est

2 2

négligeable vis-à-vis de a e, alors G/T l'est a fortiori et A peut être remplacé par a e. Les équations (40) et (41) montrent qu'alors a^ et 3^ peuvent être considérés comme nuls.

Si nous ne cherchons pas à faire intervenir les variations de l'incertitude, nous pouvons dès lors nous en tenir à un système très simple :

(50)

_ a

_Ô£ + —

- q q E (51) 6k n 6c . ~ c (52) 6EL ôq ôc 6E --- - Y — + Y --- -I- --- p r i 'c ’q c E EL q ^

C'est ce système que je proposerais volontiers pour intégration dans toute théorie qui, visant à étudier les déterminants de l'emploi à moyen terme, tiendrait compte non seulement des décisions des entreprises mais aussi des autres comportements agissant sur l'équilibre économique général.

28

-En second lieu, l'approximation permet de voir que l'effet de la profitabilité est très peu linéaire. Après approximation les équations (40) et (47) conduisent à :

(53) a = - _{q a} y =_{*q aT}

Or ces expressions décroissent vite quand on fait varier la capacité de production, à perspectives données pour la demande de biens. La chose est particulièrement visible sur la dernière ligne du tableau 1 où sont données les valeurs de y . En d'autres termes, les élasticités de la

q

capacité de production et de la demande de travail par rapport à la profitabilité sont faibles quand on part d'une situation de profitabilité satisfaisante ; elles sont au contraire très sensibles quand on part d'une situation de mauvaise profitabilité. C'est ce qu'illustre la forme très cambrée de la courbe q de la figure 3.

Au passage il est encore intéressant de noter l'expression approchée de l'élasticité de la demande de travail par rapport au coût relatif des facteurs. De (48) on déduit :

(54) Y = n T _{*c T} + rk lAig

Ainsi cette élasticité est un peu supérieure à l'élasticité de substitution.

Nous pouvons revenir, en troisième lieu, sur l'effet qu'un accroissement de l'incertitude peut avoir sur la demande de travail. L'approximation retenue permet d'écrire y^ sous la forme :

(55) Y h = 1 - s + n . I f f l i r t

yT yT T wg

Dans cette somme de trois termes, seul le second est négatif ; mais il est supérieur à 1 en valeur absolue : le fait que y soit égal au minimum de d et y implique en effet que Ey = yT soit inférieur à Ed = E. Si l'élasticité de substitution était nulle, serait négatif et un accroissement de l'incertitude détériorerait la demande de travail, ainsi que l'intuition le suggère. Mais la substitution du travail au capital fait que, à moyen terme, la demande de travail croît en fonction de l'incertitude, dès lors que l'élasticité de substitution est sensible. La condition pour qu'il en soit ainsi peut s'écrire :

rcis\ T bug + rk ^ E - y T

(56) y = n --- a--- > ---- 1— T wg E (1-T )

Si y est supérieur à 1 le membre de droite est inférieur à 1 (sur le tablieau 1 on constate que ce membre passe de 1 pour y = E à 0,09 pour y = E + a).

Deux considérations doivent être ajoutées pour préciser la portée de ce résultat. D'une part la valeur à retenir pour l'élasticité de substitution dépend de ce que l'on entend par moyen terme. Si l'horizon reste relativement court, l'élasticité de substitution à faire intervenir doit être faible puisque les conditions d'utilisation des équipements déjà installés sont assez rigides. D'autre part, le résultat obtenu concerne l'équilibre partiel des entreprises et suppose constants aussi bien les taux de rémunération w et r que le niveau espéré E de la demande de biens. L'étude de l'équilibre général peut conduire à la conclusion que l'accroissement de l'incertitude modifie les taux de rémunération et déprime la demande. Dès lors il se pourrait que l'effet sur l'emploi soit complètement renversé.

10, Agrégation

On arrêtera ici l'étude du modèle principal que l'article vise à présenter. Il reste à étudier, de façon évidemment beaucoup moins approfondie, les effets de diverses simplifications retenues dans la spécification de ce modèle. On les considérera une par une dans cette section et les suivantes.

Supposer que les lois auxquelles à conduit l f examen du modèle principal s'appliquent directement aux grandeurs agrégées et indicateurs utilisés en macroéconomie appliquée revient à négliger les difficultés de l'agrégation. Comme pour d'autres études relatives aux comportements fondamentaux, les difficultés résultent de la multiplicité des biens, des agents et des techniques productives. Il n'est pas question de les considérer toutes ici. La plupart d'entre elles sont, ou devraient être, familières et n'ont rien de spécifique aux problèmes particuliers considérés. On se limitera donc à quelques commentaires relatifs aux aspects propres de ces problèmes.

Au niveau de la firme représentative, la multiplicité des biens et des techniques a la possibilité théorique de rendre trompeuse l'image d'une substitution progressive du capital au travail au fur et à mesure que le taux de salaire réel s'élève et le taux d'intérêt réel s'abaisse. Les modifications simultanées dans les prix relatifs des divers biens peuvent, dans des cas atypiques, s'opposer à ce qui a été appelé la "capital deepening response". La chose ne serait pas mentionnée ici si elle n'avait pas donné lieu aux débats que l'on sait dans la théorie du capital. A mon avis et jusqu'à preuve du contraire, la portée pratique de cette possibilité théorique est faible, dans le contexte présent comme dans les autres considérés antérieurement.

Mais il faut s'interroger sur ce qui est propre à cet article : l'incertitude sur les débouchés futurs et le rôle de la profitabilité sur le choix des capacités de productions. L'option statique retenue suppose implicitement résolues les difficultés que peut poser l'agrégation sur une multiplicité de périodes futures. L'article de P. Artus (1984) ne conduit pas à trouver là la source d'erreurs importantes ; mais il n'a pas épuisée l'étude de la question.

La multiplicité des biens qui peuvent être produits par une entreprise sur les mêmes équipements, soit simultanément soit alternativement, complique la définition de la capacité de production ainsi que la relation entre production, demande et capacité de production. Confrontée à des demandes données sur les divers produits qu'elle peut fabriquer, aux prix auxquels elle peut alors les vendre, l'entreprise cherche évidemment à tirer le meilleur parti de ses équipements ; mais sa décision ne s'exprime pas aussi simplement que par l'équation (6) selon laquelle y est le minimum de d et y. L'étude théori­ que du problème n'a pas été faite. L'intuition suggère qu'elle n'amènerait pas à modifier fondamentalement les conclusions du modèle simple considéré ici ; mais ceci reste à vérifier. Introduisant par étapes successives des cas s'éloignant de plus en plus de celui de ce modèle, on pourrait supposer d'abord que les conditions techniques impliquent des proportionnalités fixes, qu'il s'agisse de production jointe ou de production alternative, puisque la fonction de production à court terme est séparable entre outputs et inputs.

La multiplicité des entreprises n'oblige pas à une reconsidération aussi profonde. On sait comment opère l'agrégation de lois de comportement relatives à des agents de même nature. Plus précisément, chaque entreprise a ses propres équations de comportement, ayant la forme locale des équations (38), (39) et (46), avec des coefficients a, 6 et y particuliers. La sommation de ces équations, pour

32

-obtenir par exemple la demande globale de travail, suppose que l'on tienne compte de la distribution statistique des variations individuelles des variables exogènes, ou même plutôt de la distribution jointe de ces variations et des élasticités y individuelles. Mais il n'y aurait là rien de particulier au problème considéré si on ne devait pas porter à nouveau l'attention sur l'effet de la profitabilité.

Cet effet est, comme nous l'avons vu, très peu linéaire. De ce fait la dispersion des valeurs individuelles de l'indicateur de profitabilité, appelons les q^, joue un rôle significatif. Si par exemple à la suite d'une perturbation forte des conditions économiques générales, la dispersion des q^ croît sans que leur niveau moyen ne varie, le niveau global désiré des capacités de production et celui de la demande de travail doivent diminuer : les diminutions concernant les entreprises dont la faible profitabilité décroît sont beaucoup plus importantes que les augmentations provenant des entreprises dont la forte profitabilité croît. Ceci signifie que, dans l'étude économétrique des fluctuations de l'investissement global, il faudrait faire intervenir non seulement le niveau moyen de la profitabilité, mais aussi un indicateur de sa dispersion entre les diverses entreprises.

11. Concurrence monopolistique

L'hypothèse d'une fonction de demande coudée, qui a été posée dans la section 3, est commode pour le développement et l'intelligibilité de la théorie étudiée jusqu'ici. Mais elle n'est fondamentale que pour certains des aspects des résultats obtenus, l'essentiel restant le plus souvent l'incertitude sur la demande qui s'adressera à la capacité de production. Pour s'en convaincre, on va traiter ici du cas dans lequel la fonction de demande est deux fois

differentiable et ne présente en rien l'allure d'une demande coudée. La distinction entre augmentation des débouchés et amélioration de la profitabilité disparait alors, ou devient conventionnelle. Néanmoins certaines des conclusions tirées du modèle principal subsistent.

Soit donc R(y,u) la recette marginale qui sera réalisée si la quantité produite et vendue est y. C'est la dérivée par rapport à y de la valeur des ventes S(y,u). Cette recette marginale dépend de la valeur prise par un paramètre aléatoire u, dont on écrira la loi de probabilité cumulative simplement P(u), l'intention n'étant pas ici de considérer à nouveau l'effet des variations dans le degré d'incertitude. Alors que R(y,u) est une fonction décroissante de y, on admettra que c'est une fonction croissante de u, une valeur élevée du paramètre signifiant un état favorable de la demande.

Le cas où la recette marginale serait linéaire, donc où la fonction de demande le serait aussi, permettra de rendre plus transparentes les formules obtenues. Moyennant une paramétrisation convenable de u, on peut l'écrire :

(57) R(y,u) = b(u-y) + e

où b et e sont deux nombres, b étant positif et d'autant plus élevé que l'élasticité de la demande est plus réduite.

A court terme la valeur de u sera connue. Si la capacité de production est suffisante, la production sera fixée au niveau qui égalise recette marginale et coût marginal. Sinon, la production sera égale à la capacité. En d'autres termes y sera donné par :

34

-où y sera solution de :

(59) R(y, u) = i/ug(k)

L ’équation (58) remplace donc l'équation (6), tandis que y apparaît comme une fonction croissante de u et de k, décroissante de w (le fait que y ne dépende pas uniquement de u est une caractéristique nouvelle par rapport au modèle principal, et est source de complications, comme on le verra).

Il est intéressant pour la suite de repérer la valeur du paramètre u qui est telle que la capacité de production soit juste adéquate à l'état de la demande. Cette valeur u est la solution de :

(60) R(ÿ, G) = wg(k)

C'est une fonction croissante de y et k, décroissante de w. L'introduction de u permet d'écrire :

(61) y = y si u iu

(62) y = y si u ^u

La valeur totale des ventes S(y,u), qui a pour dérivée par rapport à y la recette marginale R(y,u), intervient dans la fonction objectif W de l'entreprise de la manière suivante :

u

(63) W =

J

[s(y

,u) - wg(k)y]dP(u'

Calculant les dérivées de W par rapport à y et k, on trouve les deux expressions suivantes qui remplacent (19) et (20) :

° °

(64) — - = J [ (R(ÿ, u) - wg(k) ]dP(u) -rk

ôy u

(65) —— = - [wg'(k) T (ÿ) + r ]ÿ 6k

où T(y), espérance du taux d'utilisation de la capacité, est encore donné par l'équation (12) P(y) étant remplacé par P(u) et G(y) exprimé par

1 u A

(66) G(y) = — J ydP(u)

y

0

Ainsi, dans les conditions du premier ordre de la maximisation, l'équation (22) subsiste sans changement tandis que l'équation (21) est remplacée par :

(67) J_ [R (ÿ, u) - wg(k) ] dP(u) = rk u

(22) - î(y) g'(k) =

Mais l'équation (67) garde la même interprétation que l'équation (21) : le coût du capital d'une unité de capacité doit être exactement couvert par la contribution des cas de pleine utilisation de la capacité à l'espérance du profit brut. Pour retrouver une équation analogue à (21) on peut d'ailleurs définir le "taux de marge marginal" m comme étant l'espérance mathématique conditionnelle du profit réalisé sur une unité supplémentaire de capacité à supposer que la capacité soit pleinement utilisée :

36

-1 _

(68) m = --- J [R(y,u) - wg(k) ]dP(u)

l-P(G)

_u

L'équation (67) s'écrit alors comme l'équation (21)

(69) [l-P(u) ] m = rk

Sans reprendre ici la discussion des conditions du second ordre, on peut passer directement à l'étude des relations de statique comparée qui résultent de ce que y et k sont la solution du système défini par (67) et (22). Afin de ne pas avoir à considérer les complications résultant de l'arbitraire de la paramétrisation, on maintiendra fixe la loi de probabilité P(u). S'agissant des modifications subies par la fonction de recette marginale R, on s'en tiendra à considérer des petits déplacements exogènes 6R qui affectent de la même manière cette recette pour toutes les valeurs de y et de u. En d'autres termes, ce seront des déplacements parallèles.

Il importe de bien comprendre comment cette convention se compare avec celle retenue pour l'étude du modèle principal. Quand la fonction de demande a un coude au point (p,d), le prix p et la demande d étant eux-mêmes fonction de u, soit p(u) et d(u),la fonction de recette marginale est la constante p(u) pour y < d(u) et la constante nulle pour y > d(u). Deux types de déplacement peuvent alors être décrits et être rattachés à ceux considérés dans la section 8 : un déplacement horizontal 6d correspondant à une variation des débouchés et un déplacement vertical Sp de la partie nulle de la fonction de recette marginale, déplacement qui serait intervenu dans la section 8 pour la mesure de la variation de la profitabilité si on n'avait pas posé le modèle principal directement en termes réels. Quand la fonction de demande ne présente pas une allure coudée un déplacement vertical parallèle de la courbe de cette recette marginale diffère fort peu d'un déplacement horizontal, surtout lorsque l'on s'en tient à une étude locale. Ainsi la distinction s'estompe au point de devenir conventionnelle.

Il serait encore concevable d'étudier divers types de déplacement de la fonction R. Mais, pour autant que j'ai pu voir, ceci n'apporterait guère d'enseignements utiles. Il est préférable de s'en tenir aux variations les plus simples, celles qui affectent R de la même manière pour toutes les valeurs de y et de u. Il suffit alors de se souvenir que ces variations peuvent être interprétées soit comme affectant la profitabilité, soit comme résultant de modifications dans les perspectives de débouchés.

Commençons ici par interpréter le déplacement 6R uniquement en termes de profitabilité. Son impact doit alors intervenir dans la définition de ôq, simultanément avec ceux provoqués par les changements de coûts. Ainsi, alors que la définition (31) de ôc subsiste sans changement, la simplicité de la transposition des égalités de statique comparée requiert que (32) soit remplacé par :

(70) -^9- - _ — + ôR ~ qôw

q _ r m

Le second terme est la variation relative induite directement sur le taux de marge marginal par les changements des coûts et de la recette marginale, le seuil u restant par hypothèse inchangé, ainsi que y et k.

La différenciation de l'équation (67) conduit alors à :

(71) a + Ç J * = J a

ÿ T k q

où le coefficient a est maintenant défini par : -ÿ Ç_ Rÿ (ÿ,u)dP(u) (72) a = ---

38

-Avant d'aller plus loin, il est utile d'étudier ce coefficient, dont l'expression est a priori bien différente de celle (34) obtenue avec le modèle principal. Pour ce faire, on peut se limiter à considérer le cas de la fonction de demande linéaire (57). Le calcul est immédiat :

(73) a - if

J°° (u-u)dP(u) u

Le coefficient a est ainsi le rapport entre y et la moyenne pondérée des écarts positifs u - u, la pondération étant définie par la loi de probabilité P(u).Avec la paramétrisation correspondant à (57), les variations de u sont mesurées dans la même unité que celles de y ; il est dès lors normal de concentrer l'attention sur le cas où a est nettement plus grand que un. A titre d'exemple on peut considérer le même cas de loi normale pour P(u) que celui retenu pour le tableau 1 ; on trouve alors que a = 6,25 pour u = E et a = 12 pour u = E + a. Les valeurs de a sont donc encore plus élevées que pour le modèle principal. Elles croissent fortement aussi quand la capacité de production devient plus excédentaire.

La différenciation de l'équation (22) fait intervenir une complication suplémentaire du fait que le taux d'utilisation T(y) dépend de k et de iAi par l'intermédiaire de y, comme (66) le montre. On calcule

(74) -JLL = . G + Htù) ({R _ gSi<) _ rk_H(i! ôk

T T y y T y T2 k

O U

(75) H (G) = - JU dP(u) R'y (y>u )

Dans le cas linéaire H(ü) se ramène à P(u)/b. Quoi qu'il en soit, il apparaît que la sensibilité de T par rapport à 6R, ôw et même ôk n'est pas d'un ordre de grandeur différent de celui de sa sensibilité par rapport à Sy . S'agissant de 6R tout au moins, la chose n'est pas surprenante puisque cette variation concerne autant les débouchés que la profitabilité, ainsi qu'on l'a vu.

Tenant compte de cette différentielle de T et se plaçant dans le cas linéaire, on peut écrire l'équation suivante qui résulte de la différentiation de (22) :

(7 6 ) Ç + (£ + rkP ) 6k _ _ 6c + P . 6R-gôm

T y byT2 k c T by

où e a déjà été défini par l'équation (35).

Les deux équations (71) et (76) définissent le système des relations de statique comparée s'appliquant aux variations <5y et ôk entraî­ nées par les variations ôR, ôw, ôr de la fonction de demande et des coûts. Elles sont à rapprocher des équations (36) et (37) obtenues sur le modèle principal, étant entendu cependant qu'aucune variation de la loi de probabilité P(u) n'est maintenant considérée.

La similitude entre les systèmes (71)-(76) et (36)-(37) est évidente. Dans la matrice des coefficients des membres de gauche, les termes diagonaux ont un peu changé, le premier (a) par sa définition, le second par l'addition à e d'un terme additif positif. Mais il reste vrai que, par leurs ordres de grandeur, ses termes diagonaux l'emportent nettement sur les termes non diagonaux, qui pourraient être négligés si on voulait se contenter de lois approchées.

40

-Les premiers termes des membres de droite sont dans (71)—(76) identiques à ce qu'ils étaient dans (36)-(37). Ainsi, on peut encore dire, en un certain sens, que la profitabilité agit presque exclusivement sur la capacité de production et le coût relatif du travail par rapport au capital presque exclusivement sur l'intensité capitalistique. Cependant les deux équations (71) et (76) présentent une hétérogénéité qui peut gêner la force démonstrative de la proposition : 6R - gôw intervient dans (71) comme une des composantes de la variation de la profitabilité ; il figure au contraire dans (76) comme élément d'un terme additif, qui peut alors être interprété comme l'effet d'une variation des débouchés.

Pour une meilleure homogénéité, tout au moins dans le cas linéaire, on peut réécrire (71) sous la forme :

,-7-^ Sy G 6k ôr 6R - q6w

(77) a _ + - = - — + a -- _

---y T k r by

Sous cette écriture, l'effet des variations de la demande intervient dans (77)-(76) exactement comme dans (36)-(37). En effet dans le système s'appliquant au modèle principal, si l'écart-type a, et non le coefficient de variation h, est maintenu constant alors que l'espérance E varie, les seconds termes des membres de droite deviennent a6E/y et P6E/Ty. On retrouve les mêmes expressions dans (77)-(76) à ceci près que la variation 6E de l'espérance de la demande est maintenant remplacée par la variation (6R - gôi/O/b, qui est précisément égale à la variation de y pour k donné.

En somme, les relations de statique comparée sont très voisines de celles étudiées précédemment. La différence la plus notable résulte dans l'arbitraire de l'interprétation : alors que le modèle principal permettait une distinction nette entre les effets provenant d'une variation de la profitabilité et ceux résultant d'une variation de la demande, la distinction s'évanouit ici.

Pour terminer, notons que pour conserver la validité de l'équation (27) selon laquelle, à l'équilibre, l'indicateur q de la profitabilité doit être égal à la fonction q(y), il convient de retenir l'expression suivante du "ratio marginal de Tobin" :

(78) q = m -T--y) rk

L'équation (27) résulte en effet alors de (69). La formule de définition de q est comparable à celle donnée par la plus à droite des égalités (26) ; elle manque un peu d'élégance puisqu'elle fait intervenir le taux moyen d'utilisation de la capacité à côté du taux de marge marginal.

L'arbitraire de l'écriture des relations de statique comparée peut alors être compris comme un arbitraire dans la définition de la variation 6q à considérer. Selon (77) ce serait uniquement l'impact sur q de la variation du coût du capital, toutes les autres grandeurs étant maintenues fixes pour la mesure de cet impact. Selon (71) ce serait l'impact des variations 6R, ôw et ôr, les grandeurs de y, k et u étant maintenues fixes. La solution intermédiaire serait encore possible, qui consisterait à retenir l'impact de âw et ôr pour aboutir à la formule :

(79) i s _______ §l _ m .

q r m w

quasiment identique à la définition (32) retenue avec le modèle principal.

12. Aversion vis-à-vis du risque

En éliminant toute aversion vis-à-vis du risque, le modèle principal simplifie l'étude, mais d'une manière qui peut être jugée irréaliste. Cette section et la suivante sont donc consacrées à l'examen des changements à apporter aux résultats quand l'hypothèse de maximisation de l'espérance du profit ne suffit plus.

42

-On suppose d'abord que la firme représentative maximise plutôt l'espérance mathématique d'une fonction différentiable U de ce profit (Il s'agit du profit réel puisque le prix du produit est supposé égal à 1). La fonction objectif (17), espérance du profit tt défini par

l'équation (16), est alofs remplacée par :

- r - i ,y

(80) W = V(y) [1—P (y )] + J V(u)dp(u) O

expression dans laquelle les notations nouvelles suivantes sont retenues :

(81) \l(u) = u {[ 1 - wg(k)] u - rky}

(82) dP(u) = f (-— — ) —_{a a}

On établit alors directement que les conditions du premier ordre de la maximization ne sont plus les équations (21) et (22) mais les équations analogues :

(83) [l - P(ÿ)] [l - wg(k)] = A(ÿ) rk

(84) - T*(ÿ)g'(k) = ~_W

où les deux nouvelles fonction A(y) et T*(ÿ) sont définies par :

ÿ

(85) A(ÿ) = 1 + J X(u,ÿ)dP(u) o

i

(86) A(ÿ) T*(y) = T(y) + - J X(u,ÿ) udP(u)

z

°

tandis que X (u,y) est l'excès sur 1 du rapport des valeurs prises par l futilité marginale du profit pour y = u et y = y :

(87) 1 * X(u,ÿ) = U'([l -xg(k)]u - rkÿ } Ü ' {[l -wg(k) -rk]y}

L'aversion vis-à-vis du risque signifie que l'utilité marginale U' est décroissante. Donc X est positif pour u < y ; il est même d'autant plus élevé que la différence y-u est plus forte. Il en résulte que A(y) est supérieur à 1, ceci d'autant plus que l'aversion est plus forte et la dispersion a des aléas sur la demande plus importante. La substitution de l'équation (83) à l'équation (21) opère comme une majoration du coût du capital.

Les équations (85) et (86) permettent par ailleurs d'écrire : ÿ

(88) A(y) rT*(ÿ) - T(ÿ)] = [ X(u,ÿ)[ “ - T(ÿ)]dP(u) Ÿ

Le membre de droite est la somme de termes négatifs (pour u<Ey) et de termes positifs (pour Ey < u <y) ; mais les termes négatifs l ’emportent car leur pondération relative est plus forte que dans :

y

(89) J [ -y - T(y)] dP(u) = [l - P(ÿ)

]

[ï(ÿ)-l] < 0

p

y

44

-Ainsi T*(ÿ) est inférieur à T(ÿ). La substitution de l'équation (84) à l'équation (22) opère aussi comme une majoration du coût du capital, mais une majoration différente de celle apparaissant dans (83).

On peut encore dire que T*(ÿ) est un taux corrigé d'utilisation de la capacité, la correction consistant à pondérer d'autant plus fortement les cas de sous-utilisation que cette sous-utilisation est plus marquée.

Les relations de statique comparée impliquées par (83)-(84) sont évidemment encore plus complexes que celles résultant de (21)-(22). Aussi allons nous doublement limiter l'étude ici. D'une part nous considérerons uniquement le cas de stricte complémentarité, où k et g sont des constantes imposées par la technologie. Dans le modèle principal, ceci signifierait que l'équation (22) disparaîtrait et que l'équation (50), avec le terme additif évident en ôh, deviendrait une relation exacte ; ce serait la relation principale de statique comparée. D'autre part nous considérerons le cas où l'utilité marginale U' serait linéaire par rapport à son argument et décroîtrait à un rythme lent. En d'autre terme, nous procéderons à une étude locale au voisinage de l'absence d'aversion vis-à-vis du risque.

Posons alors, avec un choix convenable des unités :

(90) U' (ïï) = 1-£tt

£ étant de plus traité comme un infiniment petit. On en déduit directement :