Random subspace with trees for feature selection under memory
constraints
Antonio Sutera1
a.sutera@ulg.ac.be
C´elia Chˆatel2 celia.chatel@centrale-marseille.fr
Gilles Louppe3 g.louppe@nyu.edu
Louis Wehenkel1 l.wehenkel@ulg.ac.be
Pierre Geurts1 p.geurts@ulg.ac.be
1 University of Li`ege (Belgium)2 Aix-Marseille University (France)3 New York University (USA)
Keywords: feature selection, random subspace, high-dimensional spaces, random forests
1
Motivation
We consider supervised learning and feature selection problems in applications where the memory is not large enough to contain all data. Such memory con-straints can be due either to the large volume of avail-able training data or to physical limits of the system on which training is performed (eg., mobile devices). A straightforward, but often efficient, way to handle such memory constraint is to build and average an ensem-ble of models, each trained on only a random subset of both samples and features that can fit into memory. This simple ensemble approach has been shown em-pirically to be very effective in terms of predictive per-formance, eg., when combined with trees, even when samples and features are selected uniformily at random (Louppe and Geurts, 2012).
In this work, focusing on feature subsampling, we adopt a simplistic setting where we assume that only q input features (among p in total, with typically q p) can fit into memory. In this setting, we want to study ensembles of randomized decision trees trained each on a random subset of q features. In particular, we are interested in the properties of variable importance scores derived from these models and their exploitation to perform feature selection. In contrast to a purely uniform sampling of the features as in the random sub-space method (Ho, 1998), we propose in Section 2 a modified sequential random subspace approach that biases the random selection of the features at each it-eration towards features already found relevant by pre-vious models. We then show theoretically in Section 3 that this algorithm provides some interesting asymp-totic guarantees to find all relevant variables and that accumulating previously found variables can strongly reduce the number of trees needed to find these vari-ables. Section 4 concludes with an experiment.
Table 1. Sequential Random Subspace algorithm Inputs:
Data: Y the output and V , the set of all input variables (of size p). Algorithm: q, the subspace size, and T the number of iterations, α ∈ [0, 1], the percentage of memory devoted to previously found features. Tree: K, the tree randomization parameter
Output: An ensemble of T trees and a subset F of features Algorithm:
1. F = ∅
2. Repeat T times:
(a) Let Q = R ∪ C, with R a subset of min{bαqc, |F |} features randomly picked in F without replacement and C a subset of q−|R| features randomly selected in V \ R.
(b) Build a decision tree T from Q using randomiza-tion parameter K.
(c) Add to F all features from Q that get an impor-tance (significantly1) greater than zero in T .
2
Sequential random subspace
Table 1 describes the proposed sequential random sub-space (SRS) algorithm. Tree parameter K ∈ [1, q] is the number of variables sampled at each tree node for splitting (Geurts et al., 2006). Variable importance is assumed to be the MDI importance (Louppe et al., 2013). Parameter α controls the accumulation of pre-viously identified features. When α = 0, SRS reduces to the standard random subspace (RS) method (Ho, 1998). When α = 1, all previously found features are accumulated while when α < 1, some room in mem-ory is left for randomly picked features, which ensures some permanent exploration of the feature space. The potential interest of accumulating previously found variables is obvious from an accuracy point of view, as it will ensure that more and more relevant features
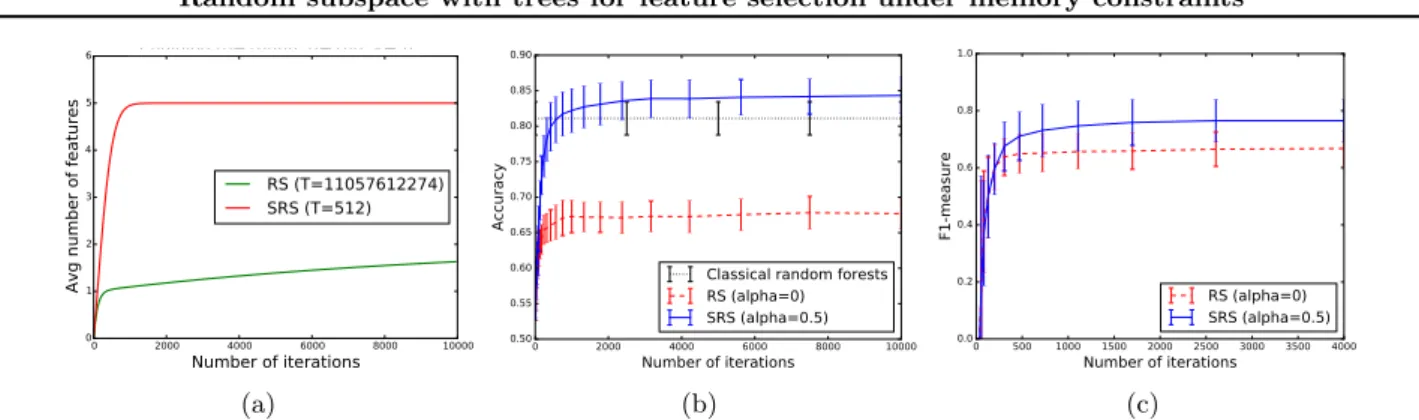
Random subspace with trees for feature selection under memory constraints (a) 0 2000 4000 6000 8000 10000 Number of iterations 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 Accuracy
Classical random forests RS (alpha=0) SRS (alpha=0.5) (b) 0 500 1000 1500 2000 2500 3000 3500 4000 Number of iterations 0.0 0.2 0.4 0.6 0.8 1.0 F1-measure RS (alpha=0) SRS (alpha=0.5) (c)
Figure 1. Left: Evolution of the number of relevant variables found (Chaining). Center: Evolution of the accuracy (Madelon dataset). As a reference, a single forest of 10000 trees. Right: Evolution of the F-measure (Madelon dataset). are given to the tree growing algorithm as iterations
proceed and therefore reduce the chance to include to-tally useless trees in the ensemble. In this work, we would like however to study this algorithm from the point of view of feature selection. Note that the RS method was proposed e.g. in (Konukoglu and Ganz, 2014; Drami´nski et al., 2016) for feature selection.
3
Theoretical analysis
In this section, we summarize our main theoretical re-sults about the proposed algorithm as a feature selec-tion method. Following (Louppe et al., 2013), these results are obtained in asymptotic sample size con-dition and assuming all features are discrete.
Soundness. We adopt here common definitions of (strong and weak) feature relevance (Kohavi and John, 1997) and denote by k ≤ p the total number of relevant variables. Building on the analysis in (Louppe et al., 2013), the following results can be proven (proofs are omitted for the sake of space):
• If k ≤ q (i.e. if all relevant variables can fit into memory), as T grows to infinity, SRS will eventually find all (and only) the relevant variables (in F ) when K = 1 (i.e., with totally randomized trees) whatever α. If K > 1, then SRS has the guarantee to find all strongly relevant variables but will potentially miss some weakly relevant ones.
• If k > q (i.e. all relevant variables can not fit into memory), SRS with K = 1 (resp. K > 1) will find all relevant (resp. all strongly relevant) variables of degree d < q(1 − α), where the degree of a rele-vant variable X is defined as the size of the smallest subset B ⊆ V such that Y ⊥6 ⊥ X|B.
Given that strongly relevant variables contain all in-formation about the output in the case of a strictly positive distribution (Nilsson et al., 2007), these re-sults show that SRS is a sound approach when the degree of relevant features is not too high, whatever
its parameters and the total number of features p. Of course, these parameters will have a strong influence on the number of trees needed to reach convergence (see next) and the performance in finite setting. Convergence. The number of trees needed by the RS algorithm (α = 0) to find relevant variables of high degree can be huge as finding them requires to sample them together with all variables in their conditioning set B. One can show however that a subset B of min-imum size such that Y ⊥6 ⊥ X|B contains only relevant variables and, under some additional assumption on the data distribution, that all features in such B have a degree strictly lower than X. This result suggests that accumulating previously found features can im-prove significantly the convergence, as each time one relevant variable is found it increases the chance to find a variable of higher degree that depends on it. By mak-ing some simplification of the tree buildmak-ing procedure, we were able to compute numerically the average num-ber of relevant variables found by SRS when T grows, in asymptotic sample size conditions. These numeri-cal simulations confirm that taking α > 0 can improve very much convergence in the presence of high degree features (see Figure 1(a) for one simulation with 5 rel-evant features Xi such that deg(Xi) = i − 1), while it
does not significantly affect convergence speed in the presence of zero degree features only.
4
Illustration
Our contribution is mainly theoretical at this stage and the empirical evaluation of the method is ongo-ing. Figures 1(b) and 1(c) nevertheless illustrate the approach on the artificial benchmark Madelon dataset (p = 500, k = 20). The left plot shows the predictive accuracy of RS vs SRS with α = .5 (with q = 50 and K = q for both methods) as T increases. The right plot evaluates the feature subset found by both meth-ods using the F 1-measure (computed wrt. relevant features). SRS is clearly superior to RS according to both criteria.
Random subspace with trees for feature selection under memory constraints
Acknowledgments
Antonio Sutera is a recipient of a FRIA grant from the FNRS (Belgium) and acknowledges its financial sup-port. This work is supported by the IUAP DYSCO, initiated by the Belgian State, Science Policy Office.
References
Drami´nski, M., Dabrowski, M. J., Diamanti, K., Koronacki, J., and Komorowski, J. (2016). Dis-covering networks of interdependent features in high-dimensional problems. In Big Data Analysis: New Algorithms for a New Society, pages 285–304. Springer.
Geurts, P., Ernst, D., and Wehenkel, L. (2006). Extremely randomized trees. Machine learning, 63(1):3–42.
Ho, T. K. (1998). The random subspace method for constructing decision forests. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 20(8):832–844.
Kohavi, R. and John, G. H. (1997). Wrappers for feature subset selection. Artificial intelligence, 97(1):273–324.
Konukoglu, E. and Ganz, M. (2014). Approximate false positive rate control in selection frequency for random forest. arXiv preprint arXiv:1410.2838. Louppe, G. and Geurts, P. (2012). Ensembles on
ran-dom patches. In Machine Learning and Knowledge Discovery in Databases, pages 346–361. Springer. Louppe, G., Wehenkel, L., Sutera, A., and Geurts,
P. (2013). Understanding variable importances in forests of randomized trees. In Advances in neural information processing.
Nilsson, R., Pe˜na, J. M., Bj¨orkegren, J., and Tegn´er, J. (2007). Consistent feature selection for pattern recognition in polynomial time. The Journal of Ma-chine Learning Research, 8:589–612.