Utilisation de la déconvolution homomorphique pour obtenir l'absorption dans la croûte terrestre

u _

•

f

\

;e

..

_•

UTILISATION

VE

LA fliCONVGLUTION

HOMOMORPHIQ.UE

POUR OBTENIR L'ABSORPTION VANS

LA CROÛTE

TERRESr~E.

St~phan

MERCURE

.

,

.

, l,

~ _-,

"Th!4-e. ~ownUe Il lA. Faiu.ul. du UtLdu GJr.a.dulu de

\ ' < ' . '

t 1

utii.vf!A6-?tl

MclJW conne c:ondUion p<J/Ltüll.e. Il

.

.

t'

ob.t:en.«çm du. ~pt6mè. de. Ma.t.tIr.U e l6 Sc..ienc.u.

'(

.

Vlpa!Lteme.Ïl.t du Sc..iUc.e.4 Glotogiqu'u,

•

~vw.(;U MeGlU., Mor&.t1r.l.aL. ,--Aoat 7975 "

~ LEi~~STiPIfM .~ ~76t

_.

. ' \ • r

,

, , " ,

t

·

_...

_"

USE OF THE ROMO~IORPHIC VECO,\/VOLUTTON TO OSTAV.J CRUSTAL ABSORPTION. •

by

", 0 Ste.pIUUl MERCURE

 :thu.Lt, .61Lbm.Ute.d to the. Fa;cd.ty

06

GJtacILUlte.

StucU.u

and Re6e.aJlC.h- o~ Mc.GUl Ulti.VeJL6Uy

.in

pcvr.:U4l

6u.l~e.nt 06 the. ~u.UtemV1.t6 6olt' the. deglte.t ~ ~

Ma4t~ 0 ~

Sc..<.e.nc.e..

h'

\

f)e.paJLtm~ 06 GeologLc.al. Sei.e.nau,

" Mon.tltut.

L.

.' 't ... ~ .. -', 4 #. " .'

..

' ... , ,

.

~ 1 1 * • MsUf.t. 1915. t ,. ' ? '

...

, ,', , . ' " f ,fil; ,1 ;:1 ,

~

-jl

..

~

of, ~.1

.'

,.

₁ ." _" ~

1

~-"

-

.

~ ~

DBCONVÇ>LUTION HOMOMORPHlQUE ET ABSORPTION DANS LA ROUTE

'.

•

\.

.

.

.

l·

i ~ • : Il:~.,: •. ' or ~ ~ , :. -~

.

~' " :J_ • " ,\ i ." ,. ,'i"" 1

.,

.,J. "

\ '

l,

,.

• 1 .s" J 1 i.;:,

,

" 0 ~

.JÎ

f

..

•

RESLl,\fÉ

Suite à un développement gén~ral

_.

de la technique de

déconvolu-"

tïon homomorphique, on a étudié conséeuti vement les hrpothèses inhérentes

à la méthode, les propriétés du'domaine du cepstre complexe et les effets

de la digitalisation des donn~es d'entrée. A pa~tir d'un développement

, '

~h~orique, on a montre qu'une fonction d'atténuation-dispersion décrivant

, ,

l'absorption subie par des ondes élastiques, se propageant au travers de

la croOte terrestre, peut 8tre isolée dans le cepstre complexe d'un

51s-mogramme. Ce ~sultat s'obtient sans imposer aucune condition

incompati-ble avec la réalité.

Afin de synthétiser un sism~gramme simulant autant que possible

les conditions réelles' d'exploration, on a eu recours au développeme~t

ma-thématique de Putterman pour engendrer une fonction d'att6nuation-dispersion

concrétisant l'effet de la croOte absorbante. On a de plus examiné les

effets"de la pondération, du ph6nomène de repli et du bruit de fond sur

les cepstres complexes tirés du sismogramme synthétique. Finalement, on

a proposé un mlcanisme de filtr~ge adapté afin d'identifier les p~ram~tres

sp6cifiques 1 la fonction d'att6nuation-dispersion de l'écorce terrestre:

en ~articulier le faeteu~ de qualité' Q •

Les techniques de d'convolution bomomo~hique et de filtrage

r

,.,

)

,

•

/

iv.

adapté s' étant/avérées satisfa~s-antes dans l'étude du sismogrammc

synthé-\

.

tique, nous

TfS

avons appliqu~es à des donn~e~ digitales provenant d'une

exploration ,\narine effectuée dans ia région du COne Laurentien, situ~e

au sud de Terre-Neuve. •

/~-" .,~ v' 5 ,

..

Following a general development of the homomorphic deconvolution

technique itself, the hypotheses inherent to the method, the properties of

its cepstral domain and the effects due ta the use of discretely sampled

data are studied in turn. Based upon a new theoretical development,

it 18 shawn that an attènuation-dispersion function ~escribing the

aQsorpt-~

ion of elastic waves propagating through the earth's crust can ùe separated from a seismogram. No assumptions incompatible with reality are required.

Futterman's mathematical development of attenuation and disper-sion in an absorptive crust 1s used in the synthesis of seismograms

simu-lating as closely as possible a real e~loration condition. The effects

of weighting, aliasing and noise on the complex cepstra obt~ined from

the synthetie seismograms are researched in detail. A matched filtering _.

_.

technique is proposed as a mechanism for discriminating the parameters "

specifie to the crustal àttenuation-d~spersion funetion : in particular

the quality factor Q.

.

The techniques shown practicable in use on synthetic seismograms'

are applied to digital marine explorati&n data obtained in the Laurentian

_..

Cone regian so~th of Newfoundland •

,"'

RÉMERCIEMENTS

Nous désirons remercier Dr.

a.G.

Jensen qui a su dirige~

habi-lement nos travaux grâce à d'innombrables discussions sur le plan

théori-que et technithéori-que.

~

Nous \reconnahsoris aussi le 1"6le jou6 par Dr. V.A. Sa\lll pour

l'intérêt démontré

A

l'égard de-notre travail tout au long de son

élaqp-~ ration et pour l'aidè financière apportée. De plus, nous appr6cions

a

sa juste valeur l'atmoSphère,yropice à l'accomplissement de ce mémoire

créé par tous les membres du D~partement des Sciences Géologiques et du

Département du Génie minier et métallurgique de l'Université McGill.

\

,

ç

Nous exprimons

a

la compagnie Imperial Oil Limitée, par

l'in-termédiaire. de Mo:psieu~ Jolm E-o Hogg. notre ~incêre gratitude pour avoir

fourni aussi généreusement des enregistrements sismiques d'une t~s

bonne qualité ainsi que des renseignements très utiles sur la g~ologie

de la région explo~e.

Nous" rendons hommage aux citoyens du Qu'bec et.Jiu Canada qui,

par l'interm6diaire du Ministlre de l'Education du _{, -} Qu~bec, du Secr6tari.t

d'Etat, de l'Université McGil1 et du Conseil National de Recherche

• (Subvention A-901? octroyée au D~. O.G. Jensen) ont supporté

financière-ment l' aut'8\4r. '.'~ " " :~ il' , :..,.. " "i

f

(

j

1-~?'

-

•

---~

--vii..

De plus, noUg tenons à'-umercier Hademoiselle Jacqueline

pour avoir dactylographié ce mémoirè, et Monsieur Selbach,

..

ice photographique de"l 'Universi té McGill, pour son travail

pho-Finalement, nous exprimons ,à tous çeux qui, de près ou de loin, participé à l~ confec~ion de ce mémoire, notre plus vive

reconnais-" ".

..

"

'1 ." .

(

,

..

:'

.

~. ... ~

..

/

TABLE OES MATIÈRES

\

RESUMÉ

i

ABSTRACT

.

.

.

REMERCIEMENTS

TABLE

VES

MATIÈRES

LISTE VES TA8LEAUX

LISTE

Ves,fIGURES

'.

"

CHAPITRE

r -

INTROVUCTION GENERALE

1.1. Introduction • . . • • 1.2. Cqntribution originale , \. .'

.

\ \

.

, \ iii v

CHAPITRE

11 - VECONVOLUTION HOMOMORPHIQUE • • • • • • • • • •

~-'2. 1. Des cri ption d'un sys taille hOl1lO}Uorphique . . . • '7

2.1.1. Vision globale du système homomorphique H 10

2.1.2.' Description du sy.st~e caractbistique D 13

2.1.3. ' Descrip~ipn du sysdme lidaire L . . 20

2'.1.4. D,escriptlon du système 0-.1 '.' • . . . . • . 21

2.2. Remarque au sujet du système caractEristique 0' • • • • 23

2.2.1. Hypothèses inh'rentes aucsystème c~ract6ristique 0 23

2.2.2. Propriétés du ceps tre complexe • 1. • • • • • • • 29

2.2.3. Considérations pratiques . . -. • ;. • . • . •... 33

2.3. Application de la d6convo1~tion homomorp~iqu~ l des

pro-blèmes sismiques . . . • . Il • • • • 1.

2.3.1. Cas d'\D1e couche inabsorbante 1 • • • • •

2;3.2. Cas d'une couche absorbante .•

2.3.3. Cas de M cou~es absorbantes

.

. .

.

.

CHAPITRE III -

ABSORPTION

ET~F~NcrION

D'ATTENUATION-DISPERSION

3.1. Evidences exp~rimè~ta1e~~ . . • . . . . • . . . • . .

3.2. Relation de disperStp~ e~,fqnction

d'atténuation-dis-persion . . . .~\. . . . 3.3. DSpendance de la fonction,V'att6nuation~dispersion ~ \ 35 37 41 46 61 63 69 81 , _, , _, , , _, , 1 , _, j \ \ " -i

\

\

..

CHAPITRE 1 V - ,\IOVELE T Q U E . . , . . . . • • • •

4.1\ Description d modèle géologique . . .

4.2" Description la fonction-source et des fonctions

4.3. 4.4. 4.5. 4.6. 4.7. 4.8. d'atténuati dispersion . . . . . . . . . . ,\ Descrîption sismogramme synthétique . . . \ Description 'cepstre complexe . . . . . . \ . . Effet de la tion sur le cepstre complexe . . . . Phénomène repli des données . . . ' . . . ~ . . Bruit de d dans le domaine du c~pstre complexe . . . Recherche 5 fonctions 4'atténuation-dispersion ~pp

ren-tes dans le domaine du cepstllé complexe . . . \ . .

4.8.1. Filtrage adapté . . . .

4.8.2. Création des filtres adaptés . . . \ . .

4.8.3. Sensibilité à la forme -et seuil de dé1,cision . " • .

4.9. Applicati0':l du' filtrage adapté. . . . . . ' '" .

CHAPITRE V - ÉTUVE V'UNE SITUATION GtOLOGIQUE RtELLE

5.1. Données si'smiques rhlles 5.2. Dispositif expérimental 5.3. Analys, des traces sismiques ,,5.4. Discus~ion . . . , .

CHAPITRE

VI

l

CON~LUSION

. .

.

.

.

~. ~. 1 t • • • • • • Il • 1

.

.

\ .

.

.

1 • • • • + • BIBL! OGRAPfH E

APPENOICE I

PROC~VuRE

VE NORMALISATION VU CEPSTRE COMPLEXE

-ix . 84 84 86 93 97 104 110 114 121 122 125 128 132 144 144 150 153 165 169 172 175

,

\

\

Table.au. no 1 2 3 4 5 •

_•

_•

LISTE DES Tr\BLEAUX

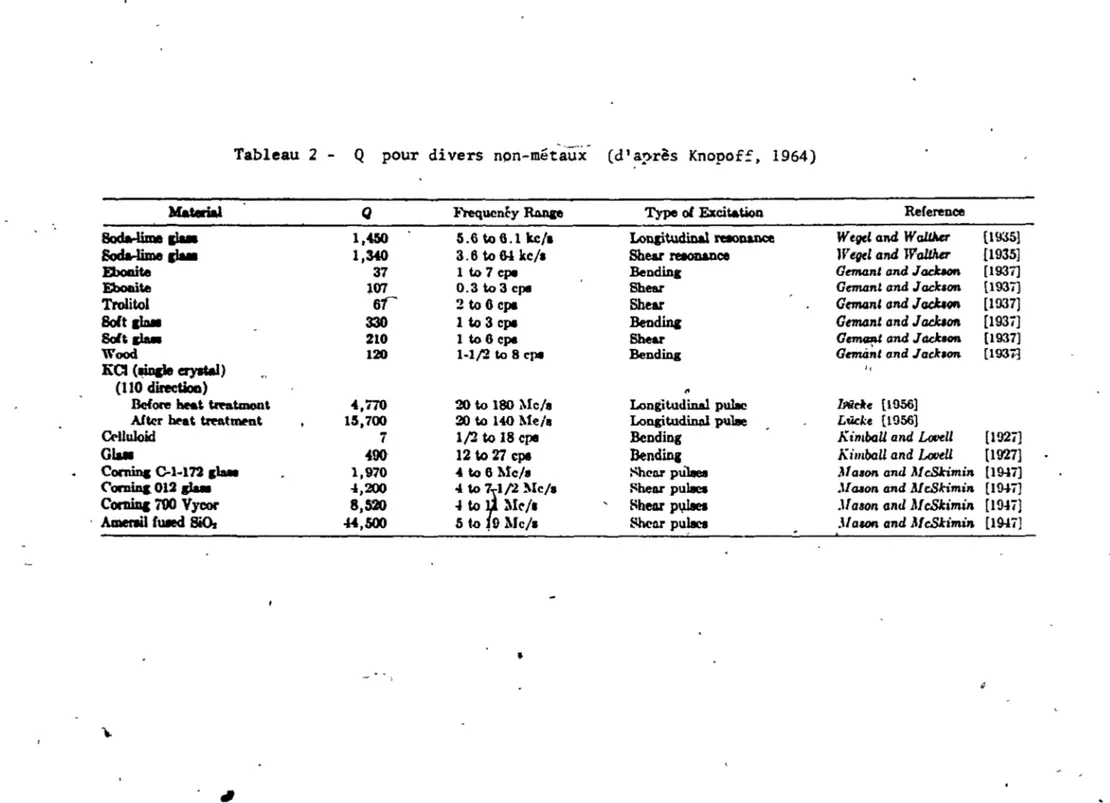
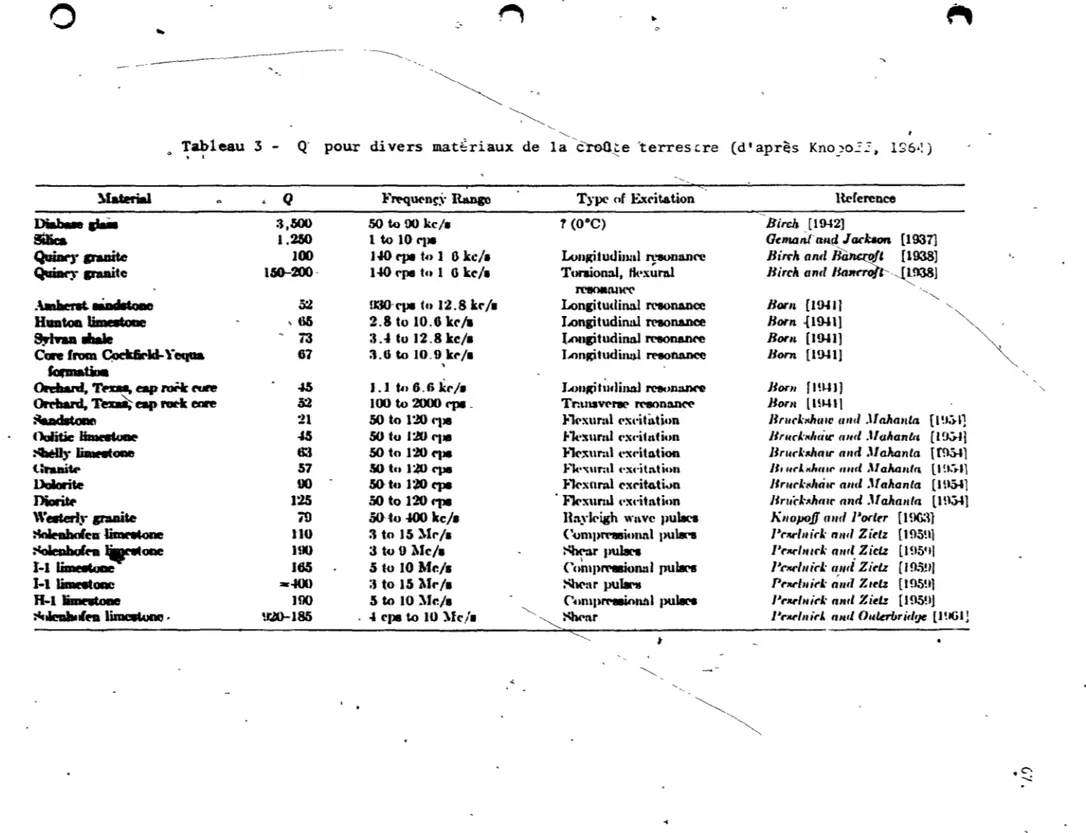
Q pour divers métaux (J'apr~s Knopoff, 1964)

Q pour divers non-métaux (d'après Knopoff, 1964)

Q pour divers mat6riaux de la croOte terrestre

(d'après Knopoff, 1964) , • . . . . .

Caractéristiques physiq,!es du podèle géologique utilisé Description de tous les échos possibles pour le modèle

choisi . . . . . . . . ' . . Page. 64 66 67 85 , 96

6 Contributions au cel'stre complexe x(n) déduites suivant

7 8 9

la th60rie 100

Résultats pour divers couples Liste des filtres adaptés cqoisis Valeur des seuils pour différents trois types de bruit de fond

; '

. .

.

~

.

G relativement aux 126 128 131

10 F,ormes étudiées pour vérifier la validité de la technique

de filtrage adap,té • . . . • . . . • . . . 135

Il Resultat dU,filtrage adapté pour le~éep5tre complexe où

R = co • • • • • • • • • • • • • • • • • t • • • • 138

12 Résultat du filtrage adapté pour le cepstre complexe où

R = 150 . • • • . • • . • . • . J • • • • • • • • • • • .. 138

13

14

1S

16

Resultat du. filtrage adapté pour le cepstre complexe où (~'

R = 100 . . . . . . . . 139

Valeurs de Qa obtenues du fil,trage adapt~ 141

Valeu~ significati~e versus Seuil S2 la

trtee

275-24 • . • . . • • • • • •

.Q. àpproxtmatif pour la trace 215-24

corresp'ondant pour . • . • '.\ • . . . . "162

...

\ \ \

. .

162 , 1 , 1

.

'

,

> '

Vi' ça

•

•

.>

LISTE VES FIGlI~ES

FLgUILe no

1 Representation d'un système linéaire de

trànsforma-t1' on T <,

- _ . 1/ 1/).- - - - • • • - _ . - - •

2 Représentation d'un système homomorphique de

trans-" _ formation H .

l'... . . .. .

5 6 7 8 9 10 11 12 13 14 IS

Repré~entation canonique d'un système homomorphique H

Représentation de la transformation en Z

R~résentation de la transformation loga~ithmique

Représentation de la transformation lineàire en z-l Représentation du système cara,ctéri,stique D

"

-Terminologie dans l~ cas de la transformation de

'Fourier et dan~ celui de l'application du système

caractéristique D . . . '". . . . . . . .

..

Représentation de la transformation linéaire L

Rep~ésentation du système Drl

~llustration du phénomène de déroulement de

arg[x(ejw)] pour un traitement continu (d'après

Oppenheim et Schafer, 1975). • • • . •

..

'\

'

Illustration, du phénomène de déroulement de

arg[x(ejw)] . pour Wl t,raitem~nt dis-cret (d'après

Oppenheim et Schafer, 1975) • . . . • . . . . • .

Décanvolution homomorphique ~'une trace sismiqde

conte-nant un écho non.dispersé (d'après Ulrych, 1971)

.

.

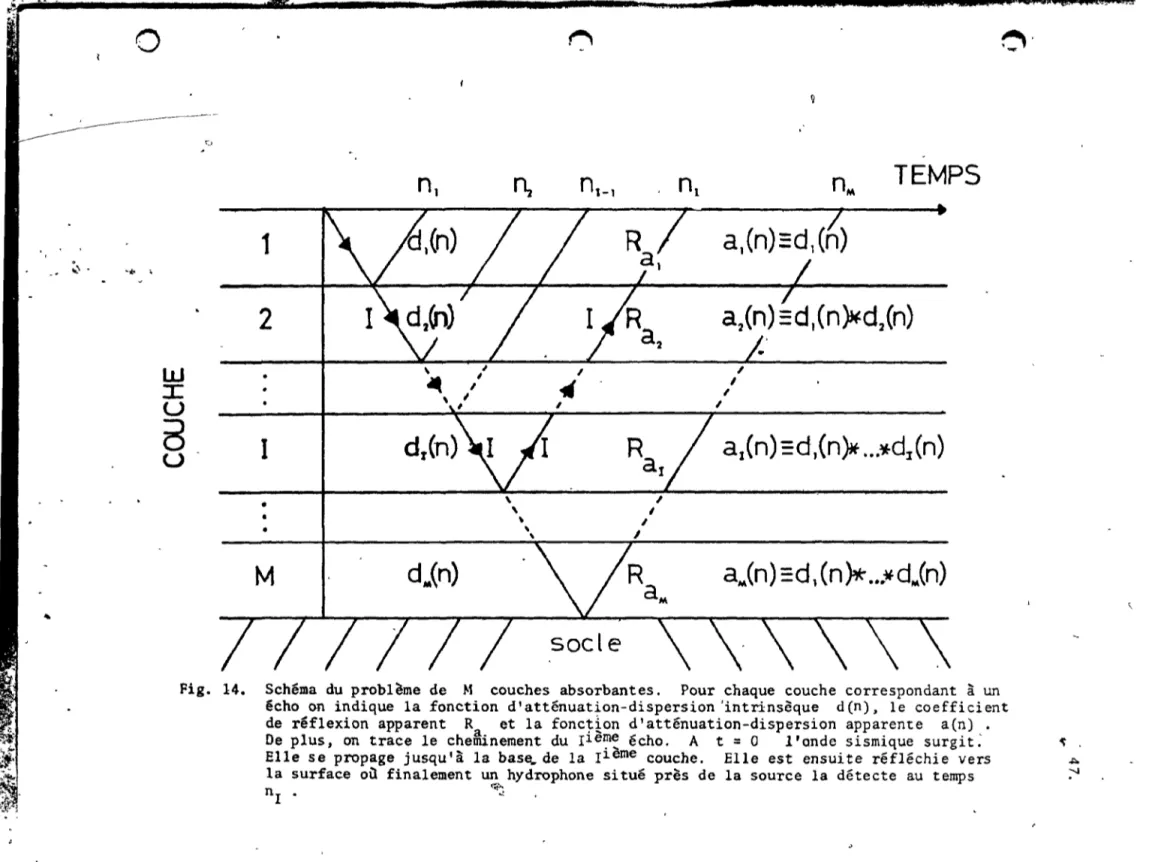
SchEma du probl"ème dé M coucheS absorb,arites .

,

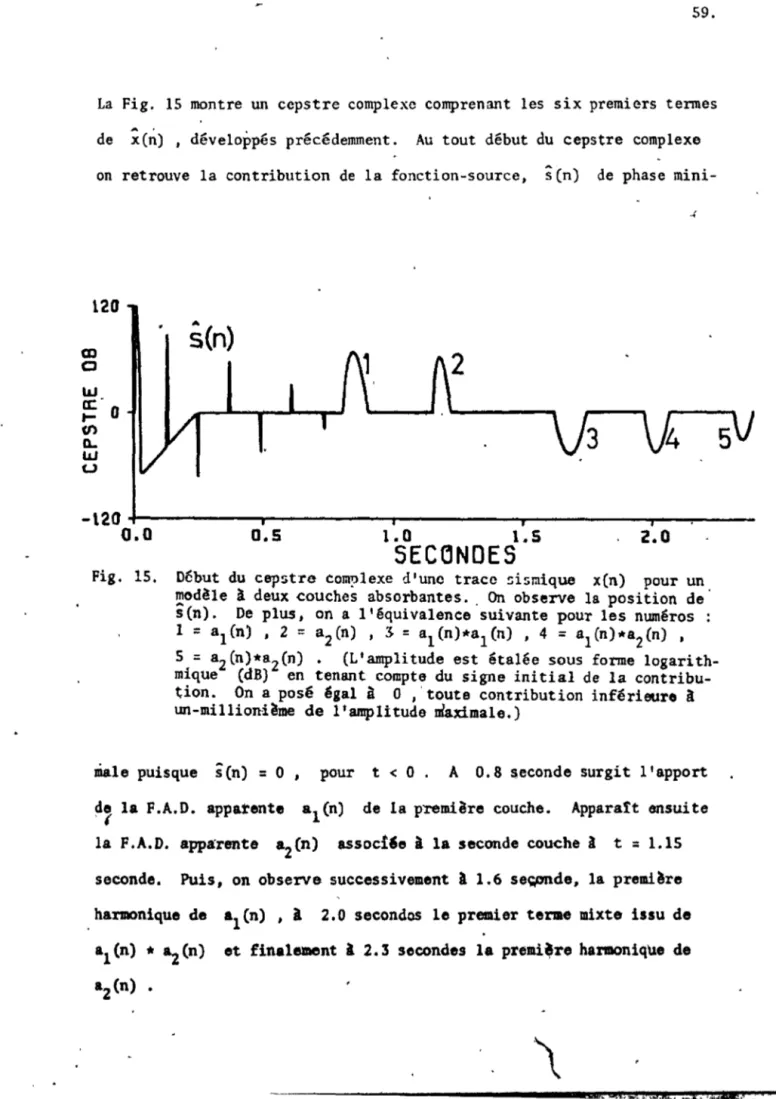
Début du .eepstre cOmplexe d'lDle trace sismique x(n)

pour lDl mod~l~

a 2 couches absorbantes

) Page 8 9 10 15 16 17

.'"

18 19 ' 20 ' 21 29 3S 1 40

_"1

47 j S9 \

-~, 16 17 18 19 20 21 22

•

_•

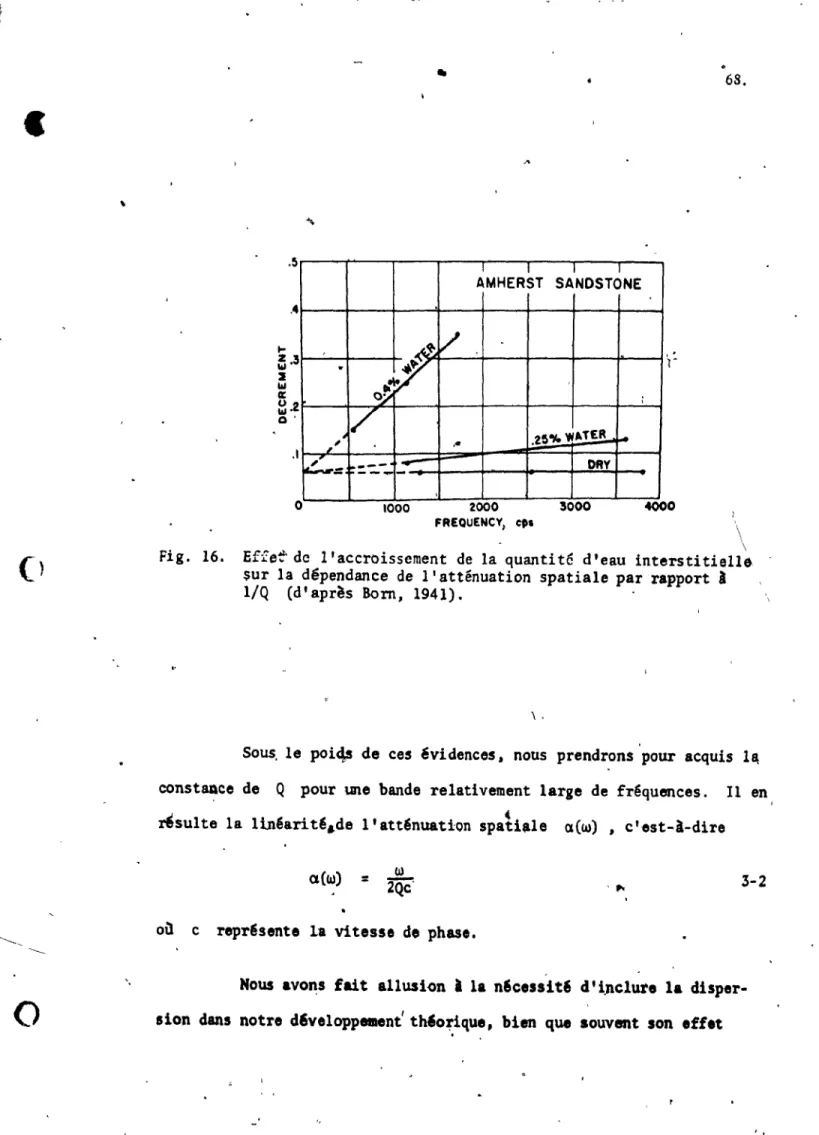
Effet de l'accroissement

dè

la quantité J'eau

intersti-tielle sûr l'atténuation spatiale (d'après Born, 1941)

Résultat de l'expérience de Wuenschel sur les argiles de

Pierre, au Colorado (d'après'> Wuenschel, 1965) . .

Diagramme montrant la fonction d'atténuation spatiale

a(w) et lm n(w) (d'après Futterman, 1962) . . .

"

Schéma de l'atténuation de l'amplitude en fonction de la

f~équence pour diverses d~stances parcourues dans un

mi-lieu absorbant . . . . . . . . . ,

Fonction d'atténuation-dispersion,

de 0.4 seconde et un 'Q égal à 2S

d(t), pour un trajet

Spectre fréquentiel d' BI!lPli tude S Cf) , de la

fonction-source

. . .

.

.

.

.

.

. .

. . .

Déve loppement de la foncHon-source et son cepstre

complexe

.

. .

. . . . .

. .

23 Fonctions d'atténuation·dispersion obtenues de la théorie

xii. 68 70

1

7S 78 81 87 90 1 de Futteman . . . . • • . . . • . . . . . 92

24 Sismogramme syTIthêtique tiré des valeurs apparaissant au

Tableau 4 • . . • • . . . . . • . . 94

2S Cepstre complexe associé au sismogramme synthétique de la

Fig. 24 . . . . . . . 101

26 Cepstres complexes de la trace sismique de la Fig. 24 pour

di vers facteurs de p~>ndération a . • . . . 106

27 ' Ex~raits des cepstres complexes de la Fig. 26 démontrant

la faible influence du facteur de pondération a sur la

_ . . . . L . forme de la fonction d

2 (n) -: • • . . . . • . • . • . . • 108

28 Cepstres complexes de la trace de la Fig. 24 pour diverses

valeurs de 'N _{. '} • . . . • . . • • . • • • •• 113

29 Cepstres complexes prpyenant de la superposi~ion de divers

niveaux de bruit à la tra~e de la Fig. 24 . • . • 118

30

, .

Bxtraits des c~stres complexes d~ la Fig. 29 illustrant

l',ffet du bruit additif sur la.forme de la fonction'

d

wu . .

,

,

,

31 32 33 34 3S 36 37 38 le • iiiif

Création d'tul filtre adapté à partir d'une fonne connue

(d' après t~thi, 1968) 1 • •

Résultat typique du filtrage adapté parfait en l'absence

de bruit (d'après Lathi, 1968) . . • .

Aspect des filtres adaptés pour diverses valeurs de

Q/sec . . _ . .

Résultat du fil ttage adapté pour le cepstre complexe de

la Fig. 29a CR = (0) • • • • •

Resû1tat du filtrage adapté pour le cepstre·complexe de'

la Fig. 29b CR

=

ISO) . . . . . • . . . . .

Résultat du filtrage adapté pour le cepstre complexe de

1ft Fig. 29c CR = 100) . . .

Carte géographique montrant la position de la région

ex-plorée (d'après Grant, 1973) . . . . . . . .

Carte précisant les dive'rs profils géologiques obtenus

dans les Maritimes jusqu'en 1971, grâce à la réfraction

(d'après Austin et Howie, 1973) • . . . . . •

xiii. 123 124 129 134 136 137 146 14,7

39 Profi~ structural et stratigraphique entre l'Ile des

Sables et Grand Palls (d'après Austin et Howie, 1973) 148

40 Profil structural coupant la région des Grand Banks

(d'après Austin et Howie, 1073 ; 'version modifiée de

Drake et al, 1959) . . . • . . . . • 148

41 Schéma précisant le dispositif technique utilisé par l'é~

quipe d'exploration . . . . . . 151

42 Cepstres complexes de trois tr~ces sismiques réelles 154

43 Traces 'sismiques utilisees pour vérifier la technique

de déconvolution homomorphique et de'filtrage adapté 156

44 Résultat du filtrage adapté pour le cepstre complexe de

la Fig. 428 . . . . . . " . " . . . 158

4S Resultat du filtrage adapté pour le cepstre complexe de

la Fig. 42b • . • . . • • • . • . • • • • . . . 15.9

46 R6sultat du filtrage adapté pour le cepstre oomplexe de

la Fig. 42c ." . . . " . . " ~ . . . . " . " . . . . 160

-,"

-

•

,

..

47 Illustration de la valeur '\ _{48 Il lus tration} procedure de . -' .~

•

•

•

ùe la. nature ùu facteur d' amp.li ~i ca ti'oh de tran:;lation b

.

i

.

..

.

.

.'

.

,.,

iors de de deux cas limites rencontres

réduction

. . .

'.

•

.

.

.

. . .

"

(

,

.

ct la ,

-xiv. 176 185 ,

,

, 1 , , 1

/,

r

o

1.1. Introduction. CHAPITRE l

INTROVUCTI0W GÉNÉRALE

•

Etant donné l'appétit .insatiable de l'Homme eu égard aux

ma-1.

tières premièr!s tant minérales qu'énergétiques, la Sismologie, d'abord

~la

Science des tremblements de terre. a vu son champ d'action s'étendre

jusqu'à englober l'exploration géophysique. Aujourd'hui quoique l'aspect

purement scientifique pe'rdure dans les secteurs gouvernementaux et acadé-miques, de plus en plus de recherche s'effectue pour le compte des

compa-gnies privées afin de développer des méthodes supérieur~s d'exploration

et d' in-te~rétation.

Il est cependant agréable de~constater que les progrês réalises

par un groupe finissent tr~s souvent par profiter à l'autre et vice versa.

Dans cette optique, le travail pré~ent6 dans le cadre de ce m~moire porte

le sceau d'une recherche l caract~re scientifique sans pour autant exclure

toute possibilité d'applicatio~ en exploration.

Essentiellement, les buts d'un sismologiste consistent à obtenir

un sismogramme dépourvu,le plus' possible de bruit de fond et à développer

des techniques d'interprétation susceptibles de tirer ~ renseignements

'utiles d'un ensemble de courbes souvent confuses. Not;re humble contribu~

'v t-ion s'insare dans la liane de pensée du second obj-ectif. Grosso modo

..

1 • \

\

\

_,

-,r

1

"

,

,

.

/

2.

nous tentons d'associcr aux principales formations g~ologiqucs un fact~u!

de qualité Q. Ce facteur indique la capacité que poss~de me couche

d'absorber l'énc~gi~ d'une onde sis~que. Ainsi, en plus des deux

dia-grammes habituels de vitesse et de densi t~ versus profondeur, nous 'aj outons

celui de facteur dc qualité versus profondeur. Cette nouvelle source d'in-formation augure d'm moyen complémentaire d'identification de la composi-tion des formacomposi-tions géologiques.

Survolons ensemble les ~verses sections forman~ l'épine,dor~ale

,

de ce mémoire. En tout premier lieu, on reconnaît qu'un sismogramme résulte

de la convolution d'me fonction-source sCn) , d'Une fo~tion a(n)

ori-ginant de la structure, de la composition et d'effets spéciaux du sous-sol

prospecté. et finalement d'une fonction rCn) _, caracterisant

l'électroni-que des appareils. Grâce à une calibration éfficace, r(n) peut être évaluée. Ceci ramène le problème à la décomposition de

r(n)

*

a(n) 1-1

où

*

décrit l'opération mathématique de convolution. Au-dessus, les n

d~crivent l'instant temporel de l'éva~uation de chaque fonction.

L'approche la plus simple à adopter pour déconvoluer l ',expression

1-1 est exposée par R.B. Rice (1962) dans un article intitulé "Inverse

,

convolution filters". Il considere la fonction a(n) conune un train

él'im-pUlsi~~s

oa

chacune est reliée au coefficient dè réflexion d'une couche.

, ,

Il ~~t'~19rs appliquer 1 la trace sismiquo un filtre inverse issu d'une

~proxi_ation de la fonction-source sen) , faute de connattre sa nature . exacte. Théoriquement, il en ressort une s6rie'd'impulsions"qui ntest

r

l'

.

'

o

autre que la fonction a(n) . Cette méthode révèle la. ~tructure de la

région explorée. x

3.

"

Dans ce mémoire nous envisageons

supposons que chaque,formatio~ agit comme

J .. ~ ".

le

pro~e

différemment. Nous 1

un "fil

tr~"

C"' est-a-dire qU'elle

modifie le signal qui la traverse. Cette altération de la forme origine de l'absorption inhérente à la matière constituant chaque section géologique. (Nous aborderons ce suj et au prochain paragraphe.) Ainsi d'un train d'

im-pulsions, la fonction a(n) devient une suite de fonctions. ChacWle est

formée par la réponse du "filtre" de chaque couche à une impulsion de Dirac.

Tout se passe comme si chaque impulsion du paragraphe précédent s'étalait

dans le (;mps de façon à presenter une image de chaque couche

plu~

conforme

à sa structure et sa composition. Puis, au lieu de recQurir à un proc6dé

de filtrage inverse, nous employons une technique non-linéaire de déconvo-_.

..

lu~iQn.appelée d6convolution hOmomorphiqu~. Cette ~éthode, exposée par

Oppenheim (1965J. consiste en l'application d'une t~ansformation permettant

de passer d'un signe convolutionnel à un signe additif (expression 1-1)

entre la fonction-source-et la fonction a(n)

.

Il en résulte une

connais-~

•

sance de la structure tout comme dans le cas précédent. Cependant, i l est

.

aussi possible de sonder la composition des formations par le biais de la

forme du "filtre" de chaque couche. ,Le second chapitre traite

exclusive-ment de la natur~ ~t de l'application d~ la deconvolution homomorphique.

Dans un troisième chapitre, nous nous efforçons de décrire

l'effet de l'absorption paxielle de P6nergie d"Wl. signal sismique paT

"

.

le milieu porteur. Au cours de catte pr'sentation les notions

d'att'nua-..

•

---~._---,-=--vu os

c

1 "

o

le;

•

t

4.

tion de l'amplitude et de dispersion de la phase t'mergent. S'appuyant sur un développement de Futtennan (1962), on formule mathématiquement

l'aspect du "filtre" rep~ésentant la réponse 'de chaque couche eu égard

à son absorption intdnsèque. De ce cheminement fhéodque apparaît une relation entre le facteur de qua l i té Q et la forme du "fi 1 tre" que désormais l'on dénote fonction d'atténuation-dispersion.

Le quatrième chapitre sert de pièce justificative à tout ce

~

\

qui fut dit dans les deux chapitres antérieurs. Au moyen d'un modèle •. on vérifie la validité des hypothèses connexes au processus de déconvo-lution homomJrphique. Au sein de cette section nous adaptons la théorie du filtrage adapté afin de pouvoir étiqueter les fonctions d'atténuation-dispersion. avec une valeur vraisemblable de Q.

Finalement, dans un dernier chapitre, nous utilisons des sismo-grammes réels fournis par la compagnie Imperial Oil Limitée pour évaluer dans quelle mesure notre théorie se vérifie. Dans un premier temps, nous détaillons où et comment les données furent colligees. A la suite de quoi 1l0us nous penchons sur les rlisultats de l'applicatiOn consecutive de la déconvolution homomorphique et du filtrage adapté à plusieurs enre-gistrements sismiques.

1.2. Contribution originale.

Le premier aspect original de ce m6moire réside dans l'utili-sation m.8me du procéd6 de déconvolution homomorphi.Que pour décoll;lposer

une trace sismique. Quoiqu'Ulrych

_.

(1971) ait définitivement adapté cette _.

(

l' ".

·0

t

.\

.

.

" s.t' ). , 5 .

.

'

méthode à 1~ Sismologie en 1972, que Stoffa, Buhl et Bryan (1974 a· et b)

l'aient employée en Sismologie marine et qu!'l tout récellunent Otis et Smith'

(1975) Y aient recouru pour étudier la forme des fonctions-source, cette

technique demeure encore peu répandue.

Cependant. la partie la plus "inédite de ce travail est composee d'lm développèment théorique. Celui-,ci prédit qu'en employant le procédé

de deconvolution homomorphique, i l s'avère possible d'extraire les

fonc-tions d'atténuation-dispersion reliées aux couches géologiques absorbantes.

Ceci s'effectue sans imposer aucUne condition irréaliste quant aux

fon~-tians traduisant l'absorption des formations.

Finalement, nous tentons de relier la forme des fonctions

d'at-ténuation-dispersion, détectées au'moyen d'un filtrage adapté, à une

pro-priété physique intrinsèque de chaque couche" soit le facteur de .qualité

Q. Cette relation s'établit grâce à la théorie de Futtermaq (l96l) sur

laquelle repose le déve1oppem~nt de nos fonctions d'atténuation-dispersion.

Il en résulte la possibilité de tracer des courbes affichant le facteur

de / qua l i 1:'6 en fonction de 1 a profond~ur.

f

4

•

;

1

(>

t,

" "

o

CHAPITRE rI VÉCONVOLUTION HOMOMORPHIQUE

Co~e nous l'avons signalé précédemment, le problème sismique

'émerge du lien non-linéaire existant entre les signaux. Si l'on omet _.

_.

\

pour le moment les multiples problèmes issus du bruit de fond, on peut

pré~endre que la mise en oeuvre d'un mécanisme, permettan~ de troquer le

signe de convolution pour celui' d' addi tion dans un domaine\quelconque, 1

constitue le meilleur moyen de rendre plus significatif un enregistrement sismique.

Crtee aux travaux d'Oppenheim (1965) et d'

oppenhe~m. S~~fer

\

et Stockham (1968), il est permds de penser qU'une telle transforma~n'

est rtialisable. _ De fait, nous trouvons dans ces réf~rènces ainsi que'

dans un 1ivr~ r~cemment publi6, écrit par Oppenheim et Schafer (1975) J ~a

base mathématique .de èette technique.

Dans une première, ~tape, on, étudiera les diverses composantes

de cet outil, en observant pas à pas leurs

effet~sur

Jne

sui te finie de

J

nombres, convolée de deux signaux quelconques. A.~a suite de quoi, on

s' attardcn-a à examiner certaines hypothèses inhérentes au d~veloppement

de la première section, quelques propriéds du nouveau domaine créé par

la transformation et des considérations li6es au caractêre discret des

données d~entr6e. Finalement, on se pench'7.a sur l'application de la

"

\

\ \

\

\

c

$ ','

,

.

"-,

" ',~ ~<

0'

" , "'f ~~': 1-'1'. t!'"

.

, ~ ~1f \ ' ,.~ ..

.

.

....

,

,

\

7.

déconvolution homomorphique à des problèmes d'origine sismique, à savoir le cas d'une couche parfai ternent élastique; sans absorption ; le cas d'une couche absorbante; le cas gênêral de M couches absorbantes .

2.1. Description d'un Système Homomorphique.

De tous les systèmes utilisés, ceux linéaires forment le groupe le plus commode à.manipul .. er, puisqu'ils se soumettent au principe de super-pos! tian. En d'autres mots, si T represente la transformation d'un sys-tème linéai~e et si Xl (n) et x

2 (n) sont les signaux d' entree, Alors

pour

to~t s'c~Îàite

c , on peut écrire :

la

et

lb

On remarque qu'ici le domaine de T contient les opErations d'addition vectori.elle et de multiplication s,calaire. Il en est' de même pour son

champ. Par consequent les espaces vectoriels du domaine et du

_.-

champ de

t

sont dés espaces additifs. La Fig. 1 sch6matise l'effet de T

.

· -~

\.

\

4 l'I! •

•

, _,

l'.

) ~'

:1

.

.

;;:

~ .:WS;)J.~

(:

·C·}

,.' Î'. Fig. 1. + T

Représentati,on d'un système linéaire de transfor-mation T avec l'addition comme operation,dans

le domaine et le champ de T.

Afin de parer à tout malentendu quant à la définition de, xl(n) 'et

x

2(n) voici une explication générale.

'1

8.

Dans un traitement discret. on suppose que le signal d'entrée

se compose d'une suite, notee x, de valeurs

discrè~es

dont le

ni~me

term~ est denoté par x(n). Formellement, nous avons

x = {xCn)}", _CIO < n < CIO , nombre entier.

Il'

Cependant, dans le but d'alléger l'écriture, on utilise xCn) au lieu

de. x pour bien marquer le caractère discontinu dans le temps des

si-gnaux en présence (OppenheiJll et Schafer, 1915, p. 8).

L'originalité des travaux déjà cités rEside dans le fait que ce

princi pe de superposi tian est eénéralid pour s'appliquer 1 tout système

non~lin6aire. !ransposant ces généralit6s l notre problame, on considare

< \ i • ~ ~ ~ '/-~

1

t '

,,, !

~

, r ~ f. , ,

/

o

;'9 .

•

Il comme une transformation d'Wl système pour 'lequ~l la convohltion,

notée _{* ,} reptésentc.l'opération entre les vecteurs dans l'espace

vec-""

toriel du domaine et du champ de Il. Par ai lIeurs, la multiplication

scalaire, dénotée par (a) o~ a est un scalaire, signifi~ la

convolu-tion d'un vecteur a fois avec lui-même (Ulrych, 1971), c'est-à-dire

Cette définition prévalant dans les deux espaces vectoriels, il nous e~

permis d'écrire le principe généralisé de superposition de la façon

sui-vante

et

\

H( (a)x

l (n)]

=

(a) H[x1 (~)J

où x1{n) et x2(n) apparti enn,en t au domaine de H.

" I I . ' ••

.

.

" ,. \ 2-2À 2-2b

Pour mieux saisir

.

le sens des Bq. 2-2a et"2-2b. la Fig. 2 montre un diagramme de la

transfor-mat ion H.

..

H

.,

Pie. 2. Repr6sentation d'un syst.llDe homomorphique avec

*

• C01lllle op6ration clans, le clomàine et le ~amp de la

transformation H. ',. \ 1 ;..'1, J , " ) "

o

l""\-' ,.. """-~ ... ~'

, .. "'r,1

10.

Dorénavant, un système qui se pliera'~tux e~igcnces du principe gcnétalisé tie stlperpoSi tion sera qualifié de système horlliômorphique. Il

' > ; ~

faut mentionner que ce principe décrit par les Eq. 2-2a et 2-2~ est par-ticulier à un système dont l'addition des vecteurs est définie comme la convolution de ceux-ci dans les deuX espaces vectoriels. En revanche, un système détermine d'une autre façon quant à ses opérati6rts d'entrée et de

\

sortie, est aussi qualifié d'homomorphique, en autant qU'il respecte les candi tians reliées au principe généralisé de superposition énumérées dans les ouvrages déjà indiqués.

2.1.1.

Oppenheim (1965) a d~montré que tout système homomorphique pos-sède- une représentation canonique. Ce groupe de systèmes, dits homomor-phiques, constitue une classe bien spêcifique au sein de tous les syst~mes .

..

La Fig. 3 illustre la représentation \'canonique.

x(n) '. ---_._---~.--- ---

.

*

,

l ,

*

1

,

1 + t + t D- 1 1 D L 1 ....

Yen)

1 x(n) 1 ,

,

1 1 • -~---~---.-H

-Fig. 3. Reprisentation canonique d'un sys~ème homoJllOr-phi que "H. ' 1 1 l 1 1 : yen l ,

,

,

)

\ "

(

l' '

o

•

./

11 .

.

Conune nous le constatons ~ la transfonnation Il. liée au

sys-tème, homom<;,rphique, consiste cT\.. une-cascl1Ùe de- trois systèmes.

, '

~

Définir

H revient donc à dé~è~iner la nature de ces trois blocs nommés

sueces-siveme~

·0:.

L et D -1 . Avant de détailler ch~cun d'eux, ii convient

r

Qd'apporter quelque~ commentaires généraux.

CA

l'avénir. ,quoique cela soit

un abus d~ langage, no~s utiliserons indifférenunent système et

transfor-1/

Le système D possède les caractéristiques suivantes

.,

2-3a

,

et j

2-3b

Se rappelant ce que l'on a dit à propos des sysdines homomorphiques, on

réalise que les Eq. 2-3a et 2-3b d'finissent une autre version du

prin-\

eipe g~n~ralisé de superposition pour lequel convolution et addition

Ii-I

n~aire correspondent à l'opération d'addition vectorielle pour le domaine

et le champ de 0 respéctive~ent. En somme, le syst~me D lest aussi

homomoYphique.

À

1

,

D'autre part, le bloc denoté L n!est qu'un simple syst~mo

lin'aire ail :

L[xl(n) +

x

_{2(n)] : L[xl(n)]} + L[x₂(n)]

~. ,

• .=

YI

(n) +

y

2 en)

~t;~

' . '

,

Cl

,/

"

'.

12.

..

et

Finalement. le système D -1 permet le passage d'un espace

, : addi tif à un espace convolutionnel. constituant' le champ de la

transfor-:"

mation H

et

Grâce aux équations

" -1

on note que ~ D effectue le traj et inverse de celUi de D

t~me V-1 constitue de fait l'inverse dû syst~me D.

Le

sys-Bien què th~orique, ce cheminement nous permet de saisir la

donn6e du problème. Nous d6sirons d~finir D de sorte qu'il effectue

le passage d'un espace convolutionnel

a

un autre additif. Une fois cette

'transfofmation obtenue, D-1 se

d~duit

automatiquement. Pour cette

rai-son D sera appelé système caratt6ristique. Alors, tout l'art d'une

bonne d~convolution homomorphique réside dans le choix judicieux du

con-tenu du bloc L • qui se compose d'une combinaison de filtres linéaires

.. passé-bas. passe-bande, passe-haut, etc. La "lection des filtres ne d6pend que de l'6tat des données d'entr6e et des r6sultats d6sir6s.

f

,

.

, , ,

-,

1

•

o

~---._~---13, 2.1.2.

Nous pouvons affirmer sans crainte d'erreur que le système D

constitue la pierre angulaire ~u processus de déconvolution ho~omorphique .

C'est pourquoi, maIgre l'existence d'articles décrivant le système D,

nous nous attarderons. à expliquer chacune do ses étapes afin 4'accorder

aux lecteurs la meilleure chance de se familiariser avec les transforma-tions employées.

Le premier point à soulever est la définition et la description _.

_..

d'une des proprietes de la transformation en Z. (Oppenheim et Schafer,

1975, chap. 2). Supposons que l'on ait trois suites répondant à la

con-dition :

xCn)

=

u(nJ

*

ven)

où u(n) et v (n) sont que 1 c,onques . On définit la transformée en Z

de xCn) ,notée Z[x(n)] ou plus

s~ent

X(z) par:

00

Z[xCn)J

=

XCz) =

!

x(n)z-n 2-4

n=-oo

où z est une variable complexe arbitraire. La transformation en Z

effectue la transposition d'une suite l un polyn6me en Z. Par

exem-ple, le coefficient de z-i est

constit~,

du terme xCi) de la suite

xCn) ,pour i positif ou n6,atif.

Il est ini'ressant de constater que la transform6e en Z de

la convolution de deux sùites Equivaut l la multiplication de la

....

o

, ~ ,

0,

.

'

•

formée en Z de chacune des suites.

Voici ~ exemple qui concrétisera cett~ affirmation.

Soit 1,1 (n),

=

CUI J U 2 )' • Soit ,v(n) = (vl'v 2) • On sait que d'où Par ailleurs, si . -1 U(z) = u l 1" u2z et Vez) = vI 1" v2z-l on obtient U(z) • Vez) d

'o'b. .

ce qui revient l 'erire

Z[u(n)

*

ven)] II. U(z) • V(Z')

=

Z[u(n)) • Z[Y(n)]

. pour tout u(n) et, v(n) •

.

.

, "

14.

,

o

"

15.

Il est ainsi possible de représenter la transformation cn Z

_.

selon le diagramme dè la Fig. 4

*

•

,Z[ J

x(n)=u(n)*v(n) , X(z)=U(z) -Vez)

Fig. 4. ~Repr6sentation ~e la ttansformation en Z modifiant

le signe de convolution en un signe de

multiplica-tion.

Pour conclure, nous consid6rerons la t r + t i o n en Z comme premil!re êtape de la définition du système D. Au sortir de Z, nous h6ritons

de deux sêries re1iêes par un signe de multiplication. En g6néral, ces

sériës se c'ornposent de nombres complexes l cause de la variable z qui

"

prend des valeurs complexes.

En second lieu, on sait que le logarithme d'un produit égale

~

la somme des logarithmes des facteurs. Sous forme de diagramme, ceci

correspond l la Pig.

s.

Pour plus de simplicit6 dans l'6criture. nous

noterons Log

(X(z»

par

X(z).

Par alileurs, avoir X(z) complexe

implique l'utilisation de

l'.

fonction logàrithmique complexe. Ceci

n6-cessite certaines c~~ditions devant 8tre rospect6es par X(z) quo l'on

examinera dans· la prochaine section. I l convient dé noter que nous

uti-liserons constamment le logarithme,n'Perion, not~ Log.

vu ça "

.

.

()

,

t Log[ ] X(z)=U(z)"V(z) . X(z)=Û(z)tV(z)

•

Fig. ,S. Représentation de la transformation logarithmique

où Log[ J équivaut à Log [ J •

e

De l'application du logari~me comple~e sur X(z) , il résulte

X(z) = Log[X(z)J = Log[U(z) • Vez)]

=

Log[U(z)] t Log[V(z)]

l

= Û(z) + Vez) •

16.

Quoique l'on évolue déjà dans un espace additif, il est

néces-saire d'adj~indre une dernière ét4pe à la définition de D. Etant donné

que X(z) est formée d'une série de puissance de~ est essentiel

de revenir à un ~sultat sous forme de suite si l'on a l'lntention de

\trait~ les donn'es de sortie. A cette fin on appliqué la

transforma-tion en Z inverse, not6e

Z •

-1 dHinie CODe suit

oil

c

est un parcours cix:culaire d'termin6 par

... a+jw

, ~ e "11' < fi) < 'II'

2-5a

2 .. Sb

inclus dans 1. ~gion de convergence de .

lez)

eO indique la valettr

""

, _,

.

" ' "

0"

, ,

1

17.

du rayon du cercle d'intégration. A nouveau, afin de simplifie~, on

~crira

... -1 0

x(n)

=

Z [A(Z)].

Pour illustrer la transformation en _-1 on a recours à la fig. 6, laquelle

-1

montre que Z peut être une transformation linéaire puïsque ~es deux

espaces vectoriels d'entrée et de sprtie de

') + -1 Z t sont additifs.

,

i

(n)::û (n)

tV

(n)

Fig. 6. Reprêsentation de la transformation linéaire en Z -1 .

I i : ' -1

En langage mathematlque,

Z

effectue les modifications suivantes

.

=

Z-l[Û(z)J + Z-l[~(Z)]

• û{n) + v,(n) •

Das l

prfsent,

il

est possible de construire le systême

carac-t!ristique D â partir d?s Fie. 4, 5 et 6. ~ Fig. 7 schbatise

1'as-.

/ .

pect global de D COD nous l'avons d6jl indiqu"fi, uni!! fois D connu

.',

.

.

,

(,

IS. ---~

*

1 1 + 1 1 " 1 • • + + 1

,

t 1 1 1 ] ] Z-l[ ] 1 1 Z[ Log[ X(z) 1 x-(n) x(n) 1 _X(z.) 1 1 1 t t \ ' 1 : ______________________________ ~---_____ J

Fig. 7. Représentation du système caractéristique D.

~out signal, fruit de la conyolution de ses éléments, peut se

décompo-ser suivant ceux-ci grâce à l'application de D.

on

appelle domaine du cepstre complexe, le domaine

quasi-tempo-rel originant de ~'application du système caractéristique, 0 sur une

sui te de valeurs discrètes ,appartenant au domaine temporel. Le mot

cepstre provient dlune analogie faite par Bogert, Healy et Tukey (1963)

...

avec le spectre de puissance. Alors qu'ilS

..

~tudiaient le logarithme du'

spectre de puissance d'un signal incluant un écho, ils observèrent que

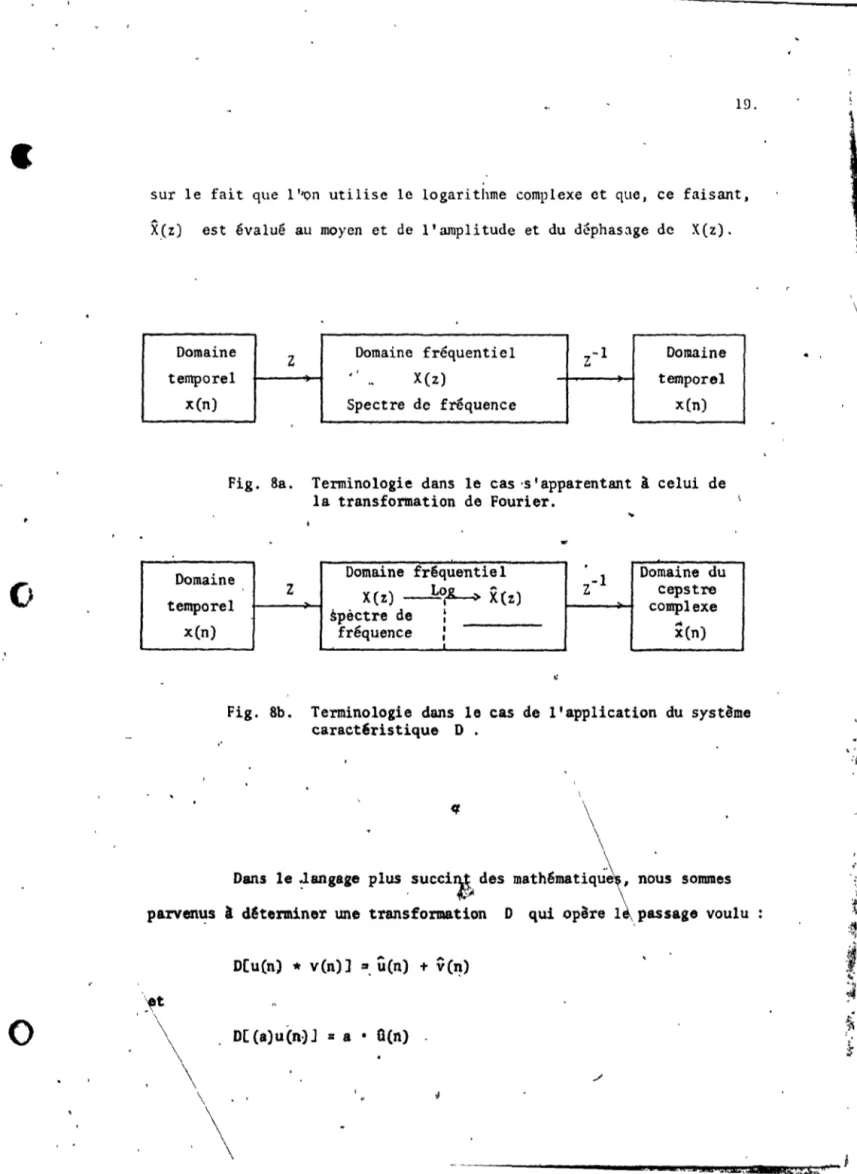
;.-...-la transform6e de Fourier de ce logarithme exhibait une contribution au temps correspondant au moment de l'arrivée de l'écho. Les Fig. Sa,et 8b tentent de démystifier cette nomenclature. Dans ces illustrations, la terminologie utilish copie .celle emp,loyée pour déc,rire la théorie des

transformations de -Fourier. Ceci ne s'avère pas lm hasard. Nous

cons-taterons plus loin dans le chapitre que l'on a recours à celle-ci pour

-'1

calculer le c,pstre complexè de nos trace$ $ismiques. Dtautre part, le

/

terme complexe rEsulte dU travail d'Oppenheim qui d6sirait ~nsi insister

.

c

û

o

--19.

sur le fait que l ''On utilise le logarithme complexe et que, ce faisant,

X{z) est évalué au moyen et de l'amplitude et du déphasage de X(z).

Domaine

Z Domaine fréquentiel

..

7-1 Domaine

temporel

.

'

X(z) temporel

,.

xCn) Spectre de fréquence x(n)

Fig. 8a. Terminologie dans le cas 's'apparentant à celui de la transformation de Fourier.

...

..

.

Domaine fr~quentiel Domaine du

Domaine -1 Z XCz) ----1..~~ X(z) Z cepstre temporel spèctre de 1 complexe xCn) ,-parven~

,

_...

fréquence 1

,

x(n)

Fig. Sb. Terminologie dans le cas de l'application du système

caractEristique D .

\

\

Dans 1. J.anga", plus SUCe!$ d ••

math6matiqÛ~.

no;" s ... s

l

d~terminer

une transformation D qui opare

l~,passage

voulu

D(u(n)

*

ven)] ~ û(n) + v(~)

D[(a)u(n~J O(n)

lCC_i§~S!Mii tt4l!1lilt:"\. !

\

~o.

où {a) représente définie dans l'cs!'Ucc'

convolution-nel. c'est-à-dire que est convoluée a fois avec elle-même.

2.1.3.

En fait peu et beaucoup mérite d'être dit aU,$ujet de cet

en-,

semble de filtres. Le seul trait commun réside dans leur caract~re

li-néaire. Mathématiquement. on a

L[x(n)] =

yen)

et on représente cette relation grâce à la' Fig. 9 . Tous les filtres

linéaires sont susceptibles d'~tre employés. La sélection dépend des

besoins de l'utilisateur eu égard à l'état des données d'entrée, quant à leur

contenu en bruit additif et convolutionnel, à leur amplitude, etc.

Nous n'aurons pas à recourir au filtrage linéaire lors de notre

recher-che des fonctions d'atténuation~dispersion. C'est pourquoi nous

n'éla-borerons pas davantage ce sujet.

+ +

L

x(n)

F!g. 9. Reprisentation de Ja transformation lingaire L .

..

()

o

\

\

\ \ \

..

\ \

\

2.1-.4.

Bien que ce système ne mette·en lumière aucun détail utile

\ pour le développement subséquent, il convient de décrire,au moins

briève-\

"

~ -1

\, ment, la na.ture du systeme D a.fin d'acquérir une vision globale de

\

\ ,

la transformation homomorphique H . La Fig. 10 schématise l'aspect

+ ~ ________________________ M _ _ _ _ _ • _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ : * 1 1 1 + + 1 1 1 1 _ _ - ... 1 ---4 Z[] Exp[ ] Z-l[ ]

Y

(n) :. 9(z) Y(z) : yen) ( : 1 1 1 1 \ ~ : ~----~---1 _\

\

Fig. 10. Représentation du système 0 -1

1""

-1

de 0 . Comme nous l'avons sp6cifi6 auparavant, connaître D signifie

-1

que D n'est plus un secret. Voici sous forme de d~ve1oppement

mathé-1 d -1

matique 'aspect e D

Soit ... yen)

=

sen)

.+ t(n)

ail ; (n) :: LÇû(n)]

, t

(n) = Lrv(n)]

alors on obtient, apris transformation en Z

Z[y(n)] = 9(z)

=

5(z) + T(z)

1

1

,"

•

A

puis prenant l'exponentiel de Vez)

expcY(z)J

=

Vez)

=

expC~(z) + T(z)]

où ~n général

=

expCS(::)] • expCT(z)] Vez) = S(z) • T(z) \

Wez)

=

LogCw(z)]

et enfih appliquant la transformation en Z inverse

Z-l[y(z)]

=

Z-ICS(z) • T(z)]

= Z-ICS (z) J

*

Z-l[T(z)]

yen)

=

s(n)

*

t·(n)

oil i l faut se rappeler qu" en général

Wez) = Z[w(n)]

Le seul point litigieux dans ce développement se situe au moment on

implicitement on ~crit :

22.

Or, cette derni~re 6quation'dScoule directement de la propriété de. la

, '

transforDation en Z v6rifi6e au moyen d'un exemple dans la section

2.1.2.

Cette demUre remarque indique la fin de la description

th6o-~ ,

)

rique du sy.t~ ~ollOmorphique

f:l.

Pourtant, i l nous reste encore 1

~mlenter certaines facettes du syst~ c~act'ristique D, le seul

"

.

.

) \

\

\

, Il , ~.

:~

'1

1

()

i r "

~

1

()

\. ~3.

que nous utiliserons en pratique dans notre recherche, ainsi qu'à d6-voiler certaines propriétés du cepstre complexe dignes de mention.

l.

2.2. Re~arques au Sujet du Syst~me Caractéristiq~e D .

Dans cette seconde section, on examinera en un premier temps les ,hypothèses implicites faites au moment du développement du système

1

caraqtéristique 0 ~ En second lieu, nous mettrons en lumière certains

traits intéressants appartenant au cepstre complexe. Finalement, il ëst

nécessaire d'exposer comment le système D \est transposé en un algorithme

.i

accessible pour.} 'ordinateur.

2.2.1.

Le chemi~ement théorique sous-jacent au 5yst~me 0 implique

trois hypothès~s. La première exige que

lez) :

Log[X(z)]

soit d~fini~ de façon unique. Car si X(z) est le résultat de la

mul-tiplication de deux pOlyn811les en

r,

tel que

X(z)

=

U(z) • Vez) J

'on, doit' pouvoir ~crir. ,

LogeX(z)]

=

~,(U(z)J + Log(V(z)]

ca

U(z) et

Vez)

sont .11 .. -... uniques.

.'

- -

-24.

Oeuxièmement, on stipule que X(z) doit être la transformée

-en Z de x(n) .

_..

Finalement, on désire que x(n) jouisse à son tour d'une

défi-nition unique. De là ressort la nécessité de déterminer une région de

convergence laquelle contiendrai~ le parcours C suivi lors de la

trans-formatlon en Z . -1 . _{, ,}

Commençons par analyser les effets de la dernière exigence. La

suite initiale finie x(n) ,.composée de N+l termes, est stable, causale

et réelle. Stable signifie

N

L

'x(n)

,2

< 00 • •

n=O Causale exprime l'idée que

x(n)

=

0 pour n < 0 •

,

,

Finalement, r~el1e souligne le fait que tous 1 es termes de la suite sont

de$ nombres reels. De l'applicatiO'n de la transformation en Z sur

x(n) , i l resulte

N

X(z) =

! ..

x(n)z -n n=O

On remarque que XCz) n'a aucune singUlarité sauf pour z

=

0 • En

- , )

vancbe, étant un polyn6me de degrE

N,

il existe

N

zéros (racines)

situ6s dans le plan Z·. Par définition de la rigion de convergence,

r6aion'où tout p8le (singularité) est absent, on déduit-que la région

re-de convergence de XCz)

4

s'étale SUr tout le plan Z excluant

z

=

0 .

"

\

-·' ••

0"

, _, . . ,

A;

Î' , ~' L, '. 25.

En général, ,cc type de SUl te dont la transform~,e en Z a des pôles ét.

\

\

des zeros à l'intérieur ct ~ l'extérieur du cercle unitaire, z

=

1

_\

est qualifiée de phase mixte.

L

Comme on s'intéresse ~ 'XCI}, le logarithme de X(z) , et que

U . .

la/fonction logarithmique commute les zeros de XC:) en pôles pour, X(z),

~

serait très commode d'évaluer la transformée de x(n) ainsi que xCn)

~ur le cercle unitaire, où

j

=

r-r .

Il faut, par conséquent: une région de convergence englobant le parcours

Izi =

l . Pour y parvenir, on a recours à un stratagème (Oppenheim,

Schafer

b~ .Stoc~ham,

1968) . On amème tous 'les zéros qui sont hors du

cercle ~itaire, à l'intérieur de cèlui-ci en pondérant la suite

d'en-tree au moyen du facteur de pondération a. Voici une explication du

mécanisme mis en br~le. Supposons que

Zo

soit le zéro le plus éloigné

de X(z) et que

IZol

> 1 • On souhaite ~d1fier X(z) de façon à ce

. ( '

que le téro le plus loin, en cons~quence tous les autres, soit ramené l

,

""

<f

~'intéri~ur d~ cercle unitaire. '~ppelons yen) la suite issue de cette

contraction et y(~ .'sa transformée en Z DU à ce changement, le

z6ro le plus

dist~

de Vez) se situe

à\~zo'

où lazol < l , i.e

-::

Y(z)'='X(a- l • z) ' •

Revenant sur nos pas. on tire l'6galit6 suivanto pour chacun des termes

des deux suites

,

_, ' ~ ,-,

o

26. yen) =

cl .

x(n) ~ CL ~ 1 . ième t

En résumé, multipliant le p ermé de la suite à phase mixte .x{n)

par un facteur de pondération aP , où a < 1 , on crée une nouvelle

suite yen) possèdant tous ses :éros à l'lntérieur du cercle unitaire.

Ceci modifie peu le contenu du message x(n) pour des temps relativement courts, comme nous ,le verrons plus tard. Nous qualifierons Une suite dont

tous les zéros et pôles sont confin~s à l'intérieur du cercle'unitaire,

de sui~e à phase minimale.

...

Si l'on revient à X(z) , maintenant que l'on a refoulé tous les

zéros à l'intérieur 4u cercle Izl

=

l , on note que X(z) ne possède plus de pôle dans la région

Ainsi, la transformation en Z inverse pr6sent6e aux Bq: 2-5a et 2-Sb

devient sur le cercle unitaire

z-l[X{ejw)]o

=

JL [

Log[X(ejw)Jejwn dw

• 2 'If -11 2-6

ce qui correspond à-la transformation de Fourier inverse de t(ej~.

Il

Y

a moyen d~ relier le proè~dé de pond6ration, pr6c6demment

décrit, à la d6finition du con~our C de l'Eq. 2-5b. Ant6rieurement

l toute pondération, lè contour C est défini par-

z

=

eO+jw , cepen4ant

l'utilisation d'un facteur de pondS ration a mane l un no~eau contour

De lA i l n'y a qu'un pas à franchir pour consid6rer a

27.'

çomme étant le facteur e cr qui permet de fixer le chemin d'intégration

à l'intérieur de la région de convergence. 'Ainsi, la pondération

cons-titue un moyen détourné de modifier le parcours

C

en vue de'conserver

le trajet simple effectué sur le cercle unitafre pour les fins de l'in-tégration de l'Eq. 2-6.

Nous avons 'dorénavant l'assurance d'un x(n) un~que, puisque

tou~e ambiguïté sur la nature de la région de convergence est levée. 'Ce-pendant, il faut maintenant analyser les èonditions que doit remplir

X(z) afin d'~re une transform~e en Z valable de x(n). A partir de

X(:l:) =' Log[XCz)]

faisant intervenir le développement en série de Laurent, on obtient

~(z)

=

_{1 zl s}

_~ 2-7

chbisissant z sur le cercle unitaire, i.e. où

,,'

z = ejw

=

cos w + j sin w

on arrive à ,

Qù xrCej") et'

'i.ï

(ej") repdsentent respectivement la partie rielle

et imaginaire de XCejw)

Exig~ant

que les teraes xCn) soient r6els, on conclut que Ir (e

jw

)

est une fonction paire et p6riodiquo en

w.

de p6riodo 2'/1' 1 de plus on tire que Xi Ce

jw

)

est une fonction impaire et p6riodique en w, de λ'riode 2'/1'

,

:j

t

,~

f

1

1

l ' i>

';'

28.

D'autre part, écrire le dé\'eloppement de Laurent (Eq. 2-7)

d'une fonction, commande que celle-ci soit analytique et par conséquent

"

continue dans la r6gion de convergence. XCz) est donc continue sur le

, cercle unitaire. Il en résulte que et doivent E!tre

continues. Or, de

A jw jw

X(e )

=

Log[X(e )J

on est forcé de demander la continuité de LogIX(ejw)\ e\ de arg[X(ejw)]

En autant qu'il n'existe aucun

~éro

sur le cercle

~itaire,

Loglx(ejw) 1

s'avère toujours une fonction continue. Le problème apparaît au niveau

de argeX(ejw)]

( \ En

outre~ r~gler

le cas de la continuité de arg[X(ejw)}

ré--0

sout par la même occasion le problème de l'unicité de

XCz).

L'obsta-cIe majeur découle du fait que

l

X. (ejw) 1

arg[X(ejw) J

=

arc tg l .

X (eJw)

r

est une fonction d. Riemann avec une

infin~

de feuillets dont la

va-leur principale, notée ARG[X(ejw)] , est définie sur l'intervalle

(-n~n). Il faut, par cons6quent, élaborer un mécanisme ajustant le

d~phasage

de X(ejw) afin de le rendre continu. La Fig. Il illustre

ce

phénom~ne

de déroulement de arg[X(ejw)] .' Dans la Fig. lIa, on #10 "(Il ,

observe l'aspect de' XiCe) ) , lors~ue continue. En comparaison, la

()

,

, ' - ~

,

.

29. 11' fi fi) -41r (cl)

~

ARG[X(.lw)J

" _'-" '-'" '-' 1

1 - I r • \ , -

7

(fi

fi) (b)

ER. 11 •. Illustration du o:1enomène de déroulement de

arg[X(ejw)1

pou~

un traitement continu:

(a) arg[X(ejw)] après l'application du

mec~isme

d,' ajustement ; (b) l' ~llure du déphasage de

• t

X (eJw) sur l'in tervall e principal, ( -n ,n)

(d'après Oppenheim et Schafer, 1975).

En conclusion, il est nécessaire, dans le but d'appliquer le

système caractéristique 0 à une suite x(n) , de rendre celle-ci

mini-male quant à sa phase, par le biais d'une pondération exponentielle. Il

'w jw

faut ensuite ajuster le d6phasag~ de X(eJ ) de sorte que arg[X(e )]

forme qne fonction continue.

2.2.2.

Tout polyn6me en z semblable l

X(z)

₌

r

n=-CII

xCn) z -1

",

(j

•

'30.

sc ramène à une fonne rationnelle; ç'est-à-dire

m. m l -1 0

L

(1 _{- akz )}

l

2-8 XCz) =

_lAI

z r k=l k=l p. _Po l -1

L

(1 - ckz )

r

k=l k=l

sont inférieurs à 1 • et où m. et m

1 0

indiquent respectivement le nombre de zéros à l'intérieur et à

l'exté-rieur du cercle unitaire, tandis que p. et

1 Po

(1

-font d'e même pour les

pôles de la série. Les facteurs dé la forme

_{'\Z' )}

'-1 et (1 - ckz ) -1

correspondent aux zeros et aux pôles à l'intérieur du cercle unitaire.

En revanche, les facteurs (1 - bkz) et (1 - dkz) sont associés aux

zéros et aux pôles situes à l'extérieur du cercle unitaire. Finalement,

le facteur zr résulte des pales et des zero"s situés à l'origine. Le

nombre r est ,égal à la différence entre le nombre de z'ras et celui de

pôles. Le développement de l'Eq. 2-8 s'applique à une suite infinie.

Dans le cas d'une suite finie~ il n'y a aucun pOle autre que l'origine

1

(Oppenheim et Schafer, 1975, p. 48 et p. SOI). La transformée en Z

s'écrit alors comme suit

mi m

X(z) =

lAI

zr

r

(1 ....

~z-l)

r

(1 - bkz)

k=l k=l 2-9

Dans l'Bq. 2-9. se trouve le factéur 1r qui représente un déphasage

soit positif soit n'gatif de la suite x{n) • Au niveau de X(e jw) ,

ce terme devient Log(ejwr) et il ajoute à &rg[x(ejw)] une

contribu-tion croissant linéairement en fonccontribu-tion de w Il en r6sulte un balayage

$ $

(l

o

•

wu

31.

étant de plus faible amplitude. Pour éviter une telle situation, on

soustrait cette composante linêaire de ,la fonction

arg[X(ej~J

avant

" -1 '" , b

d'effectuer la transformation en z .. D'un autre cote, il est possi le,

l '

comme l'a montre Ulrych (1971), de se préoccuper de ce problème après

l'obtention de x(n), en convoluant la suite x(n) avec un filtre

li-néaire variab1~ en"fonction de n qui éli~ne la participation, notée

<p(n) , de Log (ejwr) au cepstre complexe, où

<pen) :: r cos n 1T 2-10

n

Prerrant soin d'enlever z r de l'Eq. 2-9 , on arrive

a

m. II ~ -1 0 X(z)

₌

_lAI

L

(1 - _{akz )}

l

(1 - bkz) k=1 hl 1 •

De là, il est facile db dédnire, en prenant le logarithme de chaque c8t6 ,

que

m. " mo

X(z) ::

10gIA~...

t

10g(1 -

~z

-1) +

l

log Cl - bkz)

k=l k=1

Recourant aux développements en série de Laurent de

et de . -1 10g(1 - az ) GO n

= -

l

~ z-n n=l n CID n 10g(1 - az)' =

!

~

zn • n:l

1

z

1

>

1

al

l', 2-11

puis 6valuant x(n)' l partir de l'Bq. 2-11, arlce i la transformation

.

()

..

()

/ 1 J'

•

32 . xCn)

₌

log

lAI

,

n

=

0 f 2-12a~ m. n 1 a k

=

X

- \ n > 0 n ' 2-l2b k=l m -n 0" bk ::: _t

L -

n < 0 ·2-12c k=l n

Les Bq. 2-12a. b, c suggèrent les quelques propriétés du cepstre complexe que voici.

-En premier lieu, on remarque que Ix(n)1 déc~it au moins aussi

rapidement que lIn. On 6cri t

,. B

lxCn)1 < A-I-l

n -00 < n < co

où A est \me constante et B le maximum entre les 1 ~ 1 et .les Ib_k 1

Ensuite, on note que si on traite une suite finie x(n)

A

phase minimale (aucun zéro hors du ou sur le cercle unitaire), le cepstre

co~lexe de cette suite est causal, c'est-à-dire

x(n) =.0 • n < 0

"

Finalement, on constate qu'en dépit du caractère fini de x(n)

x(n) forme une suite infinie. Cette particularité acquiert ~e

impor-tance capitale lorsqu'on veut calculer

xCn)

à partir d'une suite de

valeurs discrètes.

-r 1

1

~ '-(';

.