Simulation des phénomènes de polarisation et de répulsion à partir du problème de Weber

HAL Id: hal-01542772

https://hal.archives-ouvertes.fr/hal-01542772

HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

Simulation des phénomènes de polarisation et de

répulsion à partir du problème de Weber

Luc Normand-Tellier, Xavier Ceccaldi, François Tessier

To cite this version:

Luc Normand-Tellier, Xavier Ceccaldi, François Tessier. Simulation des phénomènes de polarisation et de répulsion à partir du problème de Weber. [Rapport de recherche] Institut de mathématiques économiques ( IME). 1984, 49 p., figures. �hal-01542772�

DOCUMENT DE TRAVAIL

INSTITUT DE MATHEMATIQUES ECONOMIQUES

UNIVERSITE DE DIJON

FACULTE DE SCIENCE ECON OMIQUE ET DE GESTION 4, BOULEVARD GABRIEL - 21000 DIJON

N° 70

SIMULATION. DES PHENOMENES DE POLARISATION ET DE REPULSION A PARTIR DU PROBLEME DE WEBER

Luc-Noraand Tellier Xavier Ceccaldi François Tessier

Communication présentée au colloque de l'institut

de mathématiques économiquesde l'Université de

Dijon le 30 novembre 19 84

Luc-Normand Tellier

Professeur, Université du

Québec à Montréal,

Professeur associé, INRS-

Urbanisation

Xavier Ceccaldi, ing.

Projet Archipel

Gouvernement du Québec

François Tessier,

. Urb.

/I

rie de la localisation. Cette dernière p r opose plusieurs e x p l i c a t i o n s possibles à de tels phénomènes; la prédominance o b l i g é e des points critiques dans un espace de type réseau, la d i f f é r e n c i a t i o n de l'espace (entre autres p a r l'existence de point? de r u p t u r e ) , le jeu de la c o n c u rrence (chez Ho- telling) ou du recoupement des aires de ma r c h é (chez Losch e t C h r i s ^ a l l e r ) , l'existence d'économies externes, etc.

N o u s s o u mettons ici que les tendances à la p o l a r i s a t i o n sont si "naturelles" qu'elles a p p a r a i s s e n t d'elles-mêmes dans des con d i t i o n s idéales où aucune hypo t h è s e de contrainte ou de d i s c o n t i n u i t é particulière n'existe(si ce n'est celle de la

frict i o n de l'espace), oü ni concurrence spatiale, ni diffé­ re n c i a t i o n de l'espace, ni réseau, ni économies externes ne sont supposés.

N ous a nalysons ici, tout d'abord, les phénomènes de p o l a r i ­ sat i o n dans le contexte du problème de W e b e r (plaine u n ifor­ me indifférenciée, taux de transport constants, etc), con­

texte où le recours à des contraintes exogènes au processus de l o c a l i s a t i o n est le plus faible en théorie de la locali­ sation. Nous tenterons de démontrer, au m o y e n de simulations, que, dans ce contexte, la localisation successive de points p a r rapport à des points d'attraction^" choisis au h a s a r d et en fonction de forces de localisation déterminées aléa t o i ­ rement, donne lieu à l'apparition spontanée de phénomènes de

Les concepts de point d'attraction, de point de répul­ sion, de fonction de localisation e t de forces de loca­ lisat i o n s ont définis dans Tellier (19 84). L e u r dé f i ­ n i t i o n e s t rapidement reprise dans le texte.

l ' i m p o r t a n c e des contraintes introduites dans le système^. Nous e x a m i n e r o n s ensuite l'impact de l'introd u c t i o n de points de r é p u l s i o n dans les systèmes étudiés.

Not r e a n alyse se limitera au cas du triangle de W e b e r et uti­ l i s e r a la solution trigonométrique du probl è m e correspondant donnée p a r T e llier (19 72). Une solut i o n s i milaire sera p r o p o ­ sée p o u r le cas où des points de r é pulsion s ont c o n s i d é r é s . La f réquence des solutions au sommet sera estimée. Les sché­ mas de localisation obtenus au terme des simulations seront c a r a c t é r i s é s au moyen de différents indices et tests statistiques.

1. R a p p e l du problème de W e b e r et de sa solution t r i gonomé- trique

Le problème de Web e r consiste à loca l i s e r dans un espace b i d i m e n s i o n n e l uniforme (c'est-à-dire où l'effet d'un d é ­ p l a c e m e n t sur une distance e u c l i dienne donnée est le même dans toutes les directions) une activité dont le choix de l ocali s a t i o n est régi p a r une f o n c t i o n -objectif $ , que nous appellerons fonction de localisation, p a r rapport à une série de points prélocalisés. S'il s'agit de m i n i m i ­ ser $ (si, par exemple, comme l'examine Weber, $ est une fonct i o n de coût de t r a n s p o r t ) , le poi n t i sera considé­ ré comme un point d'attraction si <S<j,/<Sgi> 0, où gi est la distance euclidienne du p o i n t i à l'activité que nous cherchons à localiser. Le p o i n t i sera un point de ré­ p u l s i o n si 6$/ Ôgi <0.

Le p r é s e n t texte fait suite à Te l l i e r et Ceccaldi (1983), q u ' i l complète sur plusieurs points.

/3

Comme Weber l'a pressenti et comme Tellier (1972) l'a dé­

montré, la solution de ce problème est analogue à celle

d'un problème d'équilibre de forces physiques s'exerçant

dans le même espace suivant les modalités suivantes:

1)

à chaque point d'attraction ou de répulsion corres­

pond une force ;

2)

toutes les forces s'exercent sur un même point, à

savoir le point correspondant à l'activité à locali­

ser;

3)

chaque force définie par rapport à un point d'attrac­

tion est orientée vers ce point, tandis que chaque

force correspondant à un point de répulsion est

orientée en direction opposée à ce point;

4)

les intensités des diverses forces sont égales aux

valeurs <5^ /ôg^ des premières dérivées partielles de

la fonction de localisation $ par rapport aux va­

riables g-j_.

1.1 Cas de trois points d'attraction

Weber n'a analysé que le cas où les points de

du problème de localisation sont tous des points d'at­

traction.

De plus, il s'est plus particulièrement atta­

ché au cas du triangle, où seulement trois points d'at­

traction sont considérés.

La résolution du problème du

Par p o i n t de référence, nous entendons soit un point d'attraction, soit un p o i n t de répulsion.

formés par les forces de localisation sont déterminés ind é p e n d a m m e n t de la localisation des points de référen­ ce, ce qui ne peut se faire q u a n d il y a plus de trois p oints de référence. Nous p r é senterons ici la solution trigonométrique du problème du triangle i m p liquant trois p oints d'attraction qui a été utilisée au cours de nos s i m u l a t i o n s .

S u p p p s o n s le triangle de localisation A B C illustré à la figure 1, où les sommets corre s p o n d e n t à trois points d'attraction. Supposons que la fonction de localisation

$ c onsidérée est concave et doit être m inimisée (Weber 4

su ppose une telle fonction ). S oit A, B et C, les som­ mets du triangle, dont les côtés sont de longueur AB, AC et BC. Soit 0, le p o i n t de localisation optimale. Les forces de localisation d'intensités W^, W B et YIq , sont orientées respectivement vers A, B et C. Les in­ tensités W A , W B et Wç sont r e s p e c t i v e m e n t égales aux dérivées partielles et . L'équilibre

~ 5g ' 8

9c

des forces détermine les angles au centre a A , a B et ot£

La solution trigonométrique utilisée pour le calcul n u ­ m é r i q u e de simulation consiste d'abord à déterminer ces angles à partir des relations circulaires de la forme:

W A 2 - W B 2 - W C 2 cos 0^ = -

--2 Wg Wq

S u r les conditions m a t h é matiques du problème de Weber, voir C o o p e r (1968) et kuhn et Kuenne (1962).

/5

A

de c a l c u l e r les différents angles, une fois connu l'angle 1 p a r exemple, donné par:

tan î = k sin k ' 1 + k c o s k '

avec k = BC sin _ AC sin

et k' = Â + B + a c - 180°

Les angles connus, il e s t possi b l e de c a l c u l e r les coordon­ nées du point de localisation dans différents systèmes d'axes.

1.2 Cas d'un poi n t de répulsion

La force de localisation c o r r e s p o n d a n t à un p o i n t de répul­ sion e s t orientée à l'opposé de son p o i n t de référence. Son e f f e t e s t de tendre à éloig n e r la localisation optimale du p oi n t de répulsion. Dans un espace uniforme non borné, s'il n ' e x i s t e qu'un seul poi n t de référence qui se trouve être

un p o i n t de répulsion, la localisation optimale se trouvera dans n'importe quelle direction à l'infini. S'il y a deux po i n t s de référence, l'un d ' a t t r a c t i o n e t l'autre de r épul­ sion, la localisation optimale dépen d r a de l'intensité r e ­ lative des deux forces. Q u a n d la force de répulsion est p a r t o u t plus grande que la force d'attraction, la localisa­

tion optimale se retrouve à l'infini si l'espace considéré n ' e s t pas borné.

Dans le cas du triangle, si les trois points de référence sont des points de répulsion, la localisation optimale se trouve à l'infini. S'il y a un o u deux points de répulsion et que la résultante des forces de répulsion est partout plus grande que la résultante des forces d'attraction, la

n

P a r contre, si la résultante des forces d'attraction est, en certains points, plus grande que la résultante des forces de répulsion, la locali s a t i o n optimale ne se trouve, ni à l'infini, ni aux points de répulsion, ni à l' i n t é r i e u r du triangle de localisation. Elle peut se t r ouver soit à l'extérieur du triangle, soit sur un p o i n t d'attraction. Dans ce cas, les solutions trigo- no m é t riques suivantes p e u v e n t ê t r e utilisées (voir T e l l i e r et Ceccaldi (1983) e t T e l l i e r (1984)).

D^ns le cas représenté à la figure 2 où il y a deux

po i n t s d'attraction (A et B) e t un p o i n t de répulsion R, les étapes du calcul sont les suivantes.

On p e u t d'abord trouver les angles r et b à partir des relations circulaires de la forme:

Les relations trigonométriques usuelles p e r m e t t e n t ensuite de c a l c u l e r les différents angles, une fois connu l'angle

cos r

2

W

2W

W

2 p a r exemple, donné par:

tan 2 RB sin^ B * RA sin (r + b) sin (r - A) RA sin (r + b) cos (r - A) + RB sin b cos B

Les angles connus, il e s t possible de calculer les coor­ données des points de localisation dans différents systèmes d ' a x e s .

Figure 2: cas de deux points d'attr a c t i o n et d'un poi n t de répulsion

/9

Dans le cas de la figure 3, avec deux points de répulsion e t d'un point d'attraction, la solut i o n suivante est ap­ plicable, po u r v u que la force d ' a t t r a c t i o n ne soit pas s u p é r i e u r e ou égale à la somme des d eux forces de répul­ sion:

trouver les angles a et r à p a r t i r des relations c i r ­ culaires de la forme,

1 .3

Cas de deux points de répulsion

2 W R W s

- les relations trigonométriques usuelles per m e t t e n t e n ­ suite de calculer les différents angles, une fois con-

A

n u l'angle 1 par exemple, donné par:

tan 1 _ -RA sin r sin (S + R + a)______________ SA sin (a + r) + RA sin r cos (S+ R +a)

les angles connus, il est possible de calculer les coordonnées du point de l o calisation dans différents systèmes d'axes.

2. L o c a l i s a t i o n s aux sommets: e x p l i c a t i o n et fréquence

Les solutions trigonométriques que nous venons d'exposer p e r m e t t e n t de calculer le p o i n t o p timal lorsque ce p o i n t n ' e s t pas confondu avec l'un des sommets du triangle. Q u a n d les trois points de référence sont des points d'attraction, une localisation à l'un des sommets peut ê t r e observée:

R

F igure 3; cas de deux points de répu l s i o n et et d'un point d ' a t t r a c t i o n

/ I l

1) q u a n d l'une des forces e s t dominante, c'est-à-dire q u a n d son intensité est plus grande que la somme des

intensités de l'ensemble des autres forces d 'attrac­ tion dans le système; dans un tel cas, la l o calisa­ tion optimale sera au p o i n t d ' a t t r a c t i o n maximale;

2) p o u r certaines localisations relatives des sommets et certaines intensités des forces d ' attraction tel­ les que les angles au centre ne p e u v e n t se réali­ ser à l'intérieur du polygone de localisation: si

un des angles au centre calculé par la m é t h o d e trigo- n o m étrique est tel que < I , la localisation o p t i ­ male se trouve alors au sommet I.

L ' i n t r o d u c t i o n de points de répulsion dans le système de l o c a l i s a t i o n a des effets radicaux. Alors que les loca­ lisa t i o n s en dehors du triangle de localisation sont i m ­ p o s s i b l e s q u a n d les trois points de référence sont des poi n t s d'attraction, il suffit qu' u n de ces trois points s oit un point de répulsion pour que ce soit les localisa­ tions à l'intérieur du triangle qui d e v i e n n e n t impossi­ bles. Les seules localisations p ossibles communes aux d eux situations sont les localisations aux sommets. Pour q u ' u n e localisation au sommet ait l ieu q u a n d il y a un ou d e u x po i n t s de répulsion, il faut a b s o l u m e n t qu'il y ait dans le système une force d'att r a c t i o n dominante, auquel cas la localisation optimale se trouve au p o i n t d'attrac­ tion corre s p o n d a n t à cette force. La prése n c e de points de r é pulsion donne lieu à un véritable b o u l e v e r s e m e n t des s ystè m e s de localisation, aussi p e u t - o n s ' é t o n n e r que leur étude ait été fort négligée dans la littérature.

Il e s t possible, à p a r t i r des s i m u l ations réalisées, d' a p ­ p r é c i e r la fréquence appro x i m a t i v e des localisations aux s o m m e t s dans le cas de trois points d'attraction.

C et t e fréquence approximative des localisations aux som­ m e t s e s t an moyenne de 78%.

C e t t e fréquence élevée est d ' a u t a n t plus significative q u e les conditions supposées p a r W e b e r sont les moins c o n t r a i g n a n t e s qu'on puisse imaginer, tout en acceptant l'idée d'une friction de l'espace positive. Elle e x p l i ­ que d'ailleurs en bonne partie les tendances à la p o l a ­ r i s a t i o n dénotées plus loin.

3. Simulations: cas des points d'at t r a c t i o n

\

A l'aide des solutions trigono m e t r i q u e s au cas du trian­ gle présentées plus haut, des s i m u l ations o n t été faites s u r o r d i n a t e u r qui avaient p d m r but:

1) d'es t i m e r la fréquence des localisations aux sommets;

2) de voir dans quelle mesure, s u ivant divers scénarios, des phénomènes de p o l a r i s a t i o n apparaissent, c'est-à- dire dans quelle me s u r e les localisations optimales a v a i e n t tendance à s'agglomérer;

3) de v oir si la s t r u c turation de l'espace observée f a isait apparaître une h i é r a r c h i e de centres;

4) de caractériser les schémas de localisation au moyen de divers indices.

/13

Les simulations ont été faites dans le contexte d'un e s ­ pace borné, suivant un processus itératif de détermination succes­

sive des localisations optimales c o r r e s p o n d a n t à des points de références, choisis a l é a t o i r e m e n t s u i v a n t divers s cé­ narios, et a des forces de locali s a t i o n dont l'intensité a été déterminée de façon aléatoire^.

Trois scénarios ont été plus p a r t i c u l i è r e m e n t étudiés dans le cas où tous les points de référence sont des p o i n t s d'attraction. Le scénario A consiste à choisir à chaque itération trois points e t trois forces d'attrac­ tion de façon aléatoire, et ce, i n d é p e n d a m m e n t des i t é r a ­ tions précédentes. Le scénario B consiste à choisir, à chaque itération, deux points d ' a t t r a c t i o n de façon a l é a ­ toire dans l'ensemble des points de la surface et le troisième point de façon aléatoire dans l'ensemble des po i n t s déjà retenus comme localisations optimales au cours des itérations précédentes. Dans ce scénario, le ch o i x des forces d'attraction est aléatoire. Dans le s c é n a r i o C, deux des points d ' a t t r a c t i o n sont choisis a l é a t o i r e m e n t dans l'ensemble des points d ' attraction dé­ jà choisis lors des itérations précédentes, deux nouveaux po i n t s s'ajoutant à cet ensemble à chaque itération. Ces deux n o u v e a u x points sont choisis a l é a t o i r e m e n t dans l'en­ semble de la surface. Le troisième p o i n t d'attraction e s t choisi dans l'ensemble des localisations optimales, de la même façon que p o u r le scéna r i o B. Là aussi, le c h o i x des forces d'attractions est aléatoire. Ainsi, dans le scénario A, les itérations sont t o t alement i n d é ­ p e n d a n t e s les unes des autres. Dans les scénarios D et C, chaque itération est influencée p a r les itérations précédentes, le plus gra n d degré d ' i n t e r d é p e n d a n c e des ité r a t i o n s étant atteint avec le scéna r i o C.

Wesolowsky a traité le cas du problème de Weber impliquant des dis­ tances rectangulaires et des points d'attraction aléatoires.

Les trois scénarios ont été simulés sur un nombre variable d'itérations, de façon à faire r e s s o r t i r la convergence des i n dices caractérisant chacun des scénarios. L'espace con­ s i d é r é est discret et de d imension 280 points p a r 160. Les dif f é r e n t s scénarios 9 ont comparés à partir:

1) du graphique des distributions des points de localisa­ tion, selon deux formats de présentation,

2) d u calcul d'un indice de dis p e r s i o n R,

3) d'un test statistique d ' écart p a r r a pport à une dis­ tribution aléatoire de même densité;

4) du nombre de fois qu'un point, appelé alors "point de concentration", est choisi comme localisation op t i ­ male ,

5) d 'un indice de c o n c entration centrale Y appliqué à l'ensemble des points de localisation.

L ' i n d i c e de dispersion R est celui de P.J. Clark et F.C. E v a n s (1954). Il est basé sur la me s u r e de la distance au p o i n t le plus proche, p o u r chacun des points de localisa­ tion :

R = RA RE

N Z D. i=1 1 /15

où

RA

distance m o y e n n e au point le plus p roche dans la distribution é tu­ diée ,

e t RE

2

1

tion aléatoire infinie de densi­ té N/A.

o ù distance du p o i n t i au point le plus proche nombre de p o i n t s ,

superficie de l'espace borné étudié. N

A

P o u r une distribution aléatoire, R = 1. Lorsque toutes les localisations sont concentrées en un seul point, R ■ 0. La d i s t a n c e moyenne au p o i n t le plus proche, RA, sera maximale dans une distribution uniforme où chaque p o i n t occupe le s o m m e t d'un hexagone. R e s t alors égal à 2,1491 (voir P.J. C la r k e t F.C. Evans, 1954). R est é gal à 0,5 q u a n d la dis­ tance moyenne au point le plus proche e s t en moyenne deux fois plus faible que l'on p o u v a i t s'y attendre pour une d i s t r i b u t i o n aléatoire de la même densité.

L ' a p p l i c a t i o n d'un test statistique p e r m e t de vérifier si, compte tenu du nombre de points e t de la surface étudiés, on p e u t tirer, de façon significative, des conclusions sur le type de distribution étudié en calc u l a n t la valeur de son indice R. Le test est réalisé à pa r t i r de l'erreur s t a n d a r d de la courbe normale, U - (RE-RA)/s où s =

0,26136 VÂ/k e s t l'erreur s t a n d a r d de la distance moyenne au p o i n t le plus proche, p o u r une distr i b u t i o n aléatoire de densité N/A. A 99% de certitude, l'hypothêse de dis­ t r i b u t i o n aléatoire est vraie p o u r U compris entre -2,5 8 e t + 2,58.

Un indice de concentration centrale Y est calculé de la

façon suivante:

N

Y -

D./RN

i=1 1

ou

N = nombre de points étudiés

Di

m distance du point i au centre de la surface

étudiée.

k =

rayon du cercle inscrit dans l'espace rec­

tangulaire considéré (ici k = 80) (cercle

de référence arbitraire).

Lorsque tous les points sont concentrés au centre, Y = 0.

Si Y > 1 , la distance moyenne au centre est supérieure à k.

Les graphiques 1 à 24 représentent graphiquement les dis­

tributions trouvées, Chaque scénario A, B, C a été testé

pour quatre cas d'itérations (100, 200, 300 et 400 itéra­

tions) .

Les résultats sont présentés à chaque fois selon

deux formats. Chaque point de localisation est repéré,

soit par le nombre de fois où ce point est choisi, soit

par un point dont la dimension est d'autant plus grande

que le point est choisi comme localisation optimale. Les

tableaux 1 à 4 résument les principaux résultats des simu­

lations pour les scénarios étudiés, toujours dans le cas

où les trois points de référence sont des points d'attrac­

tion .

La distribution du scénario A n'est pas significativement

différente d'une distribution aléatoire.

L'indice de con­

centration des points de localisation, voisin de 1, peut

servir de référence pour l'analyse des autres scénarios.

/Il

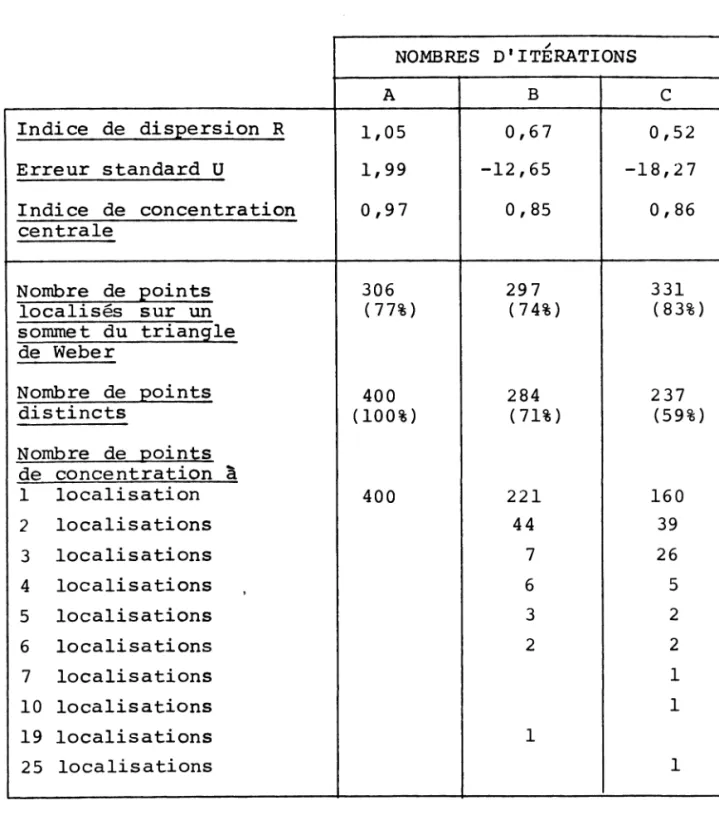
Les distributions des scénarios B et C sont signi f i c a t i ­ v e m e n t différentes d'une d i s t r i b u t i o n aléatoire et sont plus concentrées. Les hypothèses du s c é n a r i o C condui­ s e n t à la concentration la plus élevée (R = 0,52 contre R » 0,67) .

Dans les deux scénarios, des points de concentrations (des "agglomérations", pour r i o n s - n o u s dire) apparaissent. Le s c é n a r i o C donne naissance à une occ u p a t i o n de l'es­ pace très c o n c e n t r é e .

Dans ce scénario (400 i t é r a t i o n s ) , le nombre de points distincts représente 60% e n viron du nombre m a x i m u m de p oints possibles. 12 agglomérations, soit 5% du total, r e p r é s e n t e n t à elles seules 21% des localisations opti­ males; un point concentre 25 localisations, un autre 10

localisations. La h i é r a r c h i s a t i o n entre les centres e s t b i e n marquée. La suite dénombrés aléatoires perm e t ­

tant la génération des points de référence étant toujours identique, quel que soit le nombre d'itérations (et le s c é n a r i o ) , il est possible de suivre l'évolution "tem­ p orel l e " de la s t r u cturation de l'espace au travers des

itérations. Les centres a p p a r a i s s e n t e t leur taille aug­ m e n t e de façon régulière avec les itérations. Un trai­

t e m e n t s t a t i stique pe r m e t t r a i t sans doute de comparer cette h i é r a r c h i e à celles que l'on rencontre dans la l i t t é r a t u r e et é v e n t u e l l e m e n t à des cas réels.

Dans les scénarios B et C, les points de la localisation s e m b l e n t plus proches e n moyenne du poi n t central que dans le s c é n a r i o A. Des tests statistiques p e r m e t t r a i e n t de v é r i f i e r s'il existe une différence entre les deux scé­ n a r i o s du point de vue de leur c o n c e ntration centrale.

Tous ces résultats tendent vers une limite propre à c ha­ que s c é n a r i o qua n d on augmente le nombre d'itérations. D ' a u t r e s scénarios p o u r r a i e n t être étudiés, d'autres i n ­ dices calculés et d'autres tests réalisés, qui p e r m e t ­ t r a i e n t de mettre en évidence et d'a n a l y s e r les effets de s t r u c t u r a t i o n de l'espace obtenus avec un m i n i m u m d'hypo t h è s e s simples et une g é n é r a t i o n aléatoire des p r i n c i p a u x paramètres. Notons que les simulations réa­ lisées ont été effectuées à partir de points initiaux aléatoires. L'effet de contraintes posées sur ces points p o u r r a i t être intéressant à étudier. (Par exemple q u ' a r ­ r i v e - t - i l quand, sur un continent, comme l'Amérique du Nord, le processus de l o calisation débute a p a r t i r de p o i n t s d'attraction qui sont tous situés à la limite d'un espace b o r n é ? ) .

C o n c l u s i o n s

De ces premières analyses, on peut tirer les conclusions s u i v a n t e s :

1) M a l g r é les faibles contraintes qu' i l comporte, le m o d è l e de W e b e r réussit, à lui seul, à produire des phé n o m è n e s de polarisation, de conce n t r a t i o n cen­

trale et des hiérarchies de points de concentration dès que les choix successifs de localisations opti­ mal e s sont rendus i n t e r d é p e n d a n t s .

2) La tendance à la c o n c e n t r a t i o n e s t d'aut a n t plus forte que les cas de points de répulsion s ont rares e t que l'influence q u'exerce une itér a t i o n sur l'i­ tération suivante est importante.

/19

3) L ' i n t r o d u c t i o n de points de r é p u l s i o n a tendance à

freiner le processus de c o n c e n t r a t i o n centrale et peut m ê m e le renverser au p o i n t de p r o d u i r e une p o l a r i s a ­ tion "à l'envers" en faveur de la périphérie.

Ces o b s ervations sur les tendances nat u r e l l e s à la s t r u c ­ t u r a t i o n de l'espace p e u v e n t a v oir une résonnance p a r t i ­ culière, tant au niveau c o n t i n e n t a l q u ' a u n i v e a u des h i é r a r c h i e s urbaines. A u n i v e a u continental, le p h é n o ­ m è n e de concentration centrale d é c o u l a n t de la p r é d o m i ­ n a n c e des forces d ' attraction p e u t s u g g é r e r une e x p l i c a ­ tion p artielle à la croissance des villes du centre des c on t i n e n t s (comme, en A m é r i q u e du Nord, Chicago, Toronto, A t l a n t a et D a l l a s ) , alors que la cro i s s a n c e des villes

c ô t i è r e s s'expliquera m i e u x à p a r t i r de la théorie des p o i n t s de rupture.

P o u r ce qui est des hi é r a r c h i e s urbaines, on les retrou­ ve s p o n t a n é m e n t évoquées q u a n d on e x a m i n e les dis t r i b u ­ tions obtenues de points de concentration. Il semble q u e ces distributions stoc h a s t i q u e s s o i e n t conformes à

la loi rang-dimension (rank size r u l e ) . Il semble même que, plus une localisation optim a l e sera s u s ceptible d'être choisie comme p o i n t de r é f é r e n c e dans une i t é r a ­ tion ultérieure, plus le découpage de la h i é r a r c h i e sera net, c'est-à-dire plus l'écart entre les dimensions des c e ntres supérieurs, moyens et inf é r i e u r s sera prononcé.

A u n i v e a u intra-urbain, les r ésultats obtenus peuv e n t s u g g é r e r certaines e x plications à des p h é n o m è n e s de con­ c e n t r a t i o n et de répulsion. P a r exemple, le procussus i n d u i t p a r des points de répu l s i o n p e u t e x p l i q u e r en

centres-villes vers les périphéries, les forces de répulsion n a i s s a n t souvent de la c o n gestion et de la ha u s s e des v a l e u r s foncières caractéristiques des centres-villes.

NOMBRE D'ITERATIONS

100

200

300

400

Indice de dispersion R

_1,06

_1,03

_1,05

_1,05

Erreur Standard U

_1,15

_0,72

_1,55

_1,99

Indice de concentration

centrale

0,93

0,96

0,96

0,97

Nombre de points

localisés sur un

78

154

321

306

sommet du triangle

de Weber

(78%)

(77%)

(77%)

(77%)

Nombre de points

distincts

100

200

300

400

Nombre de points

de concentration à

1 localisation

100

200

300

400

TABLEAU 1:

RESULTATS DES SIMULATIONS

SCÉNARIO A

Indice de dispersion R E r r e u r s t a n d a r d U Indice de concentration c e ntrale 0, 48 -9,86 0,81 0,67 -8, 87 0,84 0,69 ■10,20 0,84 0,67 -12,65 0,85 localisés sur un s o m m e t du triangle de W e b e r N o m b r e de points d i s t i n c t s N o m b r e de points de c o n c e n t r a t i o n à 1 l o c a l i s a t i o n 2 localis a t i o n s 3 localis a t i o n s 4 l o calisations 5 localis a t i o n s 6 lo c a l i s a t i o n s 10 localis a t i o n s 14 localis a t i o n s 17 l o c a l i s a t i o n s 19 lo c a l i s a t i o n s 73 (73%) 68 (68%) 50 13 2 2 152 (75%) 141 (71%)

11

1

TA B L E A U 2: RESULTATS DES SIMUL A T I O N S SCENARIO B

N O M B R E S D ' I T E R A T I O N S 100 200 300 400 Ind i c e de d i s p e r s i o n R 0 ,54 0,45 0,47 0,52 E r r e u r s t a n d a r d U -8,86 -14,80 -17,45 -18,27 Indice de c o n c e n t r a t i o n c e n t r a l e 0,89 0, 86 0,86 0,86 N o m b r e de p o i n t s localisés sur un s o m m e t d u triangle de W e b e r 84 (84%) 168 (84%) 247 (82%) 331 (83%) N o m b r e de poin t s 57 116 178 237 d i s t i n c t s (57%) (58%) (59%) (59%) N o m b r e çle points de c o n c e n t r a t i o n à 1 l o c a l i s a t i o n 37 74 118 160 2 l o c a l i s a t i o n s 13 26 35 39 3 l o c a l i s a t i o n s 2 11 18 26 4 l o c a l i s a t i o n s 2 2 5 5 l o c a l i s a t i o n s 2 6 l o c a l i s a t i o n s 2 2 2 2 7 l o c a l i s a t i o n s 2 1 1 10 l o c a l i s a t i o n s 1 1 11 l o c a l i s a t i o n s 1 15 localisations 1 21 localis a t i o n s ₁ 25 localisations ₁

TABLEAU 3; RESULTATS DES SIMUL A T I O N S SCENA R I O C

Indice de d i s p e r s i o n R _1,05 0,67 0,52 E r r e u r s t a n d a r d U 1,99 -12,65 -18,27 Indice de c o n c e n t r a t i o n 0,97 0,85 0,86 c e ntrale N o m b r e de p o i n t s 306 297 331 localisés sur un (77%) (74%) (83%) s o m m e t du triangle de W e b e r N o m b r e de p o i n t s _{400 284 237} d i s t i n c t s _{(100%) (71%) (59%)} N o m b r e de p o ints de c o n c e n t r a t i o n à 1 l o c a l i s a t i o n ₄₀₀ 221 160 2 l o c a l i s a t i o n s 44 39 3 l o c a l i s a t i o n s 7 26 4 l o c a l i s a t i o n s 6 5 5 l o c a l i s a t i o n s 3 2 6 l o c a l i s a t i o n s 2 2 7 l o c a l i s a t i o n s 1 10 l o c a l i s a t i o n s 1 19 l o c a l i s a t i o n s 1 25 l o calisations 1

TABLEAU 4: RESULTATS DES S I M U L A T I O N S (400 ITERATIONS)

BIBLIOGRAPHIE

CLARK, P,

COOPER, ]

KUHN, H.Ï

TELLIER,

TELLIER,

TELLIER,

WEBER, A

j. et F.C. EVANS (1954) "Distance to Nearest Neighbour

as a Measure of Spatial Relationships in Populations",

Ecology, vol. 35, no.4, p. 445-453.

,. (196 8), "An Extension of the Generalized Weber Pro­

blem", Journal of Regional Science, vol. 8, no. 2,

p. 181-198.

r. et R . E . KUENNE (1962), "An Efficient Algorithm for

the Numerical Solution of the Generalized Weber Pro­

blem in Spatial Economies", Journal of Regional

Science, vol. 4, no. 2, p. 21-34.

L.-N. (1972), "The Weber Problem: Solution and Inter­

pretation", Geographical Analysis, vol 4, no. 3,

p. 215-233.

L.-N. et X. CECCALDI (1983), "Phénomènes de polarisa­

tion et de répulsion dans le contexte du problème de

Weber", communication présentée devant l'Association

canadienne des sciences régionales, à Vancouver.

L.-N. (1984), Economie spatiale, Chicoutimi, Gaétan

Morin, éditeur.

(1929), Theory of the Location of Industries, Chica­

go, University of Chicago Press, 256 pages.

W E S O L O W S K Y , G.O.

(19 77),

17,

1, p. 53.