Adaptation de maillage anisotrope : définition d'une métrique pour discrétisations de degré élevé

ELOÏSE BOITEAU

ADAPTATION DE MAILLAGE ANISOTROPE

Définition d'une métrique pour discrétisations de degré élevé

Mémoire présenté

à la Faculté des études supérieures et postdoctorales de l'Université Laval dans le cadre du programme de maîtrise en mathématiques

pour l'obtention du grade de Maître es Sciences (M.Sc.)

DEPARTEMENT DE MATHEMATIQUES ET DE STATISTIQUE FACULTÉ DE SCIENCES ET GÉNIE

UNIVERSITÉ LAVAL QUÉBEC

2012

Résumé

Ce mémoire porte sur l'adaptation de maillage par métrique. Plus précisément, on s'inté-resse à développer la métrique discutée dans l'article [10] de Pagnutti __ Ollivier-Gooch puis à voir l'amélioration d'une telle méthode d'adaptation de maillage sur la résolution numé-rique d'une équation aux dérivées partielles par éléments finis. On présente d'abord l'intuition derrière l'adaptation de maillage par métrique, d'où on introduit une approximation de l'er-reur d'interpolation. On parle de la convergence d'une solution numérique. Pour se mettre en situation, on énonce la définition d'une métrique pour ensuite introduire rapidement l'adap-tation de maillage par métrique classique et l'adapl'adap-tation hiérarchique. Puis, au vif du sujet, on explique l'approche de l'adaptation de maillage de Pagnutti & Ollivier-Gooch. On parle aussi des actions permettant d'adapter nos maillages. Enfin, on résout numériquement des équations aux dérivées partielles avec opérateur laplacien par la méthode des éléments finis sur des maillages uniformes et adaptés par nos 3 méthodes d'adaptation. On y considère des cas ID, 2D et 3D.

Avant-propos

Ce mémoire résume le travail de deux années d'études dans le programme de maîtrise en mathématiques appliquées au sein du Groupe interdisciplinaire de recherche en éléments finis (GIREF) de l'Université Laval. Ce groupe est dirigé par monsieur André Fortin et cherche à améliorer la résolution d'équations aux dérivées partielles liées à divers domaines scientifiques par la méthode des éléments finis. On y considère entre autres la déformation du bois, l'écou-lement des fluides, la diffusion de la chaleur, et le contact pneu/chaussée en partenariat avec Michelin.

Au début de mon baccalauréat, j'ai rencontré monsieur André Fortin et son groupe de re-cherche. J'ai tout de suite été impressionnée par l'équipe de travail et l'expérience scientifique qu'on y retrouvait. J'étais donc fière de me joindre aux membres du GIREF afin de collaborer à l'évolution de leur projet tout en bénéficiant de leurs connaissances et de leur aide tout au long de mes études de maîtrise.

J'aimerais remercier particulièrement mon directeur de recherche, monsieur André Fortin, qui, patiemment, a su me guider et me soutenir depuis mes débuts au GIREF, il y a de cela 4 ans déjà. J'aimerais remercier Cristian Tibirna qui s'est toujours montré disponible à m'aider et à répondre à toutes mes questions dans ma découverte de MEF++. C'est aussi grâce à Eric Chamberland que j'ai pu réaliser mon projet sur M E F + + . Son aide a grandement contribué à l'exécution de mes travaux. Merci aussi à Richard Bois pour ses bons conseils.

Merci au Fond québécois de recherche nature et technologies (FQRNT) pour la bourse de maîtrise en recherche ainsi qu'à Hydro-Québec de m'avoir appuyée financièrement.

Merci à ma famille pour leurs encouragements et leur soutien. Merci à mon petit rayon de soleil, Julianne, d'embellir mes journées.

A ma nièce, la belle et intelligente Julianne.

Table des matières

R é s u m é iii Avant-propos v Table des matières ix Table des figures xi Introduction 1 1 Concepts et rappels m a t h é m a t i q u e s 3 1.1 Adaptation et objectif 3 1.2 Terminologie 5 1.3 Erreur d'interpolation 6 1.3.1 En dimension 1 6 1.3.2 En dimension 2 7 1.4 Méthode des éléments finis 8

1.4.1 La méthode 8 1.4.2 Le choix des fonctions tests 10

1.5 Calcul de l'ordre de convergence 12

1.6 Séries de Fourier 15 1.6.1 Fourier à une variable 16

1.6.2 Fourier à deux variables 16

2 A d a p t a t i o n de maillage 19 2.1 Adaptation par métrique classique 19

2.1.1 Une métrique 19 2.1.2 Approximation linéaire 20

2.1.3 Approximation quadratique 21 2.1.4 Intersection de métriques 23

2.2 Adaptation hiérarchique 28 2.3 Méthode de Pagnutti k Ollivier-Gooch 30

2.3.1 Cas ID 30 2.3.2 Cas 2D 32

x TABLE DES MATIERES

2.3.3 Cas 3D 36 2.3.4 Cas à plusieurs variables 43

2.4 Actions sur le maillage 43 2.4.1 Division d'arête 43 2.4.2 Suppression de noeuds 44 2.4.3 Déplacement de noeuds 45 2.4.4 Retournement d'arêtes 46 3 Résolution numérique 47 3.1 Résultats en dimension 1 47 3.1.1 Interpolation linéaire 48 3.1.2 Interpolation quadratique 48 3.2 Résultats en dimension 2 52 3.2.1 Résolution linéaire 52 3.2.2 Résolution quadratique 54 3.2.3 Résolution à deux variables 61

3.3 Résultats en dimension 3 66 3.3.1 Résolution linéaire 66 3.3.2 Résolution quadratique 66 3.4 Résultats pour problème à singularité 69

3.4.1 Résolution linéaire 70 3.4.2 Résolution quadratique 70

Table des figures

1.1 Exemple d'amélioration par adaptation 4

1.2 Exemple de maillage 2D 5 1.3 Fonctions tests linéaires 11 1.4 Fonctions tests quadratiques 11

1.5 Maillages uniformes 2D 13 _*ôv

2.1 Fonctions approximation g(0,<p) 42

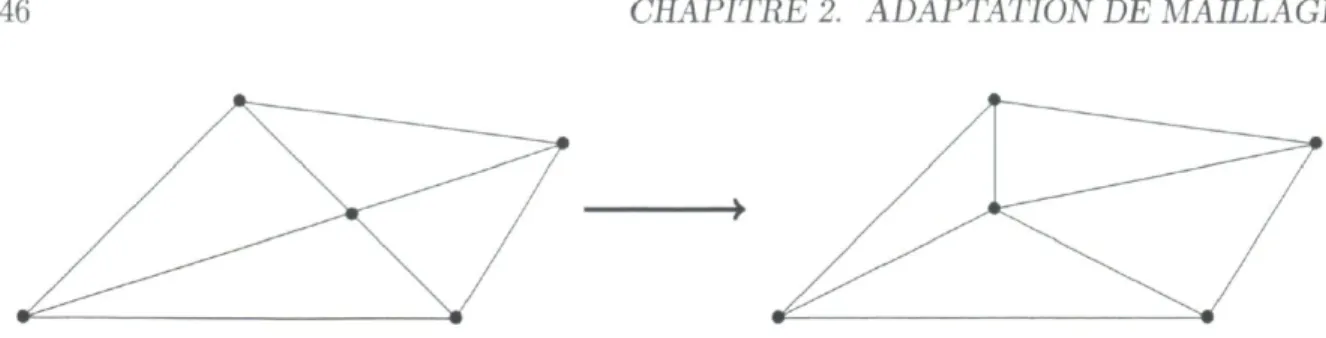
2.2 Division d'arête 44 2.3 Suppression de noeuds 45

2.4 Déplacement d'un noeud 46 2.5 Retournement d'une arête 46

3.1 f(x) = e-5 0'1"2)2 '. 47

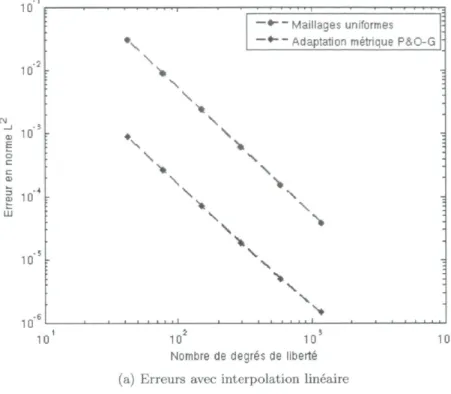
3.2 Erreurs d'interpolation en ID 49 3.3 Interpolation linéaire ID sur maillages uniformes et adaptés 50

3.4 Interpolation quadratique ID sur maillages uniformes et adaptés 51

3.5 Fonctions u\ et U2 53 3.6 Cas linéaire : erreurs de résolution 2D de u\ 55

3.7 Cas linéaire : erreurs de résolution 2D de u% 56 3.8 Cas linéaire : maillages à ~4000 sommets pour résolution de u\ 57

3.9 Cas quadratique : erreurs de résolution 2D de u\ 58 3.10 Cas quadratique : erreurs de résolution 2D de u-2 59 3.11 Cas quadratique : maillages à ~4000 sommets pour résolution de uo 60

3.12 Cas linéaire : erreurs de résolution du problème à deux variables 63 3.13 Cas quadratique : erreurs de résolution du problème à deux variables 64 3.14 Cas linéaire : maillages à ~4000 sommets pour résolution simultanée de u\ et U2 65

3.15 Cas linéaire : erreurs de résolution 3D de u 67 3.16 Cas quadratique : erreurs de résolution 3D de u 68

3.17 Domaine de résolution 69 3.18 Cas linéaire : erreurs de résolution du problème à singularité 71

3.19 Cas linéaire : maillages à ~3000 sommets pour résolution du problème à

sin-gularité 72 3.20 Cas quadratique : erreurs de résolution du problème à singularité 73

Introduction

De multiples phénomènes physiques sont observables autour de nous. Qu'on s'intéresse à la diffusion de la chaleur, la mécanique des fluides, ou encore à la déformation de matériaux sous impact, tous s'accomplissent selon les lois de la nature, des règles bien prescrites. Les mathématiques appliquées visent à modéliser ces lois et à représenter de façon abstraite le monde réel. On modélise ces comportements par des équations aux dérivées partielles que l'on souhaite résoudre.

Toutefois, la résolution explicite par quadrature n'est pas toujours possible. On décide alors de s'orienter vers la résolution numérique pour obtenir des solutions approchées. Différentes méthodes sont alors disponibles, dont la méthode des éléments finis. C'est là qu'intervient le Groupe interdisciplinaire de recherche en éléments finis (GIREF) de l'Université Laval, qui a implanté la méthode sous un code en C + + appelé M E F + + . Créé en 1996, MEF++ a gran-dement évolué et résout aujourd'hui des problèmes de type non linéaire, instationnaire, ainsi que des problèmes à plusieurs variables, en 2D et 3D.

La méthode des éléments finis s'applique sur une discrétisation du domaine de calcul. On appelle cette discrétisation un maillage et les morceaux qui le définissent sont nommés élé-ments. On désigne aussi les côtés des éléments comme étant les arêtes du maillage. Sur chaque élément, une approximation polynomiale de la solution réelle est déterminée. Plus les éléments sont petits, plus la solution approchée est précise, mais plus le temps de calcul est long pour parvenir à la solution approximative. On réclame donc des outils permettant d'améliorer la précision de la solution approchée sans trop augmenter le temps de calcul. Intervient alors l'adaptation de maillage, qui vise la conception d'une discrétisation optimale à la solution recherchée.

Lorsque la fonction solution subit peu de variations à certains endroits du domaine, il est probable qu'un grand élément puisse donner une aussi bonne approximation de la solution que plusieurs petits éléments au même emplacement. Il est alors avantageux de placer ces éléments aux endroits sujets à de plus grandes erreurs, par exemple où il y a de grandes variations. Plus est, si la solution recherchée varie rapidement dans une direction et peu de l'autre, il

2 Eloïse Boiteau

peut être utile d'avoir des éléments étirés. L'adaptation de maillage prend en compte toutes ces astuces.

Dans ce mémoire, on abordera le sujet de l'adaptation de maillage anisotrope par métrique. Au chapitre 1, on introduira la problématique de l'adaptation de maillage ainsi que la termi-nologie utilisée tout au long du mémoire. On verra comment trouver l'erreur d'interpolation d'une fonction et comment celle-ci peut être reliée à une métrique. On expliquera la méthode des éléments finis et on parlera de l'ordre de convergence des résolutions numériques. Enfin, on exposera les développements des séries de Fourier à une et deux variables, puisqu'elles seront utilisées plus loin.

Au chapitre 2, on introduira formellement la notion de métrique. On discutera sommai-rement de l'adaptation par métrique classique et de l'adaptation hiérarchique, ces méthodes étant déjà implantées au GIREF. On développera ensuite la métrique en lien avec l'erreur d'interpolation introduite par Pagnutti __ Ollivier-Gooch [10], et ce pour les cas ID, 2D, 3D et à plusieurs variables. Puis, on expliquera les procédures en lien avec la métrique qui nous permettent d'obtenir un maillage optimal à la précision du calcul.

Au chapitre 3, on présentera les résultats numériques obtenus avec MEF++. On y verra les performances des cas ID, 2D, 3D et à plusieurs variables avec approximations polynomiales de degré 1 et 2 sur les maillages uniformes et adaptés par nos 3 méthodes. De plus, on étudiera la convergence d'un problème à singularité sur un angle rentrant. On fera un bilan de la méthode d'adaptation de maillage de Pagnutti &: Ollivier-Gooch et on comparera celle-ci avec les méthodes déjà implantées au GIREF.

Chapitre 1

Concepts et rappels mathématiques

Avant de commencer à discuter du sujet de ce mémoire, il nous faut introduire la probléma-tique et présenter les bases sur lesquelles s'appuie la recherche. Nous définirons certains termes qui seront utilisés, nous donnerons un aperçu de l'intuition derrière l'adaptation de maillage par métrique dont la méthode de Pagnutti &: Ollivier-Gooch, et nous décrirons sommairement les outils mathématiques qui serviront à l'analyse des résultats numériques.

1.1 Adaptation et objectif

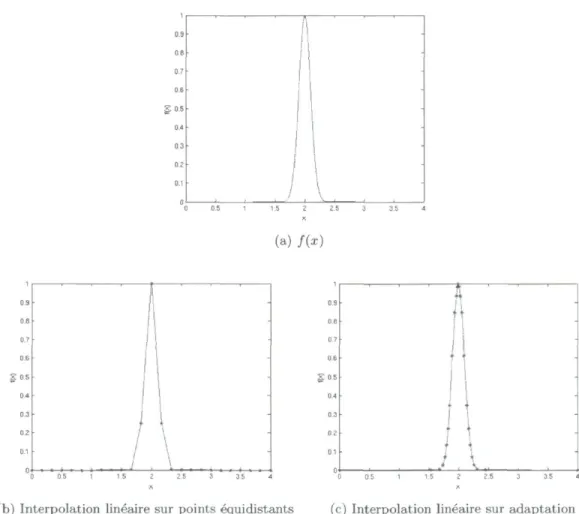
Considérons le problème suivant : soit la fonction /(x) = e-50(x-2) g u r x g ^ ^j qUe n o u s souhaitons approximer par une fonction p(x) linéaire par morceaux. Choisissons d'utiliser 25 points, que nous placerons sur le domaine, pour interpoler linéairement la fonction / ( x ) . La fonction /(x) peut être visualisée à la figure 1.1a.

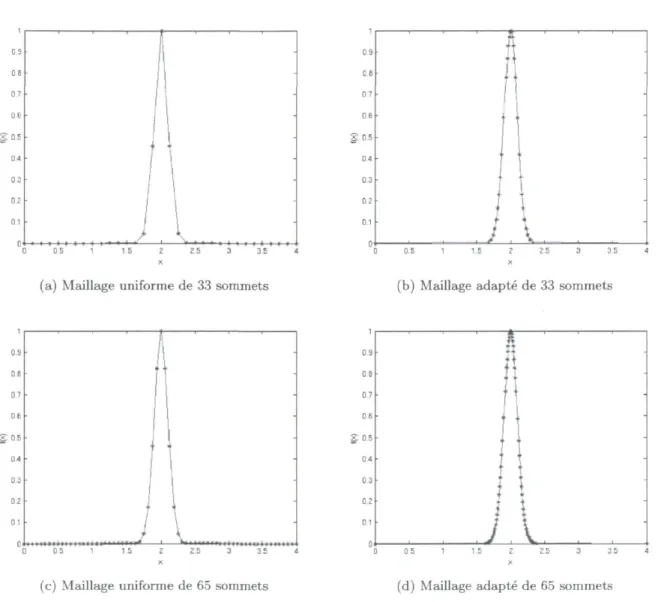
Comme première option, nous pouvons choisir de placer nos 25 points à equidistance sur [0,4]. Nous remarquons alors que notre approximation p(x), représentée à la figure 1.1b, illustre avec peu de précision la fonction / ( x ) .

Essayons donc d'interpoler linéairement /(x) sur des points différents. Cette fois-ci, nous choisissons de placer plus de points aux endroits courbes de la fonction et moins de points aux endroits relativement linéaires. Nous pouvons ainsi prévoir que l'interpolation linéaire sur ces nouveaux points sera beaucoup plus près de /(x) que l'interpolation sur les points équidistants. Constatons l'amélioration d'une telle interpolation à la figure 1.1c.

Nous appelons adaptation la façon dont nous modifions la disposition des points d'inter-polation de manière à capturer les caractéristiques de la fonction à approximer. L'objectif de l'adaptation consiste à placer un nombre indiqué de points sur un domaine de façon à ce que l'erreur entre la solution exacte et l'interpolation sur ces points soit minimisée. La position

4 CHAPITRE 1. CONCEPTS ET RAPPELS MATHEMATIQUES

de ces points d'interpolation sera différente, dépendamment de la fonction à interpoler et du type d'interpolation polynomiale (linéaire, quadratique, cubique, etc.) utilisé. Remarquons que dans les situations réelles, nous voulons résoudre un problème d'équations aux dérivées partielles. La solution exacte est alors inconnue. Il nous faut donc considérer des méthodes qui nous donneront une approximation de l'erreur sur l'interpolation.

Mais comment procéder pour arriver à un tel positionnement des points ? Un premier indice consiste à regarder le terme d'erreur de l'interpolation sur chaque intervalle de points. Nous voudrons alors cibler les endroits du domaine où l'erreur est plus élevée pour y améliorer l'interpolation. Nous verrons à la section 1.3 comment identifier ces régions du domaine. Toutefois, nous définirons d'abord quelques termes pour mieux parler d'adaptation.

es , , , rï ' ' Q_

11

1 1

1 '

1 i

J 1

i {

II

l

J

l

ï

l

-(b) Interpolation linéaire sur points équidistants (c) Interpolation linéaire sur adaptation

1.2. TERMINOLOGIE

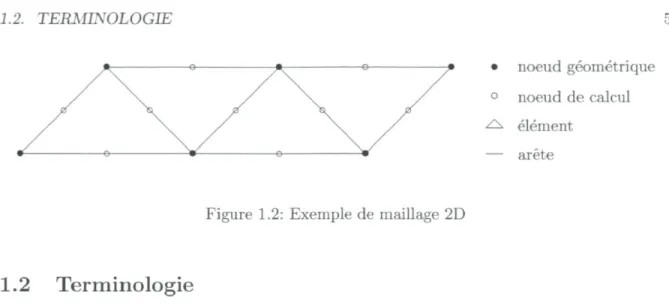
• noeud géométrique ° noeud de calcul ^ élément — arête

Figure 1.2: Exemple de maillage 2D

1.2 Terminologie

Afin de bien se préparer à la problématique, il nous faut définir certains termes qui seront employés. Nous introduisons donc les notions de maillage, élément, noeud, arête et degré de liberté.

Lors de la résolution numérique d'équations aux dérivées partielles, il nous faut discréti-ser notre domaine pour résoudre le problème sur de petits intervalles ou sous-domaines. Le maillage est ce que nous appelons la discrétisation de ce domaine. Au problème de la sec-tion 1.1, les points d'interpolasec-tion définissaient la partisec-tion qu'est le maillage. Dans le cas bidimensionnel, un maillage peut être partitionné de triangles, quadrilatères, ou toute autre forme géométrique pavant le domaine.

Un élément est un intervalle ou sous-domaine géométrique qui forme le maillage. En ID, les éléments sont des intervalles. En 2D, nous travaillons avec des éléments triangulaires ou quadrilatéraux. En 3D, les éléments sont plus communément des tétraèdres ou des hexaèdres. Toutefois, pour ce mémoire, nous utiliserons respectivement des triangles et des tétraèdres comme éléments de nos maillages 2D et 3D.

Dans les cas 2D et 3D, les éléments sont formés d'arêtes qui définissent les bords d'un élément. Un élément se définit aussi par ses sommets, ceux-ci se nommant aussi noeuds

géo-métriques du maillage.

Les noeuds de calcul sont, quant à eux, des points dont nous choisissons la position sur l'élé-ment. Ils sont liés aux inconnues de l'approximation de la fonction à déterminer. À ces noeuds, nous associons des degrés de liberté qui représenteront ces inconnues. Lors d'une résolution linéaire, nous placerons nos noeuds de calcul aux noeuds géométriques. Pour la résolution quadratique, nous y ajouterons des noeuds de calcul au milieu des arêtes du maillage.

6 CHAPITREE CONCEPTS ET RAPPELS MATHEMATIQUES

1.3 Erreur d'interpolation

Soit pn{x) le polynôme de degré n qui interpole u(x) aux points xo, xi, ..., xn. Nous souhaitons avoir une approximation de l'erreur d'interpolation En(x) telle que

u(x) =pn(x) + En(x).

Pour ce faire, introduisons la fonction

i, s (S i \ u(x) ~Pn{x)

<P(Z) = U(z) - pn{z) — xp'z)

où tp(x) = nr=o(x — X i)- Remarquons que <f>(z) possède n + 2 zéros puisque <f>(xi) = 0 pour i = 0, ...,n et 4>(x) = 0. Par le théorème de Rolle, il existe alors un £ € [x_, xn] tel que 0(n+1)(£) = 0. Cela nous permet d'écrire qu'il existe £ € [xo,xn] tel que

u

(0 -

J 4

( 0

- " ^ "

V

( o = o.

Puisque pn(x) est un polynôme de degré n, nous avons pn (£) = 0. De plus, ^(x) est un polynôme de degré n + 1 avec un coefficient directeur de valeur 1 et donc ^n + 1) ( x ) = (n + 1)!. Il existe alors £ S [x_, xn] tel que

E

(x)

(«+l)

_^i

u

(0

L'interpolation linéaire entre x_ et xi aura ainsi un terme d'erreur de la forme

Ei(x) = ±v?(t)(x-x0){x-x1) (1.2)

pour un £ G [xo,xi]. Puisque nous considérons plutôt l'erreur absolue et que h2

max |(x — £o)(x — xi)| = —

x€[x0,xi] 4

où h représente la longueur de l'élément [xo,xi], nous avons alors que

1.3. ERREUR DTNTERPOLATION 1.3.2 E n d i m e n s i o n 2

Dans le monde physique, peu de situations nous incitent à utiliser des maillages unidi-mensionnels. La plupart du temps, nous souhaitons résoudre des problèmes tridiunidi-mensionnels. Pour aborder le contexte tridimensionnel, considérons d'abord les problèmes bidimensionnels à résoudre sur des maillages à éléments triangulaires ou quadrilatéraux. Dans ces cas, nous considérons l'erreur sur les arêtes de ces éléments comme étant une bonne approximation de l'erreur sur l'élément lui-même [3].

Pour approximer l'erreur sur l'arête, nous utilisons le terme d'erreur pour le cas unidi-mensionnel trouvé à l'équation 1.1. Soit ainsi les noeuds a = (a\,a2)T et b = (b\,b2)T qui définissent l'arête ab. La fonction

7(5) = (b — a)s + a

parametrise la position d'un point sur l'arête par rapport à la variable s € [0,1]. L'erreur au point 7(5) = (x(s),y(s)) sur l'arête pour une interpolation linéaire est alors, par l'équation 1.2,

1^(7(0)

El{s) ~ 2 ds* S{S ~ l)

pour un C G [0,1].

En faisant les calculs, nous obtenons

du du dx du dy ds dx ds dy ds

du., . d u . . .

=

dx

-

dy-

-

et

d 2 u - (h n h n \ ( ë ïïïïj}\ (h^ ~ «1

__(

-ai,&_-a

) I- ^ [

-T

= ab Hu ab

où Hu est la matrice hessienne de notre fonction u à approximer. Notre approximation de l'erreur absolue sur l'arête devient

CHAPITRE 1. CONCEPTS ET RAPPELS MATHEMATIQUES

pour s G [0,1]. Puisque \s(s — 1)| < | pour s G [0,1], nous avons 1 -.T.

|_3i(s)| < - a b tf_(7(C)) a*> et donc nous évaluons

\ E \ ( x , y ) \ < c max max |(e, Hu(x, y) e ) | ,

où (x, y) est un point de l'élément K, E K est l'ensemble des arêtes de l'élément, (•, • ) est le produit scalaire usuel, c est une constante, et E\ (x, y) est l'approximation de l'erreur d'inter-polation linéaire au point (x, y). La majoration globale de l'erreur d'interd'inter-polation sur l'élément K est alors dépendante des arêtes de l'élément, tel que mentionné dans l'article [1] d'Alauzet et Frey.

Il est important de remarquer que le terme d'erreur sur l'élément ressemble particulière-ment à une métrique si la matrice hessienne Hu est définie positive. La métrique sur les arêtes est alors représentative de l'erreur sur l'élément !

Plus loin, nous définirons les étapes à la construction d'une métrique liée à l'erreur. Tout d'abord, voyons un bref aperçu de la méthode numérique que nous utiliserons pour résoudre un problème d'équations aux dérivées partielles.

1.4 Méthode des éléments finis

Nous décrirons ici brièvement la méthode des éléments finis [9], celle-ci étant la méthode que nous utiliserons pour résoudre nos équations aux dérivées partielles. Nous passerons ra-pidement sur les détails puisque la méthode des éléments finis n'est qu'un outil pour résoudre une équation aux dérivées partielles sur le maillage de notre choix.

1.4.1 L a m é t h o d e

Commençons tout d'abord en présentant l'équation différentielle ordinaire qui nous servira d'exemple.

-u"(x) = f(x), s e [0,1]

u(0) = 0 (1.3) u ( l ) = 0

La fonction /(x) est ici connue et pour simplifier, nous supposons / G I?.

1.4. METHODE DES ELEMENTS FINIS 9 différentielle par une fonction test w(x) et dïntégrer féquation sur le domaine. Notons que

la fonction test w(x) doit être dans le même espace de Hilbert que u(x) par rapport à ses conditions initiales. Pour l'exemple 1.3, nous devons avoir w(x) G Hr)([0,1]). Il s'en suit que

/ -u"(x)w(x)dx = f f{x)w(x)dx Vu; € #,J([0,1]) Jo Jo

et, en intégrant par parties le terme de gauche tout en considérant les conditions initiales,

/ u'(x)w'(x)dx= f f(x)w(x)dx Vw G Hr]([0,1]). (1.4)

Jo Jo

pour réécrire le problème 1.4 comme suit.

a(u,w) = £(w) Vu;eflo([0,l]) (1.5) Sous les hypothèses que a(-, • ) est une forme bilinéaire continue et coercive et que .(• ) est

une forme linéaire continue, le théorème de Lax-Milgram [5] nous assure une unique solution u(x)GJf/01([0,l]).

La deuxième étape consiste à approximer notre fonction u(x) par ù(x) = £_U=i Uj<fo(x) pour des fonctions (0j)n = 1 G HQ([0, 1]) choisies. Cette astuce nous permet de ramener le problème en dimension finie. En substituant u(x) par û(x) dans l'équation 1.5, nous avons

a[Y

u

<f>

,w)=e(w) Vu; G ^([0,1]).

\r=l J

l \*=1 /

_C

(/ 4>'i(x)w'(x) dx\

= yiuia(<t>i,w).

10 CHAPITRE 1. CONCEPTS ET RAPPELS MATHEMATIQUES

De plus, si nous choisissons de considérer les cas où w — 4>j pour j = 1,..., n, nous obtenons le système ^Uia^i^i) = £((p\) i=l n ^Uia{4)i,4>2) = £{<t>2) i=l Y^Uia(<t)i,(j)n) = £(4>n)

qui est équivalent au système matriciel

fa((f)i,(f)i) ... a(4>n, 4>i)\ fu{\ (£{(p\)

\a((f)i,<pn) ... a(4>n,4)n)J \un) \£(4>n)

que nous noterons

AU = L.

Ce choix de fonctions w est connu sous le nom de méthode de Ritz.

Il est alors facile de résoudre notre système matriciel afin d'obtenir la solution U. À partir des valeurs de U, nous obtenons l'approximation ù = 2~27=i ui^i de ^a solution de l'équation différentielle.

1.4.2 Le choix des fonctions tests

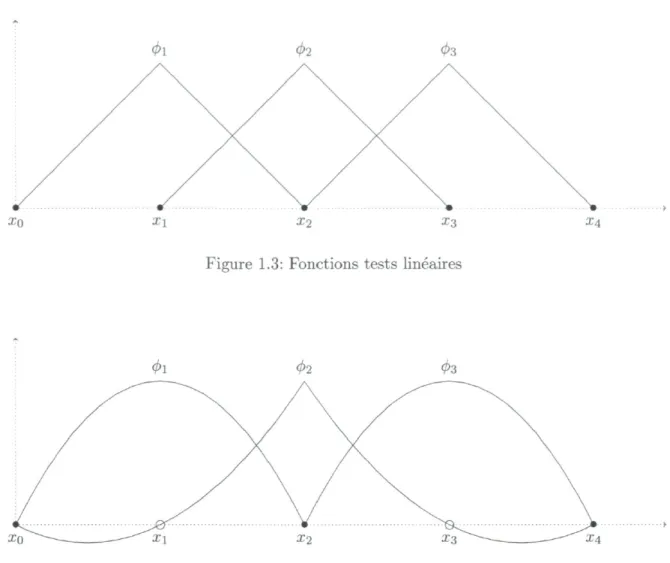
Les grandes lignes de la méthode des éléments finis sont complètes, mis à part le choix des fonctions <f>i, appelées fonctions tests. La méthode nous dit que nous devons choisir des fonctions (0i)"=1 G V (pour l'espace d'Hilbert V relatif au problème) qui nous serviront de base pour approximer la fonction u à déterminer.

Il faut d'abord établir le nombre désiré de fonctions tests. Dans le cas unidimensionnel où nous avons A^ éléments et que nous voulons approximer linéairement la fonction u(x) du problème 1.3 sur chacun d'eux, nous avons 2.V inconnues (2 inconnues par fonction affine sur N éléments) à déterminer. Il faut ensuite s'assurer de la continuité entre chaque fonc-tion affine, ce qui nous impose N — 1 contraintes. Finalement, il faut respecter les condifonc-tions aux limites û(0) = û(l) = 0, ajoutant 2 contraintes supplémentaires. Il nous reste alors 27V — (TV — 1) — 2 = N — 1 inconnues à déterminer.

1.4. METHODE DES ELEMENTS FINIS 11

Figure 1.3: Fonctions tests linéaires

Figure 1.4: Fonctions tests quadratiques

chaque noeud de calcul. Nous souhaitons donc avoir TV — 1 noeuds que nous placerons sur nos éléments et que nous noterons Xj. Nous associerons à chaque noeud X{ une fonction test linéaire par morceaux 4>i(x) telle que

(pi(Xj) = 1 SI l = J

si i ± j.

N-l

Nous aurons alors Ù(XJ) = y. uj4>j(xi) = u

12 CHAPITRE 1. CONCEPTS ET RAPPELS MATHÉMATIQUES

1.5 Calcul de l'ordre de convergence

Une étape importante de l'analyse des résultats numériques est le calcul de l'ordre de convergence de la méthode. Nous cherchons à quantifier la vitesse à laquelle la méthode converge vers la solution exacte lorsque nous utilisons des arêtes de plus en plus fines.

Soit h la longueur des arêtes d'un maillage. L'erreur sur le maillage peut alors être repré-sentée par

E(h) = chp

où c est une constante et p est l'ordre de convergence que nous recherchons. En prenant le log de chaque côté de l'expression, nous obtenons

log(E(h))=p\og(h) + log(c).

Le logarithme de l'erreur est alors représenté par une fonction affine de pente p par rapport au logarithme de h. Ainsi, en imposant des valeurs h pour nos maillages et en vérifiant l'erreur de notre solution numérique avec la solution exacte sur ces maillages, nous pouvons tracer un graphique de log(E(h)) en fonction de log(/i). La pente de ce graphique est alors l'ordre de convergence que nous recherchons.

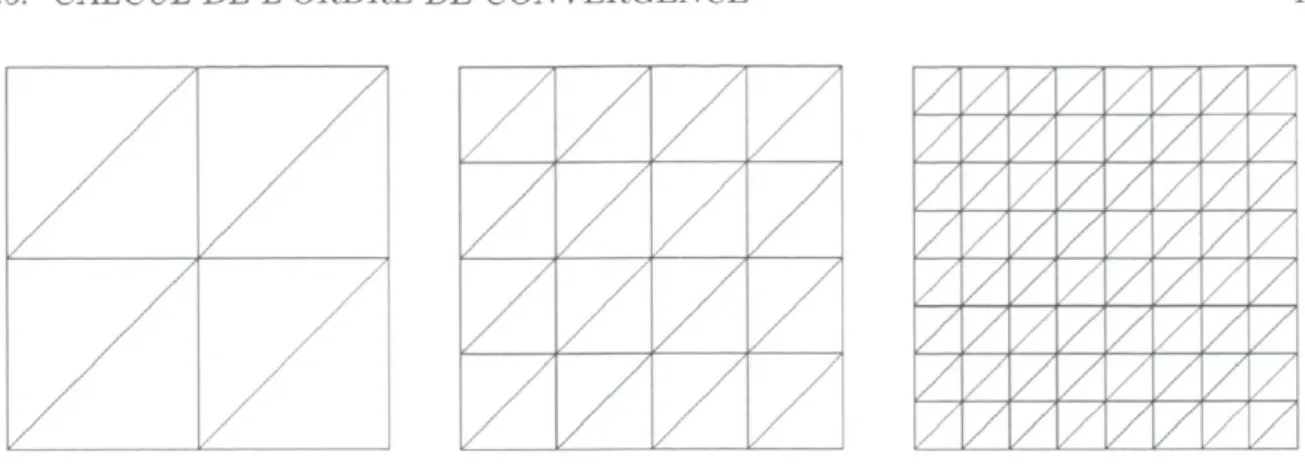
Il nous faut toutefois se demander comment nous trouverons p si la longueur de nos arêtes n'est pas constante, comme dans le cas de l'adaptation de maillage. Remarquons qu'en dimension d,

hdcx

DDL où DDL est le nombre de degrés de liberté du maillage.

Pour illustrer cette relation, prenons en exemple le cas d = 2 présenté à la figure 1.5. Supposons qu'il y a résolution linéaire sur un maillage. Lorsque la longueur h des arêtes du maillage est divisée par deux, le nombre de DDLs, étant équivalent au nombre de sommets du maillage, est à peu près doublé le long de chaque côté du maillage. Puisque nous sommes en dimension 2, le nombre de DDLs quadruple sur tout le maillage. Nous en convenons donc que lorsque la longueur h de nos arêtes est 4 fois plus petite, le nombre de DDLs est 16 fois plus grand, d'où la relation générale DDL oc ^_.

1.5. CALCUL DE L'ORDRE DE CONVERGENCE 13

/

/ / / / / / /

/

Figure 1.5: Maillages uniformes 2D

En usant de cette relation, nous pouvons déduire les équivalences suivantes. log(£) = plog(/i) + log(c)

=->G?]

\og(kxDDL) + log(c)

log(DDL) + k2.

Les variables c, k\ et &2 ci-dessus représentent des constantes.

Nous procéderons donc en faisant un graphique de log(E) sur log(DDL). De ce graphique, nous aurons à trouver la pente de la fonction relativement affine et multiplier celle-ci par —d pour obtenir l'ordre de convergence p.

Pour nos fins, nous utiliserons la norme L2 et la semi-norme H1 pour calculer l'erreur E entre u(x) et l'interpolation pn(x). Ces normes sont exprimées ci-dessous, où fl représente le domaine de calcul.

IMIi* = / h-

I

- f

Jn

= / IVUI

Le lemme de Céa [7] nous informe du taux de convergence que nous pouvons nous attendre à obtenir lors de nos résolutions par la méthode des éléments finis.

14 CHAPITRE 1. CONCEPTS ET RAPPELS MATHEMATIQUES

L e m m e d e C é a

Soit V un espace de Hilbert muni de sa norme associée \\-\\, _.(• ) une forme linéaire continue sur V, et a(-, • ) une forme bilinéaire continue et coercive sur V telle que

\a(u, v)\ < 7||u||||v||

et

a(v,v) > a\\v\\ . Considérons le problème où nous cherchons u G V telle que

a(u, v) = L(v) V. G V.

De plus, considérons le même problème sur un sous-espace de dimension finie Vh C V. Nous cherchons ici _/j G V/j. Il s'en suit alors que

7

\\u - uh\\ < -\\u- vh\\ Mvh G Vh.

a

D é m o n s t r a t i o n

Puisque a(-, • ) est a-coercive, nous avons

a\\u — Uh\\2 < a(u — Uh, u — Uh).

De plus, puisque a(-, • ) est bilinéaire, nous avons

a(u -uh,u- uh) = a(u -uh,u- vh) + a(u - uh,vh - uh) Wvh G Vh.

Notons toutefois que

a(u - uh, vh - uh) — a(u, vh - uh) - a(uh,vh - uh) = L(vh - uh) - L(vh - uh) = 0 \/vh G Vh

et donc que

a(u - uh,u - un) = a(u -uh,u- vh).

Il s'en suit alors que

Q||U - uh\\2 < a(u - uh, u - Vh) < ~f\\u - Uh\\\\u - v^W W,. G 14,

1.6. SERIES DE FOURIER 15 Remarquons que nos équations aux dérivées partielles, appliquées à la méthode des

élé-ments finis, se réduisent à la même forme (1.5) que le problème auquel s'applique le lemme de Céa. Nous pouvons donc utiliser ce lemme pour en déduire l'ordre de convergence de la méthode des éléments finis. Pour un espace Vh de fonctions polynomiales de degré n par mor-ceaux, nous considérons le problème d'interpolation comme borne pour l'erreur du problème d'éléments finis. Nous avons alors (voir Ciarlet[6])

\\u ~ uk\\L2 < Ci inf \\u — v\\L2

v€Vh

<Ci\\u-nu\\L2

< C2(u)hn+1

\u — Uhlffi < Ci inf \u — V\JJI

vevh

< C\\u — nu\fji < C2(u)hn

où n u est l'interpolation de degré n sur le maillage, Ci est une constante et C2 est fonction de la solution exacte u. Nous traiterons donc de résolutions linéaires qui convergeront à l'ordre 2 en norme L2 et à l'ordre 1 en semi-norme H1. Les résolutions quadratiques atteigneront des ordres de 3 et 2 en norme L2 et en semi-norme H1 respectivement.

Toutefois, mentionnons que C2 dépend généralement de la régularité de la solution u. Nous notons donc que les problèmes dont la solution n'est pas suffisament régulière, tel le pro-blème à singularité de la section 3.4, n'obtiendront pas nécessairement les taux de convergence optimaux.

1.6 Séries de Fourier

Au cours de notre cheminement vers l'obtention d'une métrique liée à l'erreur, nous aurons besoin des séries de Fourier. Lors de l'adaptation en 2D, nous devrons approximer une fonction à une variable par une série de Fourier partielle. Pour le cas 3D, nous aurons besoin d'une série de Fourier partielle à 2 variables. Voici donc un rappel des développements requis pour obtenir nos approximations de fonctions.

16 CHAPITRE 1. CONCEPTS ET RAPPELS MATHÉMATIQUES

1.6.1 F o u r i e r à u n e v a r i a b l e

Soit /(_•) une fonction à une variable sur [0, 2TT) à prolongement périodique. Pour obtenir sa série de Fourier F(ô) sur [0,27r], nous devons calculer (voir Tolstov[12])

i r2* ln = - / f(6) cos(n0) de TT Jo et r27T 1 fn Bn = - f(6) sin(n^) dB n Jo pour n G N.

Nous obtenons finalement

A °°

F(0) = -£ + Y, lAn cos(nô) + Bn sm(n9)}.

2

1.6.2 F o u r i e r à d e u x v a r i a b l e s

Soit f(6,<fi) une fonction à deux variables. Pour obtenir sa série de Fourier F(d,</>) à pro­ longement périodique sur [0, 2n] x [0, n], nous devons calculer (voir Tolstov[12])

O fit rlir Ajk = — / f(9, (p) cos(j0) cos(2fc0) d6d<f>, * Jo Jo BJjk = -Ô / / /(*> <t>) cos(j0) sin(2fc0) d6 d<j>, TT Jo Jo ty /»7T /•27T Cjk = -rr / /(_■,<£) sinh'c?) cos(2fc0) d0 d<p ^ Jo Jo et Djk = — / f(0,(f>)sm(j6)sm(2k<t>)ded4> n Jo Jo pour j,fc G

1.6. SERIES DE FOURIER 17 Nous obtenons finalement

A i °° i x

F(0, </>) = - ^ - + - Y }A3 J O C O S0 ' # ) + Ç»\osin(jô)] + g 5_. [ 4 u cos(2fc<£) + _30,fc sin(2fc</»)] . = i fc=i

oc oc

+ ^ ] P Aj>Jfc cos(je) cos(2k<j>) + Bj,fc cos(je) sm(2k(p) j = \ fe=i

oo oo

+ ] P ^ Cj,fc sin(j0) cos(2fc<^) + DJifc sinfj'fl) sin(2fc0). j = i fc=i

Chapitre 2

Adaptation de maillage

Nous voici au vif du sujet : l'adaption de maillage. Nous parlerons rapidement de l'adapta­ tion par métrique classique puis de l'adaptation hiérarchique, toutes deux étant des méthodes déjà implantées au GIREF. Ensuite, nous expliquerons en détails la méthode de Pagnutti & Ollivier­Gooch, une méthode d'adaptation par métrique. Nous déterminerons sa métrique, en lien avec l'erreur d'interpolation. Finalement, nous expliciterons les étapes précises menant à l'adaptation de maillage. L'adaptation est très sensible à l'ordre de ces étapes et aux critères que nous imposerons pour effectuer chaque action.

2.1 Adaptation par métrique classique

Nous définirons ici ce qu'est une métrique et nous déterminerons la métrique classique, implantée au GIREF, en lien avec l'erreur d'interpolation.

2.1.1 Une métrique

Une métrique est une mesure qui définit la distance entre deux éléments d'un ensemble. Soit donc la fonction d : (X, X ) —♦ R+. d(­, • ) est une m é t r i q u e sur X si elle satisfait, pour tout x, y et z G X, les trois propriétés suivantes :

1. d(x,y) = 0 <5 x = y

2. d(x,y) = d(y,x)

3. d(x, z) < d(x, y) + d(y, z).

Un exemple de métrique est la distance euclidienne, définie sur Rn par

20 CHAPITRE 2. ADAPTATION DE MAILLAGE Nous souhaitons créer une métrique qui sera en lien avec l'erreur d'interpolation d'une fonction u. Pour ce, considérons la métrique anisotrope dani(-,-) qui se caractérise comme

étant la distance euclidienne d'une transformation inversible L sur l'espace W1.

dam(a,b) = y/(L(b-a))T(L(b-a))

= yJ(b-a)

L

L(b-a)

En posant M = LTL, la métrique devient

da n i(a, b) = yj(b - a)TM(b - a) (2.1)

où M est une matrice symétrique définie positive.

2.1.2 A p p r o x i m a t i o n l i n é a i r e

Supposons que nous souhaitons approximer notre fonction u par une fonction linéaire par morceaux. Tel que mentionné à la section 1.3, il existe un fort lien entre l'erreur de l'approximation et la matrice hessienne de u, soit Hu. En effet, nous savons que si nous considérons un point x d'un élément K du maillage, l'erreur absolue d'interpolation |.__i(x)| en ce point aura la borne suivante

|-Ei(x)| < max max (ab,Hu(y) ab)

y^K âbcK

où ab est une arête de l'élément K et (•, • ) est le produit scalaire usuel.

Nous voudrions que notre métrique dani(- , •) soit indicatrice de l'erreur sur le maillage. Tel que mentionné à la section 1.5, si nous considérons une arête de longueur h et que nous approximons notre fonction par une fonction linéaire sur celle-ci, l'erreur de l'approximation sera proportionnelle à h2. Nous voudrions conserver cette propriété pour la mesure de longueur par métrique. Ainsi, nous voulons une métrique dani(-, • ) telle que

d>ani(a, b)2 « max |^i(x)|

xÇjab

où la longueur de l'arête au carré en mesure métrique équivaut à l'erreur sur l'arête. En considérant la borne de l'erreur sur l'arête et en choisissant

2.1. ADAPTATION PAR MÉTRIQUE CLASSIQUE 21 la mesure de longueur de l'arête ab serait directement en lien avec l'erreur d'approximation

sur l'arête. En uniformisant la longueur des arêtes du maillage par rapport à la métrique dani{-, • )i n o u s uniformiserions l'erreur sur chaque arête et donc l'erreur sur tout le maillage. Nous appelons ce processus l'adaptation par métrique.

En comparant cette métrique 2.2 à la métrique 2.1, nous identifions notre matrice M comme étant la matrice hessienne Hu de la fonction à approximer. Celle-ci est bien symé-trique mais n'est pas nécessairement définie positive. Si, en effet, la matrice M n'est pas définie positive, nous procédons de la manière suivante.

Soit la matrice symétrique M qui n'est pas définie positive. Nous procédons d'abord en diagonalisant celle-ci. Sa factorisation est alors la suivante,

M = QAQT

où Q est la matrice des vecteurs propres et A est la matrice diagonale des valeurs propres Aj de M. La prochaine étape consiste à modifier la matrice A en employant la valeur absolue sur toutes ses valeurs propres. La matrice M devient alors

M = Q\A\QT

où, dans le cas d'une matrice 2 x 2 ,

|A| =

U IH>'

De plus, s'il existe une valeur propre nulle, nous remplaçons celle-ci par une très petite valeur e > 0. La nouvelle matrice M est alors une matrice définie positive.

Remarquons que lorsque nous résolvons une équation aux dérivées partielles, la solution u est inconnue. Pour obtenir les valeurs de Hu que nous utiliserons pour définir la métrique, nous employons donc des méthodes de récupération de dérivées. Notons aussi que lorsque nous développerons nos différentes méthodes d'adaptation, toutes dérivées dont nous aurons besoin seront disponibles via différents procédés de récupération de dérivées. Pour plus d'informations sur ces méthodes, nous nous référons au mémoire [11] de Benoît Pouliot.

2.1.3 A p p r o x i m a t i o n q u a d r a t i q u e

Si toutefois nous souhaitons approximer notre fonction u par une fonction quadratique par morceaux, le processus devient plus complexe. Une première intuition nous amène à regarder le gradient de notre fonction u. Nous considérons alors que l'erreur sur le gradient est

indica-22 CHAPITRE 2. ADAPTATION DE MAILLAGE

trice de l'erreur sur la fonction u elle-même.

Puisque u est approximée par une fonction quadratique par morceaux, l'approximation de chaque composante du gradient est une fonction linéaire par morceaux. Toutefois, rien ne nous assure que ces fonctions linéaires par morceaux sont continues. Pour régler ce problème, nous pouvons projeter les morceaux de fonctions linéaires de façon à obtenir une fonction linéaire par morceaux continue pour chaque dérivée. Toutefois, cela n'est pas nécessaire puisque toute information dont nous aurons besoin sera accessible à partir de l'approximation de u.

Nous cherchons donc à définir une métrique en lien avec l'erreur de l'approximation linéaire par morceaux du gradient. Pour chaque composante du gradient, nous pouvons déterminer une telle métrique. Soit, à titre d'exemple, la première composante ux du gradient. Tel qu'admis pour les approximations linéaires par l'équation 2.2, nous avons que la métrique en lien avec l'erreur de l'approximation de ux est celle satisfaisant

dani(a,b)2 = (ab,HUx ab).

Chaque composante du gradient possède donc une métrique de la forme 2.1, indicatrice de son erreur d'approximation, ayant comme matrice M la matrice hessienne de la dérivée partielle. Chaque matrice M est alors composée de dérivées troisièmes de la fonction u.

Voici donc, en tant qu'exemple, les matrices Mx et My liées aux métriques des dérivées

premières ux et uy d'une fonction u(x,y).

Mx = My = lxxy UXxy ^xyy U3 ^ *xyy "yyyJ

Tel que mentionné plus haut, notons que, pour chaque dérivée, nous n'aurons pas à projeter les morceaux de fonctions linéaires pour en obtenir une fonction continue. Pour déterminer la matrice hessienne de chaque dérivée, nous choisissons plutôt d'effectuer une récupération des dérivées 3e à partir de l'approximation de u.

Mais que faire avec plusieurs métriques si nous n'en avons besoin que d'une? C'est là qu'intervient l'intersection de métriques, qui se charge de produire une matrice M de métrique préservant les bornes d'erreur pour chaque dérivée.

2.1. ADAPTATION PAR METRIQUE CLASSIQUE 23

2.1.4 I n t e r s e c t i o n d e m é t r i q u e s

Soit deux matrices symétriques définies positives M\ et À_2 de dimension 2 x 2 liées à deux métriques. Nous souhaitons intersecter celles-ci pour obtenir une nouvelle métrique respectant les propriétés de chacune. Pour ce, nous devons d'abord déterminer une base (ei,e2) dans laquelle nos deux matrices sont diagonales. C'est alors que nous introduisons la matrice N qui se définit comme suit.

TV = M{lM2

L e m m e 1

N est diagonalisable.

D é m o n s t r a t i o n

Nous savons que M\ est une matrice symétrique définie positive, ce qui nous permet d'affirmer que M\ est diagonalisable et donc nous pouvons écrire

Mi = QiAïQr1

-La matrice Ai est alors la matrice diagonale des valeurs propres de M\ et Q\ est sa matrice des vecteurs propres. Notons que puisque M\ est symétrique, Q\ est une matrice orthogonale, ce qui implique que Q \y = Q j .

Ecrivons M\ et Ml des manières suivantes

Mi = QiA'A'Qr

MT

= QiAf

Af

QT

et posons S — Q\ A

. La matrice N dans la base S s'écrit alors comme suit.

S~

NS = AIQ7

NQ

A~

'

= AjQr

Mf

M

g

A^

= AlQT

QiA7hf

QT

M

QiAf

= A

'QfM

<2

A

*

24 CHAPITRE 2. ADAPTATION DE MAILLAGE

Il s'en suit que S XNS est diagonalisable.

S ^ / V S = P A P "1

En revenant sur le changement de base effectué, nous obtenons la décomposition N = SPA(SP)~l.

En posant P/v = S P , nous obtenons finalement la diagonalisation N = PNA P ^ .

Mentionnons que P/v n'est pas nécessairement une matrice orthogonale.

_n

Vl V2 = V\ V2 Ai

0

0

A 2

= Ai«i J ^2 v2

Soit donc, par le lemme 1, N = P/vAP^1 la diagonalisation de la matrice N = MTl M2-Remarquons que A est la matrice diagonale des valeurs propres Aj de Af et que P/v est la matrice dont les colonnes sont les vecteurs propres Vi de N. En effet, puisque A P/v = P/vA, nous obtenons

A"

et il s'en suit que Nvi = AjU_, soit la définition de vecteurs et valeurs propres.

L e m m e 2

Les vecteurs propres Vi de N sont M\-orthogonaux si et seulement si ils sont M2-orthogonaux.

D é m o n s t r a t i o n

Remarquons que puisque les Vi et Aj sont les vecteurs et valeurs propres de N = M1_1M2, nous avons que M1_1M2fi = Ajt;. et donc

M2Vi = Aj Mit?». En multipliant l'équation par VjT, nous obtenons

VjTM2Vi = Xiv/Myvi. (2.3)

2.1. ADAPTATION PAR METRIQUE CLASSIQUE 25

L e m m e 3

Si les vecteurs propres Vi de N sont M\ -orthogonaux, alors

(k) T où P/v est la matrice des vecteurs propres de N et u\ = vC MkV{.

D é m o n s t r a t i o n

Puisque les vecteurs i;_ sont Mi­orthogonaux, ils sont aussi, par le lemme 2, Af2­orthogonaux. Comme P/v est la matrice des vecteurs propres Vi de N , remarquons alors que

f (fc) • ■ __ ■

{p%M

p

\= vjM.vj = j

:

­­

.

J 1 0 s n f j

pour fc = 1,2. Il s'en suit que P j j MkP ^ forme la matrice diagonale suivante.

P

»

M

'

P

" " ( f rf>)

D

L e m m e 4

5. /es valeurs propres Aj de A son. toutes distinctes, alors les vecteurs propres Vi sont M\-orthogonaux.

D é m o n s t r a t i o n

L'équation 2.3 nous donne l'égalité suivante.

VjTM2Vi = \iVjTM\Vi Par une permutation des indices, nous avons aussi

ViTM2Vj = XjViTMiVj. (2.4)

Notons toutefois que les matrices Mk sont symétriques et que, de ce fait, ViTMkVj = VjTMkVi

26 CHAPITRE 2. ADAPTATION DE MAILLAGE

cette égalité, l'équation 2.4 devient

Vj M2Vi = XjVj M\Vi.

En soustrayant cette dernière égalité de l'égalité 2.3, nous obtenons que

0 = (Aj - X^v/MiVi.

Soit alors i ^ j . Puisque nous affirmons que les Aj sont toutes distinctes, il en suit que (A, — Aj) T^ 0, ce qui implique

VjTM\Vi = 0.

Nous confirmons ainsi que les u_ sont Mi-orthogonaux. D

Par le lemme 4, si notre matrice N possède des valeurs propres toutes distinctes, ses vecteurs propres V{ sont donc Mi-orthogonaux. Puis, par le lemme 3, nous pouvons écrire les matrices M\ et M2 de la manière suivante, avec P/v la matrice des vecteurs propres de N.

" - ^ ( f rf)

p

»

Nous pouvons donc affirmer que les vecteurs propres de la matrice N forment une base dans laquelle les matrices M\ et M2 sont toutes deux diagonales. La base (v-y, v?) est alors la base (ei,e2) que nous recherchions.

Nous cherchons alors à déterminer une nouvelle matrice M exprimée dans la base (e_, e-i) conservant les propriétés de borne d'erreur des deux matrices M\ et Af2- Pour ce, notons qu'il existe un lien important entre les valeurs propres de chacune des matrices et 1'anisotropic de chaque métrique.

En effet, dans la direction des vecteurs propres, les valeurs propres de chaque matrice réfèrent aux bornes de l'erreur d'approximation dans chaque direction. Nous y trouvons une relation inverse où plus la valeur propre est grande, plus la borne de l'erreur est grande et plus l'arête doit être petite pour satisfaire un certain niveau d'erreur.

(fc)

2.1. ADAPTATION PAR METRIQUE CLASSIQUE 27 de chaque direction e i et e2­ La nouvelle matrice M\ C\ M2 devient

(fe) n \ m a x / ^ U = P NT "= { 1'2 n } (fc) 0 m a x /_;> *={i.2} 2 / p ­ i

et nous obtenons alors une nouvelle métrique associée qui possède les contraintes des deux métriques précédentes.

Mais que se passe­t­il si les valeurs propres Aj de N sont égales ? Pour ce, introduisons le lemme 5.

L e m m e 5

Si les valeurs propres Aj de N sont égales, alors il existe un scalaire a tel que

où Q est la matrice des vecteurs propres de M\ et les Aj sont ses valeurs propres.

D é m o n s t r a t i o n

Puisque les valeurs propres Aj de N sont égales, nous pouvons écrire sa matrice des valeurs propres A de la forme

A = al

pour a un scalaire et / la matrice identité. Nous en déduisons les égalités suivantes.

N = PvAP^1

= PN(aI)Pûl

= al

Toutefois, nous savons que N — M{" M2, d'où il découle que M± Mî = otl. De ce fait, M2 = Q M I .

28 CHAPITRE 2. ADAPTATION DE MAILLAGE

Nous en convenons donc, par le lemme 5, que si les valeurs propres de N sont égales, nous devons identifier la matrice Mk possédant les plus grandes valeurs propres. C'est alors cette matrice qui devient la matrice intersecte liée à la nouvelle métrique puisque celle-ci est plus contraignante par rapport aux bornes d'erreur.

R e m a r q u e s

Considérons aussi le cas où nous avons des matrices M\ et M . de dimension 3 x 3 . Pour déterminer leur matrice intersecte, nous généralisons la procédure du cas 2 x 2 . Toutefois, il nous faut considérer à part le cas où la matrice N possède 2 valeurs propres égales et une autre distincte. Dans ce cas, les vecteurs propres t?_ de N ne sont pas nécessairement M\-orthogonaux. En appliquant le procédé de Gram-Schmidt aux deux vecteurs Vi associés aux valeurs propres égales, nous pouvons alors construire une base dans laquelle nos 2 matrices Mi et M_ sont diagonales, tel que recherché.

Soit donc v\ et vi les vecteurs propres associés aux deux valeurs propres équivalentes de la matrice N et v& le vecteur propre associé à la valeur propre distincte. L'un des deux vecteurs ayant la même valeur propre est conservé tandis que l'autre est modifié. Nous cherchons a un scalaire tel que v^ = v\ + av? soit un vecteur remplaçant V2 et permettant aux vecteurs v\, V2 et t>3 d'être M\-orthogonaux. Dans cette base, il est alors possible d'écrire une factorisation où les matrices Afi et M2 sont diagonales. La suite est alors identique à ce qui a été appliqué dans le cas des matrices 2 x 2 .

S'il y avait raison d'avoir trois métriques à intersecter, il serait alors important d'inter-secter celles-ci par paires. Notons toutefois que la métrique résultante dépend de l'ordre dans lequel nous intersectons nos métriques. Il y a alors décision à prendre.

Pour de plus amples renseignements sur l'intersection de métriques, nous nous référons au rapport de recherche [1] d'Alauzet et Frey pour INRIA.

2.2 Adaptation hiérarchique

L'adaptation hiérarchique, décrite dans l'article [2] de Bois, Fortin et Fortin, est une toute autre méthode d'adaptation. Au lieu de définir une métrique sur notre maillage et d'unifor-miser la longueur des arêtes par rapport à celle-ci, nous tentons plutôt de gérer directement l'aspect des éléments de notre maillage, soit la position des sommets pour un élément ayant une aire fixée. Nous souhaitons positionner les sommets de façon à minimiser l'erreur en semi-norme H1 sur l'élément. Le tout revient donc à résoudre un problème de minimisation.

2.2. ADAPTATION HIERARCHIQUE 29 Soit un maillage en dimension 2 à éléments triangulaires utilisé pour déterminer

l'approxi-mation u\ de degré fc d'une fonction u. Nous souhaitons positionner les sommets Si, S2 et S3 d'un élément K d'aire A K tel que le minimum

min / | V ( u - uh) |2 (2.5)

>i,s2,s3 y_.{Si,s2,s3}

Aire(K{Si,S2,S3}) = AK

SI,S2,S3JK{SI,SJ2,S3}

sous les contraintes

f AirMKIS, .<?„ Ç,\\ = A,s

(2.6)

[ S i + S

+ S

= (0,0)

soit atteint. Remarquons que le barycentre de notre triangle K est fixé à l'origine à titre de généralisation.

Notons que la solution u est souvent inconnue. Lors d'une résolution par la méthode des éléments finis, nous souhaitons déterminer une approximation de cette erreur pour ensuite évaluer le minimum de l'équation 2.5. Pour ce, cherchons d'abord à améliorer l'approximation u£ en y ajoutant une fonction correction ch + 1 de degré fc + 1.

uh ~uh + ch

La fonction de correction c£+1 nous permet alors d'obtenir une meilleure approximation uh + ï de la solution u. La fonction de correction est alors évaluée sur un élément non-standard qui admet des degrés de liberté supplémentaires aux milieux des côtés de l'élément Pk associé aux approximations de degré fc. C'est de cette correction de degré plus élevé que vient la notion de hiérarchie.

Lorsque l'approximation améliorée ûh + de notre fonction u est obtenue, nous convenons

n«-^iin»*ii^t

-«î:iii.i = iicj

iii.i.

Le problème devient alors

JK{SU

min / |Vc£

'

h Si&iSaJK{Si,S2,S3}

sous les contraintes 2.6 précédentes. Nous pouvons ainsi déplacer les noeuds du maillage en se servant de l'estimation. L'ajout et la suppression de noeuds se font toutefois en considérant l'erreur en norme L2. Nous nous référons à l'article [8] de D'Azevedo et Simpson pour plus de détails.

30 CHAPITRE 2. ADAPTATION DE MAILLAGE

2.3 M é t h o d e de Pagnutti & Ollivier­Gooch

La méthode de Pagnutti <_. Ollivier­Gooch [10] est une méthode d'adaptation de maillage par métrique. Tout comme pour l'adaptation par métrique classique, nous considérons la métrique

dani(a, b) = y J ( b ­ a ) T M ( b ­ a ) (2.7) où M est une matrice symétrique définie positive. Nous souhaitons déterminer une matrice

M telle que la métrique sera en lien avec l'erreur d'interpolation d'une fonction u. Prenons toutefois une autre approche pour trouver celle­ci.

Notons que cette méthode ne contient pas d'intersection de métrique et se généralise fa­ cilement pour tous les degrés d'approximation. Nous y voyons alors un énorme avantage au niveau de l'exécution.

Supposons que nous souhaitons interpoler notre fonction u par des polynômes de degré n. Tel que mentionné à la section 1.5, si nous considérons une arête de longueur h, l'erreur sera proportionnelle à hn + 1. Nous voudrions conserver cette propriété pour la mesure de longueur par métrique. Ainsi, nous voulons une métrique da ni(­, • ) telle que

dna+1(a,b) = err(a,b) (2.8)

où err(a, b) est l'erreur commise sur l'arête entre les sommets a et b du maillage. Nous nous assurons alors que la même proportion entre l'erreur et la longueur métrique est gardée lorsque h varie.

En uniformisant la longueur des arêtes de notre maillage par rapport à la métrique, l'er­ reur serait semblable sur chaque arête et nous aurions une erreur presque uniforme partout sur le maillage. D'une telle façon, nous aurions aussi un ordre de convergence de n + 1, ce qui est optimal. Notre objectif sera donc de trouver une matrice symétrique définie positive M associée à la métrique da ni(­, ■ ) qui souscrira à la propriété 2.8.

Pour ce, il nous faut tout d'abord déterminer une approximation de err(a,b). Celle­ci se trouve à partir de la série de Taylor de la fonction à approximer.

2 . 3 . 1 C a s I D

En ID, la série de Taylor de la fonction u(x) autour du point a s'écrit

2.3. METHODE DE PAGNUTTI k OLLIVIER­GOOCH 31 Si nous choisissons d'approximer u(x) par un polynôme pn(x) de degré n, nous aurons

»

j/jiyujj ■ ' Utj\UjJ ~T~ u­ l u . I ^ . J . I X J | . . . | . L

n! et l'erreur sera

Pn(x) ~ u(a) + u'(a)(x ­ a) + ... + — u( n )(a)(x ­ a)T n!

P„(x) « u(x) ­ p „ ( x )

w( n + 1 )(a)(x ­ a ) "+ 1 + ^ ­ ^ r r u("+ 2 )( a ) ( x ­ a )n + 2 + (n + 1)! v 'v ' (n + 2)

- (^TT)!«

"

"(«)(—)

au point x. Ainsi, en ID, nous définissons

err(a, b) =

comme étant l'erreur entre les points a et b.

^ . . » « > ( a ) ( 6 ­ < . ) » « (2.9)

Égalisons ensuite d%nl(­ ,■) et err(­, • ) de par les expressions 2.7 et 2.9 pour obtenir la propriété 2.8. Nous voulons en déterminer la matrice M, qui est ici un scalaire positif.

<C/(a,.) = M^|6-ar

= __L_^|„(»+i)

)||

_

|n+i

,

Puisque nous considérons b ^ a, nous pouvons diviser chaque côté de l'équation par |. — a\n + 1 pour obtenir

M ^ =

4­|^+

)(a)|

ou encore

M

-((^î)ï

"

"

'

)

'

Ainsi, notre métrique devient

= l&-a|\/(7^TjîM

(o)l

2 n+1

Notons toutefois que, de cette manière, le terme wn + l> de la métrique est évalué à partir d'un seul point de l'arête. Nous souhaitons qu'il varie le long de l'arête. Pour remédier à cela, nous utilisons l'intégration pour remplacer le terme \ / ( inl1\[\u^n + 1Ka)\ ) " Pa r s a valeur

32 CHAPITRE 2. ADAPTATION DE MAILLAGE

moyenne sur l'arête, soit

\h

-a\Ja v>+i)

7

De ce fait, la métrique que nous utiliserons pour uniformiser la longueur des arêtes de notre maillage en ID sera

dani(a,b) = £ (^—L-^+^x)!) n+1 dx,

en notant que le n de l'équation réfère au n du degré de l'approximation polynomiale utilisée. 2.3.2 C a s 2 D

Pour le cas 2D, il nous faut rechercher

M=(Mn Mn)

\M_2 M22)

qui est ici une matrice 2 par 2 symétrique définie positive.

Si nous souhaitons approximer la fonction u par une fonction de polynômes de degré n par morceaux, nous définissons l'erreur sur une arête ab du maillage par les termes de degré n + 1 de la série de Taylor de la solution exacte.

En exemple, traitons le cas 2D d'une approximation linéaire par morceaux de la fonction u à déterminer. Posons a = (01,02) et b = (01,62) les noeuds de l'arête ab.

err(a,b) = \d2u, . . , ,2 92u , . . . . . . . l d2u . .0 2 d~x^{a){bl ~ Gl) + dx~dy~{a){h ~ ai)ih " a2) + 2 cV (a)( ~ U2y

Nous noterons que b est à une distance Ax = 61 — ai et Ay = .2 — «2 de a, le point de référence de la série de Taylor, pour écrire

err(Ax, Ay) 1 d2u . . . o d2u , . . . 1 d2u , . . o

2 c^(a)Ax + 5x^(a)AxAy + 2 W2 ia)Ay

La prochaine étape consiste à transformer les distances Ax et Ay en coordonnées polaires. Celles-ci deviennent Ax = Arcos^ et Ay = Arsin^. L'erreur se transforme aussi, de ce fait,

2.3. METHODE DE PAGNUTTI k OLLIVIER-GOOCH 33

en coordonnées polaires.

err(Ar, 9) = -TTOAHcosJ0 + —— {a)Arzcos9sin0 + -—T(o ArJsin^fl

2 dx2 oxoy 2 dy1

= Ar _{-^(a)cos 0 + —(a)cos0sm0+-^(a)sm 9} 1 82U 2 52U , , . 1 02U, . 2 _,

Mentionnons que lorsque nous approximons la fonction u par une fonction de polynômes de degré n par morceaux, les termes de l'erreur err(-, • ) à l'intérieur de la valeur absolue sont alors tous de degré n + 1. Ceci nous permet de mettre en évidence un facteur A rn + 1 dans err(Ar, 9). Définissons donc

err(Ar, 9) = Arn + 1f{e). (2.10)

Dans l'exemple ci-dessus, nous avons

/(*)

=

La métrique da ni(-, • ) peut aussi se transformer en coordonnées polaires. dani(a, b) = yj(b - a)TM(b - a)

dani(Ax,Ay) = ^(Ax,Ay)M(Ax,Ay)T

dani(Ar,9) = J(Arcose,Arsm9)M(Arcos9,Arsine)T

= ArJ(cose,sm9)M(cos9,sm9)T

Remarquons aussi que nous pouvons factoriser à tout coup un Ar du terme de la métrique. Définissons donc

g(9) = (cos^sin^Mtcos^sinfl)7 ,

= Mn cos2 9 + 2Mi2 sin 9 cos 6 + M22 sin2 9

ou encore pour avoir g(0) = - ( M n + M22) + r ( M n - M22) cos 20 + Mi2sin20 Z _ dani{Ar,9)=Ar^gJ¥). (2.11) (2.12)

34 CHAPITRE 2. ADAPTATION DE MAILLAGE

En comparant la métrique (2.12) et l'erreur (2.10) pour obtenir l'égalité 2.8, nous avons

d£+l(Ar,0) = Arn+lg(9)^ = Arn+1f{9) = err{Ar,e)

et donc nous voudrions que

g{9) = f(9)^i.

Puisque nous connaissons /(#), nous pouvons déterminer les premiers coefficients de

Fou-2

rier de la fonction / ( # )n + 1 - Toutefois, puisque les termes à l'intérieur de la valeur absolue de f(9) sont tous de degré n + 1, nous pouvons en conclure que f(9) sera une fonction périodique

2

de période TT, et donc f(9)n+l aussi. Il s'en suit alors que les termes impairs de sa série de Fourier doivent être nuls.

En effet, si n + 1 est un nombre pair, les termes à l'intérieur de la valeur absolue de f(9) seront de la forme fccos(<9)2psin(.')2<' et fccos(0)2p+1 sin(9)2q+l pour fc G M et p,q G N.

fc cos(0 + irfP sin(9 + ir)2q = fc(- cos(0))2P(- sin^))2* = kcos(9)2psm(9)2q

k cos(9 + vr)2p+1 sin(0 + 7r)2"+1 = fc(- cos(0))2p+1(- sm(9))2q+1

= k(- cos(fl)2p+1)(- sin(0)29+1)

= kœs(9)2p+1sm(9)2(}+1

Ces termes sont de période n et donc f(9) est aussi de période w. Autrement, si n + 1 est un nombre impair, les termes seront de la forme fccos((9)2p+1 sin(61)29 et fccos(6,)2psin(fl)2g+1 pour fc G M et p, q G N.

fc cos{9 + 7r)2p+1 sin(0 + TT)29 = fc(- cos(0))2p+1(- sm(9))2q

= -kcos(9)

sm(e)

«

k cos(fl + TT)2P sin(9 + TT)2<?+1 = fc(- cos(fl))2p(- sin(0))29+1 = -fccos(0)2psin(fl)2,?+1

En ajoutant la valeur absolue à ces termes, nous obtenons un tout de période TT. NOUS avons

encore f(9) de période TT.

2

2.3. METHODE DE PAGNUTTI k OLLIVIER­GOOCH 35 nous obtenons l'approximation

g(0) = /(0)S+î « i _ 4o + A2c o s 2 0 + P2s i n 2 0 (2.13) où Ao, A2 et S2 sont les coefficients de Fourier tels que calculés à la section 1.6.1.

Du coup, en comparant l'approximation 2.13 de o(0) avec sa définition 2.11, nous pouvons déterminer les valeurs des éléments de la matrice symétrique M, comme suit :

M n = ­A0 + A2, M12 = P2,

M22 = 2^0 - A2.

En remplaçant cette matrice M dans l'expression 2.7, nous obtenons la métrique

dani{a,b) = I 2^0 + A2 B2

que nous recherchions. Celle-ci est bel et bien en lien avec l'erreur d'interpolation, comme dicté par l'égalité 2.8. Notons que les coefficients de Fourier Ao, A2 et P2 proviennent de la

fonction f(9) composée à partir d'un développement de Taylor autour du point a.

Constatons aussi que la matrice M de la métrique est évaluée au point a et que nous souhaitons qu'elle varie le long de l'arête. Pour corriger la situation, nous appliquons une intégrale curviligne le long de l'arête sur la métrique pour obtenir la moyenne suivante.

^ — / J ( b ­ a )TM ( b ­ a ) dx ­ a \ J a v

Nous paramétrisons alors l'arête à mesurer par la fonction ~/(s) = (b — a)s + a pour s G [0,1]. L'intégrale devient alors

f sJ(b-a)

M{b-a)ds.

Les coefficients Ao, A2 et B2 de la matrice M proviennent ici de la fonction f(9) telle que développée autour du point ~f(s). Nous redéfinissons donc la métrique da ni(­, ■ ) comme étant

dani(a,b) =

36 CHAPITRE 2. ADAPTATION DE MAILLAGE

C'est cette m é t r i q u e qui sera utilisée p o u r a d a p t e r nos maillages 2D. Le n de la métrique ré­ fère a u n du degré de l'approximation polynomiale par morceaux utilisée. Il est i m p o r t a n t de noter que les coefficients de Fourier de la matrice M sont fonctions de s. Lors d e l'intégration numérique, il faudra, à chaque point d'intégration, déterminer la fonction f ( 9 ) (puisqu'elle dépend de 7 ( 5 ) ) pour en déduire la matrice M en ce point.

Enfin, il est i m p o r t a n t de s'assurer q u e la métrique soit bien définie. Pour ce, il faut que la m a t r i c e M soit définie positive en t o u t point. Ici, rien ne nous assure que c'est bien le cas. P o u r adresser ce problème, il faut s'assurer, à chaque point d'intégration, que les valeurs propres de notre m a t r i c e M soient positives. Si ce n'est pas le cas, nous devons corriger n o t r e matrice p o u r la rendre définie positive sans toutefois modifier sa n a t u r e . Nous corrigeons alors la m a t r i c e de la façon décrite à la section 2.1.2.

2 . 3 . 3 C a s 3 D

E n 3D, il nous faut chercher

M =

^ M n M12 Mi3^ M12 M2 2 M23

\ MU M23 M 3 3 /

(2.14)

qui est ici une m a t r i c e 3 x 3 symétrique. De même que pour le cas 2D, si nous souhaitons approximer la solution par une fonction de polynômes de degré n par morceaux, nous définis­ sons l'erreur sur l'arête a b p a r les termes de degré n + 1 de la série de Taylor de sa solution exacte.

En exemple, traitons le cas 3D d'une interpolation quadratique par morceaux. Posons a = (ai, a2, a3)T et b = (61, 62, 63)^ les noeuds de l'arête ab.

err(a,b) = l d3u . . . , .0 l c P u . . . . .0 l < 93n . . . . .3

6 a?W^ - *>

+ 6 cV

~

6d?

~

+ ­ 7 r ^ ( a ) ( o i ­ ai)2(62 ­ a2) + ■r­z­£­(a)(b1 ­ aj)2(63 ­ a3)

2 dx2dy

1 d3u , . . . , ., N9 1 <93u . . ., x 9 /, .

b 7-r, n n(a)(h - ai)(&2 - a.2)1 + X7r^7r(a)(°2 - «2) (h - az) 2 dx2dz

1 d3u

2dy2dz{

2 d x d y2

4cl^

(a)(6l

-

ai)(63

-

û3)2+

2cW

2.3. METHODE DE PAGNUTTI k OLLIVIER-GOOCH

err(Ax, Ay, Az) =

_{. o ( « ) ^ + z i ^ »}

_{y + ê ^ (}

₎

_{z + 0}

6 dx3 1 c^n

6 ôy 6d< 2 dx2dy (a)Ax2Ay

/ X » 2 A 1 C ^ , X A A 2 1 d3 l t / X A 2 A

+

2dxWz

2âxâ^

2ây^

1 ^ ^ / X A A 2 1 d3 u I N A A 2 d3" / N A A A

+

2âxâ?

2ây^

o^ôWz

Changeons ensuite les distances en coordonnées sphériques. Celles-ci deviennent Ax = Ar cos 9 sin (f>,

Ay = Ar sin 0 sin 0

et

Az = Ar cos (j>.

L'erreur se transforme aussi, de ce fait, en coordonnées sphériques.

err(Ar, 0, <j>) =Ar'- ^ 3 ( a ) ( c o s 0 s i n 0 )c J + - p ( a ) ( s i n . s i n ( J )d + - ^ - 3 ( a ) ( c o s ^

1 c^u 1 d3u

+ 2 ^ 2o (a)(cos0sin</>)2 (sin9sin</>) + - 2 (a)(cos0sin0)2(cos0)

1 ô3?. 1 d3u + x « a 2 (a) (c o s S s i n ^ ) (s i n °s i n^ )2 + 9 a 2a (a) (s i n^ s i n</')2(c o s0) + - ^ ^ o(a)(cos0sin<?l>)(cos<ft) + - o(a)(sin0sin<^)(cos(?!>) 2 oydz1

+

a

a

dxdydz (a) (cos 0 sin 0) (sin 0 sin 0) (cos 0)

De même que pour le cas 2D, il est possible d'extraire un facteur A rn + 1 du terme d'erreur. Définissons donc