HAL Id: hal-01544122
https://hal.archives-ouvertes.fr/hal-01544122
Submitted on 21 Jun 2017
HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
Le problème des voies de communication dans le système des places centrales
Agnès Gahitte
To cite this version:
Agnès Gahitte. Le problème des voies de communication dans le système des places centrales. [Rapport de recherche] Institut de mathématiques économiques (IME). 1988, 15 p., figures. �hal-01544122�
EQUIPE DE RECHERCHE ASSOCIEE AU C.N.R.S.
DOCUMENT DE TRAVAIL
INSTITUT DE MATHEMATIQUES ECONOMIQUES
UNIVERSITE DE DIJON
FACULTE DE SCIENCE ECON OMIQUE ET DE GESTION 4, BOULEVARD GABRIEL - 21000 DIJON
LE PROBLEME DES VOIES DE COMMUNICATION DANS LE SYSTEME DES PLACES CENTRALES
Agnès GAHITTE Avril 1988 n° 104 P a p i e r p r é s e n t é de v a n t le S é m i n a i r e D E L T A d ' a n a l y s e é c o n o m i q u e s p a t i a l e U n i v e r s i t é Erasme, R o t t e r d a m 3-4 mai 1988
LE PROBLEME DES VOIES DE
COMMUNICA TION DANS LE SYSTEME DES
PLACES CENTRALES
GAHrPTE Agnès
Institut de Mathématiques Economiques C.N.R.S et Université de Bourgogne 4, bd Gabriel - 21000 Dijon - France
Résumé : Le système de Places Centrales a fait l'objet de nombreuses études en théorie économique spatiale. Néanmoins le pay sage Löschien n'a pas été analysé du point de vue des voies de communication. Il est vrai que Lösch a été très bref sur ce sujet, et ses successeurs n'ont pas développé cet élément du paysage de Places Centrales. Le but de cette étude est d'approfondir la théorie de Lösch sur ce sujet tout en gardant un point de vue critique sur la définition qu'il a donné des voies de communication. Pour ce faire nous avons testé le modèle de Lösch, ainsi qu'un autre modèle basé sur une au tre définition de ces voies.
Mots clés: Modèle de Places Centrales - Voies de communication Théorie des régions Economiques.
L'auteur tient à remercier le Professeur Claude Ponsard pour ses commentaires, mais il reste seul responsable des erreurs qui pourraient encore s'y trouver. L'auteur tient également à remercier J.C Basaille (Centre de Calcul de l'Université de Bourgogne) pour les programmes et les tests qu'il a effectués.
LE PROBLEME DES VOIES DE COMMUNICATION DANS LE SYSTEME DES PLACES
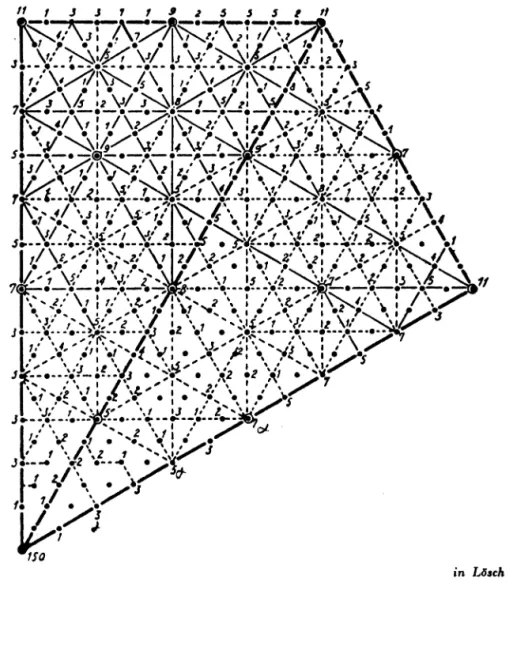
Figure 1 : Les voies de communication du paysage loschien.
INTRODUCTION
La plupart des études concernant la théorie des régions basées sur le modèle de LÆsch (1940) ont analysé le paysage en profondeur, la forme des aires de marché et de la courbe de demande, mais elles ont négligé l'étude du réseau routier construit par Lösch. Force est de constater que l'auteur lui-même a été très bref à ce sujet, Lösch (1954, p 129-130):
"en traçant les voies de communication il apparait que le trafic le plus intense (mesuré par le nombre de centres d'aires de marché par unité de longueur) se situe le long des secteurs. Ainsi douze de ces lignes se dessinent à partir de la métropole (c'est à dire que six lignes différentes se rencontrent dans la métropole). Dans le reste du paysage il n'y a jonction que de deux ou trois lignes. Des croisements dans la proximité de la métropole ne sont théoriquement pas inutiles et peu d'entre eux existent en réalité. Dans les secteurs pauvres en villes les voies de communication sont moins nombreuses et généralement moins développées. Lorsque l'on regarde l'ensemble, elles s'étalent comme une toile d'araignée autour de la métropole."
De plus Lösch affirme que dans sa figure 32 (se reporter figure 1) : 'les chiffres se réfèrent au nombre de centres qui coïncident en un point particulier. Au centre du paysage il y a cent cinquante centres d'aires de marché, tous de niveau inférieur au paysage auquel on se réfère." Lösch (p 128).
En fait l'examen de cette figure le conduit aux conclusions suivantes :
le nombre de centres le long des voies de communication en trait plein est au moins deux fois plus élevé que le long des lignes hachurées
celui correspondant aux centres qui se situent le long des droites moins épaisses est approxi mativement une fois et demi plus important que celui correspondant aux centres localisés le long des lignes hachurées.
On peut facilement voir que le trafic est plus dense dans le secteur riche en villes. Avec l'arrangement obtenu, 'le maximum de localisations coïncident, le plus grand nombre d'achats est fait localement, la somme des distances minimales entre les localisations est moindre et donc les lignes de transport sont réduites au minimum" Lösch (p 129).
Ainsi, "l'ordre a été mis en oeuvre dans nos aires de marché. La position des réseaux régionaux in dividuels n'est pas aléatoire, mais est est due à des principes économiques. On doit donc voir appa raître une métropole autour de laquelle les aires de marché et les localisations concurrentes coïncident de façon concentrique. C'est le corrolaire industriel de Von Thünen "d'Etat isolé". Nous ne devons pas l'appliquer (car c'est un concept politique) à une situation qui est tout d'abord totalement non politique" Lösch (p. 129).
Toutes ces affirmations de Lösch seront discutées ci-après. Un problème se pose si l'on analyse la phrase suivante :
'le nombre de centres sur les voies de communication en trait plein est deux fois plus élevé que le long des lignes hachurées ...."
En fait, l'importance d'une voie de communication dépend du trafic existant sur celle-ci. Si l'on ne tient compte que du nombre de centres d'aires de marché on ignore l'importance de la demande à laquelle ils ont à faire face. Par exemple prenons le point (2,2), en ce point il y a trois centres d'aires de marché (ceux-ci approvisionnent totalement trois, quatre, douze demandeurs totalement, rappe lons que si l'on prend un point quelconque (i,j) il approvionne
.2 .2 « = * + / + ij
clients entièrement. Dans notre exemple n = 3, 4, 12); prenons également le point (3,3),trois centres sont approvisionnés complètement (n = 3, 9, 27).
Le nombre de demandeurs desservis totalement sera de 3 + 4 + 12 = 19 pour le point (2,2), alors qu'il sera de 3 + 9 + 27 = 39 pour le point (3,3). Or pour Lösch les points (2,2) et (3,3) sont équivalents. En fait le trafic qui se développe à partir de ces deux points ne sera pas le même; la voie de com munication créée à partir du point (3,3) sera deux fois plus importante que celle construite à partir du point (2,2). On peut donc affirmer que ces deux points sont différents.
LE PROBLEME DES VOIES DE COMMUNICATION DANS LE SYSTEME DES PLACES
De nombreux autres exemples pourraient illustrer ce fait. On remarque ainsi que l'analyse de Lösch (dans ce^ domaine) est discutable , ses critères de choix et ses définitions Tétant également. La méthode utilisee par Lösch sera appelee méthode 1. Nous proposons dans cette étude une autre methode qui tient compte du nombre de demandeurs dans les centres d'aires de marché (ce qui cor respond au degré des centres relativement à l'ordre des centres pour la méthode 1, cf Gahitte 1987) qui portera le nom de méthode 2.
Deux configurations d aires de marche ont ete envisagées le carré et l'hexagone. Pour chacun de ces cas une formalisation a été entreprie et les espaces de références sont alors respectivement le treillis carré et le treillis hexagonal (Gahitte 1987). Au cours de cette étude nous avons traité graphi quement l'exemple de 75 et 50 fermes approvisionnées entièrement, pour le carré pour n = 50, l'hexagone n = 75, (figure 2 et 4).
Le parallélogramme considéré est limité par les points de coordonnées (0,0), (5,0), (0,5), (5,5) quelque soit le treillis considéré. Néanmoins un traitement informatique a été utilisé pour traiter des valeurs de n plus importantes, la méthode graphique étant alors inutilisable compte tenu du nombre de droites. Ia représentation graphique ne permettrait alors aucune conclusion valide car elle serait dans ce cas illisible. Pour les cas n = 1200 (pour l'hexagone) et n = 800 (pour le carré) nous avons envisagé deux cas correspondant aux deux paysages qu'il est possible de considérer, Gahitte (1987), ce sont les cas 1 (premier ij) et 2 (deuxième ij).
rL P™0» 5 E DES VOIES DE COMMUNICATION DANS LE SYSTEME DES PLACES
Chapitre 1. Le réseau routier du paysage hexagonal
Dans la figure 32 de Lösch réduite à l'exemple traite ici (figure 1 bis), les voies en trait plein sont les droites d'équation :x = 0
y = x ( c'est à dire la première bissectrice)
Pour ces droites la méthode 1 et la méthode 2 nous fournissent les résultats suivant :
méthode 1 méthode 2
x = 0 6 61
y = 0 6 61
y = x 15 100
La droite d'équation x = 0 correspond à une voie de communication qui relie six centres d'aires de marché (les extrémités relient deux points ou se situe un même nombre de centres) si l'on utilise la méthode de Lösch (méthode 1) alors qu'elle relie des centres qui approvisionnent totalement 61 demandeurs (les extrémités relient les deux points qui dans ce cadre desservent 25 clients entièrement).
Les voies hachurées sont les droites d'équation :
méthode 1 méthode 2 y = -x + 3y = -x + 5 5 31 4 103 y = -x + 6 8 46 y = -x + 4 8 72 y = 2 10 123 y = 4 11 178 x = 4 13 207
Lösch dans sa figure 32 a coupé les voies de communication en traits hachurés.
Par exemple la droite d'équation y = -x + 3 devrait relier les points (3,0) et (0,3) qui approvision nent deux centres d'aires de marché, il en est de même pour la droite y = -x + 4. Ceci s'explique par le fait que cette figure correspond au paysage complet étudié par Lösch il les a donc considéré comme négligeables relativement à d'autres droites.
Le paysage Löschien étudié ici pour n = 75 est représenté sur la figure 2.
Si l'on compare les droites citées précédemment, on peut confirmer que l'affirmation de Lösch n'est pas vérifiée car sur le réseau hachuré le nombre de centres (déterminé à l'aide de la méthode 1) n'est pas deux fois plus petit que celui qui se trouve sur les voies en trait plein.
La comparaison des deux méthodes utilisées donne les résultats cités plus haut; la conclusion n'est pas plus probante.
Selon la méthode utilisée les voies de communication les plus importantes ont comme équations dans l'ordre décroissant :
pour la méthode 1: y = x, x = 4, y = 4, y = 2, y = -x + 6, y = -x + 4, y = -x + 5, x = 0, y = 0, y = -x + 3
pour la méthode 2: y = x, x = 4, y = 4, y = 2, y = -x + 6, y = -x + 5, y = -x + 4, x = 0, y = 0, y = -x + 3
Bien entendu ces routes sont considérées comme des routes desservant des centres importants. La différence entre les résultats fournis par les deux méthodes est beaucoup plus marquée si l'on tient compte du paysage complet pour une valeur de n donnée.
Nous obtenons pour n = 75 les résultats suivants : Le réseau routier dans le paysage hexagonal (pour n = 75)
équation de la droitex = 5 méthode 2 méthode
262 8 y = x 247 15 x = 4 203 13 y = 4 178 11 y = 5 151 7 y = 4x - 15 127 5 y = -2x + 12 125 7 y = 2 123 10 i i y = 2 115 5 2x + 15 y = 5 115 5 x 4- 15 __ y = 4 113 5 y = -x + 6 113 8 y = 2x - 4 106 7 y = -x + 5-x 4- 12 103 7 y = 2 99 7 y = x + 12 95 7 y = -x 4- 7 95 5 y = 4x - 12-x + 9 95 7 y = 2 91 7 x = 3 90 8 y = 3 88 6 x + 4 y = 2 87 6 y = -2x + 9 79 7 y = i 78 6 y = x - 3 78 6 y = -x + 4 72 8 y = 0 61 6 x = 0 61 6 4x y = -y 61 1
H
v;
équation de la droite méthode 2 méthode 1
-x 4- 8 y = 2 59 5 il X 1 K> 56 5 —x + 6 y = 2 55 7 —x 4-5 y = 5 54 4 x = 2 50 8 -2 x + 14 y = 3 49 5 y = — y 2 46 4 y = -3x + 14 46 4 x + 3 y ~ a 45 3 y = -2x + 8 43 4 2r y = * T 42 2 y = -2x + 6 41 7 y = x + 3 38 6 3jc y = T 37 1 —x + 4 y== 2 31 4 X II 31 1 y = -x + 3 31 5 y = -4x + 13 29 3 y = -x 5x + 15 28 4 y = T 24 2 y = -2x + 4 24 3 y = 4x - 3 19 3 2x y = ~ 19 1 y = -3x + 7 17 3 x + 7 y = 2 17 3 5x y ~ ~2~ 16 2 —x + 3 y = 2 15 3 y = -2x + 3 15 3 y = x + 2 15 3 y = 4x - 7 14 2 x = îc 13 3 y = T 13 1 y = -x + 2 11 3 y = 4x 10 2 5x y = — 7 1 y = 2x 4 1
L'ordre est décroissant pour la méthode 2, il est clair qu'il ne correspond pas à cet ordonnancement pour l'autre méthode,
conclusion :
nombre de droites méthode 2 méthode 1
secteur riche en villes 19 1358 75
secteur pauvre en villes 16 862 67
secteur mixte 29 1908 170
frontière 1 247 15
On constate qu'il y a plus de droites dans le secteur riche en villes et le nombre de centres approvisionnés le long de celles-ci est beaucoup plus important que celui qui existe dans le secteur pauvre en villes.
Tableau 1 : Le réseau routier du paysage hexagonal n = 75 Premier ij300 1200 300Dernier ij1200 nombre de droites 19 171 1660 171 1660 I > J Secteur riche en villes méthode 1 75 1295 16591 1288 16573 méthode 2 1358 53298 2029636 57215 2016454 nombre de droites 1 1 1 1 1 I = J Frontière méthode 1 15 46 121 46 122 méthode 2 247 1894 14007 1894 14176 nombre de droites 16 146 1619 146 1619 I < J Secteur pauvre en villes méthode l 67 1047 14221 1047 14248 méthode 2 862 29462 924174 29462 928737 nombre de droites 29 385 5221 385 5221 Secteur mixte méthode 1 170 3210 58588 3200 52535 méthode 2 1908 97043 4327337 95353 4291509
Rappel : la méthode 1 tient compte du nombre de centres qui coincident en un point; la seconde méthode tient compte du nombre de demandeurs localisés dans les centres d'aires de marché.
Commentaire du tableau 1
Le secteur riche en villes contient plus de droites que le secteur pauvre en villes pour n = 75 on obtient respectivement 19 et 16 droites.
On remarque néanmoins que cette différence sectorielle est plus prononcée pour la méthode 2 (ces droites approvisionnent 1358 demandeurs totalement relativement à 862) que pour la méthode 1 (ces voies relient 75 centres d'aires de marché par rapport à 67).
Remarque concernant la seconde méthode : Dans le secteur riche en villes il existe un nombre de routes reliant des centres d'aires de marché qui est une fois et demi plus im p o rtant (si l'on
considère le nombre de demandeurs approvisionnés) que dans le secteur pauvre en villes .
Ainsi les 19 voies de communication approvisionnent au total 1358 demandeurs complètement dans le secteur riche en villes alors qu'ils ne sont que 862 (pour 16 routes) de l'autre côté de la frontière sectorielle.
la méthode de Lösch s'interprète ici plus difficilement :
Le nombre 75 correspond au nombre de centres qui se superpose dans le secteur riche en villes, il n'est que de 67 dans le secteur pauvre en villes.
Pour n = 300 et n = 1200 la première remarque s'applique encore alors que la seconde est plus prononcée :
dans le secteur riche en villes il existe des routes qui relient des centres d'offre desservant deux fois plus de demandeurs que dans le secteur situé au delà de la frontière (méthode 2 et méthode 1). Si l'on considère le degré de centres d'aires de marché (méthode 2) on remarque que quellequesoit 1 importance de l'espace considère ( n = 75, n = 300, n = 1200 ) le réseau routier du secteur riche en villes est plus dense que celui qui existe dans le modèle Löschien (méthode 1) qui tient compte de 1 ordre des centres d'offre. Un problème se pose néanmoins, on ne peut pas vérifier ou contredire 1 affirmation de Lösch citée en introduction concernant l'importance du traffic sur le réseau routier car la méthode graphique n'est pas utilisable pour de grandes valeurs de n telles 300 et 1200.
Quand aux résultats qui different selon l'utilisation du premier ou dernier (i,j) on peut affirmer que la différence existante est due aux rotations et translations effectuées pour localiser l'ensemble des points, centre d'aires de marché, dans le treillis hexagonal. Le vecteur de translation ayant une norme inférieure dans le cas 1 (premier (i,j)), il est logique qu'il y ait alors un plus grand nombre de centres desservant 169 demandeurs entièrement dans ce paysage.
Les conséquences sont plus importantes si l'on utilise la méthode 2 dans le cas 1 ( on obtient pour n = 300 des droites qui approvisionnent 58398 clients alors que pour n = 1200 elles en desservent 2029 636 ) relativement à la méthode 1 ( dans le cas 1 pour n = 300 1 295 centres d'aires de marché sont reliés par ces voies et pour n = 1200 il y a 16591 centres d'offre ) pour le secteur riche en villes, alors que l'utisation du dernier (i,j) nous fournit les résultats suivant : pour n = 300 on obtient 57215 et pour n = 1200,2016 454 avec la méthode 2 et pour n = 300 il vient 1288, pour n = 1200 on a 16573 avec la méthode 1. La même remarque s'applique si l'on considère le secteur pauvre en villes ou la frontière par exemple.
On peut donc à nouveau affirmer que l'existence des deux paysages Löschien n'est pas à négliger car ils ne sont pas équivalents.
Chapitre 2. Le réseau routier du paysage carré
Dans la treillis carré on utilise les points de coordonnées (0,0), (5,0), (0,5), (5,5) pour délimiter la partie du plan étudiée. Le nombre maximum de fermes approvisionnées sera alors de :
52 + 52 = 50
Comme pour l'hexagone, la méthode graphique étant peu lisible pour des valeurs de n assez grandes, un traitement informatique a été utilisé pour des valeurs de n égales à 200 et 800 (bien entendu il est possible d aller au delà mais l'intérêt pour cette étude était minime). Pour ce dernier cas, nous avons étudié les deux cas correspondant aux paysages cités précédemment (premier et dernier (i,j)). Les résultats sont donnés dans le tableau 2.
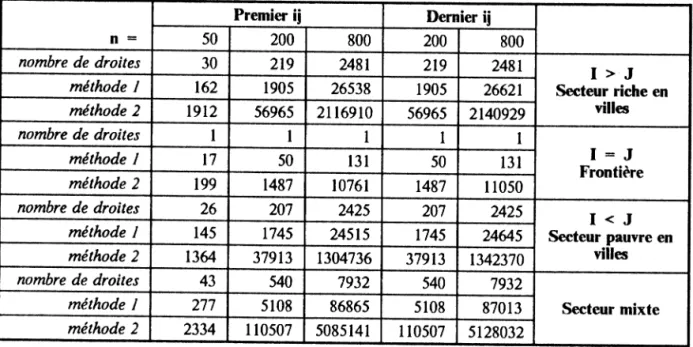
Tableau 2 : Le réseau routier du paysage carré n = 50 Premier ij200 800 200Dernier ij 800 nombre de droites 30 219 2481 219 2481 I > J Secteur riche en villes méthode 1 162 1905 26538 1905 26621 méthode 2 1912 56965 2116910 56965 2140929 nombre de droites 1 1 1 1 1 I = J Frontière méthode l 17 50 131 50 131 méthode 2 199 1487 10761 1487 11050 nombre de droites 26 207 2425 207 2425 I < J Secteur pauvre en villes méthode / 145 1745 24515 1745 24645 méthode 2 1364 37913 1304736 37913 1342370 nombre de droites 43 540 7932 540 7932 Secteur mixte méthode 1 277 5108 86865 5108 87013 méthode 2 2334 110507 5085141 110507 5128032
Rappel : la méthode 1 tient compte du nombre de centres qui coincident en un point; la seconde méthode tient compte du nombre de demandeurs localisés dans les centres d'aires de marché.
Commentaire du tableau 2
Le secteur riche en villes contient (pour n == 50) quatre droites de plus que le secteur pauvre en villes.
Les droites^ reliant les centres de même n, (n correspondant au nombre de fermes approvisionnées totalement par un centre d'offre) sont plus nombreuses dans le secteur riche, le nombre de fermes est 1,4 fois plus important (1912 offreurs approvisionnés relativement à 1364).
n = 50
(premier et dernier (i,j)) Secteur pauvre en villes
F igure 3
Nombre de centres qui coinci dent (méthode 1).
Représentation des voies de communicat ion.
Secteur riche en villes
(premier et dernier (ij)>
n = 50
Zr*J 2 V U 3 ____ 7. , S , g.Tlk
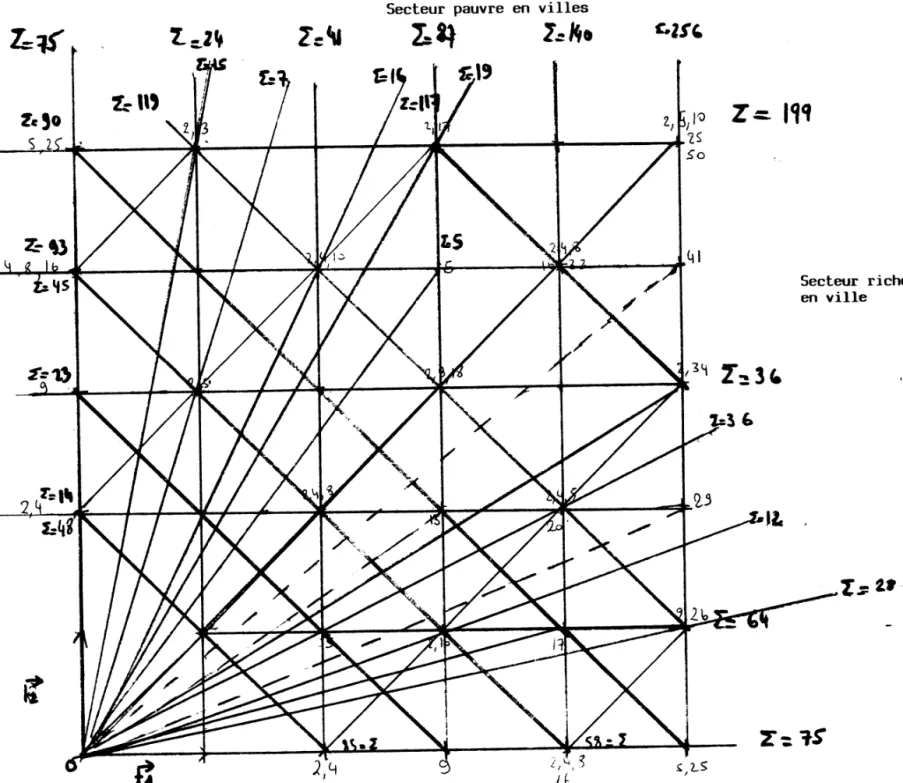
Figure 4 : Les routes reliant les centres approvisionnent le même nombre de -
demandeurs *
t«33
— xa
Secteur pauvre en villes
tjft
Secteur riche en ville
Avec la méthode de Lösch les résultats sont les suivant :
la différence sectorielle est plus faible, 162 centres reliés par les routes par rapport à 145 ( co efficient de 1,1).
Elle est conservée pour n = 200 et 800, elle a même tendance à croitre ( le coefficient est de 1,5 et 1,6) avec la méthode 2. La méthode 1 (issue de celle de Lösch) donne un coefficient de 1,09 et 1,08 pour n = 200 et 800. Dans ce cas la différence sectorielle aurait tendance a décroître faiblement.
Cette remarque est faite si l'on prend en compte le dernier (i,j), mais elles sont identiques si Ton considère le premier (i,j).
En conclusion :
Si Ton compare le nombre de demandeurs approvisionnés et le nombre de centres d'aires de marché qui coincident, on remarque que quelquesoit l'espace considéré (n = 50, 200, 800) l'existence d'un réseau routier plus dense dans le secteur riche en villes est indéniable. Le trafic est plus abondant dans ce secteur. L'importance des voies de communication est retracée dans notre étude par la méthode 2. Malheureusement la représentation graphique du réseau routier pour n = 200 et n = 800 est impossible, comme nous l'avons déjà fait remarquer pour l'hexagone. Néanmoins nous avons représenté le paysage routier pour n = 50, voir figure 4, et il est déjà fort compliqué. Si l'on se rap porte à la méthode de Lösch (méthode 1 dans notre cas), les routes en trait plein devraient avoir comme équation (figure 3) :
méthode 1 méthode 2 x = 0 9 75 y = 0 9 75 y = x 17 199 x = 5 13 256 y = 5 11 156
Les voies hachurées sont entre autres les droites d'équation :
méthode 1 méthode 2 y = -x + 4 15 95 y = 4 14 154 x = 4 14 140 y = -x + 6 14 119 y = 2 11 93 y = 3x - 10 9 123
L'affirmation de Losch ne se vérifie pas car sur les voies de communication hachurées (sur le gra phique) le nombre de centres (méthode 1) n'est pas deux fois plus faible que sur les voies en trait plein.
Les voies de communication traitées avec la méthode 1 sont classées par ordre décroissant et on ob tient le classement suivant (en fonction de leur équation de droite) :
X = y, y = -x + 4, y = 4, x = 4, y = -x + 6, x = 5, y = 2, y = 3x -10, x = 0, y = 0. Alors qu'avec la méthode 2 on obtient le résultat suivant :
x = 5, y = x, y = 5, y == 4, x = 4, y = -3x -10, y = -x + 6, y = 2, y = 4 - x, x = 0, y = 0. L'ordre est quelque peu différent et le nombre d'exaequo est beaucoup moins élevé. Cette différence est plus marquée dans la cas du carré relativement à l'hexagone. Ainsi le paysage routier carré serait différent car les voies de communication les plus importantes (par exemple) seraient représentées par les droites d'équation :
x = 5, x = y, y = 5, y = 4, x = 4 pour la méthode 2 alors que pour la méthode 1 on aurait x = y, y = -x + 4, y = 4, x = 4, y = -x 4- 6 ( les trois dernières étant de même importance). I^es voies de communication de moindre importance seraient pour la seconde méthode :
y = 3x - 10, y = -x + 6, y = 2, y = -x 4- 4 et pour la méthode 1 : x = 5, y = 5, y = 2.
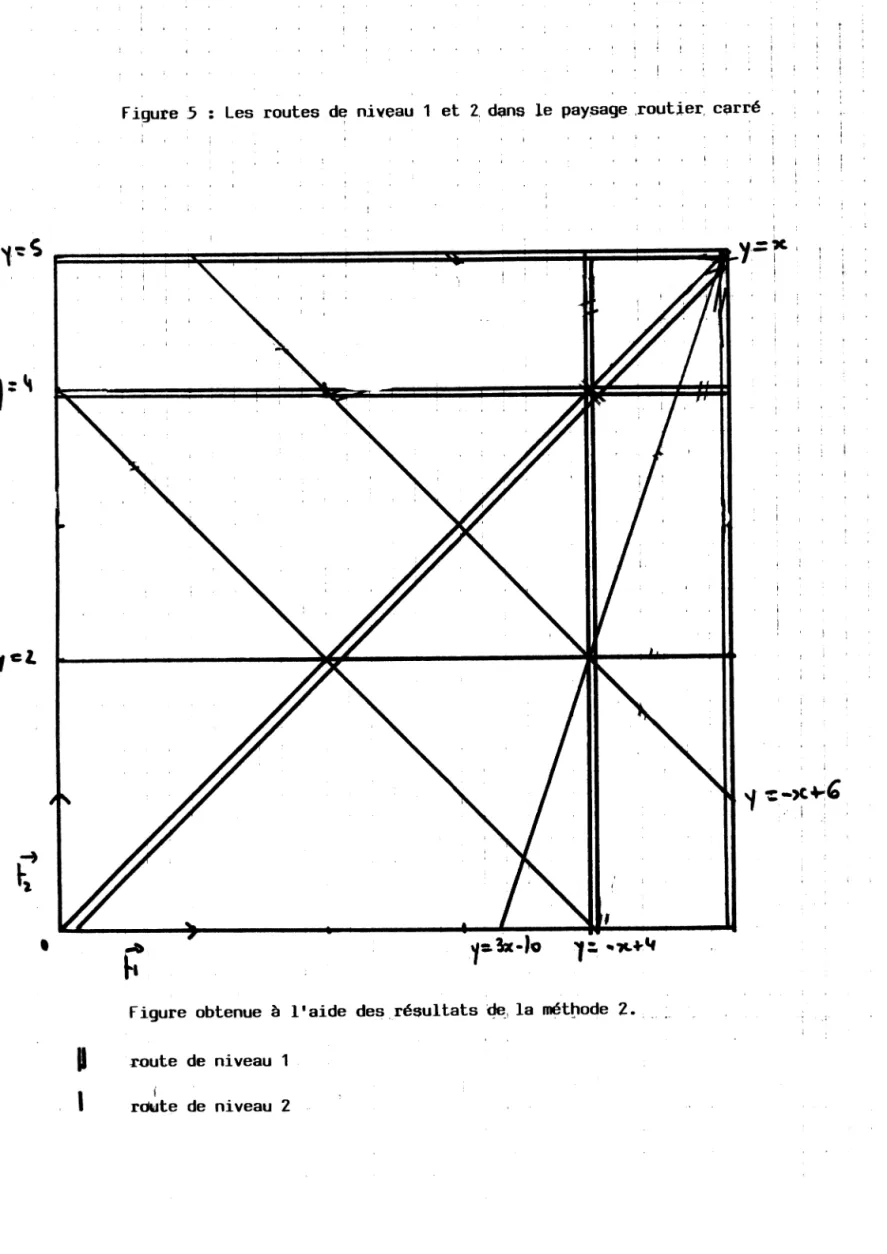
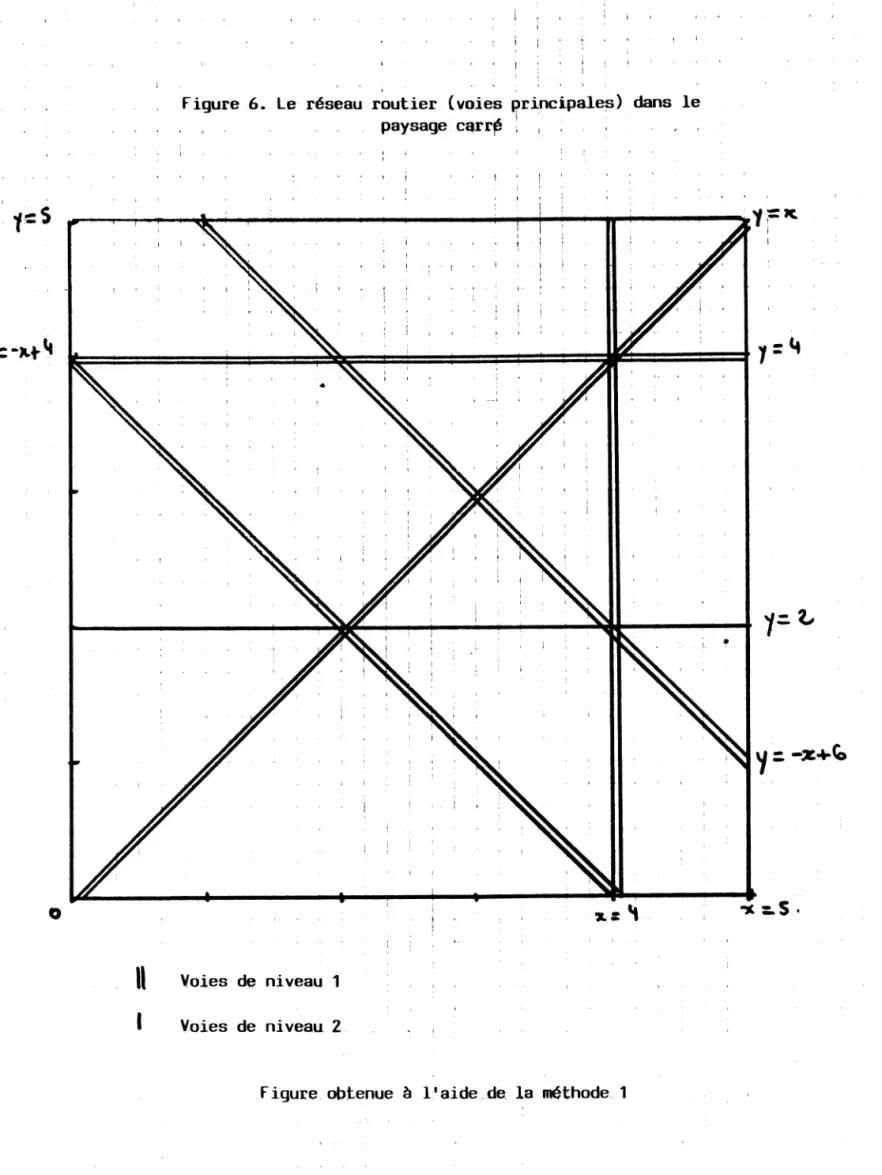
Figure 5 : Les routes de niveau 1 et 2, dans le paysage routier, carré
route de niveau 1 !
Voies de niveau 1
Voies de niveau 2
De ces résultats on tire les figures 5 et 6.
Il est clair que les deux paysages routiers obtenus ne sont pas identiques. Si l'on suppose qu'un noeud de voies de niveau 1 (correspondant aux voies de communication les plus importantes et perfor mantes) donne lieu a une ville importante, on la localisera aux points suivants :
méthode 1 méthode 2 (4,4) (4,5) (4,2) (4,4) (2,2) (5,5) (3,3) (5,4) (2,4)
En fait aucun critère n'a été défini pour déterminer les figures 5 et 6. Pour sélectionner la voie qui sera de niveau 1, 2, 3 ... nous allons utiliser un critère proche de celui de Lösch :
La voie de niveau 1 possède un nombre de centres qui coïncident (pour la méthode 1) ou un nombre de demandeurs (pour la méthode 2) au moins deux fois plus important que le nombre correspondant au paysage utilisé.
Pour la méthode 1, dans la cas n = 50 il y a cinq centres qui sont situés en (5,5). Pour la méthode 2 (et dans le même cas) le nombre sera 50 car n = 25 + 25.
Le coefficient est donc :
méthode 2 : le nombre de demandeurs approvisionnés en un point (somme des n) étant noté x il faut que
x > 2n (n = i2 + j 2)
méthode 1 : le nombre de n situé en un point étant noté y, et le nombre de centres situés en (i,j) sommet du parallélogramme étudié (avec i ^ 0 ou j # 0) étant noté z il faut que
y ^ 2z La voie de niveau 2 est telle que :
pour la méthode 1 : 3 y z < y < 2z pour la méthode 2 : 3 -y n <L x < 2n
La voie de niveau 3 est caractérisée par : pour la méthode 1 :
z ± y < \ z
pour la méthode 2 :
3
n <> x < — n
La voie de niveau 4 est telle que : pour la méthode 1 :
\ z ± y < z
pour la méthode 2 :
Y n <, x < n
La voie de niveau 5 est telle que pour la méthode 1 :
pour la méthode 2
\ z
x < \ n Pour l'hexagone seul le critère de la méthode 2 diffère car
n = i2 + j 2 + ij
Donc pour (i,j) = (5,5), n = 75; (i,j> = (10,10), n = 300; (i,j) = (20,20), n = 1200; (i,j) = (50,50), n = 7500.
Pour le carré on obtient respectivement n = 50, n = 200, n = 800, n = 5000.
Ainsi pour le paysage correspondant à n = 50 le réseau routier se présente comm suit :
• La voie de niveau 1 sera celle qui possède un nombres de centres qui coincident (méthode 1) ou un nombre de demandeurs (méthode 2) au moins deux fois plus important que le nombre correspondant au paysage utilisé, ici 50.
• Si ce nombre est compris entre 100 et 75 ce sera une voie de niveau 2. • Si il est compris entre 75 et 50 ce sera une voie de niveau 3.
• Si il est compris entre 50 et 25 la voie sera de niveau 4. • Si le nombre est inférieur à 25 le niveau de la voie sera 5. Bien entendu, plus la voie est importante plus son niveau est faible.
Les résultats obtenus pour n = 50 (méthode 2) sont les suivants :
• les voies de niveau 1 ont comme équations x = 5, y = x, y = 5, y = 4, x = 4, y - 3x- 10, y - = 5x 20, y x + 6,y x + 8,y
-(x + 5)
y = ---) y = 2x - 5.
1 a <■* * ' (3x + 10) (5jc - 10)
• les voies de niveau 2 ont comme équation y = --- —, y = —--- —t
5 3
y = -x + 4, y = 2, y = -3x + 16, x = 3, y = x - 2, y = 2x - 4, y = 3, y = -x + 16, (4* ~ 5)
x = 0, y = 0, y = ---- -— - y = - x + 5.
• les voies de niveau 3 ont comme équation par exemple y = 3x - 8,
(x + 8 ) (x + 4) (-3JC + 20)
y ----3— = — j— . y = -2x + 10, y = ---
----• les voies de niveau 4 ont comme équation par exemple y = -x + 7, y = - — ^ t
y = - 2 x + n , y = i i ± 12) , y = x +
• les voies de niveau 5 ont comme équation par exemple x = 1, y = 3x + 2, y — -5x + 10, y = 2x - 1, y = 2x, y = 3x - 2, y = -x + 2, y = 5x, y = -3x + 6, y = 3x, y = 3x - 5, y = -x + 3.
Iæs figures 7 et 8 confirment que le secteur riche en villes comporte un plus grand nombre de voies
que le secteur pauvre en villes.
Les noeuds de niveau 1 par ordre décroissant correspondent aux points : (0,0), (5,5), (2,4), (3,4), (3,3), (0,4), (5,1), (5,4), (1,5), (3,5), (4,5).
La figure 8 représente le réseau routier pour n = 50 en tenant compte de la méthode 1, le critère est ici le nombre de centres en (5,5) c'est à dire 5.
• les voies de niveau 1 ont comme équation y = x, y = 5, x = 5, x = 4, y = 4, x = 3, y = x - 2
y = -x + 6, y = -x + 4, y = 2.
• les voies de niveau 2 ont comme équation x = 2, y = x + 2, y = 3x - 10, y = -2x + 8
y - ^ ) , y - 5 x .2 0 ,y - -x + 8,x - 0, y - 0, y - M y - <i± ÎL
• les voies de niveau 3 ont comme équation par exemple y = 2x - 5 ,y = ^ ^ ,
(Sx — 10) ( —x + 16)
y = r--- y = —3.x + 16, y = --- --- y = 3x - 8,
(* + 8) (* + 4) ( —x + 20) ( —x + 12)
y - J'— y - — 2,— y = --- 5,--- ^ = 3 * - 12,j>= \,y = --- --- .
• les voies de niveau 4 ont comme équation par exemple 2y = x + 1, y = — , y = —2x+ 1 \,y = —2x + 17, j> = 5jc — 10 .
• les voies de niveau 5 ont par exemple comme équation 3y = 5x , 3y = x, y = 3x, y = 3x - 5, 3y = 2x, 4y = x, 5y = 2x, 5y = 4x.
La même conclusion s'impose, le réseau routier est plus dense dans le secteur riche en villes. Si on compare les deux figures il est clair que le réseau routier est moins important si l'on utilise la methode de Lösch. Les noeuds de niveau 1 pour la figure 8 sont par ordre décroissant les points de coordonnées :
(0,0), (4,4), (3,3), (5,5), (4,2), (4,0), (1,5), (5,2), (5,4), (4,4).
Les voies de niveau 3 sont plus nombreuses dans le paysage construit à l'aide de la méthode 1 alors que les voies de niveau 2 sont en moins grand nombre et qu'il y a autant de chemins . Le point de convergence des voies de niveau 1 n'est plus le même.
On peut donc conclure que le trafic sera plus dense si l'on considère la méthode 1.
Ainsi les deux méthodes ne sont pas équivalentes et les résultats obtenus diffèrent. Un traitement informatique tentera de sélectionner voies de niveau 1, 2, 3, 4, 5 pour des valeurs de n telles 200 et 800. Les résultats sont donnés dans les tableaux 3, 4, 5 et 6.
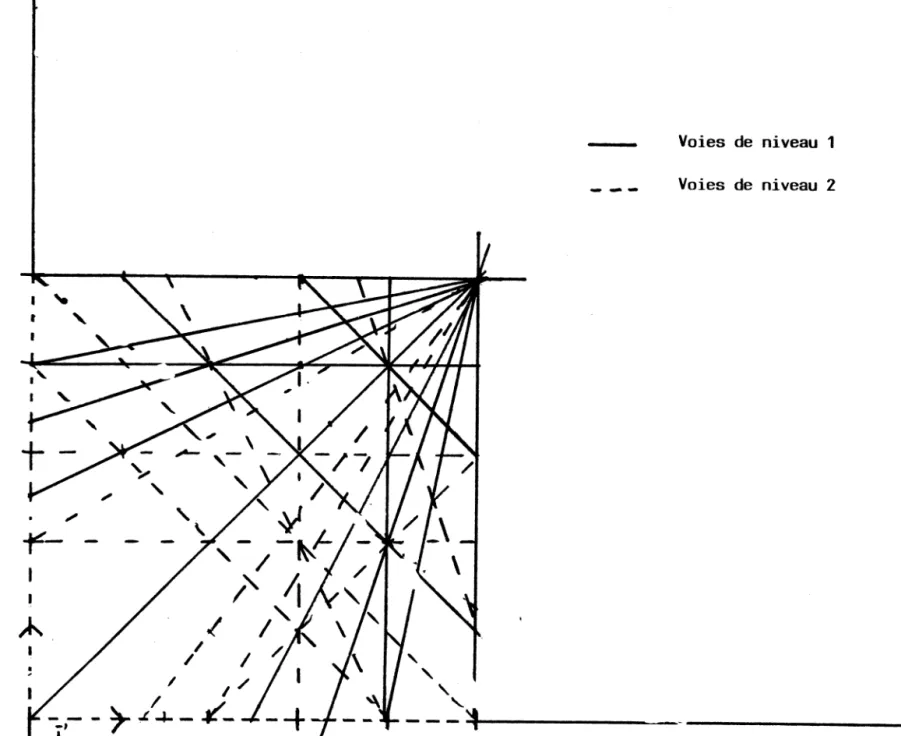
Figure 7. Les principales voies de communication du réseau routier carré traité avec la méthode 2 pour n = 50
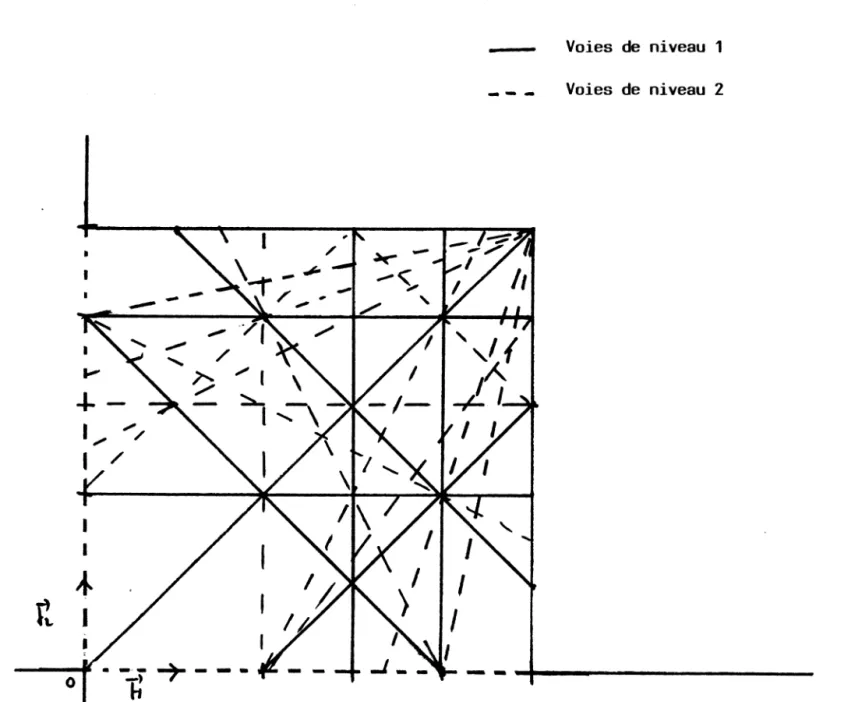
Figure 8. Les principales voies de communication du réseau routier carré traité avec la méthode 1 pour n = 50
Voies de niveau 1
Voies de niveau 2
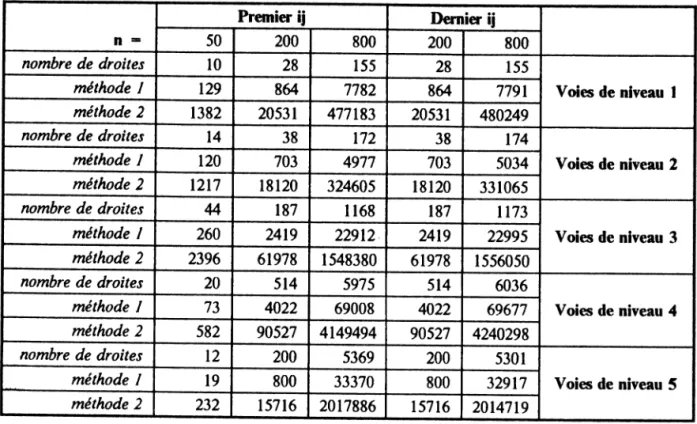
Tableau 3 : La structure du réseau routier dans le paysage carré méthode 1 n = Premier ij Dernier ij 50 200 800 200 800 nombre de droites 10 28 155 28 155 Voies de niveau 1 méthode 1 129 864 7782 864 7791 méthode 2 1382 20531 477183 20531 480249 nombre de droites 14 38 172 38 174 Voies de niveau 2 méthode 1 120 703 4977 703 5034 méthode 2 1217 18120 324605 18120 331065 nombre de droites 44 187 1168 187 1173 Voies de niveau 3 méthode 1 260 2419 22912 2419 22995 méthode 2 2396 61978 1548380 61978 1556050 nombre de droites 20 514 5975 514 6036 Voies de niveau 4 méthode I 73 4022 69008 4022 69677 méthode 2 582 90527 4149494 90527 4240298 nombre de droites 12 200 5369 200 5301 Voies de niveau 5 méthode 1 19 800 33370 800 32917 méthode 2 232 15716 2017886 15716 2014719
Rappel : la méthode 1 tient compte du nombre de centres qui coincident en un point; la seconde methode tient compte du nombre de demandeurs localisés dans les centres d'aires de marché.
Commentaire du tableau 3 :
1/utilisation de la méthode 1 nous permet de constater qu'il y a le même nombre de voies de ni veaux 1, 2 et 5; et que les voies de niveaux 3 et 4 dominent pour un paysage restreint (n = 50). Ainsi dans un tel paysage le réseau routier sera principallement composé de routes de moyenne im portance, il sera donc peu performant. Les voies de niveaux 1 et 3 relient respectivement 129 et 73 centres dont certains se superposent, alors qu'ils approvisionnent respectivement 1382 et 582 de mandeurs. Celà signifie que les voies principales relient des centres qui sont en fait plus importants que les voies de niveau 3. Cette tendance s'estompe quand le paysage grandit; dans ce cas les voies qui sont les plus nombreuses sont celles de niveau 3, 4 et 5 ( quelquesoit le cas étudié). On peut donc conclure que cette méthode permet d'obtenir un réseau routier d'importance moyenne possédant peu de voies rapides et de gmads axes (qui sont les voies de niveaux 1 et 2).
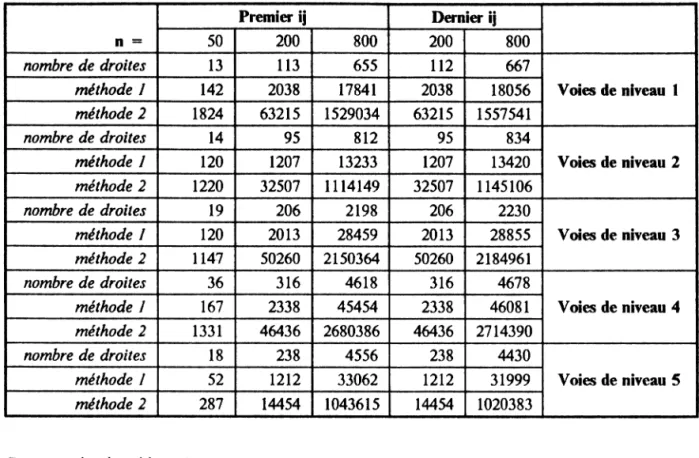
Tableau 4 : La structure du réseau routier dans le paysage carré méthode 2 n = Premier ij Dernier ij 50 200 800 200 800 nombre de droites 13 113 655 112 667 Voies de niveau 1 méthode 1 142 2038 17841 2038 18056 méthode 2 1824 63215 1529034 63215 1557541 nombre de droites 14 95 812 95 834 Voies de niveau 2 méthode I 120 1207 13233 1207 13420 méthode 2 1220 32507 1114149 32507 1145106 nombre de droites 19 206 2198 206 2230 Voies de niveau 3 méthode I 120 2013 28459 2013 28855 méthode 2 1147 50260 2150364 50260 2184961 nombre de droites 36 316 4618 316 4678 Voies de niveau 4 méthode I 167 2338 45454 2338 46081 méthode 2 1331 46436 2680386 46436 2714390 nombre de droites 18 238 4556 238 4430 Voies de niveau 5 méthode / 52 1212 33062 1212 31999 méthode 2 287 14454 1043615 14454 1020383 Commentaire du tableau 4 :
Si on considère le paysage issu de la méthode 2 (pour n = 50) il est clair que les voies de niveaux 3, 4 et 5 dominent les deux autres types de voies sont équivalents en nombre. Là encore le réseau sera peu performant. Les voies de communication de niveau 1 et 3 relient respectivement 142 et 167 centres qui se superposent alors qu'ils desservent entièrement 1824 et 1331 demandeurs. Les voies principales relient des centres beuacoup plus importants que les routes de niveau 3. Cette différence croit lorsque l'espace considéré augmente. L,es voies principales ont plus de trafic, dans ce paysage les voies 4 et 5 dominent ( dans les deux cas). Le réseau routier obtenu est plus homogène que le précédent, les voies rapides et de niveau 3 n'étant pas à négliger.
Tableau 5 : La structure du réseau routier dans le paysage hexagonal méthode 1 n -Premier ij Dernier ij 50 200 800 200 800 nombre de droites 4 59 285 58 287 Voies de niveau 1 méthode l 49 1157 9293 1140 93276 méthode 2 751 42252 855883 40921 856128 nombre de droites 5 52 407 52 406 Voies de niveau 2 méthode 1 40 608 7575 608 7540 méthode 2 587 22956 714092 22314 702830 nombre de droites 27 317 2188 316 2184 Voies de niveau 3 méthode 1 164 2579 27807 2574 27741 méthode 2 2291 83888 2563405 84023 2547961 nombre de droites 17 219 4181 221 4178 Voies de niveau 4 méthode 1 577 1136 33092 1144 33080 méthode 2 468 33294 2686696 32766 2667539 nombre de droites 12 56 1440 56 1146 Voies de niveau 5 méthode 1 17 118 5754 115 5790 méthode 2 278 4407 475078 3900 476418 Commentaire du tableau 5 :
Le paysage hexagonal ainsi obtenu ( pour n = 50) permet d'avoir un même nombre de voies de ni veaux 1 et 2 d'une part et de niveau 4 et 5 d'autre part. Néanmoins le réseau sera peu performant. Les voies de niveau 1 et 2 relient respectivement 49 et 40 centres alors qu'ils desservent totalement 751 et 582 clients. Les voies principales relient donc des centres plus importants que les voies de ni veau inférieur. Cette remarque s'appliqie en core plus pour de plus grandes valeurs de n. Dans ce cas les routes de niveaux 3 et 4 dominent, le nombre des autres voies étant très proche. Cette méthode détermine un réseau routier hexagonal modeste ayant peu de voies principales.
Tableau 6 : La structure du réseau routier dans le paysage hexagonal méthode 2 n = Premier ij Dernier ij 50 200 800 200 800 nombre de droites 5 51 330 48 323 Voies de niveau 1 méthode 1 54 929 8480 884 8292 méthode 2 1041 43040 1143224 40206 1118392 nombre de droites 7 57 519 60 517 Voies de niveau 2 méthode / 45 630 7965 668 8013 méthode 2 831 29446 1069759 31097 1065565 nombre de droites 13 115 1125 112 1112 Voies de niveau 3 méthode 1 86 1041 13860 1019 13742 méthode 2 1184 42026 1630694 40895 1613853 nombre de droites 17 231 2577 227 2574 Voies de niveau 4 méthode 1 85 1691 25326 1677 25342 méthode 2 879 50546 223241 49643 2229333 nombre de droites 23 249 3950 256 3975 Voies de niveau 5 méthode 1 57 1307 27890 1333 28089 méthode 2 440 21739 1219036 22083 1223733 Commentaire du tableau 6 :
Le paysage issu de la méthode 2 (n = 50) est caractérisé par une prédominance des voies de niveaux 3, 4 et 5; le réseau routier sera donc peu performant. Les voies de communication de niveaux 1 et 3 relient respectivement 54 et 86 centres d'aires de marché alors qu'ils approvisionnent 1041 et 1184 demandeurs totalement. On peut donc affirmer qu'en moyenne les voies principales relient des cen tres qui font face à une demande plus forte. Cette remarque s'applique encore pour des valeurs de n plus grandes: les voies principales (de niveau 1 et 2) ont un trafic important comparativement aux nombres de droites qu'elles représentent. Le réseau routier est plus homogène, les voies rapides et de niveau 3 sont présentent.
CONCLUSION
Une analyse comparative des deux paysages peut être établie par l'examen conjugué des ta bleaux 1, 2, 3, 4, 5 et 6.
Pour les deux premiers tableaux : le nombre de droites (quelquesoit la cas considéré, premier ou dernier (i,j)) est plus important pour le paysage carré; ceci est tout à fait logique car il existe beaucoup plus de "nombres Löschiens" carrés (n = P + y2) que de 'nombres Löschiens" hexagonaux (n = p + f + if)
Ainsi pour la première bissectrice le nombre de centres qui coincident (méthode 1) est légèrement supérieur dans la cas du carré, et le nombre de demandeurs (méthode 2) est également plus grand. La même remarque s'applique pour les secteurs riche et pauvre en villes, ainsi que pour le secteur mixte. On peut donc penser que le réseau routier sera plus dense dans le paysage carré, pour le vérifier il serait nécessaire de déterminer le nombre de voies de niveau 1, 2, 3, 4, 5 dans les deux paysages carré et hexagonal pour différentes valeur de n correspondant au même parrallélogramme. Rappelons que pour n = 50 (pour le carré) et n = 75 (pour l'hexagone) le parrallélogramme a les même coordonnées dans les deux cas, c'est à dire (0,0), (5,0), (0,5), (5,5). Une remarque identique peut être faite pour n = 200 et 300, et n = 800 et 1200.
Pour le carré la différence sectorielle croit avec les valeurs de n si l'on utilise la seconde méthode, alors qu'elle décroit si la première méthode est utilisée.
Pour l'hexagone elle a tendance a croitre quellequesoit la méthode utilisée.
Celà signifie pour le carré, que la méthode de Lösch semble uniformiser le réseau routier des deux secteurs, ce qui n est pas le cas si l'on prend en compte le nombre de demandeurs, c'est à dire le se conde méthode. Par contre la différence sectorielle s'atténue moins vite avec la méthode 1 dans le paysage hexagonal, mais persiste avec la méthode 2.
ces remarques sont valables pour les deux cas étudiés ici, premier et dernier (i,j).
Comparaison des tableaux 3 et 4 : pour un paysage carré de faible importance ( n = 50 ) le nombre de voies de niveaux 1, 2 et 5 dans les deux paysages sont équaivalents. Les voies de niveau 3 dominent si on utilise la première méthode alors qu'avec la seconde ce sont les voies de niveau 4. Les routes de faible importance l'emporte dans la seconde méthode, la différence est néanmoins peu flagrante car il y a le même nombre de voies principales (il y en a trois de plus dans le paysage issu de la méthode 2). Pour de plus grandes valeurs de n (200 et 800) la première remarque n'est plus valable. En effet, seules les voies de niveau 3 et 4 sont comparables en nombre. La seconde méthode nous permet d obtenir plus de voies prioritaires ( trois à quatre fois plus). Le réseau routier permettra un transport plus rapide il est donc plus performant.
Comparaison des tableaux 5 et 6 : Lorsque le paysage hexagonal est peu étendu ( n = 50 ), le nombre de voies de communication de niveaux 1 et 2 est équivalent dans les deux paysages étudiés, et avec les deux méthodes. Les voies de niveau 3 dominent si on utilise la méthode 1 alors que si on utilise l'autre méthode ce sont les voies les plus petites (niveau 5) qui dominent. Pour n = 200 ou 800 la première remarque ne s applique que pour les voies de niveau 1. La méthode 2 permet d'obtenir plus de voies de niveaux 1 et 2 donc un réseau routier plus performant.
Dans cette etude nous avons tente, a la fois de reconstruire le réseau routier déterminé graphi quement par Lösch et de proposer une autre solution pour sa construction. Le fait de tracer une voie de communication entre deux points ayant le même nombre de demandeurs n'est pas indifférent. La question que l'on se pose est alors :
Lösch a t-il eu raison de choisir cette méthode ?
En fait, si 1 on examine ceci plus en detail on ne peut s'empêcher de critiquer les critères qu'il a utilisés. Si trois centres coincident en un point, leur importance (c'est à dire le nombres de deman deurs qu'ils approvisionnent) peut être quelconque (un offreur peut être le centre d'un très grand et très petit hexagone). Homogénéiser ces données revient à perdre une partie de l'information. La différence qui existe entre les deux paysage confirme cet état de fait.
BIBLIOGRAPHIE
(1987) GAIIITTE agnes, Axiomatic and Construction of the Central Place System. (1954) LOSCII august, rrhe Economics of Location. New Haven, Yale University Press.