Competition and efficiency in congested markets

Digitized

by

the

Internet

Archive

in

2011

with

funding

from

Boston

Library

Consortium

IVIember

Libraries

HB31

_'DEWEV

.M415

'

Massachusetts

Institute

of

Technology

Department

of

Economics

Working

Paper

Series

COMPETITION

AND

EFFICIENCY

IN

CONGESTED MARKETS

Daron

Acemoglu

Asuman

Ozdaglar

Working

Paper

05-06

February

16,

2005

Revised:

January

20,

2006

Room

E52-251

50

Memorial

Drive

Cambridge,

MA

021

42

This

paper

can be

downloaded

without

charge from

the

Social

Science

Research

Network

Paper

Collectionat

Competition and

Efficiency

in

Congested

Markets^

Daron Acemoglu

Department

of

Economics,

Massachusetts

Institute of

Technology

Asuman

E.

Ozdaglar

Department

of Electrical

Engineering

and

Computer

Science

Massachusetts

Institute

of

Technology

January

20,

2006

Abstract

We

studythe efSciencyofoligopolyequilibria incongested markets.

The

moti-vatingexamplesaretheallocation ofnetworkflows inacommunication networkor

oftrafficina transportation network.

We

showthat increasing competition

among

oligopoUstscanreduceefficiency, measuredasthedifferencebetweenusers'

will-ingnesstopay anddelaycosts.

We

characterize atight

bound

of 5/6onefficiency

in pure strategyequilibria

when

thereis zero latency at zero flow anda tight

bound

of

2v^

—

2withpositivelatencyatzeroflow. These boundsaretighteven

when

thenumbersofroutesand ohgopohstsarearbitrarily large.

*We

thankXin Huang,RameshJohari,EricMaskin,Eilon Solan, NicolasStierMoses,JeanTirole,

JohnTsitsiklis,IvanWerning,

Muhamet

Yildiz, twoanonymousrefereesandparticipants atvarious

1

Introduction

We

analyzepricecompetitioninthepresenceofcongestioncosts. Consider thefollowing

environment: oneunit oftrafficcan use one of/ alternative routes.

More

traffic

on

a

particular route causesdelays,exerting anegative (congestion) externality

on

existing

traffic.^ Congestioncosts arecaptured

by

aroute-specificnon-decreasingconvexlatency

function, li(•). Profit-maximizingohgopolists set prices(tolls) fortravel

on

each route

denoted

by

Pi.

We

analyze

subgame

perfect

Nash

equilibria ofthisenvironment,

where

for eachprice vector,p, alltrafficchooses thepaththathas

minimum

(delayplus toll)

cost, li

+

Pi,

and

oligopohstschoosepricesto

maximize

profits.

The

environment

we

analyze isof practical importance for a

number

ofsettings.

These

include transportation

and communication

networks,

where

additionaluse ofa

route (path) generatesgreatercongestionforall users,

and

markets in

which

there are

"snob"effects,so thatgoods

consumed by

fewer other

consumers

are

more

valuable(see

for example, [53]).

The

key feature oftheseenvironments is the negative congestion

externalitythatusers exert

on

others. Thisexternalityhas

been

well-recognized since

the

work by

Pigou[40] ineconomics,

by

[46], [57], [5]intransportationnetworks,

and by

[36], [24], [23], [30] in

communication

networks.

More

recently,therehas

been

agrowing

literature that focuses

on

quantification of efficiency loss (referred to as the price of

anarchy) that results

from

externahties

and

strategic behavior in different classes of

problems: selfish routing (e.g., [25], [45], [10], [11], [39]

and

[15]); resource allocation

by market mechanisms

(e.g., [22], [47], [31], [59]); network design (e.g., [3]);

and

two-stagecompetitivefacilitylocationwithout congestioncosts

and

externalities(e.g.,[54]).

Nevertheless, the game-theoreticinteractions

between

(multiple) serviceproviders

and

users, orthe effects ofcompetition

among

the providers

on

the efficiency losshas not

been

consideredinnetworks with congestion (externalities). This is

an

important area

for analysis since in

most

networks congestion is a first-order issue

and

(competing)

profit-maximizingentitieschargepricesfor use. Moreover,

we

will

show

that thenature

ofthe analysischanges significantly inthepresenceofpricecompetition.

We

provide ageneral

framework

for the analysis of price competition

among

ser-vice providers^inacongested(andpotentiallycapacitated)network,studyexistence of

purestrategy

and

mixed

strategy equihbria,

and

characterize

and

quantifytheefficiency

properties ofequilibria.

There

are foursetsof

major

resultsfrom ouranalysis.

First,

though

the equilibrium of traffic assignment without prices can be highly

inefficient (e.g., [40], [45], [10]), price-settingby amonopolist internalizesthe negative

externality

and

achievesefficiency.

Second,increasingcompetitioncanincreaseinefficiency. Infact,changingthe

market

structure

from

monopoly

to

duopoly

almost always increases inefficiency. This result

contrastswith

most

existing resultsintheeconomicsliterature

where

greatercompetition

tendstoimprovethe allocation of resources(e.g. see Tirole [51]).

The

intuitionfor this

result,

which

isrelated to congestion,is illustrated

by

the

example

we

discuss below.^

^

_An

_externalityariseswhenthe actionsofthe playerinagameaffectsthe payoff ofotherplayers.

^We

useoligopolistandservice providerinterchangeablythroughoutthe paper.

^Because,inourmodel,users arehomogeneous and have aconstant reservationutility,intheabsence

Third

and most

important,

we

providetight

bounds

on theextent ofinefficiencyinthe

presenceofohgopohsticcompetition.

We

show

that

when

latency at zero flow(traffic)

is equal tozero, socialsurplus (defined as the difference

between

users' willingness to

pay

and

the delay cost) in

any

pure strategy oligopoly equilibriumis always greater

than 5/6 ofthe

maximum

socialsurplus.

When

latency at zero flow canbe positive,

there isaslightlylower

bound

of 2\f2

-

2

«

0.828. These

bounds

areindependent of

boththe

number

of routes, /, which couldbe arbitrarily large,

and

how

these routes

are distributed acrossdifferentoligopolists (i.e., ofmarketstructure). Simpleexamples

reachthesebounds.

Finally,

we

also

show

that purestrategy equilibria

may

fail to exist. This is not

surprisinginviewofthefactthat

what we

havehereisaversion ofaBertrand-Edgeworth

game

where

pure strategy equilibria do not exist in the presence of convex costs of

productionorcapacity constraints (e.g., [14], [49], [7], [56]). However,in ourohgopoly

environment

when

latency functions arelinear,a purestrategyequilibriumalwaysexists,

essentiallybecause congestionexternalities

remove

the payoff discontinuities inherentin

theBertrand-Edgeworth game. Non-existence

becomes

anissue

when

latency functions

are highly convex. In this case,

we

provethat

mixed

strategy equilibria always exist.

We

also

show

that

mixed

strategyequihbriacanlead to arbitrarilyinefficientworst-case

realizations; in particular, social surplus can

become

arbitrarily smallrelative to the

maximum

socialsurplus,

though

the average performanceof

mixed

strategyequihbria

is

much

better.

The

following

example

illustrates

some

ofour results.

Example

1 Figure 1

shows

asituation similar to theonefirst analyzed

by

Pigou[40]

tohighlighttheinefficiency

due

tocongestionexternalities.

One

unit oftrafficwilltravel

from origin

A

todestinationB, using either route 1or route2.

The

latency functions

are given

by

x^ 2

'i(a;)

=

y

,

k

(x)

=

-X.

Itisstraightforward to see that theefficientallocation [i.e.,onethatminimizesthe total

delay cost

^^hix^Xi^

is

xf

=

2/3

and

xf

—

1/3, while the (Wardrop) equilibrium

allocationthatequates delay

on

the

two

pathsis

x^^

k,.73

>

x\ and

x^^

f« .27

<

xf

.

The

sourceofthe inefficiencyisthateachunit oftraffic does notinternalizethe greater

increase indelayfromtravel

on

route 1,sothere istoo

much

use ofthisrouterelative

totheefficientallocation.

Now

consider a monopolist controlhng both routes

and

setting prices for travel to

maximize

itsprofits.

We

show

below that inthis case, themonopolist will setaprice

includinga

markup,

Xil\

(when

li isdiflFerentiable), whichexactly internalizes the

con-gestionexternality. Inotherwords,this

markup

isequivalent to thePigovian taxthata

socialplanner

would

setinorder toinducedecentralizedtraffictochoosetheefficient

al-location. Consequently,in thissimpleexample,

monopoly

priceswill_{be pf^^}

=

(2/3) -\rk

and

p^^

=

(2/3^)-I-/c, for

some

constantk.

The

resultingtraffic inthe

Wardrop

equi-hbrium

will beidenticaltothe efficientallocation, i.e.,x'^^

=

2/3

and

x^^

=

1/3.

l,(x)=x /3

1 unitof traffic

Figure 1:

A

two

link network with congestion-dependantlatency functions.

Finally, consider a

duopoly

situation,

where

each routeiscontrolled

by

a different

profit-maximizingprovider. Inthiscase,itcanbe

shown

thatequilibriumpriceswilltake

theform

_pf^

—

Xj{l[

+

/j)[seeEq.(20)inSection4],or

more

specifically,

_pf

^

^

0.61

and

p^^

^

0.44.

The

resulting equilibrium trafficis

x^^

ft; .58

<

xf and

x^^

«

.42

>

xf,

which

alsodiffers

from

theefficientallocation.

We

will

show

thatthisisgenerally the case

in the ohgopolyequilibrium. Interestingly, while in the

Wardrop

equilibrium without

prices, there

was

too

much

traffic

on

route 1,

now

there is too little traffic because

of its greater

markup.

It is also noteworthy that although the

duopoly

equilibrium

is inefficient relative to the

monopoly

equilibrium, in the

monopoly

equilibrium k is

chosen suchthatallofthe

consumer

surplusiscaptured

by

themonopolist,while in the

oligopolyequihbriumusers

may

havepositive

consumer

surplus.^

The

intuition for the inefficiency of

duopoly

relative to

monopoly

is related to a

new

source of(differential)

monopoly power

for eachduopolist,

which

theyexploit

by

distortingthepatternoftraffic;

when

provider 1, controllingroute 1,charges a higher

price,itrealizesthatthis will

push

some

trafficfromroute1toroute2,raisingcongestion

on

route2.

But

this

makes

thetrafficusing route 1

become more

"locked-in," because

theiroutside option, travel

on

theroute2,has

become

worse.^

As

aresult,theoptimal

pricethateach duopolistcharges will include

an

additional

markup

over the Pigovian

markup.

These

are Xil'2 for route 1

and

xj^j for route 2. Since these

two markups

are generally different, they will distort the pattern oftraffic

away from

the efficient

allocation. Naturally, however, prices are typicallylowerwith duopoly,so even

though

socialsurplus declines, userswillbebetteroffthanin

monopoly

(i.e.,theywill

command

apositive

consumer

surplus).

There

isalargehterature

on

modelsofcongestion

both

intransportation

and

commu-nicationnetworks (e.g. [5], [38], [44], [33], [34], [45]).^ However, very fewstudieshave

^Consumersurplusisthe differencebetweenusers'willingness topay(reservationprice)andeffective

costs, Pi

+

Zi(Xj), and is thus different from social surplus (which is the difference betweenusers'

willingness topay andlatencycost, li{xi),thusalsotakesintoaccount producersurplus/profits). See

[32].

^_{Using economics}terminology,wecouldalsosay that thedemandforroute1becomesmore

"inelas-tic". Sincethistermhaisadifferent meaninginthecommunication networksliterature (see[48]),we

do notuseithere.

®Someofthesepapersalsouse prices(or tolls)toinduce flow patterns that optimizeoverallsystem

investigated the implications ofhaving the "property rights" over routes assigned to

profit-maximizingproviders. In [4],Basar

and

Srikantanalyze

monopoly

pricingunder

specific assumptions on the utihty

and

latency functions.

He

and

Walrand

[19] study

competition

and

cooperation

among

internet service providersunder specific

demand

models. Issues ofefficientallocation of flows ortrafficacrossroutes

do

notariseinthese

papers.

Our

previous

work

[1] studiesthe

monopoly problem and

containstheefficiency

ofthe

monopoly

result, but

none

ofthe other results here.

More

recent independent

work by

[3] builds

on

[1]

and

alsostudiescompetition

among

serviceproviders. Using

adifferentmathematical approach, they providenon-tight

bounds on

theefficiency loss

forthe case ofelastictraffic. Finally, incurrentwork, [2],

we

extend

some

ofthe results

ofthispapertoanetwork withparallel-serialstructure.

In the rest of the paper,

we

use the terminology of a (communication) network,

though

all of the analysis applies to resource allocation in transportation networks,

electricity markets,

and

other economicapplications. Section 2 describes the basic

en-vironment. Section 3 brieflycharacterizesthe

monopoly

equilibrium

and

establishesits

efficiency. Section 4 defines

and

characterizesthe oligopoly equilibriawith

competing

profit-maximizing providers. Section 5containsthe

main

results

and

characterizes the

efficiency properties ofthe oligopoly equihbrium

and

provide

bounds on

efficiency.

Sec-tion 6 providesatightefficiency

bound

when

there

may

bepositivelatencyatzeroflow.

Section 7 containsconcluding

comments.

Regardingnotation,allvectors areviewedas

column

vectors,

and

inequalitiesare to

beinterpretedcomponentwise.

We

denote

by

Mf^theset ofnonnegative /-dimensional

vectors. LetCibe aclosedsubset of[0,oo)

and

let/: Cjh->

R

beaconvexfunction.

We

use df{x) todenotethesetofsubgradientsof

/

atx,

and

f~{x)

and

f'^{x) todenote

theleft

and

rightderivatives of/at x.

2

Model

We

consider anetwork with/parallel links. Let

I =

{1,..

.,/} denotethesetoflinks.

LetXidenotethe total flow

on

linki,

and

x

=

[xi,...,xj]denotethe vector oflink flows.

Each

link inthenetwork has a fiow-dependentlatency function /i(x,),which measures

the traveltime (ordelay) asa function ofthetotalflow

on

linki.

We

denotethe price

perunit flow(bandwidth)oflinki

by

_Pi. Let

p

=

[pi,..._,p/]denotethe vector ofprices.

We

are interestedinthe

problem

ofroutingdunits offlow acrossthe /links.

We

as-sume

thatthisisthe aggregateflow of

many

"small" users

and

thusadopttheWardrop's

principle (see [57]) incharacterizingtheflow distributioninthenetwork;i.e.,the flows

arerouted along paths with

minimum

effective cost, defined as the

sum

ofthelatency

atthe given flow

and

the price of that path (see the definition below).^

We

also

as-sume

that the usershave areservationutility

R

and

decidenot tosendtheirflowifthe

effectivecost exceedsthe reservationutility. This impliesthat user preferencescan be

induce optimalflows,withthe goal of choosingtollsfromthissetaccording tosecondarycriteria,e.g.,

minimizingthetotalamountoftollsor thenumberoftolledroutes; see[8],[21],[28],[27],and[20].

^Wardrop's principleisused extensivelyinmodellingtraffic behaviorintransportation networks,

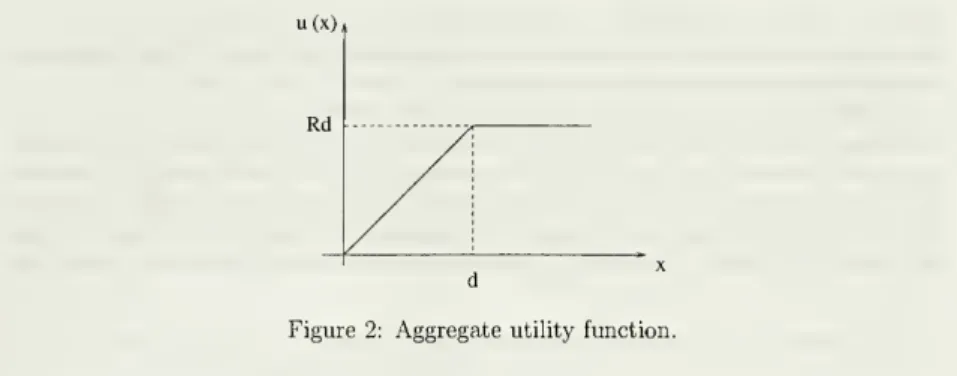
u(x)

Figure2: Aggregateutilityfunction.

represented

by

thepiecewise linearaggregateutilityfunction

u

(•)depictedinFigure2.^

To

accountforadditional side constraintsinthetrafficequihbrium problem,including

capacityconstraints

on

thelinks,

we

use thefollowing definition ofa

WE

(see[29], [26]).

Lemma

1

shows

that this definition is equivalent tothe

more

standard definition of a

WE

usedinthe literatureunder

some

assumptions.

Definition

1 For a given price vector

p

>

0,^

equilibrium

(WE)

if

a vector

x

G

arg

max

<.2_]{R~ki

xY'^)-p,)x,

is a

Wardrop

(1)

We

denotetheset of

WE

at a given

p by W{p).

Assumption

1 For eachi

£

Z, the latencyfunction _k

convex, nondecreasing,

and

satisfies /,(0)

—

0.

[0,oo) 1-^ [0,do] isclosed,^°

The

assumptionofzerolatencyatzeroflow, i.e.,/j(0)

=

0,

imphes

thatalllatencyis

due

to flow oftraffic,

and

there arenofixedlatencycosts.^^ It isadoptedto simplify the

discussion, especiallythe characterization ofequilibriumpricesin Proposition9 below.

A

trivialrelaxation ofthis assumption to ^,(0)

=

L

for all i

e

2

for

some

L

>

will

have

no

effect

on

any

ofthe results in the paper. Allowing for differential levels of

^Thissimplifyingassumptionimpliesthatallusers are "homogeneous" inthe sense thattheyhave

thesamereservationutility,R. Theanalysisbelowwillshowthat the value ofthisreservationutility

R

hasnoeffecton anyoftheresultsaslong asitisstrictly positive.

We

discuss potentialissues in

extendingthisworktouserswithelasticand heterogeneousrequirementsintheconcludingsection.

^_{Since the reservationutilityof users}

isequal toR,wecanalso restrictattention topi<

R

forall

i. Throughoutthepaper,weusep> and p £[0,

RY

interchangeably.

'''Forafunction /:R"i—»(—00,00],wesay that /isclosedifthelevel set{x\f{x

<

c)}isclosed

forevery scalarc. NotethatafunctionisclosedifandonlyifitislowersemicontinuousoverR"(see

[9],Proposition1.2.2).

''Thisassumption would be agood approximationtocommunication networks where queueingdelays

/j(0) complicates the analysis, but has littleeffect onthe

major

results. This caseis

discussedinSection6,

where

we

provideaslightlylower tight

bound

forthe inefficiency

ofohgopoly equihbria withoutthisassumption.

Another

feature of

Assumption

1 isthatit allowslatency functions tobe extended

real-valued, thus allowingfor capacityconstraints. Let Ci

—

{x

E

[0,oo) | li{x)

<

oo}

denote the effective

domain

of/,.

By

Assumption

1, Cjis a closed interval of the

form

[0, b]or[0,oo). Let

bd

—

sup^^,^, x.

Without

lossofgenerahty,

we

can

add

the constraint

Xi

6

Ciin Eq. (1). Usingthe optimality conditionsfor

problem

(1),

we

seethata vector

^WE

£i^J^ _isa

WE

_if

_and

onlyif

J^iei

^T^ —

^^'^'^thereexists

some

A

>

suchthat

K

EiGi

^^^

~d)

=

and

foralli,

R

-

_kixf"^)

_-Pi

<

A ifxf"^

-

0, (2)

=

A

iiO<xf'^

<bc„

>A

ifxr^

=

6c,.

When

the latency functions are real-valued[i.e.,Cj

=

[0,oo)],

we

obtainthe following

characterization ofa

WE,

which

isoftenusedasthedefinition ofa

WE

intheliterature.

This

lemma

states that in the

WE,

the effective costs, defined as li{xf^^)

+

pi, are

equalized

on

alllinkswithpositive flows.

Lemma

1 Let

Assumption

1 hold,

and assume

further that Ci

—

[0,oo) forall i

G

T.

Then

anonnegativevector x*

£

W{p)

if

and

onlyif

li{x*)

+

Pi

—

mm{lj{x*)

+

pj},

V

iwithX*

>

0, (3)

j

kix*)

+

Pi

<

R,

V

z withX*

>

0,

iei

withX^jgjS;*

=

dliminj{lj{xj)

+

_Pj}

<

R-Example

2 below

shows

that condition (3) in this

lemma

may

not hold

when

the

latency functions arenotreal-valued.

The

existence, uniqueness,

and

continuity

prop-ertiesofa

WE

arewell-studied (see[5], [12], [50]).

We

provideherethestandard proof

forexistence,basedonestablishingtheequivalence of

WE

and

theoptimalsolutions of

aconvexnetwork optimization problem, which

we

willrefertolater inour analysis.

Proposition

1

(Existence

and

Continuity)

Let

Assumption

1hold. For

any

price

vector

p

>

0, the set of

WE,

W{p),

is nonempty. Moreover, the correspondence

W

:

M^

^

R^

isupper semicontinuous.

Proof.

Given any

p

>

0,consider the followingoptimization

problem

maximize^>o

^

\iR

-

Pi)xi

-

_j li{z)dz\ (4)

subject to _{2_.}^i

^

d.

Inviewof

Assumption

(1)(i.e.,liisnondecreasingforall i), itcan be

shown

that the

objective function of

problem

(4) is convexoverthe constraintset,

which

is

nonempty

(since

G

Ci)

and

convex. Moreover, thefirstorder optimalityconditions of

problem

(4),whichare alsosufficientconditionsforoptimality,are identical to the

WE

optimality

conditions [cf. Eq. (2)].

Hence

a flow vector

x^^

E

W{p)

if

and

onlyifitis an optimal

solution of

problem

(4). Since the objective function of

problem

(4) is continuous

and

theconstraintsetiscompact,this

problem

hasan optimalsolution,showingthat

W{p)

isnonempty.

The

fact that

VF

is

an upper

semicontinuous correspondence at every

_p

follows

by

usingthe

Theorem

ofthe

Maximum

(see Berge [6], chapter 6) for

problem

(4).

Q.E.D.

WE

flows alsosatisfyintuitivemonotonicitypropertiesgiveninthe following

propo-sition.

The

prooffollows

from

the optimalityconditions [cf.Eq. (2)]

and

isomitted(see

[I])-Proposition

2

(Monotonicity)

Let

Assumption

1 hold. For a given

p

>

0, let

P-j

=

\PiWj-(a) For

some p

<

p, letx

£

M^(p)

and x E W{p).

Then,J^iei^^

—

Yliei^i-(b) For

some

pj

<

pj, let

x E W{pj,p^j) and x E

W{pj,p-j).

Then

Xj

>

Xj

and

Xi

<

Xi,

foralli

^

j.

(c) For

some

X

C

I,supposethatpj

<

pj forallj

E

I

and

pj

=

pjfor all_j

^

X,

and

letX

eW{P)

and

x E W{p).

Then

_Yljei^j

—

X^ief^j-For agiven price vectorp, the

WE

need not be unique in general.

The

following

example

illustrates

some

properties ofthe

WE.

Example

2 Consider a

two

linknetwork. Letthe total flowhed

=

1

and

the

reserva-tionutility

be

i?

=

1.

Assume

that the latency functions are given

by

liix)

—

MX]

=

< , . 3

^

'

^

'

\ oo otherwise.

At

the price vector (pi,P2)

—

(1,1), the set of

WE,

W{p),

is given

by

the set of ah

vectors (xi,2;2) with

<

x^

<

2/3

and

X^^Xj

<

1.

At any

price vector (pi,P2) with

Pi

>

P2

=

1,

W{p)

isgiven

by

all (0,X2) with

<

X2

<

2/3.

This

example

also illustratesthat

Lemma

1 need not hold

when

latencyfunctions

are not real-valued. Consider, for instance, the price vector (pi,P2)

=

(1

—

e,1

—

ae)

for

some

scalara

>

1. In thiscase,theunique

WE

is(xi,X2)

=

(1/3,2/3),

and

clearly

effective costs

on

the

two

routes are notequalized despitethefactthatthey

both

have

positive flows. This arises because the path with the lower effective cost is capacity

constrained, sono

more

trafficcanuse that path.

Under

further restrictions

on

the/,,the followingstandardresultfollows(proof

Proposition

3

(Uniqueness)

Let

Assumption

1 hold.

Assume

further that k is

strictly increasingover C^. For

any

price vectorp

>

0, the set of

WE,

W{p),

is a

singleton. Moreover,the function

W

:

R^

i—>

M^

iscontinuous.

Since

we

do

not

assume

thatthelatency functions are strictlyincreasing,

we

need

the following

lemma

inour analysis to dealwithnonunique

WE

flows.

Lemma

2 Let

Assumption

1hold. Fora given

p

>

0,definetheset

J={i€l|3x,

X e

W{p)

withXij^Xi}. (5)

Then

kixi)

=

0,

V

i

e

J,

V

x G Wip),

Pi

=

Pj,

V

i, j

ei.

Proof.

Consider

some

i

G

2"

and

x € W{p).

Sincei 6X, thereexists

some x 6

W{p)

suchthatXi

^

Xi-

Assume

withoutlossofgeneralitythat x,

>

Xj. Thereare

two

cases to consider:

(a) If Xk

>

Xk for all k j^ i, then X^jsi^j

>

_X^iei-^J' which

imphes

that the

WE

optimality conditions[cf. Eq. (2)] forx hold with A

=

0.

By

Eq. (2)

and

Xj

>

x,,

we

have

li{xi)

+Pz<

R,

li{xi)+Pi>R,

which

togetherimply thatli{xi)

=

li{xi).

By

Assumption

1 (i.e., kis convex

and

^.(0)

=

0),it followsthatli{xi)

=

0.

(b) IfXk

<

Xk for

some

k,

by

the

WE

optimahtyconditions,

we

obtain

k{Xi)

+

Pi

<

IkiXk)

+

Pk,

k{ii)

+Pi>

lk{xk)

+Pk-Combining

the above withXi

>

Xi

and

x^

<

x^,

we

see that li{xi)

=

k{xi),

and

hi^k)

=

hi^k)-

By

Assumption

1, this shows that li{Xi)

—

(and also that

Pi

=Pk)-Next

consider

some

z, j

G

2".

We

_will

_show

_that

pi

=

pj. Since i

E

I, thereexist

X, XE.

W{p)

suchthatXt

>

Xi.

There

arethree cases to consider:

• Xj

>

Xj. IfXk

>

Xk for all k

_^

i,j, then

X^^Xm <

d, implying thatthe

WE

optimalityconditionsholdwithA

=

0. Therefore,

we

have

k{xi)

+

Pi

<

R,

lj{xj)

+

pj

>

R,

which

togetherwithli{xi)

=

lj{xj)

=

imply thatPi

=

Pj.

• Xj

=

Xj. Since j

€

X,

by

definition there

must

exist

some

otherx

^W{p)

suchthat

Xj

^

Xj. Repeating theabove

two

stepswith Xj instead of Xj yields the desired

result.

Q.E.D.

Intuitively, this

lemma

states that ifthere exist multiple

WEs,

x,x E

W{p)

such

thatXi

^

Xi,thenthe latency function/,

must

belocallyflat

around

Xi (andXi).

Given

the assumptionthat/j(0)

=

and

the convexityoflatency functions, thisimmediately

impliesli{xi)

=

0.

We

nextdefinethesocial

problem

and

the social

optimum, which

istherouting(flow

allocation) that

would

be chosen

by

aplanner that hasfullinformation

and

fullcontrol

overthenetwork.

Definition 2

A

flow vector

x^

is asocial

optimum

ifit is

an

optimalsolution of the

socialproblem

m£iximizej:>o

y^iR

—

li{xi)jXi (6)

iei

subject to

_y.

^i

^

d-Inviewof

Assumption

1,thesocial

problem

has a continuousobjectivefunction

and

a

compact

constraintset,guaranteeingthe existence ofasocial

optimum,

x^. Moreover,

usingthe

optimaUty

conditionsfora convex

program

(see [9],Section4.7),

we

seethat

a vector

x^ E

R^

is asocial

optimum

if

and

only if

^^^jxf

<

d

and

there existsa

subgradient gi.

e

dli{xf) foreachz,

and

aA'^

>

suchthat A'^(

^jgjxf

—

d)

—

Q

and

for each2,

R

-

k{xf)

-

xfgi^

<

A^ if

xf

=

0, (7)

=

A^

ifO<xf<bc„

>A^

iixf

=

bcr

Forfuture reference, fora given vectorx

€

Mf^,

we

definethe value of the objective

functioninthe socialproblem,

S{x)

=

Y,iR-l^[x^))Xi,

(8)

asthe socialsurplus,i.e., the difference

between

users' willingnessto

pay and

the total

3

Monopoly

Equilibrium

and

Efficiency

In this section,

we assume

that a

monopoUst

service provider

owns

the / links

and

chargesaprice ofpiper unit

bandwidth on hnk

i.

We

considered arelated

problem

in

[1] foratomicusers withinelastic traffic (i.e.,theutilityfunction ofeachofa finite set

ofusers is a step function),

and

with increasing,real-valued

and

differentiablelatency

functions. Here

we

show

that similarresultsholdforthe

more

generallatency functions

and

the

demand

model

considered inSection2.

The

monopolist setsthe prices to

maximize

his profitgiven

by

n(jD,x)

^^p,Xi,

where x €

W{p). Thisdefinesatwo-stage

dynamic

pricing-congestiongame,

where

the

monopolist sets pricesanticipating the

demand

ofusers,

and

given the prices (i.e., in

eachsubgame),userschoosetheirflow vectorsaccordingto the

WE.

Definition 3

A

vector

(p^^,x^^)

>

is a

Monopoly

Equilibrium

(ME)

if

x^^

G

W{p^'^) and

liip"'^^,x'^^)

>

n(p,x),

V

p

>

0,

V

X G

W

(p)

.

Our

definition ofthe

ME

isstronger thanthestandard

subgame

perfect

Nash

equi-libriumconceptfor

dynamic

games.

With

aslightabuseof terminology,letus associate

a

subgame

perfect

Nash

equilibrium with the on-the-equilibrium-path actions of the

two-stagegame.

Definition

4

A

vector (p*,x*)

>

isa

subgame

perfect equihbrium

(SPE)

ofthe

pricing-congestion

game

ifx*

£ W{p*) and

for all

p

>

0, there exists x E

W

(p) such

that

n(p*,x*)

>

n(p,.T).

The

followingproposition

shows

thatunder

Assumption

1,the

two

solutionconcepts

coincide. Sincethe proofis not relevantfor therest oftheargument,

we

provide itin

Appendix

A.

Proposition 4

Let

Assumption

1 hold.

A

vector {p'^'^^,x'^^) isan

ME

if

and

onlyif

itisan

SPE

of the pricing-congestiongame.

Sincean

ME

(p*,x*) isan optimalsolution ofthe optimization

problem

maximizep>o,x>o

^^Pi^i

(9)

iei

subject to x

E W{p),

itis easierto

work

withthan an

SPE.

Therefore,

we

use

ME

asthe solutionconceptin

thispaper.

The

preceding

problem

has an optimalsolution,

which

establishes the existenceof

an

ME.

Moreover,

we

have:

Proposition

5 Let

Assumption

1hold.

A

vectorxisthieflowvectoratan

ME

if

and

onlyifit isa social

optimum.

Moreover, if(p,x) is

an

ME,

thenfor all iwithXi

>

0,

we

havepi

= R

—

k{xi).

This proposition therefore establishes that the flow allocation at an

ME

and

the

social

optimum

are the same. Itsproofis similar to

an

analogousresult in [1]

and

is

omitted.

In addition to the socialsurplus defined above, it is also useful to definethe

con-sumer

surplus,asthedifference

between

users'wilhngnessto

pay and

effectivecost,i.e.,

^j^^ {R

—

k{xi)—pi)xi(see[32]).

By

Proposition5, it isclearthat even

though

the

ME

achievesthesocial

optimum,

allofthe surplusiscaptured

by

the

monopohst, and

users

are just indifferent

between

sendingtheirinformationornot (i.e.,receive

no

consumer

surplus).

Our major

motivation for the study of oligopolistic settings isthat they provide

a betterapproximation to reality,

where

there istypically competition

among

service

providers.

A

secondary motivationisto seewhether anoligopolyequilibriumwillachieve

anefficient allocationlikethe

ME,

whilealsotransferring

some

orallofthe surplus to

theconsumers.

4

Oligopoly

Equilibrium

We

suppose thatthere are

S

serviceproviders, denote the set of serviceproviders

by

«S,

and assume

that eachserviceproviders

E

S

owns

a different subset X, of thelinks.

Serviceproviderscharges apricepiperunit

bandwidth on

linki EIs-

Given

thevector

of prices of links

owned by

other service providers,p_s

=

[Pili^is^ ^^^ profit of service

providersis

^s{Ps,P-s,x)

^

^PiXi,

ieis

for X

e

W{ps,p-s),

where

Ps

=

\pi]ieis-The

objective ofeachserviceprovider, like themonopolist in theprevioussection,

is to

maximize

profits. Becausetheir profits

depend on

theprices set

by

other service

providers, each service provider forms conjectures about the actions ofother service

providers, as well asthebehaviorofusers, which,

we

assume, they do accordingtothe

notion of

(subgame

perfect)

Nash

equilibrium.

We

refer to the

game

among

service

providers asthe price competitiongame.

Definition 5

A

vector [p'-'^,x^^)

>

isa(pure strategy) OligopolyEquilibrium

(OE)

if

x°^

€

W

_(p°^,p?f

)

and

forall

seS,

n,(p?^,pef,xO^)

>

n,(p3,pef,x),

vp,

>

0,

vx

G

w{p,,p'^f). (lo)

We

referto

p°^

asthe

OE

price.

As

forthe

monopoly

case,there isa close relation

between

apurestrategy

OE

and

a pure strategy

subgame

perfect equiUbrium.

Again

associating the

subgame

perfect

equilibriumwith the on-the-equilibrium-pathactions,

we

have:

Definition 6

A

vector {p*,x*)

>

isa

subgame

perfectequilibrium

(SPE)

ofthe price

competition

game

ifx* €

W

(p*)

and

there exists afunction

x

:

R^

i->

R^

such that

x{p)

e

W

(p) for all

p

>

and

foralls eS,

n,(p:,pl„a;*)>n,(p„pl„x(p3,plj)

Vp, >0.

(11)

The

followingproposition generalizesProposition4

and

enables us to

work

withthe

OE

definition,whichis

more

convenientforthesubsequentanalysis.

The

proofparallels

that ofProposition4

and

isomitted.

Proposition

6 Let

Assumption

1hold.

A

vector {p'-'^,x^^)is

an

OE

if

and

onlyif it

is

an

SPE

ofthe pricecompetitiongame.

The

pricecompetition

game

isneitherconcave nor supermodular. Therefore,classical

argumentsthat areusedto

show

the existence of apurestrategyequilibriumdo not hold

(see[16], [52]). Inthenextproposition,

we

show

thatfor linearlatency functions, there

existsapurestrategy

OE.

The

proofisprovidedintheappendix.

Proposition

7 Let

Assumption

1hold,

and assume

furtherthat the latency functions

arelinear.

Then

the pricecompetition

game

hasapurestrategy

OE.

The

existence result cannot be generalized to piecewise linear latency functions or

tolatency functions

which

are linear over theireffective domain, as illustratedin the

followingexample.

Example

3 Considera

two

linknetwork. Letthe total flowhe d

=

1.

Assume

that the

latency functions are given

by

I I \ n 1 f \

Jo

if0<x<5

for

some

e

>

and

5

>

1/2,withtheconventionthat

when

e

=

0, l2{x)

=

ooioi x

>

5.

We

first

show

that thereexists no purestrategy oligopoly equilibrium forsmall e(i.e.,

thereexists

no

purestrategy

subgame

perfectequihbrium).

The

followinglistconsiders

allcandidateohgopolyprice equilibria (pi,P2)

and

profitable unilateral deviations fore

sufficientlysmall, thusestablishingthenonexistenceofan

OE:

1. Pi

=

P2

=

0:

A

small increase in the price of provider 1 will generate positive

profits,thusprovider 1has an incentive to deviate.

2. _Pi

—

_P2

>

0: Let

x

bethe flow allocation at the

OE.

IfXi

=

1,thenprovider 2

-hasanincentive to decreaseitsprice. Ifxj

<

1,thenprovider 1has

an

incentive

todecreaseitsprice.

3.

<

_pi

_<

_P2: Player 1has anincentive to increaseitspricesinceitsflow allocation

remainsthesame.

4.

<

_P2

<

Pi'- For esufficientlysmall, theprofit function of player 2, givenpi, is

strictlyincreasing asafunction ofp2, showingthat provider 2 has

an

incentive to

increaseitsprice.

We

next

show

thata

mixed

strategy

OE

alwaysexists.

We

definea

mixed

strategy

OE

asa

mixed

strategy

subgame

perfectequilibriumofthe pricecompetition

game

(see

Dasgupta and

Maskin, [13]). Let

5"

be the spaceofall (Borel) probability measures

on [0,/?]". Let Is denote the cardinality ofT^, i.e., the

number

of links controlled

by

serviceproviders. Let/i^

€

B'^be aprobabilitymeasure,

and

denotethe vectorofthese

probabilitymeasures

by

/j,

and

the vector of these probabilitymeasures excluding s

by

Definition 7 {/j,*,x*{p))isa

mixed

strategy OligopolyEquilibrium

(OE)

ifthefunction

x*{p)

G

W

(p) forevery

p G

[0,

RY

and

/ Us{ps,p-s,x*{ps,p-s)) d{iil{ps)

X

fl*_^{p_s))

JlO,R]'

>

/ Us{Ps,P-s,X*{Ps,P-s))d{fls{Ps) XP'ls(P-s))

JlO,R\'

foralls

and

fig

€ B^\

Therefore,a

mixed

strategy

OE

simplyrequiresthat therebe noprofitable deviation

toadifferentprobability

measure

foreach ohgopoUst.

Example

3

(continued)

We

now

show

thatthe following strategyprofile is the

unique

mixed

strategy

OE

for theabove

game when

e

—

> (a

mixed

strategy

OE

also

exists

when

e

>

0,butitsstructureis

more comphcated and

lessinformative):

(

0<P<R{l-S),

fxi{p)=l

1-M«

R{l-S)<p<R,

{ 1 otherwise, (

0<P<R{l-S),

M2(P)=<

1-^

R{l-S)<p<R,

I 1 otherwise.otherwise.

Notice that ^i has

an

atom

equalto 1

—

5 ati?.

To

verifythat this profileis a

mixed

strategy

OE,

let n'

be

thedensity offj.,with the conventionthatfj,'

=

oo

when

thereis

an

atom

atthatpoint. Let

Mi

—

{p \

ji'^_(p)

>

0}.

To

establish that _{111,^2)isa

mixed

strategy equilibrium, itsufficesto

show

thatthe expectedpayoff to playeriisconstant

for all _Pi

G

Mi when

the other player choosesp_i accordingto ;U_j (see [37]). These

expectedpayoffs are

n

{pi IiJL-i)

=

/ Iii{pi,p-i,x {pi,p-i))dii-i(p_i)

.

(12)

The

WE

demand

x{pi,p2) takes the simple form of xi {pi,P2)

=

1 if Pi

<

P2

and

xi {pi,P2)

=

l

—

5iipi

>

p2-

The

exactvalue of xi (pi,P2)

=

1

whenpi

=

p2isimmaterial

sincethisevent

happens

withzero probability. It isevidentthat the expressionin (12)

is constant for allp,

€

Mj

fori

=

1,2 given /^i

and

112 above. This establishes that

{111,112) is a

mixed

strategy

OE.

Itcan alsobeverifiedthat there are

no

other

mixed

strategyequilibria.

The

next proposition,

which

is proved in

Appendix

B, estabUshes that a

mixed

strategy equilibriumalwaysexists.

Proposition

8 Let

Assumption

1hold.

Then

the pricecompetition

game

hasa

mixed

strategy

OE,

(/x°^,x°^(p)).

We

next providean explicitcharacterization ofpure strategy

OE.

Though

ofalso

independentintei'est, these results are

most

usefulforus to quantify theefficiency loss

ofoligopolyinthenextsection.

The

following

lemma

shows that an equivalent to

Lemma

1 (which required

real-valued latency functions) also holds with

more

general latency functions at the pure

strategy

OE.

Lemma

3 Let

Assumption

1hold. If(79°^,x"^^) isapurestrategy

OE,

then

/,(x°^)+pf^

=

min{L(xf^)

+

_pf^},

Vzwithxf^>0,

(13)

/i(xf^)+pf^

<

R,

Viwithxf^>0,

(14)

^xp^

<

d, (15)

with E,:ei^z°^

=

^ifminj{/j(x^°^)

+

Pj}

<

R.

Proof. Let (p°^,x'^^) bean

OE.

Since x°-^

G W{p°^),

conditions (14)

and

(15) follow

bythe definition ofa

WE.

Considercondition(13).

Assume

that thereexist

some

i,j

G

I

with

xf

^

>

0,

x°^

>

suchthat

Usingtheoptimahtyconditionsfora

WE

[cf.Eq. (2)],thisimpliesthat

xf^

=

be,-

Con-siderchanging

_pf^

to

pf

^

+

efor

some

e

>

0.

By

checkingthe optimality conditions,

we

seethat

we

can chooseesufficientlysmallsuchthat

x°^

G

W{pf^

+

e,p^f).

Hence

the

serviceprovider that

owns

linkicandeviate to

_pf

^

+

e

and

increaseitsprofits,

contra-dicting thefactthat (p'^^,x'^^) isan

OE.

Finally,

assume

to arrive at acontradiction

thatminj{/j(x?^)4-_Pj}

<

R

_{and Yliei^?^}

<

d. Usingthe optimality conditionsfora

WE

[Eq. (2)with

A

=

since

^j^ixf^

<

d],thisimpliesthat

we

must

have

xf^

—

bd

for

some

i.

With

asimilar

argument

to above, a deviation to

_pf^

+

e keepsx'-'^ asa

WE,

and

is

more

profitable,completingthe proof.

Q.E.D.

We

needthe following additionalassumptionforourpricecharacterization.

Assumption

2

Given

apurestrategy

OE

(p*^^,x^^),iffor

some

i

e

I

with

xf^ >

0,

we

haveli{xf^)

—

0, thenX^

—

{i}.

Note

thatthisassumptionisautomaticallysatisfiedifalllatency functions arestrictly

increasingorifallserviceproviders

own

onlyonelink.

Lemma

4

Let (p°^,a;°^) be a purestrategy

OE.

Let

Assumptions

1

and

2 hold. Let

Ha

denotethe profit of serviceprovider sat (jP^,x'~'^).

(a) IfUs'

>

for

some

s'

6

5,thenfls

>

foralls

E

S.

(b) If

n,

>

for

some

s

e

<S,then

_pf

^x°^

>

forallj

E

Is-Proof.

(a) For

some

j

£

Jy,define

K

=

p'^^

+

lj[x^^),whichispositive since Hgi

>

0.

Assume

Hg

=

for

some

s. Fork

E

Xg, considerthe price pk

=

K

—

e

>

ior

some

small

e

>

0. Itcan be seenthat atthe_{price vector {pk,p?.k), the}corresponding

WE

link

flow

would

satisfy Xk

>

0. Hence,serviceprovider shasanincentive todeviate to

pk at

which

hewill

make

positiveprofit,contradictingthe factthat {p'~'^,x^^) is

a purestrategy

OE.

(b) Since lis

>

0,

we

have

p^x^

>

for

some

m

E

X^.

By

Assumption

2,

we

can

assume

withoutlossofgeneralitythat Imix^^)

>

(otherwise,

we

aredone). Let j

E

Xg

and

assume

to arrive at acontradiction that

_pf^xf^

=

0.

The

profit of

serviceprovider satthe purestrategy

OE

can bewritten as

n^

=

n^

+

p,

PE OE

where

Da denotestheprofitsfromlinksotherthan

m

and

j. Let

p'^

—

K—lm{x^^)

for

some K.

Considerchangingthe prices

p^^ and

p^^

suchthatthe

new

profitis

f[g

=

Us

+

iK-

UxZ^

-

e))(x°^

-

e)

+

e{K

-

l,{e)).

Note

thate units of flow are

moved

from link

m

to link j suchthat the flows of

other links

remain

the

same

atthe

new

WE.

Hence,thechangeintheprofitis

n,

-

n,

=

iUx^^)

-

Uxl^

-

e))x^^

+

6(/„(x°^

-

e)

-

Z,(e))).

Since /^(a;^^)

>

0, ecan be chosensufficientlysmallsuchthattheaboveisstrictly

positive, contradictingthefactthat {jp^,x'-'^) isan

OE.

Q.E.D.

The

following

example

showsthat

Assumption

2 cannotbe dispensed withfor part

(b) ofthis

lemma.

Example

4

Consider athree

hnk

network with

two

providers,

where

provider 1

owns

links 1

and

3

and

provider2

owns

link2. Letthe total flow

be

d

=

1

and

the reservation

utilitybei?

=

1.

Assume

that the latency functions are given

by

^1(xi)== 0, ^2 (2^2)

=

2:2, h{x-i)

=

ax-i,

for

some

a

>

0.

Any

pricevector (pi,P2,P3)

=

(2/3,1/3,6)with6

>

2/3

and

{xi,X2,X3)

=

(2/3, 1/3,0) isa purestrategy

OE,

so^3X3

=

contraryto part (b)ofthe

lemma. To

see

why

thisisanequilibrium, notethatprovider 2isclearlyplayingabest response.

Moreover,in thisallocationIIi

=

4/9.

We

canrepresent

any

deviation of provider 1

by

(pi,P3)

=

(2/3-5,2/3-ae-5),

for

two

scalarse

and

5,whichwillinducea

WE

of(xj,X2,X3)

=

(2/3

+

6

—

e,1/3

—

5, e)

.

The

correspondingprofitofprovider1 atthisdeviationisHj

=

4/9

—

^^

<

4/9,

estab-lishingthat provider1is alsoplayinga bestresponse

and

we

haveapurestrategy

OE.

We

next establish that, under an additional mild assumption, a purestrategy

OE

willneverbeatapoint of non-differentiability of the latency functions.

Assumption

3

There

exists

some

s

E

S

such that k is real-valued

and

continuously

differentiablefor alli

£

X, .

Lemma

5 Let (p^-^,

x°^)

be an

OE

with min^

{pf^

+

lj{x°^)]

<

R

and pf

^xf

^

>

for

some

i. Let

Assumptions

1,2

and

3 hold.

Then

where

lf{x^^)

and

l~{xf^) arethe right

and

left derivatives ofthe functionU at

xf^

respectively.

Since theproofof this

lemma

islong,itisgivenin

Appendix

C.

Note

that

Assumption

3cannot be dispensed within this

lemma.

Thisisillustratedinthenext example.

Example

5 Considera

two

Hnk

network. Letthe total flowhe d

=

1

and

the

reserva-tion utilitybe/?

=

2.

Assume

that thelatency functions aregiven

by

^^(^^^^^(^)

=

_\2(x-i)

_otherwise.

Itcan beverifiedthatthe vector _(pf^,p^^)

=

(1, 1), with

(xf^,x^^)

=

(1/2,1/2) isa

purestrategy

OE, and

isat a point of non-differentiabihtyfor bothlatency functions.

We

next provideanexplicitcharacterization ofthe

OE

prices,whichis essential in

ourefficiency analysisinSection 5.

The

proofisgivenin

Appendix

D.

Proposition

9 Let{p°^,x'^^) bean

OE

suchthat

pf^xf^

>

for

some

i

e

1. Let

Assumptions

1,2,

and

3 hold.

a)

Assume

thatmiuj

{p^^

+

/j(x°^)}

<

R. Then,for alls

G

5

and

i

€

2s,

we

have

r xf^/^(xf^), ifl'^{x°^)

=

for

some

_j

^

Z„

??""={

a:P^/'(xp^)

+ _^iM^4^,

otlierwise. (^6)

b)

Assume

thatmiiij

{p°^

+

lj{xf^)}

=

R. Then, foralls

G

5

and

i GXj,

we

have

pr

>

^'^i^i^?'')- (17)

Moreover,ifthere exists

some

i

G

I

suchthat Z^

=

{i} for

some

s

G

5,then

pf^<xf^/,n:rf^)

+

_^

^ 1 • (18)

Ifthe latency functions li are all real-valued

and

continuously differentiable, then

analysis of

Karush-Kuhn-

Tuckerconditionsfor ohgopoly

problem

[problem (82) in

Ap-pendixD] immediatelyyieldsthe followingresult:

Corollary

1 Let

(p°^,x°^)

be

an

OE

suchthat

pf^xf^

>

for

some

i

G

I. Let

As-sumptions1

and

2hold.

Assume

alsothatkisreal-valued

and

continuouslydifferentiable

for alli. Then, forall s

G

5

and

i

€ls, we

have

if/;(x°^)

=

Oforsomej ^J,

otherwise.

(19)

Thiscorollary alsoimpliesthatinthe

two

linkcasewithreal-valued

and

continuously

differentiablelatency functions

and

with

minimum

effective cost lessthan R, the

OE

pricesare

P?^-xf^{l[ixn

+

l2ixr))

(20)

asclaimedinthe Introduction.

5

Efficiency

of

Oligopoly

Equilibria

This section contains our

main

results, providing tight

bounds on

the inefficiency of

oligopolyequilibria.

We

take asour

measure

ofefficiencythe ratio of thesocialsurplus of

theequilibriumflow allocation to thesocialsurplus of the social

optimum,

S{x*)/S{x^),

where

x' refers tothe

monopoly

or the oligopoly equilibrium [cf. Eq. (8)]. Section 3

established that the flow allocation at a

monopoly

equilibrium is asocial

optimum.

Hence, in congestion

games

with

monopoly

pricing, there is

no

efficiency loss.

The

following

example

showsthatthisisnotnecessarilythe casewitholigopolypricing.

Example

6 Consider a

two

linknetwork. Let thetotal flowbe d

=

1

and

thereservation

utilityhe

R=

1.

The

latency functions are given

by

3

/l(x)

=

0, l2{x)

=

-X.

The

uniquesocial

optimum

forthis

example

isx'^

=

(1,0).

The

unique

ME

(p^^,x'^^)

is x'^'^

=

(1,0)

and

p^^

=

(1,1).

As

expected, the flow allocations at the social

optimum

and

the

ME

arethesame.

Next

consideraduopoly

where

eachofthese links is

owned by

adifferent provider. UsingCorollary 1

and

Lemma

3, itfollows thatthe

flow allocation atthe

OE,

x'-'^,satisfies

/,(x?^)

+

x?^[/;(xf^)

+

Ux^^)]

=

kix^)

+

x^Ux^)

+

Ux^'')]-Solvingthistogetherwith

xf ^

+

X2^

=

1 showsthat the flow allocation at theunique

ohgopoly equilibrium is x'~^^

—

(2/3,1/3).

The

social surplus at the social

optimum,

the

monopoly

equilibrium,

and

the oligopoly equilibrium are given

by

1, 1,

and

5/6, respectively.

Before providinga

more

thoroughanalysis oftheefficiencyproperties ofthe

OE,

the

nextpropositionprovesthat, asclaimedintheIntroduction

and

suggested

by

Example

6, achange in the

market

structure from

monopoly

toduopolyin atwo linknetwork

typicallyreduces efficiency.

Proposition 10

Consider a

two

link network where each

hnk

is

owned by

a

differ-ent provider. Let

Assumption

1 hold. Let {p^^,x'^^) be a pure strategy

OE

such

that

pp^xp^

>

for

some

i

€

J

and

min^

{pf'^

+

lj{xf^)}

<

R. If Z'i(xf^)/xf^

^

/^(x°^)/x^^,then S(xO^)/S(x^)

<

1 .

Proof.

Combining

the

OE

priceswiththe

WE

conditions,

we

have

hix?")

+

x?^{l[ix?^)

+

Ux2^))

^

hix^'^)

+

xr{l[{xr)

+

Ux^)),

where

we

usethefactthatmiuj

{p°^

+

l]{x'^^)}

<

R. Moreover,

we

canuse optimality

conditions (7)toprovethata vector (xf ,xf)

>

isasocial

optimum

if

and

onlyif

/i(xf)

+

xf/'i(xf)

=

hixl)

+

xf/^(xf).

Sinceri(xf^)/xf^

^

/^(x^^)/xp^,theresult follows.

Q.E.D.

We

next quantify the efficiency of oligopoly equilibria

by

providing atight

bound

on

theefficiency loss incongestion

games

witholigopolypricing.

As we

have

shown

in

Section4, such

games

do not always have a purestrategy

OE.

Inthe following,

we

first

provide

bounds on

congestion

games

thathave purestrategyequilibria.

We

next study

efficiencyproperties of

mixed

strategyequilibria.

5.1

Pure

Strategy

Equilibria

We

consider pricecompetition

games

thathave purestrategy equilibria(this setincludes,

butissubstantially larger than,

games

withlinearlatency functions, see Section4).

We

consider latency functions thatsatisfy

Assumptions

1,2,

and

3. Let

Ci

denotethesetof

latency functionsfor which theassociated pricecompetition

game

has apurestrategy

OE

and

the individual k's satisfy

Assumptions

1,2,

and

3.^^

We

refertoan element of

the set

Cj

by

{li}iei-

Given

a parallellinknetwork with/

Unks

and

latency functions

{k}iei

S

-C/i IstOE{{li}) denote the setofflow allocations at an

OE.

We

define the

efficiencymetricat

some

x'^^

G

OE{{li})as

PV

x°^-T

l(x°^\x°^

where x^

isasocial

optimum

giventhelatency functions{li}i^j

and

R

isthe reservation

utility. In other words, our efficiency metric is the ratio ofthe social surplus in an

equihbriumrelative tothe siurplus in the social

optimum.

Following the literature

on

the "price ofanarchy",inparticular [25],

we

are interestedintheworstperformancein

an

oligopolyequihbrium,so

we

lookfora lower

bound on

inf inf^ r,{{U},x°^).

{'Oe£/

^oB^OEau))

We

firstprove

two lemmas, which

reduce theset oflatency functions thatneedto

be considered in

bounding

the efficiency metric.

The

next

lemma

allows us to use the

oligopoly price characterization giveninProposition 9.

Lemma

6 Let {p'-'^,x^^)

be

apurestrategy

OE

suchthat

pf^xf^

=

foralli

G

Z.

Then

x'~'^isa social

optimum.

Proof.

We

first

show

that

h{xf^)

=

for alli

el. Assume

that lj{x^^)

>

for

some

;

€

1. This

imphes

that

x^^

>

and

therefore

_pf^

=

0. Since lj{xf^)

>

0, itfollows

by

Lemma

2thatforall

x E

W[p),we

haveXj

=

_{xf^. Consider}increasing

_pf^

to

some

small e

>

0.

By

the

upper

semicontinuityof

W{p),

it follows that there exists

some

e

>

sufficientlysmallsuchthatforallx

6 W{e,p^^),

we

have\xj

—

x^^\

<

5for

some

5

>

0. Moreover,

by

Proposition 2,

we

have, for all

x

€

W{e,p?.f), Xi

>

xf^

forall

i7^ j. Hence, theprofitofthe provider that

owns

linkjisstrictlyhigher at price vector

{e,p^f) thanatp*^^,contradictingthefactthat

(p°^,x°^)

isan

OE.

Clearly

_xf^

>

for

some

j

and

hence

min^gijpf^

+

k{x^'^)}

=

_pf^

+

lj{xf^)

=

0,

which

implies

by

Lemma

.3that

_J^tei^?^

=

d,. Using/j(xf^)

=

0,

and

G dU{xf^)

for

all2,

we

have

R

-

_kixf^)

-

_xf

^5,.

=

i?,

V

i

G

J,

for

some

gi^

€

dli{xf^). Hence,

x°^

satisfiesthe sufficient

optimahty

conditions for a

social

optimum

[cf Eq. (7) withX^

=

R],

and

theresultfollows.

Q.E.D.

The

next

lemma

allowsus to

assume

without loss of generality that

_RYliei^f

~

Y^iei^i(^i)^f

>

s-iid

_Eiei^?^

=

dm.

thesubsequentanalysis.

Lemma

7 Let {kjiei

G

£/.

Assume

that

^^Moreexplicitly,Assumption2impliesthatifany

OE

(p'^'^,x'^^) associatedwith{li}iei has

xf^ >

andhixf^)

=

0,thenJ^

=

{i}.

either (i) _{Yliex^i(^f)^i}

~

_^^iei^f

^'^^

some

social

optimum

Xs, or (ii)

_E^eI^?^

<

^for

some

x°^

e

0^{{h}).

Then

every

x°^

G

0E{{1,}) isasocial

optimum,

implyingthat rj{{li},x'^^)

—

1.

Proof.

Assume

that

^i^xh{xf)xf

—

R^^i^jxf.

Since

x^

is asocial

optimum

and

everyx'-'^

G

OE{{k})

isafeasiblesolution to thesocial

problem

[problem(6)],

we

have

=

_{Y.^R -}

k{xf))xf

> J2iR -

h{x?''))xf'^,

V x°^

€ O^iik}).

lei lex

By

the definition ofa

WE,

we

have

xf^

>

and

i?

-

kixf^)

>

pf^

>

(where

_pf^

is

theprice oflinkiatthe

OE)

foralli. This

combined

with the precedingrelationshows

that

x°^

is asocial

optimum.

Assume

next_{that Yl^^j}

xf^ <

dfor

some

x'^^

G

OE{{li}). Letp'-^^_{bethe associated}

OE

price.

Assume

thatp^^x'^^

>

for

some

j

€

I

(otherwise

we

are

done by

Lemma

6). Since

_X^iei^?^

^

'^'

^^

have

by

Lemma

3 thatminjgjjpj

+

lj{x^^}

=

R. Moreover,

by

Lemma

4,itfollowsthatPjxf^

>

foralli

G

I. Hence,foralls

G

_{5, ((pf}^)iei,,a;°^)

is

an

optimalsolution oftheproblem

maximize((p.).g^^,:c) y^^PiXj

subject to Pi

+

li{xi)

=

R,

V

i

G

Xs,

pf^

+

liix,)^R,

^lils.

Y.xO^<d.

Substitutingfor (p^ieis inthe above,

we

obtain

maximizex>o _{2_^}

(^

~

^i{^i))^i

ieis

subject to x^

&

Ti,

M

i

^I^,

^xf'Kd,

where

Tj

=

{xj |

pf^

+

li{xi)

=

R}

is

eitherasingleton or a closedinterval. Sincethis

isaconvex problem, using the optimality conditions,

we

obtain

R

-

k{xf^)

-

xf^gi,

=0,

V

I

G

X„ V

s

G

5,

where

gi^Gdli{xf^).

By

Eq. (7), itfollowsthat

x°^

is asocial

optimum.

Q.E.D.

This

lemma

implies that in findingalower

bound on

the efficiencymetric,

we

can

restrict ourselves, without loss of generality, to latency functions {k}

G Cj

suchthat

Y^i&ik{xf)xf

<

RJ2iei^i

for

some

social

optimum

x'^,

and Xliei^?^

=

d for all

x*^^

G

OE{{li}).

By

thefollowing

lemma,

we

canalso

assume

that _YLiei^f

~

'^•

Lemma

8 Forasetoflatency functions{/,},gi,let

Assumption

1hold. Let[p'~'^_,x^^)

be an

OE

and x^

bea social

optimum.

Then

E-P'^E

Proof.

Assume

to arrive at acontradiction that_Yliei^i -^ _Yliei^i- Thisimplies

that

x^^

>

Xj for

some

j.

We

alsohave lj{x^^)

>

lj{Xj). (Otherwise,

we

would

have

lj{xj)

—

l'j{Xj)

=

0, whichyields acontradiction

by

the optimalityconditions (7)

and

thefactthat _Yliei^f"^^)- Usingthe optimality conditions(2)

and

(7),

we

obtain

R

-

_l,{xf^)

-

_pf

>R-

lj{x^)

-

x^gi^,

for

some

gi^

€

dlj{Xj).

Combining

the preceding with lj{xf^)

>

lj{xj)

and

p^^

>

xf'^lj{Xj'^) (cf.Proposition9),

we

seethat

xf-l-ixf-Xx^g,,

contradicting

x^^

>

Xj

and

completingthe proof.

Q.E.D.

5.1.1

Two

Links

We

firstconsider a parallel linknetwork with

two

links

owned by two

serviceproviders.

The

next

theorem

provides atightlower

bound

of5/6

on

r2{{li},x'-'^) [cf. Eq. (21)].

Startingwiththe two-linknetworkisuseful

two

reasons: first, thetwo-linknetwork

avoidsthe additional layer ofoptimizationoverthe allocation of links to service providers

in characterizingthe

bound on

inefficiency;

and

second,

we

willprovethe resultforthe

general case

by

reducingittotheproofofthe two-linkcase.

Although

thedetails of theproofofthe

theorem

are involved,thestructureis

straight-forward.

The

problem

offindingalower

bound

onr2{{k},x'-^^)is

an

infinite-dimensional

problem,sincetheminimizationisoverlatency functions.

The

prooffirstlower-bounds

the infinite-dimensional

problem by

theoptimalvalue ofafinite-dimensional

optimiza-tion

problem

usingtherelations

between

the flows at social

optimum

and

equihbrium,

and

convexityofthe latency functions. Itthen

shows

thatthe solutionwillinvolveone

ofthe linkshaving zero latency. Finally, usingthisfact

and

the price characterization

from

Proposition 9, itreducesthe

problem

of characterizing the

bound on

inefficiency

toa simple minimization problem, withoptimalvalue 5/6.

An

intuitionfor thisvalue

isprovidedbelow.

In the following,

we assume

withoutloss ofgenerality thatd

—

1. Also recallthat

latency functionsin

C2

satisfy

Assumptions

1,2,

and

3.

Theorem

1 Consider a

two

link network

where

each link is

owned by

a different

provider.

Then

r2{{k},x^^)

>

_^,

V

{kh=,,2

e

C2,

x^^

G O^iik}),

(22)

and

the

bound

istight,i.e.,thereexists {li}i=i,2

€

^2

and

x°^

G

OE{{li}) that attains

thelower

bound

inEq. (22).

Proof.

The

prooffollowsa

number

ofsteps:

Step 1:

We

are interestedinfindinga lower

bound

forthe

problem

inf inf r2({U,a:°^). (23)

Given {/j}

E

£2, let

x°^

£ OE{{li})

and

let x"^ be asocial

optimum.

By

Lemmas

7

and

8,

we

can

assume

that

_J2i=i^?^

—

_IZi=i^f

—

^- ^^^^implies that there exists

some

i such that

x^^

<

xf. Since the

problem

issymmetric,

we

canrestrict ourselves

to {li]

€ £2

such that x'^^

<

xf, i.e.,

we

restrict ourselves to {li} G

£2

such that

xf^

<

xf

—

efor

some

e

>

0.

We

claim

inf inf r2({/.},x°^)>infrOf(6), (24)

where

we

define

problem

(E^) as

OF, ^

R

-

hy?'^

-

hy?'^

r2,t (e)

=

mmimize

,s, (,sy>o

_{_}

_{g g}

_{_}

_{g g} (E

i^-^fyf-^fyf

subject to If

<yf{lfy,

i

=

l,2, (25) li<y?^li, i

=

l,2, (26) 'f

+

yfaf)'

=

^f

+

yfOf)', (27) ^f

+

yf(/f)'<i?, (28) 2

h

+

i[{y?''-yl)<if,

(30)

y2'"^>yf

+

e. (31)

E:

Vi

=

1, (32)

+

{Ohgopoly

Equihbrium

Constraints}t, t

=

1,2.

Problem

(E')canbe viewedasafinitedimensional

problem

thatcapturesthe

equilib-rium and

thesocial

optimum

characteristics oftheinfinitedimensional

problem

given in

Eq. (23). Thisimpliesthat instead ofoptimizingoverthe entire functionk,

we

optimize

over the possible values ofli{-)

and

dli{-) atthe equilibrium

and

the social

optimum,

which

we

denote

by

li,l^,lf,(if)' [i.e., {if)' isavariablethat representsallpossible

val-ues ofgi^ Gdli{yf)].

The

constraints ofthe

problem

guaranteethat these valuessatisfy

thenecessaryoptimality conditionsfora social

optimum

and

an

OE.

In particular,

con-ditions (25)

and

(26) capture the convexityassumption

on

li{-)

by

relatingthe values