Shannon's sampling theorem, incongruent residue classes and Plancherel's theorem

J

OURNAL DE

T

HÉORIE DES

N

OMBRES DE

B

ORDEAUX

M

AURICE

M. D

ODSON

Shannon’s sampling theorem, incongruent residue

classes and Plancherel’s theorem

Journal de Théorie des Nombres de Bordeaux, tome

14, n

o

_{2 (2002),}

p. 425-437

<http://www.numdam.org/item?id=JTNB_2002__14_2_425_0>

© Université Bordeaux 1, 2002, tous droits réservés.

L’accès aux archives de la revue « Journal de Théorie des Nombres de Bordeaux » (http://jtnb.cedram.org/) implique l’accord avec les condi-tions générales d’utilisation (http://www.numdam.org/conditions). Toute uti-lisation commerciale ou impression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit conte-nir la présente mention de copyright.

Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques

Shannon’s

_sampling

_theorem,

_incongruent

residue

classes and

Plancherel’s theorem

par MAURICE M. DODSON

Dedicated to Michel Mendis F’rance for his 65th birthday

RÉSUMÉ. On montre que la théorie de

l’échantillonnage

pour les

signaux

multi-canaux a une structure

_logique

_{qui s’apparente}

à celle de

_l’analyse

de Fourier.

ABSTRACT.

_Sampling

_theory

for multi-band

_signals

is shown to

have a

logical

structure similar to that of Fourier

_analysis.

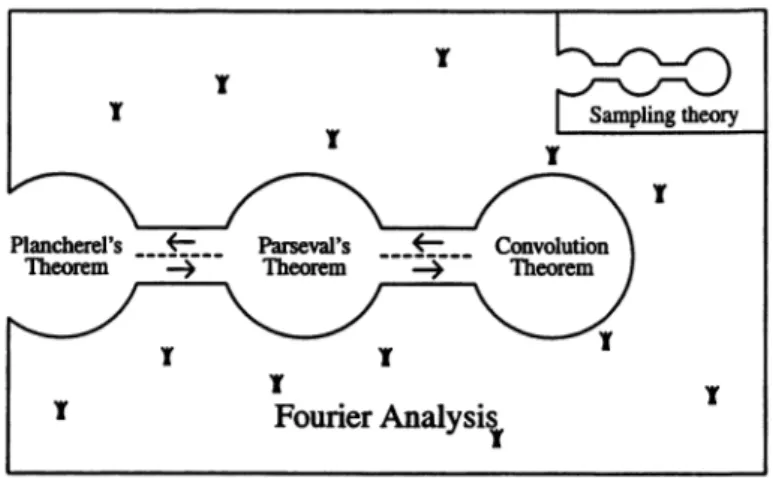
1. Introduction

In the rich and varied

_landscape

of

_mathematics,

Fourier

_analysis

occu-pies

a

_grand

and formal

_garden

(see

_Figure

1).

There is a corner of this

garden,

which borders

_{interpolation theory}

and

_{Paley-Wiener theory,}

called

sampling

theory.

This is not concerned with statistics but with informa-tion

_theory,

more

_precisely

with Shannon’s second or

_sampling

theorem.

Sometimes known as the Whittaker-Kotel’nikov-Shannon

_theorem,

it is a

cornerstone of communication

_{theory, providing}

a mathematical basis for an

_equivalence

between

_analogue

(or continuous)

_signals

and discrete

sig-nals.

In

_{applications,}

the main _purpose of Shannon’s

_sampling

theorem is to reconstruct a

_signal

from discrete

_samples.

The theorem falls

_naturally

into the

_theory

of

_{square-integrable}

functions and is

_closely

related to

Paley-Wiener

_theory.

A

_disjoint

translates condition on the Fourier transform

of the

_signal

underlies Shannon’s

_sampling

theorem and leads to a more

general

theory

sometimes called multiband

_signal

_theory

_{(see §3) .}

Plancherel’s theorem is one of the fundamental results in Fourier

_analysis

and

_implies

Parseval’s

_theorem,

which in turn

_implies

the convolution

the-orem. These three results _are,

_{however, logically equivalent}

and each could be

_regarded

as the

_starting

_point

of the

_theory

of Fourier

_analysis.

The

multiband

_theory

has a similar

_logical

structure in which

_hybrid

versions of the above three

_theorems,

_together

with the null intersection condition

FIGURE 1. The three fundamental results in Fourier

analy-sis with Plancherel’s theorem at the ’entrance’.

(see

(5) below)

and a reconstruction or

_{representation}

formula

(see (4)

be-low),

are also

equivalent.

This is

_proved

for

_{trigonometric polynomials}

which are a finite dimensional

_counterpart

of continuous

_signals.

2. Shannon’s

_sampling

theorem

An

_analogue

_signal

can be modelled

_by

a function

_{f :}

R - C

(when

_f

is a real

signal,

f(R)

C

_R).

For

_physical

_reasons, it is assumed that

_f

is

square-integrable

or has finite energy,

_i.e.,

= _oo. The

spectrum

of

_f

is

_{given by}

the Fourier transform

_{f ^ :}

_C,

where

and where

_f^

is defined as a limit if

_{f 0}

L1(lI2).

It is usual to assume that

vibrations in a

physical

_system

cannot be infinite and so the

_frequencies

of

_{analogue signals}

are taken to be bounded above.

_Signals

with bounded

spectra

are called band-limited and have the

_{representation}

where W is the maximum

_frequency

_(strictly

_speaking

W is the

supre-mum of the

_frequencies,

a

_technicality

which is

_usually

_{disregarded).}

The

sampling

theorem

_gives

the

_following

formula for the reconstruction of a

band-limited

_signal

_f

with maximum

_frequency

W in terms of the discrete values or

_samples

f (k/2W).

For each t E

_1R,

The formula

₍₁₎

_corresponds

to a

_sampling

rate of 2W

_(often

called the

Nyquist

rate,

twice the maximum

_frequency

of the

_signall).

As well as its

significance

in information

theory

and

_engineering

[17],

the

theorem has a

_{long history}

and has been

_proved

_many

_times,

for

_example

by

E.

_Borel,

E. T.

_Whittaker,

V. A.

_{Kotel’nikov,}

K. S.

Krishnan,

H.

_Raabe,

I.

_Someya

to name a selection

(more

names can be found in the articles cited

below).

However,

Shannon was the first to

_appreciate

the

_significance

of the result in his fundamental and definitive papers

[23,

24]

on the

_theory

of

communication

_(more

details can be found in the _survey articles

[6,

8,

_10,

14]

and the books

_[15,

_21]).

The article

_[10]

establishes the

_equivalence

of the

sampling

theorem to

_Cauchy’s

theorem and includes other results from

analysis;

see

[16]

also for further results.

Whittaker

_proved

the result from the

_point

of view of

_{interpolation}

the-ory

[25]

and

essentially

established formula

(1)

for a class of

analytic

func-tions

_(which

he called the Cardinal function or

series).

This assumed

_given

values at

_regular

intervals and was free of

’rapid

oscillations’. As well as

the connection with

_{interpolation}

_theory,

there are also connections with

Paley-Wiener

theory

and Fourier

_analysis

_(for

_example

₍₁₎

is

_equivalent

to the Poisson summation formula and the result also arises

_surprisingly

often in other branches of mathematics

_[8,

_19,

_22]).

3. A

_{generalisation}

of Shannon’s

_sampling

theorem

The formula

₍₁₎

can be

_{proved using}

the observation that translates

[-W, W]

+

2Wk,

k E

Z,

of the

_support

_{[-W, W]}

of the Fourier transform

fA

of

_{f essentially}

tessellate III This leads to a multiband

generalisation

of

the

_sampling

theorem to functions

_f

with Fourier transforms which vanish outside a measurable set A that satisfies the

_disjoint

translates condition

This condition

_implies

that the

_Lebesgue

measure of A is at most

I /s

[11] (see §4).

For such functions

_f

a more

general

version of

Shan-non’s

_sampling

theorem holds.

Theorem 1. Let A be a measurable subset

_of

R and _suppose that there exists an s &#x3E; 0 such that

₍₂₎

holds. Let

_f

E be continuous and suppose that the Fourier

transform

f ^

of

f

vanishes outside A. Then

1 That a _signal can be reconstructed from _samples taken at this rate was referred to _by Shannon

and

_for

each t

_{e ll§}

where the series _converges

_absolutely

and

_uniformly.

A

_proof

of this theorem and further references to earlier results are

_given

in

_[11]

where the

_approach

is based on _square

_integrable

functions _{cp :} R -+ C

which vanish outside A. A more

_general

result for stochastic processes was

obtained

_by

S. P.

_Lloyd

who showed that the

_disjoint

translates condition

was

equivalent

to a random variable

_being

determined

by

a linear

combina-tion of the

_sample

values

_[20].

For a

_{generalisation}

of Theorem 1 to abstract harmonic

_analysis,

see

[1,

_12,

18].

P. L. Butzer and A.

Gessinger

note in

_[7]

that the formula

₍₃₎

with A =

(-W, W)

implies

the Shannon’s

sampling

theorem.

_Equally,

one can first _prove the formula

(1)

and then deduce

(3)

with s =

1/2W,

_as in

[24]

_or in the abstract harmonic

_analysis

version

[18].

When

_f

is not

_continuous,

_{convergence in} norm can be deduced from an

orthogonality

argument

[18].

A common

_approach

is to use the fact that

the set k E

_7G}

is an

orthogonal

basis for

L2(-W,W)

and that

for almost

_{all q}

E

_(-W,W).

The result follows on

_taking

the inverse

Fourier transform and

_observing

that _ak =

f (k/2W)/2W.

The form of

(4),

however,

suggests

convolution. This observation is the basis of the

_parallel

between the

_logical

structures of

_sampling

_theory

and Fourier

_analysis.

4.

_Spectral

translates

The set A considered here need not be an interval but _any measurable set such that distinct translates have null

_{intersection,}

_{i. e.,}

for each non-zero

The

_possibility

of A

_containing

unbounded

_frequencies

is not excluded. For this reason, the

Paley-Wiener setting,

although

closely related,

is not suitable.

The

_{translation -y}

H

_{y + kls}

can be

regarded

as an action

by

the additive

group

Z/ son

k Orbits or cosets =

Z}

are

_disjoint

and the

factor _group

_R/(Z/s)

has

_(0,1/s)

as a

_complete

set of coset

_{representatives}

where

_ka

is the

_{unique integer}

such that a +

_ka/s

E

_(0,1/s).

Then

_v(y)

is the

_unique

element in the orbit

_{+ 7}

which falls in

_(0,1/s).

Thus v is

well

_defined,

= and

The restriction _map

_viA:

A -

_(0,1/s)

is one-one almost

_{always by}

(5)

since

_v(a)

=

v(a’)

implies

that

a-a’

_E

Z /s.

The function

VIA

is translation

by

an

_{integer multiple}

of

1/s

and so

5.

_{Plancherel-type}

theorems and the

_{general sampling}

theorem When the set A satisfies

₍₅₎

for some s &#x3E;

_0,

the _map 1,: ~4 -~

(0,1)

_given

by

where

_fxl

= x -

[x]

is the fractional

_part

of x

(~~)

is the

_integer

_part

of

x),

is an

injection

which _preserves inner

products

for almost all a E A. If

IAI

=

1/s,

then _t is a

_bijection

for almost all a E A. Thus the set

_(which

will be denoted

_L2(A))

_{of cp}

E

_{with cp vanishing}

almost

_everywhere

outside A is

_isomorphic

to

_L~([0,1)).

In the case of Shannon’s

theorem,

the

_isomorphism

is

_simply

a

_rescaling.

When

1/s,

one can consider an

auxiliary

set A which satisfies

₍₅₎

with

_JAI

and 6:

h -

[0, 1)

an

_isomorphism

almost

_everywhere.

The natural

_embedding

of

L2(A)

(C

L2 (A) )

into

_{L 2([0,1))}

is

_why

results in

_{sampling theory}

are a mixture of

Fourier series and transforms.

Plancherel’s theorem asserts that the Fourier transform is an

_isometry

on

L (R) ;

(3)

also

implies

that the _{map p:}

L (R)

-3

£2(sZ)

_{given by}

where is the restriction of

_{f :}

to is also an

_isometry.

From

the

_point

of view of

_signals,

the norm can be

_regarded

as _{energy and the}

preservation

of norm can be

_interpreted

as conservation of energy between

the

_original

_signal

and its values

_(samples)

on sZ. The factor s is the time

interval between

_samples

and so

keeps

the dimensions of the two sides of

₍₃₎

consistent.

From now on the set A C R will be assumed to have

_{positive Lebesgue}

measure. The functions

f :

1R --i- C will be restricted to

_being

_continuous,

as otherwise

nothing

can be said about values on sets of measure zero. The

inverse Fourier transform

_{of cp}

E

L2(JR)

will be denoted

_by

_cpv,

_{i. e.,}

where if

_L1(JR),

_cp

is defined as the usual limit. If

IAI

_oo, then the

transform

_given

_by

is continuous. Let

for almost

_{all y / A}.}

The

_equivalence

of the null intersection translates condition to the

ana-logues

of the three classical results of Fourier

_analysis

is now stated

(a

proof

is in

_[2]).

Theorem 2. Let A be a

Lebesgue

measurable subset and s be a

positive

real number. Then the

_following

are

_equivalent.

(1)

For each non-zero

_anteger

k

where the _{series converges} to

_f

* _g

_absolutely

and

_uniformly.

Note that

_(II)

can

_regarded

as a

’hybrid’

version of the classical

Plancherel theorem since

_by

_(11),

and

_similarly

_(III)

and

_(IV)

are versions of the Parseval and convolution

theorems.

The

_proof

that

_(I)

_implies

_(II)

relies on

_going

a little

_deeper

and

con-sidering

the set

A

which contains A and has

_Lebesgue

measure

1/5,

to obtain the

_{orthogonality}

necessary for

(11).

The

proof

that

(II)

implies

(III)

is on the same lines as the standard treatment in functional

_analysis

in which Plancherel’s theorem is

_regarded

as fundamental and the _precursor

to Parseval’s theorem and the convolution theorem

_(they

are of course all

equivalent).

Recall that

_f

E is assumed to be continuous and that

fA

E vanishes almost

everywhere

outside A. Condition

_(I)

_implies

that

_1/s

but no

explicit

use is made of this in Theorem 2.

5.1. The reconstruction formula and the translates condition. The

equivalence

of the reconstruction formula and the translates condition fol-lows from Theorem

2;

the estimate

_1/s

_{implied by}

₍₁₀₎

is used

explicitly.

Lloyd

has

_proved

a similar but more

_general

result for

stochas-tic processes

[20,

Theorem

_1].

The

_necessity

of the translates condition is related to the

_phenomenon

of

_{’aliasing’}

_[5].

Theorem 3. Let A be a measurable subset

_of

R and s E Then the

followirag

are

_equivalent.

(I)

For each non-zero

_integer

k

(II)

lls

and

_for

each

_f

E

SA,

(III)

X’

E

_SA

and each

_f

E

_SA

is

_{given by}

where the series _{converges to}

_f

_absolutely

and

_uniformly.

Since

_1/s

_implies

that

(III)

follows from

_(II)

and so _XA E

L (R)

n L (R),

whence

_{x i}

is continuous and

_xi

E

_i.e.,

XA

E

_SA.

The

_{representation}

₍₄₎

now follows from

the

_hybrid

convolution theorem

_applied

to the

_equation

6.

_{Trigonometric}

_polynomials

Trigonometric polynomials

are the finite dimensional

_counterpart

of

square

integrable

functions. The version of Shannon’s

sampling

theorem for such functions is

_given

in

_[13]

and is as follows.

Theorem 4. Let

_{f :}

lE8 ~ ~ be

_1-periodic

and let

where _cn = 0

for

Inj

_&#x3E; 0. Then

The

_counterpart

of

_parts

_(I)

and

_(III)

of Theorem 3 is a more

general

form

of Theorem

_4,

which will be stated and

_proved

to illustrate the

_arguments

without

_analytic

technicalities.

Theorem 5. Let _{p, q} be

_positive

_integers,

let J =

{jI,... ,

jp}

C Z and let

where _cj = 0

for j §

J. Then the

following

are

_equivalent:

(I)

For each non-zero

_integer

_n,

.

where the inverse Fourier

_transforms

_X’

_of

_{Xj is}

_{given by}

Proof.

First

_(I)

_implies

_(II).

For

_{given m~Z,0~m~~20131,}

consider

Then

where

_{1p X p}

is the _p x _p unit matrix. But

_by

_(18),

when

_{k l ,}

and the formula in

_(II)

follows on

_substituting

for _c; in

(17)

and

_using

the

definition of

_Xvj.

Next

_(II)

_implies

_(I).

_{By definition,}

_fA

is

_{given by}

Each r E Z can be

_expressed

as r _{= p + nq,} for

_{unique n}

E Z and _p,

0

p q. Then since

f

satisfies

(19)

and since the Fourier transform of

f (t -

c)

is k E

_Z,

it follows that

Take

_f

=

Xv

_so that for each _{t E} R and k _E

_Z,

Now for k E

_J,

_Xj(k)

= 1.

Suppose

ko

=

lo

_{+ qno E} J. Then

Of course the coefficients cj could be determined

_by

solving

the _q linear

equations in p

(~ q)

unknowns but the

_{equal spacing}

of the

_samples

_m/q

and the

_incongruence

condition allows the use of the

simpler

Hermitian

conjugate

instead of

_solving

a

_system

of linear

equations.

Theorem 4 follows

by putting

J =

{-N,

... ,

N}

and p = q = 2N + 1.

To prove the

hybrid trigonometric polynomial analogue

of Plancherel’s theorem

_{(corresponding}

to

_part

_(II)

in Theorem

_3),

further consideration must be

_given

to the set J which has to be extended to a

complete

set J of residues mod q, so that

(J)

= _q. Since J C

J,

the Fourier transform

f

of the

1-periodic

function

_{f certainly}

also vanishes outside J. Consider

=

0, ... , q -

1 runs over a

_complete

set of residues modulo where _Jk i

-q and M =

(e21ri3km/q)

is _{a q} x _q matrix. The above

_argument

and the

Riesz-Fischer theorem

_give

The usual

_argument

_involving

the

_polarisation

_identity

can be used to _prove that this

_implies

_(II).

It is

_implicit

in Theorem 2 and 3 above that if the

_sampling

theorem holds for all functions

_f

E

_SA

with Fourier transform

_supported

_throughout

_A,

then the null measure translates condition holds and the

sampling

theorem

holds for each

_f

E

SA. However,

it is shown in

_[2]

that there exist sets A

7. Conclusion

Instead of the usual

_spectral

translates conditions

₍₂₎

or

(5)

in

frequency

space, the

hybrid

Plancherel theorem

(15)

can be

_regarded

as a basis for

the

_general

_{sampling theorem,}

_allowing

_{sampling theory}

to be

_given

a

log-ical structure similar to that of Fourier

_analysis,

with the

_hybrid

versions of Plancherel’s

theorem,

Parseval’s theorem and the convolution theorem at the centre

_(note

that the theorems must hold for all functions in

_S’A).

Thus in

_{sampling theory,}

each of the theorems in

_Figure

1 is

_{replaced by}

its

_hybrid

_version,

so that in this

_approach,

the

_theory

_begins

with the

hy-brid Plancherel theorem which

_by

Theorem 2 leads to and from the

_hybrid

Parseval theorem and the

_hybrid

convolution theorem. This leads

_by

The-orem 3 to the translates condition and to the

_general

_sampling

theorem. The translates condition and the

_{general sampling}

theorem lead back to the

hybrid

Plancherel theorem

_(15),

_completing

the

_equivalence.

In addition Shannon’s theorem

_together

with the finiteness of the measure of A

_imply

the translates

condition,

which in turn

_implies

the

_hybrid

Plancherel

theo-rem. The conventional view of

_{sampling theory}

would

_place

the translates

condition at the entrance of the

_garden.

As has been

_pointed

_out,

_providing

the

_sampling

interval s satisfies

_(5),

the formula

₍₃₎

can be

interpreted

as the energy of the

_original

_{signal being}

conserved in the

_samples

_(the

information is also

_conserved,

in the sense

that the

_{original signal}

can be recovered - in

_{principle -}

from the

samples) .

The

_step

function

_{approximation a:}

R - C to

_f

is

_{given by}

It is _{immediate that its energy}

and

_hence,

_{providing s}

satisfies

_(5),

Thus the _energy of the

_original

_signal

and that of a are the _same,

_although

the

_support

of

~^

is R

_(for

non-zero

signals)

and so contains A. Moreover

the information is

_preserved

as

_{well, again}

in the sense that the

_original

signal

can be recovered in

_principle

from the values of ~.

_However,

for a

_given

_signal,

conservation of _energy alone is not sufficient to allow its

complete

reconstruction

_using

the

_sampling

formula

_(4).

Shannon’s theorem can be viewed as the result of

_passing

a train of

an ideal

_low-pass

filter. In

practice, however,

perfect impulses

and ideal

filters do not exist and the theorem cannot be

_implemented;

thus the for-mula

₍₁₎

is not often used

directly.

For

_example,

_{digital-to-analogue}

con-version in

_signal

_{processing replaces}

the

_weighted

_impulses

indicated

_by

the theorem with a

_step

function in which successive

_steps

have

amplitude

of successive

sample

values. The

_step

function

approximation a

is used in

_passing

from a

_{digital signal}

to an

analogue signal

_aA =

produced by

filtering

out all

_frequencies

_except

those in A

_(see

_[4]).

This reduces the energy of the

signal

but when A is an interval

_symmetric

about

the

_origin,

Shannon’s

_sampling

theorem can be used to show that that the

error is

_negligible

when exceeds the

_Nyquist

rate.

Placing

the

_sampling

theorem in the abstract harmonic

_{analysis setting}

reveals more

clearly

the

_underlying

_group

_structure,

the

_reciprocal

character

of the discrete

_{sampling subgroup}

and _{the discrete group of}

_translates,

as

well as the

relationship

between the

_support

of the Fourier transform and

the

_sampling

interval

_[1,

_3,

_12].

8.

_{Acknowledgements}

Thanks are due to Jean-Paul

_Allouche,

_Christophe

Doche and

Jean-Jaques

Ruch for

_organising

a _very

_interesting

and

_{enjoyable colloquium}

in honour of

Michel,

a

gifted

mathematician of

_great

humanity

and

abili-ties,

with a

_gentle

wit and interests wider than

_simply

mathematics. I am

grateful

to him for his interest in this

_topic.

I am also

grateful

to Michael

Beaty

and Rowland

_Higgins

for _many

_helpful

_discussions,

to a

commend-ably

thorough

referee and to Simon Kristensen for

_making

the

_figure

so

much better.

References

[1] M. G. _BEATY, M. M. _DODSON, Abstract harmonic _analysis and the _sampling theorem. In

Sampling theory in Fourier and _{signal analysis:Advanced topics (eds.} J. R. _Higgins and R. L.

Stens), Oxford University Press, 1999, 233-265.

[2] M. G. _BEATY, M. M. DODSON, Shannon’s _{sampling theorem,} Plancherrel’s theorem and

spectral translates, preprint, University of _York, 2002.

[3] M. G. _BEATY, M. M. _DODSON, Shannon’s _sampling theorem and abstract harmonic _analysis,

preprint, University of _York, 2002.

[4] M. G. BEATY, M. M. DODSON, J. R. _{HIGGINS, Approximating Paley-Wiener functions by}

smoothed _{step functions.} J. _{Approx. Theory} 78 _(1994), 433-445.

[5] M. G. _BEATY, J. R. _{HIGGINS, Aliasing} and Poisson summation in the _{sampling theory of}

Paley-Wiener spaces. J. Fourier Anal. Appl. 1 _(1994), 67-85.

[6] P. L. BUTZER, A _{survey of} the Whittaker-Shannon _sampling theorem and some _of its

ex-tensions. J. Math. Res. Exposition 3 _(1983), 185-212.

[7] P. L. BUTZER, A. GESSINGER, The approximate sampling theorem, Poisson’s sum _formula, a decomposition theorem for Parseval’s equation and their interconnections. In The _Heritage of P. L. _Chebyshev: a Festschrift in honor of the 70th _birthday of T. J. Rivlin, Ann. Numer. Math. 4 _(1997), 143-160.

[8] P. L. _BUTZER, M. HAUSS, R. L. STENS, The _sampling theorem and its _unique role in various

[9] P. L. BUTZER, J. R. HIGGlNS, R. L. _{STENS, Sampling theory of signal analysis.} In:

Devel-opment of mathematics _{1950-2000, Birkhäuser,} Basel, 2002, 193-234.

[10] P. L. BUTZER, G. _SCHMEISSER, R. L. STENS, An Introduction to Sampling Analysis. In:

Nonuniform _{Sampling, Theory} and Practice _(ed. F. _Marvasti), Kluwer _{Academic/Plenum}

Publishers, New York, 2000, Chapter 2, 17-121.

[11] M. M. DODSON, A. M. SILVA, Fourier analysis and the _{sampling theorem,} Proc. _Royal Irish Acad. 85A _(1985), 81-108.

[12] M. M. DODSON, A. M. SILVA, V. SOUCEK, A note on Whittaker’s cardinal series in harmonic

analysis. Proc. Edinb. Math. Soc. 29 _(1986), 349-357. [13] S. _{GOLDMAN, Information Theory. Dover,} New York, 1968.

[14] J. R. _HIGGINS, Five short stories about the cardinal _series, Bull. Amer. Math. Soc. 12 (1985), 45-89.

[15] J. R. HIGGINS, Sampling theory in Fourier and _{signal analysis:} Foundations. Clarendon

Press, Oxford, 1996.

[16] J. R. HIGGINS, G. _SCHMEISSER, J. J. _VOSS, The _sampling theorem and several equivalent

results in analysis. J. _Comput. Anal. _Appl. 2 ₍₂₀₀₀₎ 333-371.

[17] A. J. JERRI, The Shannon _sampling theorem - its various extensions and _{applications:} a

tutorial review. Proc. IEEE 65 (1977), 1565-1596.

[18] I. KLUVÁNEK, Sampling theorem in abstract harmonic analysis. Mat.-Fyz.

Gasopis

Sloven. Akad. Vied. 15 _(1965), 43-48.

[19] K. S. KRISHNAN, A simple result in _quadrature. Nature 162 _(1948), 215.

[20] S. P. _LLOYD, A _sampling theorem _{for stationary (wide sense)} stochastic _processes. Trans.

Amer. Math. Soc. 92 _(1959), 1-12.

[21] R. J. MARKS II _(ed.), Advanced _topics in Shannon _sampling and _{interpolation theory.}

Springer-Verlag, New _York, 1993.

[22] Q. I. RAHMAN, G. _SCHMEISSER, The summation _{formulae of Poisson, Plana,} Euler-Maclaurin and their relationship. J. Math. Sci. 28 _(1994), 151-171.

[23] C. E. SHANNON, A mathematical _{theory of} communication. Bell System Tech. J. 27 _(1948),

379-423, 623-656.

[24] C. E. SHANNON, Communication in the presence of noise. Proc. IRE 37 _(1949), 10-21. [25] E. T. WHITTAKER, On the _functions which are _{represented by} the expansions of the

inter-polation theory. Proc. _Roy. Soc. _Edinburgh, 35 _(1915), 181-194. Maurice M. DODSON Department of Mathematics University of York York Y010 5DD United _Kingdom E mail : _{mm.d1Iyork.ac .} uk