Cheeger
Sets
for Unit Cube: A
Numerical Solutions for L' and
£2norms
by
Mohammad Tariq Hussain
Submitted to the School of Engineering
in partial fulfillment of the requirements for the degree of
Master of Science in Computation for Design and Optimization
at the
MASSACHUSETTS INSTITUTE OF TECHNOLOGY
February 2008
@
Massachusetts Institute of Technology 2008. All rights reserved.
Author .
School of Engineering
January 18, 2008
Certified
by...
...
Gilbert Strang
Professor of Mathematics
Thesis Supervisor
-Accepted by.
... .. ..
Jaime Peraire
Professor of Aeronautics and Astronautics
Codirector, Computation for Design and Optimization Program
MAss ACHSEIN
Cheeger Sets for Unit Cube : Analytical and Numerical
Solutions for
L'
and
L
2norms
by
Mohammad Tariq Hussain
Submitted to the School of Engineering
on January 18, 2008, in partial fulfillment of the
requirements for the degree of
Master of Science in Computation for Design and Optimization
Abstract
The Cheeger constant h(Q) of a domain Q is defined as the minimum value of
IIDII/|DII
with D varying over all smooth sub-domains of Q. The D that achieves
this minimum is called the Cheeger set of Q. We present some analytical and
nu-merical work on the Cheeger set for the unit cube (Q E [-0.5,0.5]3 E R
3) using
the LY and the L2 norms for measuring |IDII. We look at the equivalent max-flow
min-cut problem for continuum flows, and use it to get numerical results for the
prob-lem. We then use these results to suggest analytical solutions to the problem and
optimize these shapes using calculus and numerical methods. Finally we make some
observations about the general shapes we get, and how they can be derived using an
algorithm similar to the one for finding Cheeger sets for domains in R
2Thesis Supervisor: Gilbert Strang
Title: Professor of Mathematics
Acknowledgments
I would like to thank my advisor, Professor Gilbert Strang, for suggesting the problem
and for his time and guidance. I would also like to thank my friend, Faisal Kashif, for the discussions and suggestions at different stages of the thesis. Finally I like to thank my parents for being there for me and for supporting me at all times. This thesis would not have been possible without the help of all of these people.
Contents
1 Introduction 7
1.1 Cheeger sets . . . . 8
1.2 Existing work . . . . 9
2 Extension of work for
R2
11 2.1 Simple extension for the L' norm . . . . 132.2 Simple extension for the £2 norm . . . . 14
2.3 A more intuitive approach for the £2 norm . . . . 17
3 Numerical Solutions 19 3.1 Max-flow min-cut problem . . . . 20
3.2 Discretization of the problem . . . . 21
3.3 Time and memory considerations . . . . 23
3.3.1 Changes . . . . 24 3.3.2 Improvements . . . . 25 3.4 R esults . . . . 26 3.4.1 Results for c . . . . 26 3.4.2 Results for £2 . . . . . . . . 27 4 Analytical Solutions 31 4.1 Analytical Solution for the L£ norm . . . . 31
4.1.1 General Shape . . . . 31
4.1.3
Comparison of Numerical and Analytical Solutions . . . .
34
4.2 Analytical Solution for the
L
2norm . . . .
36
4.2.1
G eneral Shape . . . .
36
4.2.2
O ptim ization . . . .
40
4.2.3
Comparison of Numerical and Analytical Solutions . . . .
42
4.3 Similarities between Lo and
L
2Cheeger sets . . . .
42
5 Conclusion 45
5.1
Future W ork . . . .
46
List of Figures
1-1 Optimal shapes for problem (1.1) for S E R2 using different norms . 8
1-2 Optimal shapes for problem (1.2) for the unit square . . . . 9
2-1 Extending optimal shape for £' norm . . . . 13
2-2 Optimal shape for general shape (2.6) . . . . 15
2-3 An unintuitive approach to extending the L2 results from R2 . . . . . 16
2-4 A more intuitive approach to extending the L2 results from R2 . . . . 18
3-1 Discretization grid with flows u, v and w . . . . 21
3-2 Numerical results for Cheeger set for L' norm . . . . 28
3-3 Convergence of Numerical results for Cheeger set for L2 norm . . . . 29
3-4 Numerical results for Cheeger set for L2 norm . . . . 30
4-1 General shape (2.6) . . . . 32
4-2 Optimal shape for general shape (4.1) . . . . 35
4-3 Comparison of numerical and analytical solutions for L . . . .. 35
4-4 Constructing general shape for f2 . . . . . . . . 36
4-5 General shape for L2 . . . . 38
4-6 Corner D etails . . . . 38
4-7 Projection of corner on xy-plane . . . . 40
4-8 Optimal shape for £2 ... 41
4-9 Comparison of numerical and analytical solutions for £2) . . . . 42
4-10 Two approaches for . . . . . 43
Chapter 1
Introduction
The unconstrained isoperimetric problem for a set S is defined as maximizing the
value of ||S1I for a given value of 110S11, or equivalently minimizing |10S11 for a given
||S||.
Unconstrained isoperimetric problem
min
for
f8S1|
= L.
(1.1)
||S|
For R2 this means maximizing the area
fiS|
for a given perimeter 11&Sfj = L. Theoptimal shape S that achieves this depends on the norm being used to measure the perimeter. Strang
[7]
uses the calculus of variations to prove a know result, that the optimal S is a rotated ball |t(x,y)'|ID< R,
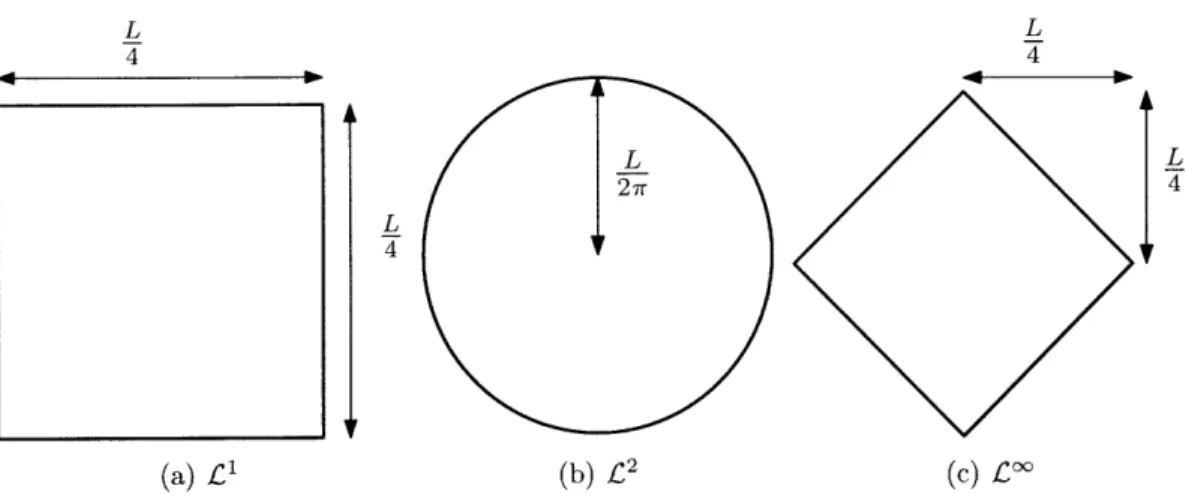
in the norm dual to the norm that defines the perimeter. Figure 1-1 shows the optimal shapes for the unconstrained isoperimetric problem for the L1, L2 and the L norms.What happens if we remove the "constraint" of fixed ||&S1| and instead require that S lies in a domain Q? The constrained isoperimetric problem for a domain Q is defined as minimizing the ratio of 18S1 to |ISf for all possible S C Q.
Constrained isoperimetric problem min for S c Q. (1.2)
L L
4 4
27r 4
L
(a) £1 (b)
L2
(c) LFigure 1-1: Optimal shapes for problem (1.1) for S E R2 using different norms
which can be solved numerically.
1.1
Cheeger
sets
The Cheeger constant h(Q) of a domain Q is defined as:
h(Q) := infll&DII (1.3)
D
IIDII
with D varying over all smooth sub-domains of Q whose boundary OD does not touch
(Q and with
II&DII
and |ID|I denoting (n - 1)- and n-dimensional Lebesgue measureof DD and D (Kawohl [4]). Kawohl [4] proves that for Q C R2 with Q convex and non-empty, there is a unique convex optimum D which can be computed by algebraic algorithms. Kawohl and Lachand-Robert present one such algorithm in [3].
For Q c R2, the unique D that attains the infimum is called the Cheeger set of
Q. The Cheeger constant h(Q) provides a lower bound A, > h2/4 for the Laplace-Dirichlet operator on Q [7]. This is also the value to which the first eigenvalue of Ap(Q) of the p-Laplacian converges to as p -- 1 [4]. Ionescu and Lachand-Robert present an
interesting application of the Cheeger problem in landslides modeling. Appleton and Talbot [1] use the dual problem to the Cheeger problem to study image segmentation with medical applications.
rR
D l=1 D l=1-2r D l=1-2R
R
JD|1 = 4 |DDI = 41 ± 2,rr |aDIC = 41 + 4R
(a) ,L (b) L2 (c) LO"
Figure 1-2: Optimal shapes for problem (1.2) for the unit square
1.2
Existing work
There is extensive work on Cheeger sets and constants for Q C R2. As mentioned above, Kawohl [4, 3] discusses the existence and uniqueness of the Cheeger set for convex, non-empty Q C R2 and also provides an algebraic algorithm for calculating the Cheeger set for such planar Q.
In this thesis, we focus on the Cheeger set for a unit cube (Q = [-0.5, 0.5]3
C
R3)using different measures of I|D 11, and so we are more interested in the different Cheeger sets (in different norms) for the unit square, rather than the Cheeger sets for general convex shapes. The Cheeger problem, for the unit square, then becomes
Minimize and
IOD11
2 andIJD~
(1.4)DC[0,112
I|DII
nDdIIDI
Strang [8] presents the minimum cuts which solve the Cheeger problem for the unit square in different norms. The results are reproduced here in Figure 1-2.
The first thing we notice about the Cheeger sets above is that in all cases the optimal D touches the boundary &Q of the square. The proof for this is trivial and is reproduced here. Assume that a shape D that does not touch the boundary 8Q is optimal. This shape can be scaled by a factor c > 1 so that it now touches the
boundary. For this new shape, the areas in the denominators of (1.4) are multiplied
by c2
off' the corners of the square. This is a special case of the algorithm to find the Cheeger set for any planer convex domain Q presented by Kawohl [3]. The algorithm in [3] only considers measurement of ||OD1| in the L2 norm, and Strang
[7]
mentions how the optimal shape in Figure 1-2(b) can be created by taking a isoperimetrix' (see Figure 1-1(b)), scaling it by an optimal scaling factor a < 1 and fitting its four pieces in the four corners of the square. We leave it to the reader to see how the same "rule" can be applied to get Figure 1-2(a) and 1-2(c) using the isoperimetrix in Figure 1-1(a) and 1-1(c) respectively.Lippert [14] used numerical methods to find a close approximation to the flow that fills the minimal cut and as a by-product of this exercise also calculated the Cheeger set (and constant) for the unit square for both the L' and the L2 norms. Lachand-Robert and Oudet [11] present a convex hull approach, a mixture of geometrical and numerical algorithms, to solve optimization problems on the space of convex functions and use their method to find the Cheeger set (in the L2 norm) of different shapes in
R3, including the cube.
In this thesis we work on the numerical and analytical solutions to the Cheeger problem (1.2) for the unit cube (Q = [-0.5, 0.5]3 C R3). We look only at the £" and
the L2 norms; the solution for the £l norm is trivial, consisting of the entire cube
similar to the results in Figure 1-2(a).
Chapter 1 provides a background of the work that formed the basis for the work in this thesis. Chapter 2 presents a simple extension of the results for the unit square (Figure 1-2). Chapter 3 mentions how the Cheeger problem can be converted to a continuum optimal flow problem, which can then be discretized and solved numeri-cally. Chapter 4 then uses the results from the numerical solutions from Chapter 3 to propose analytical solutions that approximate the numerical solutions and Chapter 5 provides a summary of the results and the conclusion.
Chapter 2
Extension of work for
R
2
We look at the constrained isoperimetric problem (1.2) for the unit cube with Q =
[-0.5, 0.5]3
c
R3. Unlike the R2 case, it is not known whether the optimum set D CQ
is unique or convex, even with Q C Rn convex for n > 3. However Q convex implies that there exists at-least one convex optimum [2]. Lachand-Robert and Oudet [11] use a convex hull approach to calculate an approximation of a convex optimum when
Q C R' is convex, and call it the Cheeger set of Q. We will use the term Cheeger set
for Q
c
R3 in a similar context.
So what does the constrained isoperimetric problem and the Cheeger set translate to for the unit cube in R3? The Cheeger problem (1.4) now changes to
Minimize
1DI
2and
aDoo(2.1)
DC[-0.5,0.5]3 ||D
II
||DI|
||DI in the denominator in (2.1) is the volume of the shape
D.
|I&D11
2and |0DII|
in the numerator in (2.1) refer to the surface area of the shape D, measured in the appropriate norm. So the Cheeger problem (2.1) for Q = [-0.5,0.5]3 C R3 is simply
finding the shape D C Q that minimizes the ratio of the surface area to the volume [11].
Surface area in the L' norm : From calculus we know that the surface area A of a smooth surface
E
with domain R is defined as :A
=JJ
|n(u,v)|| du dv
R(2.2)
For the surface E defined by z = f(x, y), and using x and y in place of u and v
respectively, we have :
&(y,
z)
a(x, y)'
n(x,
y)-
(X, y)
( , y)'
= 1,(z, x)
(x, y)
(2.3) =(1,
z, zY)For the
I1n(x,
y)
1
in
the L' norm, we have :
Iln(x,y)lKo = max{1, Izx|, zyI}
and (2.2) simplifies to :
A
=JJn(u,
v)IK
du dv
=R
iI
Rmax{1, Izxf, zyj} dx dy
Similarly, for the |1n(x, y) 1 in the L2 norm, we get :
A
J
JIn(uv)1|2
dudv
=R
S1+z2
+ zY2 dx dyR
We will use (2.4) to calculate the surface area for the analytical solutions for the L' norm. It should also be noted that for the volume, we have |DI1
1
= ||D1|2 = ||D1|00,and so we can use standard geometry to calculate the volume in any norm.
(2.4)
(2.5)
Oz Oz
(a) General Shape
Figure 2-1: Extending optim
R1 X Y + Z= R1 (z =0.5) (b) Projection on
shape for L' norm
2.1
Simple extension for the
L'
norm
We first look at the Cheeger set for the unit cube in the L" norm, and try to extend the results for the square (see Figure 1-2(c)). The most obvious extension to the "cutting-off' of the corners of the square is cutting off the corner of the cube resulting in an optimal shape defined by :
D={(x, y,z)} with
{lxi
<0.5,
Iyj
< 0.5,
IzI
< 0.5 and
JxJ + Jyj + Iz i <a -3a E [1, 1.5]
(2.6)
Figure 2-1(a) shows Dn [0,
0.5]1,
the part of the shape in the positive octant only.
We will use the area and volume from this shape to calculate the value of a that minimizes the ratio of surface area to volume. Due to symmetry, the total volume and total surface area of the optimal shape D will both be 8 times these values and hence the ratio remains the same. Figure 2-1(b) shows the projection of the shape onto the xy-plane. We see two distinct regions, with :
(0.5
z
=f(x,y)
= .y
a - x - y(x,
y) inR
1 (x, y) in R2 a) xy-planeNow the (relevant) surface area of this shape, including the planes x = 0.5 and
y = 0.5, is given by :
Surface Area = 3
max{1,1
z,
1z}
dx dy +
fmax{,IzxI,
jzy
}
dxdy
R1 R2
= 3
max{1,
0,
0} dx
dy +
fmax{1,
1,
1} dx dy
R1 R2= 3J 1 dx dy +
ffI
dxdy
R1 R2 = 3(Area of R1)
+ Area of R2= 3a
-a
2 -1.5
The volume of the shape can simply be calculated using geometry as
Volume
=0.5
-(1.5
- a)2(1.5 -a))
(2.7)
(2.8)
Now the ratio Q(a) of the values in (2.7) and (2.8) is to be minimized over 1 < a < 1.5. This was done using numerical methods and the results are shown in Figure 2-2(a). We see that a = 1 minimizes Q(a) giving a ratio of 4.8. The optimal shape (for a = 1) is shown in Figure 2-2(b). The unit cube (transparent) is shown overlapping the optimal shape. We should mention that we will find a better ratio using a different shape in Section 4.1.2.
Note : As a side note, we tried using the L' norm (I|n(u, v)I1i instead of |!n(u, v)II1") in (2.7) and the optimal value of a turned out to be 1.5. For the general shape (2.6), this means that we get the entire cube as the optimal D. This result is similar to the
L case for the unit square (see Figure 1-2(a)).
2.2
Simple extension for the L2 norm
Now we attempt to construct the general shape of the Cheeger set for a cube with
[aDO
(the surface area) measured in the L2 norm. We do this by extending theQ(a) vs a
1.08 1.1 1.15 1.2 lOS
(a) Q(a) vs a
(b) Optimal D for a = 1
Figure 2-2: Optimal shape for general shape (2.6)
5.5
'
Minimum
5
(a) A playing dice (b) Trying to replicate the corner (c) Minimal area
cov-of dice ering the broken corner
Figure 2-3: An unintuitive approach to extending the 12 results from R
2results for the square with perimeter measured in the L2 norm (see Figure 1-2(b)).
We first present an approach which is very close to the approach applied to the L*
norm, but which results in a very unintuitive shape for the Cheeger set. Just as in
Figure 2-1(a) the corners of the cube were "cut-off', for the
2norm, we can think
of using sand-paper to "round-off" the corners of a cube.
A physical example of this can be seen in playing dice (see Figure 2-3(a)). Figure
2-3(b) shows an analytical shape that tries to replicate the corner of the dice. In that
shape, the relevant corners of the 3 squares that meet at (0.5, 0.5, 0.5) have been
"rounded-off' and have been replaced by a quarter of a circle each. Notice that the
shape in Figure 2-3(b) has a "hole" in the corner that still needs to be "covered".
One approach to covering this would be to use a surface that minimizes the area.
Brakke's Surface Evolver' is a free tool used for modelling how liquid surfaces change
shape because of various forces and constraints. It can be used to find the surface
that minimizes the total surface tension (and hence the area) of a surface between a
wire-frame. Figure 2-3(c) shows the results of evolving (100 iterations) the original
corner of the cube with the 3 quarter circles as the constraints/wire-frames.
We leave this shape here and do not pursue this approach any further. We will
however revisit this shape in Section 4.3.2.3
A more intuitive approach for the
j2norm
We now present a more intuitive approach to extending the L2 results for the unit square (see Figure 1-2(b)). Remember that the shape in Figure 1-2(b) could be constructed by dividing a scaled version of the unit ball in the L2 norm (a circle) and fitting the four pieces in the four corners of the square.Similarly for the unit cube, we take a sphere (of radius r < 0.5), divide it into eight parts and fit the parts into the eight corners of the cube. This also requires us to "round-off" the edges of the cube by replacing them with quarter cylinders each of radius r. Figure 2-4(a) shows the general shape, again only for the positive octant.
This time finding the surface area and the volume is a much easier task, and we use simple geometry to find the two in terms of the radius r. The surface area of the complete shape is given by :
Surface Area = 6(Area of top surface)
+
8(Area of spherical corner)(2.9)
+ 12(Area of cylindrical edge)
= 6 + 8(-r2
2 -3r2) + 2)12( 1r(1
2 -2r)
-2r(1
-2r))
Similarly the volume is given by :
Volume =1 + 8(
1rr3
- r3) + 12(1wr2 - r2)(1 - 2r) (2.10)6 4
Now we need to minimize the ratio
Q(r)
of surface area (2.9) to the volume (2.10) over 0 < r < 0.5. This was done using numerical methods and the results are shown in Figure 2-4(b). We see that r ~~ 0.26 minimizesQ(r)
giving a ratio of 5.396778. The optimal shape (for r ~ 0.26) is shown in Figure 2-4(c). The unit cube (transparent) is shown overlapping the optimal shape. Again, we will find a better ratio using a different shape in Section 4.2.2.11
5.8 5.6 5.5 5.4 0(a) General Shape
Q(r) vs r
0.5 0.1 0.15 0.2 0. 0 3 1.5
(b) Q(r) vs r
(c) Optimal Shape for r ~ 0.26
Figure 2-4: A more intuitive approach to extending the £2 results from R2 0.3 0.4 0.45 i
Chapter 3
Numerical Solutions
Continuum flow problems are the continuous analog of the discrete network flow problems. In the discrete case, an undirected network consists of a set N of nodes and a set E of edges. Each edge has a positive capacity c,, > 0 and a feasible flow
through the edge cannot exceed the capacity of the edge. In addition to this we have conservation of flow at each node, with "flow-in=flow-out". We generally also have one or more "source" and one or more "sink" nodes. A flow through the network is defined as a set of flows on the edges. A feasible flow will fulfill the capacity constraints on edges as well as the flow conservation for each node including the source and the sink nodes.
In the continuum case, instead of being defined as a set of nodes and edges, the "network" is defined as a closed set Q C R'. The flows are given by vector fields in Q [12, 14, 6,
8].
E.g. forn
= 3 the flow would bef=
(fi(x, y, z),f
2(x, y, z), f3(x, y, z)).The conservation of flow constraints translate to equality conditions on the divergence of the flow:
Conservation of flow V - f= S (3.1)
for every point in Q. Here S represents the sources and sinks in the domain Q. Similarly the capacity constraints translate to
for every point in Q. Here C represents the capacity over the domain Q, and 11ffl represents the magnitude of the flow in the appropriate norm. E.g. for n = 3, if the magnitude of the flow is measured in the L& norm, (3.2) changes to
Illo1
00=
max{ifit,
if2L,1f3}
Cfor every point in Q.
3.1
Max-flow min-cut problem
For the general (discrete) network defined at the start of this chapter, let s and t be the source and sink nodes respectively (it is easy to show that a network with more than one source or sink nodes can be converted to a network with exactly one source node and exactly one sink node, e.g. see
[15]).
The max-flow problem seeks to find the maximum amount of flow that can be sent from s to t while maintaining flow conservation at each node and the capacity constraints on each edge (see [13, c. 6] for more details).Suppose we divide the nodes in the network into two disjoint sets S and T with
S E S, t E T and S U T = N. The capacity of this cut is defined as the sum
of the capacities of the edges which cross it. The min-cut problem seeks to find, among all possible s-t cuts, the cut with the minimum value. Ford and Fulkerson [10] demonstrated that the maximal s-t flow in a network equals the minimal s-t cut in the network.
Strang [6, 8] and Iri [12] describe the maximal flow and the minimal cut problems for continuous flows. For the continuous case the maximum flow problem is
max t: V - f= tS and 1ifi C (3.3)
t,f
If we take the source S to be a net unit source, then t gives the total net flow out of Q via
f
[14, 6]. So, in this case, (3.3) is just maximizing the total amount t of floww - -
1-V
U
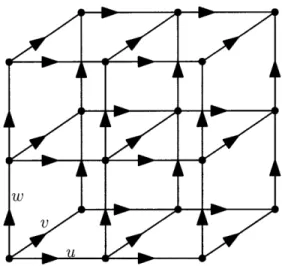
-Figure 3-1: Discretization grid with flows u, v and w
Iri [12] showed that, under very general continuity assumptions, the maximal flow is strictly equal to the minimal surface. For such a flow and surface, the flow saturates the surface uniformly. Strang [7, 8] shows how, for a net unit source S, the minimal cut is the same as the Cheeger set for Q and Grieser [5] mentions that the Cheeger constant h(Q) (see (1.3)) is equal to the optimal t that satisfies (3.3).
3.2
Discretization of the problem
Appleton and Talbot [1] have proposed an algorithm for computing the maximum flow vector
f
from a sequence of discrete problems. Lippert [14] approximates the problem by a (discrete) problem in linear optimization (with quadratic constraints for the £2 norm). Both use the same discretization step, and we use an extension ofthe discretization used in [14].
We discretize
f
= (u, v, w) into a "3D grid" over the domain Q (the cube). Wedivide the cube into N equal parts along the 3 axis. This gives (N + 1)3 distinct nodes. The flow is now considered along the edge between two consecutive nodes (see Figure 3-1). This leads to the primary variables Ui,j,k, Vi,j,k and Wi,j,k defined
These discrete flows are subject to the flow conservation :
Ui,j,k - Ui-1,j,k Vi,j,k - Vi,j-,k Wi,j~k - Wi,j,k-1
s
AX + Ay + Az - Si ,j,k
(3.4)
We also need the discrete flow f,j,k at any given point to satisfy the capacity
con-straints
Appleton and Talbot [1] and Lippert [14] use two different ways to handle this con-straint. The magnitude of the discrete flow at any given point can be obtained by considering the following approximations to the flow near a vertex.
f,7PP=
(UiJlki Vij~k, Wij,k)fJ7
=~ (U-1J,k, Vij,k, WiJ,k)to participate in the algorithm. As Lippert points out, for our case, we are only
interested in the maximum magnitude
[141
and so we define the magnitude of the flow at a point as:~fi,j,kII
= max{Iif-, lfII, l iI,| 7 , lf77[II, lf7f"Ii,Iff"II, If2gI}
(3.5)max-flow problem as follows :
Maximize t
Subject to Ui,j,k - Ui-ljk + V ,jk - Vi,j1,k + Wi,j,k - Wij,k-1 tSio,= 0
A~X Ay AZtiik
j k Kui-,j,k,i,j-1,kw i,j,k-) I 1
V
(i, j,k) E [1,
N]3with bounds 0 < t
-00 < Ui~k < oo, V(iJ, k) E
[0, N] x [1, N] x [1, N]
-00 < V < oo, V(i, j, k)C
[1,
N] x [0, N] x[1, N]
-00 <Wik < o, V(i, j, k) E [1, N] x [1, N] x [0, N]Here i(ui,j,k, Vij,k, wi,Jk)1 in the capacity constraints is to be measured in the
"ap-propriate" norm. Since finding the Cheeger set of a domain Q is identical to finding the minimum cut of Q, and the maximum flow problem is the dual of the minimum cut problem, so the "appropriate" norm for the flow is actually the dual of the norm used to find the Cheeger set (see [6]).
This means that for the Cheeger set in the L' norm, we will need to use the dual norm, the L1 norm, in the capacity constraints in the discretized problem. So, for the Cheeger set in the L£ norm, II(ui,J,kvi,jk,wiJ,k)WJ1
<
1 will give lui,J,k + IVi,j,kI +Iwi,kJ~j
< 1 and so on. This is a simple linear programming problem with linearconstraints.
Since the L2 norm is dual to itself, so for the Cheeger set in the £2 norm,
(Ui~J,k, Vi,,kiWiJ,k)2 < I will become u 2, , k + W2 < 1 and so on. This is
a quadratically constrained problem.
approximately 3N3 variables (of the form Uij,k, Vi,j,k and wij,k) and approximately
9N 3 constraints, for the problem in the L2 norm. However for the L' norm, the number of variables and constraints is larger because of the type of constraints that the Cplex/MOSEK input file formats allows. This means that even for a small N like 100, we have about 3 million variables and about 9 million constraints! It is certainly not feasible to try solving such huge problems even on commercial software
like Cplex.
3.3.1
Changes
Below we mention how we use the symmetry of the problem to make some simple modifications to the problem, making it smaller for any given N (unfortunately, the size of the problem still grows as O(N)). These changes apply to the problem in either norm.
1. The problem is symmetric about the x-, y- and the z-axis and so the first and
most obvious modification is to look at only the problem in the positive octant (like we have done in the numerical case). This does require us to define the boundary conditions, and due to the symmetry of the problem, we can see that along the z-axis, the flow in the z direction has to be zero (and similarly for the other two axes). This immediately reduces the value of N, required for any given resolution of the solution, to half, thus reducing the number of variables and constraints by a factor of 8.
2. The problem is also symmetric in the x, y and z directions, and so we can
replace Vi,j,k by Uji,k and Wi,j,k by Ukj,,. This reduces the number of variables
by a factor of 3. We call this formulation "Formulation 1" in the comparisons
below. We did not try to solve any formulations of the problem without the first two changes.
3. Now, we have only the variables in u. For these we can further decrease the
flow in the x direction and so u is symmetric in the y and z directions (also, using the relations in the previous point, we see that Ujjk = VJ,i,k W,k,i W = Uikj).
Thus replacing Ui,j,k by Ui,k,j Vj > k, we can further reduce the number of
variables by a factor of about 2.
4. The final step involves removing all the redundant constraints produced because of the replacements of variables above. This step does increase the time of the generation of the Cplex input file, but that is countered by the fact that this allows us to load and solve larger problems (meaning larger N) in Cplex. We refer to this formulation as "Formulation 2" below.
3.3.2
Improvements
The changes mentioned in the previous section lead to improvements in the following areas of the problem solution.
As mentioned above, these changes directly reduce the number of variables by a factor of 6, and the number of constraints by a factor of about 5.5. E.g. for the L2 problem with N = 50, Formulation 1 results in a total of more than 1 million
constraints, which are reduced to less than 0.2 million for Formulation 2. This directly effects the size of the input file that is generated by a similar factor. E.g The size of the generated input file for the L2 problem for N = 50, dropped from around 85MB to only 15MB when switching from Formulation 1 to Formulation 2.
The difference in file size then has a much larger effect on the time it takes for Cplex to load/read the problem. E.g. for the L2 problem with N = 50, the time it took Cplex to read the problem from the input file jumped from close to 5 minutes for Formulation 1, to under 10 seconds for Formulation 2.
Finally, there was also a gain in the time Cplex took to actually solve the problems.
E.g for the £L problem for N = 30 the solution time dropped from just under 5
minutes to 1 minute when switching from Formulation 1 to Formulation 2. The corresponding times for the norm for N =
considerable effect for larger N, keeping in mind that for N = 50 , Cplex took slightly less than 45 minutes to solve the L2 problem. This was for Formulation 2; for the same problem in Formulation 1, Cplex gave an out-of-memory error even before starting any iterations for the calculation of the solution.
Note : All stats mentioned above for the problem in the Ll norm are for the barrier
method in Cplex. The simplex method was extremely inefficient compared to the barrier method. E.g. for N = 20 (using Formulation 2), the Cplex simplex method took more than 12 minutes to find the optimal solution. The barrier method, however took less than 6 seconds to solve the same problem.
3.4
Results
The linear and quadratically constrained problems defined above were solved using MOSEK and Cplex. Due to the large number of variables and constraints (even after the improvements mentioned above), we use relatively small values of N and so the results do not have a very high resolution.
Any algorithm that solves a maximal flow problem for a discrete network, also gives the minimum cut since the "max flow saturates the minimum cut". So once we have a maximum flow, then the minimum cut is simply the set of edges that have flow equal to their capacity. The same applies to the continuous maximum flow problem and we use this to find the Cheeger set (=minimum cut) from the results of the optimization problem defined in Section 3.2.
3.4.1
Results for
L'
Solving the discretized version of the continuous maximum flow problem gives values for flow variables Ujk, Vi,j,k and Wi,j,k. Based on these values we find
fk
using (3.5).Ideally speaking, we are interested only in points (i,
j,
k) where the magnitude ofthe flow
fi,,k
is equal to the capacityCi,j,k
1. So we look at only those points with |ffij,kII > 1 - 108. This gives the approximate Cheeger set Dapp ={(i,
j,
k)||ika||
> 1 - 10-8}. The "outer surface" defined by this set of points is shown inFigure 3-2. The value of the objective function t, i.e. the maximum flow, is 4.38114966 (for N = 40).
We should note that any feasible flow gives a lower bound on the value of the Cheeger constant. This is because this is the maximum flow for (the discretized version of) the continuous max-flow problem, which is the dual problem to finding the minimum cut. Therefore this is actually just a lower bound on the value for the Cheeger constant for the unit cube in the L£ norm.
3.4.2
Results for L2
Similarly for the C2 norm, we look at only those points with > >|fjkII 1 - 10-. This
gives the approximate Cheeger set Dapprox {(i,j, k) :I
Ifi,j,kII
> 1 - 10 3}.
The"outer surface" defined by this set of points is shown in Figure 3-4. The value of the objective function t, i.e. the maximum flow, is 5.3187700759 (for N = 50). Again,
this is actually just a lower bound on the value of the Cheeger constant for the unit cube in the L2 norm.
We believe that this lower bound is far from tight. The optimal t will converge to the Cheeger constant as we increase N, but N = 50 is too small a value to give a very
good approximation to the Cheeger constant. This can also be seen from the fact that the approximate Cheeger set Dapprox =
{(i, j,
k) : I IfiJ, k I 1>-- 10-} contains almostall of the points "inside" the surface shown in Figure 3-4(a) and so the minimum cut (consisting of all saturated edges) is not a good approximation to the surface &D of the optimal shape. However we look at only the "outer surface" made by the points to approximate the Cheeger set. Also Figure 3-3 shows how the optimal value of t, the maximum flow, changes with N. We can clearly see that at N = 50, the lower
bound defined by the maximal flow is still rising.
The first thing that is to be noticed about the two shapes is that none of them is identical to the shapes proposed in Chapter 2, which simply extended the results for
Surface for numerical solution (N = 40) 0.4 0.45- 0.4-- 0.35- 0.3- 0.25- 0.2-0.15 0.1 0.05 0 0 0 . -.0 0.21.1 2 .1 2 02 .. 0.1135 0. .-4 (a) Surface
Level curves for numerical solution (N = 40)
x
(b) Contours
Figure 3-2: Numerical results for Cheeger set for L' norm
0.5 0.45 -0.4 -0.35 -0.3 -S0.25 - 0.2-0.15 0.1 0.05 - 0-0.5 0.45 0.4 0.35 O 3 0.25 0.2 0.15 0.1 0.05
Convergence of t
53
-
S25-51
N
Surface of numerical solution (N = 50) 0.5 E- 0.450--0.4,. 0.35 . 0.3, S0.25 0.2 0.15 0.1 0.05 0 00 0.1 0.1 0.2 0.2 0.3 0.3 x 0.4 0.4 0. 0.5 (a) Surface
Fig -Level r curves for numerical solution (N =50)
0.45- 0.45 0.4-- 0.4 0.35- 0.35 0.3- 0.3 A 0.25 -0.25 0.2- 0.2 0.15- 0.15 0.1 - 0.1 0.05 - 0.05 S 0 0.1 0.2 0.3 0.4 . (b) Contours
Chapter 4
Analytical Solutions
We now use the results from Chapter 3 to improve on the analytical solutions,
dis-cussed in Chapter 2, for the Cheeger problem (2.1) for the unit cube. We first present
the general shape and then the optimized shape for both the L' and the L2 norms.
As in Chapter 2, we only look at D n [0, 0.5]3, the part of the optimal shape in the
positive octant.
4.1
Analytical Solution for the L' norm
4.1.1
General Shape
We start with the shape for the LO norm as it is much simpler than the shape for the
£2
norm. It is obvious from the numerical results (see Figure 3-2), that the Cheeger
set for the unit cube in the L* norm is defined by:
x|
0.5, IyI
0.5,
Izl <0.5
and
D={(x, y, z)} with
lxI+Iyl
!
b,
jyj+ z
b,
zl +x
b
bE [0.5, 1]
IxI
+|yI +z
<
a
3a E [b,2b - 0.5]
(4.1)
Figure 4-1(a) shows the general shape, and Figure 4-1(b) shows the general shape
+ z
+z-b
x~y+z=a
(a)0.5 x
(a) General Shape
0.
(b) General Shape in relation to
"corner" of cube R4 (y = b) xy=b R3 (x + y + z = a) +x=a-05 R1 (z = 0.5) R2 ( + z =b) x (a- b b- 0.5 0.5 (c) Projection on xy-plane
Figure 4-1: General shape (2.6)
simplifies to the general shape discussed in Section 2.1 (see Figure 2-1(a)).
4.1.2
Optimization
Figure 4-1(c) shows the projection of the shape on the xy-plane. We see the following
distinct regions :
z =f(x, y)
=0.5
b - x
a - x - y b - y(x,y)
in R
1(x,y) in
R2 (x,y) in R3(x,
y) in
R4Now the relevant area of this surface, including the planes x
=
0.5 and y
=
0.5, is
given by :
Surface Area = 3
f
max{1,IzxI1,zy I}
dx dy +3
ff
max{1,
Jz
Jzj} dx dyR2
+
ff
max{1,
Iz.i,
IzI}
dx
dy
R3
max{1,
0,
0}
dx dy + 3
J
7max1, 0, 1} dx dy +
II
max{1, 1,
1}dx dy
R3=
3f
1 dx dy+3
ff1
dxdy +
ff1
dxdy
R1 R2 R3
=
3(Area of R
1) + 3(Area of R
2) + Area of R
3
=3ab
-
a2- 1.5b2(4.2)
The volume of the shape can be calculated as :
Volume
=
fz
dx dy + 2f z dx dy + Jfz dx dy
R1 R2 R3 =ff0.5
dx dy+ 2ff
b
-x
dx dy +a
-x
-y dxdy
43 R1 R2 R3 =((b
- 0.5)2 -1(2b
-a
- 0.5)2))+ ((b
-b
2)(a -b))
+
(
a3 + ab
-1a2
-a(b2)
-a)Some of the above expressions were calculated using Mathematica; we don't attempt
to simplify the expression for the volume any further since we will use numerical
methods to find the optimal value of Q(a, b), the ratio of surface area to volume. The
results are shown in Figure 4-2(a). The white region in the figure consists of invalid
pairs of (a, b) (see (4.1)).
We see that (a, b) ~ (0.83,0.78) minimizes Q(a, b) giving an optimal value of
P 4.4495 which is an improvement over the optimal value of 4.8 for the general shape
in Figure 2-1(a). The optimal shape corresponding to these values of a and b is shown
in Figure 4-2(b).
4.1.3
Comparison of Numerical and Analytical Solutions
Figure 4-3 shows the numerical and the analytical Cheeger sets (shown only for the
positive octant) for the L' norm. As we mentioned before, the maximal flow of
- 4.381 found in Section 3.4.1 gives a (not so tight) lower bound on the value of the
Cheeger constant, and the value calculated in Section 4.1.2 gives an upper bound.
So we can say that the solution to the Cheeger problem (2.1) for the L' norm is
bounded by :
4.381
<
II
4.4495
Q(a, b) for (a, b) 0.95- 5.8 0.9- - 5.6 0.85- - 5.4 0.8- - 5.2 -1 0.75- - 5 0.7 - - 4.8 0.65- - 4.6 0.6. - 4.4 0.55 - 4.2 0 0.7 0.8 09 1 1.1 1.2 1.3 1.4 1.5
(a) Q(a, b) against a and b
(b) Optimal D for (a, b) (0.83,0.78)
Figure 4-2: Optimal shape for general shape (4.1)
Surfacfo numrerical solut on (N =10)
024-02
x x
(b) Step 2
(c) Step 3 (d) Step 4
Figure 4-4: Constructing general shape for £2
4.2
Analytical Solution for the
L
2norm
Now we come to the analytical solution for the £2 norm. The analytical expression for the general shape is not obvious from the numerical results (see Figure 3-4). So we first present the rationale behind the suggested general shape and then present the results of the optimization.
4.2.1
General Shape
Constructing the General Shape
The first thing that we notice about the optimal numerical solution (see Figure 3-4) is the 3 "circular" regions on the x = 0.5, y = 0.5 and z = 0.5 planes. We use this
first step, we replace the three squares that intersect at the point (0.5, 0.5, 0.5), by a smaller "squares", each with a quarter circle of radius r1 in one corner (see top
surface in Figure 4-4(a)). The 3 (visible) edges of the original cube are replaced by (quarter) cylinders of radius r2 and length (0.5 - r1 - r2). This gives us the shape in Figure 4-4(a).
Now all we need to do is to find a surface that covers the "hole" we see in Figure 4-4(a), and whose normal is parallel to the normals of all surfaces it meets (so the resulting figure is smooth). We focus on this "hole" in Figure 4-4(b) and this will be referred to as the "corner" of the optimal shape just as 1/8th of a sphere formed the
corner of the general shape in Figure 2-4(a). The quarter circle with radius r2 marks the area where the quarter cylinders (that replace the edges) meet the "corner".
Next, we take this quarter circle (on the surface parallel to the xz-plane), where the cylinder meets the "corner", and rotate it about the line defined by {(x, y, z) :
x = y = 0.5 - r, - r2
}.
This is the line parallel to the z-axis which passes throughthe center of the quarter circle (of radius ri) on the top surface of the cube. Figure 4-4(c) shows the resulting figure.
Finally we repeat the last step symmetrically for the other two sides, to get the shape shown in Figure 4-4(d). This step does result in some overlap of the 3 surfaces created by the rotations, and this will have to be taken into account when calculating the surface area and the volume of the resulting figure.
We have now finished the construction of the corner. This gives us the completed shape shown in Figure 4-5(a). It should be noted that for r1 = 0, this shape simplifies
to the general shape discussed in Section 2.3 (see Figure 2-4(a)).
At this point we should also point out that this shape is not a perfect choice for the Cheeger set, as the view of the "corner" in Figure 4-5(b) shows. We see that the resulting figure is not convex and that by covering the "dent" in the shape, we can decrease the surface area and increase the volume thus getting a smaller value for
(a) General Shape (b) Problem with the corner
Figure 4-5: General shape for L2
(a) Dividing the "corner" (b) Part of "corner"
Figure 4-6: Corner Details
Analytical Expression for General Shape
We can think of the general shape as consisting of three planar surfaces, three
cylin-drical edges and a corner. Finding the contributions that the first two make to the
surface areas and the volumes is simple enough; geometry will give us the answers
easily. The corner is not that simple because of the overlapping mentioned above. So
before we begin the calculations of the parameters of the optimal shape, we would
like to present a method of breaking up the corner into 6 identical pieces, with each
piece being defined by surfaces with analytical expressions. We can then use calculus
to find the surface area and the volume of one piece and multiply these by 6 to get
the surface area and the volume for the corner.
Note : While describing the analytical shape for the corner, and also while cal-culating the surface area and volume of the corner, we will use the shape in Figure 4-4(d) as a reference, ignoring the fact that it is actually not positioned at the origin in the general shape (see Figure 4-4(a)). This means that we will use the corner opposite the curved surface (clearly visible in Figure 4-4(b)) as the origin, and all lengths/equations will be with reference to that. It might be a little difficult for the reader to remember this as he reads the rest of this chapter, but it simplifies the expressions a lot and we sacrifice readability over simplicity.
Figure 4-6(a) shows how the corner piece can be broken into 3 identical parts, such that in each part we have only one rotated surface to deal with. This is done by
cutting the corner with parts of the planes z = x - r1, z = y - r1 and x = y. Figure
4-6(b) then shows the details of the "top" piece (of the three parts in Figure 4-6(a)). The reader should note that this is exactly the surface we got in Figure 4-4(c) by the first of 3 rotations. The transparent part represents the portion of this piece that is covered by the other two rotated surfaces and so does not participate in the surface area or the volume.
Finally, we divide this top piece into two equal parts by the plane x = y. This gives us exactly 1/6th of the shape we refer to as the "corner" of the optimal shape.
Now the equation of the curved surface (not including the circular area on the top) is given by :
z 2 + (V/X2 + y2 - rl)2=r2
The equation of the plane dividing the valid (non-transparent) and invalid (transpar-ent) regions is given by z2 = x - r1. We now have all the pieces to calculate the area
R1 R2 R3
Figure 4-7: Projection of corner on xy-plane
4.2.2
Optimization
Figure 4.2.2 shows the projection of the corner on the xy-plane. The surface area of
the corner (Figure 4-4(d)) is then given by :
Surface Area of Corner = 6
(1irr2+J
J2 dx dy+ J dx dy+ J 2 dx dy) (4.4)R1 R2 R3
1
where 17rr2 gives the area of the circular portion at the top, and
8
+
zi
ax
(y
Similarly the volume of the corner piece is given by
Volume of Corner =
6
(8rrr 2 + zi dx dy+
JJz1 - z2 dx dy+
zi - z2 dx dy)R1 R2 R3
(4.5)
We do not attempt to simplify the expressions any further, and use numerical
integra-tion to find the values. Based on these expressions for surface area and the volume of
the corner piece, we can find the expression for Q(ri, r
2), the ratio of the total surface
area to total volume. The contribution to the surface area and the volume due to
the cylindrical edges and the planar surfaces are simple to calculate and we do not
present them here.
Q(ri, r2) for (ri, r2)
0.0
0.05 0.1 0,15 0.4 045
5.5
4.5
(a)
Q(ri,
r2) against r1and r2(b) Optimal D for (ri, r2)
(0.29,0.21)
Figure 4-8: Optimal shape for L2
Now
Q(ri,
r
2) has to be minimized over valid values of r, and r
2.
This was
done numerically and the results are shown in Figure 4-8(a). We see that (ri, r
2) ~
(0.29, 0.21) minimizes Q(ri, r
2) giving an optimal value of Q(ri, r
2) = 5.3815 which is
slightly better than the optimal value for general shape in Figure 2-4(a). The optimal
shape corresponding to these values of r
1and
r2is shown in Figure 4-8(b).
,7
0.3
6
,.I
0.2505
4 Y
(a) Numerical Solution (b) Numerical Solution
Figure 4-9: Comparison of numerical and analytical solutions for L2)
4.2.3
Comparison of Numerical and Analytical Solutions
Figure 4-9 shows the numerical and the analytical Cheeger sets (shown only for the
positive octant) for the
£2norm. As we mentioned before, the maximal flow of
~ 5.319 found in Section 3.4.2 gives a (not so tight) lower bound on the value of the
Cheeger constant, and the value calculated in Section 4.2.2 gives an upper bound. So
we can say that the solution the Cheeger problem (2.1) for the
£2norm is bounded
by:
5.319
<
IDH
2< 5.382
4.3
Similarities between
L'
and
L2
Cheeger sets
In the end we mention some observations about the shape of the analytical solutions.
Figure 4-10(a) shows the general shape based on the simple extension of the results
for the unit square. We got this shape by "cutting-off' the corner of the cube just like
the Cheeger set for the square (in the L norm) has the corners of the square cut-off.
Another way of looking at the same shape is to think of each of the 6 squares (that
form the cube) being replaced by (the general shape of) its Cheeger set (remember
that the figure only shows the first octant). This step results in "holes" where the
corners of the cube used to be. We cover these holes with a "minimal surface" to get
the shape in Figure 4-10(a).
(a) Naive approach from Section 2.1
(b) Analytical shape from Section
4.1
(c) Unit ball for L£ in R3
Figure 4-10: Two approaches for L'
Now if we "surround" this shape (similar to Kawohl's algorithm [3] for convex shapes in R2) with (a scaled) unit ball in the dual norm (shown in Figure 4-10(c)), we get the general shape in Figure 4-10(b). So (a scaled version of) the simple shape in Figure 4-10(a) is acting as the "inner Cheeger set"1 for the Cheeger set in Figure
4-10(b).
Applying the same approach to the L2 norm, the first step, of replacing each side of the cube with the (general shape of) its Cheeger set, gives us the shape in Figure 4-11(a), the shape we saw in Section 2.2. If we ignore the covering-of-the-hole step, and "surround" this shape by the unit ball in the dual norm (which is a sphere), we get exactly the shape in Figure 4-11(b), the shape we suggested and optimized in Section 4.2 above. If however we first cover the hole with a "minimal surface" (maybe as in Figure 2-3(c)), we will get a shape similar to the Figure 4-11(b), but without the non-convex portion (see Figure 4-5(b)). Again, the simple shape in Figure 4-11(a) is
(a) Naive approach from Section 2.2
(p
(b) Analytical shape from Section 4.2
Figure 4-11: The two approaches for L2
doldloffisob-- -- - L - I , - - . - -Z dw