Contrôlabilité des systèmes non linéaires en basse dimension : structure et classification

HAL Id: tel-01775714

https://hal.univ-lorraine.fr/tel-01775714

Submitted on 24 Apr 2018

HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

Contrôlabilité des systèmes non linéaires en basse

dimension : structure et classification

Jean-Claude Vivalda

To cite this version:

Jean-Claude Vivalda. Contrôlabilité des systèmes non linéaires en basse dimension : structure et classification. Mathématiques générales [math.GM]. Université Paul Verlaine - Metz, 1986. Français. �NNT : 1986METZ027S�. �tel-01775714�

AVERTISSEMENT

Ce document est le fruit d'un long travail approuvé par le jury de

soutenance et mis à disposition de l'ensemble de la

communauté universitaire élargie.

Il est soumis à la propriété intellectuelle de l'auteur. Ceci

implique une obligation de citation et de référencement lors de

l’utilisation de ce document.

D'autre part, toute contrefaçon, plagiat, reproduction illicite

encourt une poursuite pénale.

Contact : ddoc-theses-contact@univ-lorraine.fr

LIENS

Code de la Propriété Intellectuelle. articles L 122. 4

Code de la Propriété Intellectuelle. articles L 335.2- L 335.10

http://www.cfcopies.com/V2/leg/leg_droi.php

IJNIVERSITË

DH METZ

FACULTE

DES SCIENCES

THESE

DE

troisième

cycle

mention

: rnathématiques

_appliquées

contrôlabilite

_{des systèmes}

_{non lin éai}

_res

en basse

dimension

structure

et classification

par Jean-Claude

VIVALDA

l e 2 6 novembre

1 g 8 O

président : Gauthier SALLET université

de

METZ

Membres : Claude

ROGER

André ROUX

Jean-Paul

GAUTHf

ER

B I B L I O T H E O U E U N I V E R S I T A I R E D E M E T Z ₎

|

ililt

ililt

il]t

_{022 420264 6}

il]t

il]t

il]t

ililt

ililt

]il1

]]t

]il

iltl

Université de Mi:.TZ Université de METZ

Laboratoire d'Automatique de GRENOBLE

I S G M P - L a b o r a t o i r e T H E S E p r é s e n t é e à I ' U N I V E R S I T E d C M E T Z d e M é t h o d e s M a t h é m a t i q u e s d ' A n a l y s e U n i t é A s s o c i é e C N R S n " 3 9 9 p o u r o b t e n i r l e g r a d e d e D o c t e u r e n M a t h é m a t i q u e s d e s S y s t è m e s par Jean-Claude VIVALDA

CONTROLABILITE DES SYSTEMES LINEAIRES EN BASSE DIMENSION

Soutenue le 26 Novembre 1986 d e v a n t l a C o m m i s s i o n d r E x a m e n J U R Y G. SALLET C. ROGER A . R O U X J . P . G A U T H I E R G . B O R N A R D Président Examinateur Examinateur Examinateur Examinateur

BIBL,O I ngrur- r'" vrngl IAIRE

gÇostrs i

s/t 16

_l*

R ! i 1 I : : f I E l , ! I i i T l l : !':,j r.1 l' - il :.-i t ' : , :.-i t : . : I ; ' , , :.-i ' 1 - ; i t ! t ' ; r l -' j r l : ; - t - r - : i , ' 1 r r l . l . r ' : 1 1 .

C O N T R O L A B I L I T E D E S S Y S T E M E S

N O N L I N E A I R E S E N F A I B L E S D I M E N S I O N S

Structure et classification de ces systèmes

: '

1

-I N T R O D U C T -I O N

C e t t e t h è s e c o n c e r n e d e s p r o b l è m e s d e c o n t r ô l a b i l i t é d e s y s t è m e s n o n l i -n é a i r e s ; elle se décompose e-n 3 parties i-ndépe-nda-ntes :

1 ) é t u d e d e I a c o n t r ô l a b i l i t é s u r I R 3 - { O } d ' u n e p a i r e d e c h a m p s d e v e c t e u r s l i n é a i r e s o ù I ' u n d e s c h a m p s e s t n i l p o t e n t d r o r d r e 2 2 ) c l a s s i f i c a t i o n d u p o i n t d e v u e d e l a c o n t r ô l a b i l i t é d e s s y s t è m e s a f f i n e s d a n s l e plan 3 ) c l a s s i f i c a t i o n d e s s y s t è m e s q u a d r a t i q u e s d a n s I R 3 -L e c a d r e d e l ' é t u d e d e c e s s y s t è m e s e s t l e s u i v a n t : O n s e p l a c e d a n s u n e v a r i é t é d i f f é r e n t i e l l e M d e c l a s s e C - , c o n n e x e e t m a î t r i s a b l e ; u n e f a m i l l e d e c h a m p s d e v e c t e u r s s u r M e s t u n e n s e m b l e F d e c h a m p s de vecteurs de classe C-. N o u s f e r o n s a u s s i r é f é r e n c e à d e s s y s t è m e s d e l a f o r m e : i ( t ) = f ( x ( t ) , u ( t ) ) x ( 0 ) = x o L a f o n c t i o n u : I R - C e s t a p p e l é c o n t r ô l e , s i L L e s t I ' e n s e m b l e d e s t - u ( r ) c o n t r ô l e s a d m i s s i b l e s c o n t i e n t l e s f o n c t i o n s c o n s t a n t e s p a r m o r c e a u x e t e s t c o n t e n u d a n s I t e n s e m b l e d e s f o n c t i o n s m e s u r a b l e s -A u n t e l s y s t è m e o n a s s o c i e l a f a m i l l e F = { X u / u e C } o ù r x u ( x ) = f ( x , u ) D é f i n i t i o n s e t n o t a t i o n s

* Si X est un champ de vecteurs nous notons :

( t , * ) - X r ( x ) l e g r o u p e l o c a l à u n p a r a m è t r e q u ' i l e n g e n d r e

z

-Le pseudo semi-groupe engendré t ) 0, et G (F) le pseudo-groupe engendré

par les difféomorphismes locaux X, pour

S i x e s t u n é l é m e n t d e M n o u s n o t o n s I ' a c r i o n d e S ( F ) ( r e s p . d e c ( F ) ) . p a r S ( F ) . S ( F ) . x ( r e s p . G ( F ) . x ) I ' o r b i t e d e x s o u s N o u s d i r o n s q u e l a f a m i l l e F e s t c o m p l è t e m e n t c o n t r ô l a b l e s u r M ( o u t r a ' r s i t i v e ) s i S ( F ) . x = M p o u r t o u t x d e M .

L'étude des systèmes non linéaires a déjà suscité une abondante littérature er les problèmes restants sont de plus en plus difficiles. Les systèmes dits linéaires, c'est-à-dire les systèmes du type :

x ( t ) = A x ( t ) + B u , s o n t b i e n c o n n u s d e s i n g é n i e u r s x(t)elRn u e IRP m a i s o n s ' e s t r e n d u c o m p t e d e I ' i n s u f f i s a n c e d e c e s s y s t è m e s d a n s l r é t u d e d e s p r o b l è m e s c o n c r e r s ( p a r e x e m p l e l e p r o b l è m e d u s a t e l l i t e n é c e s s i t e d ' é t u d i e r d e s s y s -t è m e s q u a d r a -t i q u e s ) . D a n s l e s a n n é e s l 9 7 O d e s m a t h é m a t i c i e n s t e l s q u e L o b r y , Jurdjevic, Sùss-m a n n o n t é t a b l i l e s p r e Sùss-m i e r s r é s u l t a t s d e l a t h é o r i e . E n é t u d i a n t l a c o n t r ô l a b i l i t é s u r l e s g r o u p e s d e L i e , Jurdjevic et Sùssmann ont montré un critère de complète c o n t r ô l a b i l i t é c o n c e r n a n t l e s s y s t è m e s b i l i n é a i r e s :

I i t t ) = x ( x ( t ) )

* f o v , ( * ( t ) )

I

i ; t '

I

l u . e l R

l l

Il esr à noter que les résultats sont beaucoup plus dif f iciles à obtenir l o r s q u e le s c o n t r ô l e s u i s o n t b o r n é r ( l r i l < M p o u r i = l , . . . p ) ; d a n s l e s m ê m e s a n n é e s Lobry a établi un critère de contrôlabilité pour ces systèmes dans le cas où le champ de vecteurs X est Poisson-stable.

En 1976 Jurdjevic et Kupka ont démontré un résultat vraiment non trivial concernant les systèmes du type :

i ( t ) = ( A + u B ) x ( t ) u e l R x ( t ) e S L ( n , l R )

Dans les années suivantes Boothby a classifié les groupes G(F) transitifs sur IRn - { 0 } où F est une famille de champs de vecteurs linéaires sur IRn.

Jurdje 3 Jurdje

-vic et Kupka ont défini lréquivalence de deux systèmes F et Ft et ont mis au point des techniques permettant de remplacer un système F par un autre système F'plus grand qui lui est équivalent au point de vue de la contrôlabilité.

E n c e q u i c o n c e r n e l e s f a m i l l e s d e c h a m p s d e v e c t e u r s l i n é a i r e s , o n p e u t s i g n a l e r l e t h é o r è m e d e G a u t h i e r - B o r n a r d q u i d o n n e u n e c o n d i t i o n n é c e s - a i r e e t s u f f i s a n t e d e t r a n s i t i v i t é s u r I R n - { 0 } : c ' e s t c e t h é o r è m e q u i s e r a u t i l i s é d a n s l a l è r e p a r t i e d e n o t r e t h è s e . D a n s l a 2 è m e p a r t i e , n o u s u t i l i s e r o n s u n t h é o r è m e d t i à J u r d j e v i c - S a l l e t d o n n a n r u n c r i t è r e d e c o m p l è t e c o n t r ô l a b i l i t é p o u r l e s s y s t è m e s a f f i n e s s u r I R n l o r s q u e l e s y s t è m e l i n é a i r e a s s o c i é e s t t r a n s i t i f s u r I R n - { 0}. L a p r e m i è r e p a r t i e d e c e t r e t h è s e e s t c o n s a c r é e à l é t u d e s u r I R 3 - { 0} des p a i r e s d e c h a m p s d e v e c r e u r s l i n é a i r e s { A , B } . E t a n t d o n n é l a c o m p l e x i t é d u p r o b l è

-ffi€, il est illusoire de vouloir obtenir une classification complète, du point de vue d e l a t r a n s i t i v i t é , d e c e s p a i r e s { A , B } . N o u s n o u s s o m m e s d o n c l i m i t é s a u x p a i r e s { A , B } o ù A e s t u n c h a m p d e v e c t e u r s l i n é a i r e s q u e l c o n q u e e t B u n c h a m p d e v e c -t e u r s n i l p o -t e n -t d ' o r d r e 2 . E n u t i l i s a n t l e t h é o r è m e d e G a u t h i e r B o r n a r d , n o u s a v o n s é t a b l i d e s c o n d i t i o n s n é c e s s a i r e s e t s u f f i s a n t e s d e c o m p l è t e c o n t r ô l a b i l i t é p o u r c e t y p e d e p a i r e s -L e s c r i t è r e s o b t e n u s s o n t r e l a t i v e m e n t s i m p l e s e t s o n t d o n n é s s o u s f o r m e invariante ; il nous semble que quelque chose de profond se passe au niveau des champs nilpotents sans que nous soyons en mesure de préciser quoi.

Dans la deuxième partie, nous établissons une classif ication des systèmes affines dans le plan c'est-à-dire des systèmes du type :

i ( r ) = n x ( t ) + u ( o x ( t ) + b )

x ( t ) e I R 2 u e l R

Un article esr déjà paru sur le sujet dans la revue IEEE écrit par Narendra mais il comporte de nombreuses erreurs, crest pourquoi nous avons repris le problème - en utilisanr une méthode différente - et nous donnons des conditions nécessaires er suf f isantes (sous forme invariante) de complète contrôlabilité ; ces conditions sont purement algébriques.

Pour étudier de tels systèmes, nous avons à notre disposition le théorème de Jurdjevic-Sallet qui donne un critère de transitivité lorsque le système linéaire associé est transitif. nous avons examiné les autres cas et nous faisons apparaître

4

-que le système affine est transitif essentiellement dans les cas où le système li-néaire associé lrest aussi ainsi qu'il sera précisé plus loin. On peut conjecturer que ce résultat est encore vrai pour des dimensions supérieures.

point de

Dans la 3ème partie, nous exposons une méthode de classif ication, du v u e d e l a c o n t r ô l a b i l i t é , d e s s y s t è m e s q u a d r a t i q u e s d a n s I R 3 :

i ( t ) = Q(x(t)) + ub où Q est un champ de vecteurs UCIR

d o n t t o u t e s l e s c o m p o s a n t e s s o n t d e s p o l y n ô m e s h o m o g è n e s d r o r d r e 2 .

C e s s y s t è m e s s o n t t r è s é t u d i é s : i l s a p p a r a i s s e n t d a n s l e c o n t r ô l e d e I ' a t -t i -t u d e d u s a -t e l l i -t e m a i s i l s o n -t a u s s i l e u r i n -t é r ê -t p r o p r e p u i s q u e l a d i f f é r e n -t i e l l e e n O d u c h a m p d e v e c t e u r Q est nulle, la linéarisation nrapporte aucun renseignement : d ' o i r l a n é c e s s i t é d ' é t u d i e r d e t e l s s y s t è m e s m ê m e s i o n s e p l a c e d ' u n p o i n t d e v u e l o c a l . I c i e n c o r e n o u s u t i l i s o n s l e t h é o r è m e d e G a u t h i e r - B o r n a r d q u i p e u t s r a d a p t e r a u x s y s t è m e s c o n s t i t u é s d e c h a m p s d e v e c t e u r s h o m o g è n e s . N o t r e t r a v a i l f o u r n i t u n e m é t h o d e q u i p e r m e t d e d é c i d e r s i u n s y s t è m e q u a d r a t i q u e e s t c o n t r ô l a b l e o u n o n : c e t t e m é t h o d e p e u t a i s é m e n t a b o u t i r s u r u n a l g o r i t h m e e t ê t r e p r o g r a m m é e z u r o r d i n a t e u r .

5

-l è r e P A R T I E

CONTROLABILITE SUR IR3 - { O } D 'UNE PAIRE DE CHAMPS DE VECTEURS LINEAIRES AVEC L'UN DES CHAMPS

6

-I N T R O D U C T -I O N

E t a n t d o n n é e u n e f a m i l l e F d e c h a m p s d e v e c t e u r s l i n é a i r e s s u r I R n , l e théorème de Gauthier-Bornard donne une condition nécessaire et suf f isante de c o m p l è t e c o n t r ô l a b i l i t é p o u r F s u r I R n - { 0 } . S t a p p u y a n t s u r c e t h é o r è m e , P . A d d a a o b t e n u , d a n s s a t h è s e 3 è m e c y c l e , u n e c l a s s i f i c a t i o n , d u p o i n t d e v u e d e l a c o n t r ô l a b i l i t é , d e s p a i r e s { A , B } d e c h a m p s d e v e c t e u r s l i n é a i r e s s u r I R 2 . L e p r o b l è m e e n d i m e n s i o n 3 é t a n t b e a u c o u p p l u s c o m p l i q u é , i l e s t i l l u s o i r e d e v o u l o i r o b t e n i r u n e c l a s s i f ic a t i o n c o m p l è t e d e t e l l e s p a i r e s , c ' e s t p o u r q u o i n o u s n o u s s o m m e s b o r n é s à é t u d i e r l e s p a i r e s { A , B } o ù B e s t u n e n d o m o r p h i s m e n i l p o t e n t d ' o r d r e 2 e t A e s t q u e l c o n q u e .

Nous exposons dans cette partie des conditions nécessaires et suf f isantes d e c o m p l è t e c o n t r ô l a b i l i t é p o u r d e t e l l e s p a i r e s d a n s I R 3 - { O } ; ces conditions s o n t d o n n é e s s o u s f o r m e i n v a r i a n t e e t s o n t , s a u f d a n s u n c a s , p a r t i c u l i è r e m e n t s i m p l e s .

L a m é t h o d e d e d é m o n s t r a t i o n c o n s i s t e à e x a m i n e r t o u s l e s c a s p o s s i b l e s e t f a i t g r a n d e m e n t a p p e l à I ' i m p o r t a n t e n o t i o n d e n o r m a l e a c c e s s i b i l i t é .

7

-PLAN DE LA PARTIE I

Cette partie est divisée en 4 chapitres.

Chapitre 1 : . Après quelques généralités et le rappel de quelques notations nous introduisons la notion de contrôlabilité dilectionnelle pour les lamilles de champs de vecreurs linéaires. Les trajectoires d'une telle famille F étant homothétiques par rapport à Itorigine nous voyons que cette norion esr équivalente à la complète contrôlabilité de la famille F "projetéerr de F sur tn-t.

. Nous présentons ensuite un critère de complète contrôlabilité pour les familles de champs de vecreurs linéaires sur IRn - { 0 } dri à Gau-thier-Bornard puis une amélioration de ce critère due à G. Sallet.

. Dans le dernier paragraphe nous exposons lrimportante notion de normale accessibilité pour un système contrôlé, ce qui nous permet de donner un crirère de contrôlabilité simple pour les familles de champs de vecreurs en dimension 2 qui sera beaucoup utilisé par la suite.

Chapitre 2 : Dans ce chapitre nous exposons une condition nécessaire et suffisante de complète contrôlabilité pour une paire { A,B } de champs de vecteurs linéaires donnée sur IR3 avec A nilpotent dtordre 2 et B tel que : Spec B c IR.

Une telle paire { A,B } est complètement contrôlable sur IR3 - { 0 } si et seulement si :

i) dét (A+B-rld) I 0 pour tout tr de Spec B i i ) T r A B < 0

Chapitre 3 : Nous exposons dans ce chapitre une condition nécessaire et suffisante de complète contrôlabilité pour une paire { A,B } de champs de vecteurs linéaires sur IR3 avec A nilpotent drordre 2, Spec B ç IR et avec la valeur propre réelle de B égale à la partie réelle commune de ses

va-leurs propres non réelles.

Une telle paire { A,B } est complètement contrôlable sur IR3 - { 0 } si et seulement si :

i) dét (A+B-Àld) I 0 pour À€ Spec B 1 IR i i ) T r A B l 0

C h a p i t r e 4 :

8

-Pour terminer notre étude, nous exposons dans ce chapitre une condition n é c e s s a i r e e r s u f f i s a n t e d e _ c o m p l è t e c o n t r ô l a b i l i t é p o u r u n e f a m i l l e d e c h a m p s d e v e c t e u r s l i n é a i r e s d o n n é e s u r I R 3 a v e c A n i l p o t e n t d ' o r d r e 2 , S p e c B É IR et avec la valeur propre réelle de B différente de la p a r t i e r é e l l e c o m m u n e d e s e s v a l e u r s p r o p r e s n o n r é e l l e s -U n e t e l l e p a i r e { A , B } e s t c o m p l è t e m e n t c o n t r ô l a b l e s u r I R 3 - { 0 } si e t s e u l e m e n t s i : i ) ( À -s ) d é t ( R + e - r l d ) < 0 o u i i ) d é t ( A + B - r l d ) # 0 e t ( l - e ) t r A B < 0 o u i i i ) d é t ( A + B - À l d ) * o e t

T

_r+T,

" ' { t n r c t g l - A r c t s ï

# r .

" ) '

7 = î

ffi

o ù B s ' é c r i t T 1 = T t A B

(sii)

e t T r = T 1

dans une certaine base, ï = ft

9

-C H A P I T R E 1

GENERALITES - DEFINITIONS ET NOTATIONS

1 . 1 . S Y S T E M E S L I N E A I R E S D é f i n i t i o n S o i t F u n e f a m i l l e d e c h a m p s d e v e c t e u r s l i n é a i r e s d o n n é e s u r I R n ; n o u s n o t e r o n s S ( F ) I e s e m i - g r o u p e d e d i f f é o m o r p h i s m e s e n g e n d r é p a r F . S ( F ) e s t d é f i n i p a r :

s ( F ) = { " " o t o " " o ' o . . . o . t o o o / t y t 2 , . . . t p > 0 , A 1 , . . . o 0 . F }

N o u s n o t e r o n s G ( F ) l e g r o u p e e n g e n d r é p a r S ( F ) :

G ( s ) = { " t t o t o . . . o u ' o o o

/ t , t r , . . . t o e I R A 1 , . . . A p € F }

Accessibilité Nous dirons que le point y est accessible à partir du point x par le s y s t è m e l i n é a i r e F s ' i l e x i s t e g , é l é m e n t d u s e m i - g r o u p e S ( F ) t e l q u e y = q ( x ) .

N o t a t i o n N o u s n o t e r o n s A ( x , F ) I ' e n s e m b l e d e s p o i n t s d e I R n a c c e s s i b l e s à p a r t i r de x par le système F.

Déf inition Nous dirons que le système F est complètement contrôlable ou transitif sur IRn - { 0 }si le semi-groupe S(F) opère transitivement s u r I R n - { o } .

Aurremenr dit : F est complètement contrôlable sur IRn - { 0 } si et s e u l e m e n t s i A ( x , F ) = I R n - t 0 l p o u r t o u t x d e I R n - t 0 1 .

R e m a r q u e I l e s t é v i d e n t q u e F e s t c o m p l è t e m e n t c o n t r ô l a b l e s u r I R n - { 0 } si e r s e u l e m e n t s i - F e s t c o m p l è t e m e n t c o n t r ô l a b l e s u r I R n - t O l .

1 0

-S o i t F u n e f a m i l l e de champs de vecteurs linéaires, on note Lie(F) I'algè-bre de Lie engendrée par F. Nous dirons que F vérifie la condition du rang en un p o i n t x s i d i m L i e ( F ) ( x ) = n .

Un champ de vecteurs linéaires étant analytique, nous avons le résultat suivant :

Proposition Pour une famille de champs de vecteurs linéaires F, opère transitivement sur IRn - {0 } si er seulemenr condition du rang en tout point.

le si

g r o u p ! G ( F ) F v é r i f i e la

1.2. CONTROLABILITE DIRECTIONNELLE POUR UNE FAMILLE DE CHAMPS DE V E C T E U R S L I N E A I R E S

D é f i n i t i o n _{Une famille de champs de vecteurs linéaires F est dite contrôlable} suivant les directions si de tout point de toure demi-droite issue de I'origine on peur atteindre un point de roure demi-droite issue de I ' o r i g i n e .

Autrement dit : F esr contrôlable suivant les directions si : V ( x , y ) e I R n - { 0 } x t R n - { 0 } , 3 e e I R I t e l q u e o y e A ( x , F )

R e m a r q u o n s q u r u n e condition nécessaire pour qurun système linéaire F soit t r a n s i t i f s u r I R n - tOl est que F soit contrôlable suivanr les directions.

P r o j e c t i o n sur Sn-l

P o u r un champ de vecteurs linéaires A nous avons utA.(l *) = À etA.* pour t o u t ( r , , x ) e t R X IRn, ceci implique que les trajectoires de A sonr homothétiques p a r rapport à I'origine.

La trajectoire issue de Àx est homothétique par rapport à lrorigine à la trajectoire issue de x.

1 1 -C e s c o n s i d é r a t i o n s p e r m e t t e n t d e m o n t r e r l a p r o p o s i t i o n s u i v a n t e : L e s p r o j e c t i o n s s u r S n - l d e s t r a j e c t o i r e s d r u n c h a m p d e v e c t e u r s n é a i r e A s o n t l e s t r a j e c t o i r e s d r u n c h a m p d e v e c t e u r s A ( a p p e l é p r o j e t é d e A s u r s n - 1 ) d é f i n i p a r : À ( * ) = A ( x ) - ( A x , x ) x p o u r t o u t * d e s n - l . t A

Posons

_{e r(x) =}

ffil

oout

t

IR et x

t n - t M o n t r o n s q u e l a f a m i l l e {q ,} I R e s t u n g r o u p e à u n p a r a m è t r e d e d i f f é o m o r p h i s m e s A " S - 1 e o ( x ) = x o , ( x ) S - 1 p u , d é f i n i t i o n d e q r Proposition D é m o n s t r a t i o n

On peut alors définir paramètre est g _t en posant

Â(*)

= :t v,(*)

| ,=o

, t A \ r t A t e . x . r = A e x t A " t A . x r r - s A - - r I o o o ( x ) - Y _{t - Y s} \ " / l l e - ' x l l s A l l e t ^ e - ' x ll

ll

ll"'A.,.llll

l i -le " ( t + s ) A . x

=

lftda . .1;

c h a m p d e v e c t e u r s - 1 s u r S r r - r d o n t l e g r o u p e à A un d u t F . d pulsque ar d

iiî

/ \ A " t A x

9 r ( x / = l æ

-| -| e . * l l

l l

" r A

. * l l - ' "tA'-I,

A " t A *

l l "tA .* ll

a " t A . * , A " ' A * , " ' A . x

l l " t A . * l 1 3

( t + s ) A e ' . x ' s A ' E , X e ' r X

l l " ' A ' * l l

o n o b t i e n t

d

=dr

* ,(*) l,=o

1 2 -= A x - ( x . A x ) x d ' o ù À ( * ) R e m a r q u e

L e terme < Ax,x > est la composante radiale du vecteur Ax relativement à S n - l , Â ( * )

" r , l a " c o m p o s a n t e t a n g e n t i e l l e r ' à S n - l d u m ê m e v e c t e u r .

R e m a r q u o n s a u s s i q u e cette propriété reste vraie pour un champ de vecteurs X d o n n é s u r I R n dont toutes les composanres sont des polynômes homogènes de m ê m . e d e g r é ( l e s trajectoires de tels champs de vecteurs sont également homothéti-q u e s p a r rapport à lrorigine). Cette propriété n'est évidemment pas vérifiée par un c h a m p d e v e c t e u r s e n g é n é r a l .

P r o p o s i t i o n

il

Soient A et B deux champs o n t m ê m e p r o j e c t i o n ,u, S-1 que B = A +orld v e c t e u r s l i n é a i r e s s u r I R t , A e t B e t s e u l e m e n t s i i l e x i s t e o r r é e l t e l de s i D é m o n s t r a t i o n * Supposons B ( A * r l d ) x Supposons À x = B x donc pour ( R - g ) x = x x = f i = A x = A x = A x = A x = A x + e I d + c x + o x -- ( A x , _ ( A x , A x + o l x r x ) x p o u r x S n - l A x r x ) x - o ç X r x ) x ) x + a x ( l - < x , x > )

) x c a r l

_{l x l l z = t}

que Ax = Bx G > ( R - g ) x = pour tout * de S-1 ( < A x , x > - < B x , x > ) x t o u t x d e I R n , i l e x i s t e o ( x ) t e l q u e a ( x ) x donc A-B est une homothétie.

1 3

-On peut conclure de ce paragraphe que :

U n e f a m i l l e d e c h a m p s d e v e c t e u r s l i n é a i r e s F d o n n é e s u r I R n e s t c o n t r ô -l a b -l e s u i v a n t -l e s d i r e c t i o n s s i e t s e u -l e m e n t s i -l a f a m i -l -l e p r o j e t é e F e s t c o n t r ô -l a b -l e ^ n - 1 s u r ) 1 . 3 . L E T H E O R E M E D E G A U T H I E R - B O R N A R D C e t h é o r è m e e x p o s e u n e c o n d i t i o n n é c e s s a i r e e t s u f f i s a n t e d e c o m p l è t e c o n t r ô l a b i l i t é p o u r u n e f a m i l l e d e c h a m p s d e v e c t e u r s l i n é a i r e s . T h é o r è m e S o i t F u n e f a m i l l e d e c h a m p s d e v e c t e u r s l i n é a i r e s d o n n é e sur IRn { 0 } , F e s t c o m p l è t e m e n t c o n t r ô l a b l e s u r I R n - { 0 } si et seulement

s i :

i) F vérifie la condition du rang en au moins un point

i i ) F e s t c o n t r ô l a b l e s u i v a n t l e s d i r e c t i o n s ( c e q u i r e v i e n t à d i r e : F c o n t r ô l a b l e s u r S n - 1 )

i i i ) F a d m e t u n e d i r e c t i o n r e n t r a n t e e t u n e d i r e c t i o n s o r t a n t e .

P r é c i s o n s ce dernier point :

* F admet une direction rentrante signifie :

f x e l R " - { 0 } , f , p e S ( F ) , f À e 1 0 , 1 [ t e l s q u e s ( x ) = L *

* F admet une direction sortante signifie :

l l y e t R n - { 0 } , l o e s ( p ' ) , 1 u .

1 1 , 1 - [ t e l s q u e 0 (y ) = u y

Nous ne donnerons pas la démonstration de ce théorème qui se trouve dans

Remarques

,,

- les points i) et ii) impliquent que F vérifie la condition du rang en tout point

- si F contient un élément avec une valeur propre de partie réelle < Oet si F contient un élément avec une valeur propre de partie réelle > 0 alors le point iii) est évidemment vérifié.

1 4 -C e t h é o r è m e a é t é a m é l i o r é d e l a f a ç o n s u i v a n t e p a r G . S a l l e t : S o i t F u n e f a m i l l e d e c h a m p s d e v e c t e u r s l i n é a i r e s d o n n é e s u r a v e c n ) 3 , F e s t c o m p l è t e m e n t c o n t r ô l a b l e s u r I R n - { 0} si s e u l e m e n t s i : i ) Ë " r , t r a n s i t i f s u . S t - l i i ) S ( F ) e s t n o n b o r n é , c ' e s t - à - d i r e : . y N e l R f , f xe IRn - { 0 }, I <pe S ( F ) t e l s q u e . V e e I R * , l y e l R n - { 0 } , l Q . S ( F ) t e l s q u e T h é o r è m e D é m o n s t ra t i o n I R N e t

ll*ll

ll+(*)ll

llrll

> N

< É

c e t h é o r è m e G a u t h i e r B o r -N o u s a l l o n s m o n t r e r ^ q u e l e s e n t r a î n e n t l e s c o n d i t i o n s i ) , i i ) n a r d .

* Montrons tout d'abord que c o n d i t i o n i i i ) d u t h é o r è m e d e l i s o n s l e l e m m e s u i v a n t : c o n d i t i o n s i ) e t i i ) d e e t i i i ) d u t h é o r è m e d e les conditions i) G a u t h i e r - B o r n a r d . e t i i ) e n t r a î n e n t l a P o u r cela, nous

uti-L e m m e D é m o n s t r a t i o n

( t r , . . . t u )

n e n (t l ,

- - - , [ ) P a r a p p l i c a t i o n d u t h é o r è m e ouvert u x contenant x et un ouvert Vv

Si un système F est transitif sur un espace compact M, il existe un sous-système fini de F, transitif sur M en un temps borné.

Dtaprès un résultat de Siissmann, F est normalement transitif, crest-à-dire :

v ( x , y )

. M 2 , l x l , x 2 , . . . x k F e t ( t i , . . . r 1

) . t R T te l s q u e

1 1 . Y = X,roo ... o xf.(x) et I'application :_{' 1 ' k}

*1, o ...

"

x[ (x) est de rang

des fonctions implicites, il existe donc un contenant y tels que tout point de Vy soit

1 5 -O n a d o n c : M X M - U _{, U x X V y e t p u i s q u e} M X M e s t c o m p a c r : ( * , y ) M ' M X M = Û U x . X V y . c e o u i d é m o n t r e le l e m m e . | ' l ' l = l

A p p l i q u o n s c e l e m m e à M = 5 n - 1 et F un système de champs de vecteurs l i n é a i r e s s u r I R n : i l e x i s t e F o = { Al,...Ap } sous-système fini de F tel que Ëo soit t r a n s i t i f s u r S n - l e n t e m p s b o r n é , p a r c à n s é q u e n t p o u r I e S ( F o ) llqll est - b o r n é donc :

! ( n , e ) t * Ï

e t t o u t x d e D ' a p r è s le p o i n t i i ) l x E I R n - { 0 } , l O . S ( p ) t e l s q u e < 1

_B

$=r

q t z )

eeS(F) tels que > 1 Â D e m ê m e , l y . I R n - { 0 } , ]

il existe ç.S(Fo) tel que e (e(y)) = u t

o * * = t

| | v t l

t t t l

d o n c u € ] 1 , - [

tels que : A r( 'Ïfif

-< B pour tout e de S(Fo)

r R n - { 0 }

I lo(")

| |

l l . l l

i l e x i s t e Q e S ( F o ) t e l q u e q ( t l , ( * ) )

e r : l l q ( + ( * ) )

l l = ll,e

! o ( . ) )

l l

l l . ll

; ; a t x r 1 1

donc r.e ]0,tI

= À x

l l o ( * ) l l < B x

ll"ll

l l e ( x ) l l

ll.ll

y" g tr)

I lq o , o ( v ) l

I

I le ( v ) l

I

1 ; e t r r ; ;

l l v l l

1 6 -* _{I l n o u s r e s t e à m o n t r e r q u e l e s p o i n t s i ) e t i i ) d u t h é o r è m e e n t r a î n e n t l a c o n} -d i t i o n -d u r a n g . P o u r c e l a n o u s u t i l i s o n s l e t h é o r è m e s u i v a n t : T h é o r è m e d e M o n t g o m e r y S o i t G u n g r o u p e d e c o m p a c t e s i m p l e m e n t c o n n e x e G q u i o p è r e t r a n s i t i v e m e n t s u r ( ç , x ) c o n n e x e q u i o p è r e t r a n s i t i v e m e n t s u r u n e v a r i é t é I l e x i s t e u n s o u s - g r o u p e m a x i m a l c o m p a c t K d e L i e M . M .

est laissé invariant f = l < k x , k y > d k

J k

P o s o n s M = S n - l , S n - l e s t c o m p a c t e s i m p l e m e n t c o n n e x e ( n > 3 ) s o i t G = G ( F ) , Ë " r , t r a n s i t i f s u , S n l p a r c o n s é q u e n t l e g r o u p e G o p è r e t r a n s i t i v e -m e n t s u r S t - l p a , l ' o p é r a t i o n : G X 5 2 S2 q ( x )

rmTr

Il existe donc un sous-groupe K compact de G qui opère transitivement Soit dk une mesure de Haar définie sur K et qui soit de masse totale 1. P o u r ( x , y ) e l R n X I R n p o s o n s _{: e ( x , y ) = | <kx,ky > dk}

J k

est un produit scalaire qui

f o ( k ' x , k ' y ) = | < k k ' x , k k ' y > d k

J k

d e H a a r p a r t r a n s l a t i o n . ^ n - 1 sur )

par les éléments de K :

du fait de lrinvariance de la mesure

Appelons 5rn-1 la sphère unité relative au produit scalaire o, K opère transitivement su, St-l par l'opération décrite plus haut, donc K opère transitive-ment sur les directions, donc K opère transitivetransitive-ment sur 5rn-1 par ltopération:

K X S ' t r - l - * 5 r n - 1

( ç , * )

+ q ( x )

( p o u r t o u t ( q , x ) d e K x S ' n - l , q ( x ) e 5 r n - 1 p u i s q u e le p r o d u i t s c a l a i r e 0 e s t l a i s s é invariant par les éléments de K).

* o n p e u t d o n c d i r e q u e p o u r t o u t ( x , y ) e I R n - { 0 } , x I R n - { o } t e l s q u e ll *lle= l l r l l " , i t e x i s r e u n e t r a j e c t o i r e r p d e K C G ( F ) t e l l e q u e I ( x ) = y t l a t r a j e c t o i r e

1 7

-permettant de passer de x en y restant inscrite sur la sphère passant par x relative au produit scalaire o .

* L'hypothèse ii) du théorème assure que de toute sphère relative au produit sca-laire O on peut atteindre toute sphère relative au produit scasca-laire o grâce aux tra-j e c t o i r e s d e S ( F ) c G ( F ) .

C o n c l u s i o n L e s d e u x p o i n t s q u i p r é c è d e n t p e r m e t t e n t d ' a f f i r m e r q u e G ( F ) e s t t r a n s i t i f s u r I R 3 - { 0 i e t d o n c F v é r i f i e l a c o n d i t i o n d u r a n g e n t o u t p o i n t d e I R 3 - { o } .

Remarque Si la famille F contient un champ de vecteurs linéaire nilpotent, la l[ condition ii) du théorème est

vérifiée-D é m o n s t r a t i o n S o i t N F u n n i l p o t e n t , d a n s u n e c e r t a i n e b a s e , o n a u r a :

Mat N - _IO 1:0 _\ tes éléments de la sur-diagonale étant

lq o'-\l

\ Ô \ o /

é g a u x à 0 o u 1 .

Par conséquent la droite dtéquation

x 1 = t x t + t x i

*z=*L

* 3 = o

x - 0

n e s t u n e t r a j e c t o i r e d e N r r , N _ * ll

p o u r x j 40et tî=oona:"ffi

= t + t ( r > O )

cette quantité peut donc être rendue aussi grande que lron veut p o u r l x r o = - I t ( t > O )

t

1 8

-l -l

" t N

- * l l

I

o n a : = t f l

ll.ll

cette quantité peut être rendue aussi petite que lron veur C.e.F.D.

1 . 4 . N O R M A L E A C C E S S I B I L I T E

D é f in i t i o n _{Soit M une variété différentielle (de classe C-, connexe) er F une} famille de champs de vecteurs donnée sur M.

Nous dirons que le point y esr normalement accessible à partir du point x si :

- il existe X I ... XP dans F

- i l e x i s t " , i . . . t f R réels > 0 tels que

y = x:

_{' 1}

o...oXf,

_{. i}

( t 1 , _{t o ) - e}

M en (ti , ... ti)

( x ) e t s i

*1, o...o

I ' a p p l i c a t i o n :

xl (x) est de

p

r a n g l a d i m e n s i o n de Remarques

1) Si le point y esr normalement accessible depuis le point x depuis y, alors z esr normalement accessible depuis x. Si le

e t s i point

z est accessible y est

normale-z , a l o r s y e s t ment accessible depuis le point x er si x esr accessible depuis

normalemenr accessible depuis z.

2 ) S o i t y un point normalement accessible depuis x, par application du théorème d e s f o n c t i o n s implicites, on peut montrer ltexistence drun ouvert U x contenant x e t drun ouvert Vy contenant y tels que tout point de Vy soit normalement a c c e s s i b l e à p a r t i r de tout point de U x.

3) En particulier si le point x est normalement auto-accessible, il existe un ouvert U contenant x tel que tout point de U soit normalement accessible à partir de tout point de u par le sysrème F aussi bien que par le système opposé - F. Ainsi, dans le cas drun point normalement auto-accessible, il y a locale complète contr'-'rlabilité au voisinage de x.

Dans la L e m m e D é m o n s t r a t i o n R e m a r q u e I I e e S ( F ) t e l q u e 0 ( x r ) = x 2 d o n c z = 0 - 1 o e o q ( y ) _ 1 9 _

suite nous nous servirons abondamment du l e m m e s u i v a n t :

S o i t M u n e v a r i é t é e t F u n e f a m i l l e d e c h a m p s d e v e c t e u r s s u r M . S o i t x u n p o i n t d e M n o r m a l e m e n t a u t o - a c c e s s i b l e p a r l e s y s t è m e F. Supposons que de tout point de M on puisse atteindre un voisinage a r b i t r a i r e d e x p a r l e s y s t è m e F a i n s i q u e p a r l e s y s t è m e o p p o s é - F ' a l o r s F e s t t r a n s i t i f s u r M . x é t a n t n o r m a l e m e n t a u t o - a c c e S s i b l e , i l e x i s t e u n o u v e r t U c o n t e -n a -n t x t e l q u e t o u t p o i -n t d e U s o i t n o r m a l e m e n t a c c e s s i b l e à p a r t i r d e t o u t p o i n t d e U . S o i e n t y e t z d e u x p o i n t s d e M , J e € S ( F ) t e l q u e q ( y ) = x t I p e S ( - F ) t e l q u e 4 ' Q ) = x z o r x Z e s t a c c e s s i b l e à p a r t i r d e x , d o n c : ) ï S i l e p o i n t x e s t a t t r a c t i f p o u r u n c h a m p X d e F e t p o u r u n c h a m p y de -F, alors le lemme est vérifié.

Remarque 2 Supposons que dim M = 2, soit F une famille de champs de vecteur donné sur M. Supposons que le point y de M soit accessible à partir du point x :

J t , t 2 , . . . t p e I R * , J x l . . . X P e F t e l s q u e :

v = X 1 o . . . o x ? ' _{t l ' p} ( x ) , s i i l e x i s t e i t 1 , 2 , . - - p l t e l q u e l e s

trajectoires àe Xi et Xi*1 soient transverses au point *i+1 _{t i * 1} o o Xl (x), alors le point y est normalement accessible à partir de x . P

. rt:i : : F . 2 0 -C H A P I T R E 2 N o u s é t u d i o n s i c i l a c o n t r ô l a b i l i t é s u r I R 3 - { O } d ' u n e p a i r e { R , n } d e c h a m p s d e v e c r e u r s l i n é a i r e s o i r A e s t u n e n d o m o r p h i s m e n i l p o t e n t d r o r d r e 2 ( A I 0 e t A 2 = 0 ) e t B u n e n d o m o r p h i s m e d o n t t o u t e s l e s v a l e u r s p r o p r e s s o n t r é e l l e s . L e théorème suivant donne une condition nécessaire et suf f isante de transitivité sur I R 3 - { o } p o u r u n e t e l l e p a i r e .

T h é o r è m e 1

Remarques

S o i t A u n e n d o m o r p h i s m e n i l p o t e n t d ' o r d r e 2 d e I R 3 , B u n e n d o m o r

-?

phisme de IR" ayant toutes ses valeurs propres réelles.

La paire { A,B } est complètement contrôlable sur IR3 - { 0 } si et seulement si :

i) dét (e+g-rtO) I 0 pour tout I' de Spec (B) i i ) T r A B < 0 Puisque A est de condition équivaut Lorsque Tr AB I I de B exprime équivalent à dire, plan invariant par

t r a c e n u l l e , d o n c à : K i l l K i l l ( A , B ) = 6 x T r ( A , B ) < o A B , l a 2 è m e valeur propre ce qui est droite ou de o , d é t ( R + e - r t a ) | o p o u r t o u t e e x a c t e m e n t l a c o n d i t i o n d u r a n g ' d a n s c e c a s , q u r i l n t y a p a s d e A e t B . C e t h é o r è m e p o u r r a i t d o n c s r e x p r i m e r d e l a f a ç o n s u i v a n t e : T h é o r è m e 1 r

Rappelons enfin que, b i l i t é d e l a _ p a i r e { A , B } s u r projeté t À,g t su, 52.

La paire de champs de vecteurs linéaires {. R,a } contrôlable sur IR3 - t o I si et seulement si :

i) le système { A,B } vérifie la condition du rang sur i i ) K i l l ( A , B ) < o

est complètement

r R 3 - t 0 l

puisque A est nilpotent, établir la complète contrôla-IR3 - { o } revient à établir la transitivité du système

Nous allons démontrer le théorème précédent en étudiant tous les cas pos-sibles pour B, auparavant nous allons préciser I'allure des trajectoires de A su, 52. Dans une certaine base (i, j, k) nous avons Mat i{ =

fO 0 O\

l o o 0 l

\tooJ

2 1 -? D a n s I R " l e s t r a j e c t o i r e s d e A s o n t :

- un plan de points singuliers : le plan < j,k >

- des droites de vecteur directeur k, parcourues dans le sens des z croissants si lron esr du côté du plan où les abscisses sont positives, dans le sens décroissant sinon.

C h o i s i s s o n s c o m m e n o r m e e u c l i d i e n n e l a n o r m e r e n d a n t l a b a s e ( i , j , k ) o r t h o n o r m é e )

e t s o i t S - l a s p h è r e u n i t é a s s o c i é e .

P a r p r o j e c t i o n d e s t r a j e c t o i r e s d e A s u , 5 2 n o u s o b t e n o n s :

- un grand cercle de points singuliers : le grand cercle intersection de 52 et du p l a n < j , k >

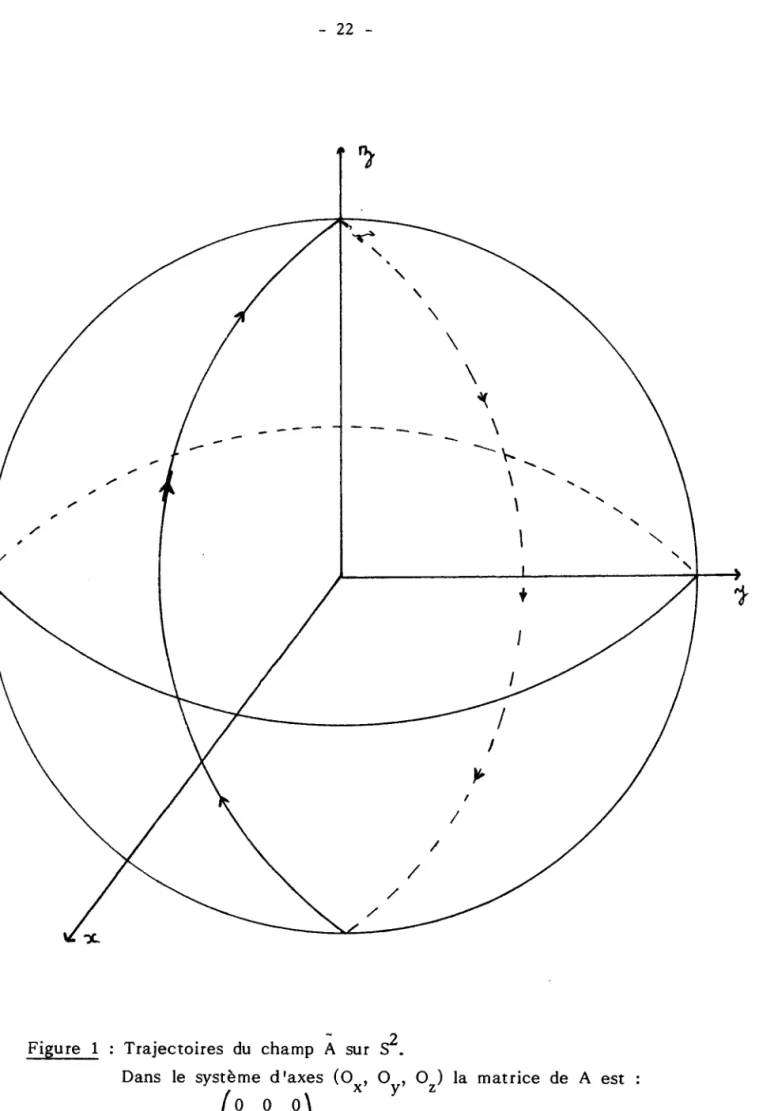
- des méridiens : ces méridiens sont parcourus dans le sens ascendant si lron est d a n s l a d e m i - s p h è r e d e s a b s c i s s e s p o s i t i v e s , d a n s l e s e n s d e s c e n d a n t s i n o n ( v o i r f i g u r e 1 ) .

: - . , : g - : . t , .i: ;*-* . t . : + -t l . ' . , : ' , , * i ' : ' ' j ' '.: E E 2 2 -\ \ . \ \

-I

I

Figure 1 : Trajectoires du champ À *, S2.

Dans le système dtaxes (O*, Or, Or) la matrice de A est :

l 0 o o l

Dans

une

certaine

base

Mat

"

=

(l

_{; i)}

2 3 -l e r c a s : B e s t u n e h o m o t h é t i e d e r a p p o r t À . I l e s t c l a i r q u e , d a n s c e c a s , l a p a i r e { A , B } n t e s t p a s c o m p l è t e m e n t c o n t r ô l a b l e s u r I R 3 - i 0 I , c a r { A , B } n e v é r i f i e p a s l a c o n d i t i o n d u rang.

Notons que dét (A+B-ÀId) = dét A = 0.

2e cas : B ne possède qu'une seule valeur propre réelle, le sous-espace propre associé étant de dimension 2.

3e cas : B ne possède qurune seule valeur propre À , le sous-espace propre associé étant de dimension 1.

/ r

1 o \

Dans

une certaine

_{base Mat e = | o ^ t I}

\ o o À /

B ayant même projection su, 52 que B-).Id, nous supposons dans la suite que tr - 0, d o n c q u e B e s t n i l p o t e n t d ' o r d r e 3 .

N o u s c h e r c h o n s t o u t d ' a b o r d à t r o u v e r u n e b a s e o ù r A e t B s r é c r i v e n t s o u s l a f o r m e l a p l u s s i m p l e p o s s i b l e .

- A e s t n i l p o t e n t d ' o r d r e 2 d o n c d i m K e r A = 2 e t I m A c K e r A - B e s t n i l p o t e n t d t o r d r e 3 d o n c d i m I m B = 2 e t K e r B c I m B

Il nty a pas, dans ce cas, complète contrôlabilité sur IR3 - t O l pour le système

{ A , B } . . f o o o \

E n e f f e t : B a m ê m e p r o j e c t i o n s u , 5 2 q u e B - À l d . M a t t a + r O ) = { o 0 1 l

\o ooJ

par conséquent le grand cercle intersection de 52 et du plan xOy est composé de points singuliers pour B et comme parmi_les orbites de A il existe également un grand cercle de points singuliers A et B ont au moins deux points singuliers en commun donc {A,B} nrest pas transitif sur 52.

S i o n a v a i t K e r B c K e r A , l a d r o i t e K e r B s e r a i t s t a b l e p a r A e t B e t i l n ' y

a u r a i t p a s t r a n s i t i v i t é d e i A , n l s u r I R 3 - { O } , e t d a n s c e c a s d é t ( R + g ) = 0 ' * Nous supposerons dans la suite que Ker B Ê

rql4 2 4 rql4

-D a n s c e c a s I m B * I m A e t o n Peut s o i t u n v e c t e u r d i r e c t e u r d e K e r B e t j

t r o u v e r u n e b a s e ( i , j ) d e I m B t e l l e q u e u n v e c t e u r d i r e c t e u r d e I m B n K e r A

-* Nous supposerons dans la suite que Im A É Im B.

D a n s c e c a s , o n p e u t t r o u v e r u n v e c t e u r k t e l q u e ( i , j ' k ) f o r m e e t t e l q u e k s o i t u n v e c t e u r d i r e c t e u r d e I m A -D a n s l a b a s e ( i , j , k ) l e s m a t r i c e s d e

/ o o o \

M a t A = l o o o l

M a t B =

\ " o o l

s t é c r i v e n t : b r \ I c ' I a v e c a r c r + 0

ol

- {0 } est équivalente à s y s t è m e { e,n } par son A e t

r:

\ o

B a ' 0 0 L a c o n t r ô l a b i l i t é d u s y s t è m e t A , B ) s u r I R 3 d u s y s t è m e { - A , - B } , q u i t t e à r e m p l a c e r l e s u p p o s e r q u e a a r c > 0 .

Kù'

A

$

t r r B

^ D a n s l e c a s o i r I m A c I m B ( i . e . j e s t v e c t e u r l e p l a n I m B e s t s t a b l e à l a f o i s p a r A e t B , l i t é d u s y s t è m e t R , g ) s u r I R 3 { o } -D a n s c e c a s d é t ( n + e ) = 0 p u i s q u e I m ( A + B ) c d i r e c t e u r d e I m A ) i l e s t c l a i r q u e e t i l n ' y a p a s c o m p l è t e c o n t r ô l a b i -I m B e t d o n c d i m

t m ( R + s )

< 2 .

une base de IR3

l a c o n t r ô l a b i l i t é opposé on peut

D a n s [ "

l''

_{l l r}

posons : 1 â ' J I

E'

k

( l r

0 0 0

Dans la base lr) nous

M a t A ce cas - i 2 5 -avons : e t M a t B =

fi:)

lz,

: )

fi

a v e c q , = a a r c ' > 0 e t b = # , C h o i s i s s o n s c o m m e n o r m e e u c l i d i e n n e l a n o r m e r e n d a n t l a b a s e ( l r , l Z , l f ) o r t h o n o r m é e e t s o i t 5 2 l a s p h è r e u n i t é a s s o c i é e . N o u s a l l o n s d é c r i r e l e s t r a j e c t o i r e s d e À " , Ë , u , 5 2 . t r a j e c t o i r e " d e  " u , 5 2 o n t é t é d é c r i t e s p l u s h a u t équations des trajectoires de B sont données par : * Les * Les x

v

z 2 = Z t

%

= z t + o = r O * ( y o + b ) t + x o yo

Les orbites de B sont :

- un axe constitué de points singuliers - des droites situées dans le plan xOy - des paraboles situées dans des plans

: I ' a x e O x

strictement parallèles à Ox strictement parallèles à xOy

O n e n d é d u i t p o u r B :

- l e s p o i n t s ( 1 , 0 , 0 ) e t ( - t , 0 , 0 ) s o n t s i n g u l i e r s - l'équateur est stable pu, Ë

- p o u r t o u t p o i n t x d e I ' h é m i s p h è r e N o r d , l i m Ë r ( x ) =

t+-@

l i m Ë

t++@

. ( x )

2 6 -1 . C a s o i r T r A B > 0 ( i . e . b > 0 ) V u l e s é q u a t i o n s d e s t r a j e c t o i r e s d e B , i l e s t c l a i r , d a n s c e c a s , q u e l e q u a d r a n t { ( * , y , ù t R 3 / x > 0 , Y > 0 e t z > 0 } e s t s t a b l e p a r A e t B ; i l n ' y a d o n c p a s c o m p l è t e c o n t r ô l a b i l i t é p o u r l e s y s t è m e { R , e } . 2 . C a s o ù T r A B < 0 ( i . e . b < 0 ) N o u s a l l o n s m o n t r e r l a t r a n s i t i v i t é d e { À , 8 } s u r 5 2 -) P o u r c e l a , n o u s d é m o n t r o n s t o u t d ' a b o r d q u e l e s p ô l e s d e S -a u t o - -a c c e s s i b l e s .

p o u r les explications qui suivent, on pourra se reporter à la C I ' o r b i t e d e B p a s s a n r p a r l e p ô l e N o r d , c e t t e o r b i t e a p o u r é q u a t i o n s t 2 / 2 * b t X =

ll'll

y -

_'

t

o ù l l . l l 2 = G Z l z * b t ) 2 * t 2 + r

|'ll

1 Z =

il'll

L"",

s o n t n o r m a l e -

-1

|

J

f i g u r e 3 . S o i t

puisque_b ( 0, il est possible d'atteindre à partir du pôle Nord et à I'aide du champ B un point M, _/.r\ tel que x, < 0, Yl > 0, zr>

0-I Y r l

lril

L a t r a j e c t o i r e d e À p a s s a n t p a r M , é t a n t l e m é r i d i e n sens descendant, il est possible d'atteindre un point M,

M, pouvant être choisie

M t p a r c o u r u d a n s l e avec xZ < 0, yZ> 0

proche de

passant par le point M, sont données par de ^ l

| *z\

\'41

arbit r a i r e m e n t e t 0 . Les X =

v

-Z = , 2 . 0 , l a l a t i t u d e o , d e équations de la trajectoire d e B ,, z, to/z * (yz + bzr)t + x,

, Z t * Y z

)rl' t t

I t . I I t t t l t t t l t r a i c n f o i r ê a ô r r n e C o t t c l e s r a . n d c e r c l e v = 0 D o u r t = r ^ = - y ^ ( t . > 0 )

2 7 -er x(to) = - y27zr, - b y, + x, = çoS 02

||'tl

||'tl

/

- c o s o r s i n z e ,

\

- 7 x i " %

- b s i n g 2 + c o s r r )

o ù 02 désigne la latitude du point MZ,9z sa

longitude-S i e 2 e s t c h o i s i s u f f i s a m m e n t p r o c h e d e 0 ( e Z . 0 ) i l e s t c l a i r q u e x ( t " ) > 0 , p a r c o n s é q u e n t , à p a r t i r d u p o i n t M ' o n p e u t a t t e i n d r e g r â c e a u c h a m p B u n p o i n t M , s i t u é d a n s I ' h é m i s p h è r e S u d e t d e l o n g i t u d e p 3 . 0 a r b i t r a i r e m e n t p r o c h e d e 0 .

* Sur l'orbite C de Ë passant par le pôle Nord, on peut trouver un point MO situé d a n s I ' h é m i s p h è r e N o r d d e l o n g i t u d e g 4 < 0 arbitrairement proche de 0 ; ce p o i n t M O é t a n t , d e p l u s , s i t u é a v a n t l e p ô l e N o r d s u r l a t r a j e c t o i r e C C h o i s i s -s o n -s q 3 = I _{4 ,} l a t r a j e c t o i r e d e A p a s s a n t p a r M , é t a n t l e m é r i d i e n d e M , Par-c o u r u d a n s l e s e n s a s Par-c e n d a n t , M o e s t a Par-c Par-c e s s i b l e à p a r t i r d e M S g r â Par-c e a u Par-c h a m p  ; le pôle Nord est accessible à partir de Mo grâce à

B-* _{N o u s a v o n s d o n c m o n t r é q u e l e p ô l e N o r d e s t a u t o - a c c e s s i b l e , l e s t r a j e c t o i r e s} d e À e t Ë é r " n , r r a n s v e r s e s e n M ' l e p ô l e N o r d e s t n o r m a l e m e n t a u t o a c c e s s i -b l e . P a r s y m é t r i e l e p ô l e S u d e s t é g a l e m e n t n o r m a l e m e n t a u t o - a c c e s s i -b l e .

I l e x i s t e d o n c u n o u v e r t Ul contenant le pôle Nord, un ouvert U, contenant le p ô l e Sud tels que tout point de U

i ( i = ! , _ Z ) s o i t n o r m a l e m e n t a c c e s s i b l e à p a r r i r d e t o u t p o i n t d e U , p a r l e s y s t è m e { A , B } a i n s i q u e p a r l e s y s t è m e o p p o s é . ) D é m o n t r o n s q u e , d e t o u t p o i n t S " , o n p e u t a t t e i n d r e u n p o i n t d e U , s y s t è m e s _{{ A , B } e t { - A , - B } .} S o i t M o u n p o i n t d e 5 2 , o n p e u t t o u j o u r s s u p p o s e r q u e M o D ' e s t p a s s i n g u -l i e r p o u r Â

" u , i l e x i s t e t > 0 t e l q u e n , {rtro) n'est pas singulier pour A. A partir d e M o , i l e s t c l a i r q u e I ' o n p e u t a t t e i n d r e u n p o i n t d e U _ l

_ o u d e U , g r â c e a u c h a m p  . S i o n a t t e i n t u n p o i n t M , d e U _{, ,} l e s y s t è m e { A , B } p e r m e t d ' a t t e i n d r e , à p a r t i r d e M l , u n p o i n t d e M , d e U Z d ' a b s c i s s e p o s i t i v e , l a t r a j e c t o i r e d e A p a s -sant par M, étant le méridien de M, parcouru dans le sens ascendant, il est_possi-b l e d ' a t t e i n d r e u n p o i n t M , d e U

t à p a r t i r d u p o i n ^ t M , e t g r â c e a u c h a m p A .

*'u"1

2 8

-Conclusion _{Il existe un ouvert U t}

')

que_tout point de S- puisse { n , n } a i n s i q u t a u s y s t è m e

à

_ p a r t i r d e t o u t p o i n t d e { R . g } e s t d o n c t r a n s i t i f s u r è t r e r a m e n é e n U _t

opposé, tout point de U . r 1 g r â c e a u s Y s t è m e s o . du pôle grâce au

-Yr est

{ A , B } , l e N o r d t e l s y s t è m e a c c e s s i b l e s y s t è m e

_ 2 9 _

Trajectoires de B sur

M a t

_{B = [: ; i)}

s2, d"n, le système draxes (ox, oY, 0z)

a v e c b > 0 F i g u r e 2 :

3 0 -/ - - - - - - { \ \ , . __ I

t

v

t

t

I {.

-l

l'1j

Nous avons représenré les trajectoires de Ë sur 52 ainsi que la jectoire drauto-accessibilité du pôle Nord.

Dans le système d'axes (0x, 0y, Oz) la matrice de B s'écrit : Figure 3 :

.È : E t 'a :G: . ' * :-i' &' :::' t ' , . L 3 1 -4e cas : B p o s s è d e d e u x v a l e u r s p r o p r e s r é e l l e s d i s t i n c t e s e e t B , l a d i m e n s i o n du sous-espace propre associé à a étant égale à 2.

Dans une certaine base Mat B =

D a n s c e c a s l e s y s r è m e { A , B } n r e s t p a s t r a n s i t i f s u r I R 3 - { 0 } - E n e f f e t , B a m ê m e p r o j e c t i o n , u , 5 2 q u e B - a I d , o r l e p l a n x O y e s t c o n s t i t u é d e p o i n t s s i n g u l i e r s p o u r B - a I d , p a r p r o j e c t i o n s u r 5 2 , o n v o i t d o n c q u e l e g r a n d _ c e r c l e i n t e r s e c t i o n d e 5 2 e t d u p l a n x O y e s t c o m p o s é d e p o i n t s s i n g u l i e r s p o u r B . P a r a i l l e u r s n o u s a v o n s v u q u e p a r m i l e s t r a j e c t o i r e s a e À s u r 5 2 s e t r o u v e é g a l e m e n t un grand cercle de points singuliers, par conséquent À et B ont au moins deux p o i n t s s i n g u l i e r s c o m m u n s , u , 5 2 , l e s y s t è m e t À , Ë I n ' e s t d o n c p a s t r a n s i t i f s u r 5 2 . N o t o n s q u e , d a n s c e c a s , d é t ( A + B - a l d ) = 0 c a r d i m ( K e r A ( t c e r ( g - o t d ) ) > o '

5e cas : B possède deux valeurs propres réelles distinctes, la dimension des sous-espaces propres étant égale à 1.

Dans une certaine base Mat B =

B a même projection sur 52 que B -cld, par conséquent on peut toujours supposer _{que o = 0 ; de plus, quitte à étudier la contrôlabilité du système { -A,-B }} a u l i e u d e { A r B } , o n p e u t t o u j o u r s s u p p o s e r q u e B > 4 .

Enfin la complète contrôlabiliré d'un système {A,B} sur IR3 - { 0 } est équivalente à la complète contrôlabilité drun système { AIB } pour tout À positif , on peut donc s u p p o s e r q u e B - a = 1 . ( : ; : )

(:;i)

O n s r e s t d r o r d r e 2 e t o ù r B donc ramené à a p o u r m a t r i c e

l o 1 o \

t l

l o o o l

l l

\ o o t J

l ' é t u d e d r u n s y s t è m e { A , B } o ù A e s t dans une certaine base :

M a t B =

3 2 N o u s c h e r c h o n s t o u t d t a b o r d u n e b a s e d e t R 3 d a n s l a q u e l l e A e t B s r é c r i -v e n t s o u s l a f o r m e l a p l u s s i m p l e p o s s i b l e . A e s t n i l p o t e n t d ' o r d r e 2 d o n c d i m K e r A = 2 e t I m A C K e r A K e r B C I m ( B - I d ) e t d i m I m ( B - I d ) = 2 S o i t P l e p l a n P = I m ( B - I d ) * _{L e p l a n P e s t s t a b l e p a r B , s i o n a v a i t I m A C P , c e p l a n s e r a i t} s t a b l e p a r A e r i l n ' y a u r a i t p a s c o m p l è t e c o n t r ô l a b i l i t é d u s y s t è m e

r R 3 - { 0 } .

D a n s c e c a s o n a u r a i t d é t ( R + B - I d ) = 0 c a r I m ( A + B - I d ) = I m ( B On suppose dans la suite que Im A fr, P

é g a l e m e n t

{ n,e } sur

- rd).

* _{D a n s c e c a s , o n p e u t t r o u v e r} - _{i s o i t u n v e c t e u r d i r e c t e u r} - (i,j) soit une base de P - _{k s o i t u n v e c t e u r d i r e c t e u r}

- _{dans cette base : Mat B =}

u n e b a s e ( i , j , k ) d e I R 3 t e l l e q u e : d e K e r B

d e l m A

ft; :)

\o orJ

Si on avait d = 0, alors le plan P engendré par i et k serait stable par B ainsi que par A car il contient llimage de A, il n'y aurait alors pas transitivité du s y s t è m e { A , B } s u r I R 3 - { O } .

D a n s c e c a s o n a u r a i t : d é t ( A + B ) = 0 p u i s q u e t m ( n + g ) C p ' . On suppose dans la suite que d I O

Posons alors : - i t C - \ . = \ _a + r / l + J 1 ,

= a K

I t

lz

lr

(::l)

(:ii)

3 3 -E l i m i n o n s e n c o r e d e u x c a s p a r t i c u l i e r s : - _{s i a = 0 , l a d r o i t e d e v e c t e u r d i r e c t e u r i e s t s t a b l e p a r A e t B , l e s y s t è m e} { A , B } n r e s t p a s t r a n s i t i f s u r I R 3 t o } -D a n s c e c a s d é t ( A + g ) = o - s i b = 0 , l a d r o i t e d e v e c r e u r d i r e c t e u r j + k e s t s t a b l e p a r A e t B , l e s y s t è m e { A , B } n r e s t d o n c p a s t r a n s i t i f s u r I R 3 - { o } . D a n s c e c a s d é t ( n + g - t d ) = o N o u s s u p p o s e r o n s d o n c , d a n s l a s u i t e , q u e a I 0 e t b l 0 D a n s c e c a s d é t ( n * e ; = a l 0 e t d é t ( A + B - l d ) = b I 0 A l l u r e d e s t r a j e c t o i r e s d e À e t Ë s u r 5 2 * _{L e s t r a j e c t o i r e . d e  s o n t :} U n g r a n d c e r c l e g r a n d C d e p o i n t s s i n g u l i e r s : C e s t l e g r a n d c e r c l e i n t e r s e c -tion de 52 et du plan d'équa-tion ax + by = Q

- Des méridiens situés de part et d'autre du grand cercle C, ces méridiens sont p a r c o u r u s d a n s d e s s e n s d i f f é r e n t s s u i v a n t q u e I ' o n e s t d a n s I ' u n e o u l r a u t r e d e m i - s p h è r e d é f i n i e Par C.

Notons D, la

$emi-+hère déterminée par le grand cercle C et contenant le point de coordonnéesf _ô1, O, la demi-sphère symétrique de Dr.

to/

- Si a > 0 les trajectoire. de À passant par les points de D, (resp. Dr) sont des méridiens parcourus dans le sens ascendant (resp.

descendants)-. Si a <0 les trajectoires de  p".rtn, par les points de Dt (resp. Dr) sont des méridiens parcourus dans le sens descendant (resp.

4 3 4 4 -L e s é q u a t i o n s d e s t r a j e c t o i r e s a e Ë s o n t d o n n é e s p a r : x ( t ) = ( y . - z o ) t + x o y ( t ) = r o " ' * y o - z o z ( t ) = T o s t . B p o s s è d e d e u x v e c t e u r s p r o p r e s : l e s v e c t e u r s e l e t e Z + e 3 . l e s p l a n s d ' é q u a t i o n s z = 0 e t y - z = 0 s o n t s t a b l e s p a r B ' On en déduit pou, Ë , - l e s p o i n t s P ( 1 , 0 , 0 ) , P ' ( - 1 , 0 , 0 ) e t Q @ , ' E / 2 , J - z / 2 ) , Q ' ( 0 , - J - z l z , - J 7 / z ) s o n t d e s p o i n t s s i n g u l i e r s p o u r B .

- l'équateur et le grand cercle intersection de 52 et du plan d'équation y - z= O sont stabl", pu.,

Ë-- le bassin d'attraction du point Q est I'hémisphère Nord l e b a s s i n d t a t t r a c t i o n d u p o i n t Q r e s t I ' h é m i s p h è r e S u d - pour le champ oPPosé - g ,

l e b a s s i n d r a r r r a c r i o n d u p o i n t P ( r e s p . P ' ) e s t l a d e m i - s p h è r e d é f in i e p a r y z < 0 ( r e s P . Y z > O )

{ \\ _ \ \ --_ I I I I

I

Nous avons représenté

r{ f a *oc ôw ôrr ôz l\rt a t

l e s t r a j e c t o i r e s

^ = [ : : : \

de À sur s2, dans le système Figure 4 :

â-T

3 6

-Nous avons représenté les

^ - - ^ . : - ^ J r ^ . . ^ - ^ - ^ , , n . t r a l e c to i r e s d u c h a m p

(:: r\

Figure 5 : À i l o t R ; sur s2, dans le

3 7

-Montrons mainrenanr que le système {A,B} est transitif sur IR3 - to} si et seulement si Tr AB < 0.

Nous montrons tout d'abord que le système {A,B } n'est pas transitif sul

7 S- dès que Tr AB ).0-l . C a s o ù T r A B = - a + b > 0 1 . 1 . C a s o ù T r A B > 0 a v e c a > 0 e t b > 0 R e m a r q u o n s t o u t d ' a b o r d q u e , p u i s q u e a > 0 , l e s t r a j e c t o i r e , a " À p a s s a n t p a r l e s p o i n t s d e D l s o n t d e s m é r i d i e n s p a r c o u r u s d a n s l e s e n s a s c e n d a n t . D t e s t , i c i , l a d e m i - s p h è r e d é f i n i e p a r : ') D 1 = { ( x , y , " ) S " f a x + b y > 0 } D r a u t r e p a r t , p u i s q u e - a + b ) 0 e t a > 0 e t b > 0 , ! > 1 â C o n s i d é r o n s a l o r s l a p a r t i e E d e l a s p h è r e d é f i n i e p a r : E = { ( * , y , r ) S 2 I y ) 0 , z > 0 e t x + y > 0 }

/ *"1

* soit Mo ly"l un point de E puisque b ) 1 on a :

l r " l

a

a x o

- + b y o > . a ( x o + y o ) > 0 d o n c l e p o i n t M o a p p a r t i e n t à D t : l e s t r a j e c t o i r e s de A passanr par les points de E sont donc des méridiens parcourus dans le sens ascendant, E est donc stable par A.

* _{M o n t r o n s q u e l a p a r t i e E e s t é g a l e m e n t s t a b l e p a r B :}

l*À

s o i t M "

[ y " l u n p o i n t d e E , l e s é q u a t i o n s d e l a t r a j e c t o i r e d e B p a s s a n t p a r lz"l

Mo sont données par :

l l . l | * t , l = ( y o - z o ) t + x o

l l . l l v ( t ) = z o ê t + y o - z o o ù l l . l 1 2

= ( ( y o - r o ) t * * ) 2 * ( r o e t * y o - r ) z * " 2 o . 2 t

3 8

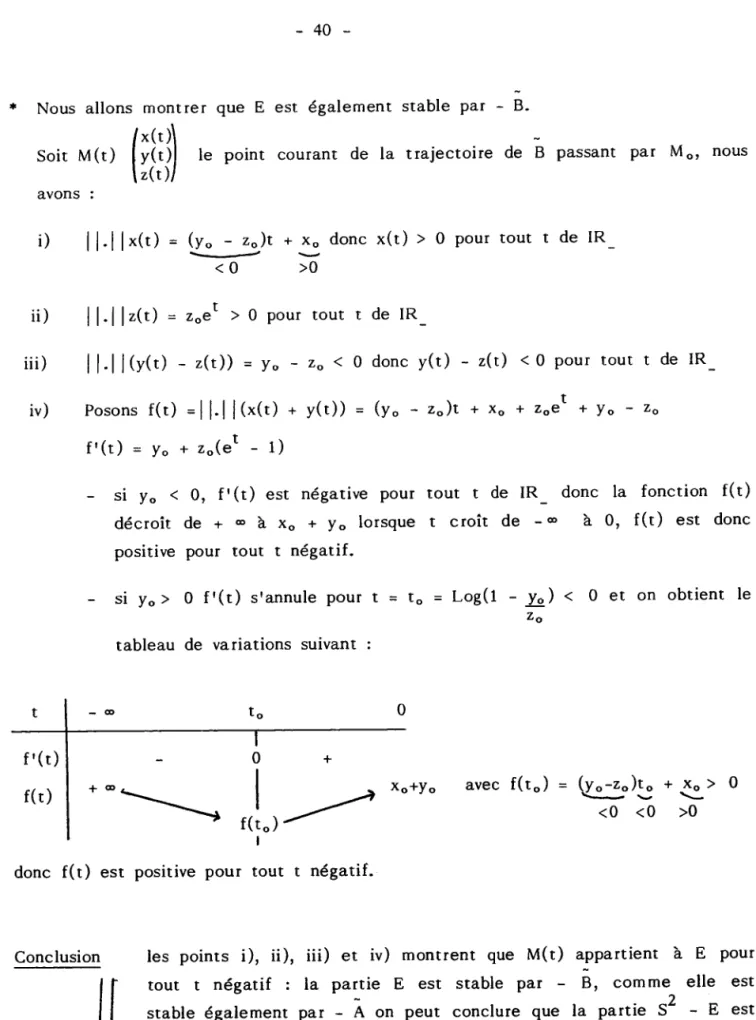
-i ) _{l l . l l y ( t ) = z o e t r y o} = 3 ( Ù ) + Y o > o >0 >0 >0 donc y(t) > 0 pour tout t

PositifI l l l r ( t ) = z o e t > 0 p o u r t o u t t p o s i t i f -P o s o n s f ( t ) = l l . l l ( * ( t ) * y ( t ) ) = ( y o - 2 , ) t f ' ( t ) = y o - r o * r o . t = g " ( d j ) * y " > 0 > 0 > 0 > 0 f ' ( t ) e s t p o s i t i v e p o u r t o u t t d e I R * d o n c l a à + - l o r s q u e t c r o î t d e 0 à + - , d o n c f ( t ) e s t t + x o + z o e t Y o - z o f o n c t i o n f c r o î t d e x o + Yo ) positive pour tout t de IR*. i i )

i i i )

Conclusion

f x ( t ) \

S i M ( t ) ly(t)l désigne le point t z ( t ) l

p a r M o , l e s p o i n t s i) , i i ) e t i i i ) à E pour tout t positif. E_ e_st stable par A, le système {Rrn }

c o u r a n t d e l a t r a j e c t o i r e d e B p a s s a n t c i - d e s s u s m o n t r e n t q u e M ( t ) a p p a r t i e n t s t a b l e p a r B , c o m m e E e s t é g a l e m e n t n ' e s t p a s t r a n s i t i f , u , 5 2 . 1 . 2 . C a s o ù T r A B > 2 0 a v e c a < 0 e t b > 0 R e m a r q u o n s t o u t d , a b o r d q u e l e s t r a j e c t o i r e s d e À p a s s a n t p a r l e s p o i n t s d e D , s o n t d e s m é r i d i e n s p a r c o u r u s d a n s l e s e n s d e s c e n d a n t . D t e s t , i c i , l a d e m i -s p h è r e d é f i n i e p a r : ) D l = {(x,y,r) S' f ax + by < 0}

Considérons la partie E de la sphère définie par : ,)

E = { ( * , y , r ) S " I x > 0 , y < 0 e t z > 0 I

/ *"1

* Si Mo lt;l est un point de E, axo + bYo < 0, le point Mo appartient donc l z o I

à Dr: la trajectoire de A passant par Mo est donc le méridien de M-o parcouru dans le sens descendant. Ceci prouve que E est stable par le champ - A'