Automatic Grid Finding in Calibration Patterns using Delaunay Triangulation

(1)

https://doi.org/10.4224/8913090

READ THESE TERMS AND CONDITIONS CAREFULLY BEFORE USING THIS WEBSITE.

https://nrc-publications.canada.ca/eng/copyright

Vous avez des questions? Nous pouvons vous aider. Pour communiquer directement avec un auteur, consultez la Questions? Contact the NRC Publications Archive team at

PublicationsArchive-ArchivesPublications@nrc-cnrc.gc.ca. If you wish to email the authors directly, please see the first page of the publication for their contact information.

NRC Publications Archive

Archives des publications du CNRC

For the publisher’s version, please access the DOI link below./ Pour consulter la version de l’éditeur, utilisez le lien DOI ci-dessous.

Access and use of this website and the material on it are subject to the Terms and Conditions set forth at

Automatic Grid Finding in Calibration Patterns using Delaunay

Triangulation

Shu, Chang; Brunton, Alan; Fiala, Mark

https://publications-cnrc.canada.ca/fra/droits

L’accès à ce site Web et l’utilisation de son contenu sont assujettis aux conditions présentées dans le site LISEZ CES CONDITIONS ATTENTIVEMENT AVANT D’UTILISER CE SITE WEB.

NRC Publications Record / Notice d'Archives des publications de CNRC:

https://nrc-publications.canada.ca/eng/view/object/?id=d0651d6a-f403-4890-a6ed-391be4169d1c https://publications-cnrc.canada.ca/fra/voir/objet/?id=d0651d6a-f403-4890-a6ed-391be4169d1c

(2)

National Research Council Canada Institute for Information Technology Conseil national de recherches Canada Institut de technologie de l'information

Automatic Grid Finding in Calibration Patterns using

Delaunay Triangulation *

Shu, C., Brunton, A., Fiala, M. August 2003

* published in NRC/ERB-1104. August 22, 2003. 17 Pages. NRC 46497.

National Research Council of Canada

Permission is granted to quote short excerpts and to reproduce figures and tables from this report, provided that the source of such material is fully acknowledged.

(3)

TECHNICAL REPORT

NRC-46497/ERB-1104 Printed August 2003

Automatic Grid Finding in Calibration

Patterns Using Delaunay

Triangulation

Chang Shu Alan Brunton Mark Fiala

Computational Video Group

Institute for Information Technology National Research Council Canada Montreal Road, Building M-50 Ottawa, Ontario, Canada K1A 0R6

(4)

NRC-46497/ERB-1104 Printed August 2003

Automatic Grid Finding in Calibration

Patterns Using Delaunay Triangulation

Chang Shu

Alan Brunton

Mark Fiala

Computational Video Group

Institute for Information Technology

National Research Council Canada

Abstract

This paper describes a technique for finding regular grids in the images of calibration patterns, a crucial step in calibrating cameras. Corner features lo-cated by a corner detector are connected using Delaunay triangulation. Pairs of neighboring triangles are combined into quadrilaterals, which are then topolog-ically filtered and ordered. We introduce a unique data structure for represent-ing both triangular and quadrilateral meshes. This mesh structure allows us to exploit the strong topological constraints in a regular grid. Experiments show that the method is able to handle images with severe radial distortions. Im-plemented on a conventional desktop, grid matching can be done in real time. The method is also applicable to marker detections for augmented reality and robot navigation.

(5)

List of Figures

1 The grid finding process . . . 5

2 Checkerboard calibration pattern . . . 6

3 Empty circumcircle . . . 7

4 Data structure for element . . . 8

5 Topological filtering. . . 9

6 Matching triangles . . . 9

7 Propagating node coordinates . . . 11

(6)

1 Introduction

The process of calibrating a camera involves determining the intrinsic parameters, such as focal length, and extrinsic parameters, such as the position and orientation of the camera with respect to a coordinate frame. This process often relies on the use of calibration patterns with known geometry. It is possible to calibrate cameras using only natural scenes, a process called autocalibration. However, when accuracy and reliability are demanded, one has to resort to the use of calibration patterns.

The first stage in calibration is to extract features from the images of patterns and match them with those of the patterns. Once the correspondences between points in the images and points in the pattern are established, the second stage is to solve for the intrinsic and extrinsic parameters by certain numerical procedures [6]. Published work has been concentrated on the second stage, for example [10, 12, 15]. Public domain code is also available [7, 14]. In contrast, there has been little study on the first stage. There, manual or user assisted methods are often used to solve the correspondence problem. With the increasing use of multiple cameras in many applications, the importance of the automatic correspondence problem has become evident.

The most commonly used calibration pattern is the checkerboard pattern. Its alternating black and white squares make strong corner features. In this paper, we use a variant of the checkerboard pattern, as shown in Figure 2. The three circles in the pattern are used for fixing the orientations.

One usual approach to processing the checkerboard pattern is to find edges and fit lines to them. Corners are found by intersecting lines. The drawback of this approach is that edges are in general curved due to radial distortions. Furthermore, the subse-quent ordering of the corners into a regular grid can be complex and unreliable. Soh et al. [9] used a regular grid pattern. They used attributed relational graph matching to arrange the centers of the black squares into a regular grid, though little detail was given in the paper. The OpenCV function, cvFindChessBoardCornerGuesses, uses a checkerboard pattern without the orientation marker, but the algorithm is not documented.

In this paper, we propose a method that exploits the topological structure of the checkerboard pattern. The main idea is to use Delaunay triangulation to connect the corner points. Neighboring pairs of triangles with similar colors are merged into quadrilaterals that match the squares in the pattern. We introduce an efficient data structure to facilitate the manipulation and traversal of the triangular and quadrilat-eral meshes. This mesh structure captures the topological information embedded in the images of the pattern. Figure 1 illustrated the main steps of the method. This approach is similar to the work of Tell and Carlsson [11] where both appearance and topological information are used for wide baseline matching. The difference in our

(7)

(a) (b)

(c) (d)

Figure 1: The grid finding process

case is that the topology is clearly known.

Our objective is to provide a calibration pattern matching method that is both robust and efficient. It should work reliably under different lighting conditions, oc-clusions, and quality of lens. It should also be fast enough so that it can be used for real-time applications such as robot navigation and augmented reality.

The rest of this paper is organized as follows. Section 2 discusses connecting fea-ture points using Delaunay triangulation and its associated data strucfea-tures. Section 3 discusses combining triangles into quadrilaterals. In section 4 we introduce a tech-nique that filters out illegal quadrilaterals. In section 5 we provide details of walking through the quadrilateral mesh to match them with the squares in the pattern. Ex-perimental results are presented in section 6. Finally, conclusions and discussions are presented in section 7.

(8)

Figure 2: Checkerboard calibration pattern

2 Feature point connectivity

We begin by finding corners in the images. Here, we use Harris’ corner detector [5], which is based on thresholding on the eigenvalues of a correlation matrix for each pixel. The checkerboard pattern gives strong corners. The positions of these corners can be found with subpixel accuracy.

Let the corner points in the image be denoted by {nk}, and the corner points in

the pattern be denoted by {Nk}. Our problem is to find a topologically compatible

map Φ : I → P such that Φ(nk) = Nk, where I is a subset of {nk} and P is a subset

of {Nk}. By topologically compatible, we mean that there exists a graph GI on I

and and a graph GP on P such that GI is homomorphic to GP .

An obvious choice for the graph GP is the regular grid that connects each corners of the square. Now, our problem is reduced to finding the graph GI that matches GP.

We start with connecting the feature points with Delaunay triangulation, and we will show that the triangular mesh thus generated can be transformed into a regular grid.

2.1 Delaunay triangulation

Given a set of points in the plane, Delaunay triangulation is the unique triangulation of the point set in which the circumcircle of every triangle is empty. The dual of Delaunay triangulation is the Voronoi diagram with the point set as the Voronoi sites. This means that in a Delaunay triangulation triangles are always formed with points that are close to each other.

(9)

Figure 3: Empty circumcircle

become general quadrilaterals. Consider a black or a white tile in the image with four corners A, B, C, and D, as shown in Figure 3. The circumcircle of the triangle ∆(A, B, C) does not contain other feature points. In fact, with the exception of point D, other feature points are quite far away from the circumcircle. Similarly, the circumcircle of triangle ∆(A, C, D) is also empty. Therefore, ∆(A, B, C) and ∆(A, C, D) are in the final Delaunay triangulation. The situation is the same in the other tiles where Delaunay triangles are formed by joining one of the diagonals of the tiles. Only in extreme cases, when the camera is pointed to the calibration pattern at a very small angle, the Delaunay triangulation may make triangles with their three corners belong to different tiles. In these cases, the corner finding is not reliable either, and therefore these images should not be used for calibration.

Delaunay triangulation is a well studied structure in computational geometry. Guibas et al. [3] gives an incremental algorithm which runs in (n log n) time. We use an early algorithm by Watson [13]. Although its worst case performance is O(n2

), in practice it runs close to linear time. We choose Watson’s algorithm because its imple-mentation is simple. For a survey of algorithms for Delaunay triangulation, see Bern and Eppstein [2]. Shewchuk [8] compares various algorithms from an implementation viewpoint.

2.2 Data structures

There are several ways to represent a mesh. The most commonly used data structure is the winged-edge data structure [1] and its variant the quad-edge data structure [4]. These data structures are capable of representing general polygons. In our case, we need only to represent meshes of uniform element type, which is either of triangle or quadrilateral. Therefore, it is possible to design simpler and more efficient data structures.

(10)

Figure 4: Data structure for element

either triangle or quadrilateral. Each element consists of an ordered lists of nodes. The nodes of an element are stored in a counter clockwise order. Each node stores its x and y coordinates as well as pointers to all the elements containing this node.

Our data structure should facilitate the efficient traversal of the meshes. Two operations are important. One is to compute the edge degree of a node, that is the number of edges incident to the node. This can be obtained from the stored elements in the nodes.

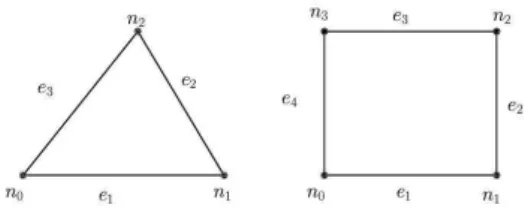
Another important operation is to find the neighboring elements sharing an edge. In our data structure, edge is a transient structure. We do not store edges. Instead, we construct them on the fly. It is easy to find the edges of an element. For a triangle element, assume its three nodes are (n0, n1, n2), its three edges are e1 = (n0, n1),

e2 = (n1, n2), and e3 = (n2, n0). Similarly, for a quadrilateral element (n0, n1, n2, n3),

its four edges are e1 = (n0, n1), e2 = (n1, n2), e3 = (n2, n3), and e4 = (n3, n0). See

Figure 4.

To find the elements sharing a common edge, all we need to do is to collect the elements stored in the two end nodes of the edge and select the elements that contain both end nodes.

3 Combining triangles

We wish to combine a pair of neighboring triangles to form a quadrilateral that cor-responds to a black or a white tile. As shown in section 2, the Delaunay triangulation will usually generate triangles by diagonalizing the tiles. From the design of the checkerboard pattern, it is clear that among the three edge-neighbors of a triangle, only one can have the same color (see Figure 6). In practice, we check for triangles with similar average colors. Note that the three tiles with circles satisfy the average color criterion.

Due to distortions, the pixels covered by a triangle may not be the same color. Since this situation always happens near the boundary of the triangle, we can simply ignore pixels with a small distance from the triangle edges.

(11)

(a) (b)

Figure 5: Topological filtering.

(12)

4 Topological filtering

When the pattern in an image does not fill up the whole frame, corners may be found outside the pattern in the environment scene. These corners will be part of the triangulation and some of the triangles may pass the color test and eventually be merged into quads (Figure 5(a)). Occasionally, due to noise, there are mismatched triangles inside the pattern area. These quads have to be pruned.

Notice that a proper node in a regular grid mesh has edge-degree of 2, 3, or 4. If a node has edge-degree more than 4, it is an illegal node. A quadrilateral that has two illegal nodes is removed from the mesh. Most of the illegal quads can be pruned by the topological filtering, since the chance of an arbitrary scene that contains feature points with regular grid topology is not very high.

We emphasize the importance of topological testing. Whenever possible, we per-form topological tests ahead of geometric tests, because topological tests are noise free. Determining topological information from geometric and appearance informa-tion always involves the use of thresholds which are difficult to choose. Different lighting conditions and different cameras may require different thresholds. We cannot eliminate the use of thresholds, but we can make use of the most reliable informa-tion, the topological informainforma-tion, first. This should be a general rule for any pattern identification system.

Figure 5 shows the effect before and after topological filtering.

5 Ordering quads - topological walking

Once we have a quadrilateral mesh, and after the topological filtering, we actually have a graph with a regular grid topology. The next step is to map nodes of the quads to the corners of the pattern. To do this, we start from an arbitrary quad and fix the coordinates of its nodes. Without loss of generality, we assume that the coordinates of the pattern’s corner are integers. Then the neighbors of the first quad can be labeled. This process is repeated in a flood-fill fashion. When all the nodes of the quads are labeled, we can find the reference quads and transform the labeled coordinates according to the reference orientation. Referring to Figure 2, we define the pattern origin as the horizontally centered white circle. The y axis points toward the other white circle. To determine orientation, however, we need only find the black circle and one white circle.

Since every quad is visited exactly once, the algorithm is O(n), where n is the number of the quads which is linear to the number of corners.

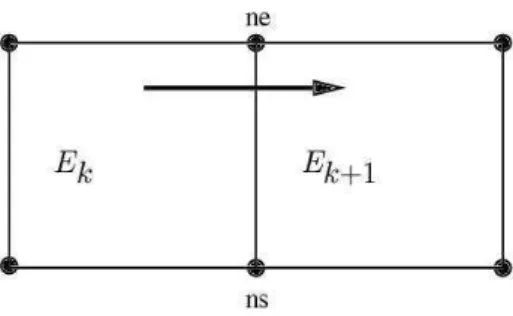
We illustrate the process of labeling node coordinates using an example of propa-gating element node coordinates from left to right (Figure 7). Suppose we have fixed the coordinates in element Ek, now we walk into its right neighbor element Ek+1

(13)

Figure 7: Propagating node coordinates

through Ek’s second edge e = (ns, ne). Let N [j] be the node with index j in element

Ek+1. As nodes ns and ne are shared by both Ek and Ek+1, we can use them to fix

the orientation of Ek+1 with respect to that of Ek. We first find the node index i of ns

in Ek+1. Then the pattern coordinates of the nodes of Ek+1 are assigned as follows.

N[i].x = ns.x N[i].y = ns.y

N[(i + 1) mod 4].x = ns.x + 1 N[(i + 1) mod 4].y = ns.y N[(i + 2) mod 4].x = ns.x + 1 N[(i + 2) mod 4].y = ns.y + 1 N[(i + 3) mod 4].x = ns.x N[(i + 3) mod 4].y = ns.y + 1

This orientation operation is equivalent to re-ordering the nodes in a quad based on its neighbors.

Note that the coordinate labeling is done using pure topological information. Hence, the algorithm works even if the the edges are curved due to radial distor-tions.

6 Experiments

The technique was tested by capturing image sequences of the calibration pattern with 12 different cameras. In each sequence the camera was moved relative to the pattern through a range of distances and orientations. The sequences were then processed on a Pentium III desktop computer with a Windows C++ program which performed the grid finding, with the result being a set of point correspondences for most of the frames in the sequence. The successfully extracted point correspondences from a sequence were then input to the OpenCV calibration function cvCalibrateCamera.

A total of 28 sequences with 12 to 52 frames, with three different resolutions were captured. Standard video (NTSC), IEEE 1394 (Firewire) and USB cameras

(14)

were used. The 12 cameras and the resolution modes used are: two color and two greyscale PointGrey DragonFly firewire cameras (640 x 480), a low-cost single board greyscale NTSC camera (416 x 484 pixels), three Intel Easycam Webcams (320 x 240 pixels) captured in greyscale, an NTSC camcorder Sharp VL-AH150U captured at 320 x 240 pixels through the NTSC input of a Intel IPro webcam, a wireless security NTSC camera also captured at 320 x 240 pixels by the Intel IPro webcam, and the camera input itself from the Intel IPro (320 x 240), and a Telemax webcam (320 x 240 pixels).

The calibration pattern from Figure 2 was printed out onto a small (20 x 25 cm) and large (150 x 150 cm) sheet, and each mounted on a flat panel. 14 of the 28 sequences were filmed aiming at the smaller pattern and the rest viewed the larger pattern.

For each frame, the vertices of the ordered quads (nodes of the mesh) were used as point correspondences where the quad number provided a pattern space coordinate. Table 1 details the success in finding these correspondences. For each sequence, the grid finding success and number of extracted correspondences is reported. Table 2 provides some statistics for each frame. Table 3 gives a breakdown of average time spent in each processing stage.

Figures 8 shows the results of grid finding on a distorted image and unwarped image after calibration.

7 Conclusions

We have presented a method for finding regular grids from calibration patterns using Delaunay triangulation. By triangulating the feature points, we create connectivi-ties between the isolating feature points. Working with a mesh data structure help exploit the topological constraints easily and greatly enhanced the robustness of the algorithm. The mesh data structure also results in a linear time algorithm for match-ing the grids.

The technique of triangulating feature points and combining them to form quadri-laterals can be applied to general marker identification in augmented reality and robot navigation. The principle of this approach is that we search for topological regulari-ties as well as appearance patterns. We may also design markers in such a way that their features have certain topological invariance under perspective transformation.

For future work, we plan to further improve the robustness and efficiency of the algorithm by adding corner validation mechanisms, more sophisticated topological filtering techniques, and optimization of the current algorithms.

(15)

(a) (b)

(c) (d)

(16)

References

[1] B. G. Baumgart. Winged-edge polyhedron representation. Technical Report STAN-CS-320, Stanford University, 1972.

[2] Marshall Bern and David Eppstein. Mesh generation and optimal triangulation. In Ding-Zhu Du and Frank Hwang, editors, Computing in Euclidean Geometry, Lecture Notes Series on Computing, Volume 1, pages 23–90. World Scientific, Singapore, 1992.

[3] Leonidas J. Guibas, Donald E. Knuth, and Micha Sharir. Randomized incremen-tal construction of Delaunay and Voronoi diagrams. Algorithmica, 7:381–643, 1992.

[4] Leonidas J. Guibas and Jorge. Stolfi. Primitives for the manipulation of general subdivisions and the computation of Voronoi diagrams. ACM Transactions on Graphics, 4(2):74–123, 1985.

[5] C. Harris and M. Stephens. A combined corner and edge detector. In Alvey Vision Conference, pages 147–151, 1988.

[6] Richard Hartley and Andrew Zisserman. Multiple View Geometry in Computer Vision. Cambridge University Press, 1998.

[7] OpenCV. Open Source Computer Vision Library. http://www.intel.com/ research/mrl/research/opencv/.

[8] Jonathan R. Shewchuk. Triangle: Engineering a 2D quality mesh generator and Delaunay triangulator. In First Workshop on Applied Computational Geometry, pages 124–133, Philadelphia, Pennsylvania, May 1996.

[9] L.M. Soh, J. Matas, and J. Kittler. Robust recognition of calibration charts. In IEE 6th International Conference on Image Processing and its Applications, pages 487–491, 1997.

[10] Peter F. Sturm and Stephen J. Maybank. On plane-based camera calibration: A general algorithm, singularities, applications. In IEEE Conference on Pattern Recognition and Computer Vision (CVPR99), volume 1, pages 432–437, 1999. [11] Dennis Tell and Stefan Carlsson. Combining appearance and topology for wide

baseline matching. In European Conference on Computer Vision (ECCV2002), LNCS 2350, pages 68–81, 2002.

(17)

[12] Roger Y. Tsai. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE Jour-nal of Robotics and Automation, 3(4):323–344, August 1987.

[13] D. F. Watson. Computing the n-dimensional Delaunay tessellation with appli-cation to Voronoi polytopes. The Computer Journal, 24(2):167–172, 1981. [14] R. Willson. Tsai Camera Calibration Software. http://www-2.cs.cmu.edu/

People/rgw/TsaiCode.html, 1995.

[15] Z. Zhang. Flexible camera calibration by viewing a plane from unknown ori-entations. In International Conference on Computer Vision (ICCV99), pages 666–673, Corfu, Greece, 1999.

(18)

Camera Frames % Located Points/ Grid Greyscale Dragonfly A 20 50% 93 Greyscale Dragonfly B 12 100% 72 Color Dragonfly A 20 95% 93 Color Dragonfly B 20 75% 81 Color Dragonfly B 20 100% 94 Low Cost NTSC 52 83% 75 Intel EasyCam A 32 81% 69 Intel EasyCam A 32 56% 57 Intel EasyCam A 32 100% 68 Intel EasyCam A 32 91% 75 Intel EasyCam A 32 97% 49 Intel EasyCam A 32 100% 55 Intel EasyCam B 32 94% 76 Intel EasyCam B 32 84% 48 Intel EasyCam B 32 72% 58 Intel EasyCam C 32 31% 66 Intel EasyCam C 32 84% 61 Intel EasyCam C 32 19% 62 Camcorder/IPro 32 19% 68 Camcorder/IPro 32 50% 75 Camcorder/IPro 32 85% 54 Wireless/IPro 32 88% 65 Wireless/IPro 32 16% 70 Wireless/IPro 32 63% 71 Intel IPro 32 94% 56 Intel IPro 32 94% 61 Telemax Webcam 32 69% 64 Telemax Webcam 32 13% 36

Table 1: Results of Automatic Grid Finding on 28 Sequences. The % Located field indicates how many of the frames in the sequence out of a total of Frames frames had a grid successfully located in them. The Points/Grid field indicates the average number of correspondences found per successfully located grid.

(19)

Frm Cnrs ∆’s Quads Pruned Points Total Quads Time (ms) 0 35 48 24 24 31 52 1 36 54 25 24 31 53 2 43 65 32 30 38 65 3 43 65 32 30 38 65 4 43 66 32 30 38 63 5 46 69 34 33 40 68 6 43 65 32 30 38 64 7 43 65 33 30 38 64 8 43 65 32 30 38 66 9 44 66 32 31 39 66 10 45 67 33 32 40 67 11 45 67 33 32 40 65 12 46 68 33 33 41 67 13 53 84 38 38 45 77 14 55 88 42 40 49 81 15 56 89 43 41 50 82 16 57 94 43 41 50 83 17 57 90 44 42 50 82 18 59 97 45 43 52 87 19 61 99 46 45 53 87 20 63 107 47 45 54 92

Table 2: Processing Stages in a Sequence for Each Image Frame. Column names: Frm – Frames, Cnrs – no. of Corners, ∆’s – no. of Triangles

Stage Average Time per Frame (ms) Harris Corner Detector 29.5 Delaunay Triangulation 1.6

Triangle Merging 15.9 Topological Filtering 19.2 Ordering Quads 16.9

Total 83.1