1
C H A P I T R E 1
N O T I O N S
D E B A S E
DÉFINITIONS GÉNÉRALES 2
1.1 DÉFINITIONS GÉNÉRALES
Le terme informatique (computer science) est un mot français désignant la science qui traite des données pour obtenir des résultats. Ce traitement est traditionnellement effectué à l’aide d’algorithmes. Un algorithme (algorithm) est une suite d’opérations à effectuer pour résoudre un problème (exemples 1.1 et 1.2). Exemple 1.1 Algorithme de résolution de l’équation ax+b = 0.
1 si a et b sont nuls, chaque nombre réel est solution et l’algorithme est terminé; 1 si a est nul et b non nul, l’équation est insoluble et l’algorithme est terminé; 2 si a est non nul, soustraire b à gauche et à droite du signe = et l’on obtient ax
= –b;
3 diviser chaque membre par a et l’on obtient le résultat cherché qui est x = –b/a.
L’algorithmique est une discipline fondamentale de l’informatique qui traite de la conception, de la réalisation et de la vérification des algorithmes. Sa pratique est rendue difficile par la rigueur qu’il est nécessaire d’appliquer, rigueur souvent négligée par les néophytes, voire parfois par les concepteurs plus expérimentés. Exemple 1.2 Algorithme de mise en marche d’une voiture.
1 mettre la clé dans le démarreur; 2 serrer le frein à main;
3 mettre le levier des vitesses au point mort;
4 répéter les opérations suivantes tant que le moteur ne tourne pas: • mettre la clé dans la position marche;
• tourner la clé dans le sens des aiguilles d’une montre; • attendre quelques secondes;
• si le moteur ne démarre pas, remettre la clé dans la position initiale; 5 enclencher la première vitesse;
6 desserrer le frein à main.
Lorsqu’un ordinateur doit exécuter un algorithme, celui-ci doit être exprimé dans un langage compréhensible par la machine. Ce langage appelé langage
machine (machine code) est composé de suites de chiffres 0 et 1 appelés bits qui
correspondent à des états distincts des circuits qui composent la machine. Or le programmeur ne peut pas exprimer des algorithmes complexes avec des 0 et des 1! Il va utiliser un langage plus proche d’une langue naturelle appelé langage de
programmation (programming language). Une fois cet algorithme codé dans un
DÉFINITIONS GÉNÉRALES 3
• soit traduit complètement en langage machine par le compilateur (compiler) pour permettre ensuite l’édition de liens;
• soit directement interprété (interpreted), c’est-à-dire que chaque ligne de code source est exécutée directement sans traduction préalable de tout le programme; cette ligne peut être traduite ou non en un langage proche du langage machine avant exécution.
La compilation (compilation) est donc une étape supplémentaire mais a l’avantage de produire un programme en langage machine. Ce programme en langage machine peut exister aussi longtemps que nécessaire. Chaque fois que le programme doit être utilisé, il le sera directement, ce qui implique que la compi-lation n’est nécessaire qu’après chaque modification du programme source.
L’interprétation (interpretation) est plus directe que la compilation, mais la traduction de chaque ligne a lieu lors de toutes les utilisations du programme.
L’édition de liens (link) est la phase pendant laquelle les différentes parties composant un programme sont réunies de manière à former un programme
exécutable. C’est au cours de cette opération que des composants préexistants, par
exemple des éléments graphiques, sont placés dans cet exécutable. Ces composants sont souvent regroupés dans une (ou plusieurs) bibliothèque(s) (library).
L’exécution (execution) d’un programme par un ordinateur consiste à exécuter les instructions machine les unes à la suite des autres. Elle sera nettement plus rapide dans le cas d’un programme compilé que pour un programme interprété.
Le déverminage (debugging) est l’activité de récupération, diagnostic et correction des erreurs de conception (logique) du programme. En d’autres termes, durant cette activité on procède à la mise au point du programme.
De manière générale, la programmation (programming) est l’art d’écrire des
programmes (programs) en langage de programmation et constitue une autre
discipline fondamentale de l’informatique. Un environnement de programmation (programming environment) ou de développement représente l’ensemble des outils logiciels (et parfois matériels) nécessaires à la conception, à la réalisation et à la maintenance d’applications complexes.
Il faut enfin définir le terme implémentation (implementation) qui regroupe toutes les caractéristiques (d’un langage de programmation) propres à un en-vironnement de programmation particulier. Parfois ce terme représente l’environ-nement lui-même.
LANGAGES DE PROGRAMMATION 4
1.2 LANGAGES DE PROGRAMMATION 1.2.1 Historique
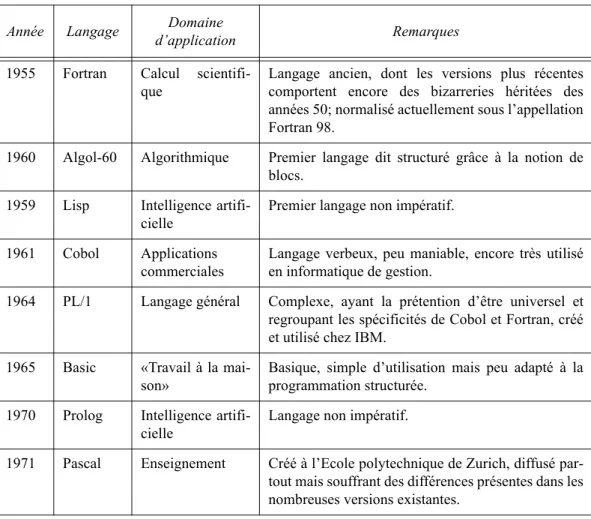
Plusieurs centaines de langages de programmation ont été proposés au cours de l’évolution de l’informatique. La majorité d’entre eux s’appliquaient à des domaines très particuliers alors que d’autres se voulaient plus généraux. Leur succès ou leur échec tient autant à leurs qualités ou leurs défauts qu’à la période où ils apparurent sur le marché ou dans les universités. Le tableau 1.1 décrit par ordre chronologique d’apparition plusieurs langages de programmation parmi les principaux utilisés jusqu’à aujourd’hui ainsi que leur principal domaine d’application. Même s’ils ne sont pas cités explicitement, il faut également mentionner les langages d’assemblage appelés assembleurs (assemblers), utilisés surtout pour programmer au niveau de la machine. Finalement, il faut préciser qu’il existe encore d’autres catégories de langages informatiques destinés par exemple à la simulation de systèmes ou à la conception de circuits électroniques.
Tableau 1.1 Principaux langages de programmation.
Année Langage d’applicationDomaine Remarques 1955 Fortran Calcul
scientifi-que
Langage ancien, dont les versions plus récentes comportent encore des bizarreries héritées des années 50; normalisé actuellement sous l’appellation Fortran 98.
1960 Algol-60 Algorithmique Premier langage dit structuré grâce à la notion de blocs.
1959 Lisp Intelligence artifi-cielle
Premier langage non impératif. 1961 Cobol Applications
commerciales
Langage verbeux, peu maniable, encore très utilisé en informatique de gestion.
1964 PL/1 Langage général Complexe, ayant la prétention d’être universel et regroupant les spécificités de Cobol et Fortran, créé et utilisé chez IBM.
1965 Basic «Travail à la mai-son»
Basique, simple d’utilisation mais peu adapté à la programmation structurée.
1970 Prolog Intelligence artifi-cielle
Langage non impératif.
1971 Pascal Enseignement Créé à l’Ecole polytechnique de Zurich, diffusé par-tout mais souffrant des différences présentes dans les nombreuses versions existantes.
LANGAGES DE PROGRAMMATION 5
1.2.2 Langage de programmation Ada
L’expérience montre que le premier langage de programmation appris est fondamental pour l’avenir d’un programmeur. En effet, les habitudes prises sont ancrées si profondément qu’il est très difficile de les modifier voire de s’en défaire! L’apprentissage de la programmation doit donc s’effectuer avec un langage forçant le programmeur à adopter de bonnes habitudes (sect. 1.3). Il est toujours plus facile d’évoluer vers de nouveaux langages lorsque ces bonnes habitudes sont acquises. Le langage Ada aide à l’apprentissage d’une bonne programmation en obligeant le programmeur à se soumettre à certaines contraintes et en lui fournissant une panoplie assez riche d’outils agréables à utiliser. Ces outils vont lui permettre de coder relativement simplement un algorithme même complexe et de refléter fidèlement sa structure. La version d’Ada présentée dans cet ouvrage est celle définie en 1995 [ARM] et normalisée ISO.
1972 C Programmation
système
Accès facile au matériel, largement diffusé; norma-lisé sous l’appellation ANSI-C.
1976 Smalltalk Langage général Programmation orientée objets, prototypage rapide. 1980 Modula-2 Programmation
système
Descendant direct de Pascal, mêmes problèmes de versions différentes.
1983 Ada Langage général Riche, utilisé pour développer des systèmes comple-xes et fiables, ainsi que pour des applications temps réel critiques; normalisé sous l’appellation Ada 83. 1984 C++ Langage général Successeur de C; permet la programmation orientée
objets; normalisé par l’ISO en 1998.
1995 Ada 95 Langage général Successeur d’Ada 83; ajoute la programmation orientée objets, par extension, etc; normalisé sous l’appellation Ada 95.
1996 Java Internet Semblable à C++, mais plus sûr; permet la program-mation d’applications classiques mais aussi d’applets.
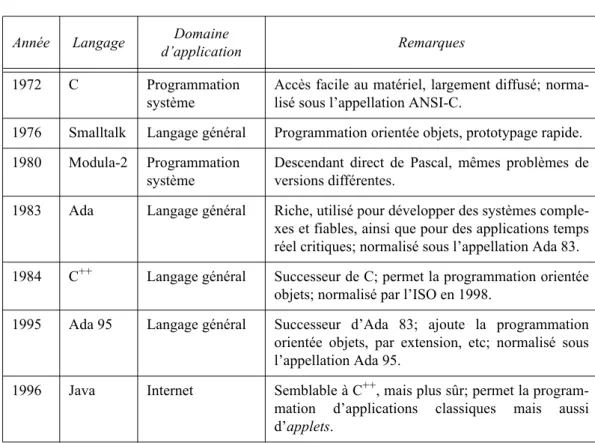
Tableau 1.1 (suite) Principaux langages de programmation.
BONNES HABITUDES DE PROGRAMMATION 6
1.3 BONNES HABITUDES DE PROGRAMMATION
Le but de tout programmeur est d’écrire des programmes justes, simples, lisibles, fiables et efficaces. Pour la justesse, la simplicité et la lisibilité, les quelques points suivants sont fondamentaux (la liste est non exhaustive!):
• Réfléchir et imaginer de bons algorithmes de résolution avant d’écrire la première ligne du programme.
• Une fois l’algorithme général trouvé, en écrire l’esquisse dans un formalisme pseudo-formel, puis préciser cette esquisse pour finalement coder l’algorithme dans le langage de programmation choisi.
• Lors du codage, choisir des noms parlants (utiliser des mnémoniques) pour représenter les objets manipulés dans le programme, commenter chaque morceau du programme de manière explicative plutôt que descriptive et tester chaque module, procédure, fonction soigneusement.
Pendant toute la démarche, adopter et appliquer systématiquement des conventions simples et cohérentes.
DE L’ANALYSE DU PROBLÈME À L’EXÉCUTION DU PROGRAMME 7
1.4 DE L’ANALYSE DU PROBLÈME À L’EXÉCUTION DU PROGRAMME
Voici une ébauche de marche à suivre pour la création de programmes à partir d’un problème donné:
1 bien lire l’énoncé du problème, être certain de bien le comprendre; 2 réfléchir au problème, déterminer les points principaux à traiter;
3 trouver un bon algorithme de résolution (sect. 1.7), l’écrire dans le formalisme choisi;
4 coder l’algorithme en un programme écrit sur papier (au moins pour son architecture principale);
5 introduire le programme dans l’ordinateur au moyen d’un éditeur de texte; 6 compiler le programme;
7 effectuer l’édition de liens du programme;
8 exécuter le programme, vérifier son bon fonctionnement par des tests significatifs.
En cas d’erreurs de compilation, il faut les corriger avec l’éditeur de texte puis recommencer le point 6. Si le programme fonctionne mais donne des résultats faux, ou si l’exécution du programme se termine par un message d’erreur, cela signifie qu’il y a des fautes de logique. Il faut réfléchir, parfois longuement, trouver l’ori-gine des fautes en particulier en s’aidant des outils de déverminage, modifier le pro-gramme en conséquence puis reprendre au point 6.
Lorsque les programmes source dépassent une page, il serait judicieux de s’habi-tuer à les concevoir et les tester par étapes. Cette façon de faire devient en effet indispensable lorsque la taille du code écrit dépasse, par exemple, deux cents li-gnes, ce qui représente encore un tout petit programme!
PROPRIÉTÉS D’UN PROGRAMME 8
1.5 PROPRIÉTÉS D’UN PROGRAMME
Lors de l’écriture d’une application, les propriétés énumérées ci-après devraient toujours guider le programmeur lors des choix qu’il devra inévitablement effectuer, que le programme soit simple ou compliqué. En effet, un code bien écrit sera toujours plus fiable, lisible, simple, juste et même efficace.
Ces propriétés sont les suivantes:
• La fiabilité (reliability) consiste à ce que les erreurs de programmation soient détectées à la compilation ou à l’exécution afin que le programme n’ait jamais de comportement imprévu. Il est naturellement préférable que le plus d’erreurs possible soient signalées à la compilation de manière à diminuer la phase de test du programme, toujours très coûteuse en temps et en argent, ainsi que le code supplémentaire généré pour la vérification de contraintes liées à l’exécution de certaines instructions. Un langage forte-ment typé répond à ce critère de fiabilité.
• La lisibilité (readability) permet de réduire la documentation associée au programme, de simplifier la correction des erreurs et de faciliter les modifications futures. Un langage permettant la construction de structures de données et disposant de structures de contrôle répond à ce critère. Rappelons cependant que les habitudes du programmeur sont au moins aussi importantes que le langage!
• La simplicité (simplicity) est un critère évident: ne jamais compliquer lorsqu’il est possible de rester simple.
• L’efficacité (efficiency) doit naturellement être suffisante afin que le programme s’exécute rapidement, mais ne doit pas constituer l’idole à laquelle tout le reste est sacrifié. Une conception bien pensée, une bonne structuration du code sont beaucoup plus importantes que l’accumulation d’astuces subtiles permettant un gain de temps minime lors de l’exécution du programme.
• Enfin, on appelle portabilité (portability) la propriété représentant l’indépendance d’une application ou d’un langage de programmation par rapport à la machine utilisée. Cette propriété joue un rôle fondamental lors de l’évolution des programmes au cours du temps. Plus un logiciel est portable, moins il sera sensible aux changements de matériels utilisés.
EXEMPLE INTRODUCTIF 9
1.6 EXEMPLE INTRODUCTIF
Une bonne introduction à l’algorithmique consiste à étudier un problème simple (exemple 1.3) dont la résolution sera effectuée en respectant la marche à suivre (sect. 1.4), restreinte aux points 1 à 4. Pour trouver un algorithme de résolu-tion, il faut appliquer une méthode et l’utiliser chaque fois qu’un problème de programmation doit être résolu.
La méthode proposée ici est connue sous le nom de méthode de décomposition
par raffinements successifs. Cet exemple va également permettre d’insister sur les
bonnes habitudes de programmation et d’introduire les premières notions de programmation en langage Ada.
Exemple 1.3 Problème simple.
Dessiner dans une fenêtre graphique une figure composée de deux formes géométriques, soit un carré et un triangle isocèle. De plus, le programme doit annoncer le début et la fin du dessin dans une fenêtre de texte.
Du fait de sa simplicité, la compréhension de ce problème est immédiate, après avoir précisé que la disposition des formes est libre. Le point 1 de la marche à suivre est fait.
MÉTHODE DE DÉCOMPOSITION PAR RAFFINEMENTS SUCCESSIFS 10
1.7 MÉTHODE DE DÉCOMPOSITION PAR RAFFINEMENTS SUCCESSIFS
Cette méthode est basée sur l’idée que, étant donné un problème à résoudre, il faut le décomposer en sous-problèmes de telle manière que:
• chaque sous-problème constitue une partie du problème donné;
• chaque sous-problème soit plus simple (à résoudre) que le problème donné; • la réunion de tous les sous-problèmes soit équivalente au problème donné. Il faut ensuite reprendre chaque sous-problème et le décomposer comme ci-dessus et recommencer jusqu’à ce que chaque sous-problème soit facile à résoudre. Une étape de cette suite de décompositions est appelée raffinement.
Une telle méthode est efficace après avoir été utilisée plusieurs fois. Lorsque les problèmes deviennent suffisamment complexes pour que la découverte d’une solu-tion ne soit plus un processus trivial, il est indispensable de l’appliquer systéma-tiquement. Elle donne en général de bons algorithmes résolvant les problèmes posés. Mais, comme toute méthode, elle a cependant ses limites. Celle-ci devient inutilisable lorsque la complexité des problèmes est tout simplement trop grande pour que la suite de raffinements soit facilement exploitable.
APPLICATION À L’EXEMPLE INTRODUCTIF 11
1.8 APPLICATION À L’EXEMPLE INTRODUCTIF 1.8.1 Considérations techniques
Selon le point 2 de la marche à suivre (sect. 1.4), il faut déterminer les points principaux à traiter. Le problème étant en partie géométrique, il faut tout d’abord savoir comment dessiner dans une fenêtre de l’écran d’un ordinateur. La documentation technique nous apprend que:
• le système de coordonnées cartésiennes a son origine au point (0, 0) situé en haut à gauche de la fenêtre graphique;
• les axes sont disposés comme le montre la figure 1.1. Figure 1.1 Axes et coordonnées cartésiennes dans une fenêtre graphique.
Ceci étant établi, il faut connaître comment faire apparaître la fenêtre, dessiner un carré et un triangle, ou au moins des segments de droite. De même, il sera nécessaire de savoir comment écrire dans la fenêtre de texte. Ces renseignements constituent le point 2 de la marche à suivre.
1.8.2 Algorithme de résolution
L’algorithme de résolution (point 3, sect. 1.4) va être déterminé en utilisant la méthode décrite dans la section 1.7. Etant donné le problème initial, on en extrait les sous-problèmes:
1 annoncer le début du dessin;
2 ouvrir, faire apparaître la fenêtre de dessin; 3 dessiner le carré;
4 dessiner le triangle isocèle; 5 annoncer la fin du dessin.
Ceci constitue le premier raffinement. Comme les points 1, 2 et 5 sont immédiatement traduisibles en Ada, ils seront laissés tels quels. Le raffinement
(0,0) X
APPLICATION À L’EXEMPLE INTRODUCTIF 12
suivant est alors:
1 annoncer le début du dessin;
2 ouvrir, faire apparaître la fenêtre de dessin;
3 choisir la position du carré, i.e. celle du sommet en haut à gauche; 4 dessiner le carré avec les côtés parallèles aux axes de coordonnées; 5 choisir la position du triangle isocèle, i.e. celle du sommet gauche;
6 dessiner le triangle isocèle sur la pointe, avec la base parallèle à l’axe des x. 7 annoncer la fin du dessin.
Afin de présenter un troisième raffinement, l’environnement Ada à disposition est supposé ne pas permettre le dessin d’un carré ou d’un triangle. La décom-position devient:
1 annoncer le début du dessin;
2 ouvrir, faire apparaître la fenêtre de dessin;
3 choisir la position du carré, i.e. celle du sommet en haut à gauche; 4 dessiner le côté supérieur depuis cette position;
5 dessiner le côté droit depuis l’extrémité droite du côté supérieur; 6 dessiner le côté inférieur depuis l’extrémité inférieure du côté droit; 7 dessiner le côté gauche depuis l’extrémité gauche du côté inférieur; 8 choisir la position du triangle isocèle, i.e. celle du sommet gauche; 9 dessiner la base depuis cette position;
10 dessiner le côté droit depuis l’extrémité droite de la base;
11 dessiner le côté gauche depuis l’extrémité inférieure du côté droit; 12 annoncer la fin du dessin.
Cette suite de raffinements s’arrête ici. En effet, même si la norme ne définit aucune opération graphique, des outils supplémentaires présents dans (presque) tous les environnements Ada permettent de dessiner un segment depuis un point courant et d’afficher un mot. La suite d’opérations 1, 2, 3.1, 3.2.1, etc., constitue un algorithme de résolution du problème donné.
1.8.3 Codage de l’algorithme en Ada
Un premier essai de codage de l’algorithme (point 4, sect. 1.4) donne le programme Exemple_Essai_1 (exemple 1.4). Il est correct, simple, fonctionne parfaitement mais est assez mal écrit. En effet, l’art de la programmation doit obéir à des conventions de style telles que celles décrites dans [AUS 95].
En particulier, il faut savoir que:
• un programme doit être lisible, ce qu’il n’est pas; • un programme doit être commenté, ce qu’il n’est pas;
• le code doit refléter les décisions prises par le programmeur, ici la grandeur des dessins et les points initiaux des dessins;
• les nombres entiers peuvent signifier n’importe quoi! Il faut préciser leur signification en leur substituant des noms parlants.
APPLICATION À L’EXEMPLE INTRODUCTIF 13
Exemple 1.4 Premier codage (maladroit) de l’algorithme obtenu. with Ada.Text_IO; use Ada.Text_IO;
with Spider; use Spider; procedure Exemple_Essai_1 is begin
Put_Line ( "Debut du dessin"); Init_Window ("Fenetre de dessin"); Move_To (30, 120); Line (50, 0); Line (0, 50); Line (– 50, 0); Line (0, – 50); Move_To (110, 120); Line (80, 0); Line (– 40, 40); Line (– 40, – 40);
Put_Line ( "Fin du dessin");
end;
Malgré son apparente complexité, l’exemple 1.5 ci-après présente un programme source bien écrit et illustrant les points énumérés précédemment. Les qualités de style de ce programme résident en particulier dans:
• les indications sur l’auteur, le but du programme (ici réduit au minimum), la date de création, les modifications éventuelles; d’autres informations générales pourraient bien entendu compléter cette introduction;
• la mention systématique de noms représentant des nombres; • les explications décrivant chaque partie du programme; • la cohérence dans le choix des identificateurs;
• la mise en page et l’alignement des lignes.
Il est vrai qu’en pratique, la production de logiciels dans des délais souvent extrêmement réduits conduit parfois à négliger l’effort de présentation du code. D’un autre côté, certaines entreprises imposent des normes strictes à respecter à la lettre. C’est le cas des industries pour lesquelles la qualité et la fiabilité du code produit est impérative comme dans le domaine spatial ou l’avionique par exemple. Exemple 1.5 Codage corrigé de l’algorithme obtenu.
-- Auteur: Dupont Jean
-- But du programme: illustrer un codage soigne -- Date de creation: 1 octobre 1999
-- Date de modification: -- Raison de la modification:
APPLICATION À L’EXEMPLE INTRODUCTIF 14
-- Pour afficher du texte dans la fenetre de texte
with Ada.Text_IO; use Ada.Text_IO;
-- Pour lire les nombres entiers donnes par l'utilisateur
with Ada.Integer_Text_IO; use Ada.Integer_Text_IO;
-- Pour travailler avec la fenetre de dessin
with Spider; use Spider;
-- Ce programme illustre un codage soigne en Ada; il dessine un -- carre et un triangle
procedure Exemple_Bien_Fait is
Droite : constant := 1; -- Pour se deplacer d'une unite
Gauche : constant := –1; -- dans les quatre directions
Haut : constant := –1; Bas : constant := 1;
-- Pour un trait vertical, le deplacement horizontal est nul A_L_Horizontale : constant := 0;
-- Pour un trait horizontal, le deplacement vertical est nul A_La_Verticale : constant := 0;
Cote_Carre : constant := 50; -- Longueur d'un cote du carre
Abscisse_Carre : Integer; -- Abscisse et ordonnee du point
Ordonnee_Carre : Integer; -- initial de dessin du carre
Demi_Base : constant := 40; -- Longueur de la demi-base du
-- triangle
Abscisse_Triangle : integer; -- Abscisse et ordonnee du point Ordonnee_Triangle : integer; -- initial de dessin du triangle
begin -- Exemple_Bien_Fait
-- Presentation du programme a l'utilisateur
Put ("Bonjour. Je vais dessiner un carre et un triangle "); Put_Line ("dans une fenetre de dessin.");
Put_Line ("Debut du dessin...");
-- Pour pouvoir dessiner dans la fenetre de dessin Init_Window ("Fenetre de dessin");
-- L'utilisateur donne le point initial de dessin du carre Put ("Donnez l'abscisse du point initial du carre: "); Get (Abscisse_Carre);
Put ("Donnez l'ordonnee du point initial du carre: "); Get (Ordonnee_Carre);
-- Dessin du carre
Move_To (Abscisse_carre, Ordonnee_Carre); Line (Cote_Carre * Droite, A_L_Horizontale); Line (A_La_Verticale, Cote_Carre * Bas); Line (Cote_Carre * Gauche, A_L_Horizontale); Line (A_La_Verticale, Cote_Carre * Haut);
-- L'utilisateur donne le point initial de dessin du triangle Put ("Donnez l'abscisse du point initial du triangle:"); Get (Abscisse_Triangle);
APPLICATION À L’EXEMPLE INTRODUCTIF 15
Get (Ordonnee_Triangle); -- Dessin du triangle.
Move_To (Abscisse_Triangle, Ordonnee_Triangle); Line (2 * Demi_Base * Droite, A_L_Horizontale); Line (Demi_Base * Gauche, Demi_Base * Bas); Line (Demi_Base * Gauche, Demi_Base * Haut); -- Message de fin du dessin et du programme Put_Line ("Fin du dessin.");
Put_Line ("Fin du programme.");
STRUCTURE D’UN PROGRAMME ADA 16
1.9 STRUCTURE D’UN PROGRAMME ADA
Un programme Ada est composé de quatre parties principales:
• La clause de contexte (context clause) qui sera développée par la suite (§ 10.5.1). Cette clause doit contenir les outils Ada que le programmeur peut utiliser sans avoir à les construire lui-même, et indispensables au fonction-nement du programme. Ces outils sont regroupés en paquetages, notion présentée ultérieurement (chap. 11). Il est nécessaire de les indiquer pour que le compilateur puisse en tenir compte lors de la phase de vérification et de traduction en code machine. La mention de ces paquetages se fera de manière intuitive en suivant les exemples fournis. Pour le programme Exemple_Bien_Fait la clause de contexte est la suivante:
with Ada.Text_IO; use Ada.Text_IO;
with Ada.Integer_Text_IO; use Ada.Integer_Text_IO; with Spider; use Spider;
• L’en-tête du programme, où est spécifié le nom du programme. Pour le programme Exemple_Bien_Fait l’en-tête est la suivante:
procedure Exemple_Bien_Fait is
• La partie déclarative (declarative part), comprise entre l’en-tête et le mot reservé begin, contenant les déclarations (declarations) des objets (constantes, variables, etc.) utilisés dans le programme. Ces objets représenteront des données traitées par le programme. La partie déclarative peut encore contenir d’autres déclarations comme des sous-programmes (chap. 4) ou encore des types (chap. 5).
• Pour le programme Exemple_Bien_Fait la partie déclarative est la suivante: Droite : constant := 1; Gauche : constant := –1; Haut : constant := –1; Bas : constant := 1; A_L_Horizontale : constant := 0; A_La_Verticale : constant := 0; Cote_Carre : constant := 50; Abscisse_Carre : Integer; Ordonnee_Carre : Integer; Demi_Base : constant := 40; Abscisse_Triangle : Integer; Ordonnee_Triangle : Integer;
Il faut noter que les déclarations sont groupées logiquement: d’abord les objets généraux pour le dessin, puis ceux concernant le carré, finalement ceux concernant le triangle.
STRUCTURE D’UN PROGRAMME ADA 17
• La partie instructions du programme, comprise entre les mots begin et end, appelée souvent corps (body). Elle contient les instructions (statements) du programme, c’est-à-dire les actions à entreprendre sur les données. Parmi celles-ci et à titre d’exemple:
Put_Line ("Debut du dessin...");
Line (Cote_Carre * Droite, A_L_Horizontale);
C’est dans cette partie que se trouve, sous forme codée, l’algorithme choisi pour résoudre le problème. Il faut encore relever le rappel du nom du programme après le end final.
Finalement, il faut insister sur le fait qu’un programme doit être documenté, en particulier par des commentaires initiaux précisant le nom de l’auteur, la date de création, etc., comme suggéré dans l’exemple 1.5. Un guide méthodologique intitulé Style et qualité des programmes Ada 95 [AUS 95], destiné aux professionnels, fournit de nombreuses indications relatives aux différents aspects de l’écriture du code source (sect. 1.11).
CONSTITUANTS D’UN PROGRAMME 18
1.10 CONSTITUANTS D’UN PROGRAMME 1.10.1 Généralités
Un programme est écrit dans un langage de programmation. Ce langage est composé de mots, symboles, commentaires, etc. Ceux-ci sont groupés en phrases dont l’ensemble compose le programme. Les phrases obéissent à des règles et ces règles déterminent de manière absolument stricte si une phrase est correcte ou non, c’est-à-dire si cette phrase respecte la syntaxe (syntax) du langage.
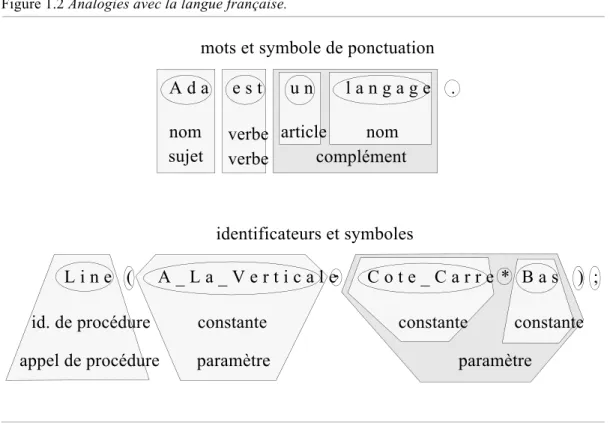
L’analogie avec les langues naturelles (français, allemand, etc.) est donc forte (fig. 1.2), la principale différence étant qu’une phrase française peut être formée de manière beaucoup moins rigoureuse et signifier néanmoins quelque chose. Or une phrase en Ada (ou tout autre langage de programmation) doit être absolument juste pour être comprise par le compilateur, sans quoi elle est obligatoirement rejetée!
Un programme Ada est composé de phrases appelées unités syntaxiques (syntactic units). Elles sont elles-mêmes constituées de mots, symboles, etc. appelés unités lexicales (lexical units). Chaque unité lexicale est une suite de caractères appartenant au jeu de caractères Ada.
Figure 1.2 Analogies avec la langue française.
1.10.2 Jeu de caractères en Ada A d a
mots et symbole de ponctuation
nom verbe article nom sujet verbe complément
L i n e
identificateurs et symboles
id. de procédure constante constante constante
appel de procédure paramètre paramètre
e s t u n l a n g a g e .
CONSTITUANTS D’UN PROGRAMME 19
Le jeu de caractères en Ada comporte les caractères décrits dans [ARM 2.1]. Cet ensemble est normalisé ISO sous le nom LATIN-1 et comporte les lettres ma-juscules et minuscules, les lettres accentuées, les chiffres, les symboles de ponc-tuation, etc. Il comprend comme sous-ensemble tous les caractères du code ASCII (§ 3.8.1). On distingue les caractères imprimables (printable characters), lisibles, comme ceux cités ci-dessus, des caractères non imprimables qui incluent les
caractères de contrôle (control characters) interprétés de manière spéciale par
l’implémentation (par exemple des caractères de contrôle comme le tabulateur horizontal (tab), le retour de chariot (return), le saut de ligne (line feed), etc.). 1.10.3 Unités lexicales en Ada
Diverses unités lexicales existent en Ada:
• Les identificateurs (identifiers), comme par exemple A, Limite_100, Cote_Carre, Put, etc. Un identificateur est un mot composé de lettres, de chiffres et du caractère _ et commençant obligatoirement par une lettre. S’il n’y a aucune limite théorique au nombre de caractères composant un identificateur, la norme Ada laisse à l’implémentation le soin de définir le nombre maximum de caractères significatifs, tout en précisant cependant que ce maximum doit être d’au moins deux cents caractères. Pour respecter les bonnes habitudes de programmation, les identificateurs doivent être par-lants pour les lecteurs du programme! Les caractères significatifs servent à différencier deux identificateurs. Il faut relever que la casse (majuscule/ minuscule) n’est pas significative!
Le langage contient des identificateurs prédéfinis (predefined identifiers) comme Integer, Float, Text_IO, Constraint_Error, etc., que le programmeur peut éventuellement redéfinir dans son programme, mais dont le but principal reste néanmoins d’être utilisés tels quels, dans les situations pour lesquelles ils ont été créés. L’annexe [ARM A.1] en donne la liste.
• Les mots réservés (reserved words) qui sont des identificateurs restreints à un usage bien défini (toujours le même!), par exemple procedure, is, begin, etc. La liste est fournie dans [ARM 2.9].
• Les symboles (symbols) formés d’un unique caractère ou de deux caractères accolés, comme
< > = <= := + – , ;
la liste exhaustive se trouve dans [ARM 2.2].
• Les commentaires (comments), c’est-à-dire n’importe quels caractères im-primables typographiés après le symbole -- et ce jusqu’à la fin de la ligne (fin de commentaire). Ils servent à expliquer le pourquoi et le comment des constructions auxquelles ils s’appliquent.
CONSTITUANTS D’UN PROGRAMME 20
• Les constantes numériques entières ou réelles ou plus simplement les nombres comme
123 –36 24E3 12.3 –234.0E3 –0.3E–2 les sections 2.2 et 2.3 définiront précisément ces constantes.
• Les constantes caractères ou plus simplement les caractères, c’est-à-dire un seul caractère imprimable entre apostrophes comme
'a' '?' 'A' '='
la section 3.8 définira précisément ces constantes.
• Les constantes chaînes de caractères ou plus simplement les chaînes de caractères, c’est-à-dire une suite d’un ou de plusieurs caractères (éventuellement aucun) entre guillemets comme
"abcd" "CARRE" "triangle de Pascal" "=" la section 9.2 définira précisément ces constantes.
Il est parfois possible, voire pratique, d’accoler deux unités lexicales. Mais en règle générale, pour augmenter la lisibilité, deux unités lexicales seront séparées par au moins un espace, une tabulation ou une fin de ligne.
1.10.4 Unités syntaxiques et diagrammes syntaxiques
Les unités syntaxiques, comme les unités lexicales d’ailleurs, peuvent être décrites par des diagrammes appelés diagrammes syntaxiques. Un diagramme
syntaxique (syntactic diagram) permet donc de décrire l’orthographe d’une unité
lexicale ou, comme son nom l’indique, la syntaxe (grammaire) d’une phrase du programme. Toute phrase est donc composée d’une séquence d’unités lexicales. Il est ainsi possible de vérifier si une instruction d’un programme en cours d’écriture est correcte en vérifiant sa syntaxe à l’aide des diagrammes syntaxiques du langage, Ada en l’occurrence.
CONSTITUANTS D’UN PROGRAMME 21
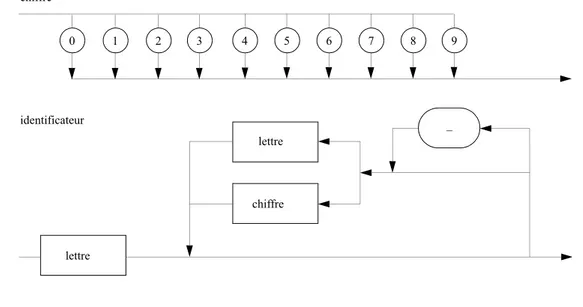
Figure 1.3 Diagrammes syntaxiques définissant un identificateur et un chiffre.
Cette vérification est simple à réaliser; il suffit de parcourir le diagramme syntaxique dans le sens des flèches. Par exemple, la figure 1.3 montre un tel diagramme, permettant de vérifier qu’un «mot» est bien un identificateur. En suivant le diagramme syntaxique on rencontre une première bulle indiquant que le premier caractère d’un identificateur doit être une lettre. Si c’est le cas l’analyse peut continuer avec un choix: soit l’identificateur ne comporte qu’une lettre et le diagramme est quitté, soit il comporte d’autres caractères (lettres, chiffres ou _ ) et il faut alors suivre les autres chemins proposés par le diagramme et vérifier au fur et à mesure s’ils peuvent correspondre aux caractères constitutifs de la suite de l’identificateur. Si le diagramme est quitté, l’unité lexicale ou syntaxique analysée est correcte. Mais si l’on reste bloqué dans le diagramme sans possibilité d’en sortir, cela correspond à une erreur d’orthographe ou de syntaxe.
Il existe trois sortes de bulles dans les diagrammes syntaxiques: les cercles, les rectangles à «coins» arrondis et ceux à angle droit. Si les coins sont à angle droit, cela signifie un renvoi à une entité syntaxique différente. Il faut ainsi se reporter à un autre digramme, pour continuer l’analyse et en revenir en cas de succès, et ainsi de suite. Si les coins sont arrondis ou si c’est un cercle, alors le contenu représente un symbole ou un mot réservé qui devra être présent tel quel dans le texte analysé. Les bulles de la figure 1.3 contenant les mots lettre et chiffre renvoient donc à deux autres diagrammes syntaxiques dont l’un des deux est donné dans la même figure. Par contre, celles contenant les chiffres de 0 à 9, ou le caractère _ montrent que ces caractères doivent apparaître tels quels dans un nombre, ou un identificateur.
lettre _ lettre chiffre identificateur chiffre 9 0 1 2 3 4 5 6 7 8
MISE EN PAGE D’UN PROGRAMME 22
1.11 MISE EN PAGE D’UN PROGRAMME
La mise en page d’un programme Ada est assez libre. Cependant, et pour des raisons évidentes de clarté et de lisibilité d’un programme, il existe des conventions de style qu’il faut respecter, décrites dans [AUS 95]. En particulier il est demandé: • de commenter chaque déclaration ou instruction importante en indiquant la raison de sa présence; ce commentaire se place avant ou à côté de la déclaration ou instruction;
• de choisir des identificateurs faciles à comprendre;
• d’assurer un degré élevé de systématique et de cohérence; • d’effectuer une seule déclaration ou instruction par ligne;
• d’indenter, c’est-à-dire de décaler vers la droite les déclarations ou instruc-tions contenues dans une autre déclaration ou instruction.
23
1.12 EXERCICES
1.12.1 Conception d’un algorithme
Ecrire un algorithme d’appel téléphonique à partir d’une cabine publique. 1.12.2 Déclarations et instructions
En Ada, peut-on mélanger des déclarations et des instructions dans une partie déclarative? Dans un corps?
1.12.3 Utilisation d’un diagramme syntaxique
Utiliser le diagramme syntaxique de la figure 1.3 pour déterminer si les termes suivants sont des identificateurs en Ada:
POINTS À RELEVER 24
1.13 POINTS À RELEVER 1.13.1 En général
• Un algorithme est une suite d’opérations à effectuer pour résoudre un problème.
• Saisie du programme, compilation, édition de liens, exécution, déverminage constituent les phases de création de tout programme.
• Algol-60, Pascal, Modula-2, Ada, Ada 95 forment une famille de langages de programmation.
• C, C++, Java forment une autre famille de langages de programmation. • Le terme Ada est utilisé dans cet ouvrage pour nommer la version 1995 du
langage de programmation Ada normalisé la première fois en 1983. • Le respect des bonnes habitudes de programmation aboutit à des
programmes plus simples et plus lisibles.
• Fiabilité, lisibilité, simplicité, justesse et efficacité des programmes sont des propriétés parmi les plus importantes.
• La méthode de décomposition par raffinements successifs aboutit à un algorithme de résolution du problème initial.
• Les unités lexicales constituent les mots du texte du programme alors que les unités syntaxiques en forment les phrases.
• Les diagrammes syntaxiques permettent de s’assurer que la syntaxe d’une construction est correcte.
• Les identificateurs nomment les entités d’un programme et doivent toujours être parlants.
• Les commentaires expliquent les raisons de la présence des constructions auxquelles ils s’appliquent.
1.13.2 En Ada
• Un programme principal Ada est constitué dans l’ordre de la clause de contexte, l’en-tête, la partie déclarative et la partie instructions.
• Les identificateurs sont composés d’une suite de lettres ou de chiffres, éventuellement séparés par le caractère _ et doivent obligatoirement commencer par une lettre.
25
C H A P I T R E 2
N O M B R E S
E T
E N T R É E S
- S O R T I E S
RAPPELS 27
2.1 RAPPELS
Un programme Ada se compose de quatre parties: • la clause de contexte;
• l’en-tête;
• la partie déclarative; • la partie instructions.
La partie déclarative contient les déclarations des objets (constantes, variables, etc.) représentant les données que l’on veut traiter. Le corps contient les ins-tructions du programme, c’est-à-dire les traitements à effectuer sur ces données. Le présent chapitre porte sur la représentation de ces données, en se limitant pour l’instant à deux catégories de nombres: les nombres entiers et réels.
TYPES ENTIERS 28
2.2 TYPES ENTIERS 2.2.1 Motivation
Les nombres entiers sont traditionnellement utilisés les premiers dans un cours d’apprentissage de la programmation. En effet, ils ne posent pas (ou peu) de problèmes. Le travail avec eux est naturel puisqu’il correspond à de l’arithmétique. Un réflexe doit cependant être acquis le plus vite possible, il est mis en évidence dans la note 2.1.
NOTE 2.1 L’ensemble des nombres entiers n’est pas infini sur un ordinateur.
Tous les nombres entiers ne sont évidemment pas utilisables sur un ordinateur; en effet, s’il existe en théorie une infinité de tels nombres, chacun d’entre eux occupe un ou quelques mots en mémoire et, de ce fait, l’ensemble des entiers représentables sur un ordinateur est fini. Généralement, les entiers sont représentés par 16 ou 32 bits, éventuel-lement 8 bits (§ 2.5.2). Les machines sur lesquelles ils occupent 64 bits ne sont encore pas très courantes.
2.2.2 Généralités
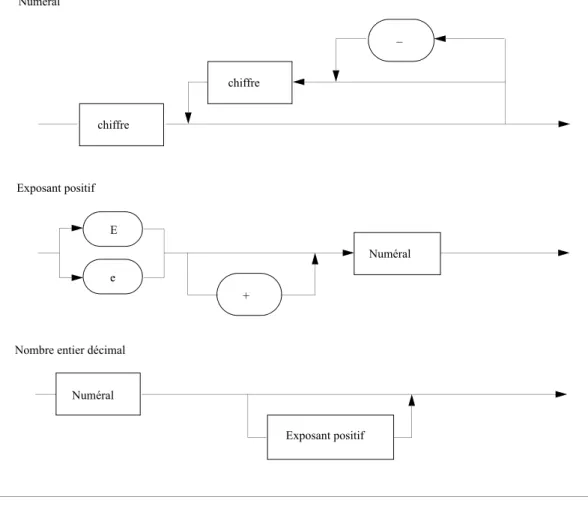
L’identificateur Integer est un identificateur prédéfini. Il signifie: «un objet (constante, variable, etc.) de type Integer contiendra un nombre entier et rien d’autre». Les variables Abscisse_Carre, Ordonnee_Carre, etc., du programme Exemple_Bien_Fait (§ 1.8.3) sont de type Integer. Le type Integer fait partie des types discrets (discrete types, [ARM 3.2]). Il faut cependant déjà mentionner qu’il existe d’autres types qu’Integer pour les entiers (§ 2.2.7). Mais tous les nombres entiers (non explicitement basés) doivent respecter la syntaxe décrite par la figure 2.1.
Les constantes entières sont les nombres entiers eux-mêmes. Ces nombres peuvent être décimaux ou basés. Un nombre basé est un nombre écrit dans une base explicitement mentionnée, comprise entre 2 et 16. Le caractère _ est utile pour la lisibilité d’un nombre mais n’a aucune signification particulière.
TYPES ENTIERS 29
Figure 2.1 Diagrammes syntaxiques définissant un nombre entier décimal.
Exemple 2.1 Nombres entiers décimaux ou basés. Nombres entiers décimaux:
10 12E6 12e6 12E+6 1_0 1_000 1_0E2 1E1_0
Le nombre entier 12 dans différentes bases (binaire, octale, décimale, hexadécimale): 2#1100# 2#0000_1100# 8#14# 10#12# 16#c# 16#C#
Les opérations arithmétiques possibles sur les valeurs entières se répartissent en deux catégories:
les opérations unaires + – abs où
chiffre Numéral
chiffre
_
Nombre entier décimal Exposant positif E Numéral + e Numéral Exposant positif
TYPES ENTIERS 30
• le symbole + représente l’identité et le symbole – l’opposé; • le mot réservé abs représente l’opération «valeur absolue»;
les opérations binaires + – * / ** rem mod où
• le symbole + représente l’addition et le symbole – la soustraction;
• le symbole * représente la multiplication et le symbole / la division (entière);
• le symbole ** représente l’exponentiation (exposant entier positif ou nul); • le mot réservé rem représente le reste de la division entière (euclidienne);
notons les relations suivantes: A rem (–B) = A rem B et (–A) rem B = –(A rem B);
• le mot réservé mod représente l’opération mathématique modulo qui ne sera
pas détaillée ici, ni d’ailleurs les différences entre mod et rem; il suffit de
préciser que mod est équivalent à rem si les deux opérandes sont positifs.
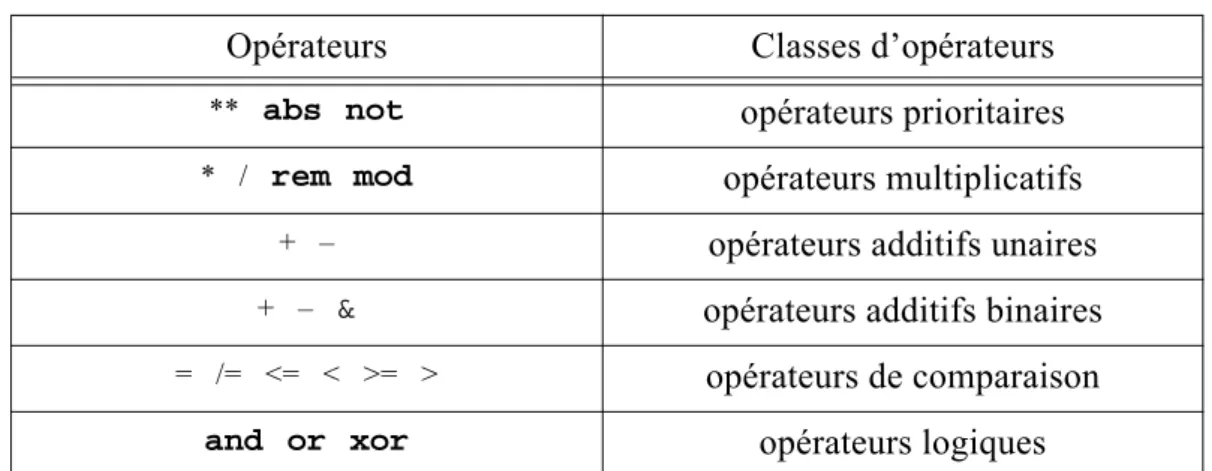
Les opérations + – * / ** abs rem mod sont appelées opérateurs
(operators), alors que les valeurs sur lesquelles ils opèrent sont les opérandes (operands).
Les expressions (expressions) entières sont des combinaisons de ces opérations. L’évaluation (le calcul) d’une expression (expression evaluation) consiste à trouver la valeur (le résultat) de l’expression. Il faut alors prendre garde au fait qu’une telle expression n’est pas toujours calculable (note 2.2)! En effet, une division par zéro est impossible ou encore l’élévation d’un nombre à une trop grande puissance provoque un débordement de capacité (overflow), c’est-à-dire l’obtention d’une valeur non représentable sur la machine utilisée (note 2.1). Lorsque le calcul de l’expression n’est pas possible, une erreur sera générée à l’exécution du programme.
NOTE 2.2 Attention aux dépassements de capacité.
En Ada, le calcul d’une expression provoquera une erreur à l’exécution (en général Constraint_Error, § 6.3.2) si la valeur obtenue n’est pas représentable sur la machine ou si elle est hors de l’intervalle des valeurs du type utilisé. Une expression doit donc être conçue de manière à ne jamais provoquer de telles erreurs. Si cette garantie ne peut pas être obtenue (utilisation de valeurs données à l’exécution, par exemple par l’utilisateur), Ada offre un mécanisme de traitement des erreurs (sect. 6.3).
Exemple 2.2 Expressions entières.
2est une expression réduite à une seule constante de valeur 2;
TYPES ENTIERS 31
3 et 4;
–2est une expression de valeur –2;
abs (–2)est une expression de valeur 2;
2 ** 8est une expression de valeur 256; 4 * 5est une expression de valeur 20; 4 / 2est une expression de valeur 2; 5 / 2est aussi une expression de valeur 2;
4 rem 2 et 4 mod 2sont deux expressions de valeur 0; 5 rem 2 et 5 mod 2sont deux expressions de valeur 1; 5 rem (–2)est une expression de valeur 1;
(–5) rem 2est une expression de valeur –1; 2 + 3 * 4est une expression qui vaut 14 (sect. 2.4); (2 + 3) * 4est une expression qui vaut 20;
Nombre + 1est une expression additionnant 1 à la valeur actuelle de la variable Nombre
(dépassement de capacité possible);
(Nombre + 10) / Nombreest une expression correcte ((dépassement de capacité
possible lors de l’adition ou si Nombre vaut 0).
Les parenthèses permettent de définir des sous-expressions et un ordre d’évaluation de celles-ci. Mais les opérateurs sont également classés en niveaux de priorité (sect. 2.4).
2.2.3 Affectation
Le mot affectation (assignment) signifie «donner une valeur à». Parler d’affectation de 3 à la variable Nombre signifie que l’on veut que la variable Nombre prenne dès lors la valeur 3. Une variable est donc un objet dont la valeur peut être modifiée au cours de l’exécution d’un programme, alors qu’une constante voit sa valeur fixée lors de sa déclaration (§ 3.9.1). Toute affectation entre valeur et variable entières s’écrit (exemple 2.3):
nom_de_variable_entière := expression_de_type_Integer;
La sémantique de n’importe quelle affectation s’exprime par un algorithme: 1 obtenir la valeur de tous les opérandes de l’expression;
2 calculer la valeur de l’expression;
3 remplacer le contenu de la variable par cette valeur.
ATTENTION: lors de l’affectation, une erreur se produira si la variable ne peut pas accueillir la valeur calculée.
Exemple 2.3 Affectations d’expressions entières à une variable entière.
-- ...
TYPES ENTIERS 32
Max : constant := 5; -- Une constante entiere
Nombre : Integer; -- Une variable entiere
begin -- Exemple_2_3
Nombre := 5; -- Affecte la valeur 5 a Nombre
Nombre := Nombre + 4; -- Affecte la valeur 9 a Nombre
Nombre := (36 / 10) * 2; -- Affecte la valeur 6 a Nombre
Nombre := Nombre / 2; -- Affecte la valeur 3 a Nombre
Nombre := Max; -- Affecte la valeur de Max a
... -- Nombre
2.2.4 Dangers liés aux variables non initialisées
Soit le morceau de programme donné dans l’exemple 2.4. Exemple 2.4 Attention aux variables non initialisées.
-- ...
procedure Exemple_2_4 is
Nombre : Integer; -- Deux variables entieres sans
valeurs
Resultat : Integer; -- initiales definies
begin -- Exemple_2_4
Resultat := Nombre + 1; ...
Que vaut Resultat après l’affectation? La réponse est que Resultat a une
valeur indéfinie (undefined value) car la valeur de Nombre n’était pas définie au moment de l’affectation. La variable non initialisée Nombre possédait en fait une valeur entière calculée à partir de la suite de bits du mot mémoire utilisé pour cette variable. L’état de ces bits dépend de l’état (électrique) de la mémoire!
L’utilisation de variables déclarées mais non initialisées, c’est-à-dire ne possédant pas de valeur définie au moment de leur utilisation, est une erreur très courante. De plus, la détection de ces erreurs est difficile puisqu’il est possible que le programme s’exécute tout de même, en produisant évidemment n’importe quels résultats à commencer par des résultats corrects! Lors de l’utilisation de la valeur d’une variable, il faut donc toujours s’assurer que cette variable possède une valeur bien définie (note 2.3).
NOTE 2.3 Toute variable doit être initialisée.
TYPES ENTIERS 33
cette valeur est toujours bien définie.
2.2.5 Attributs First, Last, Succ et Pred
Un attribut (attribute) en Ada est une construction offerte par le langage et permettant d’obtenir une certaine caractéristique d’une entité.
Les attributs First et Last sont prédéfinis et donnent la première, respectivement la dernière valeur d’un intervalle ou d’une suite; les attributs Succ et Pred sont aussi prédéfinis et fournissent la valeur suivante, respectivement précédente d’une valeur donnée entre parenthèses (exemple 2.5).
Exemple 2.5 Utilisation des attributs First, Last, Succ et Pred.
Integer'First donne le nombre le plus petit des entiers du type Integer;
Integer'Lastdonne le nombre le plus grand des entiers du type Integer;
Integer'Succ(0)donne 1;
Integer'Pred(0)donne –1;
Integer'Succ(Nombre)donne la valeur Nombre+1;
Integer'Pred(Nombre + 1)donne la valeur Nombre;
Integer'Pred(Integer'Last)donne la valeur précédent le plus grand des
entiers.
2.2.6 Généralités sur les attributs
Comme mentionné auparavant, un attribut en Ada est un outil offert par le langage qui permet d’obtenir une caractéristique d’une entité. Il faut noter la syntaxe un peu surprenante qui utilise l’apostrophe pour indiquer que l’on a affaire à un attribut placé après celle-ci, ainsi que la présence obligatoire d’un identificateur avant l’apostrophe.
Attention à la note 2.2! Par exemple Integer'Succ(Integer'Last) n’existe pas et le calcul de cette expression provoquera une erreur à la compilation du programme.
Finalement, le calcul d’un attribut est l’une des opérations les plus prioritaires dans une expression. En particulier, un attribut est calculé avant n’importe quel opérateur.
2.2.7 Types Short_Integer et Long_Integer
Le langage Ada a la particularité de fournir différents types pour, dans notre cas, traiter les nombres entiers. La norme autorise une implémentation à offrir les
TYPES ENTIERS 34
types Short_Integer et Long_Integer avec les particularités suivantes:
• le type Short_Integer a les mêmes caractéristiques qu’Integer mais l’intervalle [Short_Integer'First ; Short_Integer'Last] (ex-primé en notation mathématique) est plus petit que celui représenté par [Integer'First;Integer'Last];
• le type Long_Integer a les mêmes caractéristiques qu’Integer mais l’intervalle [Long_Integer'First;Long_Integer'Last] (exprimé en notation mathématique) est plus grand que celui représenté par [Integer'First;Integer'Last].
Exemple 2.6 Valeurs possibles pour les nombres les plus petits et les plus grands des types entiers. Avec Integer sur 16 bits:Integer'First vaut –2**15;
Integer'Last vaut 2**15–1;
Avec Short_Integer sur 8 bits:Short_Integer'First vaut –2**7; Short_Integer'Last vaut 2**7–1;
Avec Long_Integer sur 32 bits:Long_Integer'First vaut –2**31; Long_Integer'Last vaut 2**31–1;
L’existence de ces différents types entiers permet donc, en choisissant l’un plutôt que l’autre, de limiter ou d’augmenter l’intervalle des nombres entiers utilisables pour une ou plusieurs valeurs. Mais il faut toujours se rappeler que le nombre de bits, donc l’intervalle des nombres représentés, attribués à ces différents types, dépend de l’implémentation. Enfin, le langage permet de définir d’autres types entiers (sect. 6.2).
TYPES RÉELS 35
2.3 TYPES RÉELS 2.3.1 Motivation
Les nombres réels sont indispensables dans les applications dites numériques de la programmation (programmes d’analyse numérique, de statistiques, de calcul par éléments finis, de régulation numérique, etc.). Dans la majorité des autres cas, les nombres réels sont peu fréquents. Leur utilisation, sans un minimum de précautions, peut s’avérer dangereuse du fait des erreurs de calcul provoquées par leur représentation en mémoire (§ 2.5.2). Comme pour les entiers, l’ensemble des nombres réels représentables sur un ordinateur est fini.
Ces nombres réels vont être présentés sans trop de détails en commençant par les réels en virgule flottante et en laissant de côté (pour l’instant) les réels en virgule fixe.
2.3.2 Généralités
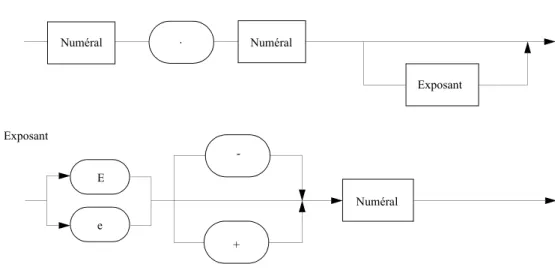
Float est un identificateur prédéfini. Il signifie «un objet (constante, variable, etc.) de type Float contiendra un nombre réel en virgule flottante et rien d’autre». Les nombres réels (non explicitement basés) doivent respecter la syntaxe donnée à la figure 2.2. Le type Float fait partie des types numériques (numeric types, [ARM 3.2]).
Les constantes réelles sont les nombres réels eux-mêmes. Ils peuvent être décimaux ou basés mais l’on ne décrira que les nombres décimaux (exemple 2.7). Le caractère _ s’utilise comme dans les nombres entiers, pour en faciliter la lecture. Figure 2.2 Diagrammes syntaxiques définissant un nombre réel décimal.
Nombre réel décimal
Numéral . Numéral Exposant Exposant E Numéral + e
-TYPES RÉELS 36
Exemple 2.7 Nombres réels décimaux (comparer avec l’exemple 2.1).
10.0 12.0E6 12.0e6 12.0E+6 12.0E–6 1_0.0 1_000.0 1_0.0E2 1.0E1_0
Les opérateurs arithmétiques possibles sur les valeurs réelles se répartissent en deux catégories:
les opérateurs unaires + – abs où
• le symbole + représente l’identité et le symbole – l’opposé; • le mot réservé abs représente l’opération «valeur absolue»;
et les opérateurs binaires + – * / ** où
• le symbole + représente l’addition et le symbole – la soustraction; • le symbole * représente la multiplication et le symbole / la division; • le symbole ** représente l’exponentiation (exposant entier positif, négatif
ou nul).
Les expressions réelles sont des combinaisons de ces opérations, comme illustré dans l’exemple 2.8.
Exemple 2.8 Expressions réelles.
1.0est une expression réduite à une seule constante de valeur 1.0 qui peut
également s’écrire 1.0e0 ou 0.1e1 ou 0.1E+1 ou encore 10.0e–1;
2.0 ** (–8)est une expression de valeur 256–1; –3.0 + 4.0est une expression de valeur 1.0; 4.3 * 5.0e0est une expression de valeur 21.5; 4.0 / 2.0est une expression de valeur 2.0;
5.0 / 2.0est une expression de valeur 2.5 (comparer avec l’exemple 2.2); 2.0 + 3.0 * 4.0est une expression qui vaut 14.0 (sect. 2.4);
2.0 + (3.0 * 4.0)est une expression qui vaut 14.0; (2.0 + 3.0) * 4.0est une expression qui vaut 20.0.
TYPES RÉELS 37
2.3.3 Affectation
L’affectation s’effectue comme pour les entiers (§ 2.2.3):
nom_de_variable_réelle := expression_de_type_Float;
2.3.4 Attributs First, Last et Digits
Comme pour les entiers, Ada offre des attributs pour les nombres réels. Les attributs First et Last ont la même signification que pour les entiers. L’attribut prédéfini Digits donne le nombre maximum de chiffres significatifs. Par exemple, et selon l’implémentation, Float'Digits peut donner la valeur 6. 2.3.5 Types Short_Float et Long_Float
De manière analogue aux entiers, la norme autorise une implémentation à offrir les types Short_Float et Long_Float avec les particularités suivantes:
• le type Short_Float a les mêmes caractéristiques que Float mais le nombre de chiffres significatifs est plus petit que celui de Float;
• le type Long_Float a les mêmes caractéristiques que Float mais le nombre de chiffres significatifs est plus grand que celui de Float, avec un minimum de 11.
L’intervalle des valeurs de ces deux types sera probablement également diffé-rent de celui de Float.
PRIORITÉ DES OPÉRATEURS ARITHMÉTIQUES 38
2.4 PRIORITÉ DES OPÉRATEURS ARITHMÉTIQUES
En mathématiques une question se pose avec une expression telle que 2+3*4: quel est le résultat de ce calcul? Est-ce 20 (addition de 2 et 3 puis multiplication par 4) ou 14 (ajouter 2 à 3*4)?
Le même problème se pose en programmation. Pour le résoudre il faut tenir compte des priorités définies dans le langage (exemple 2.9). Celles propres à Ada sont, pour les opérateurs vus jusqu’ici et dans l’ordre de priorité décroissante:
• les opérateurs ** et abs;
• les opérateurs binaires * / rem et mod ;
• les opérateurs unaires – et +; • les opérateurs binaires – et +.
Dans chacun de ces groupes les opérateurs sont de même priorité. Lors de l’évaluation d’une expression comprenant des opérateurs de même priorité, ceux-ci s’appliquent de gauche à droite.
Exemple 2.9 Applications de la priorité des opérateurs.
Integer'First + 10calcul de Integer'First puis addition de 10;
2 + 3 + 4donne 9 avec calcul de gauche à droite;
2 + 3 * 4donne 14 car la sous-expression 3*4 est d’abord évaluée (priorité de * par rapport à + );
2.0 * 3.0 / 4.0donne 1.5 car l’expression est calculée de gauche à droite
(opérateurs de même priorité);
2 * 3 + 4 / 3donne 7 car la sous-expression 2*3 est d’abord évaluée puis la sous-expression 4/3 est calculée enfin l’addition des résultats partiels 6 et 1 est effectuée.
Il est naturellement possible de préciser l’ordre d’évaluation (c’est-à-dire l’ordre de calcul des constituants) d’une expression en utilisant les parenthèses ( et ) comme en mathématiques. Les sous-expressions entre parenthèses sont alors calculées en priorité (exemple 2.10).
Exemple 2.10 Parenthèses, expressions et priorités des opérateurs.
(2 + 3) * 4 2+3 donne 5, multiplié par 4 donne 20;
2 + (3 * 4)3*4 donne 12, ajouté à 2 donne 14 (parenthèses inutiles); 3 * (1 + 2) + 41+2 donne 3, multiplié par 3 donne 9, ajouté à 4 donne 13;
abs (–2.0)donne 2.0, avec les parenthèses indispensables;
PRIORITÉ DES OPÉRATEURS ARITHMÉTIQUES 39
5.0 ** (–2)donne 25.0–1, avec les parenthèses indispensables; (2 ** 3) ** 4donne 4096, avec les parenthèses indispensables.
Les parenthèses des quatre derniers exemples sont indispensables pour respecter la syntaxe Ada car en écrivant par exemple 3.0*–2.0, l’ordre de priorité imposerait de calculer d’abord 3.0*–, ce qui n’a aucun sens!
REMARQUES RELATIVES AUX TYPES ENTIERS ET RÉELS 40
2.5 REMARQUES RELATIVES AUX TYPES ENTIERS ET RÉELS 2.5.1 Conversions de types
Il est interdit par la norme d’écrire des expressions composées d’un mélange d’opérandes entiers et réels. S’il est nécessaire de former de telles expressions, alors il faut décider si leur valeur sera entière ou réelle et utiliser des conversions explicites de type (exemple 2.11) entre Integer et Float pour s’assurer que chaque sous-expression (opérande opérateur opérande) est formée d’opérandes de même type. Une conversion explicite de type a la forme:
nom_de_type ( expression ) où
• le nom_de_type sert à convertir la valeur de l’expression en une valeur de ce type.
Exemple 2.11 Exemples de conversions explicites entre Integer et Float.
Float ( 5 )5 est converti en 5.0;
Integer ( 2.03 )2.03 est converti en 2;
Float ( –800 ) / 2.5E2l’expression vaut –3.2;
Integer ( 3.5 ) 3.5 est converti en 4;
Integer ( –2.5 ) –2.5 est converti en –3.
La conversion d’une valeur réelle en une valeur entière est faite par arrondi vers l’entier le plus proche.
2.5.2 Valeurs entières et réelles utilisables en Ada
Les valeurs entières utilisables sont celles comprises dans l’intervalle [System.Min_Int;System.Max_Int] (en notation mathématique) dont les deux bornes ont bien entendu une valeur dépendant de l’ordinateur et du compilateur Ada utilisé. Sans entrer maintenant dans les détails, il faut souligner que les constantes Min_Int et Max_Int sont mises à disposition par le paquetage prédéfini System (sect. 19.3). Tous les types entiers ont leur domaine de définition (§ 2.2.7) inclus dans l’intervalle ci-dessus.
Les valeurs réelles en virgule flottante utilisables dépendent de la représentation en mémoire des nombres réels. Un tel nombre est enregistré sous forme d’une mantisse et d’un exposant, le tout implémenté généralement sur 32 ou 64 bits. Par exemple, le nombre 0.10012e13 est pour le programmeur constitué de 0.10012 pour la mantisse et de 13 pour l’exposant. Mais en réalité, le nombre de chiffres significatifs est en relation avec le nombre de bits dédiés à la représentation de la mantisse; les bits restants sont eux utilisés pour l’exposant.
REMARQUES RELATIVES AUX TYPES ENTIERS ET RÉELS 41
Dans tous les cas il faut se méfier lors de calculs avec les nombres réels, particulièrement si ces nombres sont grands ou petits. En effet, une addition telle que 1.0e45 + 1.0e–40 donne 1.0e45 !
RAPPEL: les décimales dont la position excède le nombre de chiffres signi-ficatifs ne signifient plus rien!
DIALOGUE PROGRAMME-UTILISATEUR 42
2.6 DIALOGUE PROGRAMME-UTILISATEUR 2.6.1 Motivation
La qualité du dialogue entre l’utilisateur et un logiciel est une propriété fondamentale d’une partie dudit logiciel appelée interface homme-machine (user interface). Ce dialogue est rendu possible par l’existence de périphériques spécialisés comme le clavier, la souris, le microphone, etc., qui permettent l’entrée d’informations dans la machine, et de périphériques comme l’écran, l’imprimante, le traceur ou les hauts-parleurs qui permettent la sortie de résultats ou de messages pour l’utilisateur. L’importance du dialogue réside dans le fait que plus celui-ci est compréhensible, cohérent et agréable, plus l’utilisateur acceptera ou aura envie d’utiliser le logiciel. Sans vouloir approfondir ici la notion de dialogue (cela ne fait pas partie d’une introduction à la programmation), il faut simplement mentionner qu’il consiste entre autres pour l’utilisateur en:
• l’introduction des données; • la commande du logiciel;
• la compréhension du déroulement des opérations; • la compréhension des résultats obtenus;
et pour le programme, en:
• la demande des données nécessaires à son exécution; • la production de résultats lisibles et clairement présentés; • la quittance des opérations importantes effectuées;
• la mise en garde de l’utilisateur en cas de donnée erronée;
• la mise en garde de l’utilisateur en cas de commande erronée ou dan-gereuse.
Même s’il existe des logiciels spécialisés de conception et de réalisation d’interfaces homme-machine, la programmation d’un dialogue textuel en Ada se basera sur les outils de base que sont d’une part les deux opérations Get et Get_Line (§ 9.2.3) pour la lecture de données (nombres, caractères...), d’autre part Put et Put_Line pour l’affichage de messages ou de résultats. Ces quatre opérations sont mises à disposition dans des paquetages (sect. 10.2) prédéfinis, spécialisés dans les entrées-sorties de texte tels que Ada.Text_IO, les entrées-sorties d’entiers Ada.Integer_Text_IO ou de réels Ada.Float_Text_IO.
Dans nos programmes et pour des raisons de simplicité, l’utilisation d’autres mécanismes indispensables à tout interface homme-machine actuel ou futur com-me la souris, la reconnaissance vocale, les écrans tactiles, etc., sera complètecom-ment ignorée.
2.6.2 Lecture de nombres entiers ou réels
DIALOGUE PROGRAMME-UTILISATEUR 43
quelques principes cités au paragraphe 2.6.1, le programme doit, dans l’ordre: • afficher un message clair à l’utilisateur pour lui indiquer ce qu’il doit faire; • attendre que l’utilisateur ait introduit la valeur;
• lire la valeur;
• vérifier la validité de la valeur obtenue (§ 6.3.5); • reprendre son exécution.
L’exemple 2.12 illustre l’utilisation des opérations d’entrées-sorties et réalise une ébauche de dialogue entre le programme et l’utilisateur. Il faut bien comprendre que ce dialogue obéit à un protocole fixé dans le programme et que l’utilisateur doit suivre.
Exemple 2.12 Ebauche de dialogue entre un programme et son utilisateur. with Ada.Text_IO;
with Ada.Integer_Text_IO; with Ada.Float_Text_IO;
-- Calcul du volume d'un mur de briques
procedure Ebauche_Dialogue is
-- Nombre de briques en longueur Longueur_Mur : Integer;
-- Nombre de briques en hauteur Hauteur_Mur : Integer;
-- Dimensions d'une brique Longueur_Brique : Float; Largeur_Brique : Float; Hauteur_Brique : Float; -- Volume du mur de briques Volume : Float; -- Autres declarations... ... begin -- Ebauche_Dialogue -- Presentation du programme... ...
-- Obtenir le nombre de briques formant le mur en longueur Ada.Text_IO.Put ( "Donnez le nombre de briques " );
Ada.Text_IO.Put ( "(longueur du mur): " ); Ada.Integer_Text_IO.Get ( Longueur_Mur );
-- Obtenir le nombre de briques formant le mur en hauteur Ada.Text_IO.Put ( "Donnez le nombre de briques " );
Ada.Text_IO.Put ( "(hauteur du mur): " ); Ada.Integer_Text_IO.Get ( Hauteur_Mur ); -- Obtenir les dimensions d'une brique
Ada.Text_IO.Put ( "Donnez les dimensions d'une brique. " ); Ada.Text_IO.Put ( "La longueur: " );
DIALOGUE PROGRAMME-UTILISATEUR 44
Ada.Float_Text_IO.Get ( Longueur_Brique ); Ada.Text_IO.Put ( "La largeur: " );
Ada.Float_Text_IO.Get ( Largeur_Brique ); Ada.Text_IO.Put ( "La hauteur: " );
Ada.Float_Text_IO.Get ( Hauteur_Brique ); -- Calcul du volume du mur
Volume := Longueur_Brique * Largeur_Brique * Hauteur_Brique * Float ( Longueur_Mur * Hauteur_Mur );
-- Montrer a l'utilisateur la valeur du volume du mur
Ada.Text_IO.Put ( " Le volume du mur de briques vaut : " ); Ada.Float_Text_IO.Put ( Volume );
Ada.Text_IO.New_Line; ...
end Ebauche_Dialogue;
Comment la lecture des dimensions d’une brique et du mur est-elle effectuée? L’exemple de la figure 2.3 va illustrer cette opération.
Figure 2.3 Lecture de valeurs données par l’utilisateur.
Après l’exécution de Ada.Float_Text_IO.Get(Longueur_Brique); la variable Longueur_Brique vaut 30.0, Largeur_Brique et Hauteur_Brique sont indéfinies.
Après l’exécution de Ada.Float_Text_IO.Get(Largeur_Brique); la variable Largeur_Brique vaut 20.0, Longueur_Brique garde sa valeur 30.0 et Hauteur_Brique est encore indéfinie.
Après l’exécution de Ada.Float_Text_IO.Get(Hauteur_Brique); la variable Hauteur_Brique vaut 15.5, Longueur_Brique et Largeur_Brique conservent leur valeur.
Les valeurs ont été lues par le programme en respectant l’ordre dans lequel elles
programme ce que l’utilisateur a donné
Ada.Float_Text_IO.Get(Longueur_Brique); Ada.Float_Text_IO.Get(Largeur_Brique); Ada.Float_Text_IO.Get(Hauteur_Brique);