Contribution à la Théorie des Gaz Dilués-Dégénérés

HAL Id: tel-00011907

https://tel.archives-ouvertes.fr/tel-00011907

Submitted on 10 Mar 2006

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

Peter Gruter

To cite this version:

Peter Gruter. Contribution à la Théorie des Gaz Dilués-Dégénérés. Physique Atomique [physics.atom-ph]. Université Paris Sud - Paris XI, 1996. Français. �tel-00011907�

24,

Rue Lhomond - 75231 PARIS CEDEX 05

Tél. (33-1) 47 07 54 13

UNIVERSITÉ

DE

PARIS

SUD

U.F.R.

SCIENTIFIQUE

D’ORSAY

DÉPARTEMENT

DE

_PHYSIQUE

DE

L’ÉCOLE

NORMALE

SUPÉRIEURE

THÈSE

présentée

pour obtenir

le GRADE de DOCTEUR EN SCIENCES

de

l’UNIVERSITÉ

PARIS XI ORSAY

par

Peter

Grüter

Intitulé:

Contribution à

la

Théorie

des

Gaz

_{Dilués-Dégénérés}

Soutenue le 11 Juillet 1996 devant la Commission d’examen :

M. Roger BALIAN

M. Bernard JANCOVICI

M. Franck

_LALOË,

Directeur de Thèse M.

_Maciej

_LEWENSTEIN,

_Rapporteur

M.

_Jacques

_MAGNEN,

_Rapporteur

U.F.R.

SCIENTIFIQUE

D’ORSAY

DÉPARTEMENT

DE

_PHYSIQUE

DE

L’ÉCOLE

NORMALE

SUPÉRIEURE

THÈSE

présentée

pour obtenir

le GRADE de DOCTEUR EN SCIENCES

de

l’UNIVERSITÉ

PARIS XI ORSAY

par

Peter

Grüter

Intitulé:

Contribution à

la

Théorie

des

Gaz

_{Dilués-Dégénérés}

Soutenue le 11 Juillet 1996 devant la Commission d’examen :

M. Roger BALIAN

M. Bernard JANCOVICI

M. Franck

_LALOË,

Directeur de Thèse M.

_Maciej

LEWENSTEIN,

_Rapporteur

Ich lasse dich im

Überfluß

Von Wonne und von Freuden.

[...]

J’ai été chaleureusement accueilli au Laboratoire Kastler

Brossel,

ce dont

je

tiens à

remercier ses directeurs

successifs,

_Jacques

Dupont-Roc

et Michèle Leduc.

Je voudrais

_témoigner

de ma

plus

grande

reconnaissance envers Franck Laloë

_qui

m’a

guidé pendant

toute la durée de ma thèse par son

enthousiasme,

sa

_patience,

sa

préci-sion et son intuition

_physique

_que

je

n’ai

jamais

cessé d’admirer.

Des discussions avec

_Roger

_Balian,

Yvan

Castin,

David

_Ceperley,

_Jacques

Dupont-Roc,

Werner

Krauth,

Alexander

_Meyerovich,

William

_Mullin,

Pierre-Jean

_Nacher,

Phi-lippe

Nozières et Géneviève Tastevin ont été d’une

_grande

aide et ont fourni des idées stimulantes. Je souhaite leur

_exprimer

toute ma

_gratitude.

Tous les membres du laboratoire ont contribué aux travaux

_présentés

ici en créant une

ambiance amicale et

_{encouragante,}

_{si nécessaire pour} le bon avancement de ce _genre

de

_projet.

En

_particulier,

_je

souhaite en remercier Maxime Ben

Dahan,

Pierre

Des-biolles,

Benoît

Demolder,

Simone

Kulin,

Eric

Stolz,

Pippa Storey,

Pascal

_Szriftgiser

et

_Bérengère

Villard.

L’équipe

informatique

du

_{départment, Thierry Besançon,}

Cécile

Combier,

et Zaïre

Dissi,

a joué

un rôle

_important

_pour l’avancement de mes travaux. Je voudrais ici leur

exprimer

ma reconnaissance. Je voudrais envoyer un merci

_particulier

à Zaïre et les

équipes techniques

du

_{département qui}

ont contribué au maintien de mon vélo en état

de marche - afin de

_permettre

le bon avancement des travaux

_présentés

ici - avec de

nombreux

conseils,

des astuces

_pratiques

et une _pompe.

Mes remerciements vont à toutes les _personnes

_qui

ont

_accepté

de faire

_partie

de mon

jury,

en

particulier Maciej

Lewenstein et

_{Jacques Magnen qui}

ont non seulement

ac-cepté

le rôle de

_rapporteur,

mais m’ont aussi fait bénéficier de _{nombreuses remarques.} Enfin mais surtout,

je

veux remercier Sandrine et ma

famille,

de leur

_patience

et leur soutien.

i

1 Les

_systèmes

_quantiques

dilués 1

1.1 Situation

_{expérimentale ...}

1

1.2

_Approches

_{théoriques ...}

3

1.2.1

_{Approches inspirées}

de la matière condensée ... 3

1.2.2

_{Pseudopotentiel...}

4

1.2.3 Les

_{développements}

en

agrégats

... 6

1.2.4 Motivation de notre travail ... 8

1.3 Les bases de notre

_description

_théorique

... 9

1.3.1 Généralisation de la formule de Beth-Uhlenbeck ... 9

1.3.2

_Propriétés

à courte distance ... 10

1.3.3

_{Propriétés thermodynamiques}

... 10

2 La méthode des

_opérateurs

d’Ursell 13 Introduction au

_{chapitre ...}

13

Article 1

_(en

_anglais)

2.1 Introduction ... 17 2.2

_Opérateurs

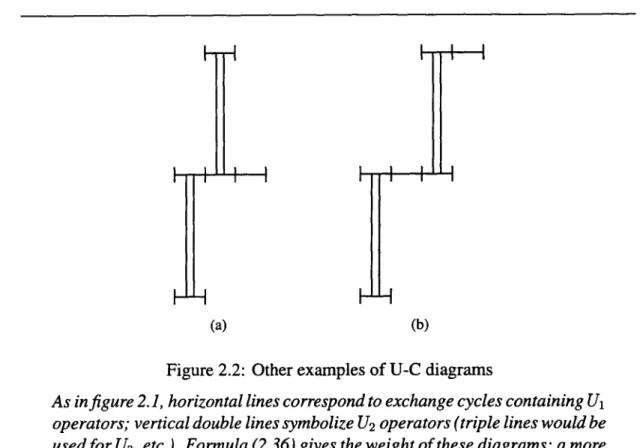
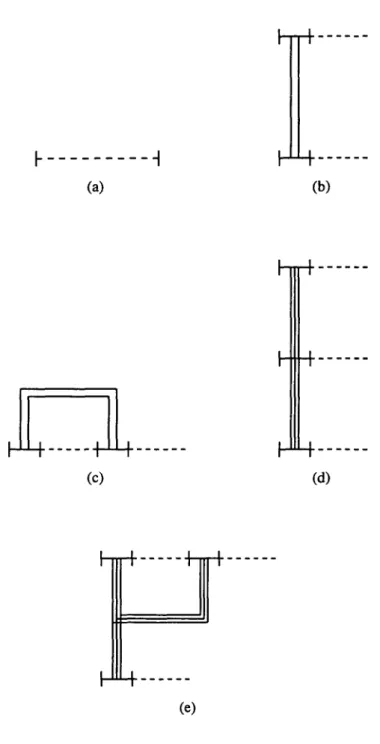
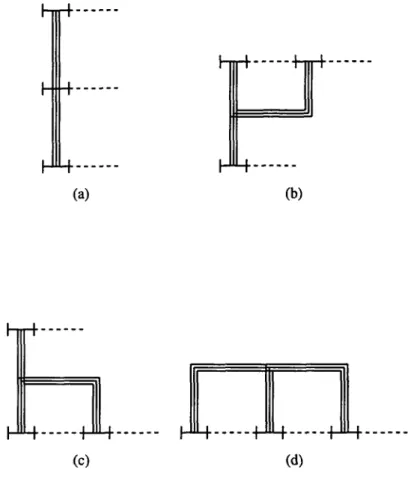
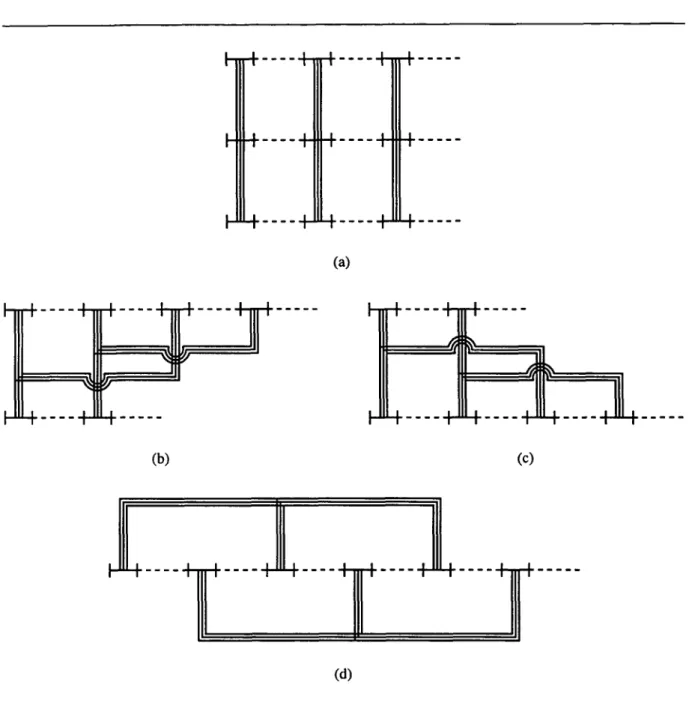
d’Ursell ... 18 2.3

_{Diagrammes ...}

21 2.3.1 Définition et

_comptage

... 21 2.3.2 Deux sommations ... 24 2.4

_{Systèmes dilués dégénérés ...}

27 2.4.1 Gaz

_parfait

... 27 2.4.2 Première correction ... 29

2.4.3 Correction d’ordre suivant ... 34

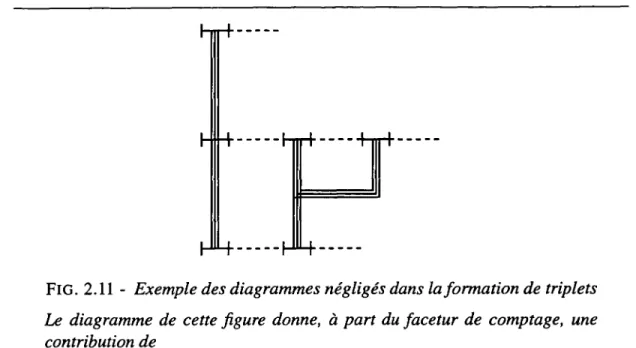
2.A

_Règles

de construction des

_diagrammes

... 40

2.B Deux

_exemples

... 42

Fin de l’article 2.6 Condensation de

_{paires, triplets, ...}

43

2.6.1 Les classes de la formation de

_paires

... 43

2.6.2 Discussion ... 48

2.6.3 Autres canaux de condensation ... 48

3 Les

_opérateurs

densité réduits 51 Introduction au

_{chapitre ...}

51

Article 2

_(en

_anglais)

3.1 Introduction ... 53

3.2 Calcul des

_opérateurs

réduits ... 54

3.2.1

_Opérateur

densité à une

particule ...

55

3.2.2

_Opérateur

densité à deux

_particules

... 56

3.3

_Application

au

gaz dilué ...

57

3.3.1 Gaz

_parfait

... 57

3.3.2 Première correction ... 59

3.3.3 Deuxième ordre en

U

2

... 64

3.3.4 Premier ordre en

U

3

... 66

3.4

_Répulsion

forte à courte

_portée

... 67

3.4.1 Ordre

_{zéro en U}

₂

... 68

3.4.2 Premier ordre en

_U

₂

... 69

3.4.3 Termes suivants ... 73

3.4.4 Résumé ... 77

3.5 Discussion ... 78

3.A Variation du

_potentiel

d’interaction ... 79

Fin de l’article 3.6 Le cas de formation de

_{paires ...}

82

4 Grandeurs

_{thermodynamiques}

et

_longueur

d’Ursell 85

Introduction au

_{chapitre ...}

85

Article 3

_(en

_anglais)

4.1 Introduction ... 87

4.2 Le

_potentiel

de l’ensemble

_{grand-canonique}

... 89

4.2.1 Notation ... 89

4.2.2

_{Approximations}

_pour le

_potentiel

_{thermodynamique}

... 90

4.2.3 Particules

_{sans spin ...}

91

4.2.4

_Spins

... 93

4.2.5 Etats liés ... 93

4.3 Particules

_{à spin}

_1/2

... 95

4.3.1 Densité de

_particules,

_énergie,

aimantation ... 96

4.3.2 Discussion ... 98 4.4 Eléments de matrice de

_U

₂

... 99 4.4.1

_{Longueur d’Ursell}

... 100 4.4.2 Potentiel en marches ... 102 4.4.3

_Sphères

dures ...

103 4.5

Discussion ...

108 Fin de l’article 4.6

U

2

pour

sphères

dures ...

109

4.6.1

Les fonctions d’onde ...

111

4.6.2

_[U

₂

_]

_rel

en

_{représentation}

_position

... 122

4.6.3

_U

₂

en

_{représentation}

_impulsion

... 122

5 Calcul

_numérique

de

_{température critique}

d’un _gaz de bosons 127 5.1

_{Les intégrales de chemin ... 128}

5.1.1

_{L’opérateur densité ... 129}

5.1.2

_{Symétrisation ... 134}

5.2

_{Repérage de la transition ... 134}

5.2.2

_Energie

libre de torsion ... 140 5.3 Résultats ... 141 5.3.1 Le calcul

_{numérique ... 142}

5.3.2 Discussion ... 143 Conclusion 145

Appendices

A Lien avec la théorie de Hartree-Fock 147 B

_Approche

de théorie de

_{champs (Beliaev)}

151 B.1 Fonctions _{de Green pour} des bosons ... 151

B.2

_Règles

de

_Feynman

et fonctions de Green ... 154

B.3 Potentiel effectif ... 158

B.4 Potentiel de

_sphères

dures ... 162

C Notations 167

Bibliographie

171

Index 176

1

LES

SYSTÈMES

QUANTIQUES

DÉGÉNÉRÉS

MAIS

DILUÉS

sont

principalement

caractérisés

par deux

propriétés.

En

premier

lieu,

ils sont le

siège

des effets

quan-tiques

collectifs,

liés à la

_{symétrisation}

des états des

_particules

et au recouvrement de leurs

_paquets

_d’onde;

en second

lieu,

les interactions ne

_perturbent

le

_système

_que

fai-blement en ce sens _{que les collisions} entre

_particules

sont rares, même

_si,

_pendant

une

collision,

les

_particules

concernées

_peuvent

sentir un

potentiel

d’interaction très fort.

Ces

_{systèmes physiques}

se

_prêtent

bien à une étude

_théorique

et il est _{naturel que les}

livres d’introduction à la

_{physique statistique}

en citent des

approches

théoriques

di-verses. Ce n’est toutefois _que

_depuis

_{peu de}

_temps

_{que les}

_{expérimentateurs}

ont réussi à en

préparer

des échantillons.

Les travaux

_présentés

dans cette thèse ont _pour

_objectif

d’élaborer des outils

théo-riques adaptés spécifiquement

à l’étude de ce

_type

de

_système,

et ainsi de contribuer à

une

compréhension plus profonde

des

_phénomènes

_physiques

se

_produisant

dans un

domaine

_qui

se trouve à la croisée de la matière condensée et de la

_{physique atomique.}

1.1 Situation

_{expérimentale}

Un des domaines d’intérêt de la

_{physique atomique}

est,

_depuis

un certain

_temps,

le

re-froidissement et le

_piégeage

d’atomes au _{moyen de} faisceaux laser. L’un des buts

prin-cipaux

est d’atteindre des densités et des

_{températures}

dans un échantillon d’atomes

bosoniques

conduisant à la condensation de Bose-Einstein

_{([ 1];}

_pour une revue récente

( 1993)

des recherches sur ce domaine voir

_[2]).

Cette

_phase

condensée est caractérisée par l’accumulation d’un nombre

macroscopique

de

_particules

dans l’état de

_plus

basse

énergie.

Dans les

_{liquides quantiques}

elle se manifeste _par l’effet de

superfluidité

_(cas

de

₄

_He)

ou de

supraconductivité

_(paires

de

_Cooper

formées _{par les} électrons

conduc-teurs des

_métaux).

Mais la densité élevée de tels

_systèmes

rend difficile la

_séparation

des effets

_quantiques

et

_{d’interaction,}

ce

_qui

_explique

l’intérêt

_porté

vers les

systèmes

dilués ou ce

_problème

est moins ardu.

Pour refroidir des atomes, on a recours

(le

cas échéant seulement

_pendant

une

_phase

de

_{préparation)}

à une utilisation

_adéquate

des interactions entre atomes et lumière. Le transfert

_{d’impulsion}

de la lumière vers des atomes a été mise en évidence pour la

première

fois en 1933

_([3])

dans une

expérience

qui

a

permis

d’obtenir une déviation

d’un

_{jet atomique.}

Le

_principe

des méthodes de _{ralentissement par effet}

_Doppler

est

le suivant:

_quand

un atome dans son état fondamental est éclairé _par un laser se

pro-pageant en sens

opposé,

d’une

_{fréquence légèrement}

_plus

faible

_qu’une

_fréquence

de transition de l’atome vers un état

excité,

l’atome

_peut

absorber un

_photon

_(dont

la

fré-quence

apparente

est

_augmentée

_{par l’effet}

_Doppler).

La transmission de

_{l’impulsion}

du

_photon

à l’atome freine ce dernier. Lors de la désexcitation

_qui

_suit,

le

_photon

est

émis dans une direction

arbitraire; donc,

en _moyenne, ce _{processus d’émission}

spon-tanée ne

change

_pas la

vitesse,

et le résultat

_global

est _{que les} atomes sont ralentis. Pour des atomes neutres, le

refroidissement,

c’est à dire la diminution du mouvement

thermique

autour _{d’une vitesse moyenne, par} ce _processus a été

_{proposé ([4])}

en

1975,

mais il a fallu attendre les années 80 pour la

première

réalisation

expérimentale

([5]).

Depuis,

les travaux sur le refroidissement

laser,

en matière

_{expérimentale}

et

_théorique,

ayant

pour but l’obtention des densités de

plus

en

_plus

élevées,

n’ont pas cessé. Au cours des années 1987-88 il est _{apparu que les}

_{températures}

obtenues _par les

expé-riences sur le refroidissement

_Doppler

étaient bien au-dessous de la limite

_théorique

attendue,

la

_température

minimale observée étant

_plutôt

_{donnée par}

_l’énergie

de recul dû à l’émission

_spontanée

d’un seul

_photon.

En

1989,

une

_explication

en a été donnée en termes d’un effet nouveau,

l’effet Sisyphe ([6]).

La

première

mise en évidence du

refroidissement des atomes en dessous de cette

_température

de recul a été obtenue par

la méthode du

_Piégeage

Cohérent de

_{Population Sélectif}

en Vitesse

([7])

en 1988. Le

refroidissement

par

effet

Raman,

une autre méthode

_permettant

de s’affranchir de la limite de la

_température

de

_recul,

a vu le

_jour

en 1992

([8]).

Pour

_pouvoir

atteindre un

régime

dégénéré

et _{pour détecter les atomes, il} est utile de les confiner dans une

_région

de

_l’espace

à l’aide d’un

_{piège atomique.}

Le

_premier

_piège

(magnétostatique)

pour des atomes neutres a été construit en 1985 par une

_équipe

de chercheurs américains

_([9]).

La

_profondeur

en

énergie

du

piège

étant très

faible,

ils

n’obtenaient

_{cependant qu’une}

basse densité des

_{particules préalablement}

refroidies par laser. A

partir

de 1987

([10])

l’utilisation du

piège

magnéto-optique

a

permis

d’at-teindre des densités

_{beaucoup plus}

élévées en utilisant des

_{champs magnétiques}

_qui

rendent la force de radiation de la lumière

_dépendante

de la

_position

_spatiale.

Il est

_depuis

_{apparu que les méthodes} de

_piégeage

et de refroidissement laser n’étaient pas suffisantes pour obtenir la condensation de Bose-Einstein dans un _{gaz dilué. Les}

expérimentateurs

se sont alors tournés vers une

technique supplémentaire,

issue des

travaux sur

_{l’hydrogène}

_polarisé:

le

_{refroidissement évaporatif.}

_Incidemment,

c’est

entre autres _par ce mécanisme _que les substances se refroidissent dans la vie courante:

la

_température

du thé dans une tasse baisse au cours du

_temps

_par la

_perte

des

molé-cules les

_plus

chaudes

_qui

sont

_emportées

_{par le} courant d’air au-dessus de la tasse.

Sous l’effet des

interactions,

la distribution

_d’énergie

des molécules restantes

_s’ajuste

au fur et à mesure, de sorte

_qu’il

_y a

_toujours

des

_particules

_prêtes

à être

_évaporées

dans la _queue de haute

_énergie

de la distribution de Maxwell-Boltzmann.

_L’équipe

de refroidissement

_{d’Hydrogène polarisé}

au MIT a été la

première

de proposer

l’ap-plication

de ce

_principe

aux atomes

_piégés

_([11,12]).

En raison des difficultés de ces

expériences (préparation

du

_H~,

détection

etc.),

c’est

_cependant

avec des atomes al-calins que cette

_technique

a été

complètement

couronnée de succès et la condensation de _{Bose-Einstein observée pour} la

_première

fois de

_façon

directe.

1

1. Cette transition de _phase a été observée dans un _{système analogue,} constitué d’un gaz d’excitons, des

composés binaires de _porteurs de _charge

_positive

et _négative à l’intérieur des semi-conducteurs excités par une forte radiation laser _{([13] (paires d’excitons)} et _{[14]). Cependant,} la durée de vie très courte de

ces _{paires empêche} des mesures _précises sur les effets collectifs dans un état _{d’équilibre} thermodyna-mique qui ne _peut être que métastable.

Pendant le refroidissement

_évaporatif,

la hauteur du

_potentiel

_qui

_sépare

l’échantillon d’atomes

_piégés

de l’extérieur est continûment réduite. En

_pratique,

une variante de

la méthode utilise un

_champ

de

_{radiofréquence}

selon une

_technique

proposée

_par

Prit-chard que nous ne décrivons pas ici. Les atomes

_qui

se trouvent en haut de la

distri-bution

_thermique

_peuvent

alors franchir la barrière de

_potentiel

et s’enfuir amenant

avec eux

plus

_que

l’énergie

thermique

_{moyenne par}

particule.

Au cours du

_temps

le

niveau de la barrière est abaissé

_(de

manière assez lente _pour

_permettre

aux atomes de

se

rethermaliser,

mais aussi assez

_rapide

à cause des

_pertes

du

piège)

de sorte _que la

température

diminue.

Pour le moment ce sont _{les groupes travaillant} sur le Rubidium

_([15])

et le Sodium

([16])

qui

ont atteint le

_régime

de condensation de Bose-Einstein. Un certain doute

règne

encore concernant les

_expériences

avec du Lithium

([17]),

la

question

étant de

savoir si la transition a été vraiment atteinte. En

revanche,

ce cas du lithium

_présente

actuellement un intérêt

particulier,

du fait que la

longueur

de diffusion est

_négative.

Ceci _pose un

problème théorique

intéressant de stabilité de l’état condensé

(voir

_par

exemple

[18]

ou

_[19]).

1.2

_Approches

_théoriques

Nous

_présentons

dans ce mémoire une contribution au traitement

_théorique

des _gaz

quantiques.

Les méthodes habituelles dans ce domaine sont _{pour la}

_plupart

_originaires

de la

_physique

de la matière

_condensée,

où elles ont été

_employés

avec succès pour la

description

des

_{liquides quantiques}

comme

3

He

ou

4

He.

Elles _{sont, bien}

_sûr,

_également

très utiles _{pour décrire} les _gaz

_quantiques;

_cependant

il est

_possible

d’aller au-delà et

de

_développer

une

_{comprehension plus microscopique}

en

_exploitant

le fait que ces

systèmes

sont dilués.

1.2.1

_Approches

_inspirées

de la matière condensée

La théorie de Landau

_([20:

_{§§1-4,6,25])}

fournit une

_{description macroscopique}

des

propriétés

des

_{liquides quantiques proche}

de la

_température

nulle. Elle introduit le

concept

des

_{quasi-particules, qui}

sont

_porteuses

_{des excitations élémentaires du}

sys-tème. Ces

_{quasi-particules}

obéissent à une

_statistique

_{quantique imposée}

_{par les}

pro-priétés physiques

du

_système.

_L’énergie

ou toute autre

_grandeur

calculée est donnée par une fonctionnelle de la fonction de distribution des

_{quasi-particules}

faisant interve-nir des constantes d’interaction

_(les

« constantes de

_{Landau »).}

Pour un _gaz

dilué,

ces

constantes

_peuvent

être déterminées

_{jusqu’ à}

un certain

ordre,

à

partir

de la

longueur

du

diffusion,

et cela _{même pour des}

_{potentiels divergents}

à courte distance

_(quelquefois

appelé

« _ansatz de renormalisation » de Landau :

après

avoir fait _un calcul habituel

de

_perturbation

en

_potentiel

on

_remplace

les

_{expressions - divergentes}

le cas échéant

- en fonction du

potentiel

par des

expressions

en fonction des éléments de la matrice

de collision T et obtient un résultat

fini).

Beliaev et Galitskii

_{([21-23]) transposent}

les méthodes de la théorie

_quantique

des

champs

(électrodynamique

quantique)

aux

_problèmes

à N _{corps à}

_température

nulle. Pour traiter des

_potentiels

du

_type

de

_sphères

_dures,

ils resomment toute une classe de

diagrammes

de

_Feynman,

du

_type

échelle,

incluant de cette

_façon

des termes

_jusqu’à

l’ordre infini en

_puissances

de

potentiel.

Ainsi,

ils arrivent à obtenir un

_{développement}

en termes d’un

_potentiel

_effectif,

lui-même

fini,

qui

représente

une

_amplitude

de

diffu-sion

_{généralisée}

tenant en

_compte

la

_présence

des autres

_particules.

Ce

_potentiel

effec-tif _{s’obtient par la solution} d’une

_{équation intégrale}

faisant intervenir les

_amplitudes

de _{diffusion à deux corps}

_(on-

et

_off-shell),

finies même pour des

_potentiels

fortement

répulsifs

(voir

l’annexe B pour

plus

de

_détails).

Des

_système

dilués de bosons à

_température

nulle se décrivent avec une assez bonne

approximation

par un Hamiltonien modèle

qui

se laisse

diagonaliser

_par une

trans-formation

de

_{Bogoliubov, qui remplace}

les

_opérateurs

création/annihilation

_agissant

sur le condensat par un nombre

complexe.

On utilise

également

l’équation de

Gross-Pitaevskii,

une

équation

de

Schrödinger

non-linéaire _pour la fonction d’onde d’un

con-ensat de Bose-Einstein non-uniforme dans

_l’espace

_(la

_première

_application

en a été

la

_description

des vortex dans le

4

He

_superfluide

([24,25])).

Dans les

_approches

de

_champ

_moyen

_chaque

_particule

se

déplace

dans un

potentiel

effectif à un _{corps créé par l’interaction}

moyennée

avec les autres atomes. Cette

ap-proximation

en termes de

_particules

_{indépendantes,}

souvent _{utilisée par}

_exemple

en

physique

atomique

ou nucléaire dans le cadre de

_{l’approximation}

de

Hartree-Fock,

donne des résultats en bon accord avec les observations pour de nombreux

_systèmes

physiques

différents. Dans la

_pratique,

il s’avère difficile de résoudre les

_équations

couplées

pour déterminer les fonctions d’onde et le

champ

moyen de manière auto-cohérente

_{(voir [26],}

section

10,

et à

_température

finie: sections

_27-29).

En ce

_qui

concerne les méthodes

_numériques,

le

_champ

est tellement vaste _que nous ne

citons que

quelques

exemples,

développés

notamment _pour

_comprendre

la

superflui-dité de

4

He.

McMillan a déterminé des

énergies

et _{fractions condensées par} une

ap-proche

variationelle

_([27]).

Kalos,

_Levesque

et Verlet ont utilisé une méthode Monte

Carlo pour des fonctions de Green afin d’évaluer des

_énergies

exactes

_([28,29]).

Nous

présentons l’approche

des

_intégrales

de chemin _{déterminées par} une méthode de

Monte

_Carlo,

mise en oeuvre _par

_Ceperley,

en

plus

de détail dans la section

5,

dans

laquelle

nous calculons la

_{température critique}

des _gaz de bosons.

Toutes les manières d’aborder le

_problème

à N _corps

_{présentées jusqu’ici}

ont été éla-borées avec un but

_principal

_{d’application}

aux

liquides.

Bien

qu’il

soit bien sûr

pos-sible de les utiliser aussi _{pour des}

_systèmes

_{gazeux, deux} méthodes existent

_qui

sont

conçues pour ces cas en

_particulier

et

_qui

tirent

_profit

de la faiblesse de l’interaction faible dès le début du

_{développement.}

Nous les décrivons

_plus

en détail dans les

sec-tions

_qui

suivent.

1.2.2

_{Pseudopotentiel}

Dans une série d’articles

_([30-34]),

_Huang,

Lee et

_Yang

reformulent le

_problème

de N

_particules

en interaction faible à l’aide de la notion de

_{« pseudopotentiel}

_»,

_qui

ne

fait intervenir _que les

_déphasages

de collision

_~

_l

_(k).

L’idée est de

_remplacer

le

poten-tiel d’interaction _par une condition aux limites sur la fonction

_d’onde,

_qui

_{par ailleurs} se

_comporte

comme celle de

_particules

libres. Provenant initialement de la

_physique

nucléaire

_{([35, 36]),}

ces méthodes se limitaient alors au

problème

à deux corps et au

traitement des collisions dans

_{l’approximation}

de

_Born,

_{restrictions que}

_Huang,

Lee

et

_Yang

ont ensuite surmontées.

Ces auteurs donnent

_{l’expression}

suivante pour le

pseudopotentiel

(non-hermitien

2

)

associé à un

potentiel

d’interaction du

_type

de

sphères

dures de diamètre

a:

3

Pour que cette théorie reste

_valable,

_{il faut que} la

_perturbation

du

_{potentiel (réel)}

sur

la fonction d’onde reste suffisamment limitée dans

_l’espace;

l’étendue de cette

pertur-bation pourra être assimilée à la

largeur

infinitésimale d’un

_pic

delta à _{condition que} l’extension

_spatiale

du

_potentiel

soit

_négligeable

_par

_rapport

à un

_paquet

d’onde dont

la taille est

_comparable

à la

_longueur

de de

_Broglie,

ce

qui implique:

(la longueur

d’onde

_thermique

03BB

T

est _{definie pour des}

_particules

de masse m à

tem-pérature

T _{par :}

où

k

B

est la constante de

Boltzmann)

Appliquant

la condition aux limites

_(1.1)

au

problème

à N

particules (tronquée

au

pre-mier ordre en

_a),

ces auteurs calculent

_l’énergie

de l’état fondamental d’un _{gaz de}

bo-sons

jusqu’à

l’ordre 3 en

a;

4

pour

un _{gaz de} fermions ils trouvent la correction à la fonction d’état en ordre 2 et la fonction de corrélation

_(aux

distances entre

_particules

comparables

à la

_portée

du

_potentiel

et aux distances très

grandes).

Malgré

ces

résultats,

qui

sont obtenus d’une

_façon

assez

directe,

cette théorie

_présente

cependant

des limitations inhérentes

_qui

rendent son extension aux ordres suivants

dif-ficile. En

_premier

lieu,

même si

_{l’expression}

formelle

(1.1)

est _{donnée pour} toutes les valeurs de

l,

en

pratique

le calcul des contributions des ondes

partielles

d’ordres

supé-rieurs n’est pas

effectué,

ce

_qui

se traduit dans la condition suivante _{pour les} moments

relatifs k:

2. _{L’opérateur}

_(~/~r)r

_{n’est pas hermitique,} c’est à dire _qu’il existent des fonctions d’onde

_{<r|~>}

et

_{<r|03B8>}

telles que <~ | (~/~r)r

| 03B8> ~ <03B8 | (~/~r)r |

~>. Même si la façon par laquelle l’opérateur du

pseu-dopotentiel a été obtenu assure _que ses _{valeurs propres} sont _réelles, son caractère non-hermitien interdit

l’utilisation de _techniques variationelles afin de déterminer ces valeurs propres ([30]).

3. m est la masse d’une _particule, k _correspond au vecteur d’onde.

4. Pour des intéraction de _sphères dures, on _{peut développer:}

1/

(k)]

0

[-k cot ~

= _{a +}

1 3 (ka)

2

a

₊ ... Dans l’état fondamental _{non-perturbé,} toutes les _particules ont un moment

_cinétique

nul de sorte _que

la contribution en k2 _{n’intervient pas. Des} collisions dans l’onde l = 1 sont interdites _{par la symmetrie}

En

second,

la méthode n’inclut que des collisions à deux _corps; il _{n’est pas évident} de voir comment il serait

_possible

d’en

_élargir

le

_champ

_{d’application.}

Enfin,

la distorsion de la fonction d’onde à « l’intérieur du

potentiel

d’ interaction _{» est}

ignorée.

5

Il

_est donc

possible

que des effets

physiques

soient

négligés

par le

concept

même de la théorie du

pseudopotentiel.

En

fait,

c’est cette méthode sous la forme la

plus simple,

en

remplaçant

le

_potentiel

d’interaction par le

potentiel

effectif

suivant

6

:

qui

est habituellement à la base des travaux

_théoriques

sur la condensation de

Bose-Einstein dans les _gaz

_atomiques

(voir

par

exemple

[18,37,38]).

1.2.3 Les

_{développements}

en

agrégats

Dans la suite nous

_présentons

les méthodes dites de

_{développement}

en

agrégats

(ou

« clusters

»).

Elles constituent le

point

de

départ

des travaux de cette thèse et sont

construites pour fournir directement des

développements

en densité.

Nous nous intéressons aux _gaz

dilués,

c’est à dire aux

systèmes

_pour

_lesquels

la

_portée

du

_potentiel

est

_beaucoup

_{plus petite}

_{que la} distance _moyenne entre

_particules:

en introduisant la densité de

_{particules n}

=

N/V

et la

_longueur

b caractérisant _la por-tée du

_potentiel

d’interaction

_V

_int

_(|r

₁

_-

_|),

₂

_r

i.e. une distance entre

_particules

à

_partir

de

_laquelle

le

_potentiel

_peut

être

_négligé

devant les autres

_énergies

du

_problème.

Le

produit

n

1/3

b

est

_{supposé petit,}

cas _pour

_lequel

il

_paraît

naturel de construire un

déve-loppement

des

_grandeurs

_{thermodynamiques}

en

puissances

de ce

paramètre.

Ursell a

présenté

en 1927

_([39:

_§5])

une méthode de calcul de la fonction de

partition

pour un _gaz

_{classique qui}

est basée exactement sur cette idée. Il

_développe

la fonction de

_partition

à l’aide des fonctions

_u

_(n)

_qui

sont non-nulles seulement si n

_particules

sont

_proches

l’une de

_l’autre,

autrement

_dit,

si elles forment un

_agrégat.

Dans un _gaz

dilué

_pourtant

les collisions à

_plus

_{de deux corps} sont extrêmement rares et _par

consé-quent

le

développement

peut

être arrêté

après

quelques

termes seulement.

_Mayer

et

Mayer

ont rendu

_l’approche

_plus

_{systématique}

_([40])

et fourni une

_{représentation}

gra-phique

des termes du

_{développement.}

La

_{première généralisation}

aux

systèmes

_quantiques

a été faite _{par Uhlenbeck} et Beth

en 1936

_([41,42]).

Ils se limitent au

_premier

ordre

_(seulement

des collisions à deux

5. Bien sûr, cette distorsion est invisible _{pour des sphères} dures, le _type de _{potentiel que Huang,} Lee et

Yang ont étudié, puisque, dans ce cas, la fonction d’onde est totalement exclue du _potentiel.

6. L’ omission de _{l’opérateur}

_(~/~r)r

ne _{change pas l’effet du pseudopotentiel} si celui-ci

_agit

sur des

fonc-tions d’onde _qui se _{comportent regulièrement} à _{l’origme (Contre-exemple:} une fonction d’onde _qui devient _{proportionnelle} à a +

_b/r

au _{voisinage de l’origine)}

corps

interviennent)

et aux _gaz faiblement

dégénérés,

_pour

lesquels

la

_longueur

d’onde

thermique

03BB

T

est

_{beaucoup plus}

_petite

_que la _{distance moyenne} entre

_particules:

En

effet,

le caractère

_quantique

_{n’intervient que par le fait que les}

_opérateurs

associés à

_l’énergie

_cinétique

et à

_l’énergie

_potentielle

ne commutent _{pas, ainsi que par}

l’uti-lisation des fonctions d’onde

_{symétrisées}

_pour le calcul des fonctions _u(2). La corré-lation

_quantique

des deux

_particules

subissant la collision avec toutes les autres est

complètement négligée.

Ils calculent le deuxième coefficient du viriel

_B(T),

_la pre-mière correction à la

_pression

_après

_{la contribution du gaz}

_parfait

_{pour des}

_systèmes

dilués:

Dans cette

_première

_correction,

deux contributions

_d’origines

différentes

_peuvent

être

distinguées:

Le

_premier

terme est de nature

_purement

_statistique;

il est de

_signe

_opposé

_pour des bosons et _pour des fermions. Le deuxième terme tient

_compte

des effets du

_potentiel

d’interaction. Son calcul fait intervenir la différence entre la densité d’états du

_système

(à

deux

_corps)

en interaction et celle du

_système

sans

interaction ;

cette différence

s’ex-prime

en fonction des

_déphasages

de collision

~

l

(k).

Beth et Uhlenbeck obtiennent alors le résultat suivant :

(La

somme sur

_{l porte}

sur les nombres

_pairs

_pour des bosons et sur les nombres

_impairs

pour des

fermions;

B

lié

(T)

donne la contribution des états liés le cas

échéant)

Ce résultat est

_remarquable

en ce sens

_{qu’il exprime}

de

_façon

exacte une

_grandeur

macroscopique uniquement

en fonction des

_paramètres

_{microscopiques.}

Pour _des par-ticules

_bosoniques,

à basse

_{température,}

seules les collisions en onde s sont

impor-tantes, la somme sur l se réduit alors à un seul terme.

_{L’intégration}

sur k fait

_disparaître

une

_puissance

de

03BB

T

et introduit - comme

/dk

0

d~

varie peu

_comparé

à

e

-03BB2

T

k2/203C0 -un nouveau

paramètre

du

_potentiel,

la

_longueur

a =

d~

0

/dk

(dans

le _cas d’un

po-tentiel de

_sphères

_dures,

a

correspond

au diamètre des

_sphères).

Par

_conséquent,

le

terme

int

n03BB

3

T

B

est

_{approximativement proportionnel}

à

_.

_na03BB

_T

₂

Le

_produit

_a03BB

₂

_T

corres-pond

donc au

_paramètre

du

_{développement}

en interaction.

Kahn et Uhlenbeck ont

_poursuivi

ce travail et donné un

_approche

_plus

méthodique

incluant les ordres suivants

_([43]).

Ils ont

_{également essayé}

_{d’appliquer}

le

développe-ment aux _gaz

parfaits

en

régime

de condensation Bose-Einstein et démontré

qu’effec-tivement le

_{développement}

mène à une condensation des bosons dans l’état à moment

cinétique

nul: la

_pression

reste constante _{pour des densités au-dessus d’un certain seuil}

critique.

La méthode de collisions binaires de Lee et

_Yang

est la continuation de ces études

([44-46]

et

[47:

section

9.7]).

Comme nous, ces auteurs cherchent à

_distinguer

deux

étapes

dans leur étude en introduisant un

_système

auxiliaire de

_particules

discernables.

Mais ils effectuent un calcul en termes d’éléments de

matrice,

et ne font pas le même

usage que nous des

_{cycles d’échange.}

Aussi leur méthode est elle relativement

com-pliquée,

en

_particulier

lors

qu’ils

tiennent

approximativement

_compte

d’effets à trois

corps et

_plus

_(qui

sont _{traités par des}

_{intégrations}

sur la

_température

inverse

_03B2).

Se-lon leurs termes, « les

propriétés

de convergence de leurs

développements

ne sont _pas

bien

_{comprises » .}

_Cependant,

et comme nous le _verrons, ils obtiennent certains

re-sultats

_qui

sont

_identiques

aux nôtres

_(la

formule de Beth Uhlenbeck

généralisée),

ce

dont nous nous sommes d’ailleurs rendu

_compte

_après

les avoir obtenus

independam-ment. En

revanche,

dans bien d’autres cas, leurs calculs sont

_trop

_compliqués

et ne

permettent

pas d’aboutir à un resultat

qui

soit

comparable

aux nôtres.

1.2.4 Motivation de notre travail

Le vaste

_champ

de théories

_permettant

de traiter les

_{systèmes quantiques}

dilués,

dont

nous avons seulement pu discuter les

_plus

_marquantes,

nous fournit des outils

théo-riques

parfaitement

satisfaisants,

bien que

parfois

difficiles à mettre en oeuvre.

_Quelles

sont alors les motivations de ce travail? Nous limitons cette étude aux _gaz

_quantiques

dilués,

ce

qui

est évidemment une

simplification

_par

comparaison

avec un traitement

incluant les

_{liquides. Exploitant}

cette

_{simplification}

dès le commencement, nous

cher-chons à construire une

_{description plus}

cohérente du

_système

_physique,

contenant à la fois ses

propriétés

_{thermodynamiques macroscopiques (grand potentiel}

_par

_exemple)

et ses

_{propriétés microscopiques (opérateurs}

densité

reduits,

à un ou à deux

_corps).

En

particulier,

les corrélations entre

_particules

sont

_prises

en

_compte

de

_façon

_detaillée,

même lors

_qu’elles

sont fortes à courte distance sous l’effet de

_repulsions

du

_type

coeur

dur. Ce dernier

_point

necessite evidemment un traitement

non-perturbatif

du

poten-tiel d’interaction. Nous verrons

_qu’une

telle

_description

est effectivement

_possible

en

termes

_{d’opérateurs}

d’Ursell,

inspirés

des fonctions d’Ursell habituelles en

_mécanique

statistique quantiques,

mais mieux

_adaptés

à un cas où le

degré

de

dégénérescence

du

gaz n’est pas nécessairement faible. Ainsi obtiendrons nous des

expressions

systéma-tiques

du

_grand

_potentiel

et des

_opérateurs

densité

reduits,

au sein d’un même cadre

théorique.

Ces resultats sont néanmoins limités à un _gaz restant au dessus du

_point

de

conden-sation de Bose-Einstein

_(ou

_{d’appariement}

_{BCS pour} des

_{fermions). Cependant,}

nous avons

_également

abordé l’étude de ces

phénomènes

de

condensation;

en

_particulier

nous montrons comment le formalisme des

_opérateurs

d’Ursell

_permet

très

directe-ment de mettre en évidence le

_phénomène

de condensation

_BCS,

_par une

générali-sation toute naturelle de la condensation de bosons. De même d’autres « canaux de

Nous nous sommes aussi intéressé au

problème

de condensation

_superfluide

dans un

gaz de bosons. Guidés par le formalisme des

opérateurs

d’Ursell,

nous avons obtenu

certains resultats

_numériques

concernant la

_{température critique. Cependant,}

faute de

temps,

l’étude des gaz condensés n’a pas été

complétée

de

façon

aussi

systématique

et nos resultats n’ont _pas encore le même caractère

_méthodique

_qu’au

dessus du

_point

de condensation.

L’ensemble de notre travail est décrit dans la suite de ce mémoire.

1.3 Les bases de notre

_description

_théorique

Notre but est _{donc de pousser l’idée du}

_{développpement}

en

agrégats

plus

loin que dans

les traitement

_{classiques (fonction}

_d’Ursell).

Ceux-ci

_requièrent

deux conditions de

validité, (1.6)

et

_(1.7),

_{alors que} nous désirons nous affranchir de la seconde.

1.3.1 Généralisation de la formule de Beth-Uhlenbeck

La formule de

_{Beth-Uhlenbeck,}

_qui

donne le deuxième coefficient du viriel d’un _gaz

non-dégénéré,

peut

être

_{généralisée}

à des

_dégrées

de

_{dégénérescence plus}

élévés. L’élaboration et la

_description

de ce

formalisme,

_que nous avons

_baptisée

« Méthode

des

_opérateurs

d’Ursell », fait

l’objet

du

chapitre

2.

La méthode se base sur des

opérateurs

_agissant

sur un

_système

auxiliaire de

_particules

discernables,

que nous

_appelons

les «

opérateurs

d’Ursell _{», et}

_qui

_permettent

de

dé-velopper

la fonction de

_partition

en une série où le

_paramètre

de

_{développpement}

fait intervenir la

_portée

du

_potentiel,

_{mais pas} son intensité

_(il

reste

_convergent

même _pour des

_potentiels

fortement

_répulsifs).

Le

_{premier opérateur}

d’Ursell

_agit

sur une

parti-cule,

et tient

_compte

de

_{l’énergie cinétique}

_{ainsi que,} le cas

_échéant,

d’un

_potentiel

extérieur;

le

deuxième,

opérant

sur deux

_particules,

contient tous les effets du

poten-tiel

_pendant

une collision

binaire,

le troisième ceux des collisions à trois

_particules

et

ainsi de suite.

Les

_opérateurs

tenant en

_compte

les interactions

_(les

_opérateurs

d’ordre

_supérieur

à

1)

font intervenir non seulement les effets

_{asymptotiques}

des collisions sur les fonc-tions d’onde

_{(déphasages),}

mais aussi leur

_comportement

à courte distance

_{qui joue}

un rôle dans les corrélations entre

_particules.

En utilisant les

_opérateurs

_d’Ursell,

nous

classons les effets du

_potentiel

selon le nombre de

_particules

mises en

jeu

dans les

collisions,

ce

_qui

nous

_permet

de trouver des

_{approximations}

_propices

à l’étude des

systèmes

dilués.

Ce traitement des interactions est suivi d’une deuxième

_{opération indépendante}

-qui

tient

_compte

de la

_{symétrisation}

_quantique.

Nous

_exprimons

les

_opérateurs

symé-triseur/antisymétriseur

en

_cycles

_{d’échange. Après}

un

_regroupement

des termes nous

parvenons à resommer sur ces

_cycles

d’une

_façon

_exacte, ce

_qui

nous

_permet

de

trai-ter des

_systèmes

de

_{dégénérescence}

élevée. Afin de

_{systématiser}

les sommations et

approximations

à

effectuer,

nous introduisons une

représentation graphique.

gaz

parfait

sont obtenues de cette manière. Il est

_possible

de choisir

_{l’approximation}

à

employer

en fonction du

problème

à étudier de sorte

_qu’on

_peut

se concentrer sur les

effets

_importants.

La

_première

correction est _{valable pour} un _{gaz dilué} et

_généralise

la formule de Beth-Uhlenbeck en introduisant des facteurs

d’occupation

de

l’espace

des

impulsions.

D’autres

corrections,

par

exemple

d’ordre

plus

élévé en

portée

du

poten-tiel,

ou des sommations

_permettant

de

_reproduire

l’appariement

des

paires

de

Cooper,

sont calculées.

1.3.2

_Propriétés

à courte distance

Les éléments de matrice

_diagonaux

des

_opérateurs

de densité réduits à un

_(ou

deux

corps)

donnent la

_probabilité

_pour

_qu’une

_{(respectivement}

_{deux) parmi}

un

_grand

nom-bre de

_particules

d’un ensemble

_{thermodynamique}

se trouvent dans des _états

quan-tiques

spécifiés.

Ils

_permettent

ainsi de sonder le

_système

à une échelle

_{microscopique.}

Dans le cadre de notre formalisme nous obtenons les

opérateurs

densité en

_imposant

une variation aux

opérateurs

d’Ursell à un _{corps de}

l’expression

de la fonction de

par-tition. De cette

_façon,

nous obtenons ces

opérateurs

dans les

approximations

succes-sives,

_partant

à l’ordre le

_plus

bas de

_{l’expression}

valable _{pour le gaz}

_parfait

_(voir

cha-pitre

3).

La

_première

correction

_s’applique

aux _gaz dilués. Pour la

calculer,

nous _prenons comme

_point

de

_départ

la formule de la fonction de

_partition

du

_premier

ordre en

por-tée du

_potentiel.

Nous obtenons une

_expression

_pour

_{l’opérateur}

à un _corps

qui

fait

intervenir la trace sur une deuxième

particule

liés avec le

_premier

_par un

_opérateur

d’Ursell à deux corps, et

_qui

ressemble donc à un résultat des méthodes de

_champ

moyen. Dans le terme correctif de

_{l’opérateur}

à deux

_particules,

deux

_parties

sont à

distinguer:

la

_première

contient

_également

une trace sur une

particule

auxiliaire

_qui

introduit une contribution d’interaction

moyennée;

dans la

seconde,

en

revanche,

les

deux

_particules

ressentent directement l’interaction _par un

_opérateur

d’Ursell à deux

corps. Cette

partie

contient toutes les corrélations

_qui

sont

_importantes

à courte dis-tance,

lorsque

le

_champ

_moyen créé _{par les}

_particules

autour cesse d’être

_{prédominant.}

Comme une

première application

nous déterminons la fonction de corrélation à deux

corps pour un _gaz de

sphères

dures. En tenons

_compte

des

_{diagrammes jusqu’à}

l’ordre deux en

_portée

du

_potentiel,

nous vérifions

_qu’en

effet la

_probabilité

de trouver deux

particules

à une distance inférieure au diamètre des

_sphères

dures s’annule. C’est à

notre connaissance la

_première

fois

_qu’une

_expression

_générale

de cette

_propriété

non-perturbative

est obtenue. 1.3.3

_Propriétés

_{thermodynamiques}

Le

_chapitre

4 décrit les résultats _que nous avons obtenus _pour les différentes

_grandeurs

thermodynamiques

utilisant le

_premier

terme de notre

_{développement.}

Les traces sont

explicitées

en

_intégrales

sur les états d’onde

_libre,

_plus

une somme des contributions dues aux états liés.

_{Quelques grandeurs,}

comme _par

_exemple

la

_pression,

la densité ou

la

_{susceptibilité magnétique,}

sont

_explicitées

en fonction

_{d’opérateurs}

d’Ursell à deux

Les

_expressions

obtenues ressemblent à celles évaluées au

_premier

ordre des méthodes

habituelles de

_perturbation

en

_potentiel,

la différence

_principale

étant que, dans toutes

les

_expressions,

les éléments de matrice du

_potentiel

d’interaction sont

_remplacés

_par

un

_opérateur

d’Ursell à deux

_{particules (qui}

lui-même contient tous les ordres en

po-tentiel).

Il est alors

_important

d’étudier le

_comportement

de cet

_opérateur.

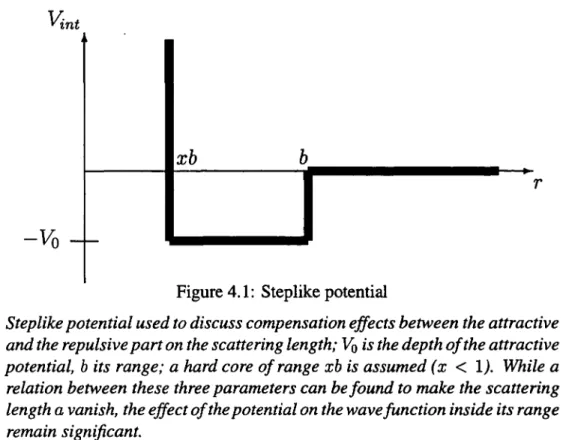
A titre

d’exemple

nous _{comparons les éléments} de matrice de cet

_opérateur

_pour un _gaz de

sphères

dures avec des

_prédictions

de la théorie des

_{pseudopotentiels (dans}

l’approxi-mation de

_(1.5)).

Il se trouve _{que pour des}

_bosons,

dans le domaine de validité des

pseudopotentiels

(1.2)

et

_(1.4),

on n’observe pas de différence

_appréciable

entre les deux

résultats,

tandis

_qu’un

_phénomène

étonnant se

_produit

_pour les

_fermions,

du fait

de l’existence de la

_sphère

de Fermi

_qui

introduit une nouvelle échelle

_{d’énergie:}

_pour

des moments

_{cinétiques k}

de l’ordre du moment de Fermi

_k

_F

_,

l’élément de matrice de

l’opérateur

d’Ursell

_change

de

_signe,

tout comme si les interactions

_pourraient

devenir attractives à

_température

suffisamment basse.

Les

_expressions

sont exactes au

_premier

ordre dans le «

paramètre

de dilution »

n

1/3

b

pourvu que le

degré

de

dégénérescence,

fixé par le

produit

n

1/3

03BB

T

,

ne soit pas

_trop

élevé;

elles cessent d’être valable si les

_particules

commencent à atteindre le

_régime

de condensation de Bose-Einstein ou de

_paires

de fermions. En

_effet,

_quand

on se

rap-proche

de la

_température

_critique,

les termes de notre

_{développement}

commencent à

diverger

et cela d’autant

_{plus rapidement}

_{que les} termes sont d’ordre élevé.

Au

_chapitre

5 nous _exposons les resultats d’une étude de la condensation de

13 Introduction au

_chapitre

LA

FONCTION DE PARTITION est une fonction

génératrice

qui

contient toute

l’in-formation

d’un ensemble

_{thermodynamique}

_{([48: 7.1,3]).}

Dans ce

chapitre

nous

montrons comment on

_peut

calculer cette fonction _pour un

système

dilué à l’aide du

formalisme des

_opérateurs

d’Ursell. La fonction de

_partition

_Z

_gc

de l’ensemble

grand-canonique

est _{donnée par :}

Dans cette

formule,

la trace s’effectue sur le nombre de

_particules

N et les états des

particules

discernables,

03B2

désigne

la

_{« température}

inverse

_{» (k}

_B

_T)

_-1

_,

z la

fugacité

e

03B203BC

où 03BC

est le

_{potentiel chimique,}

et

_N

_N

l’hamiltonien _pour N

_{particules interagissant}

par un

potentiel

V

int

:

Le

_symétriseur

S

N

s’applique

pour des

particules bosoniques,

l’antisymétriseur A

N

pour des fermions.

Comme nous l’avons

déja

dit,

nous calculons

_Z

_gc

en deux

_étapes.

Dans un

premier

temps,

les interactions sont _{traitées pour} un

_système

auxiliaire de

_particules

discer-nables en se servant d’un

_{développement}

en

agrégats inspirée

des méthodes citées

dans la section

1.2.3,

puis

la

_statistique

entre en

_jeu

et les

symétriseurs/antisymétri-seurs sont

_développés

en

_cycles

_d’échange

C

l

.

Cette démarche est _{à opposer} aux

cal-culs

antérieurs,

où les effets d’interaction et de

_statistique

sont

_incorporés

dans un seul

traitement,

ce

qui

rend

plus

difficile la

prise

en

_compte

d’un taux de

_{dégénérescence}

élevé

_{puisqu’elle}

demanderait la resommation d’un très

_grand

nombre de coefficients

du viriel.

L’élaboration et la

_{description précise}

de cette démarche fait

_l’objet

d’un _article pu-blié

_([49])

_que nous

_reproduisons

dans la suite.

Ici,

nous ne donnons

_qu’un

résumé

simplifié.

on définit une hiérarchie

_{d’opérateurs}

d’« Ursell

» U

q

,

dont les

premiers

membres

s’écrivent:

Pour un

_{potentiel qui}

tend suffisamment vite vers zéro

_quand

la distance entre

parti-cules

croit,

ces

opérateurs

_transposent

dans le domaine

quantique

la

propriété

de

l’«

_{agrégativité »}

(«

clustering »

en

anglais)

des fonctions d’Ursell

classiques :

leurs

élements de matrice s’annulent en

représentation

positions lorsque

les

particules

sont

éloignées

l’une de l’autre. En termes des

_U

_q

_{l’opérateur}

K

N

s’exprime

par :

Chaque

terme de la somme est un

produit

de

m’

1

opérateurs

U

1

,

de

m’

2

opérateurs

U

2

,

... , et ainsi de suite. La

sommation,

schématisée par

03A3

{U}

,

consiste en une somme

sur toutes les différents ensembles

_{m’

₁

_,

_m’

₂

_{, ... ,}

_m’

_N

_}

_conformes

avec la condition :

et toutes les

_{possibilités non-équivalentes}

de distribuer les N

_particules

_{dans les}

argu-ments des

_U

_q

_.

On _{remarque que,} même _{pour des}

_potentiels

_{divergents (potentiels atomiques}

à courte

distance entre

_particules

_par

_exemple),

aucun des termes de

_(2.5)

ne

_présente

un

com-portement

singulier,

ce

qui

est à _opposer aux

_{développements}

habituels en

puissances

du

_potentiel.

De

_façon

_analogue

le

_{symétriseur/antisymétriseur}

de

_(2.1)

est

_développé

en

_cycles

d’échange :

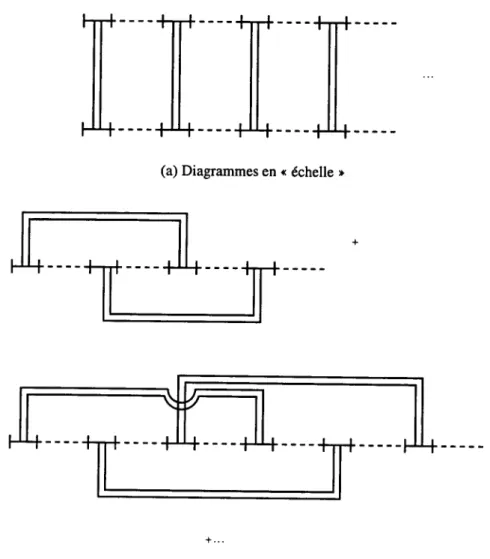
Pour le

_{symétriseur S}

_N

_(bosons)

le

_{facteur ~}

vaut

+1,

pour

l’antisymétriseur

A

N

(fer-mions), ~ prend

la valeur 20141. La somme

symbolique

sur

{C}

_porte

_également

sur les

configurations possibles,

à condition

_d’adapter

la notion de

_{non-équivalence}

de deux

distributions.

1

1. Les _{cycles d’échange} sont invariant _{uniquement par} rotation _{cyclique des arguments, alors que} toutes