Micromechanical Modelling of Heterogenous Porous Materials with Application to Oolitic Rocks

(1)

HAL Id: tel-01487018

https://tel.archives-ouvertes.fr/tel-01487018

Submitted on 10 Mar 2017

HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

Micromechanical Modelling of Heterogenous Porous

Materials with Application to Oolitic Rocks

Fengjuan Chen

To cite this version:

Fengjuan Chen. Micromechanical Modelling of Heterogenous Porous Materials with Application to Oolitic Rocks. Materials. Université de Lorraine, 2016. English. �NNT : 2016LORR0134�. �tel-01487018�

(2)

AVERTISSEMENT

Ce document est le fruit d'un long travail approuvé par le jury de

soutenance et mis à disposition de l'ensemble de la

communauté universitaire élargie.

Il est soumis à la propriété intellectuelle de l'auteur. Ceci

implique une obligation de citation et de référencement lors de

l’utilisation de ce document.

D'autre part, toute contrefaçon, plagiat, reproduction illicite

encourt une poursuite pénale.

Contact : ddoc-theses-contact@univ-lorraine.fr

LIENS

Code de la Propriété Intellectuelle. articles L 122. 4

Code de la Propriété Intellectuelle. articles L 335.2- L 335.10

http://www.cfcopies.com/V2/leg/leg_droi.php

(3)

Thèse de DOCTORAT

Préparée à L’Université de Lorraine - Laboratoire Georessources –UMR7359

Présentée par Fengjuan CHEN Pour obtenir le grade de Docteur en SCIENCES

DE L’UNIVERSITE DE LORRAINE Spécialité

Mécanique - Génie Civil

Modélisation Micromécanique de Milieux Poreux Hétérogènes et

Applications aux Roches Oolithiques

Ph-D Thesis

Micromechanical Modelling of Heterogeneous Porous Materials

with Application to Oolitic Rocks

Soutenance publiquement le 24 Octobre 2016

Jury composé de

M.KACHANOV Professeur Tufts University, USA Rapporteur V.KUSHCH Professeur Ukraine National Academy of Science, UA Rapporteur Y.GUEGUEN Professeur Ecole Nationale Supérieure, Paris, France Examinateur I.SEVOSTIANOV Professeur New Mexico State University, USA Examinateur A.GIRAUD Professeur ENSG, Nancy, France Directeur D.GRGIC Maître de conférences ENSG, Nancy, France Co-directeur

(4)

(5)

III

For my father, for my mother,

"It's not that I'm so smart, it's just that I stay with problems longer "

(6)

(7)

V

Acknowledgement

Considering the challenge, I would not accomplish my Ph.D. without supports from many individuals. My appreciation goes out to them, and I would like to acknowledge some of them here.

I would like to express my most sincere gratitude to my supervisors Prof. Albert Giraud and Dr. Dragan Grgic for their full supports throughout my doctoral study at multiscale hydrogeomechanical group of Georessources laboratory of university of Lorraine. Their constructive scientific suggestions, friendly encouragements and particularly their great patience for a young researcher, supported me to enjoy my research and life in my Ph.D.

I would like to express my appreciation to the committee of my Ph.D. defense, most of them have traveled to France to attend my final defense. Their insightful suggestions and valuable remarks enriched my knowledge and encouraged me for a further exploration.

My gratitude goes to Prof. Mark Kachanov and Prof. Volodymyr Kushch for their constructive report and indications. I’m grateful for the presence of Prof. Yves Guguén as the president of the defense committee.

I would like to thank Prof. Igor Sevostianov. It is my honor for his presence, as well as his kindness supports and helps. As a mentor of my research carrier and life, he has warmly welcomed me several times during my Ph.D. to his team at New Mexico State University. Without his innovative ideas and his programmatic proposals, our works would have no opportunity for publication; also my dissertation would lose a part of knowledge contribution.

I would like also to thank every member of Georessources laboratory for their kindness. Finally, this dissertation is dedicated to my parents for their permanent love, support and encouragement.

(8)

(9)

VII

Abstract

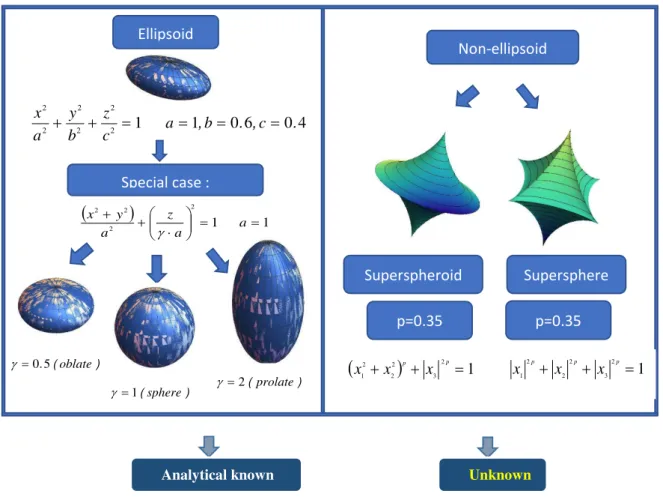
Focusing on the effect of shape factor on the overall effective properties of heterogeneous materials, the 1st_{and the 2}nd_{Eshelby problem related to 3-D non-ellipsoidal inhomogeneities} with a specific application to oolitic rocks have been discussed in the current work. Particular attention is focused on concaves shapes such as supersphere and superspheroid. For rocks, they may represent pores or solid mineral materials embbeded in the surrounding rock matrix.

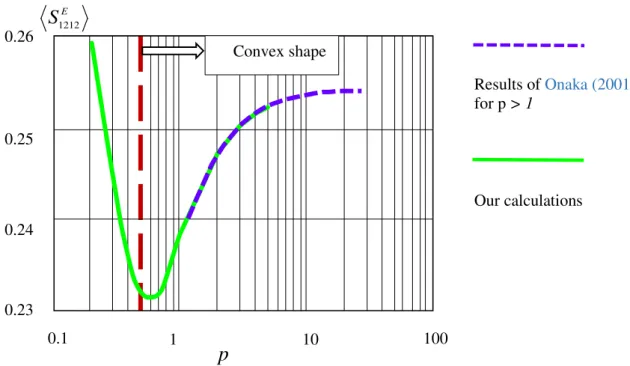
In the 1st_{Eshelby problem, Eshelby tensor interrelates the resulting strain about inclusion and} eigenstrain that would have been experienced inside the inclusion without any external contraire. Calculations of this tensor for superspherical pores– both concave and convex shapes – are performed numerically. Results are given by an integration of derivation of Green’s tensor over volume of the inclusion. Comparisons with the results of Onaka (2001) for convex superspheres show that the performed calculations have an accuracy better than 1%. The current calculations have been done to complete his results.

In the 2nd_{Eshelby problem, property contribution tensors that characterizes the contribution} of an individual inhomogeneity on the overall physical properties have been numerically calculated by using Finite Element Method (FEM). Property contribution tensors of 3D non ellipsoidal inhomogeneities, such as supersphere and superspheroid, have been obtained. Simplified analytical relations have been derived for both compliance contribution tensor and resistivity contribution tensor.

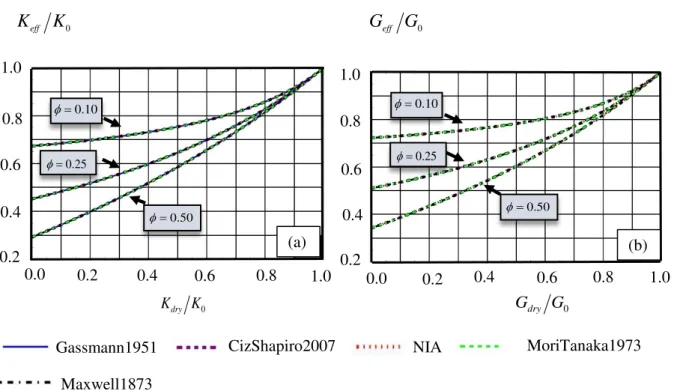
Property contribution tensors have been used to estimate effective elastic properties and effective conductivity of random heterogeneous materials, in the framework of Non-Interaction Approximation, Mori-Tanaka scheme and Maxwell scheme.

Two applications in the field of geomechanics and geophysics have been done. The first application concerns the evaluation of the effective thermal conductivity of oolitic rocks is performed to complete the work of Sevostianov and Giraud (2013) for effective elastic properties. A two step homogenization model has been developed by considering two distinct classes of pores: microporosity (intra oolitic porosity) and meso porosity (inter oolitic porosity). Maxwell homogenization scheme formulated in terms of resistivity contribution tensor has been used for the transition from meso to macroscale. Concave inter oolitic pores of superspherical shape have been taken into account by using resistivity contribution tensor obtained thanks to FEM modelling. Two limiting cases have been considered: ‘dry case’ (air saturated pores) and ‘wet case’ (water liquid saturated pores). Comparisons with experimental data show that

(10)

VIII

variations of effective thermal conductivity with porosity in the most sensitive case of air saturated porosity are correctly reproduced.

Applicability of the replacement relations, initially derived by Sevostianov and Kachanov (2007) for ellipsoidal inhomogeneities, to non-ellipsoidal ones has been investigated. It is the second application of newly obtained results on property contribution tensors.

We have considered 3D inhomogeneities of superspherical shape. From the results, it has been seen that these relations are valid only in the convex domain, with an accuracy better than 10%. Replacement relations can not be used in the concave domain for such particular 3D shape. Keywords: Homogenization, heterogeneous material, inhomogeneity, concave, supersphere, superspheroid, effective elasticity, effective thermal conductivity, cross-property connection.

(11)

IX

List of figures

FIG.0.1: OBSERVATIONS AU MEB SUR LE CALCAIRE OOLITIQUE DE LAVOUX (LA PREMIERE IMAGE EN HAUT A GAUCHE CORRESPOND A UNE SECTION POLIE) (GRGIC 2011). ... XXVIII FIG.0.2: UN MACRO-PORE CONCAVE ILLUSTRE CETTE IMAGE MEB DU CALCAIRE OOLITIQUE DE LAVOUX ... XXVIII FIG.0.3: (A).COMPARAISON DES RESULTATS NUMERIQUES ACTUEL DES PORES SUPERSPHERIQUES AVEC CEUX D’ONAKA (2001) POUR LA FORME CONVEXE (B). DEPENDANCE DES TRACES DU TENSEUR DE HILL SUR LE COEFFICIENT DE FORME (CHEN ET AL. 2015A). ... XXXI FIG.0.4: MODELE NUMERIQUE D’UN MATERIAU SOLIDE CONTENANT UNE INHOMOGENEITE ISOLEE DU TYPE SUPERSPHERE (1/8 DE L’INHOMOGENEITE) (A) ET DU TYPE SUPERSPHEROÏDE (INHOMOGENEITE ENTIERE) (B) ET LEURS CHAMPS DE DEPLACEMENTS. ... XXXIII FIG.0.5: TENSEUR DE SOUPLESSE EVALUEPAR LES DEUX METHODES DE NORMALISATION (A) SUPERSPHERE (B) SUPERSPHEROÏDE (CHEN ET AL.2015 B) ... XXXIV FIG.0.6: TENSEUR DE RESISTIVITE EVALUE PAR LES DEUX METHODES DE NORMALISATION (A) SUPERSPHERE (B) SUPERSPHEROÏDE (SEVOSTIANOV ET AL.2016) ... XXXV FIG.0.7: POUR CERTAINES FRACTIONS VOLUMIQUES ϕ, DEPENDANCE DU MODULE D’ELASTICITE ISOSTATIQUE ET DU MODULE DE CISAILLEMENT SUR LES PROPRIETES ELASTIQUES DES CALCITES CONTENANT DES PORES VIDES PAR DES SCHEMAS D’HOMOGENEISATIONS DIFFERENTS. ... XXXVII FIG.1.1: METHOD OF MULTIPLE SCALES (MICRO » MINI » MACRO) (GUÉGUEN AND PALCIAUSKAS 1992) ... 4 FIG.1.2: REAL HETEROGENEOUS MEDIUM (LEFT) AND EFFECTIVE HOMOGENEOUS MEDIUM (RIGHT). (GUÉGUEN AND PALCIAUSKAS 1992) ... 4 FIG.1.3: ILLUSTRATION OF ELLIPSOIDAL AND NON-ELLIPSOIDAL SHAPES ... 6 FIG.1.4: LOW MAGNIFICATION SEM IMAGES OF IRON ORE (IRONSTONE) SHOWING THE OOLITIC TEXTURE. CORTEXES ARE MADE BY POROUS AND CONCENTRIC LAYERS OF GOETHITE. (A) CRACK SURFACE. (B) POLISHED THIN SECTION. (GRGIC 2001). ... 7

(16)

XIV

FIG.1.5: HIGH MAGNIFICATION SEM IMAGES OF OOLITIC IRON CORE SHOWING CONCAVE INTER-OOLITIC CARBONATE CRYSTALS. ... 7 FIG.1.6: HIGH MAGNIFICATION SEM IMAGE OF OOLITIC IRON ORE SHOWING A CONCAVE INTER-OOLITIC CRYSTAL OF SIDERITE. (GRGIC ET AL. 2013) ... 8 FIG.1.7: LOW AND HIGH MAGNIFICATION SEM OBSERVATIONS ON OOLITIC LAVOUX LIMESTONE (THE FIRST IMAGE CORRESPONDS TO A POLISHED THIN SECTION). (GRGIC 2011) ... 8 FIG.1.8: SEM IMAGE OF OOLITIC LAVOUX LIMESTONE SHOWING A CONCAVE MACRO-PORE. ... 9 FIG.2.1: VOLUME OF THE SUPERSPHERE INDEPENDENT ON THE CONCAVITY PARAMETER P (SUPERSPHERE WITH P=0.35 IS SHOWN IN THE RIGHT) ... 26 FIG.2.2: SHAPE OF CONVEX SUPERSPHERES AT SEVERAL VALUES OF P (IMAGES PRODUCED BY GOCAD) ... 27 FIG.2.3: ONE-EIGHT OF SPHERE OF UNIT RADIUS PRODUCED BY GOCAD AND THE MESH USED ... 28 FIG.2.4: FUNCTION F (P), DEFINED BY (2.8), CALCULATED WITH DIFFERENT MESH DENSITY, COMPARED TO RESULTS OF ONAKA (2001). ... 28 FIG.2.5: COMPARISON OF THE CALCULATED E

S1212 WITH MESH DENSITY 80 NODES PER EDGE WITH

THE RESULTS OF ONAKA (2001) ... 29 FIG.2.6: CONCAVE HYPERSPHERES (IMAGES PRODUCED BY GOCAD). ... 30 FIG.2.7: NON-ZERO COMPONENTS OF THE AVERAGE ESHELBY TENSOR FOR DIFFERENT VALUES OF P ... 30 FIG.2.8: TRACES OF THE HILL TENSOR FOR DIFFERENT VALUES OF P ... 32 FIG.2.9: NORMALIZED STRAIN ENERGY FOR EIGENSTRAIN OF TYPE A AND B FOR CONCAVE SUPERSPHERICAL PORES, COMPARED WITH THE ONE OF ONAKA (2001) FOR CONVEX RANGE. ... 36 FIG.3.1: (A) REMOTELY LOADING AND THE BOUNDARY CONDITIONS FOR ELASTICITY PROBLEMS (B) HEAT FLUX VECTORS AND THE GRADIENT OF TEMPERATURE FOR THERMAL CONDUCTIVITY PROBLEMS. ... 44 FIG.3.2: DIFFERENT SUPERSPHERICAL SHAPE AT DIFFERENT VALUES OF P. INSET: DEPENDENCE OF THE SUPERSPHERE VOLUME ON P ... 49 FIG.3.3: REFERENCE MESH FOR CONCAVE SUPERSPHERE (P=0.35) (1/8 F THE MESHED SUPERSPHERE ON THE LEFT, DETAILS AT THE TOP RIGHT CORNER AND THREE-NODES TRIANGULAR FINITE ELEMENTS ON THE SURFACE AT THE BOTTOM RIGHT CORNER) ... 50

(17)

XV

FIG.3.4: NON-ZERO COMPONENT OF COMPLIANCE CONTRIBUTION TENSOR FOR DIFFERENT VALUES OF P (FROM 0.2 TO 5) ... 53 FIG.3.5: LINEAR APPROXIMATION OF THE NON-ZERO COMPONENTS OF THE COMPLIANCE CONTRIBUTION TENSOR NORMALIZED ACCORDING TO (2.32). R-SQUARED VALUES OF THE APPROXIMATIONS ARE INDICATED ... 53 FIG.3.6: DEPENDENCE OF THE RESISTIVITY CONTRIBUTION TENSOR ON P (A) AND ITS LINEAR APPROXIMATION (B). ... 54 FIG.4.1: BOUNDARY CONDITIONS FOR MODELLING OF MATERIALS CONTAINING CONCAVE SUPERSPHEROIDAL PORES ... 66 FIG.4.2: TEMPERATURE GRADIENT AND CONVECTION OF HEAT FLUX FOR THERMAL CONDUCTIVITY PROBLEMS ... 66 FIG.4.3: PORES OF CONCAVE SHAPES TYPICAL IN ROCK MECHANICS: (A) SANDSTONE (FROM EMMANUEL ET AL. 2010); (B) HARZBURGITE (FROM WARK ET AL.2003) ... 68 FIG.4.4: AXISYMMETRIC SUPERSPHEROID (“SUPEREGG”) FOR DIFFERENT VALUES OF P. ... 71 FIG.4.5: (A) TOTAL SURFACE AREAS OF A SUPERSPHEROID OF CONCAVITY P AND OBLATE SPHEROID OF ASPECT RATIO γ NORMALIZED TO THE SURFACE AREA OF THE SUPERSCRIBED UNIT SPHERE: (B) NORMALIZED VOLUMES OF THE SUPERSPHEROID AND SPHEROID ... 71 FIG.4.6: 3D REFERENCE FINITE ELEMENT MESH FOR CONCAVE SUPEREGG (P=0.3) ... 74 FIG.4.7: NON-ZERO COMPONENT OF COMPLIANCE CONTRIBUTION TENSOR (A) AND RESISTIVITY CONTRIBUTION TENSOR (B) AS FUNCTIONS OF THE CONCAVITY PARAMETER P ... 75 FIG.4.8: LINEAR APPROXIMATION OF THE NON-ZERO COMPONENTS OF THE COMPLIANCE CONTRIBUTION TENSOR (A) AND RESISTIVITY CONTRIBUTION TENSOR (B) NORMALIZED ACCORDING TO (4.14) AND (4.15) ... 79 FIG.4.9: NON-ZERO COMPONENTS OF THE COMPLIANCE CONTRIBUTION TENSOR OF OBLATE SPHEROIDAL PORE USING NORMALIZATION (4.14) ... 79 FIG.4.10: COMPARISON OF APPROXIMATION (4.23) WITH NUMERICAL VALUES OF NON-ZERO COMPONENTS OF THE COMPLIANCE CONTRIBUTION TENSOR FOR A SUPERSPHERICAL PORE ... 80 FIG.4.11: (A) DEPENDENCE OF THE RESISTIVITY CONTRIBUTION TENSOR FOR A SPHEROIDAL PORE NORMALIZED ACCORDING TO (4.15). (B) COMPARISON OF THE APPROXIMATION (4.24) WITH NUMERICAL RESULTS ... 81

(18)

XVI

FIG.5.1: SCANNING ELECTRON MICROSCOPY (SEM) IMAGES OF LAVOUX LIMESTONE (SEE GIRAUD AND SEVOSTIANOV 2013). ... 94 FIG.5.2: FIRST HOMOGENIZATION STEP: MICROPORES INSIDE OOLITE CORE ARE HOMOGENIZED BY USING SELF-CONSISTENT METHOD (2D REPRESENTATION OF A 3D MICROSTRUCTURE) ... 97 FIG.5.3: SECOND HOMOGENIZATION STEP: TRANSITION FROM MESOSCALE TO MACROSCALE WITH MAXWELL HOMOGENIZATION METHOD, CASE OF SIMPLIFIED MODEL (ELLIPSOIDAL APPROXIMATION FOR ALL THE PORES). ... 100 FIG.5.4: MESOPOROSITY: ELLIPSOIDAL PORES (B1) AND CONCAVE PORES (B2) (GIRAUD AND SEVOSTIANOV 2013) ... 100 FIG.5.5: PORES SATURATED WITH AIR: EXPERIMENTAL THERMAL CONDUCTIVITY AS A FUNCTION OF POROSITY, FOR PURE CALCITIC LIMESTONES (ROBERTSON 1988) ... 101 FIG.5.6: PORES SATURATED WITH WATER LIQUID: EXPERIMENTAL THERMAL CONDUCTIVITY AS A FUNCTION OF POROSITY FOR PURE CALCITIC LIMESTONES (ROBERTSON 1988) ... 101 FIG.5.7: PORES SATURATED WITH AIR: EFFECTIVE THERMAL AS A FUNCTION OF MESOPOROSITY WITH B2=RANDOM DISTRIBUTION CRACKS (OBLATEγ =0.05) ... 103 FIG.5.8: PORES SATURATED WITH AIR: EFFECTIVE THERMAL CONDUCTIVITY AS A FUNCTION OF MESOPOROSITY WITH B2=RANDOM DISTRIBUTION OF NEEDLES (PROLATEγ =20)... 103 FIG.5.9: PORES SATURATED WITH LIQUID WATER: EFFECTIVE THERMAL CONDUCTIVITY AS A FUNCTION OF MESOPOROSITY WITH B2=RANDOM DISTRIBUTION OF CRACKS (OBLATEγ =0.05) .... 103 FIG.5.10: PORES SATURATED WITH LIQUID WATER: EFFECTIVE THERMAL CONDUCTIVITY AS A FUNCTION OF MESOPOROSITY WITH B2 RANDOM DISTRIBUTION OF NEEDLES (PROLATEγ =20) .... 103 FIG.5.11: PORES SATURATED WITH AIR: EFFECTIVE THERMAL CONDUCTIVITY AS A FUNCTION OF MESOPOROSITY WITH B2=RANDOM DISTRIBUTION OF SUPERSPHERE ( p=0.35) ... 105 FIG.5.12: PORES SATURATED WITH LIQUID WATER: EFFECTIVE THERMAL CONDUCTIVITY AS A FUNCTION OF MESOPOROSITY WITH B2 DISTRIBUTION OF SUPERSPHERES (p=0.35) ... 105 FIG.5.13: PORES SATURATED WITH AIR: RESISTIVITY CONTRIBUTION TENSOR OF SPHEROID AS A FUNCTION OF PORE ASPECT RATIOγ , COMPARISON WITH SUPERSPHERE ( , 2 =0.529

−air SP b

H )

(19)

XVII

FIG.5.14: PORES SATURATED WITH LIQUID WATER: RESISTIVITY CONTRIBUTION TENSOR OF SPHEROID AS A FUNCTION OF PORE ASPECT RATIO γ ,COMPARISON WITH SUPERSPHERE ( p=0.35 ,

448 0 2 = . −lq SP b H ) ... 105

FIG.6.1: SUPERSPHERICAL INHOMOGENEITY FOR DIFFERENT VALUES OF P ... 113 FIG.6.2: DEPENDENCES OF F (P) DEFINED BY EQUATION (6.20) (A) AND COMPONENT P1212 OF HILL’S

TENSOR GIVEN BY (6.19) (B) ON THE CONCAVITY PARAMETER P ... 117 FIG.6.3: COMPARISON OF THE COMPONENTS OF THE COMPLIANCE CONTRIBUTION TENSOR CALCULATED BY EQUATION (6.22B) WITH ONES OBTAINED BY CHEN ET AL. (2015B) USING FEM ... 118 FIG.6.4: DEPENDENCE OF THE BULK MODULI OF CALCITE WITH CRUDE OIL FILLED PORES ON THE BULK MODULUS OF DRY CALCITE AT SEVERAL VOLUME FRACTIONS OF PORES CALCULATED BY DIFFERENT METHODS ... 123 FIG.6.5: DEPENDENCE OF THE BULK AND SHEAR MODULI OF CALCITE WITH CLAY FILLED PORES ON THE ELASTIC PROPERTIES OF DRY CALCITE AT SEVERAL VOLUME FRACTIONS OF PORES CALCULATED BY DIFFERENT METHODS... 124 FIG.6.6: DEPENDENCE OF THE BULK MODULI OF CALCITE WITH CRUDE OIL FILLED PORES ON THE VOLUME FRACTIONS OF PORES AT SEVERAL VALUES OF THE BULK MODULUS OF DRY CALCITE CALCULATED BY DIFFERENT METHODS ... 124 FIG.6.7: DEPENDENCE OF THE BULK AND SHEAR MODULI OF CALCITE WITH CLAY FILLED PORES ON THE VOLUME FRACTIONS OF PORES AT SEVERAL VALUES OF THE ELASTIC MODULI OF DRY CALCITE CALCULATED BY DIFFERENT METHODS ... 125

(20)

(21)

XIX

List of tables

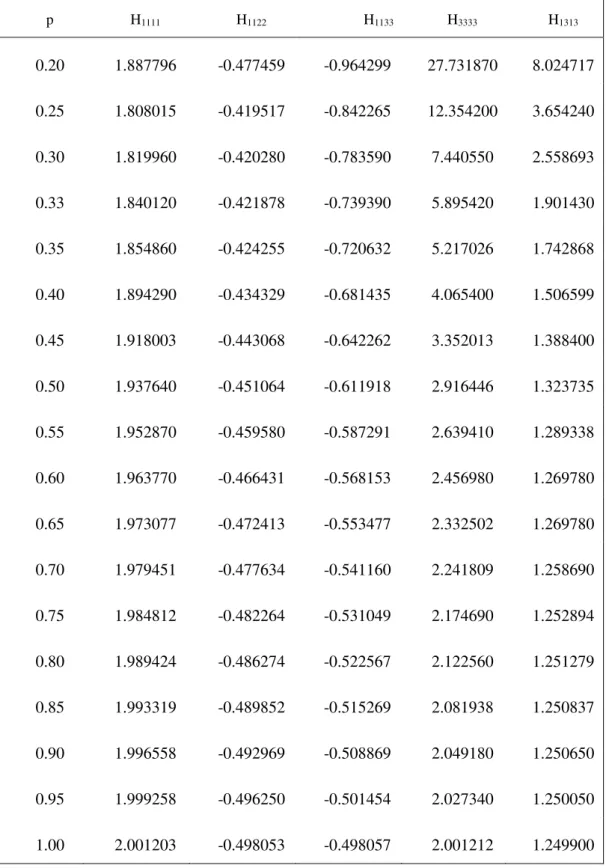
TABLE B1. CALCULATED COMPONENTS OF THE COMPLIANCE CONTRIBUTION TENSOR AND THE RESISTIVITY CONTRIBUTION TENSOR ... 147 TABLE B2. NUMBER OF ELEMENTS AND NODES OF T3 MESH ... 148 TABLE D1. CALCULATED COMPONENTS OF THE COMPLIANCE CONTRIBUTION TENSOR ... 153 TABLE D2. NUMBER OF ELEMENTS AND NODES OF THE MESH B (MORE REFINED ON SUPERSPHEROID SURFACE) ... 154 TABLE D3. RELATIVE ERRORS ON COMPONENTS OF COMPLIANCE TENSOR BETWEEN MESH A AND MESH B ... 155 TABLE D4. COMPONENTS OF RESISTIVITY CONTRIBUTION TENSOR OF SUPERSPHEROID ... 156 TABLE E1: EXACT VALUES OF DIMENSION LESS VOLUME AND SURFACE AREA OF A SUPERSPHEROID (A =1, ) FOR CONCAVITY PARAMETER ) ... 157 TABLE F1. COMPONENTS OF THE COMPLIANCE CONTRIBUTION TENSOR FOR A SUPERSPHERICAL PORE:

ijkl

H ′ CALCULATED BY (3.67) FROM COMPONENTS OF HILL TENSOR AND H_ijkl CALCULATED BY FEM 161 TABLE F2. MATERIAL PROPERTIES USED FOR CALCULATION OF THE EFFECTIVE PROPERTIES. ... 162

(22)

(23)

XXI

List of notations

σ Stress vector ε Strain vector C B A, , Shape factor p _{Concavity parameter} γ _{Aspect ratio} c b

a, , semi-principal axes of length *

ij

ε

Eigenstrain inside inclusion

Ω Domain occupied by inclusion or inhomogeneity Ω

∂ Surface of inclusion or inhomogeneity

E

S

Eshelby tensor

. . . Average over volume

) , , (

x

₁

x

₂

x

₃

=

x

Position vector of a point on the surface

ij

ε Component of resulting strain around inclusion

G Green’s function

kl

δ Kronecker delta symbol *

V Volume of inclusion or inhomogeneity

V Volume of matrix including inhomogeneity

0

V Volume of the unit sphere

Γ Euler gamma function

0

(24)

XXII

P ,Q Hill’s tensor

µ,λ Lamé parameters

0

C

Stiffness tensor of matrix

1

C Stiffness tensor of inhomogeneity

0

S

Compliance tensor of matrix

1

S Compliance tensor of inhomogeneity

H Compliance contribution tensor

N Stiffness contribution tensor

ε

∆ Extra strain due to inhomogeneity

∞

σ

Remotely applied stress

T

∇ Temperature gradient

q _{Heat flux vector}

R Resistivity contribution tensor

n Inward unit normal vector to the boundary

x

e ,ey,e z Basis unit normal vectors

u Displacement vector

i

S Surface area of i-th element

*

S The total surface area of the superspheroid

∗

L Certain characteristic length of inhomogeneity J Fourth-rank unit tensor

0

G Shear modulus of matrix

0

K Bulk modulus of matrix

0

k ,λ 0 Thermal conductivity of matrix 1

(25)

XXIII

η

_{Geometric parameter of concavity parameter}

k

α

,

α

_G,

H

_K,

H

_G Function of Poisson’s ratio

ϕ, f Porosity

el

N Number of finite elements on boundary surface

G

n Number of Gauss integration points per elements

i G i G i G

w ,ξ ,η Weights and coordinates of Gauss integration points

) (j el op

h Function of u0 and n0

L

, L1,L2 Distance from the center of inhomogeneity

g

_{Shape factor in terms of function of the spheroid’s aspect ratio}

I Λ,

P, Upper case bold symbols refer to second order tensors

σ ε,

a, Lower case bold symbols refer to first order tensors

I

0

λ conductivity of the oolite at the mesoscale a

λ conductivity of the intra-oolitic porous phase 0

λ conductivity of micritic solid grains

i

P Pressure inside the inhomogeneities produced by external load i

τ

Deviatoric stresses inside the inhomogeneities i

γ Deviatoric strains inside the inhomogeneities

i

e

Pressure inside the inhomogeneities produced by the corresponding volumetric strains

(26)

(27)

XXV

(28)

(29)

XXVII

0.1 Contexte

Ce travail se place dans le cadre de l’homogénéisation des milieux hétérogènes aléatoires, naturels ou synthétiques.

Les méthodes de changement d’échelle ou d’homogénéisation sont utilisées pour définir des propriétés effectives, propriétés élastiques, conductivité, à une échelle dite "macroscopique" où le matériau hétérogène peut être considéré comme un matériau homogène équivalent. Ces méthodes permettent de remonter au niveau des propriétés effectives les informations microstructurales : propriétés physiques des constituants, effets de forme, taille, et de distribution spatiale etc. Elles seront utilisées dans ce travail, dans le cadre des approches dites par tenseurs d’Eshelby basées sur la solution du problème fondamental d’une inclusion, ou hétérogénéité isolée en milieu infini.

Les applications envisagées concernent principalement les matériaux hétérogènes de type roches poreuses. Les matériaux poreux peuvent d’ailleurs être vus comme un cas particulier de matériaux hétérogènes dont certains composants sont constitués de fluides (air et/ou eau liquide, hydrocarbure etc.).

Les hétérogénéités, ou inhomogénéités (les deux termes sont synonymes dans ce qui suit), représentent aussi bien des composants solides (inclusions minérales solides) que fluides (pores). A titre d’exemple dans le cas des argilites, les hétérogénéités minérales solides peuvent représenter des cristaux de calcite, quartz, etc. noyées dans une matrice argileuse.

On s’intéressera en particulier aux roches carbonatées poreuses, et plus précisément aux calcaires oolithiques, largement étudiées dans le cadre de l'étude de faisabilité du stockage géologique de gaz tels que le dioxyde de carbone CO2 (Sterpenich et al. 2009, Makhloufi et al.

2013, Grgic 2011). Le calcaire oolithique de Lavoux (Nguyen et al. 2011, Giraud et al. 2012) a été choisi en tant que roche de référence pour les applications des modèles micromécaniques analytiques et numériques.

Le calcaire oolithique est principalement composé de calcite et sa microstructure est caractérisée par un ensemble d’oolithes cimentées par des cristaux de calcite syntaxiale (calcite spathique d’une taille de plusieurs centaines de micromètres). L’observation au MEB (microscopie électronique à balayage) de cette roche a montré (1) deux types de pores : micro à l’intérieur des oolites et macro (avec une taille maximale de 100 µm) entre les oolithes (Fig.0.2). Certains macro-pores ont une forme concave. (2) Les oolites sont constituées de

(30)

XXVIII

couches concentriques de micro-calcite (avec une taille moyenne d'environ 3 µm) et leur diamètre moyen est d'environ 400 µm (Fig. 0.1 ) (Grgic 2011).

Fig.0.1: Observations au MEB sur le calcaire oolitique de Lavoux (la première image en haut à gauche correspond à une section polie) (Grgic 2011).

Fig.0.2: Un macro-pore concave illustré cette image MEB du calcaire oolitique de Lavoux

La plupart des méthodes d’homogénéisation des milieux aléatoires utilisées dans le cadre des approches d’Eshelby sont basées sur la solution fondamentale de l’hétérogénéité ou inhomogénéité ellipsoïdale isolée en milieu infini, obtenue par Eshelby (1957, 1961). Par

(31)

XXIX

conséquence les inhomogénéités sont généralement supposées ellipsoïdales dans ce type d’approche.

Des extensions aux hétérogénéités isolées de formes non ellipsoïdales ont été étudiées ces dernières décennies, par exemple, les polygones et polyèdres (Rodin 1996), des pores de formes irrégulières de matériaux composites carbone-carbone (Drach et al. 2011), des fissures planes (Fabrikant 1989, Sevostianov et Kachanov 2002), des fissures planes recoupées (Grechka, Vasconselos et Kachanov 2006), des fissures non planes (Mear, Sevostianov et Kachanov 2007) et des fissures traversant les pores (Kachanov et Sevostianov 2012).

L’exemple des roches oolithiques montre l’insuffisance d’une représentation ellipsoidale, et par conséquence convexe, des hétérogénéités.

La représentation ellipsoidale, 3D, est riche dans le sens où inclut de manière exacte ou approchée des géométries aussi différentes que les sphères, sphéroides, les ‘aiguilles’, les cylindres de sections elliptique ou circulaire, les fissures circulaires (et le cas limite ‘penny shaped crack’) ou planes. Une limitation de cette représentation est la convexité de la courbure de sa surface. Les observations de microstructure de roches oolithiques mettent notamment en évidence des formes concaves pour les matériaux de remplissage inter oolithique, que ce soit les pores inter oolithiques ou des remplissages de type calcite syntaxiale.

0.2 Objectifs de la thèse

L'objectif de ce travail est d'étudier les effets de formes d’hétérogénéités tridimensionnelles non ellipsoïdales sur les propriétés effectives de matériaux hétérogènes. Plus précisément nous cherchons à caractériser les paramètres géométriques dont l’influence sur les propriétés effectives est majeure : coefficients de forme (ou rapport d’aspect), concavité ou convexité, etc. De nombreuses études ont été réalisées dans le cas bidimensionnel mais très peu dans le cas tridimensionnel qui nous intéresse. Cela est dû au fait que des méthodes de résolution numérique (éléments finis notamment) doivent être utilisées dans le cas tridimensionnel pour résoudre le problème de l’inhomogénéité isolée en milieu infini, dans le cas des problèmes élastiques ou de diffusion linéaire stationnaire, dès que la forme de l’inhomogénéité est non ellipsoïdale (et concave en particulier).

Une attention particulière est portée dans ce travail aux formes concaves. Comme discutée par Giraud et Sevostianov (2013), la forme concave de pore et de cristaux inter-oolithiques du calcaire oolithique de Lavoux (France) est décrite de manière approchée par l’équation de la

(32)

XXX

supersphère x₁2p + x₂2p + x₃2p ≤1 avec p le coefficient de forme (Onaka 2001, 2012, Zohdi et Wriggers 2008). Elle est un cas particulier de la forme générale de type superellipsoïde. La supersphère et les tenseurs de contributions associés respectent une symétrie cubique. On ne considèrera que des distributions isotropes d’inhomogénéités supersphériques, ce qui correspond à un matériau effectif (macroscopique) isotrope. L’anisotropie effective n’est pas étudiée dans ce travail.

Une autre forme, également convexe ou concave, le supersphéroïde, décrite par l’équation

(

2

)

₃2

1

2 2 1

+

≤

p p

x

. Cette forme respecte une symétrie de révolution, et les tenseurs de contribution associés respectent la symétrie isotrope transverse (ceci dans le cas où la matrice environnante est isotrope). De manière similaire au cas de la supersphère, on ne considèrera dans ce travail que des distributions isotropes d’inhomogénéités supersphéroidales ce qui, combiné à une isotropie des constituants, conduit à un matériau effectif isotrope.

Les applications envisagées concernent les géomatériaux de type roches hétérogènes. Les tenseurs de contribution élastique sont déterminés numériquement. Sur cette base, les relations simplifiées sont fournies pour l'utilisation de ces résultats dans le cadre des méthodes de type EMA (Effective Medium Approximation) telles que les approximations NIA (Non Interation Approximation), Maxwell, Mori-Tanaka.

0.3 Problèmes d’Eshelby

0.3.1 Le premier problème d’Eshelby pour des inclusions 3-D non ellipsoïdales

J.D. Eshelby a déterminé la solution élastique autour et à l'intérieur d'une inclusion ellipsoïdale isolée dans une matrice élastique isotrope infinie (Eshelby 1957). Dans ce cas précis, à la fois l'inclusion et la matrice sont constituées du même matériau. Ce problème fondamental est connu comme le premier problème d’Eshelby ou problème de l'inclusion. Eshelby a démontré un résultat d'une importance majeure en micromécanique : l'uniformité des champs de contraintes et de déformations autour et à l'intérieur de l'inclusion ellipsoïdale soumise à un chargement uniforme aux limites infinies.

Dans le cas des formes non ellipsoïdales et en particulier pour les formes non ellipsoïdales concaves tridimensionnelles étudiées dans cette thèse, cette uniformité n'est plus vraie. Ces nouveaux résultats sont fournis par des approches numériques dans la gamme concave et

(33)

XXXI

convexe dans le domaine élastique (Chen et al. 2015 a), cependant ils ne sont pas liés aux propriétés effectives.

La fonction de Green exacte (solution de Kelvin en élasticité linéaire isotrope) est intégrée numériquement à la surface de l'inclusion supersphérique afin d’obtenir le tenseur d’Eshelby moyen (Rodin 1996, Mura 1987, Maekenscoff 1998, Onaka 2001). Du fait de la symétrie cubique de la supersphère et des relations importantes proposées par Milgrom and Shtrikman (1992), une seule composante non nulle doit être évaluée.

Fig.0.3: (a).Comparaison des résultats numériques actuel des pores supersphériques avec ceux d’Onaka (2001)

pour la forme convexe(b). Dépendance des traces du tenseur de Hill sur le coefficient de forme (Chen et al. 2015a). 0.1 1.0 10 100

p

Results of Onaka (2001) for p > 1 Our calculations 0.23 0.24 0.25 0.26 Convex (a) 0.2 0 1.00 0.020 0.025 0.030 0.035 0.040 0.045 Traces

p

2.00 3.00 4.00 5.00 (b)

(34)

XXXII

Une comparaison est faite, à titre de validation de la méthode d’intégration numérique développée, avec les résultats d’Onaka (2001) pour la supersphère de forme convexe (ligne en pointillés sur le graphique de la figure 0.3a), et le taux d'erreur est inférieur à 1%. Les calculs actuels sont effectués pour compléter les résultats d’Onaka (2001).

Le tenseur de Hill est lié au tenseur d’Eshelby par une relation linéaire, des nouveaux résultats concernant les traces du tenseur de Hill montrent qu’ils sont fortement dépendants du coefficient de forme (Fig. 0.3b), surtout dans le domaine de concave.

0.3.2 Le deuxième problème d’Eshelby pour des hétérogénéités 3-D non ellipsoïdales

Le deuxième problème d’Eshelby ou le problème de l'inhomogénéité est beaucoup plus important pour les applications aux matériaux hétérogènes. On considère dans ce cas une matrice élastique infinie, contenant une hétérogénéité constituée par un matériau élastique ayant des propriétés différentes, soumise à une charge uniforme (contrainte ou déformation) aux limites infinies.

On peut souligner que les deux problèmes d’Eshelby sont reliés par de simples relations linéaires uniquement dans le cas particulier des inclusions ou des hétérogénéités ellipsoïdales. Cela est dû à la propriété d'uniformité des champs de contrainte et de déformation qui ne vaut que pour les formes ellipsoïdales (c’est la conjecture d’Eshelby, voir parmi de nombreuses références Ammari et al. 2010). En raison de l'équivalence mathématique entre les deux problèmes d'Eshelby pour l'hétérogénéité de forme ellipsoïdale, différents tenseurs caractérisant les interactions élastiques peuvent être utilisés, car ils sont liés les uns aux autres par des relations linéaires : le tenseur d'Eshelby, le tenseur de Hill, le tenseur de rigidité et le tenseur de souplesse (Hill 1965, Walpole 1969, Kunin and Sosnina 1971, Sevostianov and Kachanov 1999, 2002, 2007).

Cependant, l’équivalence n'est plus vraie dans le cas des formes non ellipsoïdales. Il faut alors définir soigneusement les tenseurs propres caractérisant les propriétés élastiques entre l’hétérogénéité et la matrice environnante. Le deuxième problème d’Eshelby est au coeur des travaux de cette thèse.

La méthode des éléments finis est utilisée pour résoudre le problème de l’inhomogénéité du type supersphère ou supersphéroïde, isolé dans une matrice infinie, et obtenir le tenseur de souplesse (Hill 1963, Kachanov et al. 1994). Les résultats sont donnés par l’intégration du produit vectoriel sur le volume de l’hétérogénéité. Pour le problème d’élasticité, il s’agit du

(35)

XXXIII

vecteur de déplacement et du vecteur normal. Les champs de déplacement pour la supersphère et le supersphéroïde sont illustrés sur la figure 0.4.

Fig.0.4: Modèle numérique d’un matériau solide contenant une inhomogénéité isolée du type supersphère (1/8 de l’inhomogénéité) (a) et du type supersphéroïde (inhomogénéité entière) (b) et leurs champs de déplacements.

Deux méthodes de normalisation sont souvent appliquées. Dans le cas où on s’intéresse à l’effet du volume donné sur le coefficient de forme, le tenseur Hest formulé en termes de ratio

V

V_*/ où V_*est le volume d’hétérogénéité et V est le volume total de la matrice y compris l’hétérogénéité. Autrement, si on s’intéresse à l’effet du coefficient de forme de l’hétérogénéité

(a) : supersphère

(36)

XXXIV

sur le tenseur, tenseur est formulé en termes de où est généralement considéré comme la distance la plus longue entre deux indices de l’hétérogénéité.

La première méthode de normalisation n’est pas adaptée au cas limite où le volume de l’inhomogénéité V* tend vers zéro, ce qui inclut en partiulier les fissures.

Les résultats pour la supersphère et le supersphéroïde sont illustrés sur la figure 0.5 (Chen et al. 2015 b).

ijkl

H H~_ijkl

Fig.0.5: Tenseur de souplesse évaluépar les deux méthodes de normalisation (a) supersphère (b) supersphéroïde

(Chen et al.2015 b) H L_*3/V L* 0.2 0.4 0.6 0.8 1.0 0.0 2.0 4.0 6.0 8.0 10.0 998587 0 4 1 5 2 1111 1111 . R H~ p H~ S = − = 998564 0 4 1 5 2 1212 1212 . R H~ p H~ S = − = 998183 0 4 1 5 2 1122 1122 . R H~ p H~ S = − − = − 0.0 2.0 4.0 6.0 8.0 0.0 1.0 2.0 3.0 4.0 5.0 1111 H 1212 H 1122 H 3333 0H~ E 1313 0H~ E 1111 0H~ E 1122 0H~ E 1133 0H~ E p 30 20 10 0 -10 0.2 0.4 0.6 0.8 1.0 0.2 0.4 0.6 0.8 1.0 3.0 2.0 1.0 0 -1.0 3333 0H E 1313 0H E 1111 0H E 1122 0H E 1133 0H E p p p (a) : supersphère (b) : supersphéroïd

(37)

XXXV

Les problèmes linéaires de conductivité/résistivité thermique sont étudiés en utilisant la même méthodologie (Sevostianov et Kachanov 2002). L’intégration est donnée par le produit vectoriel du gradient de température et du vecteur normal. De même, le tenseur de résistivité est également évalué par deux méthodes de normalisation (Sevostianov et al. 2016), les résultats sont illustrés sur la figure 0.6 (Chen et al. 2015 b). L’analyse des invariants du tenseur de contribution à la souplesse H ("compliance contribution tenseur") de la supersphère et du supersphéroïde est également présentée.

Fig.0.6: Tenseur de résistivité évalué par les deux méthodes de normalisation (a) supersphère (b) supersphéroïde (Sevostianov et al.2016) 9917 0 4 1 5 2 11 11 . ~ ~ = − − = R R p R S (a) : supersphère 3.0 2.5 2.0 1.5 1.0 0.0 1.0 2.0 3.0 4.0 5.0 0.0 0.2 0.4 0.6 0.8 1.0 0.5 1.0 1.5 2.0 p p 33 0R~ k 11 0R~ k 33 0R k 11 0R k (b) : supersphéroïd 0.2 0.4 0.6 0.8 1.0 p 20 15 10 5 0 0.2 0.4 0.6 0.8 1.0 2.0 1.5 1.0 0.5 0 p

(38)

XXXVI

0.4 Applications aux roches hétérogènes

Les résultats théoriques et numériques concernant les tenseurs de résistivité et compliance sont +appliqués aux propriétés effectives de roches hétérogènes, via les méthodes d’homogénéisation des milieux aléatoires. Ces applications envisagées dans ce travail concernent les propriétés effectives des roches hétérogènes, d’une part la conductivité thermique et, d’autre part les propriétés élastiques et poroélastiques.

La conductivité thermique effective des roches oolithiques est discutée en utilisant le schéma de Maxwell récemment reformulé par I. Sevostianov et coauteurs (Sevostianov et Giraud 2013,

Sevostianov 2014).

Ces résultats ont fait l’objet d’une publication, Giraud et al. (2015). Le modèle proposé initialement par Giraud et Sevostianov (2013) pour des hétérogénéités ayant une forme concave, par exemple la forme supersphérique, est appliqué dans ce papier. Le schéma de Maxwell est formulé en terme de tenseur de résistivité. Par rapport aux travaux antérieurs sur les matériaux étudiés, les calcaires oolithiques, la nouveauté est la prise en compte de la forme concave et 3D de certains pores inter oolithiques. Les tendances obtenues sont cohérentes avec les données bibliographiques pour la conductivité thermique de ce type de matériau, dans deux cas particuliers : le cas sec (les pores sont saturés d’air) et le cas humide (les pores sont saturés à l’eau liquide). Un point à noter est que le modèle morphologique présenté dans Giraud et Sevostianov (2013) pour l’estimation des propriétés effectives élastiques a été utilisé pour la conductivité thermique.

La seconde application présentée concerne l’extension des relations dites de substitution, établies par Sevostianov et Kachanov (2007), Les applications dans le cas d’hétérogénéités ellipsoïdales isotropes et/ou anisotropes au cas non ellipsoidal. Ces relations concernent des hétérogénéités de même forme mais de paramètres élastiques différents (par exemple pores saturés ou secs et matrice solide). Appliquées aux tenseurs de souplesse, ces relations permettent de définir dans un cadre général anisotrope les relations de compatibilité micro-macro dites de Biot-Gassmann, très importantes en poroélasticité linéaire. La nouveauté est la prise en compte d’hétérogénéités 3D de forme non ellipsoidales et les résultats ont fait l’objet d’un article récemment soumis à IJSS (soumis en mai 2016, en cours d’expertise).

(39)

XXXVII

Fig.0.7: Pour certaines fractions volumiques ϕ, dépendance du module d’élasticité isostatique et du module de cisaillement sur les propriétés élastiques des calcites contenant des pores vides par des schémas

d’homogénéisations différents.

La comparaison des résultats estimés par ces relations avec ceux qui sont fournis par la méthode aux éléments finis montre que ces relations de substitution ne sont utilisables, avec une erreur relative inférieure à 10 %, dans le cas non ellipsoidal et pour des formes de type supersphère, que pour des hétérogénéités de forme convexe. Dans le cas contraire, en particulier dans le domaine concave, l’erreur relative est importante et ces relations ne peuvent être utilisées. 0 K K_eff 0 K Kdry 50 . 0 = φ 25 . 0 = φ 10 . 0 = φ (a) 0 G Gdry 0 G G_eff 10 . 0 = φ 25 . 0 = φ 50 . 0 = φ (b) 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 1.0 0.8 0.6 0.4 0.2 0.0 0.2 0.4 0.6 0.8 1.0 p p

Gassmann1951 CizShapiro2007 NIA MoriTanaka1973

(40)

XXXVIII

Les applications de ses résultats concernent les propriétés effectives élastiques et poroélastiques de roches réservoirs contenant des hétérogénéités remplies par des argiles ou par des fluides (gaz, eau, huiles, etc.). A titre d’exemple, le module d’incompressibilité et le module de cisaillement estimés par ces relations sont illustrés sur la figure 0.7.

0.5 Conclusions et perspectives

Dans le cadre de l’étude des propriétés effectives des matériaux hétérogènes, le travail présenté concerne des hétérogénéités tridimensionnelles, non ellipsoïdales de formes concave et/ou convexe, telles que supersphère et supersphéroïde.

Les tenseurs de contribution d’une hétérogénéité isolée, contribution à la souplesse d’une part (problème élastique) et à la résistivité d’autre part (problème de diffusion linéaire stationnaire), sont calculés numériquement par éléments finis. Les nouveaux résultats obtenus ont permis de proposer des relations analytiques approchées et utiles dans le cadre des méthodes d’homogénéisation dites EMA (Effective Medium Approximation) : en citera en particulier les schémas NIA (Non Interaction Approximation), Maxwell, Mori-Tanaka.

Concernant les applications aux roches hétérogènes, les propriétés effectives thermiques des roches hétérogènes telles que les calcaires oolitiques ont été evaluées pour compléter l’analyse de Giraud et Sevostianov (2013) dans les problèmes d’élasticité. En outre, les relations de substitution initialement proposées par Sevostianov and Kachanov (2007) ont été élargies aux hétérogénéités non ellipsoïdales .

Un résultat important est que, dans le cas de formes de type supersphère, ces relations simplifiées ne peuvent être utilisées que dans le cas convexe (le seuil limite de validité considéré est de 10 % d’écart relatif).

Parmi les perspectives, on citera l’extension des résultats présentés aux roches isotropes transverses telles que les argilites, marnes ou schistes.

La prise en compte d’hétérogénéités 3D de forme concave telles que celles étudiées dans ce travail, mais dans le cas de matériaux hétérogènes à constituants anisotropes d’une part et à anisotropie effective d’autre part sera une perspective importante pour les roche

(41)

Part 1 Introduction

(42)

(43)

3

ChaPter 1 I

General framework

1.1 Background Context

Many natural substances and man-made materials are heterogeneous, their physical properties depend on volume fraction, distribution, orientation and individual properties of their constituted elements. Oolitic rocks (e.g., limestone, ironstone) are typical examples of such materials.

Heterogeneity of materials can be considered differently depending on the scales of measurement: micro-, mini- and macroscale. At microscale, all components, such as the skeletal portion which is often solid and pores which are generally filled with a liquid or gas of porous materials, can be observed. At miniscale or called as mesoscale, a representative volume element (RVE) that constitutes a sufficiently large, statistically representative pattern of the microstructure should be considered, it is the smallest volume over which a measurement could be acquired that will yield a value representative of the whole. At macroscale, a solution for the posed problem may be found. Method of multiple scales raises a possibility to evaluate macroscopic behaviors of heterogeneous materials via their microstructures (Fig. 1.1). This method can be applied to a medium that are heterogeneous in small scale, but homogeneous in big scale.

In other words, in the context of effective problems, effective properties of such material are shown by an integration of physical parameters over the volume of RVE, the latter parameters could be, for example, loading rate, displacement, temperature, etc. This procedure is called homogenization where the real heterogeneous materials is considered to be equivalent to a homogeneous material with certain effective properties (Fig. 1.2). Homogeneity (statistic) is therefore a necessary condition to apply this homogenization approach.

(44)

Ch.1: General framework

4

Porous carbonate rocks such as oolitic limestones are extensively investigated in the framework of feasibility study of geological storage of residual gases such as carbon dioxide CO2 (Sterpenich et al. 2009, Makhloufi et al. 2013). The Lavoux limestone (Nguyen et al. 2011,

Giraud et al. 2012) will be chosen as a reference rock for applications of analytical and numerical micromechanical models.

Fig.1.1: Method of multiple scales (micro » mini » macro) (Guéguen and Palciauskas 1992)

.

Fig.1.2: Real heterogeneous medium (left) and effective homogeneous medium (right). (Guéguen and Palciauskas 1992)

Effect of shape paramter on the overall properties of materials containing 3-D non-ellipsoidal inhomogeneities will be mainly discussed in this work.

Staring from the simplest case of ellipsoid, its general description with semi-principal axes of length a, b, c is:

1

2 2 3 2 2 2 2 2 1

+

=

c

x

b

x

a

x

(1.1) 100 µm 1 mm 1 cm

(45)

5

In numerous literatures, inhomogeneities contained in solid materials are typically assumed to be ellipsoids of the same identical aspect ratio, this unrealistic assumption is widely responsible for insufficient linkage between methods of micromechanics and materials science applications. A special case of ellipsoid is described by the following equation witha =b,γ =c/ a , namely spheroid:

1

2 2 3 2 2 2 2 2 1

+

=

) (

a

γ

x

a

x

a

x

(1.2)

It is oblate with aspect ratio

γ

<

1

, prolate with

γ

>

1

and spherical with

γ

=

1

, analytical solutions of effective problems related to these shapes are well known (Mura 1987, Nemat Nasser and Hori 1993, Kachanov et al. 2003). In limiting cases, the shape becomes strongly oblate (

γ

<<

1

) including perfectly rigid disk and crack-like pore (flat cracks, no-flat cracks, intersected and branched cracks). Otherwise, it becomes strongly prolate (

γ

>>

1

) including perfectly rigid cylindrical fiber and cylindrical pore.

Only limited number of numerical results and approximated estimates are known for 3-D non-ellipsoidal inhomogeneities since the end of 20th_{century. Several shapes such as polygons} and polyhedral (Rodin 1996), pores of irregular shapes of carbon-carbon composite materials (Drach et al. 2011), planar cracks (Fabrikant 1989, Sevostianov and Kachanov 2002), intersecting planar cracks (Grechka, Vasconselos and Kachanov 2006), non-planar cracks (Mear, Sevostianov and Kachanov 2007) and cracks growing from pores (Kachanov and Sevostianov 2012) have been discussed.

Particular attention is paid to concave shapes, the only one that has been discussed in the litteratures is supersphere (Onaka 2001, 2012, Zohdi and Wriggers 2008, Eq.9.2) and it is a particular case of superellipsoid:

1

2 3 2 2 2 1

+

=

p p p

x

_(1.3)

where p is called concavity parameter. While, another concave shape, namely superspheroid, which respects axisymmetric symmetry describing by:

(

2

)

₃2

1

2 2 1

+

=

p p

x

(1.4)

(46)

6

Fig.1.3: Illustration of ellipsoidal and non-ellipsoidal shapes

Grgic (2001) showed, from SEM (Scanning Electron Microscopy) observations on iron ore (i.e., oolitic ironstone from Lorraine, France), that some macro-pores and inter-oolitic crystallized minerals of carbonate composition (calcite, siderite) have concave shapes (Fig. 1.4). Other SEM observations done in GeoRessources Laboratory show high magnifications images of these concave carbonate crystals (Fig. 1.5). Calcite and siderite fill the pores between oolitic prolate spheroidal grains (oolites). Figure 1.6 shows a SEM image of a very characteristic concave inter-oolitic crystal of siderite between 3 oolites of prolate spheroid shape (Grgic et al. 2013).

Figure 1.7 represents some SEM images of an oolitic limestone (from Lavoux, France). This rock is mainly composed of calcite and its microstructure is characterized by an assembly of (almost spherical) oolites cemented by large syntaxial crystals of calcite (sparry calcite of several hundred µm of size). There are two kinds of pores: micro inside oolites and macro between oolites. Oolites are made up of concentric layers of micro-calcite (with an average size around 3 µm) and their mean diameter is about 400 µm. Generally speaking, the diameter l of

Ellipsoid Non-ellipsoid Superspheroid Supersphere Special case : p=0.35 p=0.35 4 0 6 0 1 1 2 2 2 2 2 2 . , . , = = = = + + a b c c z b y a x ( ) 2 ₁ ₁ 2 2 2 = =       ⋅ + + a a z a y x γ

Analytical known Unknown

) ( .5 oblate 0 = γ ) (prolate 2 = γ ) (sphere 1 = γ

(

)

2 1 3 2 2 2 1 + + = p p x x x 32 1 2 2 2 1 + + = p p p x x x

(47)

7

concentric layers are in the range of 100 µm < l < 1000 µm. Figure 1.8 shows a concave macro-pore (with a maximum size of 100 µm) between oolitic grains.

Fig.1.4: Low magnification SEM images of iron ore (ironstone) showing the oolitic texture. Cortexes are made by porous and concentric layers of goethite. (a) Crack surface. (b) Polished thin section. (Grgic 2001).

(48)

8

Fig.1.6: High magnification SEM image of oolitic iron ore showing a concave inter-oolitic crystal of siderite. (Grgic et al. 2013)

Fig.1.7: Low and high magnification SEM observations on oolitic Lavoux limestone (the first image corresponds to a polished thin section). (Grgic 2011)

(49)

9

Fig.1.8: SEM image of oolitic Lavoux limestone showing a concave macro-pore.

1.2 Fundamental Eshelby problems

In the 1950s, J. D. Eshelby determined the elastic field about and within an isolated ellipsoidal inclusion embedded in an infinite isotropic elastic matrix (see Eshelby 1957). It is worth to emphasize that both inclusion and matrix are constituted by the same material.

This fundamental problem is known as the First Eshelby problem or the Inclusion problem. Eshelby has obtained result of major importance in micromechanics: uniformity of strain and stress fields inside and around ellipsoidal inclusion submitted to remotely uniform loading.

The Second Eshelby problem or the Inhomogeneity problem is much more important for practical applications concerning heterogeneous materials. One considers in this case an infinite elastic matrix, containing an ellipsoidal inhomogeneity constituted by an elastic material with different properties, submitted to uniform remote loading (uniform stress or uniform strain imposed on infinite boundary).

It may be emphasized that the two problems are equivalent only in the particular case of ellipsoidal inclusions or inhomogeneities as it is related to the property of uniformity of stress and strain fields which holds only for ellipsoidal shapes (this is known as Eshelby’s conjecture, see among many others Ammari et al. 2010).

(50)

10

Concerning rock materials, inhomogeneities may represent pores (elastic material with zero elastic moduli) or solid mineral inhomogeneities (for example inclusions of calcite, quartz etc. in argillaceous rocks) embedded in a surrounding rock matrix.

Due to the mathematical equivalence between the two Eshelby problems for inhomogeneities of ellipsoidal shapes, different tensor characterizing elastic interactions may be used as they are related to each other by linear relations: Eshelby tensor, Hill tensor, stiffness contribution tensor of compliance contribution tensor (Hill 1965, Walpole 1969, Kunin and Sosnina 1971,

Sevostianov and Kachanov 1999, 2002, 2007).

However, this is not the case for non-ellipsoidal shapes and in particular for the 3-D non- ellipsoidal shapes investigated in this work. One has to carefully define the proper tensors characterizing elastic between inhomogeneity and the surrounding matrix and the second Eshelby problem will be the focus of the work.

New results will be provided for the first Eshelby problem of superspherical inclusion mainly to complete previous work of Onaka (Onaka 2001) in the convex range but the results (averaged Eshelby tensor), will be not used in homogenization scheme as it would be irrelevant.

For the second Eshelby problem, the proper tensors are the stiffness contribution tensor or the compliance contribution tensors defined by Sevostianov and Kachanov (2011, 2013).

To the author’s knowledge analytical results are only available in the case of ellipsoidal inhomogeneities embedded in an isotropic matrix, or aligned ellipsoidal inhomogeneities aligned in the direction of a transversely isotropic matrix (Withers 1989, Sevostianov et al. 2005,

Levin and Markov 2005)

Due to this, semi analytical and numerical method will be used to solve the Eshelby problems related to non-ellipsoidal inclusions and inhomogeneities:

The exact elastic Green function will be numerically integrated on the surface of the superspherical inclusion for the first Eshelby problem to obtain the averaged Eshelby tensor (Rodin 1996, Mura 1987, Maekenscoff 1998, Onaka 2001)

The finite element method will be used to solve the problem of the isolated superspherical and/or superspheroidal inhomogeneity and to obtain the compliance contribution tensor (Hill 1963, Kachanov et al. 1994)

The linear conductivity/resistivity problems will be investigated by using the same methodology (Sevostianov and Kachanov 2002)

(51)

11

1.3 Homogenization schemes

By neglecting interaction effects, Non-Interaction Approximation (NIA) constitutes the simplest approach for effective problems, taking advantage of its simplicity, the main focus could be addressed to the shape effect of shape factor. Its accuracy holds for low concentration of inhomogeneity. Importance of NIA approach is shown in two aspects: (1) it constitutes the basic building block for other approximation schemes that account interactions by placing non-interacting inhomogeneities into certain "effective environment" (effective matrix or effective field). (2) the explicit cross-property interrelating changes in the elastic and conductive properties due to inhomogeneities that are established in NIA remains efficient at substantial concentrations (since interactions produce similar effects on each of the two properties).

Mori-Tanaka scheme and Maxwell scheme are largely investigated in the case where the interaction affects could be accounted at substantial concentration. Their accuracies are generally appreciated, in particular, Maxwell scheme is considered to be the most accurate homogenization scheme. Interactions are taken into account by the following manners: (1) In Mori-Tanaka scheme, the isolated inhomogeneity is assumed to be subjected to an effective stress field. (2) In Maxwell scheme, the far field generated due to the inhomogeneities is equal to the far field produced by a fictitious domain of certain shape that possesses unknown effective properties.

1.4 Goals of the thesis

The main focus of this work is to investigate the effect of the concavity parameter of 3-D non-ellipsoidal inhomogeneities on the overall effective properties in the framework of Eshelby tensor approach and micromechanics of random heterogeneous media. To the author’s acknowledge this is novel in 3D context as many results are available in 2D case. Property contribution tensors will be determined numerically by using appropriate numerical method such as finite element. On this basis, approximate simplified relations will be provided for use of these results in NIA, Maxwell, Mori-Tanaka approximations.

As previously mentioned, 3D inhomogeneites (solid or fluid filled pores) of concave shapes may be observed in rock materials such as oolitic rocks. Applications of newly calculated property contribution tensors to effective properties of such heterogeneous materials, via relevant homogenization schemes, will be presented. It completes previous known results, for such materials based on ellipsoidal approximation for all inhomogenities shapes.

(52)

12

1.5 Organization of the work

Four parts are involved in this work. In Part 1, background and the theoretical frameworks are briefly overviewed. In Part 2, property contribution tensor such as compliance contribution tensor in elasticity problems and resistivity contribution tensor in thermal conductivity problems will be carefully discussed. Numerical calculations are performed for superspherical and superspheroidal pores with the pursuit of high precision. Three papers related to Eshelby

tensor, compliance contribution tensor, resistivity contribution tensor published from 2015 to

2016 in I.J.E.S will be shown entirely (IJES: International Journal of Engineering Science) In Part 3, relative applications in the field of rock mechanics and geophysics will be illustrated. Effective thermal conductivity of oolitic rocks is discussed by using the reformulated Maxwell homogenization approach (paper published in International Journal of Rock Mechanics and Mining Sciences (2015)). The accuracy of the replacement relations for materials with non-ellipsoidal inhomogeneities is verified (paper submitted to International Journal of Solids and Structures I.J.S.S. April/2016).

To conclude, in Part 4, some essential results that have been done in this work will be reminded and a brief perspective of the future work will be mentioned.

(53)

13

Part 2 Property contribution tensors of material

containing 3-D non-ellipsoidal inhomogeneities

(54)

(55)

15

Preface

"

E

shelby problems" and their explicit results of uniformity of strain and stress fields around and inside region Ω occupied by an ellipsoidal inclusion or inhomogeneity submitted to a remotely uniform loading at infinity lead to remarkable revolutions in solid mechanics and in micromechanics of the 20th century.

Both inclusion- and inhomogeneity problem are involved in "Eshelby problems. Solution of inclusion problem such as the resulting strain around Ω is interrelated to an natural existing eigenstrain by a fourth-rank Eshelby tensor

S

E or Hill’s tensor P , whereas solution of inhomogeneity problem are given by property contribution tensor, which turns into by compliance contribution tensorHin elasticity problems or by resistivity contribution tensorR in thermal conductivity problems. If Ω is ellipsoidal, both problems are mathematically equivalent and their solutions are interrelated by linear equations.

Nevertheless, one has to carefully distinguish the differences between the two Eshelby problems for non-ellipsoidal inhomogeneities, in particular for 3-D cases. In the context of effective problems, only property contribution tensors characterizing contribution of individual inhomogeneity on the overall effective properties are involved in homogenization schemes.

(56)

(57)

17

ChaPter 2 II

Eshelby tensor of concave superspherical inclusions

For determining the elastic fields of homogeneous materials containing non-ellipsoidal regions of the same elastic properties, the first Eshelby problem has been largely investigated. It could be traced back to its original proposition of Eshelby (1957, 1961) who considered only ellipsoidal shapes for isotropic medium.

This chapter is motived by the work of Onaka (2001) who considered a particular 3-D non-ellipsoidal superspherical shape of convex curvature (with concavity parameter _{� ≥ 1). The} novelty of the presented work concerns the extension to concave domain. As an example, concave superspherical shape (with _{� < 1) is useful to model filling materials between spheres} as it may be observed in oolithic rocks (oolithes are nearly spheroidal or spherical grains).

After a brief introduction of fundamental physics of the first Eshelby problem in section 1, new computational results for concave superspherical pores will be provided in section 2, to end this chapter, discussions about the related issues and some short remarks will be proposed in section 3.

(58)