Automate des préfixes-suffixes associé à une substitution primitive

J

OURNAL DE

T

HÉORIE DES

N

OMBRES DE

B

ORDEAUX

V

INCENT

C

ANTERINI

A

NNE

S

IEGEL

Automate des préfixes-suffixes associé à une

substitution primitive

Journal de Théorie des Nombres de Bordeaux, tome

13, n

o

_{2 (2001),}

p. 353-369

<http://www.numdam.org/item?id=JTNB_2001__13_2_353_0>

© Université Bordeaux 1, 2001, tous droits réservés.

L’accès aux archives de la revue « Journal de Théorie des Nombres de Bordeaux » (http://jtnb.cedram.org/) implique l’accord avec les condi-tions générales d’utilisation (http://www.numdam.org/conditions). Toute uti-lisation commerciale ou impression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit conte-nir la présente mention de copyright.

Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques

Automate

des

_{préfixes-suffixes}

associé à

une

substitution

_primitive

par VINCENT CANTERINI et ANNE SIEGEL

RÉSUMÉ. On

_explicite

une

_conjugaison

en mesure entre le

déca-lage

sur le

système dynamique

associé à une substitution

primi-tive et une transformation

_adique

sur le _support d’un sous-shift de

type

fini,

à savoir l’ensemble des chemins d’un automate dit des

préfixes-suffixes.

En caractérisant les

_préimages

_par la

conjugai-son des chemins

_périodiques

de

_{l’automate,}

on montre que cette

conjugaison

est

_injective

sauf sur un ensemble

_{dénombrable,}

sur

lequel

elle est finie-à-un. On en déduit l’existence d’une suite de

partitions du

_{système qui}

est

_{génératrice}

en mesure et une

appli-cation aux fractals de

Rauzy

est donnée.

ABSTRACT. _{We prove} that a

_dynamical

_system 03A9

_arising

from a

primitive substitution is

_{measurably conjugate}

to an adic trans-formation on a subshift of finite _type defined as the set of

_paths

on a

_graph.

The

_conjugation

map is one-to-one except on the orbit

of

_{periodic points}

of

_03A9,

on which it is finite-to-one. We deduce a

sequence of

partitions

of 03A9 which is is

_generating

in measure. An

application

to

_Rauzy

fractals is

_given.

0. Introduction

Soit une substitution sur un

alphabet

fini. On obtient un

système

dy-namique

symbolique

en considérant

_{l’opérateur}

de

_décalage

S sur l’ensemble

Q des mots dont le

_langage

est inclus dans l’ensemble des facteurs des itérés de c~ sur les lettres de

_{l’alphabet.}

Notre

_objectif

est de décrire de manière

plus explicite

ce

_{système dynamique lorsqu’il}

est minimal et de mettre en

évidence la

_dynamique

de la numération associée à cette substitution. De nombreux auteurs se sont intéressés à ces

_questions

(E.

Coven et

M. Keane

_[2],

J. Martin

_[14],

M.

_Dekking

_[3]

entre

_autres).

En

_1882,

G.

_Rauzy

a introduit un automate des

_préfixes.

Cette notion lui a

per-mis en

particulier

de décrire

précisément

la

dynamique

du

_système

associé

à la substitution

_12,

_{u(2) =}

_13,

_{u(3) =}

1 et d’en déduire que

ce

système

est

_conjugué

en mesure à une rotation sur un tore

_(voir

_[18]).

Dans

_[19],

l’auteur annonce _que l’automate des

_préfixes

_permet

de décrire

de manière semblable toute la classe des substitutions

_primitives

de

_type

Pisot. Les travaux de B. Mossé

_[15]

sur la reconnaissabilité des substitutions

impliquent

que cette affirmation est incorrecte en toute

généralité.

Notre

but est de mettre en

place

un véritable outil _pour décrire les

_systèmes

sub-stitutifs

_minimaux,

en nous

inspirant

de la méthode

proposée

_par G.

_Rauzy.

Plus

_{précisément,}

si tous les éléments du

_système

unilatéral

_{(S2, S)}

ad-mettent une

décomposition unique

sous la forme w =

su(v),

où s est le suffixe de

_l’image

_u(b)

d’une lettre b telle _que bv E

_0,

alors

_{l’application}

w e v

_apparaît

comme

_{l’opération}

inverse de la substitution. Une telle

opération

se trouve aussi dans les travaux de J. Martin

_[14]

et bien d’autres mais elle est

_{généralement}

définie de manière

_incomplète.

Dans cet

_article,

la notion

_précédente

est

_remplacée

_par celle de désnbstitution

_qui

_permet

de décrire la

_dynamique

du

_décalage

sur SZ.

On considère non _pas, comme le font la

_plupart

des

_auteurs,

le

_système

symbolique

unilatéral associé à une

substitution,

mais le

_système

_bilatéral,

où les suites sont indexées _par Z. La

_projection

_canonique

du

_système

bilatéral sur le

_système

unilatéral est alors

_injective

sauf sur un ensemble

fini de

_points

où les fibres sont finies.

Les résultats de

_[15]

_impliquent

_que tout mot du

_système

bilatéral est

l’image

par ~, éventuellement décalée un

petit

nombre de

fois,

d’un

unique

autre mot de n. Autrement

_dit,

tout mot w de n

_peut-être

_découpé

de manière

_unique

sous la forme suivante :

1.. , 1 1

le mot v = ... ... V-l.VOVl ... Vn ...

appartenant

à S2. On

appelle

dé-substitution

_{l’application 8}

_qui

à w associe le mot v. A cette désubstitution

est naturellement associée la

_partition

de 11 suivant le

_découpage

de

sous la forme _{w_k ... W-1}

1 WO wl

... Wl, c’est-à-dire selon les ensembles

suivants où

_[a]

_désigne

l’ensemble des mots du

_système

dont la lettre d’indice 0 _{est a, et}

_Ipl

la

_longueur

du mot fini _{p :}

.. 1 .

On

_{appelle développement}

en

préfixes-suffixes l’application

r

qui

à un

point w

de Si associe sa

_trajectoire

suivant la

_partition

ci-dessus sous l’action

de la désubstitution 0. Nous montrons au théorème 5.2 et au corollaire 5.2

que r est une bonne

_{représentation}

de S2 :

Théorème.

_{L’application}

r est continue

_surjective

de S2 dans

_l’espace

d’un

_sous-shift

de

_type

_fini

D

_défini

comme l’ensemble des chemins d’un

l’orbite des

_points

de S2

_périodiques

_pour la substitution _a, où les

_fibres

sont

finies.

En

_{particulier, la}

_partition

Í2 sous la

forme

U

est markovi-enne

pour la

désubstitution 0.

Le sous-shift de

_type

fini D

_peut-être

vu comme un

_compact

markovien

stationnaire au sens d’A. Vershik

[21].

La substitution

_permet

de définir un

ordre naturel sur les

triplets

(p,

_a,

s)

tels

qu’il

existe une lettre b vérifiant

pas

= cr(6).

A

partir

de cet

ordre,

on obtient une transformation

adique

T sur

D,

dont on montre

_qu’elle

est une bonne

_description

du

décalage

S sur Í2. Plus

_{précisément,}

le théorème 5.1 et la

_proposition

5.1

_{s’expriment}

comme suit :

Proposition. L’application

r

_conjugue

le

_décalage

S’ sur Í2 avec une

trans-formation adique

sur le

sous-shift

de

_type

fini

D. A

_contrario,

la

désubsti-est

_conjuguée

par r à un

simple décalage

sur D.

Nous retrouvons ainsi de manière constructive et

_explicite

le fait _que tout

système

substitutif minimal est

_conjugué

en mesure à une transformation

adique

sur un

_compact

de Markov

[12, 5].

Le fait _{que r} soit un

isomorphisme

_permet

d’interpréter dynamiquement

et de

_{généraliser}

les résultats de

_[4]

sur les échelles de numération associées au

_point

fixe d’une substitution. En

_{conséquence :}

Corollaire. Pour tout soit E

_N,

a E

Les Pk

forment

une suite de

_partitions

génératrice

en mesure.

L’automate des

_{préfixes-suffixes}

_permettant

de définir le sous-shift de

type

fini D est la forme la

plus complète

des automates du même

_type

qui apparaissent

dans la littérature.

_Ainsi,

la donnée de cet automate est

équivalente

à celle du

_{graphe dirigé}

défini _par C. Holton et L. Zamboni dans

[8]

pour étudier la dimension de Hausdorff de

représentations

géométriques

unidimensionnelles de substitutions. Ces deux auteurs étudient

indépen-damment et

_rapidement

dans

_[9]

des

_propriétés

du

_{graphe dirigé qui}

re-coupent

une

_partie

des résultats

_{précédents.}

Cet _{automate est par} construction une extension de l’automate des

préfi-xes et de l’ automate des

suffixes

définis _par G.

Rauzy

dans

[18,

19]

_pour

représenter

des

_systèmes

substitutifs de

_type

Pisot par des

échanges

de

morceaux dans

_l’espace

euclidien. Les sous-shifts déterminés _par ces deux

derniers automates ne sont _que

_sofiques,

ce

_qui

_empêche

l’obtention de résultats sur

_{l’injectivité}

des

_{représentations.}

L’automate des

préfixes-suffixe,

par

contre,

détermine un sous-shift de

_type

fini. Ceci est le

point-clé utilisé dans

_[1]

_pour étudier

_{l’injectivité}

de

_{représentations}

_{géométriques}

de

_{systèmes substitutifs,}

ces

représentations

étant définies via le sous-shift

L’automate des

_{préfixes-suffixes}

se retrouve sous forme codée dans les

travaux en théorie des nombres

_développés

à

_partir

de l’automate de

G.

_{Rauzy :}

tout d’abord ceux de J.-M. Dumont et A. Thomas

_[4],

sur

des échelles de numérations associées à certaines substitutions

_{définies ;}

ensuite leurs

_{développement}

_par V. Sirvent

_[20]

pour exhiber certaines

pro-priétés

du fractal de

_Rauzy.

Citons enfin la définition _par T. Kamae dans

[10]

de pavages colorés à

partir

d’une substitution

_pondérée,

_{l’agencement}

des

_pavés

étant défini _par des

_règles

_proches

des transitions de l’automate des

_préfixes,

mais non

explicitées.

Pour

_finir,

dans le domaine de la théorie des

_langages,

l’automate des

préfixes-suffixes

se

_projette

d’une

_part

sur l’automate défini _par A. Maes

[13]

dans ses travaux sur la décidabilité de théories

_{arithmétiques,}

et d’autre

part

sur l’automate défini _par P. Narbel

[16]

_pour étudier la frontière d’un

langage

à

_partir

de la

_description

sous forme d’arbre de l’ensemble des

chemins de son automate.

Remerciements. Nous tenons à remercier V. Berthé et P. Arnoux _pour leurs

_suggestions

tout au

long

de la rédaction de cet article. Nous

remer-cions

_également

les

_rapporteurs

_pour nous avoir

_indiqué

la référence

[10]

et

pour leurs remarques

judicieuses

sur le manuscrit.

1.

_{Système dynamique}

substitutif

Soit ,~4. un

alphabet fini,

,~4* l’ensemble des mots finis sur ,A.. On note

,~1.+

=

.4* B

où -

désigne

le mot vide de ,~l*. La

longueur

d’un mot

fini u est notée

_lui.

On

_appelle

mot

_infini

bil atéral tout élément w de On écrit un tel mot en le

pointant

entre et wo, _par

exemple

w =

... W-2W-l.WOW1 .... On note l’ensemble des mots infini unilatéraux

indexés _par les entiers strictement

_négatifs,

et l’ensemble des mots infinis unilatéraux indexés _par les entiers

_positifs

ou nul. Les ensembles _pour

M =

Z, N,

-N* _sont munis du

produit

des

_topologies

discrètes _sur A.

On

_appelle

13

_{= ~ n.v ; u}

E ~4* U E ,,4* U l’ensemble de

tous les mots

_pointés

_pouvant

être construits à

_partir

de .~. Cet ensemble contient

A+

et

_s’injecte

_{canoniquement}

dans où s est un

symbole

supplémentaire,

en

complétant

tout élément

qui

n’est _pas indexé _par

Z _par le

_symbole

s.

On dit

_qu’une

suite wn d’éléments de B converge vers w E Z3 si les

_images

des wn par

l’injection

canonique convergent

dans vers

l’image

de w. On _remarque

_qu’une

telle définition est cohérente avec la _convergence

dans

_AM,

_pour M =

Z, N,

-N*.

(lorsque u

est

_vide,

le

_cylindre

est

_simplement

noté

_{w~ ) .}

Ils sont ouverts et

fermés et forment une base de la

_topologie

de

Une substitutzon est ici un

morphisme a

_pour la concaténation du

mo-noïde libre

_{r4*, qui}

envoie ,4 sur

,A.+

et tel

_qu’il

existe une lettre a de r4.

vérifiant

_limn,,,.

₁

= _-f-oo. La substitution a _se

_prolonge

de manière

naturelle à l’ensemble des mots infinis

AZ

par :

Un mot infini u de

4z

pour

lequel

il existe un entier k non nul vérifiant

01 k (U) = u

est

_appelé

un

_point

_périodique

de u

(point

_fixe

si =

u).

On

note

_Oper

l’ensemble des

_points

_périodiques

de la substitution.

_Ainsi,

_Oper

est l’ensemble des mots w de la forme w =

adn(b).adn(a),

où _a

et b sont deux lettres et d un entier tels _que

ad(a)

commence _{par a,}

od(b)

finit _par

_b,

et ba

_apparaît

dans

_l’image

_par

~d

d’une lettre.

On note ,5’ le

_décalage

sur

qui

à tout mot w = associe le _mot

Sw =

(wi+,)iEz.

On

appelle

_point

S-périodique

_{tout mot w} de

A7’

tel

qu’il

existe h &#x3E; 1 avec w. Une substitution a est dite

_{S-périodique}

s’il existe un

point périodique

de u

_qui

soit

également S-périodique.

Le

_langage

_f-(w)

d’un mot infini w est l’ensemble de tous les mots finis

_qui

apparaissent

dans w. Le

système dynamique symbolique engendré

_par un

mot infini bilatéral u est le

_couple

_{(0(’11,),8),}

où

_{w

E C

Notons _que l’ensemble est

_{l’adhérence,}

dans de l’orbite de

u sous l’action de

_{,S ;}

il est

_compact

_pour la

_topologie

induite _par celle de

47’

et la restriction de S’ à encore notée

S,

est un

homéomorphisme.

On

remarque que est fini si et seulement si u est un

_point

_{S-périodique.}

Une substitution or est dite

_primitive

s’il existe un entier naturel 1~ tel

que

uk (a)

contient une occurrence de b _pour tout

_couple

_{(a, b)}

E

,A.2.

Si a~

est

_primitive,

_Qper

est fini et non vide. Soit u un

_{point périodique}

de _~,

alors ne

dépend

_pas de u : on le note

Q,

et

(0, S)

est

_appelé

le

_système

dynamique symbolique engendré

par ~. De

même,

£(u)

ne

_dépend

_pas de

u, on le note aussi

_f-(Ç2).

Si la substitution est

_primitive,

le

_système

(Q, S)

est m2nimal : il ne

_possède

_pas de fermé non trivial _{invariant par} S’. Ce

_système

est

_un2quement

_{ergodique :}

il existe une

_unique

mesure

de

_probabilité

S-invariante sur

Q,

la mesure d’un

_cylindre

_[u.v]

étant la

fréquence d’apparition

du mot uv dans

n’importe

quel

élément de Q. On

renvoie le lecteur à

_[17]

_pour

_plus

de

_{développements}

sur ce

_sujet.

Dans la

_suite,

nous ne considèrerons _que des substitutions

_primitives

et

2. Désubstitution et

_{développement}

en

préfixes-suffixes

Soit or une substitution

_primitive

non

S-périodique

sur

l’alphabet

,~l =

~ l, 2, ... , d}

et soit

_(!1,

_S)

le

_{système symbolique engendré}

_par ~. Par

com-pacité,

tout mot de Q se

_décompose

sous la forme w = avec

k où v E SZ et vo est la lettre d’indice 0 de v. L’unicité de

cette

_{décomposition}

est assurée _par un résultat de

[15],

où l’auteur _prouve

que toute substitution

primitive

non

S-périodique

vérifie une

propriété

de

reeonnazssabilité

_bilatérale,

_que nous utiliserons sous la forme suivante :

w rv w , v

-Si on note _p =

W-k ...

W-1 le

préfixe

de

a(vo)

de

longueur

k et s le suffixe

wl ... wl, la connaissance du

couple

(v, k)

est

_équivalente

à celle de v et de la factorisation de

_o-(vo)

sous la forme _pwos. Introduisons l’ensemble de ces

découpages :

Définition 2.1. Soit

_{(11, S)}

le

_système

_{d ynamique symbolique engendré}

_par

une substitution _a,

primitive

non

_{S-périodique.}

On

_appelle

désubstitution

l’application

8 : SZ -~ n

_définie

_par

On

_{note ’Y :}

S2 --~ P

_{l’application}

suivante :

L’existence et la continuité de ces

_applications

découlent directement de

[15].

Ceci

_justifie

le choix de travailler sur un

système dynamique

bilatère

plutôt qu’avec

des mots unilatéraux. En

_fait,

suivant

_[15],

pour certaines substitutions - _par

_exemple

_Q(1)

= 1112 _et

Q(2)

= 12 - la

décomposition

sous la forme w =

Sk(a(v))

n’est _pas

_unique

_{pour tous} les _mots unilatéraux

du

_{système dynamique,}

et il est

_impossible

de définir un

unique

désubstitué

dans ce cas.

Les ensembles

_{~y-1 (p, a, s)}

_pour

_{(P, a, s)}

E P définissent une

partition

finie de S2. Nous allons nous intéresser aux itinéraires des

_points

de S2 dans

cette

_partition

sous l’action de la désubstitution B.

Définition 2.2. On note r : S2 ~

P~

l’application

continue

_définie

_par

On

_appelle

_{développement}

en

préfixes-suffixes

de w la suite

r(w).

Deux

_problèmes

se

_{posent :}

identifier

lr(Ç2)

et déterminer si r est

in-jective.

Nous montrerons que

r(52)

est entièrement décrit _par la

_propriété

suivante.

Remarque

2.1. Si w Ena _pour

_{développement}

_{r(w) =}

_{(pi, ai,}

alors

Relativement à

_{l’injectivité}

de

_r,

notons la _remarque suivante.

Remarque

2.2. Soit w E 11 et

_{r(w) =}

son

développement.

Si les

_préfixes

_{pi et} les

_suffixes

si ne sont pas tous vides à

_partir

d’un certain

rang, alors w est la limite de la suite des mots

_finis

suivants :

Si les

_préfixes

ou les suffixes sont vides à

_partir

d’un certain _rang, les

mots finis ci-dessus ne

_convergent

_pas vers un mot bi-infini. Les éléments de n

_qui

sont dans ce cas seront identifiés aux sections 4 et 5. On note

dans la _remarque suivante

_qu’il

en existe :

Remarque

2.3. Les

_{développements}

_(pi,

_ai, des

_points

de n

périodi-ques pour or sont tels _{que pi} = _e

pour tout entier i. Les

développements

des

antécédents _par le

_décalage

S de ces

points

sont tels _{que si} = _e

pour tout

entier i .

3. Automate des

_{préfixes-suffixes}

Les

_propriétés

des

_r(w),

où w E

_{Q, exprimées}

à la _{remarque 2.1} amènent à définir l’automate suivant.

Définition 3.1. L’automate des

_{préfixes-suffixes}

_Au

associé à la substitu-tion o, est

_défini

comme suit :

. A _est l’ensemble des états. Tous les états _{sont initiaux.}

. P est l’ensemble des

_étiquettes.

. Il existe _une

_flèche

_entre les états _{a et b}

_étiquetée

par e =

(p,

a,

s)

si

u(b)

=

pas.

La matrice

_{d’adjacence}

du

_{graphe dirigé}

_sous-jacent

à

_Au

est la matrice de _u, dont le coefficient

_{(i, j )}

est le nombre d’occurrences de la lettre i dans Si or est

_primitive,

l’automate

_Au

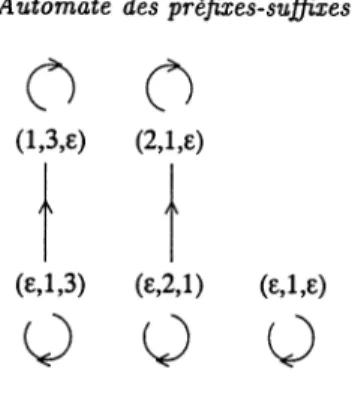
est fortement connexe. La

_figure

1

donne un

exemple

d’un tel automate.

Définition 3.2. Un élément

_(ei)i&#x3E;o

de

~~

est dit admissible s’il

_s’agit

d’un mot

_infini

reconnu _par l’automate des

préfixes-suffixes.

On note D l’ensemble des éléments de

7~~

_qui

sont admissibles.

Un chemin est

_étiqueté

_par les ei =

(pi, ai, si)

si _et seulement _si

piaisi pour tout i

positif.

On en déduit _{que D} est le sous-shift de

_type

fini

de

P~

pour

lequel

les mots interdits sont toutes les

paires

d’étiquettes

qui

FIGURE 1. automate des

_{préfixes-suffixes}

_{pour : 1} ~

21,2~13,3~1

Proposition

3.1. L’ensemble D muni du

_décalage

de

PN

est un

sous-shift

de

_type

_fini

associé à la matrice

_Mv

=

définie

par

On

_peut

maintenant

_{répondre partiellement}

à la

_question

sur

_l’image

de

r et de son

injectivité.

Proposition

3.2. On a

r(!1)

C D. De

_plus,

r est

_injective

sur

r-1(D B

D~),

et

_{D B}

_D,

C

_r(f2),

avec

De

= _E

D

_i

(3 io

_E

io, pi

=

c)

_ou

(B1 i

_~

_io,

si =

c)}.

Preuve. Le fait d’avoir

_r(S2)

C D est une

_conséquence

directe de la

remar-que 2.1.

L’injectivité

de r sur

r-1(V B

D,)

provient

de la formule

(2).

Si

e = _ai, la suite des mots

Q2(si)

con-verge vers un mot infini zu de

47.

Celui-ci a tous ses facteurs dans

G(S2)

et

_appartient

ainsi à S2. La définition de r

_implique

_r(w)

= e et donc 0

Les

_{problèmes posés}

la

_{surjectivité}

et

_{l’injectivité}

de r se ramènent donc

à l’étude

_précise

de

_r-1Dé.

Par

_application

du

_décalage

_(voir

section

_5),

ceci revient à étudier les mots de S2 dont les

_{développements}

ont tous leurs

préfixes

ou tous leurs suffixes vides.

4.

_{Développement}

des

_{points périodiques}

Le but de cette section est de montrer _que les inclusions

_r(Ç2per)

C

Dmin

Si

_(é,

ai,

si)i

E les ai forment une suite

périodique, puisque

l’auto-mate défini sur _par a - b si commence _par a est codéterministe. Ceci

_{implique qu’il}

_y a au

_plus

d éléments dans De

_{même, Dmaz}

contient au

_plus

d éléments. On en déduit aussi :

Lemme 4.1. Soit w E Q. Le

_{développement}

_{r(w) _ (pi,}

_ai,

_si)i&#x3E;o

est dans

Dmin

(respectivement

si et seulement si w E

_Qper

_{(respectivement}

Sw E

_Qper).

Preuve. Les _{preuves pour} et

_Vmax

étant

_analogues,

examinons

seule-ment le cas des

_préfixes

vides. On sait

_déjà

_que C

1Jmin.

Récipro-quement,

si _{pi = e pour} tout

_i,

la suite

_(ai)i

est

_périodique.

Soit 1

sa

_période.

La

_{partie positive}

w+

est alors

_uniquement

déterminée _par

w+ -

WOWJ ° ° ° *

limnPoe

Les désubstitués

vi

= de w sont tels

que v’

= =

Si

_bi

= est la lettre d’indice -1 du _mot

vi,

la suite _est

périodique

puisque

pib2.

Si m est sa

_période,

comme w =

u"(vl),

la

partie

w- de w indexée

_{négativement}

se termine par tous les ce

_qui

im-plique

... W-2W-l = w- =

limj_oo

=

om

UZ (b2+rra ) )

=

olm (w-) .

En définitive w = _{w- .}

w+ =

_E

Qper.

0

Théorème 4.1. On a

, . ’

Preuve. Si e =

si)i

_E les lettres

ai forment une suite

périodi-que. Soit 1 sa

période.

Il existe un mot fini W tel _que =

aoW .

Soit

_{bo E}

A tel _que

_{boao E}

_f-(Ç2)

_{et bi}

les lettres définies _par =

où les

_v

sont des mots finis. Comme

_l’alphabet

,~4 est

_fini,

il existe

_jo

&#x3E;

_io

tels _que

_bio

= Par définition des

b2,

_{on a}

a(jo-io)l(bio)

=

=

Viobjo.

Ainsi,

~ k =

jo -

io

et V =

Vio

sont tels

que

Vbio.

Puisque

boao E

.~(SZ),

on a

_bioao

E Le fait que

akl(bioao)

= _avec W et V _non vides

par

primitivité

(quitte

à

remplacer

kl _par un

multiple),

entraîne donc _{que w} =

Ainsi,

r (w)

E De

_plus,

les définitions de 8

_{et q}

_impliquent

directement _que les lettres d’indice 0 des

O’w

sont les _ai, ce

_qui

_{prouve que}

r(w) =

e.

Dans le cas où e =

(pi,

ai,

é)i

E i la lettre ao vérifie

al

(ao) -

Vao,

et on obtient une lettre telle _que

akl(bio)

= _avec

aobio

E

f-(ç2)-Ainsi, W

=

Qper

et vérifie e =

On a ainsi

_prouvé

_que

_1Jmin

C et _que

Drnax

C

_{r (}

ce

Notons que r n’est pas nécessairement une

bijection

de

Í2per

sur ou

de sur

_Vmax,

comme le montre

_l’exemple

_suivant,

où

et

_DmaT

sont de cardinal différent.

Exemple

4.1 La substitution u : 1 ~

_21,

2 ~

_13,

3 ~ 1

_possède

deux

points périodiques

ui et u2

(de

période

2)

tandis que

IM1, M2}

et

Dmaz =

{M},

avec :

La section suivante

_permet

de ramener l’étude de

_De

à celle de

Dmjn

et et de

_régler

ainsi les

_problèmes

de la

_{surjectivité}

de F dans D et de

son

injectivité

en mesure.

5. Ordre et successeur

Sur des

_supports

de sous-shifts de

_type

fini semblables à

_D,

A. M. Ver-shik

_[21]

utilise la

_terminologie

des

_compacts

markoviens

_et,

à

_partir

d’un ordre arbitraire sur

l’alphabet,

définit un ordre sur le

_support

du sous-shift

et un _passage au successeur

_{appelé transformation adique,}

en raison de la

similarité avec les odomètres. Cette transformation fut d’abord introduite sur les

_diagrammes

de Brattelli

[7, 21],

et a

_permis

d’étudier le _groupe de

dimension des

_systèmes

substitutifs

_[5].

Dans cette

_section,

nous étudions

la

_{transformation adique}

obtenue sur

D,

l’ordre ~ sur 7~ étant défini

na-turellement à

_partir

de la substitution.

Plus

_{précisément,}

_pour deux éléments

_(p,

_a,

_s)

et

_(q,

_b,

_r)

de

_~,

on _{pose :}

(3i

Sur l’automate des

_{préfixes-suffixes}

deux

_étiquettes

sont

_comparables

si,

et seulement

_si,

elles

_marquent

des transitions arrivant au même état.

Pour cet

_ordre,

un élément

(p,

_a,

s)

est minimal. si son

_préfixe

_p est vide et

maximal si son suffixe s est vide.

Ainsi,

en

_chaque

état de

l’automate,

ar-rivent une

unique

arête minimale e =

(e, a,

s)

_{et une}

unique

arête maximale

f

=

(p,

_b,

é).

Remarquons

que si

(p, a, s)

n’est pas

maximal,

alors l’élément

(q, b, r)

de 7~ défini par pas =

qbr

_et

ipl

_{+ 1 =}

lql

_est le

plus petit

des

majorants

stricts de

_(p,

_a,

_s).

Reprenons

la substitution u :

_{1 t-7 21, 2 t-7 13, 3 t-7 1,}

l’ordre « est

FIGURE 2. ordre « pour o, : 1 M

_21,

2 r-7

_13,

3 r-7 1

L’ordre sur P

_permet

de définir sur D un ordre

_{lexicographique}

inverse encore noté - : si et sont deux suites de

_D,

on _pose

Un élément de D est minimal

_{(respectivement maximal)}

si _pour

tout

_i,

ei est minimal

(respectivement maximal)

dans

P,

c’est-à-dire que

tous les

_préfixes

_{(respectivement suffixes)}

de

_(ei)i

sont vides. L’ensemble des éléments minimaux de D est donc celui des éléments maximaux

Vmax.

Le théorème 4.1

_signifie

alors _{que w} est

_périodique

_pour u si et

seulement si son

développement

r(w)

est

_minimal,

ou encore si et seulement

si est maximal.

Définition 5.1. Soit e =

(ei)i

_E

D ~

_et

io le

_plus

_petit

entier tel

que n’est pas maximale.

L’image

de e _par

_{l’application}

successeur T :

D B

D est l’élément

_T(e)

=

f

de D

défini

par :

Notons _{que, si}

_{e 1}

_1)max,

alors

_T(e)

est le

_plus

_petit

des

_majorants

stricts de e. La définition de T

implique

facilement le résultat suivant :

Théorème 5.1. Le successeur T est une

bijection

de

D B

_Dmax

dans

D B

un élément de Q tel _que Sw n’est _pas

périodique

_{pour ar,}

alors

Revenons sur

l’exemple

de la substitution a : 1 H-

_21,

2 H-

_13,

3 H- 1. Le

_point

_mi =

[(~,2, l)(c, 1,3)]~

_E D s’écrit :

et ainsi

_T7(ml)

=

r(S7Ul).

Une solution naturelle pour définir le successeur d’un

_point

maximal

serait de lui associer un

point

minimal. Ceci est

généralement impossible,

puisque

pour la

plupart

des

substitutions,

le nombre de

points

minimaux diff’ere de celui des

_points

_maximaux,

comme dans le cas

_déjà

vu de la

substitution o, : 1 ~

_21,

2 ~

_13,

3 ~ 1.

Dans le cas

particulier

où u est une substitution _propre

(id

est ne

possède

qu’un

seul

_point

_{périodique),}

_{l’application}

successeur T est définie sur tout

D en

_posant

_Pmin, où _{pm;n est}

l’unique

_point

minimal de D et p?.,.ta~

l’unique

point

maximal. Le

système dynamique

(D, T)

est alors un

odomètre

_{généralisé}

_(voir

_{~6~ ) .}

Le successeur

_permet

de relier

De

à

Tmjn

et la définition de T

implique

facilement

_qu’un

élément de D a tous ses

_préfixes

(respectivement

suffixes)

vides à

_partir

d’un _{certain rang si} et seulement s’il

_appartient

à l’orbite

_positive

_{(respectivement négative)}

_par T de

_Dmjn

(respectivement

1

Corollaire 5.1.

De ce

_{qui précède,}

on déduit _que r est une bonne

représentation

de Í1 :

Théorème 5.2. Si a est une substitution

_primitive

et non

S-périodique,

l’application

r est continue

_surjective

de Ç2 sur le

_support

du

sous-shift

de

type

fini

D. Elle est

_injective

sur

S2

UkEZsknper

et est donc

_injective

en mesure. De

_plus,

_{pour tout} d

_EV,

on a card

(

r-1

(d) ) :5

card

(

Í1per ).

Dans le cas

_particulier

d’une substitution _{propre, r} est un

homéomor-phisme

et on retrouve un résultat de

[5]

disant _que

(0, ,S’)

est

topologique-ment

_isomorphe

à une

application adique

sur le

_support

d’un sous-shift de

type

fini. L’intérêt de notre résultat _{est que}

_{l’isomorphisme}

est constructif. Cette étude sera

complète lorsqu’on

aura déterminé comment r

_agit

sur

la désubstitution 0 et la substitution or. Par

construction,

r o 8 est le

décalage

T sur D.

_{L’application}

r o _or,

_qui

est

_plus

ou moins l’inverse de

r o

0,

devrait donc être l’inverse du

_décalage

T sur D.

Or,

D est constitué de suites indexées _par

_N,

et

T -1

n’est _pas défini sur D : un élément de D

peut-être prolongé

de différentes manières vers la

_gauche.

La

_proposition

suivante

_signifie

_que le fait

_{d’appliquer}

r o 0 revient à choisir le

plus

petit

des

_{prolongements}

à

_gauche.

Proposition

5.1. Soit T le

_décalage

sur D et _{p : D -~ D}

_{l’application}

définie

comme un

prolongement

minimal à

gauche

_par

p(e2)i

= _avec

1 -- - -

-Les dieux

_diagrammes

suivants sont

_commutatifs.

p 1

Ces résultats

_{s’interprètent dynamiquement}

_par le fait _que le

_système

(Q, 0)

admet une

_partition

markovienne

(voir

[11],

_partie

6.5).

Corollaire 5.2. La

_partition

de Q _par les ensembles

est une

_partition

de Markov de

(0,

0)

en mesure.

Preuve. Les ensembles

_{~y-1 (p,}

a,

s)

sont des ouverts-fermés de Ç2

disjoints

deux à deux _par définition et continuité

_{de q.}

Alors

_(D,

_T)

est le

_système

symbolique correspondant

à la

_{partition, puisque}

r est

_surjective

et

_{(D, T)}

est le sous-shift de

_type

fini de matrice

_MD

_{(formule (3.1 ) ) .}

Ceci assure _que

~(7’~~) )

est l’union des

_y-1

_(q,

_b,

_r)

pour - l.

Enfin,

si

e = _E

D,

par définition de r on a =

qui

est

_{presque-sûrement}

réduit à un

_point.

D

6. Echelles de numération et

_{partition génératrice}

Pour tout b e

_,~1.,

soit

_(b)

= _E

D ;

_ao =

bl

l’ensemble

des

_étiquettes

des chemins de l’automate

_qui

_partent

de l’état b. Une

notons _{eo, ... ,}

_ep&#x3E;

un

cylindre

de

longueur

_{p +} 1 de D. Les

cylindres

de

D et ceux de S2 sont liés _par la relation suivante.

Proposition

6.1. Soient a E ,A et Pour tout n

lak(a)l,

il existe un

unique

chemin de

longueurs

k de

A,, étiqueté

_{eo, ... , ek-l et} arrivant en

l’état a, tel que

r(

C _{ep, ... ,}

Preuve. L’unicité du chemin est évidente. L’existence du chemin se _prouve

par

l’algorithme glouton

suivant.

Si _ak = _a et nk = _n, on a _nk

lok (ak) 1 -

Soit le

_plus

_{long préfixe}

de

Q(ak)

tel _{que nk et} défini _par =

Pk-lak-lSk-1-Alors

_(Pk-1,

_ak-1,

_Sk-1)

_étiquette

une arête de l’automate _{entre ak-l et ak,}

.. - - -.. J

Par choix de Pk-1 on a ce

_qui

assure

_qu’on

_peut

réitérer le _processus et obtenir une suite de lettres _ai,

_{d’étiquettes}

(p2,

_a2,

s2)

de l’automate _{entre a2} et ai+1, et

d’entiers ni

vérifiant ni =

1

tels _{que :}

La

_{surjectivité}

de r

_permet

de

_préciser

la

_proposition

6.1 en identifiant

les

_préimages

des

_cylindres

de D.

Corollaire 6.1. Soit

_{(ei)i« _ (pi,}

ai,

Si)ik

un chemin de

longueur

k + 1 de l’automate des

_{préfixes-suffixes.}

Si n =

’ak(pk)1

+ ~ ~ ~ + +

_IPOI,

alors

l’union étant

_disjointe.

Corollaire 6.2. Soit a une lettre de A telle _que

a(a) =

av avec v E

,~4~

Alors _{pour tout} entier n, il existe dans

Aa

un

_unique

cherrtin arrivant en

a noté

(po,

_ao,

so)

...

(Pk-1,

ak-l,

Sk-1),

avec e, tel que n s’écrive :

On retrouve

_ici,

comme cas

_particulier,

la

_{décomposition}

définie dans

[4]

d’un entier n dans la "base" de numération associée au

_point

fixe d’une

de

_[4]

et les échelles de numération associées à une substitution comme des

structures

_{sous-jacentes}

à la

_dynamique

de la désubstitution 0 sur SZ.

Les

_cylindres

_{eo, ... , ek-,&#x3E; de}

_longueur

k forment une

_partition

géné-ratrice

_canonique

de D.

_{L’injectivité}

de

_r,

sauf sur un ensemble

dénom-brable,

permet

de remonter cette

_{partition génératrice}

en une

_partition

de

0,

constituée des

_préimages

des

_cylindres

de

_D,

c’est-à-dire les sn Cette

_partition

n’est _pas

_topologique,

dans la mesure où il est nécessaire d’isoler un nombre dénombrable de

_{points qui}

ne sont _pas

_séparés

_par la

partition.

Ce résultat

_généralise

celui obtenu dans

_[5],

où les auteurs définissent

une

partition

topologiquement génératrice

dans le cas d’une substitution

propre.

Proposition

6.2. Soir a une substitution

_primitive

et Q le

_système

sub-stitutif

associé à a.

Pour tout soit

_{Ak =}

n E

_N,

a E

_A,

n Les

Ak

forment

une suite de

partitions

génératrice

en mesure.

Plus

_{précisément,}

il existe un ensemble

N

dénombrable tel _{que pour tout}

entier

_k,

_{S~ ~}

J1Î

= où l’union _est

_disjointe.

Pour _toute suite avec

Ck

E

_Ak,

_nCk

est réduit à 0 ou 1

_point

ou bien consiste en

un nombre

_fini

de

_points

de

N.

Preuve. Soit

_11~

_{pour tout}

_k,

des sous-ensembles

_appartenant

à chacune des

_partitions.

_D’après

la

_proposition

_6.1,

est inclus dans

un

_unique

_cylindre

de D de

_longueur

k.

Ainsi,

est inclus dans l’intersection de

_cylindres

de

_longueur

croissante de

_{D, qui}

soit est

_vide,

soit contient un

unique

élément de D. Dans le cas non

_vide,

on a

Soit

N

l’union dans Q des orbites des

_points

_périodiques

pour o. Selon

le théorème

_5.2,

si e E

_D,

est vide. Si e E

_{D B}

_De,

est

réduit à une

_point.

Si e E

_D,,

est fini et inclus dans

N.

La suite de

_{partitions ~1~}

_sépare

ainsi tout

_point

de l’ensemble de mesure

pleine n B

N.

D

Concernant les

_{partitions Ak ,}

on notera que pour tout

Ck

E

_1~~

et

_Ck+l

E

est inclus ou strictement

_disjoint

de

Ck.

Application Reprenons l’exemple

de la substitution u : 1 H

_21,

2 H

13,

3 r-t 1.

_L’objectif

est de

_représenter

D par un

_compact

de C sur

_lequel

le successeur

_{s’interprète}

comme un

_échange

de 3 morceaux. Le

_polynôme

caractéristique

de sa matrice d’incidence est

X3 - X2 - X -

1

_(voir

_[1]

pour

plus

de

détails).

Notons a une racine de module inférieur à 1. Soit

et soit la fonction

, , . , ,

définie _par

FIGURE 3. Fractal de

_Rauzy

_{pour u :}

On vérifie que

et _que les

_images

des

_cylindres

_.~Z

=

p(1),

_pour i =

l, 2, 3,

sont

disjointes

_en mesure dans le

plan. L’image 0

(cf.

figure

3),

_qui

a une structure

auto-similaire,

est ainsi stable _par

_l’échange

de morceaux défini sur chacun des

~Z

par z H z +

_5(i).

_{L’application}

_p étant

_injective

en _mesure, on obtient

bien _que le

_support

du sous-shift D muni de

_{l’application}

successeur T est

conjugué

en mesure à un

échange

de morceaux dans le

_compact

,~’.

Enfin le fractal .~’ se

_projette

sur le tore de sorte _que les

_projections

des

Ô(i)

soient

_égales.

Ainsi le

_{système dynamique}

_{(D, 8)}

admet _pour facteur

une translation du tore

’li~ .

Cet

_exemple

est

_{généralisé}

dans

_[1].

Plus

_{précisément,}

à toute substitution

_primitive

de

_{type Pisot,}

sont

as-sociées deux

_{représentations géométriques explicites}

des

_systèmes

dynami-ques

(D, T)

et

_{(Q, S),}

l’une est une translation minimale sur un

_tore,

l’autre

est un

_échange

de morceaux euclidien. Les

propriétés

de r démontrées ici

permettent

de _{prouver que} la

_{représentation}

_par un

_échange

de morceaux

est

_injective

en mesure

lorsque

la substitution vérifie une condition

combi-natoire.

Bibliographie

[1] V. _CANTERINI, A. _SIEGEL, Geometric _{representation of primitive} substitutions _of Pisot type.

[2] E. M. _COVEN, M. S. KEANE, The structure _of substitution minimal sets. Trans. Amer. Math. Soc. 162 _(1971), 89-102.

[3] F. M. _DEKKING, The _{spectrum of dynamical systems arising from} substitutions of constant

length. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 41 _(1978), 221-239.

[4] J.-M. _DUMONT, A. _{THOMAS, Systèmes} de numération et _{fonctions fractales relatifs} aux

substitutions. Theoret. _Comput. Sci. 65 _(1989), 153-169.

[5] F. _DURAND, B. HOST, C. SKAU, Substitutional _{dynamical systems,} Bratteli diagrams and dimension groups. Ergodic Theory Dynam. Systems 19 _(1999), 953-993.

[6] P. J. GRABNER, P. LIARDET, R. F. TICHY, Odometers and _systems of numeration. Acta Arith. 70 _(1995), 103-123.

[7] R. H. HERMAN, I. F. PUTNAM, C. F. SKAU, Ordered Bratteli _diagrams, dimension groups and topological dynamics. Internat. J. Math. 3 _(1992), 827-864.

[8] C. HOLTON, L. Q. ZAMBONI, Geometric realizations _of substitutions. Bull. Soc. Math. France

126 _(1998), 149-179.

[9] C. HOLTON, L. Q. ZAMBONI, Directed _graphs and substitutions. _Preprint, 1999.

[10] T. KAMAE, Linear expansions, strictly ergodic homogeneous cocycles and _fractals. Israel J. Math. 106 _(1998), 313-337.

[11] D. LIND, B. _MARCUS, An introduction to _{symbolic dynamics} and _{coding. Cambridge} Uni-versity Press, Cambridge, 1995.

[12] A. N. _{LIVSHITS, Sufficient} conditions _for weak mixing of substitutions and of stationary

adic transformations. Mat. Zametki 44 _(1988), 785-793. English translation: Math. Notes

44 _(1988), 920-925.

[13] A. MAES, Morphic predicates and applications to the _{decidability of} arithmetic theories. Thèse de doctorat, Université de _{Mons-Hainault,} 1999.

[14] J. C. _MARTIN, Minimal flows arising from substitutions _of non-constant _length. Math.

Sys-tems _{Theory 7 (1973),} 73-82.

[15] B. _MOSSÉ, Reconnaissabilité des substitutions et _complexité des suites _{automatiques.} Bull. Soc. Math. France 124, (1996), 329-346.

[16] P. NARBEL, The boundary of iterated morphisms on _{free semi-groups.} Internat. J. Algebra

Comput. 6 _(1996), 229-260.

[17] M. _QUEFFÉLEC, Substitution dynamical systems-spectral analysis. Lecture Notes in Math-ematics _{1294, Springer-Verlag, Berlin,} 1987.

[18] G. RAUZY, Nombres _algébriques et substitutions. Bull. Soc. Math. France 110 _(1982), 147-178.

[19] G. _RAUZY, Rotations sur les _groupes, nombres _{algébriques,} et substitutions. Dans Séminaire de Théorie des _Nombres, 1987-1988 _{(Talence, 1987-1988),} Univ. Bordeaux _{I, Talence,} 1988.

Exp. No. 21.

[20] V. F. _SIRVENT, Modelos _geométricos asociados a substituciones. _Trabajo de ascenso, Uni-versidad Simón _Bolivar, 1998.

[21] A. M. _{VERSHIK, Uniform algebraic approximation of shift} and _{multiplication} operators.

Dokl. Akad. Nauk SSSR 259 _(1981), 526-529. English translation: Soviet Math. Dokl. 24

(1981), 97-100.

Vincent CANTERINI CESAME Bâtiment Euler Université _Catholique de Louvain Avenue G. Lemaire, 4 1348 Louvain-la-Neuve Belgique E-mail : canteriniOanma.ucl.ac.be Anne SIEGEL IRMAR Bât. 22-23 Université Rennes 1 Campus de Beaulieu 35042 Rennes Cedex France E-mail : _{siegelbaths.univ-rennesl.fr}