Modélisation de la convection à faible nomre de Prandtl

MINISTÈRE DE L’ENSEIGNEMENT SUPÉRIEUR ET DE LA RECHERCHE SCIENTIFIQUE

UNIVERSITÉ MENTOURI – CONSTANTINE FACULTÉ DES SCIENCES DE L’INGÉNIEUR

DÉPARTEMENT DE GÉNIE MÉCANIQUE

N° d’ordre :

Série :

MÉMOIRE

Présenté pour obtenir le diplôme de Magister

En Génie Mécanique

MODÉLISATION DE LA CONVECTION A FAIBLE

NOMBRE DE PRANDTL

OPTION :

Thermo-fluides

Par :

DJIMLI Samir

Soutenu le : … /… /… Devant le jury :

Président : R. BESSAIH Prof. Université Mentouri – Constantine Directeur du Mémoire : M. KADJA Prof. Université Mentouri – Constantine Rapporteur : S. BENISSAAD M.C. Université Mentouri – Constantine Examinateurs : K. TALBI M.C. Université Mentouri – Constantine O. KHOLAI M.C. Université Mentouri – Constantine

DEDICACES

A mes chers parents, mes frères et

mes sœurs, mes amis et mes collègues

Remerciements

Je tien à exprimer ma reconnaissance à Messieurs M. KADJA et S.

BENISSAAD, d’avoir

diriger ce travail de recherche. Leurs suggestions, leurs conseils et leurs critiques m’ont permis l’élaboration de ce travail. Qu’ils soient rassurés de mes remerciements les plus respectueux.

Ma gratitude s’adresse à Mr R. BESSAIH, Professeur à l’Université Mentouri-Constantine, pour avoir accepter la présidence du jury. Je remercie vivement Mr K. TALBI Maître de Conférences à l’Université Mentouri-Constantine et Mr O. KHOLAI Maître de Conférences à l’Université Mentouri-Constantine, qui ont accepté de faire partie du jury.

J’adresse, également, mes remerciements à mes enseignants et collègues du Département de Génie Mécanique

SOMMAIRE Remerciement………...………..i Dédicaces………ii Sommaire………...…………...iii Nomenclature………..………...………..iv I. Introduction générale……….….……...1

Chapitre I : Généralités et Bibliographie

I.1 Généralité……….3

I.1.1 Convection………..…3

I.1.1.1 Convection dans les cavités……….4

I.1.1.1.1 Cavité avec gradient de température vertical………4

I.1.1.1.2 Cavité avec gradient de température horizontal………5

I.1.2 Les fluides à faible nombre de Pr (les métaux Liquide)……….6

I.1.2.1 Propriétés de quelques métaux liquides………...7

I.1.2.1.1 Le Gallium………7

I.1.2.1.2 Le Mercure……….. ……….7

I.1.2.2 Applications des métaux liquides………8

I.1.2.2.1 Les méthodes d'élaboration des monocristaux………..8

I.1.2.2.2 Refroidissement des composants électroniques………..11

I.2 Synthèse bibliographique………..12

Chapitre II : Modèle Mathématique et Présentation du Fluent

II.1 Modèle Mathématique………16

II.1.1 Configuration………16

II.1.2 Equations gouvernantes………17

II.1.3 Modèle mathématique du problème étudié………...18

II.1.3.1 Equations dimensionnelles……….………...18

II.1.3.2 Equations adimensionnelles………...20

II.2 Présentation des logiciels Gambit et fluent...23

II.2.1 Préprocesseur Gambit……….23

II.2.2 Code Fluent……….27

II.2.3 Condition aux limites utilisée par le code FLUENT………...………29

II.2.4 Modelé Numérique utilisée par le code FLUENT………..30

Chapitre III : Résultats et discussions

III. 1 Validation du code……….…………...36

III.1.1 Régime stationnaire……….……….36

III.1.2 Régime instationnaire………...42

III.2 Influence du nombre de Prandtl………..………….44

III.3 Etude du Mercure………..50

III.3.1 Simulation en 2D……….50

III.3.1.1 influence du nombre de Grashof (due à la variation du gradient de température ΔT)………50

III.3.1.2 Influence du nombre de Rayleigh ….……….…54

III.3.1.3 Régime instationnaire ….………...……….…60

III.3.1.4 Régime turbulent……….62

III.3.1.5 Influence du rapport d'aspect………..64

III.3.2 Simulation en 3D……….69

Conclusion

Conclusion………71

Références

Références………...………...….…….73 Résumes………...………...….…….75

Annexe

Nomenclature

A Rapport d'aspect, A=L /H

Ap,Ae,Aw,As,An Coefficients de l'équation algébrique de transport discrétisée.

A(│P│) Fonction de schéma numérique.

Cp Chaleur spécifique à pression constante, [J/kg.K]

De,Dw,Dn,Ds Flux diffusifs aux interfaces e, w, n,s de l'équation de transport

discrétisée.

Fe ,Fw,Fn,Fs Flux convectifs aux interfaces e, w, n,s de l'équation de transport

discrétisée.

Fi Force suivant la direction i par unité de volume, [N.m-3]

g Accélération de la pesanteur, [m.s-2]

H Hauteur de la cavité, [m]

i,j Coordonnées logiques des points.

L Longueur de la cavité, [m]

Nu Nombre de Nusselt.

P' Pression hydrodynamique, [Pa]

P Pression totale, [Pa]

Pr Nombre de Prandtl, Pr = ν/α

Ra Nombre de Rayleigh,

Ra= gβΔTH

4

/ναL

Gr Nombre Grashof, Gr=Ra/Pr

S Terme source de l'équation de transport discrétisée.

T Température dimensionnelle, [K]

t Temps dimensionnel, [s]

U,V Composantes de la vitesse adimensionnelles.

u,v Composantes de la vitesse dimensionnelles, [m.s-1]

X,Y Coordonnées cartésiennes adimensionnelles.

Symboles grecs

α Diffusivité thermique, [m2.s-1]

β Coefficient d'expansion thermique à pression constante, [K-1]

λ Conductivité thermique, [W.m-1.K-1] Φ Variable dépendante. μ Viscosité dynamique, [kg.m-1.s-1] υ Viscosité cinématique, [m2.s-1] θ Température adimensionnelle. ρ Masse volumique, [kg.m-3] τ Temps adimensionnel.

ψ Fonction de courant adimensionnelle.

Δτ Incrément du temps adimensionnel.

ΔT Différence de température, [K] Γ Coefficient de diffusivité. Indices et exposants c Paroi chaude. cr Valeur critique. f Paroi froide.

nb Nœuds adjacents : Est, West, Nord et Sud (E, W, N, S)

* Valeur adimensionnelle.

Rouge chaude

INTRODUCTION GENERALE

L’utilisation de logiciels pour la résolution de problèmes physiques est de nos jours très fréquents. En effet, dans la plus part des ces problèmes, surtout la résolution de phénomènes (transfert de chaleur, rayonnement, changement de phase…) couplés à la mécanique des fluides n’est possible que sous certaines hypothèses simplificatrices qui ne permettent pas de faire une étude plus réelle des phénomènes physiques observés expérimentalement.

L’objectif de ce travail est de faire une étude de la convection naturelle dans une cavité rectangulaire avec FLUENT ; contenant un fluide à faible Prandtl (métal liquide) et soumise à un gradient horizontal de température. La convection naturelle dans les métaux liquides a fait l'objet d'études menées par les métallurgistes et les ingénieurs des réacteurs nucléaires parce que les métaux liquides sont un excellent milieu de transfert de chaleur. Puis faire une investigation pour observer les limites du logiciel.

L'intérêt pour l'étude de ce problème est également son implication dans la croissance des cristaux destinés à la fabrication des semi-conducteurs. En effet, l'apparition de la convection pendant la croissance cristalline peut conduire à des inhomogénéités qui conduisent à des striations et à des défauts qui affectent la qualité des cristaux obtenus par les techniques de Bridgman et de Czochralski. Les oscillations de température dues aux instabilités de l'écoulement dans les métaux liquides induisent également un refroidissement non uniforme au niveau du front de la solidification. Dans ce cas, la convection est étudiée dans le but de l'éviter ou de la réduire.

En plus de cet aspect pratique, l'étude des écoulements convectifs dans les métaux liquides présente un intérêt certain du point de vue recherche fondamentale. En effet ce type de fluides opaques à basses températures de fusion (par exemple 302,8 K pour le gallium) sont des fluides à bas nombre de Prandtl (Pr) et leurs comportements lorsqu'ils sont soumis à des gradients de température sont assez différents de ceux observés dans les fluides à haut nombre de Pr (tel que l'eau).

De nombreuses études ont été menées ces dernières années et qui ont permis de mieux comprendre les comportements des métaux liquides lorsqu'ils sont sollicités thermiquement.

Les résultas expérimentaux de la convection naturelle et de transfert de chaleur dans les métaux liquides sont très limités à cause de la difficulté à mener des mesures dans ce type de fluides opaques, Seuls le nombre de Nusselt moyen ou la variation temporelle de la température sont disponibles dans la littérature. Ces résultats ont été corrélés en fonction des nombres de Grashof ou de Rayleigh.

Notre étude est présentée en trois chapitres :

Le premier chapitre est consacré à des généralités sur les métaux liquides, leurs descriptions ainsi que leurs applications. Une synthèse bibliographique sur la convection naturelle dans les cavités contenant des métaux liquides est également présentée.

Le deuxième chapitre présente la modélisation du problème et présentation de code du calcule Fluent

Le dernier chapitre est consacré à la présentation des résultats numériques avec des interprétations et comparaisons avec les résultats contenus dans la littérature, Dans le cadre de cette étude, on a considéré l'influence des paramètres suivants :

• Le type de fluide utilisé (gallium, mercure, eau, air), • Le gradient de température appliqué (nombre de Grashof), • Le confinement de la couche fluide (rapport d'aspect), Sur:

• Le taux de transfert de chaleur par convection (nombre de Nusselt), • Les structures convectives qui apparaissent,

I. Généralité et Bibliographie

I.1 GENERALITE

I.1.1 Convection

La convection caractérise la propagation de la chaleur dans un fluide, gaz ou liquide, dont les molécules sont en mouvement (Figure1.1).

Imaginons un solide baignant dans un fluide en mouvement. Si le solide et le fluide ne sont pas à la même température, de la chaleur est échangée entre le solide et les particules fluides qui sont à son contact. Cet échange se fait par conduction. Mais la particule de fluide, dès qu’elle a échangé de la chaleur, se déplace et est remplacée, au contact du solide, par une autre particule. Par ailleurs, la particule fluide initiale rencontre, au cours de son déplacement, d’autres particules fluides avec lesquelles elle échange de la chaleur par conduction. Le mécanisme élémentaire de transfert de chaleur est la conduction thermique mais le phénomène global, qui est la convection thermique, résulte de la combinaison de cette conduction avec les mouvements du fluide qui obéissent à des lois spécifiques. Deux types de convection sont généralement distingués :

La convection naturelle dans laquelle le mouvement résulte de la variation de la masse volumique du fluide avec la température ; cette variation crée un champ de forces gravitationnelles qui conditionne les déplacements des particules du fluide.

La convection forcée dans laquelle le mouvement est provoquée par un procédé mécanique indépendant des phénomènes thermiques ; c’est donc un gradient de pression extérieur qui provoque les déplacements des particules du fluide. L’étude de la transmission de chaleur par convection est donc étroitement liée à celle de l’écoulement des fluides.

Les applications du transfert de chaleur par convection sont beaucoup trop nombreuses pour que l’on puisse envisager de les citer toutes. Elles interviennent chaque fois que l’on chauffe ou que l’on refroidit un liquide ou un gaz, qu’il s’agisse de faire bouillir de l’eau dans une casserole, du radiateur de chauffage central, du radiateur associé au moteur d’une voiture ou de l’échangeur dans un procédé, évaporateur ou condenseur. La convection s’applique même si la surface d’échange n’est pas matérialisée par une paroi, ce qui est le cas des condenseurs par mélange ou des réfrigérants atmosphériques.

I.1.1.1 Convection dans les cavités

Une revue de la littérature montre que la cavité rectangulaire est un exemple de configuration extensivement étudiée [1]…[5]. Les travaux s’y rattachant sont en fait si nombreux et variés qu’il devient impensable de les citer tous. De plus, malgré cette abondance apparente, le problème reste loin d’être épuisé. La poursuite de la recherche se rapportant au cas de la cavité rectangulaire apporte souvent des renseignements précieux et montre que les connaissances déjà acquises restent loin d’être suffisantes pour prédire correctement l’état de l’écoulement du fluide et le transfert de chaleur dans de telles configurations. Aussi, la recherche actuelle témoigne-t-elle de la carence relative des études se rapportant aux fluides à faible nombre de Prandtl.

I.1.1.1.1 Cavité avec gradient de température vertical

La cavité horizontale chauffée par le bas et refroidie par le haut correspond à la configuration de la convection de Rayleigh-Bénard qui traite de la stabilité et le mouvement d'un fluide, confiné entre deux plaques horizontales, maintenues à des températures uniformes et distinctes et soumis au champ de la gravitation. La convection de Rayleigh-Renard a une longue et riche histoire, elle a été étudiée durant des décennies aussi bien pour ses différentes applications industrielles que du point de vue recherche fondamentale. Le mécanisme de base de cette convection est comme suit (Figure 1.2)

Une perturbation fait monter rapidement une particule de façon qu'elle garde sa masse volumique constante (Figure1.2). Deux cas peuvent se produire :

- Si ρ2> ρ1, la force d'Archimède est inférieure à son poids, la particule redescend, le mouvement est stable.

- Si ρ2 < ρ1, la force d'Archimède est supérieure à son poids, la particule continue à monter, le mouvement est instable. Au delà d'une valeur critique de l'écart de température, des rouleaux contra - rotatifs, d'axes horizontaux apparaissent au sein du fluide (Figure 1.3)

.

I.1.1.1.2 Cavité avec gradient de température horizontal

Dans cette configuration, les parois verticales sont chauffée et refroidie, alors que les parois horizontales sont considérées comme adiabatiques (Figure 1.4). L'écoulement est alors monocellulaire avec le fluide ascendant le long de la paroi chaude et descendant suivant la paroi froide. Pour Ra ≤ 103, le transfert de la chaleur est principalement par conduction dans le fluide et le nombre de Nusselt est égal à l’unité [6]. C'est cette dernière configuration qui fera l'objet de notre étude avec des cavités qui contiennent un fluide à faible Pr (métal liquide) comme fluide de convection.

Figure (1.3) : Schéma représentant les rouleaux de la convection de Rayleigh-Bénard

ρ

1

ρ

2

Figure (1.2) : Schéma représentant la particule et le mécanisme de base de la

I.1.2 Les fluides à faible nombre de Pr (les métaux Liquide)

Pour avoir une idée de la différence entre les fluides usuels, ayant des Pr élevés, et les métaux liquides à bas Pr ; nous donnons (Tableau (I.1)) à titre d'exemple les caractéristiques d'un liquide à haut nombre de Pr (eau, Pr =1,72) et d'un métal liquide à bas nombre de Pr (sodium, Pr = 0,0072).

Tableau (I.1) : Propriétés Thermo physique de l’eau et du sodium [7].

Ces caractéristiques ne diffèrent fortement que par la conductivité et la viscosité et, corrélativement, par le nombre de Prandtl.

Au sein de la classe des métaux liquides, les caractéristiques peuvent être très variables (voir en Annexe les figures (1, 2, 3, 4, 5,6)). Mais la conductivité thermique λ est toujours beaucoup plus grande que celle des fluides ordinaires et Pr<<l.

Les coefficients de convection des métaux liquides sont pour les mêmes surfaces d'échange et les mêmes écarts de température, beaucoup plus élevés que ceux des autres fluides ; d'où leur utilisation dans les applications qui font intervenir de très fortes densités de flux (refroidissement des réacteurs nucléaire notamment) [7].

ρ μxl04 _λ Cp βx104 νx107 Pr Eau à 100°C 958 2,81 0,68 4205 7,42 2,8 1,72 Na à 200°C 1130 4,4 81,5 1335 2,57 3,9 0,0072 Paroi Adiabatique Paroi Froide Paroi Adiabatique Paroi Chaude

Figure (1.4) : Schéma de la convection dans une cavité avec gradient de

I.1.2.1 Propriétés de quelques métaux liquides I.1.2.1.1 Le Gallium

Généralement, la bauxite est considérée comme la meilleure source de la production de gallium. Le Gallium est un métal liquide qui a un bas nombre Prandtl (Pr = 0,025 à 300K) et a un point de fusion de 29,78°C.

Le Gallium a plusieurs propriétés qui lui donnent l’avantage, sur le silicium dans beaucoup d'applications. Ces avantages sont particulièrement appréciés dans les applications de l'optoélectronique. Le gallium arsenic (GaAs) est ainsi utilisé pour fabriquer des diodes de laser, applications pour lequel le silicium ne peut être utilisé. Le GaAs et le silicium peuvent convertir la lumière en énergie électrique, ce qui les rend utiles pour la fabrication des photodiodes et des cellules solaires, mais le GaAs peut convertir plus de lumière disponible en énergie électrique.

Le gallium arsenic est environ dix fois plus résistant à la radiation que le silicium. Cette résistance est essentielle dans les utilisations dans l'espace où les composants sont exposés aux intenses radiations du soleil [8,16].

I.1.2.1.2 Le Mercure

En comparaison avec d'autres métaux, le mercure et ses minerais sont rares dans la croûte terrestre.

Le mercure élémentaire possède les caractéristiques d'un métal lourd et précieux. Il a de grandes conductivités électrique et thermique et une faible pénétrabilité à la lumière. II est malléable à l'état solide. Son poids spécifique est plus élevé que celui du plomb et il est relativement résistant aux influences chimiques. Propriété particulière du mercure, il se présente sous forme liquide à des températures beaucoup plus basses que les autres métaux, le point de fusion se situe à -38,84°C et la température d'ébullition à 356,5°C. Il est ainsi le seul métal qui est liquide à température ambiante. Il possède en outre un coefficient de dilatation thermique élevé, proportionnel à la température entre 0 et 100°C. Les domaines d'utilisation du mercure et de ses composés sont nombreux et très divers : instruments de mesure et de contrôle, fabrication des tubes fluorescents, etc.…Le grand inconvénient du mercure est qu'il est toxique, ce qui a conduit à une forte diminution de son utilisation au cours des dernières années [9 ,16].

L'oxyde mercurique qui existe sous deux variétés (jaune et rouge) d'une même espèce cristalline est très peu soluble dans l'eau, il se décompose sous l'effet de la lumière ou de hautes températures en mercure et oxygène.

Le sulfure mercurique qui existe sous deux formes cristallines allotropies (rouge et noire) est pratiquement insoluble dans l'eau.

Le chlorure mercurique, qui se présente sous forme de cristaux nacrés à saveur métallique désagréable, est facilement soluble dans l'eau, l'oxyde de d’éthyle et l'acétate d'éthyle, très soluble dans les alcools et l'acétone. Les solutions aqueuses sont légèrement acides par suite de l'hydrolyse du sel. Les cristaux émettent des vapeurs dès la température ordinaire.

Le sulfate mercurique, poudre cristalline blanche noircissant à la lumière, s'hydrolyse dès qu'il est en contact avec l'eau, avec formation de sulfate basique jaune, insoluble et d'acide sulfurique.

I.1.2.2 Applications aux métaux liquides

Quelques auteurs se sont intéressés aux problèmes de la convection naturelle dans une cavité rectangulaire contenant du métal liquide. Ces travaux étaient principalement justifiés par la nécessité de contrôler la croissance des cristaux destinés à la fabrication des semi-conducteurs ou d'améliorer le refroidissement des composants électroniques [10,16].

I.1.2.2.1 Les méthodes d'élaboration des monocristaux

Semi-conducteur est le nom donné à un matériau caractérisé par des propriétés particulières, il s'agit d'un cristal qui conduit l'électricité mieux qu'un isolant et moins bien qu'un métal.

Dans la vie quotidienne, le terme semi-conducteur évoque l'ensemble des composants, dispositifs et même des systèmes microélectroniques ou électroniques, fabriqués à partir d'éléments semi-conducteurs.

Le principe des méthodes d'élaboration des monocristaux est de provoquer la solidification progressive d'une masse plus ou moins grande de métal liquide à partir d'un cristal « germe » unique [11,16]. La plupart des cristaux élaborés sont produits par les méthodes de Bridgman et de Czochralski qui vont être brièvement décrites dans ce qui suit :

a. La méthode de Bridgman. On distingue deux types :

i/ Technique de bridgman-stockbarger verticale

Le principe de la technique de Bridgman-Stokbarger est illustré dans la figure (1.5.a), avec un exemple schématique de la réalisation pratique dans la figure (1.5.b). Le métal est fondu dans un creuset scellé de verre ou de quartz. L'ampoule se déplace dans un four dans lequel un gradient de température est établi. Elle passe ainsi progressivement d'une zone chaude au-dessus du point de fusion Tm dans une zone froide au-dessous du point de fusion.

Le composé est solidifié progressivement à partir de l'extrémité inférieure de l'ampoule. En pratique, on utilise un four tubulaire vertical à deux zones de chauffage éventuellement séparées par un déflecteur thermique [11,12,16].

ii/ Technique de bridgman-stockbarger horizontale

Le principe de la technique de bridgman-stockbarger horizontale est semblable à celui de la technique verticale. Le matériau en fusion est contenu dans un creuset en forme de « bateau allongé ». Il est progressivement solidifié à partir d'une extrémité (figure 1.6). Cette technique est utilisée, par exemple, pour la production industrielle de monocristaux de gallium arsenic dont le diamètre peut atteindre plusieurs centimètres [11,12,16].

b. Méthode de Czochralski

Le procédé impliquant cette méthode est souvent désigné sous le nom d'étirage de cristaux. Pour un matériau donné, le premier procédé décrit par Czochralski en 1918 est encore aujourd'hui la méthode de croissance de cristaux la plus rapide.

L'étirage de cristaux est également la méthode qui produit un cristal de bonne qualité du point de vue pureté et homogénéité. Actuellement, la moitié des cristaux de haute qualité sont produits en utilisant la méthode de Czochralski.

Par exemple la plupart des cristaux de silicium utilisés en microélectronique sont produits par cette méthode. Les cristaux les plus courants ont généralement des diamètres d'au moins 50 mm, les plus gros peuvent atteindre 200 mm de diamètre. Le principe du procédé est illustré dans la figure (1.7) et se déroule de la manière suivante : du silicium polycristallin est chauffé dans un creuset de verre de silice, au dessus du point de fusion du silicium,

Tm =1420OC. Après homogénéisation de la masse fondue, un « germe » monocristallin est

plongé depuis le haut, partiellement fondu, puis retiré graduellement. La formation d'un étranglement par diminution du diamètre favorise l'élimination des défauts. Le diamètre du monocristal en croissance est ensuite augmenté par la réduction de la vitesse de tirage. Des monocristaux de diamètre de l'ordre de 15-20 cm et de 1-2 m de long sont ainsi fabriqués.

Les perfectionnements de la technique de tirage consistent à agir principalement sur les courants de convection dans le bain liquide. Ainsi, l'écoulement au voisinage de l'interface solide/liquide influence le processus de croissance et la qualité structurale du cristal. En plus des courants de convections naturels liés aux gradients de température et aux tensions superficielles, interviennent des convections forcées causées par les rotations respectives du cristal et du creuset, ainsi que par le tirage du cristal [11,12,16].

I.1.2.2.2 Refroidissement des composants électroniques

Dans un tout autre ordre d'idée, la miniaturisation croissante des circuits électroniques demande une dissipation de plus en plus efficace de la chaleur qui y est générée. Il s'agit en fait d'un des principaux obstacles à surmonter afin d'augmenter la puissance des ordinateurs et de l'électronique en général. Pour sa simplicité, le système de refroidissement actuellement le plus courant est la convection (naturelle ou forcée) en utilisant l'air ambiant. Un MCP

(a) (b) (c)

Germe Cou

Monocristal

Silicium fondu dans un creuset en verre de silice Figure (1.7) : Schéma de principe de la méthode de Czochralski

(matériau à changement de phase), peut alors absorber une grande quantité de chaleur en fondant, ce qui en fait une alternative très intéressante pour dissiper la chaleur émanant des composants électroniques. Étant donné que le phénomène de fusion se produit à l'intérieur d'une plage de température étroite, il est alors possible de contrôler la température de ces composantes. La quantité de chaleur dissipée serait aussi de beaucoup supérieurs à ce qu'il est possible d'obtenir en refroidissant les composants électroniques par l'air ambiant. II suffirait donc de juxtaposer à ces composants une enceinte de MCP qui permettrait de dissiper l'énergie produite par les sources de chaleur pour un temps d'utilisation donné. Ce système est particulièrement bien adapté à l'utilisation cyclique d'équipements électroniques. Le MCP peut alors céder sa chaleur (en se ressolidifiant) pendant la période d'inactivité [10,16].

I.2 SYNTHESE BIBLIOGRAPHIQUE

Après cette préface, nous exposons chronologiquement quelques travaux disponibles dans la littérature qui traite l’écoulement avec transfert de chaleur par convection naturelle, dans les enceintes rectangulaires.

Stewarl et Weinberg [1] furent parmi les premiers à étudier la convection naturelle au sein d'une cavité rectangulaire bidimensionnelle avec des parois horizontales isolées, et des parois verticales isothermes, pour des nombres de Prandtl qui varient de 0,0127 (étain liquide) à 10,0 (eau) avec un nombre de Grashof qui varie de 2x103 à 2x107 en (2D). Ils ont comparé le comportement de l'écoulement dans plusieurs types de fluides, et ont démontré que le comportement de l'écoulement dans les métaux liquides est différent de celui des fluides usuels.

Stewarl & Weinberg [2] ont étudié expérimentalement la distribution de température et le transfert de la chaleur dans une cavité rectangulaire remplie d'étain liquide.

Viskanta et al. [3] ont développé un modèle numérique à trois dimensions pour la convection naturelle dans un métal liquide (Pr =0,02) dans une cavité et ils ont comparé leurs résultats avec des résultats expérimentaux.

Wolff et al. [4] ont étudié expérimentale et numérique du transfert de la chaleur dans des cavités verticales en 2D, remplies de métaux liquides. Les expériences ont été menées dans deux enceintes différentes avec deux parois latérales opposées qui sont maintenues à des températures différentes et les autres parois isolées. L'étain et le gallium ont été utilisés comme fluides de convection. Pour plusieurs valeurs des paramètres de contrôles (Gr, Ra.), ils ont trouvé que la convection naturelle dans les métaux liquides est considérablement différente de celle dans les fluides à haut nombre de Prandtl. L'écoulement est alors caractérisé par une grande cellule de convection dans Le centre et de petites cellules de circulation dans les coins de la cavité. Leurs résultats numériques n'étaient pas en accord avec les mesures expérimentales, en particulier au centre de la cavité, le besoin pour des simulations numériques à trois dimensions précises s'est fait donc sentir. Malgré que Viskanta et al. [3] ont menés des simulations en 3D, ils ont mentionnés que leurs résultats numériques étaient préliminaires et ont besoin d'un raffinement du maillage. Wolff et al. [4] ont également insisté sur le besoin de simulations numériques à trois dimensions plus précises.

Derhail & Koster [5] ont simulé numériquement et en 3D l'écoulement dans une cavité avec le gallium liquide comme fluide de convection. Ils ont comparé les résultats numériques obtenus aux résultats expérimentaux qu'ils ont obtenus par la technique de la radioscopie.

Juel et al. [13] ont mené une étude expérimentale et numérique en 3D qui a montré l'importance de l'effet de la troisième dimension sur l'écoulement convectif du gallium liquide.

Les études expérimentales dans des cavités avec des parois latérales chauffées différemment et remplies de métal liquide, avec de hauts nombres de Ra, sont très limitées. La plupart des études ont été menées en régime laminaire. Wolf et al. [4] ont mesuré les profils de température dans une cavité remplie d'étain liquide (Pr = 0,011) pour Ra=3,66x105. Leurs résultats ont montré que l'écoulement fluctue, mais aucune analyse supplémentaire n'a été menée pour vérifier si l'écoulement était turbulent ou non. Mohamad et Viskanta [14] ont examiné la convection naturelle turbulente de l'écoulement, dans des cavités avec des gradients de température horizontal et vertical, avec des fluides à bas nombre Prandtl. Ils ont montré des profils de température mesurés dans une cavité remplie de gallium (Pr =0,0208), pour Ra = 1,08x106. Des résultats en simulations numérique directe (DNS) et avec le modèle

k-ε en 2D ont été comparés aux résultats expérimentaux. Pour la cavité avec un gradient de température horizontal, les résultats du transfert de chaleur peuvent être corrélés en fonction du nombre de Boussinesq (B=Ra x Pr). Une corrélation a été suggérée pour l'écoulement turbulent pour les cavités de rapport d'aspect de 1 jusqu'à 1/6 et pour Ra> 5x103 et Pr allant de 0,022 à 0,005. Ils ont également trouvé que l'écoulement dans les cavités, chauffées différentiellement et avec un rapport de forme égal à l'unité, devient turbulent pour

B= 4,8xl03.

Wakashima et al. [15] ont obtenus numériquement une solution idéale dite «Benchmark» de la convection naturelle tridimensionnelle de l’air dans une enceinte cubique, chauffée différentiellement par les deux parois verticales et les autres sont adiabatiques. Les calculs ont été effectués pour trois nombres de Rayleigh 104 ,105 et 106. La méthode de résolution est TSM (time space method) proposée par Saitoh en 1991. Cette méthode est basée sur la discrétisation du quatrième ordre des termes spatiaux et troisième ordre en arrière des termes temporels. La stabilité numérique de cette méthode est assurée et le choix du pas de temps est arbitraire. Ce travail peut être utilisé pour valider les performances et l’exactitude de n’importe quelle méthode numérique.

Ibrir [16] a étudié la convection naturelle dans une enceinte rectangulaire de dimension 0,091x0,063 contenant du Mercure et soumise à un gradient horizontal de température a l’aide de code ANSYS (éléments fins). Pour plusieurs valeurs des paramètres de contrôles (Gr. Ra. A), elle a trouvée que la convection naturelle dans le Mercure est considérablement différente de celle dans les fluides à haut nombre de Prandtl (eau, air).

L’objectif de l’étude menée par Boutout [17] était la détermination des instabilités hydrodynamiques et thermiques qui apparaissent pour une certaine valeur du nombre de Rayleigh critique, Racr, lors du refroidissement à air d’un et de deux composants

électroniques, montés dans une enceinte rectangulaire, ayant un rapport d’aspect égale à 4 et aussi d’analyser l’effet de l’espace entre deux sources de chaleur et le rapport des conductivités thermiques (conductivité thermique du composant/conductivité thermique du fluide) sur la valeur de Racr. Cette étude permettra de donner des informations aux

expérimentateurs et industriels sur les valeurs de Racr et les différentes bifurcations obtenues

pour la géométrie considérée, afin d’optimiser le refroidissement et le prolongement de la vie des composants électroniques.

Ces dernières années, des études ont été menées sur la transmission de chaleur par convection naturelle en présence de champs magnétiques [18,19]. Un exemple de ces recherches, les travaux de Juel et al. [19], qui ont présenté les résultats d'une étude numérique sur les effets d'un champ magnétique sur la convection dans le gallium liquide. Le champ magnétique a été appliqué suivant une direction perpendiculaire à l'écoulement principal, ce qui a réduit la convection. Ils ont trouvé un bon accord entre les résultats numériques et expérimentaux. Ils ont montré aussi que les oscillations observées même à des gradients de températures élevés peuvent être supprimées par l'application du champ magnétique.

D'après cette recherche bibliographique, on a constaté que la plupart des études sur les métaux liquides dans les cavités, soumises à un gradient horizontal de températures ont été menées avec l'étain ou le gallium liquides comme fluide de convection. Le mercure qui n'a pas été considéré par ces études, fera ainsi l'objet d'une partie importante de notre travail.

II. Modèle Mathématique et Présentation du Fluent

Dans ce chapitre, nous présentons la configuration considéré dans cette étude ainsi que les équations gouvernantes et les conditions initiales et aux limites du phénomène physique étudié.

II.1 Modèle Mathématique

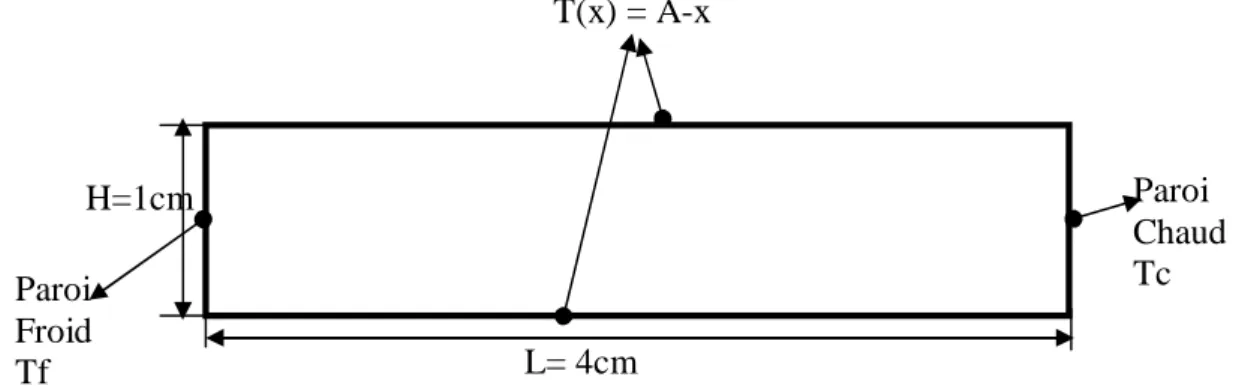
II.1.1 Configuration

Une enceinte rectangulaire de dimension L×H et de rapport d’aspect A=L/H=4 contient un fluide à faible nombre de Prandtl (mercury, gallium,….), chauffée différentiélement et les autres parois sont adiabatiques figure (2.1), avec un maillage de 200x50

Les équations régissant l'écoulement sont les équations de continuité, de Navier Stokes et l'équation d'énergie, qui expriment la conservation de masse, de quantité de mouvement et d'énergie. Pour une formulation simple du problème, nous allons considérer quelques approximations entre autres les approximations de Boussinesq.

Nous supposons alors que l'influence de la variation de la masse volumique n'est prise en compte que par l'intermédiaire des forces de volume; le fluide étant supposé newtonien, et incompressible Parois adiabatiques Paroi Froide Tf Paroi Chaude Tc L= 4cm H=1cm

II.1.2 Equations gouvernantes

Les équations qui gouvernent le phénomène de convection naturelle dans l’enceinte sont :

II.1.2.1 L’équation de continuité

Elle déduite du principe de conservation de masse et s’exprime sous forme tensorielle comme suit : 0 ) ( = ∂ ∂ + ∂ ∂ j j u x t ρ ρ (II.1) (j=1, 2, 3 : indice de sommation)

Pour un fluide Newtonien incompressible, l’équation (II.1) se réduit à : =0 ∂ ∂ j j x u (II.2)

II.1.2.2 Les équations de quantité de mouvement

D’après la deuxième loi fondamentale de la dynamique, le taux temporaire de changement de quantité de mouvement d’une particule fluide est égal à la somme des forces extérieures sur cette particule. L’équation de la dynamique sous forme tensorielle s’écrit alors comme suit :             ∂ ∂ + ∂ ∂ ∂ ∂ + ∂ ∂ − = ∂ ∂ + ∂ ∂ i j j i j i i j i j i x u u u x x p F x u u u t µ ρ ρ ) ( ) ( (II.3) Où : ) ( u_i t ρ ∂ ∂

: Représente le taux de variation de la quantité de mouvement.

) ( _{j i} j u u x ρ ∂ ∂

: Représente le taux nette de transport de quantité de mouvement suivant la direction i, par mouvement du fluide.

i

F : Représente les force du volume suivant la direction i.

i

x p ∂

∂

: Représente les forces dûe à la pression.

              ∂ ∂ + ∂ ∂ ∂ ∂ i j j i j x u u u

x µ : Représente les forces nettes de viscosité.

L’équation (II.3) représente la conservation de quantité de mouvement (équation de Navier Stokes) d’un fluide visqueux incompressible pour un régime transitoire.

II.1.2.3 L’équation de l’énergie

Elle est obtenue par l’application du premier principe de la thermodynamique. Cette équation pour un fluide Newtonien incompressible, s’écrit sous la forme suivante :

2 2 ) ( j j j x T T u x t T ∂ ∂ = ∂ ∂ + ∂ ∂ _α (II.4) Où : P C K ρ α = α : La diffusivité thermique. K : La conductivité thermique. P

C : La chaleur spécifique à pression constante.

II.1.3 Modèle mathématique du problème étudié

II.1.3.1 Equations dimensionnelles

Considérons l’équation de quantité de mouvement suivant y qui est parallèle au vecteur de gravité g. g y v y x v x y p vv y uv x t v _{µ µ ρ} ρ − ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ + ∂ ∂ − =       ∂ ∂ + ∂ ∂ + ∂ ∂ ) ( ) ( ) ( ) ( (II.5) Sachant que : gy p p' = +ρ₀ (II.6) Avec : : ' p Pression hydrodynamique. : p Pression totale. gy 0 ρ : Pression hydrostatique. On a encore : y p ∂ ∂ − = g y p 0 ' ρ + ∂ ∂ − (II.7) Rajoutant aux deux membres de l’équation (II.7) le terme (−ρg) on obtient :

y p ∂ ∂ − +(−ρg)= g y p ) ( ₀ ' ρ ρ − + ∂ ∂ − (II.8)

On écrit le terme droit de l’équation (II.8) sous la forme : g y p ) (ρ₀ −ρ + ∂ ∂ −

Négligeant la Pression P’ mais considérant que p est la pression hydrodynamique. On considère l’hypothèse de Boussinesq qui exige que :

0

ρ

ρ = Dans tous les termes des équations de mouvement, sauf dans le terme de gravité(−ρg), et en supposant que la masse volumique varie linéairement avec la température. En faisant un développement de Taylor d’ordre 1 de la masse volumique, on obtient :

) ( ) ( 2 0 0 T T T T _P − + ∆ ∂ ∂ + =ρ ρ ο ρ (II.8.a) ) ( ) ( 1 2 0 0 0 0 T T T T _P − + ∆ ∂ ∂ + = ρ ρ ο ρ ρ ρ (II.8.b) D’où: ) ( ₀ 0 0 =− T−T −ρ βρ ρ (II.9) Avec : T ∂ ∂ − = ρ ρ β 0 1 (II.10) β : Le coefficient d’expansion thermique.

En substituant l’équation (II.10) dans (II.8) on aura : ) ( ) ( _{0 0}g T T₀ y p g y p _{+ −} ∂ ∂ − = − + ∂ ∂ − ρ ρ ρ β (II.11) Avec les hypothèses du fluide Newtonien incompressible, l’hypothèse de Boussinesq est vérifiée, la convection naturelle bidimensionnelle se modélise alors comme suit :

• Equation de continuité : =0 ∂ ∂ + ∂ ∂ y v x u (II.12) • Equation de quantité de mouvement suivant la direction X :

₀ ( ) ( ) ( ) ( ) y u y x u x x p vu y uu x t u ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ + ∂ ∂ − =       ∂ ∂ + ∂ ∂ + ∂ ∂ _{µ µ} ρ (II.13)

• Equation de quantité de mouvement suivant la direction Y : 0 ( ) ( ) ( ) ( ) 0g (T Tf) y v y x v x y p vv y uv x t v − + ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ + ∂ ∂ − =       ∂ ∂ + ∂ ∂ + ∂ ∂ _{µ µ ρ β} ρ (II.14) • Equation de l’énergie : 0 ( ) ( ) ( ) ( ) y T K y x T K x vT y uT x t T Cp ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ =       ∂ ∂ + ∂ ∂ + ∂ ∂ ρ (II.15)

II.1.3.2 Equations adimensionnelles

Au lieu de parler des coordonnées x, y d’une particule à l’instant t, de composante u, v d’une vitesse et de pression p, nous utiliserons de nouvelles variables définies de la manière suivante : f c f T T T T H p P H v V H u U H t H y Y H x X − − = = = = = = = θ α ρ α α α τ 2 0 2 ) / ( , ) / ( , ) / ( ) / ( , , (II.16)

L’emploi des variables réduites dans les équations (II.12-II.15) permet de s’approcher de la réalité des phénomènes physiques, car leurs existences et leurs déroulements sont indépendants du système d’unités de mesure utilisé. Les équations adimensionnelles deviennent alors :

• Equation de continuité : =0 ∂ ∂ + ∂ ∂ Y V X U (II.17)

• Equation de quantité de mouvement suivant la direction X :       ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ + ∂ ∂ − = ∂ ∂ + ∂ ∂ + ∂ ∂ ) ( ) ( Pr Y U Y X U X X P Y U V X U U U τ (II.18)

• Equation de quantité de mouvement suivant la direction Y : Ra A Y V Y X V X Y P Y V V X V U V . . Pr . ) ( ) ( Pr θ τ _ +     ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ + ∂ ∂ − = ∂ ∂ + ∂ ∂ + ∂ ∂ (II.19) • Equation d’énergie : ( ) ( ) Y Y X X Y V X U ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ = ∂ ∂ + ∂ ∂ + ∂ ∂ θ θ θ θ τ θ (II.20) Avec :

ü A=L/H : le rapport d’aspect de la cavité ü Pr = ν/α : le nombre de Prandtl

ü Ra= gβΔTH4

/ναL : le nombre de Rayleigh

• Nombre de Prandtl :

Pr =

ν

/

α

= viscosité cinématique/diffusivité thermique

Le nombre de Prandtl est donc le rapport de 2 grandeurs ayant les mêmes dimensions, soient m2/s. La viscosité cinématique représente la diffusion de la vitesse (qui dépend des forces visqueuses) alors que la diffusivité thermique est la capacité du fluide de conduire de la chaleur. Aussi, Pr nous donnera une indication sur le rapport des effets thermiques et visqueux.

Avec un Pr donné, il est possible de savoir à quel type de fluides nous avons à faire.

• Nombre de Rayleigh:

Ra= gβΔTH

4

/ναL

• Gradient de température dans le champ de gravite (direction y) Le nombre de Rayleigh est directement lié à la convection.

La convection a lieu lorsque la poussée d’Archimède (due à la hausse de température) crée le mouvement du fluide.

Cependant, il faut que cette force d’Archimède soit assez grande pour contrer les forces visqueuses qui s’opposent au mouvement de la particule.

De plus, si l’équilibre thermique est atteint, il n’y a plus de force d’Archimède. La capacité d’une particule d’entrer en équilibre avec son environnement plus ou moins rapidement dépend de sa diffusivité thermique (α)

Ra nous donne le rapport entre le temps pour que la chaleur diffuse et celui pour que la particule entre en mouvement.

• Gradient de température dans une direction différente de la gravite

Dans ce cas, il y a convection naturelle quelque soit la valeur de Ra parce que les particules de fluide n’ont pas à lutter contre la force de gravité pour se déplacer.

II.1.4 Modèles de turbulence

II y'a quatre modèles de turbulence dans le code Fluent • Spalart-Allmaras (1 équation)

• K-epsilon (2 équations) • K-Omega (2 équations) • Reynolds Stress (5 équations)

Pour notre simulation en régime turbulent, on a utilisé le modèle K-epsilon standard à deux équations de transport qui est le plus utilisé et qui donne, en général, de bons résultats dans les configurations simples.

Les équations standard de l'énergie cinétique turbulente (K), et de son taux de dissipation (ε) ont respectivement la forme suivante :

Equation de l’énergie cinétique turbulente K :

ε σ ε σ ν µ µ ₋ ∂ ∂     ∂ ∂ + ∂ ∂ +         ∂ ∂         + ∂ ∂ = ∂ ∂ + ∂ ∂ k i i k k i k k k k k K x U x U x U k C x k k C x x k U t k 2 2 (II.21) Equation de la dissipation ε : k C x U x U x U k C C x k C x x U t _k i i k k i k k k k K 2 2 1 2 ε ε ε σ ν ε ε ε µ ε µ ₋ ∂ ∂       ∂ ∂ + ∂ ∂ +         ∂ ∂         + ∂ ∂ = ∂ ∂ + ∂ ∂ (II.22)

Les valeurs des coefficients du modèle k-ε standard sont :

II.2 Présentation des logiciels Gambit et fluent

II.2.1 Préprocesseur Gambit

C'est un préprocesseur intégré pour l'analyse en CFD (computational fluid dynamics), il permet de générer un maillage structuré ou non structuré en coordonnées cartésiennes, polaires, cylindriques ou axisymétriques, Il peut réaliser des maillages complexes en deux ou trois dimensions avec des mailles de type rectangle ou triangle.

Il peut être utilisé pour construire une géométrie et lui générer un maillage Eventuellement, une géométrie d'un autre logiciel de CAO peut être importée dans ce préprocesseur. Les options de génération de maillage de Gambit offrent une flexibilité de choix. On peut décomposer la géométrie en plusieurs parties pour générer un maillage structuré. Sinon, Gambit génère automatiquement un maillage non structuré adapté au type de géométrie construite. Avec les outils de vérification du maillage, les défauts sont facilement détectés.

-Interface de gambit

C'est une interface facile à manipuler .elle est décomposé en plusieurs parties

a. Fenêtre d'outils d'opération:

Chaque bouton de cette fenêtre correspond à une fonction bien définie figure (2.3)

a.l. Construction de la géométrie

Elle est créée à partir de points, de cotés, de surfaces, de volumes ou d'un groupe de tous ces éléments. On peut effectuer des opérations d'union, d'intersection, de séparation d'effacement de décomposition figure (2.4).

a.2. Génération de maillage

Cette fonction permet la génération de tous types de maillage, la manipulation du maillage généré et même la création d'une couche limite s'il y a lieu figure (2.5).

Figure (2.3)

Figure (2.5) Figure (2.4)

a.3. Incorporation des conditions aux limites

Plusieurs types de conditions aux limites sont disponibles selon le problème traité. A noter que l'espace maillé est pris par défaut comme étant fluide figure (2.6).

a.4. Boutons d'outils

Ils permettent de spécifier le système de coordonnée par exemple ou d'autres opérations spécifiques figure (2.7).

Figure (2.7) b. Fenêtre de contrôle global

Elle concerne l'orientation, l'affichage, la lumière et la vérification du maillage figure (2.8)

Figure (2.8) Figure (2.6)

c. fenêtre des descriptions

Elle concerne l'orientation, l'affichage, la lumière et la vérification du maillage figure (2.9)

d. Fenêtre de la liste des commandes

Elle contient la liste des commandes antérieures. Si nécessaire, on peut ajouter une commande écrite pour être exécutée figure (2.10)

e -types des fichiers qui sont crées par gambit Quatre fichiers sont crées par daufant :

- nom-fichier.dbs : database qui contient toutes les informations nécessaires à Gambit pour créer le maillage.

- nom-fichier.jou : journal file qui contient les commandes que l'on a effectuées.

- nom-fichier.trn : transcript file qui contient les messages donnés dans la fenêtre de dialogue Transcript.

-nom-fichier.lok : pour l'utilisation.

Le fichier le plus important crée par l'utilisateur prend l'extension nom-fichier .msh Figure (2.9)

II.2.2 Code Fluent

Fluent est un programme informatique conçu pour la simulation des écoulements de fluide et du transfert de chaleur dans des géométries complexes.

II présente une grande flexibilité des résultats et une adaptation avec n'importe quel type de maillage. Il permet le raffinement du maillage en fonction des conditions aux limites, des dimensions et même des résultats déjà obtenue. Cela est très utile dans la région à gradients importants (couches limites, couches à cisaillement libre).

Fluent écrit en langage C, il emploie toute la flexibilité et la puissance qu'offre ce langage. Il utilise l'architecture serveur client nécessaire au calcul parallèle sur plusieurs machines

Fluent dispose d'un outil de graphisme pour l'affichage des résultats et leur exploitation. On peut aussi exporter les résultats vers un autre logiciel de graphisme, et l'option UDF permet de résoudre des équations additionnelles ou des termes sources additionnelles définies par l'utilisateur.

-Interface du code Fluent

On peut démarrer 4 versions de Fluent 2D, 3D, 2DDP, 3DDP ayants la même interface figure (2.11).

• 2D (2 Dimensions)

• 2DDP (2 Dimensions Double Précision) • 3D (3 Dimensions)

• 3DDP (3 Dimensions Double Précision) Figure (2.11)

Les fonctions (figure (2.12)) disponibles pour la procédure numérique sont :

File: pour les opérations concernant les fichiers: lecture, sauvegarde, importation...etc. Grid : pour la vérification et la manipulation du maillage et de la géométrie.

Define : pour définir les phénomènes physiques, les matériaux et les conditions aux limites. Solve : pour choisir les équations à résoudre, les schémas de discrétisations, les facteurs de sous relaxation, les critères de convergence et pour initialiser et procéder au calcul.

Adapt : pour l'adaptation du maillage selon plusieurs paramètres.

Surface: pour créer des points, des lignes et des plans nécessaires à l'affichage des résultats. Display et plot: pour l'exploitation des résultats.

Report : pour afficher des rapports contenant les détails du problème traité. Parallel : pour le calcul parallèle.

Help : pour l'exploitation du contenu du code. Figure (I-14)

II.2.3 Condition aux limites utilisée par le code FLUENT

Pour le code Fluent les types disponibles des conditions aux limites sont classés comme suite a) Conditions d'entrée et de sortie de l'écoulement : pression d'entrée (pressure inlet), vitesse de l'entrée (velocity inlet), débit massique à l'entrée (mass flow inlet), admission (intake), pression de sortie (pressure outlet) ; sortie (outflow), champ de pression lointain (pressure far-field), échappement (exhaust)

b) Mur et conditions du pole : mur (wall), axe de symétrie (axis), conditions périodique, plan de symétrie (symétrie).

c) Cellules des zones internes : fluide ou solide (de différent type). d) Condition des faces internes : ventilation, radiation, mur intérieur.

Mais si on parle d'une façon plus générale nous aurons quatre types de conditions aux limites ou chacun d'eux nécessite une étude approfondie :

1-- à l'entrée du domaine : la valeur du variable est connue.

2-- à la sortie du domaine : soit qu'en connaît la valeur de le variable donné ou on suppose que

le régime est établi.

3-- à la paroi : soit on connaît la valeur de la variable posée (la vitesse ou la température par

exemple), soit on connaît d'autres grandeurs physiques (gradient de vitesse, flux thermique).

4--Sur l’axe de symétrie : où le gradient de la variable posé suivant la direction perpendiculaire à

II.2.4 Modèle Numérique utilisée par le code FLUENT

Le code Fluent utilisé la méthode des volumes finis pour discrétiser les équations de transport. Dans cette méthode, on intègre des équations de conservation que l’on applique sur chaque volume de contrôle élémentaire. A partir des variables connues aux centres des volumes, on évalue les flux aux surfaces des volumes par interpolation. La grille est a priori quelconque, permettant ainsi de traiter des écoulements à géométrie complexe. Cette méthode donne de très bon résultat, car elle garantie la conservation des bilans massique et thermique sur tout le domaine étudié.

II.2.4.1 Maillage

Les équations différentielles ponctuelles qui gouvernent notre phénomène sont écrites dans chaque point du domaine physique. Pour les projeter sur ce domaine nous construisons une grille divisée en un certain nombre de volumes finis, et en chaque volume, on considère des points situés en son milieu. Les faces d’un volume de contrôle typique sont localisées au point e, w, n, s (Fig 2.13). Notons P le centre du volume de contrôle considéré et E, W, N, S sont les centres des volumes de contrôles adjacents situés respectivement à l’Est, l’Ouest, le Nord et le Sud de celui contenant P. Les quantités scalaires (pression et température) sont stockées aux centres des volumes finis (Fig 2.14). Par contre, les quantités vectorielles (composantes u et v) sont stockées respectivement aux faces Est et Nord (Fig 2.14) et (Fig 2.15). Pour éviter certains problèmes numériques, les équations de quantité de mouvement sont résolues dans des volumes finis décalées vers la droite pour l’impulsion suivant X et vers le haut pour l’impulsion suivant Y.

E W S N e w s n P

Figure (2.13): Volume de contrôle bidimensionnel.

Ue E P

Figure (2.14): Volume de contrôle décalé vers la droite. Ue W N S Vn E P Ue W N S

II.2.4.2 Intégration d’une équation générale de transport

II.2.4.2.1

Equation générale de transport

Considérons l’équation de transport de la variable φ :

φ φ φ τ φ S X X U X_j j _{j j} _+      ∂ ∂ Γ ∂ ∂ = ∂ ∂ + ∂ ∂ ) ( (II.23) (j : indice de somme ; i=1, 2 dans le cas bidimensionnel)

τ φ ∂ ∂ : Le terme transitoire. ) ( _jφ j U X ∂ ∂

: Le transport par convection de φ .

    ∂ ∂ Γ ∂ ∂ J j X X φ

: Le transport par diffusion deφ .

φ

S : Le terme source.

Pour notre problème nous donnons la définition deφ ,Γ et S_φ dans le tableau suivant : Table II.1 : Définition de φ , Γ et S_φ des équations gouvernantes.

Equation φ Γ S_φ

Continuité 1 0 0

Quantité de mouvement suivant X U Pr

X P ∂

∂ − Quantité de mouvement suivant Y

V Pr A Ra Y P . Prθ + ∂ ∂ − Energie θ 1 0

II.2.4.2.2

Intégration sur un volume de contrôle typique

Pour obtenir l’équation de discrétisation de la variable dépendante φ dans un volume cartésien bidimensionnel, on intègre l’équation générale de transport (équation (II.21)) sur un volume de contrôle (Fig 2.16) :

τ τ τ τ τ φ τ τ τ φ τ τ τ τ τ τ τ τ τ dXdYd S dXdYd Y J dXdYd X J dXdYd n s e w n s e w y n s e w x n s e w

∫ ∫∫

∫ ∫∫

∫ ∫∫

∫ ∫∫

∆ +∆ +∆ +∆ + = ∂ ∂ + ∂ ∂ + ∂ ∂ (II.24) Avec : X U J_x ∂ ∂ Γ − = φ φ Y V J_y ∂ ∂ Γ − = φ φ

Le résultat de l’intégration de l’équation (II.22) et la division par ∆τ donne : Y X S J J J J Y X sn n n n w n e n P n P ∆ ∆ + − + − = ∆ ∆ ∆ − + + + + + φ τ φ φ 1 1 1 1 1 (II.25) Où : n et n+1 correspondant les incréments du temps τ etτ +∆τ.

Y X Y U J e e e e _∂ ∆ ∂ Γ − ∆ = φ φ Y X Y U J w w w w ∆ ∂ ∂ Γ − ∆ = φ φ (II.26) X Y X V J n n n n ∆ ∂ ∂ Γ − ∆ = φ φ X Y X V J s s s s ∆ ∂ ∂ Γ − ∆ = φ φ

Les quantitésJ ,_e J ,_w J et_n J sont les flux aux interfaces (e,w,n,s). Le terme _s S est supposé être _φ constant dans le volume de contrôle. S est évalué au centre du volume de contrôle. _φ

II.2.4.2.3 Les Schémas numériques

Nous allons présenter une forme générale de l’équation algébrique discrétisée où le flux total de convection et diffusion est calculé par une fonctionA( P), on peut écrire l'équation discrétisée sous forme compact comme :

1 + n P P Aφ =A_Eφ +_En+1 A_Wφ +_Wn+1 A_Nφ +_Nn+1 A_Sφ +b (II.27) _Sn+1 Avec : ) 0 , max( ) ( e e e E D A P F A = + − ) 0 , max( ) ( w w w W D A P F A = + (II.28) ) 0 , max( ) ( n n n N D A P F A = + − ) 0 , max( ) ( s s s S D A P F A = + b S X Y n ∆ ∆ ∆ + =( ) τ φ φ τ ∆ ∆ ∆ + − + − + + + + = A A A A F F F F X Y A_{P E W N S} ( _{e w n s}) (II.29) w J n J e J s

J

X ∆ W E N S Y ∆ n dY s dY e dX w dX s w _e n

Figure (2.16) : Volume de contrôle typique. P

Y U F_e = _e∆ X V F_n = _n∆ (II.28) X V F_s = _s∆ Y dX D e e e ∆ Γ = Y dX D w w w ∆ Γ = (II.29) X dY D n n n ∆ Γ = X dY D s s s ∆ Γ = e e e D F P = , w w w D F P = , n n n D F P = et s s s D F P = .

Où : (Fe ,Fw ,Fn ,Fs) , (De ,Dw ,Dn ,Ds) et (Pe ,Pw ,Pn ,Ps ) sont respectivement, les flux

convectifs et diffusifs, et les nombres de Peclet aux interfaces e,w,n et s • Fonction A( P) pour différents schémas numériques

Le tableau ci-dessous donne les expressions de la fonction A( P) pour différents schémas numériques.

Table II.2 : Fonction A( P) pour différents schémas numériques.

Schéma _{Formule de la fonction A( P)}

Différences centrées Upwind Hybrid Power Law Exponentiel 1-0.5 P 1 Max [0, 1-0.5 P ] Max [0, (1-0.1 P )5] P / [exp ( P )-1]

Dans le présent travail nous utilisons :

Ø Le schéma power-law ce schéma est mieux placé pour capter les phénomènes physiques de transfert de chaleur,

Ø Le schéma de discrétisation du couplement Pression vitesse est le SIMPLE,

Ø

Le Critère de convergence utilise par FLUENT est la sous-relaxation.

Y U F_w= _w∆

III. Résultats et Discussions

III. 1 Validation du code

III.1.1 Régime stationnaire

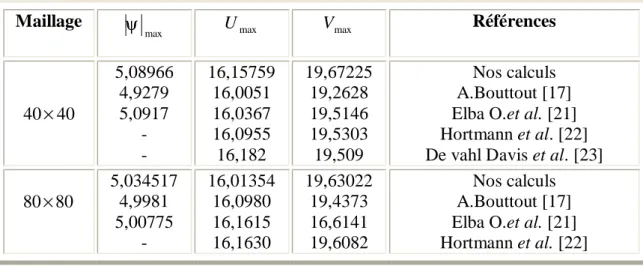
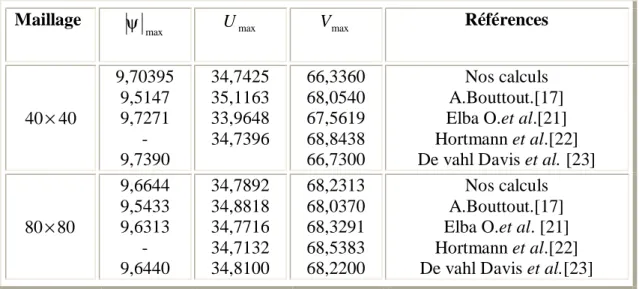
Afin d’élaborer une comparaison constructive et objective des résultats obtenus par nos simulations numériques avec des travaux expérimentaux disponibles dans la littérature, et de donner des interprétations aux phénomènes observés, il est utile de valider au préalable le code de calcul Fluent

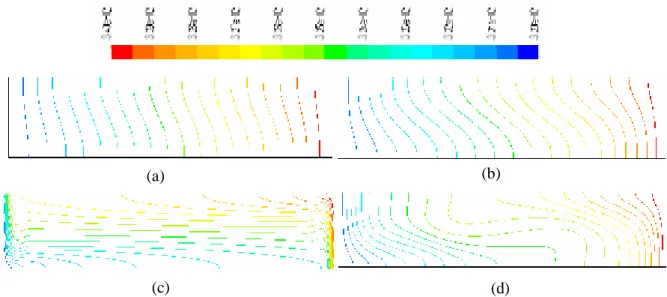
La première étape consiste à valider notre simulation numérique en comparant nos résultats avec ceux de Derbail & Koster [5] et de Koster et al. [20]. Pour cela, on a employé les mêmes conditions figure (3.1) (fluide de convection: gallium, cavité rectangulaire de dimensions (0,050x0, 035x0,002), régime laminaire, ΔT=60 K et Gr = l,86x107) que Derbail & Koster [5] qui ont obtenus leurs résultats avec le code numérique FIDAP (Figures 3.2.a) et Koster et al. [20] qui ont obtenus des résultats expérimentaux en utilisant la technique de radioscopie (Figures (3.2.b)).

Les figures 3.2.a et 3.2.b, montrent que nos champs de températures et de vitesse sont en bon accord avec les résultats expérimentant et numériques obtenus en [20,5].

5 cm Paroi Froide 3.5 cm 0.2 cm Paroi Chaude

.

Figure (3.2.a): champs de vitesse pour le gallium Gr = l,86x107

(a) résultat numérique de Derbail & Koster [5] (b)Résultat de notre calcul (code Fluent)

(a) Résultat numérique de Elba O.et al. [21] (b) Résultat expérimental de Juel et al. [14]

(c) Résultat de notre calcul (code Fluent)