Diffuse double-layer interaction for nonspherical colloidal particles

Diffuse Double-Layer Interaction for Nonspherical

Colloidal Particles

by

Mark Jhon

Submitted to the Department of Materials Science and Engineering in partial fulfillment of the requirements for the degree of Bachelor of Science in Materials Science and Engineering

at the

MASSACHUSETTS INSTITUTE OF TECHNOLOGY

@

The author hereby grants to MIT permission to reproduce and distribute publicly paper and electronic copies of this thesis document

The author hereby grants to MIT permission to reproduce and to distribute publicly paper and electronic copies of this thesi3 document in whole or in part in any medium now known or hereafter created,

in whole or in part.

A uthor ...

Signature redacted

Department of Materials Scdence/and Engineering

Signature redacted

C ertified by ...

...

C ertified by ...

Tiesis Supervisor

Signature redacted

Richard L. Smith

AMAX Assistant Professor of Materials Science and Engineering

Accepted by...

JUL

10 2017

n

I

Thesis Supervisor

Signature redacted...

Chairman, Undergraduate Thesis Committee

Diffuse Double-Layer Interaction for Nonspherical Colloidal

Particles

by

Mark Jhon

Submitted to the Department of Materials Science and Engineering on May 25, 2001, in partial fulfillment of the

requirements for the degree of

Bachelor of Science in Materials Science and Engineering

Abstract

The DLVO theory of colloids is used to consider the stability of clay colloid parti-cles. An approach to colloid physics using classical electrostatic methods is presented. Specifically, the electrical double layer is examined using computational methods. To this end, the Poisson-Boltzman equation is solved numerically for geometries corre-sponding to interacting clay particles. The interaction energies of double layers is calculated for several particle configurations.

Thesis Supervisor: W. Craig Carter

Title: Thomas Lord Associate Professor of Materials Science and Engineering Thesis Supervisor: Richard L. Smith

Acknowledgments

The author would like thank Professor Carter and Professor Smith for their guidance during this project.

Contents

Abstract

Acknowledgments List of Figures List of Tables

1 Introduction and Background

1.1 Clay Particles . . . . 1.2 Clay Surface Charges . . . .

1.3 DLVO Stability Theory . . . .

1.4 Electrical double layer . . . .

1.5 Double layer energies . . . .

2 Computation of Double Layer

2.1 Boundary conditions . . . . 2.2 Electrical Double Layer of Isolated Sphere . . . .

2.3 Double Layer of 2-D Isolated Platlet . . . . 2.4 Double Layer of Two Interacting Platlets . . . .

3 Results

3.1 Potential of Isolated Sphere . . . .

3.2 Potential of Isolated Platelet . . . .

3.3 Interaction Energy of Two Platelets . . . .

3 5 9 11 13 . . . . 13 . . . . 14 . . . . 15 . . . . 15 . . . . 18 21 22 23 23 24 25 25 26 27

4 Discussion 29

4.1 Error A nalysis . . . . 29

4.2 Conclusions . . . . 30

List of Figures

1-1 Schematic of clay structures . . . . 14 2-1 Schematic of Laponite particle . . . . 22 2-2 Diagram of two particle experiment. . . . . 24

3-1 Double layer energy vs. Nondimensional edge charge strength . . . . 26

3-2 Total double layer energy of two particle system . . . . 28

3-3 Interaction energy of double layers . . . . 28

4-1 Detailed representation of platelet . . . . 29 A-1 Contour plot of potential surrounding single particle for zero edge charge 31

A-2 Contour plot of potential about single particle for edge charge of 30 . 32

A-3 Contour plot of potential about single particle for edge charge of 50 . 32

List of Tables

3.1 Electrical double layer of sphere . . . . 25 3.2 Sim ulation tim es . . . . 27

Chapter 1

Introduction and Background

During the manufacture of ceramics, most forms of processing begin by mixing clay particles with an electrolyte. The particles may become suspended in solution, creat-ing a colloidal solution, or sol. The properties of the sol are important because they limit the processing of the clay. In this system, there are two main forces governing the particles, specifically the electric double layer and van der Waals interactions. If these two forces are described completely, it should be possible to predict the properties of the colloidal solution.

In order to understand the behavior of sols with realistic particle shapes, a general means for their investigation is required. This study numerically solves the governing equations for the double layer given boundary conditions corresponding to a plate-like clay particle using a finite differencing technique.

1.1

Clay Particles

Macroscopic clay particles generally fall into three basic categories of shapes: plate, lath, and needle-like. For instance, smectite clays have a plate-like habit, which are typically 1 nm thick and several hundred nanometers wide. On the other hand, attapulgite (palygorskite) crystallizes in the form of long needles.

The asymmetric shape of the clay particles leads to to self assembly of the particles. There are three main structures that may form, depending on the relative strengths

of the interactions between the particles. If they pack edge-to-edge, they can form a chain structure. If they pack face-to-edge, they may form a house-of-cards. The face-to-face packing of the clay particles is called the deck-of-cards structure. These three structures are depicted in two dimensions in Figure 1-1.

Face-to-face Face-to-edge Edge-to-edge

Figure 1-1: Schematic of clay structures

1.2

Clay Surface Charges

When a clay particle is immersed in an electrolyte, it will acquire a charge on its surface. However, different parts of the particle can take on different surface charge. The mechanism for clay particles acquiring charge in an electrolyte is mainly deter-mined by ionic reactions of the surface groups on the particle. Surface complexes will form differently on the edges of the particle than on the faces due to the presence of broken bonds on the edge.

For instance, surface charges have been measured for the case of kaolinite in a NaCl solution. The surface is measured as having a negative charge, due to the presence of isomorphous substituted Al in the siloxane surface. The surface reaction is

AlOH+ = AlOH + H+ (1.1)

with a pK = 4.04 [7]. The edge has a net positive charge, due to the presence of SiOH and AlOH sites in the crystal lattice, with pK = 6.3. This is a highly pH dependant

efffect, and may be controlled by changing the composition of the solvent. However, the negative charge on the face of the particle typically dominates the overall charge

1.3

DLVO Stability Theory

The Deryaguin-Landau-Verwey-Overbeek (DLVO) theory is the basis for determining the behavior of colloidal suspensions [3, 10]. It predicts the conditions at which a colloid will remain stable, where the particles will remain suspended in solution. The DLVO theory states that a van der Waals attractive force is balanced by a repulsive electrostatic interaction. Closed form expressions adequately describing the van der Waals interaction have been found for a number of geometries. The van der Waals force typically follows a scaling law of d-" where the distance between two particles is given by 2d and n ~ 3 - 4.

However, it is difficult to change the magnitude of the van der Waals interaction. This makes the effect of the electrostatic interaction more important. Because of the charge on the colloid particle, a layer of ions is formed around the particle. This is called the electrical double layer. The stability of a colloid may be altered by changing the strength of the double layer interaction between particles.

1.4

Electrical double layer

A mean field model is used, where the charge distribution on the surface of the particle

is assumed to be continuous. The charge density about a particle can be determined using the Poisson equation,

V2

o 47p (1.2)

where

4

used. This is equivalent to assuming that the number of small ions is so large that the

addition of one ion does not change the mean potential. This is done by ignoring the work that is done by bringing two ions together. Assuming a Boltzmann distribution

is equivalent to stating that the bulk concentration vi of an ion species i is given by

vi = ni exp zie' (1.3)

(_kBT)

Where e is the electronic charge, kB is the Boltzmann constant, zi is the valence of the ion, and ni is the ion concentration far away from the particle. It is possible to relate the charge density p to the species concentration vi through the expression

p = evizi + Pc (1.4)

where pc is a function of position, and is zero everywhere except for the volume of the clay particle. Here, it takes on the value of the charge density of the clay particle. Because the charge density is related to the the species concentration, by summing over all species, (1.2) may be rewritten as

v2v = Enizi exp ze (1.5)

B _(kB1.5

The Poisson-Boltzmann (PB) equation, Eq. 1.5 is accepted as a good model for distances much larger than the size of the ions [10]. Additionally, for symmetric, single valent electrolytes, the PB equation is valid even for extremely small distances.

By integrating the PB equation, it is possible to find the diffuse electrical double

layer surrounding the colloid particle. The geometry of the particle complicates this calculation.

The PB equation can be integrated exactly for the case of the infinite wall. How-ever, for more complex geometries, because of the nonlinearity of Eq. 1.5, inte-gration is not straightforward. For more complex geometries, various linearizations have been used in order to simplify the calculation. This is the basis for linearized Poisson-Boltzmann (LPB) theory. The standard method is to assume that the surface potential is very small in comparison to thermal energy, such that

Z~ev) < 1 _(1.6)

This is often called the Debye-Huckel (DH) approximation. Using this condition, the PB equation may then be solved as:

V0= n2)(1.7)

with the inverse Debye length r, equal to,

S2 = - niz? 2(1.8)

kBTE

In this limit, the PB equation may easily integrated into an exponential form, yielding

V' = Oo exp(x) (1.9)

However, de Carvalho et al. have shown that in systems where the macroions hold a relative large charge, the interparticular forces determined by LPB theory differ significantly from solving the full PB equation [8].

Using simple boundary conditions such as constant surface potential, numerical solutions for the nonlinear PB equation can be found using reasonable time limits

[9, 11]. For spherical particles, the classical numerical computation was done by

Loeb, Overbeek and Wiersema and was published as a set of tables for a wide range of parameters [1]. Their results have been replicated using a variety of numerical and analytical techniques, including a network thermodynamics model. Both numerical and analytic solutions have been found for cylindrical particles in certain limiting conditions.

There are two particular phenomena in clays which have not been dealt with completely. First, there are edge effects due to the finite size of the particle. de Carvalho et al. began to explore this subject in a semianalytical approach utilizing Green's functions [8]. However, they only considered the case of parallel plates, ignoring the possibility of tilted particles. Second, the fact that the edges have a different charge from the faces of the platelets has been ignored until now.

1.5

Double layer energies

It is possible to calculate the free energy of the double layer around a spherical particle, as derived by Levine [5]. This expression is

< = - 2 _{(All + X)dV (1.10)}

47ra2

where X is an electrostatic potential energy and Arl is the osmotic pressure. We notice that this expression considers both electrostatic energy as well as chemical potential (in the osmotic pressure term).

The energy densities x and Azl have been calculated to be

/ JJ= kBT [(v -n+) +(v- -n-)] (.1

x

The total energy of the system also includes the electrostatic repulsion between the particles as well as the van der Waals force. This is not considered in this calculation. The lack of symmetry in the two-particle system restricts the techniques that may be used to determine the double layer energy of the system. Monte Carlo calculations

have been done using this form to estimate the force felt by arbitrarily shaped particles [6]. However, this approach uses LPB theory.

The overlapping of the double layer of two particles will create an interaction energy V(H). This double layer interaction energy is given by

V(H) = Esys - 2Ec, (1.13)

where Ey, is the energy of the system as calculated by Eq. 1.10 and E" is the interaction energy of a single isolated particle. For spherical particles at a separation H, V(H) has been calculated using Derjaguin's approximation,

where a is the radius of the particles and Vpj is the potential energy of the double layer of a single sphere, found using the PB equation.

Chapter 2

Computation of Double Layer

The first step to solving the PB equation is to rewrite all terms in nondimensional form. The following change of variables is made: a reduced potential is defined in the form q = eo/kBT and a reduced permitivitty is defined in the form E = EkBT/e2

These two substitutions reduce the general PB equation to the form

V2_{q =-- nizi exp (-ziq) - 47p, (2.1)}

eE

This equation may be further simplified by writing it in more useful in a reduced distance, using ir = ri/A with the inverse Debye length rs defined as in Eq. 1.8 and

A2 _{Z+ + z} (2.2)

2z_

By writing VR as the gradient in this reduced basis, we can rewrite Eq. 1.5 as zq _ e-z+q 4wper2

VR 2z 2 (2.3)

Eq. 2.3 is the equation which we attempt to solve numerically. The substitution to

the reduced distance basis may be applied to the double layer energy as well. The

expression for the double layer energy

#

/

=Y dV (VRq)2 + z2 (ez _ -z- (

1

where y is a function of z+, z_, n+, n-, c, T. That is, it is independant of position.

Therefore, without calculating y, it is possible to compare free energies of two systems with different geometries.

2.1

Boundary conditions

This model uses a number of simplifying assumptions. First, it assumes that the macroion concentration is low, so that the interaction of at most two particles are considered. Further, simplified boundary conditions are utilized.

T

I

n

Tinm

K )

25 nm

Figure 2-1: Schematic of Laponite particle

This experiment specifically considers Laponite, which is a commonly studied, synthetic clay. This choice was made because surface charge data is easily available, and the particles are further very regularly shaped. Laponite particles are cylindrical plates in platy habit, and are cylindrical in shape. The particles are about 1 nm thick and about 25 nm wide, as shown in figure 2-1. On these length scales, it is a reasonable approximation to assume that the particle has no height, and may be visualized as a circle of charge with no thickness. This simulation assumes a 2-d picture, so the particle will be idealized as two positive point charges separated by a line of negative charge.

Although most existing approaches to solving the PB equation use constant poten-tial boundary conditions for the particle surface, the clay system is more accurately modeled using constant surface charge boundary conditions. The total charge on the platelet is taken to be Ze where Z ~ 1000 [4]. The charge density on the surface of the Laponite particle is taken to be uniform, such that

4Ze

where d is the diameter of the platelet. In our two dimensional approximation, each mesh element must hold a charge of 12 , where 1 is the length of each element. The boundary condition on the particle surface is to use pc = 12a.

2.2

Electrical Double Layer of Isolated Sphere

The first part of this project calculated the potential around an isolated sphere ac-cording to the PB equation. This effort replicated the of LOW tables in order to better understand the problem and, as a practical concern, to be able to calculate ion concentrations in the double layer for arbitrary distances. The LOW algorithm was followed as outlined in [1]. The double layer is assumed to be spherically symmetric, allowing the PB equation to be rewritten in terms of the radial distance, r. This algorithm was implemented in ANSI C.

2.3

Double Layer of 2-D Isolated Platlet

The second part of this study was to solve the PB equation for an isolated Laponite platelet. To solve this problem, we utilized a multigrid finite difference solution to the PB equation. This method incorporated a full approximation scheme (FAS) for nonlinear equations. This algorithm solves the equation on a very coarse mesh, and successively relaxes the solution so that it solves the equation on the finest mesh.

The convergence of the FAS solution is known to be very good for PB-type equa-tions This was implemented by modifying a routine in Numerical Recipes in C to solve the discretized PB lattice equation [12]. This was also implemented in ANSI C. Simulations were run on a Sun Ultra 10.

Although a commercial PDE solver was available, it did not prove to be useful. The MatLab software package, by the MathWorks company, uses a finite element method which has relatively poor convergence for the PB equation. The large number of elements needed for an accurate calculation imply that it is not practical for this application.

The choice of the FAS method was inspired by computations done by Coalson, who noted that because the PB equation has no saddle points, it has a unique solution, and may be solved by any minimization method [2]. However, different algorithms yield different convergence rates. The FAS method has relatively fast convergence.

The FAS algorithm limits meshes to square grids of size 2", because it uses an array of coarser grids. All simulations were run using a grid size of 1024 x 1024 elements. The colloid particle was picked to be 100 mesh elements long.

2.4

Double Layer of Two Interacting Platlets

In this part of the experiment, the interaction energy between two particles was mea-sured. The generalized experiment is shown in Figure 2-2. Neumann-type boundary conditions were used, where the potential at the edge of the box was set to zero. In

Y

Figure 2-2: Diagram of two particle experiment.

this experiment, the two relative position coordinates x and y and the misorientation between the particles is 0. The interaction energy is measured by solving the PB equation for the system of two particles, then subtracting twice of the energy of the single particle. This avoids using a geometry based approximation such as Derjaguin's method.

Because of the relatively large number of calculations necessary for a two-particle system, simulations were run using a grid size of 512 x 512 elements.

Chapter 3

Results

3.1

Potential of Isolated Sphere

The LOW tables were compared to the data generated by our implementation of the LOW algorithm. The data generated by our implementation of the LOW algorithm was fairly close to the published data points, although some small variations were observed. Sample data points between the LOW tables and our impletmentation of the algorithm are compared in Table 3.1. This compares the reduced potential y for several values of 1/q at z+ = z_= 1 and using Y = 0.999000

The two sets of values are precise to 1 part in 104, implying that the algorithm was implemented correctly. The differences are assumed to be because of different

Table 3.1: Electrical double layer of sphere

y from [1] Calculated y 0.3 0.001182 0.001182 1 0.040616 0.040618 2 0.133941 0.133943 3 0.237377 0.237379 4 0.344050 0.344054 5 0.452168 0.452173 6 0.561061 0.561067 7 0.670420 0.670427

precision in library functions such as exponentials.

3.2

Potential of Isolated Platelet

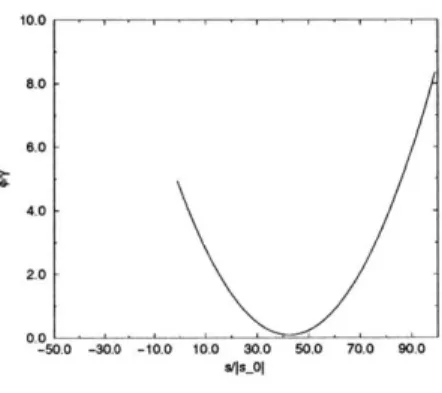
The potential around single platelets was measured for various initial conditions. Because the charge on the edge of the platelet is highly pH dependant, it may take on a range of values. This calculation was made in order to show the range of charges in which the double layer switches sign. The boundary conditions used were to place a negative charge of so = -1000 on each element on the particle surface, then to

vary the edge charge from s = so to s = -100so. The double layer energy was measured and plotted as a function of edge charge strength. Further, contour plots

10.0 8.0 8.0 4.0 2.0 0. -50.0 -30.0 -10.0 10.0 30.0 50.0 70.0 90.0

Figure 3-1: Double layer energy vs. Nondimensional edge charge strength

of the potential were made at representative strengths of the edge charge. These may be found in Appendix A. It is important to note that for the parameters tested, the double layer does not switch sign locally until the graph in Figure 3-1 reaches its local minimum. Here, the charge density on the tips is about 45 times that of the charge on the surface.

In this case, the total charge on the particle surface is approximately equal to the charge on the edges. This is not a realistic scenario. Under the parameters tested, the double layer will not locally change sign.

In addition to calculating double layer energies, speed benchmarks were taken. Because large a large number of geometries were modeled, the available computational

Table 3.2: Simulation times Elapsed time Mesh size

0.23s 64 x 64 0.99 s 128 x 128 3.38 s 256 x 256 15.23 s 512 x 512 67.74 s 1024 x 1024 1004.49 s 2048 x 2048

power limits this calculation. In other words, it is not possible to increase the mesh size indefinitely. An increase of mesh size from 1024 to 2048 corresponds to an increase of 15 minutes per double layer energy calculation (See Table 3.2). This would make calculations impractical.

3.3

Interaction Energy of Two Platelets

This experiment tracks two particles at constant y while varying both x and 0. This was done for a particle with no charge on the edge. The double layer energies of the total system are shown in Figure 3-2. Notice that each of the different orientations have different asymptotic behavior at large r. They appear to be approaching slightly different values. It is necessary to find the interaction energies by themselves by Notice that these interaction energies are very similar for all orientations. The interaction energy of the 0 = 900 case is slightly higher, but not significantly.

2.0 1.8 1.6 1.4 1.2 1.0 1 0.05 0.10

Figure 3-2: Total double layer energy of two particle system

0.8 0.6 0.4 0.2 0.0 0.05 0.10 0.15 d

Figure 3-3: Interaction energy of double layers

- 0 ..---.--.- 1 0 ---- 20 - - - 30 40 - - - 50 G--O 60 x-x 70 0---* 80 B-E 90 0.25 0.15 d 0.20 --0 10 20 ---- 30 40 50 0 060 x-x 70 0--80 -A 2 0.20 0.25 ) 1~ 6

Chapter 4

Discussion

4.1

Error Analysis

Much of the error from the two-particle calculation comes about because a fixed size square mesh is used. Because the model deals with platelets at an arbitrary angle, at certain angles the platelet is not exactly aligned with the mesh. It must be approximated, as shown in Figure 4-1. In this diagram, the black line represents

At angle 0 At angle 0 + E

Figure 4-1: Detailed representation of platelet

the model platelet, while the gray boxes represent the values of the mesh elements. Notice that with a small change in the orientation of the platelet, the number of mesh elements that the particle lies on changes. However, this effect is minimized by examining the interaction energy.

The finite size of the simulation box also affects the calculated double layer energy values. Because of the boundary conditions on the simulation box, the potential is forced to zero at the edges. Therefore, the curvature of the potential is increased.

As the electrostatic component of the double layer energy is related to the slope of the potential through Eq. 1.12, the double layer energy is overstated if the particle is close enough to the edge of the simulation box. To minimize this effect, calculations were repeated in a larger box to minimize boundary effects.

It is lastly important to note that the 2-dimensional nature of the calculation is not completely physically valid. However, it should give us insight into the physics of the real system without solving the entire problem. Doing the full 3-d calculation would require an extra rotational degree of freedom. This would make interpretation of the results more difficult.

4.2

Conclusions

This study comprises only a first step in a full study of the colloid system. There are a number of ways in which this research may be further extended. For instance, the van der Waals interaction must still be added to the electrostatic interaction. In addition, the full 3-d system may be solved. Finally, once the force-position curves are calculated, a simulation may be constructed which predicts the behavior of a many colloid particle system.

The methods used in the study of ceramic particles may be applied to other colloid systems, such as chain-folded polymer crystals.

Appendix A

Contour plots of single particle

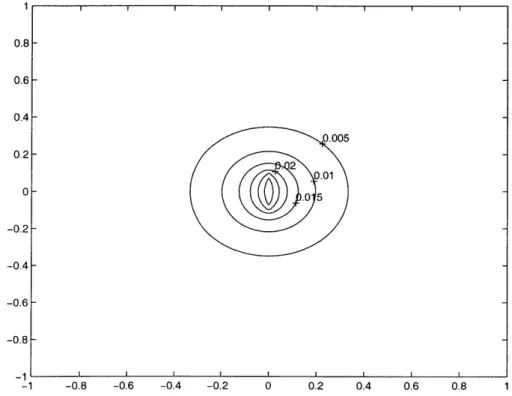
0.8- 0.6- 0.4- 0.2-0 -0.2- -0.4- -0.6- -0.8--1 0.005 .2 - .0 0 0 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8

Figure A-1: Contour plot of potential surrounding single particle for zero edge charge

1

1 - 0.8- 0.6- 0.4- 0.2- 0- -0.2- -0.4- -0.6- -0.8--1: -1 A-2: -0.6 -0.4 -0.2 plot of potential 0 0.2 0.4 0.6

about single particle for

0.8 1

edge charge of 50

0005

-0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

Contour plot of potential about single particle for edge charge of 30 Figure 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 A-3: -0 -. 0.000 .005 05 Figure -0.8 Contour

1 0.8 0.6 0.4 0.2 0 -0.2 -0.4- -0.6- -0.8--1 -1 Figure A-4: -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

Contour plot of potential about single particle for edge charge of 80

33 -01 -0.005 0.0 5 - T0.01

-Bibliography

[1] J. Th. G. Overbeek A. L. Loeb and P. H. Wiesama. The Electical Double Layer

Around a Spherical Colloid Particle. Massachusetts Institute of Technology,

Cambridge, 1961.

[2] R. D. Coalson and A. Duncan, 1992.

[3] B. V. Derjaguin and L. D. Landau. Acta Physiochim., 14:633, 1941.

[4] Laponite Inorganics. Laponite technical bulletin 1104/90/a.

[5] S. Levine. Proc. Phys. Soc., page 781, 1951.

[6] S. Reymann M. A. Koenders. J. Colloid Inter. Sci., 225:299-306, 2000.

[7] W. Strumm P.W. Schindler. The surface chemistry of oxides, hydroxides and oxide minerals. In Aquatic surface chemistry, pages 88-100. Wiley-Interscience, New York, 1987.

[8] E. Trizac R. J. F. Leote de Carvalho and J. P. Hansen. Nonlinear

poisson-boltzmann theory of a wigner-seitz model for swollen clays. Phys. Rev. E,

61(2):1634-1647, 2000.

[9] J. E. Sanchez-Sanchez and Lozada-Cassou. Chem. Phys. Lett., 190:202, 1992. [10] E. J. W. Verwey and J. Th. G. Overbeek. Theory of the Stability of Lyophobic

Colloids. Elsevier, Amsterdam, 1948.

[12] W. T. Vetterling W. H. Press, S. A. Teukolsky and B. P. Flannery. Numerical

Recipes in C, chapter 19, pages 827-888. Cambridge University Press, New York,