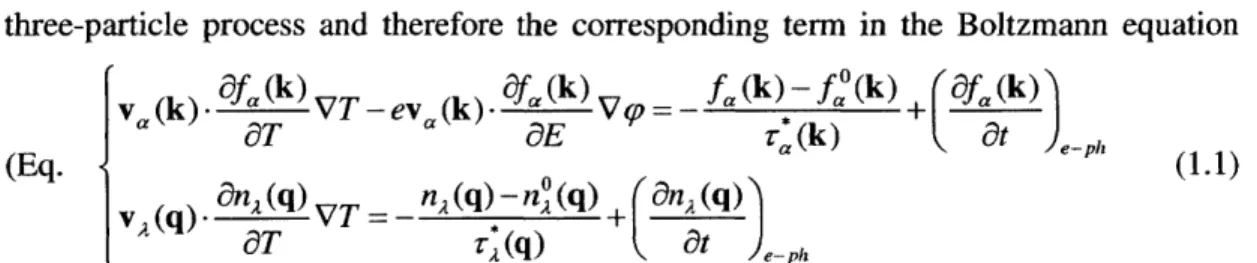Ab initio simulation and optimization of phonon drag
effect for lower-temperature thermoelectric energy
conversion
by
Jiawei Zhou
Submitted to the Department of Mechanical Engineering
in partial fulfillment of the requirements for the degree of
Master of Science in Mechanical Engineering
at the
MASSACHUSETTS INSTITUTE OF TECHNOLOGY
ARCHNES
MA A 1 T NQTITUTEJUL 3
0
2015
LIBRARIES
JUNE 2015
Massachusetts Institute of Technology 2015. All rights reserved.
AuthorSignature
red acted
A uth or
... . . . ..
. . . . .
.r
...
....-
---Department of Mechanical Engineering
7
May 8, 2015
Certified by ...
Signature
Gang Chen
Carl Richard Soderberg Professor of Power Engineering
Accepted by ...
Thesis Supervisor
Signature redacted
David E. Hardt
Chairman, Department Committee on Graduate Students
MITLibraries
77 Massachusetts Avenue Cambridge, MA 02139 http://Iibraries.mit.edu/ask
DISCLAIMER NOTICE
Due to the condition of the original material, there are unavoidable
flaws in this reproduction. We have made every effort possible to
provide you with the best copy available.
Thank you.
The images contained in this document are of the
best quality available.
Ab initio simulation and optimization of phonon drag effect for
lower-temperature thermoelectric energy conversion
by
Jiawei Zhou
Submitted to the Department of Mechanical Engineering on May 8, 2015, in partial fulfillment of
the requirements for the degree of Master of Science in Mechanical Engineering
Abstract
In recent years, extensive efforts have been devoted to searching for materials with high thermoelectric (TE) efficiency above room temperature for converting heat into electricity. These efforts have led to significant advances with a record-high zT above 2. However, the pursuit of higher TE performance at lower temperatures for cooling and refrigeration applications receives much less attention. Today's most widely-used thermoelectric materials below room temperature are still (Bi,Sb)2(Te,Se)3 material system, discovered
60 years ago with a maximum zT around 1. This thesis develops the first-principles
simulation tools to study the phonon drag effect - a coupling phenomenon between electrons and non-equilibrium phonons - that leads to a large Seebeck coefficient at low temperatures. Phonon drag effect is simulated successfully from first-principles for the first time and results compare well with experimental data on silicon. While the common wisdom always connects a significant phonon drag effect to a high thermal conductivity, a key insight revealed from the simulation is that phonons contributing to phonon drag and to thermal conductivity do not spectrally overlap. Even in a heavily-doped silicon sample with 1019 cm-3 doping concentration, phonon drag still contributes to -50% of the total Seebeck coefficient. By selectively scattering phonons contributing to heat conduction but not to phonon drag, a large improvement in thermoelectric figure of merit zT is possible. An ideal phonon filter is shown to tremendously enhance zT of n-type silicon at room temperature by a factor of 20 to -0.25, and the enhancement reaches 70 times at lOOK. A practical phonon filtering method based on nanocluster scattering is shown to enhance zT due to reduced thermal conductivity and optimized phonon drag effect. This work opens up a new venue towards better themoelectrics by harnessing non-equilibrium phonons. More material systems can be systematically studied with the developed simulation tools.
Thesis Supervisor: Gang Chen
Title: Head of the Department of Mechanical Engineering and Carl Richard Soderberg Professor of Power Engineering
Dedication
Acknowledgement
This thesis work would be simply impossible without the help and advice from various people I have met from the first day I entered the graduate school. Firstly, I would like to thank my thesis advisor, Prof. Gang Chen, who provides me the great opportunity to work in a wonderful and exciting research environment, points out the possible directions in the long-term and helps with the tiny problems I met during the research, even though he has to squeeze out his time from the commitments to the department among other things. His inspiring vision and scientific rigor always helps me to shape my research habits. Secondly, I would like to thank Mr. Sangyeop Lee and Mr. Bolin Liao, who are knowledgeable seniors I have learned from. I have spent many hours bothering them on the details and understandings of the density functional theory as well as the transport property calculations based on it. It is hard to imagine how I would move from knowing nothing to the phonon transport and later the electron-phonon interaction without their
advice and patience. I would also like to thank my labmates in the nanoengineering group for their generous help, especially Mr. Samuel Huberman, Mr. Lee Weinstein, Dr. Yuan
Yang, Ms. Yi Huang and Dr. Yanfei Xu. I would also like to thank Prof. Mildred S.
Dresselhaus who has pointed to me a different perspective of phonon drag and shared with me her stories in the thermoelectric research.
Finally, I want to thank my family for their support, and many friends outside my research field, for who I would not list the names but who have painted wonderful colors to the sky of my research life.
Contents
Chapter 1. Introduction ... 13
1.1. Coupled electron-phonon Boltzmann equation... 15
1.1.1. Picture of Boltzmann equation ... 15
1.1.2. Electron-phonon interaction... 18
1.1.3. Scattering rates due to electron-phonon interaction... 21
1.2. Phonon drag effect ... 26
1.3. Kelvin relation for phonon drag ... 30
1.4 Experimental investigation into phonon drag ... 32
1.5 Organization of thesis... 34
Chapter 2. Ab initio approach for transport property calculations ... 36
2.1. Density functional theory ... 36
2.2. Electron-phonon interaction... 39
2.2.1. W annier function-based interpolation scheme ... 39
2.2.2. Electron scattering by phonons ... 42
2.2.3. Phonon scattering by electrons... 45
2.3. Phonon-phonon interaction ... 46
2.4. Impurity scattering ... 48
2.5. Phonon drag modeling ... 49
Chapter 3. Simulation of phonon drag ... 51
3.1. Intrinsic phonon drag ... 51
3.2. Saturation effect ... 52
3.2.1. Reduction of phonon drag at high doping concentrations... 52
3.2.2. Cause of saturation effect... 55
3.3. M ode contribution to phonon drag... 57
3.3.1. Phonon mode contribution ... 57
3.3.2. Electron mode contribution... 59
3.3.3. Effect of normal scattering and Umklapp scattering ... 60
Chapter 4. Optimization of phonon drag ... 63
4.1. Preferable phonon modes for phonon drag ... 63
4.1.1. Optimization of n-type silicon with ideal phonon filters... 64
4.1.2. Optimization of p-type silicon with ideal phonon filters... 67
4.2. Other Phonon filters ... 69
4.2.1. Nanocluster scattering for frequency selectivity ... 69
C hapter 5. Conclusion... 75
5.1. Summ ary ... 75
5.2. Future work...75
List of Figures
Figure 1-1. (a) Illustration of the collision between electrons and phonons, (b) transitions
shown in the electronic band and (c) corresponding phonon modes in the phonon dispersion ... 18
Figure 2-1. Temperature dependence of the calculated intrinsic mobility in n-type and p-type silicon compared with that of sufficiently pure samples from the experiment. . 45 Figure 2-2. Temperature dependence of the thermal conductivity of pure silicon com pared with the experim ent... 48
Figure 3-1. Intrinsic phonon drag effect for (a) electrons and (b) holes in lightly-doped
silico n ... 52
Figure 3-2. Calculated Seebeck coefficient with respect to doping concentrations for (a) n-type silicon and (b) p-type silicon at 300K and 200K on a semilog plot... 54 Figure 3-3. Phonon scattering rates due to phonon-phonon interaction (red points) and electron-phonon interaction (blue points)... 56
Figure 3-4. Phonon mode-specific accumulated contributions to the phonon drag Seebeck coefficient and the thermal conductivity with respect to (a) phonon frequency,
(b) phonon wavelength and (c) phonon mean free path.. ... 58
Figure 3-5. Accumulated contribution to electrical conductivity, diffusive Seebeck coefficient and phonon drag Seebeck coefficient, with respect to (a) electron band energy,
(b) electron wavelength and (c) electron mean free path.. ... 61 Figure 3-6. Electron mode contribution to the phonon drag effect for (a) n-type silicon
and (b) p-type silicon, as well as (c) the phonon mode contribution to the phonon drag effect for n-type silicon... 62 Figure 4-1. Distribution of preferable phonon modes in wave vector and phonon frequency...65
Figure 4-2. (a) Contribution of the most preferable modes to the phonon drag Seebeck coefficient at different reduced thermal conductivity values and (b) the enhancement of the factor S2
/ K as a function of doping concentration when phonon modes are
selectively scattered ... 67
Figure 4-3. (a) The enhancement of zT compared to bulk crystal achieved by selecting preferable modes at 300K for n-type silicon with respect to the doping concentration and
(b) the zT enhancement at a doping concentration of 4 x 10' cm-3 as a function of the
tem perature.. ... 68
Figure 4-4. (a) Contribution of preferable modes to the phonon drag Seebeck coefficient at different reduced values of the thermal conductivity and (b) the enhancement of the factor S2 / K as doping concentration for p-type silicon... 69
volume fraction of nanoclusters using phonon frequency selectivity for n-type silicon with a doping concentration of 1019 cm-3
at (a) 300K and (b) 200K... 73
Figure 4-6. The enhancement of the thermoelectric figure of merit zT if single impurities are used to scatter short-wavelength phonons preferentially... 74
List of Tables
Table 1-1. Prefactors for different types of electron-phonon collisions... 22
Table 2-1. Scattering mechanisms for electrons and phonons ... 49
Table 2-2. Parameters used in determining the electron and phonon relaxation times as
Chapter 1. Introduction
Understanding the transport properties of solids has a main focus on the interaction between various elementary excitations, among which the interplay between electrons and phonons has played a significant role in particular phenomena such as superconductivity' and the metal-insulator transition2
. The electron-phonon interaction (EPI) problem was first studied by Bloch3, Sommerfeld and Bethe , who all assumed the phonons to be in equilibrium (so-called "Bloch condition") when calculating the scattering rates of electrons caused by EPI, because of the frequent phonon-phonon Umklapp scattering. This assumption is well justified and widely adopted for the determination of transport properties of electrons at higher temperatures5,6, including the electrical conductivity and diffusive Seebeck coefficient. Below the Debye temperature, however, the phonon-phonon Umklapp process is largely suppressed, and this assumption becomes questionable. The significance of non-equilibrium phonons on the electrical transport properties and especially the Seebeck coefficient was first recognized by Gurevich7. The experimental evidence given later by Frederikse8 and by Geballe and Hull9 clearly showed an "anomalous" peak of the Seebeck coefficient at around 40K in germanium. To address this unusual observation, Herring proposed that the non-equilibrium phonons can deliver excessive momenta to the electron system via the EP1'0". This process generates an extra electrical current in the same direction as the heat flow, as if the electrons were dragged along by phonons. Therefore this effect has been dubbed "phonon drag"'0, which makes itself distinct from the normal diffusive contribution to the Seebeck coefficient derived from the diffusion of electrons. Subsequent explorations revealed that this effect exists in various materials systems, including simple semiconductors like silicon1-14 and InSb 1'1 among other
newly-emerged ones1'7 19, layered structures like Bi20 and Bi2Se32 1, lower-dimension
phonon drag is responsible for the extremely high Seebeck coefficient experimentally found in FeSb22 -28. In parallel, the theoretical picture for phonon drag has been
confirmed and further refined by more detailed theoretical models5,29-34
.
The efficiency of thermoelectric materials is characterized by the figure of merit zT, defined as zT = oS2T/Ir, where o-,S,T,iK are the electrical conductivity, Seebeck coefficient, thermal conductivity and absolute temperature, respectively. Thermoelectric energy conversion at lower temperatures (around and below 300K) can benefit a wide range of applications including refrigeration, air conditioning and cryogenic cooling35
but is also challenging mainly because the normal Seebeck coefficient drops in magnitude while the thermal conductivity increases as temperature decreases. It is therefore tempting to make use of the phonon drag effect for higher-efficiency thermoelectrics in the lower-temperature range via boosting the Seebeck coefficient. Straightforward as it seems, controversies exist as to whether zT can be enhanced at all by utilizing the phonon drag effect. Theoretical models36 concluded that the optimal zT achievable using the phonon drag effect is much smaller than 1, while the experiment on silicon nanowires has suggested the possibility of reaching zT of 1 at 200K37. The major concern lies in the fact
that significant phonon drag requires phonons to be far away from their equilibrium when subject to a given temperature gradient (or equivalently, with long mean free paths), which usually implies high thermal conductivity. So far it is not clear whether it is possible to decouple the contributions, i.e. keeping a high Seebeck coefficient while reducing the lattice thermal conductivity, the latter of which has recently become a common strategy in increasing the thermoelectric efficiency 340. A further opposition to
the use of phonon drag comes as increased doping concentration leads to reduced phonon drag, known as the saturation effect'0 . It has been generally believed that in samples with high doping concentration (crucial in obtaining high electrical conductivity), the phonon drag almost vanishes, which however is an incorrect opinion as we will show later.
The key information for a better understanding here is a mode-by-mode analysis of phonon contributions to phonon drag and thermal conductivity. With the recent development of first-principles simulation tools442 , the mode-specific contributions to the thermal conductivity have now become accessible. Obtaining the same information for phonon drag, however, can be exceedingly challenging. Ab initio calculation of the EPI, even when the Bloch condition is assumed, has already been proven difficult due to the ultra-dense sampling mesh entailed, only becoming tractable recently thanks to the invention of an interpolation scheme based on maximally localized Wannier functions4344.
A further step towards the phonon drag calculation requires an accurate description of the
non-equilibrium phonon distributions when calculating EPI, thus combining the above-mentioned two calculations, in addition to more stringent convergence conditions. We will undertake the task of examining the detailed phonon mode contributions to the phonon drag effect in silicon from first-principles and also explore new possibilities for improving thermoelectric efficiency based on the information thus revealed. In this chapter the theoretical formalism is given first for the phonon drag effect, which allows us to distinguish the contributions from different phonon modes. Henceforth, we will provide the justification of our calculation by looking at the temperature and carrier concentration dependence of the phonon drag effect compared with experiments. We then show that the phonon drag effect can be engineered to enhance the Seebeck coefficient while largely reducing the thermal conductivity by identifying the "preferable" phonon modes and filtering out others. An ideal phonon filter is demonstrated to increase zT in n-type silicon by a factor of 20 to -0.25 at room temperature, with the enhancement reaching 70 times at lOOK.
1.1. Coupled electron-phonon Boltzmann equation
1.1.1. Picture of Boltzmann equation
distributions in the real space and momentum space45. A major approximation is made
when the single particle distribution function is used to represent all the particles in the system, therefore simplifying the problem into a differential equation known as the Boltzmann equation. Simply speaking, Boltzmann equation describes the balance of the transition of one particle between various available states. There are two major causes for these transitions. One is coming from the forces (or potential gradients in a more general sense) acting on the particles, with examples including electric fields for electrons and temperature gradients for both electrons and phonons. The other originates from the interaction between the particles, also called scatterings. For convenience, the terms of the former type in the Boltzmann equation are often called drift terms while those of the latter type are referred as collision terms4 6
.
In equilibrium, the distribution functions for electrons and phonons are described by Fermi-Dirac and Bose-Einstein statistics respectively45. As the macroscopic fields start to drive the system, electrons and phonons will move away from the equilibrium, and the degree of the non-equilibrium will be determined by the strength of the scatterings5. In
general, the dynamics of electrons and phonons are coupled to each other due to the electron-phonon interaction which will become clear in later chapters, and the corresponding coupled Boltzmann equations in the steady-state can be expressed as4 6
a, (k) VT - (k)f f(k)
-f(k)f (k) (fa(k)
aT
aE T(k) &at(1.1)
V,()-I(q)q) VT = - na - ()
at(q
aT
rA(q)at
)e,,where T is the temperature, e is the electron charge, p is the electrochemical potential (incorporating electric potential and chemical potential) and the velocity vectors v for electrons ( v, (k)) and for phonons (V A(q)) are specified with wave vectors k (for electrons) and q (for phonons), as well as band number a and branch number A (in the following we will restrict our discussion to periodic solids where the Bloch band
theory applies).
f
and N represent the distribution functions for electrons and phonons respectively, with equilibrium state (labeled with a superscript 0) described by1
fO(k)
= 1-A)IkBT +1(1.2)
N"(q) = 1
For electrons, the external driving forces include the electrochemical potential gradient VV and temperature gradient VT, each of which leads to a current of electron flow4 5, while for phonons the only external driving force comes from the temperature gradient. Besides of the drift terms on the left-hand-side of Eq.
,()
VT
eva( k)a(k)vPf,(k)-f
(k) 9fa(k)aT {Va~)Af aE
E
Ta k~k~e~ph * (k) + t )e_,h (1.1), there8n (q) n,(q)-nO(q)
+rT)
(q)T
r*(q) at e-phare also collision terms on the right-hand-side, which describe the various scattering events experienced by electrons and phonons. For both electrons and phonons, there are various mechanisms that can make transitions from one state to another. Among these processes, the electron-phonon interaction is most important for our problem because it couples the electron and phonon systems, which essentially leads to the interesting phonon drag effect as we will see below. For this reason, we have separated them out from other terms contributing to the scattering events. Apart from the electron-phonon interaction, we have also considered electron-impurity scattering, phonon-impurity scattering as well as phonon-phonon scattering processes in Eq.
V,(k)- VT -ev, (k)- VP= fa(k> - ,f +k)
aT aE 11)& a(1.1). , Note
V nt (q)- q) = n.(q)-no(q) + n (q)1.
ot
aT
rz(q)
at e-phvariable ( * (k) for electrons and * (q) for phonons), called mode-dependent relaxation time. For electrons, z*(k) only includes electron-impurity scattering, while for phonons r*(q) considers both phonon-impurity scattering and phonon-phonon scattering, added together according to Matthiessen's rule. Previously it has been pointed out that in certain materials4 7'48 (for example diamond and graphene) such relaxation time model is not
accurate enough to describe the thermal transport properties. However, generally this relaxation time model leads to good agreement for the thermal transport across a wide range of materials49-53, and has been recently used to study the electrical transport in silicon4'4 , the material we will focus on in this thesis. The use of the relaxation time model will be further justified as we compare the simulation results with the experiments.
1.1.2. Electron-phonon interaction
The electron-phonon interaction couples the electron and phonon systems, and is the key factor that leads to the phonon drag effect5. In the lowest order approximation, electrons and phonons lie in their eigenstates, described by the electronic band and phonon dispersion respectively. Because electrons sit in an environment of atoms, the atomic vibrations (phonons) will therefore affect the movement of electrons. In the particle language, this means electrons can collide with phonons, making transition from one state to another (Figure 1-1). During these processes, energy and crystal momentum conservation need to be satisfied, which impose the conditions on which processes are allowed.
(a)
(b)
Ii
(c)
k
ek e+hk+qW22
Figure 1-1. (a) Illustration of the collision between electrons and phonons, (b) transitions shown in the electronic band and (c) corresponding phonon modes in the phonon dispersion. In part (a) k1 is the initial
state of the electron, which is scattered to the final state k2 via the absorption of a phonon mode q.
As we see from the illustration in Figure 1-1, the electron-phonon interaction is a three-particle process and therefore the corresponding term in the Boltzmann equation
afa(k) Vfe(k).(k) f, (k)f-f,(k) (fa(k)
va(k)- VT--eva(k)- c zVCP=- + a ep
(Eq.
aT
(k)(1.1)v(q). - VT=(q) T n,(q)-no(q) an,(q)
aT
r*(q)at
)_,iinvolves distribution functions in three different states: the initial electron state, the final
electron state and the participating phonon, each characterized by fka, fk,,' and n,,,
respectively. The rate of the transition processes (also called the scattering rate) depends on the occupation numbers of these states and typically involves prefactors like
fk, (1 - fk,,),2 (k -* k' via phonon absorption), which means for an electron to absorb
one phonon, the probability of the scattering is proportional to the probability of finding the electron at the initial state, the probability that there is position available for the electron at the final state and the number of phonons, which essentially derives from the quantum statistics of electrons and phonons.
The coupling between electrons and phonons is described by the coupling matrix element in the language of quantum mechanics. The eigenstates mentioned before for electrons and phonons are only approximations to the true states of the system. This is because in the real system, the Hamiltonian will deviate from the ideal case and eigenstates assumed for each are not true eigenstates of the whole system5. However, since usually the deviation is small, we can regard this as a perturbation to the original solutions and therefore use perturbation theory to determine the real dynamics of the system. Electron-phonon interaction is one of such perturbations, which means that the Hamiltonian, which represents the total energy of the system, has non-zero overlap
between the electron and phonon states. In an intuitive way, Bloch wrote down the contribution to the total energy due to the combined effect of electrons and phonons5 4
SE = urR -E (1.3)
_11
rR 0 r,R
where u is the displacement of the atom, r describes different sub-lattice atomic sites, R distinguishes different unit cells, and E is the total energy of the system. A simple explanation of this equation is that, as the atoms in the system move around, the electrons will adjust themselves to find the lowest energy for that atom configuration and therefore the total energy also changes. Born-Oppenheimer approximation is often assumed5,
which states that as the atoms vibrate, electrons respond so fast that they almost see a static atomic configuration and therefore finds the lowest energy corresponding to that configuration. This simplifies the problem because electrons and phonons still have their own eigenstates, and are only coupled to each other via coupling matrix element. Models go beyond this approximation often consider "vibron" which is a combined state of electron and phonon in a general sense5 5
(Note that there are also different types of vibrons suited for different problems). For our problem, the Born-Oppenheimer approximation applies well and we will restrict our discussion to this picture.
aE
The explicit coupling term, as given in Eq. SE = IUrR
rR r,R (1.3), will not be useful for the transport property until we consider how it is incorporated
into the Boltzmann equation. This is accomplished by applying the Fermi's golden rule, which determines the transition probability (or scattering rate) when the perturbation induces coupling between different eigenstates (electrons and phonons in our case). As a first step, Eq. SE IUr,R - (1.3) needs a more
r,R rR
explicit expression. As shown by Ziman5 6, the intuitive expression given by Bloch can
F
we regard uR as operator acting on the phonon eigenstates while as operator
OI"r,R
acting on the electron states. This simple interpretation clearly couples the electron and phonon system as we expect, and the electron-phonon coupling matrix element can be
explicitly described by
(n,, 1u n)-(k'aq,,Vjka) (1.4)
where we have transformed the change of the energy due to the displacement of one
OE
single atom to the potential change due to a collective atomic motion
ar,R
corresponding to a certain phonon mode with wave vector q and branch number A (defined as @qV ), which varies in the real space and will be referred as the (phonon-induced) perturbed potential.
Ika)
andIk'f8)
describe different states that are coupled through the perturbation, andjnq,)
represents the phonon state (Note that it is characterized by the number of phonons and the final state can only differ by one). The first term in Eq. (n, I u In,,)-(k'p8jjVjka) (1.4) essentially leads to the proportionality to the number of phonons as we mentioned before for the scattering rate. The second term, which includes electron states and perturbed potential, is the key element that is required for describing the scattering rates in the Boltzmann equation and thus the calculation of transport properties. For convenience, we define the electron-phonon interaction matrix element asgf6A(k,k,q) =
(
j
(k',6
I
OqV Ika) (1.5)2mco,1/
which only differs from Eq. (nqA 1 li n,) -
(k'pJ
V ka) (1.4) byh
g,6(k,k',q)= -(k'fiVaqAVka) (1.5) h is the Planck
constant and m is the electron mass.
1.1.3. Scattering rates due to electron-phonon interaction
With the electron-phonon matrix element written down, now we can apply the Fermi's golden rule to calculate the scattering rates due to the electron-phonon interaction. More specifically, the EPI-induced scattering terms (last terms in Eq.
() " T v,(k) (k)
f,(k)-f(k)
8fa(k)
V(k)a VT ev(k)aE ((k) +at
) n(I. are V,(q)(q)q)VT=-n z(q + a aT rj(q) &)e-ph t described by-jga,(k,k',q)j nqAfka 0- fkf,)S(k'-k - q + G)6(E,, - Eka - hoqA)
(af1(k)
2rr - A(kk',q)2(n., + 1)fka(1 - fk,,)S(k'--k + q + G)8(Ek,, - Ek, + hpqA)at
,_-h h k'#lqA + ga,,, (k',k,q) ( a- fk, A ,,(k-k'-q+G)(E, -
E, -hcq2)+
ga,,
(k',k, q)1 (nqA + 1)(1 - fka)fkg(k -k'+ q + G)S(Eka - Ek,, + hcoq)-Iga,
(k~k',q) nff(1 -fk)(k'-k -q+G)(E - Eka - ho) + n(k,)k2,cq) +1g(n(kk',q) (n + ()f -(1-f 6)(k'- k + q+ G) (E , -Es +hC
anA(q) 2;r I E 12ka )qA)at )ep, h 2 kak'fl g-,4(k',k, q) n1a (1- fkG)fkS(k -k' - q + G)(Eka - Ek, - hcoqA)
+ga,(k',k,q)1 (nq, +1)(1 - fka)f,6S(k -k'+
q
+ G)6(Eka - E,, + h cq)(1.6)
where the electron-phonon interaction matrix element g,6A(k,k',q) is defined in Eq.
gafpA(k,k',q)= .(k'fiaqAVjka) (1.5).
In Eq. (1.6),
Ekcand
2mocWo
Ek,, describes the energy of electron states and c,, describes the phonon frequency. The energy conservation is imposed by the last delta function while the crystal momentum
conservation is included by the delta function next to it, which describes either Umklapp process or normal process depending on whether extra reciprocal lattice vectors are required to bring the difference of the wave vectors to zero. Note that for the scattering rate for phonons there is an extra 1/2. This is because when k and k' go over the Brillouin zone each k, ->k 2 process is counted twice (let k = k, and k'=k2 or vice
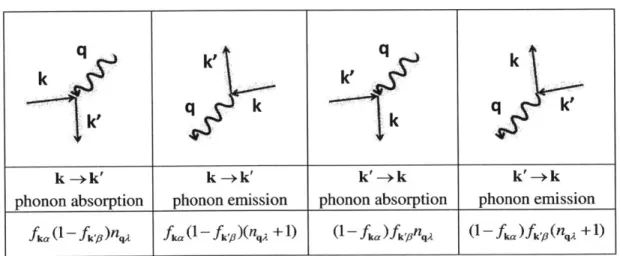
versa). Here we want to make simple comments on the physical meanings of these complicated expressions. As we expect, the scattering rates involve the distribution functions of three different states, and the dependences are clearly different for different types of processes. For the electron as an example, we list in the following the corresponding prefactors for different processes, which are similar to the phonon
absorption process (k --+ k' via phonon absorption) we mentioned above.
Table 1-1. Prefactors for different types of electron-phonon collisions
q
qk
k
k
q
k
kq
k -> k' k -> k' k' -> k k' -> k
phonon absorption phonon emission phonon absorption phonon emission
fka (1- fk'/O)qA fA (1- fki)(qI + 1) (1 f ka )fkyJOnq (1 f ka ) fk'pO(qA + 1)
Besides, the energy and crystal momentum conservation are seen as the delta functions, automatically imposed when applying the Fermi's golden rule. The scattering rate is proportional to the magnitude squared of the electron-phonon coupling matrix element and therefore the coupling matrix serves as a quantitative parameter that determines the strength of the interaction between electrons and phonons.
The solution of the Boltzmann equation described by Eq. V, (k)- "kVT - ev, (k) - " (k)
f,
(k) -fa
(k) +f()VT
aE
*a(k) &t )1_V a(q)n()VT=-na -n + na
aT rA(q) (
at
e-phcombined with Eq. (1.6) is not as straightforward as it seems. This is because it is a non-linear equation and it is generally harder to find its solutions in a robust way than solving linear equations. However, we note that in equilibrium, all distribution functions should take their equilibrium values and the scattering rates therefore vanish, because otherwise the state of the system will move away from the equilibrium (see Eq.
F
A,(k)vTev\.fa(k)v8k'
fa(k)-f
0(k)
r8fa(k)~
Va (k)- VT - ev, (k) V(P= f, k +
T
(k)
+at
)e-ph (1.1)). Thisan( (q) VT = (q) -n +(q) an t(q)
A (q) _ph-t
inspires one to take the lowest order approximation for Eq. (1.6), or the first order deviation of the distribution functions, which gives rise to the widely-used linearized Boltzmann equation:
f
([Ik):[
- F (k', q A) -Afk, + (ka,qA)- Af + F (ka,k'8)- An e~)-ph k',,qA I- k',,qA k',,qA
I,,
(q)
=I
[Gk.(k'/, qA) -Afka +Gk,,(ka,qA)- Afk]- Gq (ka,k'fl) -Anq
S e-ph ka.k'l ka,k'f
(1.7)
Fk, (k'#, qA) = [n,,+ fk",fl _(n,, +- fkg"l +
F..,,(ka, qA) = [no, + I-
fo,,)
r_ + (nq I +f,0a
F,,(ka, k'8)=
f
0 - [(Akfl 0a)-f9 -f~ UAka + (k~fl- Aa
+(1.8)
Gk,(k'#, qA)= - n +f")
+(n,,2+-f") Gs,,(ka~q) n +- fk' )H - n4+ -fk)1 G,fl(ka,k'p) = [(n - 0,H - (no - 0a with HrS=
hga,,(k,k,q)
-g(Ek, Eka -h2)-.5(k'-k-q)
S= hIg,(k,k',).5(E,, -E + h coq,2)-.(k'-k+q)
denoting processes due to the absorption of a phonon Wq2 and the emission of a phonon,
respectively. The first-order deviations Afa fk ,, - Af = fk', -f and
AnqA = n2 - n", characterize the non-equilibrium state of electrons and phonons. Note
that in Eq.
Ff
k) [ZF(k'6,qA) -Afk, + Z [F,,(ka,qA)-Afki]+ I [F,(ka,k',6)-An,
e-ph k', qA - k',,q k# qA
anG(q) ),(k'_,q)Af,+Gk,,(ka,q)-Af,]--
Gqjka,k'p) An,
eat -ph kak', _kak', I
(1.7) we have re-grouped the contributions so that the dependence of the scattering rates
on each non-equilibrium state is clearly seen. For normal electrical property calculations, the relaxation time approximation is often used. This approximation naturally arises if we assume that for the electron scattering (first line in Eq.
_ (k) F(k'p,qA) Afka + [Fk ,,(ka,qx) Afkfl] + [Fq,(ka,k'p) -Anqx] a -p h k',,qA k',,q k ,q
t () [G a (k'/,q). Afka +Gk.,(ka,q2). Afk,]- Gq (ka,k')] Anfq2
(1.7)) only the distribution of the initial state of the electron deviates from the equilibrium ( Afgk # 0 ) and that of the final electron state and of phonons remain at equilibrium (Afk,'a =0, An, =0 ), which is essentially the Bloch condition. In this case, the prefactor
before Afk, can be defined as 1/ (k). The relaxation time ir.-P(k) is what is
usually called the electron-phonon relaxation time (for electrons), which determines the intrinsic mobility of one material. We should also note that Afkf, is essentially neglected because the terms containing Afkf sum up to approximately zero. In metals and for elastic scattering with impurities, this approximation is not valid and therefore an extra correction term (1- cos 0) is often added to the electron-phonon relaxation time, which
6
is called the momentum relaxation time .In semiconductors, however, it is proved, based on deformation potential models, that for nearly isotropic scattering, the neglect of AfJ,
will not cause much difference. It has also been shown758 that without considering
Afk,,, good agreement for the electrical properties in silicon with experiments can be
achieved, justifying the approximation that terms containing Afk,'O can be neglected.
A more important perturbation term from equilibrium comes in the evaluation of the
assumption Anfq =0. It is clear that this assumption makes non-equilibrium phonons have no effect on the electron system. When phonons are far away from the equilibrium, assuming Anq,, to be zero is no longer valid. These non-equilibrium phonons described
by non-zero Anq2 in the electron system (the last term in the first line of Eq.
=f
(k)F -
j(k'p,
q Af + I Fk,,(ka, g)- Af + F,(ka,k'p)-Anq, ]a
t
),-ph _k',,A I[k', k',,A
On, (q) ) ~=ph
[kG,
(k'?, qA) -Afk, + Gk, (ka,q)- fl.J - Gq,(ka,k'8)j- An,The above picture describing the phonon drag effect is based on the Seebeck effect, where a temperature gradient induces a phonon heat flow (characterized by non-zero An,), which delivers part of its momenta to the electron system and gives rise to an extra current. Because of the Kelvin relation H = TS, an extra contribution to the
Seebeck coefficient also implies an extra Peltier coefficient. This is manifested by the first two terms in the second line of Eq.
af
(k) -[ Fk,(k'pf,qqA) Afk, + Z [F,,(ka,qA)-Afk,]+ I [F,(ka,k'p)8 -qAn]S he-ph k6qA j k',qA k',6qA
an, (q) =I [Gka(k'p,qA)- Aft. + G.,(ka, q)- fAfk,]- Ga(ka,k'p)- An,
2
at )-ph ka,k'$ _ka,k'#
(1.7), which transfer the momenta of the electron system to phonons when an electrical
current is applied through the system. We will discuss the Kelvin relation later with more details.
If we look at the last term in the second line of Eq.
-k -I Fk (k'8, qA)j- Afka +Z [F ,O(ka, q2)- Af + I F (ka,k'p) -An ,
at -ph k'#,qA k'p,qA k'p~qA
an,, (q) I [Gka (k'f, qA) -Afk, + Gk. (ka,qA)- Afk,]- Gq,(ka,k'p) -An,
at ),_ph ka,k'l ka,k# I.
(1.7), the prefactor of AnqA in the phonon Boltzmann equation can be readily written as 1 / r7-Ph(q) (just as the definition of electron-phonon relaxation time for electrons),
which denotes the process that phonons are scattered by electrons at equilibrium. As a result, higher doping concentrations (more free electrons) lead to stronger scattering for phonons. Normally when considering the phonon relaxation times, the electron-phonon scattering is neglected because phonon-phonon scattering dominates the scattering processes. However, as the doping concentration increases, there will be increasing probability that phonons get scattered by electrons. It is found from the simulation that this phonon scattering by electrons account for some fraction of the reduction of the thermal conductivity in heavily-doped materials59. Furthermore, as we will see in later
chapters, it is also responsible for the reduction of the phonon drag effect in heavily-doped samples compared to lightly-doped samples (the saturation effect).
Having discussed the meaning of each term in Eq. Va(k)-
af"(k)
VT aT v (q)- an(q) VTaT
-ev,(k) - " EK
=-nA(q) -n (q) + r(q)f,(k)-
f(k)
r (k)ang(q)
Nat
)e_,h +( aat
e(k))
)ep/
(1.1) and Eq.
af, (k) =-[
Fa(k'#, qA) -Afk
I
t )e-ph k'$,,A kIa'an
2(q)
I-Z [Gk (k'#,qX)-Afka+ at e-ph ka,k'#+ I [Fk(ka,q)-Afkj+ F
[pt(ka,k'fl)-An,,
k',,A k'#,,A
Gk.,(ka,qA)-Afk,, - Gq,(ka,k'8) -An ,
ka,k'p I
(1.7), now we want to make the inclusion of these scattering terms more compact by
rearranging them. If we incorporate the first term of the right-hand-side in the first line of
Eq.
tf
(k) -[I:
Fk,, (k'8, qA) -Afka a e- ph _k',,A I an(q) Z [G,(k'8,q )Afa+ at e-ph ka,k'+ I [F,,,(ka,q2)-Afk,]+ I [F2(ka,k'6)- An,,
k'6,qA k',Aq
Gk,,(ka,q)-AfkJ- - Gq,(ka,k'p)]-An,
2
ka,k' I
(1.7) and the last term in the second line of Eq.
t
[(k) -Z F(k'8,qA) -Af + Z [F,,(ka,qA)-Afkf]+ [F(ka,k'p)-Anq1
)e-ph k'qA k',,A k',,A
at
[Gk (k',q2)- Afa +G,, (ka,qA)- Af - 2 '
),-ph ka,k'# ka,k'6I
(1.7) into the relaxation times
v,(k) '(kVT-eva(k)J- "V( =0
VA(q)-n VT=- n. (q)-n ) n
aT r*(q) at
coupled Boltzmann equation now becomes
we already
k)-f
(k)
r,(k)Je-ph
have in Eq. f(k)N
at
)e_,h(1.1),
the
t
" =_f - "(k)-f:(k)+
Z
[FkF,,(ka,qA) - Afk,,]+ Z [F,2(ka,k'p)-Anqjat
d,,ft r,(k) k,',qA k,8,qAang(q)n,, (q) -no ()S -(q +
Z
[Gk,(k'p,qA)-Afka +G,,(ka,qA)- Afk,)o
at
,ri A(q) ka,k7,((1.9)
where new relaxation times include part of the electron-phonon coupling (scattering of electrons by equilibrium phonons as well as scattering of phonons by equilibrium electrons) = +F,(k'O, qA) r()r(k) 'Oq'-a (k) (1.10) = -- k) + GqA(ka,k'p8) A) r,(q) kak
and the remaining terms describe the coupling between non-equilibrium states in the electron and phonon systems.
1.2. Phonon drag effect
We have above derived the coupled electron-phonon Boltzmann equation in a compact
form as shown in Eq.
", = k - O "k + Z [Fk,,(ka,qA)- Afk,,]+ Z [F,,(ka,k'p)- Anqj
at
ift r,(k) k'/,qA k,,,q2an-(q) n, (q)-no(q) + I [Gk.(k'pqA)- Afk, +G, (ka, qA) -Afkj
at
),if, Tr(q) kak'p(1.9). The electron relaxation time ra (k) incorporates electron-impurity scattering and
electron scattering by equilibrium phonons, while the phonon relaxation time T. (q)
contains phonon-phonon interaction, phonon-impurity scattering and phonon scattering
by equilibrium electrons. The coupling through the non-equilibrium distribution is
t
=- "(k f(k+ I
fF,( [ (ka,qA)-Afk,,]+ F [, (ka,k'8)-LAnq,,
at
dft -r,(k) kflqAn. 2(q) - no(q) + Z [Gka(k'fl,qA)- Afka +Gk (ka,qA)- Afkf]
at
)dri r(q)(1.9), which are responsible for the phonon drag effect. In this section we will derive the
phonon drag Seebeck coefficient based on these equations.
We will adopt the Peltier picture, where an isothermal electric field is applied to drive the coupled electron-phonon system. We choose this approach because it directly provides the phonon drag contribution from each phonon mode. The derivation based on the Seebeck effect will be discussed in the next section, which clearly shows that the fundamental relation between the Seebeck coeffient S and Peltier coefficient I
-Kelvin relation - still applies to the phonon drag effect.
For the Peltier effect, a non-equilibrium distribution of electrons Afk, is generated first by the electric field, which will then drive the phonons away from the equilibrium. However, the determination of Afk, requires the knowledge of Anq. , which also appears in the electron Boltzmann equation and makes solving fully-coupled Boltzmann equations a formidable task. One further step towards solving Eq.
" = " ,f (k) , -+ 1 [F1,,(ka,q2) -Afk,,]+ E [F2(ka,k'p)- Anq,
at
raf T,(k) k,',qA k,,,Aan(q)J - (q) -ni(q) + [Gka(k'f,q2)
Afka +Gk,,(ka,qA)- Afk,]
at
)dri rA(q) ka,k'#(1.9) is to realize that the influence of the current-induced non-equilibrium phonons on
the phonon drag effect, indirectly through affecting the non-equilibrium electrons, is a higher-order effect, which can be justified by the fact that the phonon drag phenomenon is found to have a small influence on the electrical conductivity. Therefore for the electron system, we can then assume that phonons are at equilibrium (An,, =0 can be assumed in the first line of Eq.
[ =)t,(k - " ) "(k) + Z [Fk, (ka,qA)- Afk,,]+ I [F,,(ka,k')#)-An ]
rft
,ra (k) k,',q k,6,,A
An
2(q) n2(q)-n"(q) + Z [Gk,(k'#,q)- AfG +Gk,,(ka, q)- Af],,)
&t ,,rr(q) ka.k,/
(1.9) and note that for the Peltier effect the phonon drag comes in through the last term in
the second line of Eq.
"a = k) -) "(k) + I [F,,(ka,qA)-Afk,,]+
I
[F2(ka,k'i)-Anq2]
at )dft ra (k) k,',qA k/J,qA
n,,(q) n q
S( n2(q)-n(q) + [Gka(k'p,q) -Afka +G,,(ka,q)- Afk,)]
at drif, -rA(q) ka,k',i
(1.9) instead of the last term in the first line). As a result, the electron-phonon Boltzmann
equation can be partially decoupled, which leads to a feasible computational approach for calculating Sph (phonon drag contribution to the Seebeck coefficient). Now the electron distribution function can be directly written down using the relaxation time model
Afea e avk = - (see Eq.
V,(k) (VT-ev(k) "(k) f,(k) _f_(k) (
aT a E r(k) +
at
)e_,h01 T(qk) -a
eno(1.1);
hereVA (q)- VT=-n A)- (q) + n~q
IT -r(q)
at
)e-phwe also assume that the term F,(ka,qA)-Afk,,] will vanish, which is a
k',f,qA
commonly used approximation as discussed in section 1.1.3). The normal electrical conductivity and Peltier coefficient (related to the normal Seebeck coefficient via the Kelvin relation II= TS) can be obtained by looking at the charge current and energy current induced by such a non-equilibrium electron distribution, respectively:
< af=V(E- ka kI 2
3
"."
(E -pfkaOr13Nk kA )/(V) 3Nk I aka DE)
KNk k(-lVxafc;a/ 3Nk ka J(1)
= e (E f1)Va "
3o7Nk ka k &E)
where o- is the electrical conductivity, H is the Peltier coefficient due to diffusion of electrons and Nk is the number of points in the discrete reciprocal space mesh for electrons. The Peltier coefficient shown here, only includes the energy current of the electrons, and will be denoted as "diffusive" Peltier coefficient Haif in the later part (and corresponding diffusive Seebeck coefficient Sdaff). Besides this, the energy current also has its origin in the phonon heat flow. As we have discussed, in the isothermal condition the phonons acquire the momentum via the electron-phonon coupling shown by the last term in the second line of Eq.
" =- , ( + Z [F,,(ka,qA)-Afkfl]+ I [F,(ka,k'#f)-An]
at
)dri, -r (k) k,,,, k',f.qAI(n,(q)
_ _n (q) - n (q) +Z
[Gka, (k'6,q)- Afka + Gk,, (ka, q2)- Afk,,)at
,drift -r(q) ka,kfl(1.9) and lead to an extra heat flow, which manifests the "phonon drag" effect (In this
case "electron drag" might be a more suitable word). Given the electron distribution
Afka, the phonon Boltzmann equation now becomes
n,(q)-no(q) +eV r= af[G#
-(q) +e rp kaG ,(k'fJ, q2)re Vka +Gk,, (ka,q),rkv, E
kaf(q)
Lak,
aE
aE
(1.12) where the drift term vanishes because there is no temperature gradient. It can be readily solved to obtain the phonon distribution function
An,(q) = r( - G (k'V,qk)va " +Gk,,(ka,qA)rkv,, V W
ka,k', f l
(1.13)
Considering the heat flow described by q= hoqvq,,AnA and the Kelvin relation, we finally arrive at the formula describing the phonon drag Seebeck coefficient:
Sph= 2 2 Jhq,~qAq~.* (TkaVka _'kfiVkflk41kfllq
h
3onNkNq kT q
L-
,kakf,fa(1.14)
with HI= r gafl(k,k',q) .(Ek, - Eka - hoq)- 5(k'-k -q)
where e is the electron charge, u is the electrical conductivity, 0 is the unit cell volume, Nk and Nq are the number of points in the discrete reciprocal space mesh for electrons and phonons, and the term inside the bracket of Eq. (1.14) is the phonon drag contribution (neglecting the common prefactor) from each phonon mode. Equation (1.14) essentially describes the momentum delivery from non-equilibrium phonons to the electron system via EPI. The total Seebeck coefficient is obtained by summing the diffusion contribution and the phonon drag contribution, i.e. S = Sdif + .ph*
Here we briefly comment on the various models used by previous work to study the
10
phonon drag effect. In Herring's original paper , an intuitive formula was used to estimate the phonon drag magnitude, which is proportional to the relaxation time of phonons that can deliver the momenta to the electron system and inversely proportional to the relaxation time of the electrons. A more rigorous analysis based on solving coupled electron-phonon Boltzmann equation was also discussed, with the results mostly focused on the scaling analysis'0. Following this, Ziman introduced a variational method to solve the coupled electron-phonon Boltzmann equations5, by first recasting the Boltzmann equation into a variational form describing the entropy generation rate in the system. Therefore solving the Boltzmann equation, in Ziman's approach, becomes a functional minimization problem. Using this method, Ziman showed the order of magnitude of the
phonon drag Seebeck coefficient in metals is around a few kBT . Bailyn further extended this variational method to study the phonon drag with more details 29. There are some major assumptions used by Bailyn: (1) For phonons, dominant phonon-phonon scattering is represented by relaxation time approximation; (2) For electrons, impurity scattering (and possibly electron-electron scattering) is represented by relaxation time approximation; (3) The electron-phonon interaction is represented by transition
probabilities, with assumed perturbation potential. The first two assumptions also serve as the basis in our derivation, but the model of deformation potential is no longer required because the information of perturbed potential can be obtained from first principles calculations.
Our formula presented above is identical to the results given by Cantrell and Butcher32
who assumed weak electron-phonon coupling to ignore the effects of non-equilibrium phonons back on the phonon system (Seebeck picture). It was argued for GaAs that the electron-phonon scattering indeed can be neglected when considering the phonon transport. However, our previous derivation has shown that this assumption can be relaxed and in later chapters we will demonstrate that a wider agreement with experiment can be achieved within this formalism. Particularly, we will study the whole doping concentration range with the saturation effect taken into account, which is crucial for evaluating the thermoelectric property (typical thermoelectric materials have high doping concentrations) but not examined by previous work.
1.3. Kelvin relation for phonon drag
The above derivation is based on the Peltier picture, for which an isothermal electric field drives a charge current, which transfers the momenta to the phonon system and gives rise to an extra heat flow. Here we want to further clarify the phonon drag effect in the context of the Seebeck effect, which completes the picture and provides a clear proof for the Kelvin relation applied to the phonon drag effect.
For the Seebeck effect, a temperature gradient drives the phonon flow, which then transfer their momenta to the electron system via the non-zero Anfl appearing in the electron Boltzmann equation (last term in the first line of Eq.
= - f a(k)f(k) + Z[F,(ka,q)-Afk, ]+ [q,(ka,k'6).Anq,
at drift
-a
k,(k) k',,2- 2(q) - nG(q) + I [G, (k'fl,qI) Afk, +G,,,(ka,qA)- Afkf)
at
)drif, - TA(q) k,k', fk,(1.9)). Similar as before, we realize that the influence of non-equilibrium electrons on the
phonon drag effect, indirectly through affecting the non-equilibrium phonons, is a higher-order effect (i.e. Afk, 0 can be assumed in the phonon Boltzmann equation).
Accordingly the non-equilibrium phonon distribution can be directly expressed as
n0
AnqA2 = rqAv,2-VT q, and the electron Boltzmann equation in Eq.
aT
a=ak - kL(k) + Z [F,(ka,qA)- Afk,,]+ [,(ka,k'6)- Anq,]
at
drft r,t (k) k,',q W,6,Bngn ()n(q) - n"(q)
a )
=- ) ) + I [Gk,(k',q2)- Afk, +Gkfl(ka,qZ)- Afk,,]at
,,, (q) ka,kf,(1.9) can then be readily solved given the phonon distribution function (for the electron
Boltzmann equation we again assume that the term [,(ka,qA)- Afk, F ] will
vanish). Considering the electrical current density described by
j
= e Vkagfka, afrka
some rearrangements we will find that the same equation (Eq. (1.14)) is derived, describing the phonon drag contribution to the Seebeck coefficient.
We note that the two methods' merging into the same result is not a coincidence. In fact the Kelvin relation can be derived from a more fundamental law - the Onsager's reciprocity theorem. This theorem states that linear reciprocal processes (examples include thermoelectrics, piezoelectrics, pyroelectrics, etc.) are not independent of each other, and simple relationships can be established essentially originating from the detailed
balance under the time-reversal symmetry. In our problem, since the time-reversal symmetry is not broken, the Kelvin relation should still applies as for the normal diffusive Seebeck coefficient (and Peltier coefficient).
1.4
Experimental investigation into phonon drag
Apart from the experimental work mentioned in the beginning of the introduction in which the phonon drag is discovered in various materials, here we discuss some of other experimental work that dived into the details of the phonon drag, which potentially lead to further manipulation of the phonon drag effect.
One difficulty associated with phonon drag is that simple thermopower measurement cannot distinguish between the contribution from the diffusion of electrons and the phonon drag effect. At low temperatures, it is believed the phonon drag dominates the measured Seebeck coefficient since theoretical models predict a low value for the diffusive Seebeck coefficient. At higher temperatures (for example around room temperature), however, the phonon drag effect becomes weaker, and as a result there is ambiguity in how much the phonon drag contributes to the total Seebeck coefficient. The experimental work by Trzcinski et. al. seeks to provide such information by "quenching" the phonon drag contribution at room temperature 60. They designed a point contact device where two tips make contact only at a small region, where the temperature gradient is applied across the point contact and the voltage bewteen the two ends is measured. Because phonons that contribute to phonon drag typically have long mean free path (a qualitative understanding since Herring's work'0), it is expected that the Seebeck coefficient will decrease as the phonon drag makes less contribution if the contact area is reduced. In this way, they found that the phonon drag still plays a role at room temperature. However, because it is not clear how much the point contact geometry destroys the phonon drag, it is hard to reach quantitative conclusion on the contribution of the phonon drag.