SEPTEMBER 1991
LIDS-P-2066
APPLICATION OF MULTIVARIABLE DESIGN TECHNIQUES TO
ROBUST CONTROL OF A LARGE-SCALE SYSTEMS
by
Kelly D. Hammett, John R. Dowdle, Michael Athans
and Karl W. Flueckiger
AIAA-91.2833;Cp
APPLICATION OF MULTIVARIABLE DESIGN TECHNIQUES TO
ROBUST CONTROL OF A LARGE-SCALE SYSTEM*
Kelly D. Hammett *, John R. Dowdlet, Michael Athans , and Karl W. FlueckigerL
The Charles Stark Draper Laboratory, inc.
555 Technology Square
Cambridge, MA 02139
AbstractReducing plant order consequently introduces unmodeled Typical issues and tradeoffs resulting from dynamics into the system, which must then be application of various modern multivariable controller accounted for via stability and performance robustness design techniques to large-scale systems are illustrated considerations. Additionally, parametric errors in the herein by synthesis of robust H2 optimal, H,- optimal, open-loop system model invariably exist, and their and H.. loop-shaped compensators for a space-based laser effects must be considered. The lightly damped nature of bearmr control example problem using reduced-order typical large-scale systems is also a design issue of models. A design framework is adopted which allows concern, leading to extremely slow oscillatory transient stability robustness in the presence of resulting responses, and, due to the location of lightly damped poles near the complex plane imaginary-axis, potential
neglected dynamics to be guaranteed via unstructured
uncertainty representation and the Small Gain Theorem,n obtaining closed-loop stability andor and performance robustness to be independently verified.
Infinity-norm bounds on two closed-loop transfernfunctions provide the key figures-of-merit foer This paper addresses several of the above issues in
functions provide the key figures-of-merit for
the context of multivariable feedback design for a chosen
guaranteeing the desired stability robustness and nominal context of muluvaable feedback design for a chosen performance A final design is obtained conditions. example problem. The results presented in this paperperformance conditions. A final design is obtained
which is verified to meet nominal performance st control ofinuing research effort focusing on specifications, and is also seen to possess robustness of robust control of large-scale systems. Previous both stability and performance to dynamics truncated in researchl discussed mode ultivaiable design
the model reduction process. The effects of open-loop methodologies, and addressed possible application t pole parametric uncertainty are also examined, the main primary mirror beam jitter control of a space-based laser result observed being a severe degradation in closed-loop (SBL). In a subsequent work2, H, optimization and
system performance. reduced-order models were employed to perform
requirements analysis for the combined beam jitter and 1. Introduction segment phasing aspects of the SBL beam control problem, and preliminary H2/H,. designs were The complexity of large-scale dynamic systems examined. The results given in this paper extend the provides a challenging proving ground for modem results of the previous research to include application of multivariable control system analysis and design loop-shaping design methodologies to 6btain a final techniques. High plant dimensionality inherent in large- design which meets specified beam jitter/segment scale systems can lead to breakdowns in numerics of phasing performance objectives, and possesses both state-space algorithms or intolerably long computational stability and performance robustness to modeling errors times, necessitating use of model reduction techniques. introduced during the model reduction process. Additionally, the effects of open-loop pole parametric This paper was prepared by the authors under uncertainty on closed-loop stability and performance are Independent Research and Development funding at The investigated. In Section 2 of this paper, details of the Charles Stark Draper Laboratory, Inc. SBL analyzed are given. Section 3 describes the ** 1 Lt. Kelly Hammett (USAF) is a C.S. Draper application of model reduction techniques, and Section 4 Laboratory Fellow, graduate student at the covers the robustness analysis and compensator Massachusetts Institute of Technology, Cambridge, synthesis methods used for control system design. MA, and Student Member AIAA. Section 5 presents results of controller synthesis t John Dowdle is Chief, Flight Systems Section, utilizing various compensator design techniques, C.S. Draper Laboratory, Cambridge, MA. comparison of which allows selection of a best design.
t Michael Athans is a Professor of Electrical Section 6 then verifies performance of the chosen Engineering, Massachusetts Institute of Technology, compensator design via time-domain simulation with
Cambridge, MA. stochastic disturbance inputs. Finally, Section 7
£ Karl Flueckiger is a member of the Technical Staff concludes the paper by addressing performance C.S Drap aborato kiger Cambridge, MA. robustness and parametric uncertainty issues.
chosen for illustration of design issues is a wide-field-of each primary mirror segment in three orthogonal view rapid-retargeting space-based laser (SBL) with directions, thereby enabling desired Cool unCon o0
features typical of large-scale flexible space structures. be accomplished The secondary mi.rror Ismaled as a
Before proceeding further, a brief and somewhat general rigid body kinenatically mounted by cmntrd atum to description of an assumed SBL physical system concept the tripod metering truss, although the secondary mirror and relevant terminology is presented to facilitate actuators are not employed in this study. Te bulkhead
discussion. and metering trusses are modeled using beam bending
elements, and additional lumped masses arm included in The envisioned spacecraft includes both the flexible the finite element model to account for all nonstructral forward body, referred to as the beam expander assembly masses, such as the mirror electronics and target tracker. (BEA, see Figure 1) due to its primary purpose of laser
beam pointing and magnification, and the aftbody, which houses the laser generating equipment and satellite attitude control system. While these two major components necessarily interact dynamically, the
analysis of the forward body is the most critical due to 4
its structural flexibility and importance to beam control functions, and, therefore, this study addresses only the
performance of the beam expander with the structural 1
model "isolated" from the aftbody. The role of the aftbody is limited to imparting two vibrational torque disturbances to the forebody via an imperfect gimbal isolation subsystem, thereby necessitating active feedback control of the BEA optics. A finite element model of the BEA, described in Section 2, was derived to facilitate control system design.
t.4m
Figure 2. Primary Mirror Segments and
BACXa LPEro^iRv suwo:~rr Segment Phasing Measurement Locations.
:YI-zt ,b,:~ ~ ~SECONOARY Since the ultimate objective of a space-based laser is
.
//1/ MD)M
to destroy targets by the efficient transfer of energy, MA" God l omen optimizing worst-case laser wavefront quality and
-'-U -r - - - pointing performance in the presence of the assumed
fl w.Om
to an
C Of
torque disturbances is identified as the primary SBL1
.t-a to1.0 961 a z m control system requirement. Therefore, for a given level
80T0 I\v xUESw of disturbance torque (characterized by a bound on its
r r~10.0 M \\\Y
z
root-mean-square (RMS) value), system performancespecifications are identified as minimizing RMS beam deviation from the desired aimpoint (jitter control) and simultaneous minimization of RMS longitudinal
tZ0 m separations between primary mirror segment edges
(segment phasing). Such segment edge separations Figure 1. SBL BEA Concept. induce destructive optical interference, aberrating the laser wavefront, and thereby degrading beam quality.
2. The SBL Model Note that laser beam wavefront aberration due to
deformation of the primary milror segments themselves The optical design of the SBL beam expander is not considered in this study. An outgoing wavefront consists of a 10-m diameter paraboloidal primary mirror sensor (OWS), collocated with the secondary mirror, with a 12-m focal length and a confocal secondary mirror measures line-of-sight (LOS) jitter errors in the plane with a 0.8-m focal length and a 0.67-m diameter. Due normal to the line of sight, while six segment edge to deployment and manufacturing limitations, the sensors provide information necessary for segment primary mirror is composed of four segments or petals phasing control (reference Figure 2).
attached to rigid reaction structure plates (one center and
three outer segments, see Figure 2). Each segment Finite element analysis provides a modal model of reaction structure is in turn kinematically mounted by the system, consisting of 195 structural modes, which six segment position actuators to a graphite-epoxy in turn is readily transformed into a state-space system bulkhead truss. The six segment position actuators per representation consisting of 390 states, i.e.,
petal provide six independent degrees-of-freedom for
y = Cx + Dr system input/output behavior as the first 68 states,'ad may thus be removed from the system model. 7
where x represents the system's 390 states, y consists of
the 2 LOS jitter sensor measurements at the OWS and 6 . . segment phasing edge gap measurements, and r is a I concatenation of the primary mirror's 24 rigid body 0 segment position actuator commands and 2 disturbance
inputs creating moments ?bout the base of the mirror. I (A damping ratio, C, of 0.005 is assumed for all
structural modes.) This linear state-space model can be " ' employed in model reduction techniques and modern
multivariable linear systems analysis, as illustrated in Sections 3 and 4.
3. Model Reduction
0 0o 100 15o 20o 250o 1300
Due to the large dimension of the state-space model c e oa a
developed, reduction of model order is necessary to ease
the computational requirements associated with control Figure 3. B&T Reduced Order Model Absolute Error. system design. A thorough and systematic treatment of
reduced-order model (ROM) development was published Additionally, examination of individual by Moore3. The technique proposed by Moore, which observability and controllability gramians from the is often called balance and truncate (B&T), uses a state- separate disturbances and actuators reveals that while the space representation (A,B,C,D) of the plant describing six rigid body mode pairs are very observable in the the relationship between the inputs, states, and system outputs, they are almost totally uncontrollable measurements in which the respective steady-state from the system segment position actuator inputs. controllability and observability gramians Consequently, rigid body motion of the BEA must be controlled by other actuators, and, therefore, the rigid body modes can be removed from the system model. P = exp(At) BBTexp(ATt) dt Doing so yields a 56 state ROM of the BEA for control
;Jo
system design purposes. The maximum singular valuebode plots for the full-order model (FOM) and the 56-state ROM, both with the 12 rigid body 56-states removed,
Q
= exp(ATt)CTCexp(At) dt appear in Figure 4. As is evident from the figure,application of the B&T method gives a ROM that includes the important low-frequency structural modes, are diagonal and equal. The diagonal elements of the while neglecting the much higher frequency bending gramians, referred to as Hankel singular values (HSVs), mode dynamics.
provide the basis for model reduction. Large HSVs correspond to states that are easily controlled and observed, while small HSVs define states that are difficult to control and observe. Thus, the state-space model can be partitioned into strongly and weakly
controllable/observable states and the subspace of s 0 FM
weakly controllable/observable states may be deleted. In Figure 3, a plot of absolute modeling error
versus ROM order for the SBL BEA model, as measured : by the infinity-norm, is given for the B&T method.* A 20 significant knee in this plot is seen at order 12 where all 0
six rigid body mode pairs of the BEA are included in the 101 1
ROM, and another pronounced knee is found for a ROM UQUY ()
of 34 mode pairs (68 states). This suggests that states
beyond the 68-state level are not as significant to the Figure 4. Full-Order and 56-State ROM Maximum Singular Value Frequency Responses. Let Gk denote a kth order ROM approximation to 4. A Framework for Robust Control System Design the plant, G. The absolute error is given by IIG -Gkll,,,
where l1TIT1 indicates the HO-norm (or infinity-norm) of Model reduction introduces errors into the design T (i.e., the maximum singular value of the transfer model that must be accounted for in system stability and
techniques that ensure both stability and performance in
the presence of modeling errors are required. For the 2 i
SBL BEA segment phasing/jitter control problem, analysis with the well-known Small Gain Theorem (SGT) in combination with an appropriate controller
design technique such as H2 or H, optimal control G (3Y provides a suitable framework for robust control system
design. Such a framework is convenient because it
allows both stability robustness constraints and nominal Figure 6. ROM with Modeling Error. performance conditions to be simply posed in terms of
bounds on infinity-norms of certain transfer functions. Since the disturbance torques (and assumed measurement noise) provide the primary limitations on how small the segment phasing and LOS errors may be kept, nominal system performance can be characterized in terms of the frequency-dependent transfer from a combined disturbance
vector, d, to a combined LOS and segment phasing error vector, e, while stability robustness may be guaranteed
in terms of the following argument. For the system G (s) depicted in Figure 5, the Small Gain Theorem states that
the nominally stable plant M(s) is stable for all stable u
perturbations A(s) if IIM(s)llollA(s)Ill < 1. Y
/- i(|)- :C ,2 Figure 7. 3-Block Open-Loop Plant.
These nominal performance and stability robustness Figure 5. Topology for the Small Gain Theorem. conditions may be restated more clearly by considering Figure 8, which illustrates the closed-loop transfer Consider Figure 6, where G(s) represents the open-loop function from w and d to z and e, obtained from setting
plant ROM transfer matrix, AM(S) is the error due to u = K(s)y. model reduction modeled as a multiplicative error at the
plant output, u represents the actuator commands, and y
includes the measured LOS and segment phasing errors. M(S) Further, assume without loss of generality that
IIAM(s)IIl < 1i. The block diagram of Figure 6 can be
augmented to include the disturbance and performance
signals, d and e respectively, as shown in Figure 7, and z
scaling may be performed so that the disturbance is RMS bounded by unity (i.e., cd < 1) and nominal
performance specifications are met if ae < 1. Since the d T(s) e infinity-norm of a system transfer function bounds the
ratio of the associated output/input RMS values, an Hoo
performance optimization problem may be constructed
to minimize the infinity-norm of the closed-loop transfer Figure 8. Closed-Loop Transfer Function. from d to e, and if this quantity can be made less than 1
(implying nominal performance specifications are met), Since the closed-loop transfer function, T(s), can be then stability robustness may be ensured via the SGT by partitioned such that
verifying that IIM(s)ilJllAM(s)l 0o < 1.
z = 1 [_Tl l(s) T1 2(S)
[w]
le] = T21 (s) T22(s) ld
then, in the context of the framework discussed above, * Scaling of Am is easily incorporated into the plant nominal system performance specifications are met as by augmenting frequency-dependent weighting functions long as
ITT22(s)ll, <_ 1 from Figure 9, both controllers result in achieving nominal performance specifications (closed-loop transfer and stability robustness is ensured if infinity-norm from d to e less than 1 (0 dB)), but the Hoo response is flatter and has a smaller infinity-norm (5
irT1 (s)II <c 1 dB less) than the H2design, indicating better worst-case disturbance rejection properties. From Figure 10 it is A two-Riccati equation algorithm4, commonly clear that both unconstrained bandwidth designs violate referred to as y-iteration, provides an efficient solution the stability robustness test of the SGT. This seems to to the H,4 optimization problem. Also, although be occurring due to high gain being injected by the performance objectives for the example problem controllers at high frequencies, where a large modeling considered have been posed as minimizing the infinity- error exists due to neglected high-frequency dynamics. norm of a certain transfer function, the design framework m
presented is compatible with other controller synthesis
techniques such as H2 optimal control, for which I standard solution methods are well known.
Additionally, another suitable compensator synthesis
technique is HF loop-shaping, which results from y , .
augmenting frequency-dependent weighting functions to . . ...-.
the system errors and/or controls, and applying the y- z3 .02
iteration procedure to the resulting augmented plant. Results of application of all three of these design methods to the BEA segment phasing/jitter control problem are presented in Section 5.
Before leaving this section, however, it should be FREQUENCY (rad/s) mentioned that the framework for robust control system
design presented here addresses only stability robustness Figure 9. Open- and Closed-Loop Transfer from d to e. issues, and allows no general provisions for testing the
robustness of performance. Performance robustness, or the guaranteeing of system performance in the presence of uncertainty, is not specifically designed for in the example problem. Performance robustness of the final design selected is, however, independently assessed in
Section 7 for certain known types of system errors. '
5. Compensator Designs
Results of application of the various compensator H-2
synthesis techniques are now presented. Arbitrary H
bounds selected for the allowable RMS values of the
disturbance torque, segment phasing, and LOS error ... - ____
vectors are 0.35 Newton-meters (N-m), 0.15 FReOUENCY (r-a)
micrometers (pm), and 0.10 microradians (prad)
respectively. Insignificant sensor noise is assumed. For Figure 10. Closed-Loop Transfer About AM (T Dl). purposes of convenient comparison, only maximum
singular value response plots of the T1 1and T22 blocks To verify this, consider Figure 11, which shows the of each design and associated compensators are shown. maximum singular value frequency responses of the Note that the disturbance and error vetors have been unconstrained bandwidth H2/H, compensators. The
scaled as described in Section 4 so that
ad,
ae < 1.high bandwidth nature of these compensators is obvious Figures 9 and 10 show open- and closed-loop from the figure, as they can be seen to indeed inject very transfer maximum singular value plots from d to e and high gain at high frequencies, creating a possibility for about AM, respectively, for unconstrained bandwidth H2 excitation of the truncated bending mode dynamics, andleading to possible instability due to high-frequency gain considerations. Thus, from Figure 11 it is obvious why said to be of unconstrained bandwidth because although the unconstrained bandwidth closed-loop systems violate both the H2and H,,o optimal control algorithms require the stability robustness test of the Small Gain Theorem. inclusion of some multiple of all the controls in the
system error (performance) vector, for these designs that multiple was chosen to be very small. As can be seen
H-mtH
SIW 11
-H-2
FREQUENCY (radl&) FREQUENCY (rd/s)
Figure 11. Unconstrained Bandwidth Compensator Figure 12. Open- and Closed-Loop Transfer From d to e Maximum Singular Value Frequency Responses. (Controls Penalized).
Traditional means of overcoming this high gain, . high frequency problem involve increasing the constant
multiple control penalty portion of the system error 'u
vector to a significant level. This tends to limit the H f i
amount of gain injected by the compensator at all Ha2
frequencies so that the system bandwidth is decreased,
which is desirable from a stability robustness point of v view, but also has the undesirable consequence of
degrading low-frequency performance. Stability / robustness is obtained via this technique by increasing
the penalty weighting on u until the gain injected at high frequencies diminishes enough to offset the large modeling error present.
FREQUENCY (rad,)
Figures 12 and 13 show open- and closed-loop
transfer maximum singular value plots from d to e and Figure 13. Closed-Loop Transfer About AM (T11) about AM, respectively, for H2 and Ho designs with an (Controls Penalized).
error vector that has been augmented with a suitably
large control penalty term. The figures indicate that (40 dB) drop in gain injected at low frequencies as stability robustness is attained with both designs by compared to the unconstrained bandwidth designs frequency-independent penalization of u, but at a price of (reference Figure 11), resulting in the robust designs' sacrificing about one order of magnitude (20 dB) in observed degradation in nominal performance. This is closed-loop d to e infinity-norm, so that nominal the expected result of constant control penalty, which performance specifications are no longer met. Thus, acts at low as well as at high frequency.
although the constant control penalty reduced bandwidth
designs are robustly stable to the truncated dynamics and
do outperform the open-loop system, their disturbance rejection performance properties are unacceptable.
To gain more insight into how stability robustness
H-has been achieved with these designs, consider Figure
14, which shows the maximum singular value frequency M responses of the robust H2 and H,o reduced bandwidth z M compensators. The most significant point to be
observed from the figure is that now both compensators S are rolling off the injected gain at a frequency of -100
rad/s, which allows the designs to meet the stability
robustness test of the Small Gain Theorem. Also V . .u .
important to note is the over two orders of magnitude FREQUENCY (rads)
Figure 14. Robust Compensator Maximum Singular Value Frequency Responses.
From the results presented thus far, it can be seen 3
-that penalizing the system control at all frequencies m
proves effective in attaining closed-loop stability -robustness, but results in an unacceptable degradation of
system disturbance rejection performance, particularly at
low frequencies. Alternate means of achieving stability U ·
robustness without greatly sacrificing achievable
performance are therefore required. From Figures 11 and Z 14, it seems that what is needed is a methodology that
induces the compensator to inject higher gain at low n frequencies (thereby improving performance), while still
forcing a fast roll-off of gain at high frequencies in order to meet the stability robustness constraint This design,
objective suggests the use of frequency-dependent design FREQUENCY (rads)
techniques, otherwise known as loop-shaping methods.
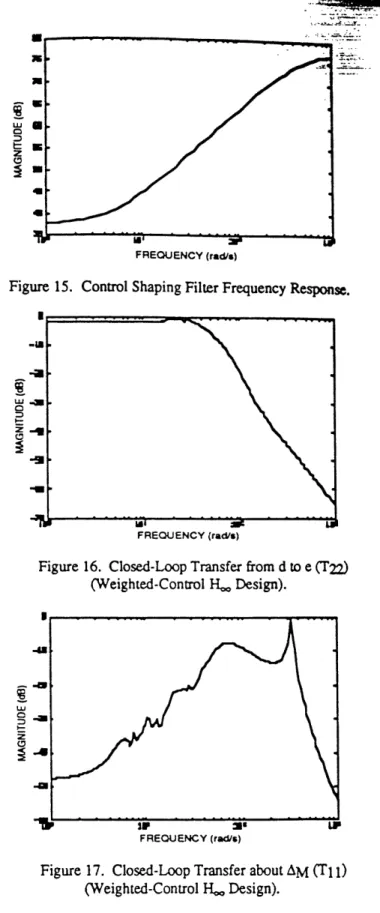
Figure 15. Control Shaping Filter Frequency Response. As mentioned previously, the technique of H,
loop-shaping is carried out by augmenting frequency- .
dependent weighting functions to the system -u
performance vector, and subsequent solution of the H, Riccati equations in the y-iteration process. For the problem at hand, the results shown thus far suggest that frequency-dependent penalty of the controls portion of -the performance vector offers hope for an acceptable -solution to be obtained. Penalizing the controls significantly more at high frequencies than at low frequencies should allow the design to inject high gain at
low frequencies, thereby improving low-frequency -disturbance rejection properties, while simultaneously
forcing the compensator to roll-off the high-frequency
-gain so as to meet the stability robustness constraint. FREQUENCY (rad/a)
Such a design is now presented
Such a design is now presented. Figure 16. Closed-Loop Transfer from d to e (T22) Consider Figure 15, which shows the singular value (Weighted-Control H,~ Design).
frequency response for a single-input/single-output control weighting function with a zero at s = -5 rad/s, a pole at s = -500 rad/s, and a dc gain of 77, selected to
meet the above criteria and arrived at via trial and error
-iteration. Figures 16 and 17 show the closed-loop
transfers from d to e and about AM for the -H,o loop- a
shaped design obtained by augmenting the dynamics of !/ the above control weighting transfer function to every
control channel of the open-loop model and solving the H,~ Riccati equations. As can be seen from Figure 16, the maximum singular values of the T2 2block are less than 1 (0 dB) at all frequencies, so that the H.,,
loop-shaped control design obtained meets nominal
performance specifications. Similarly, Figure 17
indicates that the H, loop-shaped control design is FREOUENCY (rd/)
guaranteed to be robustly stable. Thus, this design is Figure 17. Closed-Loop Transfer about AM (T11)
dee m ed acceptable. (Weighted-Control H,,, Design).
Figure 18 shows the maximum singular value
frequency response of the weighted-control H,, design higher gain maintained by the loop-shaped H, compensator. The most significant difference between compensator over the low-frequency region. This allows the frequency response of this compensator and the the H, loop-shaped control compensator to meet robust H2/Hh, compensator responses is the markedly performance specifications in the frequency range where the other designs do not Further, it is the ability of the Ho. loop-shaped control compensator to preserve high gain through -100 rad/s and still roll-off fast enough to
meet the stability robustness constraint that is especially Figures 19 and 20 show representative time crucial to the success of this design. Finally, Figure 18 responses of two BEA torque disturbances, generated by indicates that there is a region of particularly high passing white noise through a simple first-order low compensator gain between -18 and 30 rad/s, including pass filter with bandwidth just greater than the what appears to be a very lightly-damped compensator bandwidth of the loop-shaped Hoo closed-loop system. pole at -28 rad/s. The clear presence of this pole seems The random nature of the torque disturbances is obvious to indicate that the compensator is performing some from the plots, as any two consecutive values seem to type of critical pole-zero cancellation of the plant be highly uncorrelated. The RMS values of the torque dynamics at -28 rad/s, in order to extend the design's disturbances also seem to be accurately represented, as it disturbance rejection capability to higher frequencies. appears that 95 percent of the values lie within the 30 margins of : 0.75 N-m (note that two individual torque RMS values of 0.25 N-m combine to yield the chosen 0.35 N-m torque vector RMS value).
LI
A4
FREQUENCY (rad/)
-I
Figure 18. H,o Loop-Shaped Control Compensator A -s s .'s i at i i
Maximum Singular Values. nm (sc)
6. Design Simulation Figure 19. Torque Disturbance 1 Time Response. In this section, the HI loop-shaped control e
compensator obtained in Section 5 is validated via time domain simulation. Representative time responses are presented which illustrate characteristic system behavior under the influence of filtered white noise disturbances and demonstrate satisfaction of nominal performance
specifications. Open- and closed-loop results are presented simultaneously in order to facilitate
comparison between the two cases.
Since large-scale flexible space structures like the SBL envisioned here have yet to be built and tested, the
time-domain nature and spectral properties of the torque %- B!1 L: a ; .
disturbances and measurement noise present in the BEA 'ime (s:c)
system are not precisely known. Therefore, the
assumption is made that the disturbances can be Figure 20. Torque Disturbance 2 Time Response. represented as random processes with typically broadband
spectral characteristics and bounded RMS values. One Figures 21 and 22 respectively show the open- and convenient way of modeling such processes is to closed-loop segment phasing errors at measurement represent them as outputs of linear-time-invariant low- position 4 (reference Figure 2) resulting from pass systems driven by white noise, otherwise known as application of the disturbance torques of Figures 19 and colored noise processes. As long as the bandwidth of 20. From the figures, it can be seen that, on the the coloring filter is selected to be greater than the average, the open-loop response is significantly larger bandwidth of the system being driven, colored noise than the closed-loop response, as expected. In fact, the inputs may be used to excite all system natural largest amplitude of the open-loop error is more than frequencies. Modeling the system disturbances as twenty times the magnitude of the largest closed-loop colored noises therefore allows the dominant frequency- error amplitude, indicating a significant improvement in dependent behavior of the system to be elicited. performance between the closed and open-loop systems.
jagged than its closed-loop counterpart, or in general It is well-known that optimal controllers alter the
more slowly time varying. This can be interpreted as behavior of the open-loop plant via the mechanism of meaning that the open-loop error is dominated by low- "approximate plant inversion", in which undesirable frequency components, while the closed-loop error is system poles and zeros are respectively cancelled with dominated by higher-frequency components. Since the compensator zeros and poles, and the best system compensator employed in the closed-loop system was response achievable is then obtained via selection of any designed specifically to reject low-frequency additional compensator pole/zero locations. One disturbances, this interpretation makes sense. Also note obvious flaw in such a design methodology is that that both these error time responses are significantly less uncertainty invariably exists in the location of the open-jagged than the torque disturbances. This effect can be loop poles, due to approximations and errors in the attributed to the high-frequency attenuation resulting modeling process. If the true system poles are not from passing the colored-noise disturbances through a exactly the same as those of the design model, then the lower-bandwidth system. As a final remark, note that a multivariable pole-zero cancellations employed by plant-rough estimate of the closed-loop RMS position 4 inverting techniques are not likely to be completely segment phasing error of 0.02 gm projected into a 6 successful, and may even lead to serious degradations in element segment phasing vector yields a total RMS nominal system stability and performance. It is thus of value of 0.05 mun. Since this value is significantly less interest to the designer to somehow assess the potential than the specified segment phasing performance bound impact of open-loop pole location errors prior to of 0.15 gpm, it appears that the H, loop-shaped control compensator implementation. Therefore, in this section design can indeed be seen to meet nominal performance it is demonstrated how the Small Gain Theorem may be specifications. used to assess the stability robustness of the weighted-control H- loop-shaped compensator closed-loop system ... to five percent parametric uncertainty in the open-loop finite-element model stiffness matrix elements,
8·
^corresponding to two and one-half percent parametricuncertainty in the open-loop natural frequencies. Since
ta I
l
althe
Small Gain Theorem is known to be conservative,the actual effects of open-loop pole location errors on closed-loop stability for two specific perturbed natural frequency models is then directly verified via
c1h
Vtlll § 1lzl l lcomputation of the closed-loop poles. Finally, , 11 _ V V l robustness of performance of non-perturbed and perturbed models is assessed via computation of closed-loop d to e transfer function frequency responses.
lbs 4 4MS 3
Time (s) As discussed in Section 5, the Small Gain Theorem
may be used to conservatively assess the stability Figure 21. Open-Loop Position 4 Segment Phasing robustness of any system containing uncertainty, as Error Time Response. long as that uncertainty may be gain-bounded as a function of frequency. In particular, a framework has been developed for testing the stability robustness of systems where the only uncertainty in the plant is
,m lmodeled as a multiplicative error at the plant output. As
was previously developed, stability robustness of such an uncertain system may be guaranteed by ensuring that the infinity-norm of the closed-loop transfer about the uncertainty block, IITl
l(s)ll
I, is less than one, as long as the infinity-norm of the uncertainty block is unity bounded. Consider Figure 23, which shows the maximum singular value frequency responses of,~ll1 I.m
·
multiplicative errors, AM(s), at the plant output for twoperturbed natural frequency systems, and of a transfer .Ms i Bt o -'xc i~ al .1 a !.function which effectively bounds both the errors. As
Time (sec) can be seen from Figure 23, the nominal design model possesses large errors at high-frequency due to model-Figure 22. Closed-Loop Position 4 Segment Phasing reduction truncation of the high-frequency modes (as was Error Time Response. previously the case for the unperturbed system), but now 7. Performance Robustness and Effects of there is also significant error at low frequency due to the Open-Loop Pole Parametric Uncertainty difference between modeled and "actual" open-loop
stability robustness test of the Small Gain Theorem.
The conservatism of the SGT is thus made apparent. Severe degradations in closed-loop performance do
U F(s) F however result, as can be seen from Figures 25 and 26 below, which show the maximum singular value closed-loop d to e transfers for the systems with respectively five percent greater and less stiffness than the original model. The figuree clearly illustrate the importance of i I / feeding the precise location of the open-loop poles and
W
10
q|JJ
-m "rr / I Yzeros to the optimal control problem. Note that even in
.r 14 (s/ the presence of open-loop natural frequency parametric
uncertainty, closed-loop performance specifications are met at low frequency, and the degraded higher frequency performance is, in general, still superior to that of the
FREOUENCY (radhs) open-loop system.
Figure 23. Perturbed System Multiplicative Errors at the Plant Output and Bounding Transfer Function
-Frequency Responses.
Figure 24 shows the closed-loop transfer maximum singular values about the delta block for the perturbed
plant models. As can clearly be seen from the figure,
il
the maximum singular values of the closed-loop transfer a about the uncertainty block exceed unity (O dB) overalmost all of the frequency range of interest. Figure 24 therefore indicates that the closed-loop system is not guaranteed to be robustly stable to two and one-half
percent error in open-loop natural frequencies according ... .'. ; . to the sufficient test of the Small Gain Theorem. The FREQUENCY (rad/s)
Small Gain Theorem is based purely on gain
considerations, however, and is known to be Figure 25. Closed-Loop Transfer from d to e (T22) conservative. Therefore, the actual closed-loop systems (5% More Stiff Open-Loop System).
4g 1 n a
-UrIf UJU
FREQUENCY (radh) FREQUENCY (rad")
Figure 24. Closed-Loop Transfer about AM (T11) Figure 26. Closed-Loop Transfer from d to e (T22) (Perturbed Open-Loop Natural Frequency Systems). (5% Less Stiff Open-Loop System).
using the perturbed natural frequency models and Since performance specifications are not met in the weighted-control H. loop-shaped compensator may be presence of two and one-half percent open-loop natural formed, and the closed-loop poles and d to e transfer frequency parametric uncertainty, the closed-loop system function maximum singular value frequency responses does not possess robustness of performance to these computed to verify the actual effects of the parametric types of structured parameter errors. This observation uncertainty. In doing this for the two perturbed open- raises the question of whether or not the closed-loop loop models chosen, the resulting closed-loop systems system displays robustness of performance to the errors are found to be stable, in spite of the indications of the due to truncation of modes brought about by model
reduction. To answer this question, consider Figure 27, 1. Flueckiger, K., Dowdle, J. and Henderson, T., "A which shows the closed-loop frequency response from d Control System Design Methodology for Large-Scale to e for the full-order model with no parametric Interconnected Systems", Proceedings of the 1990 uncertainty. As can be seen from the figure, the system American Control Conference, San Diego, CA,
pp.428-does indeed possess robust performance for the errors due 434.
to model reduction. 2. Hammett, K., Dowdle, J., Athans, M., and
Flueckiger, K., "Robust Control System Synthesis for Space-Based Laser Beam Control", to appear Proceedings
.~ of the 1991 American Control Conference, Boston, MA.
3. Moore, B.C., "Principle Component Analysis in
__ Linear Systems: Controllability, Observability and
Model Reduction," IEEE Trans. on Auto. Control, Vol.
-_ AC-26, pp. 17-32, 1981.
4. Glover, K. and Doyle, J., "State-Space Formulae
;z J "for All Stabilizing Controllers that Satisfy an I-IH-norm
Bound and Relations to Risk Sensitivity," Systems &
Control Letters, 11(1988) 167-172, North-Holland.
FREQUENCY (rad/s)
Figure 27. Closed-Loop Transfer from d to e (T22) (Full-Order Open-Loop System).
8. Conclusions
In this paper, the utility of applying optimal controller synthesis methodologies in conjunction with model reduction techniques and the stability robustness test of the Small Gain Theorem to robust control of large-scale systems has been demonstrated, and several interesting consequences of adopting this design approach have been illustrated. Controller design for large-scale systems necessitates reduction of model order, and in this paper ideally performing but unconstrained bandwidth designs were developed for a space-based laser example problem to illustrate the dangers of totally ignoring the effects of the resulting unmodeled dynamics. In particular, the Small Gain Theorem was used to show the strong possibility of closed-loop instability for these designs. Reduction of closed-loop bandwidth via constant control penalty was seen to achieve guaranteed stability robustness, but at an unacceptable cost of large sacrifices in performance. The added degrees-of-freedom afforded by Ho loop-shaping techniques were then used to overcome this problem, resulting in a design meeting both robust stability and nominal performance conditions. However, severe degradations in performance were seen to result from parametric uncertainty in open-loop pole/zcro locations, illustrating the fact that one should not realistically expect ideal performance in a practical setting. Finally, although it had not been specifically designed for, the H,, loop-shaping design was seen to possess performance robustness to the dynamics removed in the model reduction process.