Approche numérique à l’usage du physicien pour résoudre les équations différentielles ordinaires. III. Cas d’équations différentielles aux dérivées ordinaires du second ordre en dimension 2. Application aux oscillateurs harmoniques/anharmoniques, et au

HAL Id: cel-02164507

https://hal.archives-ouvertes.fr/cel-02164507

Submitted on 25 Jun 2019

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

Approche numérique à l’usage du physicien pour

résoudre les équations différentielles ordinaires. III. Cas

d’équations différentielles aux dérivées ordinaires du

second ordre en dimension 2. Application aux

oscillateurs harmoniques/anharmoniques, et au

mouvement Képlérien dans le plan

Hubert Baty

To cite this version:

Hubert Baty. Approche numérique à l’usage du physicien pour résoudre les équations différentielles

ordinaires. III. Cas d’équations différentielles aux dérivées ordinaires du second ordre en dimension 2.

Application aux oscillateurs harmoniques/anharmoniques, et au mouvement Képlérien dans le plan.

Licence. France. 2019. �cel-02164507�

Approche numérique à l’usage du physicien pour résoudre

les équations différentielles ordinaires.

III. Cas d’équations différentielles aux dérivées ordinaires

du second ordre en dimension

2. Application aux

oscillateurs harmoniques/anharmoniques, et au

mouvement Képlérien dans le plan

Hubert Baty

June 25, 2019

Abstract

Le but de ce chapitre est d’étendre les méthodes numériques étudiées au chapitre précé-dent (Runge-Kutta et symplectiques) à des systèmes en dimension 2. Le but final est l’intégration numérique de la trajectoire d’une particule dans un potentiel de type Képlérien (correspondant à la loi de la gravitation universelle de Newton). La propriété physique supplémentaire que les schémas numériques doivent essayer d’assurer pour les systèmes considérés ici, est la conservation du moment cinétique. Cette propriété est fondamentale (comme nous le verrons) pour la stabilité des orbites.

1

Equation de l’oscillateur harmonique en dimension 2

1.1

Equation normalisée

L’oscillateur harmonique en dimension 2 est représenté par l’équation différentielle vectorielle (normalisée),

¨ ~

r = −~r, (1)

avec ~r le vecteur position radial (ayant pour coordonnées x et y dans le plan du mouvement). Alors que la résolution analytique requiert (car plus naturel) d’utiliser un repère polaire, nous allons utiliser un repère cartésien pour l’intégration numérique. Ce qui conduit à décomposer l’équation suivant deux directions:

˙ x = vx, ˙ vx= −x, ˙ y = vy, ˙ vy= −y. (2) Le vecteur vitesse est en effet ~v = ˙~r, ayant pour composantes vx= ˙x et vy = ˙y. La nouveauté à

-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 y x

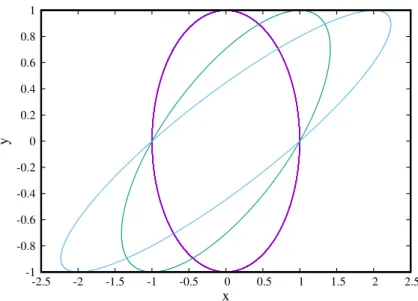
Figure 1: Oscillateur harmonique bidimensionnel. Trajectoire obtenue dans l’espace réel pour trois jeux différents de conditions initiales ayant en commun (x0= 1, y0= 0).

est le moment cinétique normalisé, ~σ = ~r × ~v. Cette propriété provient du théorême du moment cinétique, qui implique que la dérivée temporelle du moment cinétique est nulle pour une force radiale (−~r ici), car le moment de la force est lui même nul.

1.2

Solution analytique et propriétés

La solution générale pour l’oscillateur harmonique à 2 dimensions (pour x(t) et y(t)) est similaire à la solution vue pour l’oscillateur harmonique à 1 dimension (combinaison d’une fonction cosinus et fonction sinus assortie des conditions initiales pour chaque direction). La conservation de l’énergie E doit aussi être assurée le long d’une trajectoire, avec E = (v2

x+ v2y)/2 + (x2+ y2)/2

maintenant. En effet le potentiel (l’énergie potentielle) est maintenant U (x, y) = (x2_{+ y}2_)/2.

Quant au moment cinétique (qui est aussi conservé), sa norme sécrit σ = xvy− yvx. On rappelle

que la conservation de la direction de ~σ implique que le mouvement se fait dans un plan qui lui est perpendiculaire, alors que la conservation de sa norme implique la loi des aires (vitesse aréolaire constante).

Des exemples de trajectoire sont visibles sur la figure 1 dans l’espace physique (x, y). Les trajectoires dans l’espace des vitesses (vx, vy) donnent exactement la même figure (non

mon-trée). On obtient donc des ellipses dont le centre de force est le centre géométrique O(0, 0), correspondant à des solutions périodiques de période égale à 2π (à cause de notre normalisation du temps).

1.3

Solution numérique

Comme pour le chapitre précédent, nous nous focaliserons sur l’emploi des deux types de méth-odes principales vues avant (Runge-Kutta et symplectiques). Nous pourrons alors tester si la conservation de l’énergie et du moment cinétique sont assurées par les schémas.

-1.5 -1 -0.5 0 0.5 1 -1.5 -1 -0.5 0 0.5 1 1.5 y x RK2 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 0 50 100 150 200 250 300 350 t E moment

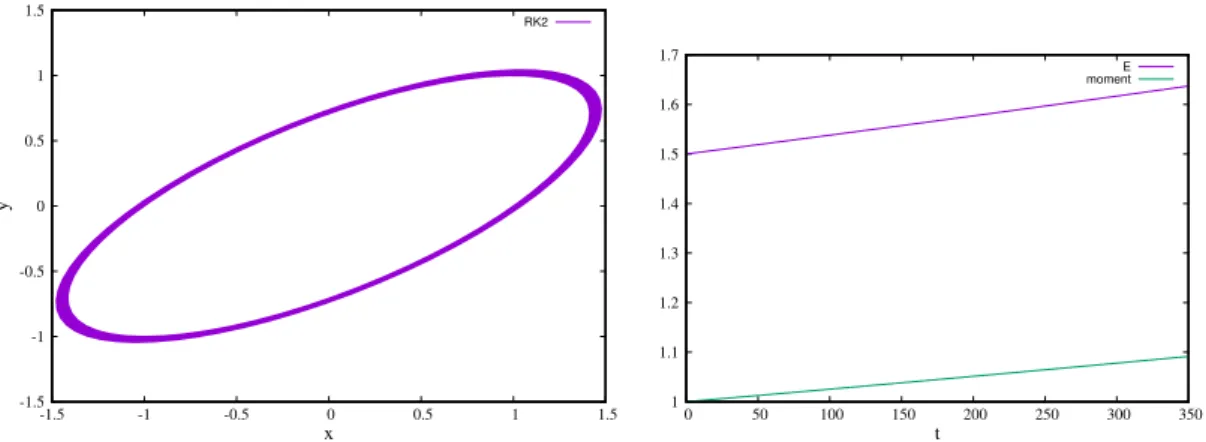
Figure 2: Oscillateur harmonique 2D. A gauche, trajectoire obtenue dans le plan avec RK2 et un pas h = 0.1. A droite, énergie E et moment cinétique σ correspondants au cours du temps.

Comme illustré sur la figure 2 en utilisant RK2 pour une trajectoire, les schémas de type Runge-Kutta ne conservent ni l’énergie ni le moment cinétique. Ce qui conduit comme con-séquence à des trajectoires non fermées qui s’agrandissent car l’énergie augmente continuelle-ment au cours du temps (pour RK2). On peut vérifier que pour RK4, l’énergie et le mocontinuelle-ment cinétique varient en sens inverse (diminuent au cours du temps), et la trajectoire tend vers le centre de force asymptotiquement quand le temps tend vers l’infini. Cette tendance avait aussi été observée pour l’oscillateur 1D. Cet effet peut bien sûr être minimisé en diminuant le pas de temps d’intégration ou/et en utilisant un schéma d’ordre plus élevé, tout en intégrant pas trop longtemps. Cependant, dans des problèmes où certains aspects de la dynamique (comportement chaotique par exemple) doivent être analysés avec précaution, on n’oublie trop souvent que les schémas de Runge-Kutta peuvent modifier considérablement les résultats.

On vérifie que l’emploi d’une méthode symplectique (SY2) permet de corriger les travers de RK2 (voir figure 3). En effet, la trajectoire est maintenant fermé, l’énergie se conserve avec de petites oscillations (dont l’amplitude dépend du pas de temps utilisé). Et surtout, le moment cinétique est conservée aux erreurs d’arrondi près. Une démonstration de la conservation exacte du moment cinétique par l’emploi d’une méthode symplectique (d’ordre 1) est consultable en Annexe (pour l’oscillateur 2D).

2

Oscillateur anharmonique en dimension 2

On peut aussi comparer les deux types de méthode sur l’exemple d’un oscillateur anharmonique correspondant au mouvement d’une particule dans un potentiel de type U (x, y) = (x6+ y6)/6. La force n’étant plus radiale, le moment cinétique n’est plus constant, mais l’énergie totale E = (v2x+ v2y)/2 + U (x, y) reste constante au cours du temps (une constante du mouvement). Ce

-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 -1.5 -1 -0.5 0 0.5 1 1.5 y x SY2 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 0 50 100 150 200 250 300 350 t E moment

Figure 3: Oscillateur harmonique 2D. A gauche, trajectoire obtenue dans le plan avec SY2 et un pas h = 0.1. A droite, l’énergie E et moment cinétique σ correspondants au cours du temps. On note que l’énergie oscille autour d’une valeur moyenne constante.

-1.5 -1 -0.5 0 0.5 1 1.5 -1.5 -1 -0.5 0 0.5 1 1.5 y x -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 -1.5 -1 -0.5 0 0.5 1 1.5 vy vx

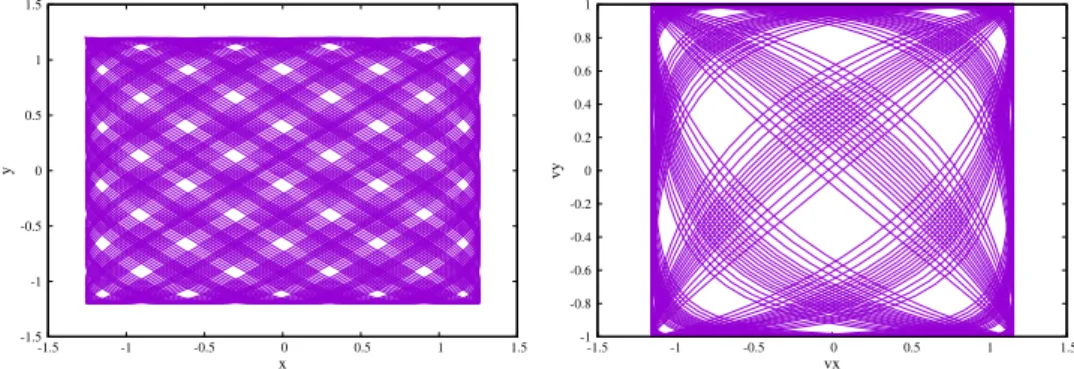
Figure 4: Oscillateur anharmonique bidimensionnel. Exemple de trajectoire exacte dans l’espace réel , dans l’espace (x, y) (figure de gauche), et dans l’espace des vitesses (vx, vy) (figure de

droite).

qui conduit au système suivant: suivant deux directions:

˙ x = vx, ˙ vx= −x5, ˙ y = vy, ˙ vy= −y5. (3) Un exemple de trajectoire typique obtenue est visible sur la figure 4. On constate que la trajectoire balaye au cours du temps une surface contenue dans un rectangle dans l’espace réel aussi bien que dans l’espace des vitesses. Le résultat est relativement artistique.

-2 -1.5 -1 -0.5 0 0.5 1 1.5 -1.5 -1 -0.5 0 0.5 1 1.5 y x 0 1 2 3 4 5 6 7 8 9 0 50 100 150 200 250 E t E(t)

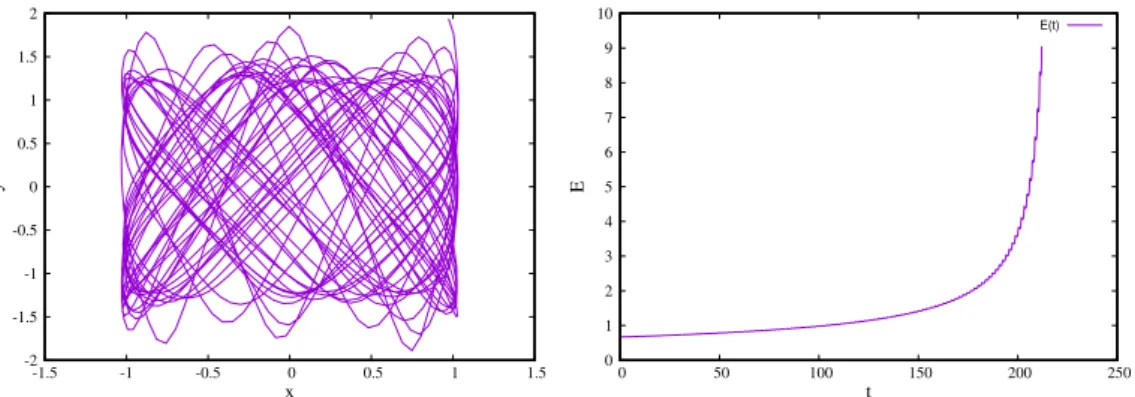
Figure 5: Oscillateur anharmonique bidimensionnel. Trajectoire numérique obtenue dans l’espace réel pour un jeu de conditions initiales dans l’espace (x, y) par le schéma RK2 avec un pas d’intégration h = 0.1 (figure de gauche), et l’évolution de l’énergie correspondante au cours du temps (figure de droite).

2.1

Solution numérique

L’utilisation d’une méthode numérique de type Runge-Kutta (RK2) illustrée sur la figure 5, mon-tre que la trajectoire s’éloigne de façon catastrophique du rectangle en correspondance avec une augmentation exponentielle de l’énergie. Si on poursuit de quelques pas de temps l’intégration, on ne pourra pas échapper à un ’crash’ du calcul. Bien sûr, ce problème sera retardé si on emploie un pas de temps plus petit et/ou une méthode d’ordre plus élevé, mais ceci démontre clairement les travers des Runge-Kutta sur ce type de problème avec un exemple de force hautement non-linéaire (exposant 5). Pour RK4, une fois de plus, l’énergie diminue au lieu d’augmenter (non montré), et la trajectoire tend vers le centre de force asymptotiquement quand le temps tend vers l’infini.

Par contre, pour la méthode symplectique (SY2), l’intégration de la même trajectoire montre maintenant qu’elle reste confinée dans un rectangle en accord avec la conservation de l’énergie (aux oscillations près) comme on peut le constater sur la figure 6. Ainsi, ce test illustre parfaite-ment la nette supériorité des méthodes symplectiques.

3

Mouvement Képlérien dans le plan

Maintenant, on s’intéresse au mouvement d’une particule se déplaçant dans un potentiel grav-itationnel (correspondant à la loi de la gravitation universelle de Newton) U (x, y) = −k/r2_,

avec r = (x2_{+ y}2₎1/2_{la distance au centre de force et k une constante englobant notamment la}

constante de la gravitation. L’équation du mouvement à intégrer est alors, ¨

~r = −k~r/r3. (4)

Les solutions analytiques sont bien connues et ont conduit aux fameuses lois de Kepler, inspirant ainsi Newton pour déduire sa loi de la gravitation expliquant ces solutions observées par Kepler. Les trajectoires fermées sont des ellipses dont le centre de force est situé à un des deux foyers. Le moment cinétique se conserve (force radiale) impliquant la seconde loi de Kepler (loi des aires). Enfin, l’énergie totale (cinétique et potentielle) est encore une constante du mouvement du fait de l’absence de dissipation.

-1.5 -1 -0.5 0 0.5 1 1.5 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 y x 0.661 0.662 0.663 0.664 0.665 0.666 0.667 0.668 0.669 0 50 100 150 200 250 E t E(t)

Figure 6: Oscillateur anharmonique bidimensionnel. Trajectoire numérique obtenue dans l’espace réel pour un jeu de conditions initiales dans l’espace (x, y) par le schéma SY2 avec un pas d’intégration h = 0.1 (figure de gauche), et l’évolution de l’énergie correspondante (figure de droite).

Bien que le problème se résolve analytiquement en utilisant un repère polaire, pour l’intégration numérique on utilise les coordonnées cartésiennes conduisant alors à,

˙ x = vx, ˙ vx= −x/(x2+ y2)3/2, ˙ y = vy, ˙ vy= −y/(x2+ y2)3/2, (5) avec la normalisation k = 1.

3.1

Solution numérique par les méthodes de type Runge-Kutta

D’après les tests précédents, nous nous attendons à des résultats pour lesquels, ni le moment cinétique, ni l’énergie totale ne seront conservées le long du mouvement.

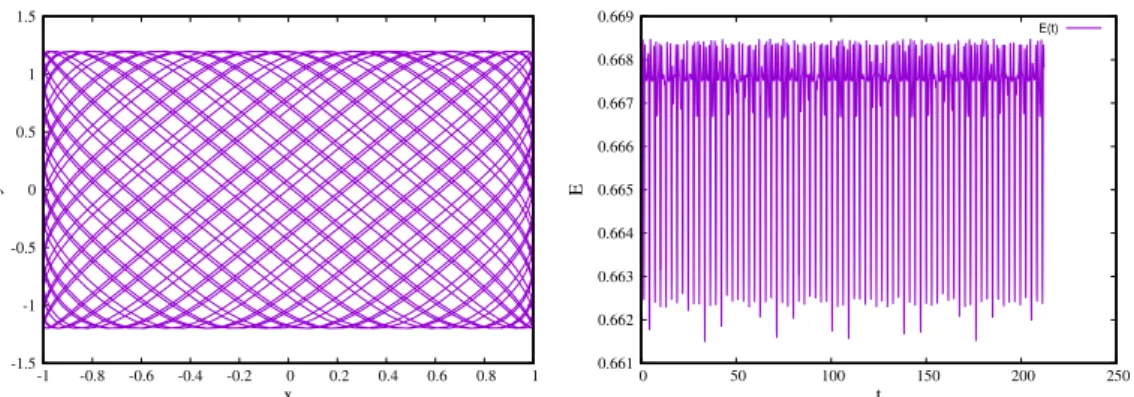
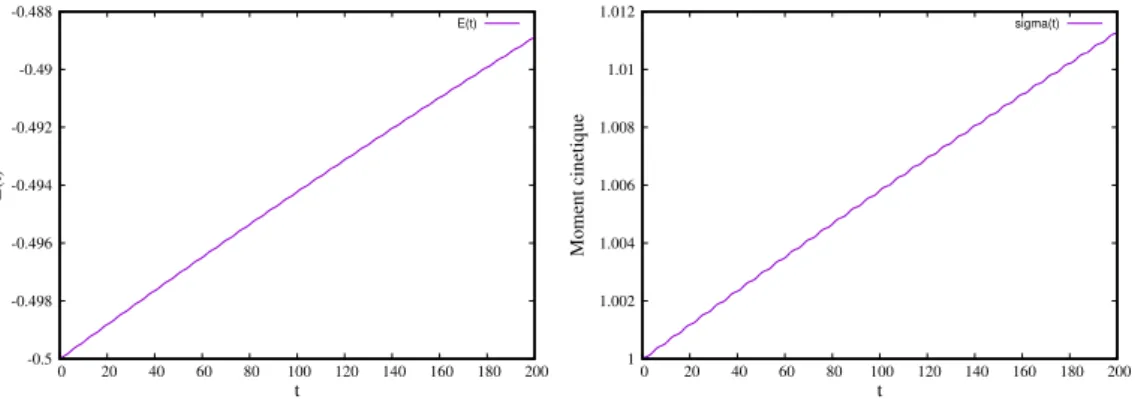
Prenons tout d’abord le schéma RK2, et initialisons le mouvement sur une orbite circulaire avec x(0) = 1, y(0) = 0, vx(0) = 0, et vy(0) = 1. Les résultats obtenus avec un pas de temps

relativement grossier (h = 0.1) sur la figure 7 mettent en évidence que la trajectoire ne reste pas fermée. En fait, elle s’agrandit dans l’espace réel en accord avec l’augmentation continuelle du moment cinétique et de l’énergie au cours du temps. La trajectoire dans l’espace des vitesses (quant à, elle) rétrécit car la particule explore des régions de plus en plus éloignées du centre de force. Une intégration plus longue conduit bien évidemment à une trajectoire qui s’échappe, avec une énergie totale qui tend vers zéro. Il est aussi intéressant de tester sur une orbite initiallement elliptique. Le résultat obtenu est similaire avec en plus une précession importante (voir figure 9) provoquée par des oscillations importantes du moment cinétique et de l’énergie.

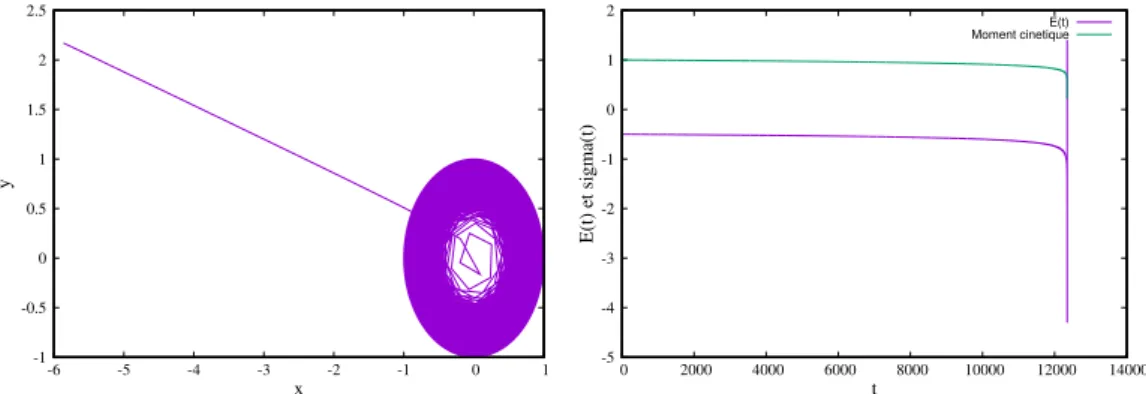
Nous avons vu précédemment que le comportement pour RK4 diffère de RK2, avec une diminution de l’énergie totale au cours du temps ainsi que du moment cinétique. La trajectoire Képlérienne ne déroge pas à cette règle. En effet, ceci est illustré sur la figure 10. Cependant, lorsque la trajectoire s’approche trop près du centre de force, la particule ’rebondit’ car la force tend alors vers l’infini (c’est en fait une collision), et repart alors vers l’infini selon une trajectoire ouverte.

-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 vy vx -1.5 -1 -0.5 0 0.5 1 -1.5 -1 -0.5 0 0.5 1 1.5 y x

Figure 7: Trajectoire circulaire Képlérienne. Exemple de trajectoire numérique obtenue par RK2, dans l’espace (x, y) (figure de gauche), et dans l’espace des vitesses (vx, vy) (figure de droite).

-0.5 -0.498 -0.496 -0.494 -0.492 -0.49 -0.488 0 20 40 60 80 100 120 140 160 180 200 E(t) t E(t) 1 1.002 1.004 1.006 1.008 1.01 1.012 0 20 40 60 80 100 120 140 160 180 200 Moment cinetique t sigma(t)

Figure 8: Trajectoire circulaire Képlérienne. Evolution de l’énergie totale au cours du temps E(t) (figure de gauche) et du moment cinétique (figure de droite), pour la trajectoire numérique (par RK2) obtenue sur la figure précédente.

-1.5 -1 -0.5 0 0.5 1 1.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 y x 1.098 1.099 1.1 1.101 1.102 1.103 1.104 1.105 0 20 40 60 80 100 120 140 160 180 200 Moment cinetique t sigma(t)

Figure 9: Trajectoire elliptique Képlérienne. Trajectoire numérique obtenue dans l’espace réel pour un jeu de conditions initiales dans l’espace (x, y) par le schéma RK2 avec un pas d’intégration h = 0.1 (figure de gauche), et l’évolution du moment cinétique (figure de droite).

-1 -0.5 0 0.5 1 1.5 2 2.5 -6 -5 -4 -3 -2 -1 0 1 y x -5 -4 -3 -2 -1 0 1 2 0 2000 4000 6000 8000 10000 12000 14000 E(t) et sigma(t) t E(t) Moment cinetique

Figure 10: Trajectoire circulaire Képlérienne. Trajectoire numérique obtenue dans l’espace réel pour un jeu de conditions initiales dans l’espace (x, y) par le schéma RK4 avec un pas d’intégration h = 0.2 (figure de gauche), et évolution de l’énergie totale et du moment cinétique (figure de droite).

3.2

Solution numérique par les méthodes symplectiques

D’après les tests précédents, nous nous attendons à des résultats montrant la conservation exacte du moment cinétique, ainsi que pour l’énergie totale mais avec des oscillations temporelles autour d’une valeur moyenne constante.

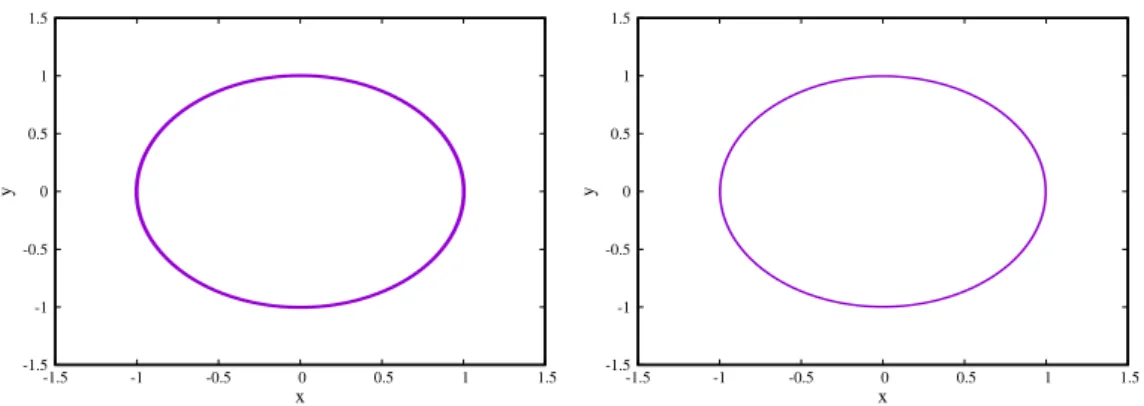
Tout ceci est vérifié aussi bien pour la méthode d’ordre 2 (SY2) que celle d’ordre 4 (SY4). Pour s’en convaincre, il suffit de consulter les figures 11-12. En effet, en intégrant la même trajectoire initialle que celle obtenue pour RK4 précédemment et les mêmes conditions (pas de temps et temps final identiques), on constate que la trajectoire reste fermée et circulaire. Elle est légèrement épaissie pour SY2, car pour ce pas d’intégration grossier, l’énergie totale oscille avec une amplitude plus grande que pour SY4 (non montré). Quant au moment cinétique, il est conservé à la précision machine près pour SY2 aussi bien que pour SY4. La légère dégradation observée pour SY4 versus SY2 est attribuée aux erreurs d’arrondis qui peuvent intervenir pour un pas trop petit et/ou une méthode d’ordre élevé. Le test pour une orbite elliptique (comme pour le cas avec RK2) donnera aussi une précéssion d’origine numérique liée à l’oscillation en énergie qui diminue rapidement pour un pas de temps plus petit ou en utilisant un ordre plus élevé (SY4). Cependant, l’orbite restera confinée et ne s’échappera pas contrairement aux résultats obtenus avec les Runge-Kutta.

Ainsi, il faut retenir qu’il faut toujours vérifiér la convergence des résultats avec le pas de temps, même avec l’emploi des méthodes symplectiques.

3.3

Sections de Poincaré

Pour aider à diagnostiquer l’effet du numérique sur la solution, il est possible d’utiliser un outil supplémentaire, appelé section de Poincaré, du nom du célèbre mathématicien/physicien Henri Poincaré. En effet, nous avons vu que l’énergie totale se conserve pour les exemples précédents. Ceci se traduit par la conservation du volume dans l’espace des phases (voir chapitre 2). En dimension 2 pour l’espace réel, l’espace des phases est un espace à 4 dimensions, compliquant ainsi la visualisation des trajectoires. Or, ces systèmes dit Hamiltoniens ont aussi la propriété de conserver l’aire dans un sous-espace des phases à 2 dimensions, par exemple (x, vx). Pour

-1.5 -1 -0.5 0 0.5 1 -1.5 -1 -0.5 0 0.5 1 1.5 y x -1.5 -1 -0.5 0 0.5 1 -1.5 -1 -0.5 0 0.5 1 1.5 y x

Figure 11: Trajectoire circulaire Képlérienne. Trajectoire numérique obtenue dans l’espace réel pour un jeu de conditions initiales dans l’espace (x, y) par les schémas SY2 (figure de gauche) et SY4 (figure de droite) avec un pas d’intégration h = 0.2 et un temps final tf = 12350 (comme

pour la figure 10). 0.99999999999995 0.99999999999996 0.99999999999997 0.99999999999998 0.99999999999999 1.00000000000000 1.00000000000001 1.00000000000002 0 2000 4000 6000 8000 10000 12000 14000

t

Figure 12: Trajectoire circulaire Képlérienne de la figure 11 obtenue par SY2 et SY4. Evolution du moment cinétique.

y = 0) dite application du premier retour qui sera obtenue (pour une trajectoire donnée) par intersection des trajectoires avec ce plan. Comme l’énergie totale est aussi fixée (car déterminée par les conditions initiales), la variable manquante (donc vy) est automatiquement déterminée

pour ce plan, car E est une fonction des 4 variables.

Il suffit ainsi d’examiner la répartition de ces intersections successives au cours du temps dans le plan y = 0, pour différents jeux de conditions initiales correspondants à une énergie totale donnée. Par exemple, une trajectoire périodique fermée donnera deux points dans ce plan, et un seul si on considère en plus un sens de traversée donné (positif ou négatif). Ceci est illustré sur la figure 13. Ce point est appelé point fixe.

La mise en pratique pour une trajectoire circulaire (d’énergie totale E = −0.5) passant en principe à chaque franchissement du plan y = 0 par le point x = 1, Vx = 0 est illustrée sur la

figure 14 en utilisant RK2 et SY2. Les résultats montrent une dispersion autour de ce point fixe. Si on intègre plus longtemps, la dispersion reste la même en balayant toujours la même aire mais de façon plus dense. L’aire balayée est bi-dimensionnelle pour RK2, alors que pour SY2 elle se réduit à une courbe bien définie. Lorsque le pas de temps employé est diminué, cette aire tend vers le point fixe comme attendu (en comparant les deux figures). La dispersion bi-dimensionnelle par RK2 se traduit par l’introduction d’un comportement chaotique dont l’origine est numérique (voir chapitre suivant).

Enfin, un dernier test est visible sur la figure 15 pour une trajectoire elliptique en utilisant RK2 versus RK4. Les résultats sont similaires ceux montrés juste auparavant.

A

Conservation du moment cinétique par une méthode

numérique symplectique sur l’exemple de l’oscillateur 2D

Pour rendre les calculs le plus simple possible, nous allons utiliser la méthode symplectique d’ordre 1 (SY1 aussi appelée explicite-implicite car la vitesse est d’abord implémentée par Euler explicite puis la position par Euler implicite) au lieu de SY2. Cependant, le résultat reste valable aussi pour les schémas d’ordre plus élevés.

La discrétisation temporelle de SY1 pour l’oscillateur 2D conduit à,

un+1= un− hxn vn+1= vn− hyn, (6)

et

xn+1= xn+ hun+1 yn+1= yn+ hvn+1, (7)

avec les notations u pour la composante vx, et v pour la composante vy de la vitesse.

Ainsi le moment cinétique calculé par le schéma à l’instant tn+1s’écrit, σn+1= xn+1vn+1−

yn+1un+1. Il se déduit alors à partir de σn= xnvn−ynunen vérifiant σn+1= σnpar construction

du schéma. En effet on obtient, σn+1= σn+ h(vnun+1− unvn+1) − h2(ynun+1− xnvn+1), puis

σn+1 = σn+ h(vnun− hvnxn− unvn+ hunyn) − h2(ynun− hxnyn− xnvn+ hxnyn), et enfin

dx/dt

y

x

P

P

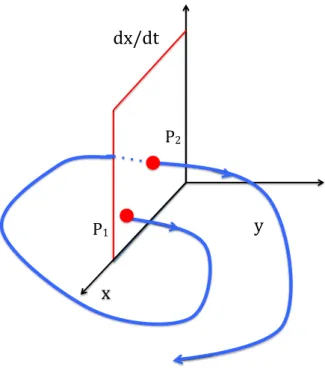
Figure 13: Sections de Poincaré : principe de construction montrant comment on obtient les intersections successives de la trajectoire tridimensionnelle dans l’espace (x, y, dx/dt) pour une énergie totale E donnée) avec un plan (ici y = 0), en ne gardant que le sens passant avec dy/dt > 0, et notées P1, P2, etc ...

-0.05 -0.04 -0.03 -0.02 -0.01 0 0.01 0.02 0.03 0.04 0.05 0.06 0.995 1 1.005 1.01 1.015 1.02 1.025 1.03 1.035 Vx x RK2 SY2 -0.005 -0.004 -0.003 -0.002 -0.001 0 0.001 0.002 0.003 0.004 0.005 0.99998 0.99999 1.00000 1.00001 1.00002 1.00003 1.00004 Vx x RK2 SY2

Figure 14: Sections de Poincaré obtenues pour une trajectoire circulaire ayant une énergie totale E = −0.5, en utilisant RK2 versus SY2 avec un pas de temps h = 0.05 (figure de gauche) et h = 0.005 (figure de droite), pour un temps final tf = 2500 correspondant à 400 tours environ.

-0.6 -0.4 -0.2 0 0.2 0.4 0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 y x -0.006 -0.004 -0.002 0 0.002 0.004 0.006 0.99996 0.99997 0.99997 0.99998 0.99998 0.99999 0.99999 1.00000 1.00000 Vx x SY4 RK4

Figure 15: Trajectoire elliptique (figure de gauche) obtenue par RK4 et SY4 avec un pas de temps h = 0.005 pour un temps final tf = 25000 (correspondant à 4000 tours environ). Sections